Abstract
In multispecies electrolyte solutions, each individual species can migrate according to its specific ionic properties. This process is called electrochemical migration or electro-diffusion and is well-described by the Nernst–Planck equation. The common approach for solving the corresponding mathematical system is based on the null current (NC) assumption, which expresses the electric potential in terms of charges and concentrations of chemical components. This assumption has a great advantage as it eliminates the electric potential from the Nernst–Planck equation. However, the NC assumption has limited capacities in describing electro-diffusion processes when the domain is subjected to an external electric field. The validity of the NC assumption could be questionable, even in the absence of an external electric field. This topic has never been investigated in the past. The main goal of this work is to evaluate the validity of the NC assumption and to understand its effect on the model outputs. Thus, we present a new reactive transport model that allows for a reliable representation of the electrochemical migration process. This model is based on the Nernst–Planck and Poisson (NPP) equations which are solved together. We also implement a model based on the NC assumption. Both models have been validated by comparison with CrunchFlow, based on several benchmarks. The results show that in the case of high sorptivity, the NC assumption is no longer valid. Therefore, in the case of sorption processes, the NPP should be used to simulate coulombic interactions.
1. Introduction
Mass transfer accompanied by chemical reactions, or reactive transport (RT), in porous media is central to a wide range of applications in the fields of geology, hydrogeology, engineering, and environmental research. For instance, RT processes are encountered in geological carbon dioxide sequestration [1,2], geothermal systems [3,4], groundwater pollution [5], and nuclear waste disposals [6,7].
Several applications involving RT processes reveal the necessity of the development of new models to better describe the chemical processes. Many modern codes have extensive capabilities and have been used to simulate RT in different applications and at different scales. In particular, CrunchFlow [8], Phreeqc [9], TOUGHREACT [10], MIN3P [11], PHT3D [12,13], and PHAST [14] exemplify the RT simulators established in previous years. In recent years, significant advances have been achieved in the development of RT codes due to the increase of capability in coupling transport simulators with geochemical reactive codes. For instance, modules have been developed that couple Phreeqc, a widely used geochemical package [15,16], to other simulators [17,18].
Most of the RT codes mentioned above, neglect the coulombic interactions between the charged particles, as they are based on the classical Fick’s law. However, it is well known that coulombic interactions processes cannot be simulated with Fick’s law that assumes a constant diffusion coefficient for each dissolved species. This classical view assumes that the movements of each dissolved species in a system are merely based on concentration gradients. However, in a multicomponent electrolyte solution, each individual dissolved species migrates differently according to its ionic properties such as charge, ionic size, or ionic mobility [19]. Therefore, the features of a multicomponent electrolyte system cannot be fully represented by Fick’s law, and including electrochemical migration to a multicomponent reactive transport model requires a departure from Fick’s law by the use of the Nernst–Planck equation (Equation (1) in Section 2.1). This equation takes into account the ionic interactions by including the electric field generated by such interactions. Among the previous studies on electrochemical migration, more attention is given to the electro-diffusion process where the diffusion of charged particles is combined with their migration in a self-consistent electric field [20,21,22,23,24]. The common assumption in these studies is that no electric current is passing through the domain. This assumption is known as the null current (NC) assumption (Equations (7) and (8) in Section 2.2). It leads to an explicit expression of the electric field in terms of species concentration (Equation (10) in Section 2.2). The advantage of the NC assumption is that it simplifies the numerical solution of the system of governing equations by reducing the number of unknowns. The NC assumption is widely used in the literature because it makes easy the implementation of the coulombic interactions processes into existing numerical codes. Indeed, the electro-diffusion processes are represented with the standard Fick’s law, but with specific diffusion coefficients that depend on concentrations. In recent years, the NC assumption-based models have been used to solve problems with higher levels of sophistication and non-linearity. For instance, three benchmarks are presented in [25]. These benchmarks are used to provide accurate analyses on the role of electrochemical migration in the mass transport processes. A 2D multicomponent reactive transport model is developed in [18] takes the electrostatic interactions during transport of charged ions in physically and chemically heterogeneous porous media into account. In [26] a multidimensional modeling approach is proposed, illustrating the importance of coulombic coupling in diffusive-dispersive Nernst–Planck-based fluxes in one, two, and three-dimensional porous media domains.
Despite the popularity of the NC assumption and its major contribution in simulating and understanding the electrostatic processes, this assumption is not able to describe a domain subjected to an external field. In this case, the total electric field represented by the Nernst–Planck equation is affected by both internal interactions of ions (liquid junction potential) and an externally applied electric field [27,28]. In addition, the elimination of the electric field from the transport equation makes the description of electro diffusion processes independent from the permittivity of the medium and dielectric properties of the porous media. Moreover, the NC assumption is not physically valid when the charged species participating in the mass fluxes are not the total charged species existing in the domain [29]. The aforementioned challenges of the NC assumption can be avoided by using a more general approach that couples the Nernst–Planck equation with the Poisson equation (NPP). In the Poisson equation, the electric field is linked to the total ionic concentration of species in the system and the dielectric property of the medium. This approach is rarely used in reactive transport codes because it cannot be easily implemented in existing codes.
Despite the common use of the NC assumption in models dealing with reactive transport and electro-diffusion, the validity of this assumption is questionable. Thus, the main goal of this work is to evaluate the validity of the NC assumption by comparing it to a full model based on the NPP equations. To the best of our knowledge, this topic has never been investigated in the past. Thus, we first present a comprehensive formulation of the NPP equations. We develop a (1D/2D) finite element model to solve these equations, using the mathematical module of COMSOL Multiphysics. With the same module, we also develop a (1D/2D) finite element model based on the NC assumption. We validate the developed models based on common benchmarks and we compare them in different configurations of RT to evaluate the validity of the NC assumption.
2. Mathematical and Numerical Models
2.1. General NPP Model
The Nernst–Planck equation in combination with the conservation of mass equation is used to describe the migration of interacting species. It accounts for molecular diffusion, electro-diffusion, and advection:
where is the total concentration of ith species, is the time, [mol/m2·s] is the total mass flux, [m2/s] is the species-dependent diffusion coefficient, [mol/m3] is the dissolved concentration of ith species, [C/mol] is the Faraday constant, [J/K·mol] is the gas constant, is the absolute temperature, is the charge number, is the electric potential and [m/s] is the Darcy’s velocity.
The Poisson equation, giving the electrical potential as function of electrical charges, is as follows:
where [F/m] is the permittivity of the porous medium.
The permittivity of the domain depends on the soil porosity and permittivity of the solid grains. According to the averaging method [30], the bulk permittivity, representing the porous medium, is given as follows:
where is the porosity of the porous medium, and are the relative permittivity of water and solid grains, respectively and (= [F/m]) is the vacuum permittivity. The permittivity of water is higher than that of solid grains. Thus, in saturated porous media, the increase of porosity leads to an increase in the average permittivity of porous media. We neglect the effect of sorption on the permittivity of the solid grains.
The NC assumption could be invalid in the case of sorption processes that occur with the cations dissolved in multicomponent electrolyte systems due to the negatively charged surfaces of clay soils [29]. The model used for simulating adsorptive reactive transport is given here. For the sake of simplicity, linear isotherms have been considered in this study. The sorbed concentration at each time step is therefore defined as a constant ratio of the total concentration of each species. The total concentration for the species having sorption is detailed as follows:
where, [mol/m3] and [mol/kg] are the dissolved and sorbed concentration of the ith species, respectively. [kg/m3] is the bulk density of the medium.
As is common in the literature, we assume that the porosity is not affected by the sorption processes and consequently, the permittivity used in NPP models is not affected by the sorption. Therefore, the continuity equation of each species is as follows:
Using the sorption capacity, (), the above equation can be rewritten as follows:
2.2. Electro-Neutrality and NC Assumption
Two physical requirements of the electro-neutrality are: (i) the total charge should be zero at every point of the domain and (ii) no electric current should pass through the domain. The following equations satisfy these two conditions, respectively:
Various views of electro-neutrality have been discussed in the literature. It has been defined as Equation (7) in [23]. However, Equation (8) is introduced as the only requirement of electro-neutrality in [21]. These assumptions are investigated in [24], and it has been shown that both are strictly equivalent and lead to the same formulation as long as there is no initial electric charge and no electric current imposed to the domain.
In this work, the considered benchmarks deal with no initial charge no external electric field in the domain. Thus, both approaches of the NC assumption are equivalent, and we employ Equation (8). We substitute the Nernst–Planck flux from Equation (1) in this equation. The following expression for the electric field can be obtained:
where is the total number of dissolved species.
If one assumes local electro-neutrality of the solution, Equation (9) can be simplified to:
Equation (10) represents the classical form of the electro diffusion model. is substituted into the electro diffusion term of the Nernst–Planck model (Equation (1)). Therefore, electric potential does not appear as an unknown in the final system of equations. This means that only dissolved species concentrations should be calculated. This simplifies the implementation of coulombic effects into existing RT codes. However, the validity of the expression linking the electric potential to the dissolved species concentrations cannot be valid in general. The validity of this expression, which in other words is the validity of the NC assumption, will be discussed in the next sections.
2.3. Equivalency of NPP Systems and Null Current Assumption Models
It has been proven that the local electro-neutrality and null-current assumptions are equivalent. We show here that the NPP approach can be reduced to both previous approaches for some conditions. Rearranging the Poisson equation gives:
This equation shows that if , then . This means that, in a media with low dielectric permittivity and/or with a smooth distribution of electrical potential, the Poisson formulation leads to the local electro-neutrality assumption. Considering the value of [C/mol] and that of permittivity used in this work makes this assumption more reliable.
2.4. Numerical Models
Two numerical models (1D and 2D) have been developed based on the NPP equations and the NC assumption, respectively. The model based on the NPP equations is denoted NPP-model, while the model based on the NC assumption is called NC-model. Both models have been developed using the framework of the finite elements COMSOL multiphysics. COMSOL is a software that can be used to simulate problems involving multi-physical processes. It has two options to implement a model. In the first option, called the ‘wizard model’, a model can be developed by selecting physics available in COMSOL. In the second option, called “blank model”, a model can be developed by specifying the governing mathematical equation. In this case, COMSOL can be seen as an advanced finite element library for solving coupled partial differential equations. Electro-diffusion physics is not included in COMSOL. The implementation of the NPP and NC-models, with the ‘wizard model’ option, is not an easy task. The NC model can be developed using the physics of the module ‘Transport of Diluted Species in Porous media—tds’, by assuming a variable molecular diffusion, which is a function of the concentrations. The NPP model can be developed by coupling physics from the modules ‘Transport of Diluted Species in Porous media—tds’ and ‘Electric Currents—ec’. However, coupling these modules in COMSOL does not allow for considering the electro-diffusion processes. To achieve that, the electro-diffusion term should be defined as a source term in the mass transport equation. However, this implementation with the ‘wizard model’ can only work for examples dealing with Dirichlet boundary conditions. In the case of the Neumann boundary condition (i.e., a constant total mass flux), the electro diffusive flux cannot be counted in the total mass flux as it is calculated as a source term. Thus, due to this limitation, the NPP-model has been developed with the mathematic modules in COMSOL (‘blank model’). For mathematical consistency, we also developed the NC-model in the same way. For the NPP model, we choose the ‘General PDE form—g’ from the PDE interfaces in mathematic modules to implement the mass conservation equation. We define all terms separately, with the total species concentrations as dependent variables. The ‘General PDE form—g’ is coupled with the ‘Poisson’s equation—poeq’ module in the classical PDEs group of mathematic modules. In the ‘poeq’ module, the electric potential is defined as the dependent variable, and it appears directly in the mass flux defined in the mass balance equation. Therefore, there is the possibility of formulating a complete definition of the mass flux consisting of all the Nernst–Planck equation terms. For the classical NC model, the only requirement is a mass balance equation given in the ‘General PDE form—g’ module. The electric potential can be expressed as a function of dissolved species concentrations as shown before.
3. Verification
To gain confidence in the correctness of the NPP and NC models developed with COMSOL, we compare these models with the results of three benchmarks presented in [25]. These comparisons also allow for investigating the validity of the NC assumption. In [25], these three benchmarks have been simulated based on the NC assumption with three reactive transport codes: CrunchFlow, MIN3P, and PHREEQC. Since the results for these three simulators agreed well with each other, here we compare the results of our COMSOL models only with CrunchFlow. Besides electro-diffusion, benchmarks 1 and 2 deal with pure diffusion processes, while benchmark 3 deals with advection and molecular diffusion. Benchmarks 1 and 2 are in 1D, while benchmark 3 is a 2D problem. The chemical systems of these benchmarks as well as a summary of the physical processes are presented in Table 1. The detailed explanations on three benchmarks (i.e., boundary conditions, initial conditions, and physical parameters) are given in Appendix A. We should mention that benchmarks 1 and 3 involve both Neumann and Dirichlet boundary conditions. As explained in the introduction, Neumann boundary conditions are the main reason for using the blank model in COMSOL. For the three benchmarks, the relative permittivity of water and soil to vacuum permittivity are considered to be equal to 80 and 52 at the temperature of 20 °C Benchmark 1 deals with pure water (porosity = 1). Thus, the equivalent to the absolute permittivity is equal to that of water. For benchmarks 2 and 3, the porosity is set to 0.5. The bulk permittivity is calculated with the weighted averaging method as in Equation (4).

Table 1.
Summary of the three multicomponent reactive benchmarks.
The results of the developed NPP and NC models, for the 1D benchmarks, are presented in Figure 1. Similarly, the results of the 2D benchmarks are presented in Figure 2. The figures show also the solutions obtained with CrunchFlow in [25]. Figure 1 and Figure 2 show that the three solutions are indistinguishable. This confirms, on the one hand, the correctness of the implementation of the NPP and NC-models in COMSOL, and on the other hand, the equivalency between the NPP and NC-models. These results confirm the validity of the NC assumption for cases dealing with aqueous transport processes. In such cases, the total concentrations of charges are the ones participating in the mass flux. Therefore, the electric field calculated with the NC assumption on the mass flux is equivalent to a general case where the electric field is calculated from the total charges existing in the domain, which is the same approach used in the NPP model. This similarity between the NPP and NC approaches for calculation of the electric field as the origin of electrochemical migration through the domain, leads to the same results for both NPP and NC models.
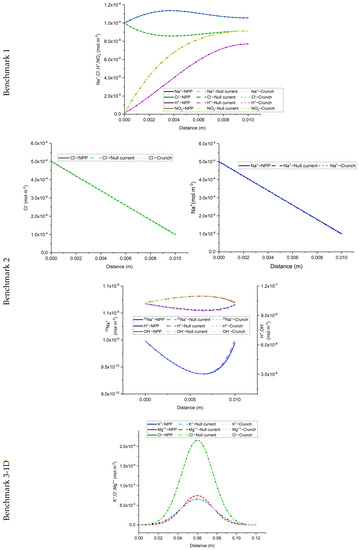
Figure 1.
Comparison of the concentration results of the NPP, NC, and ‘Crunch’ models for the three 1D benchmarks. Dashed and continuous lines are indistinguishable showing perfect agreement between models.
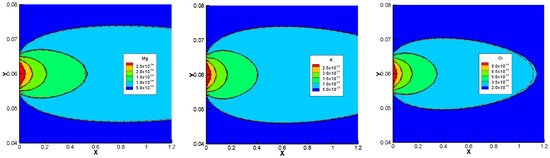
Figure 2.
Comparison of the concentration results of the NPP (Colors), NC (solid black lines), and ‘Crunch’ (dashed red lines) models for 2D simulations of benchmark 3.
4. Effect of Adsorption Reactions
The results of the previous section confirm the validity of the NC assumption in the case of reactive transport of aqueous species. However, it is well-known that transport processes are usually affected by sorption processes, due to the charge difference between the dissolved electrolyte systems and the surfaces of clay soils. When sorption processes occur, the charged species involved in the mass fluxes becomes different from the total charged species existing in the domain. In this case, the NC assumption could become invalid. Thus, the main goal of this section is to investigate the validity of the NC assumption in the case of adsorption reactions.
To do so, we consider sorption processes in the three benchmarks presented in the previous section. To observe the sorption effects, the porosity of all benchmarks is set to be 0.5. In this study, we have considered a linear sorption model with a constant sorption capacity for each test case (Equation (6)). To quantify and analyze the effects of sorption, we used two test cases, defined as ‘test case 1’ and ‘test case 2’ with low and high sorption capacity, respectively. For low and high sorption capacity, sorption capacities of 5 × 10−5 and 10−4 [m3/kg] are considered, respectively. The domain is initially set to be at zero charges. All the other parameters, the boundary, and initial conditions are kept the same as in the previous section. The same COMSOL models used in the previous section are modified to include adsorption reactions and then used in the simulation of the different test cases in this section. The results are discussed in the next sections, in terms of total concentration, total charge, total current, and electrical currents, respectively.
4.1. Total Concentration
The total concentration results of the NPP and NC-models for the three benchmarks defined with sorption are shown in Figure 3 and Figure 4. As we can see, the results of the two approaches are different and the differences are more significant in test case 2 for each benchmark, due to the higher sorption capacity considered for this test case. Some jumps appear in the results of the total concentration of the NC-model which also implies jumps in the results of dissolved and sorbed concentration. A mesh sensitivity analysis has been performed to obtain mesh-independent solutions and to ensure that these differences are not related to numerical artifacts. The jumps are mostly happening in the areas where the imposed initial concentration changes. For instance, in benchmark 1, jumps take place on the left, where the initial species concentration changes, to preserve higher and lower amounts for positive and negative charges, respectively. This can be explained by the underestimation of positive charges in the formulation of the electric field by the NC-model. In benchmark 2, the jumps take place in the middle of the domain, where the initial conditions for total species concentration change. Since benchmark 2 is a steady-state problem, the initial condition does not affect the final results. Figure 5 compares the results of the total concentration of the NPP and NC models with the initial condition for the species concentrations in the NC-model. A linear initial condition is assumed on the domain. There are no jumps in the total concentration results of the NC-model with linear initial conditions in this benchmark. However, the total concentrations of the species with electro-diffusion as the driving force which are and (no initial gradient of concentration is imposed for these species) are different in the NPP and NC-models, with lower amounts of cations and higher amounts of anions in the NC, because this approach does not consider the total amounts of cations in the formulation of the electric field.
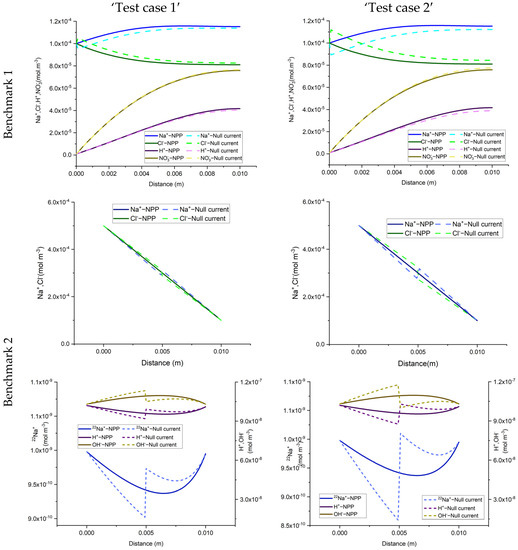
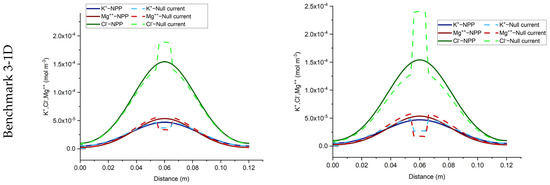
Figure 3.
Comparison of total concentration results of the NPP and NC-models for 1D simulations of the three benchmarks in the case of adsorption reactions. Test case 1 deals with low sorptivity while test case 2 deals with high sorptivity.
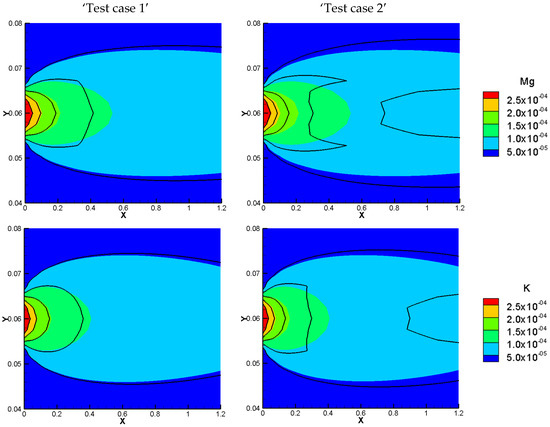
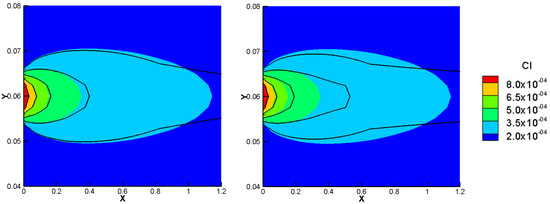
Figure 4.
Comparison of total concentration results of the NPP (Colors) and NC (Lines) models for simulation of benchmark 3-2D with sorption: low sorptivity (test case 1—left), high sorptivity (test case 2—right).
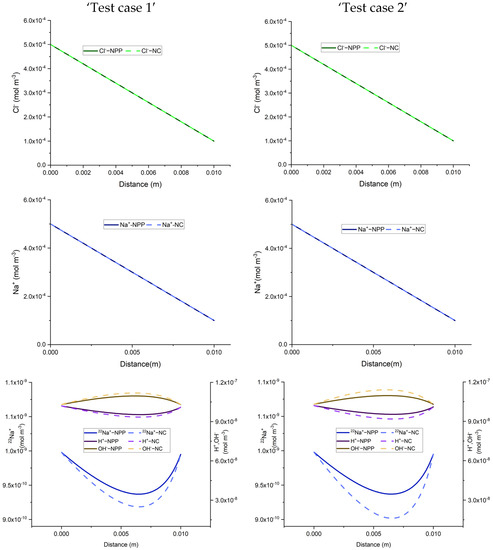
Figure 5.
Comparison of total concentration results of the NPP and NC models for Benchmark 2 with linear initial condition Figure 1.—left), high sorptivity (test case 2—right).
In benchmark 3 (1D), the jumps can be seen for the NC-model around the 1 cm middle source that has been applied to the domain as an initial injection of ions to assure the electrolyte solution. This is because the jumps in the NC-model preserve lower concentrations for cations and higher concentrations for anions. For the 2D case, the same trend of preservation for cations and anions is seen in parallel to the inlet Dirichlet boundary.
In the three benchmarks, we can see that the total positive charge is underestimated in the NC-model and consequently, the total negative charge is overestimated. Although currently there is no experimental evidence for the full-validation of these results, the NPP-model with taking both sorbed and dissolved ionic species into account for the calculation of electric field is theoretically more reliable. Therefore, in the applications of solute transport, especially clay soils, the NPP model can be more representative of the physical processes than the classical NC-model. It is well-known that the null current assumption is not valid near charged interfaces. This can be seen as an interpretation of the results presented here. In fact, the cations adsorbed at the surfaces of the solid grains can be seen as local charged interfaces, leading to the invalidity of the NC model.
4.2. Total Electric Current
For a better understanding of the difference between the NPP and NC models, we investigate the total electrical current. In this section, we plot the total electrical current through the domain calculated as which has been assumed to be equal to zero in the NC assumption. Figure 6 shows the total electrical current for 1D simulations. Obviously, the total electrical current for the NC-model is zero in all 1D test cases. We presented it only for the no sorption case. For the NPP model, however, the total electrical current deviates from zero, when considering sorption. This value increases by increasing the sorption capacity in the model.
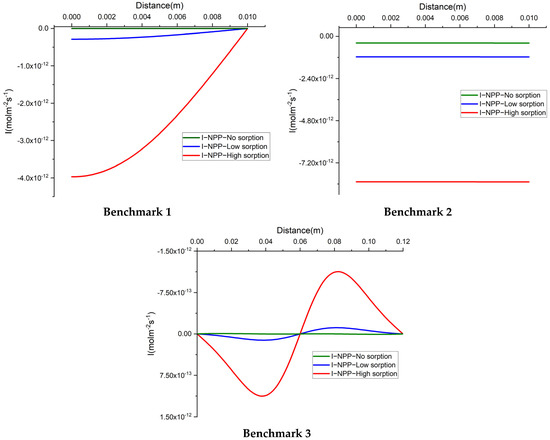
Figure 6.
The total electrical current for the 1D benchmarks with the NPP and NC-models.
The total electrical currents of the 2D benchmark calculated with horizontal and vertical fluxes are shown in Figure 7. Fluxes in the horizontal and vertical directions are denoted ‘Ix’ and ‘Iy’, respectively. For the case without sorption, the values for Ix and Iy for both models are too small, and they are considered to be zero in the numerical simulations and are not shown. By introducing sorption to the model and increasing it, the total electrical current in both directions increases in the NPP model. In the NC models, since the electro diffusion is considered only in the vertical direction, the total electrical current for the vertical direction is equal to zero and is not shown. For the horizontal direction, the only considered flux is the advective flux. Therefore, in this direction, the electrical current in both approaches receives a value. The results for the total electrical current in the horizontal direction for NC and NPP models are in the same order of magnitude. However, they are not the same due to the differences in the total concentration results which brings the differences in dissolved concentration results.
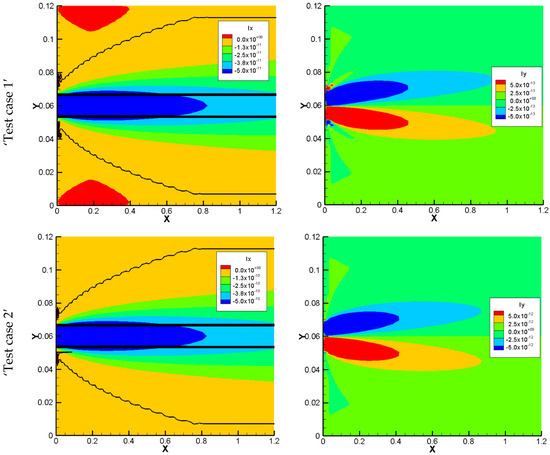
Figure 7.
The total electrical current for the 2D benchmark in the horizontal (left) and vertical directions (right). The NPP model is represented with colors and the NC model with lines: low sorptivity (test case 1), high sorptivity (test case).
4.3. Total Charge
For a better understanding of the NPP and NC models, we investigate in this section the total charge in the domain as, which is defined as: . Total charges for the 1D benchmarks are plotted in Figure 8. The results show that, for the NPP-model, the total charge in the domain tends to stay equal to zero. Therefore, in the areas with Dirichlet boundary conditions in benchmark 1 and benchmark 2, there are some jumps in the results of the total charge for the NPP-model because the non-zero total charge only exists at the Dirichlet boundary of the domain. However, for the NC-model we see that the amount of total charge increases with increasing sorption capacity. There are also some jumps in the results of the NC model in benchmark 3, in the area with a significant change in the initial concentration. Therefore, for the NC-model, despite the assumption of initial electro-neutrality in total concentration for all the test cases, the whole domain deviates from electro-neutrality as we introduce sorption to the model and increase it.
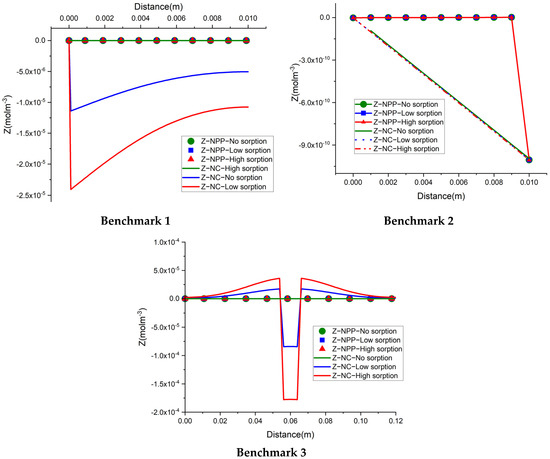
Figure 8.
The total charge for the 1D benchmarks with the NPP and NC-models.
Figure 9 shows the total charge for the 2D benchmark, calculated by the NC-model. For the NPP models, the total charge for all the test cases (with or without) sorption is very small, and in numerical modeling, they are considered as zero. It is the same for the case without sorption in the NC-model. Therefore, in 2D, the total charge calculated with the NPP approach for all test cases and the total charge calculated with the NC approach for the case without sorption is not shown here.
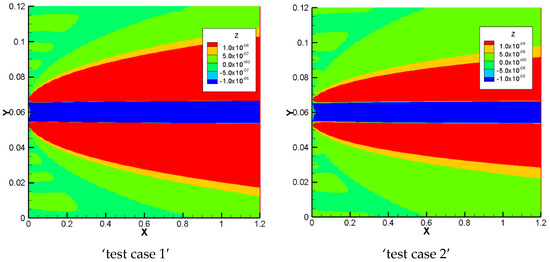
Figure 9.
The total charge for the 2D benchmark with the NC-model: low sorptivity (test case 1), high sorptivity (test case 2).
The results are consistent with [24], proving that for no sorption involvement in the electro-diffusion process, NC and zero charge assumptions are equivalent. For the cases with sorption, as is shown in Figure 9, the NC-model shows the total charge to increase with increasing sorption capacity resulting in non-electroneutrality. Indeed, the NC-model maintains a null current (or no charge according to [24]) for the water phase but allows charge accumulation on the solid phase. Thus, Figure 9 exhibits the sorbed charges in the case of the NC-model.
4.4. Electric Field
We also investigate the electrical field, for a deep understanding of the difference between the NC and NPP-models. In the NC models, the electric field is represented as a function of dissolved concentrations. For the NPP models, however, it is calculated from the derivative of electric potential as which is linked to the total concentrations. The results of the electric field for the 1D benchmarks are plotted in Figure 10. For the cases without sorption, the NC and NPP models for the three 1D benchmarks agree well. By increasing the sorption capacity in benchmarks 1 and 2, the results of the two approaches become different and in benchmark 3, some jumps appear in the areas of a high concentration gradient. The electric fields for the 2D case of benchmark 3 calculated by the NPP and NC-models are shown in Figure 11a,b, respectively. As we can see, for the NPP-model, in benchmark 3, either 1D or 2D, the electric field does not depend on sorption capacity. As shown in Figure 11b, there are some oscillations in the electric field obtained from the NC assumption because of the dependence of the electric field on the concentration gradient, which may require a finer mesh. These oscillations increase with increasing sorption capacity for the NC-model.
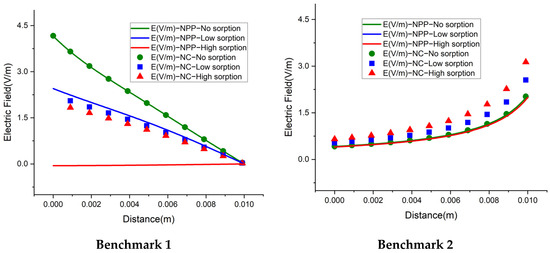
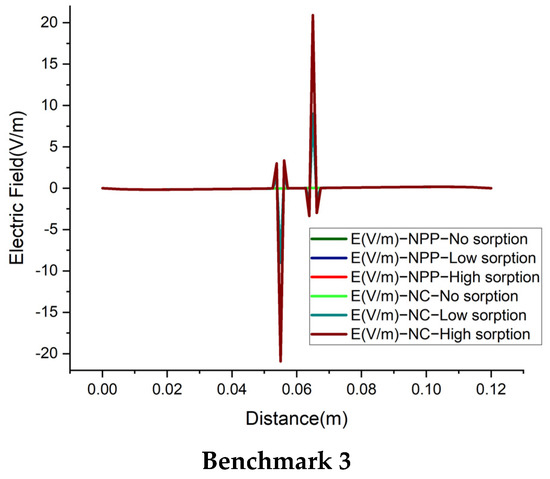
Figure 10.
The electric field for the 1D benchmarks with the NPP and NC-models.
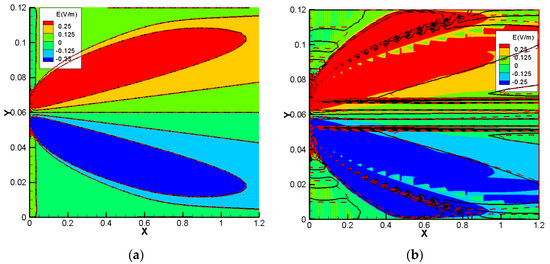
Figure 11.
Benchmark3-2D. (a) The electric field with the NPP-model for the case of no sorption (colors), low sorption (black lines), and high sorption (red dashed lines). (b) The electric field with the NC-model for the case of no sorption (colors), low sorption (black lines), and high sorption (red dashed lines).
5. Conclusions
Processes of adsorptive reactive transport with electro-diffusion are investigated. These processes can be modeled using the Nernst–Planck equation, involving advective and diffusive fluxes, accompanied by an electro-diffusion flux which considers the electric potential effects. In the literature, the system of equations is often solved using the null current assumption. This assumption allows for eliminating the electrical potential from the governing equations and for representing the electro-diffusion processes with a diffusion coefficient that is a function of concentrations. This simplification is highly important as it allows for easy implementation of the electro-diffusion processes in existing codes of reactive transport. In this work, we present a comprehensive formulation of the governing equations without any assumption of null current or charge, by coupling the Nernst–Planck equation to the Poisson equation giving the electrical potential as a function of electrical charges. A 1D and 2D finite element models are developed using COMSOL multi-physics. Numerical test cases, based on common benchmarks, show that the new approach, based on the Poisson equation, leads to similar results as the usual null current approach if the electrical charge is only considered for the water phase. However, this work proved that important differences between both approaches occur when dissolved species create electric flow. Our results show a significant difference between the null current and Poisson equation approaches in the case of adsorption reactions. In contrast to the null current assumption, the new approach allows for considering the existence of an external electric field and/or electromigration through media with heterogeneities on dielectric permittivity. The existing benchmarks for electro-diffusion are based on the NC assumption. The results presented in this paper can be used as a new benchmark without this assumption.
The current work is based on numerical simulations. A full analysis has been performed to ensure numerical consistency of the solutions, but better confidence in the results can be obtained by confronting numerical simulation to laboratory experiments. This work shows, based on a case of sorption processes, the limitation of the NC assumption. However, this limitation could be not limited to adsorption processes. Further studies with more generic analysis can be performed to fully understand the validity of the NC assumption. In the current model, we assume the permittivity of solid grains is constant. However, this permittivity can be affected by the sorption processes. The effect of sorption on permittivity could be an important topic for further investigations. While showing the invalidity of the null current assumption in the case of adsorption reactions, this paper could motivate further works on finding an appropriate simplification that will be helpful in implementing electrochemical migration processes in existing reactive transport codes. As discussed in the previous section, this paper presents new results for benchmarking. However, the investigated benchmarks involve Dirichlet or Neumann boundary conditions. Thus, developing new benchmarks with different types of boundary conditions [31,32] is worth further investigations.
Author Contributions
Conceptualization, S.T. and M.F.; methodology, J.C. and M.W.S.; software, S.T.; validation, S.T. and H.M.B.; investigation, S.T.; resources, H.M.B. and M.F.; writing—original draft preparation, S.T.; writing—review and editing, M.F. and M.W.S.; supervision, M.F. and J.C.; funding acquisition, M.F., J.C. and H.M.B. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
No new data were created or analyzed in this study. Data sharing is not applicable to this article.
Conflicts of Interest
The authors declare no conflict of interest.
Appendix A. Benchmarks Description (Boundary and Initial Conditions and Chemical System)
- Parameters, boundary, and initial conditions for Benchmark 1

Figure A1.
Configuration of benchmark 1.

Table A1.
Boundary and initial conditions, chemical system, and parameters for benchmark 1.
Table A1.
Boundary and initial conditions, chemical system, and parameters for benchmark 1.
| Species | Left Boundary Condition (mM) | Initial Condition (mM) |
|---|---|---|
| 0.001 | 0.1 | |
| 0.1 | 0.1 | |
| 0.1 | 0.1 | |
| 0.001 | 0.1 | |
| Parameters | ||
| Permittivity [F/m] | ||
| Molecular diffusion coefficients [m2/s] | : 1.33 × 10−9 | |
| : 2.03 × 10−9 | ||
| : 1.9 × 10−9 | ||
| : 9.31 × 10−9 | ||
- 2.
- Parameters, boundary, and initial conditions for Benchmark 2

Figure A2.
Configuration of benchmark 2.

Table A2.
Boundary and initial conditions, chemical system, and parameters for benchmark 2.
Table A2.
Boundary and initial conditions, chemical system, and parameters for benchmark 2.
| Species | Left Boundary Condition (mM) (Initial Condition in the Left Half of the Domain) | Right Boundary Condition (mM) (Initial Condition in the Right Half of the Domain) |
|---|---|---|
| 1 × 10−4 | 1 × 10−4 | |
| 0.5 | 0.1 | |
| 1 × 10−6 | 1 × 10−6 | |
| 0.5 | 0.1 | |
| 1 × 10−4 | 1 × 10−4 | |
| Parameters | ||
| Permittivity [F/m] | 5.85 × 10−10 | |
| Molecular diffusion coefficients [m2/s] | : 9.31 × 10−9 | |
| : 1.33 × 10−9 | ||
| : 2.03 × 10−9 | ||
| : 5.27 × 10−9 | ||
- 3.
- Parameters and Boundary and initial conditions for Benchmark 3
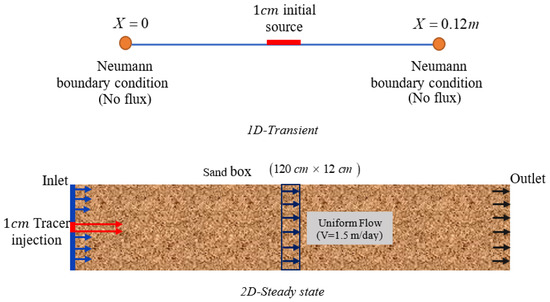
Figure A3.
Configuration of benchmark 3.

Table A3.
Boundary and initial conditions, chemical system, and parameters for benchmark 3.
Table A3.
Boundary and initial conditions, chemical system, and parameters for benchmark 3.
| Species | Initial Source (1D) and the Tracer Injection Ports (mM) | Initial Condition (1D) and Remaining Injection Ports (2D) (mM) |
|---|---|---|
| 0.29 | 1 × 10−6 | |
| 0.29 | 1 × 10−6 | |
| 0.87 | 3 × 10−6 | |
| Parameters | ||
| Permittivity [F/m] | 5.85 × 10−10 | |
| Molecular diffusion coefficients [m2/s] | : 1.77 × 10−9 | |
| : 6.26 × 10−10 | ||
| : 2.03 × 10−9 | ||
| Transverse dispersion coefficients [m2/s] | : 2.405 × 10−9 | |
| : 1.745 × 10−9 | ||
| : 2.425 × 10−9 | ||
References
- Babaei, M.; Islam, A. Convective-Reactive CO2 Dissolution in Aquifers With Mass Transfer with Immobile Water. Water Resour. Res. 2018, 54, 9585–9604. [Google Scholar] [CrossRef] [Green Version]
- Islam, A.; Korrani, A.K.N.; Sepehrnoori, K.; Patzek, T. Effects of geochemical reaction on double diffusive natural convection of CO2 in brine saturated geothermal reservoir. Int. J. Heat Mass Transf. 2014, 77, 519–528. [Google Scholar] [CrossRef]
- Kim, J.; Sonnenthal, E.; Rutqvist, J. A sequential implicit algorithm of chemo-thermo-poro-mechanics for fractured geothermal reservoirs. Comput. Geosci. 2015, 76, 59–71. [Google Scholar] [CrossRef] [Green Version]
- Erfani, H.; Joekar-Niasar, V.; Farajzadeh, R. Impact of microheterogeneity on upscaling reactive transport in geothermal energy. ACS Earth Space Chem. 2019, 3, 2045–2057. [Google Scholar] [CrossRef] [Green Version]
- Van der Lee, J.H.; Roorda, L.D.; Beckerman, H.; Lankhorst, G.J.; Bouter, L.M. Improving the Action Research Arm test: A unidimensional hierarchical scale. Clin. Rehabil. 2002, 16, 646–653. [Google Scholar] [CrossRef] [Green Version]
- Van der Lee, J.; De Windt, L.; Lagneau, V.; Goblet, P. Module-oriented modeling of reactive transport with HYTEC. Comput. Geosci. 2003, 29, 265–275. [Google Scholar] [CrossRef]
- Spycher, N.F.; Sonnenthal, E.L.; Apps, J.A. Fluid flow and reactive transport around potential nuclear waste emplacement tunnels at Yucca Mountain, Nevada. J. Contam. Hydrol. 2003, 62, 653–673. [Google Scholar] [CrossRef] [Green Version]
- Steefel, C.I.; Lasaga, A.C. A coupled model for transport of multiple chemical species and kinetic precipitation/dissolution reactions with application to reactive flow in single phase hydrothermal systems. Am. J. Sci. 1994, 294, 529–592. [Google Scholar] [CrossRef]
- Parkhurst, D.L.; Appelo, C.A.J. User’s guide to PHREEQC (Version 2): A computer program for speciation, batch-reaction, one-dimensional transport, and inverse geochemical calculations. Water Resour. Investig. Rep. 1999, 99, 312. [Google Scholar]
- Xu, T.; Sonnenthal, E.; Spycher, N.; Pruess, K. TOUGHREACT User’s Guide: A Simulation Program for Non-Isothermal Multiphase Reactive Geochemical Transport in Variable Saturated Geologic Media; Lawrence Berkeley National Lab.: Berkeley, CA, USA, 2004.
- Mayer, K.U.; Frind, E.O.; Blowes, D.W. Multicomponent reactive transport modeling in variably saturated porous media using a generalized formulation for kinetically controlled reactions: Reactive transport modeling in variably saturated media. Water Resour. Res. 2002, 38, 13–1–13–21. [Google Scholar] [CrossRef]
- Prommer, H.; Barry, D.A.; Zheng, C. MODFLOW/MT3DMS-Based Reactive Multicomponent Transport Modeling. Ground Water 2003, 41, 247–257. [Google Scholar] [CrossRef] [PubMed]
- Post, V.E.A.; Prommer, H. Multicomponent reactive transport simulation of the Elder problem: Effects of chemical reactions on salt plume development: Reactive elder problem. Water Resour. Res. 2007, 43, W10404. [Google Scholar] [CrossRef]
- Parkhurst, D.L.; Kipp, K.L.; Engesgaard, P.; Charlton, S.R. Phast, a program for simulating ground-waterflow, solute transport, and multicomponent geochemical reactions. US Geol. Surv. Tech. Methods 2004, 6, A8. [Google Scholar]
- Charlton, S.R.; Parkhurst, D.L. Modules based on the geochemical model PHREEQC for use in scripting and programming languages. Comput. Geosci. 2011, 37, 1653–1663. [Google Scholar] [CrossRef]
- Parkhurst, D.L.; Wissmeier, L. PhreeqcRM: A reaction module for transport simulators based on the geochemical model PHREEQC. Adv. Water Resour. 2015, 83, 176–189. [Google Scholar] [CrossRef]
- Kazemi Nia Korrani, A.; Sepehrnoori, K.; Delshad, M. A Novel Mechanistic Approach for Modeling Low Salinity Water Injection. In Proceedings of the SPE Annual Technical Conference and Exhibition, SPE, New Orleans, LA, USA, 30 September–2 October 2013; p. D021S021R007. [Google Scholar]
- Muniruzzaman, M.; Rolle, M. Modeling multicomponent ionic transport in groundwater with IPhreeqc coupling: Electrostatic interactions and geochemical reactions in homogeneous and heterogeneous domains. Adv. Water Resour. 2016, 98, 1–15. [Google Scholar] [CrossRef] [Green Version]
- Cussler, E.L.; Cussler, E.L. Diffusion: Mass Transfer in Fluid Systems; Cambridge University Press: Cambridge, UK, 2009; ISBN 0-521-87121-2. [Google Scholar]
- Rubinstein, I. Electro-Diffusion of Ions; SIAM: Philadelphia, PA, USA, 1990; ISBN 0-89871-245-9. [Google Scholar]
- Ben-Yaakov, S. Diffusion of Sea Water Ions—I. Diffusion of Sea Water into a Dilute Solution. Geochim. Cosmochim. Acta 1972, 36, 1395–1406. [Google Scholar] [CrossRef]
- Katz, A.; Ben-Yaakov, S. Diffusion of Seawater Ions. Part II. The Role of Activity Coefficients and Ion Pairing. Mar. Chem. 1980, 8, 263–280. [Google Scholar] [CrossRef]
- Lasaga, A.C. Multicomponent Exchange and Diffusion in Silicates. Geochim. Cosmochim. Acta 1979, 43, 455–469. [Google Scholar] [CrossRef]
- Boudreau, B.P.; Meysman, F.J.R.; Middelburg, J.J. Multicomponent Ionic Diffusion in Porewaters: Coulombic Effects Revisited. Earth Planet. Sci. Lett. 2004, 222, 653–666. [Google Scholar] [CrossRef]
- Rasouli, P.; Steefel, C.I.; Mayer, K.U.; Rolle, M. Benchmarks for multicomponent diffusion and electrochemical migration. Comput. Geosci 2015, 19, 523–533. [Google Scholar] [CrossRef] [Green Version]
- Rolle, M.; Sprocati, R.; Masi, M.; Jin, B.; Muniruzzaman, M. Nernst-Planck-based Description of Transport, Coulombic Interactions, and Geochemical Reactions in Porous Media: Modeling Approach and Benchmark Experiments. Water Resour. Res. 2018, 54, 3176–3195. [Google Scholar] [CrossRef] [Green Version]
- Frizon, F.; Lorente, S.; Ollivier, J.P.; Thouvenot, P. Transport model for the nuclear decontamination of cementitious materials. Comput. Mater. Sci. 2003, 27, 507–516. [Google Scholar] [CrossRef]
- Maineult, A.; Bernabé, Y.; Ackerer, P. Detection of advected concentration and pH fronts from self-potential measurements: Detection of concentration or pH fronts. J. Geophys. Res. 2005, 110, B11205. [Google Scholar] [CrossRef]
- Birgersson, M.; Karnland, O. Ion equilibrium between montmorillonite interlayer space and an external solution—Consequences for diffusional transport. Geochim. Cosmochim. Acta 2009, 73, 1908–1923. [Google Scholar] [CrossRef]
- Brovelli, A.; Cassiani, G. Effective permittivity of porous media: A critical analysis of the complex refractive index model. Geophys. Prospect. 2008, 56, 715–727. [Google Scholar] [CrossRef]
- Berardi, M.; Difonzo, F.V. Strong Solutions for Richards’ Equation with Cauchy Conditions and Constant Pressure Gradient. Environ. Fluid Mech. 2020, 20, 165–174. [Google Scholar] [CrossRef]
- Choquet, C. Semi-Classical Solutions for a Nonlinear Coupled Elliptic-Parabolic Problem. Bull. Aust. Math. Soc. 2007, 76, 369–396. [Google Scholar] [CrossRef] [Green Version]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).