Resistance Analysis of Morphologies in Headwater Mountain Streams
Abstract
:1. Introduction
2. Materials and Methods
2.1. River Reach
2.2. Empirical Resistance Equations
2.3. Statistical Performance Metrics
2.4. Determination of NDHG Parameters
2.5. Variance Decomposition Methodology (VDM)
2.6. Test with Data from Literature
3. Results
3.1. Best Fitting Equation
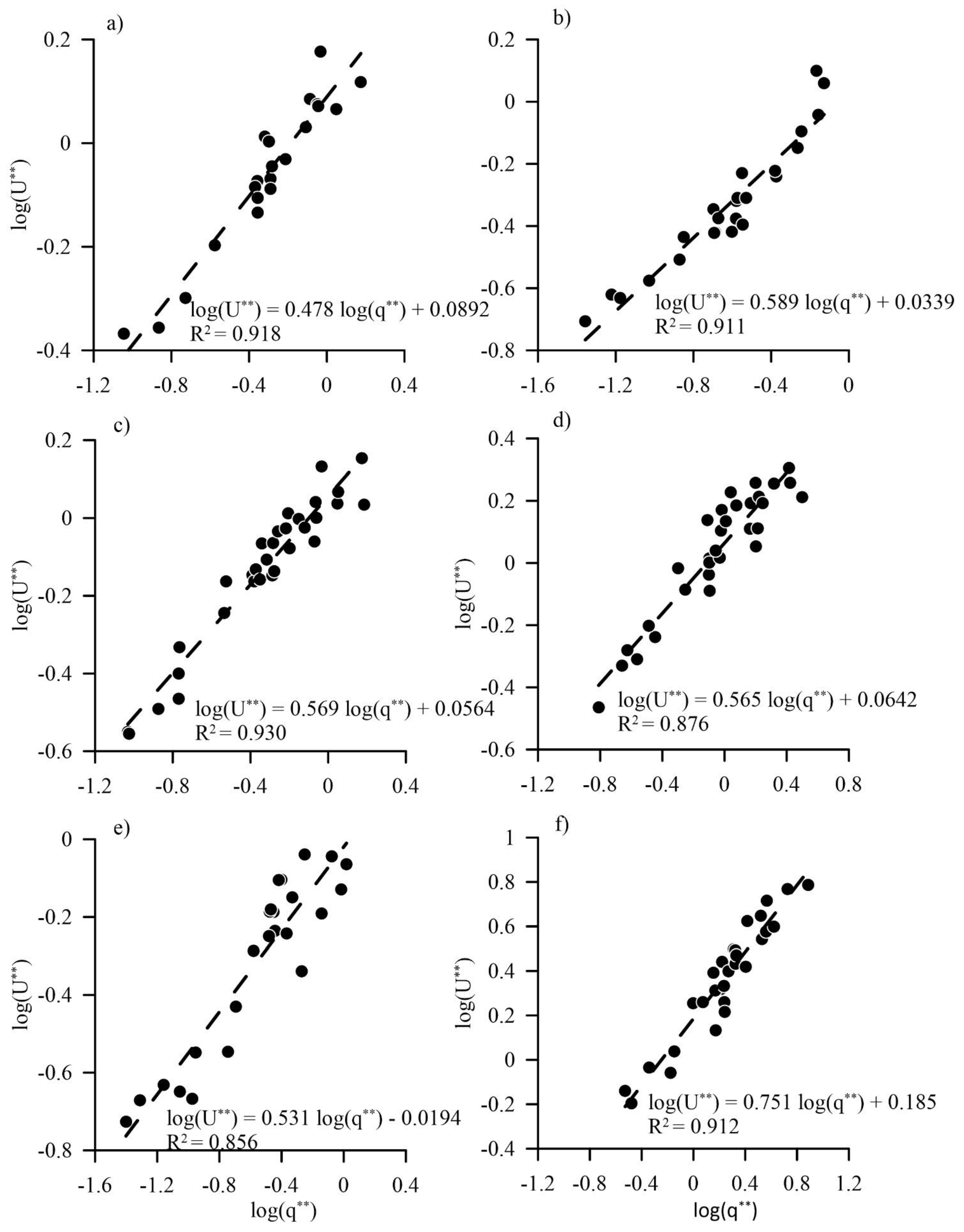
3.2. Estimation of NDHG Parameters
3.3. Variance Decomposition Methodology (VDM)
3.4. Test with Data from Literature
4. Discussion
4.1. Characteristics of NDHG Equations
4.2. NDHG Parameters
4.3. Variance Decomposition Methodology (VDM)
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Comiti, F.; Mao, L.; Wilcox, A.; Wohl, E.E.; Lenzi, M.A. Field-derived relationships for flow velocity and resistance in high-gradient streams. J. Hydrol. 2007, 340, 48–62. [Google Scholar] [CrossRef]
- Aberle, J.; Smart, G.M. The influence of roughness structure on flow resistance on steep slopes. J. Hydraul. Res. 2003, 41, 259–269. [Google Scholar] [CrossRef]
- Papanicolaou, A.N.; Bdour, A.; Wicklein, E. One-dimensional hydrodynamic/sediment transport model applicable to steep mountain streams. J. Hydraul. Res. 2004, 42, 357–375. [Google Scholar] [CrossRef]
- Ferguson, R. Flow resistance equations for gravel- and boulder-bed streams. Water Resour. Res. 2007, 43. [Google Scholar] [CrossRef] [Green Version]
- Bathurst, J.C. At-a-site variation and minimum flow resistance for mountain rivers. J. Hydrol. 2002, 269, 11–26. [Google Scholar] [CrossRef]
- Chin, A.; Wohl, E. Toward a theory for step pools in stream channels. Prog. Phys. Geogr. 2005, 29, 275–296. [Google Scholar] [CrossRef]
- Curran, J.H.; Wohl, E.E. Large woody debris and flow resistance in Step-pool channels, Cascade Range, Washington. Geomorphology 2003, 51, 141–157. [Google Scholar] [CrossRef]
- David, G.C.L.; Wohl, E.; Yochum, S.E.; Bledsoe, B.P. Controls on spatial variations in flow resistance along steep mountain streams. Water Resour. Res. 2010, 46. [Google Scholar] [CrossRef] [Green Version]
- MacFarlane, W.A.; Wohl, E. Influence of step composition on step geometry and flow resistance in Step-pool streams of the Washington Cascades. Water Resour. Res. 2003, 39. [Google Scholar] [CrossRef] [Green Version]
- Montgomery, D.R.; Buffington, J.M. Channel-reach morphology in mountain drainage basins. Geol. Soc. Am. Bull. 1997, 109, 596–611. [Google Scholar] [CrossRef]
- Nitsche, M.; Rickenmann, D.; Kirchner, J.W.; Turowski, J.M.; Badoux, A. Macroroughness and variations in reach-averaged flow resistance in steep mountain streams. Water Resour. Res. 2012, 48. [Google Scholar] [CrossRef] [Green Version]
- Rickenmann, D.; Recking, A. Evaluation of flow resistance in gravel-bed rivers through a large field data set. Water Resour. Res. 2011, 47, W07538. [Google Scholar] [CrossRef] [Green Version]
- Comiti, F.; Cadol, D.; Wohl, E. Flow regimes, bed morphology, and flow resistance in self-formed Step-pool channels. Water Resour. Res. 2009, 45, 1–18. [Google Scholar] [CrossRef]
- Zimmermann, A. Flow resistance in steep streams: An experimental study. Water Resour. Res. 2010, 46. [Google Scholar] [CrossRef]
- Jarrett, R.D. Hydraulics of high-gradient streams. J. Hydraul. Eng. 1984, 110, 1519–1539. [Google Scholar] [CrossRef]
- Bathurst, J.C. Flow Resistance Estimation in Mountain Rivers. J. Hydraul. Eng. 1985, 111, 625–643. [Google Scholar] [CrossRef]
- Maxwell, A.R.; Papanicolaou, A.N. Step-pool morphology in high-gradient streams. Int. J. Sediment Res. 2001, 16, 380–390. [Google Scholar]
- Lee, A.J.; Ferguson, R.I. Velocity and flow resistance in Step-pool streams. Geomorphology 2002, 46, 59–71. [Google Scholar] [CrossRef]
- Romero, M.; Revollo, N.; Molina, J. Flow resistance in steep mountain rivers in Bolivia. J. Hydrodyn. Ser. B 2010, 22, 702–707. [Google Scholar] [CrossRef]
- Wohl, E. Mountain Rivers Revisited; American Geophysical Union: Washington, DC, USA, 2013; ISBN 9781118665572. [Google Scholar]
- Hudson, R.; Fraser, J. Introduction to salt dilution gauging for streamflow measurement, Part IV: The mass balance (or dry injection) method. Streamline Watershed Manag. Bull. 2005, 9, 6–12. [Google Scholar]
- Moore, R.D.D. Slug injection using salt in solution. Streamline Watershed Manag. Bull. 2005, 8, 1–6. [Google Scholar]
- Wilcox, A.C.; Wohl, E.E. Flow resistance dynamics in Step-pool stream channels: 1. Large woody debris and controls on total resistance. Water Resour. Res. 2006, 42. [Google Scholar] [CrossRef] [Green Version]
- Bathurst, J.C. Slope-area Discharge Gaging in Mountain Rivers. J. Hydraul. Eng. 1986, 112, 376–391. [Google Scholar] [CrossRef]
- Bunte, K.; Abt, S.R. Sampling Surface and Subsurface Particle-Size Distributions in Wadable Gravel- and Cobble-Bed Streams for Analyses in Sediment Transport, Hydraulics, and Streambed Monitoring; US Department of Agriculture; Forest Service; Rocky Mountain Research Station: Fort Collins, CO, USA, 2001; ISBN RMRS-GTR-74.
- Chai, T.; Draxler, R.R. Root mean square error (RMSE) or mean absolute error (MAE)? -Arguments against avoiding RMSE in the literature. Geosci. Model Dev. 2014, 7, 1247–1250. [Google Scholar] [CrossRef] [Green Version]
- Willmott, C.J.; Matsuura, K. Advantages of the mean absolute error (MAE) over the root mean square error (RMSE) in assessing average model performance. Clim. Res. 2005, 30, 79–82. [Google Scholar] [CrossRef]
- McCuen, R.H.; Knight, Z.; Cutter, A.G. Evaluation of the Nash–Sutcliffe Efficiency Index. J. Hydrol. Eng. 2006, 11, 597–602. [Google Scholar] [CrossRef]
- Merz, R.; Blöschl, G. Regionalisation of catchment model parameters. J. Hydrol. 2004, 287, 95–123. [Google Scholar] [CrossRef] [Green Version]
- Nayak, P.C.; Venkatesh, B.; Krishna, B.; Jain, S.K. Rainfall-runoff modeling using conceptual, data driven, and wavelet based computing approach. J. Hydrol. 2013, 493, 57–67. [Google Scholar] [CrossRef]
- Ritter, A.; Muñoz-Carpena, R. Performance evaluation of hydrological models: Statistical significance for reducing subjectivity in goodness-of-fit assessments. J. Hydrol. 2013, 480, 33–45. [Google Scholar] [CrossRef]
- Parker, G.; Wilcock, P.R.; Paola, C.; Dietrich, W.E.; Pitlick, J. Physical basis for quasi-universal relations describing bankfull hydraulic geometry of single-thread gravel bed rivers. J. Geophys. Res. Earth Surf. 2007, 112. [Google Scholar] [CrossRef]
- Parker, G.; Toro-Escobar, C.M.; Ramey, M.; Beck, S. Effect of Floodwater Extraction on Mountain Stream Morphology. J. Hydraul. Eng. 2003, 129, 885–895. [Google Scholar] [CrossRef]
- Marcus, W.A.; Roberts, K.; Harvey, L.; Tackman, G. An Evaluation of Methods for Estimating Manning’s n in Small Mountain Streams. Mt. Res. Dev. 1992, 12, 227–239. [Google Scholar] [CrossRef]
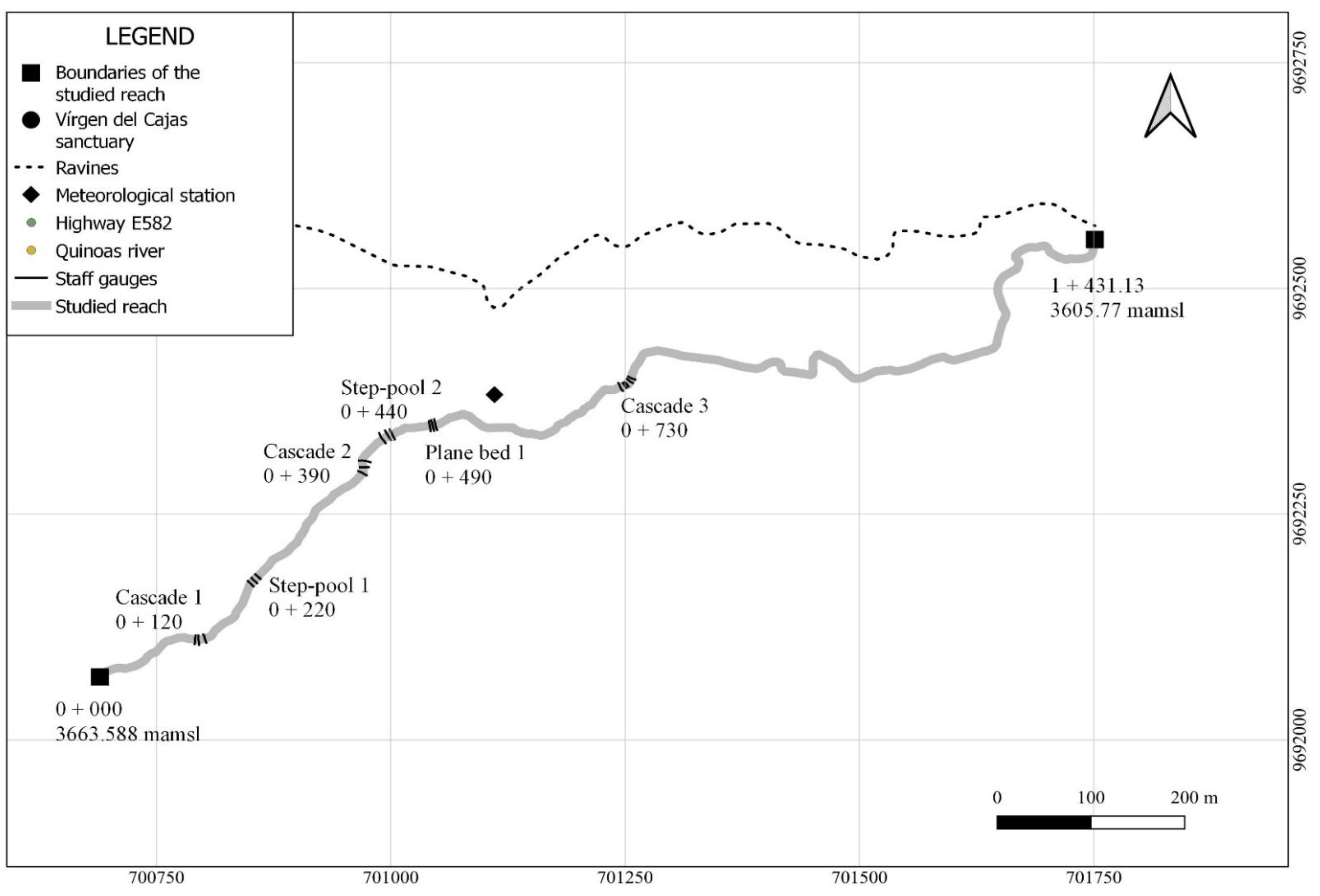


| Profile | Picture |
|---|---|
Plain bed |  |
Cascade |  |
Step-pool |  |
| Reach | Length (m) | S0 (%) | sΔz (m) 1 | s (m) 2 | k3 (m) 3 | dstep (m) 4 | lstep (m) 4 | Measured Manning Range |
|---|---|---|---|---|---|---|---|---|
| Cascade 1 | 11.95 | 8.82% | 0.041 | 0.022 | 0.287 | 0.120–0.264 | ||
| Step-pool 1 | 12.22 | 6.10% | 0.288 | 0.177 | 0.435 | 0.491 | 6.61 | 0.108–0.414 |
| Cascade 2 | 14.58 | 9.30% | 0.282 | 0.179 | 1.299 | 0.139–0.510 | ||
| Step-pool 2 | 11.82 | 8.08% | 0.197 | 0.107 | 0.336 | 0.442 | 3.49 | 0.178–0.472 |
| Plane-bed 1 | 6.26 | 3.16% | 0.039 | 0.017 | 0.197 | 0.036–0.242 | ||
| Cascade 3 | 18.08 | 8.50% | 0.427 | 0.214 | 0.474 | 0.142–0.456 |
| Reference | Code | Type of Resistance | Equation |
|---|---|---|---|
| [16] | BA1985 | Total resistance | D84 corresponds to the 84th percentile of the grain-size distribution. d is the mean water depth |
| [5] | BA2002 | Grain-skin | S0 is bed slope |
| [17] | MaPa2002 | Total resistance in Step-pool | |
| [18] | LFe2002 | Total resistance in Step-pool | Dxx corresponds to the xxth percentile of the grain-size distribution. s, s∆z, k3, lstep, and dstep has been define in Table 1 and Table 2 |
| [2] | AbSm2003 | Total resistance in Step-pool | |
| [4] | (a) FeVPE2007 (b) FeNHGE2007 | Grain-skin | (a) Variable Power Equation (b) Nondimensional Hydraulic Geometry Deep flow: Shallow Flow: U* and q*: ; Dxx = D84 |
| [1] | Co2007 | Total resistance in Step-pool and Cascade | |
| [13] | Co2009 | Total resistance in Step-pool | Nappe flow Skimming flow All data U* and q*: ; Dxx = D84 |
| [19] | Ro2010 | Grain-skin | |
| [14] | (1) Zi12010 (2) Zi22010 | Total resistance in self-formed Cascade reaches | (1) (2) U* and q*: ; Dxx = D84 w is water surface width |
| [12] | RiRe2011 | Total resistance |
| Morphology | Name | RMSE | RMSElog | PE | SX | MAE | EF |
|---|---|---|---|---|---|---|---|
| Cascade | Zi12010 | 0.061 | 0.066 | 0 | 16.761 | 0.046 | 0.834 |
| FeNHGE2007 | 0.102 | 0.099 | 0 | 26.936 | 0.078 | 0.536 | |
| Co2007 | 0.104 | 0.127 | 1 | 25.546 | 0.078 | 0.514 | |
| Step-pool | Zi12010 | 0.085 | 0.096 | 0 | 26.582 | 0.062 | 0.731 |
| FeNHGE2007 | 0.137 | 0.132 | 1 | 39.106 | 0.102 | 0.294 | |
| RiRe2011 | 0.141 | 0.137 | 1 | 40.786 | 0.107 | 0.253 | |
| Plane-bed | Co2009 | 0.153 | 0.102 | 0 | 28.914 | 0.108 | 0.631 |
| FeNHGE2007 | 0.162 | 0.116 | 0 | 23.485 | 0.122 | 0.585 | |
| RiRe2011 | 0.164 | 0.117 | 0 | 23.719 | 0.123 | 0.577 |
| Morphology | m | a | S0 | a1 | a2 | a3 | a2/a3 |
|---|---|---|---|---|---|---|---|
| Cascade 1 | 0.478 | 0.089 | 0.088 | 2.31 | 0.48 | 0.26 | 1.83 |
| Cascade 2 | 0.590 | 0.034 | 0.093 | 1.76 | 0.59 | 0.21 | 2.88 |
| Cascade 3 | 0.569 | 0.056 | 0.085 | 1.94 | 0.57 | 0.22 | 2.64 |
| Plane-bed 1 | 0.751 | 0.185 | 0.032 | 2.36 | 0.75 | 0.12 | 6.02 |
| Step-pool 1 | 0.565 | 0.064 | 0.061 | 2.13 | 0.57 | 0.22 | 2.60 |
| Step-pool 2 | 0.531 | −0.019 | 0.081 | 1.73 | 0.53 | 0.23 | 2.26 |
| Morphology | Name | RMSE | RMSElog | PE | SX | MAE | EF |
|---|---|---|---|---|---|---|---|
| Cascade | NDHGCA | 0.055 | 0.052 | 0 | 11.865 | 0.037 | 0.863 |
| Step-pool | NDHGSP | 0.070 | 0.076 | 0 | 18.208 | 0.052 | 0.817 |
| Plane-bed | NDHGPB | 0.098 | 0.076 | 0 | 19.101 | 0.076 | 0.848 |
| Cascade | Step-Pool | Plane-Bed | ||||
|---|---|---|---|---|---|---|
| Term | Value | % | Value | % | Value | % |
| Se2Yo | 8.986 × 10−5 | 3.336 | 6.786 × 10−5 | 1.367 | 1.532 × 10−4 | 2.532 |
| Se2Y | 0.00260 | 96.664 | 0.00490 | 98.633 | 0.00590 | 97.468 |
| Se2Y-Yo | 0.00269 | 100.00 | 0.00496 | 100.00 | 0.00605 | 100.00 |
| Method | RMSEa (%) | MAEa (%) | EF |
|---|---|---|---|
| Zi12010 | 53 | 43 | 0.296 |
| NHDGlit | 19 | 13 | 0.910 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Cedillo, S.; Sánchez-Cordero, E.; Timbe, L.; Samaniego, E.; Alvarado, A. Resistance Analysis of Morphologies in Headwater Mountain Streams. Water 2021, 13, 2207. https://doi.org/10.3390/w13162207
Cedillo S, Sánchez-Cordero E, Timbe L, Samaniego E, Alvarado A. Resistance Analysis of Morphologies in Headwater Mountain Streams. Water. 2021; 13(16):2207. https://doi.org/10.3390/w13162207
Chicago/Turabian StyleCedillo, Sebastián, Esteban Sánchez-Cordero, Luis Timbe, Esteban Samaniego, and Andrés Alvarado. 2021. "Resistance Analysis of Morphologies in Headwater Mountain Streams" Water 13, no. 16: 2207. https://doi.org/10.3390/w13162207
APA StyleCedillo, S., Sánchez-Cordero, E., Timbe, L., Samaniego, E., & Alvarado, A. (2021). Resistance Analysis of Morphologies in Headwater Mountain Streams. Water, 13(16), 2207. https://doi.org/10.3390/w13162207






