Analysis of Existing Equations for Calculating the Settling Velocity
Abstract
:1. Introduction
2. Existing Equations for Settling Velocity of Sediments
3. Data Description
4. Results and Discussions
4.1. Performances of Existing Equations
4.2. Statistical Performance Analysis of Equations
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Gibbs, R.J.; Matthews, M.D.; Link, D.A. The relationship between sphere size and settling velocity. J. Sediment. Res. 1971, 41, 7–18. [Google Scholar]
- Ruby, W. Settling velocities of gravel, sand and silt particles. Am. J. Sci. 1933, 25, 325–338. [Google Scholar] [CrossRef]
- Zanke, U. Berechnung der Sinkgeschwindigkeiten von Sedimenten; Heft 46, Seite 243; Franzius-Institut für Wasserbau und Küsteningenieurwesen: Hannover, Germany, 1977. [Google Scholar]
- Hallermeier, R.J. Terminal settling velocity of commonly occurring sand grains. Sedimentology 1981, 28, 859–865. [Google Scholar] [CrossRef]
- Rijn, L.C.V. Sediment transport, part II: Suspended load transport. J. Hydraul. Eng. 1984, 110, 1613–1641. [Google Scholar] [CrossRef]
- Zhu, L.J.; Cheng, N.S. Settlement of Sediment Particles; Resp. Rep., Dept of River and Harbor Eng. Nanjing Hydr. Res. Inst.: Nanjing, China, 1993. (In Chinese) [Google Scholar]
- Cheng, N.S. Simplified Settling Velocity Formula for Sediment Particle. J. Hydraul. Eng. 1997, 123, 149–152. [Google Scholar] [CrossRef]
- Jiménez, J.A.; Madsen, O.S. A simple formula to estimate settling velocity of natural sediments. J. Waterw. Port Coast. Ocean Eng. 2003, 129, 70–78. [Google Scholar] [CrossRef] [Green Version]
- Zhang, R.J. River Dynamics; Industry Press: Beijing, China, 1961. (In Chinese) [Google Scholar]
- Julien, P.Y. Erosion and Sedimentation; Cambridge University Press: Cambridge, UK, 2010. [Google Scholar]
- Pandey, M.; Sharma, P.K.; Ahmad, Z.; Singh, U.K.; Karna, N. Three-dimensional velocity measurements around bridge piers in gravel bed. Mar. Georesour. Geotechnol. 2018, 36, 663–676. [Google Scholar] [CrossRef]
- Soulsby, R. Dynamics of Marine Sands: A Manual for Practical Applications; Thomas Telford: Telford, UK, 1997. [Google Scholar]
- Pourshahbaz, H.; Abbasi, S.; Pandey, M.; Pu, J.H.; Taghvaei, P.; Tofangdar, N. Morphology and hydrodynamics numerical simulation around groynes. ISH J. Hydraul. Eng. 2020, 1–9. [Google Scholar] [CrossRef]
- Ahrens, J.P. A fall-velocity equation. J. Waterw. Port Coast. Ocean Eng. 2000, 126, 99–102. [Google Scholar] [CrossRef]
- Wu, W.; Wang, S.S. Formulas for sediment porosity and settling velocity. J. Hydraul. Eng. 2006, 132, 858–862. [Google Scholar] [CrossRef]
- Camenen, B. Simple and general formula for the settling velocity of particles. J. Hydraul. Eng. 2007, 133, 229–233. [Google Scholar] [CrossRef]
- Stokes, G.G. On the effect of the internal friction of fluids on the motion of pendulums. Trans. Camb. Phil. Soc. 1851, 9, 8–106. [Google Scholar]
- Dietrich, W.E. Settling velocity of natural particles. Water Resour. Res. 1982, 18, 1615–1626. [Google Scholar] [CrossRef]
- Engelund, F.; Hansen, E. A Monograph on Sediment Transport in Alluvial Streams; Technical University of Denmark: Copenhagen, Denmark, 1967. [Google Scholar]
- Raudkivi, A.J. Loose Boundary Hydraulics, 3rd ed.; Technical report; Pergamon Press: Oxford, UK, 1990. [Google Scholar]
- Zegzhda, A.P. Settlement of Sand Gravel Particles in Still Water; Izv. NIIG, 12; Moscow, Russia, 1934. (In Russian) [Google Scholar]
- Arkangel’skii, B.V. Experimental Study of Accuracy of Hydraulic Coarseness Scale of Particles; Isv. NHG, 15; 1935. [Google Scholar]
- Sarkisyan, A.A. Deposition of Sediment in a Turbulent Stream; Izd. AN SSSR: Moscow, Russia, 1958. (In Russian) [Google Scholar]
- Briggs, L.I.; McCulloch, D.S.; Moser, F. The hydraulic shape of sand particles. J. Sediment. Res. 1962, 32, 645–656. [Google Scholar]
- Amit, K.; Sharma, M.P.; Rai, S.P. A novel approach for river health assessment of Chambal using fuzzy modeling, India. Desalination Water Treat. 2017, 58, 72–79. [Google Scholar]
- Pandey, M.; Lam, W.H.; Cui, Y.; Khan, M.A.; Singh, U.K.; Ahmad, Z. Scour around Spur Dike in Sand–Gravel Mixture Bed. Water 2019, 11, 1417. [Google Scholar] [CrossRef] [Green Version]
- Kumar, A.; Cabral-Pinto, M.; Kumar, M.; Dinis, P.A. Estimation of risk to the eco-environment and human health of using heavy metals in the Uttarakhand Himalaya, India. Appl. Sci. 2020, 10, 7078. [Google Scholar] [CrossRef]
- Singh, R.K.; Pandey, M.; Pu, J.H.; Pasupuleti, S.; Villuri, V.G.K. Experimental study of clear-water contraction scour. Water Supply 2020, 20, 943–952. [Google Scholar] [CrossRef]
- Kumar, A.; Mishra, S.; Taxak, A.K.; Pandey, R.; Yu, Z.G. Nature rejuvenation: Long-term (1989–2016) vs short-term memory approach based appraisal of water quality of the upper part of Ganga River, India. Environ. Technol. Innov. 2020, 20, 101164. [Google Scholar] [CrossRef] [PubMed]
- Singh, U.K.; Ahmad, Z.; Kumar, A.; Pandey, M. Incipient motion for gravel particles in cohesionless sediment mixtures. Iran. J. Sci. Technol. Trans. Civ. Eng. 2019, 43, 253–262. [Google Scholar] [CrossRef]
- Mishra, S.; Kumar, A.; Shukla, P. Estimation of heavy metal contamination in the Hindon River, India: An environmetric approach. Appl. Water Sci. 2021, 11, 2. [Google Scholar] [CrossRef]
- Singh, P.; Kumar, A.; Mishra, S. Performance evaluation of conservation plan for freshwater lakes in India through a scoring methodology. Environ. Dev. Sustain. 2021, 23, 3787–3810. [Google Scholar] [CrossRef]
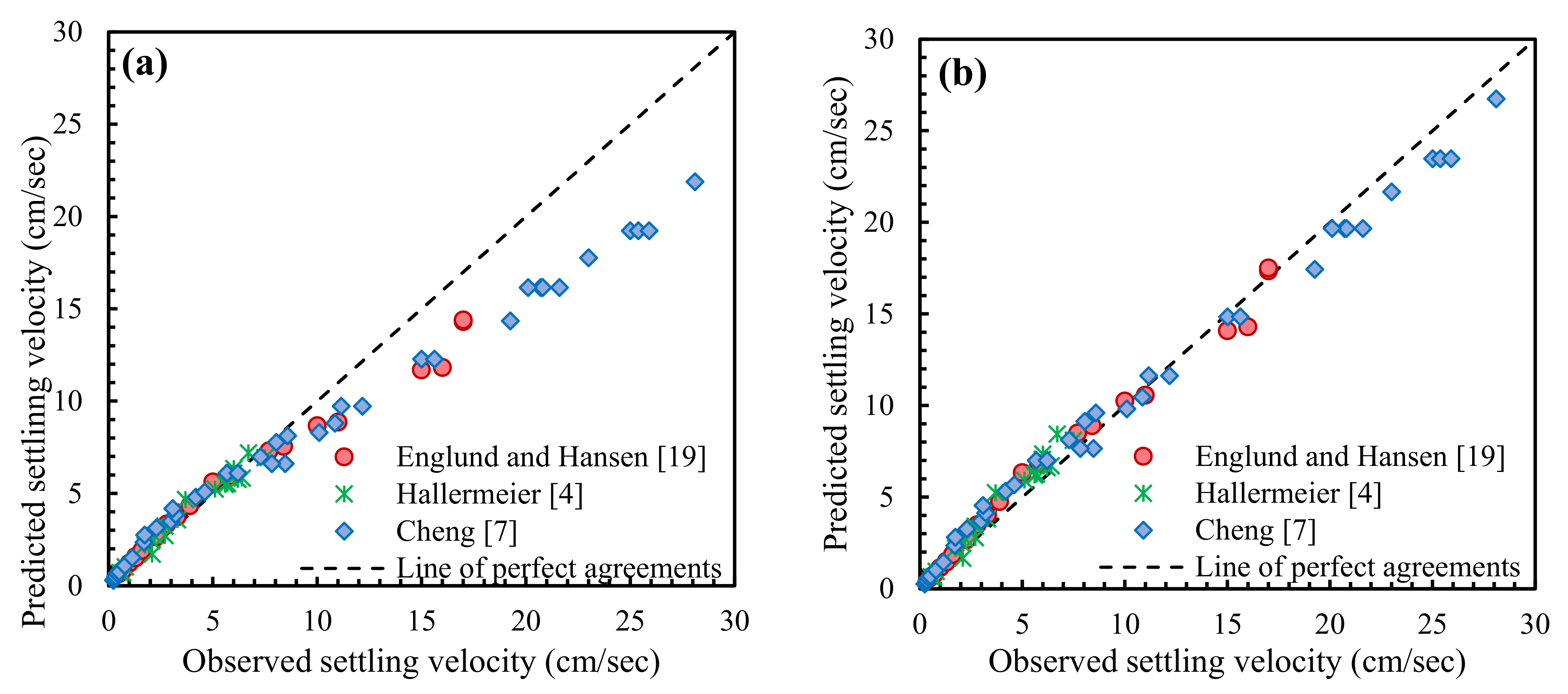
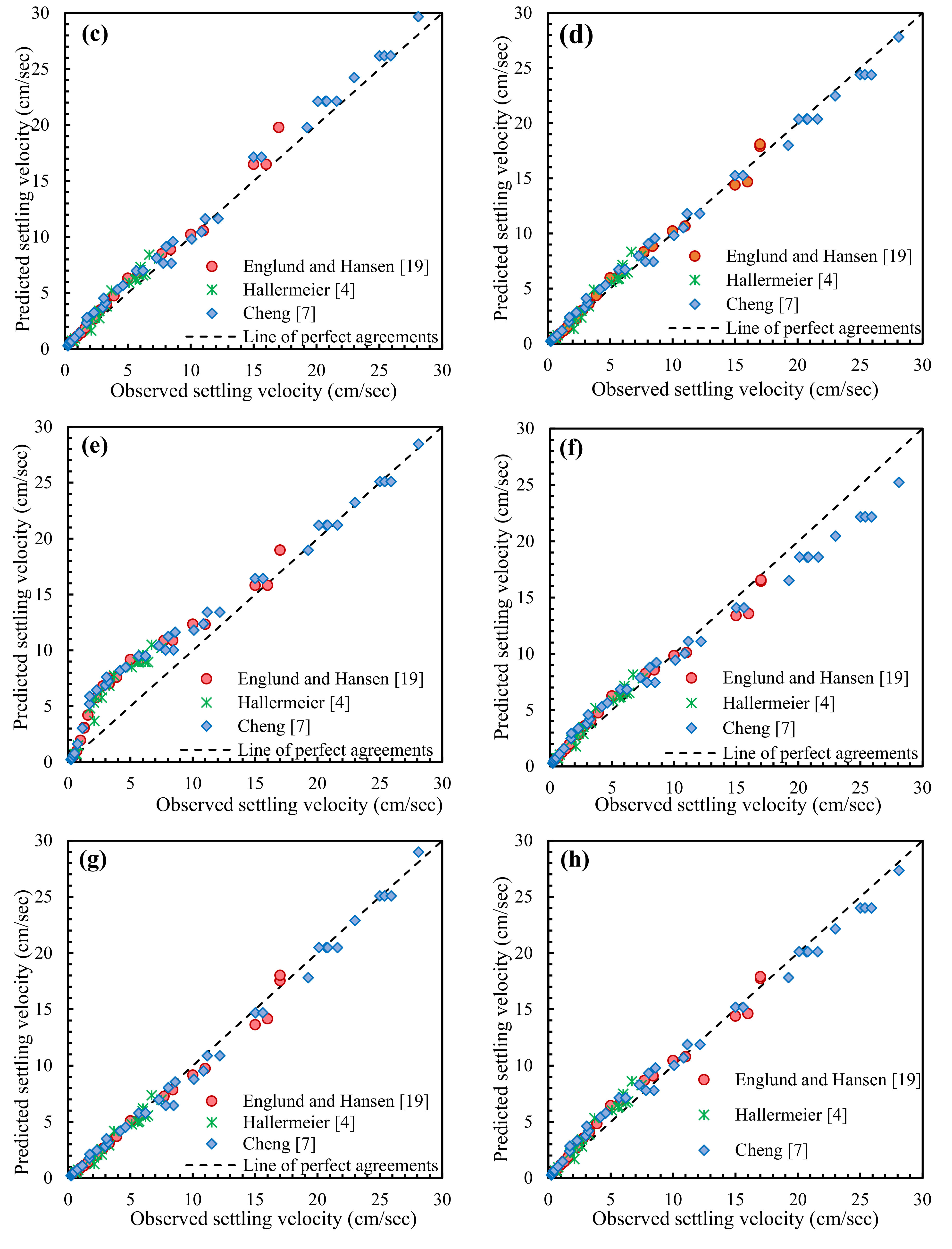

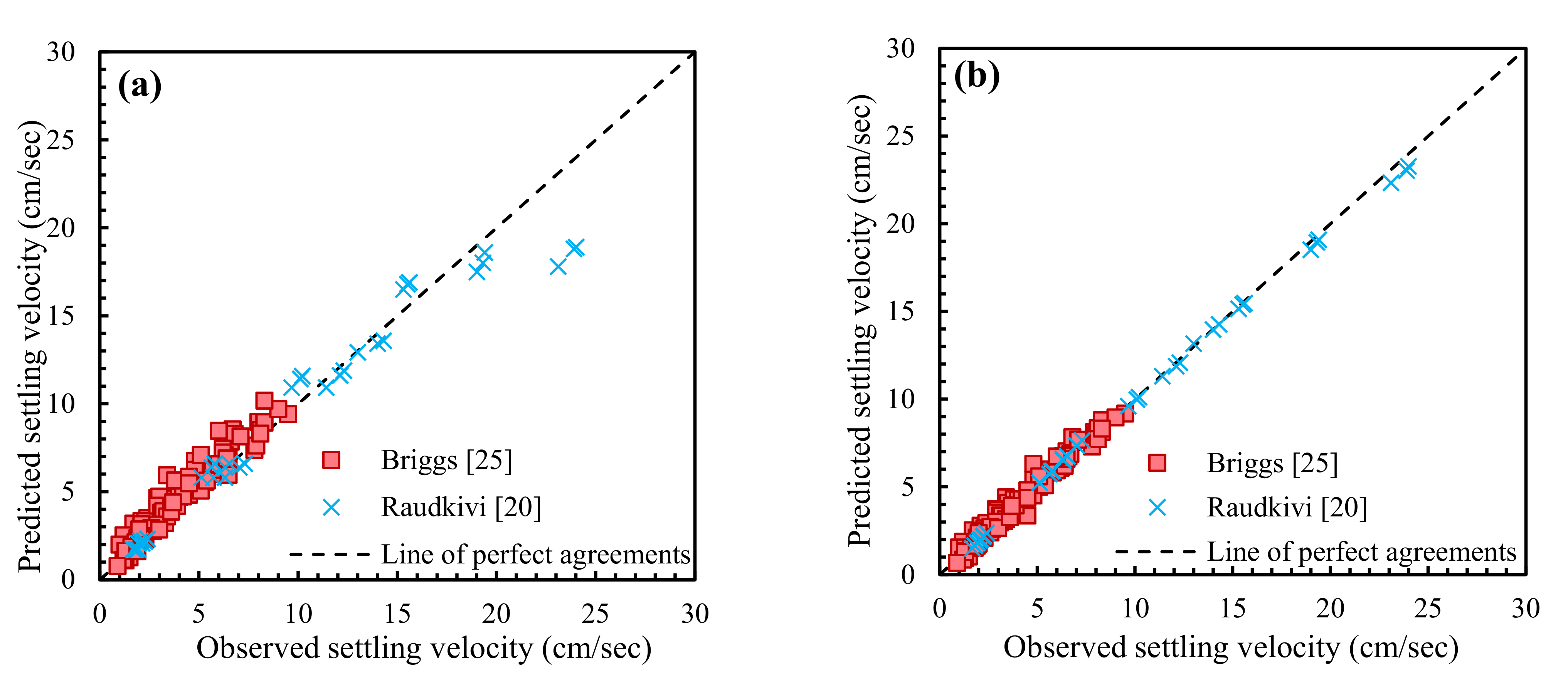
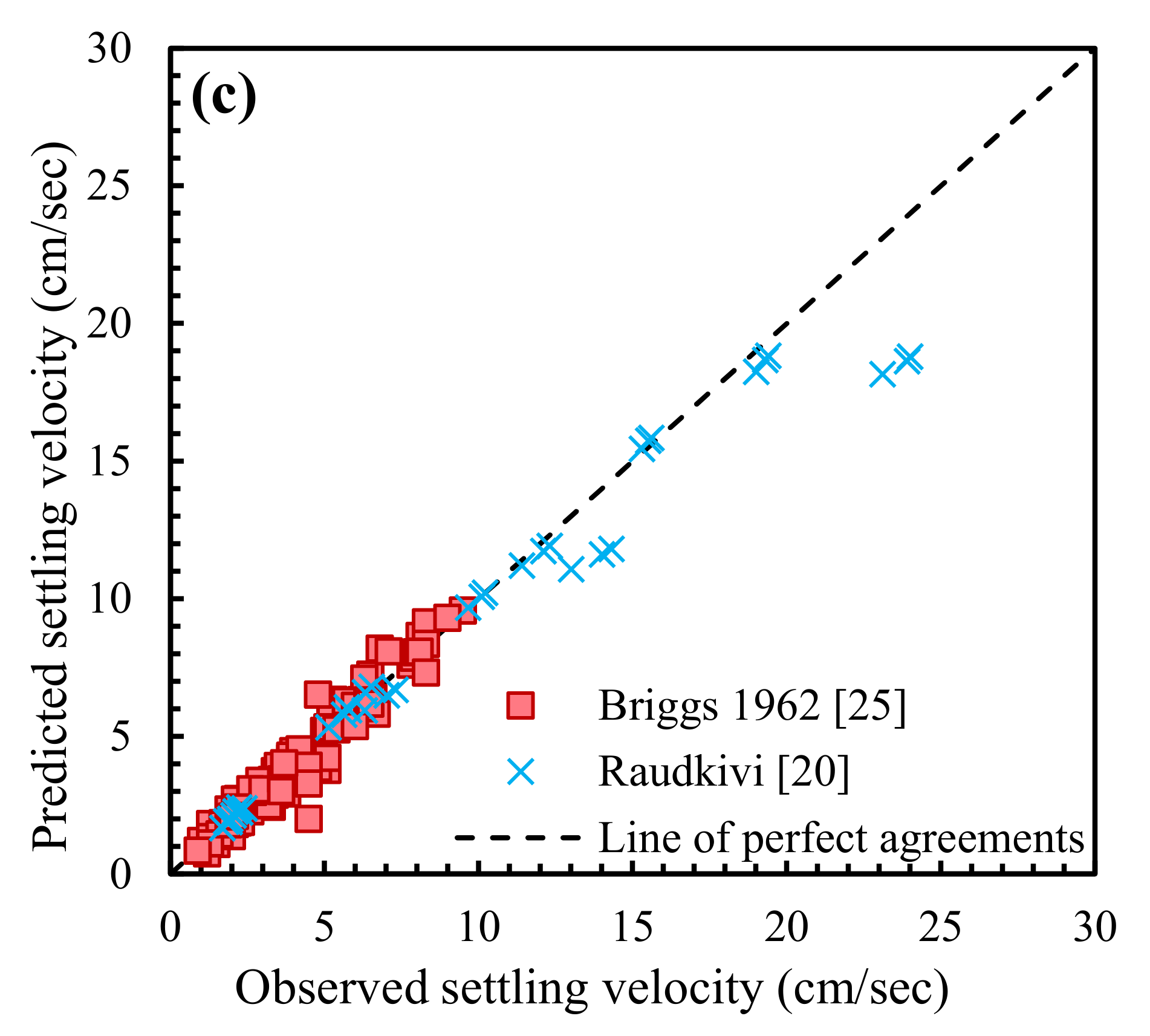
| Parameters | No. of Data | d (mm) | S (-) | CSF (-) | |||
|---|---|---|---|---|---|---|---|
| Authors | |||||||
| Briggs [24] | 110 | 0.09–0.5 | 3.97–5.07 | 0.049–0.881 | 0.01 | 0.9–9.5 | |
| Engelund and Hansen [19] | 21 | 0.01–2.0 | 2.65 | 0.7 | 0.01–0.0131 | 0.5–17.0 | |
| Hallermeier [4] | 21 | 0.09–1.3 | 2.65 | 0.7 | 0.0084–0.0114 | 0.54–14 | |
| Raudkivi [20] | 36 | 0.2–2.0 | 2.65 | 0.5–0.9 | 0.009–0.0131 | 1.68–24.0 | |
| Cheng [7] | 38 | 0.06–4.5 | 2.65 | 0.7 | 0.0114–0.0141 | 0.235–28.1 | |
| Researchers | NSE | KGE | PBIAS | MAE | R2 |
|---|---|---|---|---|---|
| Wu and Wang [15] with Sf | 0.9937 | 0.976 | −1.06 | 0.2691 | 0.9942 |
| Wu and Wang [15] without Sf | 0.9931 | 0.9616 | −1.463 | 0.4107 | 0.9948 |
| Camenen [16] without Sf | 0.9936 | 0.9733 | −2.3895 | 0.4376 | 0.9944 |
| Jimenez and Madsen [8] without Sf | 0.9929 | 0.9512 | 2.6308 | 0.4164 | 0.9952 |
| Cheng [7] without Sf | 0.9924 | 0.96 | 3.8275 | 0.4342 | 0.9941 |
| Zhang [9] without Sf | 0.9925 | 0.964 | −1.7206 | 0.4835 | 0.9937 |
| Zanke [3] without Sf | 0.9847 | 0.9143 | −2.4174 | 0.7276 | 0.9914 |
| Soulsby [12] without Sf | 0.9861 | 0.9241 | −4.5574 | 0.7057 | 0.9915 |
| Rijn [5] without Sf | 0.9824 | 0.8998 | −9.1874 | 0.7705 | 0.9933 |
| Camenen [16] with Sf | 0.9581 | 0.8958 | 3.4168 | 0.5018 | 0.9661 |
| Julien [10] without Sf | 0.9714 | 0.8582 | 1.0309 | 0.9229 | 0.9901 |
| Jimenez and Madsen [8] with Sf | 0.9234 | 0.8648 | −6.1132 | 0.8406 | 0.9354 |
| Ruby [2] without Sf | 0.9069 | 0.7104 | 12.4768 | 1.3657 | 0.989 |
| Zhu and Cheng [6] without Sf | 0.8707 | 0.7057 | −28.4017 | 2.1954 | 0.9599 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Shankar, M.S.; Pandey, M.; Shukla, A.K. Analysis of Existing Equations for Calculating the Settling Velocity. Water 2021, 13, 1987. https://doi.org/10.3390/w13141987
Shankar MS, Pandey M, Shukla AK. Analysis of Existing Equations for Calculating the Settling Velocity. Water. 2021; 13(14):1987. https://doi.org/10.3390/w13141987
Chicago/Turabian StyleShankar, M. Shiva, Manish Pandey, and Anoop Kumar Shukla. 2021. "Analysis of Existing Equations for Calculating the Settling Velocity" Water 13, no. 14: 1987. https://doi.org/10.3390/w13141987








