Abstract
New technologies for water pressurized systems try to implement the introduction of strategies for the improvement of the sustainable indicators. One of these technologies is the implementation of pumps working as turbines. The use of these recovery machines was proposed some years ago, and the interest in this technology has increased over the last years. The simulation of these machines is necessary when analyzing pressurized water systems, or when optimization procedures are proposed for their management, great care must be taken. In these cases, the knowledge of the operation curves is crucial to reach accurate results. This study proposes different regression expressions to define three operational curves when the machines operate under variable rotational speed. These curves are the best efficiency head, the best power-head and the best power flow. The here proposed methods were compared with other five published methods. The comparison shows the proposed method was the best when it is compared with the rest of the published procedures, reducing the error values between 8 and 20%.
1. Introduction
The use of micro-hydropower systems is key to improve the energy efficiency in water pressurized systems. The accuracy of the energy analyses is also very important in the complete analysis of these energy improvements [1]. Pump working as turbines (PATs) are hydraulic machines, which are commonly recommended to be used as recovery machines in water pressurized systems [2]. These favorable aspects were defined by different published researches in which the feasibility, simple operation, availability in the market and great range of applications are some of the most important characteristics of these systems, when they are compared with classical machines such as Francis or Pelton turbine. However, the use of these recovery machines has the main disadvantage joined to low efficiency compared to classical machines [3]. The knowledge of their characteristic curves (i.e., head, efficiency and power) is difficult to know in advance if water managers look in the manufacturer catalogue.
The lack of this information has been a challenge, in which researchers tried to fill this shortage by proposing empirical expressions [4]. These functions are based on the development of the experimental tests. These helped to understand better the operating of these machines when these recovery systems operate as turbine [5]. The need to establish these equations are focused on two main aspects: (i) the knowledge of the best operation point of the machine (BEP) when it operates as turbine and the water manager only knows the characteristic curves in pump mode; and (ii) the need to regulate the rotational speed of the machine to maximize the recovered energy of the system when variable operation strategy is applied.
The first challenge was studied by different researchers. Ref. [6] established a common empirical equation to estimate the best efficiency point of the machine when it operates as a turbine from a pump. These expressions and the empirical equations proposed by [7] are the most used last years. However, other published researches focused on their effort to improve these expressions. Ref. [8] proposed computational fluid dynamics analysis to characterize and improve the accuracy of these methods, which tried to predict the operational point. Different methods were reviewed by [9], who proposed empirical expressions using the greater database, particularly 181 different PATs. The proposed expressions estimated the BEP operation as a turbine with errors lower than the rest of the methods reviewed by [3]. In this line, Ref. [10] defined regression expression to estimate the curve of head and efficiency when the rotational speed changes by modification of the affinity laws, improving the results obtained in others researches [11].
The use of these empirical equations focuses on improving the simulation of PAT systems operating under variable rotational speed. Ref. [2] showed the need to know these curves in the energy estimation strategies in the water systems. The analysis of the hydropower potential contributes to incorporate sustainable measurements in which the water-energy nexus acquires relevance in the water management of the systems [12]. When micro-hydropower systems are analyzed, the effectiveness increases when the variable operation strategy (VOS) is applied [13]. Therefore, the improvement in the estimation of the operational curves makes sense to search for the best strategy to maximize the recovered energy by the recovery system [14].
The knowledge of expressions, which allow water managers to use with software and optimization procedure will improve the decision making in the water systems [15]. The future strategies should be focused on improving sustainability as well as the alignment of the operation indicators with the sustainable development goals [16]. The research is focused on the development of regression expressions. These equations define the generated power as a function of the flow under variable rotational speed. These curves are: (i) the best efficiency head, proposed by [17] and (ii) the best power curve proposed in this research, which is key in the maximization of energy. Besides, the research compiles the great database used by researchers to analyze the PATs systems operating under variable rotational speed. This research considers 15 different machines, which were tested on 87 different rotational speeds. The proposed regression equations, which are based on non-dimensional parameters is validated by the error analysis compared to other published methods, obtaining better approaches.
2. Material and Methods
2.1. Hydraulic Mathematical Development
The modification of the affinity laws is recommendable when the characteristic curves must be estimated by water managers, n accordance with the aforementioned references. The characteristics curves are head curve (HC), efficiency curve (EC) and power curve (PC). These curves are defined by the following expression:
where is the recovered head in nominal rotational speed in m w.c. (water column); is the flow rate in m3/s; is the efficiency of the machine; is the generated power in kW. The rest of the coefficients (A, B, C, ,,, , , , ,, and ) are the coefficients, which define the HC, EC and PC of the pump working as the turbine.
The variation of the rotational speed is defined by affinity laws when classical concepts are considered. The definition of the affinity laws is based on the analysis of the congruence parabola (), which was defined and applied by [18]. This parabola is defined by the following expression:
Considering an operation point (), when the congruence parabola concept is applied, the affinity laws are defined by the following expressions [18]:
where is the new rotational speed in rpm, is the nominal rotational speed in rpm; is the circulating flow when the rotational speed is ; is the recovered head when the machine operates for a flow equal to in m w.c.; is the new efficiency of the machine when it operates in .
Different published researches established the need to modify these affinity laws to better address the estimation of the characteristics curves of the machine. These affinity laws can be defined using dimensionless numbers of the machines (q, h, e and p) [19], which enable the establishment of the operation function for determining any rotational speed.
where are operation functions for different rotational speed (α), is any flow value of PAT in m3/s. This value is inside of the VOS; is the recovered head for this flow in m w.c. when the machine operates at the ratio of rotational speed equal to ; is the efficiency for values of , and is the shaft power in this operation point in kW; , , and are referred to any point of the characteristic curve of the machine when it is operating at nominal rotational speed (i.e., α = 1).
The curves for any rotational speed inside of the VOS were defined by [10], who established the following expressions:
This relationship between q and Q is linear and it is determined by the slope m. The m value will adopt a constant value according to the curve analyzed (best efficiency head, BEH; best power head, BPH or best power flow, BPF) [19,20]. Any value of has an associated line, which has a slope equal to m (Figure 1a).
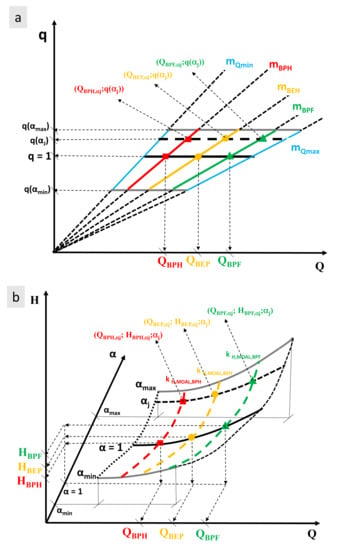
Figure 1.
(a) m coefficient; (b) VOS zone.
The m value remains constant either in affinity laws or modified affinity laws, changing the q expression. When the VOS is defined by affinity laws, q is equal to . If the modified affinity laws (MOAL) are used, q is a function both and [10]. The m value is defined by the following expression:
The m parameter enables to simplify the development of expressions, which are used to develop the expression when a machine operates under variable rotational speed.
The variation of the rotational speed inside of the VOS is defined by the previously cited congruence parabola (CP). This CP enables to define the change the rotational speed. Besides, when these CPs are used, they help to define the analytical curves of the characteristic curves (head, efficiency and power) both the application of the affinity laws and modified affinity laws (Figure 1b). These new curves were called the modified affinity laws (MOAL) [20,21,22]. When coefficients of the congruence parabola () are operated comparing between affinity laws (AL) and modified affinity laws, the following expressions are obtained. The modification of these expressions is defined in Table 1.

Table 1.
Definition of the curves as a function of parameter.
Each congruence parabola has one m parameter, which is associated to an value. The m parameter enables the estimation of the curves H-Q, -Q and P-Q, directly. This m is the unknown value, and it should be solved for the different operational curves inside of the VOS zone. Once, m or are known, the estimation of the characteristic curves is possible and therefore, the definition of the following curves is feasible.
Best efficiency head (BEH), defined by [18], this curve is the line, which establishes the value in which the efficiency is maximum for a defined flow. The analysis of this equation is defined in the following:
Considering Equations (2), (5) and (9):
As the relationship between and Q is , considering Equations (16) and (17), the expression enables to calculate the m parameter is:
Best power head (BPH), this curve is the line, which establishes the value in which the power is maximum for a defined flow [20,21]. The analysis of this equation is defined in the following
Considering Equations (1), (2), (5) and (9):
As the relationship between and Q is , considering Equations (16) and (17), the expression enables to calculate the m parameter is:
Best power flow (BPF), this curve is the line, which establishes the value in which the power is maximum for a defined. The analysis of this equation is defined in the following
Considering Equations (1), (2), (5) and (9):
As the relationship between and Q is , considering Equations (16) and (17), the expression enables to calculate the m parameter is:
Once, the three curves (BEH, BPH and BPF) are known, the knowledge of the m parameter is demonstrated it can be solved by a polynomial equation, which has the next typology:
Table 2 summarizes the value of the different coefficients for BEH, BPH and BPF as a function of the characteristic curve when they operate in nominal conditions. The introduction of the ‘m’ parameter simplifies the analysis of the mathematical expressions that allow to study of the behaviour of the machines along the VOS zone, facilitating the analysis in situations different from the nominal regime.

Table 2.
Coefficients for the knowledge of the m parameters.
2.2. Methodology
The proposed methodology is based on ten different steps (Figure 2). This figure contains two different phases. The first phase analyses the experimental database from Steps A to D. The second phase considers the analytical procedure to define the best equation to establish the operation curves of the machine from Steps E to J.
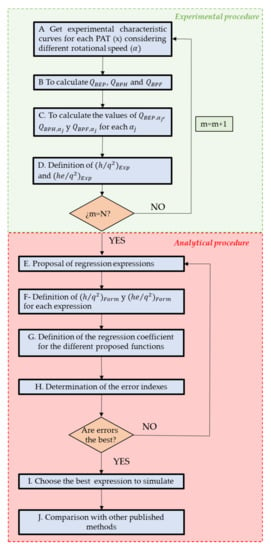
Figure 2.
The methodology proposed to reach the expressions.
Step A. Using the different experimental database, the characteristic curves are obtained for each machine as well as considering different rotational speeds.
Step B. When the curves are known, the procedure determines the flow for the different curves when the machine operates on nominal rotational speed. The flow values are: (i) best efficiency head (, (ii) best power head (), and (iii) best power flow ().
Step C. Defined the three flow values in step B, the procedure defines these flow values for the different values of the rotational speed (), which were tested experimentally. Therefore, , and are determined.
Step D. The non-dimensional parameters, and , are defined using the experimental database for different values of the rotational speed.
Step E. It is the first step of the second phase, where the best regression expression will be defined. In this step, different functions are proposed and analysed using the database. Table 3 shows the regression expression, which is used in the procedure.

Table 3.
Proposed functions to be analysed.
Step F. Once the proposed regression expression is defined in the previous step, the values of and are estimated for each , defining the error indexes, which enable to choose of the best regression expression to define the proposed functions (BEH, BPH and BPF).
Step G. Definition of the regression expression for and .
Step H. The error indexes were estimated for each function when the dimensionless parameters (and ) were applied to BEH, BPH and BPF. The error indexes are defined in Table 4.

Table 4.
Error indexes used in the analysis.
Step I. The function, which minimizes the errors is defined to establish the BEH, BPH and BPF.
Step J. The chosen function is compared with other published methods, comparing the error indexes, which were defined in Step H to show the accuracy between this study, other published methods and experimental tests when BEH, BPH and BPQ are defined both analytical and experimental.
2.3. Materials
The analytical development described here was applied to different machines, which were tested in different published experimental tests. In this case, the used machines were fifteen PATs, which have a specific speed between 5.67 and 50.71 rpm (m, kW). The nominal rotational speed was between 800 and 3000 rpm. The non-dimensional curves of the machines are shown in Figure 3. The number of experimental curves (RS) was 87. These curves were tested for different rotational speed. The use of the experimental data enabled to interpolation of more than 10,000 parabolas. All curves were used to define the regression expressions except ID11, which was used to compare the empirical equations with the experimental data.
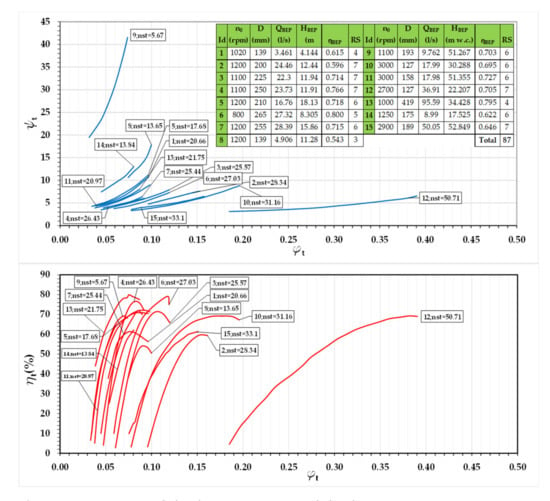
Figure 3.
Experimental database. Experimental database. ID1 [23]; ID2-ID4 [24]; ID5-ID7 [21]; ID8 [25]; ID9 [26]; ID10-ID12 [27]; ID13 [28]; ID14 [2]; ID15 [3].
3. Results
3.1. Definition of the Regression Expression to Define
The regression expressions propose for and are shown in Table 5. It shows the different values of the for each function . These ten functions are used to estimate the BEH, BPH and BPF curves using the and the dimensionless coefficient for each machine. The estimation considered all experimental rotational speed of the PATs, considering their characteristic curves.

Table 5.
Proposed expression for the dimensionless numbers.
When these curves are defined, the error indexes were calculated comparing them with each experimental value and calculating the mean value (Table 6 and Table 7). Table 6 shows the average error indexes when the non-dimensional parameter, , was calculated for the different 10 proposed functions. When the BEH curve is analysed, the function which showed the minimum average error was . RMSE, MAD and MRD were 0.1035, 0.0735 and 0.0628, respectively. However, the second function was , which the error difference was 2.4% and 4.7% for RMSE and MAD respectively, while the MRD was better for , reducing a −0.94% compared to .

Table 6.
Average error indexes for applied.

Table 7.
Average error indexes for .
When BPH are analyzed, the best fitting function was . When considering BPF, was the expression with less error but the is near such as BEH case. However, considering the analysis developed by [10], was chosen to define the characteristic curve of the machine when other methods were compared to define the BEH, BPH and BPF. This comparison will show in Section 3.2. Therefore, when the head curve is defined the function will be the following expression:
Besides, includes both ratio of the rotational speed ( and the ratio between Q/QBEP. The ‘’ parameter also did other formulations in the published literature. Besides, this study adds another parameter, Q/QBEP. It considers the distance to the working zone of the maximum efficiencies).
Table 7 shows the average errors for RMSE, MAD, MRD and BIAS when the non−dimensional value of he/q2 is calculated. In this case, was the expression, in which the errors were low when BEH and BPH are observed. In all cases, BIAS values were low, and this index was between 0 and . These values are no significant because they show average errors, which are less than 3% when the head curve and power curve are estimated.
To develop the comparison of methods, was chosen to define the power curve of the machine, according to the expression shown in Table 1. The following expression enables estimating the power when the head curve and efficiency curve are known in nominal conditions.
3.2. Comparison of the Proposal Study vs. Other Published Methods Applied to BEH, BPH and BPF
The proposed methodology was compared with five different published methods. These were: (i) classical affinity laws [18]; (ii) Carravetta et al. [22]; (iii) Fecarotta et al. [20]; (iv) Pérez−Sánchez et al. [17]; and (v) Tahani et al. [11].
The last cited methods were operated to get the best efficiency head, best power head and best power flow. The BEH, BPH and BPF for each method were compared with the experimental database for each machine. In all cases, when the average error indexes were calculated, the proposal of non−dimensional parameters (i.e., h/q2 and he/q2) showed the minor error values of BEH, BPH and BPF.
Figure 4a,b shows error indexes classified in the different methods. When the non−dimensional parameter, (he/q2), is observed similar results were obtained. The proposed functions were the best compared to the other five methods. RMSE, MAD and MRD were 0.067, 0.051 and 0.054, respectively. When these error indexes were compared with the second-best value (affinity laws or Carravetta’s method), the error values decreased between 26.5, 28.8 and 25.4%. For BPH, the trend of the results was similar. The proposed method was the most accurate, decreasing the errors between 25 and 32% compared with the second-best-option functions (Carravetta’s). When BPF was analyzed, RMSE, MAD and MRD decreased 14.3, 12.4 and 13.4%, respectively. The use of MOALs demonstrated better accuracy in the operational curves when these results are compared with the affinity laws, which are simpler, but they showed higher errors [11,17,19,22]. Figure 4 shows the decrease of the error in the different curves. Therefore, although the expressions use high degree equations, they improve the simulation of the PATs when they operate under variable rotational speeds.
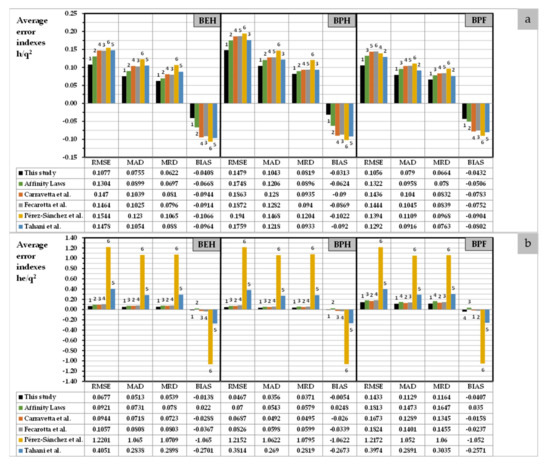
Figure 4.
(a) Error indexes for the different methods applied to h/q2; (b) error indexes for the different methods applied to he/q2.
If h/q2 (Figure 4a) is considered for BEH, the RMSE, MAD and MRS errors were 0.1077, 0.0755 and 0.622, respectively. These errors decreased between 17.4, 16 and 0.7% respectively, compared to the second-best method (affinity laws). If the BPH is analyzed similar results were obtained. The proposed functions were the best and the error indexes were reduced between 9 and 16% compared to the second−best method. When the error indexes were calculated for the BPF, the proposed study was the best, and the error values decreased 20.1, 17.5 and 14.9% for RMSE, MAD and MRD respectively.
When h/q2 is analysed in Figure 4a, the proposed regression expression showed errors between 8.6% and 49.8% less than the obtained errors by application of the affinity laws, which was the second−best method for BEH and BPH, being the third when BPF was calculated. RMSE value was 0.1 for BEH and BPF, while it was 0.148 when BPH was estimated. If the MAD and MRD were analysed in this table, these values were around 0.07 and 0.06 respectively when BEH was compared. If BPH is compared, the MAD and MRD errors 0.1 and 0.08 respectively when they were 0.12 and 0.09 when the second−best method (affinity laws) is compared.
A similar analysis can be developed by looking at Figure 4b. The proposed expression regressions were the best when BEH, BPH and BPF were defined using all previous cited methods and the errors calculated. If BEH is analyzed, the proposed expressions in this research reduced the error indexes (RMSE, MAD and MRD) by around 30% compared to Affinity laws and Carravetta’s method, which were the second and third best methods for this BEH curve. In this curve, the BIAS was near −1%. If BPH is analyzed, a similar analysis was done. The error indexes reduced between 33 and 36% the error of the second−best method, while the BIAS value was 0.5% for BPH. Finally, if BPF is observed, the proposed expressions decreased the error indexes. Particularly, RMSE, MAD and MRD decreased 21, 23 and 30% respectively between the proposed method and Carravetta’s method.
If BPF is analyzed, RMSE error was 0.14. It decreased by 14% compared to the second−best method (Carravetta´s method). MAD and MRD got similar values, which were reduced by 12.4 and 14.1%, respectively.
Both parameters, h/q2 and he/q2 showed the proposed regression using F6 enabled to estimate the best efficiency head, best power head and best power flow. Three lines are strategic considerations when water managers define operations rules to maximize the energy recovery using micro hydropower systems.
3.3. Application of the Proposed Curves to Experimental Machine
The proposed empirical regressions were applied to a tested experimental machine to show the accuracy of the expressions applied in real case studies. In this case, the tested machine was NK−140 125/127 [28], being a specific speed in turbine mode of 31.16 rpm (m, kW). Its BEP operating as the turbine was 17.99 l/s, 30.31 m w.c. with an efficiency of 0.695. The machine was tested on six different rotational speed, being 3000 rpm its nominal rotational speed. Figure 5a shows the head as a function of the flow of the BEH. The m value for this machine is 0.056. If this curve is analyzed, Figure 5b shows the curve, which defines the power as a function of the flow. Both figures show good accuracy when making visual comparison. When the error was measured, RMSE and MRD were 0.077 and 0.059 respectively, being BIAS equal to 0.0585. If the head curve is analyzed using the proposed expressions in NK−140 125/127, the average error values of RMSE and MRD were 0.2195 and 0.0096, respectively. The error values decreased around 65.6% in both errors when they were compared to affinity laws. When the power curve is analyzed, RMSE and MRD were 0.0123 and 0.005 respectively. These errors decreased and MRD errors decreased around 82.6% compared to affinity laws. The expressions indicate the good fit for the whole range of nst when Figure 4 and Figure 5 are considered and the errors are evaluated.
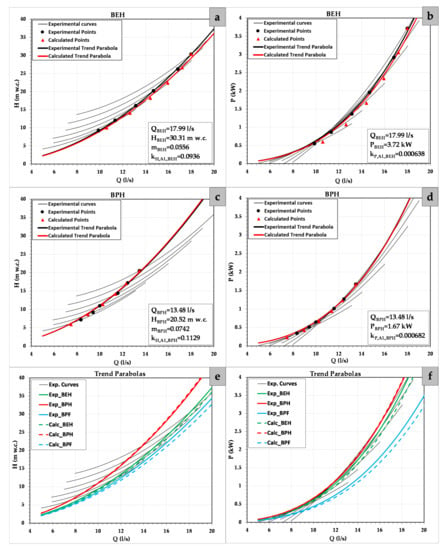
Figure 5.
(a) H−Q for BEH; (b) P−Q for BEH; (c) H−Q for BPH; (d) P−Q for BPH; (e) H−Q for BEH, BPH and BPF; (f) P−Q for BEH, BPH and BPF.
Figure 5c shows the operation curve (H−Q), representing the best power head. This is the most important curve since the operation based on this curve is the best to maximize the recovered energy, when variable operation strategy is applied in a water pressurized systems. Comparison of the power curve between the estimated and experimental BPH values (Figure 5d) also shows a good fit.
Figure 5e,f show the difference between trend parabolas and tested curves when BEH, BPH and BPF were considered both the curves (i.e., head and power curve). These three curves (i.e., BEH, BPH and BPF) are the curves, which should be considered when regulation strategies want to be considered to maximize the recovered energy.
4. Conclusions
The present research proposed a new modification of the affinity laws (MOAL) when applied to pumps working as turbines. These new expressions were compared to the rest of the published methods and affinity laws, showing the best results in the estimation of the best efficiency head, best power head and best power flow. Analyses of these curves in other published researches showed that they are key in the operation of the recovery systems to maximize recovered energy. Therefore, the modified affinity laws proposed in this study were found to decrease the error indexes by 8 to 30% compared with existing methods, and can help water system managers to improve the accuracy of energy predictions.
The analysis of the different tested curves as well as the consideration of the analytical expressions showed the importance of the value. This value should be considered when the machine is chosen, and it is always greater than . Therefore, the PATs system could operate under the best power head conditions when the constrain ‘’ is satisfied.
Incorporating these curves (i.e., BEH, BPH and BPF) when the potential recovery is analyzed by water managers is crucial to get the best results, when the BPH achieves the best results in terms of recovered energy. However, the analysis of BEH and/or BPF is recommended because it can be useful when the recovered energy is not the main goal to be achieved and other factors such as valves regulation or sustainable measures are considered.
These MOAL were validated when the specific speeds of the PATs systems were between 5 and 50 rpm using 15 different machines and 87 different rotational speed. The analysis showed the need to increase the tests applied on axial machines to increase the operating range by the research community. Future researches should focus on developing axial machines analyses. These machines are significant in the water pressurized systems because there are many potential recovery points in which the flow is high, but the recoverable head is low, and therefore, the recovery systems should be established by axial machines.
Author Contributions
Conceptualization, P.A.L.-J. and M.P.-S.; methodology, C.A.M.Á. and F.-J.S.-R.; software, writing—original draft preparation, C.A.M.Á. and M.P.-S.; writing—review and editing, M.P.-S. and P.A.L.-J.; visualization M.P.-S.; supervision, P.A.L.-J. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
Not applicable.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Da Silveira, A.P.P.; Mata-Lima, H. Energy audit in water supply systems: A proposal of integrated approach towards energy efficiency. Water Policy 2020, 22, 1126–1141. [Google Scholar] [CrossRef]
- Postacchini, M.; Darvini, G.; Finizio, F.; Pelagalli, L.; Soldini, L.; Di Giuseppe, E. Hydropower generation through pump as turbine: Experimental study and potential application to small-scale WDN. Water 2020, 12, 958. [Google Scholar] [CrossRef] [Green Version]
- Pugliese, F.; De Paola, F.; Fontana, N.; Giugni, M.; Marini, G. Experimental characterization of two Pumps As Turbines for hydropower generation. Renew. Energy 2016, 99, 180–187. [Google Scholar] [CrossRef]
- Kim, J.W.; Suh, J.W.; Choi, Y.S.; Lee, K.Y.; Kim, J.H.; Kanemoto, T.; Kim, J.H. Simultaneous efficiency improvement of pump and turbine modes for a counter-rotating type pump-turbine. Adv. Mech. Eng. 2016, 8, 1–14. [Google Scholar] [CrossRef] [Green Version]
- Binama, M.; Su, W.T.; Li, X.B.; Li, F.C.; Wei, X.Z.; An, S. Investigation on pump as turbine (PAT) technical aspects for micro hydropower schemes: A state-of-the-art review. Renew. Sustain. Energy Rev. 2017, 79, 148–179. [Google Scholar] [CrossRef]
- Ortiz Flórez, R.; Abella Jiménez, J. Máquinas Hidráulicas Reversibles Aplicadas a Micro Centrales Hidroeléctricas. IEEE Lat. Am. Trans. 2008, 6, 170–175. [Google Scholar]
- Sharma, K. Small Hydroelectric Project-Use of Centrifugal Pumps as Turbines; Kirloskar: Bangalore, India, 1985. [Google Scholar]
- Derakhshan, S.; Nourbakhsh, A. Experimental study of characteristic curves of centrifugal pumps working as turbines in different specific speeds. Exp. Therm. Fluid Sci. 2008, 32, 800–807. [Google Scholar] [CrossRef]
- Pérez-Sánchez, M.; Sánchez-Romero, F.J.; Ramos, H.M.; López-Jiménez, P.A. Improved Planning of Energy Recovery in Water Systems Using a New Analytic Approach to PAT Performance Curves. Water 2020, 12, 468. [Google Scholar] [CrossRef] [Green Version]
- Plua, F.A.; Sánchez-Romero, F.J.; Hidalgo, V.; López-Jiménez, P.A.; Pérez-Sánchez, M. New expressions to apply the variation operation strategy in engineering tools using pumps working as turbines. Mathematics 2021, 9, 860. [Google Scholar] [CrossRef]
- Tahani, M.; Kandi, A.; Moghimi, M.; Houreh, S.D. Rotational speed variation assessment of centrifugal pump-as-turbine as an energy utilization device under water distribution network condition. Energy 2020, 213, 118502. [Google Scholar] [CrossRef]
- Chen, S.; Chen, B. Urban energy–water nexus: A network perspective. Appl. Energy 2016, 184, 905–914. [Google Scholar] [CrossRef]
- Carravetta, A.; Del Giudice, G.; Fecarotta, O.; Ramos, H. Pump as Turbine (PAT) Design in Water Distribution Network by System Effectiveness. Water 2013, 5, 1211–1225. [Google Scholar] [CrossRef] [Green Version]
- Ebrahimi, S.; Riasi, A.; Kandi, A. Selection optimization of variable speed pump as turbine (PAT) for energy recovery and pressure management. Energy Convers. Manag. 2021, 227, 113586. [Google Scholar] [CrossRef]
- Man, Y.; Han, Y.; Liu, Y.; Lin, R.; Ren, J. Multi-criteria decision making for sustainability assessment of boxboard production: A life cycle perspective considering water consumption, energy consumption, GHG emissions, and internal costs. J. Environ. Manag. 2020, 255, 109860. [Google Scholar] [CrossRef]
- Niet, T.; Arianpoo, N.; Kuling, K.; Wright, A.S. Embedding the United Nations sustainable development goals into energy systems analysis: Expanding the food–energy–water nexus. Energy Sustain. Soc. 2021, 11, 1–12. [Google Scholar] [CrossRef]
- Pérez-Sánchez, M.; López-Jiménez, P.A.; Ramos, H.M. Modified Affinity Laws in Hydraulic Machines towards the Best Efficiency Line. Water Resour. Manag. 2018, 32, 829–844. [Google Scholar] [CrossRef] [Green Version]
- Mataix, C. Turbomáquinas Hidráulicas; Universidad Pontificia Comillas: Madrid, Spain, 2009; ISBN 978-84-8468-252-3. [Google Scholar]
- Fecarotta, O.; Carravetta, A.; Ramos, H.M.; Martino, R. An improved affinity model to enhance variable operating strategy for pumps used as turbines. J. Hydraul. Res. 2016, 54, 332–341. [Google Scholar] [CrossRef]
- Hyypiä, J. Hydraulic energy recovery by replacing a control valve with a centrifugal pump used as a turbine. Ph.D. Thesis, Lappeenranta University of Technology, Lappeenranta, Finland, 2016. [Google Scholar]
- Nygren, L. Hydraulic Energy Harvesting with Variable-Speed-Driven Centrifugal Pump as Turbine. Master’s Thesis, Lappeenranta University of Technology, Lappeenranta, Finland, 2017. [Google Scholar]
- Carravetta, A.; Conte, M.C.; Fecarotta, O.; Ramos, H.M. Evaluation of PAT performances by modified affinity law. Procedia Eng. 2014, 89, 581–587. [Google Scholar] [CrossRef] [Green Version]
- KSB. “PATs Curves,” Catalogue. 2019. Available online: https://www.ksb.com/es-es/productos/catalogo-de-productos (accessed on 5 July 2021).
- Jain, S.V.; Swarnkar, A.; Motwani, K.H.; Patel, R.N. Effects of impeller diameter and rotational speed on performance of pump running in turbine mode. Energy Convers. Manag. 2015, 89, 808–824. [Google Scholar] [CrossRef]
- Abazariyan, S.; Rafee, R.; Derakhshan, S. Experimental study of viscosity effects on a pump as turbine performance. Renew. Energy 2018, 127, 539–547. [Google Scholar] [CrossRef]
- Kramer, M.; Terheiden, K.; Wieprecht, S. Pumps as turbines for efficient energy recovery in water supply networks. Renew. Energy 2018, 122, 17–25. [Google Scholar] [CrossRef] [Green Version]
- Delgado, J.; Ferreira, J.P.; Covas, D.I.C.; Avellan, F. Variable speed operation of centrifugal pumps running as turbines. Experimental investigation. Renew. Energy 2019, 142, 437–450. [Google Scholar] [CrossRef]
- Stefanizzi, M.; Torresi, M.; Fortunato, B.; Camporeale, S.M. Experimental investigation and performance prediction modeling of a single stage centrifugal pump operating as turbine. Energy Procedia 2017, 126, 589–596. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).