Abstract
While hydropower in California is one the main sources of renewable energy, population growth has continuously increased demand for energy. In addition, recent droughts reduced the amount of available water behind the hydropower dams to provide the water head needed to run the turbines in hydropower plants. A more sustainable alternative, instead of developing new infrastructure, is to enhance the daily operation of reservoirs to support hydropower generation. This study suggests a new optimal operation policy for Folsom Reservoir in California and hydropower plants, which maximizes hydropower generation and reduces flood risk. This study demonstrates the application of the cellular automata (CeA) approach to optimize the daily hydropower operation of Folsom Reservoir. The reservoir operation is a nonlinear problem, where the hydropower generation and elevation-area-storage functions are the main nonlinearity to accurately represent the daily operation of the system. Moreover, the performance of the CeA approach under two extreme climate conditions, wet and dry, was evaluated and compared to the operation during normal conditions. Results showed that the CeA approach provides more efficient solutions in comparison to the commonly used evolutionary optimization algorithms. For the size of the non-linear optimization problem designed in this study, CeA outperformed genetic algorithm for finding optimal solutions for different climate conditions. Results of CeA showed that although the annual average inflow to the reservoir during the dry period was about 30% less than the normal condition, CeA offered about a 20% reduction in average hydropower generation. The new operation policy offered by CeA can partly compensate for the loss of the snowpack in California’s Sierra Nevada under a warming climate. The approach and its outcomes support an informed decision-making process and provide practical reservoir operational guideline to remediate the adverse effects of hydroclimatic changes in the future.
1. Introduction
Hydropower is one of the renewable energy sources that supplies about 16% of total electricity generation and 85% of all renewable electricity globally [1]. However, hydroclimate variability has a profound impact on water-dependent energy production. Limited water availability associated with droughts constrain the generation of energy in reservoir hydropower plants, especially in arid and semi-arid regions. The optimal operation of hydropower plants is become increasingly important and has led to an increase in the total number of published works in this field during the past two decades e.g., [2,3,4,5,6,7]. In California, about 9% to 30% (average 15%) of electricity is generated by hydropower [8]. From this portion, about 50% of the state’s hydroelectric power is generated by flows from the Sierra Nevada Mountain Range in the eastern part of the Central Valley of California [9].
California’s developed water supply relies heavily on surface storage that depends on streamflow timing and volume, which in turn depends strongly on the timing and volume of Sierra Nevada snowmelt. The topographic gradients from mountain peaks to the valley floor have provided excellent hydropower opportunities. Due to climate warming, however, more precipitation is falling as rain, rather than snow, and the snow is melting sooner [10], leaving less reservoir storage during peak hydropower demands in summer, even if total precipitation does not decrease. These same impacts to snowpack driven water systems are also occurring elsewhere in the western United States [11,12,13]. Due to the expected occurrence of persistent and heavy rainfalls from atmospheric rivers coming off the Pacific, high peak flows must be anticipated in winter. Thus, during the winter and spring, water must be released for purposes other than hydropower generation [14]. Thus, while the losses in snowpack systems result in less water stored in the surface hydropower reservoir systems, and therefore, less energy generation, there is a need for more optimal operation of reservoirs to compensate for the losses. This requires a better understanding and representation of complex and often non-linear relationships in hydropower system operations.
Optimizing the operation of a hydropower system in a finer temporal resolution (daily and sub daily) is a complex task due to the size of the problem, high non-linearity in the objective function, non-linearity, and complexity of the constraints, trapping in local optima and the curse of dimensionality. The problem we are dealing with in this study is the multi-year daily operation of a reservoir for aa non-linear hydropower objective and non-linear constraints. Different methods have been examined to evaluate the effectiveness of re-operating or optimizing the operation of reservoirs in order to maximize the benefits, especially hydropower generation, in particular using optimization methods e.g., [15,16,17,18]. Researchers have tested classic optimization approaches such as linear programming (LP) [19,20], non-linear programming (NLP) [21,22], and dynamic programming (DP) [23,24] to solve reservoir operation problems in different forms. However, these studies also simplified objective functions and constraints in a linear model, which makes them unsuitable for optimizing hydropower generation [25]. In order to optimally operate the reservoir system though, a daily model is needed, which represents the non-linear behavior of the system to better reflect changes in the timing and magnitude of water availability in the reservoir, especially during extreme events. To continue, two main deficiencies of existing optimization models for hydropower generation are touched and a new alternative method is offered.
- Different optimization research studies [26,27] or commonly used simulation models for planners (e.g., CalSim II [28]) have employed the LP/DP and piecewise linearization methods to simplify the simulation of reservoir systems. However, linear programing often disregards the nonlinear and unsmooth representation of reservoir operation optimization problems, which leads to large errors in the optimization process [29]. One of the largest errors in these problems appears by linearization of the hydropower generation and the reservoir’s elevation–storage relationship nonlinearity [30]. Here, polynomial functions are used to express the hydropower generation equation and bathymetry (elevation-area-storage relationship) of the reservoir, rather than using the traditional piecewise linearization method.
- There are drawbacks associated with the classic optimization methods in order to solve large scale nonlinear optimization problems. In confronting the shortcomings of classical optimization methods, evolutionary algorithms (EAs) have been used to solve water resources management problems. Genetic algorithms (GAs) [3,31], particle swarm optimization (PSO) [32,33], ant colony optimization (ACO) [34,35], invasive weed optimization [36], and genetic programming (GP) [37] have been extensively used for the optimal operation of hydropower reservoirs. Different studies have investigated the application of EAs for discontinuous, non-differentiable, and non-convex problems. However, EAs are not able to converge for large problems, or often converge to a near-global optimal solution for many types of problems. These methods need extensive processing times to converge to a solution and are unable to exploit the entire decision variable space.
Therefore, to address these complexities, more advanced optimization techniques to improve the operation of hydropower systems are required [29,36] (Ming et al. 2015; Azizipour et al. 2016). An effective optimization algorithm was proposed to solve the reservoir operation problems, called cellular automata (CeA) [38]. They employed the CeA approach for optimal water supply and hydropower operation of a single reservoir system and compared the results with those obtained by GA, PSO, and ACO. The results confirm that CeA is superior to the search methods of other EAs in finding optimal solutions. One of the advantages of CeA over EAs is that CeA offers less computational effort and processing time to converge to an optimal solution. This paper explores the CeA approach to maximizing hydropower generation while improving the reservoir operations and maintaining essential services such as flood risk management. The non-linear optimization of reservoir operation is done in a daily time step by the CeA. This significantly increases the total number of decision variables, reservoir storage. Importantly, existing EA methods are unable to handle such a large number of decision variables because of the much more intense computational burden.
This paper is followed by presenting methods to operate reservoirs for hydropower generation in a fine temporal scale and non-linear and complex problems. The CeA approach is introduced as an alternative method to improve the reservoir’s operation. Section 2 presents the formulation of the optimization problem and offers more detail about the proposed CeA optimization approach. The CeA method is then applied to a case study that is later described in this paper. The Folsom Reservoir in California was selected to further investigate the application of the CeA method to optimize the hydropower generation. Section 3 explains the configuration of the Folsom Reservoir. The results of this study are shown in Section 4, where the optimization approach is tested for three different hydrologic patterns. These time periods are selected from observed wet, normal, and dry historical hydrologic records. Within each scenario, the inflow to the reservoir varies in time and volume to ensure exposure of the system to a broad range of possible hydroclimatic circumstances. Finally, Section 5 includes a summary of the research methods, results and discussion, and presents the limitations and future work.
2. Methods
Various research studies have verified the capability of the CeA approach in solving complicated reservoir operation problems over EAs [39,40]. However, in this study, the GA was only used as a benchmark for validation purposes and the intent was not to make a comprehensive comparison between methods. We emphasize that the GA is only used for validation purposes, and not for comprehensive comparison and judgment about its capability, which was beyond the scope of the current study. The first objective of the operation in this study was hydropower generation. This is considered as the main objective function for the optimization problem formulation. The second (auxiliary) objective is improving the reservoir’s operation under normal reservoir services including reducing flood risk and water supply. The auxiliary objectives were embedded into the optimization formulation as constraints to represent the normal level of the reservoir’s services.
2.1. Mathematical Formulation
Linearizing the nonlinear functions of hydropower generation, elevation–storage relationship, and maximum capacity of release from different reservoir outlets will generate large errors in the optimization of the reservoir’s operation [25,30]. The problem is considered as a single objective optimization problem in which the first goal is maximizing the hydropower generation (Equation (1)), while the latter objective is embedded to the optimization problem as constraints, flood management. The objective function of the problem is, therefore, written as
In this equation, F is the objective function of a single reservoir problem; N is the number of periods; Pt is the power generated by the hydroelectric plant at period t (MW); and Icap is the installed capacity of hydropower plant (MW). This objective function is subjected to the following constraints:
- Mass balance equation for the reservoir:where St, Qt, Rt, Lt and Spillt are storage of the reservoir, inflow to the reservoir, the released water from the reservoir, evaporation losses, and spill from reservoir, all at period t, respectively. Evaporation losses are calculated based on monthly evaporation rate in cm multiplied by the variable monthly surface area of the reservoir with respect to the simulated storage in time step t.
- Physical Constraints:where Smin is the minimum reservoir capacity based on the engineering design of the dam; is the minimum water release; and is the maximum water release from the reservoir, all in million cubic meters (MCM).
- Top of Conservation Level:The flood control purpose of the operation is considered through the satisfaction of these constraints. According to the existing rule curve, the capacity related to the top of the conservation level is taken as the maximum possible reservoir storage at period t, , and it varies with time.
- Power Equation:where g is gravity acceleration equal to 9.81 m/s2; η is the efficiency of the hydroelectric plant; Pf is the plant capacity factor (actual electrical energy output over a given period of time to the maximum possible electrical energy output over that period); and ht is the effective head of the hydropower plant in meter during time t, which is calculated aswhere Ht and TWLt are the elevation of water in the reservoir and downstream water elevation of the hydroelectric plant at period t, respectively.
- Bathymetry:The relationship between storage volume and water elevation is indicated by Equation (8). Additionally, Equation (9) represents the tailwater elevation based on downstream discharge (cms), Dt. The constant coefficients a1, a2, a3, a4, b1, b2, b3, and b4 are obtained by fitting the above equations into the available data.
2.2. Optimization Approach—Cellular Automata (CeA)
In this study, the cellular automata (CeA) based optimization approach was proposed for optimal hydropower operation and flood control of the Folsom Reservoir. The CeA is composed of a regular grid of cells. Each cell can carry one of the finite numbers of states, which is described for the system. For example, each cell can take on a value of 0 or 1. Then, the grid can be formed by joining various sets of cells that identify the dimensions of the grid cells. Neighborhood cells of a cell are those sets of cells that surround the specified cell. The initial values of cells describe the initial state of the grid cells. The new generation of solutions at the next time step can be developed by introducing fixed rules (generally, a mathematical function) that estimate the new state of each cell. The rules can be described based on the previous state of the specified cell and the states of neighborhood cells. Generally, the rules are kept the same for all the cells within a grid and do not change over time. Therefore, in order to use the concept of CeA for any optimization problem, four components of the CeA should be defined including the cell, cell state, cell neighbors, and updating rule. For this particular problem, the cells are taken as discrete points in time representing the start and the end of each period of the operation. In the CeA optimization approach, the cell state represents the decision variable of the optimization problem, which in this study was taken as the reservoir storage. The surrounding cells are considered as the neighborhood cells.
To derive the updating rule for an arbitrary cell, j, a local objective function should be defined based on the objective function of the problem, earlier defined in Equation (1). This local objective function is:
where j and k denote the cell number and iteration level, respectively. It should be mentioned that a penalty approach is used to satisfy the constraints on the local level, with a penalty parameter of α and constraint violation of CVj for an arbitrary cell j. The constraint violation of CVj is calculated as
where
Updating the rules for cell j is derived by calling for the local objective function (Equation (10)) that should be minimized with respect to the cell state, Sj, while all other cell states are kept constant. This leads to an updating rule in the form of:
where and B is a binary parameter with the value of 1 if the solution in the cell j is feasible, and 0 if otherwise. Starting with randomly generated initial values for all the cell states, for j = 1, 2, …, N, the updated values of the jth cell states were obtained by using the updating rule defined in Equation (14). Once was calculated for all cells, j = 1, 2, …, N, the states of all cells were updated at the same time. This process is continued until the convergence criterion is met. It should be noted that the constraints of minimum and maximum allowable storages, defined by Equations (3) and (5), were applied as box constraints, while the constraints over minimum and maximum releases from the reservoir were satisfied using a penalty approach. The optimization framework and the CeA approach to solve it was all coded in MATLAB and is accessible on GitHub (https://github.com/erfangoharian/ accessed on 20 February 2021).
3. Case Study: Folsom Reservoir
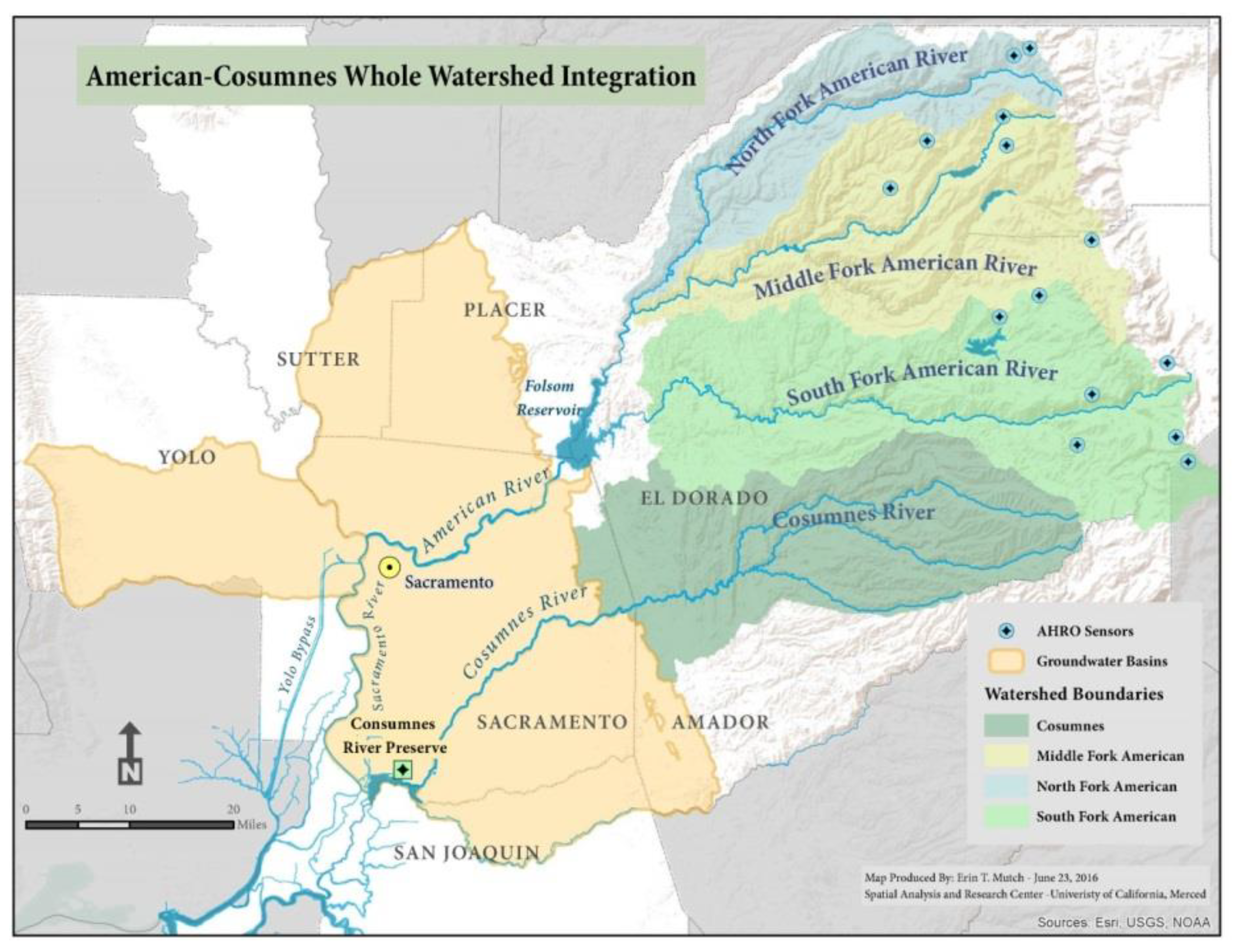
Located 40 km (25 mi) northeast of Sacramento, CA (Figure 1), the Folsom Reservoir was built by the U.S. Army Corps of Engineers (USACE) in 1956. The reservoir provides thee water supply for irrigation and municipal demand, controls flooding events, generates hydropower, and regulates downstream environmental flows. The U.S. Bureau of Reclamation (USBR) operates and maintains the reservoir as an integrated part of the Central Valley Project (CVP) [41]. The average annual inflow to the Folsom Reservoir is about 3330 million cubic meters (MCM) (2.7 million acre-feet (af)), which is the sum of flows from three tributaries of the American River (North, Central, and South forks in Figure 1). About 90% of precipitation in the American River Basin falls in an approximately 4821 km2 drainage area during the wet season (November–April) [42].
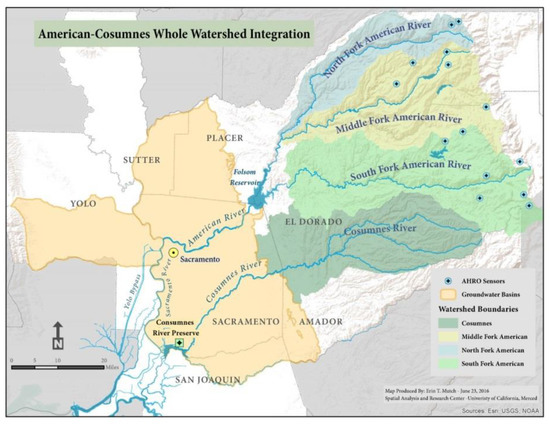
Figure 1.
Map of study area: American-Cosumnes Watershed and Folsom Reservoir.
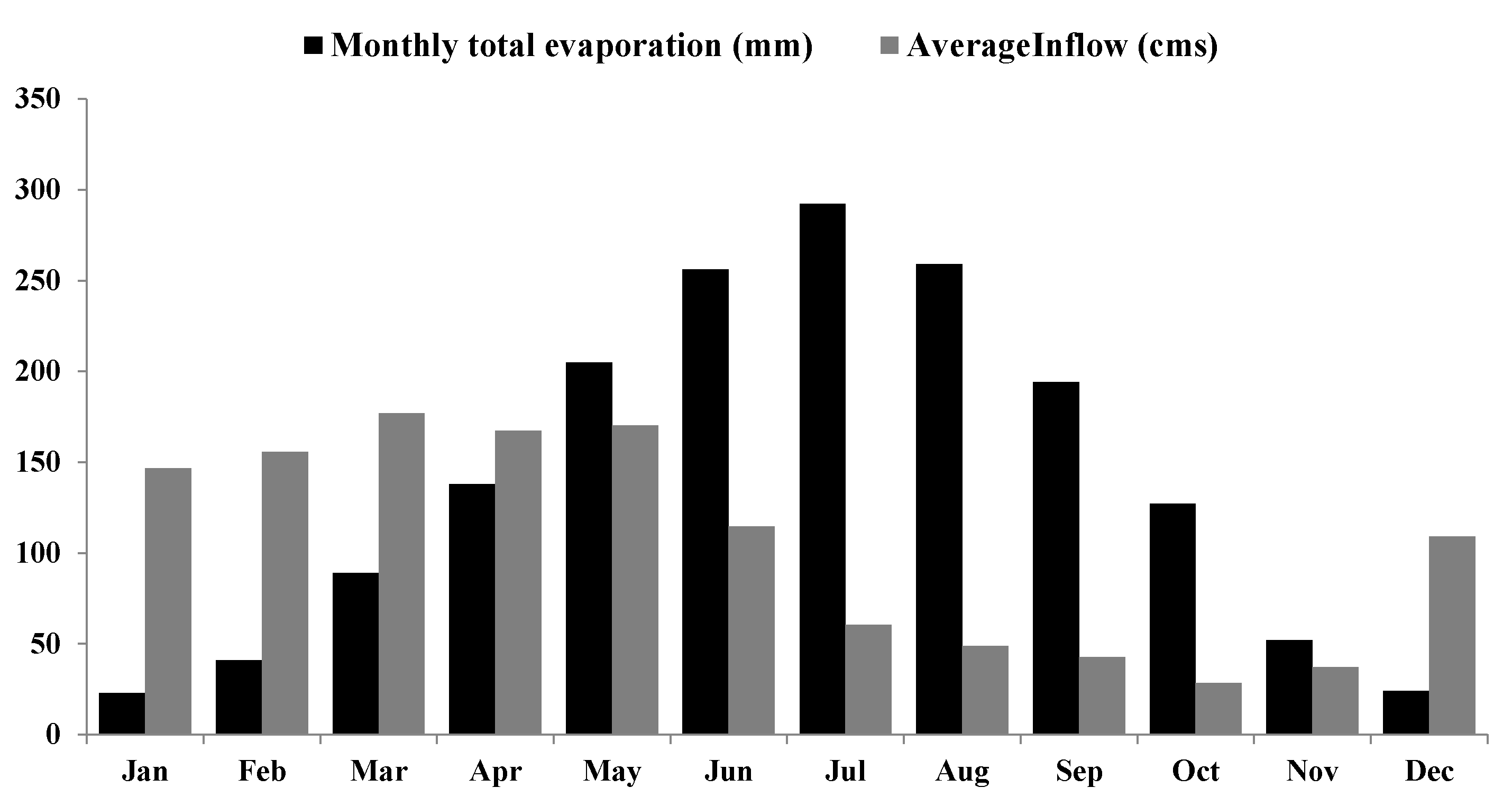
Table 1 shows the characteristics of the American River Basin. The total capacity of the reservoir is about 1205 MCM (977,000 af) at a reservoir water surface elevation of 142 m (466 ft). The reservoir’s total capacity is about one-third of the average discharge from the American River Basin. Hence, the total annual average releases from the reservoir are about 2097 MCM (1.7 million acre-feet). Figure 2 shows monthly reservoir evaporation and inflow. The dam’s spillway consists of eight tainter gates (five service gates and three emergency spillway gates) with a total capacity of 16,056 cubic meters per second (cms) (567,000 cubic feet per second (cfs)) at the 145 m (475 ft) level to prevent flooding events (Table 2).

Table 1.
Characteristics of the American River Basin.
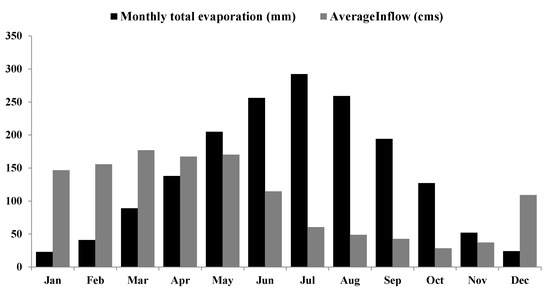
Figure 2.
Long-term monthly average of inflow to the Folsom Reservoir and evaporation.

Table 2.
Outlet structure characteristics of the Folsom Reservoir.
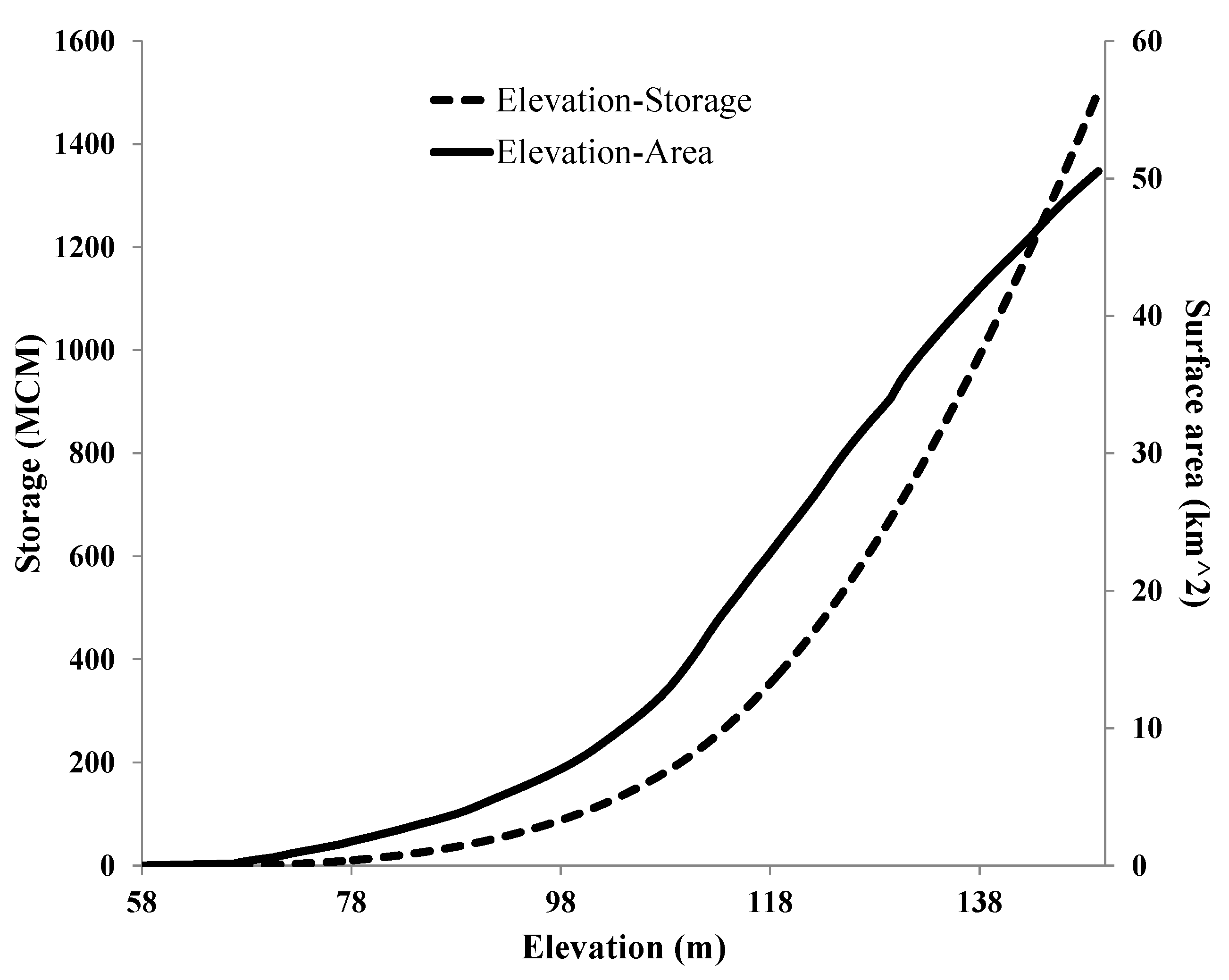
As previously mentioned, linearizing the nonlinear functions of hydropower generation, elevation–storage relationship, and maximum capacity of release from different reservoir outlets will generate large errors in the optimization of the reservoir’s operation. In this study, the bathymetry (Figure 3) and tailwater elevation were estimated using polynomial functions to better represent the operation of the reservoir system. Moreover, the hydropower generation equation is a polynomial function. Downstream of the reservoir, levees accept the flow rate up to 3256 cms (115,000 cfs). The hydropower generated from Folsom Dam (installed capacity of 198 Megawatt) supplies about 10% of the power used in Sacramento, average annual generation 691,358 MWh [41]. The system is operated by a combination of simulation/optimization models by the California Department of Water Resources (DWR) and supervised by the U.S. Bureau of Reclamation such as CalSim and HEC-ResSim (full discussion in [14]). The Folsom Dam regulates the American River flow for water supply, power, flood control, fish and wildlife, and recreation. During emergency flood events, releases from the reservoir for a short period of time (almost three days) can be increased up to 4531 cms (160,000 cfs). There are three power penstocks that transfer water from the reservoir to hydroelectric turbines for hydropower generation (Table 2). The maximum capacity of each hydropower penstock is about 241cms (8500 cfs) with a vertical drop of approximately 91 m (300 ft). The plant factor and power plant efficiency were assumed to be 25% and 85%, respectively.
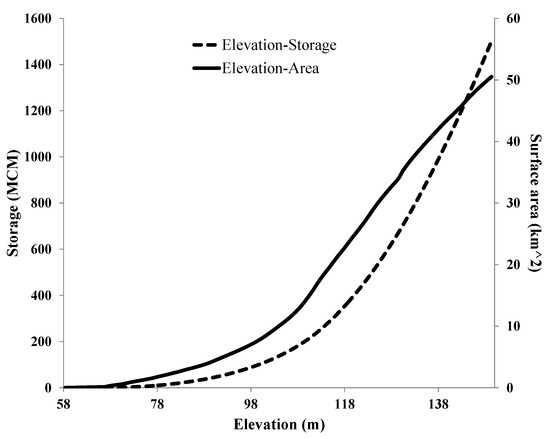
Figure 3.
Elevation–area–storage of Folsom Reservoir.
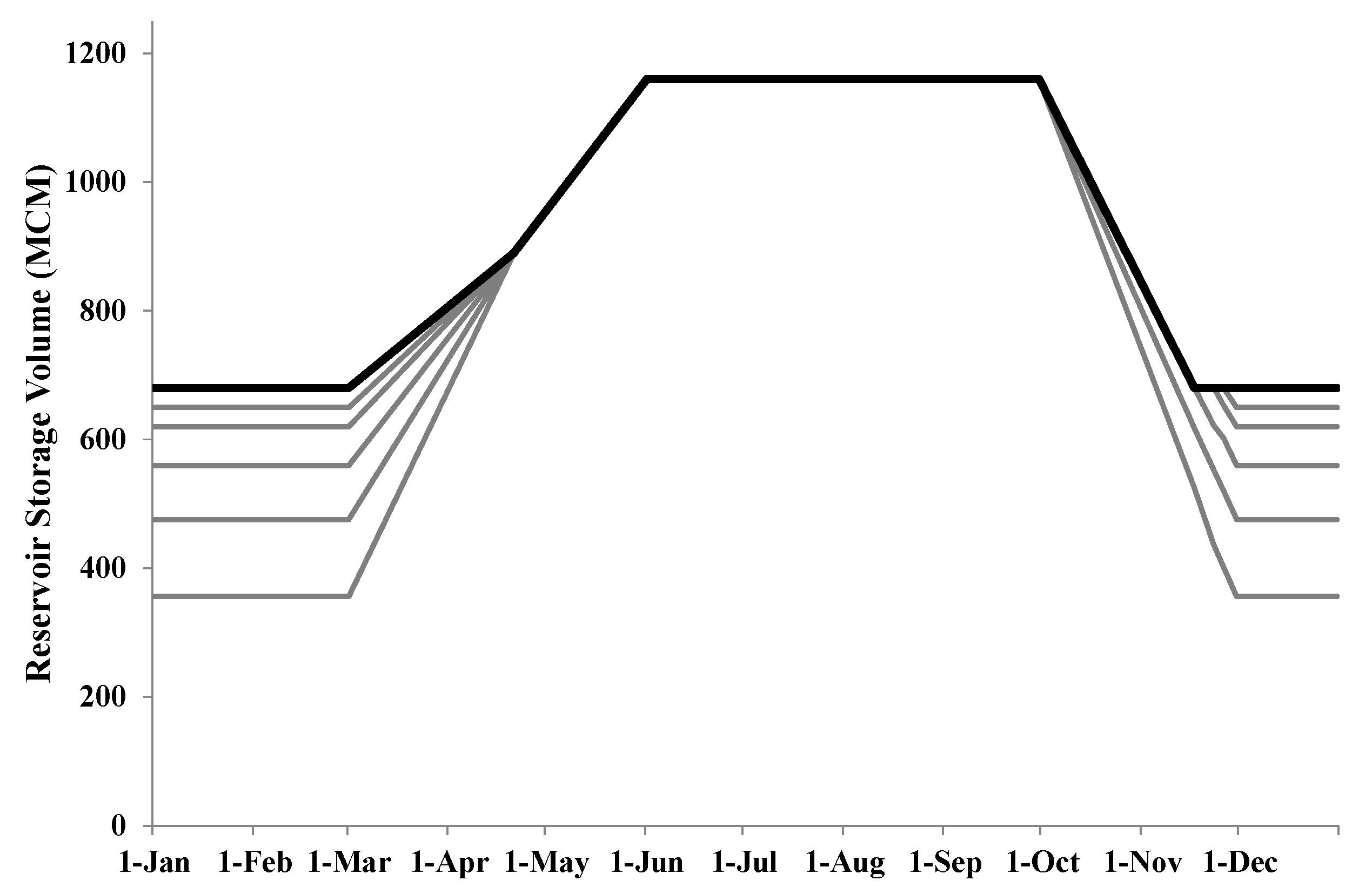
The Folsom Reservoir, as the main flood control structure in the Sacramento metropolitan area, is operated by USACE and the Sacramento Flood Control Agency (SAFCA) for the flood control at the Folsom Facility. However, the USBR tries to regulate releases from the reservoir to maximize hydropower generation by taking into account the limitations from the flood space requirements that are enforced by USACE (Figure 4). Therefore, these entities operate the reservoir more or less in a seasonal fashion. The existing rule curve for the Folsom Reservoir is presented in Figure 4. During the dry season, from the beginning of June through to the end of September, flood control constraints are not executed and there is no need for flood space in the Folsom Reservoir. During this time, USBR operates the system to supply irrigation and urban demands, generate hydropower, and meet the temperature regulations for downstream aquatic habitats. Thus, during the dry season, no space is designated for flood control. During the transition months, October 1 through to the mid/end of November, USACE starts to drawdown the reservoir to provide enough space for the winter flood events. Refilling Folsom begins early in March and continues with variable rates up to the end of May, when the reservoir reaches its maximum capacity. Therefore, during the wet season (December through to the end of February), the flood control storage should be kept at its maximum designated space. This space is variable from 493 to 839 MCM. Although the rate of drawdown and refill and total flood control capacity are variable (Figure 4), this study selected the single rule curve with the flood control space of 493 MCM (solid black line in Figure 4). This assumption was due to the lack of information regarding the available storage in the three upstream reservoirs (French Meadows, Hell Hole, and Union Valley Reservoirs). Having more information from the headwater can potentially inform the reservoir operation. For example, in case of flooding events, water can be pre-released from the reservoir earlier to provide enough space for the upcoming high peak inflow to the Folsom Reservoir. In addition, to protect downstream fishes in the lower American River, Reclamation needs to manage releases from Folsom in order to meet water temperature standards based on the National Oceanic and Atmospheric Administration (NOAA) Fisheries (around or less than 18 °C during Jun through Nov) [41]. The minimum environmental requirements and additional information concerning downstream needs are presented in the Results section.
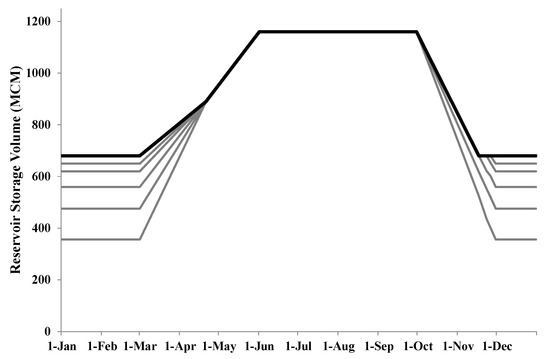
Figure 4.
Current rule-curve and top of conservation (TOC) of Folsom Reservoir (gray lines are alternative TOC lines based on the varying rule curve).
4. Results
4.1. Hydroclimate Scenarios
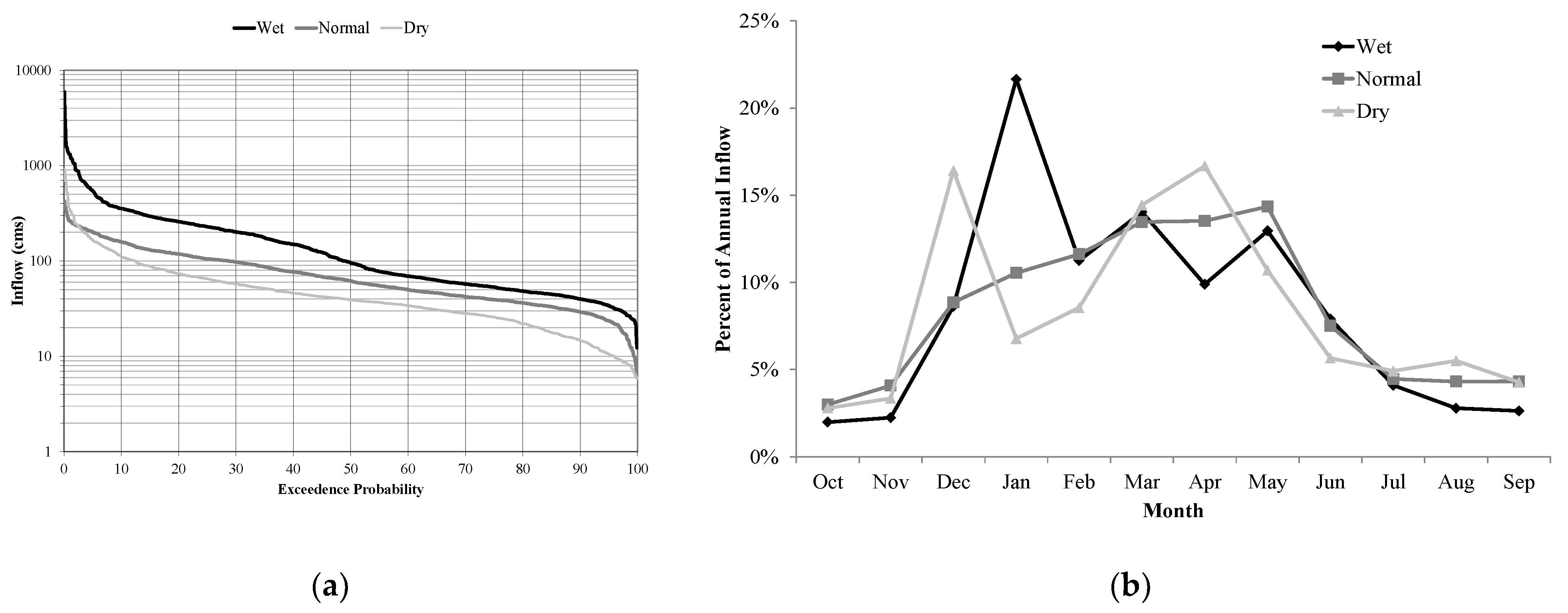
The optimization model was run for three climate scenarios, each three-year period, to estimate optimal daily energy generation. The model was run in daily mode for three historical climate periods including the normal, wet, and dry conditions. These periods were selected based on the classification of the Sacramento River Index (SRI), which is used by California Department of Water Resources (CADWR) to determine hydrologic year types. Three-year periods of dry (recent drought in California: 2012–2014), normal (2002–2004), and wet (1995–1997) were considered to illustrate the efficiency and effectiveness of the proposed method for different ranges of climate conditions including extremes like drought and flood. The intra-annual and inter-annual variabilities of the reservoir inflow under these conditions are shown in Figure 5a,b respectively.
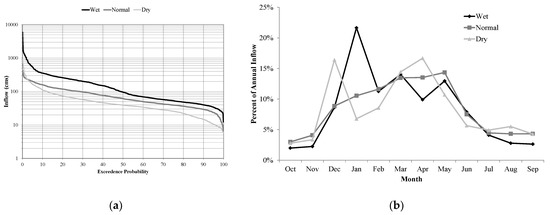
Figure 5.
Inflow to the Folsom Reservoir during wet, normal, and dry periods. (a) Exceedance probability; (b) Monthly average.
The exceedance probability plots of different inflows under different hydrologic conditions show that the inflow ranged from about 6cms to 6000 cms within the study time periods. This shows the high intra-annual variability of the inflows to the Folsom Reservoir. Since monthly runoff patterns vary by the hydrologic year type, Figure 5b represents these inter-annual changes. The reservoir’s monthly inflows in this figure indicate that although all the scenarios had the same low flow/base flow during June–November, the main difference stems from the hydroclimatic conditions during the wet season, December–May. During extreme events, dry and wet years, runoff peaks occur earlier and at a higher magnitude. This is mainly because despite the dry condition, during normal years, the snowpack is larger and lasts longer. During the dry years, and due to higher temperature, most of the precipitation falls as rain rather than snow, and also the existing snowpack melts earlier. In contrast, the wet scenario has high peaks in January due to atmospheric river events. During such events, most of the precipitation falls as rain during a short period of time in January.
4.2. CeA Optimization Results
The intra- and inter-annual variations of timing and volume of the reservoir inflow and the uncertainty associated with them complicate the operation of the reservoir, especially when the objectives are in conflict with each other. To maximize water supply during the dry season, peak inflows during the high flow season should be stored in the reservoir in order to be released later during the high energy demand season. However, storing more water during the high flow season means a higher risk of flooding during this time period. Flooding, in this study, is defined as a reservoir water level that is above the level required by the rule curve. The proposed CeA optimization approach, based on the minimization of the objective function and satisfaction of constraints, increases the benefits of hydropower generation by taking into consideration the allowance space of flood control. Table 3 indicates how the inflow, release from reservoir, available storage, hydropower generation, and the objective function (Equation (1)) vary for different climate scenarios while the system’s operation is optimized.

Table 3.
Optimization results: Annual average for different scenarios.
The main objective of the optimization problem is minimizing the deviation of power generation from the installed capacity, defined by Equation (1). Hence, the objective function value was greater for the dry scenario and lower for the wet scenario. Although annual inflow for the wet scenario was 130% higher than the normal scenario, the hydropower generation was only about 4% higher and average available water in the reservoir was quite the same. This was mainly due to using the full capacity of the turbines and permissible reservoir capacity (conservation zone). Under the dry scenario, system faces a reduction of about 21% in hydropower generation. Due to the decrease in the inflow and maintaining an acceptable head in storage, release is decreased proportionally. This leads to a lower energy generation under the dry scenario. Because the reservoir flood control space should be kept empty, the peak flows from earlier snowmelt and rainfall events should be bypassed from the reservoir. This leads to a reduction in the total energy production during the months when energy demand is higher. Moreover, under the dry scenario, the annual storage was quite the same (2% decrease compared to the normal scenario), while the hydropower production was about 21% less than the normal scenario. It should be noted that the average annual generation based on the current operation of the reservoir is about 691,358 MWh. More information about hydropower generation during extreme climate conditions requires further investigation. In this study, the normal condition scenario was assumed as the status quo for the comparison with extreme climate conditions. This indicates that hydropower generation is related not only to the releases from the reservoirs through turbines, but also the head above the turbines in the reservoir.
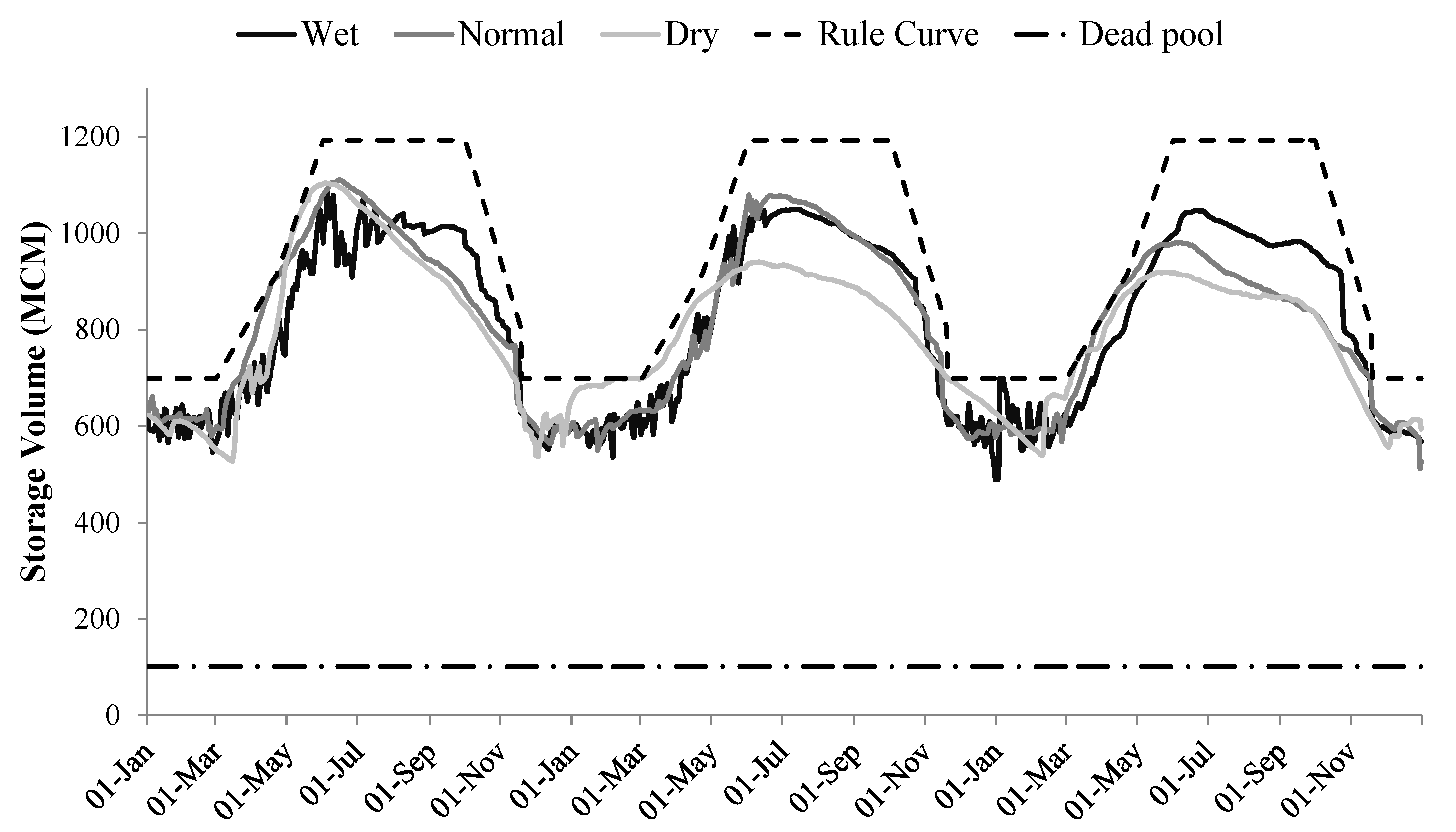
Figure 6 shows the top of the conservation, flood, and dead pools, and the daily storage simulations of the Folsom Reservoir under different climate conditions. This figure illustrates the obligatory storage for flood control, which is kept empty during the optimization runs, regardless of the climate conditions. The importance of the secondary objective considered in the reservoir operation in this study was to force the optimization to keep the flood zone empty. This term was included as a constraint in the optimization formulation. This is more interesting when one realizes that during the wet period, based on historical records, there were multiple flooding events in the downstream and within the reservoir (violations from constraints). However, as shown in Figure 6, under the wet scenario, these flows (flooding events) were damped by pre-release from the reservoir to keep the reservoir empty for the upcoming peak flows. It should be noted that there was only one event where the release from the reservoir was violated from the maximum capacity of the downstream. This evidence presents a chief improvement in the reservoir operation, in terms of flood control, in daily mode by using the CeA optimization approach. Figure 6 also shows that the optimization tends to keep the reservoir storage full (up to the top of the conservation level), while safely avoiding water level entering the flood zone (the constraint in optimization). Moreover, all the scenarios had the same end of period water storage (450–480 MCM) in the reservoir, while they maximized the hydropower generation regardless of the hydroclimate condition. As is clear from Figure 6, during the dry seasons, even for wet years, the reservoir storage did not reach the maximum level and nor did the reservoir completely empty out. The reason behind this is that the CeA tries to balance the need for the water supply demand in the downstream and at the same time, keeps an optimal water level behind the dam to create enough head for hydropower generation during the high energy and water demand periods.
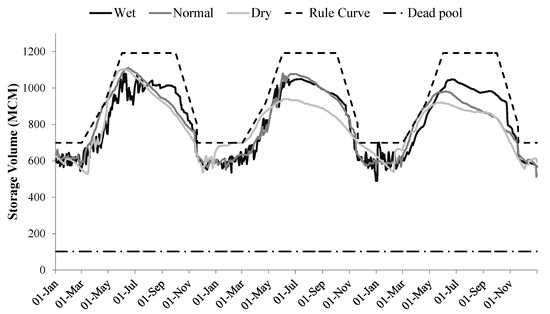
Figure 6.
Folsom Reservoir storage during the wet, normal, and dry periods from the optimization model.
Another important factor to keep the reservoir service at an acceptable level is the reliability of the system to meet other requirements. The Folsom Reservoir should meet the local agricultural and municipal demands as well as the minimum flow requirement downstream of the reservoir. These two main requirements are fully met in all the optimization runs. The minimum environmental flow (MEF), in this study, was assumed to be the same for all the climate scenarios. However, the MEF is not constant during a year and this value was about 14 cms from January through to mid-September, and 28 cms for the rest of the year. The MEF should be checked at the confluence of the American River and Sacramento River. Even during the drought, the downstream environmental flow as well as the local demand were met for the optimization time period.
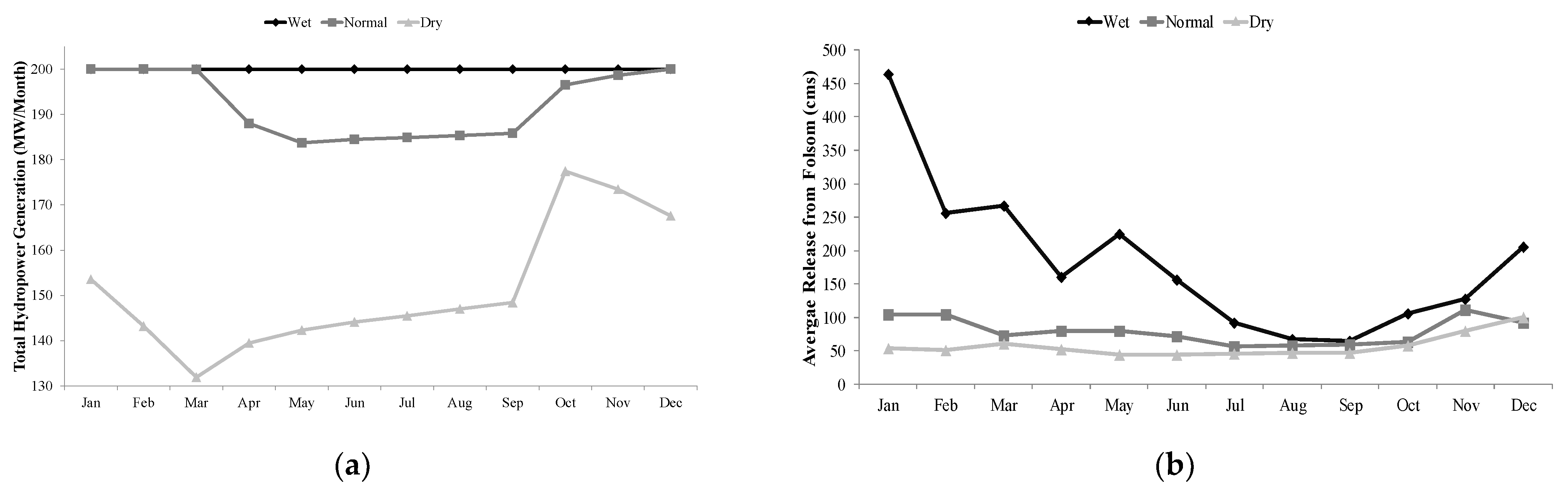
Figure 7a shows the average monthly hydropower generation from the model, and Figure 7b shows the releases from the Folsom Reservoir under different climate scenarios. Results were averaged monthly during the three-year periods of different scenarios. Although the optimization proposes the maximum hydropower generation under the wet scenario, the timing and magnitude of hydropower generation under normal and dry scenarios differed significantly (Figure 7a). These changes provide an important insight into the sensitivity of the hydropower generation and its timing to the changes in climate conditions. The optimization suggests a lower amount of hydropower generation during the winters (when there is enough water in the reservoir) to store more water in the reservoir for the summers. However, the summer energy generation in both of these scenarios was still less than the wet scenario due to the reduction in the total inflow and availability of water. A comparison of the hydropower generation (Figure 7a) and releases (Figure 7b) for the wet scenario indicated that release was significantly decreased after March (until October), but the hydropower generation was still high. This is due to the higher level of water in the storage, which makes enough head to generate more hydropower. Figure 4 shows that the filling period for the reservoir starts in March; therefore, at this time, there is enough water (head above the turbines) in the reservoir for turbines to perform at full capacity and generate more hydropower. As soon as the drawdown is started (October), release from the reservoir is increased in order to make up for the lower head in the reservoir. If there is a higher permissible storage capacity (less flood capacity and higher conservation level) under normal conditions, there is a likelihood of less release during December to March, and therefore, result in an increase in energy generation later during April–November. This is also true for the dry scenario. The reservoir can store more water during the wet season of a dry year and discharge it later through turbines during April–October. Additionally, releases from the reservoir under normal and dry scenarios are similar, but with different hydropower generation. This confirms the importance and sensitivity of the generated hydropower in such a reservoir (and similar reservoir with inter- and intra-annual variability of storage and head) to the head above the turbines. Consequently, the tradeoff between the head and release is a decisive factor in the optimization of the reservoirs’ operation to maximize the hydropower generation.
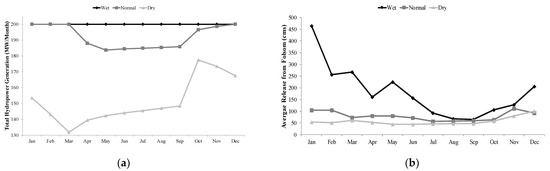
Figure 7.
Monthly average of (a) generated hydropower and (b) release from the Folsom Reservoir during wet, normal, and dry periods based on the optimization model.
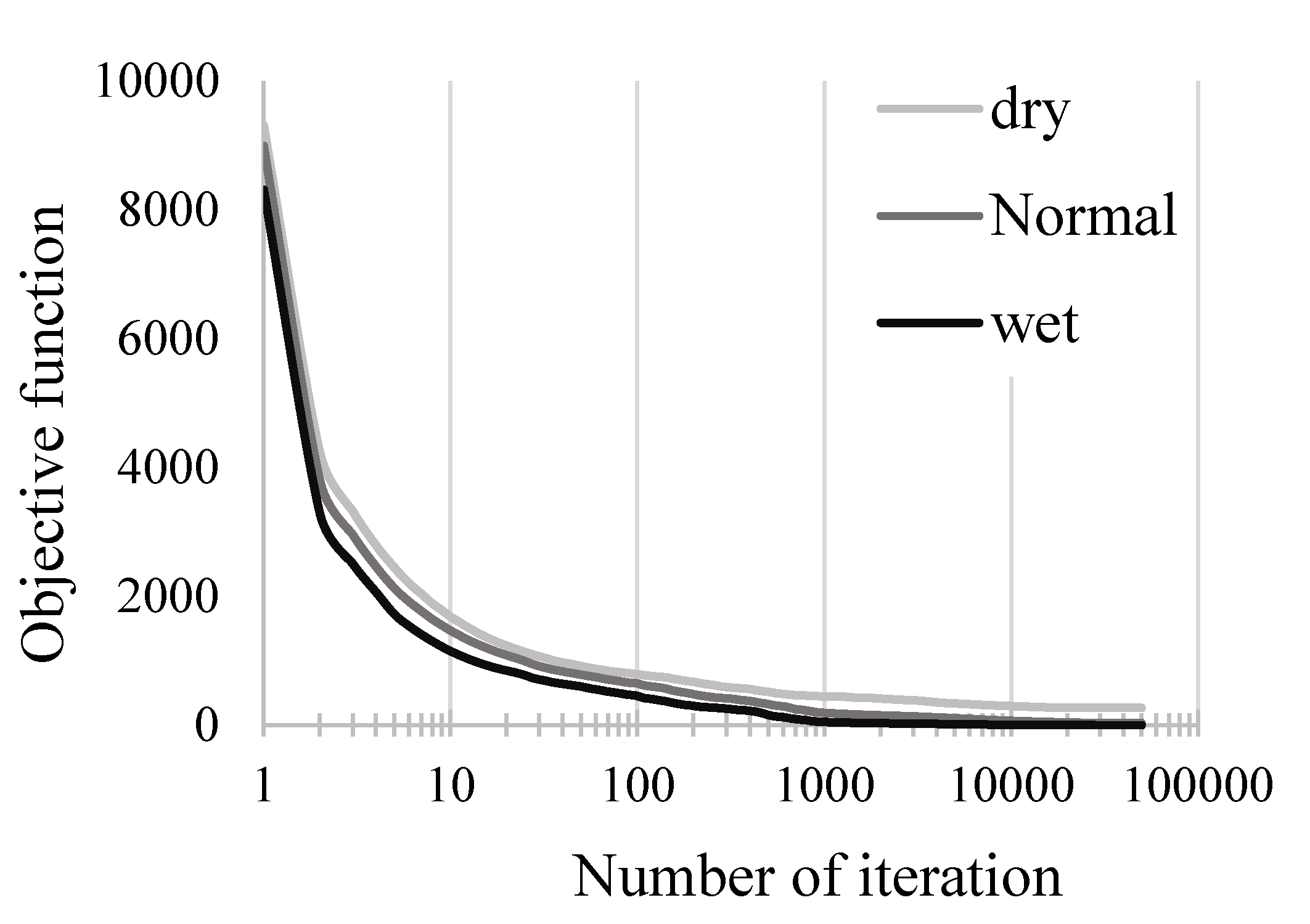
The convergence curves of the proposed method under wet, normal, and dry climate conditions are illustrated in Figure 8. The CeA requires about 15,000, 5000, and 1200 iterations for dry, normal, and wet conditions, respectively, to achieve feasible solutions (the number of iterations are presented with log axis in Figure 8 to better represent the convergences).
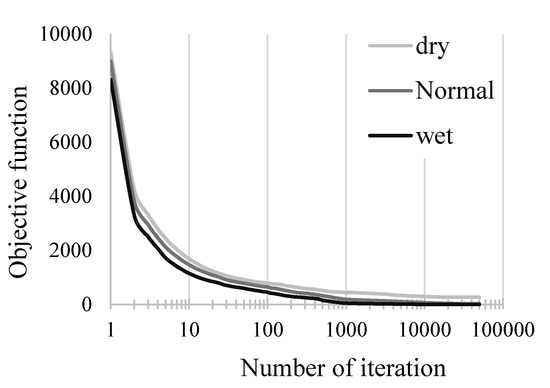
Figure 8.
Convergence curves of cellular automata optimization for wet, normal, and dry conditions.
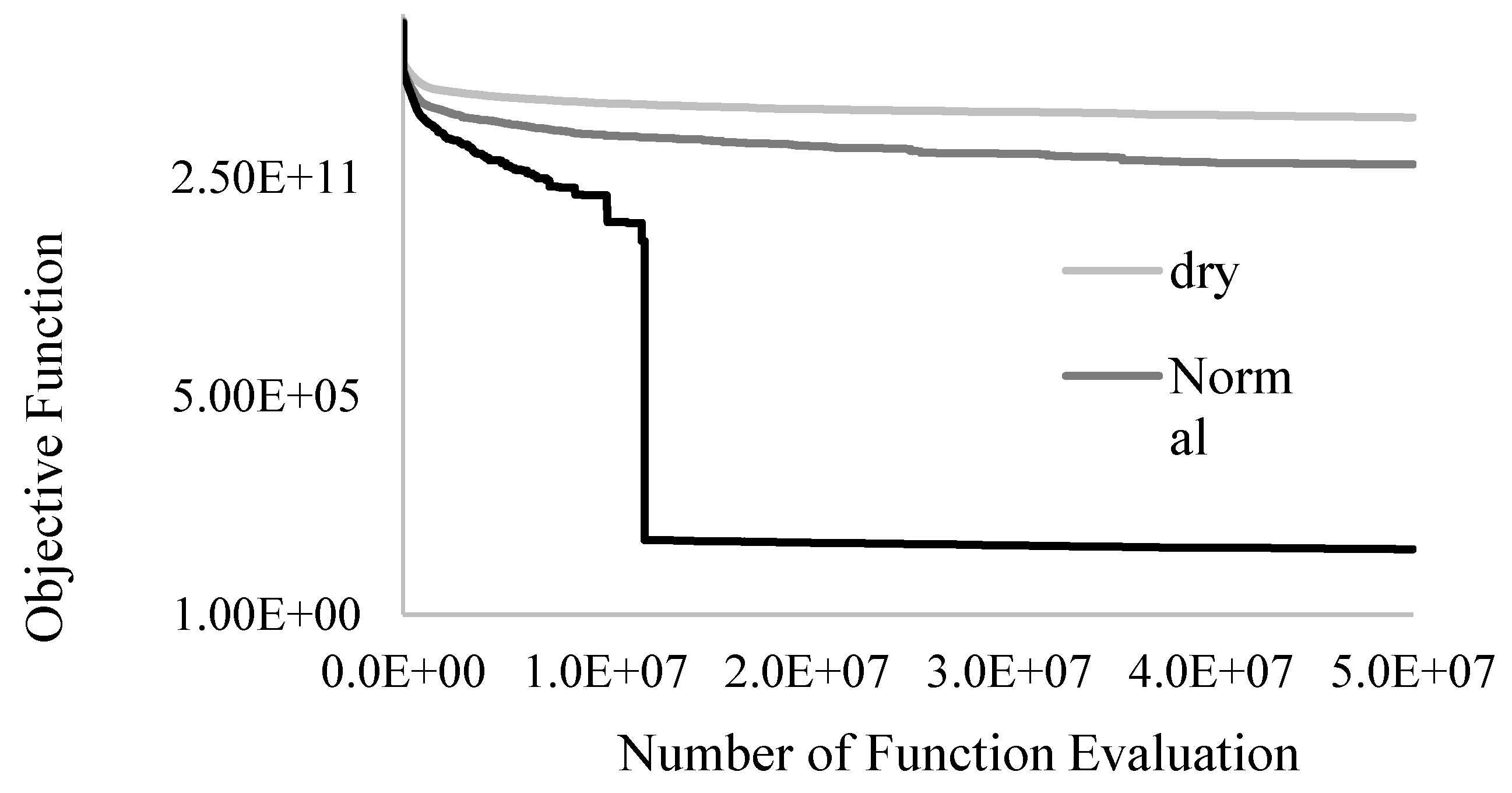
For validation purposes, genetic algorithm (GA) was employed to solve the same problem. The storage volume of the reservoir was considered as the decision variable for the GA [43,44]. The GA’s model parameters and operators were already fine-tuned during preliminary tests. The Roulette Wheel selection procedure was picked for selection, a single-point crossover with a probability of 0.8 with random weighted averaging after the crossover, and a 1-bit mutation procedure with a probability of 0.2 were used to produce the off-springs. Population size was set to 500 for operation under all climatic conditions, and an exhaustive maximum number of generations equal to 100,000 was used for all runs to ensure the convergence of GA. The convergence curves of GA for different climate conditions are presented in Figure 9. As shown in the figure, GA could not find any feasible solution for dry and normal conditions up to 50,000,000 function evaluations. This could be attributed to the fact that solving large-scale (non-deterministic polynomial-time) NP-hard optimization problems using evolutionary algorithms would be extremely challenging, if not impossible. It should be noted that the solution with no constraint violation is taken as a feasible solution, which is not necessarily the optimal or even near-optimal solution. The iteration at which the feasible solution is found can be simply identified by tracking the constraint violation. However, it is not recognizable in this figure, since there may be only a slight difference between objective functions with a feasible solution and one with a very small constraint violation.
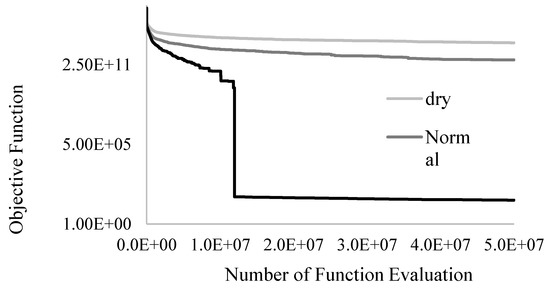
Figure 9.
Convergence curve of GA for wet, normal, and dry conditions.
Table 4 summarizes the optimization results of the proposed CeA method along with those obtained from GA. CeA produced superior solutions compared to GA for the wet climate condition with 0.02 of CPU runtime required by GA (Table 4). It is interesting to note that for normal and dry conditions, GA was not able to find any feasible solution with 82 and 110 times the computational efforts required by CeA.

Table 4.
Comparison of CeA and GA optimization results for different climate conditions.
Finally, it can be concluded from the results that the design and current operation of the reservoir system was based on the historical stationary conditions, which does not account for the higher flows during the wet years. The stationary assumptions do not just include the climate conditions, but also an estimation error in the land-cover, land-use changes, infrastructure aging, river modifications, etc. [45]. The magnitude of flow during the wet season in the American River Basin has had an increasing trend during the past 100 years and is expected to continue [46]. Therefore, the necessity of re-operation of the reservoir and revision of the rule-curve studies are significant in order to adapt the operation of the reservoir system to these changes. The optimal operation of a reservoir system using new techniques that can more efficiently solve complex and non-linear problems should be seriously considered in future studies.
5. Summary and Conclusions
Longer drought periods and frequent high flow events are becoming the new normal hydroclimate condition in California. The new condition threatens great changes in the availability of water resources and thereupon changes in food and energy resources in the state of California. California’s commitments to deliver 50 per cent of their electricity from clean, renewable sources by 2030, alongside mismatches between the state’s water supply and demand, is likely to be affected by climate change and will require integrated management solutions. Hydropower produces a major part of the total electricity in the state. Consequently, changes in the available water and energy sources call for more thoughtful research about the future portfolio of water and energy in California. As the temperature increases, snowpack-driven water systems are more susceptible to these changes. The Sierra Nevada’s snowpack melts earlier and faster, while the surface water storage in the Central Valley can carry only a limited amount of water in a short time. Surface reservoir hydropower plants play a great role in hydroelectricity production. Water should be pre-released or released immediately after facing high peak flows in order to protect lands and cities from flooding. Therefore, energy spills from the surface reservoir hydropower plants increase significantly under these hydroclimate circumstances. While the expansion of surface reservoirs is a straight-forward solution, it is not a cost-effective and sustainable solution. Mismatches between the timing and magnitude of water and energy demands and water availability and hydropower generation significantly affect the efficiency of the infrastructure development solutions. On the other hand, soft solutions like the management of demands or optimal operation of surface reservoirs and hydropower systems would be more practical and likeminded. However, dealing with such a complex, uncertain, and non-linear system is not an easy task.
The focus of this study was to better understand the changes of hydropower generation during extreme years in California under extreme hydroclimatic conditions. We suggest using a new optimization approach, cellular automata, to optimally operate the hydropower systems under different hydroclimate conditions. While the GA was not able to find feasible solutions for dry and normal conditions, the CeA approach achieved a near optimal solution with much less computational effort. The application of the optimization method and the model were tested for the daily operation of the Folsom Reservoir in Northern California. Two objectives were considered for the optimal operation of the reservoir. While the first objective was to maximize the electricity generation, the auxiliary objective of the reservoir operation was considered as a reduction in the flood risk and was embedded as a constraint in the optimization formulation. The CeA’s results indicate that changes in runoff during the wet season can be accommodated by the available surface storage capacity of the Folsom Reservoir during the normal years. However, the energy production is limited to the maximum installed capacity of turbines during the wet years. While the energy spills increased during the wet seasons under wet and normal scenarios, during a drought season, the energy production was 25% less than the maximum and 20% less than normal hydropower generations. Recent changes in inter- and intra-annual water availability in California have exacerbated the conditions. The lower-elevation reservoirs in California including the Folsom Reservoir, have been designed and built under stationary assumptions and mainly for flood control and water supply purposes. Therefore, the existing reservoir rule curves, which indicate the required flood capacity in the reservoir during the wet season, need to be adapted to changes in hydroclimatic conditions. Although decreasing the flood control space during the dry years is still associated with flooding risks, it can compensate for part of the changes in snowmelts, the real-time optimization and forecast informed reservoir operation concepts can increase hydropower production in California. Therefore, future studies should investigate the possible improvement in the operation of reservoirs and hydropower systems by coupling the proposed CeA optimization approach with the forced input streamflow forecast information from the California Nevada River Forecast Center.
Author Contributions
Conceptualization, E.G. and S.S.-S.; Methodology, E.G., M.A. and S.S.-S.; Coding, E.G. and M.A.; Analysis, E.G., M.A., S.S.-S. and G.F.; Resources, S.S.-S. and G.F.; Writing—original draft preparation, E.G. and M.A.; Writing—review and editing, S.S.-S. and G.F.; Visualization, E.G. and M.A.; Supervision, S.S.-S. and G.F.; Funding acquisition, G.F. All authors have read and agreed to the published version of the manuscript.
Funding
We acknowledge support from the UC Office of the President’s Multi-Campus Research Programs and Initiatives (MR-15-328473) through UC Water, the University of California Water Security and Sustainability Research Initiative.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
The optimization code generated for this study along with some of the results and data are available online (https://github.com/erfangoharian accessed on 20 February 2021). The rest of the data, models, and codes generated or used during the study are available from the corresponding author by request.
Acknowledgments
We acknowledge support from the University of California (UC) Office of the President’s Multi-Campus Research Programs and Initiatives (MR-15-328473) through UC Water, the University of California Water Security and Sustainability Research Initiative.
Conflicts of Interest
The authors declare no conflicts of interest.
References
- IEA. Medium-Term Renewable Energy Market. Report 2015; OECD/IEA: Paris, France, 2015. [Google Scholar]
- Barros, M.T.; Tsai, F.T.; Yang, S.L.; Lopes, J.E.; Yeh, W.W. Optimization of large-scale hydropower system operations. J. Water Resour. Plan. Manag. 2003, 129, 178–188. [Google Scholar] [CrossRef]
- Cheng, C.-T.; Wang, W.-C.; Xu, D.-M.; Chau, K.W. Optimizing hydropower reservoir operation using hybrid genetic algorithm and chaos. Water Resour. Manag. 2008, 22, 895–909. [Google Scholar] [CrossRef] [Green Version]
- Yurtal, R.; Seckin, G.; Ardiclioglu, G. Hydropower optimization for the lower Seyhan system in Turkey using dynamic programming. Water Int. 2005, 30, 522–529. [Google Scholar] [CrossRef]
- Olivares, M.A.; Lund, J.R. Representing energy price variability in long-and medium-term hydropower optimization. J. Water Resour. Plan. Manag. 2011, 138, 606–613. [Google Scholar] [CrossRef]
- Li, F.-F.; Shoemaker, C.A.; Wei, J.-H.; Fu, X.-D. Estimating maximal annual energy given heterogeneous hydropower generating units with application to the three gorges system. J. Water Resour. Plan. Manag. 2013, 139, 265–276. [Google Scholar] [CrossRef]
- Côté, P.; Leconte, R. Comparison of stochastic optimization algorithms for hydropower reservoir operation with ensemble streamflow prediction. J. Water Resour. Plan. Manag. 2015, 142, 04015046. [Google Scholar] [CrossRef]
- Aspen Environmental Group; Cubed, M. Potential Changes in Hydropower Production from Global Climate Change in California and the Western United States; CEC-700-2005-010, June 2005; California Climate Change Center: Sacramento, CA, USA, 2005; Available online: https://relicensing.pcwa.net/var/www/html/public_html/documents/Library/PCWA-L-208.pdf (accessed on 30 February 2021).
- Vicuña, S.; Leonardson, R.; Hanemann, M.W.; Dale, L.L.; Dracup, J.A. Climate change impacts on high elevation hydropower generation in California’s Sierra Nevada: A case study in the upper american river. Clim. Chang. 2008, 28 (Suppl. 1), 123–137. [Google Scholar] [CrossRef]
- Vicuna, S.; Maurer, E.P.; Joyce, B.; Dracup, J.A.; Purkey, D. The sensitivity of California water resources to climate change scenarios. JAWRA J. Am. Water Resour. Assoc. 2007, 43, 482–498. [Google Scholar] [CrossRef]
- Cayan, D.R.; Maurer, E.P.; Dettinger, M.D.; Tyree, M.; Hayhoe, K. Climate change Scenarios for the California region. Clim. Chang. 2008, 87, S21–S42. [Google Scholar] [CrossRef]
- Goharian, E.; Burian, S.J.; Bardsley, T.; Strong, C. Incorporating potential severity into vulnerability assessment of water supply systems under climate change conditions. J. Water Resour. Plan. Manag. 2016, 142, 04015051. [Google Scholar] [CrossRef]
- Goharian, E.; Burian, S.J.; Lillywhite, J.; Hile, R. Vulnerability assessment to support integrated water resources management of metropolitan water supply systems. J. Water Resour. Plan. Manag. 2017, 143, 04016080. [Google Scholar] [CrossRef] [Green Version]
- Goharian, E.; Azizipour, M.; Sandoval-Soils, S.; Fogg, G.E. Surface reservoir reoperation for managed aquifer recharge: Folsom reservoir system. J. Water Resour. Plan. Manag. 2020, 146, 04020095. [Google Scholar] [CrossRef]
- Bai, T.; Kan, Y.-B.; Chang, J.-X.; Huang, Q.; Chang, F.-J. Fusing feasible search space into PSO for multi-objective cascade reservoir optimization. Appl. Soft Comput. 2017, 51, 328–340. [Google Scholar] [CrossRef]
- Uen, T.-S.; Chang, F.-J.; Zhou, Y.; Tsai, W.-P. Exploring synergistic benefits of Water-Food-Energy Nexus through multi-objective reservoir optimization schemes. Sci. Total Environ. 2018, 633, 341–351. [Google Scholar] [CrossRef]
- Zhou, Y.; Guo, S.; Chang, F.J.; Xu, C.Y. Boosting hydropower output of mega cascade reservoirs using an evolutionary algorithm with successive approximation. Appl. Energy 2018, 228, 1726–1739. [Google Scholar] [CrossRef]
- Zhou, Y.; Guo, S.; Xu, C.Y.; Chang, F.J.; Chen, H.; Liu, P.; Ming, B. Stimulate hydropower output of mega cascade reservoirs using an improved Kidney Algorithm. J. Clean. Prod. 2020, 244, 118613. [Google Scholar] [CrossRef]
- Madani, K.; Lund, J.R. Estimated impacts of climate warming on California’s high-elevation hydropower. Clim. Chang. 2009, 102, 521–538. [Google Scholar] [CrossRef] [Green Version]
- Belsnes, M.M.; Wolfgang, O.; Follestad, T.; Aasgård, E.K. Applying successive linear programming for stochastic short-term hydropower optimization. Electr. Power Syst. Res. 2016, 130, 167–180. [Google Scholar] [CrossRef] [Green Version]
- Arnold, E.; Tatjewski, P.; Wołochowicz, P. Two methods for large-scale nonlinear optimization and their comparison on a case study of hydropower optimization. J. Optim. Theory Appl. 1994, 81, 221–248. [Google Scholar] [CrossRef]
- Schluter, M.; Savitsky, A.G.; Mckinney, D.C.; Lieth, H. Optimizing long-term water allocation in the Amudarya River delta: A water management model for ecological impact assessment. Environ. Modeling Softw. 2004, 20, 529–545. [Google Scholar] [CrossRef]
- Allen, R.B.; Bridgeman, S.G. Dynamic programming in hydropower scheduling. J. Water Resour. Plan. Manag. 1986, 112, 339–353. [Google Scholar] [CrossRef]
- Delipetrev, B.; Jonoski, A.; Solomatine, D.P. A novel nested stochastic dynamic programming (nSDP) and nested reinforcement learning (nRL) algorithm for multipurpose reservoir optimization. J. Hydroinform. 2017, 19, 47–61. [Google Scholar] [CrossRef]
- Labadie, J.W. Optimal operation of multireservoir systems: State-of-the-art review. J. Water Resour. Plan. Manag. 2004, 130, 93–111. [Google Scholar] [CrossRef]
- Mariño, M.A.; Mohammadi, B. Reservoir operation by linear and dynamic programming. J. Water Resour. Plan. Manag. 1983, 109, 303–319. [Google Scholar] [CrossRef]
- Yao, H.; Georgakakos, A.P. ACF River Basin: Climate and Demand Change Impacts and Mitigation Measures; Georgia Institute of Technology: Atlanta, GA, USA, 2011. [Google Scholar]
- Ferreira, I.C.; Tanaka, S.K.; Hollinshead, S.P.; Lund, J.R. Musings on a model: CalSim II in California’s water community. In San Francisco Estuary and Watershed Science; University of California: Oakland, CA, USA, 2005; Volume 3. [Google Scholar]
- Ming, B.; Chang, J.X.; Huang, Q.; Wang, Y.M.; Huang, S.Z. Optimal operation of multi-reservoir system based on cuckoo search algorithm. Water Resour. Manag. 2015, 29, 5671–5687. [Google Scholar] [CrossRef]
- Bayón, L.; Grau, J.M.; Ruiz, M.M.; Suárez, P.M. Influence of the elevation-storage curve in the optimization of hydroplants. Int. J. Simul. Multidiscip. Des. Optim. 2009, 3, 326–331. [Google Scholar] [CrossRef]
- Oliveira, R.; Loucks, D.P. Operating rules for multireservoir systems. Water Resour. Res. 1997, 33, 839–852. [Google Scholar] [CrossRef]
- Zhang, X.; Yu, X.; Qin, H. Optimal operation of multi-reservoir hydropower systems using enhanced comprehensive learning particle swarm optimization. J. Hydro-Environ. Res. 2016, 10, 50–63. [Google Scholar] [CrossRef]
- Kiruthiga, D.; Amudha, T. Optimal Reservoir Release for Hydropower Generation Maximization Using Particle Swarm Optimization. Innovations in Bio-Inspired Computing and Applications; Springer International Publishing: Cham, Switzerland, 2016; pp. 577–585. [Google Scholar]
- Kumar, D.N.; Reddy, M.J. Ant colony optimization for multi-purpose reservoir operation. Water Resour. Manag. 2006, 20, 879–898. [Google Scholar] [CrossRef]
- Moeini, R.; Afshar, M.H. Extension of the constrained ant colony optimization algorithms for the optimal operation of multi-reservoir systems. J. Hydroinform. 2013, 15, 155–173. [Google Scholar] [CrossRef] [Green Version]
- Azizipour, M.; Ghalenoei, V.; Afshar, M.H.; Solis, S.S. Optimal operation of hydropower reservoir systems using weed optimization algorithm. Water Resour. Manag. 2016, 30, 3995–4009. [Google Scholar] [CrossRef]
- Akbari-Alashti, H.; Bozorg-Haddad, O.; Mariño, M.A. Application of fixed length gene genetic programming (FLGGP) in hydropower reservoir operation. Water Resour. Manag. 2015, 29, 3357–3370. [Google Scholar] [CrossRef]
- Afshar, M.H.; Shahidi, M. Optimal solution of large-scale reservoir-operation problems: Cellular-automata versus heuristic-search methods. Eng. Optim. 2009, 41, 275–293. [Google Scholar] [CrossRef]
- Azizipour, M.; Afshar, M.H. Adaptive hybrid genetic algorithm and cellular automata method for reliability-based reservoir operation. J. Water Resour. Plan. Manag. 2017, 143, 04017046. [Google Scholar] [CrossRef]
- Azizipour, M.; Afshar, M.H. Reliability-based operation of reservoirs: A hybrid genetic algorithm and cellular automata method. Soft Comput. 2018, 22, 6461–6471. [Google Scholar] [CrossRef]
- USBR (US Bureau of Reclamation). Folsom Dam. 2019. Available online: https://www.usbr.gov/projects/index.php?id=74 (accessed on 16 September 2020).
- Maher, K.M. Potential Use of Real-Time Information for Flood Operation Rules for Folsom Reservoir; University of California: Davis, CA, USA, 2011. [Google Scholar]
- Deb, K.; Pratap, A.; Agarwal, S.; Meyarivan, T.A.M.T. A fast and elitist multiobjective genetic algorithm: NSGA-II. IEEE Trans. Evol. Comput. 2002, 6, 182–197. [Google Scholar] [CrossRef] [Green Version]
- Jothiprakash, V.; Shanthi, G. Single reservoir operating policies using genetic algorithm. Water Resour. Manag. 2006, 20, 917–929. [Google Scholar] [CrossRef]
- Milly, P.C.D.; Betancourt, J.; Falkenmark, M.; Hirsch, R.M.; Kundzewicz, Z.W.; Lettenmaier, D.P.; Stouffer, R.J. Stationarity is dead: Whither water management? Science 2008, 319, 573–574. [Google Scholar] [CrossRef] [PubMed]
- Goharian, E.; Gailey, R.; Maples, S.; Sandoval-Solis, S.; Fogg, G. Maximizing whole watershed storage through optimized reservoir reoperation and managed aquifer recharge. In Proceedings of the EGU General Assembly Conference Abstracts, Vienna, Austria, 4–13 April 2018; Volume 20, p. 867. [Google Scholar]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).