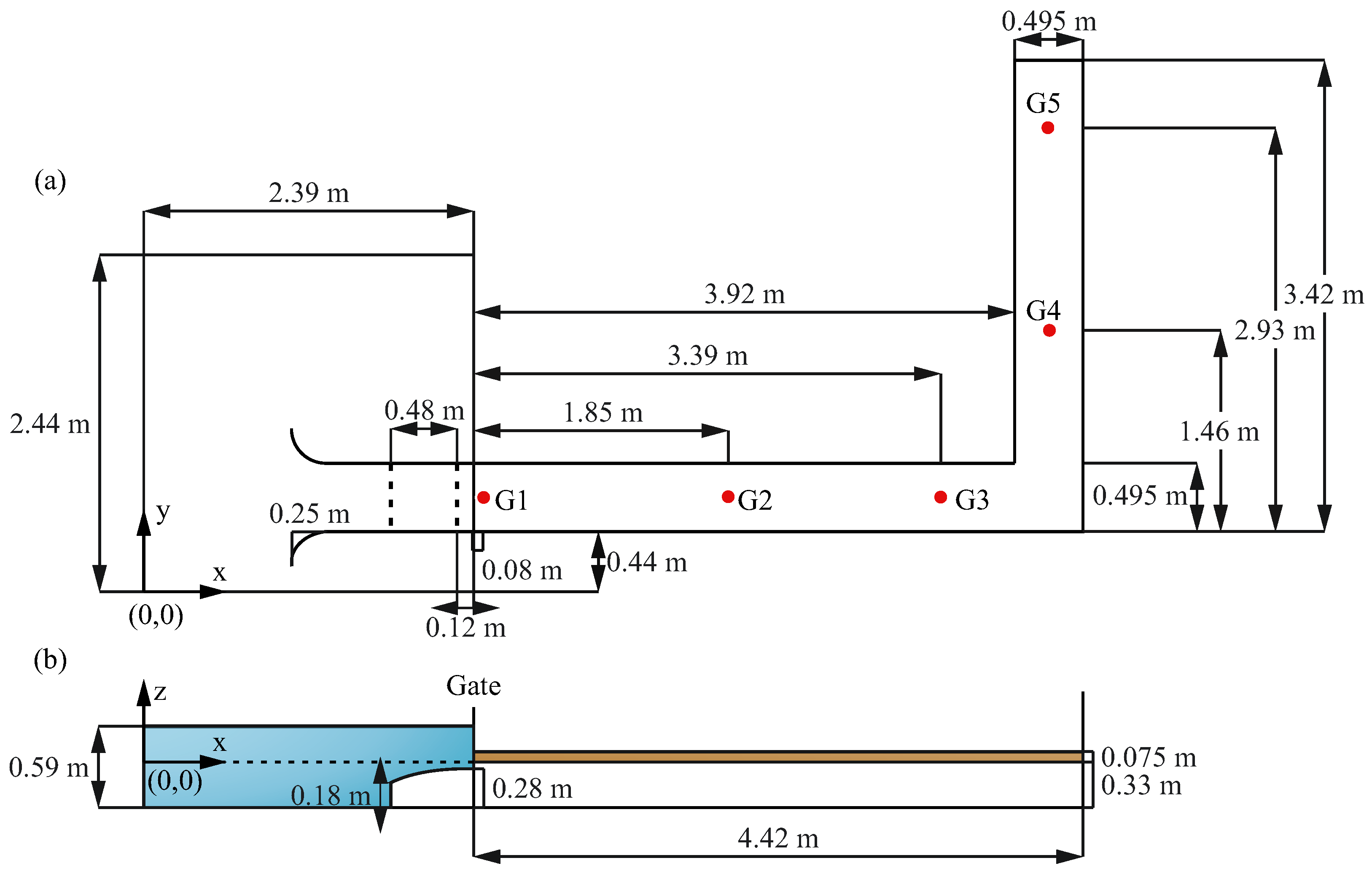
4.1. Comparison between the Roe- and HLLC-Based Capacity Models
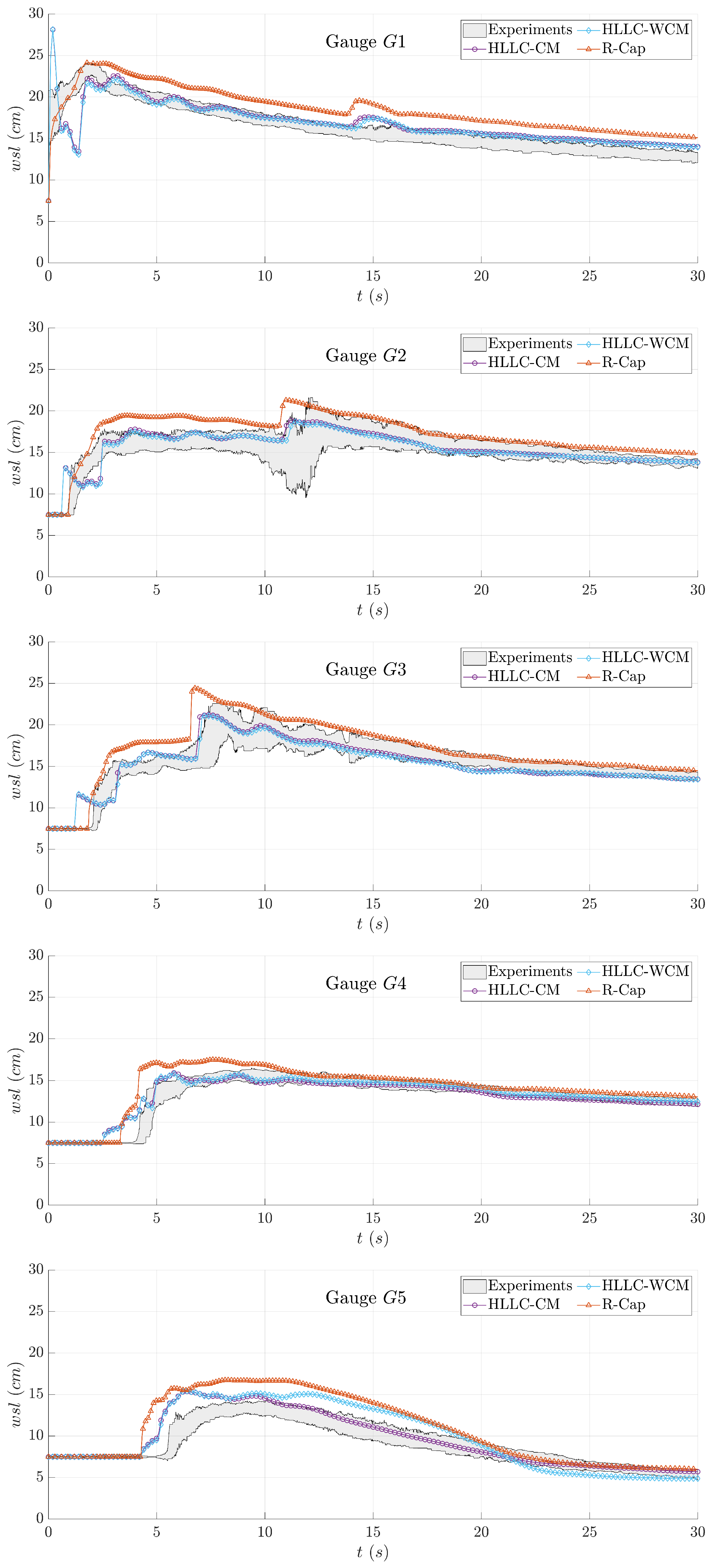
Figure 3 shows the temporal evolution of the water surface level (
) at the gauge points measured during the experiment. The arrival time of the dam-break wave was well predicted at the gauge points
,
, and
, located upstream of the corner region, with the Roe- and HLLC-based models. However, at the gauge points placed downstream of the corner region (
and
), all the numerical models showed a shorter arrival time of the dam-break wave than those observed in the laboratory. Furthermore, the R-Cap model showed a slightly higher
than the HLLC solvers, especially at the wavefront, for all the gauge points measured. Nevertheless, the transient flow structure was reasonably well predicted by all the numerical models.
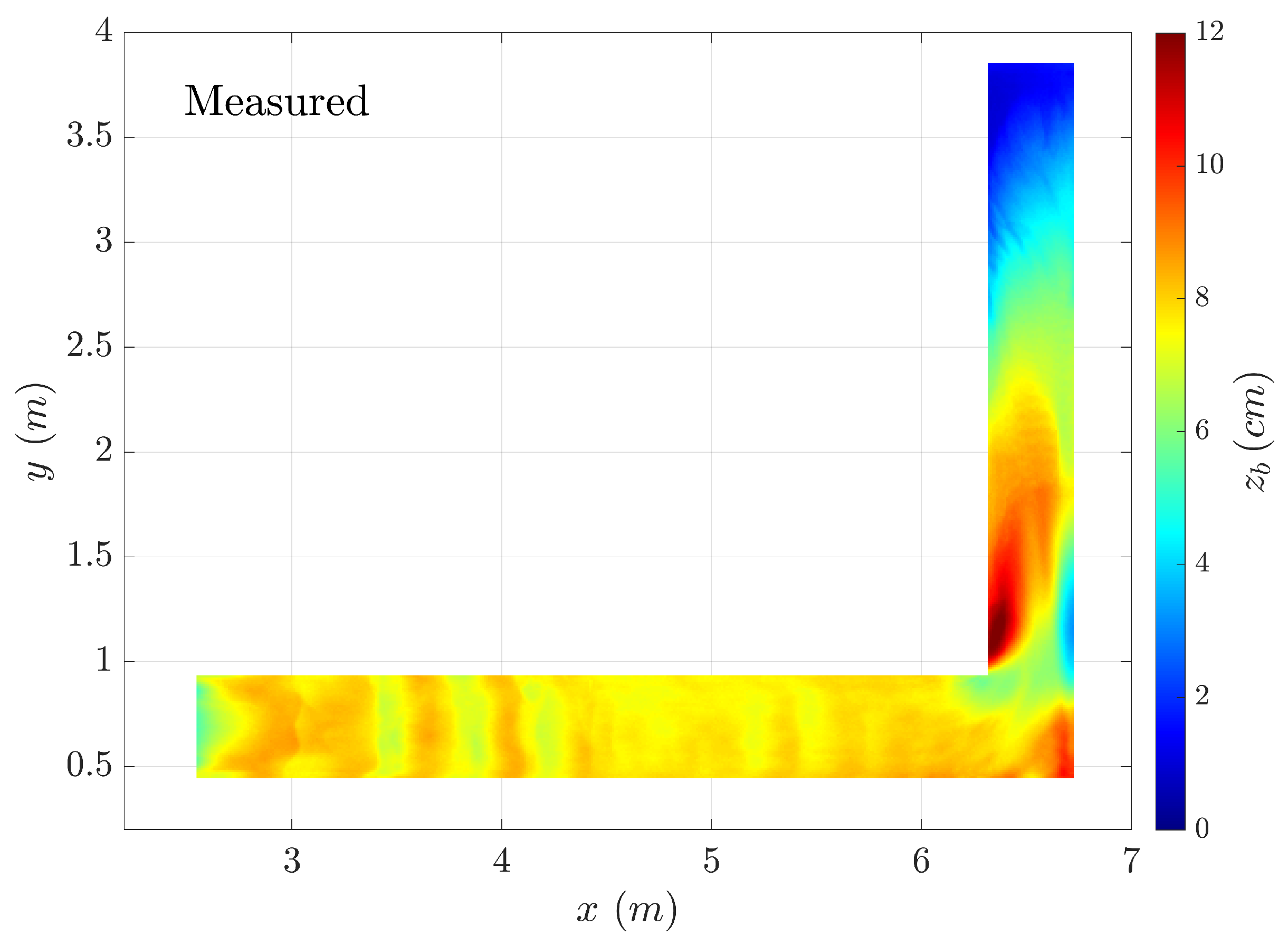
In order to assess the performance of the different numerical schemes to predict the bed changes caused by the dam-break wave, the final bed elevation obtained with the R-Cap- and HLLC-based solvers was compared against the photogrammetry measurements.
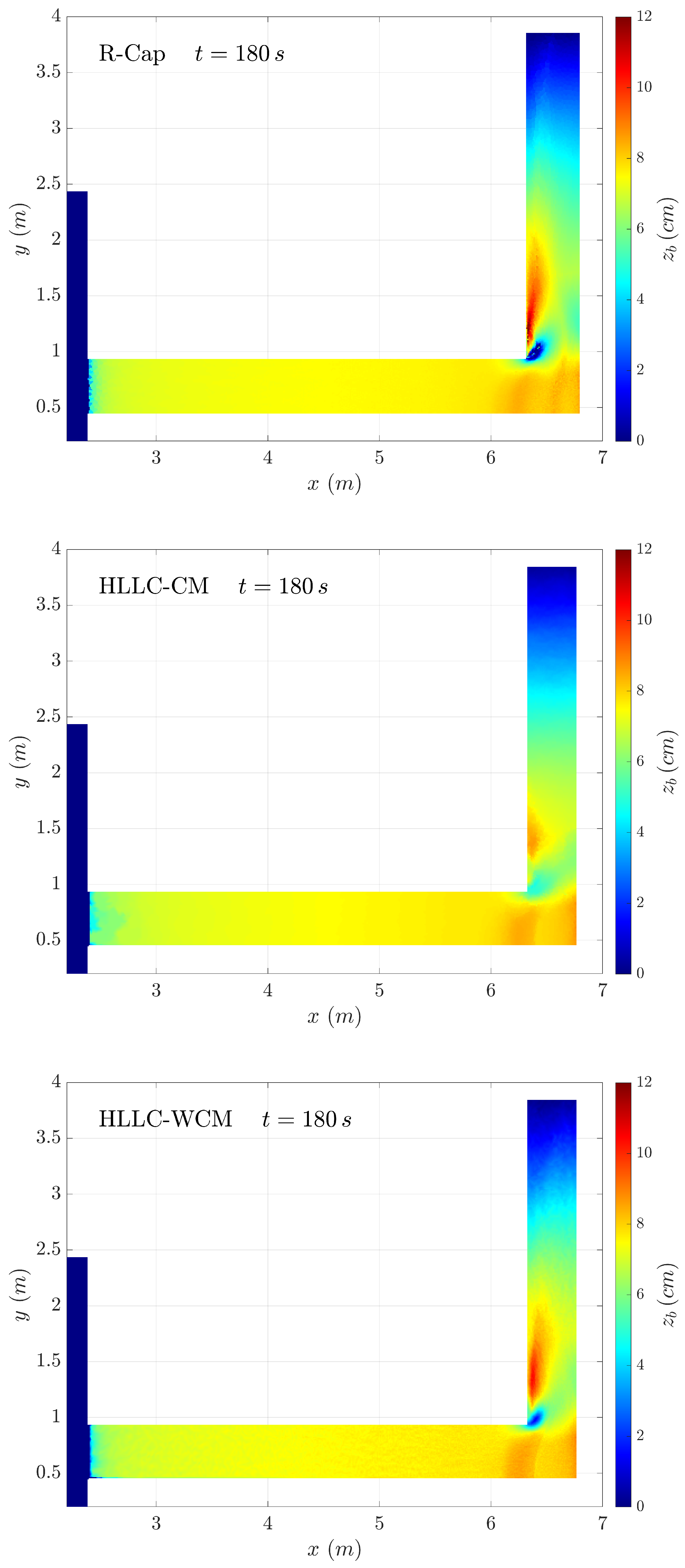
Figure 4 shows the 2D maps of the bed elevation
obtained with the R-Cap- and HLLC-based models at the final time
s. Several common aspects should be pointed out for the three models:
First, the three models were able to predict the bed degradation close to the outlet boundary reasonably well. However, none of them were able to obtain the bed forms observed in the experimental measurements at the beginning of the inlet reach;
Second, the R-Cap and the HLLC-WCM reproduced the main structures observed in the experiments for the final bed elevation well. However, the HLLC-CM led to a highly diffusive estimation of the bedload flux at the intercell edges, and the model was not able to reproduce the main features of the measured topography (see
Figure 2). However, none of the schemes were able to accurately predict the absolute accumulation of bed material observed in the experiments downstream of the inner corner, nor the depth in the opposite eroded region;
Third, the R-Cap and HLLC-WCM computed a marked eroded zone close to the inner corner. Although slight erosion was observed in this region in the laboratory, both numerical models overestimated the bed degradation. That was in reality due to the formation and development of a 3D vortex downstream of the inner corner. Such a vortex cannot correctly be reproduced by depth-averaged models, which would neglect some vertical recirculation, which would itself hamper the erosion near the inner corner. Relaxing the assumption of a hydrostatic pressure distribution along the flow column might help to improve the accuracy of the numerical model predictions, since the vertical accelerations within the flow play an important role in this region.
Table 4 shows the global RMSE for the computed bed level
2D maps with respect to the photogrammetric data in
Figure 2. The HLLC-WCM showed the lowest RMSE, followed by the R-Cap and the HLLC-CM. Since only a limited area—i.e., the bend region and roughly two meters downstream of it—was subject to large differences between the models, no model performed strikingly better than any other when looking at the RMSE. Nevertheless, these results were in line with the visual observations made previously.
In order to quantitatively identify the performance of the schemes more locally, final bed profiles taken along
m (A),
m (B), and
m (C) were obtained with the three numerical models and compared against the photogrammetric data, as shown in
Figure 5.
Regarding Profile (A), the R-Cap model approximated the maximum of the accumulation region better than the HLLC-based models. However, the depth of the overeroded region close to the inner corner also increased with the R-Cap solver due to its lower numerical diffusion. Eventually, the R-Cap model showed the lowest RMSE for the bed level
along this profile (
cm), whereas the HLLC-based models showed higher errors (see
Table 5).
The HLLC-WCM performed slightly better than the R-Cap model along Profile (B) (see
Figure 5), with RMSEs of
cm and
cm, respectively. The main reason for this similar performance was that the HLLC-WCM scheme better approximated the accumulation height in the outer corner upstream region and the bed slope at the outlet reach of the channel, whereas the R-Cap model slightly improved the prediction of the erosion zone downstream of the outer corner. However, the HLLC-CM again performed worse than the others (
cm), especially in the erosion zone downstream of the outer corner.
Finally, the three model performed quite similarly along Profile (C), with an RMSE below
cm and were able to predict the general trend of the bed change, as is shown in
Figure 5. However, none of them were able to approximate the formation of dunes in the inlet reach of the channel. The formation of this kind of bed form is directly related to the vertical structure of the flow near the bed surface [
19] and is hence difficult to mimic using depth-averaged bedload transport models.
4.2. Application of the R-NCap Model
The main feature of the R-NCap model is the progressive adaptation of the bedload transport rate
to the local flow conditions until the equilibrium transport state is reached, contrary to the capacity models, which assume instantaneous adaptation. The celerity of this adaptation is controlled by the entrainment and detention constants
and
, respectively, but also directly depends on the dimensionless Shields stress excess
at the bed interface [
22]. This is one of the main differences between the proposed R-NCap scheme and other nonequilibrium bedload models, which assume a constant value for the adaptation length
[
19,
31,
40] and compute the entrainment rate as:
where
is the modulus of the equilibrium bedload rate (9).
Comparing the proposed R-NCap with former noncapacity models based on Equation (45) for the formulation of Meyer-Peter and Müller [
26], it can be easily derived that the equivalent adaptation length applied by the R-NCap models scales with:
and hence, the equivalent adaptation length increases at regions where the boundary Shields stress excess is high. Furthermore, the smaller the entrainment constant
, the larger the adaptation length
is.
This property of the R-NCap model was used to improve the numerical prediction in the inner corner region. One of the main flaws in the numerical results obtained with the capacity R-Cap and HLLC-WCM models was the appearance of a marked overeroded region near the inner corner. This overeroded zone was not observed in the experimental measurements. The simulation showed that the marked erosion happened at the first stages of the dam-break progress throughout the corner region, when a vortex was formed downstream of the inner corner. The right panel of
Figure 6 shows the velocity vectors at the corner region for the R-Cap simulation at
s. The formation of the vortex was clearly associated with the appearance of the overeroded zone, but by neglecting vertical features, the sediment was highly sheared and eventually advected downstream.
Moreover, the changes in the flow direction in the inner corner region led to high bed Shields stresses, which contributed to increasing the erosion within this region. The left panel of
Figure 6 is a 2D map of the maximum values of bed Shields stress excess
as computed by the R-Cap model. The maximum
was around
in most of the channel, but increased in the inner corner region until reaching a maximum value greater than
, leading to a high erosion in this zone.
Considering the 2D map of the maximum
recorded for the R-Cap model and the features of the sediment used in this experiment, we analyzed the sensitivity of the R-NCap model by setting the entrainment and detention constants,
and
, respectively, to the values summarized in
Table 6. Therefore, four simulations using the R-NCap model were carried out, varying the entrainment constant from
to
, but maintaining the
ratio equal to 20. It is worth mentioning that, considering the characteristic maximum value of the bed Shields stress excess
recorded for the simulation with the R-Cap model, the ratio
was chosen to ensure that the relation between the characteristic thickness of the bedload transport layer under equilibrium conditions and the sediment diameter remained
(15) for all the simulations from T0 to T4.
Therefore, as decreased, the characteristic value of the equivalent adaptation length increased from cm for the case T1 to cm for the case T4. The increment of the adaptation length means that the spatial and temporal delay between the actual bedload transport rate and the flow carrying capacity became larger, and hence, the nonequilibrium states were enabled. Note that these values for the ratio and the adaptation length only corresponded to the inner corner region, where the bed Shields stress was higher during the first stages of the dam-break wave. In other regions of the channel, the equivalent would be shorter and the ratio smaller.
Figure 7 shows the final topography at time
s. When the R-NCap model was applied, the adaptation of the actual bedload solid rate to the flow capacity in the inner corner region became noninstantaneous. Hence, the appearance of the overeroded zone was not only delayed in time, but also moved further downstream of the inner corner. As
decreased, the noncapacity state in that region was enabled, until the formation of the overeroded zone was avoided. The other main features of the topography observed in the laboratory were maintained, even if alterations in the bed level
results also occurred in other regions of the channel.
Table 7 shows the global RMSE for the numerical topographies computed with the R-NCap model with respect to the photogrammetric data (
Figure 2). The improvement of the global performance using the R-NCap model was not marked, but an optimal value for the entrainment constant
could be found, corresponding to Test T2. Once again, the difference between the models may look limited regarding this indicator, because of the close results that they showed before the bend (
Figure 5C), but it highlights the importance of properly calibrating the model. Poor calibration choices could indeed lead to worse results with the R-NCap than with the R-Cap model.
The final bed level
computed with the R-NCap model is plotted along the profiles in
Figure 8. The results from the R-Cap model and the photogrammetric data are also depicted for comparison purposes. For Profile (A), the activation of the nonequilibrium states led to the avoidance of the overeroded zone, but a spatial delay of the accumulation zone was also predicted, as well as a reduction of the accumulation height. Furthermore, the prediction of the bed slope at the outlet reach of the channel was increasingly worse as
decreased. Despite the gain of accuracy allowed by the noncapacity feature near the inner corner, these worse and worse slope predictions led to higher RMSE values for the R-NCap model than for the R-Cap one along that profile (see
Table 8).
For Profile (B), the R-NCap model improved the prediction of the bed slope in the channel outlet reach without significantly affecting other regions (see
Figure 8). This also improved the RMSE of the bed level
with respect to the photogrammetric data along this profile, in comparison with the R-Cap model, as highlighted by
Table 8. The best agreement was given for
with a ratio
.