Comparison of Empirical and Analytical Solutions for Open-Channel Flow Velocity with Common Grass Species in Taiwan
Abstract
:1. Introduction
2. Materials and Methods
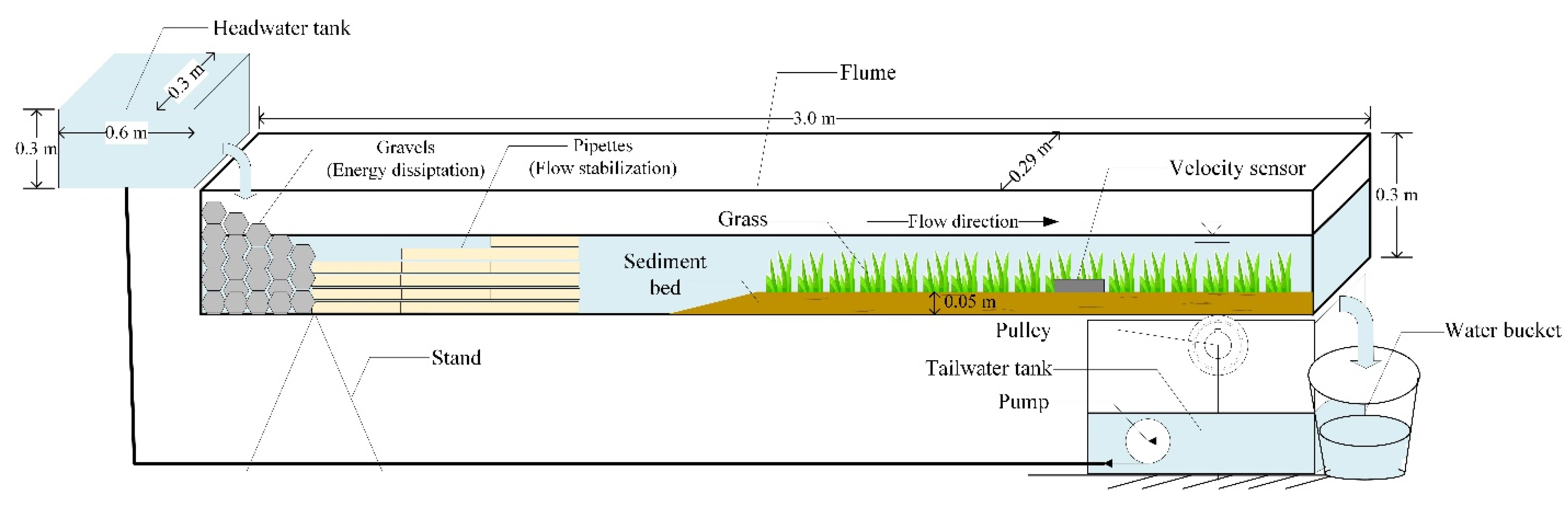
2.1. Flume Experiment Apparatus
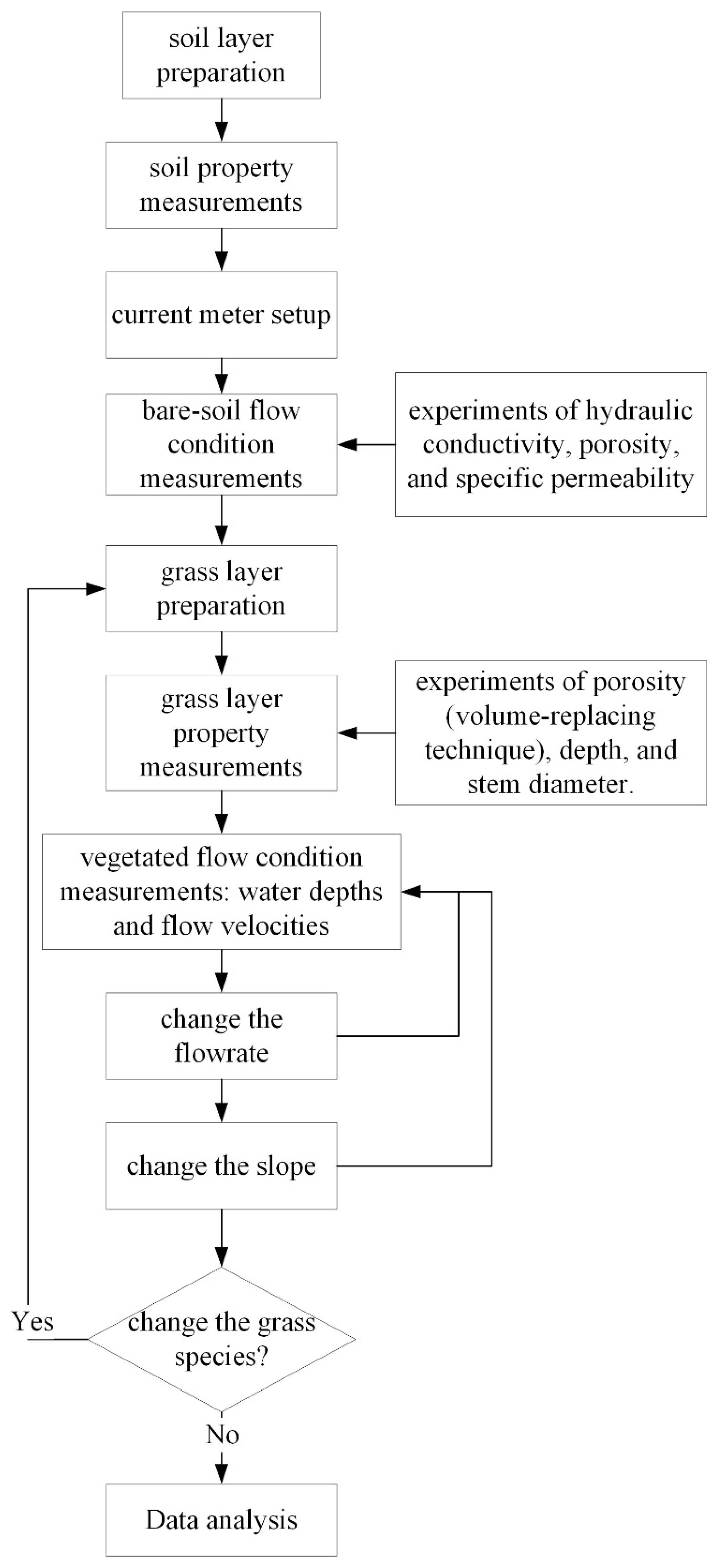
2.2. Experimental Procedure
2.3. Measurements of Soil Layer Properties
2.4. Measurements of Grass Layer Properties
2.5. Flow Velocity Measurements
2.5.1. Ultrasonic Current Meter
2.5.2. Electromagnetic Current Meter
2.5.3. The Bucket Method
2.5.4. Manning’s Equation
2.5.5. Analytical Solution for Water Flow Passing a Grass Layer
3. Results
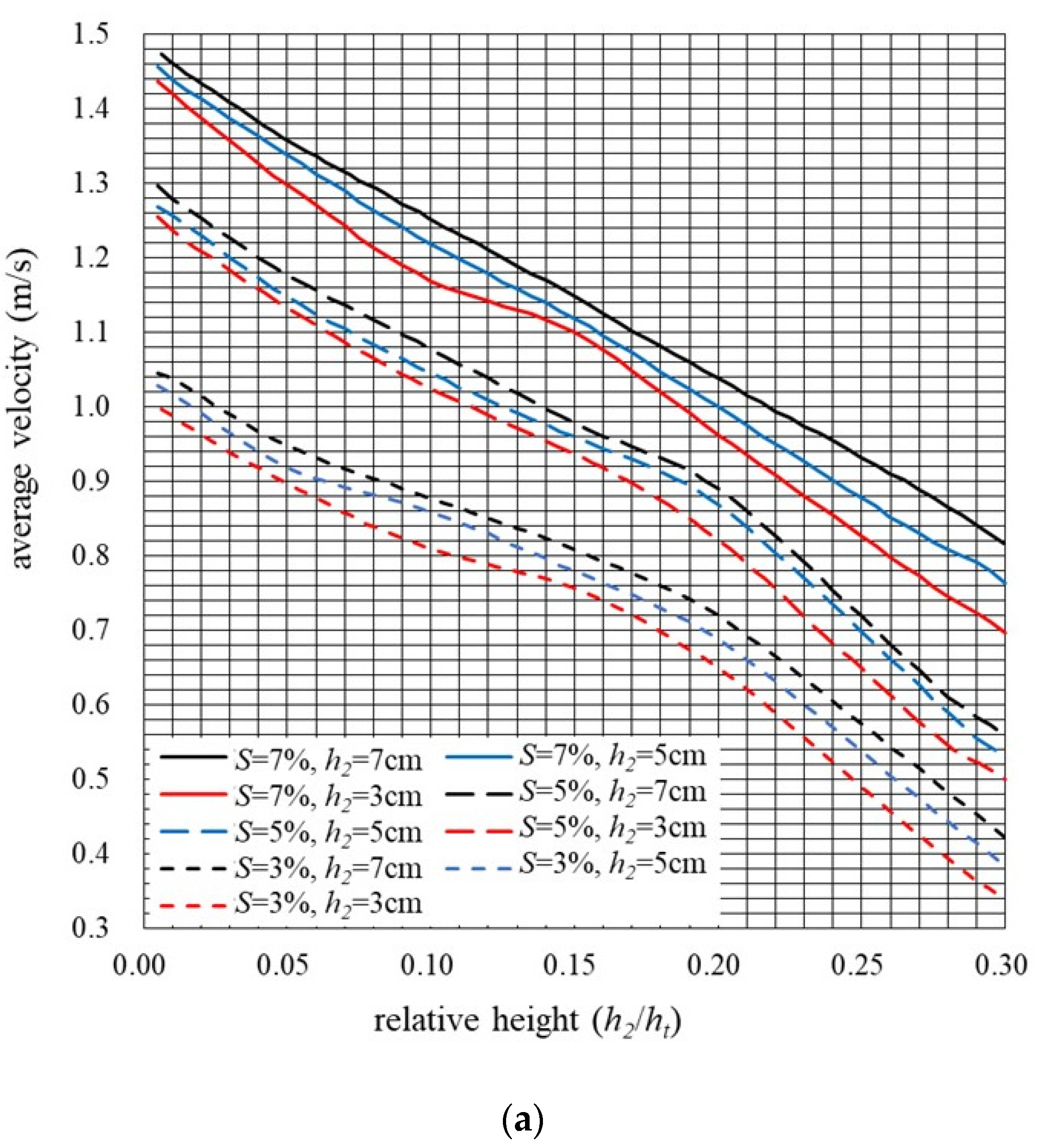
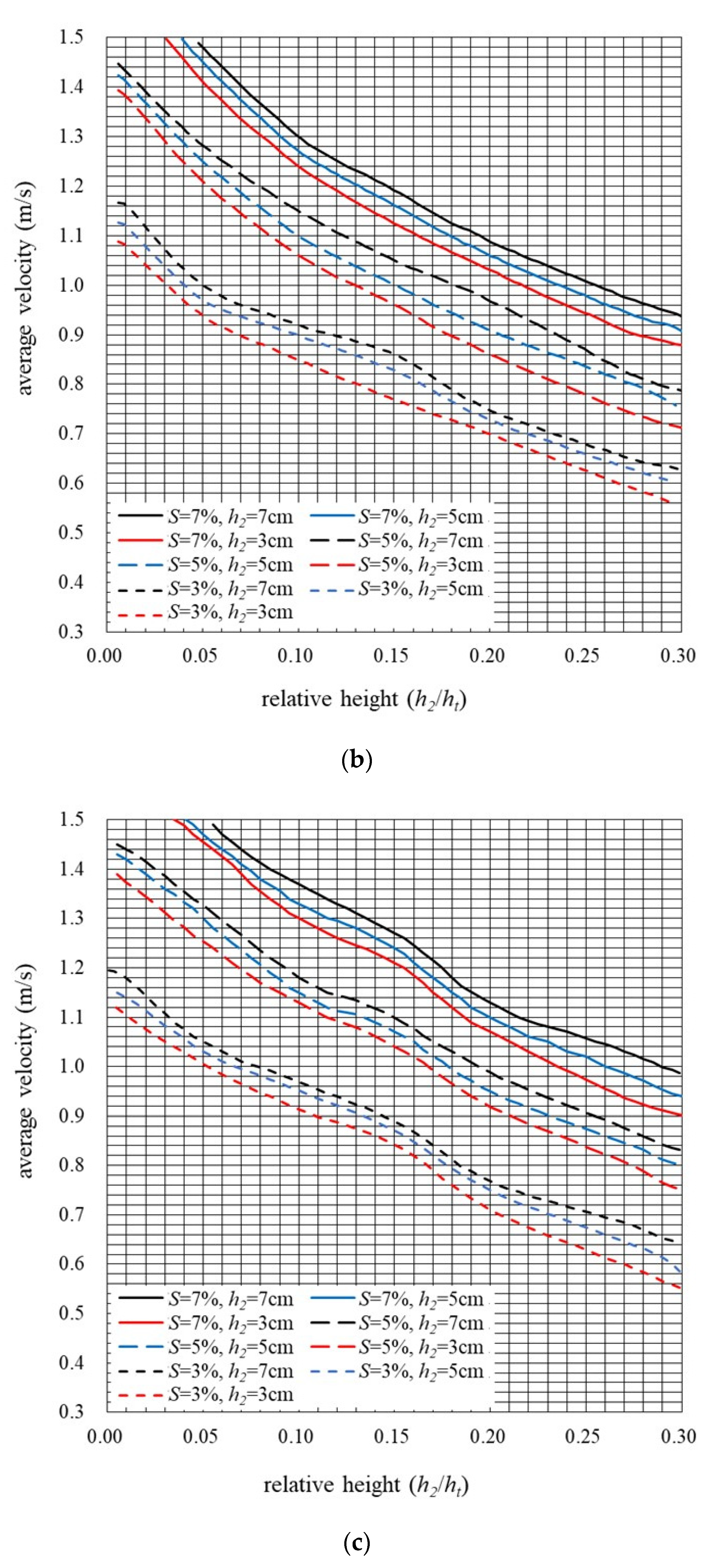
3.1. Average Flow Velocities with Different Relative Heights
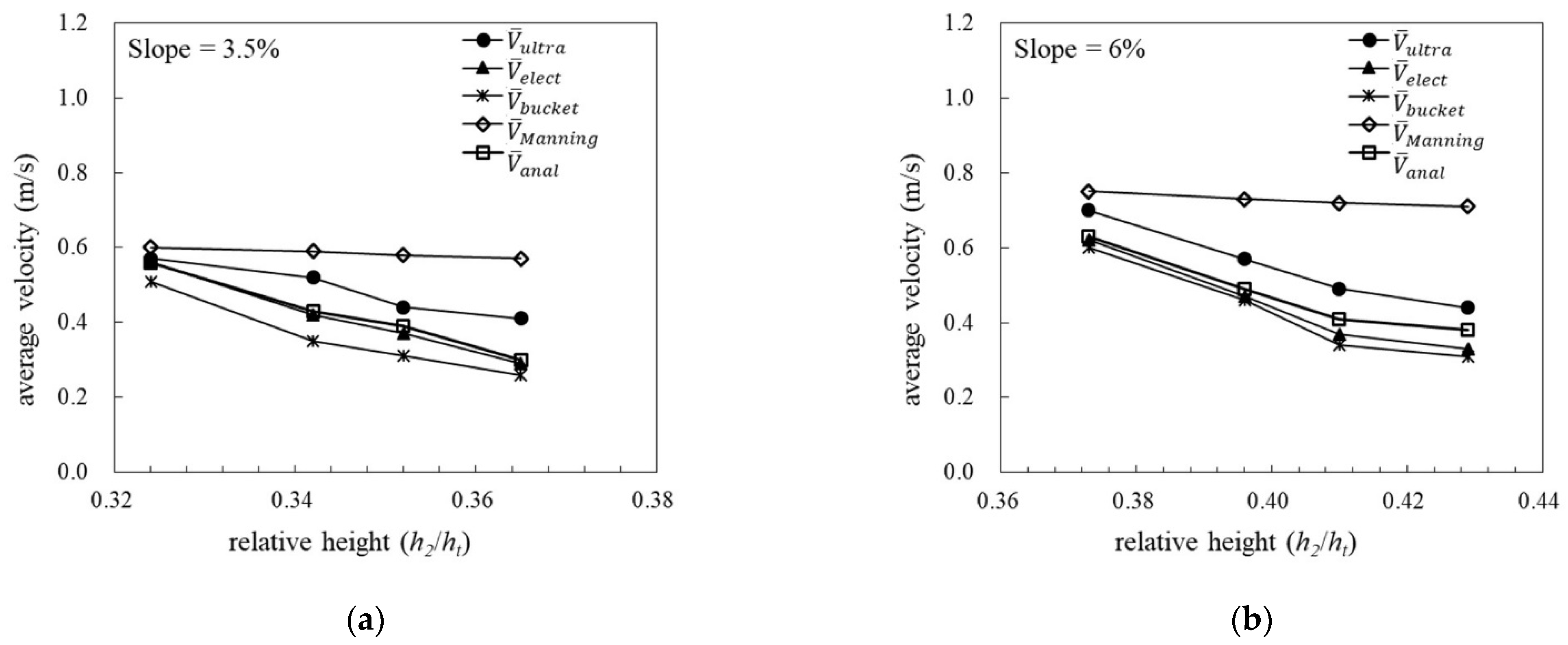
3.1.1. Velocity Variation in Cases of Centipede Grass
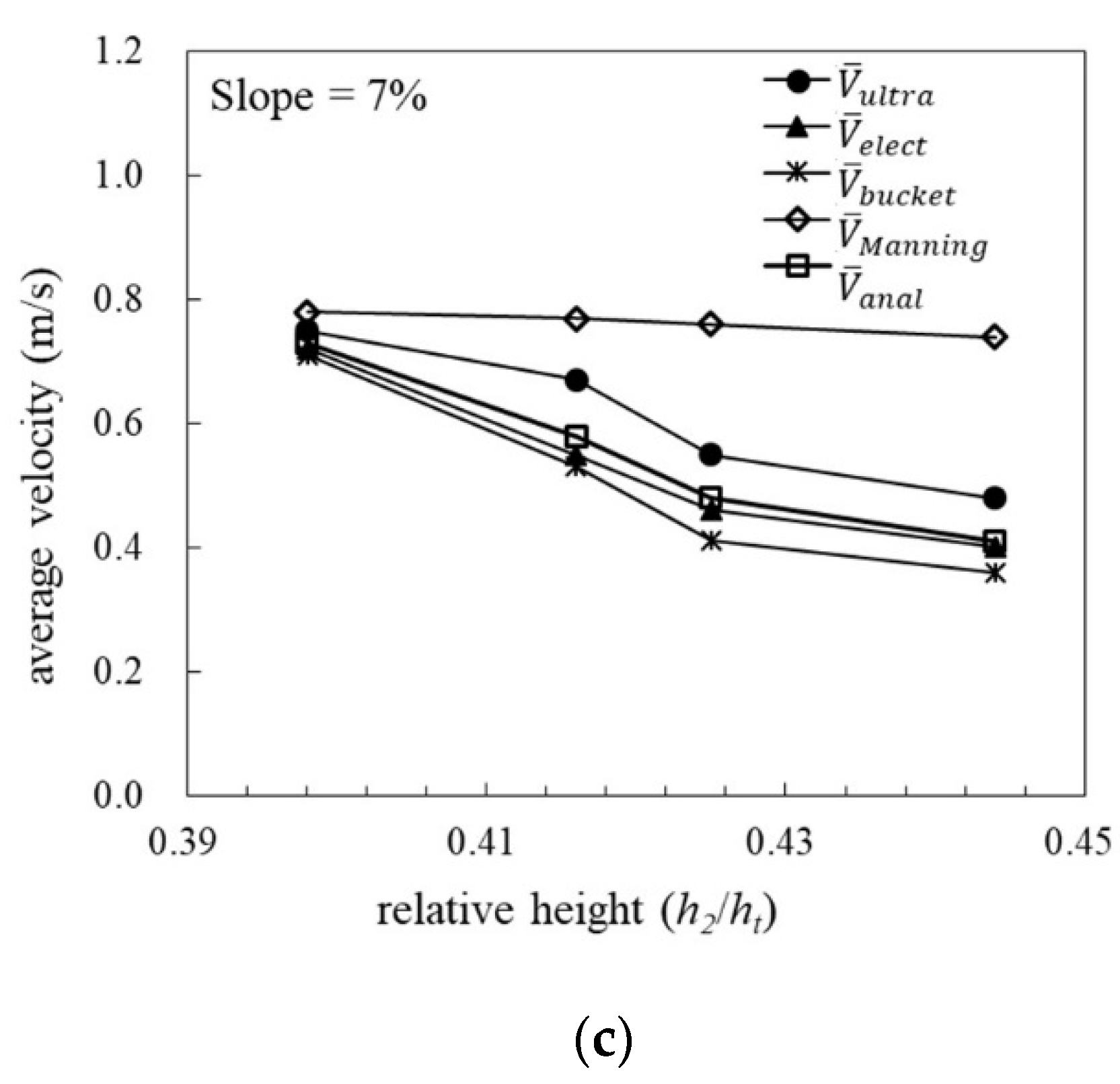
3.1.2. Velocity Variation in Cases of Bermuda Grass
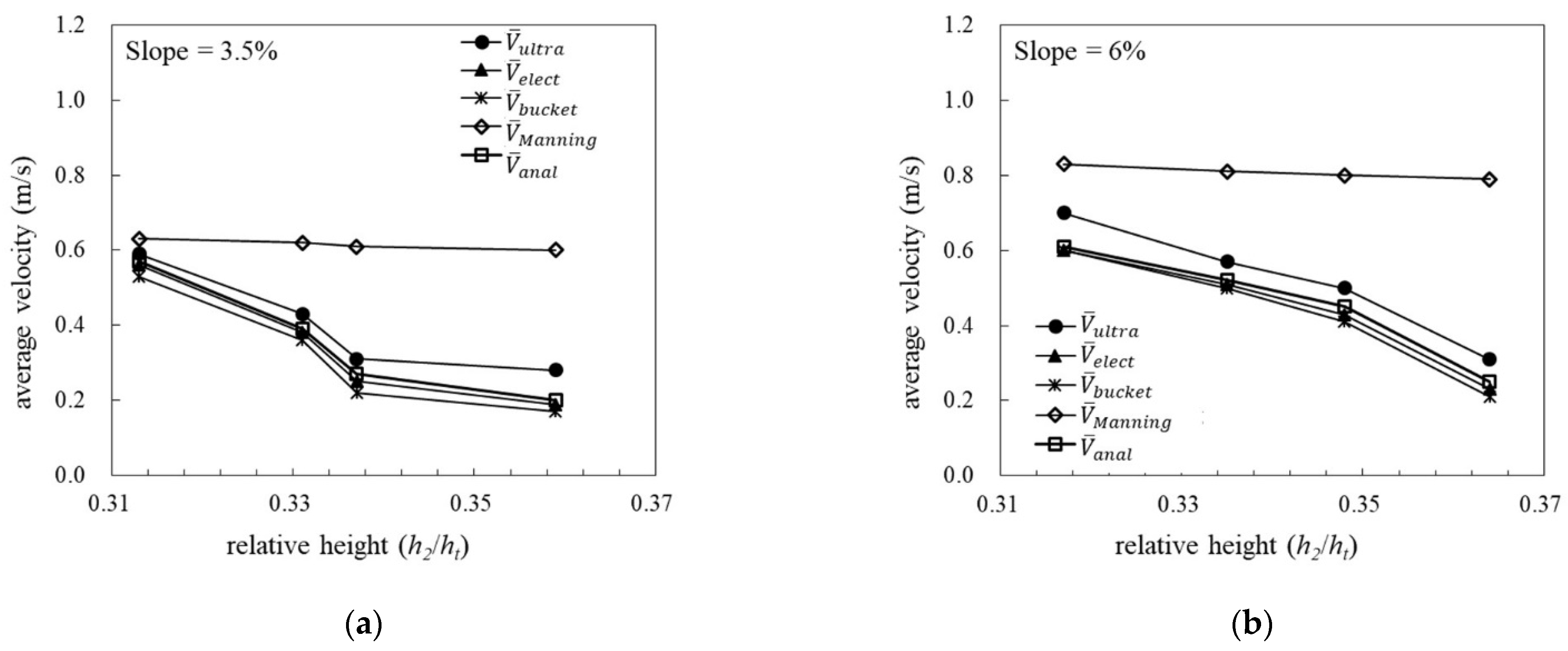
3.1.3. Velocity Variation in Cases of Carpet Grass
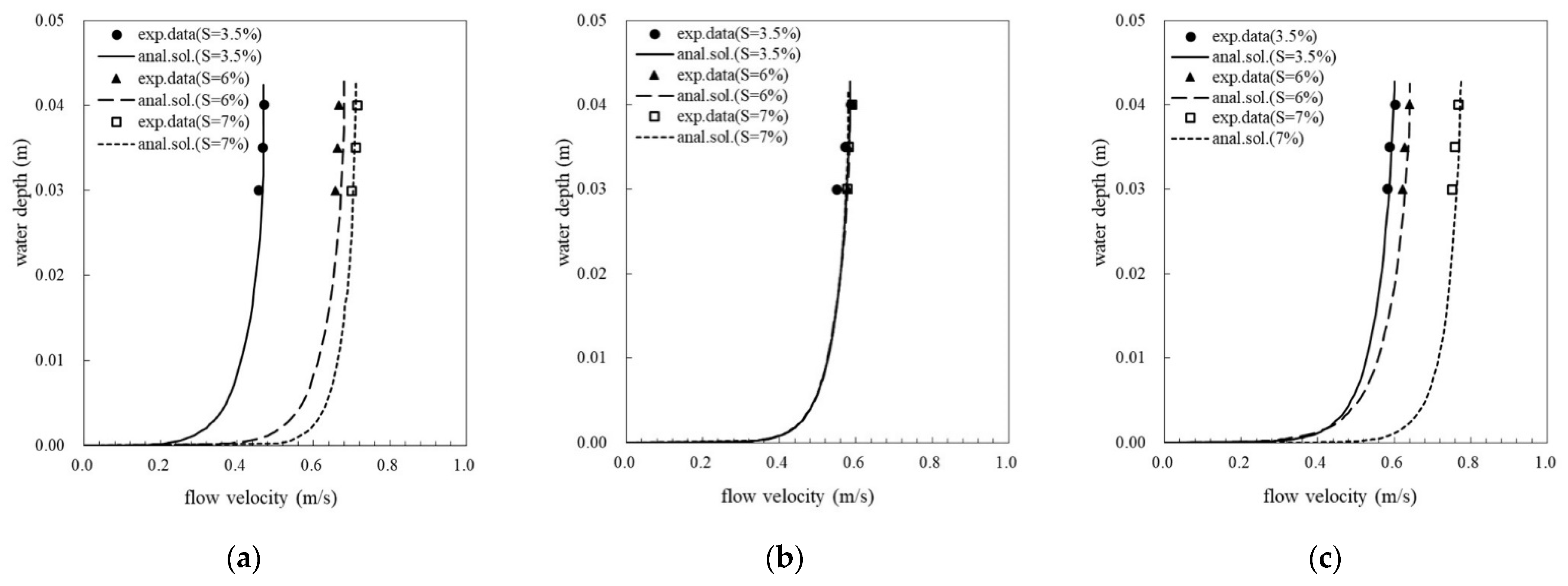
3.2. Velocity Profiles with Different Grass Species
4. Discussion
4.1. Comparison of Average Flow Velocity among the Three Grass Species
4.2. Comparison between Measured Values and the Analytical Solution of Average Flow Velocity
4.3. Comparison between Measured Values and Manning’s Estimations of Average Flow Velocity
4.4. Application to Grassed Channel Design
- From Manning’s equation, ,where ; .Take the suggested Manning’s n of Centipede grass, 0.055, in the Soil and Water Conservation Handbook [3], and thus, .
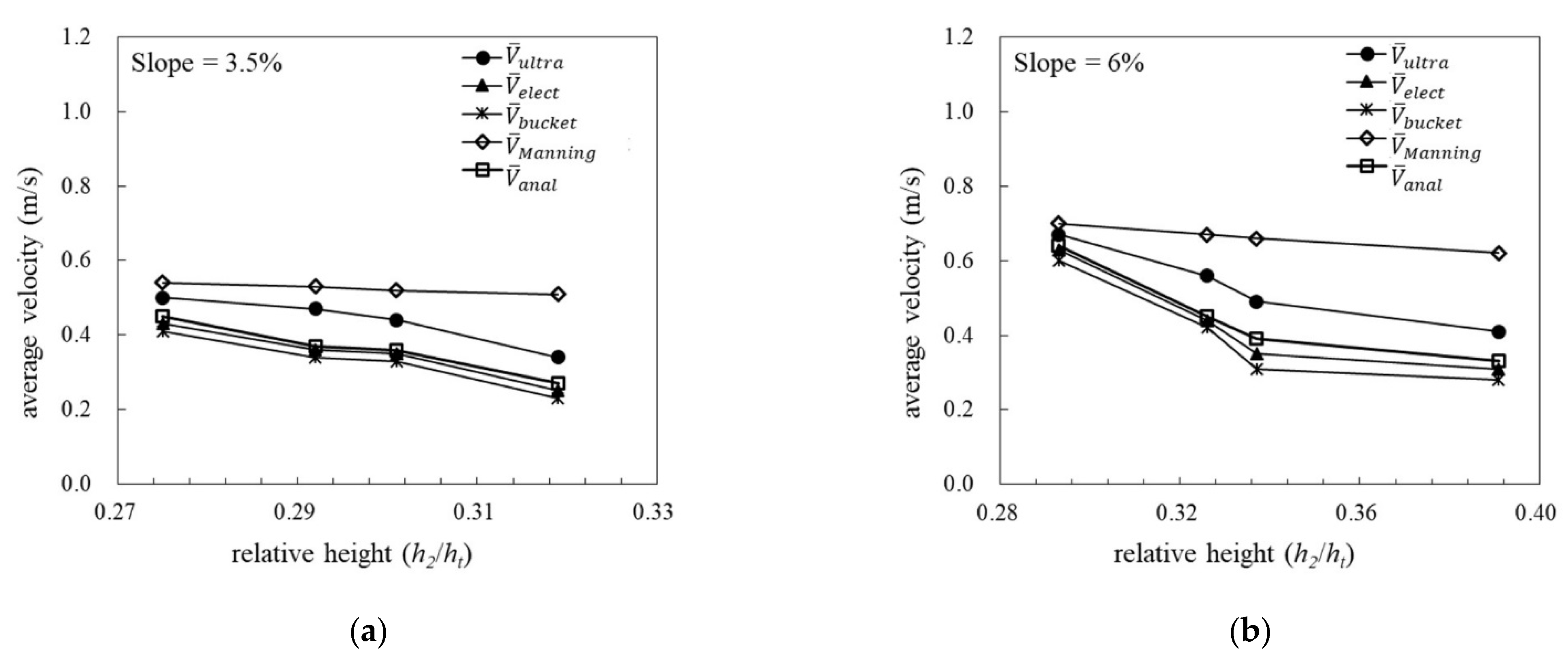
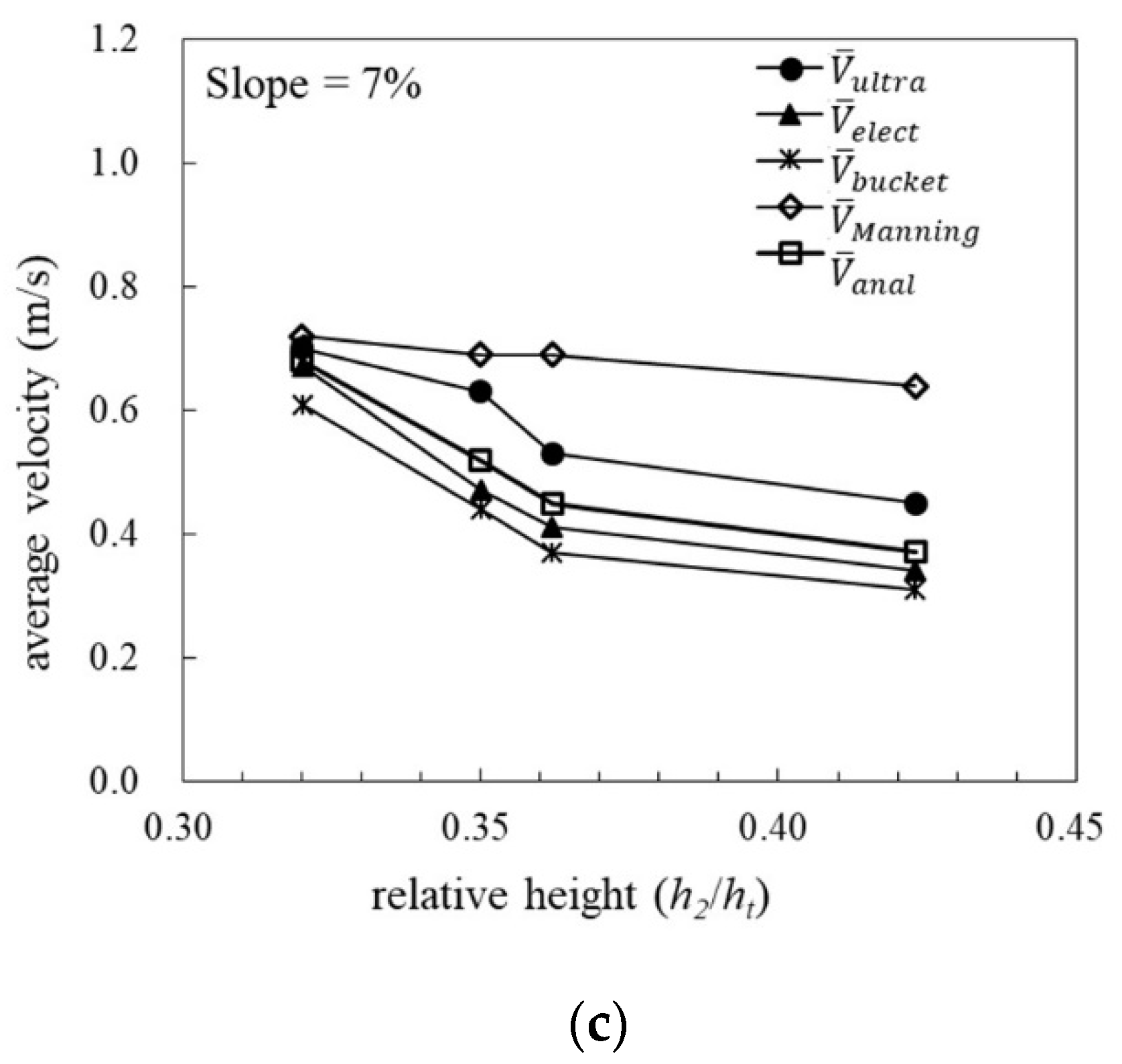
- Given that the grass layer height () is 0.05 m and the water depth () is 0.182 m, .From Figure 7a, .
- Thus, .
- Compare and , and find . This result implies that the flowrate calculated by Manning’s equation may be overestimated for grassed channel flows.
- Revise Manning’s n using the average velocity measured by the bucket method (Figure 3a), , , and thus .
- Revise Manning’s n using the average velocity calculated by the analytical solution, , , and thus .
- Compare , , and , we find that both and are larger than . This result implies that Manning’s coefficient should be larger than the suggested value in the Soil and Water Conservation Handbook [3] in Taiwan.
5. Conclusions
- The comparison between the five evaluating methods suggested that the average velocity evaluated from the different methods showed a general trend of in all the flow conditions. In the cases of a red soil bed (soil layer porosity of around 60%) and 3.5% slope, the values of varied from 0.92 to 1 and varied from 0.51 to 0.63. When the slope was 6%, varied from 0.86 to 0.99 and varied from 0.29 to 0.90. When the slope changed to 7%, varied from 0.91 to 0.99 and varied from 0.33 to 0.93. Therefore, the experimental values of flow velocity () fitted the analytical solution () very well, whereas generally overestimated the grassed flow velocity.
- Based on the relationships between the average flow and relative height (), Centipede grass showed the best flow decelerating effect when , and Carpet grass showed the best effect in cases of . Thus, Centipede grass or Carpet grass may be more effective when grassed channels are used to decelerate flow and enhance water infiltration for water conservancy, whereas Bermuda grass may be more suitable for grassed channels used to release floods for disaster prevention.
- The average velocity in grassed flow was found to be significantly affected by the morphological characteristics of grass, such as the height and porosity of the grass layer. Manning’s equation considered the roughness in channels using Manning’s coefficient, n, and thus was unable to properly reflect the grass layer characteristic effects on the flow velocity.
- The flow velocity profiles estimated using the analytical method matched well with the velocities observed at different water depths in grassed flow. Therefore, the experimental results will be beneficial for the verification of mathematical methods, including analytic solutions and numerical models of grassed flow. For application, we extended the analytical solution of flow velocity to grassed flow with three grass species and proposed curves of the average flow velocity against the relative height of the grass layer. When planning for a drainage system on hillslopes in Taiwan, the proposed curves can be used as references for grassed channel flowrate design in cases of red bed soil; 3% to 7% slopes; and grass species of Centipede grass, Bermuda grass, and Carpet grass.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Chang, C.-T.; Harrison, J.F.; Huang, Y.-C. Modeling typhoon-induced alterations on river sediment transport and turbidity based on dynamic landslide inventories: Gaoping river basin, Taiwan. Water 2015, 7, 6910–6930. [Google Scholar] [CrossRef] [Green Version]
- Chiang, L.-C.; Wang, Y.-C.; Liao, C.-J. Spatiotemporal Variation of Sediment Export from Multiple Taiwan Watersheds. Int. J. Environ. Res. Public Health 2019, 16, 1610. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Soil and Water Conservation Bureau. Soil and Water Conservation Handbook; Soil and Water Conservation Bureau, Council of Agriculture: Executive Yuan, Taiwan, 2005.
- Chow, V.T. Open-Channel Hydraulics; McGraw–Hill: New York, NY, USA, 1959. [Google Scholar]
- Samani, J.M.V.; Kouwen, N. Stability and Erosion in Grassed Channels. J. Hydraul. Eng. 2002, 128, 40–45. [Google Scholar] [CrossRef]
- Kirby, J.T.; Durrans, S.R.; Pitt, R.; Johnson, P.D. Hydraulic Resistance in Grass Swales Designed for Small Flow Conveyance. J. Hydraul. Eng. 2005, 131, 65–68. [Google Scholar] [CrossRef]
- Abood, M.A.; Yusuf, B.; Mohammed, T.; Ghazali, A. Manning roughness coefficient for grassed channel. Suranaree J. Sci. Technol. 2006, 13, 317–330. [Google Scholar]
- Fischenich, J.C. Resistance Due to Vegetation; EMRRP Technical Notes Collection (ERDC TN-EMRRP-SR-07); U.S. Army Engineer Research and Development Center: Vicksburg, MS, USA, 2000. [Google Scholar]
- Wu, F.C.; Shen, H.W.; Chou, Y.J. Variation of roughness coefficient for unsubmerged and submerged vegetation. J. Hydraul. Eng. 1999, 125, 934–942. [Google Scholar] [CrossRef] [Green Version]
- Abdelsalam, M.W.; Khattab, F.A.; Khalifa, A.A.; Bakry, F.M. Flow capacity through wide and submerged vegetation channels. J. Irrig. Drain. Eng. 1992, 150, 25–44. [Google Scholar]
- Kouwen, N.; Unny, E.T. Flexible roughness in open channels. J. Hydraul. Div. 1973, 99, 713–729. [Google Scholar] [CrossRef]
- Petryk, S.; Bosmajian, G. Analysis of flow through vegetation. J. Hydraul. Div. 1975, 101, 871–884. [Google Scholar] [CrossRef]
- Shih, S.F.; Rahi, G.S. Seasonal variations of Manning’s roughness coefficient in subtropical marsh. Trans. ASAE 1982, 25, 116–119. [Google Scholar] [CrossRef] [Green Version]
- Thompson, G.T.; Roberson, J.A. Theory of flow resistance for vegetated channels. Trans. ASAE 1976, 19, 288–293. [Google Scholar] [CrossRef]
- Maghdam, F.; Kouwen, N. Nonrigid, nonsubmerged vegetation roughnees on flood plains. J. Hydraul. Eng. 1997, 123, 51–56. [Google Scholar] [CrossRef]
- Righetii, M.; Armanini, A. Flow resistance in open channel flows with sparsely distribution bushes. J. Hydrol. 2002, 269, 55–64. [Google Scholar] [CrossRef]
- Palmer, V.J. A Method for Designing Vegetated Waterways. Agric. Eng. 1945, 26, 516–520. [Google Scholar]
- Cox, M.B.; Palmer, V.J. Results of Tests on Vegetated Waterways, and Methods of Field Application; Miscellaneous Publication No. MP-12; Oklahoma Agricultural Experiment Station, Oklahoma State University: Stillwater, Oklahoma, 1948; pp. 1–43. [Google Scholar]
- Ree, W.O.; Palmer, V.J. Flow of water in channels protected by vegetative linings. USDA Tech. Bull. 1949, 967, 115. [Google Scholar]
- USDA, Soil Conservation Service. Handbook of Channel Design for Soil and Water Conservation; SCS-TP-61; USDA, Soil Conservation Service: Washington, DC, USA, 1947; p. 34, Revised 1954.
- Temple, D.M. Flow Retardance of Submerged Grass Channel Linings. Trans. ASAE 1982, 25, 1300–1303. [Google Scholar] [CrossRef]
- Temple, D.M. Flow Resistance of Grassed Channel Banks. Appl. Eng. Agric. ASAE 1999, 15, 129–133. [Google Scholar] [CrossRef]
- Temple, D.M.; Cook, K.R.; Neilsen, M.L.; Yenna, S.K.R. Design of Grassed Channels: Procedure and Software Update. Am. Soc. Agric. Biol. Eng. 2003, 032099. [Google Scholar]
- Choong, P.K.; Deepak, T.J.; Raman, B. Determining Coefficient of Discharge and Coefficient of Roughness for Short Grass Bed and Concrete Bed. Int. J. Trend Sci. Res. Dev. 2018, 23–33. [Google Scholar]
- Rizalihadi, M.; Shaskia, N.; Asharly, H. The effect of ratio between rigid plant height and water depth on the manning’s coefficient in open channel. In IOP Conference Series: Materials Science and Engineering; IOP Publishing: Bristol, UK, 2018; Volume 352, p. 012039. [Google Scholar] [CrossRef]
- Rizalihadi, M.; Ziana; Shaskia, N. Approaching model of Manning’s coefficient due to an Effect of density and height of vegetation in open channel. In IOP Conference Series: Materials Science and Engineering; IOP Publishing: Bristol, UK, 2019; Volume 523, p. 012033. [Google Scholar] [CrossRef]
- Wang, W.-J.; Peng, W.-Q.; Huai, W.-X.; Qu, X.-D.; Dong, F.; Feng, J. Roughness height of submerged vegetation in flow based on spatial structure. J. Hydrodyn. 2018, 30, 531–534. [Google Scholar] [CrossRef]
- Wang, W.-J.; Peng, W.-Q.; Huai, W.-X.; Katul, G.G.; Liu, X.-B.; Qu, X.-D.; Dong, F. Friction factor for turbulent open channel flow covered by vegetation. Sci. Rep. 2019, 9, 5178. [Google Scholar] [CrossRef] [PubMed]
- Wang, W.-J.; Cui, X.-Y.; Dong, F.; Peng, W.-Q.; Han, Z.; Huang, A.-P.; Chen, X.-K.; Si, Y. Predictions of bulk velocity for open channel flow through submerged vegetation. J. Hydrodyn. 2020, 42241. [Google Scholar] [CrossRef]
- Hsieh, P.-C.; Shiu, Y.-S. Analytical solutions for water flow passing over a vegetal area. Adv. Water Resour. 2006, 29, 1257–1266. [Google Scholar] [CrossRef]
| Grass Species | Parameters (Unit) | Values |
|---|---|---|
| Centipede grass (Eremochloa ophiuroides) | Height (m) | 0.031 |
| Porosity (-) | 0.715 | |
| Specific permeability (m2) | 1.765 × 10−7 | |
| Manning’s n a (-) | 0.055 | |
| Bermuda grass (Cynodon dactylon) | Height (m) | 0.036 |
| Porosity (-) | 0.947 | |
| Specific permeability (m2) | 2.941 × 10−7 | |
| Manning’s n b (-) | 0.05 | |
| Carpet grass (Axonopus) | Height (m) | 0.041 |
| Porosity (-) | 0.781 | |
| Specific permeability (m2) | 1.987 × 10−6 | |
| Manning’s n a (-) | 0.05 |
| Grass Species | Slope (%) | ||||
|---|---|---|---|---|---|
| Centipede grass | 3.5 | 0.44 | 0.08 | 0.79 | 0.14 |
| 6 | 0.52 | 0.12 | 1.04 | 0.20 | |
| 7 | 0.58 | 0.16 | 1.01 | 0.29 | |
| Bermuda grass | 3.5 | 0.51 | 0.21 | 0.91 | 0.25 |
| 6 | 0.49 | 0.08 | 1.20 | 0.20 | |
| 7 | 0.44 | 0.12 | 1.04 | 0.19 | |
| Carpet grass | 3.5 | 0.33 | 0.10 | 1.18 | 0.15 |
| 6 | 0.36 | 0.05 | 1.51 | 0.11 | |
| 7 | 0.25 | 0.08 | 1.38 | 0.11 | |
| RMSE | 0.447 | 0.120 | 1.138 | 0.191 | |
| Grass Species | Slope | ||||
|---|---|---|---|---|---|
| Centipede grass | 3.5% | 0.319 | 0.85 | 1.25 | 0.92 |
| 0.301 | 0.91 | 1.22 | 0.97 | ||
| 0.292 | 0.93 | 1.28 | 0.98 | ||
| 0.275 | 0.92 | 1.12 | 0.96 | ||
| 6% | 0.391 | 0.84 | 1.23 | 0.93 | |
| 0.337 | 0.80 | 1.26 | 0.90 | ||
| 0.326 | 0.93 | 1.23 | 0.97 | ||
| 0.293 | 0.93 | 1.04 | 0.98 | ||
| 7% | 0.423 | 0.83 | 1.20 | 0.91 | |
| 0.362 | 0.82 | 1.18 | 0.91 | ||
| 0.350 | 0.85 | 1.22 | 0.91 | ||
| 0.320 | 0.90 | 1.03 | 0.99 | ||
| Bermuda grass | 3.5% | 0.365 | 0.86 | 1.36 | 0.96 |
| 0.352 | 0.79 | 1.12 | 0.94 | ||
| 0.342 | 0.82 | 1.22 | 0.98 | ||
| 0.324 | 0.91 | 1.02 | 1.00 | ||
| 6% | 0.429 | 0.81 | 1.14 | 0.86 | |
| 0.410 | 0.84 | 1.21 | 0.91 | ||
| 0.396 | 0.95 | 1.17 | 0.97 | ||
| 0.373 | 0.95 | 1.10 | 0.98 | ||
| 7% | 0.444 | 0.87 | 1.16 | 0.97 | |
| 0.425 | 0.85 | 1.14 | 0.95 | ||
| 0.416 | 0.91 | 1.15 | 0.94 | ||
| 0.398 | 0.97 | 1.03 | 0.99 | ||
| Carpet grass | 3.5% | 0.359 | 0.84 | 1.39 | 0.94 |
| 0.337 | 0.82 | 1.15 | 0.93 | ||
| 0.331 | 0.92 | 1.09 | 0.97 | ||
| 0.313 | 0.93 | 1.04 | 0.98 | ||
| 6% | 0.364 | 0.84 | 1.24 | 0.92 | |
| 0.348 | 0.92 | 1.12 | 0.96 | ||
| 0.335 | 0.96 | 1.09 | 0.97 | ||
| 0.317 | 0.99 | 1.15 | 0.99 | ||
| 7% | 0.393 | 0.95 | 1.10 | 0.98 | |
| 0.374 | 0.96 | 1.04 | 0.98 | ||
| 0.368 | 0.93 | 1.08 | 0.98 | ||
| 0.346 | 0.94 | 1.05 | 0.99 |
| Grass Species | Slope | ||||
|---|---|---|---|---|---|
| Centipede grass | 3.5% | 0.319 | 0.45 | 0.67 | 0.51 |
| 0.301 | 0.63 | 0.84 | 0.52 | ||
| 0.292 | 0.64 | 0.89 | 0.53 | ||
| 0.275 | 0.76 | 0.93 | 0.54 | ||
| 6% | 0.391 | 0.45 | 0.66 | 0.50 | |
| 0.337 | 0.47 | 0.74 | 0.53 | ||
| 0.326 | 0.63 | 0.84 | 0.66 | ||
| 0.293 | 0.86 | 0.96 | 0.90 | ||
| 7% | 0.423 | 0.48 | 0.70 | 0.53 | |
| 0.362 | 0.54 | 0.77 | 0.60 | ||
| 0.350 | 0.63 | 0.91 | 0.68 | ||
| 0.320 | 0.85 | 0.97 | 0.93 | ||
| Bermuda grass | 3.5% | 0.365 | 0.46 | 0.72 | 0.57 |
| 0.352 | 0.54 | 0.76 | 0.58 | ||
| 0.342 | 0.60 | 0.89 | 0.59 | ||
| 0.324 | 0.85 | 0.95 | 0.60 | ||
| 6% | 0.429 | 0.44 | 0.62 | 0.47 | |
| 0.410 | 0.47 | 0.68 | 0.51 | ||
| 0.396 | 0.63 | 0.78 | 0.65 | ||
| 0.373 | 0.80 | 0.94 | 0.83 | ||
| 7% | 0.444 | 0.48 | 0.64 | 0.54 | |
| 0.425 | 0.54 | 0.73 | 0.61 | ||
| 0.416 | 0.69 | 0.88 | 0.72 | ||
| 0.398 | 0.91 | 0.96 | 0.92 | ||
| Carpet grass | 3.5% | 0.359 | 0.28 | 0.47 | 0.60 |
| 0.337 | 0.36 | 0.51 | 0.61 | ||
| 0.331 | 0.58 | 0.69 | 0.62 | ||
| 0.313 | 0.84 | 0.94 | 0.63 | ||
| 6% | 0.364 | 0.27 | 0.39 | 0.29 | |
| 0.348 | 0.51 | 0.63 | 0.54 | ||
| 0.335 | 0.62 | 0.70 | 0.63 | ||
| 0.317 | 0.72 | 0.84 | 0.72 | ||
| 7% | 0.393 | 0.32 | 0.37 | 0.33 | |
| 0.374 | 0.53 | 0.58 | 0.54 | ||
| 0.368 | 0.68 | 0.79 | 0.71 | ||
| 0.346 | 0.81 | 0.91 | 0.85 |
| Grass Species | Centipede Grass | Bermuda Grass | Carpet Grass | ||
|---|---|---|---|---|---|
| Porosity | |||||
| Height (m) | |||||
| 0.02 | 0.710 | 0.944 | 0.765 | ||
| 0.03 | 0.715 | 0.947 | 0.770 | ||
| 0.04 | 0.718 | 0.949 | 0.779 | ||
| 0.05 | 0.720 | 0.951 | 0.783 | ||
| 0.06 | 0.725 | 0.955 | 0.792 | ||
| 0.07 | 0.729 | 0.957 | 0.796 | ||
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Hsieh, P.-C.; Lin, Y.-C.; Wang, Y.-C. Comparison of Empirical and Analytical Solutions for Open-Channel Flow Velocity with Common Grass Species in Taiwan. Water 2021, 13, 1839. https://doi.org/10.3390/w13131839
Hsieh P-C, Lin Y-C, Wang Y-C. Comparison of Empirical and Analytical Solutions for Open-Channel Flow Velocity with Common Grass Species in Taiwan. Water. 2021; 13(13):1839. https://doi.org/10.3390/w13131839
Chicago/Turabian StyleHsieh, Ping-Cheng, Yi-Cheng Lin, and Yung-Chieh Wang. 2021. "Comparison of Empirical and Analytical Solutions for Open-Channel Flow Velocity with Common Grass Species in Taiwan" Water 13, no. 13: 1839. https://doi.org/10.3390/w13131839






