Assessing the Extinction Risk of Heterocypris incongruens (Crustacea: Ostracoda) in Climate Change with Sensitivity and Uncertainty Analysis
Abstract
:1. Introduction
2. Materials and Methods
2.1. Potential Hydroperiod and Hydroperiod Unpredictability
2.2. Clonal Lineages
2.3. Cohen’s Model, Egg Bank Dynamics and Extinction Rate
2.4. Factor Fixing: Morris’ Method
2.5. Uncertainty Analysis, Regionalized Sensitivity Analysis (RSA) and Global Sensitivity Analysis (GSA)
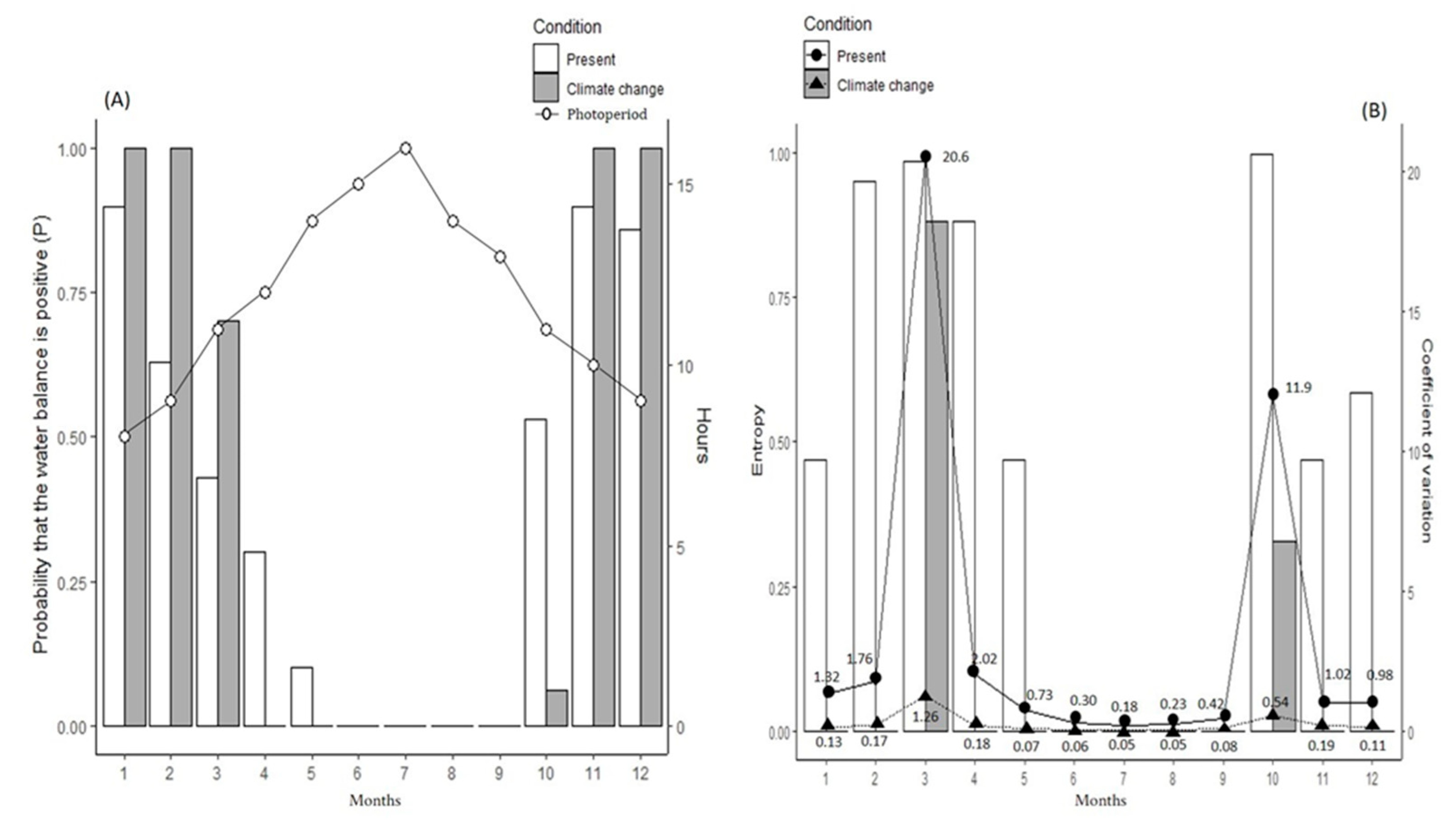
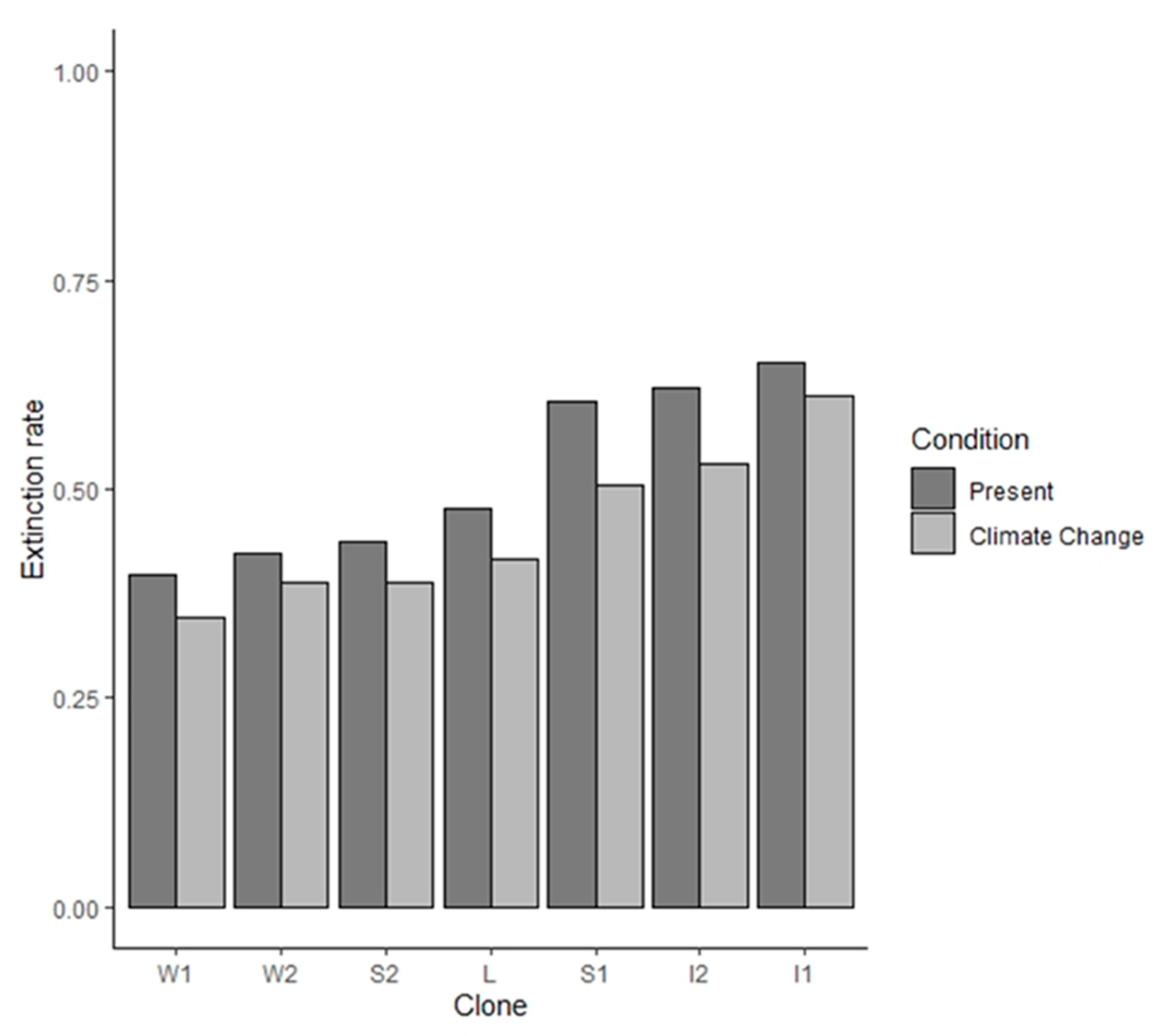
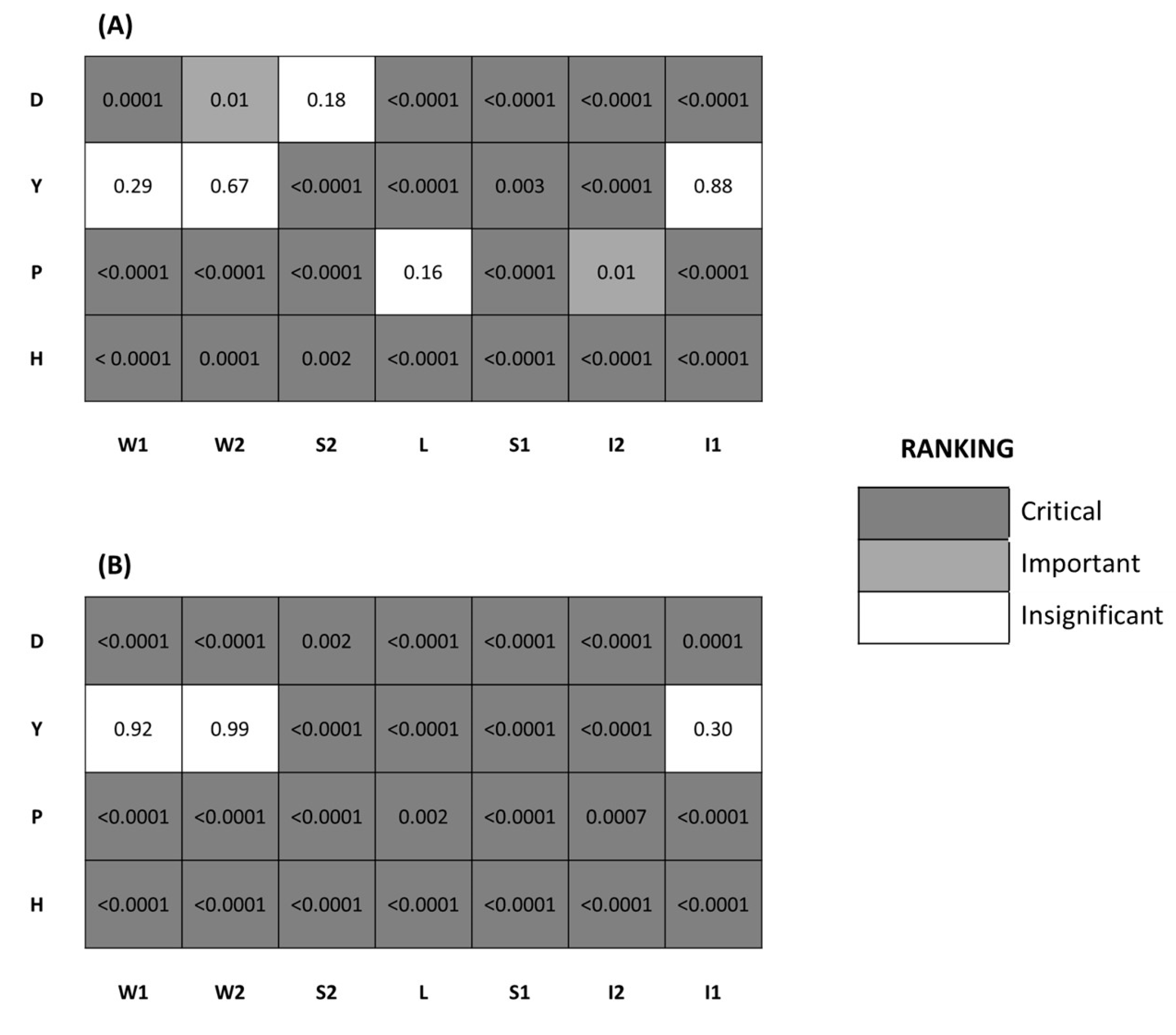
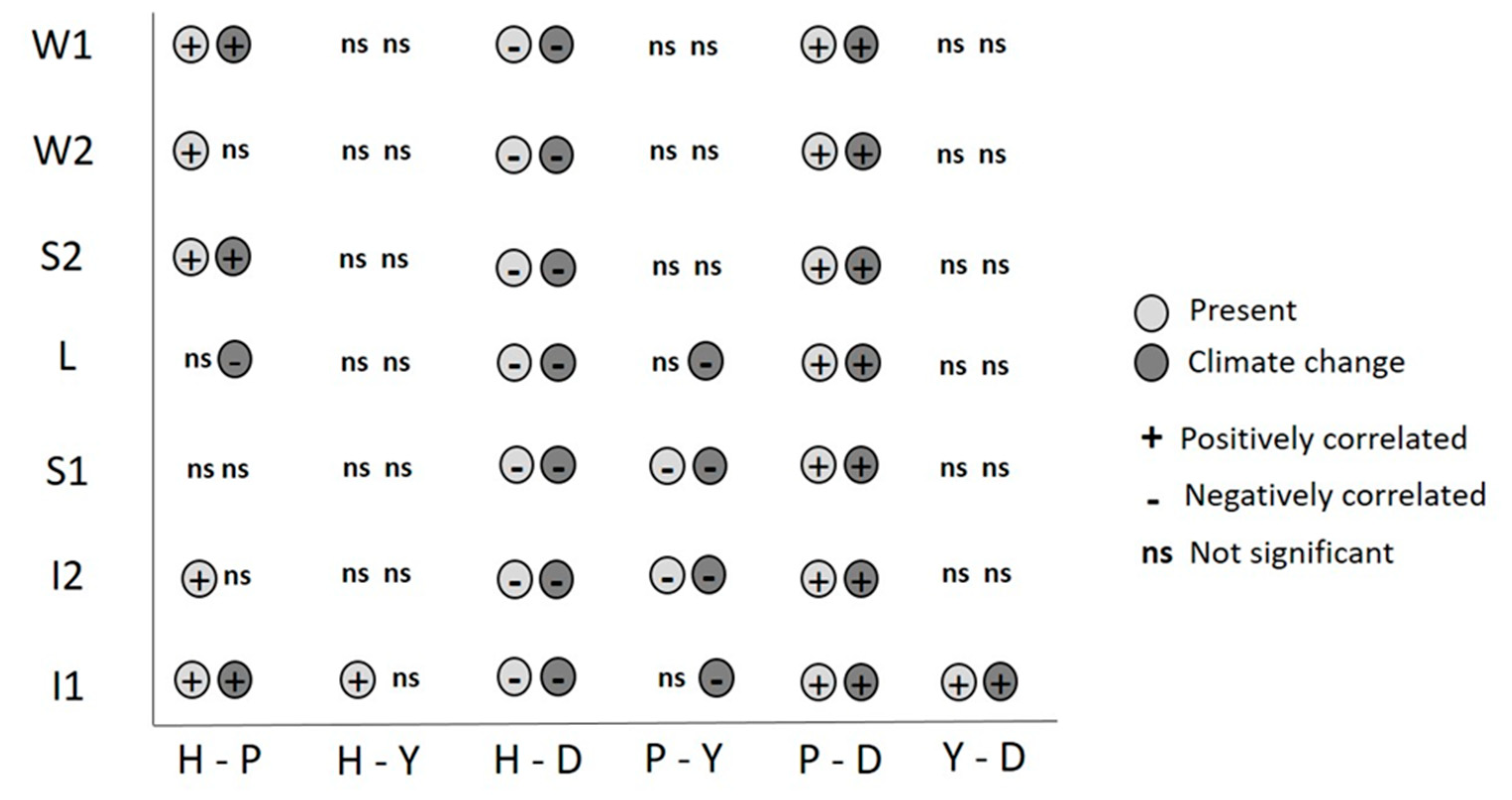
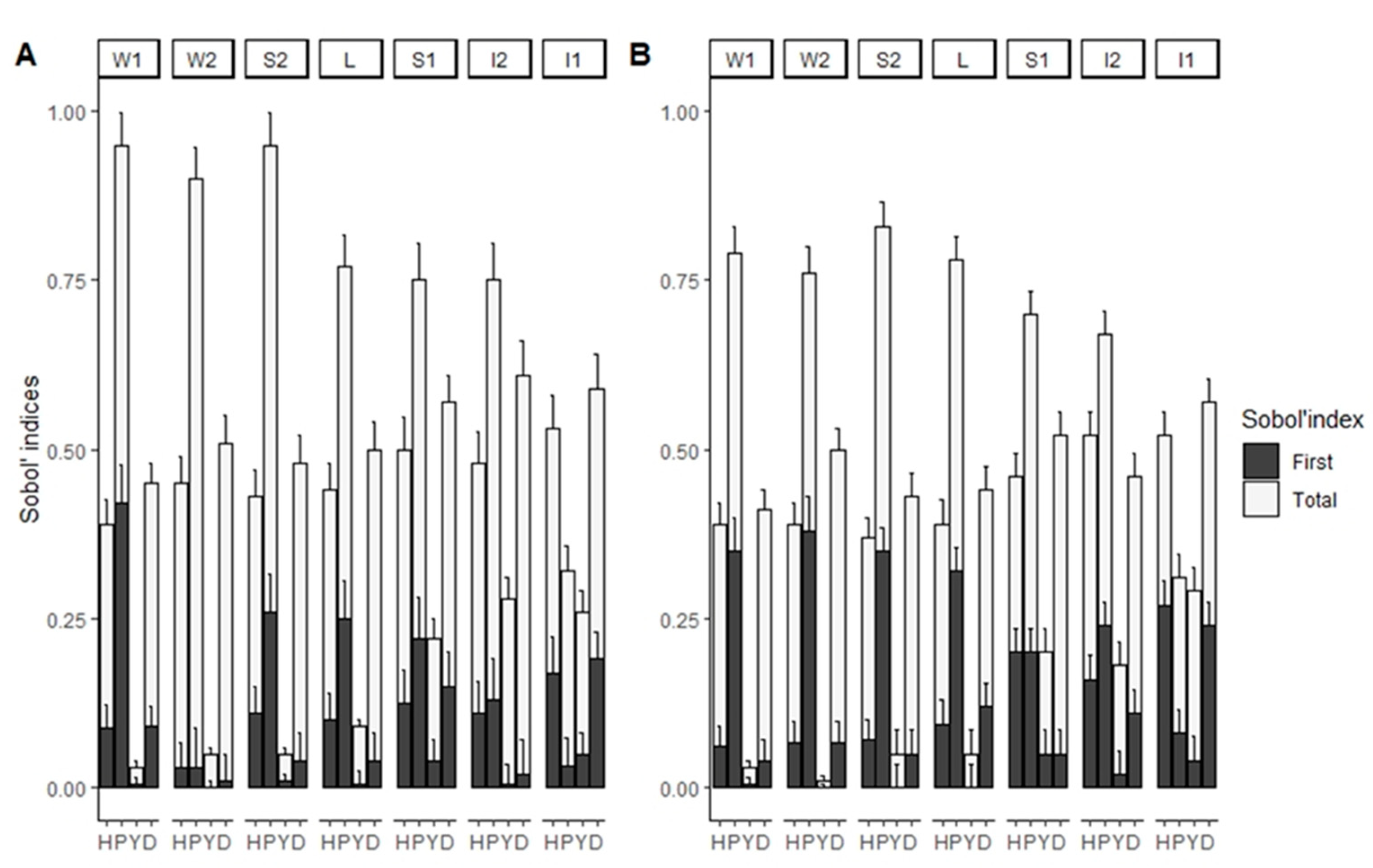
3. Results
4. Discussion
5. Conclusions
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Urban, M.C. Accelerating extinction risk from climate change. Science 2015, 348, 571–573. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Vadadi-Fülöp, C.; Sipkay, C.; Mészáros, G.; Hufnagel, L. Climate change and freshwater zooplankton: What does it boil down to? Aquat. Ecol. 2012, 46, 501–519. [Google Scholar] [CrossRef] [Green Version]
- Wiens, J.J. Climate-Related Local Extinctions Are Already Widespread among Plant and Animal Species. PLoS Biol. 2016, 14, 1–18. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Catullo, R.A.; Llewelyn, J.; Phillips, B.L.; Moritz, C.C. The Potential for Rapid Evolution under Anthropogenic Climate Change. Curr. Biol. 2019, 29, R996–R1007. [Google Scholar] [CrossRef]
- Diniz-Filho, J.A.F.; Bini, L.M. Will life find a way out? Evolutionary rescue and Darwinian adaptation to climate change. Perspect. Ecol. Conserv. 2019, 17, 117–121. [Google Scholar] [CrossRef]
- Gienapp, P.; Teplitsky, C.; Alho, J.S.; Mills, J.A.; Merilä, J. Climate change and evolution: Disentangling environmental and genetic responses. Mol. Ecol. 2008, 17, 167–178. [Google Scholar] [CrossRef]
- Hoffmann, A.A.; Sgró, C.M. Climate change and evolutionary adaptation. Nature 2011, 470, 479–485. [Google Scholar] [CrossRef]
- Moritz, C.; Agudo, R. The future of species under climate change: Resilience or decline? Science 2013, 341, 504–508. [Google Scholar] [CrossRef]
- Román-Palacios, C.; Wiens, J.J. Recent responses to climate change reveal the drivers of species extinction and survival. Proc. Natl. Acad. Sci. USA 2020, 117, 4211–4217. [Google Scholar] [CrossRef] [PubMed]
- Waldvogel, A.; Feldmeyer, B.; Rolshausen, G.; Exposito-Alonso, M.; Rellstab, C.; Kofler, R.; Mock, T.; Schmid, K.; Schmitt, I.; Bataillon, T.; et al. Evolutionary genomics can improve prediction of species’ responses to climate change. Evol. Lett. 2020, 4, 4–18. [Google Scholar] [CrossRef]
- Williams, S.E.; Shoo, L.P.; Isaac, J.L.; Hoffmann, A.A.; Langham, G. Towards an integrated framework for assessing the vulnerability of species to climate change. PLoS Biol. 2008, 6. [Google Scholar] [CrossRef] [PubMed]
- Carvalho, S.B.; Torres, J.; Tarroso, P.; Velo-Antón, G. Genes on the edge: A framework to detect genetic diversity imperiled by climate change. Glob. Chang. Biol. 2019, 25, 4034–4047. [Google Scholar] [CrossRef]
- Razgour, O.; Forester, B.; Taggart, J.B.; Bekaert, M.; Juste, J.; Ibáñez, C.; Puechmaille, S.J.; Novella-Fernandez, R.; Alberdi, A.; Manel, S. Considering adaptive genetic variation in climate change vulnerability assessment reduces species range loss projections. Proc. Natl. Acad. Sci. USA 2019, 116, 10418–10423. [Google Scholar] [CrossRef] [Green Version]
- Matesanz, S.; Ramírez-Valiente, J.A. A review and meta-analysis of intraspecific differences in phenotypic plasticity: Implications to forecast plant responses to climate change. Glob. Ecol. Biogeogr. 2019, 28, 1682–1694. [Google Scholar] [CrossRef]
- Brendonck, L.; Pinceel, T.; Ortells, R. Dormancy and dispersal as mediators of zooplankton population and community dynamics along a hydrological disturbance gradient in inland temporary pools. Hydrobiologia 2017, 796, 201–222. [Google Scholar] [CrossRef]
- Brock, M.A.; Nielsen, D.L.; Shiel, R.J.; Green, J.D.; Langley, J.D. Drought and aquatic community resilience: The role of eggs and seeds in sediments of temporary wetlands. Freshw. Biol. 2003, 48, 1207–1218. [Google Scholar] [CrossRef]
- Cáceres, C.E. Seasonal dynamics and interspecific competition in Oneida Lake Daphnia. Oecologia 1998, 115, 233–244. [Google Scholar] [CrossRef] [PubMed]
- De Meester, L.; Declerck, S.; Stoks, R.; Louette, G.; Van De Meutter, F.; De Bie, T.; Michels, E.; Brendonck, L. Ponds and pools as model systems in conservation biology, ecology and evolutionary biology. Aquat. Conserv. Mar. Freshw. Ecosyst. 2005, 15, 715–725. [Google Scholar] [CrossRef]
- Brendonck, L.; De Meester, L. Egg banks in freshwater zooplankton: Evolutionary and ecological archives in the sediment. Hydrobiologia 2003, 491, 65–84. [Google Scholar] [CrossRef]
- De Stasio, B.T. The seed bank of a freshwater crustacean: Copepodology for the plant ecologist. Ecology 1989, 70, 1377–1389. [Google Scholar] [CrossRef]
- Hairston, N.G.; De Stasio, B.T. Rate of evolution slowed by a dormant propagule pool. Nature 1988, 336, 239–242. [Google Scholar] [CrossRef]
- Cohen, D. Optimizing reproduction in a randomly varying environment. J. Theor. Biol. 1966, 12, 119–129. [Google Scholar] [CrossRef]
- García-Roger, E.M.; Serra, M.; Carmona, M.J. Bet-hedging in diapausing egg hatching of temporary rotifer populations—A review of models and new insights. Int. Rev. Hydrobiol. 2014, 99, 96–106. [Google Scholar] [CrossRef]
- Maffei, C.; Vagaggini, D.; Zarattini, P.; Mura, G. The dormancy problem for Crustacea Anostraca: A rigorous model connecting hatching strategies and environmental conditions. Ecol. Modell. 2005, 185, 469–481. [Google Scholar] [CrossRef]
- Spencer, M.; Colegrave, N.; Schwartz, S.S. Hatching fraction and timing of resting stage production in seasonal environments: Effects of density dependence and uncertain season length. J. Evol. Biol. 2001, 14, 357–367. [Google Scholar] [CrossRef]
- Gianuca, A.T.; Declerck, S.A.J.; Lemmens, P.; De Meester, L. Effects of dispersal and environmental heterogeneity on the replacement and nestedness components of β-diversity. Ecology 2017, 98, 525–533. [Google Scholar] [CrossRef]
- Childs, D.Z.; Metcalf, C.J.E.; Rees, M. Evolutionary bet-hedging in the real world: Empirical evidence and challenges revealed by plants. Proc. R. Soc. B Biol. Sci. 2010, 277, 3055–3064. [Google Scholar] [CrossRef] [Green Version]
- Gremer, J.R.; Venable, D.L. Bet hedging in desert winter annual plants: Optimal germination strategies in a variable environment. Ecol. Lett. 2014, 17, 380–387. [Google Scholar] [CrossRef]
- Simons, A.M. Modes of response to environmental change and the elusive empirical evidence for bet hedging. Proc. R. Soc. B Biol. Sci. 2011, 278, 1601–1609. [Google Scholar] [CrossRef] [Green Version]
- Pinceel, T.; Vanschoenwinkel, B.; Hawinkel, W.; Tuytens, K.; Brendonck, L. Aridity promotes bet hedging via delayed hatching: A case study with two temporary pond crustaceans along a latitudinal gradient. Oecologia 2017, 184, 161–170. [Google Scholar] [CrossRef]
- Saiah, H.; Perrin, N. Autumnal vs Spring Hatching in the Fairy Shrimp Siphonophanes grubii (Dybowski) (Crustacea, Anostraca): Diversified Bet-Hedging Strategy? Funct. Ecol. 1990, 4, 769. [Google Scholar] [CrossRef]
- Ripley, B.J.; Holtz, J.; Simovich, M.A. Cyst bank life-history model for a fairy shrimp from ephemeral ponds. Freshw. Biol. 2004, 49, 221–231. [Google Scholar] [CrossRef]
- Rossi, V.; Gandolfi, A.; Menozzi, P. Mother’s Age and Hatching Phenology Strategy of Heterocypris incongruens (Crustacea: Ostracoda) in Unpredictable Environment. J. Exp. Zool. Part A Ecol. Genet. Physiol. 2016, 325, 701–712. [Google Scholar] [CrossRef] [PubMed]
- Pearson, R.G.; Stanton, J.C.; Shoemaker, K.T.; Aiello-Lammens, M.E.; Ersts, P.J.; Horning, N.; Fordham, D.A.; Raxworthy, C.J.; Ryu, H.Y.; Mcnees, J.; et al. Life history and spatial traits predict extinction risk due to climate change. Nat. Clim. Chang. 2014, 4, 217–221. [Google Scholar] [CrossRef] [Green Version]
- Pyke, C.R. Assessing climate change impacts on vernal pool ecosystems and endemic branchiopods. Ecosystems 2005, 8, 95–105. [Google Scholar] [CrossRef]
- Stoks, R.; Geerts, A.N.; De Meester, L. Evolutionary and plastic responses of freshwater invertebrates to climate change: Realized patterns and future potential. Evol. Appl. 2014, 7, 42–55. [Google Scholar] [CrossRef]
- Pinceel, T.; Vanschoenwinkel, B.; Brendonck, L.; Buschke, F. Modelling the sensitivity of life history traits to climate change in a temporary pool crustacean. Sci. Rep. 2016, 6, 1–5. [Google Scholar] [CrossRef] [Green Version]
- Meisch, C. Freshwater Ostracoda of Western and Central Europe; Spektrum Akademischer Verlag: Heidelberg, Germany, 2000. [Google Scholar]
- Rossi, V.; Benassi, G.; Belletti, F.; Menozzi, P. Colonization, population dynamics, predatory behaviour and cannibalism in Heterocypris incongruens (Crustacea: Ostracoda). J. Limnol. 2011, 70, 102–108. [Google Scholar] [CrossRef]
- Rossi, V.; Menozzi, P. The Clonal Ecology of Heterocypris incongruens (Ostracoda). Oikos 1990, 57, 388. [Google Scholar] [CrossRef]
- Rossi, V.; Gandolfi, A.; Menozzi, P. Egg diapause and clonal structure in parthenogenetic populations of Heterocypris incongruens (Ostracoda). Hydrobiologia 1996, 320, 45–54. [Google Scholar] [CrossRef]
- Rossi, V.; Gandolfi, A.; Baraldi, F.; Bellavere, C.; Menozzi, P. Phylogenetic relationships of coexisting Heterocypris (Crustacea, Ostracoda) lineages with different reproductive modes from Lampedusa Island (Italy). Mol. Phylogenet. Evol. 2007, 44, 1273–1283. [Google Scholar] [CrossRef] [PubMed]
- Rossi, V.; Menozzi, P. The Clonal Ecology of Heterocypris incongruens (Ostracoda): Life-History Traits and Photoperiod. Funct. Ecol. 1993, 7, 177. [Google Scholar] [CrossRef]
- Rossi, V.; Martorella, A.; Menozzi, P. Hatching phenology and voltinism of Heterocypris barbara (Crustacea: Ostracoda) from Lampedusa (Sicily, Italy). J. Limnol. 2013, 72, 227–237. [Google Scholar] [CrossRef] [Green Version]
- Rossi, V.; Albini, D.; Benassi, G.; Menozzi, P. To rest in hydration: Hatching phenology of resting eggs of Heterocypris incongruens (crustacea: Ostracoda). Fundam. Appl. Limnol. 2012, 181, 49–58. [Google Scholar] [CrossRef]
- Bellin, N.; Groppi, M.; Rossi, V. A model of egg bank dynamics in ephemeral ponds. Ecol. Modell. 2020, 430, 109126. [Google Scholar] [CrossRef]
- Saltelli, A.; Ratto, M.; Andres, T.; Campolongo, F.; Cariboni, J.; Gatelli, D.; Saisana, M.; Tarantola, S. Global Sensitivity Analysis: The Primer; John Wiley and Sons, Inc.: Hoboken, NJ, USA, 2008. [Google Scholar]
- Marino, S.; Hogue, I.B.; Ray, C.J.; Kirschner, D.E. A methodology for performing global uncertainty and sensitivity analysis in systems biology. J. Theor. Biol. 2008, 254, 178–196. [Google Scholar] [CrossRef] [Green Version]
- Convertino, M.; Muñoz-Carpena, R.; Chu-Agor, M.L.; Kiker, G.A.; Linkov, I. Untangling drivers of species distributions: Global sensitivity and uncertainty analyses of MaxEnt. Environ. Model. Softw. 2014, 51, 296–309. [Google Scholar] [CrossRef]
- Pianosi, F.; Beven, K.; Freer, J.; Hall, J.W.; Rougier, J.; Stephenson, D.B.; Wagener, T. Sensitivity analysis of environmental models: A systematic review with practical workflow. Environ. Model. Softw. 2016, 79, 214–232. [Google Scholar] [CrossRef]
- Dazzi, C.; Costantini, E. (Eds.) The Soils of Italy, 1st ed.; Springer: Dordrecht, The Netherlands, 2013. [Google Scholar]
- Celico, P. Prospezioni Idrogeologiche Vol. I e II.; Liguori Editore: Napoli, Italy, 1988. [Google Scholar]
- Rossi, M.; Donnini, M. Estimation of regional scale effective infiltration using an open source hydrogeological balance model and free/open data. Environ. Model. Softw. 2018, 104, 153–170. [Google Scholar] [CrossRef]
- Trouet, V.; Van Oldenborgh, G.J. KNMI climate explorer: A web-based research tool for high-resolution paleoclimatology. Tree-Ring Res. 2013, 69, 3–13. [Google Scholar] [CrossRef] [Green Version]
- Fifth assessment report of the intergovernmental panel on climate change. In IPCC Climate Change 2014: Synthesis Report; IPCC: Geneva, Switzerland, 2014.
- Rossi, V.; Benassi, G.; Veneri, M.; Bellavere, C.; Menozzi, P.; Moroni, A.; Mckenzie, K.G. Ostracoda of the Italian ricefields thirty years on: New synthesis and hypothesis. J. Limnol. 2003, 62, 1. [Google Scholar] [CrossRef] [Green Version]
- Team, R.C. R: A Language and Environment for Statistical Computing; R Foundation for Statistical Computing: Vienna, Austria, 2017. [Google Scholar]
- Helton, J.C.; Davis, F.J. Latin hypercube sampling and the propagation of uncertainty in analyses of complex systems. Reliab. Eng. Syst. Saf. 2003, 81, 23–69. [Google Scholar] [CrossRef] [Green Version]
- Saltelli, A.; Tarantola, S.; Campolongo, F.; Ratto, M. Sensitivity Analysis in Practice: A Guide to Assessing Scientific Models; Wiley: Hoboken, NJ, USA, 2004; ISBN 0470870931. [Google Scholar]
- Saltelli, A.; Annoni, P.; Azzini, I.; Campolongo, F.; Ratto, M.; Tarantola, S. Variance based sensitivity analysis of model output. Design and estimator for the total sensitivity index. Comput. Phys. Commun. 2010, 181, 259–270. [Google Scholar] [CrossRef]
- King, J.L.; Simovich, M.A.; Brusca, R.C. Species richness, endemism and ecology of crustacean assemblages in Northern California vernal pools. Hydrobiologia 1996, 328, 85–116. [Google Scholar] [CrossRef]
- Wiggins, G.B.; Rosemary, J.M.; Smith, I.M. Evolutionary and Ecological Strategies of Animals in Annual Temporary Pools; Archiv für Hydrobiologie; Schweizerbart: Stuttgart, Germany, 1980. [Google Scholar]
- Williams, D.D. The Biology of Temporary Waters; Oxford University Press: Oxford, UK, 2006. [Google Scholar]
- Moss, B. Climate change, nutrient pollution and the bargain of Dr Faustus. Freshw. Biol. 2010, 55, 175–187. [Google Scholar] [CrossRef]
- Tuytens, K.; Vanschoenwinkel, B.; Waterkeyn, A.; Brendonck, L. Predictions of climate change infer increased environmental harshness and altered connectivity in a cluster of temporary pools. Freshw. Biol. 2014, 59, 955–968. [Google Scholar] [CrossRef]
- Evans, M.E.K.; Dennehy, J.J. Germ banking: Bet-hedging and variable release from egg and seed dormancy. Q. Rev. Biol. 2005, 80, 431–451. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Gyllström, M.; Hansson, L.A. Dormancy in freshwater zooplankton: Induction, termination and the importance of benthic-pelagic coupling. Aquat. Sci. 2004, 66, 274–295. [Google Scholar] [CrossRef]
- Nunney, L. The effective size of annual plant populations: The interaction of a seed bank with fluctuating population size in maintaining genetic variation. Am. Nat. 2002, 160, 195–204. [Google Scholar] [CrossRef]
- Rossi, V.; Benassi, G.; Leonardi, S.; Piotti, A.; Menozzi, P. Clonal diversity of Heterocypris incongruens (Crustacea: Ostracoda) in Northern Italian ricefields. Arch. Hydrobiol. 2006, 166, 225–240. [Google Scholar] [CrossRef]
- Kindvall, O.; Gärdenfors, U. Temporal extrapolation of PVA results in relation to the IUCN red list criterion E. Conserv. Biol. 2003, 17, 316–321. [Google Scholar] [CrossRef]
- Bradshaw, W.E.; Holzapfel, C.M. Evolution of animal photoperiodism. Annu. Rev. Ecol. Evol. Syst. 2007, 38, 1–25. [Google Scholar] [CrossRef]
- Dawson, A.; King, V.M.; Bentley, G.E.; Ball, G.F. Photoperiodic control of seasonality in birds. J. Biol. Rhythms 2001, 16, 365–380. [Google Scholar] [CrossRef] [PubMed]
- Nielsen, M.E.; Kingsolver, J.G. Compensating for climate change–Induced cue-environment mismatches: Evidence for contemporary evolution of a photoperiodic reaction norm in Colias butterflies. Ecol. Lett. 2020, 23, 1129–1136. [Google Scholar] [CrossRef] [Green Version]
- Nylin, S. Induction of diapause and seasonal morphs in butterflies and other insects: Knowns, unknowns and the challenge of integration. Physiol. Entomol. 2013, 38, 96–104. [Google Scholar] [CrossRef] [Green Version]
- Walton, J.C.; Weil, Z.M.; Nelson, R.J. Influence of photoperiod on hormones, behavior, and immune function. Front. Neuroendocrinol. 2011, 32, 303–319. [Google Scholar] [CrossRef] [Green Version]
- Bradshaw, W.E.; Holzapfel, C.M. Light, time, and the physiology of biotic response to rapid climate change in animals. Annu. Rev. Physiol. 2009, 72, 147–166. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Grevstad, F.S.; Coop, L.B. The consequences of photoperiodism for organisms in new climates. Ecol. Appl. 2015, 25, 1506–1517. [Google Scholar] [CrossRef]
- Dupuis, A.P.; Hann, B.J. Climate change, diapause termination and zooplankton population dynamics: An experimental and modelling approach. Freshw. Biol. 2009, 54, 221–235. [Google Scholar] [CrossRef]
- Rossi, V.; Rozzi, M.C.; Menozzi, P. Life strategy differences among electrophoretic clones of Heterocypris incongruens (Crustacea, Ostracoda). Verandlungen des Int. Verain Limnol. 1991, 24, 2816–2819. [Google Scholar] [CrossRef]
- Gillooly, J.F.; Charnov, E.L.; West, G.B.; Savage, V.M.; Brown, J.H. Effects of size and temperature on developmental time. Nature 2002, 417, 70–73. [Google Scholar] [CrossRef] [PubMed]
- Vanschoenwinkel, B.; Brendonck, L.; Pinceel, T.; Dupriez, P.; Waterkeyn, A. Rediscovery of Branchipus schaefferi (Branchiopoda: Anostraca) in Belgium—Notes on habitat requirements and conservation management. Belgian J. Zool. 2013, 143, 3–14. [Google Scholar]
- Schindler, D.W. The cumulative effects of climate warming and other human stresses on Canadian freshwaters in the new millennium. Can. J. Fish. Aquat. Sci. 2001, 58, 18–29. [Google Scholar] [CrossRef]
- Rossi, V.; Martorella, A.; Scudieri, D.; Menozzi, P. Seasonal niche partitioning and coexistence of amphimictic and parthenogenetic lineages of Heterocypris barbara (Crustacea: Ostracoda). Can. J. Zool. 2017, 95, 7–14. [Google Scholar] [CrossRef]
- Halse, S.A.; Ruprecht, J.K.; Pinder, A.M. Salinisation and prospects for biodiversity in rivers and wetlands of south-west Western Australia. Aust. J. Bot. 2003, 51, 673–688. [Google Scholar] [CrossRef]
- Loureiro, C.; Pereira, J.L.; Pedrosa, M.A.; Gonçalves, F.; Castro, B.B. Competitive Outcome of Daphnia-Simocephalus Experimental Microcosms: Salinity versus Priority Effects. PLoS ONE 2013, 8, e70572. [Google Scholar] [CrossRef] [PubMed]
- Wellborn, G.A.; Skelly, D.K.; Werner, E.E. Mechanisms creating community structure across a freshwater habitat gradient. Annu. Rev. Ecol. Syst. 1996, 27, 337–363. [Google Scholar] [CrossRef] [Green Version]
- Simons, A.M. Playing smart vs. playing safe: The joint expression of phenotypic plasticity and potential bet hedging across and within thermal environments. J. Evol. Biol. 2014, 27, 1047–1056. [Google Scholar] [CrossRef] [PubMed]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Bellin, N.; Spezzano, R.; Rossi, V. Assessing the Extinction Risk of Heterocypris incongruens (Crustacea: Ostracoda) in Climate Change with Sensitivity and Uncertainty Analysis. Water 2021, 13, 1828. https://doi.org/10.3390/w13131828
Bellin N, Spezzano R, Rossi V. Assessing the Extinction Risk of Heterocypris incongruens (Crustacea: Ostracoda) in Climate Change with Sensitivity and Uncertainty Analysis. Water. 2021; 13(13):1828. https://doi.org/10.3390/w13131828
Chicago/Turabian StyleBellin, Nicolò, Rachele Spezzano, and Valeria Rossi. 2021. "Assessing the Extinction Risk of Heterocypris incongruens (Crustacea: Ostracoda) in Climate Change with Sensitivity and Uncertainty Analysis" Water 13, no. 13: 1828. https://doi.org/10.3390/w13131828
APA StyleBellin, N., Spezzano, R., & Rossi, V. (2021). Assessing the Extinction Risk of Heterocypris incongruens (Crustacea: Ostracoda) in Climate Change with Sensitivity and Uncertainty Analysis. Water, 13(13), 1828. https://doi.org/10.3390/w13131828






