Reservoir Scheduling Using a Multi-Objective Cuckoo Search Algorithm under Climate Change in Jinsha River, China
Abstract
:1. Introduction
2. Methods
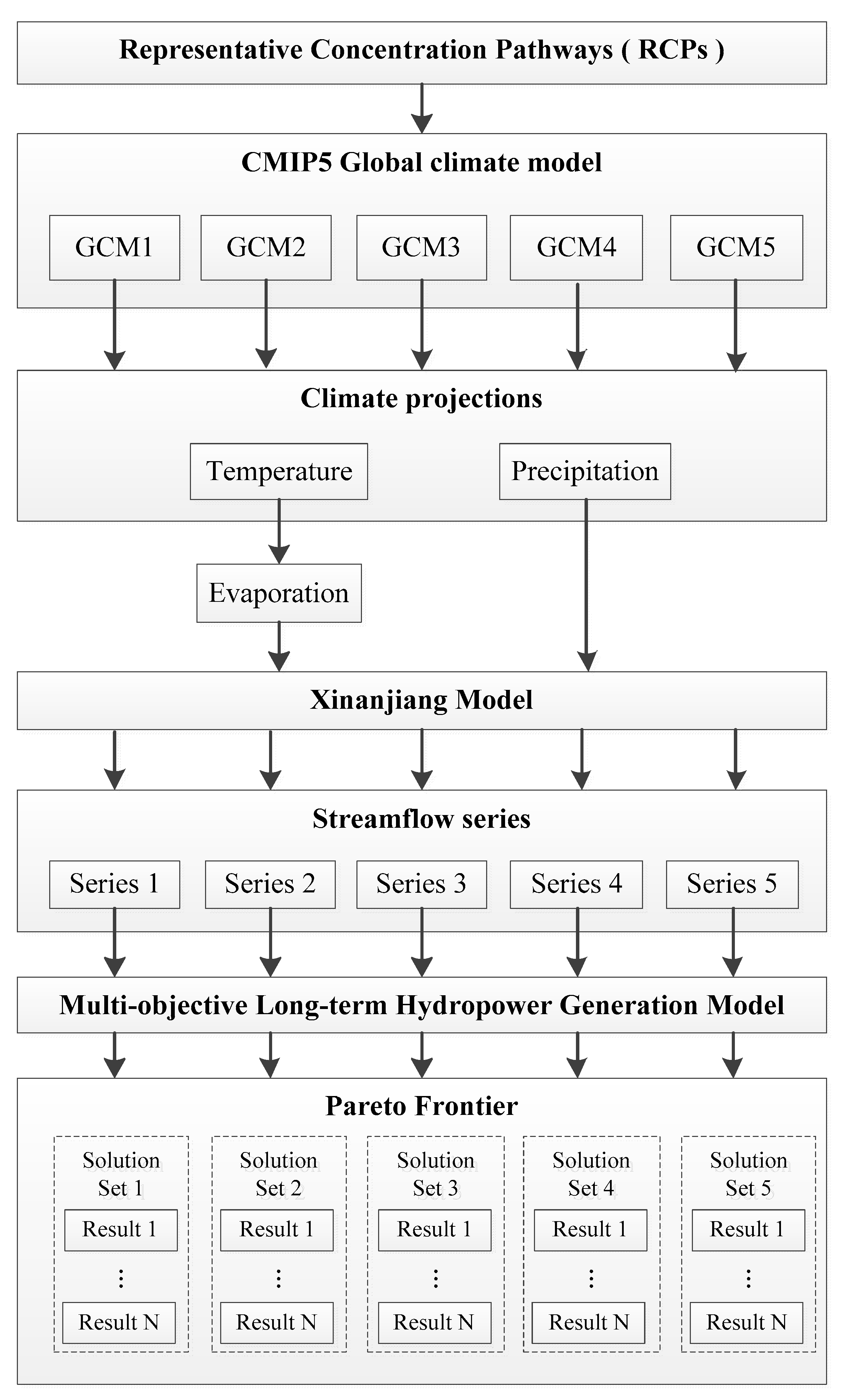
2.1. Estimating Climate Change Impacts on Hydropower
2.2. Improved Multi-Objective Cuckoo Search Algorithm
2.2.1. NGSA-II
- (1)
- Randomly generate an initial population of size N. Then, sort the initial population using the non-dominated method.
- (2)
- Generate new subpopulations through selection, crossover, and mutation operations of the evolutionary algorithm.
- (3)
- Merge the parent and child populations and select the most fit individuals to form the next-generation population based on a dominance relationship and crowding degree.
- (4)
- Repeat the above processes until the termination condition is met.
2.2.2. Improved Cuckoo Search
- (1)
- Dynamic parameter adjustment strategy
- (2)
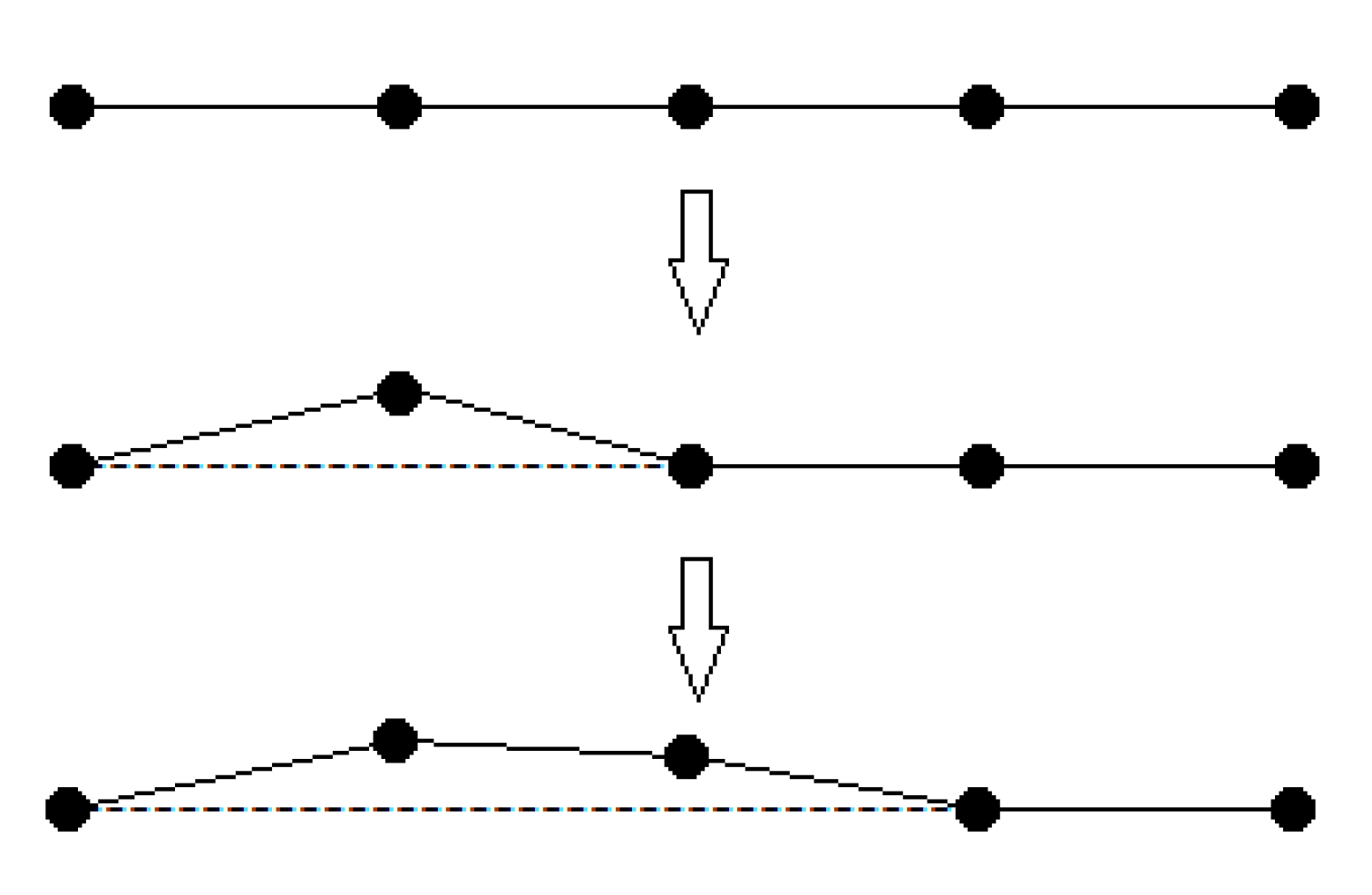
- Differential strategy for Lévy flight
- (3)
- Revised solution
| Algorithm 1. Improved cuckoo search |
| Objective function |
| Initialize default parameters |
| Generate initial population of n host nests |
| While (t < MaxEvaluation) or (stop criterion) |
| Select two solution from host nests randomly |
| For d=1,…, D do |
| End for |
| If |
| Replace xi by the new solution |
| End if |
| If |
| Init the worst nest |
| End if |
| End while |
2.2.3. Multi-Objective Cuckoo Search
- (1)
- Generate a random initial population, and classify the individuals using the non-dominated sorting method. A new population can then be generated using the ICS algorithm.
- (2)
- Merge the parent and child populations, employ a fast, non-dominated sorting and crowding degree calculation in the mixed population, and select the most fit individuals to form the next generation.
- (3)
- Repeat the processes above until the termination conditions are met.
2.3. Gradient Multi-Objective Cuckoo Search for Reservoir Scheduling
2.3.1. Power Generation Objective
2.3.2. Residual Load Variance Objective
2.3.3. Constraints
- (1)
- Hydraulic connection (Equation (7)):where (m³/s) is the inflow of reservoir i at time t; (m³/s) is the outflow of reservoir i − 1 at time t, (m³/s) is the interval inflow between reservoir i − 1 and i; (m³/s) is the spillage of the upstream reservoir i − 1, and (m³/s) is the generation flow of the upstream reservoir i − 1.
- (2)
- Water-balance constraint (Equation (8)):where Vi,t (m³) is the storage of reservoir i in time t.
- (3)
- Water-level constraints (Equations (9) and (10)):where (m) and (m) are the lower and upper bounds of the water level, respectively; and (m) is the limitation of the water-level variation.
- (4)
- Outflow constraint (Equation (11)):where (m³/s) and (m³/s) are the minimum and maximum outflows of reservoir i, respectively.
- (5)
- Output constraint (Equation (12)):where (kW∙h) and (kW∙h) are the minimum and maximum power output of reservoir i, respectively.
- (6)
- Boundary condition (Equation (13)):where (m) and (m) are the initial and terminal water levels of reservoir i, respectively.
2.3.4. Solution Encoding and Initialization
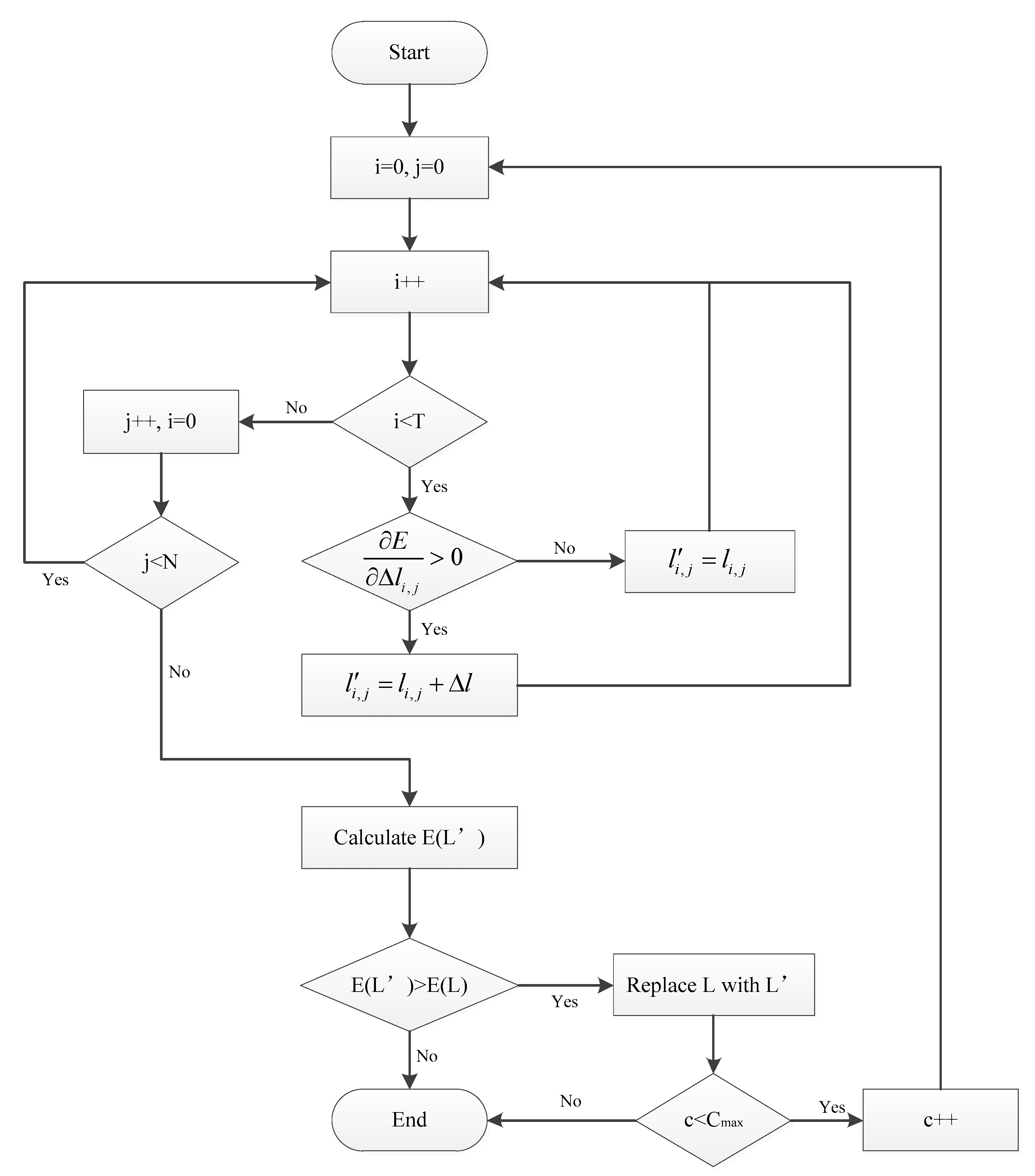
2.3.5. Gradient Search Strategy
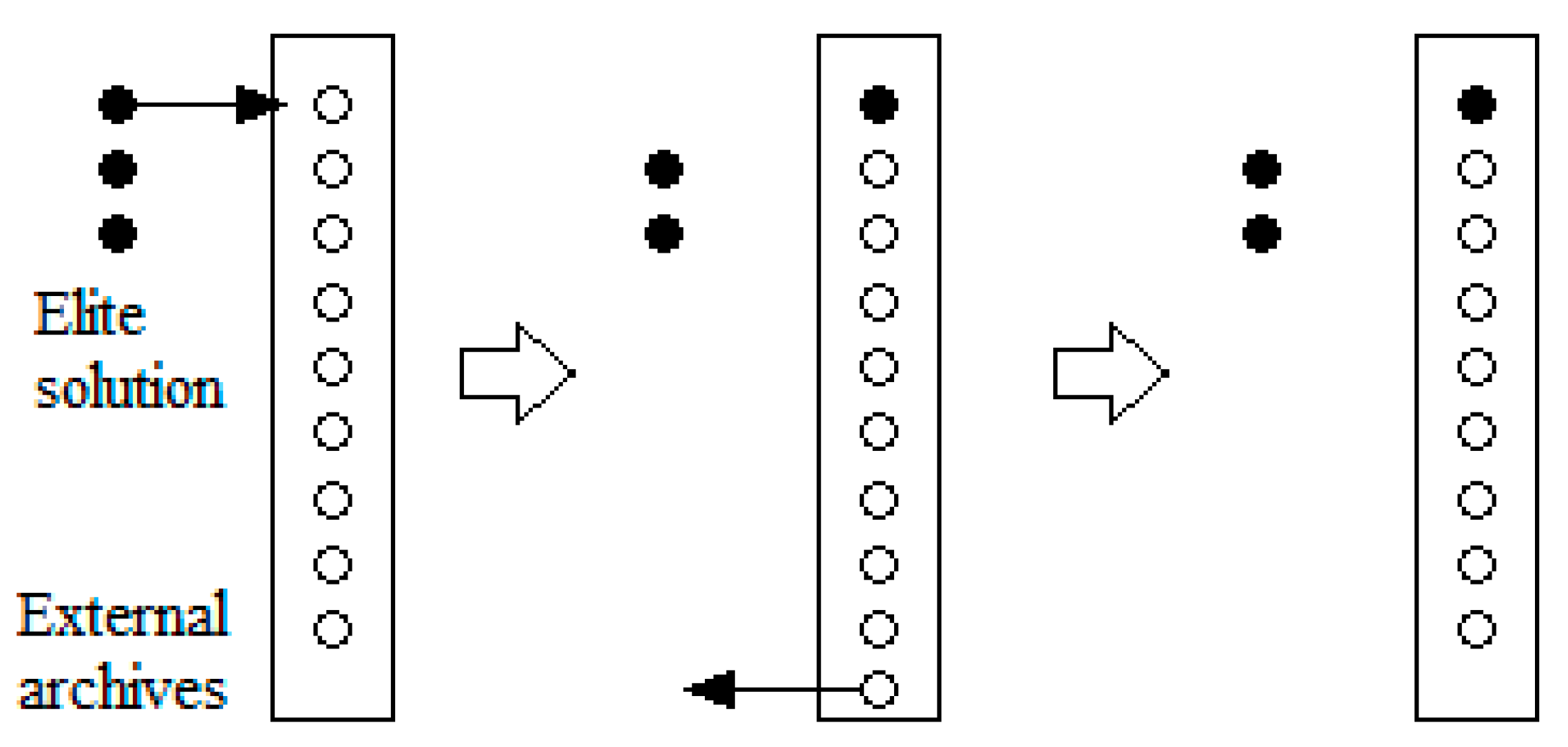
2.3.6. Single Entry External Archive
2.3.7. Self-Tuning Divergent Operator Strategy
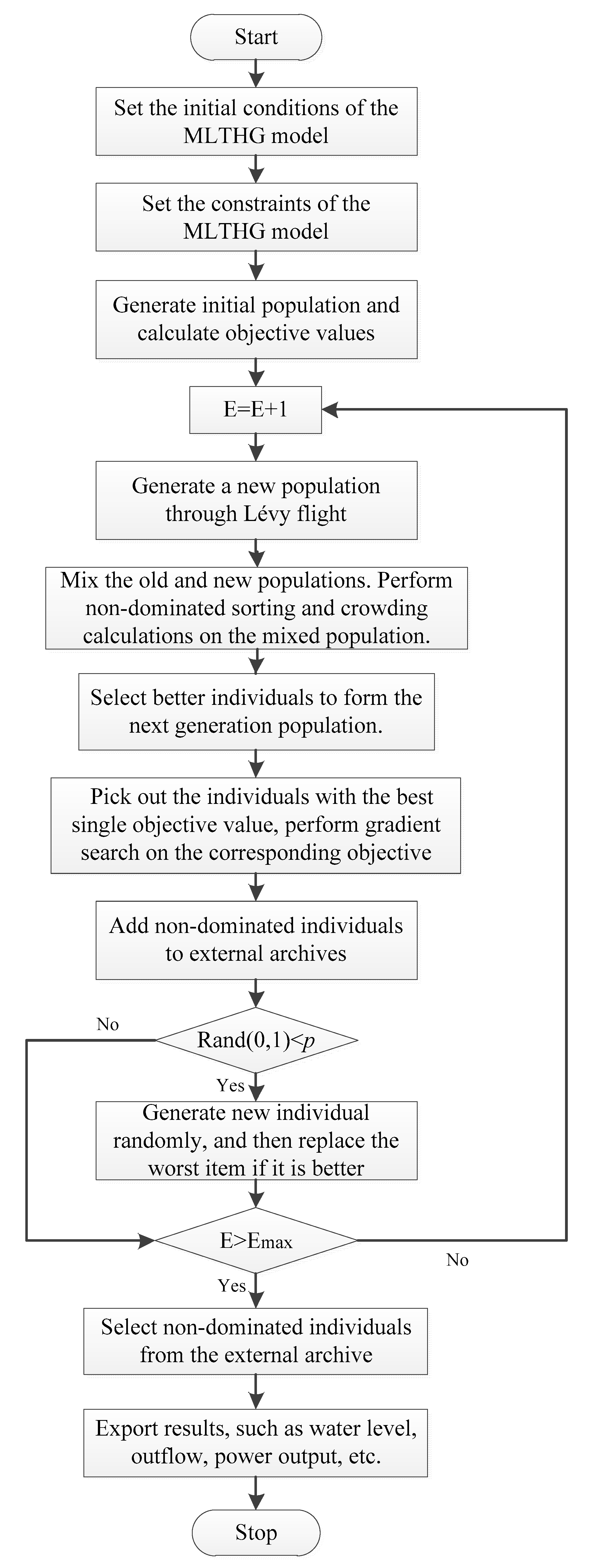
2.3.8. Procedures of Solving MLTHG with Gradient Based MoCS
- (1)
- Set the initial conditions of the MLTHG model, including incoming water, water level of each hydropower station in the initial time period and the end time period.
- (2)
- Set up the constraints of the MLTHG model, including the maximum outflow, minimum outflow, maximum water level, minimum water level, and water level variation in each period of each hydropower station. The setting of water level constraints needs to consider the flood control requirements in the flood season.
- (3)
- Set the parameters of the GMoCS algorithm.
- (4)
- Generate a random individual according to Equations (14) and (15), calculate its objective values and check whether it meets all constraints. If the constraints are met, added it to the initial population. Generate other new individuals using the same method until the population size is reached.
- (5)
- Generate new individual by Lévy flight.
- (6)
- Calculate objective values of the new individual and check whether it meets all constraints. If the new individual does not meet the constraints, try to adjust the water level to make it meet the constraints.
- (7)
- Mix the old and new populations. Perform non-dominated sorting and crowding calculations on the mixed population. Select better individuals to form the next generation population.
- (8)
- Select the individual with the largest power generation and perform gradient search for the power generation objective. Then, select the individual with the smallest residual load variance, and perform gradient search for the residual load variance objective.
- (9)
- Select non-dominated individuals from the next generation population. Insert the non-dominated individuals into the external archives one by one, while replacing the worst individual with a better random individual with a certain probability.
- (10)
- Repeat steps 3–9 until the termination condition is met.
- (11)
- Select non-dominated individuals from the external archive set as the Pareto optimal frontier. Export time series data of these individuals, including water level, outflow, power output, etc.
2.4. MLTHG in Jinsha River
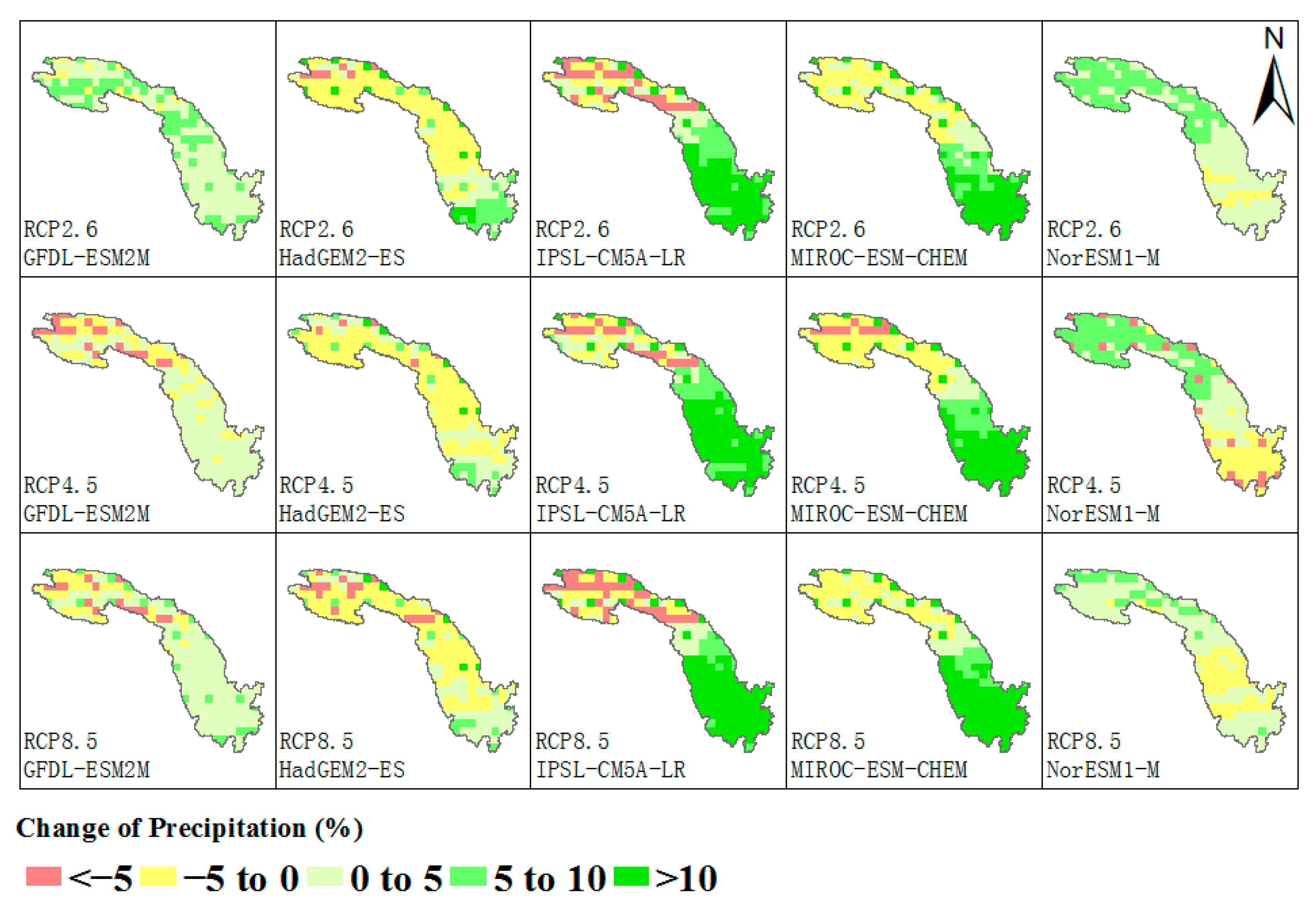
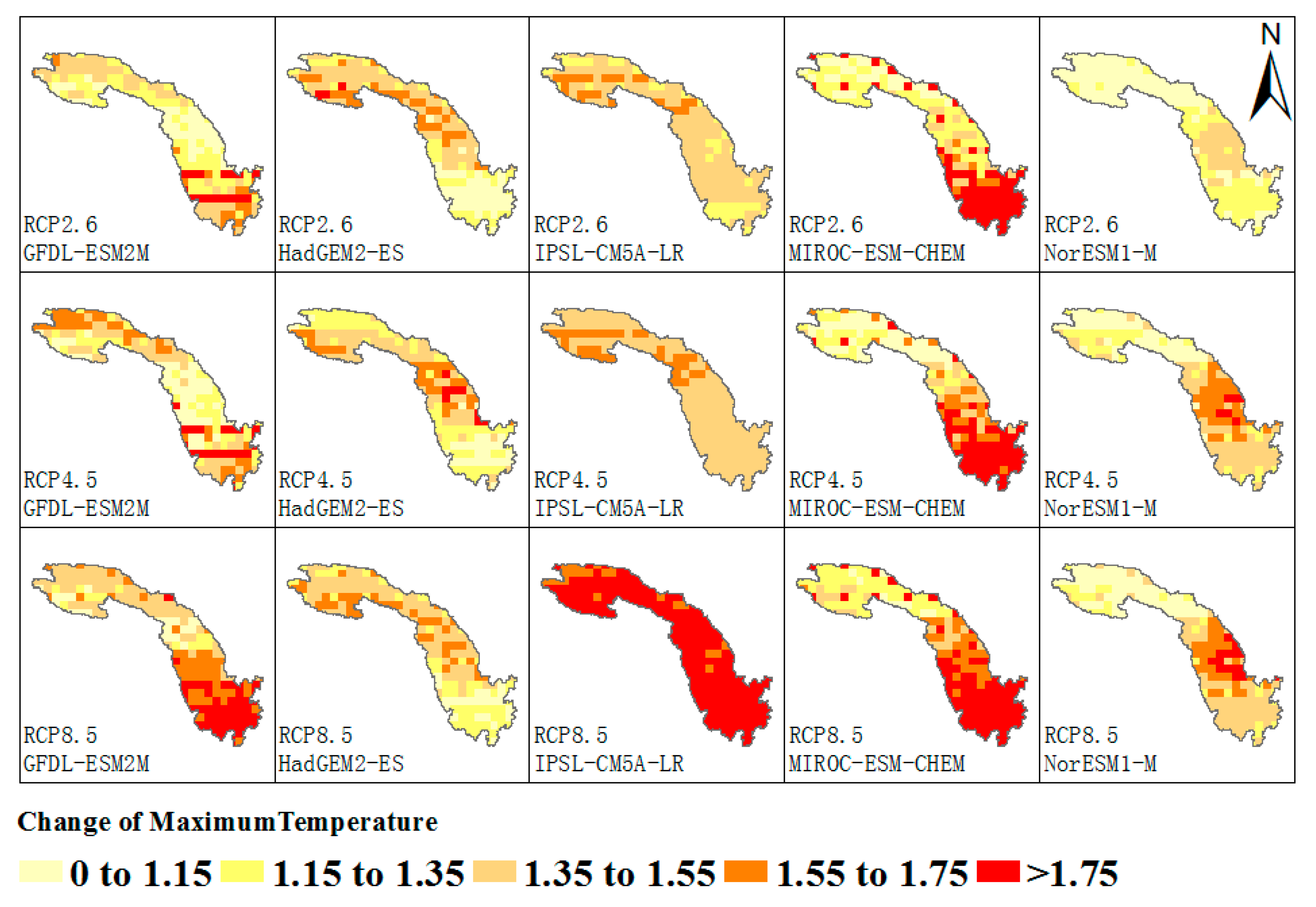
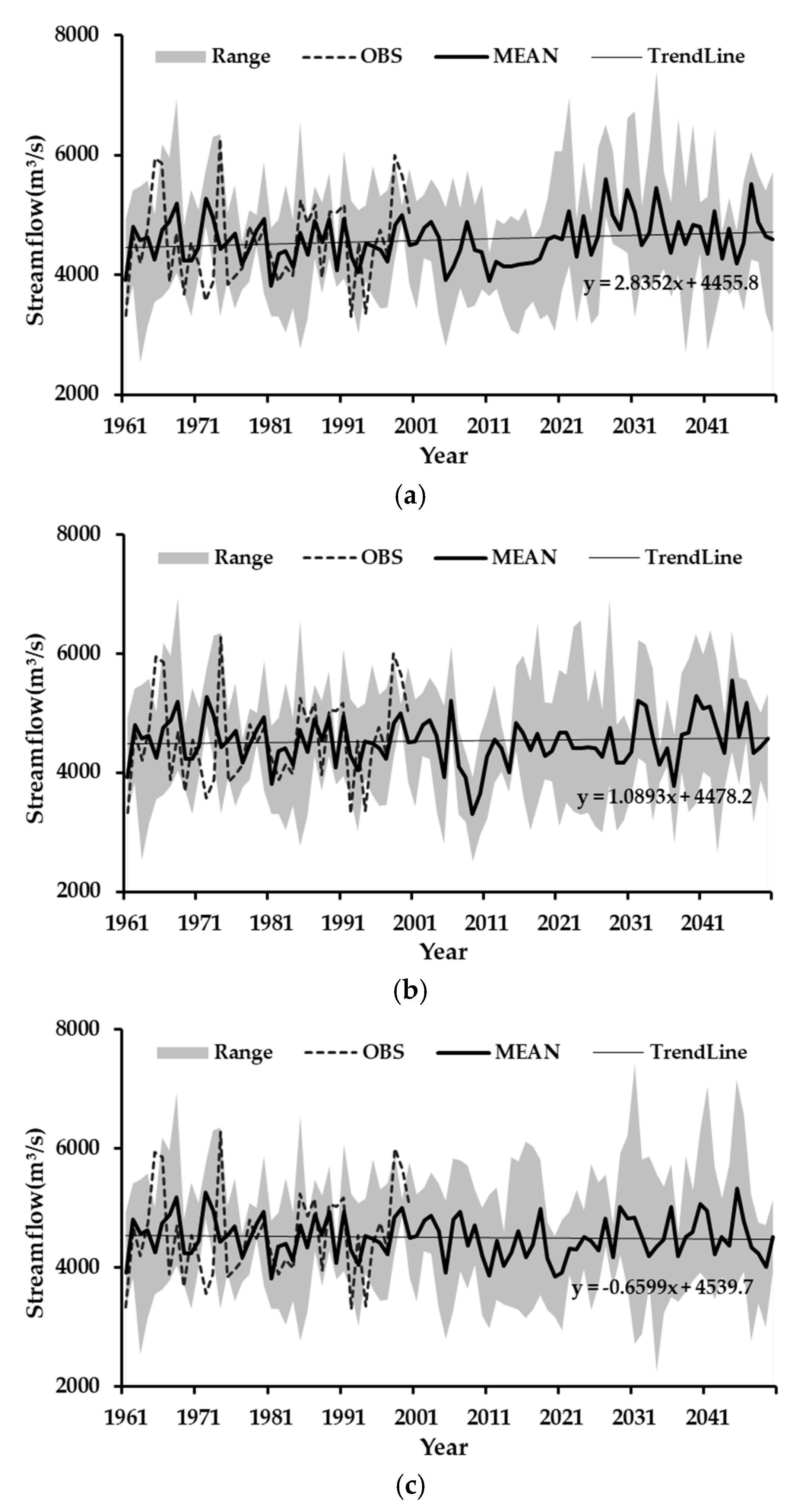
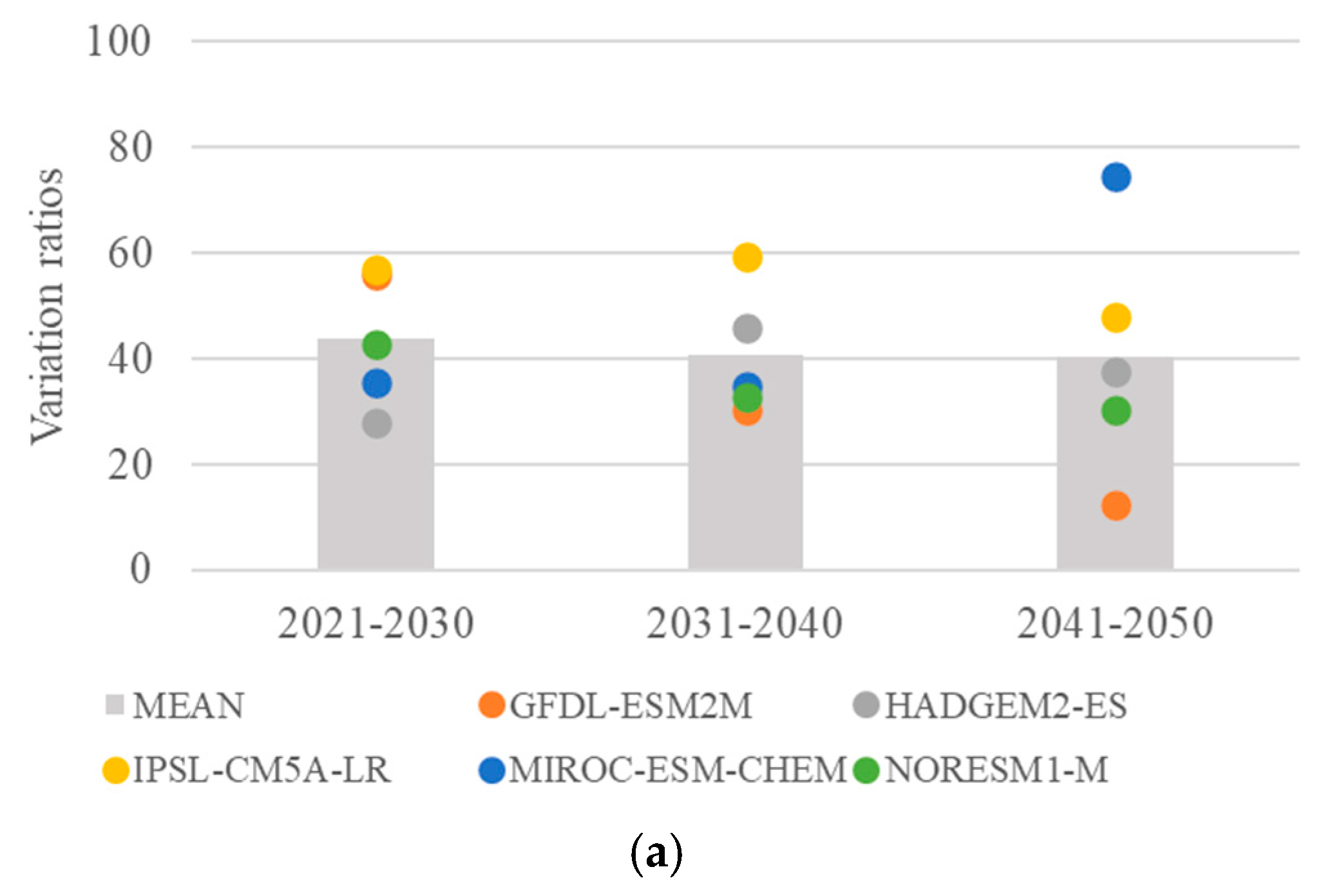
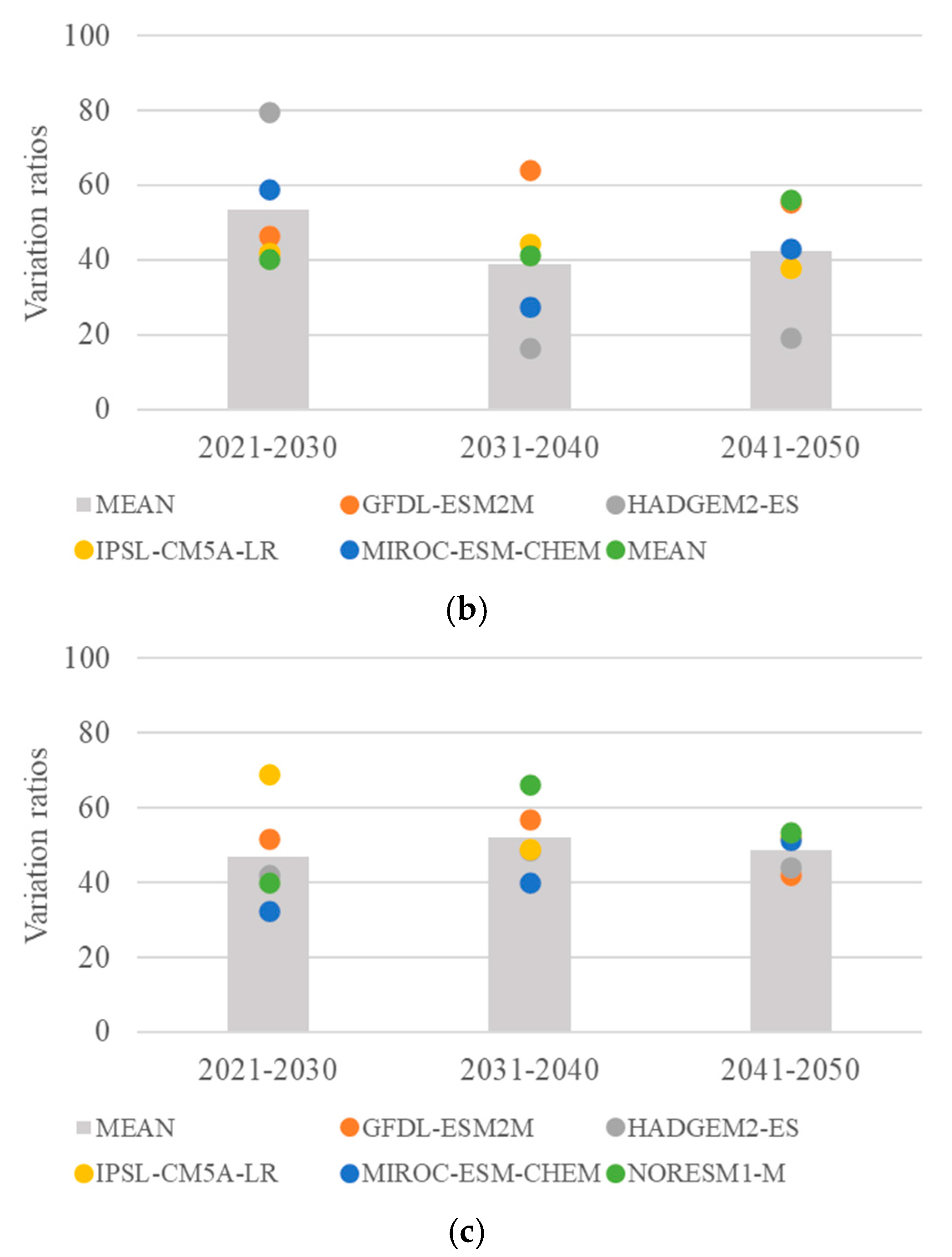
2.4.1. The Projection of Streamflow in the Context of Climate Change
2.4.2. Modeling of MLTHG in Jinsha River
3. Results and Discussion
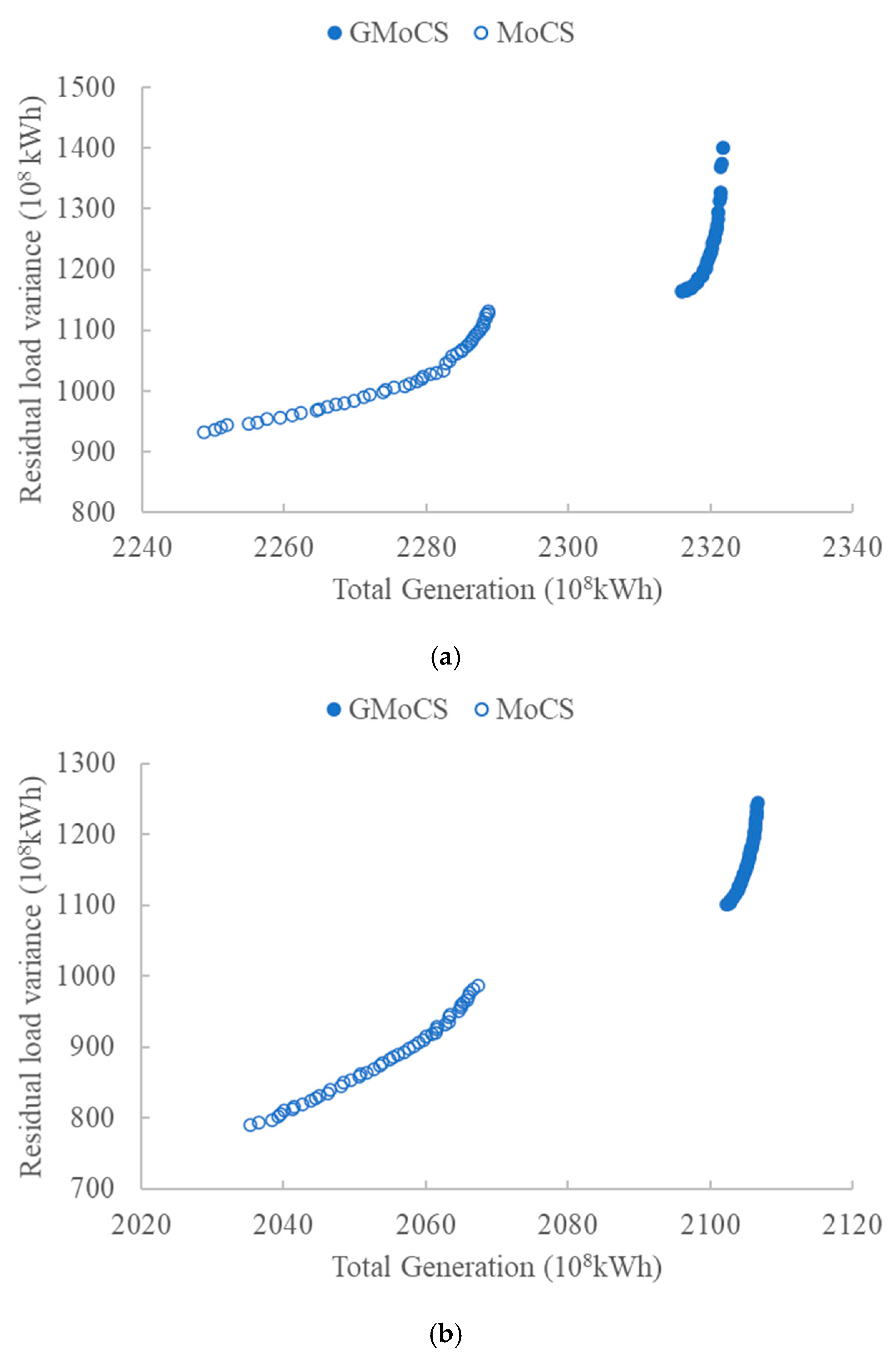
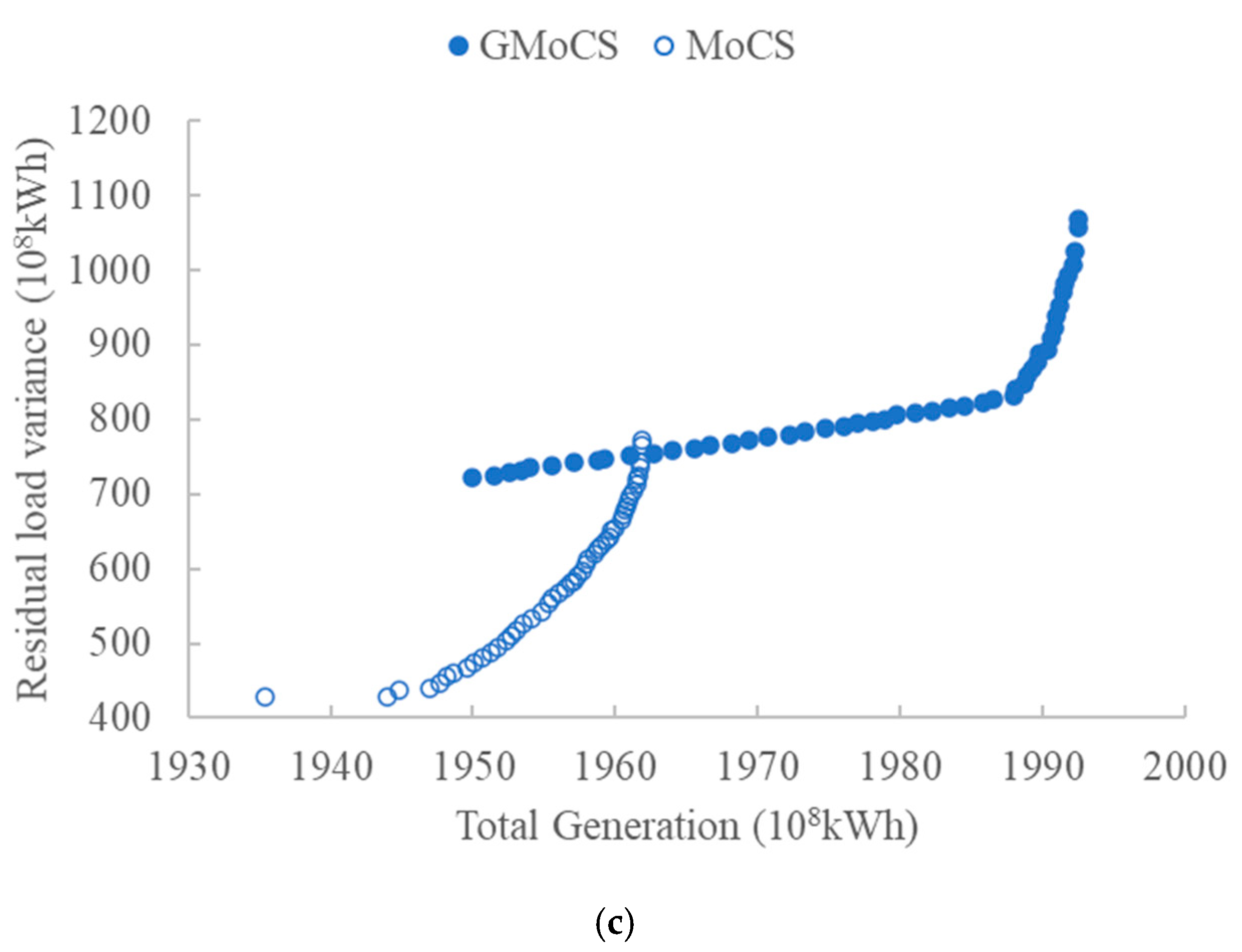
3.1. Performance of GMoCS
3.2. Climate Change on Multi-Objective Scheduling of Cascade Hydropower Stations
3.2.1. Power Generation Objective
3.2.2. Residual Load Variance Objective
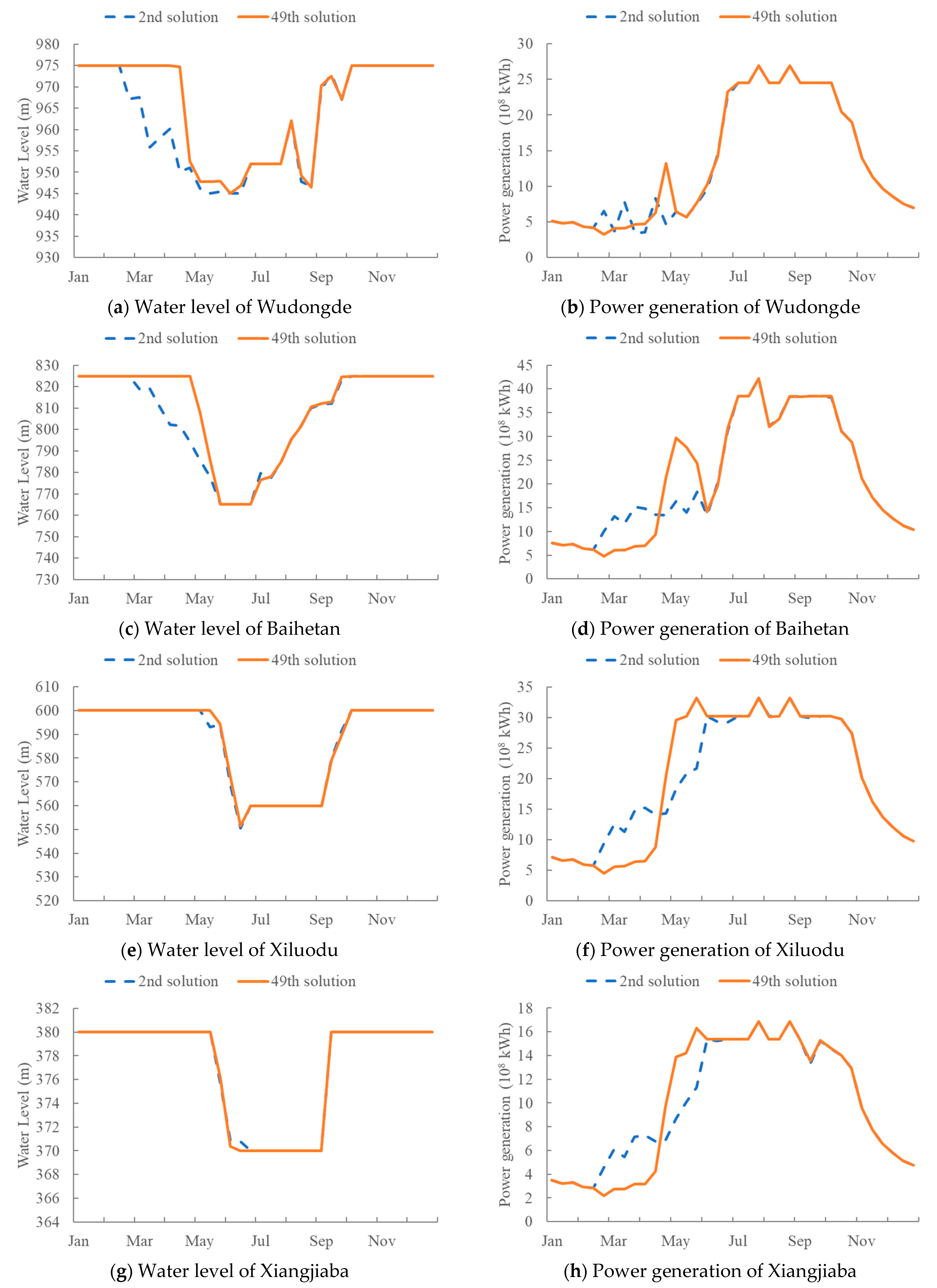
3.2.3. Combination of the Two Objectives
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Mendes, C.A.B.; Beluco, A.; Canales, F.A. Some important uncertainties related to climate change in projections for the Brazilian hydropower expansion in the Amazon. Energy 2017, 141, 123–138. [Google Scholar] [CrossRef]
- Fan, J.-L.; Hu, J.-W.; Zhang, X.; Kong, L.-S.; Li, F.; Mi, Z. Impacts of climate change on hydropower generation in China. Math. Comput. Simul. 2020, 167, 4–18. [Google Scholar] [CrossRef]
- Gaudard, L.; Romerio, F.; Valle, F.; Gorret, R.; Maran, S.; Ravazzani, G.; Stoffel, M.; Volonterio, M. Climate change impacts on hydropower in the Swiss and Italian Alps. Sci. Total Environ. 2013, 493. [Google Scholar] [CrossRef]
- Chang, J.; Wang, X.; Li, Y.; Wang, Y.; Zhang, H. Hydropower plant operation rules optimization response to climate change. Energy 2018, 160, 886–897. [Google Scholar] [CrossRef]
- Zhong, W.; Guo, J.; Chen, L.; Zhou, J.; Zhang, J.; Wang, D. Future hydropower generation prediction of large-scale reservoirs in the upper Yangtze River basin under climate change. J. Hydrol. 2020, 588, 125013. [Google Scholar] [CrossRef]
- Qin, P.; Xu, H.; Liu, M.; Du, L.; Xiao, C.; Liu, L.; Tarroja, B. Climate change impacts on Three Gorges Reservoir impoundment and hydropower generation. J. Hydrol. 2020, 580, 123922. [Google Scholar] [CrossRef]
- Kim, K.; Jeong, H.; Ha, S.; Bang, S.; Bae, D.-H.; Kim, H. Investment timing decisions in hydropower adaptation projects using climate scenarios: A case study of South Korea. J. Clean. Prod. 2017, 142, 1827–1836. [Google Scholar] [CrossRef]
- Boehlert, B.; Strzepek, K.M.; Gebretsadik, Y.; Swanson, R.; McCluskey, A.; Neumann, J.E.; McFarland, J.; Martinich, J. Climate change impacts and greenhouse gas mitigation effects on U.S. hydropower generation. Appl. Energy 2016, 183, 1511–1519. [Google Scholar] [CrossRef] [Green Version]
- Huang, S.; Krysanova, V.; Hattermann, F. Projections of climate change impacts on floods and droughts in Germany using an ensemble of climate change scenarios. Reg. Environ. Chang. 2014, 15. [Google Scholar] [CrossRef]
- Mezosi, G.; Bata, T.; Meyer, B.; Blanka, V.; Ladányi, Z. Climate Change Impacts on Environmental Hazards on the Great Hungarian Plain, Carpathian Basin. Int. J. Disaster Risk Sci. 2014, 5, 136–146. [Google Scholar] [CrossRef] [Green Version]
- Hasan, M.M.; Wyseure, G. Impact of climate change on hydropower generation in Rio Jubones Basin, Ecuador. Water Sci. Eng. 2018, 11, 157–166. [Google Scholar] [CrossRef]
- Falchetta, G.; Gernaat, D.E.H.J.; Hunt, J.; Sterl, S. Hydropower dependency and climate change in sub-Saharan Africa: A nexus framework and evidence-based review. J. Clean. Prod. 2019, 231, 1399–1417. [Google Scholar] [CrossRef] [Green Version]
- Lu, S.; Dai, W.; Tang, Y.; Guo, M. A review of the impact of hydropower reservoirs on global climate change. Sci. Total Environ. 2020, 711, 134996. [Google Scholar] [CrossRef]
- IPCC; McDowell, G.; Barr, I. ‘High Mountain Areas’ Chapter—IPCC Special Report on the Oceans and Cryosphere in a Changing Climate (SROCC); IPCC: Geneva, Switzerland, 2019. [Google Scholar]
- Mishra, S.K.; Hayse, J.; Veselka, T.; Yan, E.; Kayastha, R.B.; LaGory, K.; McDonald, K.; Steiner, N. An integrated assessment approach for estimating the economic impacts of climate change on River systems: An application to hydropower and fisheries in a Himalayan River, Trishuli. Environ. Sci. Policy 2018, 87, 102–111. [Google Scholar] [CrossRef]
- Feldbauer, J.; Kneis, D.; Hegewald, T.; Berendonk, T.U.; Petzoldt, T. Managing climate change in drinking water reservoirs: Potentials and limitations of dynamic withdrawal strategies. Environ. Sci. Eur. 2020, 32, 48. [Google Scholar] [CrossRef] [Green Version]
- Helfer, F.; Lemckert, C.; Zhang, H. Impacts of climate change on temperature and evaporation from a large reservoir in Australia. J. Hydrol. 2012, 475, 365–378. [Google Scholar] [CrossRef] [Green Version]
- Shu, J.; Qu, J.; Motha, R.; Xu, J.; Dong, D. Impacts of climate change on hydropower development and sustainability: A review. IOP Conf. Ser. Earth Environ. Sci. 2018, 163, 012126. [Google Scholar] [CrossRef]
- Turner, S.W.D.; Hejazi, M.; Kim, S.H.; Clarke, L.; Edmonds, J. Climate impacts on hydropower and consequences for global electricity supply investment needs. Energy 2017, 141, 2081–2090. [Google Scholar] [CrossRef]
- Nam, W.-H.; Kim, T.; Hong, E.-M.; Choi, J.-Y. Regional Climate Change Impacts on Irrigation Vulnerable Season Shifts in Agricultural Water Availability for South Korea. Water 2017, 9, 735. [Google Scholar] [CrossRef] [Green Version]
- Carvajal, P.E.; Li, F.G.N.; Soria, R.; Cronin, J.; Anandarajah, G.; Mulugetta, Y. Large hydropower, decarbonisation and climate change uncertainty: Modelling power sector pathways for Ecuador. Energy Strategy Rev. 2019, 23, 86–99. [Google Scholar] [CrossRef]
- Chilkoti, V.; Bolisetti, T.; Balachandar, R. Climate change impact assessment on hydropower generation using multi-model climate ensemble. Renew. Energy 2017, 109, 510–517. [Google Scholar] [CrossRef]
- Sample, J.E.; Duncan, N.; Ferguson, M.; Cooksley, S. Scotland׳s hydropower: Current capacity, future potential and the possible impacts of climate change. Renew. Sustain. Energy Rev. 2015, 52, 111–122. [Google Scholar] [CrossRef]
- Pereira-Cardenal, S.; Madsen, H.; Arnbjerg-Nielsen, K.; Riegels, N.; Jensen, R.; Mo, B.; Wangensteen, I.; Bauer-Gottwein, P. Assessing climate change impacts on the Iberian power system using a coupled water-power model. Clim. Chang. 2014, 126, 351–364. [Google Scholar] [CrossRef]
- González-Villela, R.; Martínez, M.J.M.; Sepúlveda, J.S.S. Effects of climate change on the environmental flows in the Conchos River (Chihuahua, Mexico). Ecohydrol. Hydrobiol. 2018, 18, 431–440. [Google Scholar] [CrossRef]
- Givati, A.; Thirel, G.; Rosenfeld, D.; Paz, D. Climate change impacts on streamflow at the upper Jordan River based on an ensemble of regional climate models. J. Hydrol. Reg. Stud. 2019, 21, 92–109. [Google Scholar] [CrossRef]
- Clifton, C.F.; Day, K.T.; Luce, C.H.; Grant, G.E.; Safeeq, M.; Halofsky, J.E.; Staab, B.P. Effects of climate change on hydrology and water resources in the Blue Mountains, Oregon, USA. Clim. Serv. 2018, 10, 9–19. [Google Scholar] [CrossRef]
- Bhatta, B.; Shrestha, S.; Shrestha, P.K.; Talchabhadel, R. Evaluation and application of a SWAT model to assess the climate change impact on the hydrology of the Himalayan River Basin. CATENA 2019, 181, 104082. [Google Scholar] [CrossRef]
- de Queiroz, A.R.; Faria, V.A.D.; Lima, L.M.M.; Lima, J.W.M. Hydropower revenues under the threat of climate change in Brazil. Renew. Energy 2019, 133, 873–882. [Google Scholar] [CrossRef]
- Arango-Aramburo, S.; Turner, S.W.D.; Daenzer, K.; Ríos-Ocampo, J.P.; Hejazi, M.I.; Kober, T.; Álvarez-Espinosa, A.C.; Romero-Otalora, G.D.; van der Zwaan, B. Climate impacts on hydropower in Colombia: A multi-model assessment of power sector adaptation pathways. Energy Policy 2019, 128, 179–188. [Google Scholar] [CrossRef]
- Zhai, M.Y.; Lin, Q.G.; Huang, G.H.; Zhu, L.; An, K.; Li, G.C.; Huang, Y.F. Adaptation of Cascade Hydropower Station Scheduling on A Headwater Stream of the Yangtze River under Changing Climate Conditions. Water 2017, 9, 293. [Google Scholar] [CrossRef] [Green Version]
- Zhang, W.; Liu, P.; Wang, H.; Lei, X.; Feng, M. Operating rules of irrigation reservoir under climate change and its application for the Dongwushi Reservoir in China. J. Hydro-Environ. Res. 2017, 16, 34–44. [Google Scholar] [CrossRef]
- Yang, X.S.; Deb, S. Cuckoo Search via Levy Flights. Mathematics 2010, 210–214. [Google Scholar]
- Geressu, R.; Harou, J. Reservoir system expansion scheduling under conflicting interests. Environ. Model. Softw. 2019, 118, 201–210. [Google Scholar] [CrossRef]
- Feng, Y.; Zhou, J.; Mo, L.; Wang, C.; Yuan, Z.; Wu, J. A Gradient-Based Cuckoo Search Algorithm for a Reservoir-Generation Scheduling Problem. Algorithms 2018, 11, 36. [Google Scholar] [CrossRef] [Green Version]
- Warszawski, L.; Frieler, K.; Huber, V.; Piontek, F.; Serdeczny, O.; Schewe, J. The Inter-Sectoral Impact Model Intercomparison Project (ISI-MIP): Project framework. Proc. Natl. Acad. Sci. USA 2014, 111, 3228–3232. [Google Scholar] [CrossRef] [Green Version]
- Hempel, S.; Frieler, K.; Warszawski, L.; Schewe, J.; Piontek, F. A trend-preserving bias correction—The ISI-MIP approach. Earth Syst. Dyn. 2013, 4, 219–236. [Google Scholar] [CrossRef] [Green Version]
- Berti, A.; Tardivo, G.; Chiaudani, A.; Rech, F.; Borin, M. Assessing reference evapotranspiration by the Hargreaves method in north-eastern Italy. Agric. Water Manag. 2014, 140, 20–25. [Google Scholar] [CrossRef]
- Feng, Y.; Zhou, J.; Mo, L.; Yuan, Z.; Zhang, P.; Jiang, W.; Wang, C.; Wang, Y. Long-Term Hydropower Generation of Cascade Reservoirs under Future Climate Changes in Jinsha River in Southwest China. Water 2018, 10, 235. [Google Scholar] [CrossRef] [Green Version]


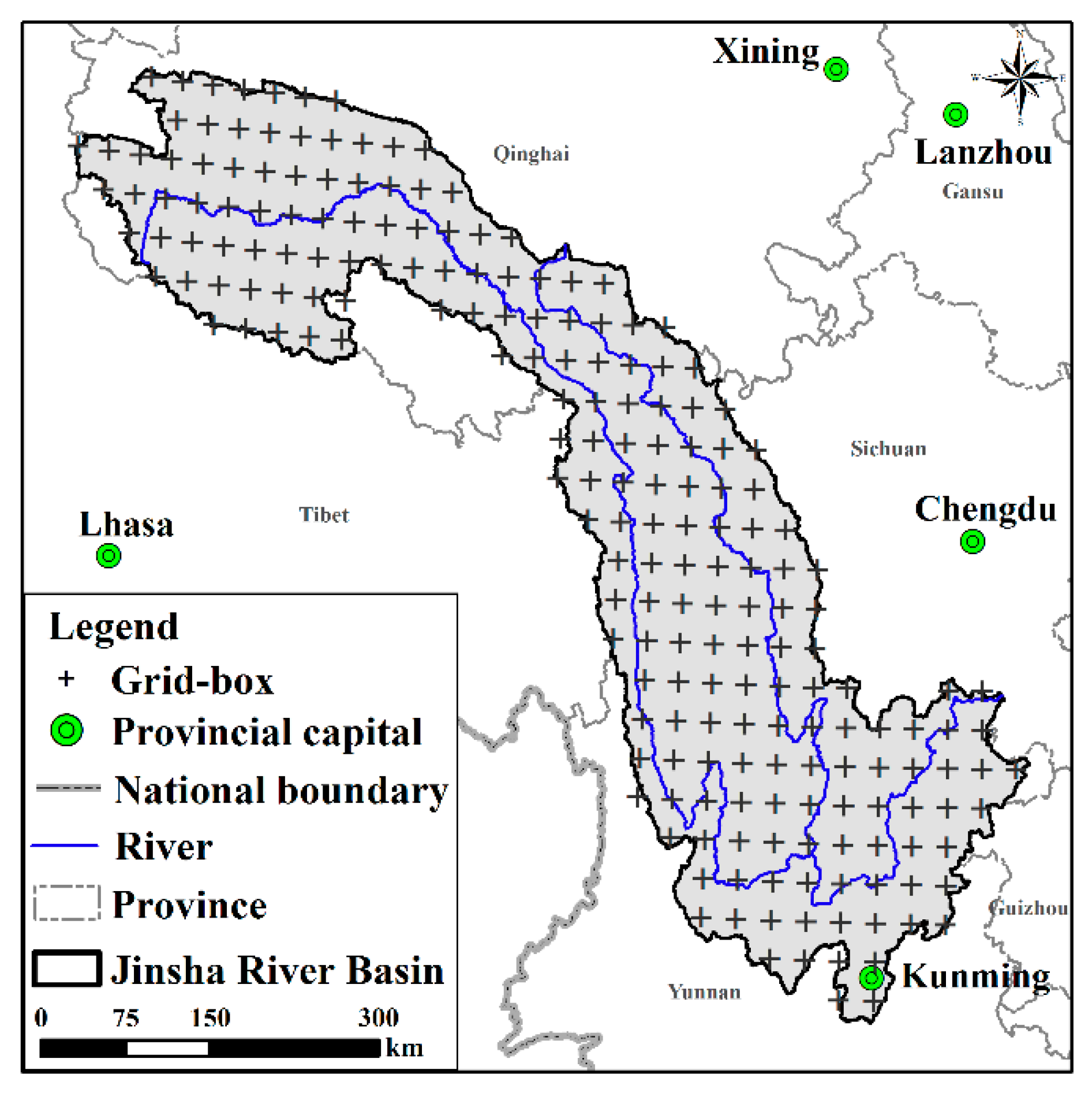
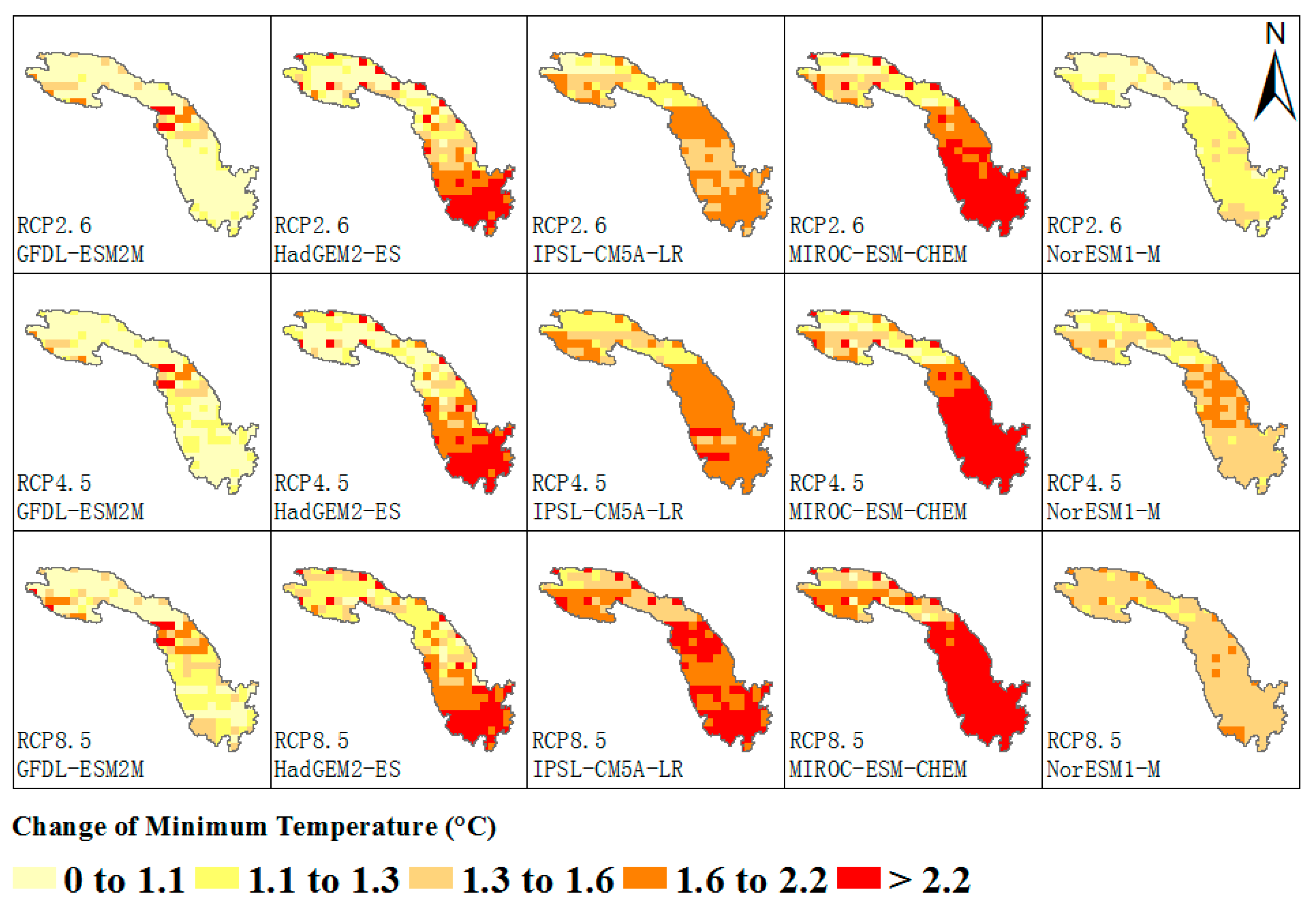
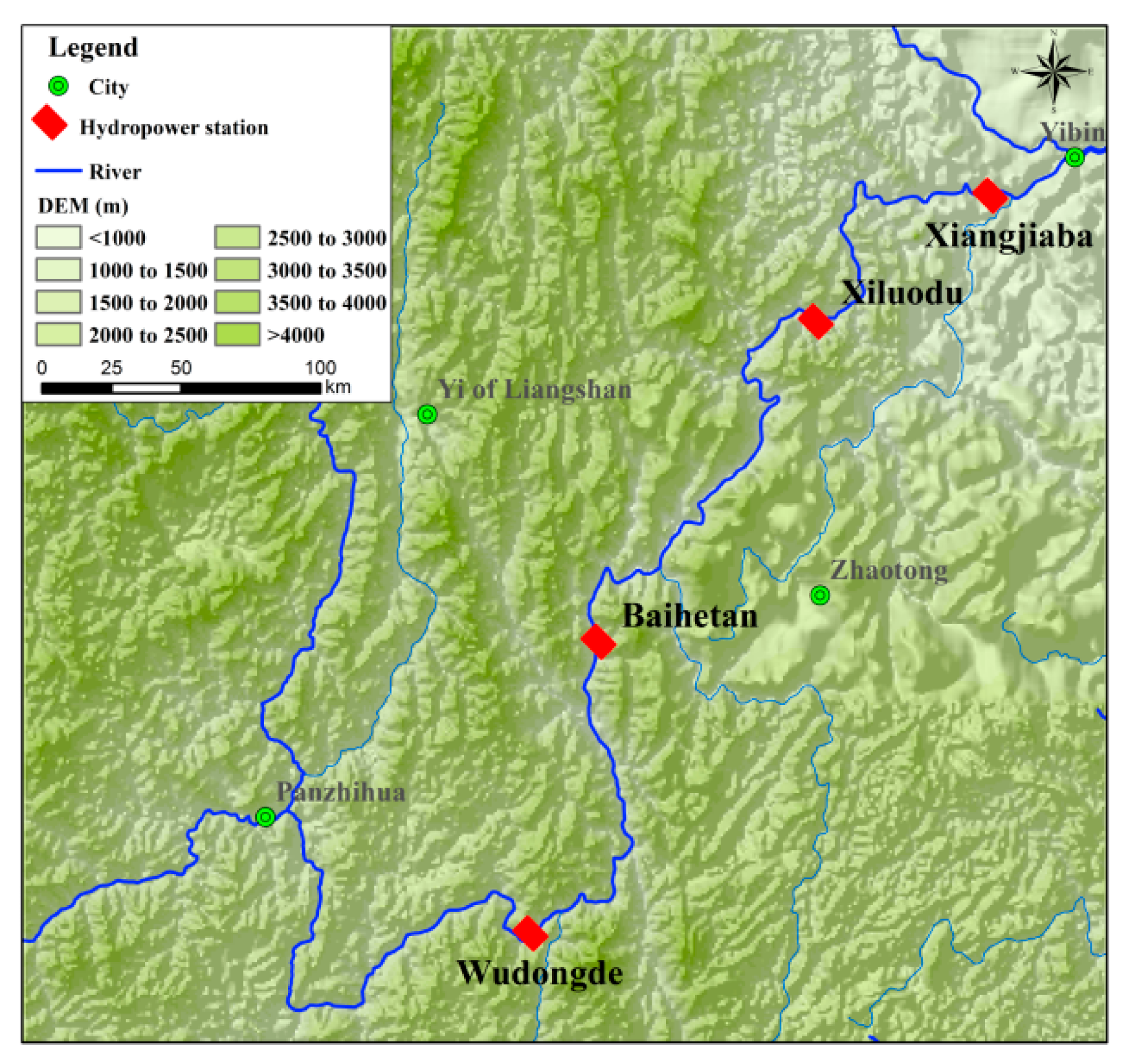
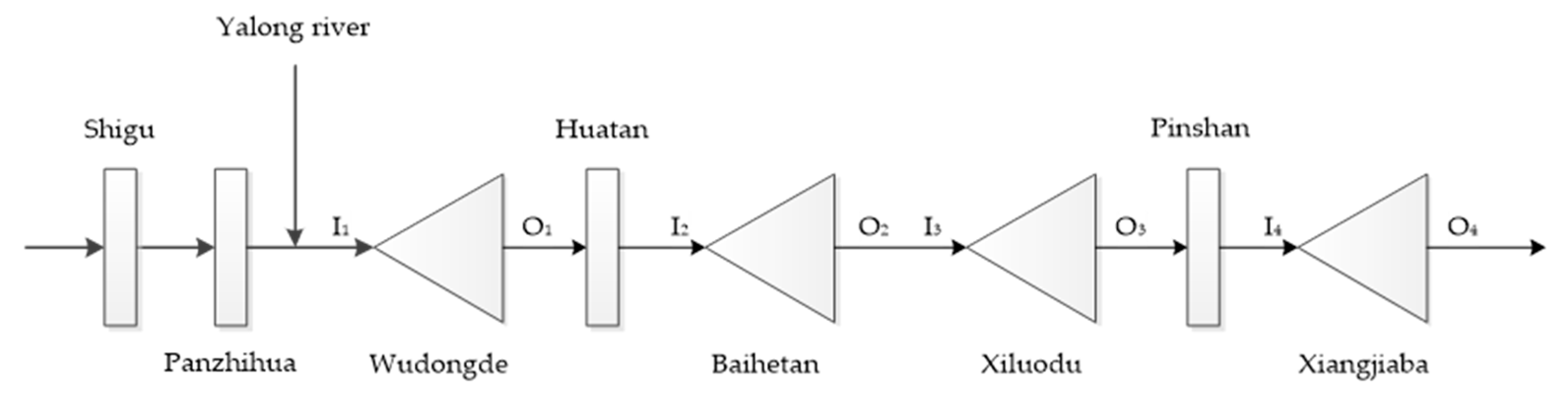
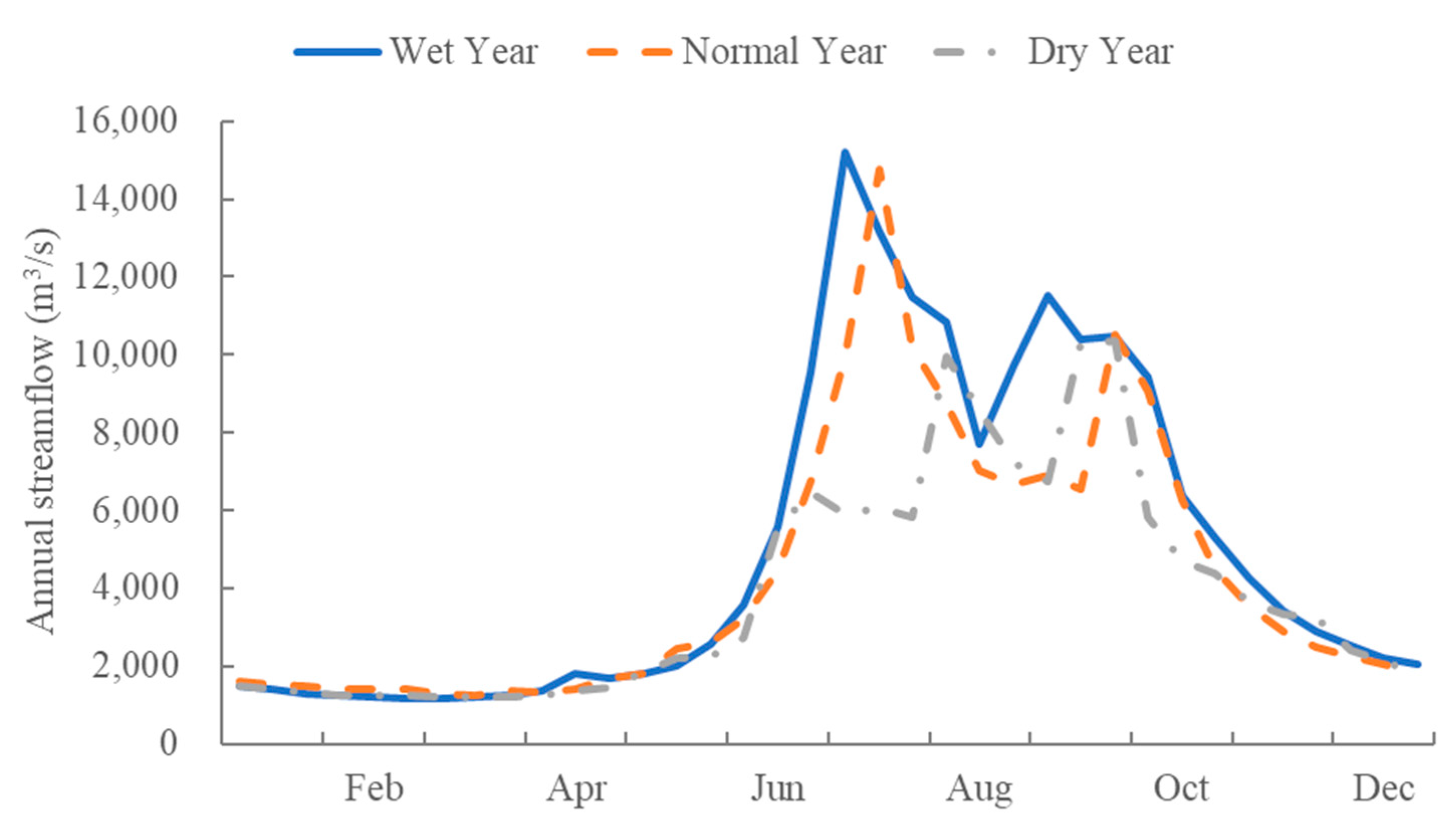
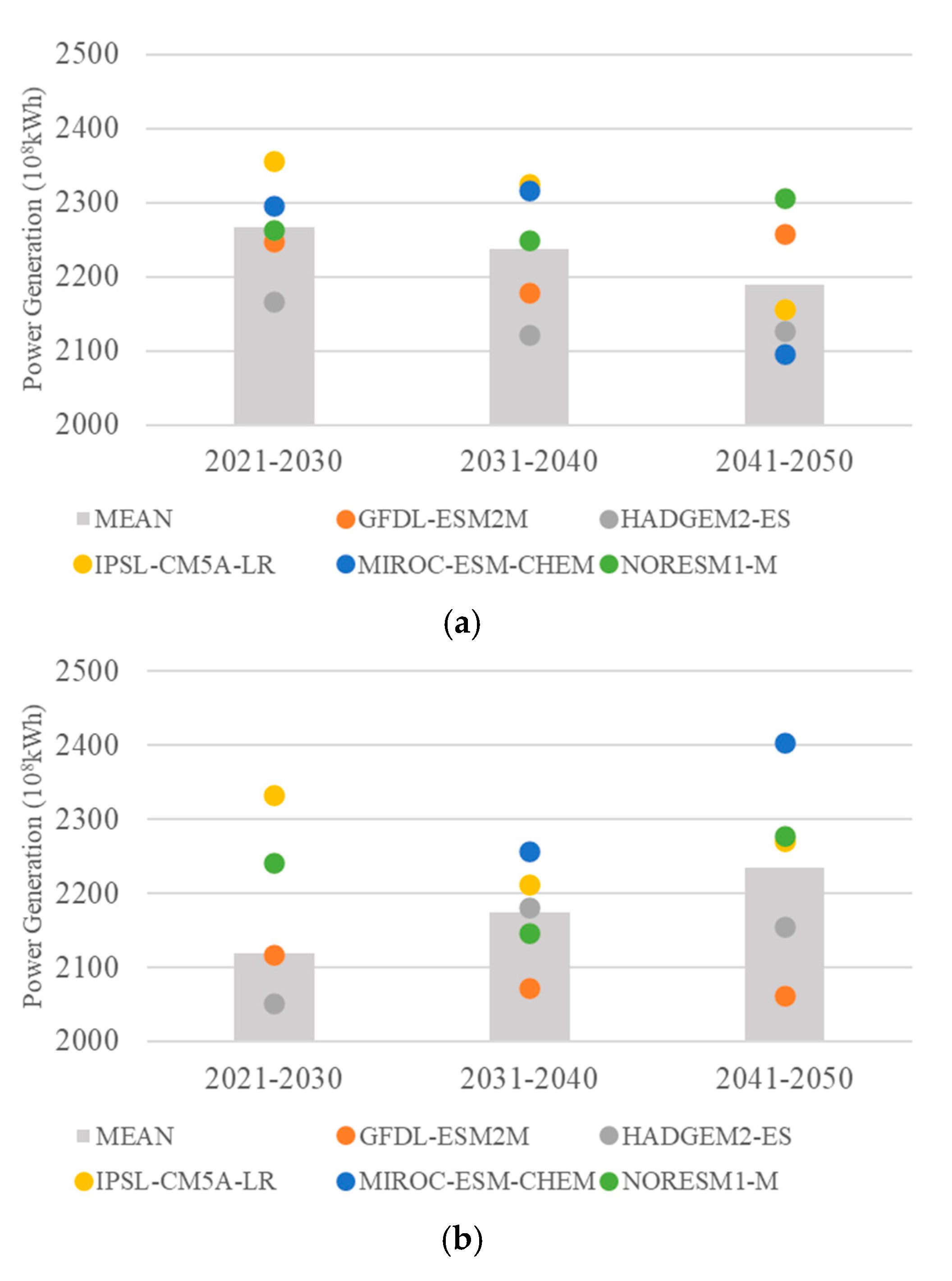
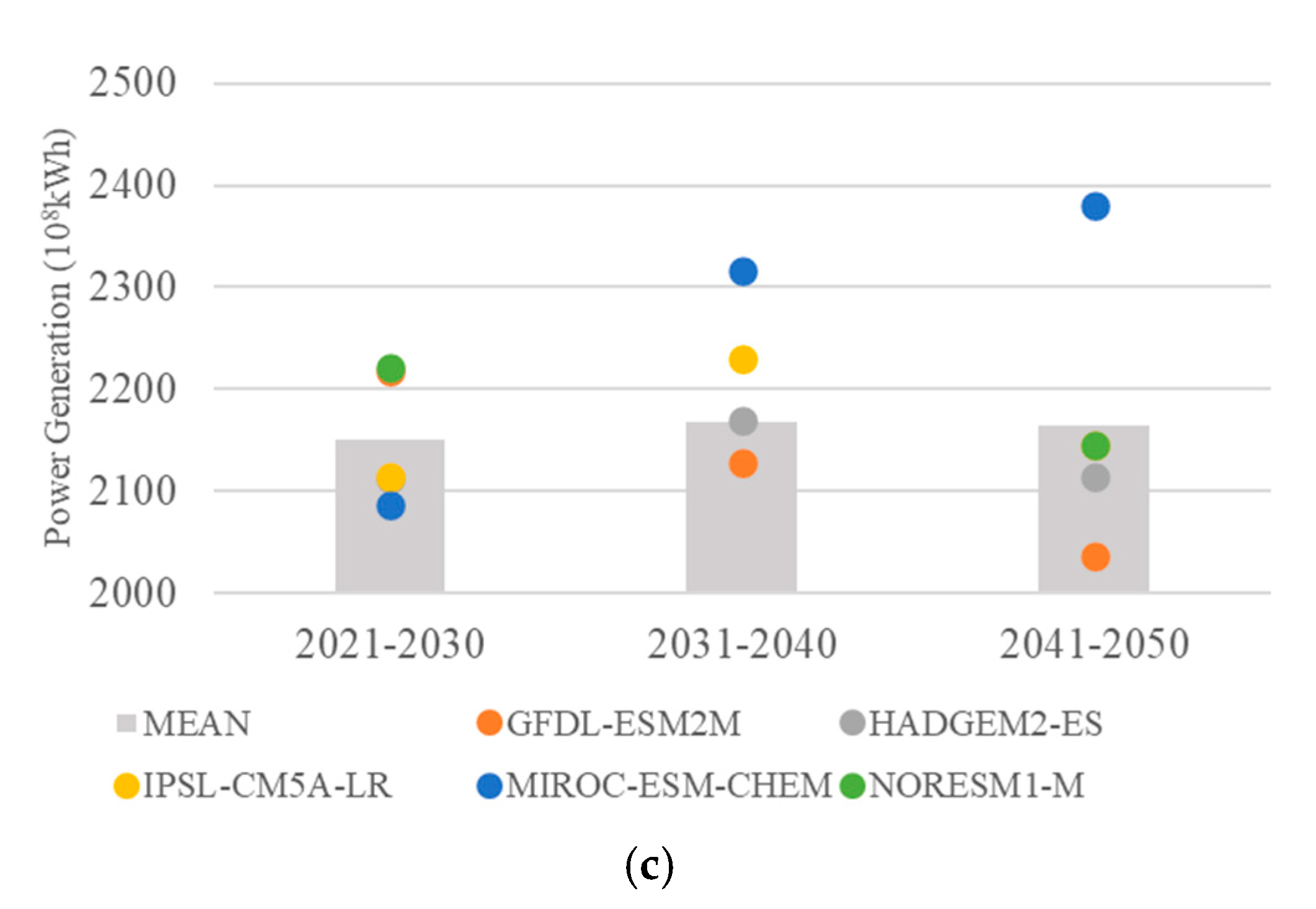
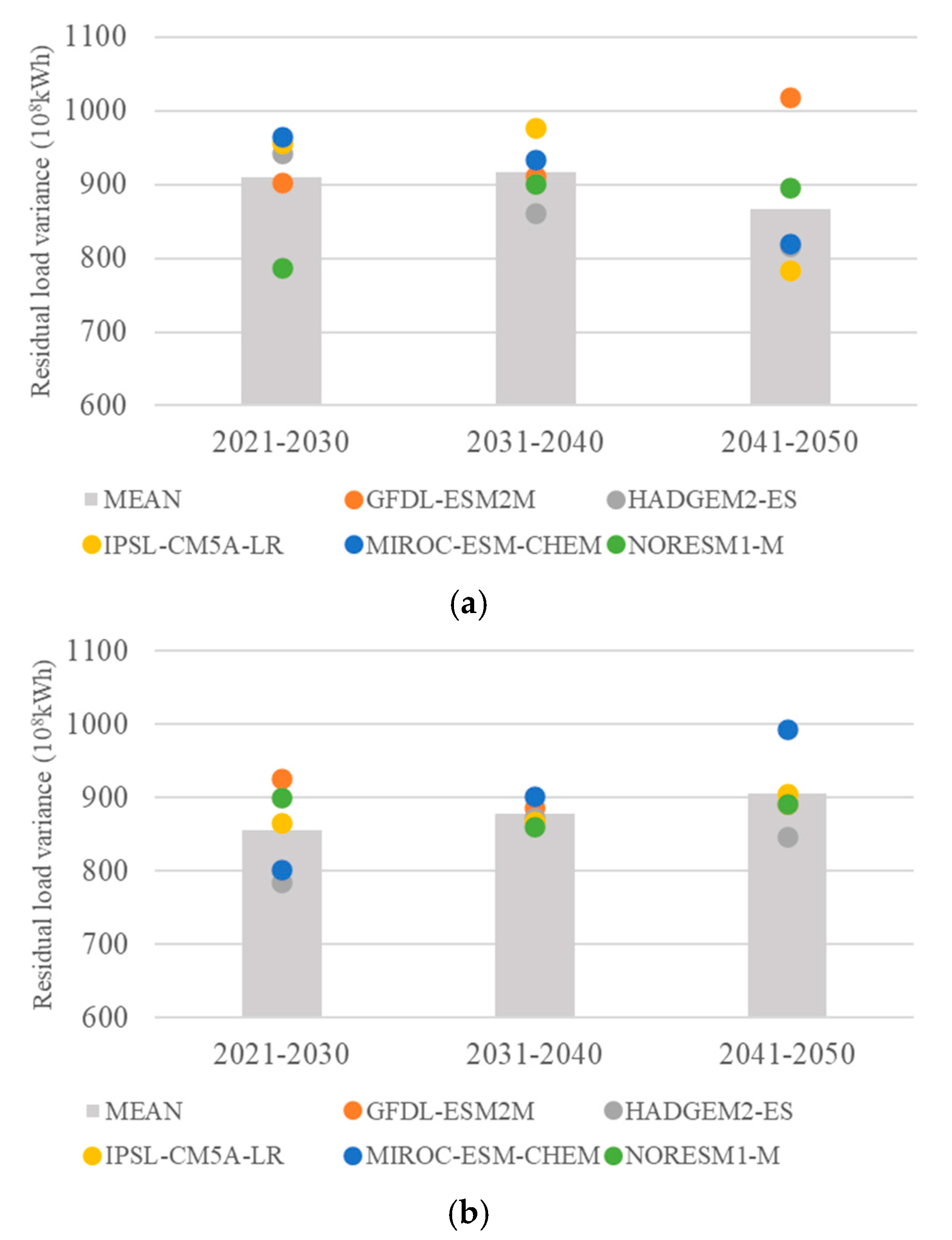
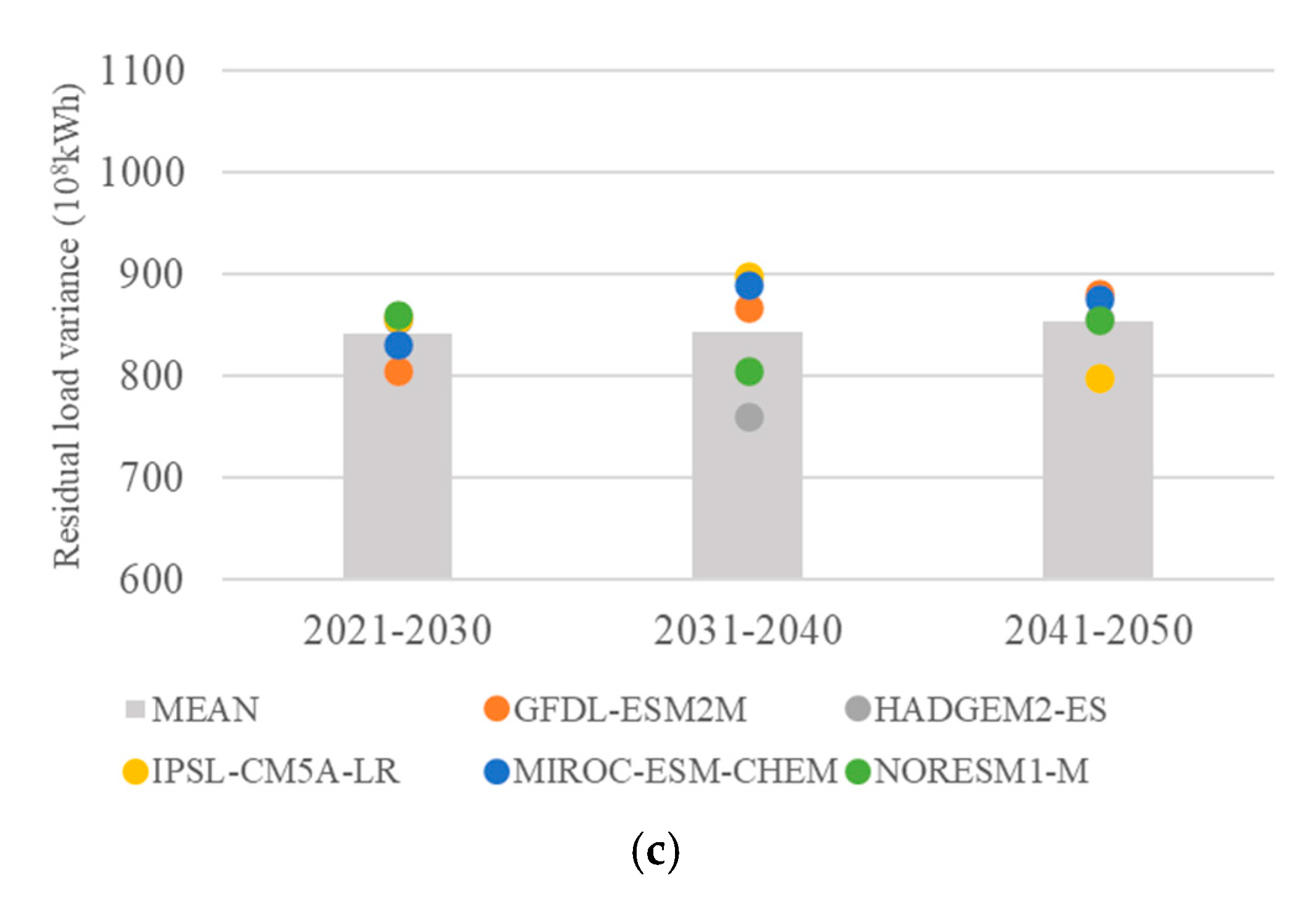
| Parameters | Wudongde | Baihetan | Xiluodu | Xiangjiaba |
|---|---|---|---|---|
| Dead water level (m) | 945 | 765 | 540 | 370 |
| Normal water level (m) | 977 | 825 | 600 | 380 |
| Flood limit water level (m) | 952 | 785 | 560 | 370 |
| Installed capacity (104 kw) | 1020 | 1600 | 1260 | 600 |
| Total capacity (108 m3) | 74.08 | 206.27 | 126.7 | 51.63 |
| Minimum outflow (m3·s−1) | 906 | 905 | 1500 | 1500 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Feng, Y.; Xu, J.; Hong, Y.; Wang, Y.; Yuan, Z.; Wang, C. Reservoir Scheduling Using a Multi-Objective Cuckoo Search Algorithm under Climate Change in Jinsha River, China. Water 2021, 13, 1803. https://doi.org/10.3390/w13131803
Feng Y, Xu J, Hong Y, Wang Y, Yuan Z, Wang C. Reservoir Scheduling Using a Multi-Objective Cuckoo Search Algorithm under Climate Change in Jinsha River, China. Water. 2021; 13(13):1803. https://doi.org/10.3390/w13131803
Chicago/Turabian StyleFeng, Yu, Jijun Xu, Yang Hong, Yongqiang Wang, Zhe Yuan, and Chao Wang. 2021. "Reservoir Scheduling Using a Multi-Objective Cuckoo Search Algorithm under Climate Change in Jinsha River, China" Water 13, no. 13: 1803. https://doi.org/10.3390/w13131803
APA StyleFeng, Y., Xu, J., Hong, Y., Wang, Y., Yuan, Z., & Wang, C. (2021). Reservoir Scheduling Using a Multi-Objective Cuckoo Search Algorithm under Climate Change in Jinsha River, China. Water, 13(13), 1803. https://doi.org/10.3390/w13131803






