Retrieving and Verifying Three-Dimensional Surface Motion Displacement of Mountain Glacier from Sentinel-1 Imagery Using Optimized Method
Abstract
:1. Introduction
2. Study Site and Materials
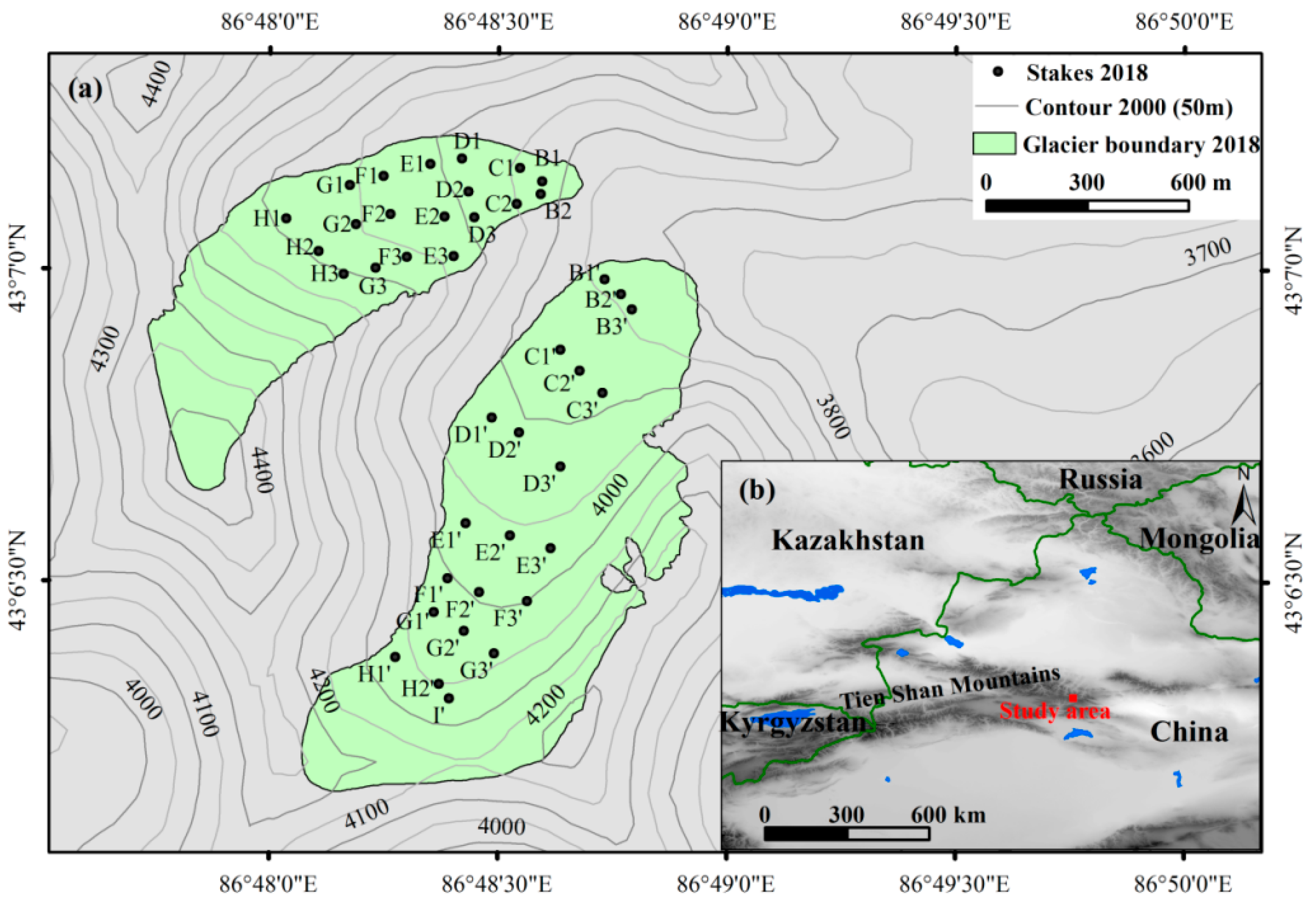
2.1. Study Site
2.2. Materials
2.2.1. Sentinel-1 Ascending and Descending Orbits Data
2.2.2. Measurement Data
3. Methodology
3.1. Offset Tracking
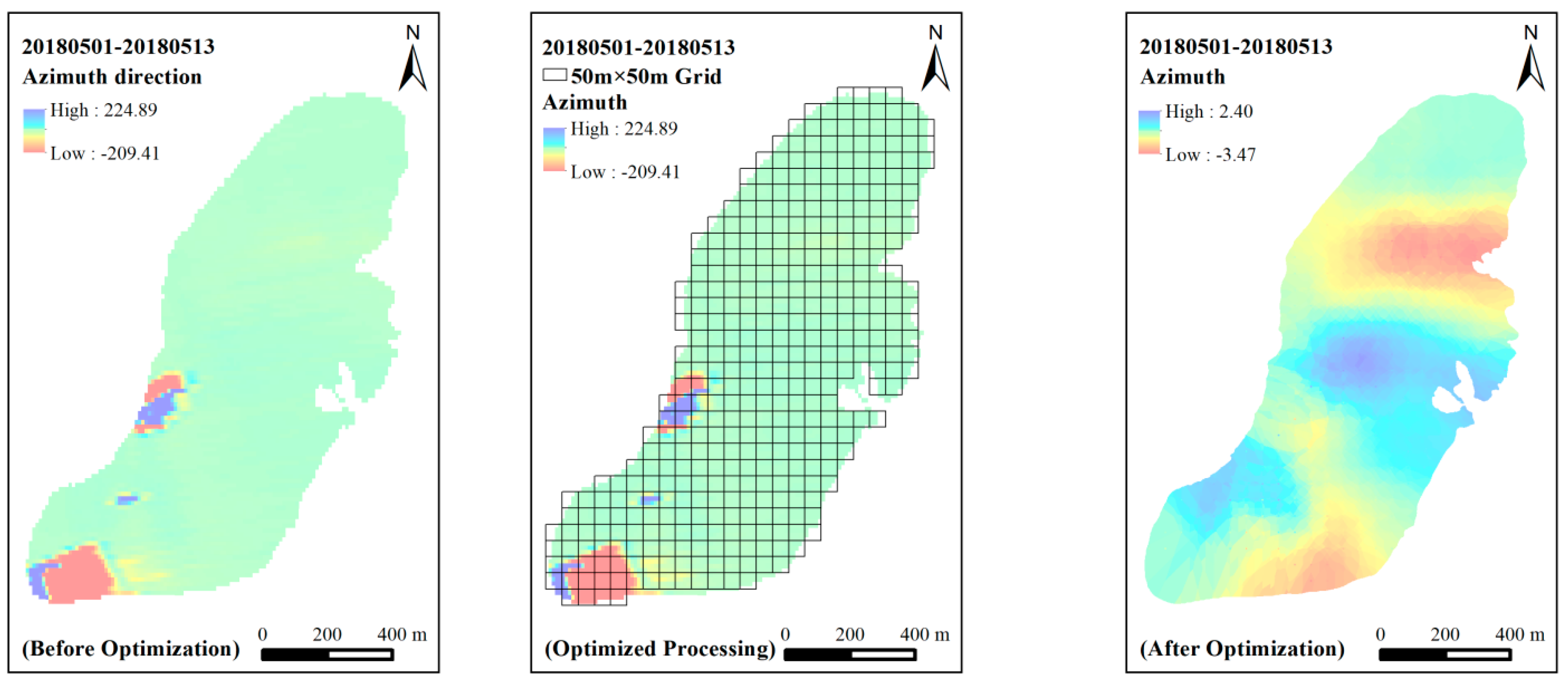
3.2. Optimizing the Offset Tracking Results by Means of Iterative Filtering
3.3. OT-SBAS Technology
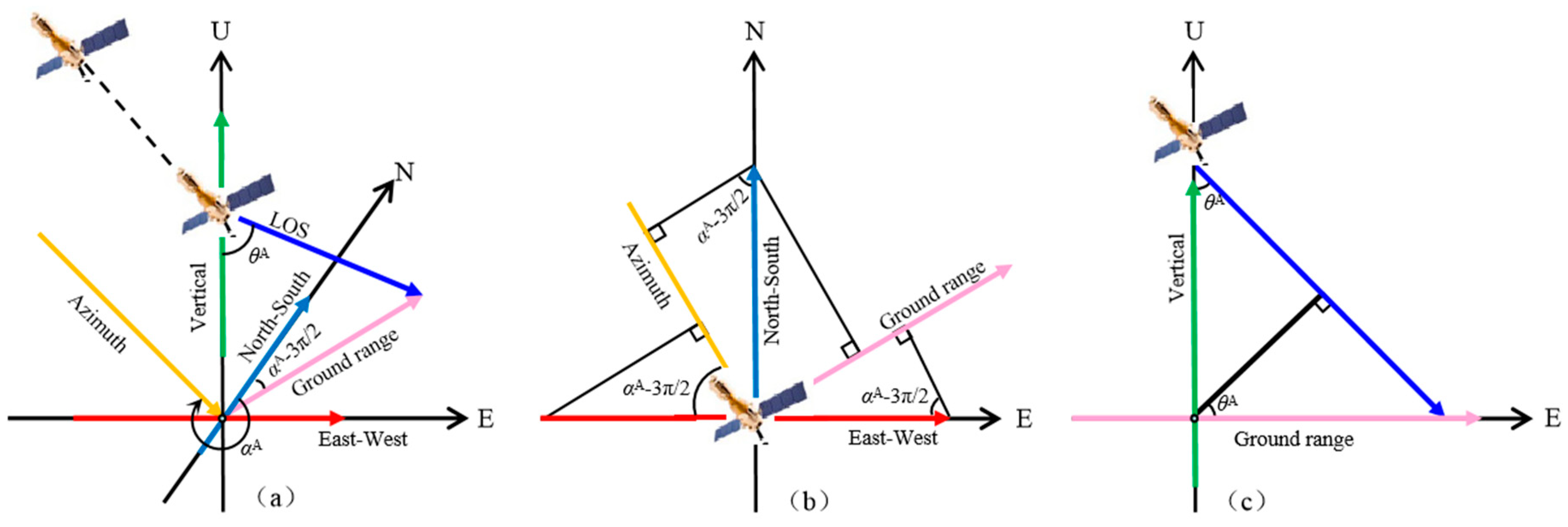
3.4. Conversion of 3D Surface Motion Displacement of Glacier
4. Results and Discussion
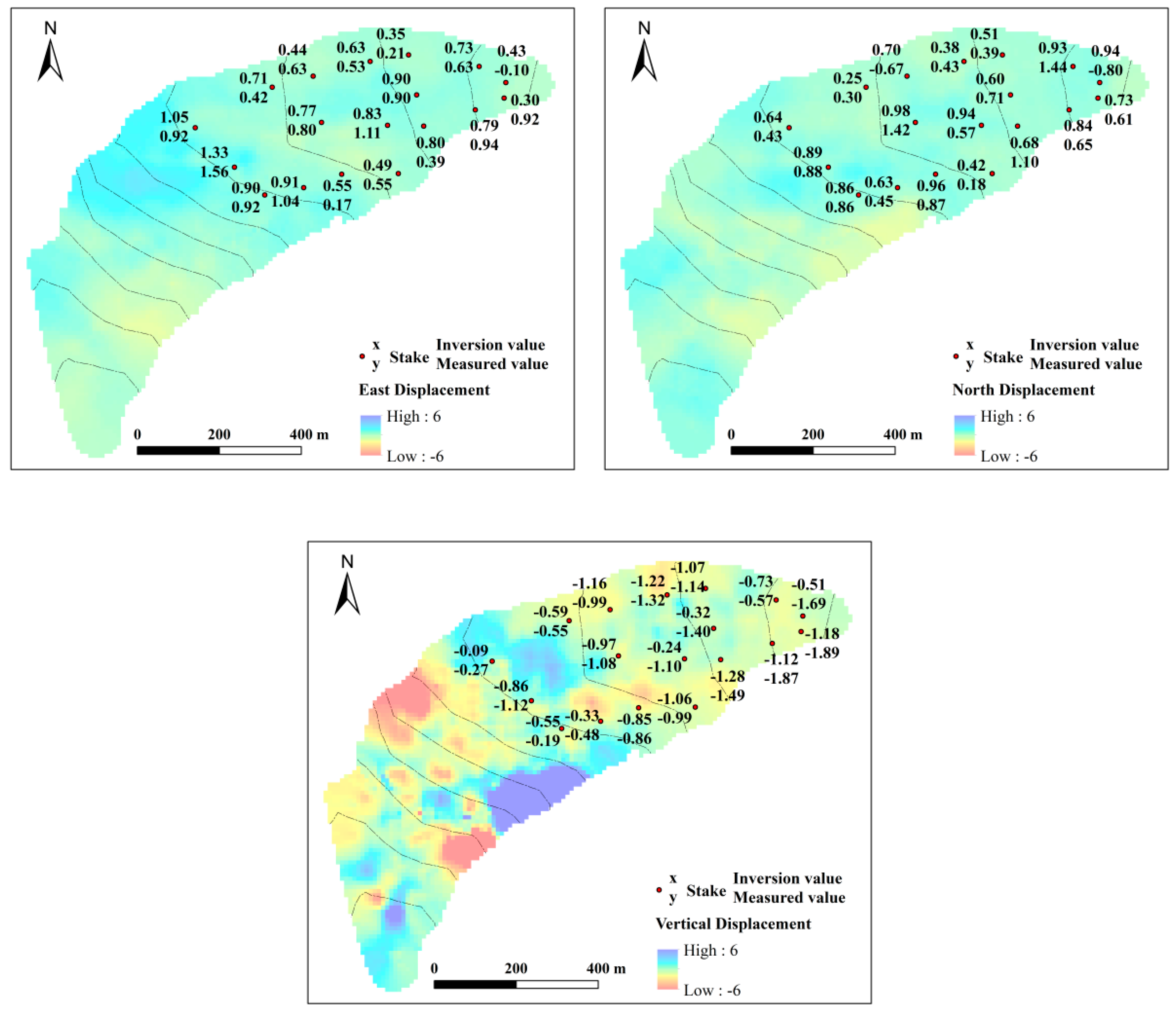
4.1. Comparison between the Inversion Value and the Measured Value
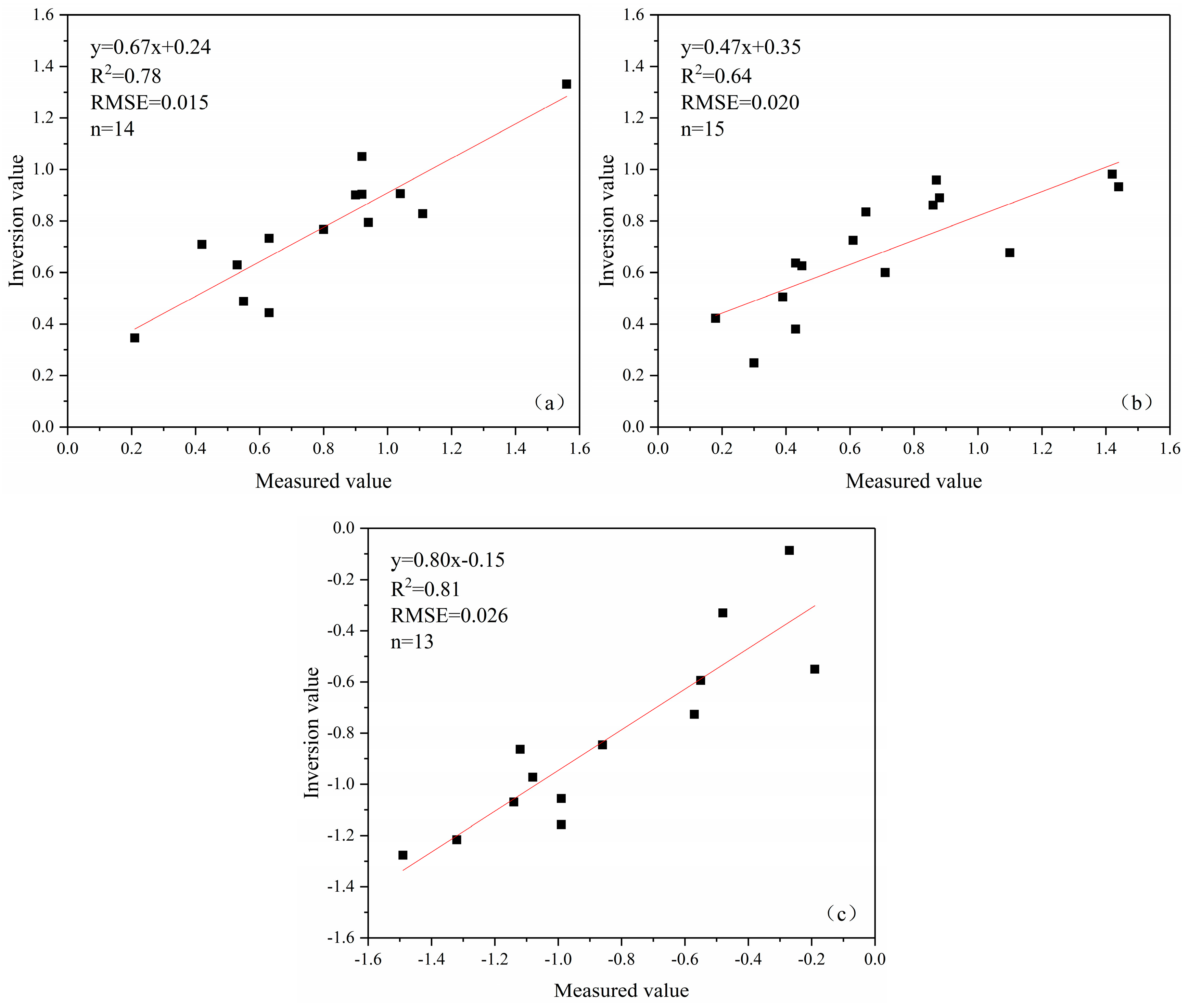
4.2. Accuracy Evaluation of Inversion Results
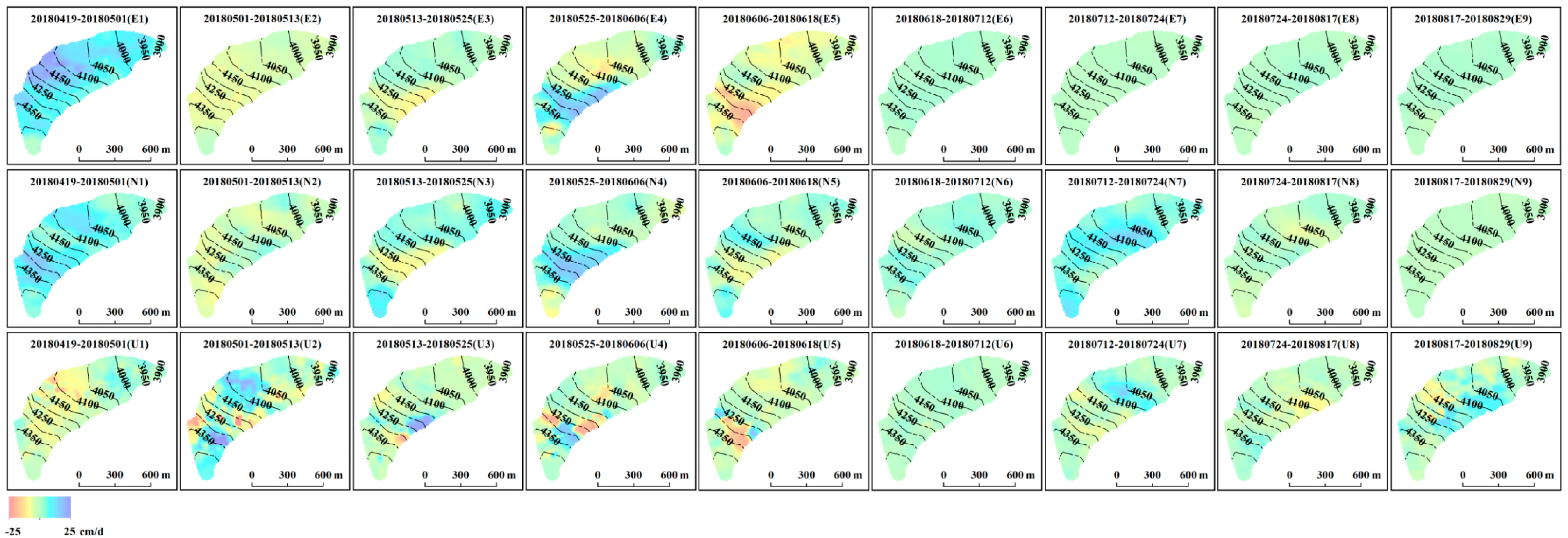
4.3. Distribution of the 3D Surface Motion Velocity of UG1
5. Conclusions and Outlook
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Appendix A
| Satellite | Track Directions | Track | Acquired Time | Polarization Mode | Incidence Angle/° |
|---|---|---|---|---|---|
| Sentinel-1A | Ascending | Track_114 | 19 April 2018 | VV | 41.444 |
| 1 May 2018 | VV | 41.441 | |||
| 13 May 2018 | VV | 41.447 | |||
| 25 May 2018 | VV | 41.450 | |||
| 6 June 2018 | VV | 41.447 | |||
| 18 June 2018 | VV | 41.446 | |||
| 12 July 2018 | VV | 41.441 | |||
| 24 July 2018 | VV | 41.446 | |||
| 17 August 2018 | VV | 41.450 | |||
| 29 August 2018 | VV | 41.448 | |||
| Sentinel-1B | Descending | Track_19 | 19 April 2018 | VV | 43.851 |
| 1 May 2018 | VV | 43.843 | |||
| 13 May 2018 | VV | 43.845 | |||
| 25 May 2018 | VV | 43.848 | |||
| 6 June 2018 | VV | 43.853 | |||
| 18 June 2018 | VV | 43.850 | |||
| 12 July 2018 | VV | 43.847 | |||
| 24 July 2018 | VV | 43.846 | |||
| 17 August 2018 | VV | 43.849 | |||
| 29 August 2018 | VV | 43.850 |
| Track Directions | Primary Images | Secondary Images | Baseline (m) | Time Intervals (day) |
|---|---|---|---|---|
| Ascending | 19 April 2018 | 1 May 2018 | 45.814 | 12 |
| 19 April 2018 | 13 May 2018 | −51.462 | 24 | |
| 19 April 2018 | 25 May 2018 | −97.520 | 36 | |
| 1 May 2018 | 13 May 2018 | −93.673 | 12 | |
| 1 May 2018 | 25 May 2018 | −141.855 | 24 | |
| 1 May 2018 | 6 June 2018 | −91.351 | 36 | |
| 13 May 2018 | 25 May 2018 | −48.964 | 12 | |
| 13 May 2018 | 6 June 2018 | 18.352 | 24 | |
| 13 May 2018 | 18 June 2018 | 31.388 | 36 | |
| 25 May 2018 | 6 June 2018 | 52.916 | 12 | |
| 25 May 2018 | 18 June 2018 | 76.525 | 24 | |
| 6 June 2018 | 18 June 2018 | 25.262 | 12 | |
| 6 June 2018 | 12 July 2018 | 100.125 | 36 | |
| 18 June 2018 | 12 July 2018 | 74.758 | 24 | |
| 18 June 2018 | 24 July 2018 | 3.160 | 36 | |
| 12 July 2018 | 24 July 2018 | −74.824 | 12 | |
| 12 July 2018 | 17 August 2018 | −141.608 | 36 | |
| 24 July 2018 | 17 August 2018 | −67.225 | 24 | |
| 24 July 2018 | 29 August 2018 | −39.664 | 36 | |
| 17 August 2018 | 29 August 2018 | 27.249 | 12 | |
| Descending | 19 April 2018 | 1 May 2018 | 143.474 | 12 |
| 19 April 2018 | 13 May 2018 | 101.273 | 24 | |
| 19 April 2018 | 25 May 2018 | 56.725 | 36 | |
| 1 May 2018 | 13 May 2018 | −42.507 | 12 | |
| 1 May 2018 | 25 May 2018 | −88.337 | 24 | |
| 1 May 2018 | 6 June 2018 | −168.091 | 36 | |
| 13 May 2018 | 25 May 2018 | −45.842 | 12 | |
| 13 May 2018 | 6 June 2018 | −125.828 | 24 | |
| 13 May 2018 | 18 June 2018 | −73.370 | 36 | |
| 25 May 2018 | 6 June 2018 | −80.777 | 12 | |
| 25 May 2018 | 18 June 2018 | −29.639 | 24 | |
| 6 June 2018 | 18 June 2018 | 52.497 | 12 | |
| 6 June 2018 | 12 July 2018 | 101.450 | 36 | |
| 18 June 2018 | 12 July 2018 | 49.405 | 24 | |
| 18 June 2018 | 24 July 2018 | 59.532 | 36 | |
| 12 July 2018 | 24 July 2018 | 18.759 | 12 | |
| 12 July 2018 | 17 August 2018 | −36.185 | 36 | |
| 24 July 2018 | 17 August 2018 | −43.193 | 24 | |
| 24 July 2018 | 29 August 2018 | −72.274 | 36 | |
| 17 August 2018 | 29 August 2018 | −30.089 | 12 |
References
- Shi, Y.F.; Huang, M.H.; Yao, T.D.; Deng, Y.X. Glaciers and Their Environments in China: The Present, Past and Future; Science Press: Beijing, China, 2000; ISBN 7030081269. [Google Scholar]
- Thiel, K.; Arndt, A.; Wang, P.; Li, H.; Li, Z.; Schneider, C. Modeling of Mass Balance Variability and Its Impact on Water Discharge from the Urumqi Glacier No. 1 Catchment, Tian Shan, China. Water 2020, 12, 3297. [Google Scholar] [CrossRef]
- Benn, D.I.; Warren, C.R.; Mottra, R.H. Calving processes and the dynamics of calving glaciers. Earth-Sci. Rev. 2007, 82, 144–179. [Google Scholar] [CrossRef]
- Paul, F.; Bolch, T.; Kääb, A.; Nagler, T. The glaciers climate change initiative: Methods for creating glacier area, elevation change and velocity products. Remote Sens. Environ. 2015, 162, 408–426. [Google Scholar] [CrossRef] [Green Version]
- Guan, W.J.; Cao, B.; Pan, B.T. Research of glacier flow velocity: Current situation and prospects. J. Glaciol. Geocryol. 2020, 42, 1101–1114. (In Chinese) [Google Scholar]
- Xu, S.Q.; E, D.C.; Wang, S.D. Glacier movement monitoring on Nelson Ice Cap, Antarctica. J. Geomatics 1988, 4, 30–35. (In Chinese) [Google Scholar]
- Jing, Z.F.; Zhou, Z.M.; Liu, L. Progress of the Research on Glacier Velocities in China. J. Glaciol. Geocryol. 2010, 32, 749–754. (In Chinese) [Google Scholar]
- Dehecq, A.; Gourmelen, N.; Gardner, A.S.; Brun, F.; Goldberg, D.; Nienow, P.W.; Berthier, E.; Vincent, C.; Wagnon, P.; Trouvé, E. Twenty-first century glacier slowdown driven by mass loss in High Mountain Asia. Nat. Geosci. 2019, 13, 2189–2202. [Google Scholar] [CrossRef]
- Rydt, J.D.; Reese, R.; Fernando, P.; Gudmundsson, G.H. Drivers of Pine Island Glacier speed-up between 1996 and 2016. Cryosphere 2021, 15, 113–132. [Google Scholar] [CrossRef]
- Lei, Y.B.; Yao, T.D.; Tian, L.D.; Sheng, Y.W.; Zhu, L.; Liao, J.J.; Zhao, H.B.; Yang, W.; Yang, K.; Berthier, E.; et al. Response of downstream lakes to Aru glacier collapses on the western Tibetan Plateau. Cryosphere 2020, 15, 199–214. [Google Scholar] [CrossRef]
- Mohr, J.J.; Reeh, N.; Madsen, S.N. Three-dimensional glacial flow and surface elevation measured with radar interferometry. Nature 1998, 391, 273–276. [Google Scholar] [CrossRef]
- Gudmundsson, S.; Gudmundsson, M.T.; Björnsson, H.; Sigmundsson, F.; Rott, H.; Carstensen, J.M. Three-dimensional glacier surface motion maps at the Gja’lp eruption site, Iceland, inferred from combining InSAR and other ice-displacement data. Ann. Glaciol. 2002, 34, 315–322. [Google Scholar] [CrossRef] [Green Version]
- Mohr, J.J.; Reeh, N.; Madsen, S.N. Accuracy of three-dimensional glacier surface velocities derived from radar interferometry and ice-sounding radar measurements. J. Glaciol. 2003, 49, 210–222. [Google Scholar] [CrossRef]
- Magnússon, E.; Rott, H.; Björnsson, H.; Roberts, M.J. Unsteady Glacier Flow Revealed by Multi-Source Satellite Data. In Proceedings of the Agu Fall Meeting, San Francisco, CA, USA, 1–15 December 2006. [Google Scholar]
- Gray, L. Using multiple RADARSAT InSAR pairs to estimate a full three-dimensional solution for glacial ice movement. Geophys. Res. Lett. 2011, 38, L05502. [Google Scholar] [CrossRef]
- Hu, J.; Li, Z.W.; Li, J.; Zhang, L.; Ding, X.L.; Zhu, J.J.; Sun, Q. 3-D movement mapping of the alpine glacier in Qinghai-Tibetan Plateau by integrating D-InSAR, MAI and Offset-Tracking: Case study of the Dongkemadi Glacier. Glob. Planet. Chang. 2014, 118, 62–68. [Google Scholar] [CrossRef]
- Reeh, N.; Madsen, S.N.; Mohr, J.J. Combining SAR interferometry and the equation of continuity to estimate the three-dimensional glacier surface-velocity vector. J. Glaciol. 1999, 45, 533–538. [Google Scholar] [CrossRef] [Green Version]
- Li, J.; Li, Z.W.; Wu, L.X.; Xu, B.; Hu, J.; Zhou, Y.S.; Miao, Z.L. Deriving a time series of 3D glacier motion to investigate interactions of a large mountain glacial system with its glacial lake: Use of Synthetic Aperture Radar Pixel Offset-Small Baseline Subset technique. J. Hydrol. 2018, 559, 596–608. [Google Scholar] [CrossRef]
- Yang, L.Y.; Zhao, C.Y.; Zhong, L.; Yang, C.S.; Zhang, Q. Three-Dimensional Time Series Movement of the Cuolangma Glaciers, Southern Tibet with Sentinel-1 Imagery. Remote Sens. 2020, 12, 3466. [Google Scholar] [CrossRef]
- Bolch, T. Climate change and glacier retreat in northern Tien Shan(Kazakhstan/Kyrgyzstan) using remote sensing data. Glob. Planet. Chang. 2007, 56, 1–12. [Google Scholar] [CrossRef]
- Shen, Y.P.; Wang, G.Y.; Ding, Y.J.; Mao, W.Y.; Liu, S.Y.; Wang, S.D.; Mamatkanov, D.M. Changes in Glacier Mass Balance in Watershed of Sary Jaz-Kumarik Rivers of Tianshan Mountains in 1957–2006 and Their Impact on Water Resources and Trend to End of the 21th Century. J. Glaciol. Geocryol. 2009, 31, 792–800. (In Chinese) [Google Scholar]
- Kääb, A.; Berthier, E.; Nuth, C.; Gardelle, J. Contrasting patterns of early twenty-first-century glacier mass change in the Himalayas. Nature 2012, 488, 495–498. [Google Scholar] [CrossRef] [PubMed]
- Gardelle, J.; Berthier, E.; Amaud, Y. Slight mass gain of Karakoram glaciers in the early twenty-first century. Nat. Geosci. 2012, 5, 322–325. [Google Scholar] [CrossRef]
- Immerzeel, W.W.; Kraaijenbrink, P.; Shea, J.M.; Shrestha, A.B. High-resolution monitoring of Himalayan glacier dynamics using unmanned aerial vehicles. Remote Sens. Environ. 2014, 150, 93–103. [Google Scholar] [CrossRef]
- Jiang, Z.L.; Wang, L.; Zhang, Z.; Liu, S.Y.; Zhang, Y.; Tang, Z.G.; Wei, J.F.; Huang, D.N.; Zhang, S.S. Surface elecation changes of Yengisogat Glacier between 2000 and 2014. Arid Land Geograph. 2020, 43, 12–19. (In Chinese) [Google Scholar]
- LI, Z.J.; Wang, N.L.; Chen, A.A.; Liu, K. Remote sensing monitoring of glacier changes in Shyok basin of the Karakoram Mountains, 1993–2016. J.Glaciol. Geocryol. 2019, 41, 770–782. (In Chinese) [Google Scholar]
- Xu, A.W.; Yang, T.B.; Wang, C.Q.; Ji, Q. Variation of glaciers in the Shaksgam River Basin, Karakoram Mountains during 1978–2015. Prog. Geograph. 2016, 35, 878–888. (In Chinese) [Google Scholar]
- Yao, T.D.; Thompson, L.; Yang, W. Different glacier status with atmospheric circulations in Tibetan Plateau and surroundings. Nat. Clim. Chang. 2012, 2, 663–667. [Google Scholar] [CrossRef]
- Fujita, K.; Ageta, Y. Effect of summer accumulation on glacier mass balance on the Tibetan Plateau revealed by mass-balance model. J. Glaciol. 2000, 46, 244–252. [Google Scholar] [CrossRef] [Green Version]
- Zhao, Q.D.; Ding, Y.J.; Wang, J.; Gao, H.K. Projecting climate change impacts on hydrological processes on the Tibetan Plateau with model calibration against the glacier inventory data and observed streamflow. J. Hydrol. 2019, 573, 60–81. [Google Scholar] [CrossRef]
- Wang, X.N.; Yang, T.B.; Tian, H.Z.; Jiang, S. Response of glacier variation in the southern Altai Mountains to climate change during the last 40 years. J. Arid Land Res. Environ. 2013, 27, 77–82. (In Chinese) [Google Scholar]
- Wang, P.Y.; Li, Z.Q.; Li, H.L.; Wang, W.B. Characteristics of a partially debris-covered glacier and its response to atmospheric warming in Mt. Tomor, Tien Shan, China. Glob. Planet. Chang. 2017, 159, 11–24. [Google Scholar] [CrossRef]
- Xu, C.H.; Li, Z.Q.; Li, H.L.; Wang, F.T.; Zhou, P. Long-range terrestrial laser scanning measurements of annual and intra-annual mass balances for Urumqi glacier No. 1, eastern Tien Shan, China. Cryosphere 2019, 13, 2361–2383. [Google Scholar] [CrossRef] [Green Version]
- Yao, X.J.; Liu, S.Y.; Guo, W.Q.; Huai, B.J.; Sun, M.P.; Xu, J.L. Glacier change of Altay Mountain in China from 1960 to 2009-Based on the Second Glacier Inventory of China. J. Nat. Resour. 2012, 27, 1734–1745. (In Chinese) [Google Scholar]
- Wang, Y.Q.; Zhao, J.; Li, Z.Q.; Zhang, M.J. Glacier changes in the Sawuer Mountain during 1977-2017 and their response to climate change. J. Nat. Resour. 2019, 34, 802–814. (In Chinese) [Google Scholar]
- Jin, H.A.; Yao, X.J.; Zhang, D.H. A dataset of glacier length in Chinese Altay Mountains from 1959 to 2016. Sci. Data Bank 2019, 4, 168–175. (In Chinese) [Google Scholar]
- Huai, B.J.; Li, Z.Q.; Wang, F.T.; Wang, P.Y.; Li, K.M. Ice thickness distribution and ice volume estimation of Muz Taw Glacier in Sawir Mountains. Earth Sci. 2016, 41, 757–764. (In Chinese) [Google Scholar]
- Li, Z.Q.; Shen, Y.P.; Wang, F.T.; Li, H.L.; Dong, Z.W.; Wang, W.B.; Wang, L. Response of Glacier Melting to Climate Change-Take Urumqi Glacier No. 1 as an Example. J. Glaciol. Geocryol. 2007, 29, 333–342. (In Chinese) [Google Scholar]
- Li, Z.Q.; Shen, Y.P.; Wang, F.T.; Li, H.L.; Dong, Z.W.; Wang, W.B.; Wang, L. Response of melting ice to Climate Change in the Glacier No. 1 at the headwaters of Urumqi River, Tianshan Mountain. Adv. Clim. Change Res. 2007, 3, 132–137. (In Chinese) [Google Scholar]
- Li, Z.Q.; Wang, W.B.; Zhang, M.J.; Wang, F.T. Observed changes in streamflow at the headwaters of the Urumqi River, eastern Tianshan, central Asia. Hydrol. Process. 2010, 24, 217–224. [Google Scholar] [CrossRef]
- Li, Z.Q.; Li, H.L.; Chen, Y.N. Mechanisms and simulation of accelerated shrinkage of continental glaciers: A case study of Urumqi Glacier No. 1 in eastern Tianshan, Central Asia. J. Earth Sci. 2011, 22, 423–430. [Google Scholar] [CrossRef]
- Xu, C.H.; Li, Z.Q.; Wang, P.Y.; Anjumab, M.N.; LI, H.L.; Wang, F.T. Detailed comparison of glaciological and geodetic mass balances for Urumqi glacier No. 1, eastern Tien Shan, China, from 1981 to 2015. Cold Reg. Sci. Technol. 2018, 155, 137–148. [Google Scholar] [CrossRef]
- Wang, P.Y.; Li, Z.Q.; Li, H.L.; Wang, W.B.; Yao, H.B. Comparison of glaciological and geodetic mass balance at Urumqi glacier No. 1, Tian Shan, central Asia. Glob. Planet. Chang. 2014, 114, 14–22. [Google Scholar] [CrossRef]
- Wang, P.Y.; Li, Z.Q.; Schneider, C.; Li, H.L.; Hamm, A.; Jin, S.; Xu, C.H.; Li, H.L.; Yue, X.Y.; Yang, M. A Test Study of an Energy and Mass Balance Model Application to a Site on Urumqi Glacier No. 1, Chinese Tian Shan. Water 2020, 12, 2865. [Google Scholar] [CrossRef]
- Li, H.L.; Ng, F.; Li, Z.Q.; Qin, D.H. An extended “perfect-plasticity” method for estimating ice thickness along the flow line of mountain glaciers. J. Geophys. Res. Earth Surf. 2012, 117, 1020–1030. [Google Scholar] [CrossRef] [Green Version]
- Yue, X.Y.; Li, Z.Q.; Zhao, J.; Li, H.L.; Wang, P.Y.; Wang, L. Changes in the End-of-Summer Snow Line Altitude of Summer-Accumulation-Type Glaciers in the Eastern Tien Shan Mountains from 1994 to 2016. Remote Sens. 2021, 13, 1080. [Google Scholar] [CrossRef]
- Jia, Y.F.; Li, Z.Q.; Jin, S.; Xu, C.H.; Deng, H.J.; Zhang, M.J. Runoff Changes from Urumqi Glacier No. 1 over the Past 60 Years, Eastern Tianshan, Central Asia. Water 2020, 12, 1286. [Google Scholar] [CrossRef]
- Liu, S.Y.; Yao, X.J.; Guo, W.Q.; Xu, J.L.; Shangguan, D.H.; Wei, J.F.; Bao, W.J.; Wu, Z.L. The contemporary glaciers in China based on the Second Chinese Glacier Inventory. Acta Geograph. Sin. 2015, 70, 3–16. (In Chinese) [Google Scholar]
- Wang, P.Y.; Li, Z.Q.; Zhou, P.; Li, H.L.; Yu, G.B.; Xu, C.H.; Wang, L. Long-term change in ice velocity of Urumqi Glacier No. 1, Tian Shan, China. Cold Reg. Sci. Technol. 2018, 145, 177–184. [Google Scholar] [CrossRef]
- Luckman, A.; Quincey, D.; Bevan, S. The potential of satellite radar interferometry and feature tracking for monitoring flow rates of Himalayan glaciers. Remote Sens. Environ. 2007, 111, 172–181. [Google Scholar] [CrossRef]
- Strozzi, T.; Luckman, A.; Murray, T. Glacier motion estimation using SAR offset-tracking procedures. IEEE Trans. Geosci. Remote Sens. 2002, 40, 2384–2391. [Google Scholar] [CrossRef] [Green Version]
- Bindschadler, R.; Vornberger, P.; Blankenship, D.; Scambos, T.; Jacobel, R. Surface velocity and mass balance of Ice Streams D and E, West Antarctica. J. Glaciol. 1996, 42, 461–475. [Google Scholar] [CrossRef] [Green Version]
- Yasuda, T.; Furuya, M. Short-Term glacier velocity changes at West Kunlun Shan, Northwest Tibet, detected by synthetic aperture radar data. Remote Sens. Environ. 2013, 128, 87–106. [Google Scholar] [CrossRef] [Green Version]
- Michel, R.; Avouac, J.P.; Taboury, J. Measuring ground displacements from SAR amplitude images: Application to the Landers earthquake. Geophys. Res. Lett. 1999, 26, 875–878. [Google Scholar] [CrossRef] [Green Version]
- Yang, Z.F.; Li, Z.W.; Zhu, J.J.; Preusse, A.; Yi, H.W.; Hu, J.; Feng, G.C.; Papst, M. Retrieving 3-D Large Displacements of Mining Areas from a Single Amplitude Pair of SAR Using Offset Tracking. Remote Sens. 2017, 9, 338. [Google Scholar] [CrossRef] [Green Version]
- Neelmeijer, J.; Motagh, M.; Wetzel, H.U. Estimating Spatial and Temporal Variability in Surface Kinematics of the Inylchek Glacier, Central Asia, using TerraSAR–X Data. Remote Sens. 2014, 6, 9239–9259. [Google Scholar] [CrossRef] [Green Version]
- Jung, H.S.; Lu, Z.Y.; Won, J.; Poland, M.P.; Miklius, A. Mapping Three-Dimensional Surface Deformation by Combining Multiple-Aperture Interferometry and Conventional Interferometry: Application to the June 2007 Eruption of Kilauea Volcano, Hawaii. IEEE Geosci. Remote Sens. Lett. 2011, 8, 34–38. [Google Scholar] [CrossRef]
- Wang, X.Z.; Tao, B.Z.; Qiu, W.N.; Yao, Y.B. Advanced Surveying Adjustment; Surveying Press: Beijing, China, 2006; ISBN 9787503013966. [Google Scholar]
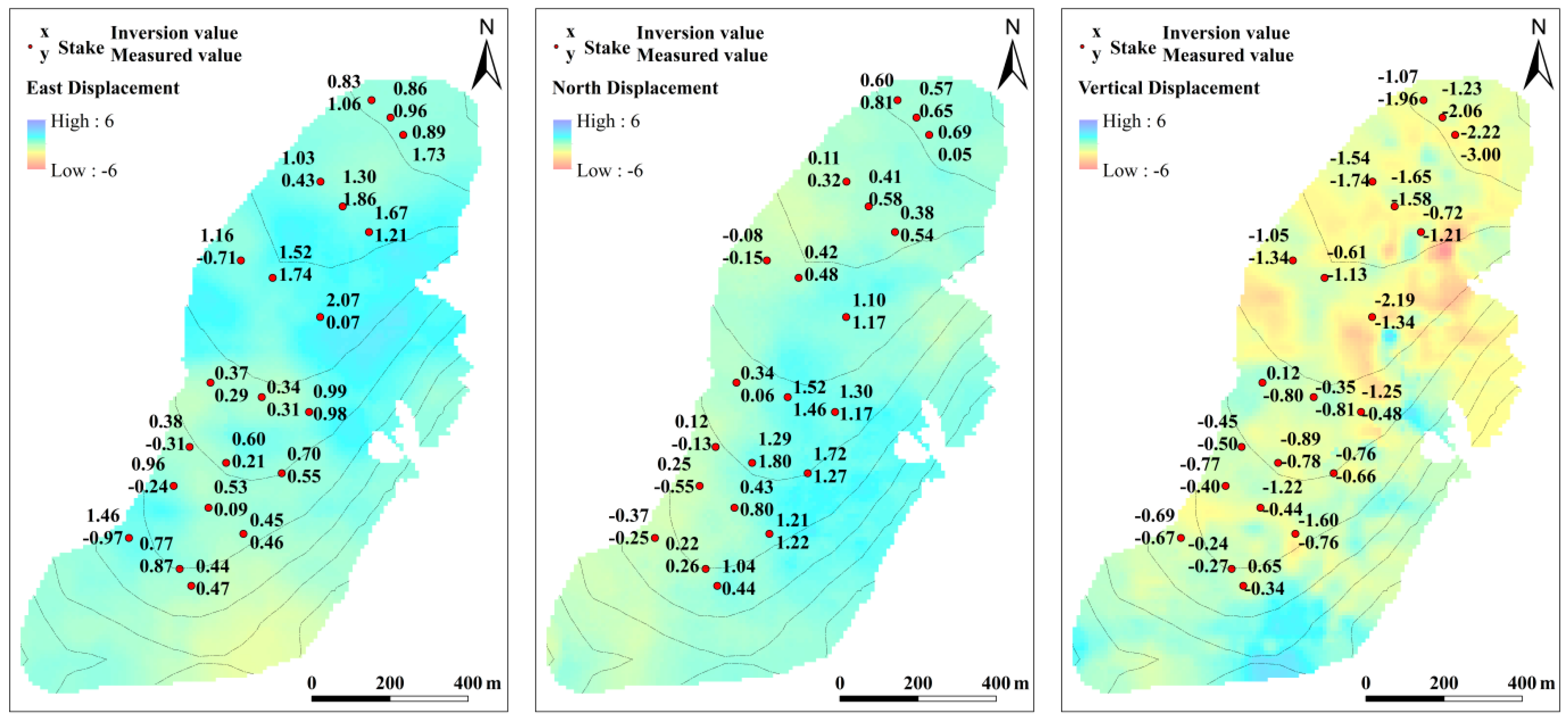
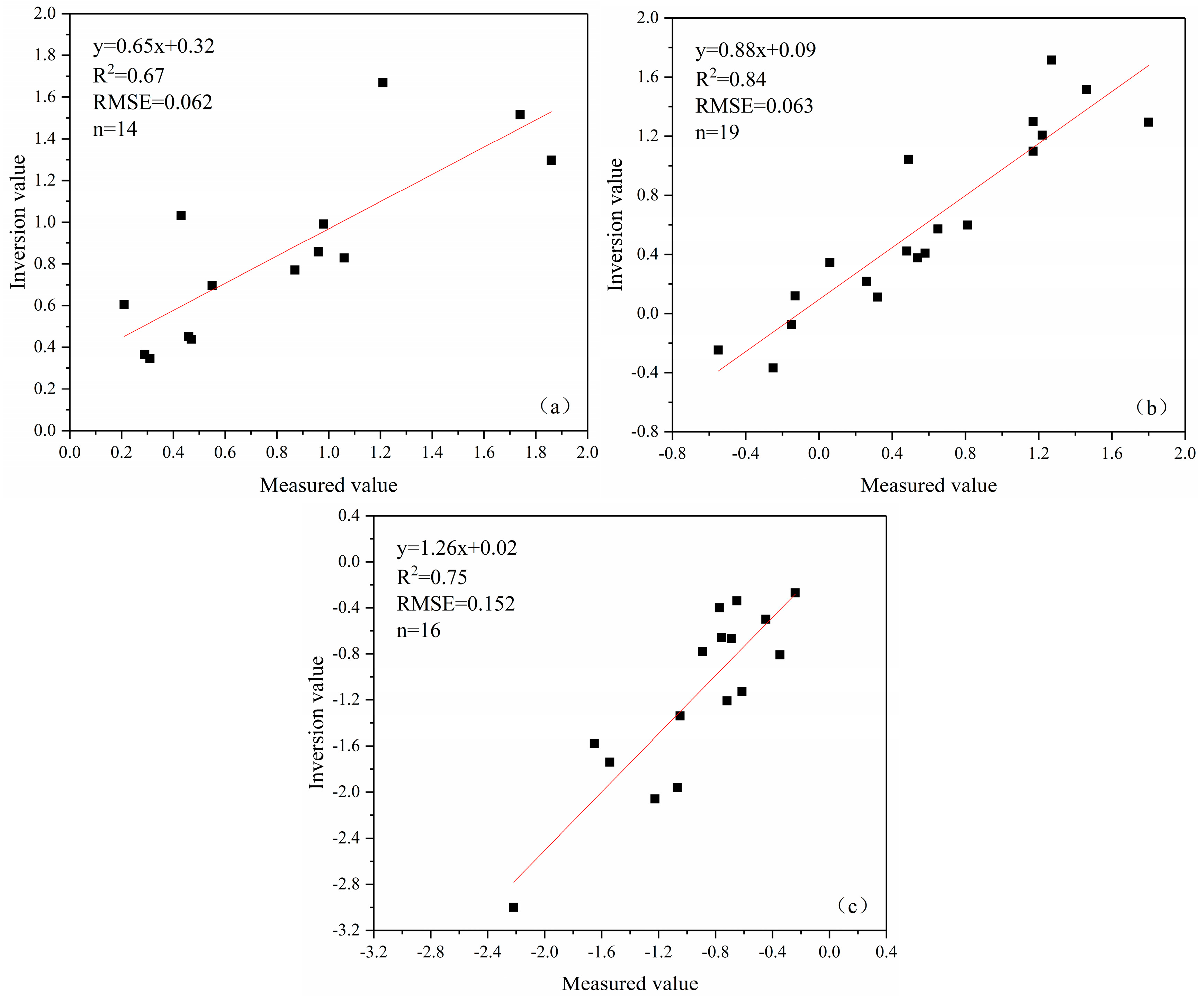
| Stakes | East | North | Vertical | |||
|---|---|---|---|---|---|---|
| Inversion Value | Measured Value | Inversion Value | Measured Value | Inversion Value | Measured Value | |
| B1′ | 0.83 | 1.06 | 0.60 | 0.81 | −1.07 | −1.96 |
| B2′ | 0.86 | 0.96 | 0.57 | 0.65 | −1.23 | −2.06 |
| B3′ | 0.89 | 1.73 | 0.69 | 0.05 | −2.22 | −3.00 |
| C1′ | 1.03 | 0.43 | 0.11 | 0.32 | −1.54 | −1.74 |
| C2′ | 1.30 | 1.86 | 0.41 | 0.58 | −1.65 | −1.58 |
| C3′ | 1.67 | 1.21 | 0.38 | 0.54 | −0.72 | −1.21 |
| D1′ | 1.16 | −0.71 | −0.08 | −0.15 | −1.05 | −1.34 |
| D2′ | 1.52 | 1.74 | 0.42 | 0.48 | −0.61 | −1.13 |
| D3′ | 2.07 | 0.07 | 1.10 | 1.17 | −2.19 | −1.34 |
| E1′ | 0.37 | 0.29 | 0.34 | 0.06 | 0.12 | −0.80 |
| E2′ | 0.34 | 0.31 | 1.52 | 1.46 | −0.35 | −0.81 |
| E3′ | 0.99 | 0.98 | 1.30 | 1.17 | −1.25 | −0.48 |
| F1′ | 0.38 | −0.31 | 0.12 | −0.13 | −0.45 | −0.50 |
| F2′ | 0.60 | 0.21 | 1.29 | 1.80 | −0.89 | −0.78 |
| F3′ | 0.70 | 0.55 | 1.72 | 1.27 | −0.76 | −0.66 |
| G1′ | 0.96 | −0.24 | 0.25 | −0.55 | −0.77 | −0.40 |
| G2′ | 0.53 | 0.09 | 0.43 | 0.80 | −1.22 | −0.44 |
| G3′ | 0.45 | 0.46 | 1.21 | 1.22 | −1.60 | −0.76 |
| H1′ | 1.46 | −0.97 | −0.37 | −0.25 | −0.69 | −0.67 |
| H2′ | 0.77 | 0.87 | 0.22 | 0.26 | −0.24 | −0.27 |
| I′ | 0.44 | 0.47 | 1.04 | 0.49 | 0.65 | −0.34 |
| Stakes | East | North | Vertical | |||
|---|---|---|---|---|---|---|
| Inversion Value | Measured Value | Inversion Value | Measured Value | Inversion Value | Measured Value | |
| B1 | 0.43 | −0.10 | 0.94 | −0.80 | −0.51 | −1.69 |
| B2 | 0.30 | 0.92 | 0.73 | 0.61 | −1.18 | −1.89 |
| C1 | 0.73 | 0.63 | 0.93 | 1.44 | −0.73 | −0.57 |
| C2 | 0.79 | 0.94 | 0.84 | 0.65 | −1.12 | −1.87 |
| D1 | 0.35 | 0.21 | 0.51 | 0.39 | −1.07 | −1.14 |
| D2 | 0.90 | 0.90 | 0.60 | 0.71 | −0.32 | −1.40 |
| D3 | 0.80 | 0.39 | 0.68 | 1.10 | −1.28 | −1.49 |
| E1 | 0.63 | 0.53 | 0.38 | 0.43 | −1.22 | −1.32 |
| E2 | 0.83 | 1.11 | 0.94 | 0.57 | −0.24 | −1.10 |
| E3 | 0.49 | 0.55 | 0.42 | 0.18 | −1.06 | −0.99 |
| F1 | 0.44 | 0.63 | 0.70 | −0.67 | −1.16 | −0.99 |
| F2 | 0.77 | 0.80 | 0.98 | 1.42 | −0.97 | −1.08 |
| F3 | 0.55 | 0.17 | 0.96 | 0.87 | −0.85 | −0.86 |
| G1 | 0.71 | 0.42 | 0.25 | 0.30 | −0.59 | −0.55 |
| G3 | 0.91 | 1.04 | 0.63 | 0.45 | −0.33 | −0.48 |
| H1 | 1.05 | 0.92 | 0.64 | 0.43 | −0.09 | −0.27 |
| H2 | 1.33 | 1.56 | 0.89 | 0.88 | −0.86 | −1.12 |
| H3 | 0.90 | 0.92 | 0.86 | 0.86 | −0.55 | −0.19 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, Y.; Zhao, J.; Li, Z.; Zhang, M.; Wang, Y.; Liu, J.; Yang, J.; Yang, Z. Retrieving and Verifying Three-Dimensional Surface Motion Displacement of Mountain Glacier from Sentinel-1 Imagery Using Optimized Method. Water 2021, 13, 1793. https://doi.org/10.3390/w13131793
Wang Y, Zhao J, Li Z, Zhang M, Wang Y, Liu J, Yang J, Yang Z. Retrieving and Verifying Three-Dimensional Surface Motion Displacement of Mountain Glacier from Sentinel-1 Imagery Using Optimized Method. Water. 2021; 13(13):1793. https://doi.org/10.3390/w13131793
Chicago/Turabian StyleWang, Yanqiang, Jun Zhao, Zhongqin Li, Mingjun Zhang, Yuchun Wang, Jialiang Liu, Jianxia Yang, and Zhihui Yang. 2021. "Retrieving and Verifying Three-Dimensional Surface Motion Displacement of Mountain Glacier from Sentinel-1 Imagery Using Optimized Method" Water 13, no. 13: 1793. https://doi.org/10.3390/w13131793
APA StyleWang, Y., Zhao, J., Li, Z., Zhang, M., Wang, Y., Liu, J., Yang, J., & Yang, Z. (2021). Retrieving and Verifying Three-Dimensional Surface Motion Displacement of Mountain Glacier from Sentinel-1 Imagery Using Optimized Method. Water, 13(13), 1793. https://doi.org/10.3390/w13131793






