Evaluation of FAO-56 Procedures for Estimating Reference Evapotranspiration Using Missing Climatic Data for a Brazilian Tropical Savanna
Abstract
:1. Introduction
2. Materials and Methods
2.1. Study Area
2.2. Micrometeorological Measurements
2.3. Penman–Monteith Method and FAO Procedures When Climatic Data Are Missing
2.4. Hargreaves–Samani Method
2.5. ETo with Missing Climatic Data
2.6. Performance Evaluation
3. Results and Discussion
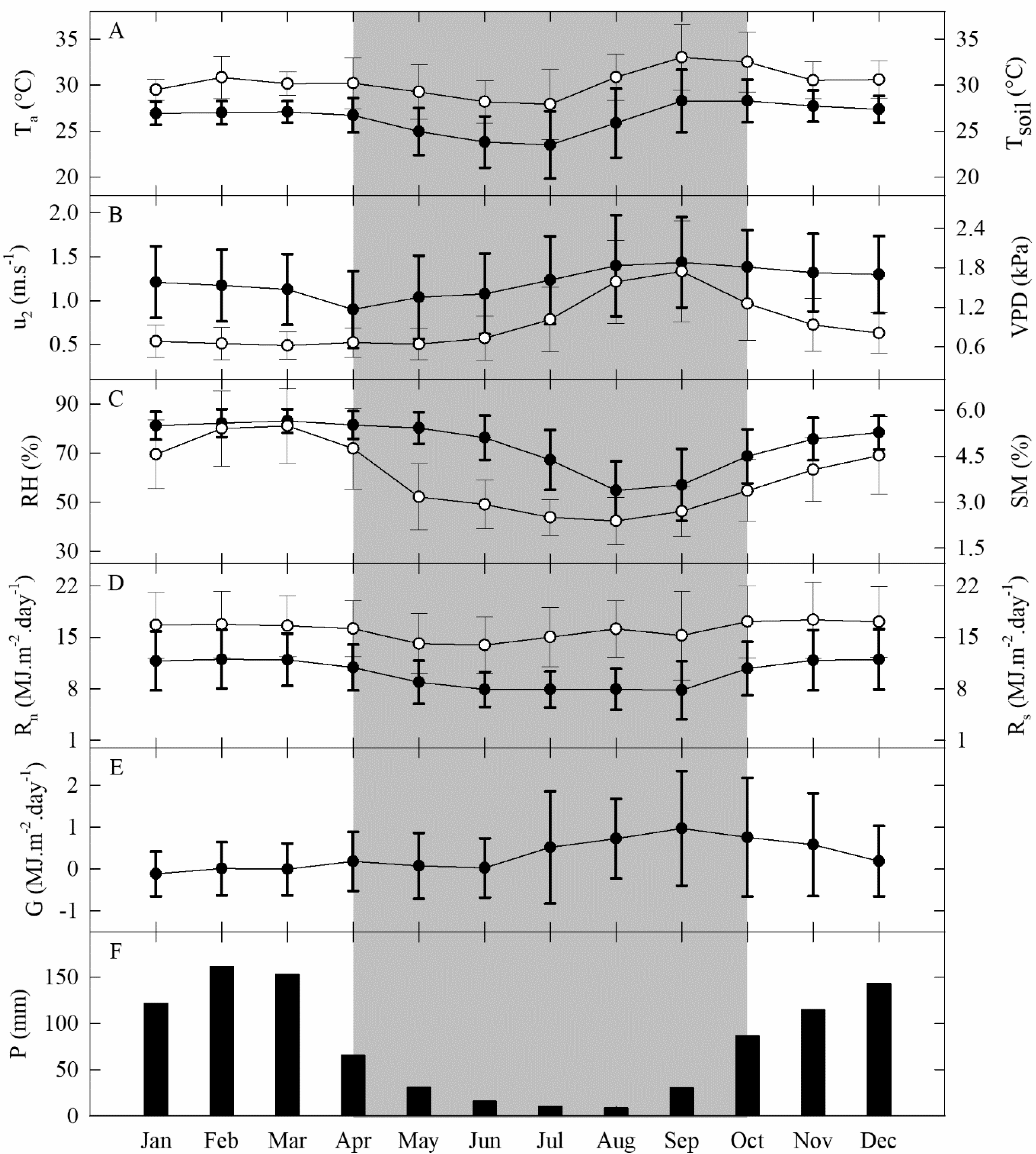
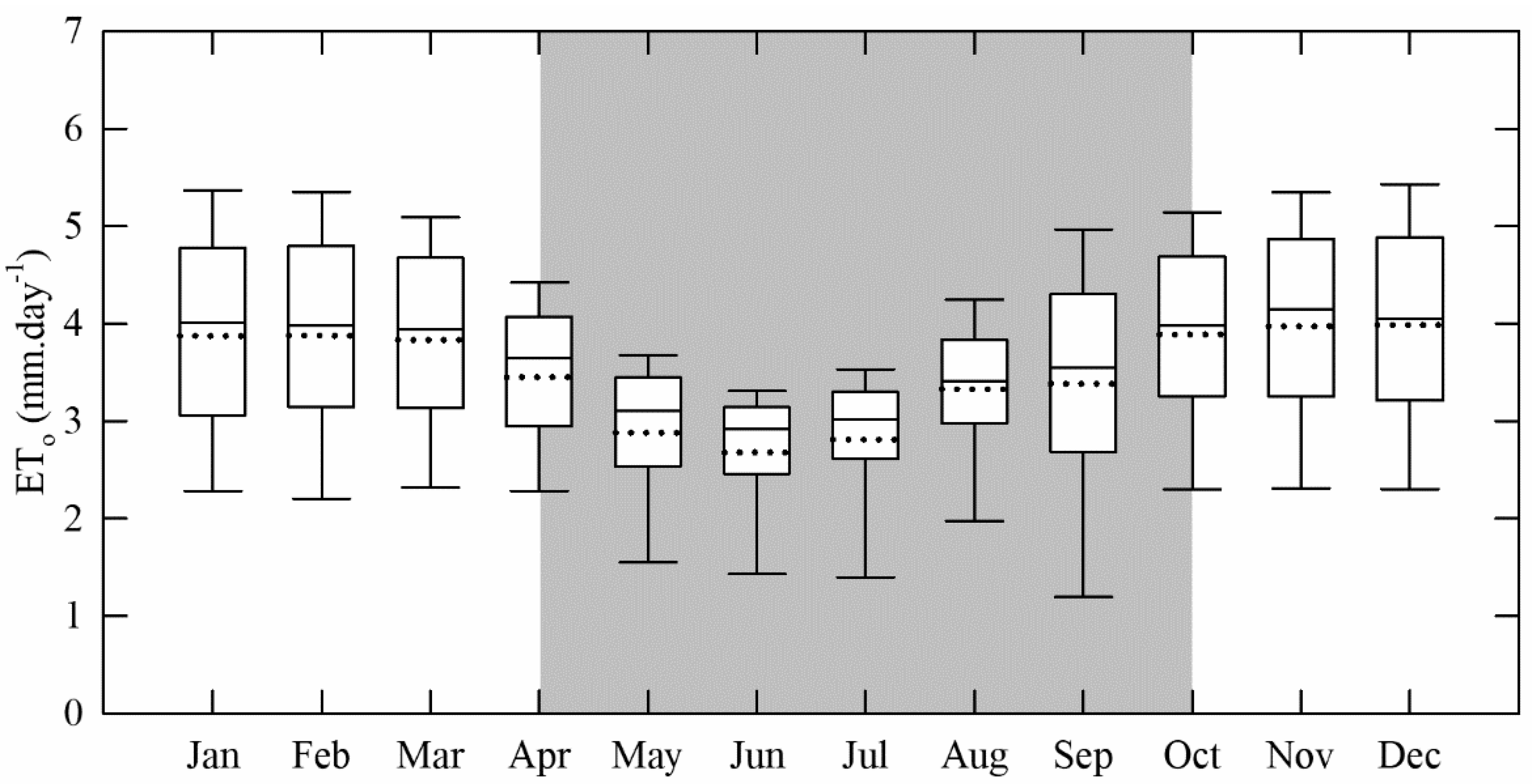
3.1. Seasonal Variation in Micrometeorological Condition
3.2. ETo Estimates with Limited Climatic Data
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Giambelluca, T.W.; Scholz, F.G.; Bucci, S.J.; Meinzer, F.C.; Goldstein, G.; Hoffmann, W.A.; Franco, A.C.; Buchert, M.P. Evapotranspiration and energy balance of Brazilian savannas with contrasting tree density. Agric. For. Meteorol. 2009, 149, 1365–1376. [Google Scholar] [CrossRef]
- Nóbrega, R.L.B.; Guzha, A.C.; Lamparter, G.; Amorim, R.S.S.; Couto, E.G.; Hughes, H.J.; Jungkunst, H.F.; Gerold, G. Impacts of land-use and land-cover change on stream hydrochemistry in the Cerrado and Amazon biomes. Sci. Total Environ. 2018, 635, 259–274. [Google Scholar] [CrossRef] [PubMed]
- Oliveira, P.T.S.; Nearing, M.A.; Moran, M.S.; Goodrich, D.C.; Wendland, E.; Gupta, H.V. Trends in water balance components across the Brazilian Cerrado. Water Resour. Res. 2014, 50, 7100–7114. [Google Scholar] [CrossRef] [Green Version]
- Rodrigues, T.R.; Vourlitis, G.L.; Lobo, F.D.A.; de Oliveira, R.G.; Nogueira, J.D.S. Seasonal variation in energy balance and canopy conductance for a tropical savanna ecosystem of south central Mato Grosso, Brazil. J. Geophys. Res. Biogeosci. 2014, 119, 1–13. [Google Scholar] [CrossRef]
- Silva, J.B.; Gaio, D.C.; Curado, L.F.A.; Nogueira, J.D.S.; Valle Júnior, L.C.G.; Rodrigues, T.R. Evaluation of methods for estimating atmospheric emissivity in Mato-Grossense Cerrado. Ambient. Agua Interdiscip. J. Appl. Sci. 2019, 14, 1. [Google Scholar] [CrossRef]
- Valle Júnior, L.C.G.; Ventura, T.M.; Gomes, R.S.R.; de Nogueira, J.S.; de Lobo, F.A.; Vourlitis, G.L.; Rodrigues, T.R. Comparative assessment of modelled and empirical reference evapotranspiration methods for a brazilian savanna. Agric. Water Manag. 2020, 232, 106040. [Google Scholar] [CrossRef]
- Doorenbos, J.; Pruitt, W.O. Guidelines for Predicting Crop Water Requirements; FAO Irrigation and Drainage Paper no.24; FAO: Rome, Italy, 1977; ISBN 92-5-100279-7. [Google Scholar]
- Allen, R.G. Assessing Integrity of Weather Data for Reference Evapotranspiration Estimation. J. Irrig. Drain. Eng. 1996, 122, 97–106. [Google Scholar] [CrossRef]
- Dong, Q.; Wang, W.; Shao, Q.; Xing, W.; Ding, Y.; Fu, J. The response of reference evapotranspiration to climate change in Xinjiang, China: Historical changes, driving forces, and future projections. Int. J. Climatol. 2020, 40, 235–254. [Google Scholar] [CrossRef]
- Droogers, P.; Allen, R.G. Estimating reference evapotranspiration under inaccurate data conditions. Irrig. Drain. Syst. 2002, 16, 33–45. [Google Scholar] [CrossRef]
- Hargreaves, G.H. Defining and Using Reference Evapotranspiration. J. Irrig. Drain. Eng. 1994, 120, 1132–1139. [Google Scholar] [CrossRef]
- She, D.; Xia, J.; Zhang, Y. Changes in reference evapotranspiration and its driving factors in the middle reaches of Yellow River Basin, China. Sci. Total Environ. 2017, 607–608, 1151–1162. [Google Scholar] [CrossRef]
- Tyagi, N.; Sharma, D.; Luthra, S. Determination of evapotranspiration and crop coefficients of rice and sunflower with lysimeter. Agric. Water Manag. 2000, 45, 41–54. [Google Scholar] [CrossRef]
- Allen, R.G.; Smith, M.; Pereira, L.S.; Perrier, A. An Update for the Calculation of Reference Evapotranspiration. ICID Bull. 1994, 43, 35–92. [Google Scholar]
- Martins, D.S.; Paredes, P.; Raziei, T.; Pires, C.; Cadima, J.; Pereira, L.S. Assessing reference evapotranspiration estimation from reanalysis weather products. An application to the Iberian Peninsula. Int. J. Climatol. 2017, 37, 2378–2397. [Google Scholar] [CrossRef]
- Sharifi, A.; Dinpashoh, Y. Sensitivity Analysis of the Penman-Monteith reference Crop Evapotranspiration to Climatic Variables in Iran. Water Resour. Manag. 2014, 28, 5465–5476. [Google Scholar] [CrossRef]
- Allen, R.G.; Pereira, L.S.; Raes, D.; Smith, M. Crop Evapotranspiration: Guidelines for Computing Crop Water Requirements; FAO Irrigation and Drainage Paper no. 56; FAO: Rome, Italy, 1998; ISBN 92-5-104219-5. [Google Scholar]
- Xu, C.; Gong, L.; Jiang, T.; Chen, D.; Singh, V.P. Analysis of spatial distribution and temporal trend of reference evapotranspiration and pan evaporation in Changjiang (Yangtze River) catchment. J. Hydrol. 2006, 327, 81–93. [Google Scholar] [CrossRef]
- Almorox, J.; Grieser, J. Calibration of the Hargreaves-Samani method for the calculation of reference evapotranspiration in different Köppen climate classes. Hydrol. Res. 2016, 47, 521–531. [Google Scholar] [CrossRef] [Green Version]
- Srivastava, A.; Sahoo, B.; Raghuwanshi, N.S.; Singh, R. Evaluation of Variable-Infiltration Capacity Model and MODIS-Terra Satellite-Derived Grid-Scale Evapotranspiration Estimates in a River Basin with Tropical Monsoon-Type Climatology. J. Irrig. Drain. Eng. 2017, 143, 04017028. [Google Scholar] [CrossRef] [Green Version]
- Blaney, H.F.; Criddle, W.D. Determining Water Requirements in Irrigated Areas from Climatological and Irrigation Data; United States Department of Agriculture: Washington, DC, USA, 1950. [Google Scholar]
- Hargreaves, G.H.; Samani, Z.A. Reference Crop Evapotranspiration from Temperature. Appl. Eng. Agric. 1985, 1, 96–99. [Google Scholar] [CrossRef]
- Jensen, M.E.; Haise, H.R. Estimating evapotranspiration from solar radiation. J. Irrig. Drain. 1963, 4, 15–41. [Google Scholar] [CrossRef]
- Priestley, C.H.B.; Taylor, R.J. On the Assessment of Surface Heat Flux and Evaporation Using Large-Scale Parameters. Mon. Weather Rev. 1972, 100, 81–92. [Google Scholar] [CrossRef]
- Bourletsikas, A.; Argyrokastritis, I.; Proutsos, N. Comparative evaluation of 24 reference evapotranspiration equations applied on an evergreen-broadleaved forest. Hydrol. Res. 2017, nh2017232. [Google Scholar] [CrossRef]
- Shafieiyoun, E.; Gheysari, M.; Khiadani, M.; Koupai, J.A.; Shojaei, P.; Moomkesh, M. Assessment of reference evapotranspiration across an arid urban environment having poor data monitoring system. Hydrol. Process. 2020, 34, 4000–4016. [Google Scholar] [CrossRef]
- Shiri, J. Modeling reference evapotranspiration in island environments: Assessing the practical implications. J. Hydrol. 2019, 570, 265–280. [Google Scholar] [CrossRef]
- Tabari, H.; Grismer, M.E.; Trajkovic, S. Comparative analysis of 31 reference evapotranspiration methods under humid conditions. Irrig. Sci. 2013, 31, 107–117. [Google Scholar] [CrossRef]
- Zhang, Q.; Cui, N.; Feng, Y.; Gong, D.; Hu, X. Improvement of Makkink model for reference evapotranspiration estimation using temperature data in Northwest China. J. Hydrol. 2018, 566, 264–273. [Google Scholar] [CrossRef]
- Dinpashoh, Y.; Jhajharia, D.; Fakheri-Fard, A.; Singh, V.P.; Kahya, E. Trends in reference crop evapotranspiration over Iran. J. Hydrol. 2011, 399, 422–433. [Google Scholar] [CrossRef]
- Gong, L.; Xu, C.; Chen, D.; Halldin, S.; Chen, Y.D. Sensitivity of the Penman–Monteith reference evapotranspiration to key climatic variables in the Changjiang (Yangtze River) basin. J. Hydrol. 2006, 329, 620–629. [Google Scholar] [CrossRef]
- Srivastava, A.; Sahoo, B.; Raghuwanshi, N.S.; Chatterjee, C. Modelling the dynamics of evapotranspiration using Variable Infiltration Capacity model and regionally calibrated Hargreaves approach. Irrig. Sci. 2018, 36, 289–300. [Google Scholar] [CrossRef]
- Kumari, N.; Srivastava, A. An Approach for Estimation of Evapotranspiration by Standardizing Parsimonious Method. Agric. Res. 2020, 9, 301–309. [Google Scholar] [CrossRef]
- Oudin, L.; Hervieu, F.; Michel, C.; Perrin, C.; Andréassian, V.; Anctil, F.; Loumagne, C. Which potential evapotranspiration input for a lumped rainfall-runoff model? Part 2—Towards a simple and efficient potential evapotranspiration model for rainfall-runoff modelling. J. Hydrol. 2005, 303, 290–306. [Google Scholar] [CrossRef]
- Čadro, S.; Uzunović, M.; Žurovec, J.; Žurovec, O. Validation and calibration of various reference evapotranspiration alternative methods under the climate conditions of Bosnia and Herzegovina. Int. Soil Water Conserv. Res. 2017, 5, 309–324. [Google Scholar] [CrossRef]
- Djaman, K.; Irmak, S.; Asce, M.; Futakuchi, K. Daily Reference Evapotranspiration Estimation under Limited Data in Eastern Africa. J. Irrig. Drain. Eng. 2016, 1–13. [Google Scholar] [CrossRef]
- Jabloun, M.; Sahli, A. Evaluation of FAO-56 methodology for estimating reference evapotranspiration using limited climatic data. Application to Tunisia. Agric. Water Manag. 2008, 95, 707–715. [Google Scholar] [CrossRef]
- Popova, Z.; Kercheva, M.; Pereira, L.S. Validation of the FAO methodology for computing ETo with limited data. Application to south Bulgaria. Irrig. Drain. 2006, 55, 201–215. [Google Scholar] [CrossRef]
- Raziei, T.; Pereira, L.S. Spatial variability analysis of reference evapotranspiration in Iran utilizing fine resolution gridded datasets. Agric. Water Manag. 2013, 126, 104–118. [Google Scholar] [CrossRef] [Green Version]
- Raziei, T.; Pereira, L.S. Estimation of ETo with Hargreaves–Samani and FAO-PM temperature methods for a wide range of climates in Iran. Agric. Water Manag. 2013, 121, 1–18. [Google Scholar] [CrossRef]
- Todorovic, M.; Karic, B.; Pereira, L.S. Reference evapotranspiration estimate with limited weather data across a range of Mediterranean climates. J. Hydrol. 2013, 481, 166–176. [Google Scholar] [CrossRef] [Green Version]
- Ferreira, L.B.; da Cunha, F.F.; de Oliveira, R.A.; Fernandes Filho, E.I. Estimation of reference evapotranspiration in Brazil with limited meteorological data using ANN and SVM—A new approach. J. Hydrol. 2019, 572, 556–570. [Google Scholar] [CrossRef]
- Karimi, S.; Kisi, O.; Kim, S.; Nazemi, A.H.; Shiri, J. Modelling daily reference evapotranspiration in humid locations of South Korea using local and cross-station data management scenarios. Int. J. Climatol. 2017, 37, 3238–3246. [Google Scholar] [CrossRef]
- Mattar, M.A. Using gene expression programming in monthly reference evapotranspiration modeling: A case study in Egypt. Agric. Water Manag. 2018, 198, 28–38. [Google Scholar] [CrossRef]
- Mehdizadeh, S.; Behmanesh, J.; Khalili, K. Using MARS, SVM, GEP and empirical equations for estimation of monthly mean reference evapotranspiration. Comput. Electron. Agric. 2017, 139, 103–114. [Google Scholar] [CrossRef]
- Salam, R.; Islam, A.R.M.T. Potential of RT, bagging and RS ensemble learning algorithms for reference evapotranspiration prediction using climatic data-limited humid region in Bangladesh. J. Hydrol. 2020, 590, 125241. [Google Scholar] [CrossRef]
- Kisi, O. Pan evaporation modeling using least square support vector machine, multivariate adaptive regression splines and M5 model tree. J. Hydrol. 2015, 528, 312–320. [Google Scholar] [CrossRef]
- Wang, L.; Kisi, O.; Hu, B.; Bilal, M.; Zounemat-Kermani, M.; Li, H. Evaporation modelling using different machine learning techniques. Int. J. Climatol. 2017, 37, 1076–1092. [Google Scholar] [CrossRef]
- Wang, L.; Kisi, O.; Zounemat-Kermani, M.; Li, H. Pan evaporation modeling using six different heuristic computing methods in different climates of China. J. Hydrol. 2017, 544, 407–427. [Google Scholar] [CrossRef]
- Rodrigues, T.R.; Vourlitis, G.L.; de Lobo, F.A.; Santanna, F.B.; de Arruda, P.H.Z.; de Nogueira, J.S. Modeling canopy conductance under contrasting seasonal conditions for a tropical savanna ecosystem of south central Mato Grosso, Brazil. Agric. For. Meteorol. 2016, 218, 218–219–229. [Google Scholar] [CrossRef] [Green Version]
- Alvares, C.A.; Stape, J.L.; Sentelhas, P.C.; de Moraes Gonçalves, J.L.; Sparovek, G. Köppen’s climate classification map for Brazil. Meteorol. Z. 2013, 22, 711–728. [Google Scholar] [CrossRef]
- Vourlitis, G.L.; da Rocha, H.R. Flux Dynamics in the Cerrado and Cerrado—Forest Transition of Brazil. In Ecosystem Function in Global Savannas: Measurement and Modeling at Landscape to Global Scales; Hill, M.J., Hanan, N.P., Eds.; CRC, Inc.: Boca Raton, FL, USA, 2011; pp. 97–116. [Google Scholar]
- Willmott, C.J. Some Comments on the Evaluation of Model Performance. Bull. Am. Meteorol. Soc. 1982, 63, 1309–1313. [Google Scholar] [CrossRef] [Green Version]
- Hutyra, L.R.; Munger, J.W.; Nobre, C.A.; Saleska, S.R.; Vieira, S.A.; Wofsy, S.C. Climatic variability and vegetation vulnerability in Amazônia. Geophys. Res. Lett. 2005, 32, L24712. [Google Scholar] [CrossRef] [Green Version]
- Rodrigues, T.R.; Curado, L.F.A.; Pereira, V.M.R.; Sanches, L.; Nogueira, J.S. Hourly interaction between wind speed and energy fluxes in Brazilian wetlands—Mato Grosso—Brazil. An. Acad. Bras. Cienc. 2016, 88, 2195–2209. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Grace, J.; Malhi, Y.; Lloyd, J.; McIntyre, J.; Miranda, A.C.; Meir, P.; Miranda, H.S. The use of eddy covariance to infer the net carbon dioxide uptake of Brazilian rain forest. Glob. Chang. Biol. 1996, 2, 209–217. [Google Scholar] [CrossRef]
- Machado, L.A.T.; Laurent, H.; Dessay, N.; Miranda, I. Seasonal and diurnal variability of convection over the Amazonia: A comparison of different vegetation types and large scale forcing. Theor. Appl. Climatol. 2004, 78, 61–77. [Google Scholar] [CrossRef]
- Rodrigues, T.R.; de Paulo, S.R.; Novais, J.W.Z.; Curado, L.F.; Nogueira, J.S.; de Oliveira, R.G.; Lobo, F.D.; Vourlitis, G.L. Temporal Patterns of Energy Balance for a Brazilian Tropical Savanna under Contrasting Seasonal Conditions. Int. J. Atmos. Sci. 2013, 2013, 1–9. [Google Scholar] [CrossRef] [Green Version]
- Djaman, K.; Irmak, S.; Kabenge, I.; Futakuchi, K. Evaluation of FAO-56 Penman-Monteith Model with Limited Data and the Valiantzas Models for Estimating Grass-Reference Evapotranspiration in Sahelian Conditions. J. Irrig. Drain. Eng. 2016, 142, 04016044. [Google Scholar] [CrossRef]
- Sentelhas, P.C.; Gillespie, T.J.; Santos, E.A. Evaluation of FAO Penman–Monteith and alternative methods for estimating reference evapotranspiration with missing data in Southern Ontario, Canada. Agric. Water Manag. 2010, 97, 635–644. [Google Scholar] [CrossRef]
- Córdova, M.; Carrillo-Rojas, G.; Crespo, P.; Wilcox, B.; Célleri, R. Evaluation of the Penman-Monteith (FAO 56 PM) Method for Calculating Reference Evapotranspiration Using Limited Data. Mt. Res. Dev. 2015, 35, 230–239. [Google Scholar] [CrossRef] [Green Version]
- Sun, J.; Wang, G.; Sun, X.; Lin, S.; Hu, Z.; Huang, K. Elevation-dependent changes in reference evapotranspiration due to climate change. Hydrol. Process. 2020, 34, 5580–5594. [Google Scholar] [CrossRef]
- Aladenola, O.O.; Madramootoo, C.A. Evaluation of solar radiation estimation methods for reference evapotranspiration estimation in Canada. Theor. Appl. Climatol. 2014, 118, 377–385. [Google Scholar] [CrossRef]
- Jahani, B.; Dinpashoh, Y.; Raisi Nafchi, A. Evaluation and development of empirical models for estimating daily solar radiation. Renew. Sustain. Energy Rev. 2017, 73, 878–891. [Google Scholar] [CrossRef]
- Trnka, M.; Žalud, Z.; Eitzinger, J.; Dubrovský, M. Global solar radiation in Central European lowlands estimated by various empirical formulae. Agric. For. Meteorol. 2005, 131, 54–76. [Google Scholar] [CrossRef]
- Cai, J.; Liu, Y.; Lei, T.; Pereira, L.S. Estimating reference evapotranspiration with the FAO Penman–Monteith equation using daily weather forecast messages. Agric. For. Meteorol. 2007, 145, 22–35. [Google Scholar] [CrossRef]
- Paredes, P.; Martins, D.S.; Pereira, L.S.; Cadima, J.; Pires, C. Accuracy of daily estimation of grass reference evapotranspiration using ERA-Interim reanalysis products with assessment of alternative bias correction schemes. Agric. Water Manag. 2018, 210, 340–353. [Google Scholar] [CrossRef]
- Salam, R.; Islam, A.R.M.T.; Pham, Q.B.; Dehghani, M.; Al-Ansari, N.; Linh, N.T.T. The optimal alternative for quantifying reference evapotranspiration in climatic sub-regions of Bangladesh. Sci. Rep. 2020, 10, 20171. [Google Scholar] [CrossRef]
- de Oliveira, R.G.; Valle Júnior, L.C.G.; da Silva, J.B.; Espíndola, D.A.L.F.; Lopes, R.D.; Nogueira, J.S.; Curado, L.F.A.; Rodrigues, T.R. Temporal trend changes in reference evapotranspiration contrasting different land uses in southern Amazon basin. Agric. Water Manag. 2021, 250, 106815. [Google Scholar] [CrossRef]
- Jhajharia, D.; Dinpashoh, Y.; Kahya, E.; Singh, V.P.; Fakheri-Fard, A. Trends in reference evapotranspiration in the humid region of northeast India. Hydrol. Process. 2012, 26, 421–435. [Google Scholar] [CrossRef]
- Almorox, J.; Senatore, A.; Quej, V.H.; Mendicino, G. Worldwide assessment of the Penman–Monteith temperature approach for the estimation of monthly reference evapotranspiration. Theor. Appl. Climatol. 2018, 131, 693–703. [Google Scholar] [CrossRef]
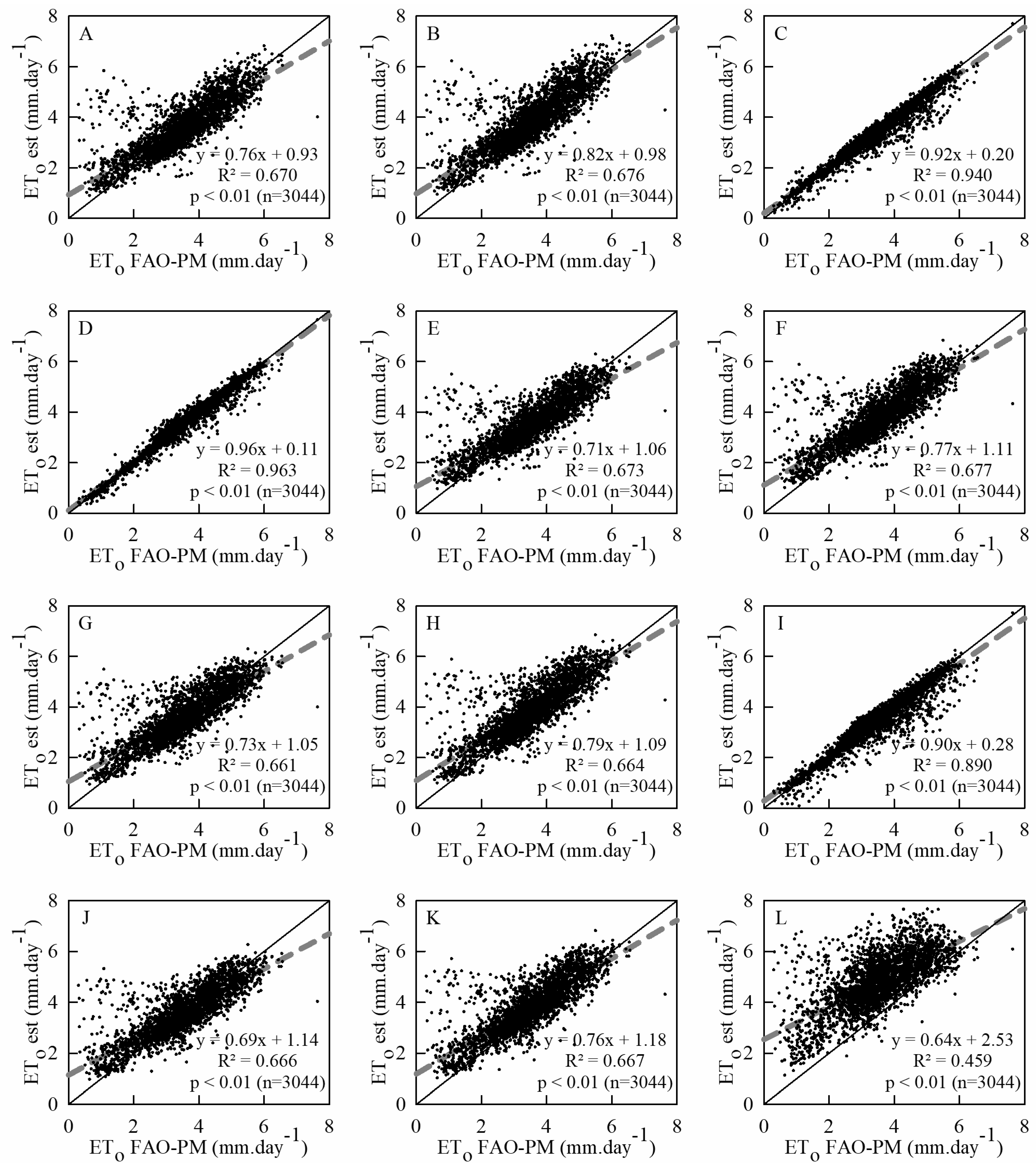
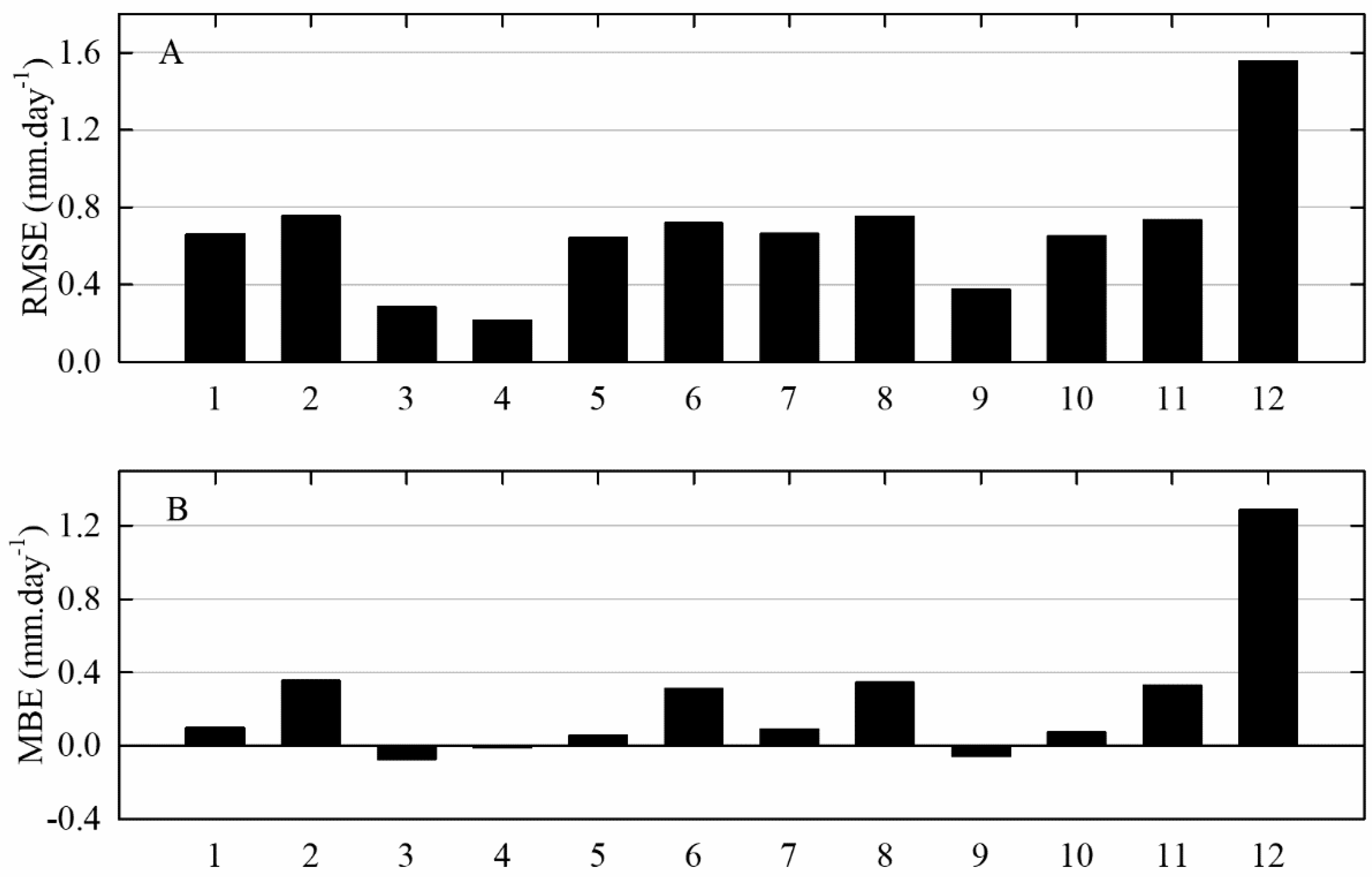

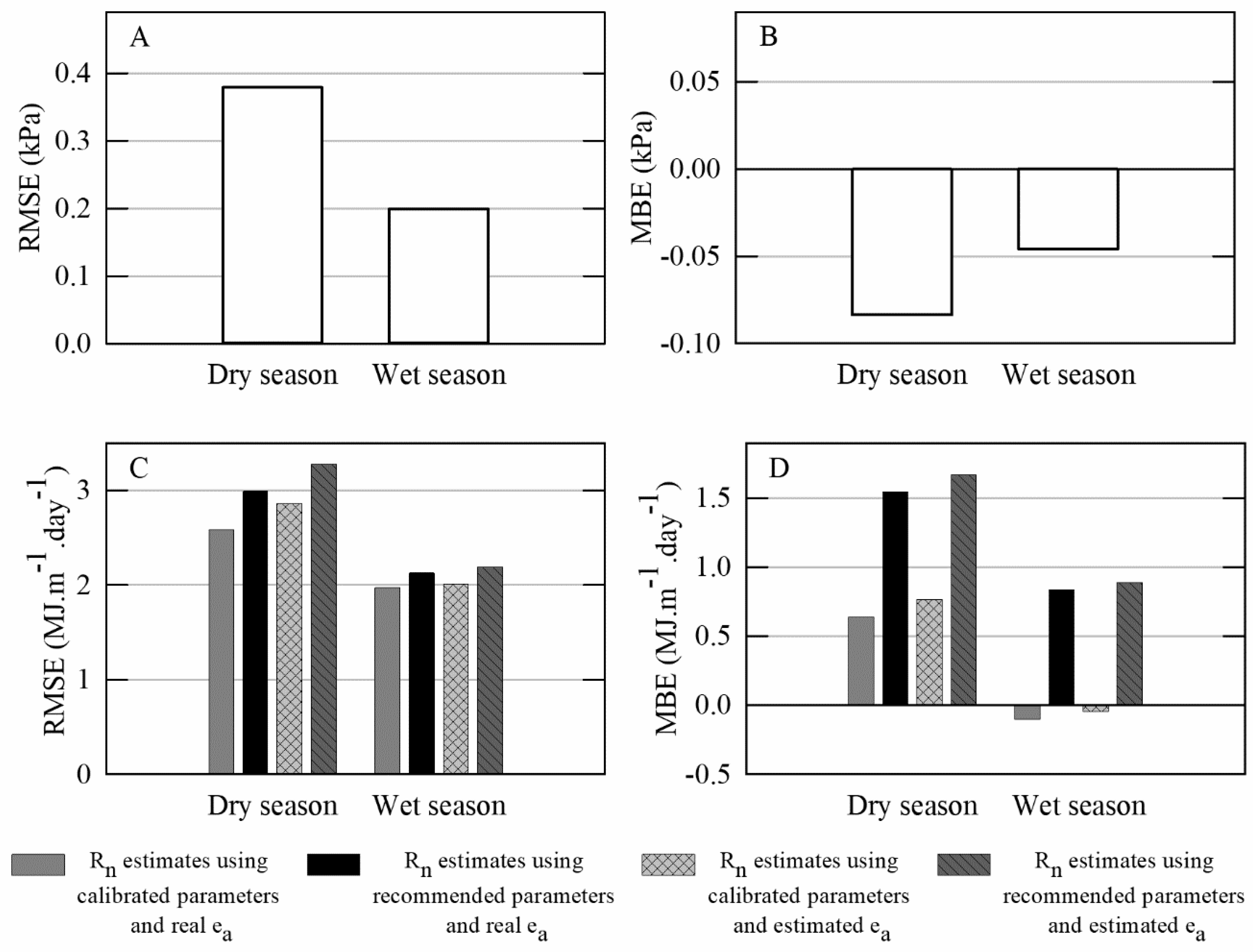
| Method | Symbol | Calculation of ETo |
|---|---|---|
| FAO-PM, no radiation data (using calibrated parameters to estimate Rs) | Rs-a | ETo (Equation (1)); Rn (Equation (12)); as and bs calibrated |
| FAO-PM, no radiation data (using recommended parameters to estimate Rs) | Rs-b | ETo (Equation (1)); Rn (Equation (12)), as and bs recommended |
| FAO-PM, no relative air humidity data | RH | ETo (Equation (1)); ea (Equation (13)) |
| FAO-PM. no wind speed data | WS | ETo (Equation (1)); u2 calculated by daily mean wind speed |
| Hargreaves–Samani | HS | ETo (Equation (14)) |
| Method | d | r | RMSE (mm.day−1) | MBE (mm.day−1) |
|---|---|---|---|---|
| Rs-a | 0.90 | 0.82 | 0.66 | 0.10 |
| Rs-b | 0.88 | 0.82 | 0.75 | 0.35 |
| RH | 0.98 | 0.97 | 0.28 | −0.07 |
| WS | 0.99 | 0.98 | 0.21 | −0.01 |
| RS-a and RH | 0.90 | 0.82 | 0.64 | 0.05 |
| RS-b and RH | 0.89 | 0.82 | 0.72 | 0.31 |
| RS-a and WS | 0.90 | 0.81 | 0.66 | 0.09 |
| RS-b and WS | 0.88 | 0.82 | 0.75 | 0.34 |
| RH and WS | 0.97 | 0.94 | 0.37 | −0.06 |
| RS-a, RH, and WS | 0.90 | 0.82 | 0.65 | 0.07 |
| RS-b, RH, and WS | 0.88 | 0.82 | 0.73 | 0.33 |
| HS | 0.64 | 0.68 | 1.56 | 1.29 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Valle Júnior, L.C.G.d.; Vourlitis, G.L.; Curado, L.F.A.; Palácios, R.d.S.; Nogueira, J.d.S.; Lobo, F.d.A.; Islam, A.R.M.T.; Rodrigues, T.R. Evaluation of FAO-56 Procedures for Estimating Reference Evapotranspiration Using Missing Climatic Data for a Brazilian Tropical Savanna. Water 2021, 13, 1763. https://doi.org/10.3390/w13131763
Valle Júnior LCGd, Vourlitis GL, Curado LFA, Palácios RdS, Nogueira JdS, Lobo FdA, Islam ARMT, Rodrigues TR. Evaluation of FAO-56 Procedures for Estimating Reference Evapotranspiration Using Missing Climatic Data for a Brazilian Tropical Savanna. Water. 2021; 13(13):1763. https://doi.org/10.3390/w13131763
Chicago/Turabian StyleValle Júnior, Luiz Claudio Galvão do, George L. Vourlitis, Leone Francisco Amorim Curado, Rafael da Silva Palácios, José de S. Nogueira, Francisco de A. Lobo, Abu Reza Md Towfiqul Islam, and Thiago Rangel Rodrigues. 2021. "Evaluation of FAO-56 Procedures for Estimating Reference Evapotranspiration Using Missing Climatic Data for a Brazilian Tropical Savanna" Water 13, no. 13: 1763. https://doi.org/10.3390/w13131763
APA StyleValle Júnior, L. C. G. d., Vourlitis, G. L., Curado, L. F. A., Palácios, R. d. S., Nogueira, J. d. S., Lobo, F. d. A., Islam, A. R. M. T., & Rodrigues, T. R. (2021). Evaluation of FAO-56 Procedures for Estimating Reference Evapotranspiration Using Missing Climatic Data for a Brazilian Tropical Savanna. Water, 13(13), 1763. https://doi.org/10.3390/w13131763








