A New Dam-Break Outflow-Rate Concept and Its Installation to a Hydro-Morphodynamics Simulation Model Based on FDM (An Example on Amagase Dam of Japan)
Abstract
:1. Introduction
2. Calculation Methods
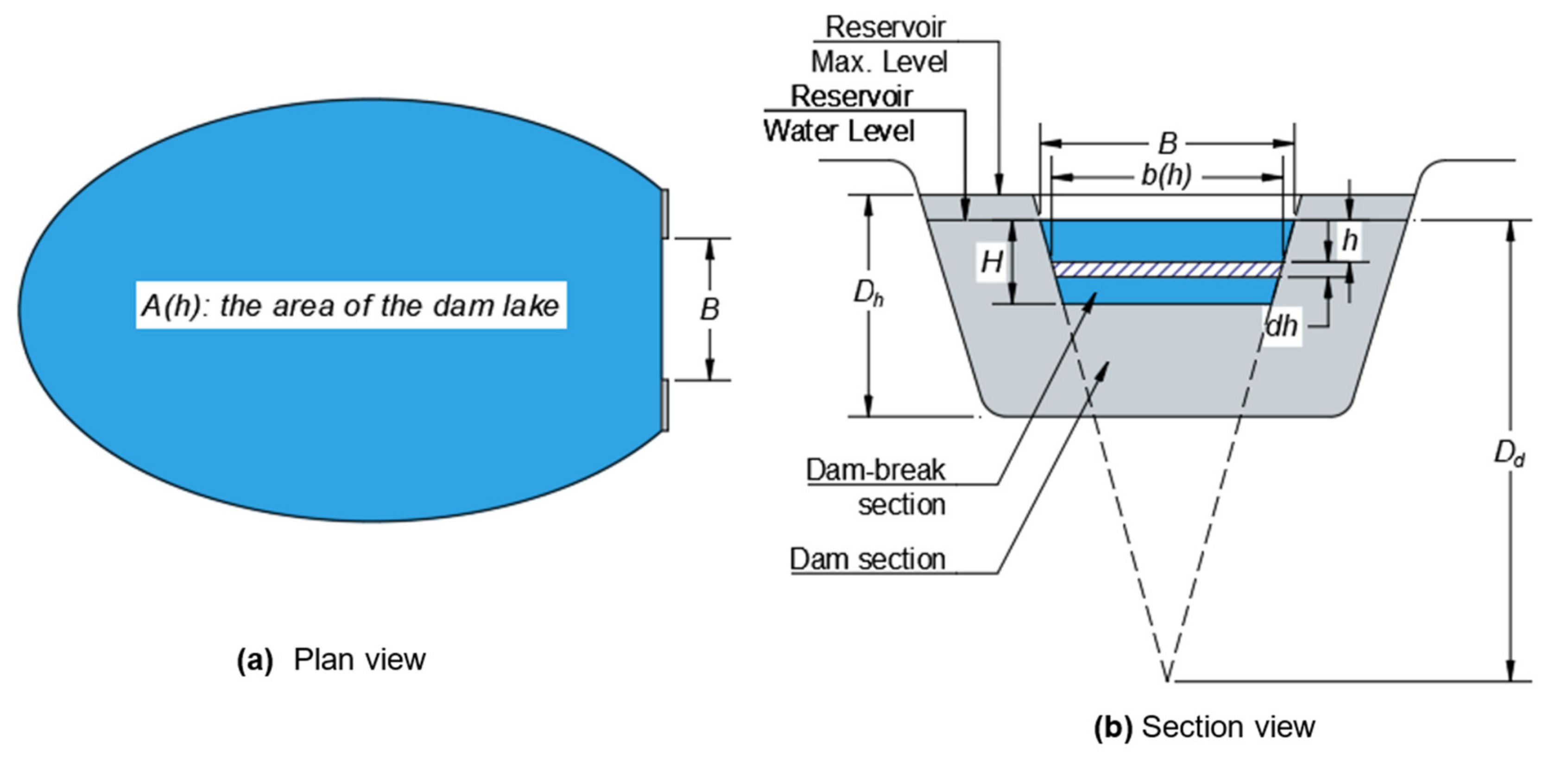
2.1. New Model of Dam-Break Out-Flow Rate
2.2. Existing Numerical Simulation Model
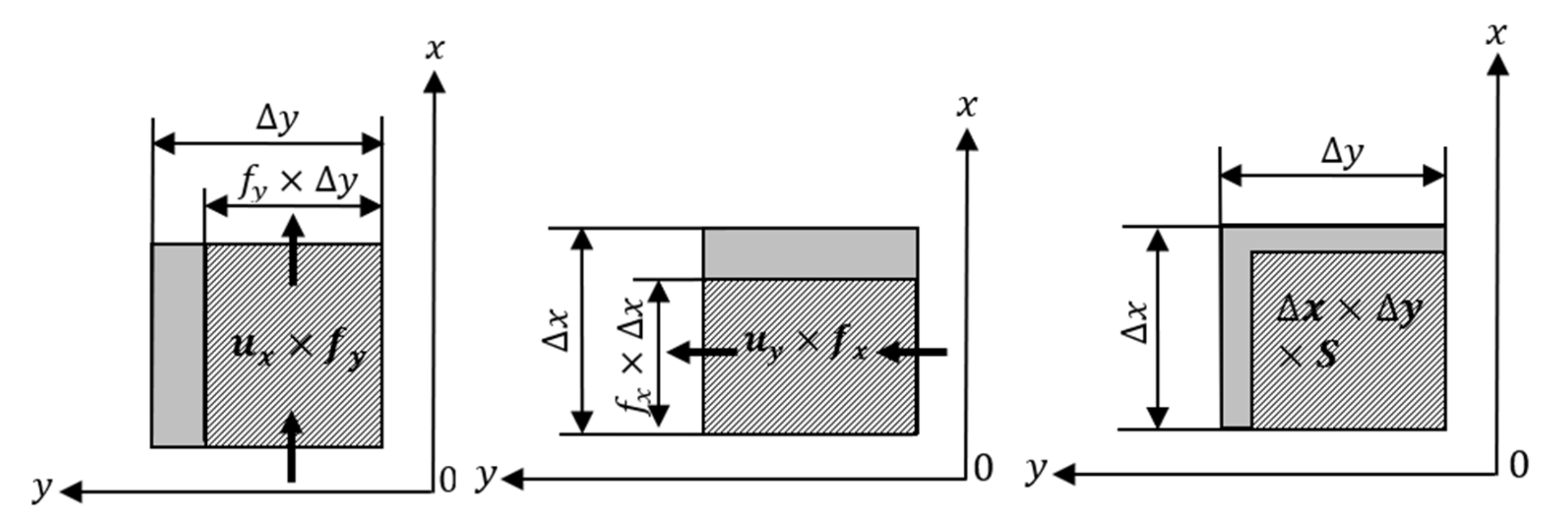
2.2.1. Numerical Model for Fluid Motion
2.2.2. Numerical Model for Topographical Change
3. Methods for Evaluation of Empirical Coefficients
3.1. Evaluation of the Break-Shape Coefficient of the Outflow Rate Equation
3.2. Rational Evaluation of the Coefficient of Bed-Load Transport Rate
4. Verification and Application of the Proposed Concept
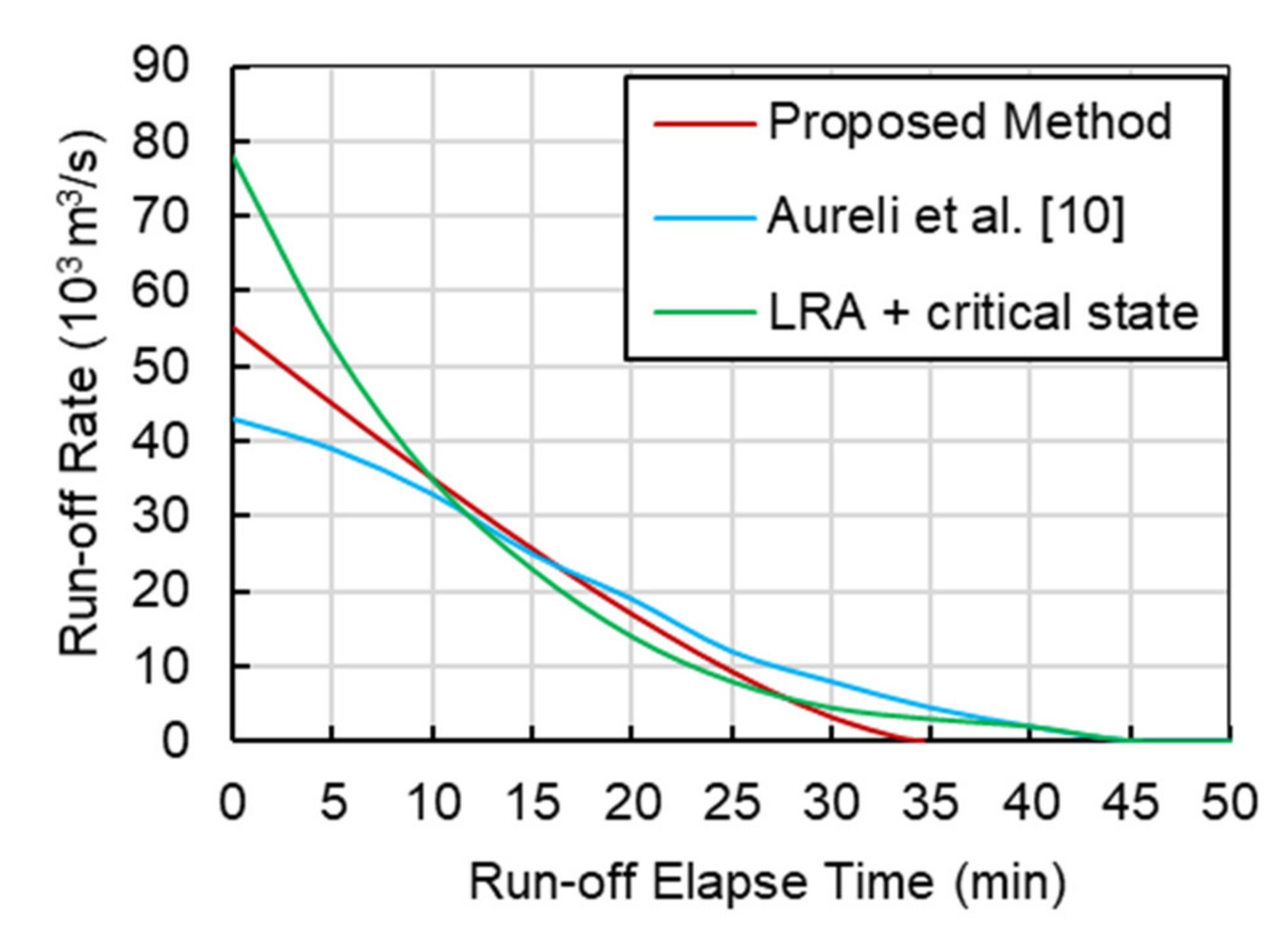
4.1. Malpasset Dam-Break Hydrograph
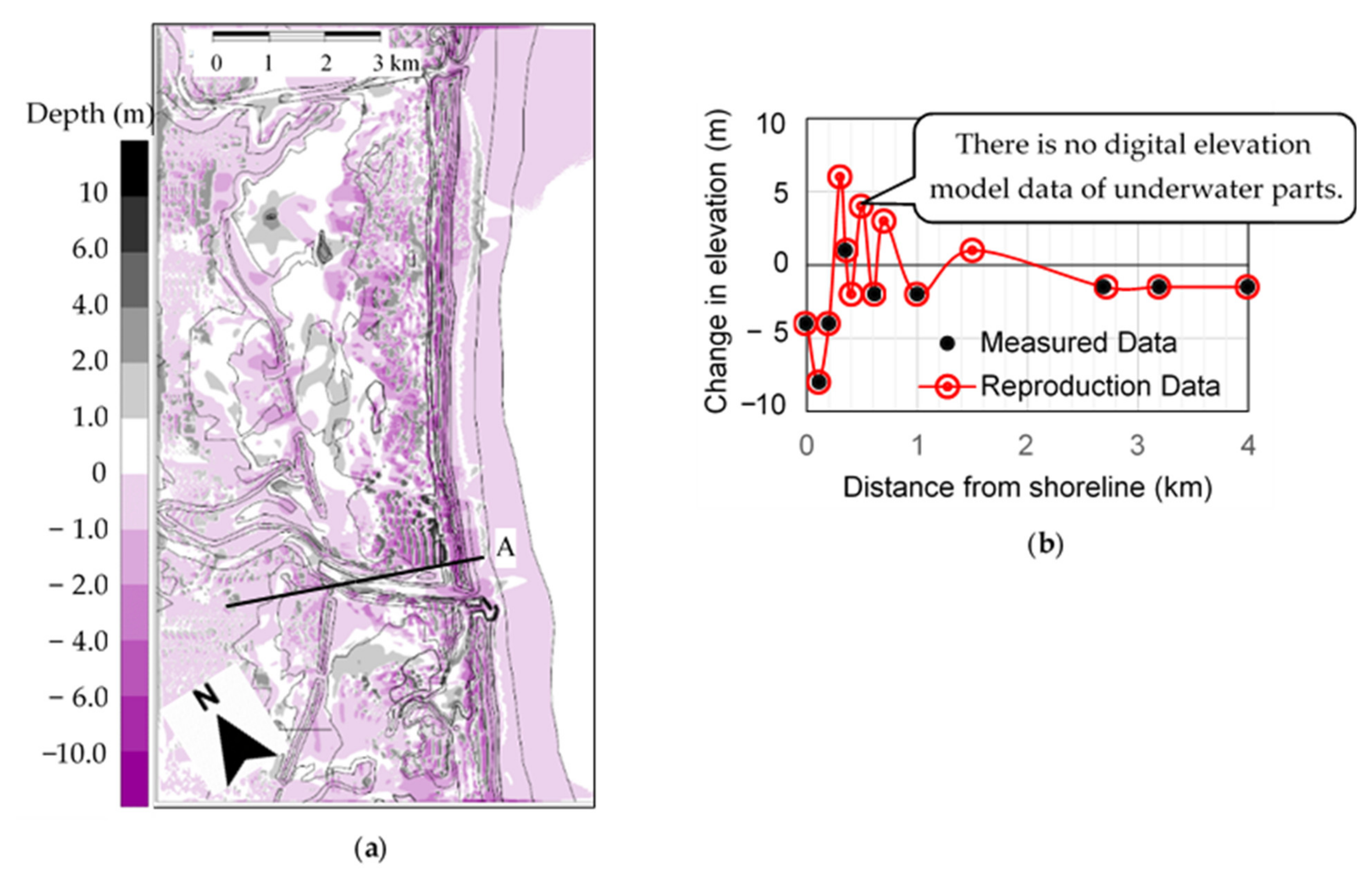
4.2. Hydro-Morphodynamics Simulation in Sendai-Natori Coast
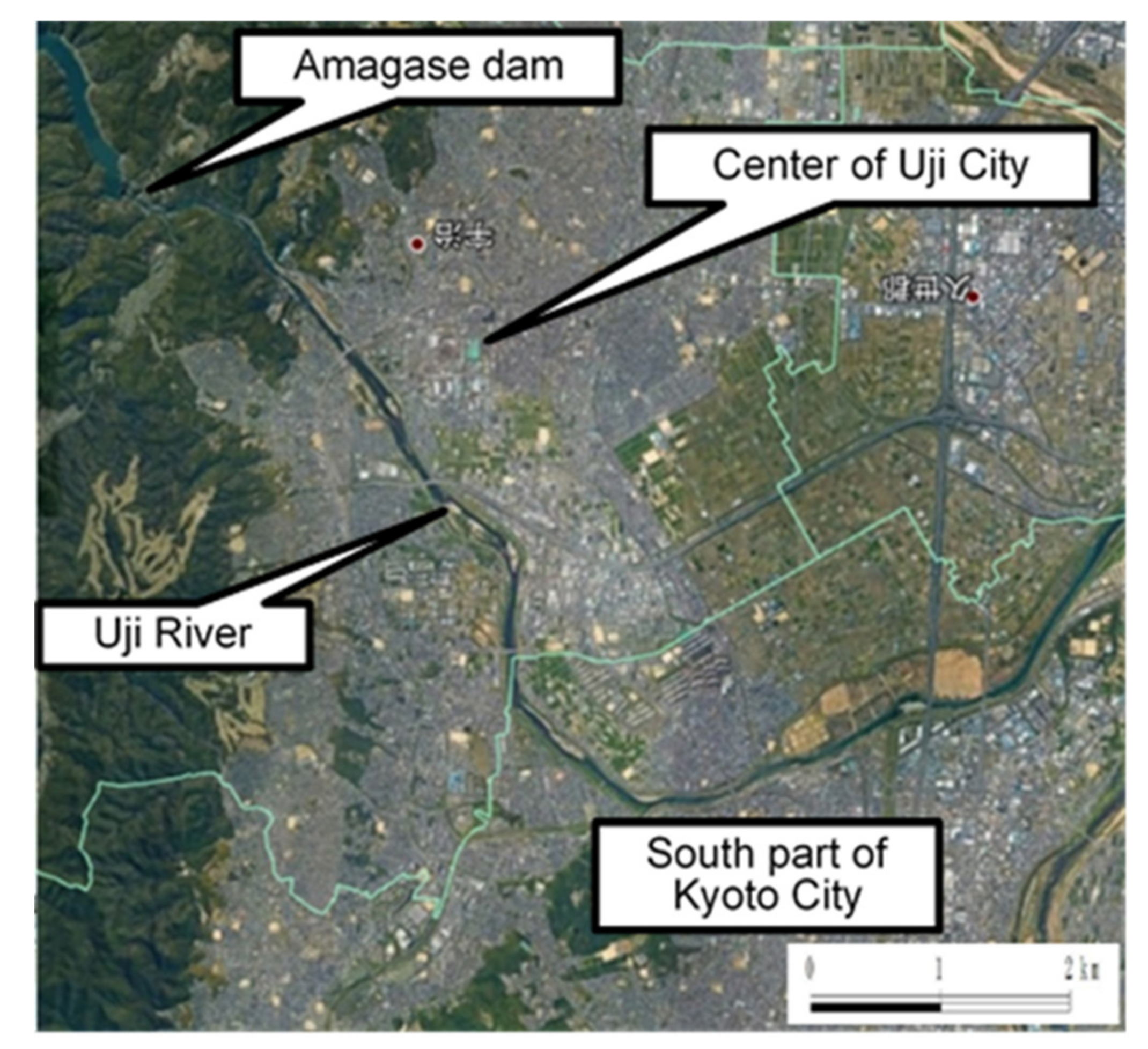
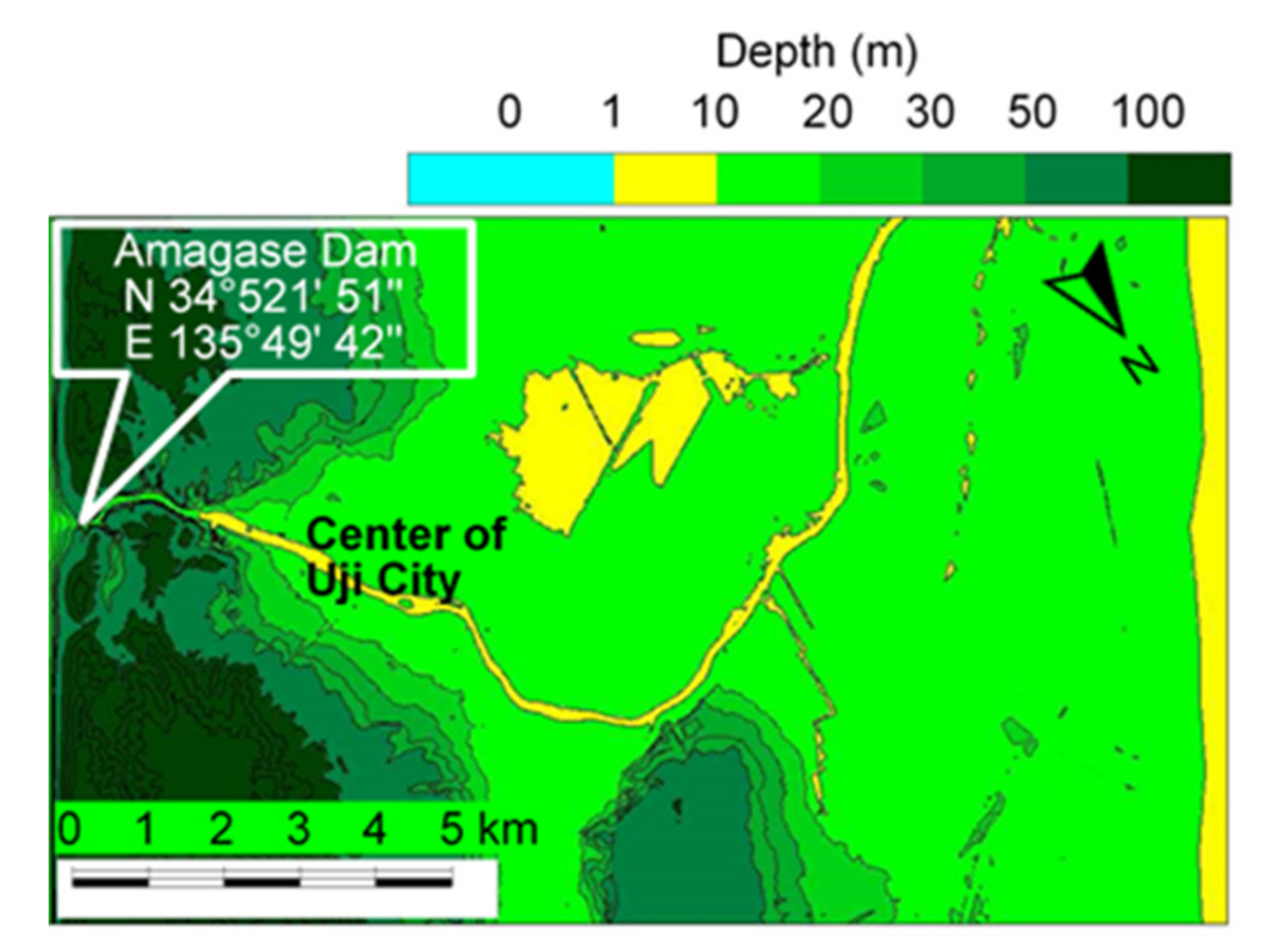
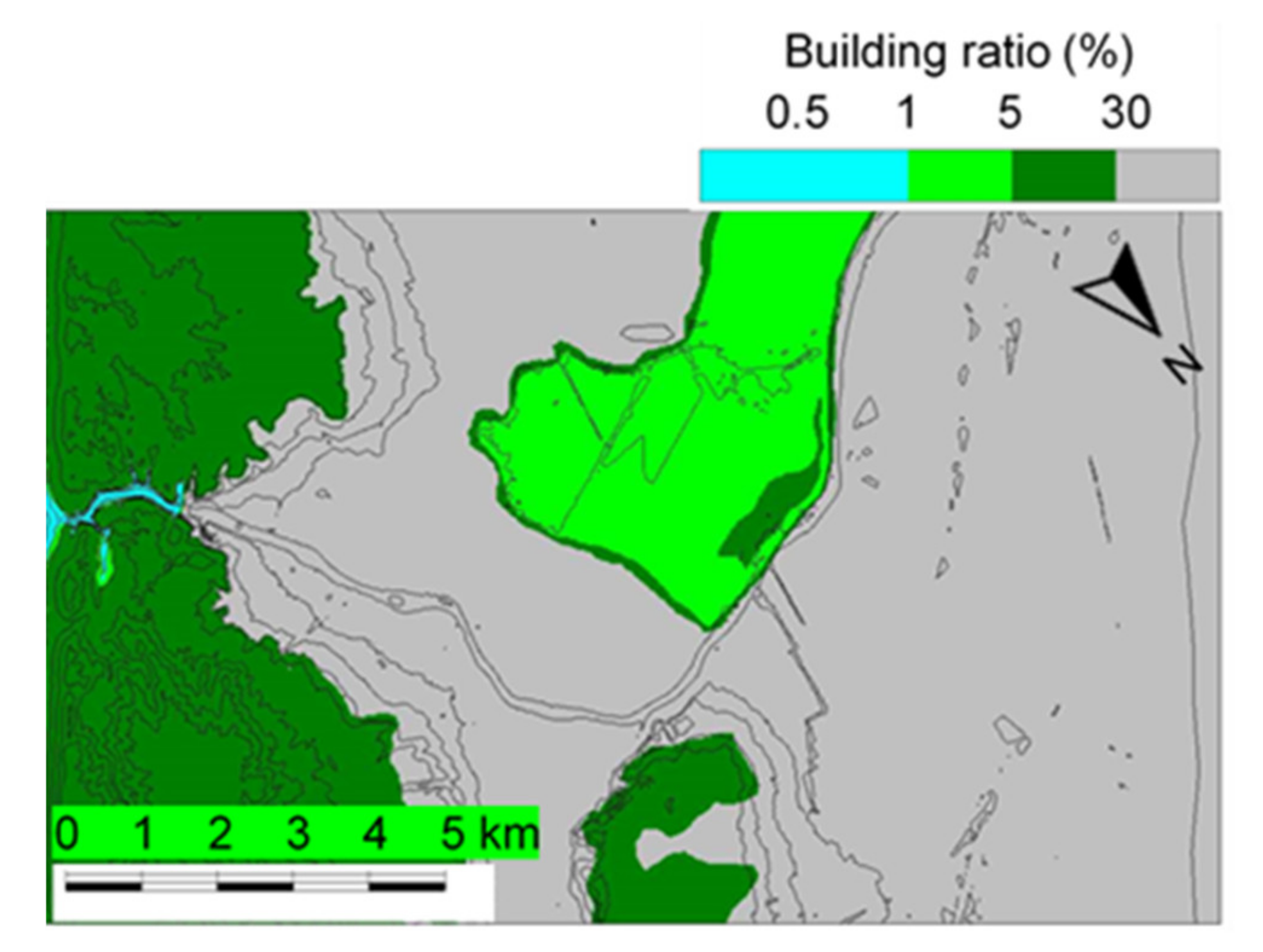
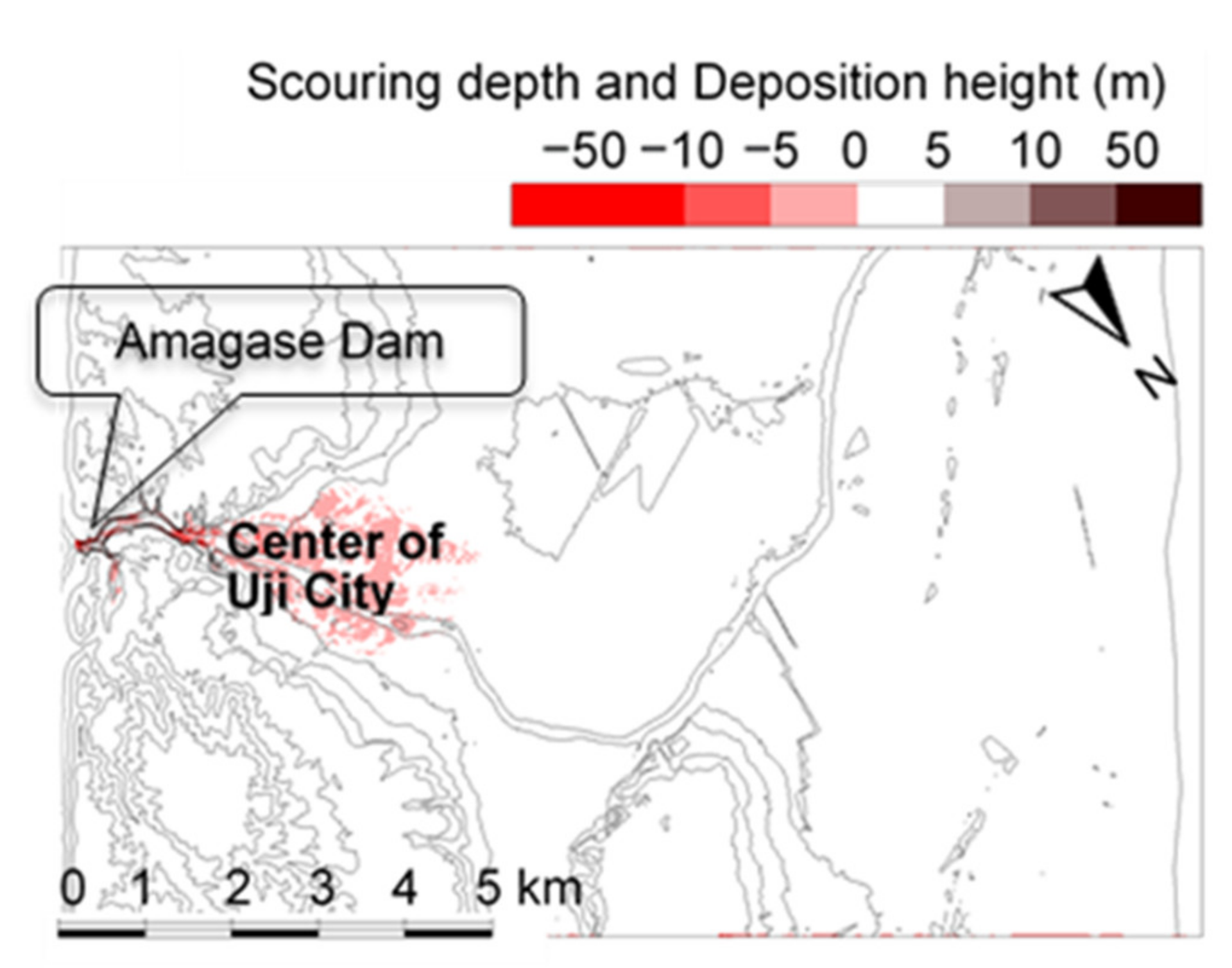
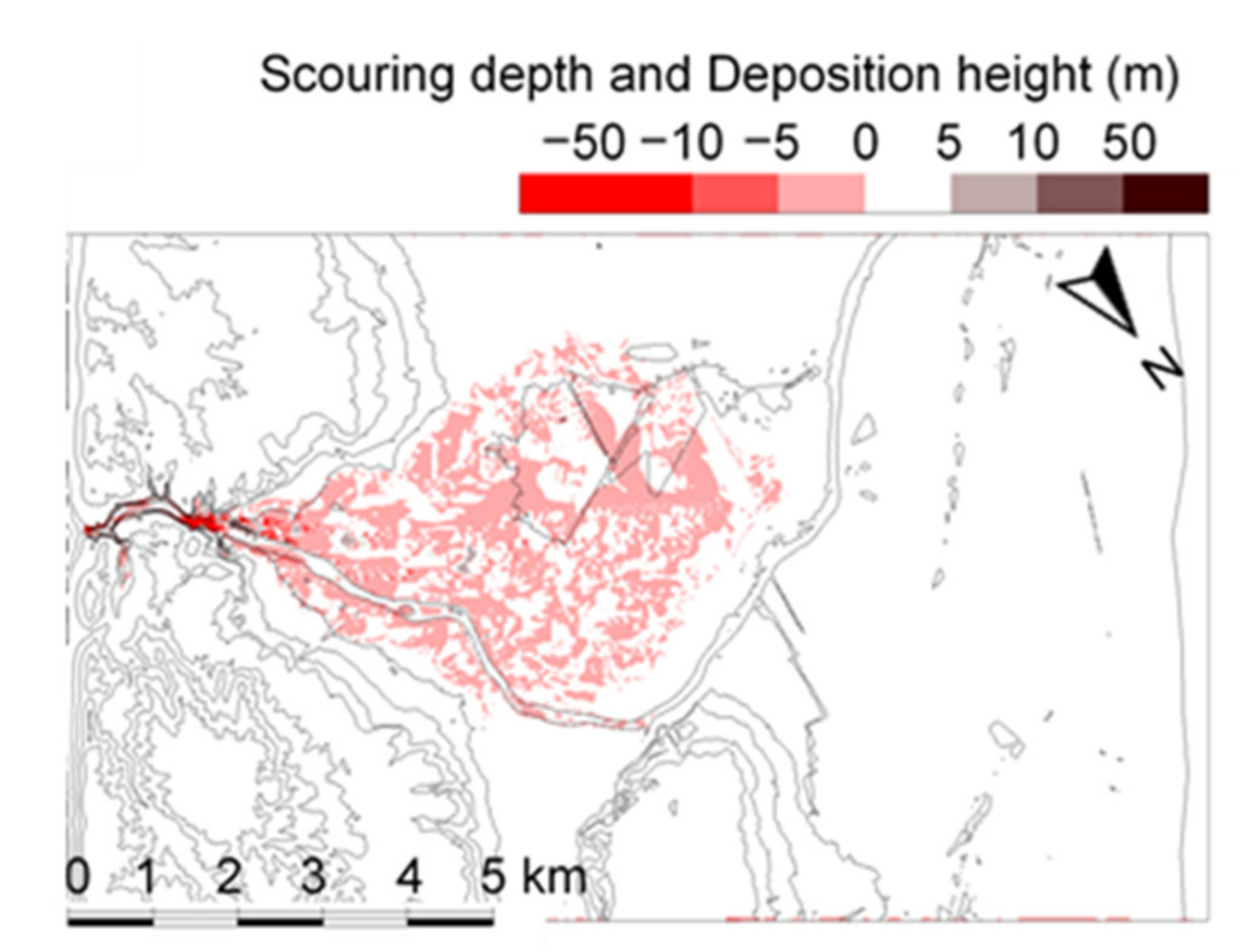
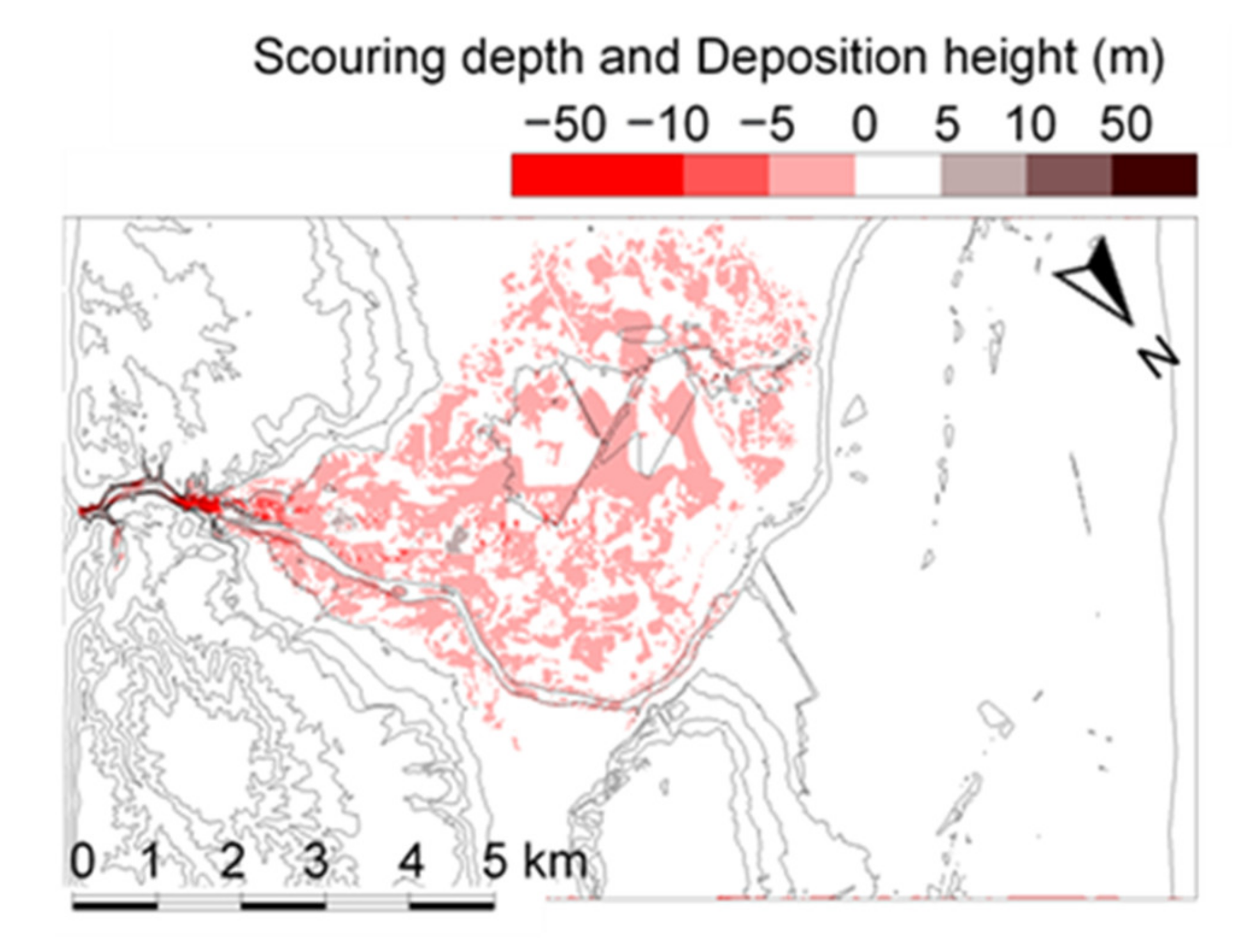
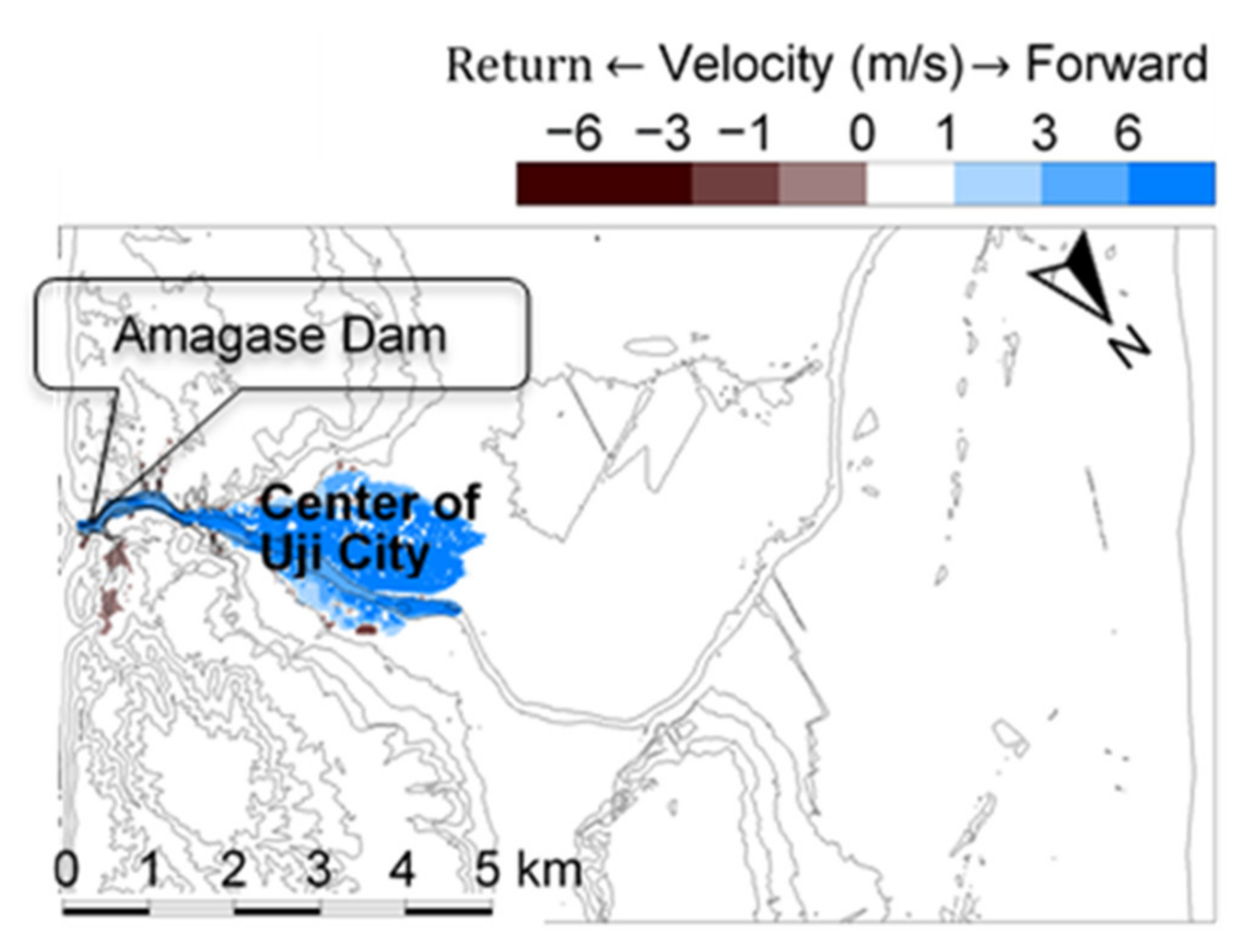
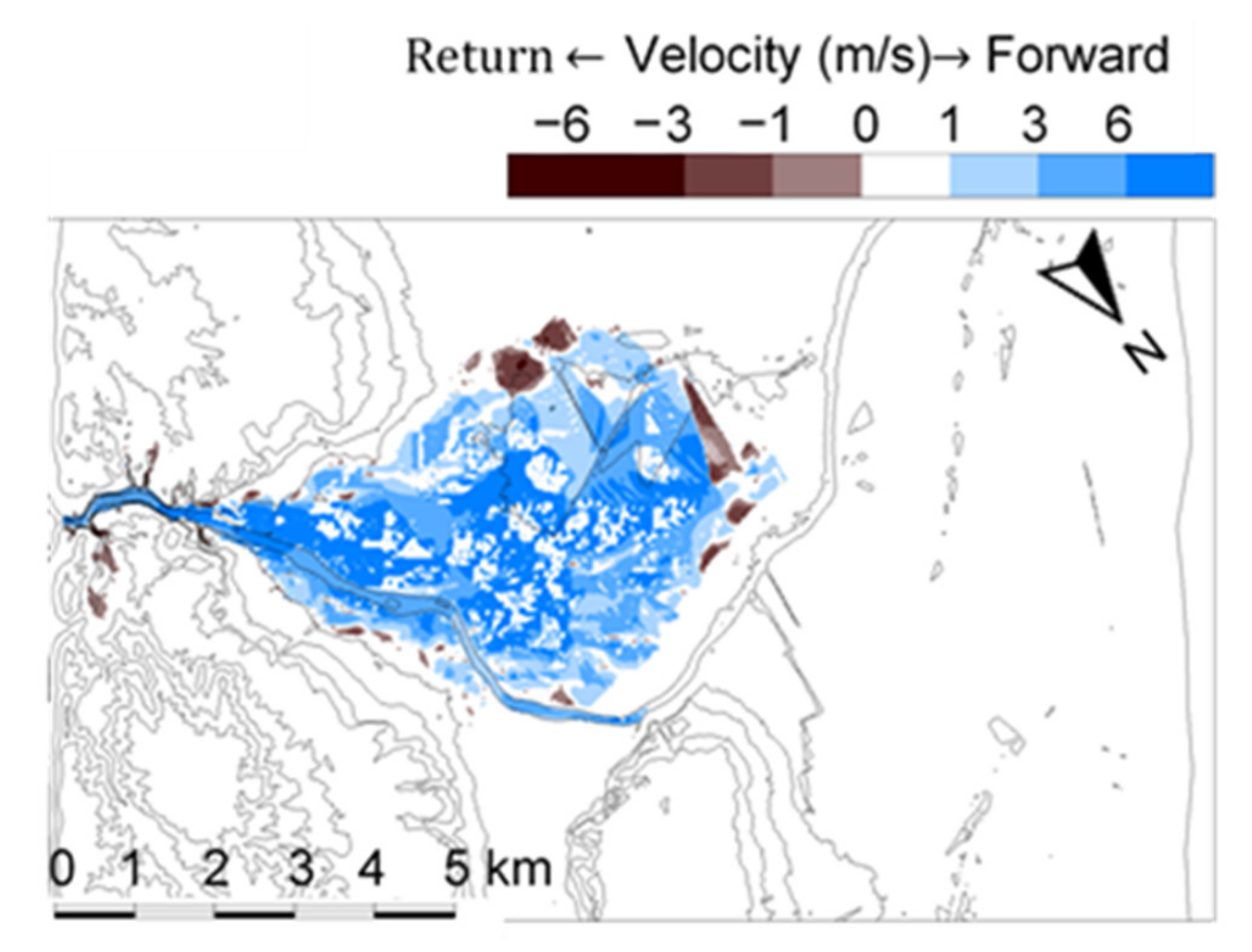
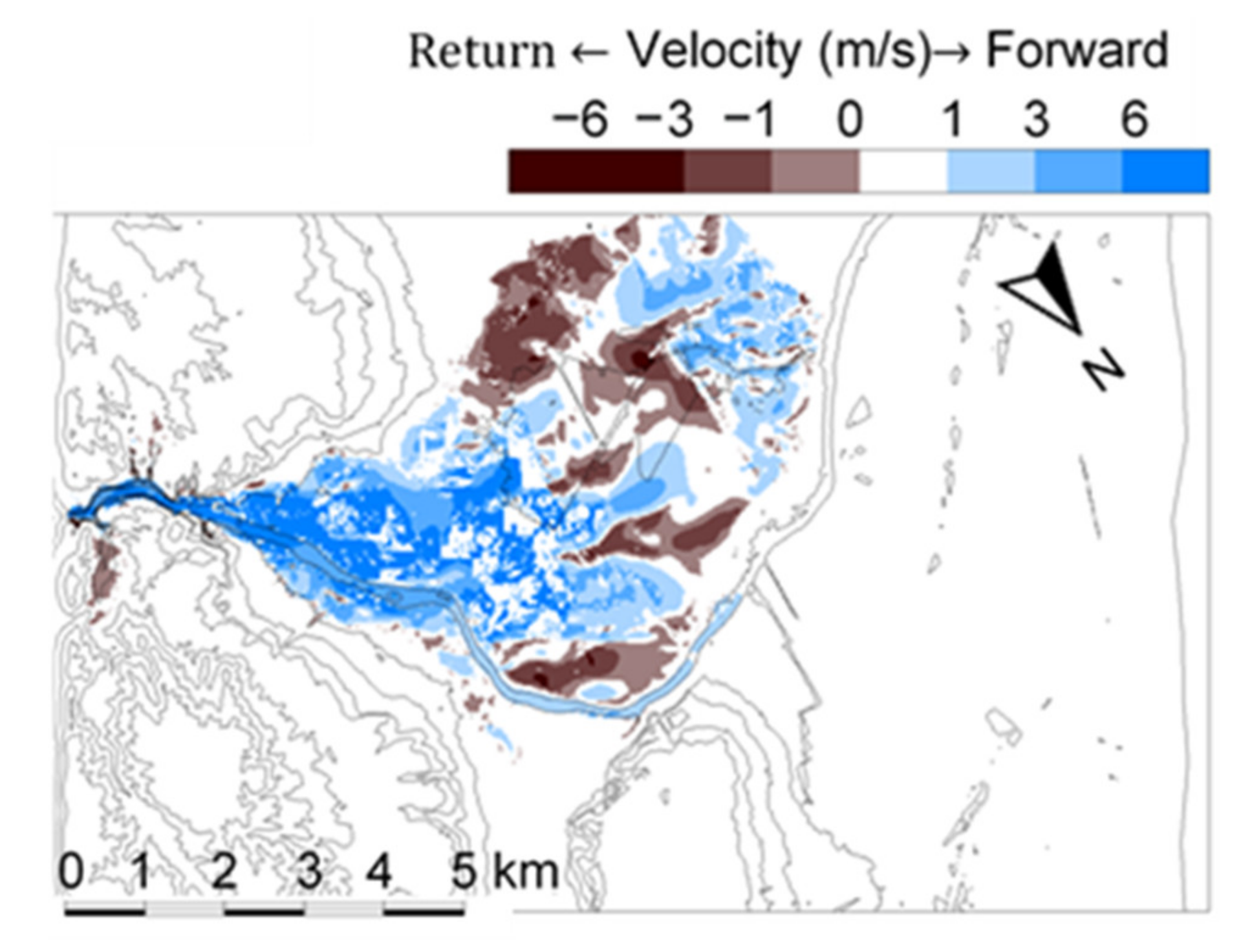
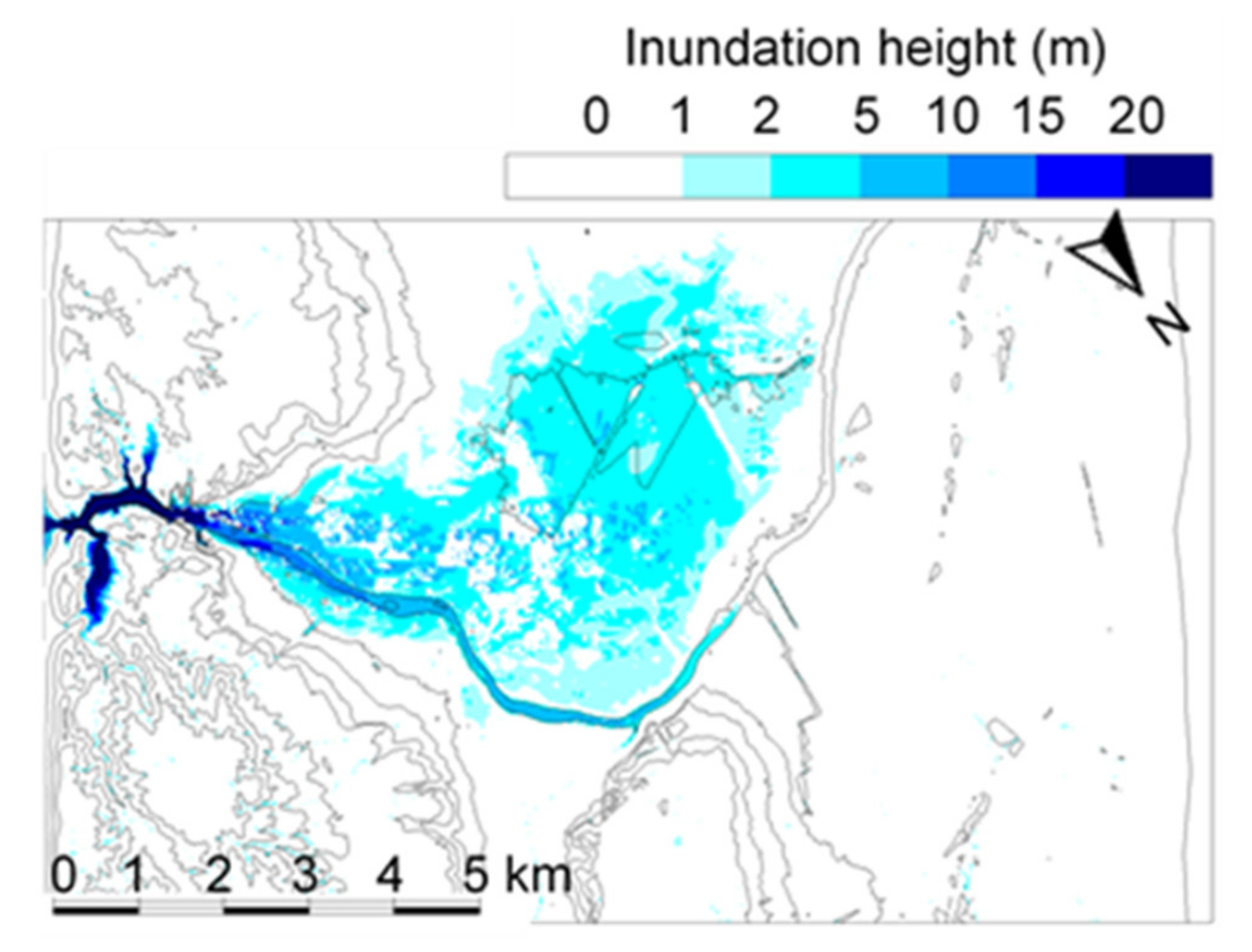
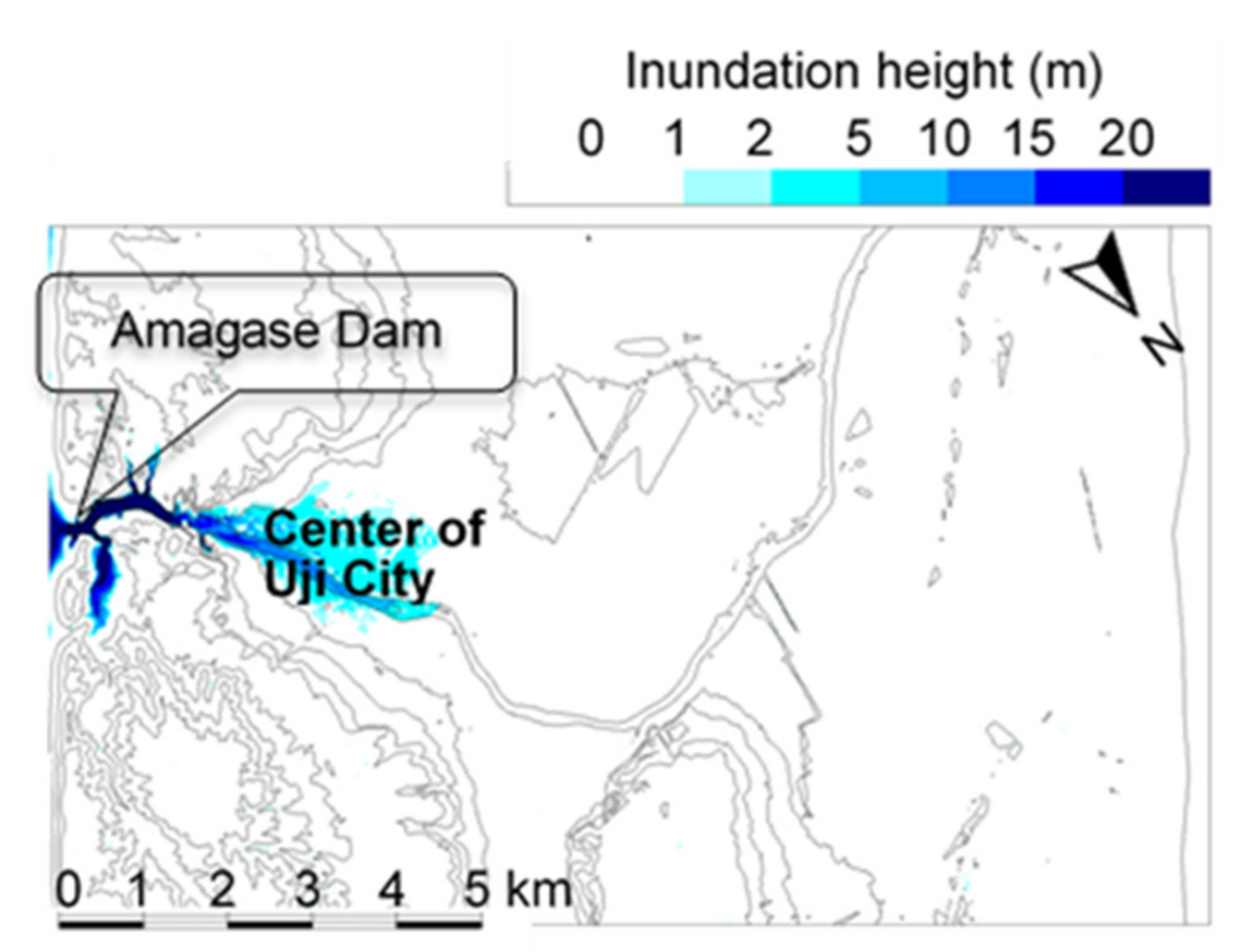
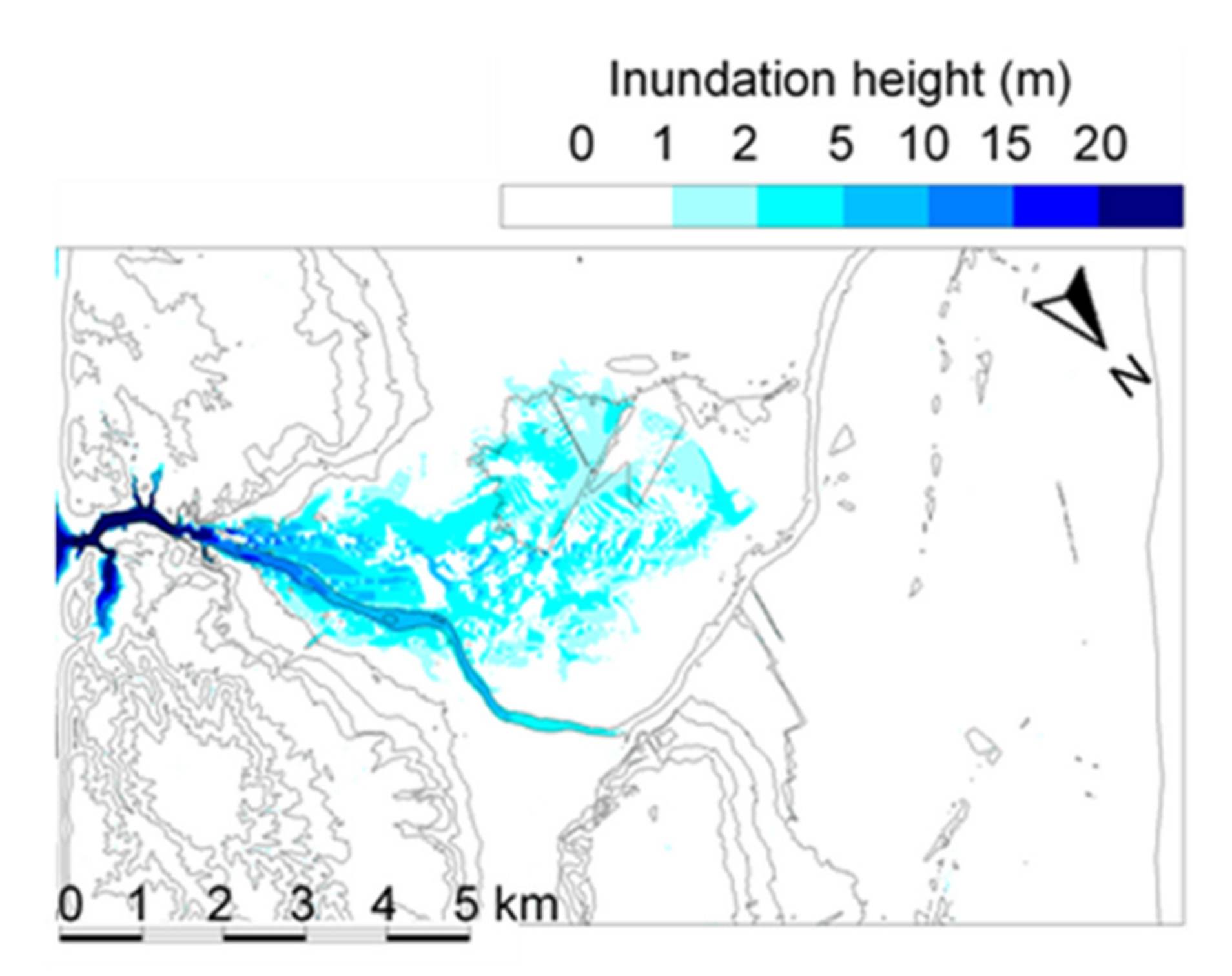
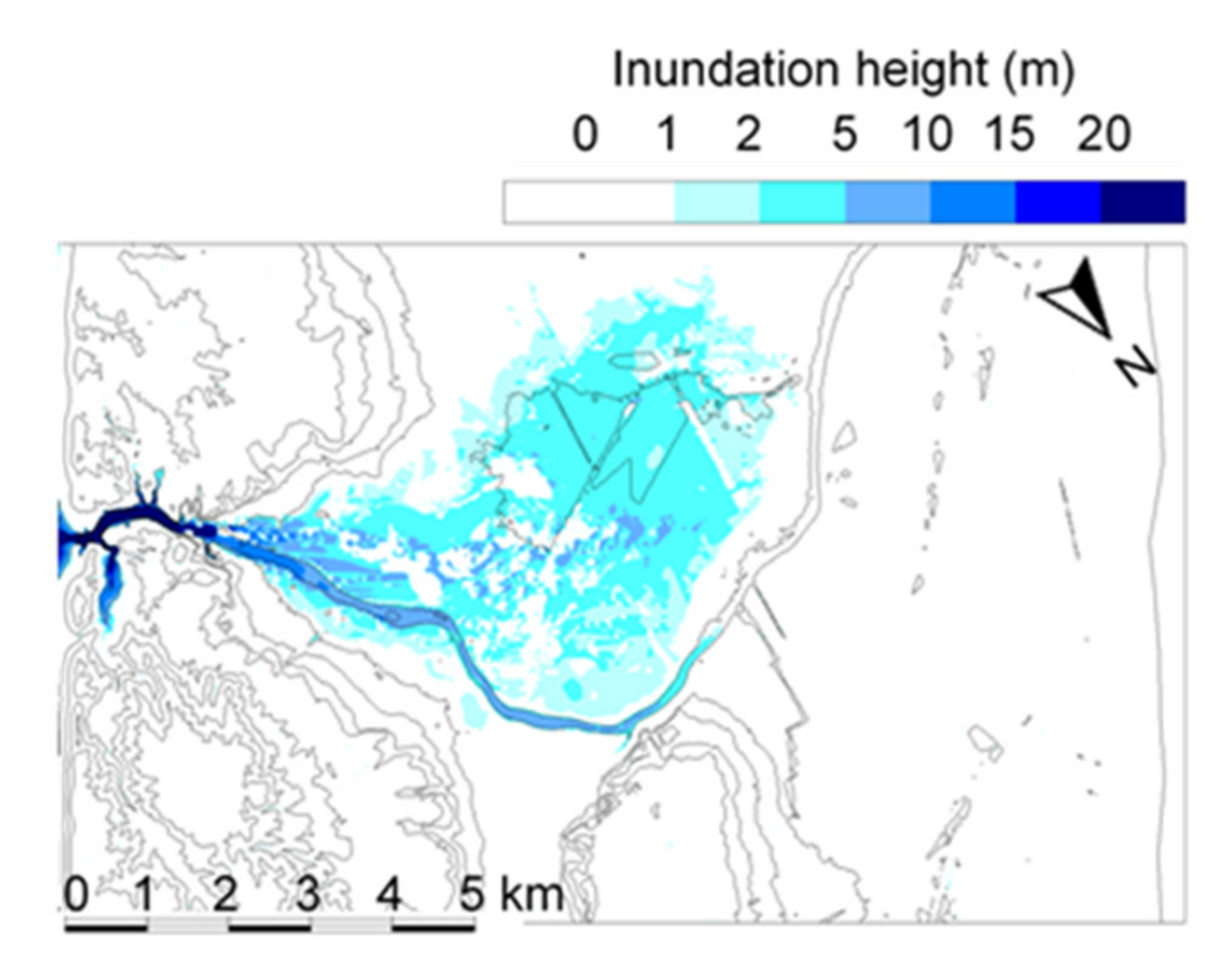
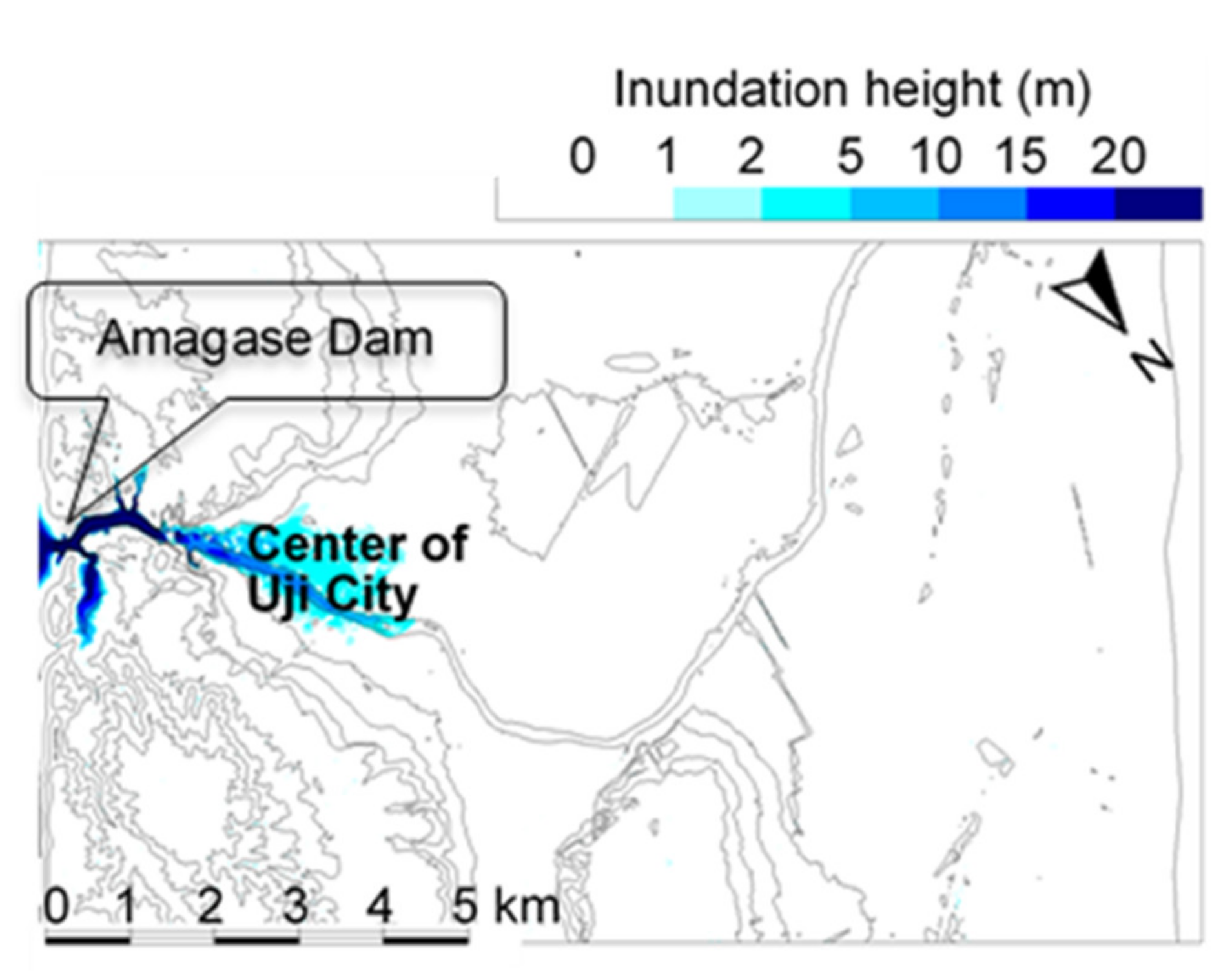
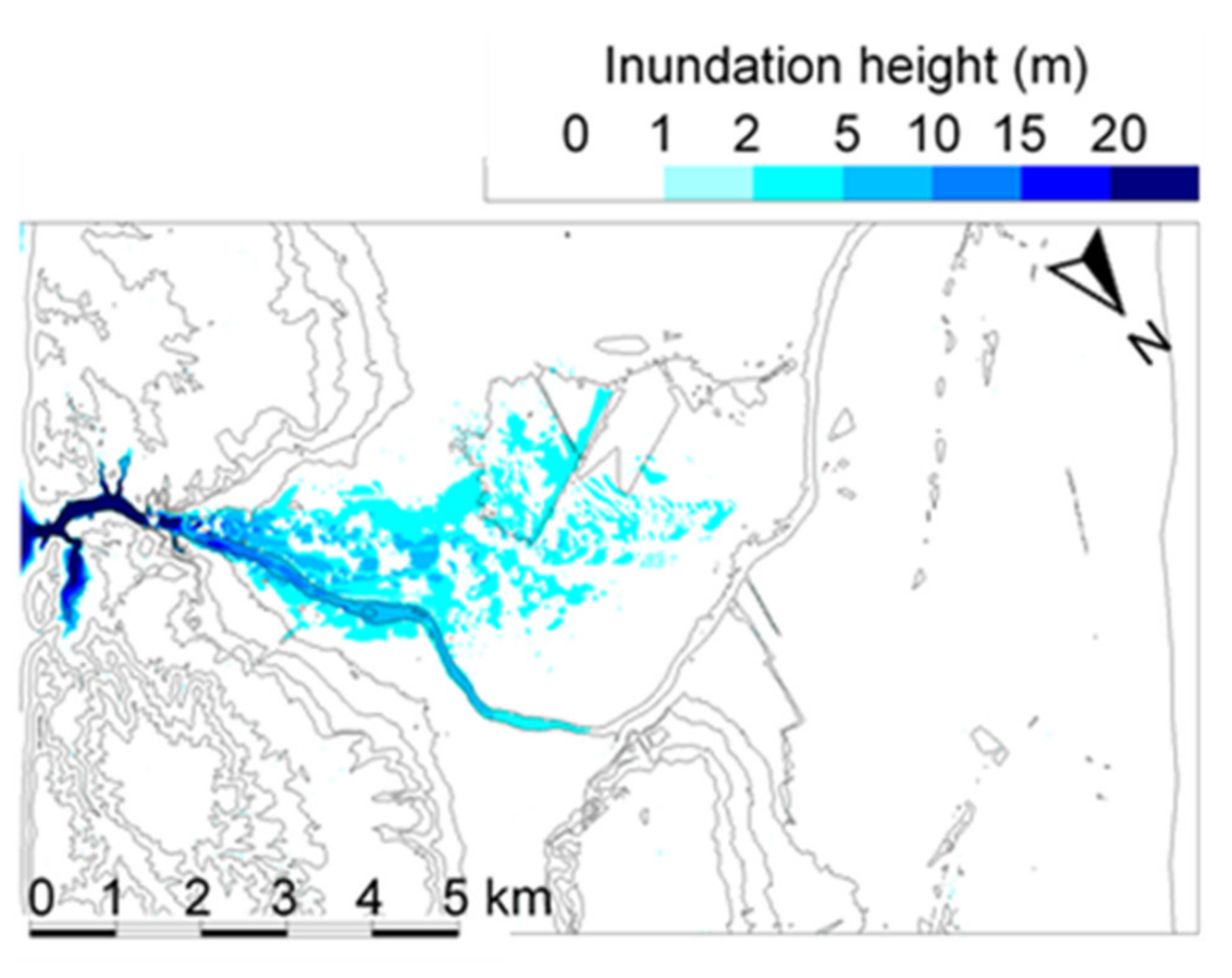
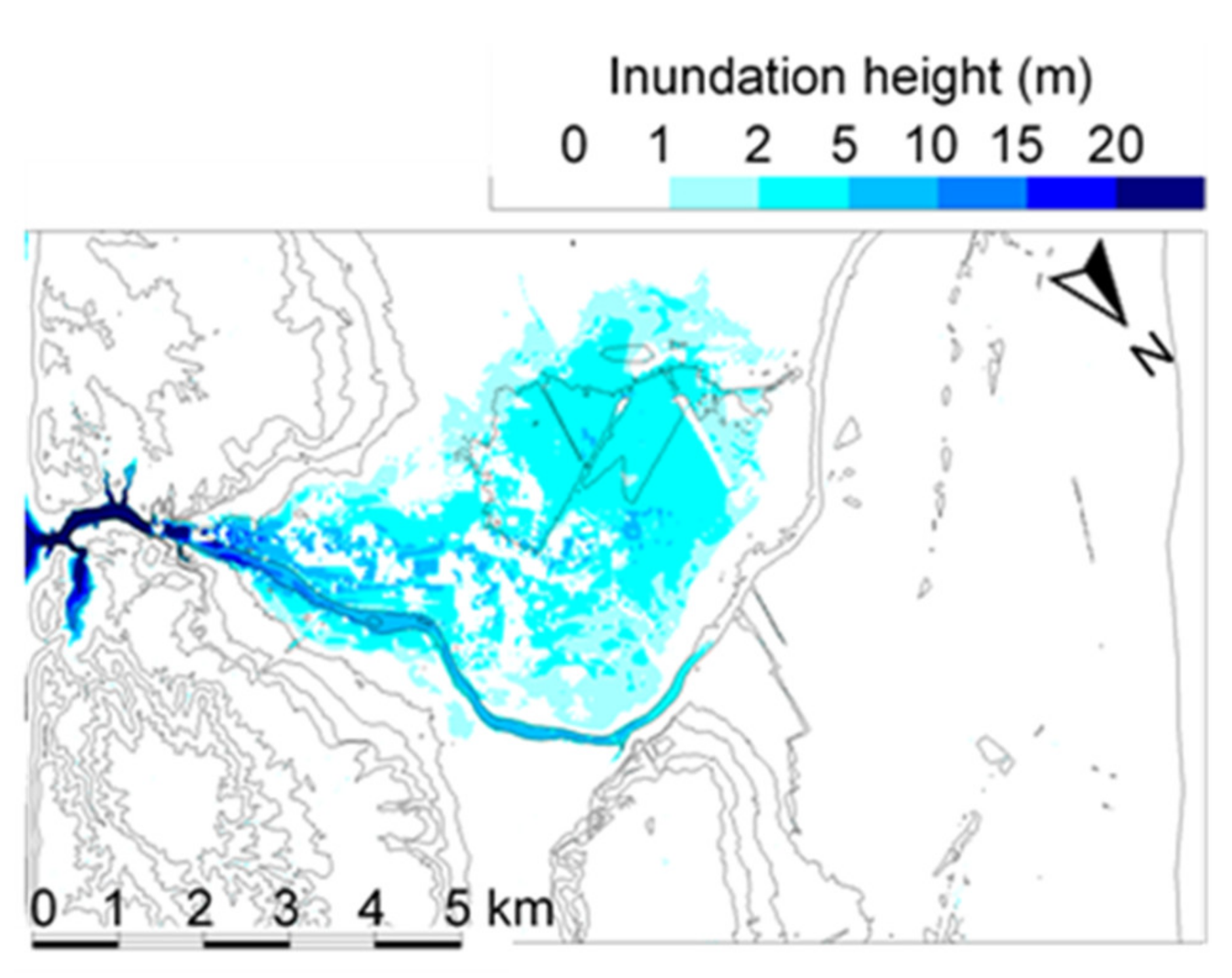
4.3. Dam-Break Hydro-Morphodynamics Simulation (Amagase Dam)
- , using Figure 5,
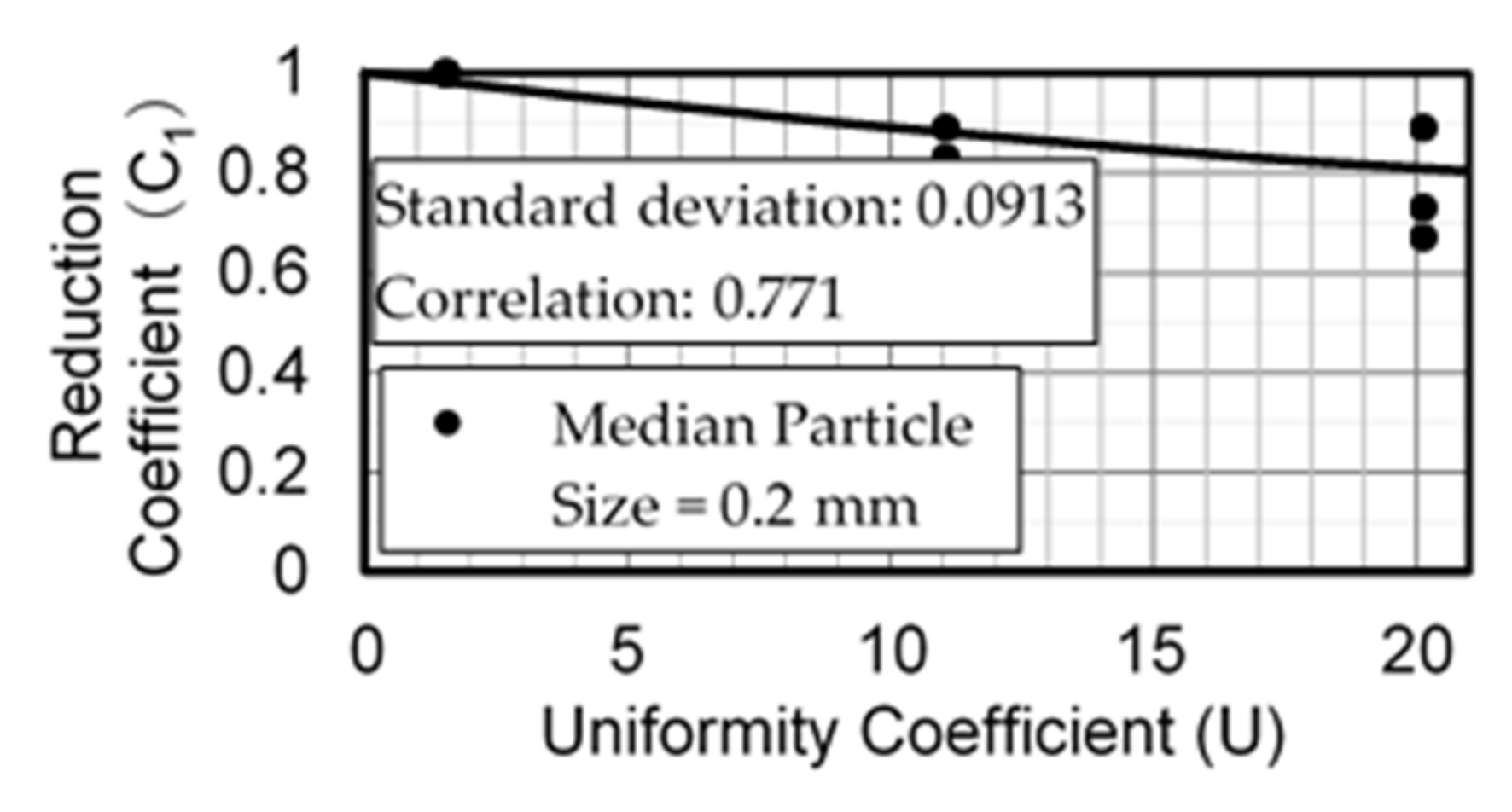
- Uniformity coefficient, . Using Figure 6,
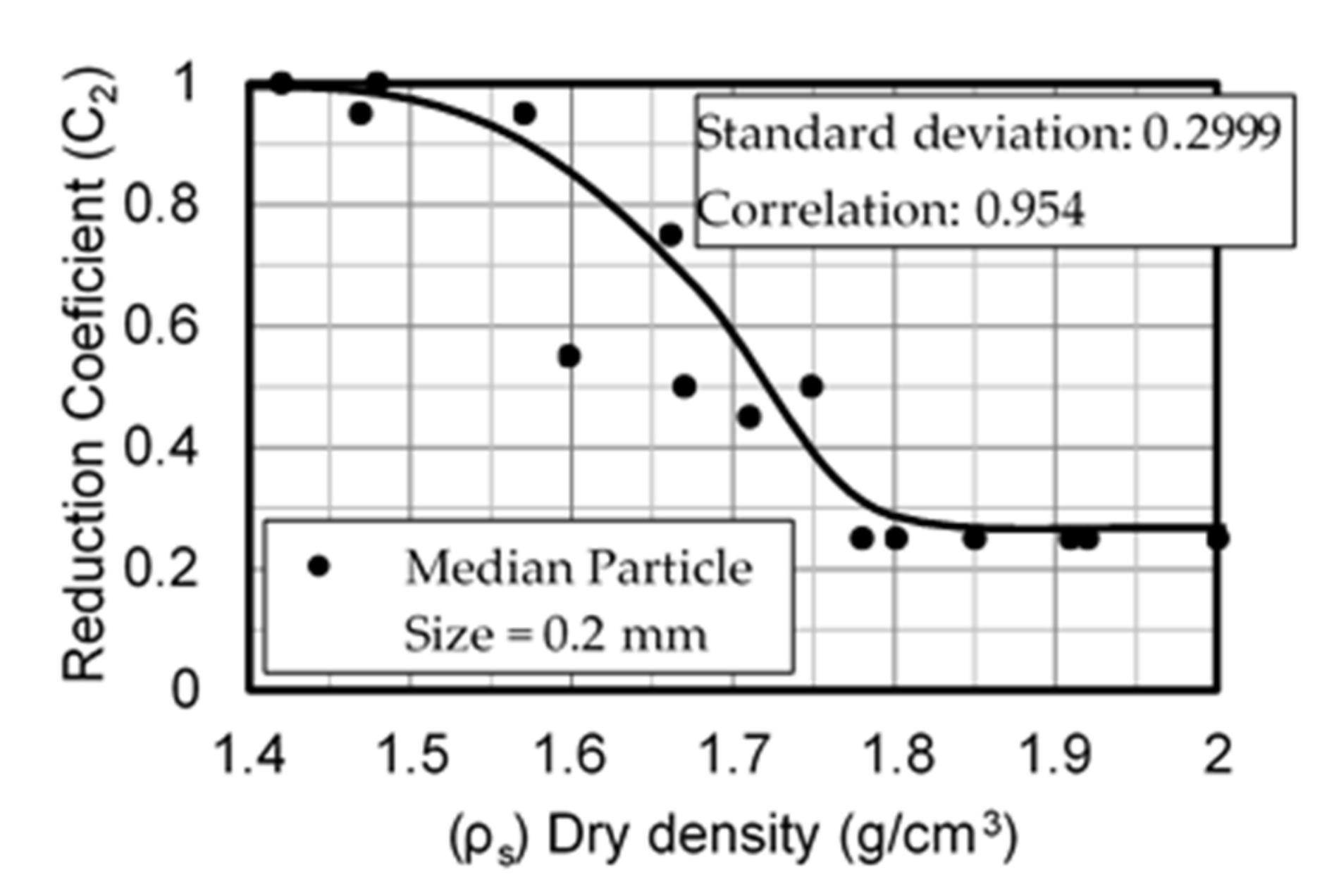
- Dry density . Using Figure 7,
- From Equation (27), .
- , using Figure 5,
- Uniformity coefficient, . Using Figure 6,
- Dry density . Using Figure 7,
- From Equation (27), .
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Psomiadis, E.; Tomanis, L.; Kavvadias, A.; Soulis, K.X.; Charizopoulos, N.; Michas, S. Potential Dam Breach Analysis and Flood Wave Risk Assessment Using HEC-RAS and Remote Sensing Data: A Multicriteria Approach. Water 2021, 13, 364. [Google Scholar] [CrossRef]
- Wahl, T.L. Predicting Embankment Dam Breach Parameters—A Needs Assessment. In Proceedings of the XXVIIth IAHR Congress, San Francisco, CA, USA, 10–15 August 1997. [Google Scholar]
- Pilotti, M.; Tomirotti, M.; Valerio, G.; Bacchi, B. Simplified Method for the Characterization of the Hydrograph following a Sudden Partial Dam Break. J. Hydraul. Eng. 2010, 136, 693–704. [Google Scholar] [CrossRef]
- Costa, J.E. Floods from Dam Failures; Open-File Report; U.S. Geological Survey: Denver, CO, USA, 1985. [Google Scholar]
- Gary, G. Using HEC-RAS for Dam Break Studies; US Army Corps of Engineers: Washington, DC, USA, 2014. [Google Scholar]
- Wurbs, R.A. Dam-Breach Flood Wave Models. J. Hydraul. Eng. 1987, 113, 29–46. [Google Scholar] [CrossRef]
- Bazin, H. Recherches Expérimentales relatives aux remous et à la propagation des ondes [Experimental research on the hydraulic jump and on wave propagation]. Deux. Partie Rech. Hydraul. Darcy Baz. Dunod Paris 1865, 2, 148. [Google Scholar]
- Ritter, A. Die Fortpflanzung der Wasserwellen. [The propagation of water waves]. Z. Ver. Dtsch. Ing. 1892, 3633, 947–954. [Google Scholar]
- Su, S.-T.; Barnes, A.H. Geometric and Frictional Effects on Sudden Releases. J. Hydraul. Div. 1970, 96, 2185–2200. [Google Scholar] [CrossRef]
- Aureli, F.; Maranzoni, A.; Mignosa, P. A semi-analytical method for predicting the outflow hydrograph due to dam-break in natural valleys. Adv. Water Resour. 2013, 63, 38–44. [Google Scholar] [CrossRef]
- Saberi, O.; Zenz, G. Empirical Relationship for Calculate Outflow Hydrograph of Embankment Dam Failure due to Overtopping Flow. Int. J. Hydraul. Eng. 2015, 4, 45–53. [Google Scholar]
- Basheer, T.A.; Wayayok, A.; Yusuf, B.; Kamal, R. Dam breach parameters and their influence on flood hydrographs for mosul dam. J. Eng. Sci. Technol. 2017, 12, 14. [Google Scholar]
- Hakimzadeh, H.; Nourani, V.; Amini, A.B. Genetic Programming Simulation of Dam Breach Hydrograph and Peak Outflow Discharge. J. Hydrol. Eng. 2014, 19, 757–768. [Google Scholar] [CrossRef]
- Wahl, T.L. Prediction of Embankment Dam Breach Parameters—A Literature Review and Needs Assessment; Dam Safety Office: Denver, CO, USA, 1998. [Google Scholar]
- Ca, V.T.; Yamamoto, Y.; Charusrojthanadech, N. Improvement of Prediction Methods of Coastal Scour and Erosion due to Tsunami Back-flow. In Proceedings of the International Society of Offshore and Polar Engineers (ISOPE), Beijing, China, 20 June 2010. ISOPE-I-10-510. [Google Scholar]
- Suetsugi, T.; Kuriki, M. Research on Application for Flood Disaster Prevention and Simulation of Flooding Flow by Means of New Flood Simulation Model. Doboku Gakkai Ronbunshu 1998, 593, 41–50. [Google Scholar] [CrossRef] [Green Version]
- Ribberink, J.S. Bed-load transport for steady flows and unsteady oscillatory flows. Coast. Eng. 1998, 34, 59–82. [Google Scholar] [CrossRef]
- Yokoyama, Y.; Tanabe, H.; Torii, K.; Kato, F.; Yamamoto, Y.; Vu, T.C.; Arimura, J. A quantitative evaluation of scour depth near coastal structures. In Proceedings of the Coastal Engineering 2002; World Scientific Publishing Company: Cardiff, UK, 2003; pp. 1830–1841. [Google Scholar]
- Ahmadi, S.M.; Yamamoto, Y.; Ca, V.T. Rational Evaluation Methods of Topographical Change and Building Destruction in the Inundation Area by a Huge Tsunami. J. Mar. Sci. Eng. 2020, 8, 762. [Google Scholar] [CrossRef]
- Van Rijn, L.C. Principles of Sediment Transport in Rivers, Estuaries and Coastal Seas. 1: Principles of Sediment Transport in Rivers, Estuaries and Coastal Seas; Aqua Publications: Amsterdam, The Netherlands, 1993; ISBN 978-90-800356-2-1. [Google Scholar]
- Van Rijn, L.C. Sediment Transport, Part I: Bed Load Transport. J. Hydraul. Eng. 1984, 110, 1431–1456. [Google Scholar] [CrossRef] [Green Version]
- Van Rijn, L.C. Sediment Transport, Part II: Suspended Load Transport. J. Hydraul. Eng. 1984, 110, 1613–1641. [Google Scholar] [CrossRef]
- Van Rijn, L.C. Sediment Transport, Part III: Bed forms and Alluvial Roughness. J. Hydraul. Eng. 1984, 110, 1733–1754. [Google Scholar] [CrossRef]
- Richard Soulsby Dynamics of Marine Sands; Thomas Telford Ltd: London, UK, 1997; ISBN 978-0-7277-2584-4.
- Zyserman, J.A.; Fredsøe, J. Data Analysis of Bed Concentration of Suspended Sediment. J. Hydraul. Eng. 1994, 120, 1021–1042. [Google Scholar] [CrossRef]
- Bates, P.D.; De Roo, A.P.J. A simple raster-based model for flood inundation simulation. J. Hydrol. 2000, 236, 54–77. [Google Scholar] [CrossRef]
- Amicarelli, A.; Manenti, S.; Albano, R.; Agate, G.; Paggi, M.; Longoni, L.; Mirauda, D.; Ziane, L.; Viccione, G.; Todeschini, S.; et al. SPHERA v.9.0.0: A Computational Fluid Dynamics research code, based on the Smoothed Particle Hydrodynamics mesh-less method. Comput. Phys. Commun. 2020, 250, 107157. [Google Scholar] [CrossRef]
- He, G.; Chai, J.; Qin, Y.; Xu, Z.; Li, S. Evaluation of Dam Break Social Impact Assessments Based on an Improved Variable Fuzzy Set Model. Water 2020, 12, 970. [Google Scholar] [CrossRef] [Green Version]
- Kocaman, S.; Dal, K. A New Experimental Study and SPH Comparison for the Sequential Dam-Break Problem. J. Mar. Sci. Eng. 2020, 8, 905. [Google Scholar] [CrossRef]
- Goutal, N. The Malpasset dam failure. An overview and test case definition. In Proceedings of the 4th CADAM Meeting, Zaragoza, Spain, 18–19 November 1999; pp. 18–19. [Google Scholar]
- Alcrudo, F.; Gil, F. The Malpasset dam break case study. In Proceedings of the 4th CADAM Meeting, Zaragoza, Spain, 18–19 November 1999; pp. 18–19. [Google Scholar]
- Hervouet, J.-M.; Petitjean, A. Malpasset dam-break revisited with two-dimensional computations. J. Hydraul. Res. 1999, 37, 777–788. [Google Scholar] [CrossRef]
- Valiani, A.; Caleffi, V.; Zanni, A. Case Study: Malpasset Dam-Break Simulation using a Two-Dimensional Finite Volume Method. J. Hydraul. Eng. 2002, 128, 460–472. [Google Scholar] [CrossRef]
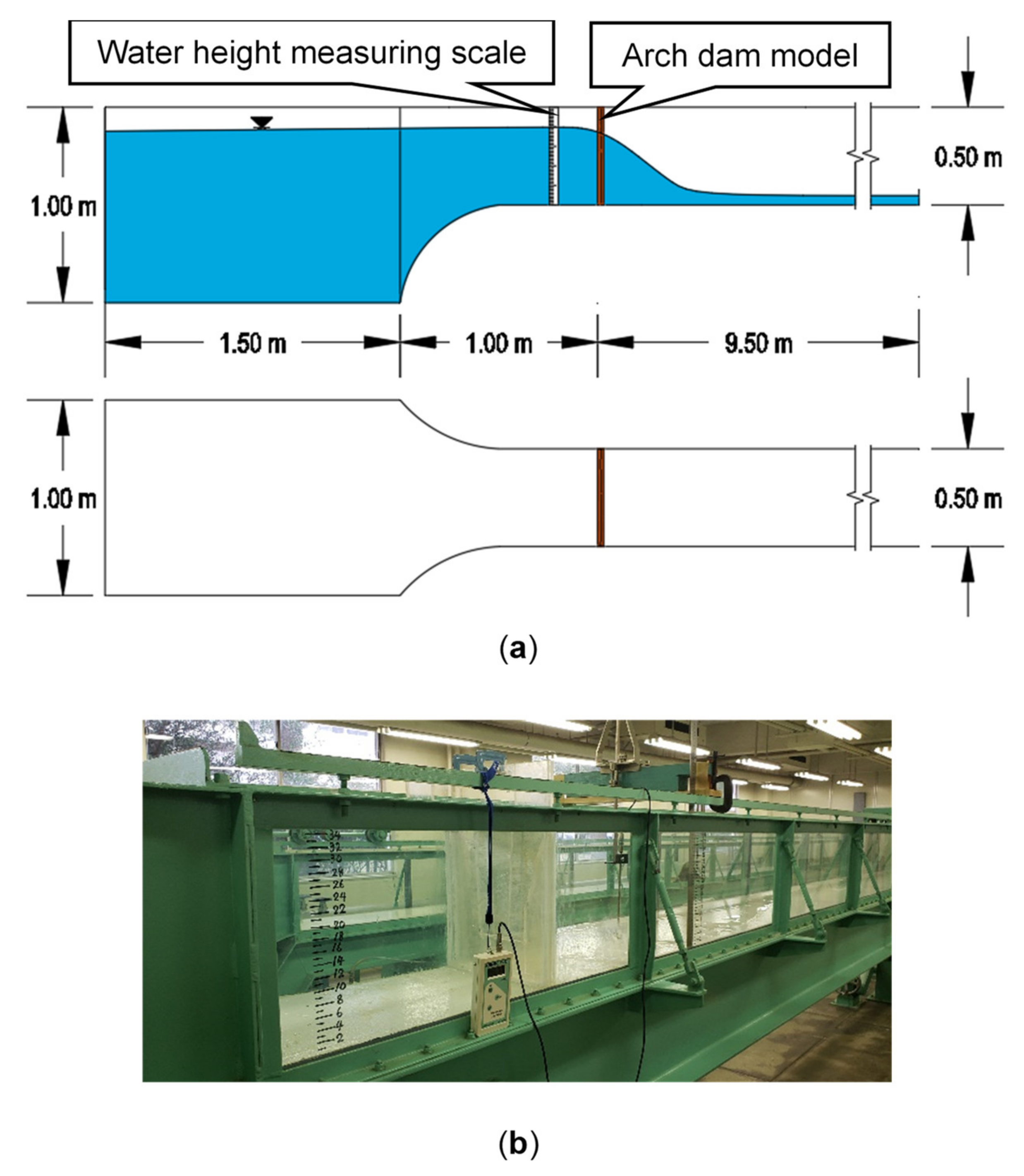
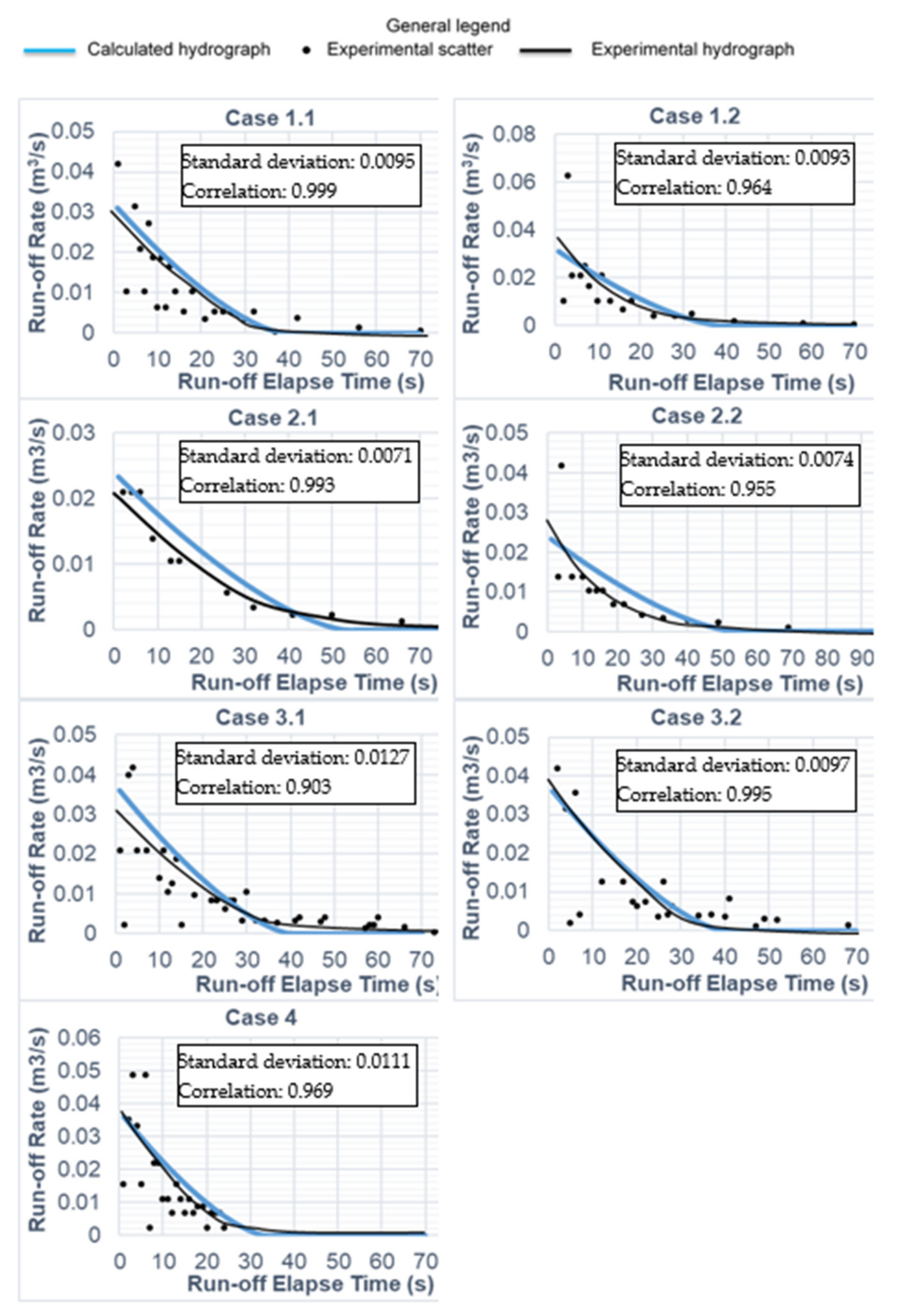




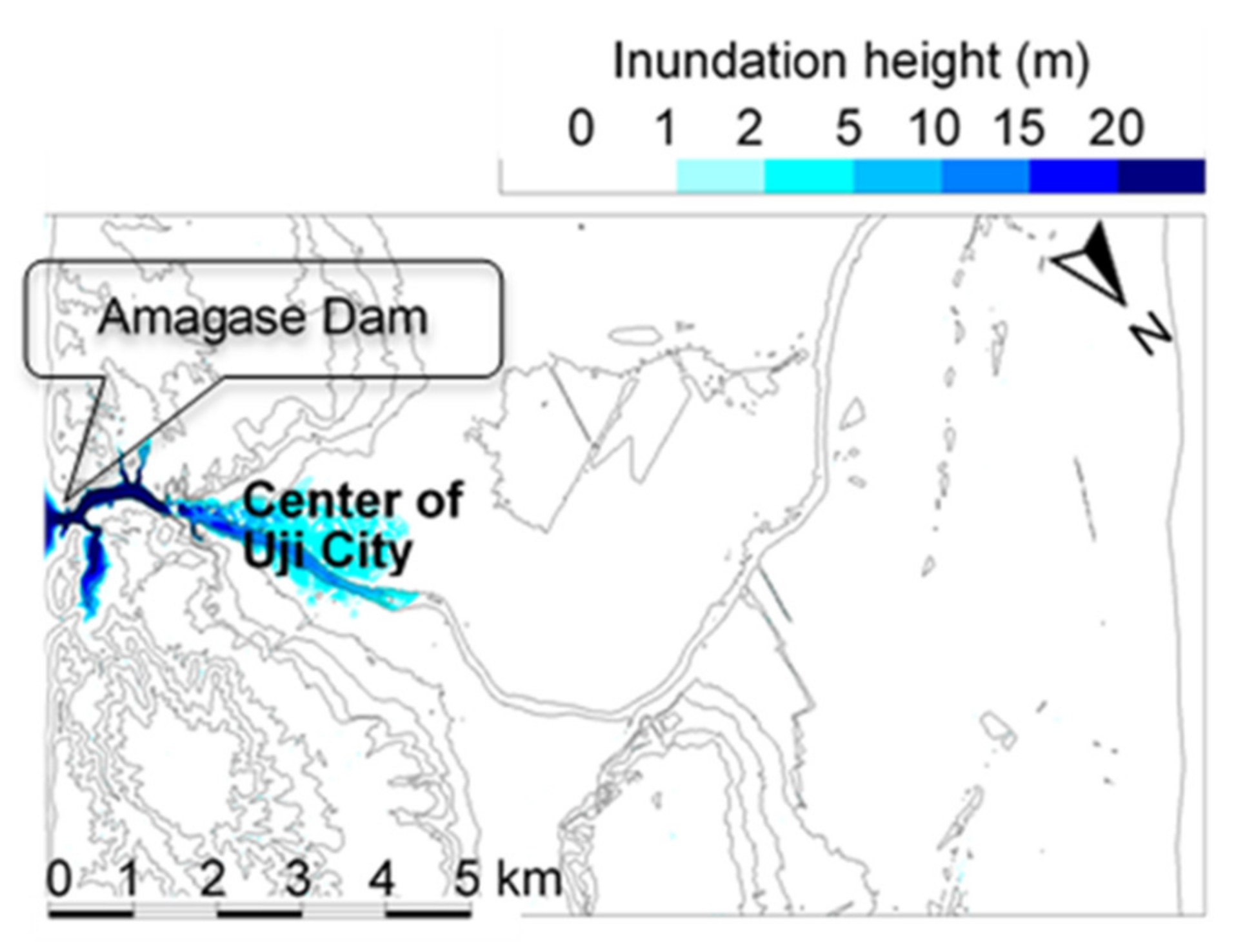
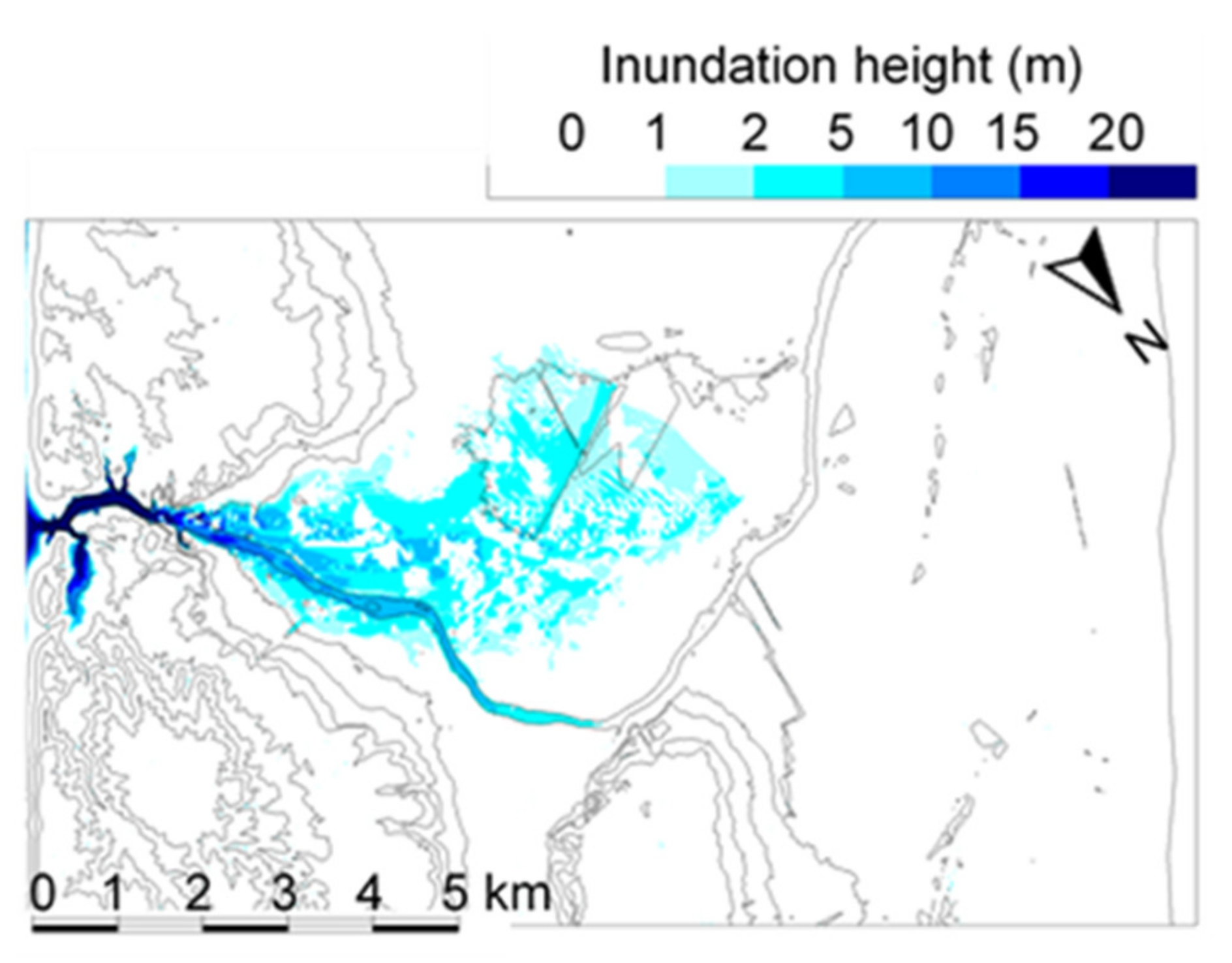
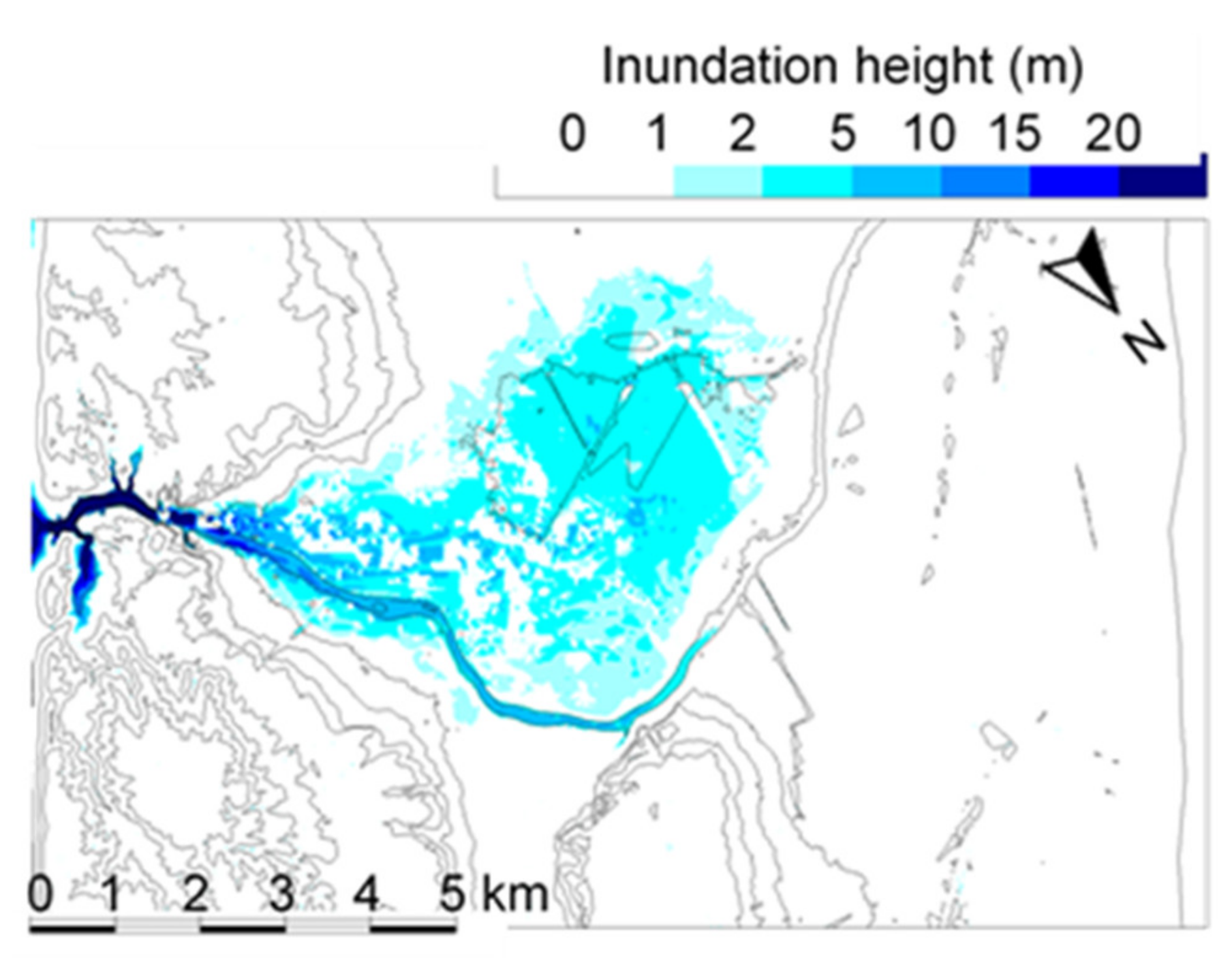
| Case | Description | Break Dimensions | c | |||
|---|---|---|---|---|---|---|
| B (m) | H (m) | Dd (m) | Break Section Thickness (cm) | |||
| I.1 | Trapezoidal | 0.30 | 0.25 | 6 | 3.0 | 0.30 |
| 1.2 | Trapezoidal | 0.30 | 0.25 | 6 | 3.0 | 0.30 |
| 2.1 | Trapezoidal | 0.30 | 0.25 | 4 | 3.0 | 0.20 |
| 2.2 | Trapezoidal | 0.30 | 0.25 | 4 | 3.0 | 0.20 |
| 3.1 | Trapezoidal | 0.20 | 0.30 | 10 | 3.0 | 0.35 |
| 3.2 | Trapezoidal | 0.20 | 0.30 | 10 | 3.0 | 0.35 |
| 4 | Triangle | 0.20 | 0.30 | 1 | 0.2 | 0.50 |
| Case 1 | Case 2 | Case 3 | Case 4 | |
|---|---|---|---|---|
| Broken width and height (m) | 100 × 50 | 50 × 50 | 50 × 25 | 100 × 25 |
| Broken area (sq. m) | 2500 | 1250 | 625 | 1250 |
| Dam reservoir area (sq. m) | 1,880,000 | 1,880,000 | 1,880,000 | 1,880,000 |
| Water height behind the dam (m) | 68 | 68 | 68 | 68 |
| Mesh size (m) | 20 × 20 | 20 × 20 | 20 × 20 | 20 × 20 |
| Descriptions | Case 1 | Case 2 | Case 3 | Case 4 |
|---|---|---|---|---|
| Inundation area 10 min from the start of the calculation (m2) | 4.4 × 106 | 3.6 × 106 | 2.9 × 106 | 3.0 × 106 |
| Inundation area 20 min from the start of the calculation (m2) | 1.6 × 107 | 1.4 × 107 | 1.3 × 107 | 1.3 × 107 |
| Inundation area 30 min from the start of the calculation (m2) | 2.2 × 107 | 2.0 × 107 | 2.0 × 107 | 2.0 × 107 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ahmadi, S.M.; Yamamoto, Y. A New Dam-Break Outflow-Rate Concept and Its Installation to a Hydro-Morphodynamics Simulation Model Based on FDM (An Example on Amagase Dam of Japan). Water 2021, 13, 1759. https://doi.org/10.3390/w13131759
Ahmadi SM, Yamamoto Y. A New Dam-Break Outflow-Rate Concept and Its Installation to a Hydro-Morphodynamics Simulation Model Based on FDM (An Example on Amagase Dam of Japan). Water. 2021; 13(13):1759. https://doi.org/10.3390/w13131759
Chicago/Turabian StyleAhmadi, Sayed Masihullah, and Yoshimichi Yamamoto. 2021. "A New Dam-Break Outflow-Rate Concept and Its Installation to a Hydro-Morphodynamics Simulation Model Based on FDM (An Example on Amagase Dam of Japan)" Water 13, no. 13: 1759. https://doi.org/10.3390/w13131759
APA StyleAhmadi, S. M., & Yamamoto, Y. (2021). A New Dam-Break Outflow-Rate Concept and Its Installation to a Hydro-Morphodynamics Simulation Model Based on FDM (An Example on Amagase Dam of Japan). Water, 13(13), 1759. https://doi.org/10.3390/w13131759






