Interactions between Tandem Cylinders in an Open Channel: Impact on Mean and Turbulent Flow Characteristics
Abstract
:1. Introduction
2. Materials and Methods
2.1. Experimental Setup
2.2. ADV Measurements and Analysis
3. Results and Discussion
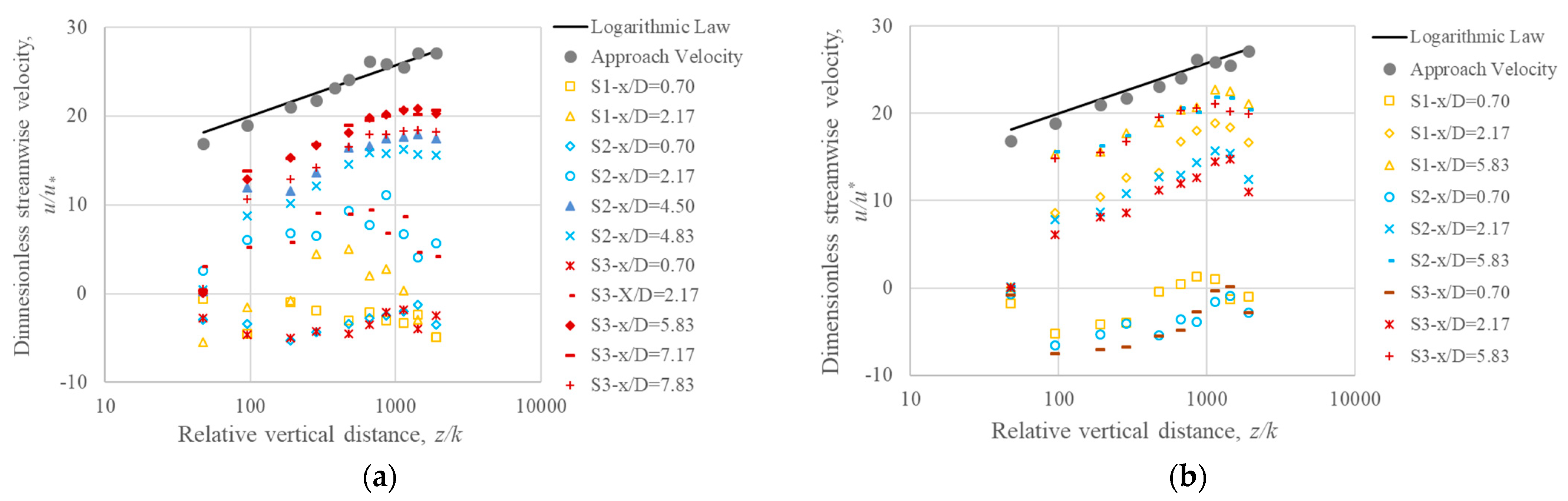
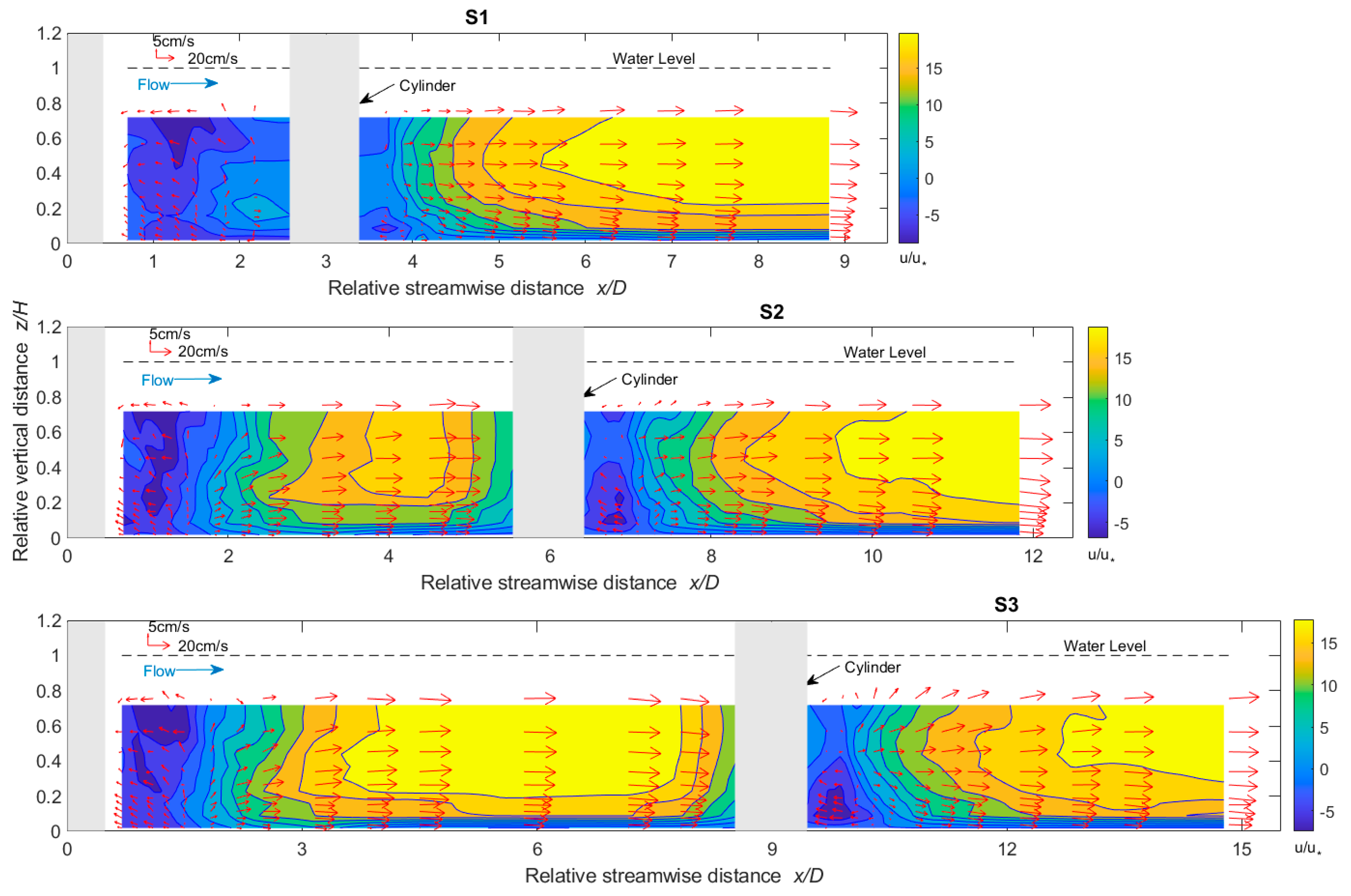
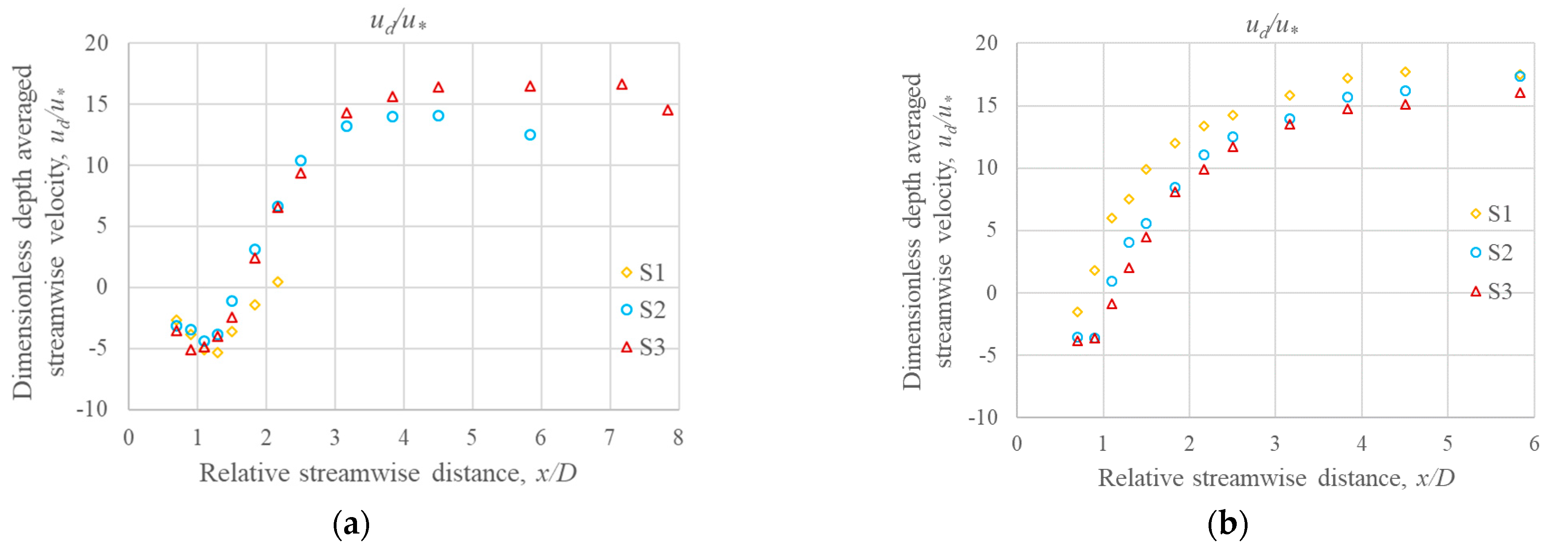
3.1. Mean Flow Characteristics
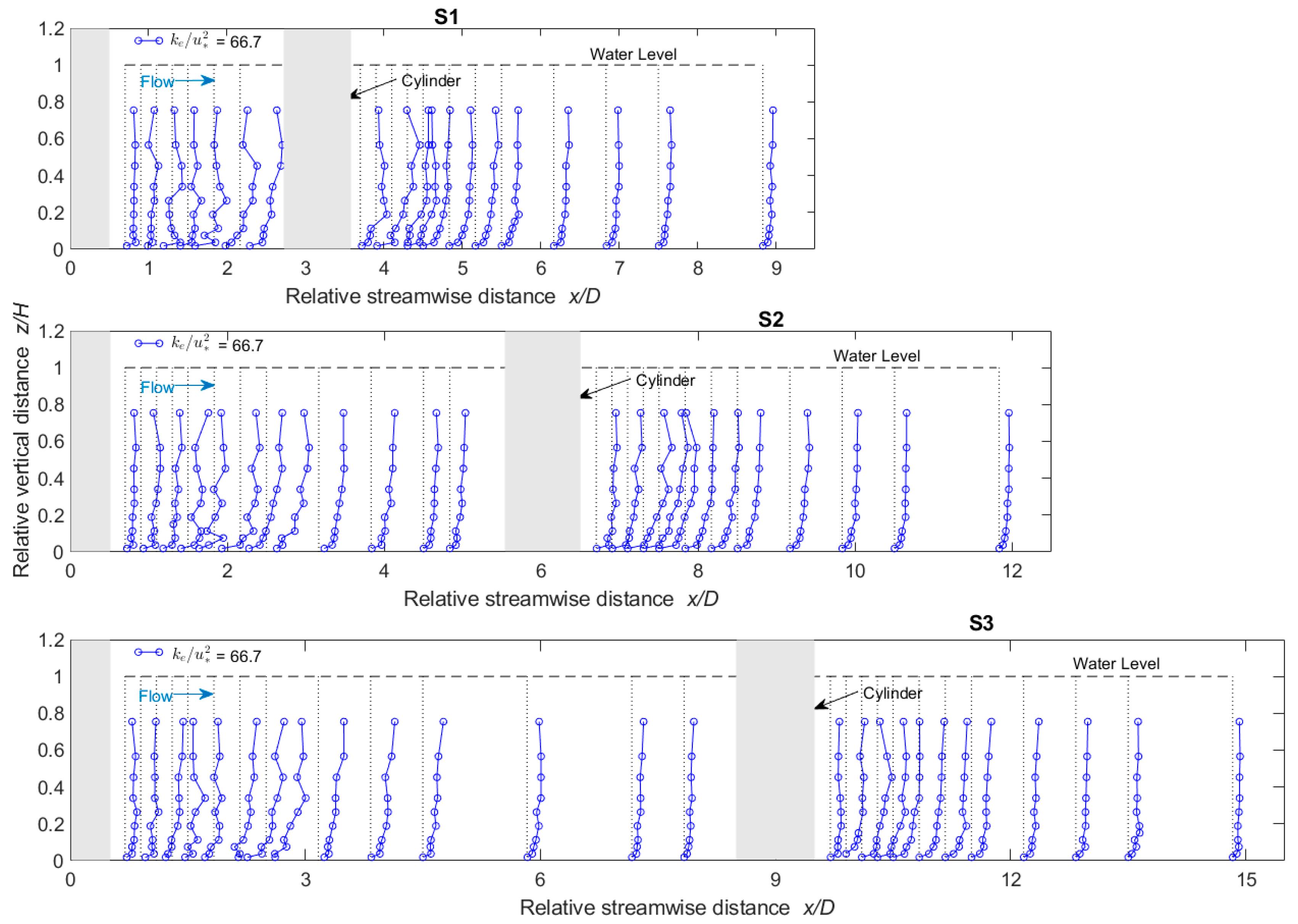
3.2. Turbulent Flow Characteristics
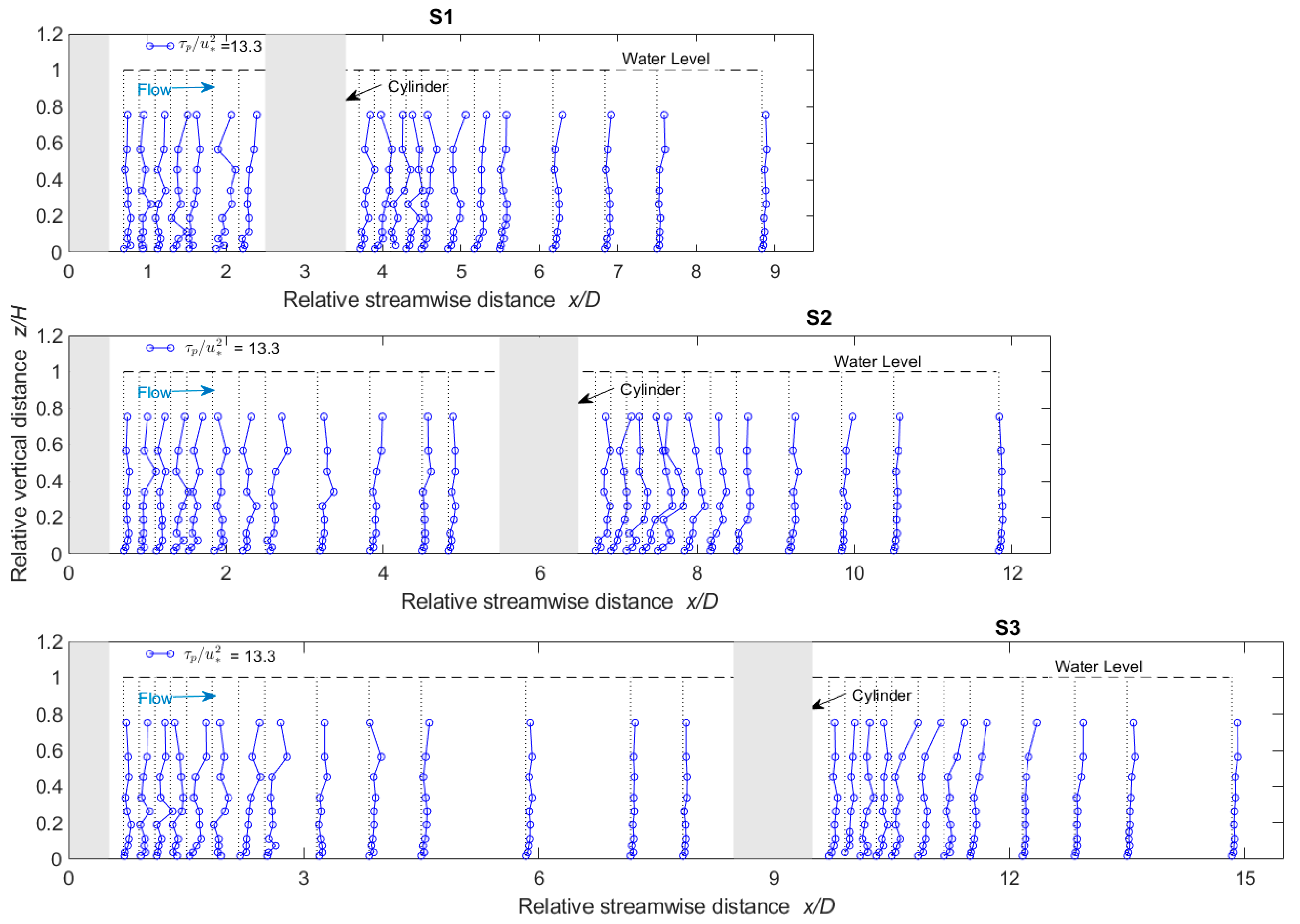
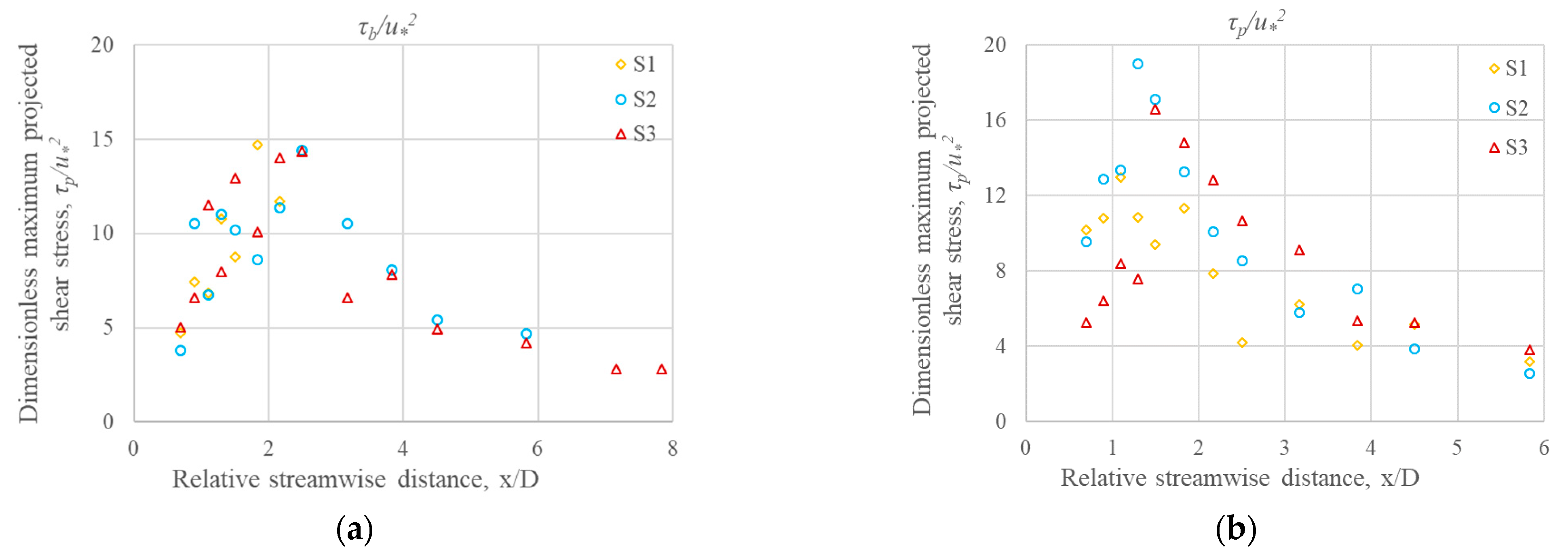
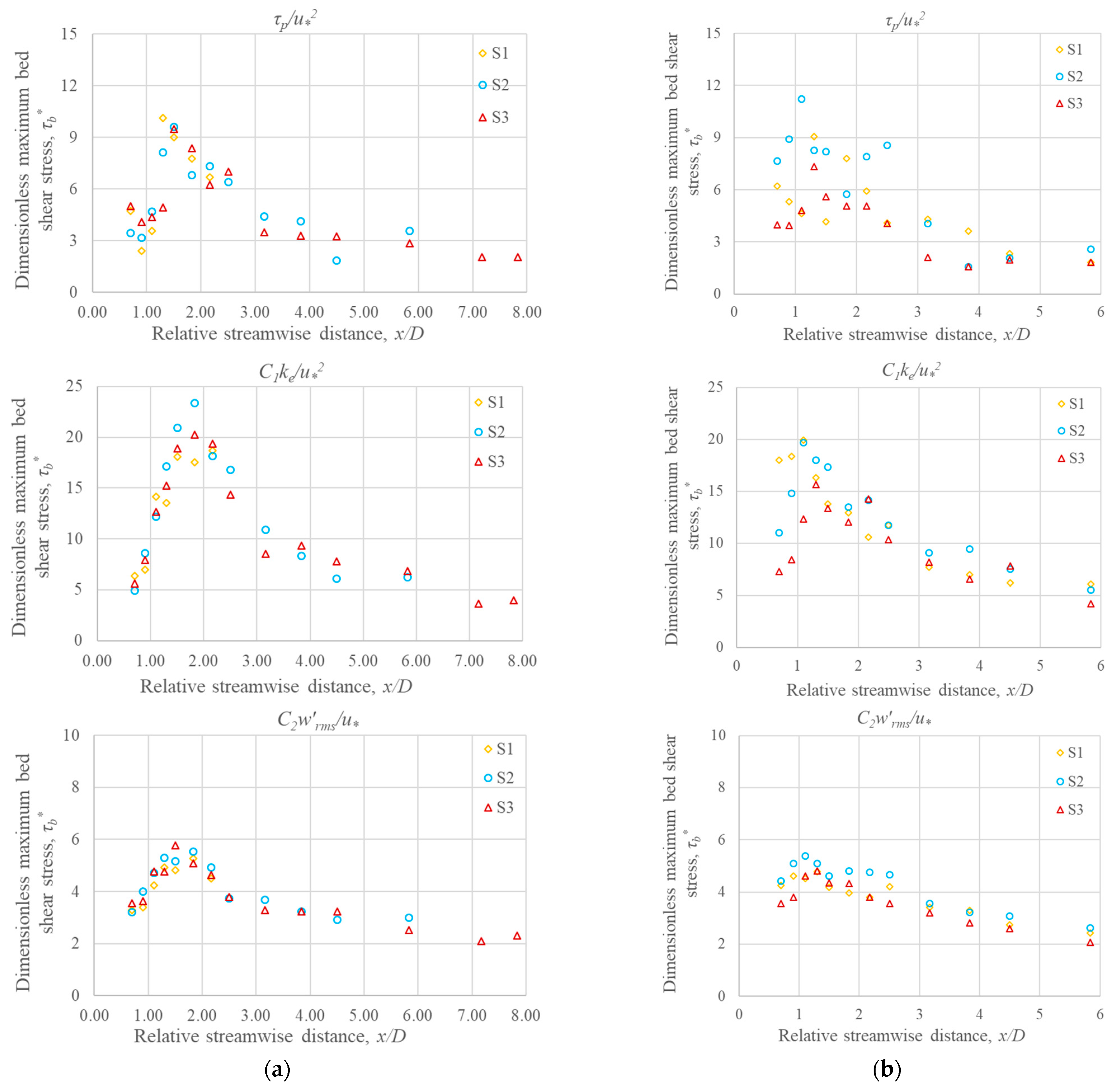
3.3. Near-Bed Shear Stress
4. Conclusions
- The analysis of vertical profiles of streamwise normalized velocity revealed that the rate of flow development downstream was faster than that midstream. The midstream profiles were influenced by the downstream cylinder in all scenarios.
- The flow recirculation zones midstream (x/D~1.50–1.80) were larger and stronger than those downstream (x/D~0.90–1.30). The longest recirculation zone in S1 midstream was affected by the downstream cylinder, and there was zero interruption from the downstream cylinder in S2 and S3.
- The length of the recirculation zone increased with the increase in c/c spacing of cylinders. The rate of flow development to achieve cross-sectional mean velocity became slower with increasing c/c spacing.
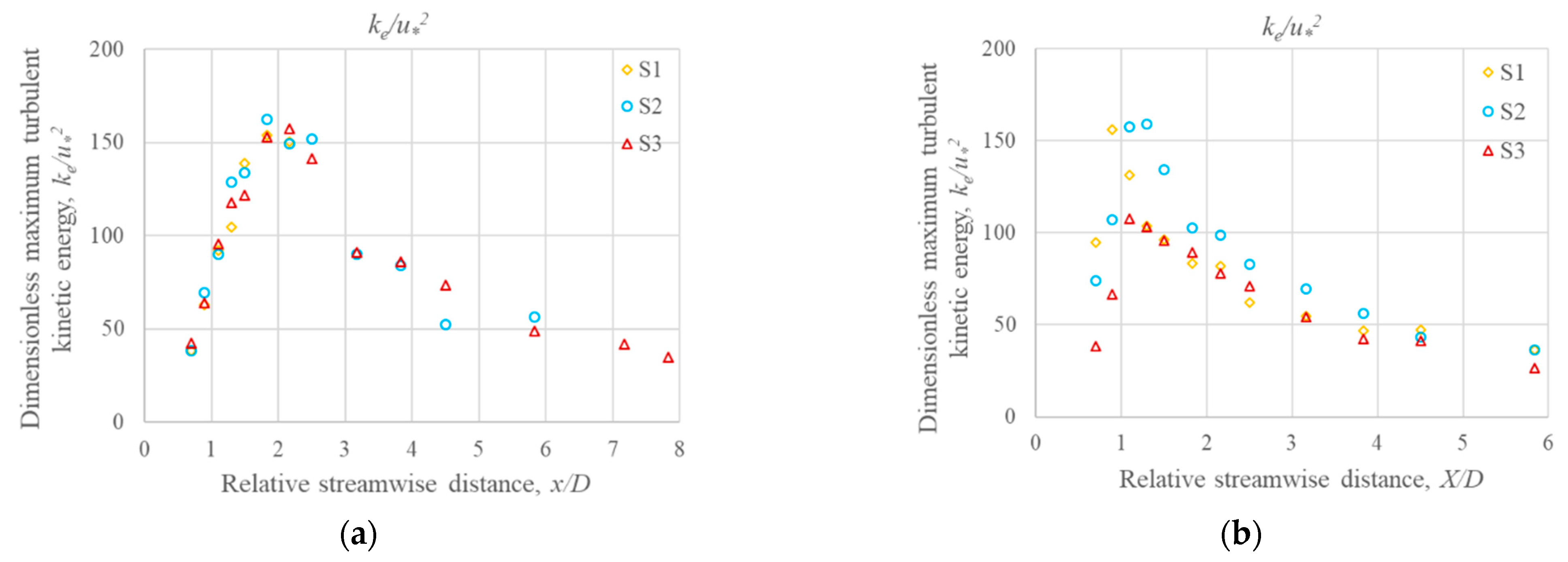
- The maximum turbulent kinetic energy for all three scenarios occurred approximately near the end of their respective recirculation zones. The midstream ke had a significant influence on the ke in downstream.
- The variation of resultant Reynolds shear stress was relatively chaotic as compared to the turbulent kinetic energy. The maximum shear stresses occurred within the recirculation zone for all scenarios.
- The peaks of dimensionless maximum near-bed shear stress () were higher (5–20%) and occurred over an extended length of about 0.5D in midstream as compared to the peaks of downstream, which occurred over a short length of 0.2D. The highest value of in the TKE method was about 50% and 70% higher than that in the Reynolds and modified TKE methods, respectively.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Zhou, Y.; Yiu, M.W. Flow structure, momentum and heat transport in a two-tandem-cylinder wake. J. Fluid Mech. 2006, 548, 17–48. [Google Scholar] [CrossRef] [Green Version]
- Heidari, M. Wake Characteristics of Single and Tandem Emergent Cylinders in Shallow Open Channel Flow. Ph.D. Thesis, University of Windsor, Windsor, ON, Canada, 2016. Available online: https://scholar.uwindsor.ca/etd/5733 (accessed on 24 January 2021).
- Nosier, M.A.; Elbaz, A.R.; Fetouh, T.A.; El-Gabry, L.A. Characteristics of turbulent wakes generated by twin parallel cylinders. J. Fluids Eng. 2012, 134, 121201. [Google Scholar] [CrossRef]
- AlQadi, I.; AlHazmy, M.; Al-Bahi, A.; Rodi, W. Large eddy simulation of flow past tandem cylinders in a channel. Flow Turbul. Combust. 2015, 95, 621–643. [Google Scholar] [CrossRef]
- Shamloo, H.; Rajaratnam, N.; Katopodis, C. Hydraulics of simple habitat structures. J. Hydraul. Res. 2001, 39, 351–366. [Google Scholar] [CrossRef]
- Sadeque, M.F.; Rajaratnam, N.; Loewen, M.R. Shallow turbulent wakes behind bed-mounted cylinders in open channels. J. Hydraul. Res. 2009, 47, 727–743. [Google Scholar] [CrossRef]
- Rostamy, N.; Sumner, D.; Bergstrom, D.J.; Bugg, J.D. Local flow field of a surface-mounted finite circular cylinder. J. Fluids Struct. 2012, 34, 105–122. [Google Scholar] [CrossRef]
- Zdravkovich, M.M. The effects of the interference between circular cylinders in cross flow. J. Fluids Struct. 1987, 1, 239–261. [Google Scholar] [CrossRef]
- Sharman, B.; Lien, F.S.; Davidson, L.; Norberg, C. Numerical predictions of low Reynolds number flows over two tandem circular cylinders. Int. J. Numer. Meth. Fluids 2005, 47, 423–447. [Google Scholar] [CrossRef]
- Papaioannou, G.V.; Yue, D.K.P.; Triantafyllou, M.S.; Karniadakis, G.E. Three-dimensionality effects in flow around two tandem cylinders. J. Fluid Mech. 2006, 558, 387–413. [Google Scholar] [CrossRef] [Green Version]
- Lin, J.C.; Yang, Y.; Rockwell, D. Flow past two cylinders in tandem: Instantaneous and averaged flow structure. J. Fluids Struct. 2002, 16, 1059–1071. [Google Scholar] [CrossRef]
- Pinarbasi, A.; Pinar, E.; Akilli, H.; Ince, E. Shallow water experiments of flow past two identical square cylinders in tandem. Eur. J. Mech. B/Fluids 2015, 49, 100–107. [Google Scholar] [CrossRef]
- Akilli, H.; Rockwell, D. Vortex formation from a cylinder in shallow water. Phys. Fluids 2002, 14, 2957–2967. [Google Scholar] [CrossRef]
- Gao, Y.; Yu, D.; Tan, S.; Wang, X.; Hao, Z. Experimental study on the near wake behind two side-by-side cylinders of unequal diameters. Fluid Dyn. Res. 2010, 42, 055509. [Google Scholar] [CrossRef]
- Kirkil, G.; Constantinescu, G. A numerical study of the laminar necklace vortex system and its effect on the wake for a circular cylinder. Phys. Fluids 2012, 24, 073602. [Google Scholar] [CrossRef]
- Kirkil, G.; Constantinescu, G. Effects of cylinder Reynolds number on the turbulent horseshoe vortex system and near wake of a surface-mounted circular cylinder. Phys. Fluids 2015, 27, 075102. [Google Scholar] [CrossRef] [Green Version]
- Nezu, I.; Nakagawa, H. Turbulence in Open-Channel Flows; Balkema: Rotterdam, The Netherlands, 1993. [Google Scholar]
- Baki, A.B.M.; Zhang, W.; Zhu, D.Z.; Rajaratnam, N. Flow structures in the vicinity of a submerged boulder within a boulder array. J. Hydraul. Eng. 2016, 143, 04016104. [Google Scholar] [CrossRef]
- Biron, P.M.; Robson, C.; Lapointe, M.F.; Gaskin, S.J. Comparing different methods of bed shear stress estimates in simple and complex flow fields. Earth Surf. Process. Landf. J. Br. Geomorphol. Res. Group 2004, 29, 1403–1415. [Google Scholar] [CrossRef]
- Strom, K.B.; Papanicolaou, A.N. ADV measurements around a cluster microform in a shallow mountain stream. J. Hydraul. Eng. 2007, 12, 1379–1389. [Google Scholar] [CrossRef]
- Wahl, T.L. WinADV Version 2.028: A Windows-Based Viewing and Post-Processing Utility for ADV Files; User’s Manuals and On-Line Help Provided with the Software. 2002. Available online: http://www.usbr.gov/wrrl/twahl/winadv/ (accessed on 24 January 2021).
- Goring, D.G.; Nikora, V.I. Despiking acoustic Doppler velocimeter data. J. Hydraul. Eng. 2002, 128, 117–126. [Google Scholar] [CrossRef] [Green Version]
- Kim, S.C.; Friedrichs, C.T.; Maa, J.Y.; Wright, L.D. Estimating bottom stress in tidal boundary layer from acoustic Doppler velocimeter data. J. Hydraul. Eng. 2000, 126, 399–406. [Google Scholar] [CrossRef] [Green Version]
- Papanicolaou, A.N.; Kramer, C.M.; Tsakiris, A.G.; Stoesser, T.; Bomminayuni, S.; Chen, Z. Effects of a fully submerged boulder within a boulder array on the mean and turbulent flow fields: Implications to bedload transport. Acta Geophys. 2012, 60, 1502–1546. [Google Scholar] [CrossRef]
- Zexing, X.; Chenling, Z.; Qiang, Y.; Xiekang, W.; Xufeng, Y. Hydrodynamics and bed morphological characteristics around a boulder in a gravel stream. Water Supply 2020, 20, 397–407. [Google Scholar] [CrossRef]
- Dey, S.; Sarkar, S.; Bose, S.K.; Tait, S.; Castro-Orgaz, O. Wall-wake flows downstream of a sphere placed on a plane rough wall. J. Hydraul. Eng. 2011, 137, 1173–1189. [Google Scholar] [CrossRef]
- Baki, A.B.M.; Zhu, D.Z.; Rajaratnam, N. Turbulence characteristics in a rock-ramp-type fish pass. J. Hydraul. Eng. 2015, 141, 04014075. [Google Scholar] [CrossRef]
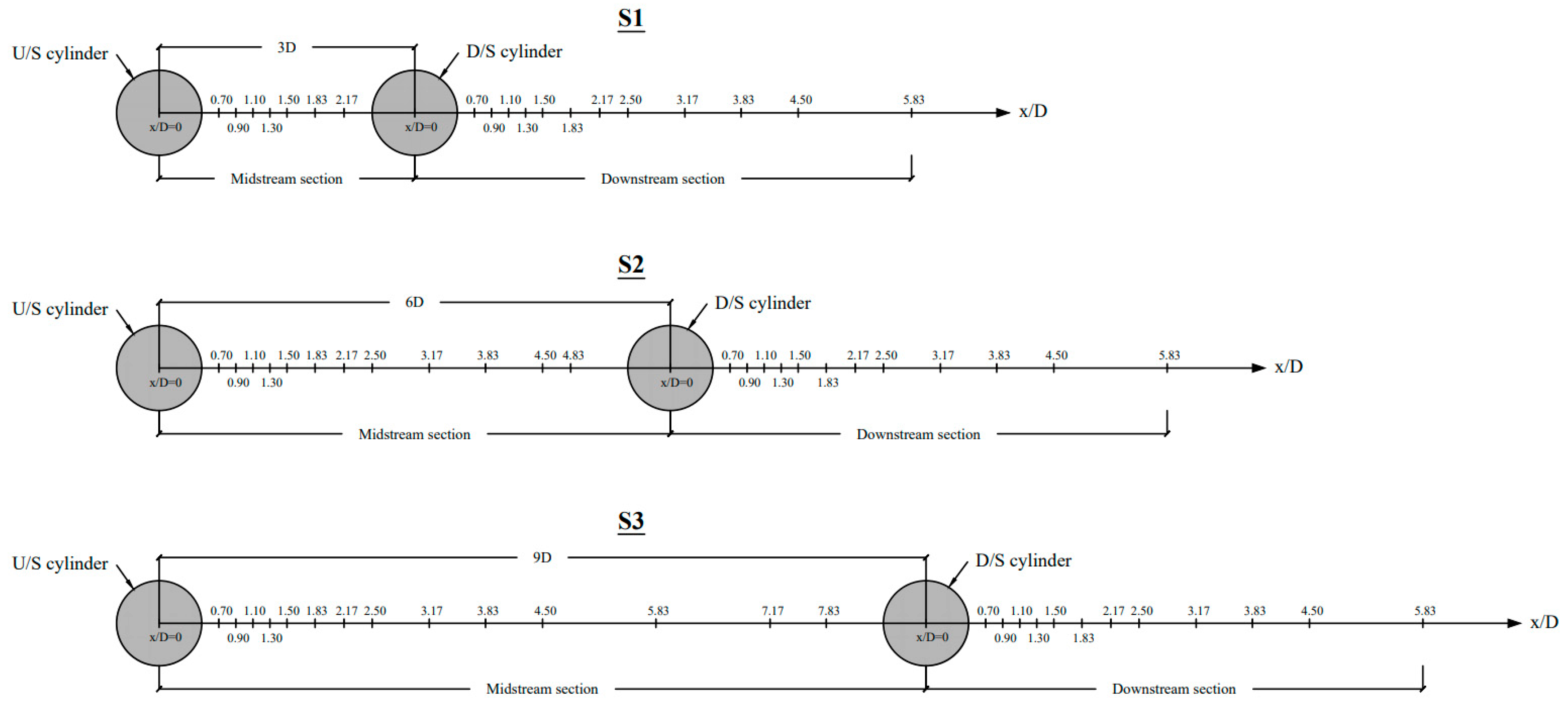
| Experimental Scenarios | Cylinder Diameter (D) | Cylinder Spacing * | Flow Rate | Approach Water Depth (H) | Approach Flow Velocity θ | Reynolds Number Ϯ (Rd) | Shear Velocity ± (u *) | Average | Average | Data Retained |
|---|---|---|---|---|---|---|---|---|---|---|
| COR | SNR | |||||||||
| - | (cm) | (times) | (m3/s) | (cm) | (cm/s) | - | (cm/s) | (%) | (dB) | (%) |
| S1 | 15 | 3D | 0.069 | 26.5 | 35.3 | 52,900 | 1.4 | 80.6 | 16.7 | 90.1 |
| S2 | 15 | 6D | 0.069 | 26.5 | 35.3 | 52,900 | 1.4 | 80.6 | 16.9 | 90.4 |
| S3 | 15 | 9D | 0.069 | 26.5 | 35.3 | 52,900 | 1.4 | 78.3 | 15.6 | 91.2 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zobeyer, H.; Baki, A.B.M.; Nowrin, S.N. Interactions between Tandem Cylinders in an Open Channel: Impact on Mean and Turbulent Flow Characteristics. Water 2021, 13, 1718. https://doi.org/10.3390/w13131718
Zobeyer H, Baki ABM, Nowrin SN. Interactions between Tandem Cylinders in an Open Channel: Impact on Mean and Turbulent Flow Characteristics. Water. 2021; 13(13):1718. https://doi.org/10.3390/w13131718
Chicago/Turabian StyleZobeyer, Hasan, Abul B. M. Baki, and Saika Nowshin Nowrin. 2021. "Interactions between Tandem Cylinders in an Open Channel: Impact on Mean and Turbulent Flow Characteristics" Water 13, no. 13: 1718. https://doi.org/10.3390/w13131718
APA StyleZobeyer, H., Baki, A. B. M., & Nowrin, S. N. (2021). Interactions between Tandem Cylinders in an Open Channel: Impact on Mean and Turbulent Flow Characteristics. Water, 13(13), 1718. https://doi.org/10.3390/w13131718






