Discharge Calculation of Side Weirs with Several Weir Fields Considering the Undisturbed Normal Flow Depth in the Channel
Abstract
:1. Introduction
1.1. Discharge Behaviour at Side Weirs in the Context of Flood Risk Management
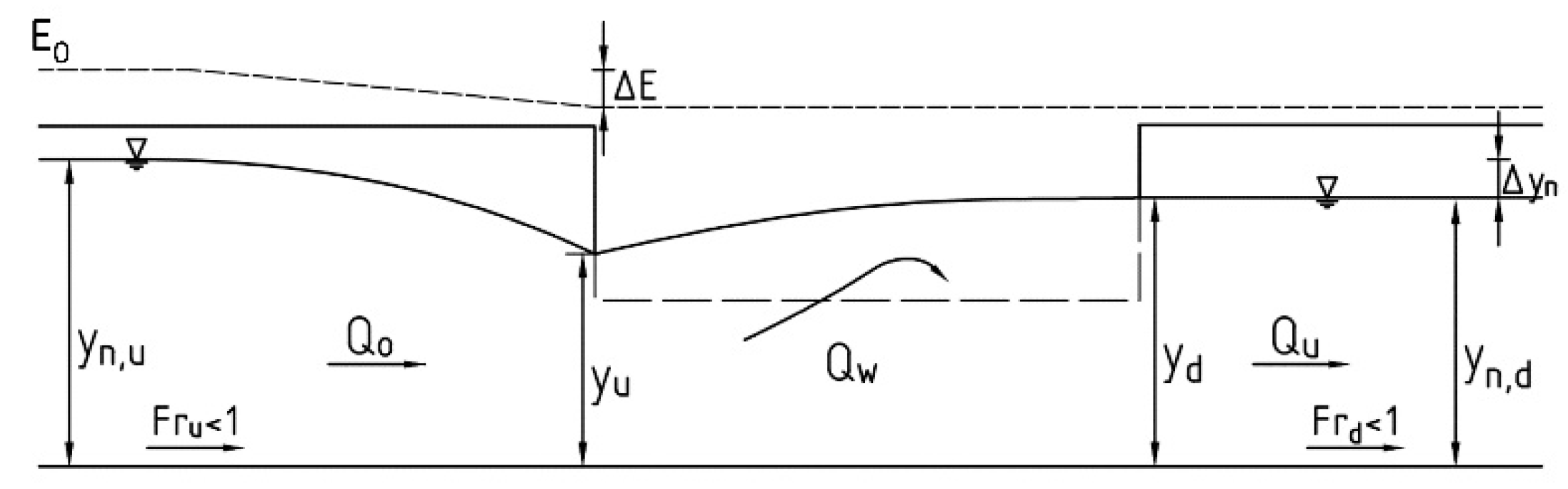
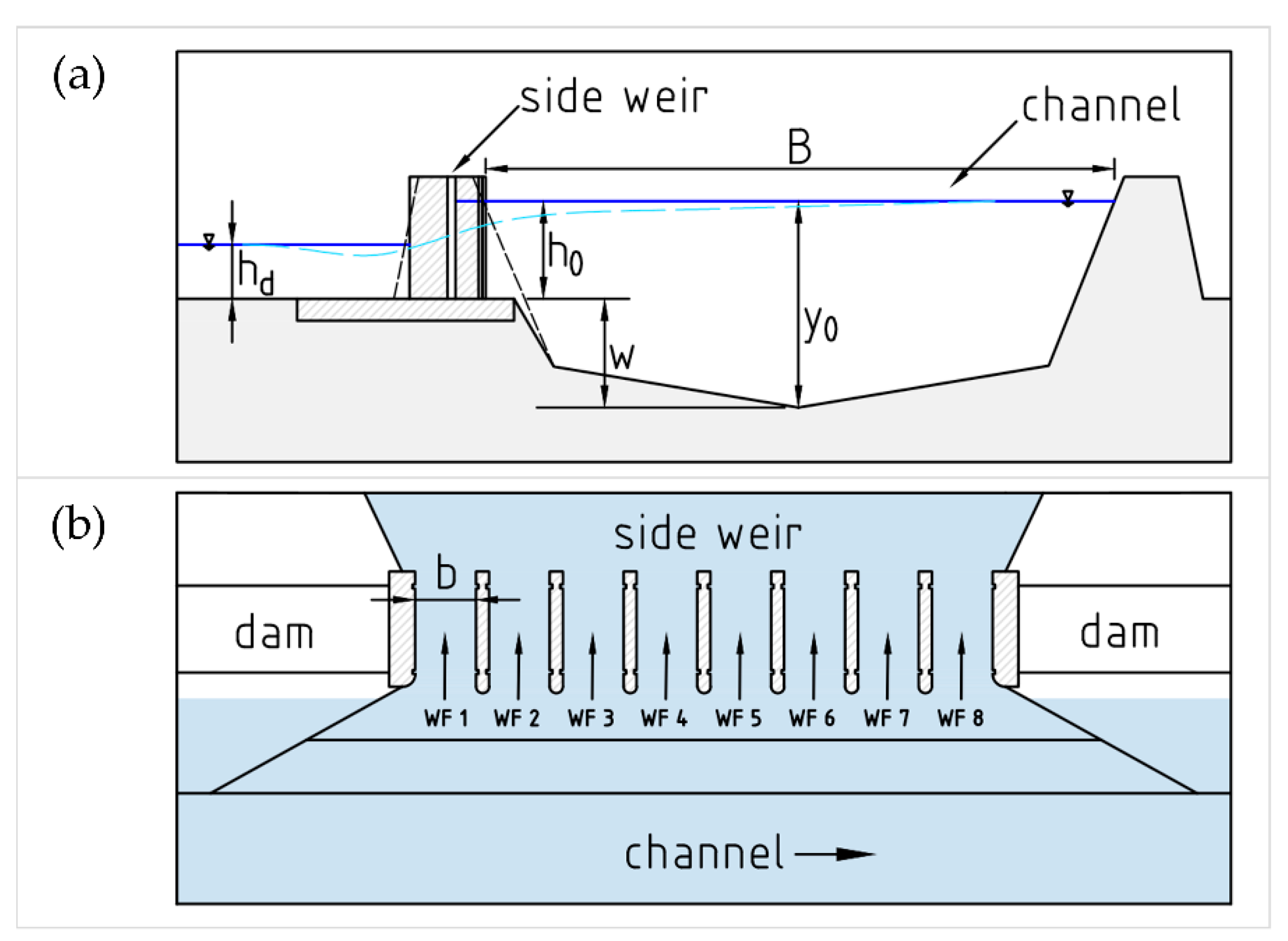
1.2. Theoretical Background
2. Materials and Methods
2.1. Discharge Coefficient
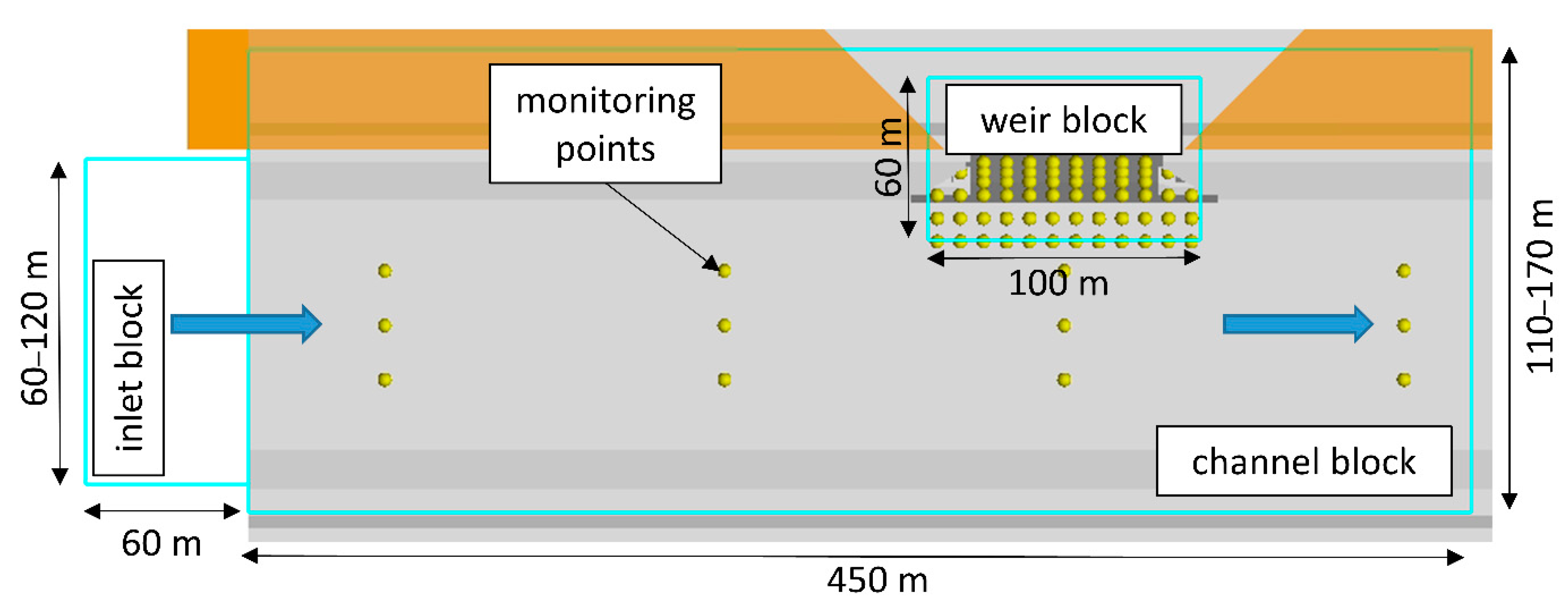
2.2. Numerical Model
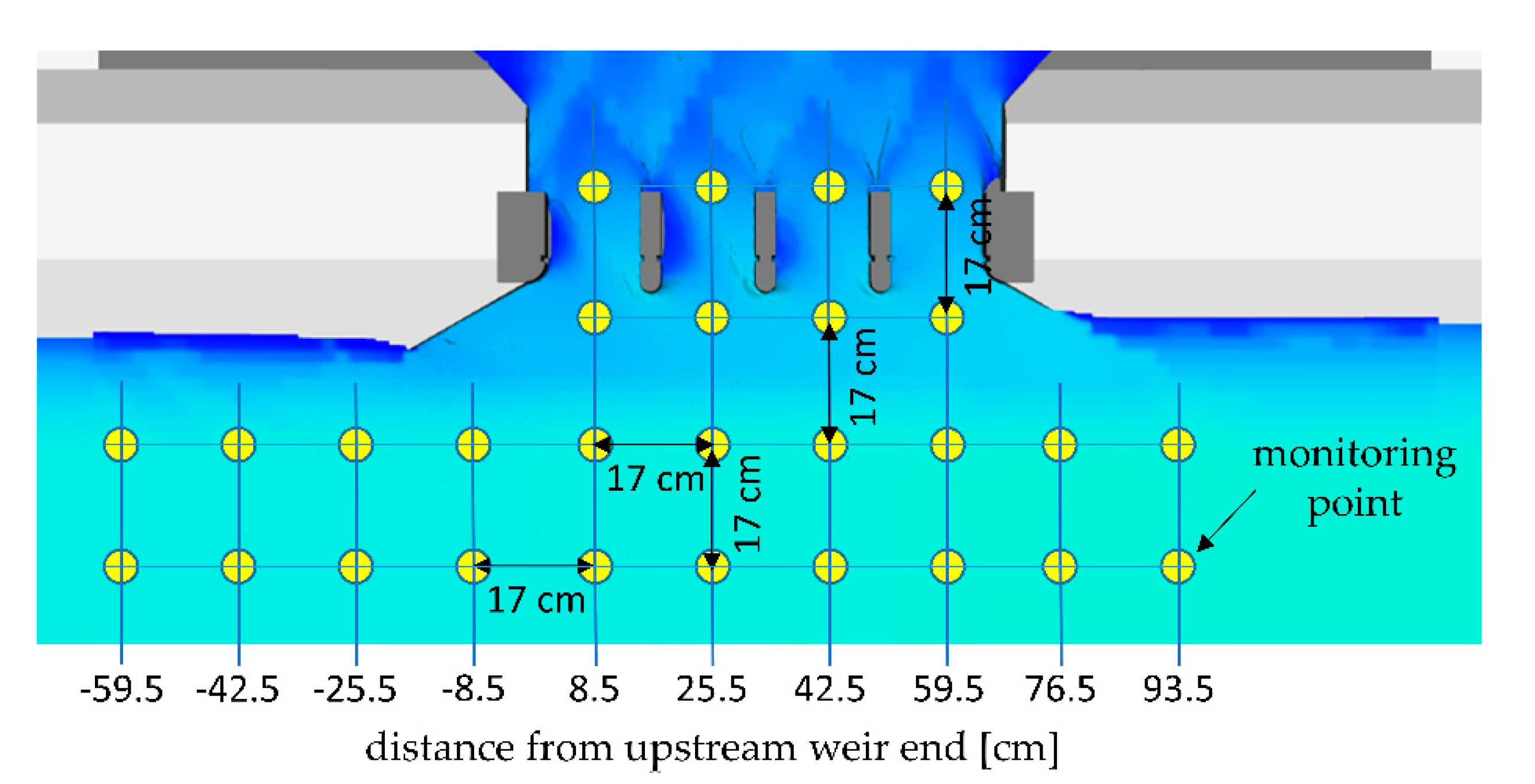
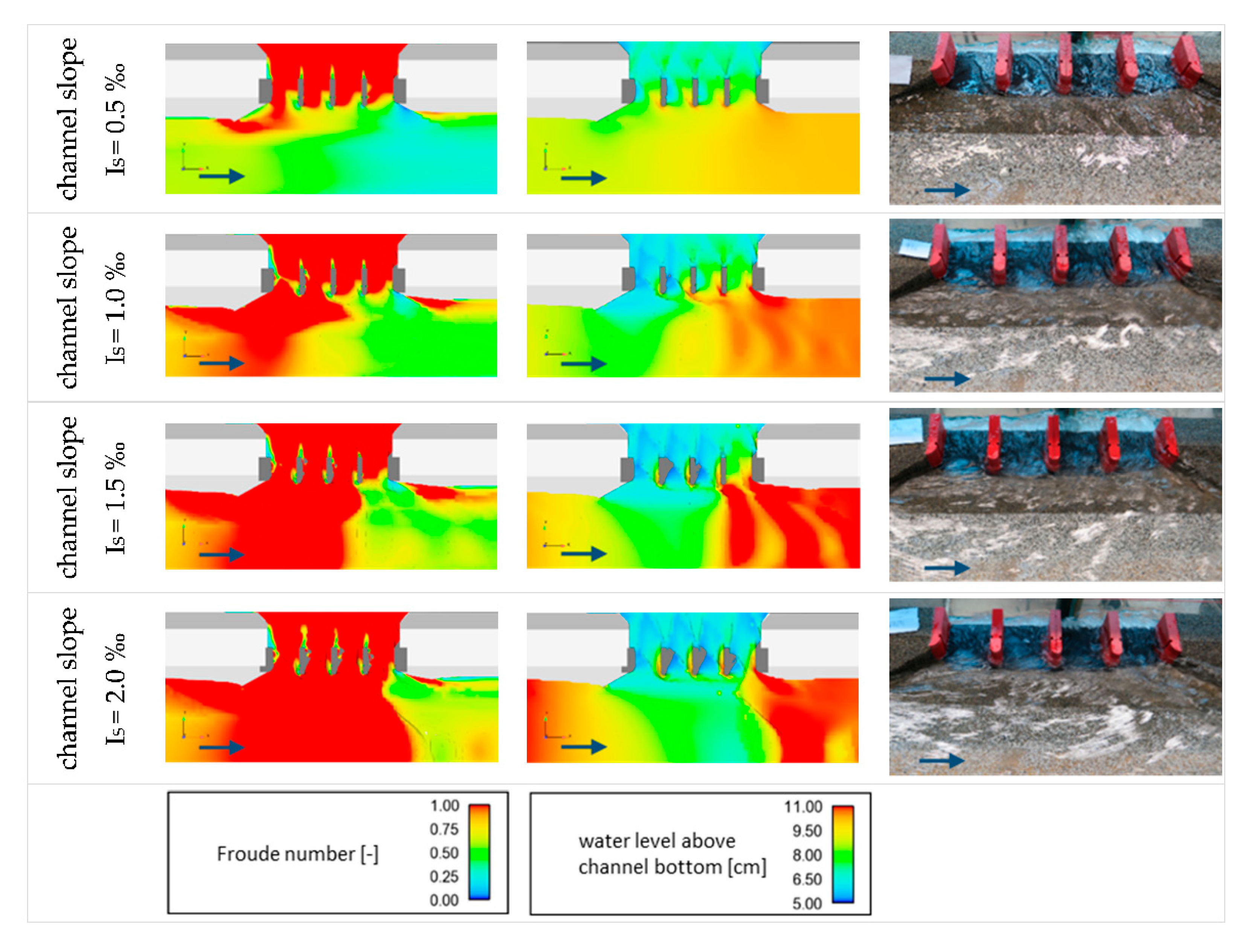
2.3. Validation of the Numerical Simulation Results with a Physical Scale Model
3. Results
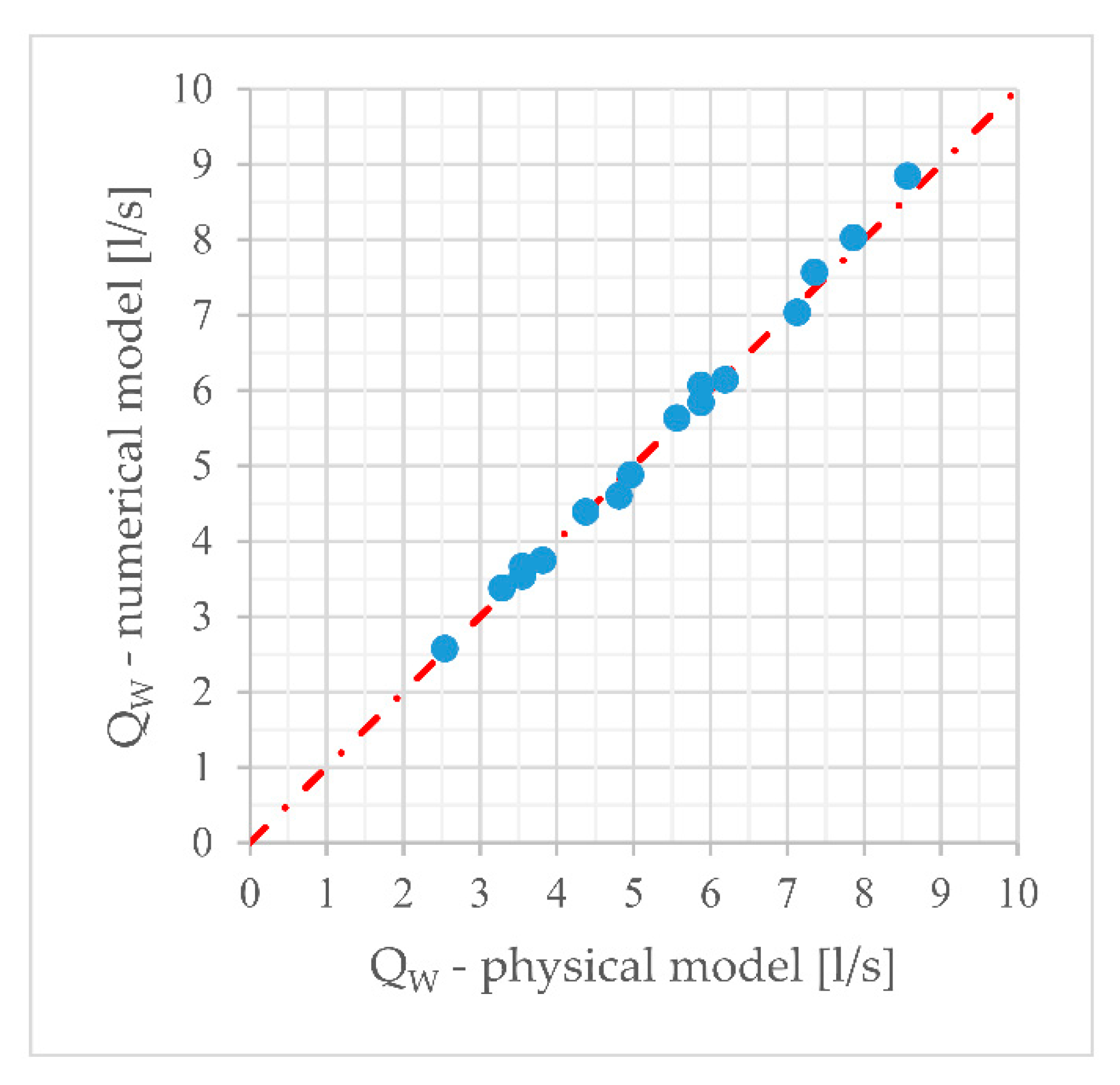
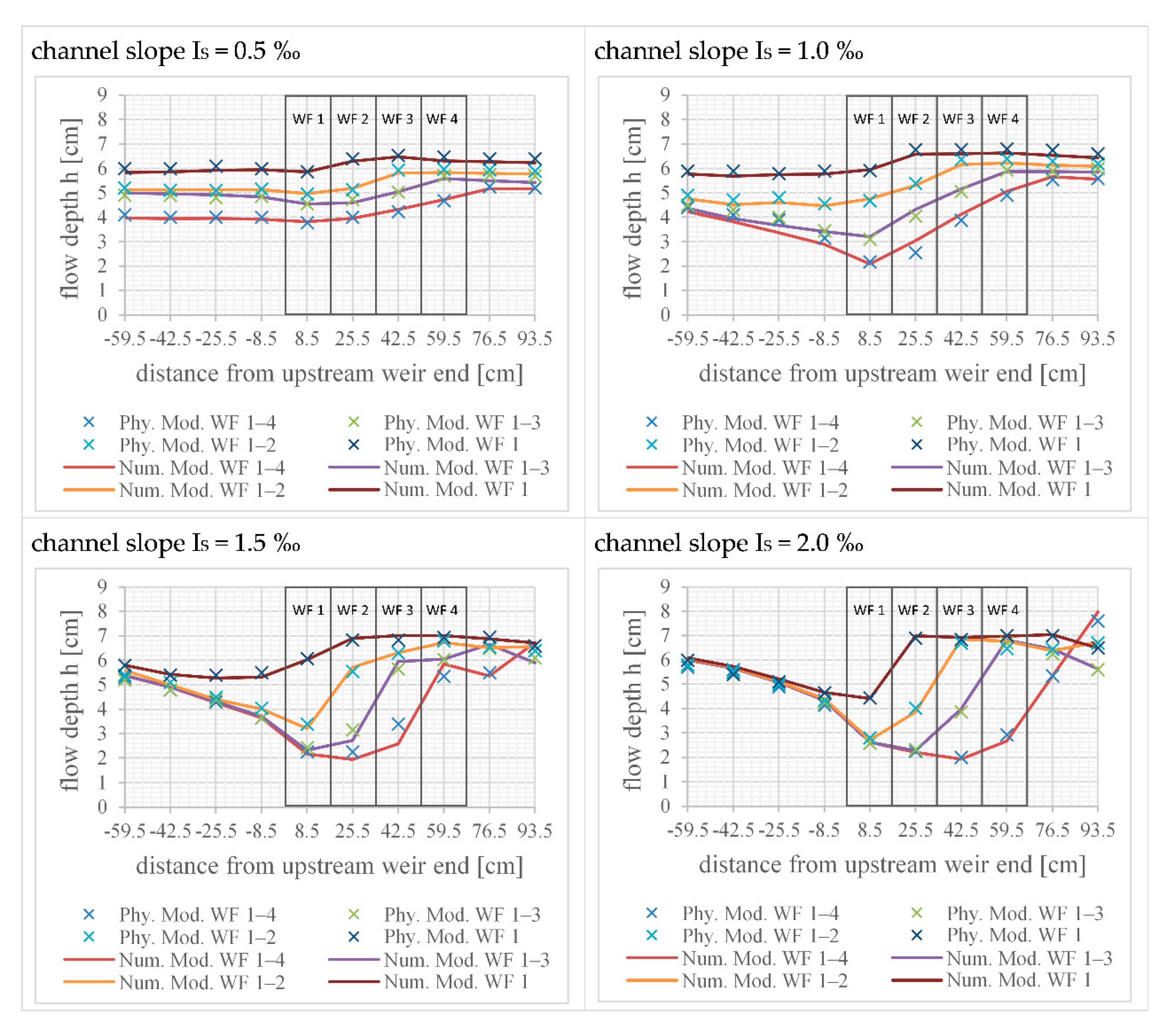
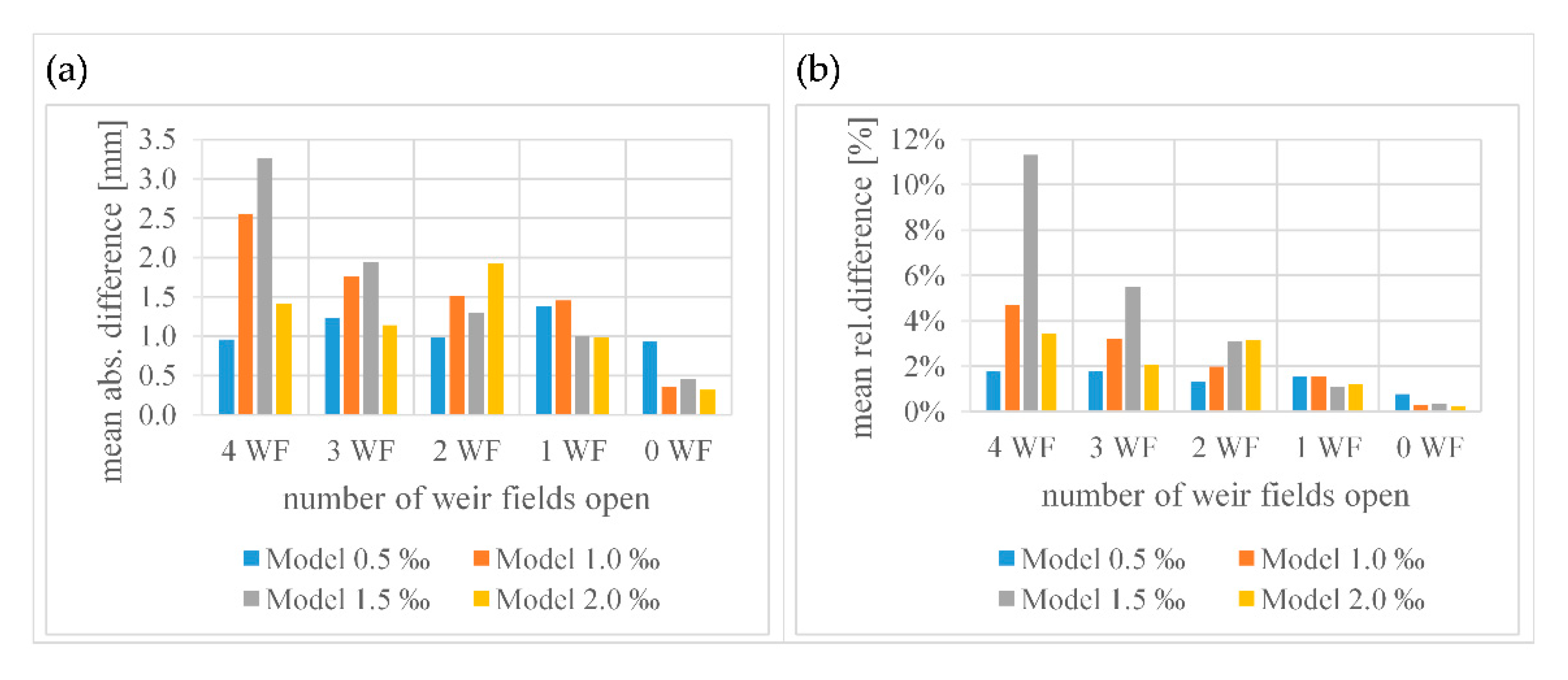
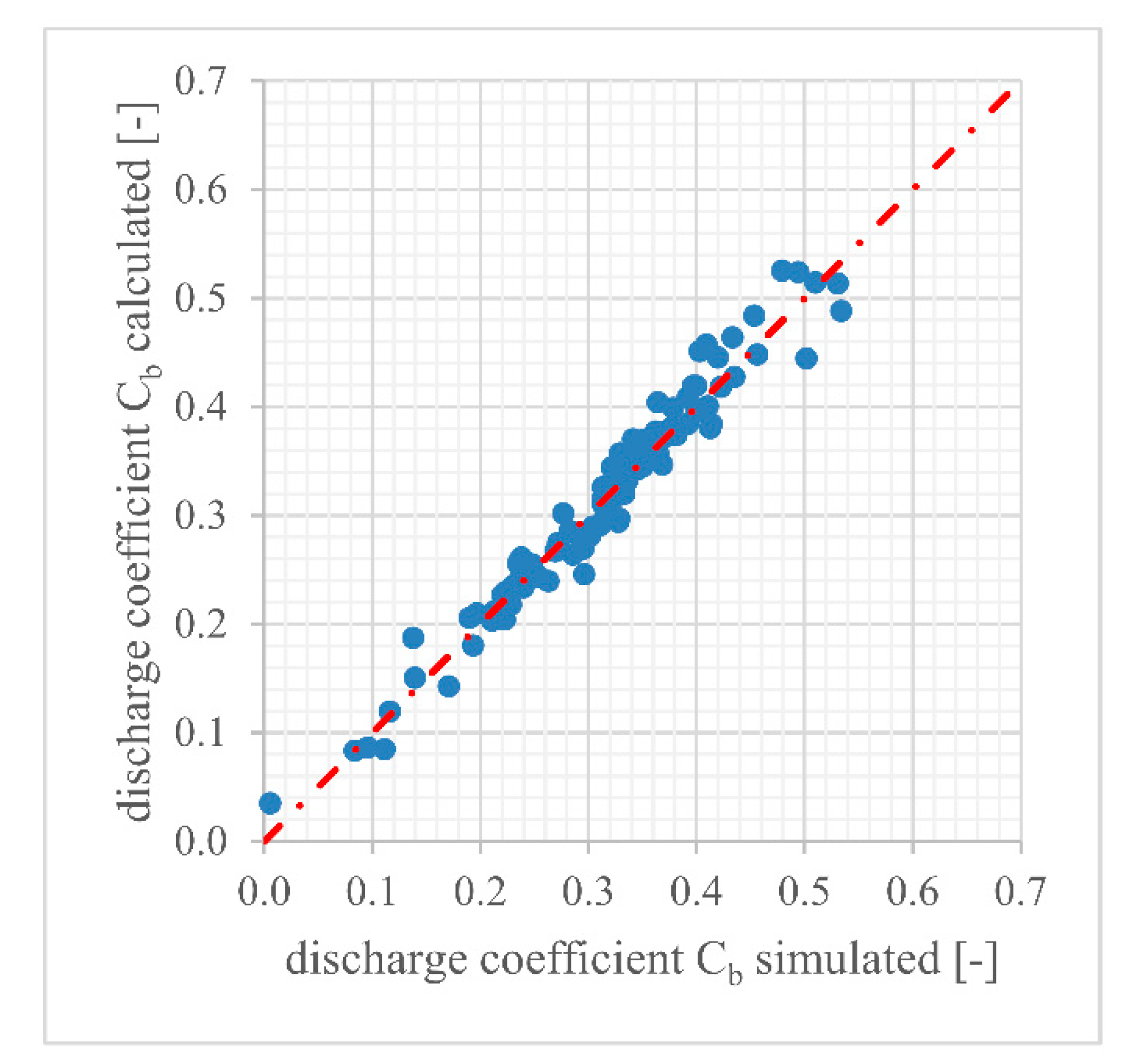
3.1. Comparison of the Numerical and Physical Model Results
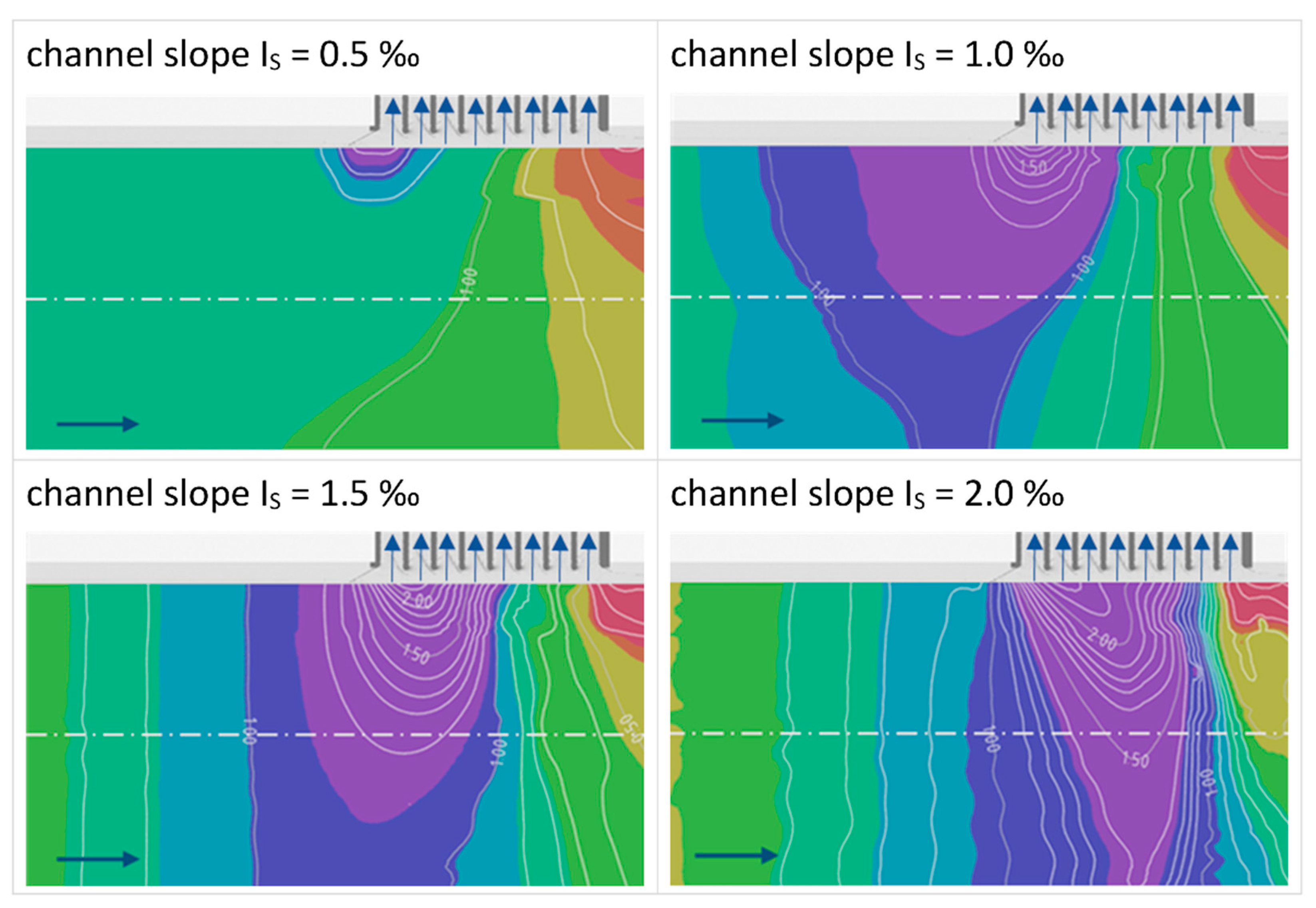
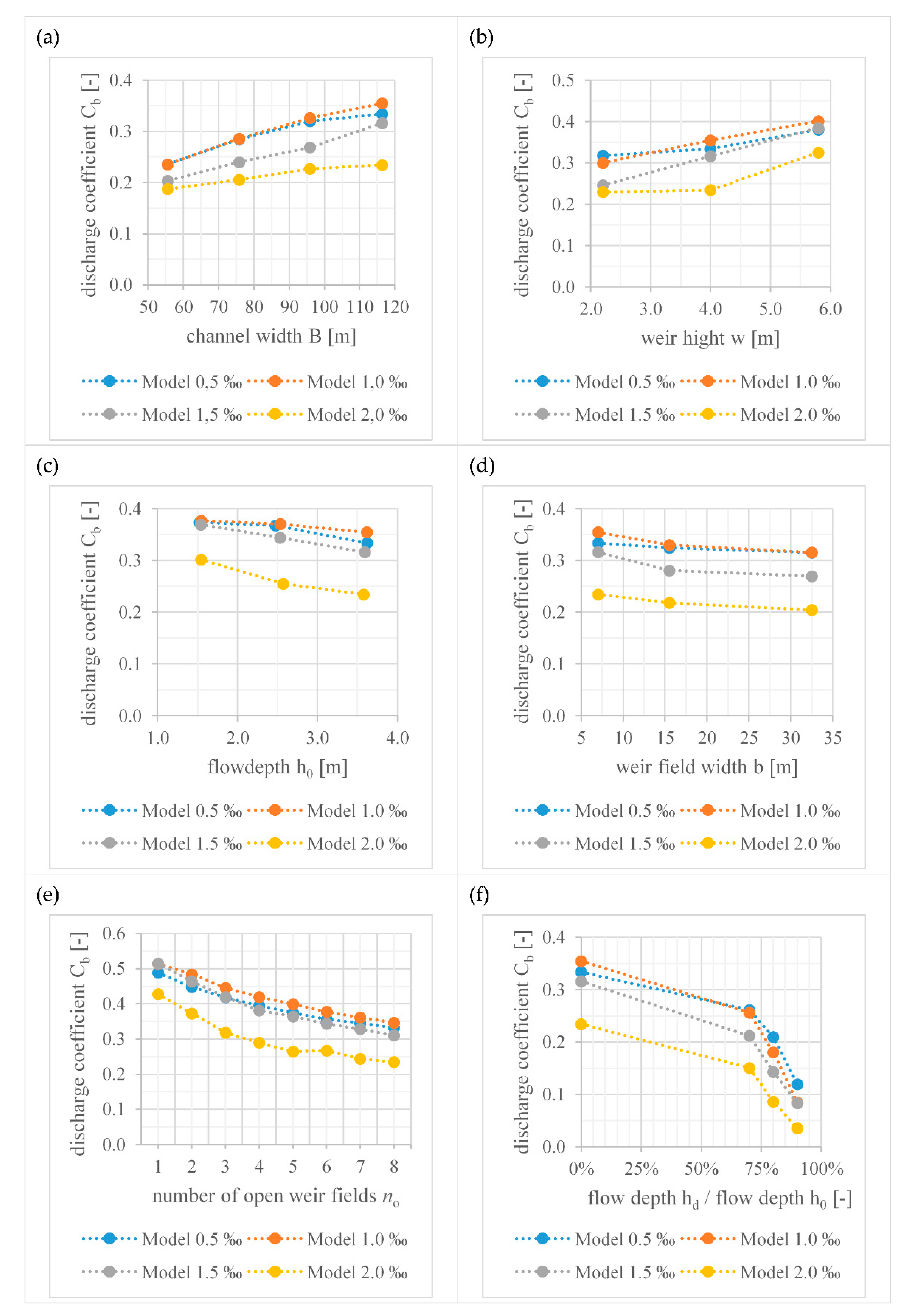
3.2. Influence of Single Parameters on the Discharge Coefficient
3.3. Regression Analysis
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- May, R.W.P.; Bromwich, B.C.; Gasowski, Y.; Rickard, C.E. Hydraulic Design of Side Weirs, 1st ed.; Thomas Telford: London, UK, 2003; ISBN 978-0-7277-3167-8. [Google Scholar]
- De Marchi, G. Saggio di teoria sul funzionamento deglistramazzi laterali. L’Energia Elettr. 1934, 11, 849–854. [Google Scholar]
- Borghei, S.M.; Jalili, M.R.; Ghodsian, M. Discharge Coefficient for Sharp-Crested Side Weir in Subcritical Flow. J. Hydraul. Eng. 1999, 125, 1051–1056. [Google Scholar] [CrossRef]
- Cheong, H. Discharge Coefficient of Lateral Diversion from Trapezoidal Channel. J. Irrig. Drain. Eng. 1991, 117, 461–475. [Google Scholar] [CrossRef]
- Hager, W.H. Lateral Outflow Over Side Weirs. J. Hydraul. Eng. 1987, 113, 491–504. [Google Scholar] [CrossRef] [Green Version]
- Ranga Raju, K.G.; Gupta, S.K.; Prasad, B. Side Weir in Rectangular Channel. J. Hydraul. Div. 1979, 105, 547–554. [Google Scholar] [CrossRef]
- Singh, R.; Manivannan, D.; Satyanarayana, T. Discharge Coefficient of Rectangular Side Weirs. J. Irrig. Drain. Eng. 1994, 120, 814–819. [Google Scholar] [CrossRef]
- Subramanya, K.; Awasthy, S.C. Spatially Varied Flow over Side-Weirs. J. Hydraul. Div. 1972, 98, 1–10. [Google Scholar] [CrossRef]
- Di Bacco, M.; Scorzini, A.R. Are We Correctly Using Discharge Coefficients for Side Weirs? Insights from a Numerical Investigation. Water 2019, 11, 2585. [Google Scholar] [CrossRef] [Green Version]
- El-Khashab, A.; Smith, K.V. Experimental Investigation of Flow over Side Weirs. J. Hydraul. Div. 1976, 102, 1255–1268. [Google Scholar] [CrossRef]
- Emiroglu, M.E.; Ikinciogullari, E. Determination of Discharge Capacity of Rectangular Side Weirs Using Schmidt Approach. Flow Meas. Instrum. 2016, 50, 158–168. [Google Scholar] [CrossRef]
- Namaee, M.R.; Jalaledini, M.S.; Habibi, M.; Yazdi, S.R.S.; Azar, M.G. Discharge Coefficient of a Broad Crested Side Weir in an Earthen Channel. Water Sci. Technol. Water Supply 2013, 13, 166–177. [Google Scholar] [CrossRef]
- Říha, J.; Zachoval, Z. Flow characteristics at trapezoidal broad-crested side weir. J. Hydrol. Hydromech. 2015, 63, 164–171. [Google Scholar] [CrossRef] [Green Version]
- Uyumaz, A.; Muslu, Y. Flow Over Side Weirs in Circular Channels. J. Hydraul. Eng. 1985, 111, 144–160. [Google Scholar] [CrossRef]
- Castro-Orgaz, O.; Hager, W. Subcritical Side-Weir Flow at High Lateral Discharge. J. Hydraul. Eng. 2012, 138, 777–787. [Google Scholar] [CrossRef] [Green Version]
- Crispino, G.; Cozzolino, L.; Della Morte, R.; Gisonni, C. Supercritical Low-Crested Bilateral Weirs: Hydraulics and Design Procedure. J. Appl. Water Eng. Res. 2015, 3, 35–42. [Google Scholar] [CrossRef]
- Chow, V.T. Open-Channel Hydraulics; McGraw-Hill: New York, NY, USA, 1959. [Google Scholar]
- Poleni, G. De Motu Aquae Mixto Libri Duo; Kessinger Publishing: Padova, Italy, 1717. [Google Scholar]
- Schmidt, M. Gerinnehydraulik; Bauverlag GmbH: Wiesbaden, Germany, 1957. [Google Scholar]
- Dominguez, F.J. Hidraulica; Editorial Universitaria: Santiago, Chile, 1999. [Google Scholar]
- Shariq, A.; Hussain, A.; Ansari, M.A. Lateral Flow through the Sharp Crested Side Rectangular Weirs in Open Channels. Flow Meas. Instrum. 2018, 59, 8–17. [Google Scholar] [CrossRef]
- Martin, H.; Pohl, R. Technische Hydromechanik 4—Hydraulische und numerische Modelle, 3rd ed.; Beuth Verlag GmbH: Berlin, Germany, 2015. [Google Scholar]
- SPSS IBM. SPSS Statistics for Windows; Version 24.0; IBM Corp.: Armonk, NY, USA, 2016. [Google Scholar]
- Flow Science, Inc. FLOW-3D® Solver; Version 11.2; Flow Science, Inc.: Santa Fe, NM, USA, 2017. [Google Scholar]
- Hirt, C.W.; Nichols, B.D. Volume of Fluid (VOF) Method for the Dynamics of Free Boundaries. J. Comput. Phys. 1981, 39, 201–225. [Google Scholar] [CrossRef]
- Launder, B.E.; Spalding, D.B. The Numerical Computation of Turbulent Flows. Comput. Methods Appl. Mech. Eng. 1974, 3, 269–289. [Google Scholar] [CrossRef]
- Aigner, D.; Bollrich, G. Handbuch der Hydraulik für Wasserbau und Wasserwirtschaft, 1st ed.; Beuth Verlag GmbH Berlin: Zurich, Vienna, 2015. [Google Scholar]

| Parameters | Dimension |
|---|---|
| Channel roughness kSt | 40 (m1/3/s) |
| Channel slope Is | 0.5, 1.0, 1.5, 2.0 (‰) |
| Froude number Fr at norm flow conditions | 0.35, 0.50, 0.65, 0.80 (-) |
| Channel width B | 56, 76, 96, 116 (m) |
| Flow depth h0 | 1.6, 2.6, 3.6 (m) |
| Flow depth underwater of the weir hd | 0.0, 0.7*h0, 0.8*h0, 0.9*h0 (m) |
| Weir field width b | 7.0, 15.5, 32.5 (m) |
| Weir height w | 2.2, 4.0, 5.8 (m) |
| Number of open weir fields no | 1–8 (-) |
| Parameters | Dimensions Numerical Model/Physical Model (1:50) |
|---|---|
| Channel slope Is | 0.5, 1.0, 1.5, 2.0 (‰) |
| Froude number Fr | 0.35, 0.50, 0.65, 0.80 (-) |
| Channel width B | 16.0 (m)/32.0 (cm) |
| Flow depth h0 | 3.6 (m)/7.2 (cm) |
| Flow depth underwater of the weir hd | 0.0 (m)/0.0 (cm) |
| Weir field width b | 7.0 (m)/14 (cm) |
| Weir height w | 2.5 (m)/5 (cm) |
| Number of open weir fields no | 0–4 (-) |
| Variables Included in the Analysis | R | R² | Standard Error | Equation |
|---|---|---|---|---|
| 0.664 | 0.414 | 0.076 | (10) | |
| 0.866 | 0.749 | 0.050 | (11) | |
| 0.943 | 0.888 | 0.034 | (12) | |
| 0.954 | 0.911 | 0.030 | (13) | |
| 0.977 | 0.954 | 0.022 | (14) |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lindermuth, A.; Ostrander, T.S.P.; Achleitner, S.; Gems, B.; Aufleger, M. Discharge Calculation of Side Weirs with Several Weir Fields Considering the Undisturbed Normal Flow Depth in the Channel. Water 2021, 13, 1717. https://doi.org/10.3390/w13131717
Lindermuth A, Ostrander TSP, Achleitner S, Gems B, Aufleger M. Discharge Calculation of Side Weirs with Several Weir Fields Considering the Undisturbed Normal Flow Depth in the Channel. Water. 2021; 13(13):1717. https://doi.org/10.3390/w13131717
Chicago/Turabian StyleLindermuth, Adrian, Théo St. Pierre Ostrander, Stefan Achleitner, Bernhard Gems, and Markus Aufleger. 2021. "Discharge Calculation of Side Weirs with Several Weir Fields Considering the Undisturbed Normal Flow Depth in the Channel" Water 13, no. 13: 1717. https://doi.org/10.3390/w13131717
APA StyleLindermuth, A., Ostrander, T. S. P., Achleitner, S., Gems, B., & Aufleger, M. (2021). Discharge Calculation of Side Weirs with Several Weir Fields Considering the Undisturbed Normal Flow Depth in the Channel. Water, 13(13), 1717. https://doi.org/10.3390/w13131717








