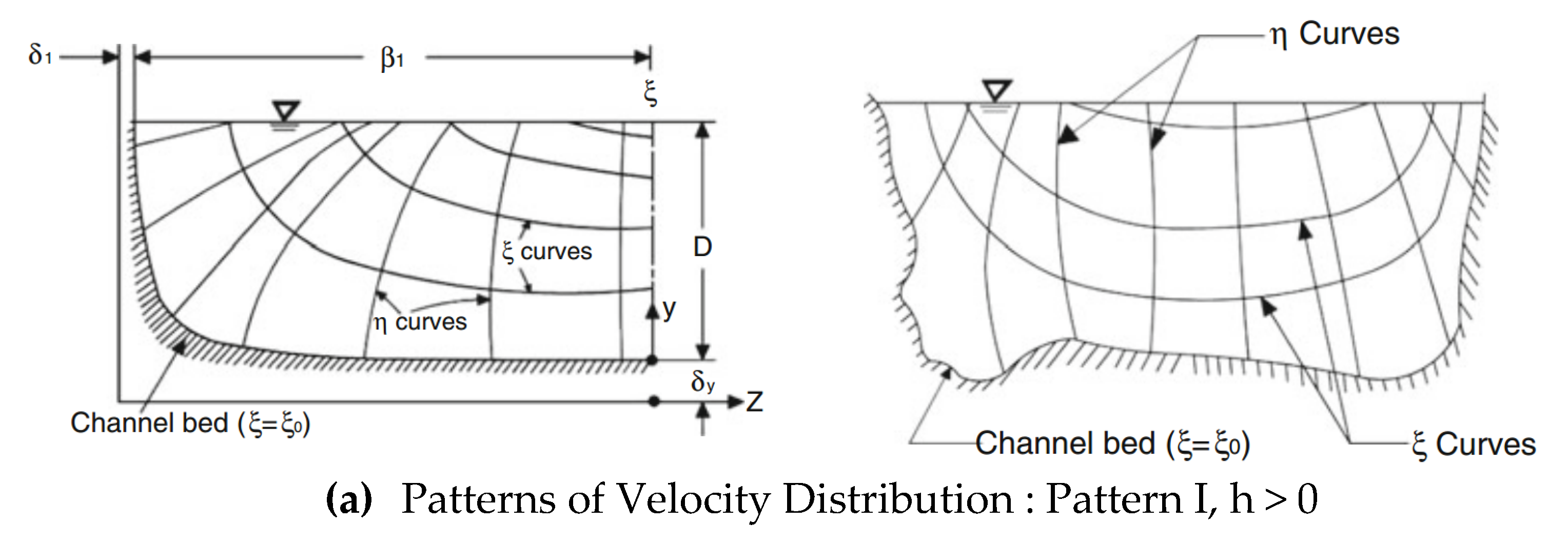
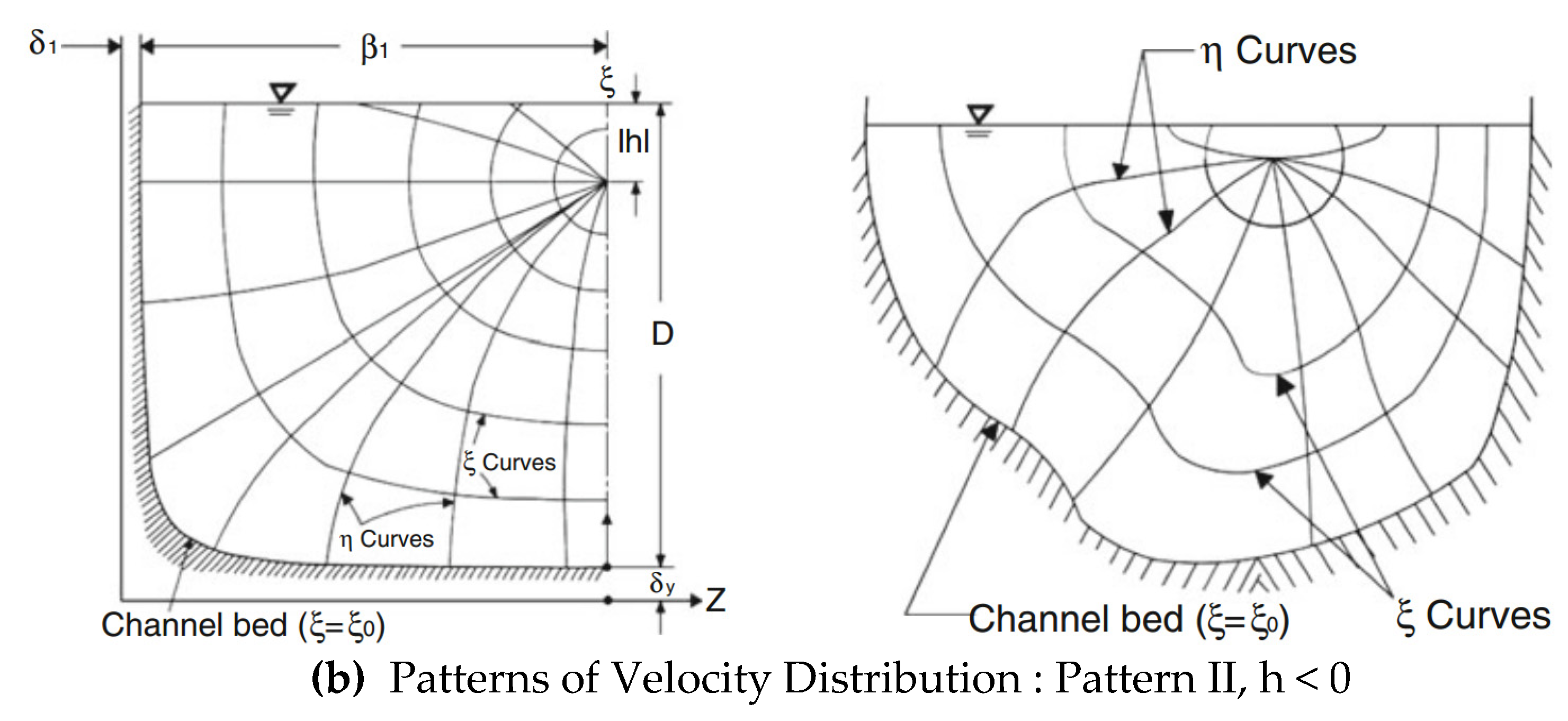
A Study on the Friction Factor and Reynolds Number Relationship for Flow in Smooth and Rough Channels
Abstract
:1. Introduction
2. Theoretical Background
2.1. Existing Friction Loss Coefficient
2.2. New Friction Coefficient Using Entropy
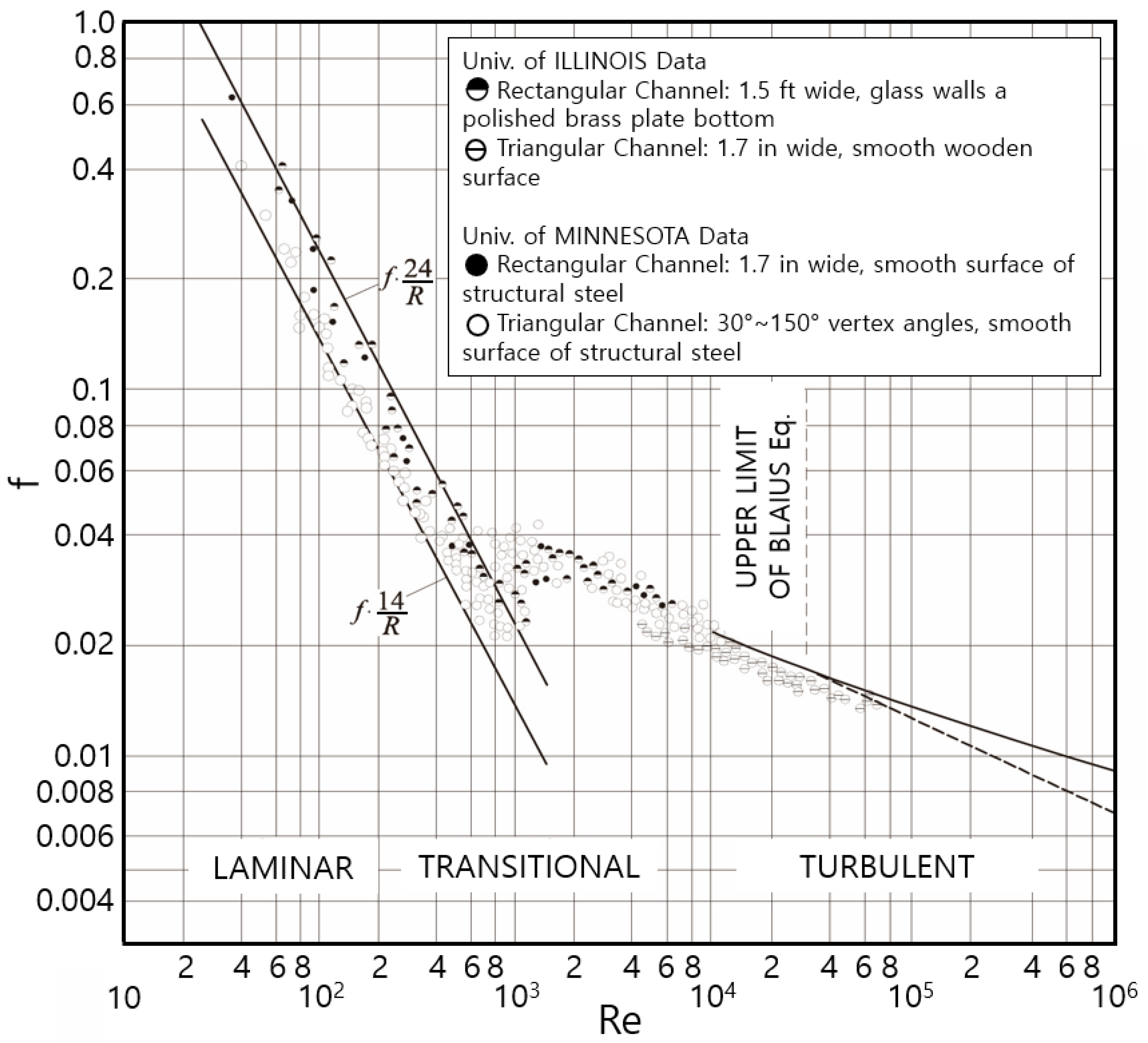
3. Experimental Data
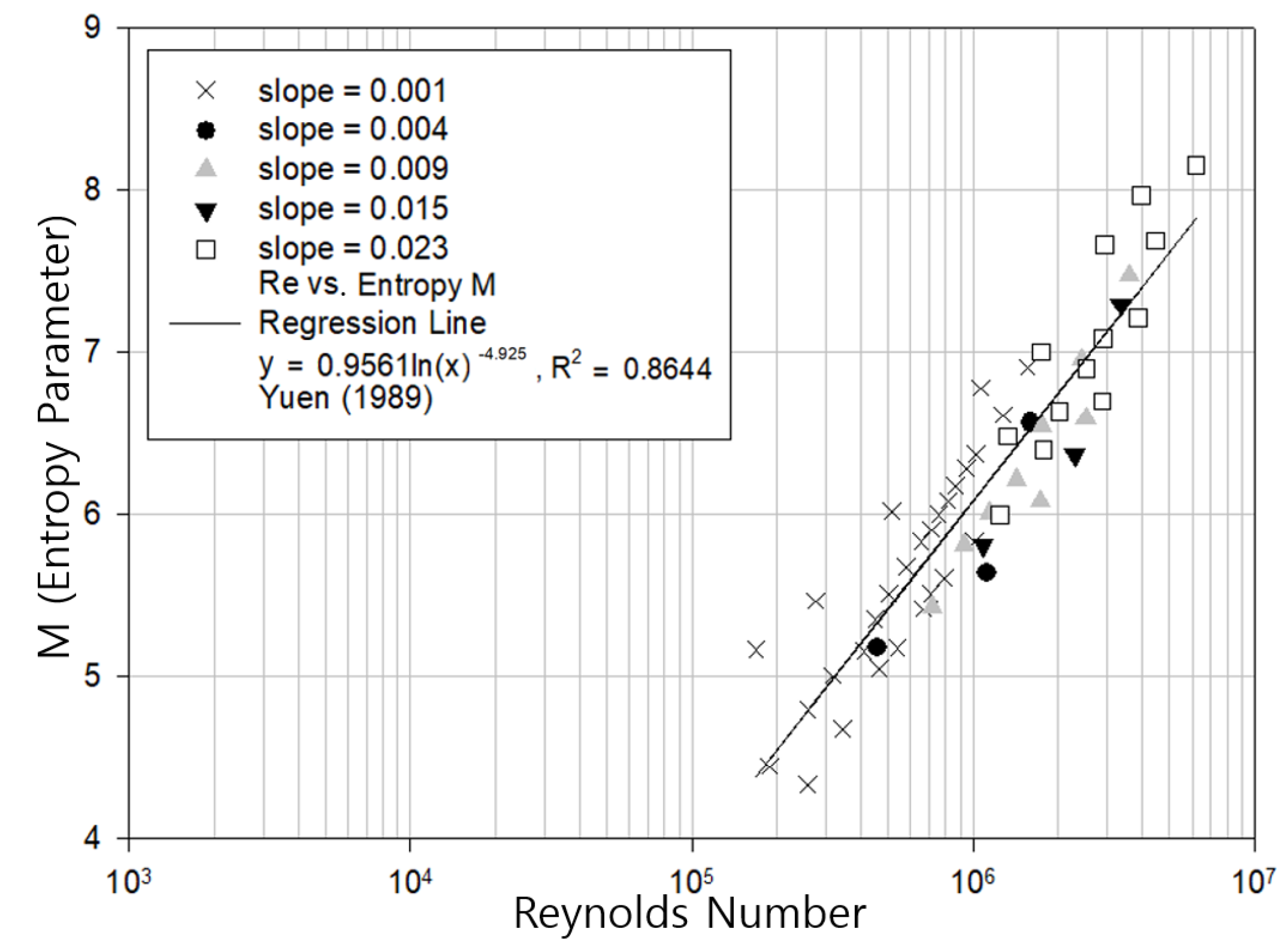
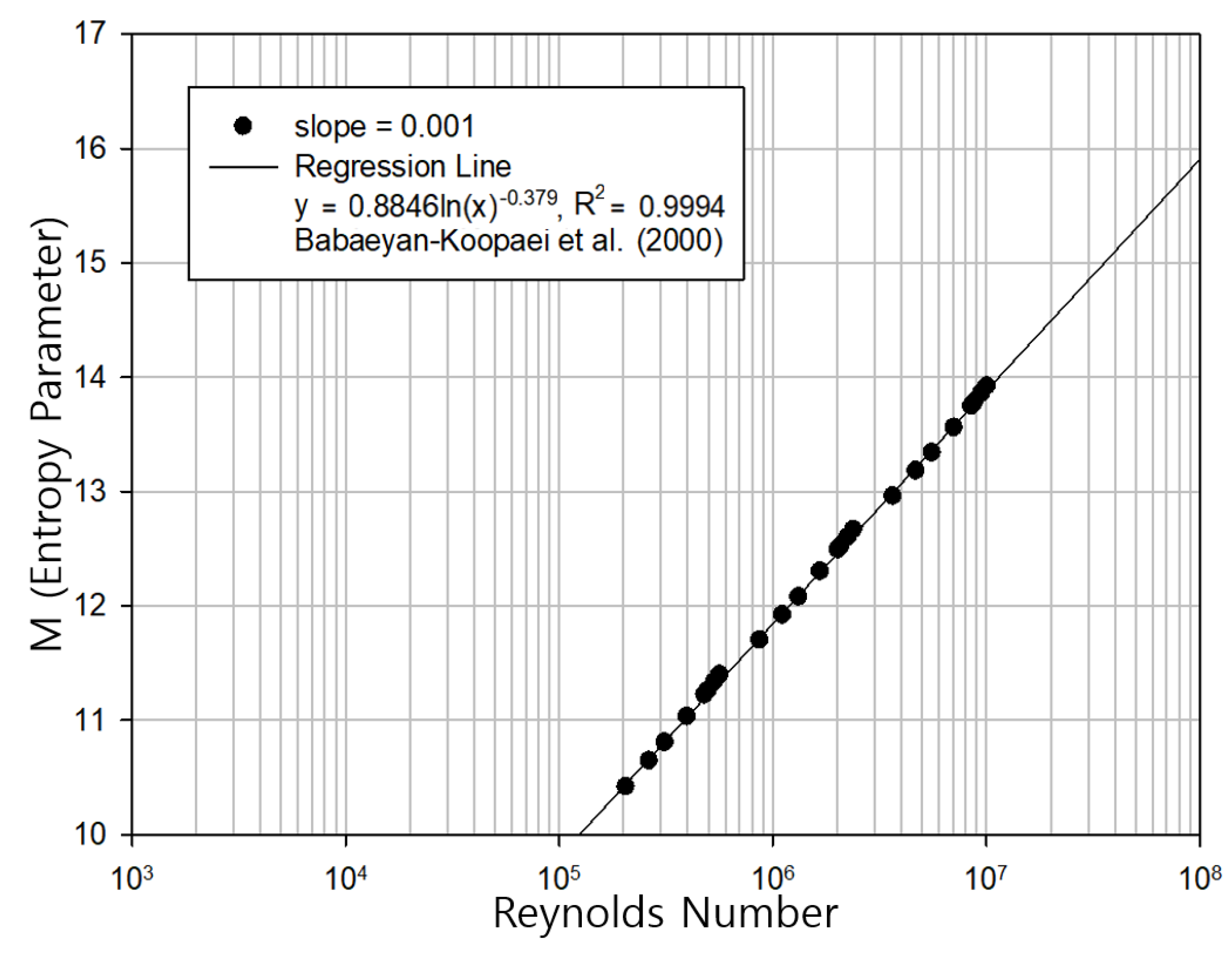
4. Estimation of the Entropy Parameter, M
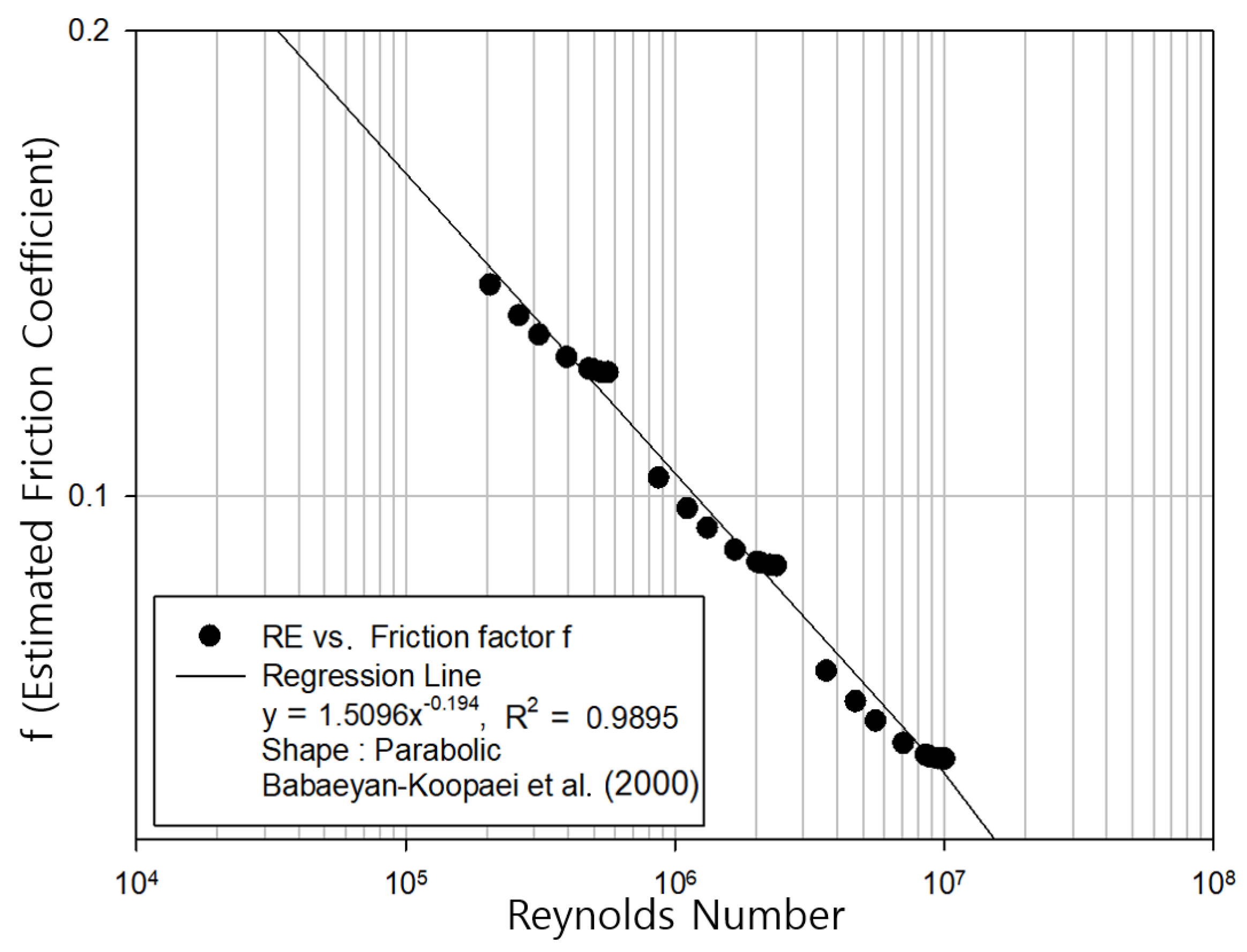
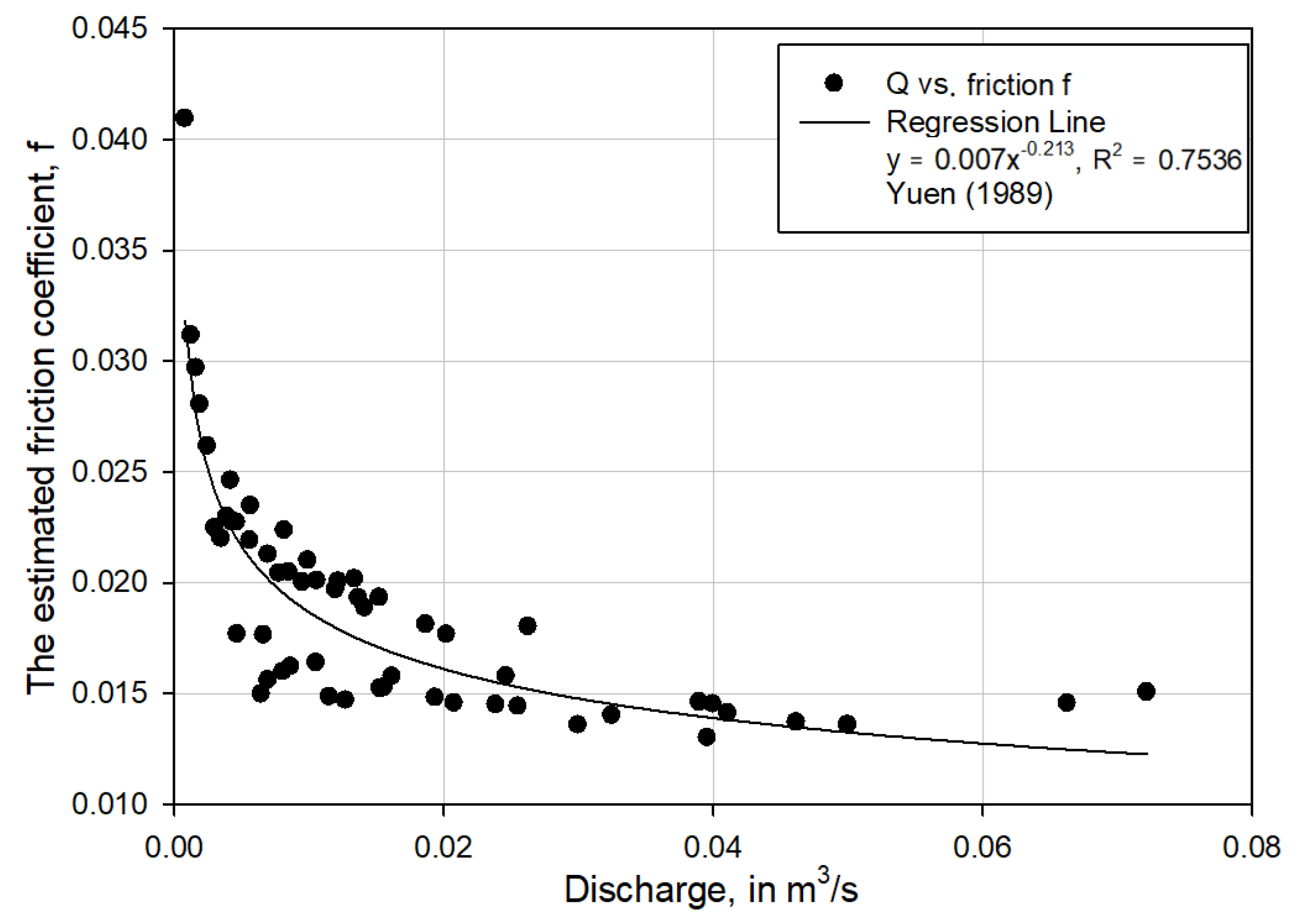
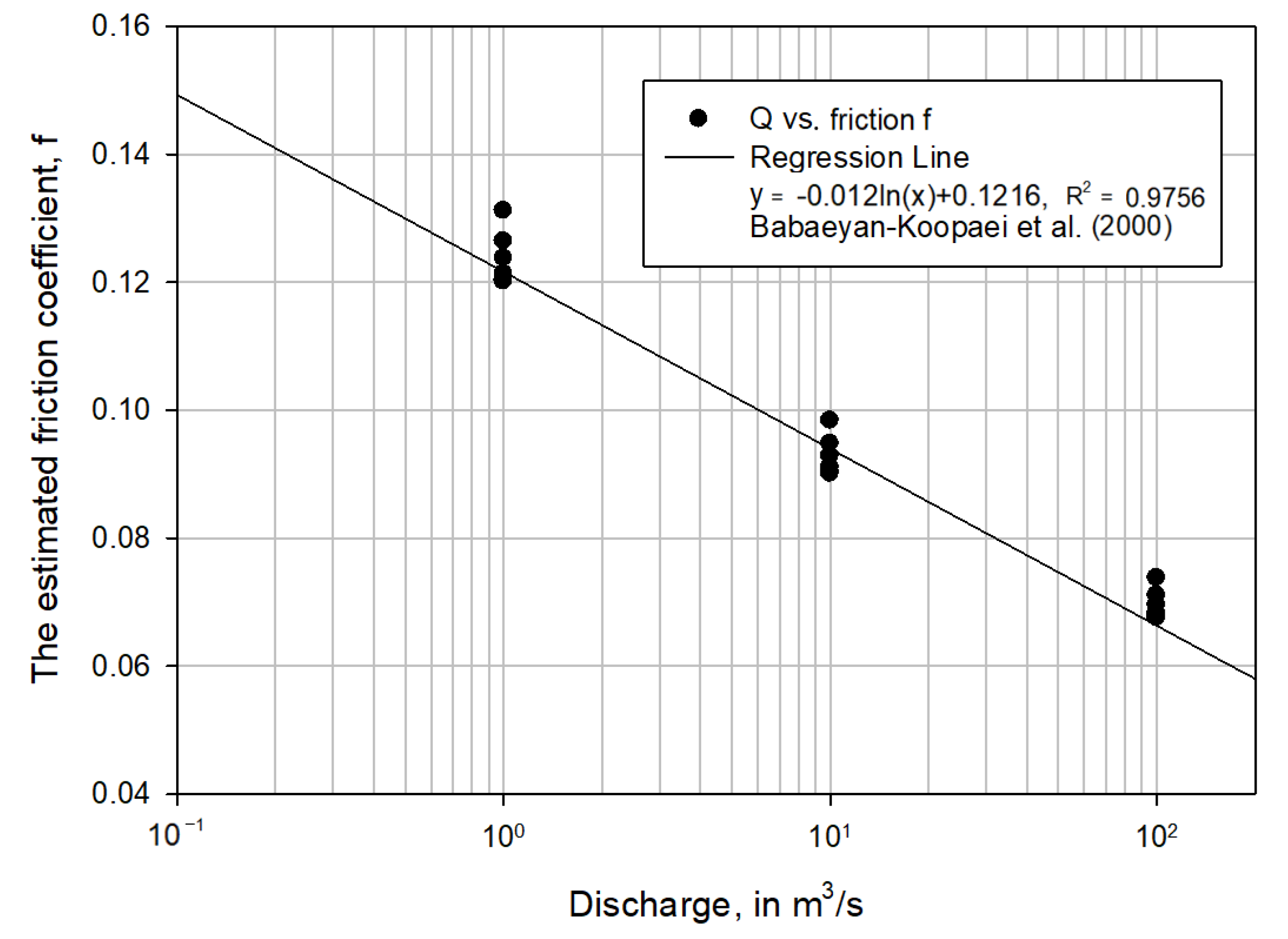
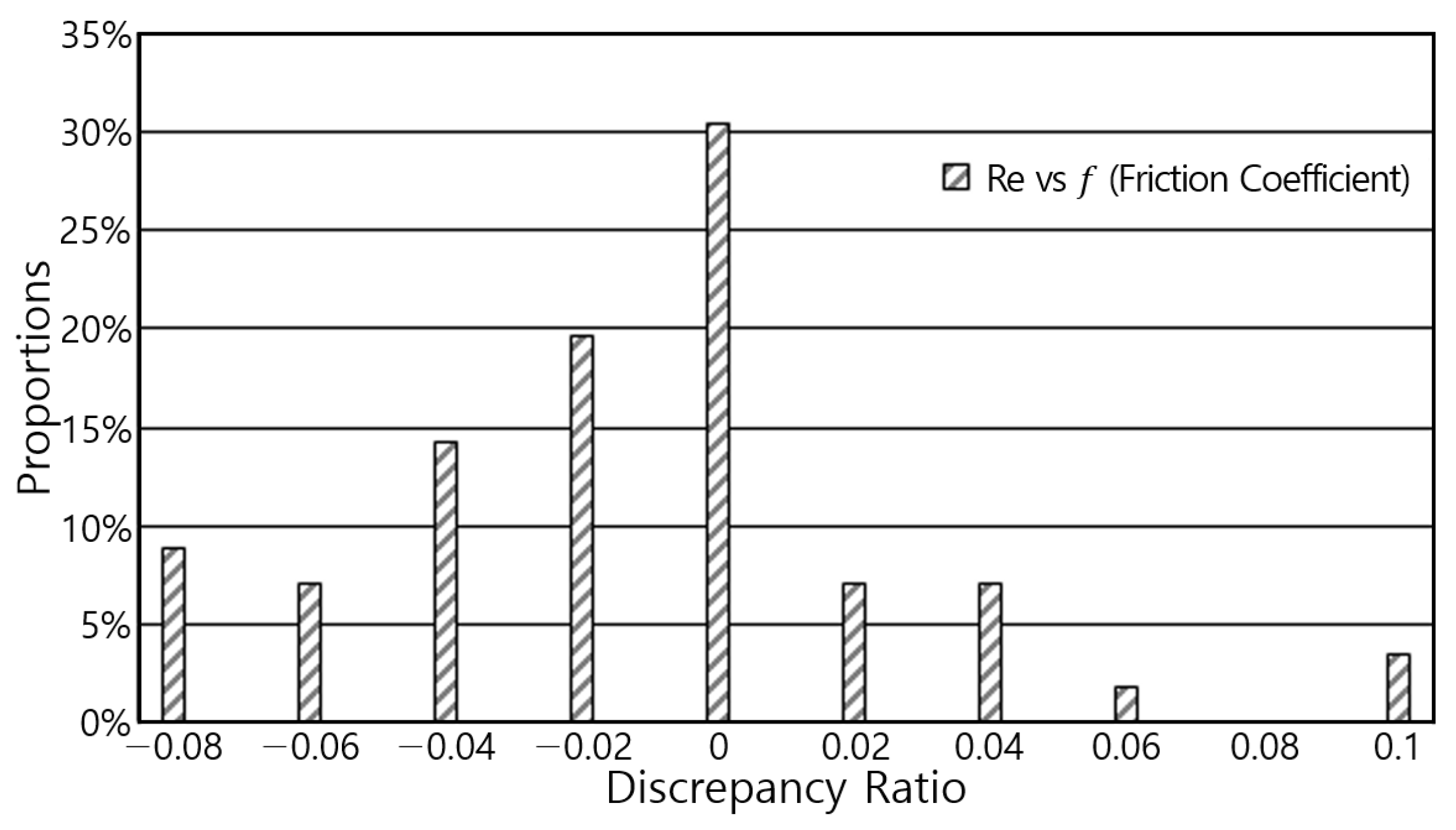
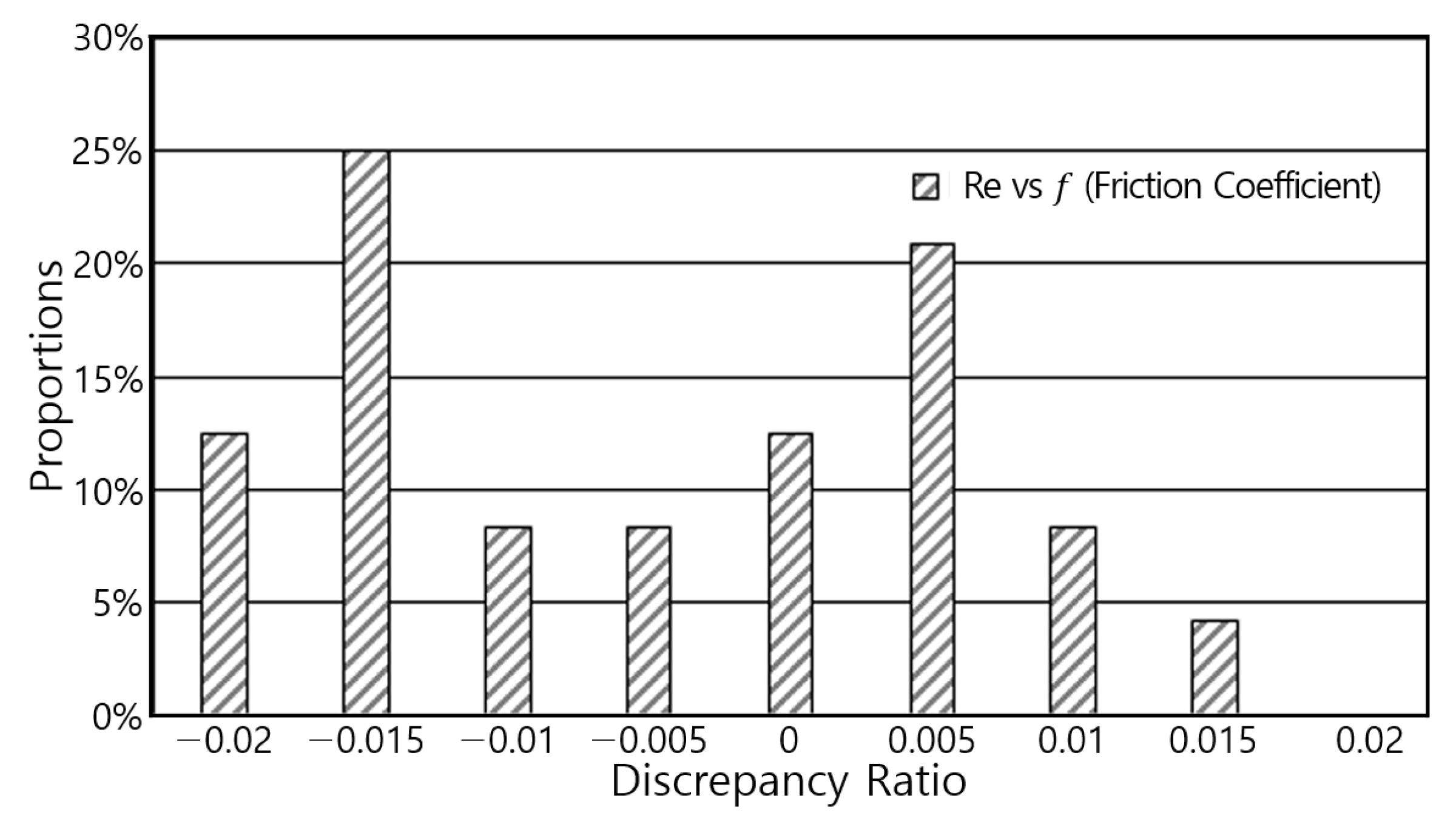
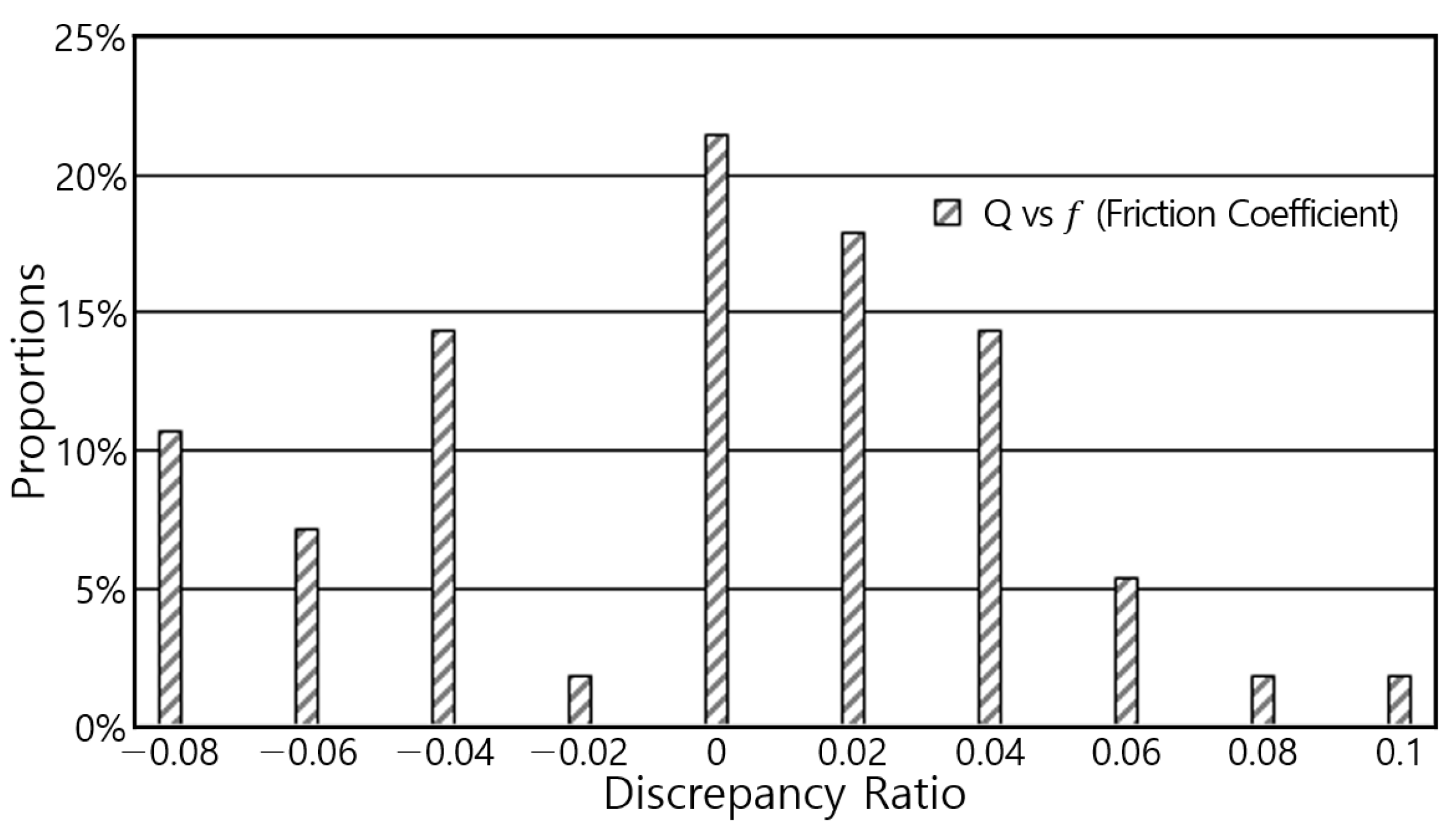
5. Results Analysis
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Acknowledgments
Conflicts of Interest
References
- Darcy, H.; Bazin, H. Recherches Hydrauliques; Enterprises par M.H. D’Arcy; Imprimerie Nationale: Paris, France, 1865. [Google Scholar]
- Yu, K.K. Particle Tracking of Suspended-Sediment Velocities in Open-Channel Flow. Ph.D. Thesis, Civil and Environmental Engineering, University of Iowa, Iowa City, IA, USA, 2004. [Google Scholar]
- Bazin, H.E. Recherches Experimentales sur Lecoulement de Leau dans les Canaux Decouverts; Memoire Presentes par Divers Savants al Academie des Sciences: Paris, France, 1865. [Google Scholar]
- Bazin, H.E. Etude d’une nouvelle formule pour calculer le debit des canaux decouverts. In Annales des Ponts et Chaussées; P. Vicq-Dunod: Paris, France, 1897; Volume 14, pp. 20–70. [Google Scholar]
- Varwick, F. Zur Fließformel für offene Künstliche Gerinne; Dresden University: Dresden, Germany, 1945. (In German) [Google Scholar]
- Manning, R.; Griffith, J.P.; Pigot, T.F.; Vernon-Harcourt, L.F. On the Flow of Water in Open Channels and Pipes; Transaction of the Institution of Civil Engineers of Ireland: Dublin, Ireland, 1890; Volume 20. [Google Scholar]
- Ganguillet, E.; Kutter, W.R. An investigation to establish a new general formula for uniform flow of water in canals and rivers. Z. Oesterreichischen Ing. Archit. Ver. 1869, 21, 6–25. [Google Scholar]
- Chezy, A. Thesis on the Velocity of the Flow in a Given Ditch; des Ponts et Chaussees, Library in France: Paris, France, 1775; Volume 847. [Google Scholar]
- Chow, V.T. Open-Channel Hydraulics; Mcgrow-Hill Civil Engineering Series; McGraw-Hill: Tokyo, Japan, 1959. [Google Scholar]
- Choo, T.H.; Yoon, H.C.; Lee, S.J. An estimation of discharge using mean velocity derived through Chiu’s velocity equation. Environ. Earth Sci. 2013, 69, 247–256. [Google Scholar] [CrossRef]
- Chiu, C.L. Velocity distribution in open channel flow. J. Hydraul. Eng. 1988, 115, 576–594. [Google Scholar] [CrossRef]
- Chiu, C.L. Application of entropy concept in open-channel flow study. J. Hydraul. Eng. 1991, 117, 615–628. [Google Scholar] [CrossRef]
- Blasius, H. Das Ähnlichkeitsgesetz bei Reibungsvorgängen in Flüssigkeiten; Forschungsheft des Vereins Deutscher Ingenieure: Berlin, Germany, 1913; Volume 131. [Google Scholar]
- Kảrmản, T. Mechanische Ähnlichkeit und turbulenz. In Proceedings of the 3rd International Congress for Applied Mechanics, Stockholm, Sweden, 24–29 August 1930; Volume 1, pp. 85–93. [Google Scholar]
- Prandtl, L. >The Mechanics of Viscous Fluids; Durand, B., Ed.; Aerodynamic Theory Springer: Berlin, Germany, 1935; Volume III, division G. 142. [Google Scholar]
- Nikuradse, J. Gesetzmassigkeiten der turbulenten Stromung in glatten Rohren; Ver Deutsch. Ing. Forschungsheft: Berlin, Germany, 1932; Volume 356. [Google Scholar]
- Ryu, H.J.; Kim, J.H.; Lee, B.H.; Lee, W.H.; Jang, I.S. Choisin Hydrography; Donghwa, Korea, 2007. [Google Scholar]
- Shannon, C.E. A mathematical theory of communication. Bell Syst. Tech. J. 1948, 27, 379–423. [Google Scholar] [CrossRef] [Green Version]
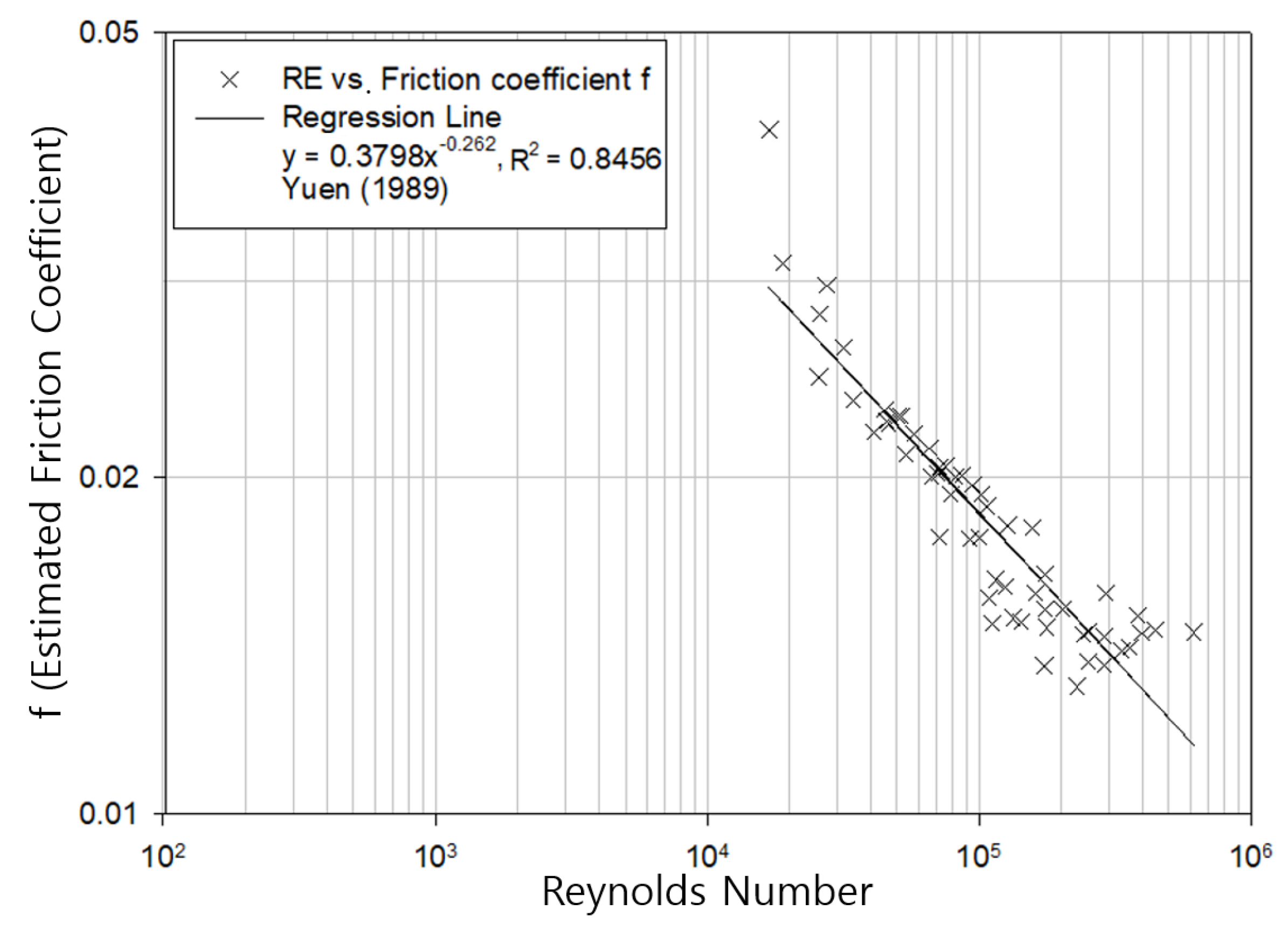
- Yuen, W.H. A Study of Boundary Shear Stress, Flow Resistance and Momentum Transfer in Open Channels with Simple and Compound Trapezoidal cross Section. Ph.D. Thesis, Department of Civil Engineering, University of Birmingham, Birmingham, UK, 1989. [Google Scholar]
- Babaeyan-Koopaei, K.; Valentine, E.M.; Swailes, D.C. Optimal design of parabolic-bottomed triangle canals. J. Irrig. Drain. Eng. 2000, 126, 408–411. [Google Scholar] [CrossRef]
- Moramarco, T.; Saltalippi, C.; Singh, V.P. Estimation of mean velocity in natural channels based on Chiu’s velocity distribution equation. J. Hydrol. Eng. 2004, 9, 442–450. [Google Scholar] [CrossRef]
- Moramarco, T.; Singh, V.P. Formulation of the entropy parameter based on hydraulic and geometric characteristics of river cross sections. J. Hydraul. Eng. 2010, 15, 852–858. [Google Scholar] [CrossRef]
- Choo, Y.M.; Yun, G.S.; Choo, T.H.; Kwon, Y.B.; Sim, S.Y. Study of shear stress in laminar pipe flow using entropy concept. Environ. Earth Sci. 2017, 76, 1–27. [Google Scholar] [CrossRef]
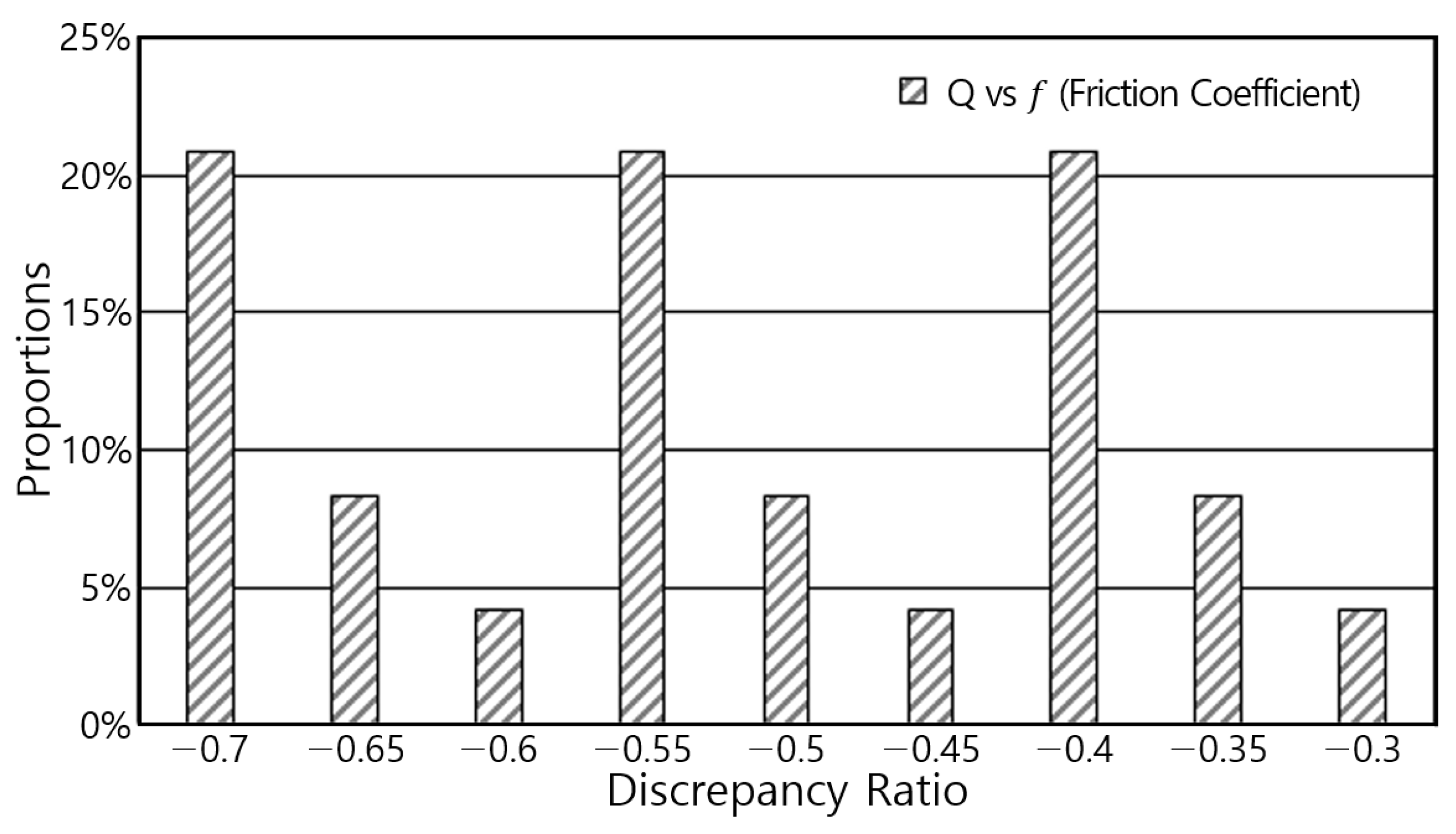
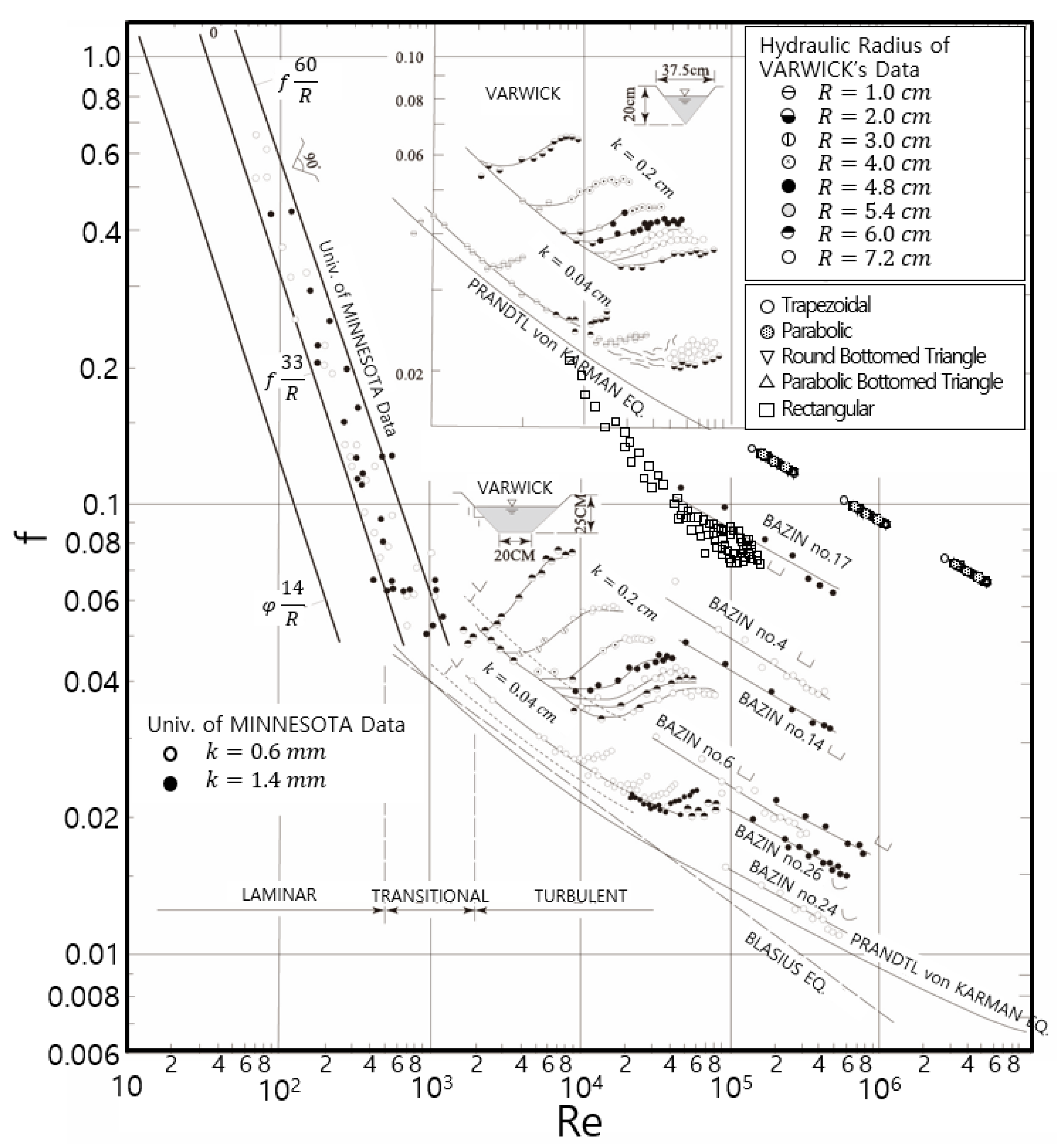
| Data | Cross-Section Shape | Channel Slope | Reynolds Number Range |
|---|---|---|---|
| Yuen [19] | Rectangular | 0.001 | 16,920~156,400 |
| 0.004 | 45,770~160,900 | ||
| 0.009 | 71,450~358,000 | ||
| 0.015 | 108,600~335,000 | ||
| 0.023 | 124,400~618,300 | ||
| Babaeyan-Koopaei [20] | Trapezoidal | 0.001 | 167,000~4,474,000 |
| Parabolic | 0.001 | 135,000~4,630,000 | |
| Round-bottomed triangle | 0.001 | 167,000~4,684,000 | |
| Parabolic-bottomed triangle | 0.001 | 167,000~4,630,000 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Choo, Y.-M.; Kim, J.-G.; Park, S.-H. A Study on the Friction Factor and Reynolds Number Relationship for Flow in Smooth and Rough Channels. Water 2021, 13, 1714. https://doi.org/10.3390/w13121714
Choo Y-M, Kim J-G, Park S-H. A Study on the Friction Factor and Reynolds Number Relationship for Flow in Smooth and Rough Channels. Water. 2021; 13(12):1714. https://doi.org/10.3390/w13121714
Chicago/Turabian StyleChoo, Yeon-Moon, Jong-Gu Kim, and Sang-Ho Park. 2021. "A Study on the Friction Factor and Reynolds Number Relationship for Flow in Smooth and Rough Channels" Water 13, no. 12: 1714. https://doi.org/10.3390/w13121714
APA StyleChoo, Y.-M., Kim, J.-G., & Park, S.-H. (2021). A Study on the Friction Factor and Reynolds Number Relationship for Flow in Smooth and Rough Channels. Water, 13(12), 1714. https://doi.org/10.3390/w13121714