Estimation of the Average Retention Time of Precipitation at the Surface of a Catchment Area for Lake Biwa
Abstract
1. Introduction
2. Methods
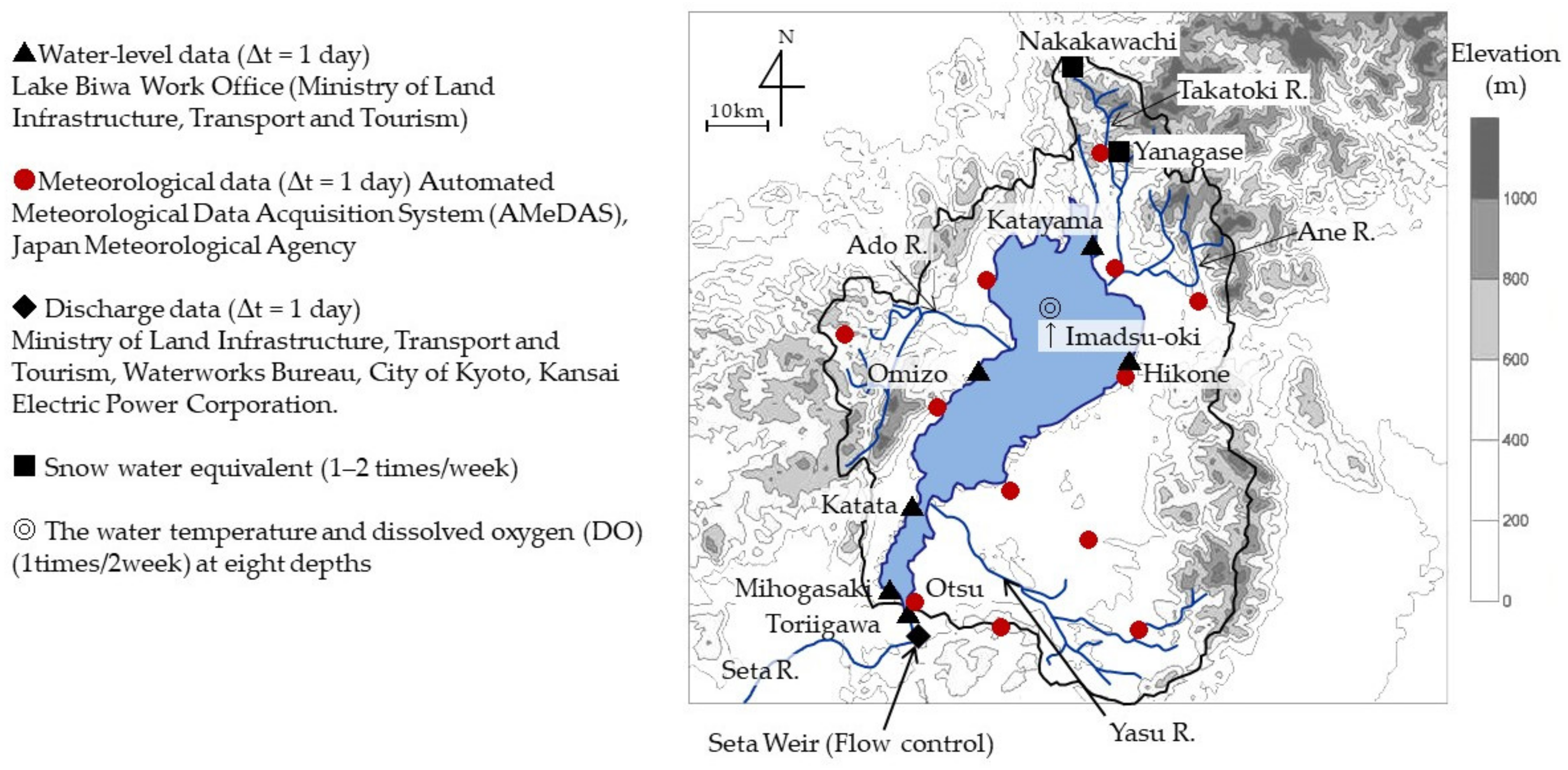
2.1. Site Information
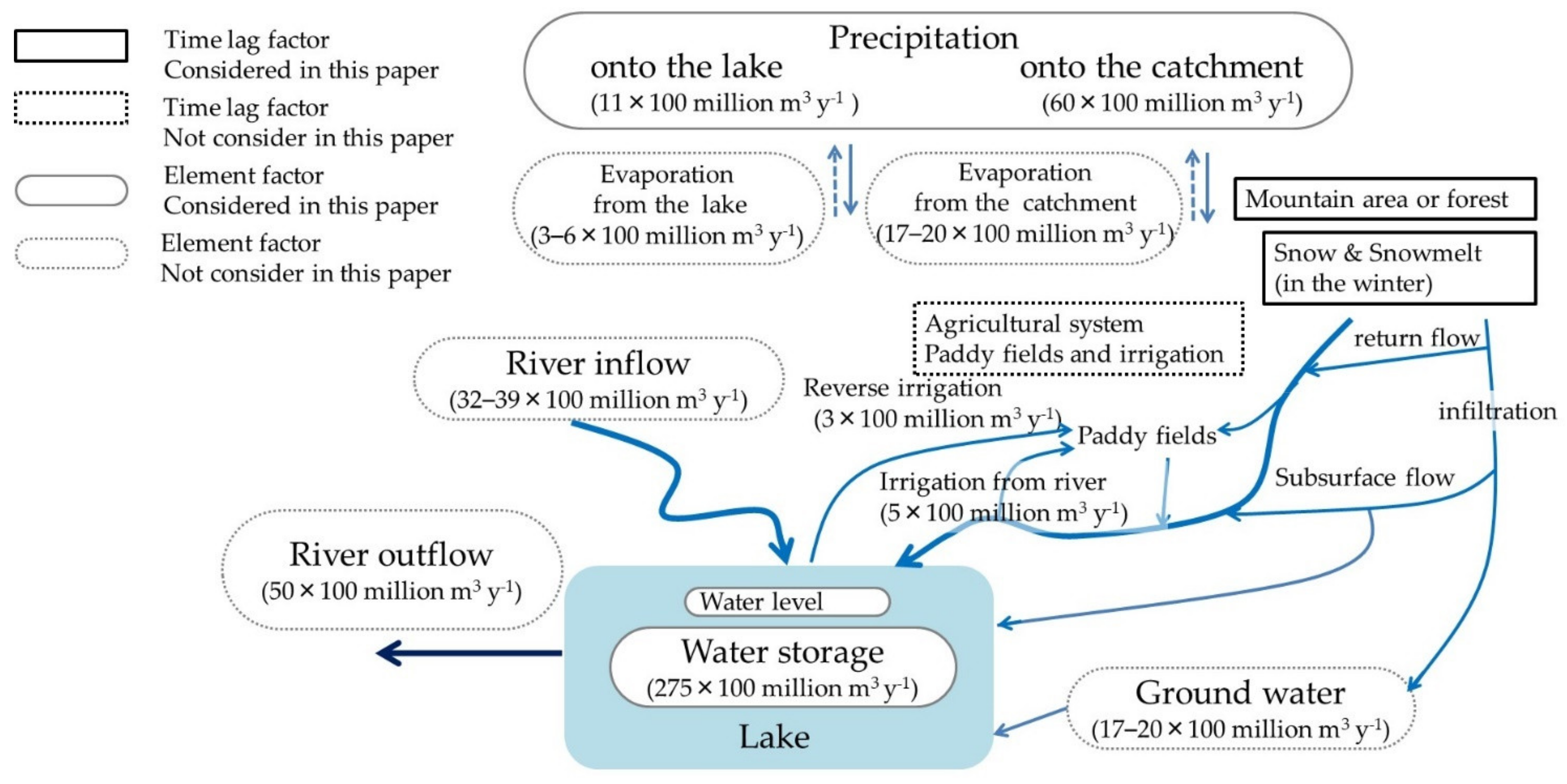
2.2. Water Flow from the Catchment Area to Lake Biwa and Its Water Balance
2.3. Data Acquisition
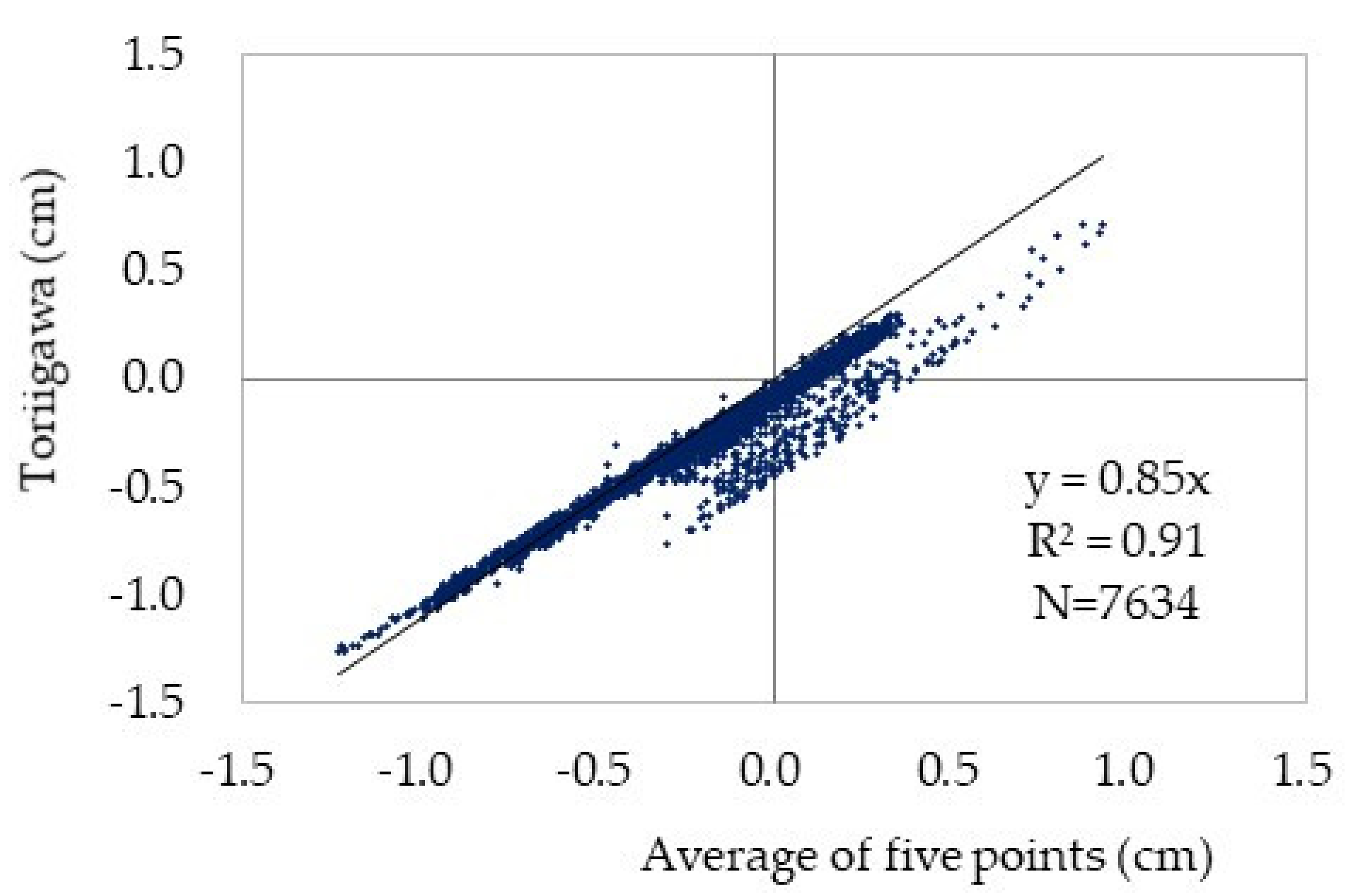
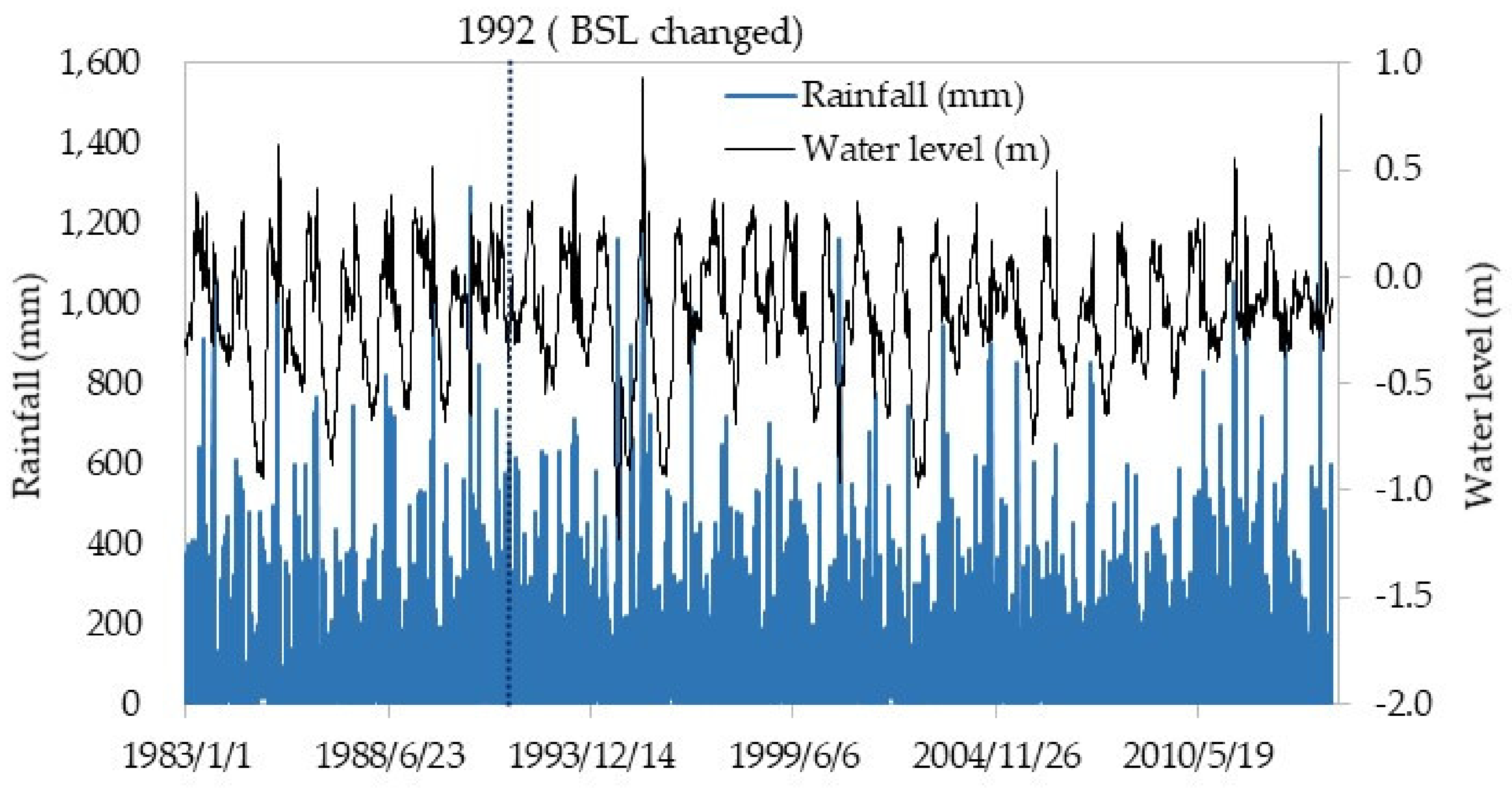
2.3.1. Water Level
2.3.2. Outflow from Lake Biwa
2.3.3. Precipitation
2.3.4. Snow Density and Snow Water Equivalent
2.3.5. Dissolved Oxygen and Water Temperature
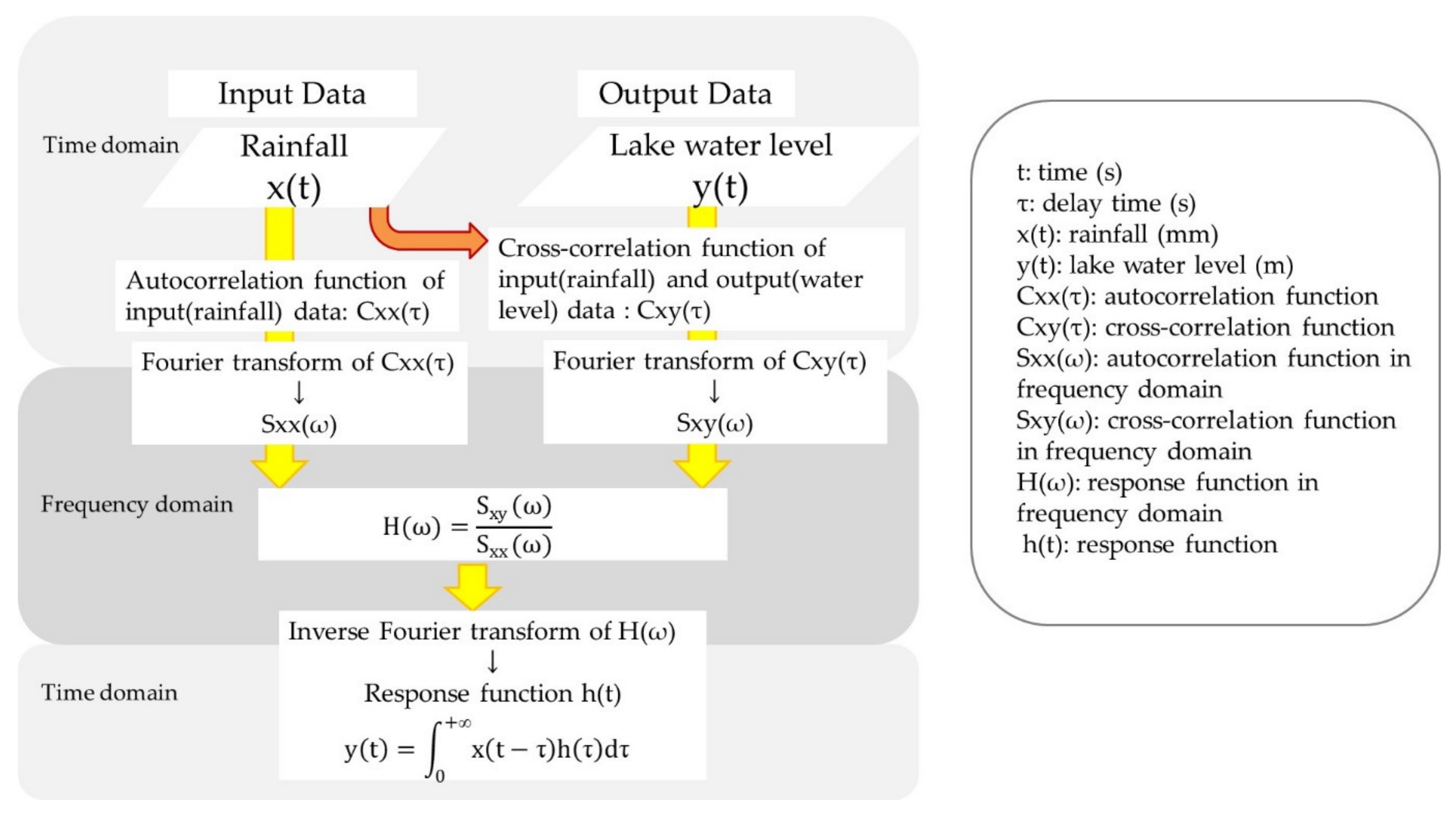
2.4. Impulse Response Function
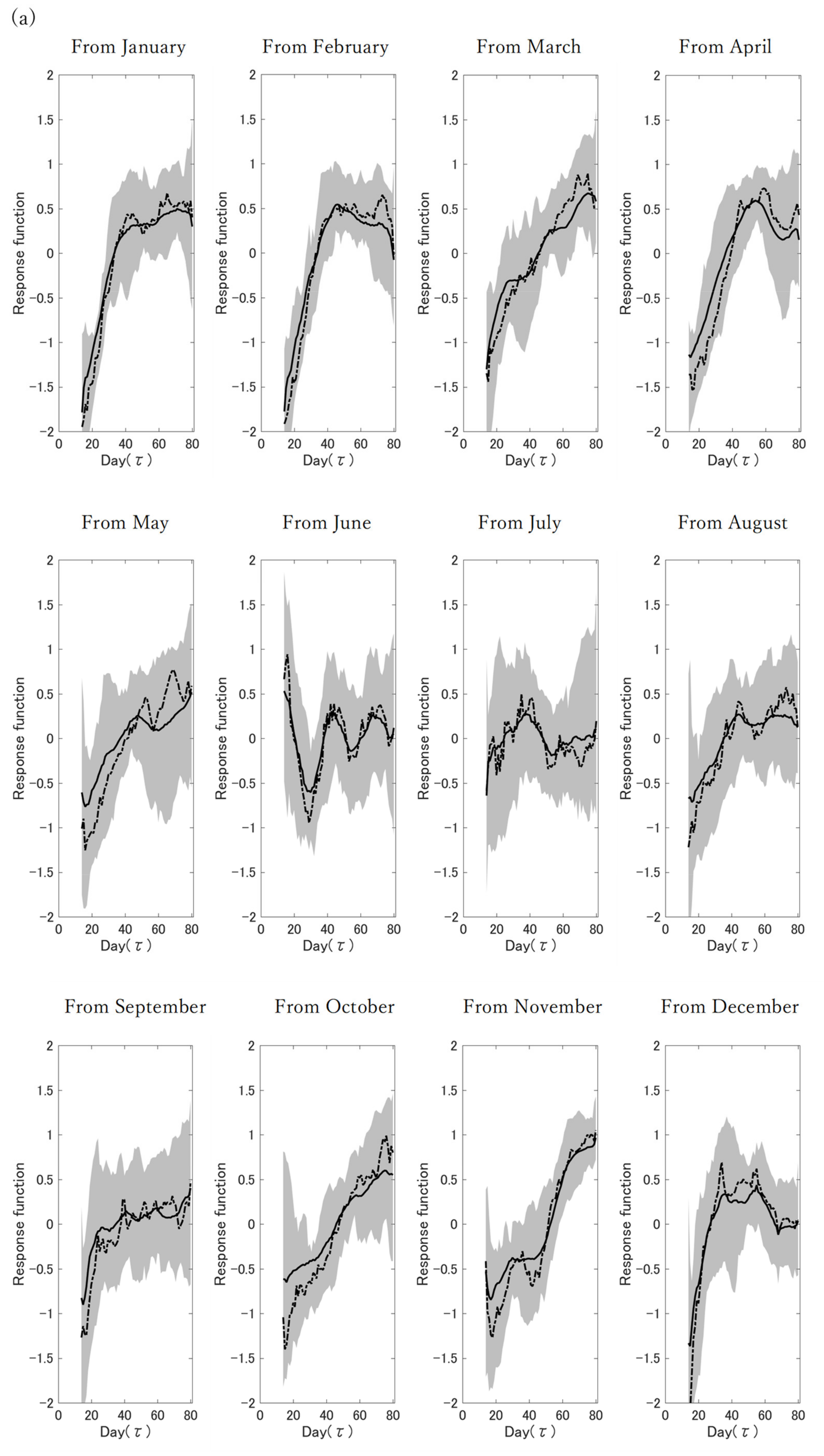
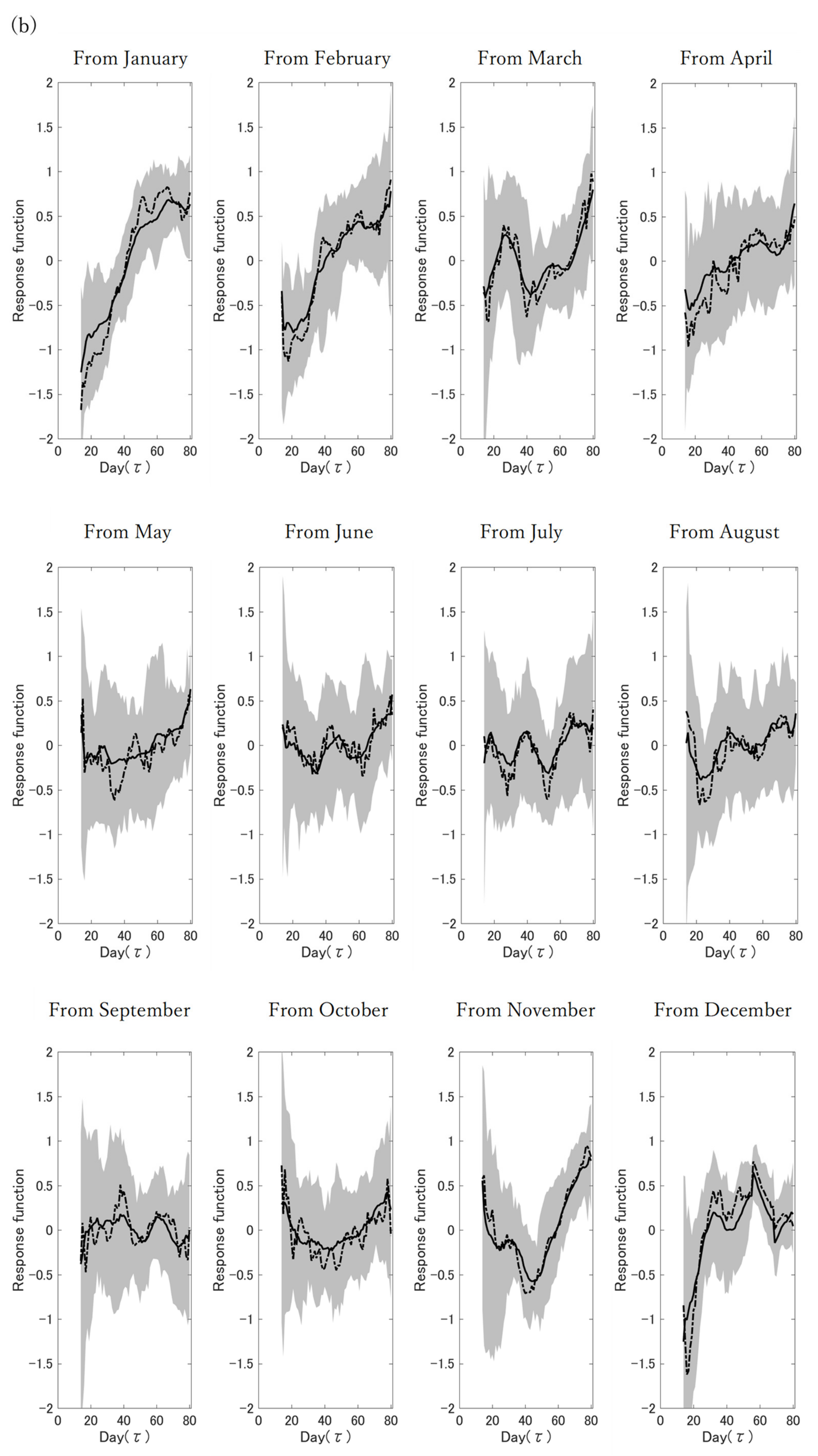
3. Results and Discussion
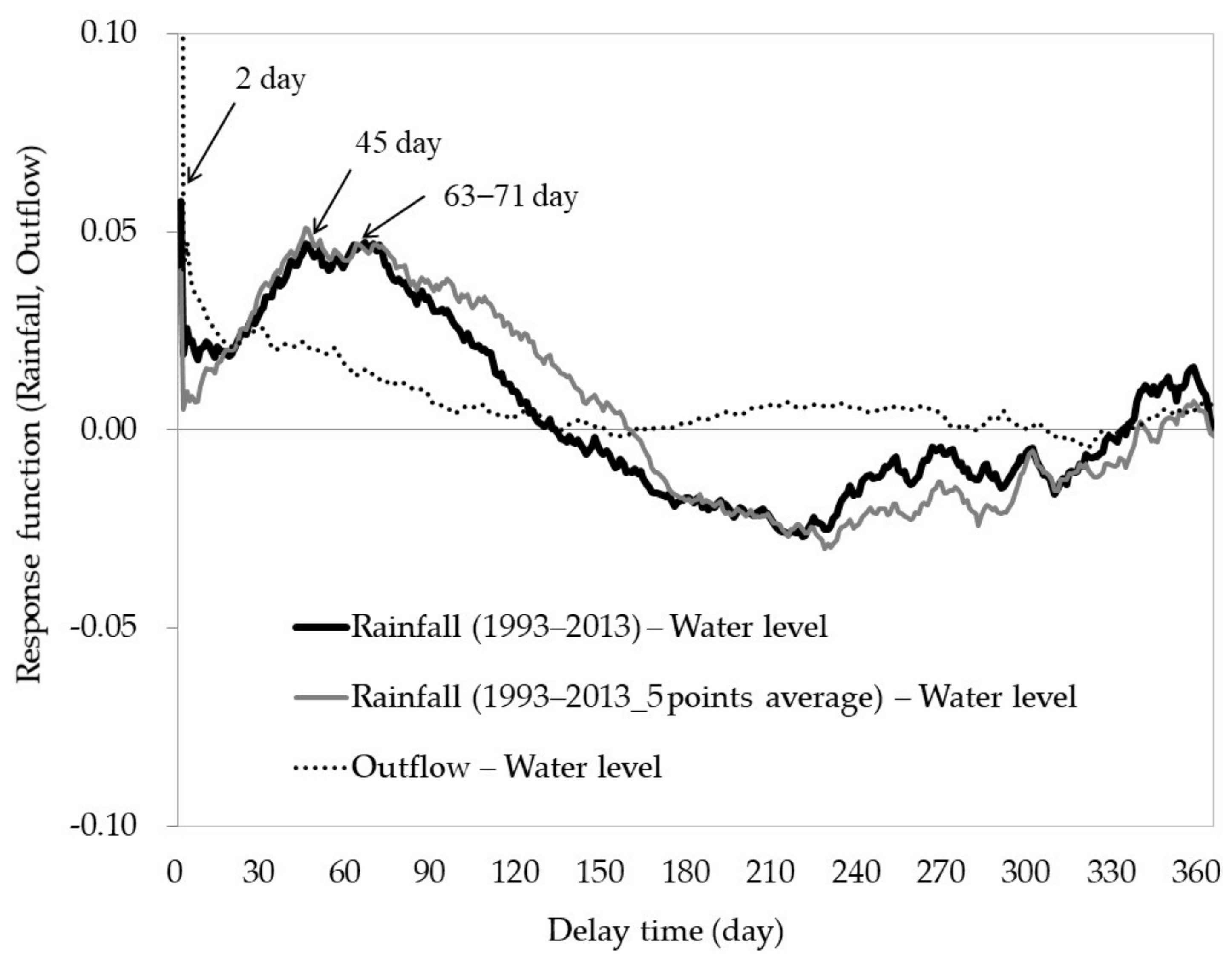
3.1. Data Assimilation and Calculation of the Response Function
3.2. Identification of the Peaks Calculated Using the Response Function
3.3. Calculation of the Seasonal Response Function
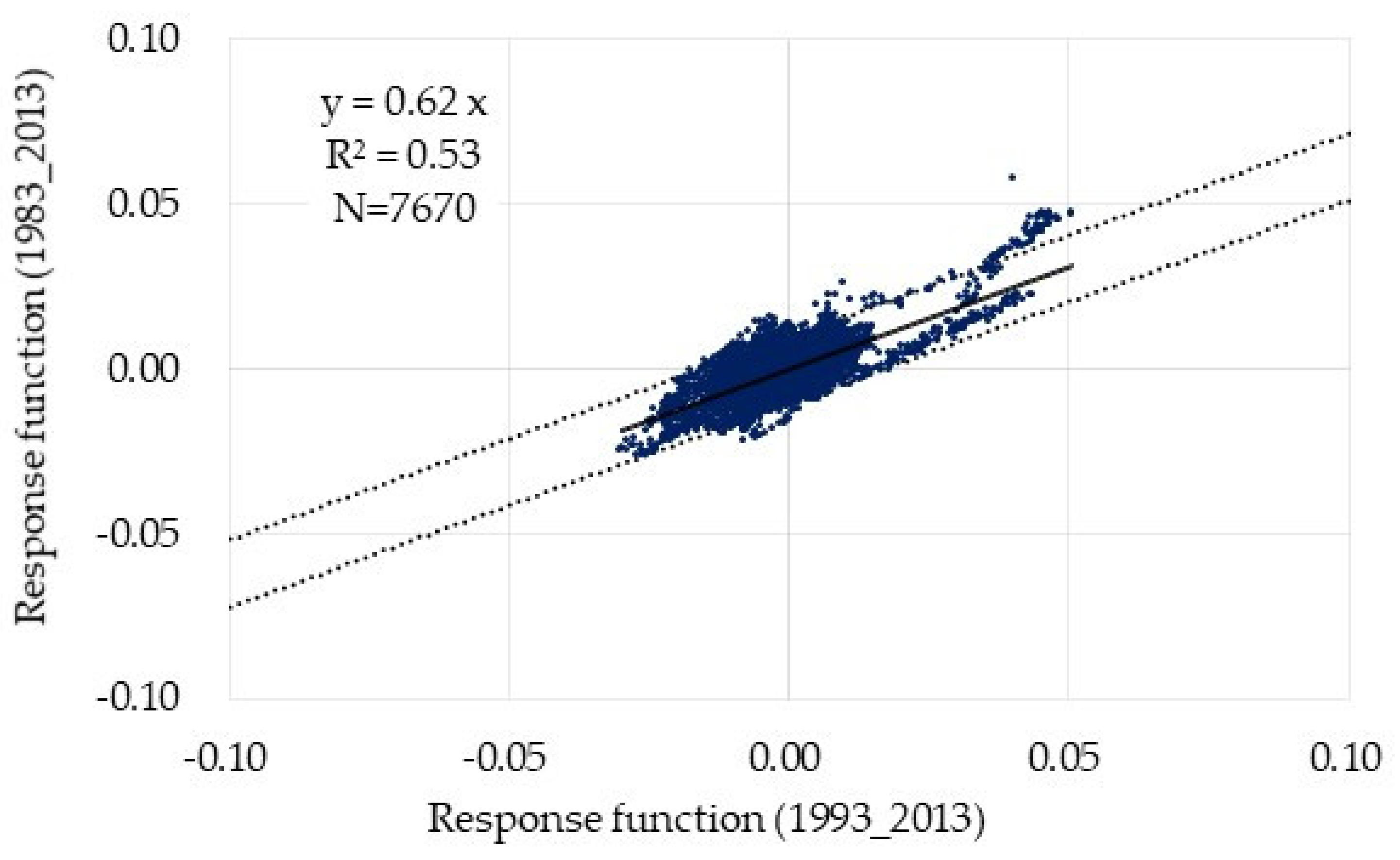
3.4. Use of the 30 Year Data
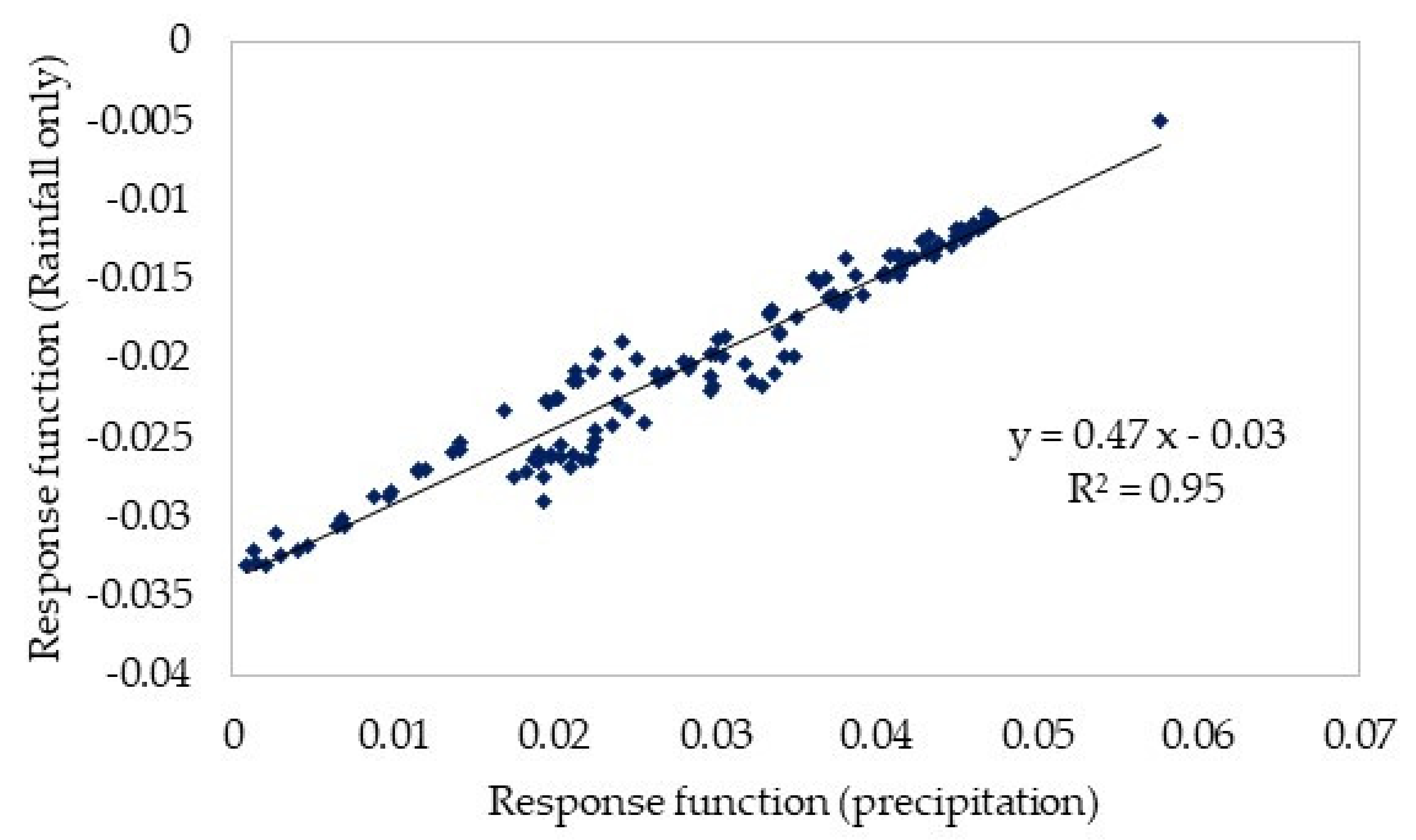
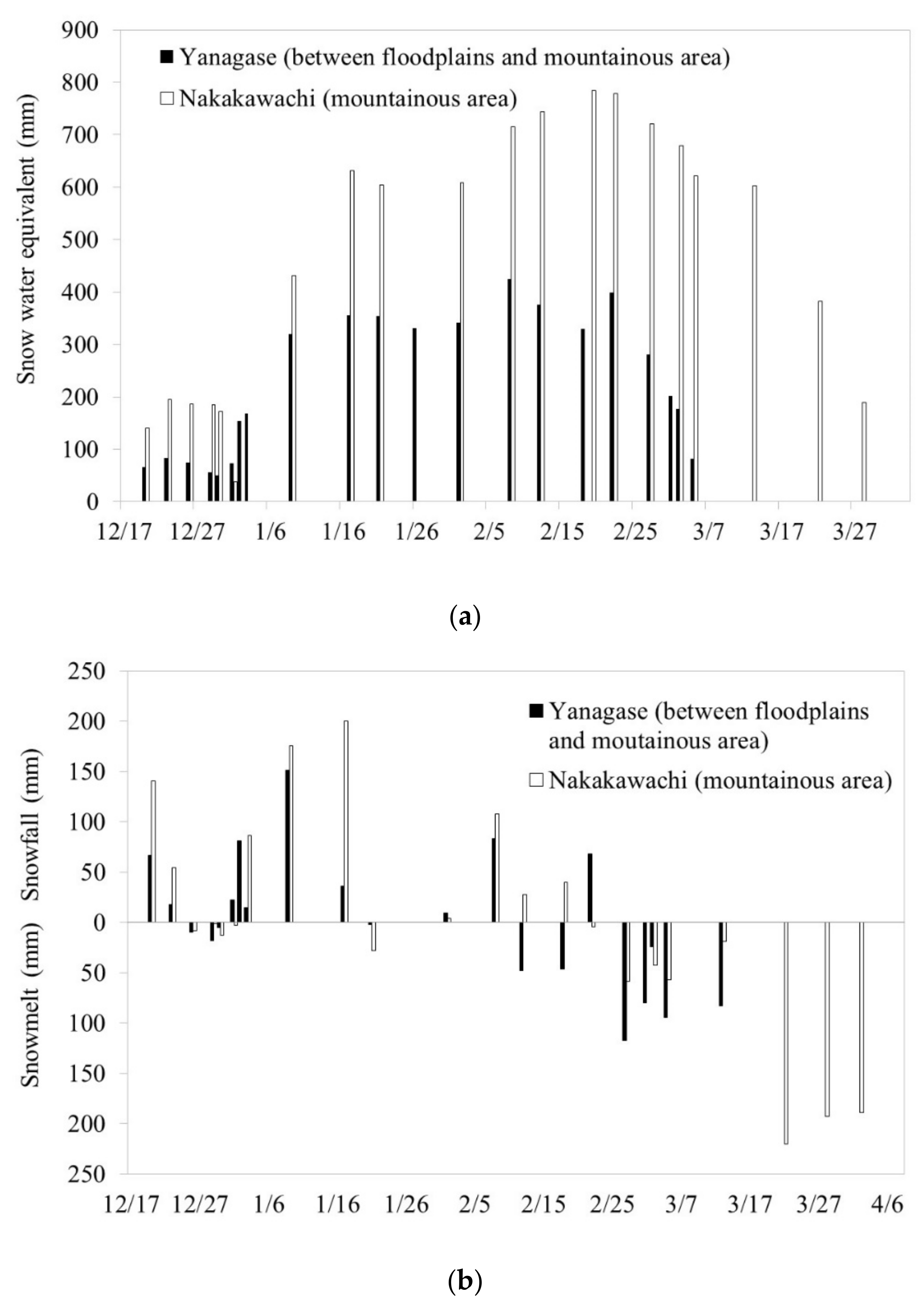
3.5. Inflow Due to Snowmelt Water
4. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Appendix A
References
- Ostrovsky, I.; Rimmer, A.; Yacobi, Z.Y.; Nishri, A.; Sukenik, A.; Hadas, O.; Zohary, T. Long-Term Changes in The lake Kinneret Ecosystem: The Effects of Climate Change and Anthropogenic Factors. Climatic Change and Global Warming of Inland Waters: Impacts and Mitigation for Ecosystems and SOCIETIES; Goldman, R.C., Kumagai, M.M., Robarts, D.R., Eds.; John Wiley & Sons: West Sussex, UK, 2013; Volume 16, pp. 271–291. [Google Scholar]
- Micklin, P.P. Desiccation of the Aral Sea: A water management disaster in the Soviet Union. Science 1988, 241, 1170–1176. [Google Scholar] [CrossRef]
- Micklin, P.M. The Aral Sea disaster. Annu. Rev. Earth Planet. Sci. 2007, 35, 47–72. [Google Scholar] [CrossRef]
- Zohary, T.; Ostrovsky, I. Ecological impacts of excessive water level fluctuations in stratified freshwater lakes. Inland Waters 2011, 1, 47–59. [Google Scholar] [CrossRef]
- Wine, M.L.; Rimmer, A.; Laronne, J.B. Agriculture, diversions, and drought shrinking Galilee Sea. Sci. Total Environ. 2019, 651, 70–83. [Google Scholar] [CrossRef]
- AghaKouchak, A.; Norouzi, H.; Madani, K.; Mirchi, A.; Azarderakhsh, M.; Nazemi, A.; Nasrollahi, N.; Farahmand, A.; Mehran, A.; Hasanzadeh, E. Aral Sea syndrome desiccates Lake Urmia: Call for action. J. Great Lakes Res. 2015, 41, 307–311. [Google Scholar] [CrossRef]
- Alborzi, A.; Mirchi, A.; Moftakhari, H.; Mallakpour, I.; Alian, S.; Nazemi, A.; Hassanzadeh, E.; Mazdiyasni, O.; Ashraf, S.; Madani, K. Climate-informed environmental inflows to revive a drying lake facing meteorological and anthropogenic droughts. Environ. Res. Lett. 2018, 13. [Google Scholar] [CrossRef]
- Chaudhari, S.; Felfelani, F.; Shin, S.; Pokhrel, Y. Climate and anthropogenic contributions to the desiccation of the second largest saline lake in the twentieth century. J. Hydrol. 2018, 560, 342–353. [Google Scholar] [CrossRef]
- Khazaei, B.; Khatami, S.; Alemohammad, S.H.; Rashidi, L.; Wu, C.; Madani, K.; Kalantari, Z.; Destouni, G.; Aghakouchak, A. Climatic or regionally induced by humans? Tracing hydro-climatic and landuse changes to better understand the Lake Urmia tragedy. J. Hydrol. 2019, 569, 203–217. [Google Scholar] [CrossRef]
- Moore, J.N. Recent desiccation of Western Great Basin Saline Lakes: Lessons from Lake Abert, Oregon, U.S.A. Sci. Total Environ. 2016, 554–555, 142–154. [Google Scholar] [CrossRef] [PubMed]
- Tsai, C.; Miki, T.; Chang, C.W.; Ishikawa, K.; Ichise, S.; Kumagai, M.; Hsieh, C.H. Phytoplankton functional group dynamics explain species abundance distribution in a directionally changing environment. Ecology 2014, 95, 3335–3343. [Google Scholar] [CrossRef]
- Wantzen, K.M.; Rothhaupt, K.O.; Mörtl, M.; Cantonati, M.; G.-Tóth, L.; Fischer, P. Ecological effects of water-level fluctuations in lakes: An urgent issue. Hydrobiologia 2008, 613, 1–4. [Google Scholar] [CrossRef]
- Gownaris, N.J.; Rountos, K.J.; Kaufman, L.; Kolding, J.; Lwiza, K.M.M.; Pikitch, E.K. Water level fluctuations and the ecosystem functioning of lakes. J. Great Lakes Res. 2018, 44, 1154–1163. [Google Scholar] [CrossRef]
- Gronewold, A.D.; Rood, R.B. Recent water level changes across Earth’s largest lake system and implications for future variability. J. Great Lakes Res. 2019, 45, 1–3. [Google Scholar] [CrossRef]
- Geraldes, A.M.; Boavida, M.J. Seasonal water level fluctuations: Implications for reservoir limnology and management. Lakes Reserv. Res. Manag. 2005, 10, 59–69. [Google Scholar] [CrossRef]
- Valdespino-Castillo, M.P.; Merino-Ibarra, M.; Jiménez-Contreras, J.; Fermín, S.; Castillo-Sandoval, S.F.; Ramírez-Zierold, A.J. Community metabolism in a deep (stratified) tropical reservoir during a period of high water-level fluctuations. Environ. Monit. Assess. 2014, 186, 6505–6520. [Google Scholar] [CrossRef] [PubMed]
- Yang, J.; Lv, H.; Yang, J.; Liu, L.; Yu, X.; Chen, H. Decline in water level boosts cyanobacteria dominance in subtropical reservoirs. Sci. Total Environ. 2016, 557–558, 445–452. [Google Scholar] [CrossRef]
- Mizuno, T.; Otuska, T.; Ogawa, M.; Funao, T.; Kanao, S.; Maehata, M. Spawning migration triggers in round crucian carp Carassius auratus glandoculis and water level fluctuations in Lake Biwa. Jpn. J. Conserv. Ecol. 2010, 15, 211–217. (In Japanese) [Google Scholar]
- Sato, Y.; Nishino, M. Model analysis of the impact on spawning of cyprinid fishes by water level manipulation and prediction of the effect of measures. Wetl. Res. 2010, 1, 17–31. (In Japanese) [Google Scholar]
- Fujioka, Y.; Taguchi, T.; Kikko, T. Spawning time, spawning frequency, and spawned egg number in a multiple-spawning fish, the honmoroko Gnathopogon caerulescens. Nippon Suisan Gakkaishi 2013, 79, 31–37. (In Japanese) [Google Scholar] [CrossRef][Green Version]
- Kikko, T.; Nemoto, M.; Ban, S.; Saegusa, J.; Sawada, N.; Ishizaki, D.; Nakahashi, T.; Teramoto, N.; Fujioka, Y. Efficient rearing of larvae and juveniles of Honmoroko Gnathopogon caerulescens in paddy fields. Aquac. Sci. 2013, 61, 303–309. [Google Scholar]
- Iwaki, M.; Yamashiki, Y.; Muraoka, K.; Toda, T.; Jiao, C.; Kumagai, M. Effect of rainfall-influenced river influx on lake water levels: Time scale analysis based on impulse response function in the Lake Biwa catchment area. Inland Waters 2020, 10, 283–294. [Google Scholar] [CrossRef]
- Iwaki, M.; Kumagai, M.; Jao, C.; Nishi, K. Evaluation of river inflows during heavy precipitation based on water level changes in a large lake. Jpn. J. Limnol. 2014, 75, 87–98. (In Japanese) [Google Scholar] [CrossRef]
- Yokoki, H.; Kuwahara, Y.; Hanawa, N.; Gunji, M.; Tomura, T.; Hirayama, A.; Miura, N. Estimation of the future flood and inundation risk on Japanese major Rivers Basins caused by climate change. Chikyu Kankyo Assoc. Int. Res. Initiat. Environ. Stud. 2009, 14, 237–246. (In Japanese) [Google Scholar] [CrossRef][Green Version]
- Delbart, C.; Valdés, D.; Barbecot, F.; Tognelli, A.; Couchoux, L. Spatial organization of the impulse response in a karst aquifer. J. Hydrol. 2016, 537, 18–26. [Google Scholar] [CrossRef]
- Hocking, M.; Kelly, B.F.J. Groundwater recharge and time lag measurement through Vertosols using impulse functions. J. Hydrol. 2016, 535, 22–35. [Google Scholar] [CrossRef]
- Sakamoto, M.; Kumagai, M. Lakes and Drainage Basins in East Asia Monsoon Area; Nagoya University Press: Nagoya, Japan, 2006; p. 186. (In Japanese) [Google Scholar]
- Haga, H. Confirmation of surface area of the southern basin of Lake Biwa Japan. Jpn. J. Limnol. 2006, 67, 123–126. (In Japanese) [Google Scholar] [CrossRef]
- Muramoto, Y.; Michiue, M. Characteristics of alternating current between south and north basin in Lake Biwa. Anu. Dis. Prev. Res. Inst. Kyoto Univ. 1978, 21, 263–276. (In Japanese) [Google Scholar]
- Fujino, Y. Water Budget. An Introduction to Limnology of Lake Biwa; Mori, S., Ed.; CiNii: Kyoto, Japan, 1980; pp. 19–26. (In Japanese) [Google Scholar]
- Kawabata, H. Groundwater infiltration into the lake. Environ. Sci. Res. Rep. 1982, S704, 29–36. (In Japanese) [Google Scholar]
- Biwako Handbook. Fluctuation of Lake Biwa; The Editorial Committee of Biwako Handbook, Ed.; Shiga Prefecture: Shiga, Japan, 2010; p. 192. (In Japanese) [Google Scholar]
- Kotoda, K. The estimation method of lake evaporation using climatological data. In Report of the Hydraulic Experiment University of Tsukuba Environmental Research Center Papers; University of Tsukuba: Tsukuba, Japan, 1977; pp. 53–65. (In Japanese) [Google Scholar]
- Ikebuchi, S.; Seki, M.; Ohtoh, A. Evaporation from Lake Biwa. J. Hydrol. 1988, 102, 427–449. [Google Scholar] [CrossRef]
- Iwaki, M. Estimation of the Distribution of Snow Water Equivalent in the North Catchment Area of Lake Biwa. Ph.D. Thesis, The University of Shiga Prefecture, Shiga, Japan, 2003. [Google Scholar]
- Shiga Prefecture. White Paper on the Environmental of Shiga Prefecture; Shiga Prefecture: Shiga, Japan, 2010. (In Japanese) [Google Scholar]
- Hidaka, K. The Theory of Applied Integral Equation; Kawakita Press: Tokyo, Japan, 1943. (In Japanese) [Google Scholar]
- Hino, M. Spectrum Analysis; Asakura Press: Tokyo, Japan, 1977. (In Japanese) [Google Scholar]
- Iwaki, M.; Hida, Y.; Ueno, K.; Saijyo, M. Observation of snow water equivalent in the North catchment area of Lake Biwa. Lakes Reserv. Res. Manag. 2011, 16, 215–221. [Google Scholar] [CrossRef]
- Kumagai, M.; Fushimi, H. Inflows Due to Snowmelt: Coastal and Estuarine Studies; Okuda, S., Imberger, J., Kumagai, M., Eds.; The American Geophysical Union: Washington, WA, USA, 1995; Volume 48, pp. 129–139. [Google Scholar]
- Chaffe, P.L.B.; Yamashiki, Y.; Takara, K.; Kato, M.; Iwaki, M. Influence of the Ane River Basin on Dissolved Oxygen Concentration of Lake Biwa: Sensitivity Study of the Biwa–3D model. Anu. Dis. Prev. Res. Inst. Kyoto Univ. 2010, 53, 91–96. [Google Scholar]
- Chaffe, P.L.B.; Yamashiki, Y.; Takara, K.; Iwaki, M. A comparison of simple snowmelt models for the Ane River Basin. Anu. Dis. Prev. Res. Inst. Kyoto Univ. 2011, 54, 113–118. [Google Scholar]
- Chaffe, P.L.B.; Yamashiki, Y.; Takara, K.; Iwaki, M. Measurement and modeling of the snowmelt in the Ane river basin. J. Jpn. Soc. Civil Eng. 2012, 68, 223–228. [Google Scholar] [CrossRef]

| Date | Weather | Snow Depth (cm) | Snow Water Equivalent (mm) | Snow Density (kg·m−3) | Air Temperature (°C) | Surface Snow Temperature (°C) |
|---|---|---|---|---|---|---|
| 24 February 2002 | Sunny | 82.6 | 36.5 | 0.442 | 2.9 | −1.0 |
| 28 February 2002 | Cloudy | 74.6 | 32.9 | 0.441 | 1.7 | −0.9 |
| 5 March 2002 | Cloudy | 59.4 | 25.9 | 0.436 | 1.5 | −2.1 |
| 14 March 2002 | Rainy | 20.5 | 8.6 | 0.418 | 5.4 | −2.2 |
| 17 March 2002 | Sunny | 10.1 | 4.6 | 0.454 | 13.2 | −3.0 |
| Water Temperature (°C) | |||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Observation Point | Depth\Month-Year | Oct-09 | Nov-09 | Dec-09 | Jan-10 | Feb-10 | Mar-10 | Apr-10 | May-10 | ||||||||
| The center of Imadsu-oki | 0.5m | 22.7 | 20 | 17.7 | 14.6 | 13.4 | 11.4 | 10.0 | 8.7 | 8.3 | 7.9 | 8.2 | 8.1 | 9.1 | 10.4 | 14.4 | 16.8 |
| 5 m | 22.6 | 19.6 | 17.0 | 14.6 | 13.4 | 11.4 | 10.0 | 8.7 | 8.3 | 7.9 | 7.9 | 8.1 | 8.6 | 9.1 | 12.9 | 12.9 | |
| 10 m | 22.6 | 19.6 | 17.0 | 14.6 | 13.4 | 11.4 | 10.0 | 8.7 | 8.3 | 7.9 | 7.9 | 8.1 | 8.2 | 8.8 | 12.4 | 11.1 | |
| 15 m | 22.2 | 19.6 | 16.9 | 14.6 | 13.4 | 11.4 | 10.0 | 8.7 | 8.3 | 7.9 | 7.8 | 8.0 | 8.2 | 8.7 | 11.5 | 10.6 | |
| 20 m | 13.9 | 17.4 | 16.8 | 14.6 | 13.4 | 11.4 | 9.9 | 8.7 | 8.3 | 7.9 | 7.9 | 7.9 | 8.2 | 8.7 | 11.2 | 10.1 | |
| 30 m | 9.8 | 9.8 | 10.5 | 11.2 | 10.2 | 11.4 | 9.9 | 8.6 | 8.3 | 7.9 | 7.9 | 7.9 | 8.2 | 8.6 | 9.4 | 9.4 | |
| 40 m | 8.8 | 8.5 | 8.9 | 8.8 | 8.8 | 10.1 | 9.9 | 8.6 | 8.3 | 7.9 | 7.9 | 7.8 | 8.2 | 8.4 | 8.8 | 8.9 | |
| 60 m | 8.3 | 8.0 | 8.1 | 8.2 | 8.1 | 8.4 | 8.8 | 8.6 | 8.3 | 7.9 | 7.6 | 7.7 | 8.0 | 8.1 | 8.3 | 8.5 | |
| 80 m | 8.2 | 7.9 | 7.9 | 7.9 | 7.9 | 8.2 | 8.3 | 8.4 | 8.3 | 7.7 | 7.5 | 7.6 | 7.6 | 7.9 | 8.0 | 7.9 | |
| Bottom from l m | 8.1 | 7.8 | 7.8 | 7.9 | 7.9 | 8.1 | 8.2 | 8.3 | 8.3 | 1.6 | 7.5 | 7.6 | 7.6 | 7.8 | 7.8 | 7.9 | |
| Dissolved Oxygen (mg/L) | |||||||||||||||||
| Observation Point | Depth\Month-Year | Oct-09 | Nov-09 | Dec-09 | Jan-10 | Feb-10 | Mar-10 | Apr-10 | May-10 | ||||||||
| The center of Imadsu-oki | 0.5m | 8.7 | 9.2 | 9.4 | 10.0 | 10.4 | 10.5 | 9.8 | 9.7 | 10.6 | 11.1 | 11.6 | 12.0 | 12.0 | 12.1 | 11.3 | 10.6 |
| 5 m | 8.7 | 9.2 | 9.6 | 9.9 | 10.3 | 10.5 | 9.8 | 9.7 | 10.6 | 11.1 | 11.6 | 12.0 | 12.0 | 12.3 | 11.8 | 11.1 | |
| 10 m | 8.5 | 9.0 | 9.4 | 9.9 | 10.2 | 10.5 | 9.8 | 9.6 | 10.5 | 11.0 | 11.6 | 11.9 | 12.0 | 12.4 | 11.6 | 10.9 | |
| 15 m | 7.7 | 8.9 | 9.4 | 9.9 | 10.3 | 10.4 | 9.7 | 9.7 | 10.5 | 11.0 | 11.7 | 11.8 | 12.0 | 12.3 | 11.6 | 10.9 | |
| 20 m | 5.9 | 7.5 | 8.8 | 9.8 | 10.3 | 10.4 | 9.7 | 9.6 | 10.5 | 11.0 | 11.6 | 11.8 | 11.9 | 12.1 | 11.6 | 10.6 | |
| 30 m | 7.8 | 7.7 | 7.1 | 7.1 | 8.9 | 10.3 | 9.6 | 9.6 | 10.5 | 11.0 | 11.6 | 11.8 | 11.8 | 12.0 | 11.2 | 10.5 | |
| 40 m | 8.1 | 8.6 | 7.3 | 6.8 | 7.3 | 9.3 | 9.1 | 10.1 | 10.5 | 11.0 | 11.2 | 11.6 | 11.8 | 11.8 | 11.0 | 10.3 | |
| 60 m | 9.2 | 9.0 | 8.3 | 7.0 | 6.6 | 7.0 | 6.4 | 10.1 | 10.5 | 10.9 | 11.2 | 11.0 | 11.2 | 11.5 | 10.7 | 10.2 | |
| 80 m | 6.9 | 7.6 | 7.2 | 5.8 | 4.1 | 5.2 | 5.6 | 6.9 | 10.4 | 11.2 | 11.0 | 10.9 | 10.1 | 10.6 | 9.9 | 9.2 | |
| Bottom from l m | 2.5 | 3.6 | 4.1 | 3.8 | 3.6 | 2.8 | 5.0 | 3.9 | 10.2 | 11.1 | 11.0 | 11.0 | 10.0 | 10 2 | 9.3 | 8.8 | |
| Snow Water Equivalent (mm) | |||||||||||||||||
| Observation Point | Month-Year | Oct-09 | Nov-09 | Dec-09 | Jan-10 | Feb-10 | Mar-10 | Apr-10 | May-10 | ||||||||
| 12/1 | 12/23 | 1/9 | 1/21 | 2/8 | 2/22 | 3/5 | 3/22 | 4/2 | |||||||||
| Yanagase | Mid-mountain areas | 0 | 84 | 320 | 354 | 424 | 398 | 83 | 0 | 0 | |||||||
| Nakakawachi | Mountain areas | 0 | 195 | 432 | 604 | 716 | 779 | 621 | 382 | 0 | |||||||
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Iwaki, M.; Yamashiki, Y.; Toda, T.; Jiao, C.; Kumagai, M. Estimation of the Average Retention Time of Precipitation at the Surface of a Catchment Area for Lake Biwa. Water 2021, 13, 1711. https://doi.org/10.3390/w13121711
Iwaki M, Yamashiki Y, Toda T, Jiao C, Kumagai M. Estimation of the Average Retention Time of Precipitation at the Surface of a Catchment Area for Lake Biwa. Water. 2021; 13(12):1711. https://doi.org/10.3390/w13121711
Chicago/Turabian StyleIwaki, Maho, Yosuke Yamashiki, Takashi Toda, Chunmeng Jiao, and Michio Kumagai. 2021. "Estimation of the Average Retention Time of Precipitation at the Surface of a Catchment Area for Lake Biwa" Water 13, no. 12: 1711. https://doi.org/10.3390/w13121711
APA StyleIwaki, M., Yamashiki, Y., Toda, T., Jiao, C., & Kumagai, M. (2021). Estimation of the Average Retention Time of Precipitation at the Surface of a Catchment Area for Lake Biwa. Water, 13(12), 1711. https://doi.org/10.3390/w13121711






