Economic Determinants of Industrial Water Demand: A Review of the Applied Research Literature
Abstract
1. Introduction
2. A General Overview
3. Methodological Issues
3.1. Data and Problems Linked to Lack of Information
3.2. Specification of Water Price
3.3. The Estimated Function
3.4. Estimation Techniques
4. Elasticities Obtained
4.1. Total Intake Water and Publicly Supplied Water
4.2. Other Water Inputs: Self-Supplied and Recirculated Water
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- UN Environment. Global Environment Outlook—GEO-6: Healthy Planet, Healthy People; United Nations Environment Programme (UNEP): Nairobi, Kenya, 2019. [Google Scholar]
- World Bank. Water Resources Management; World Bank: Washington, DC, USA, 1993. [Google Scholar]
- Organisation for Economic Co-operation and Development (OECD). Managing Water for All. An OECD Perspective on Pricing and Financing; OECD Publishing: Paris, France, 2009. [Google Scholar]
- European Environment Agency (EEA). Towards Efficient Use of Water Resources in Europe; EEA Report 1/2012; EEA: Copenhagen, Denmark, 2012.
- United Nations World Water Assessment Programme (WWAP). The United Nations World Water Development Report 2017: Wastewater: The Untapped Resource; UNESCO: Paris, France, 2017. [Google Scholar]
- Renzetti, S. Commercial and industrial water demands. In The Economics of Water Demand; Renzetti, S., Ed.; Kluwer Academic: London, UK, 2002; pp. 35–49. [Google Scholar]
- De Gispert, C. The Economic Analysis of Industrial Water Demand: A Review. Environ. Plan. C Gov. Policy 2004, 22, 15–30. [Google Scholar] [CrossRef]
- Worthington, A. Commercial and industrial water demand estimation: Theoretical and methodological guidelines for applied economics research. Estud. Econ. Apl. 2010, 28, 237–258. [Google Scholar]
- Arbués, F.; García Valiñas, M.A.; Martínez-Espiñeira, R. Estimation of residential water demand: A state-of-the-art review. J. Socio Econ. 2003, 32, 81–102. [Google Scholar] [CrossRef]
- Dalhuisen, J.M.; Florax, R.J.G.M.; de Groot, H.L.F.; Nijkamp, P. Price and income elasticity of residential water demand: A meta-analysis. Land Econ. 2003, 79, 292–308. [Google Scholar] [CrossRef]
- Worthington, A.C.; Hoffman, M. An empirical survey of residential water demand modeling. J. Econ. Surv. 2008, 22, 842–871. [Google Scholar] [CrossRef]
- Nauges, C.; Whittington, D. Estimation of water demand in developing countries: An overview. World Bank Res. Obs. 2009, 25, 263–294. [Google Scholar] [CrossRef]
- Sebri, M. A meta-analysis of residential water demand studies. Environ. Dev. Sustain. 2013, 16, 499–520. [Google Scholar] [CrossRef]
- Bich-Ngoc, N.; Teller, J. A review of residential water consumption determinants. In Computational Science and Its Applications–ICCSA 2018, Melbourne, Australia, 2–5 July 2018; Gervasi, O., Murgante, B., Misra, S., Stankova, E., Torre, C.M., Rocha, A.M.A.C., Taniar, D., Apduhan, B.O., Tarantino, E., Ryu, Y., Eds.; Springer: Cham, Germany, 2018; pp. 685–696. [Google Scholar]
- Marzano, R.; Rougé, C.; Garrone, P.; Grilli, L.; Harou, J.; Pulido-Valazquez, M. Determinants of the price response to residential water tariffs: Meta-analysis and beyond. Environ. Model. Softw. 2018, 101, 236–248. [Google Scholar] [CrossRef]
- Dige, G.; De Paoli, G.; Agenais, A.L.; Strosser, P.; Anzaldua, G.; Rouillard, J.; Trolzsch, J.; Hizmann, M. Pricing and Non-Pricing Measures for Managing Water Demand in Europe; Service Contract No 3415/B2015/EEA.56130; European Environment Agency: Copenhagen, Denmark, 2017.
- Turnovsky, S. The demand for water: Some empirical evidence on consumers’ commodity uncertain in supply. Water Resour. Res. 1969, 5, 350–361. [Google Scholar] [CrossRef]
- Grebenstein, C.R.; Field, B.C. Substituting for water inputs in U.S. manufacturing. Water Resour. Res. 1979, 15, 228–232. [Google Scholar] [CrossRef]
- Berndt, E.; Wood, D.O. Technology, prices, and the derived demand for energy. Rev. Econ. Stat. 1975, 57, 376–384. [Google Scholar] [CrossRef]
- Griffin, J.M.; Gregory, P.R. An intercountry translog model of energy substitution responses. Am. Econ. Rev. 1976, 66, 845–857. [Google Scholar]
- Moroney, J.R.; Toevs, A. Factor costs and factor use: An analysis of labour, capital and natural resource inputs. South. Econ. J. 1977, 44, 222–239. [Google Scholar] [CrossRef]
- Babin, F.J.; Willis, C.E.; Allen, G. Estimation of substitution possibilities between water and other production inputs. Am. J. Agric. Econ. 1982, 64, 148–151. [Google Scholar] [CrossRef]
- Ziegler, J.A.; Bell, S.E. Estimating demand for intake water by self-supplied firms. Water Resour. Res. 1984, 20, 4–8. [Google Scholar] [CrossRef]
- Dupont, D.P.; Renzetti, S. Water use in the Canadian food processing industry. Can. J. Agric. Econ. 1998, 46, 83–92. [Google Scholar] [CrossRef]
- Malla, P.B.; Gopalakrishnan, C. The economics of urban water demand: The case of industrial and commercial water use in Hawaii. Int. J. Water Resour. Dev. 1999, 15, 367–374. [Google Scholar] [CrossRef]
- Linz, T.; Tsegai, D.W. Industrial Water Demand Analysis in the Middle Olifants Sub-Basin of South Africa; Center for Development Research (ZEF), Bonn University: Bonn, Germany, 2009. [Google Scholar]
- Lynne, G.D. Water price responsiveness and administrative regulation: The Florida example. South. J. Agric. Econ. 1977, 9, 137–143. [Google Scholar] [CrossRef]
- Lynne, G.D.; Luppold, W.; Kiker, C. Water price responsiveness of commercial establishments. J. Am. Water Resour. Assoc. 1978, 14, 719–729. [Google Scholar] [CrossRef]
- Hussain, I.; Thrikawala, S.; Barker, R. Economic analysis of residential, commercial and industrial uses of water in Sri Lanka. Water Int. 2002, 27, 183–193. [Google Scholar] [CrossRef]
- Angulo, A.M.; Atwi, M.; Barberán, R.; Mur, J. Economic analysis of the water demand in the hotels and restaurants sector: Shadow prices and elasticities. Water Resour. Res. 2014, 50, 6577–6591. [Google Scholar] [CrossRef]
- Deyà-Tortella, B.; Garcia, C.; Nilsson, W.; Tirado, D. The effect of the water tariff structures on the water consumption in Mallorcan hotels. Water Resour. Res. 2016, 52, 6386–6403. [Google Scholar] [CrossRef]
- Wang, H.; Lall, S. Valuing water for Chinese industries: A marginal productivity analysis. Appl. Econ. 2002, 34, 759–765. [Google Scholar] [CrossRef]
- Dachraoui, K.; Harchaoui, T.M. Water Use, Shadow Prices and the Canadian Business Sector Productivity Performance; Statistics Canada: Ottawa, ON, Canada, 2004.
- Nahman, A.; De Lange, W. Valuing Water for South African Industries: A Production Function Approach; CSIR Report No. CSIR/NRE/SUSET/ER/2012/0049/A; Council for Scientific and Industrial Research: Pretoria, South Africa, 2012. [Google Scholar]
- Gracia-de-Rentería, P.; Barberán, R.; Mur, J. Urban water demand for industrial uses in Spain. Urban Water J. 2019, 16, 114–124. [Google Scholar] [CrossRef]
- Gracia-de-Rentería, P.; Barberán, R.; Mur, J. Urban water demand for manufacturing, construction and service industries. A microdata analysis. AQUA-Water Infrastruct. Ecosyst. Soc. 2021, 70, 274–288. [Google Scholar]
- Revollo-Fernández, D.A.; Rodríguez-Tapia, L.; Morales-Novelo, J.A. Economic value of water in the manufacturing industry located in the Valley of Mexico Basin, Mexico. Water Resour. Econ. 2020, 30, 100138. [Google Scholar] [CrossRef]
- Vásquez-Lavín, F.; Vargas, L.; Hernández, J.I.; Ponce, R.D. Water demand in the Chilean manufacturing industry: Analysis of the economic value of water and demand elasticities. Water Resour. Econ. 2020, 32, 100159. [Google Scholar] [CrossRef]
- Dupont, D.P.; Renzetti, S. The role of water in manufacturing. Environ. Resour. Econ. 2001, 18, 411–432. [Google Scholar] [CrossRef]
- Féres, J.; Reynaud, A. Assessing the impact of environmental regulation on industrial water use: Evidence from Brazil. Land Econ. 2005, 81, 396–411. [Google Scholar] [CrossRef]
- Kumar, S. Analysing industrial water demand in India: An input distance function approach. Water Policy 2006, 8, 15–29. [Google Scholar] [CrossRef]
- Vallés, J.; Zárate, A. Environmental taxation and industrial water use in Spain. Investig. Reg. 2013, 34, 133–164. [Google Scholar]
- Nauges, C.; Strand, J. Estimation of non-tap water demand in Central American cities. Resour. Energy Econ. 2007, 29, 165–182. [Google Scholar] [CrossRef]
- Cheesman, J.; Bennett, J.; Son, T.V.H. Estimating household water demand using revealed and contingent behaviors: Evidence from Vietnam. Water Resour. Res. 2008, 44, W11428. [Google Scholar] [CrossRef]
- Nauges, C.; Van der Berg, C. Demand for piped and non-piped water supply services: Evidence from Southwest Sri Lanka. Environ. Resour. Econ. 2009, 42, 535–549. [Google Scholar] [CrossRef]
- Coulibaly, L.; Jakus, P.M.; Keith, J.E. Modeling water demand when households have multiple sources of water. Water Resour. Res. 2014, 50, 6002–6014. [Google Scholar] [CrossRef]
- De Rooy, J. Price responsiveness of the industrial demand for water. Water Resour. Res. 1974, 10, 403–406. [Google Scholar] [CrossRef]
- Renzetti, S. An econometric study of industrial water demands in British Columbia, Canada. Water Resour. Res. 1988, 24, 1569–1573. [Google Scholar] [CrossRef]
- Renzetti, S. Estimating the structure of industrial water demands: The case of Canadian manufacturing. Land Econ. 1992, 68, 396–404. [Google Scholar] [CrossRef]
- Bruneau, J.; Renzetti, S.; Villeneuve, M. Manufacturing firms’ demand for water recirculation. Can. J. Agric. Econ. 2010, 58, 515–530. [Google Scholar] [CrossRef]
- Féres, J.; Reynaud, A.; Thomas, A. Water reuse in Brazilian manufacturing firms. Appl. Econ. 2012, 44, 1417–1427. [Google Scholar] [CrossRef]
- Bruneau, J.; Renzetti, S. A panel study of water recirculation in manufacturing plants. Can. Water Resour. J. 2014, 39, 384–394. [Google Scholar] [CrossRef]
- Renzetti, S. Examining the differences in self- and publicly supplied firms’ water demands. Land Econ. 1993, 69, 181–188. [Google Scholar] [CrossRef]
- Reynaud, A. An econometric estimation of industrial water demand in France. Environ. Resour. Econ. 2003, 25, 213–232. [Google Scholar] [CrossRef]
- Gracia-de-Rentería, P.; Barberán, R.; Mur, J. The groundwater demand for industrial uses in areas with access to drinking publicly-supplied water: A microdata analysis. Water 2020, 12, 198. [Google Scholar] [CrossRef]
- Arbués, F.; García-Valiñas, M.A.; Villanúa, I. Making decisions on industrial water sources: The case of Zaragoza, Spain. Urban Water J. 2020, 17, 122–135. [Google Scholar] [CrossRef]
- Tobarra-González, M.A. The Value of Water in the Manufacture Industry and its Implications for Water Demand Policies. The Case of Chile. Estud. Econ. Apl. 2018, 36, 945–960. [Google Scholar] [CrossRef]
- Moeltner, K.; Stoddard, S. A panel data analysis of commercial customers’ water price responsiveness under block rates. Water Resour. Res. 2004, 40, W01401. [Google Scholar] [CrossRef]
- Arbués, F.; García-Valiñas, M.A.; Villanúa, I. Urban water demand for service and industrial use: The case of Zaragoza. Water Resour. Manag. 2010, 24, 4033–4048. [Google Scholar] [CrossRef]
- Zhou, Y.; Tol, R.S.J. Water use in China’s Domestic, Industrial and Agricultural Sectors: An Empirical Analysis; Working Paper FNU-67; Research Unit Sustainability and Global Change, Hamburg University and Centre for Marine and Atmospheric Science: Hamburg, Germany, 2005. [Google Scholar]
- Bell, D.R.; Griffin, R.C. An Economic Investigation of Urban Water Demand in the U.S; Technical Report TR-331; Texas Water Resources Institute, Texas A&M University: College Station, TX, USA, 2008. [Google Scholar]
- Canizales, R.; Bravo, H.M. Estudio Sobre Valoración Económica y Financiera del Agua Para el Uso Industrial del Organismo de Cuenca Lema Santiago Pacífico; Technical Report; Conagua: Mexico, DF, USA, 2011. [Google Scholar]
- Schneider, M.; Whitlatch, E.E. User-specific water demand elasticities. J. Water Resour. Plan. Manag. 1991, 117, 52–73. [Google Scholar] [CrossRef]
- Onjala, J. Industrial Water Demand in Kenya: Industry Behavior When Tariffs are Not Binding; Working Paper; Roskilde University: Roskilde, Denmark, 2001. [Google Scholar]
- Mitchell, G.; McDonald, T.; Wattage, P.; Williamson, P. A standard industrial classification coded strategic planning model of industrial and commercial water demand for U.K. regions. Water Environ. J. 2000, 14, 226–232. [Google Scholar] [CrossRef]
- Gómez-Ugalde, S.C.; Mora-Flores, J.; García-Salazar, J.A.; Valdivia-Alcalá, R. Demanda de agua para uso residencial y comercial. Terra Latinoam. 2012, 30, 337–342. [Google Scholar]
- Stone, J.C.; Whittington, D. Industrial Water Demands. In Modeling Water Demands; Kindler, J., Russell, C.S., Eds.; Academic Press: London, UK, 1984; pp. 51–100. [Google Scholar]
- Christensen, L.R.; Jorgeson, D.W. The measurement of U.S. real capital input, 1929–1967. Rev. Income Wealth 1969, 15, 293–320. [Google Scholar] [CrossRef]
- Gaudet, G.O.; May, J.D.; McFetridge, D.G. Optimal capital accumulation: The neoclassical framework in a Canadian context. Rev. Econ. Stat. 1976, 58, 269–273. [Google Scholar] [CrossRef]
- García-Valiñas, M.A. Fijación de precios para el servicio municipal de suministro de agua: Un ejercicio de análisis de bienestar. Hacienda Pública Española 2005, 172, 119–142. [Google Scholar]
- Organisation for Economic Co-operation and Development (OECD). Pricing Water Resources and Water and Sanitation Services; OECD Publishing: Paris, France, 2010. [Google Scholar]
- Gibbs, K. Price variable in residential water demand models. Water Resour. Res. 1978, 14, 15–18. [Google Scholar] [CrossRef]
- Billings, R.B.; Agthe, D.E. Price elasticities for water: A case of increasing block rates. Land Econ. 1980, 56, 73–84. [Google Scholar] [CrossRef]
- Foster, H.S.; Beattie, B. Urban residential demand for water in the United States: Reply. Land Econ. 1981, 57, 257–265. [Google Scholar] [CrossRef]
- Opaluch, J.J. Urban residential demand for water in the United States: Further discussion. Land Econ. 1982, 58, 224–227. [Google Scholar] [CrossRef]
- Nieswiadomy, M.L.; Molina, D.J. A note on price perception in water demand models. Land Econ. 1991, 67, 352–359. [Google Scholar] [CrossRef]
- Barkatullah, N. OLS and Instrumental Variable Price Elasticity Estimates for Water in Mixed-Effects Model Under Multiple Tariff Structure; Working Paper No. 226; Department of Economics, University of Sydney: Sydney, Australia, 1996. [Google Scholar]
- Martínez-Espiñeira, R. Price specification issues under block tariffs: A Spanish case study. Water Policy 2003, 5, 237–256. [Google Scholar] [CrossRef]
- Taylor, R.G.; McKean, J.R.; Young, R.A. Alternative price specifications for estimating residential water demand with fixed fees. Land Econ. 2004, 80, 463–475. [Google Scholar] [CrossRef]
- Ruijs, A.; Zimmermann, A.; Van der Berg, M. Demand and distributional effects of water pricing policies. Ecol. Econ. 2008, 66, 506–516. [Google Scholar] [CrossRef]
- Baerenklau, K.A.; Schwabe, K.A.; Dinar, A. The residential water demand effect of increasing block rate water budgets. Land Econ. 2014, 90, 683–699. [Google Scholar] [CrossRef]
- Williams, M.; Suh, B. The demand for urban water by customer class. Appl. Econ. 1986, 18, 1275–1289. [Google Scholar] [CrossRef]
- Taylor, L.D. The demand for electricity: A survey. Bell J. Econ. 1975, 6, 74–110. [Google Scholar] [CrossRef]
- Nordin, J.A. A proposed modification of Taylor’s demand analysis: Comment. Bell J. Econ. 1976, 7, 719–721. [Google Scholar] [CrossRef]
- Shin, J.S. Perception of price when price information is costly: Evidence for residential electricity demand. Rev. Econ. Stat. 1985, 67, 591–598. [Google Scholar] [CrossRef]
- Polzin, P.E. The specification of price in studies of consumer demand under block price scheduling: Additional empirical evidence. Land Econ. 1984, 60, 306–309. [Google Scholar] [CrossRef]
- Borenstein, S. To What Electricity Price do Consumers Respond? Residential Demand Elasticity under Increasing-Block Pricing; Working Paper; University of California at Berkeley: Berkeley, CA, USA, 2009. [Google Scholar]
- Ito, K. Do consumers respond to marginal or average price? Evidence from nonlinear electricity pricing. Am. Econ. Rev. 2014, 104, 537–563. [Google Scholar] [CrossRef]
- Binet, M.E.; Carlevaro, F.; Paul, M. Estimation of residential water demand with imperfect price perception. Environ. Resour. Econ. 2014, 59, 561–581. [Google Scholar] [CrossRef]
- Wichman, C.J. Perceived price in residential water demand: Evidence from a natural experiment. J. Econ. Behav. Organ. 2014, 107, 308–323. [Google Scholar] [CrossRef]
- Almendarez-Hernández, M.A.; Avilés, G.; Hernández, V.; Ortega-Rubio, S.; Beltrán, L.F. Residential water demand in a Mexican biosphere reserve: Evidence of the effects of perceived price. Water 2016, 8, 428. [Google Scholar] [CrossRef]
- Arbués, F.; Barberán, R.; Villanúa, I. Price impact on urban residential water demand: A dynamic panel data approach. Water Resour. Res. 2004, 40, W11402. [Google Scholar] [CrossRef]
- Chambers, R. Applied Production Analysis: A Dual Approach; Cambridge University Press: Cambridge, UK, 1988. [Google Scholar]
- Christensen, L.R.; Jorgeson, D.W.; Lau, L.J. Conjugate duality and the trascendental logarithmic production function. Econometrica 1971, 39, 255–256. [Google Scholar]
- Revankar, N.S. A class of variable elasticity of substitution production functions. Econometrica 1971, 39, 61–71. [Google Scholar] [CrossRef]
- McCarthy, M.D. Approximation of the CES production function: A comment. Int. Econ. Rev. 1967, 8, 190–192. [Google Scholar] [CrossRef]
- Diewert, W.E. An application of the Shephard duality theorem: A generalized Leontief production function. J. Political Econ. 1971, 79, 481–507. [Google Scholar] [CrossRef]
- Cardoso, M.L. Modeling Portuguese Water Demand with Quantile Regression. Ph.D. Thesis, University Institute of Lisbon, Lisbon, Portugal, 2013. [Google Scholar]
- Siddiquee, M.S.H.; Ahamed, R. Exploring Water Consumption in Dhaka City Using Instrumental Variables Regression Approaches. Environ. Process. 2020, 7, 1255–1275. [Google Scholar] [CrossRef]
- Höglund, L. Household demand for water in Sweden with implications of a potential tax on water use. Water Resour. Res. 1999, 35, 3853–3863. [Google Scholar] [CrossRef]
- Nauges, C.; Thomas, A. Long-run study of residential water consumption with an application to a sample of French communities. Environ. Resour. Econ. 2003, 26, 25–43. [Google Scholar] [CrossRef]
- Martínez-Espiñeira, R. An estimation of residential water demand using co-integration and error correction techniques. J. Appl. Econ. 2007, 10, 161–184. [Google Scholar] [CrossRef]
- Zaied, Y.B.; Binet, M.E. Modeling seasonality in residential water demand: The case of Tunisia. Appl. Econ. 2015, 47, 1983–1996. [Google Scholar] [CrossRef]
- Zaied, Y.B.; Cheikh, N.B. Modeling regional water consumption in Tunisia using panel cointegration second generation tests. J. Quant. Econ. 2015, 13, 237–251. [Google Scholar] [CrossRef]
- Brookshire, D.S.; Burness, H.S.; Chermak, J.M.; Krause, K. Western urban water demand. Nat. Resour. J. 2002, 42, 873–898. [Google Scholar]
- Guerrero, H. Industrial Water Demand in Mexico: Econometric Analysis and Implications for Water Management Policy. Ph.D. Thesis, Université de Toulouse 1, Toulouse, France, 2005. [Google Scholar]
- General Assembly. Transforming Our World: The 2030 Agenda for Sustainable Development; Agenda items 15 and 116; United Nations, A/RES/70/1: New York, NY, USA, 2015. [Google Scholar]
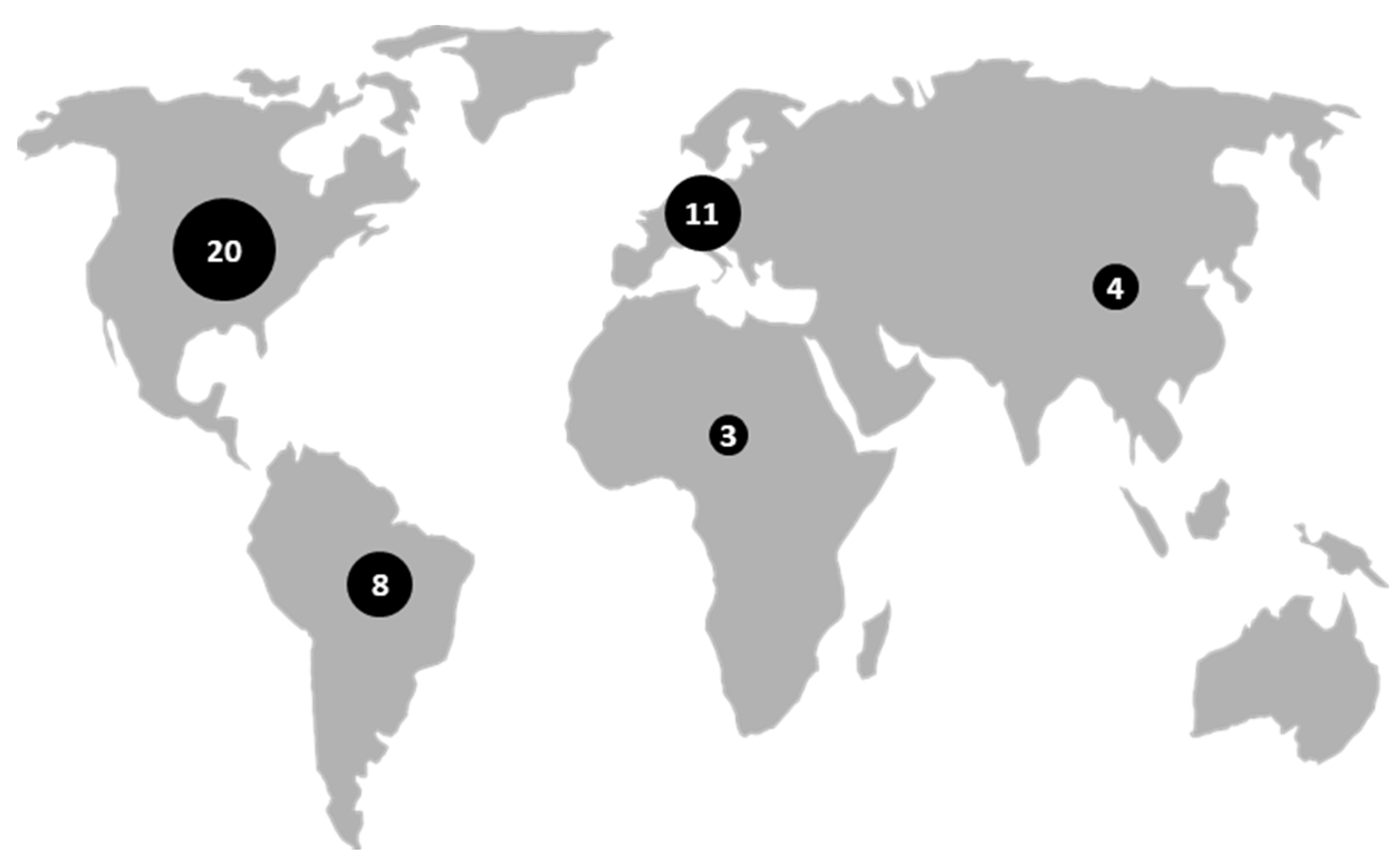
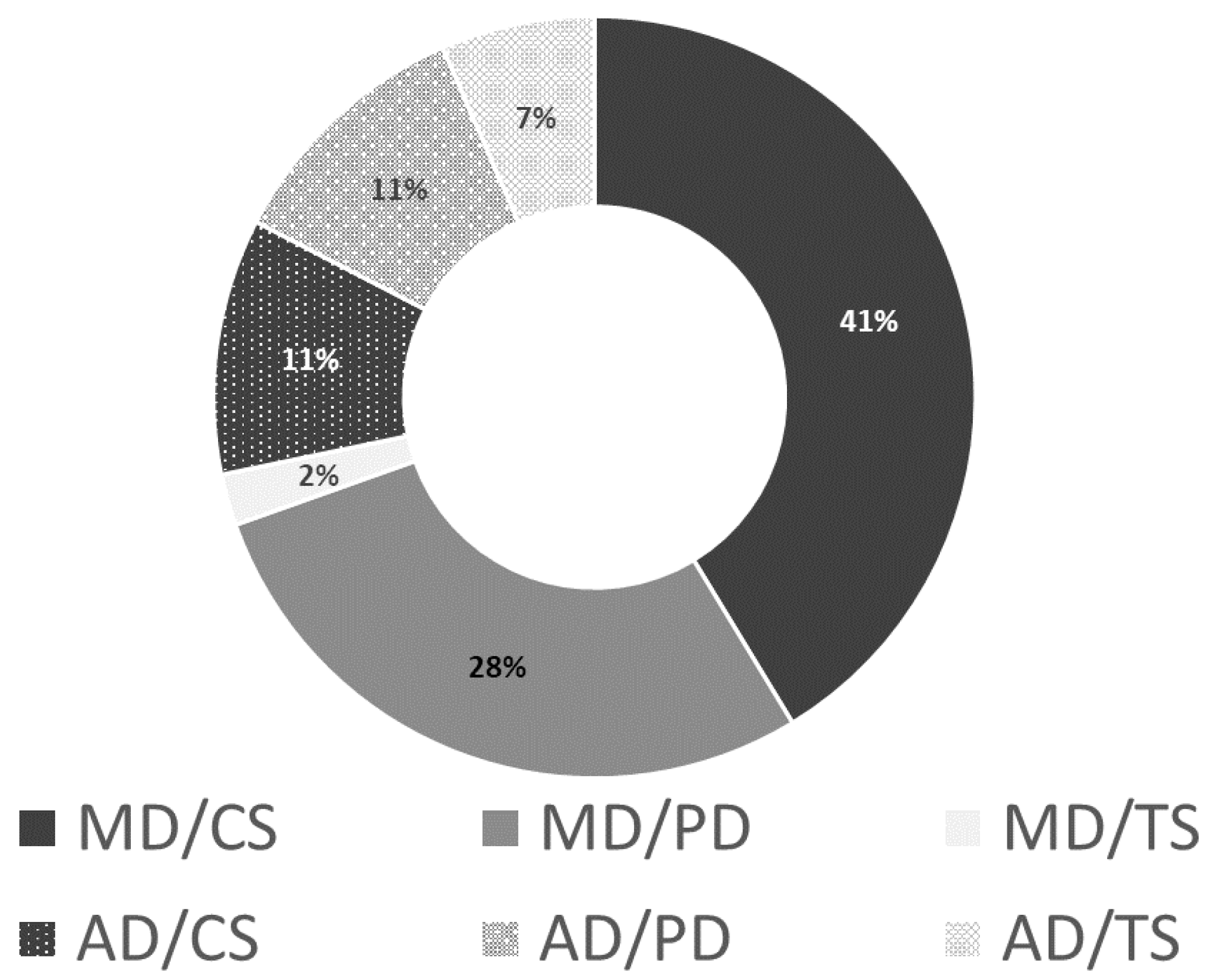
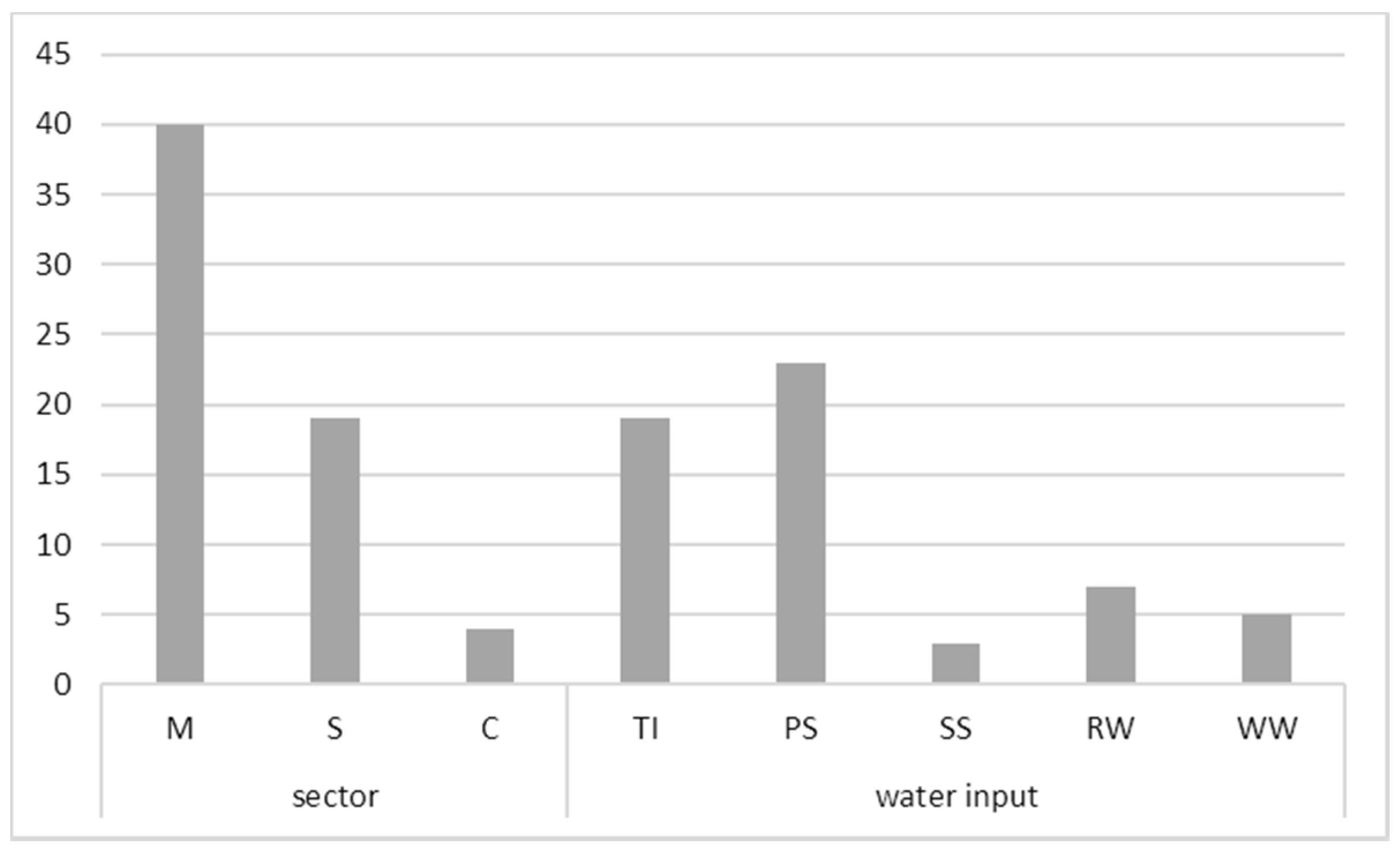
| Reference | Country | Years | Periodicity | Type of Data | Sample | Sector (Number of Subsectors) | Water Input |
|---|---|---|---|---|---|---|---|
| Angulo et al. (2014) | Spain | 1995–2006 | Annual | MD/PD | 676 firms | Hotels and restaurants (3) | PS |
| Arbués et al. (2010) | Spain | 1996–2000 | Quarterly | MD/PD | 298 firms | M and S | PS |
| Babin et al. (1982) | USA | 1973 | Annual | MD/CS | 245 firms | M (6) | PS |
| Bell and Griffin (2008) | USA | 1995–2005 | Monthly | AD/PD | 210 cities | M and S (2) | PS |
| Bruneau and Renzetti (2014) | Canada | 1986, 1991, 1996 | Annual | MD/PD | 2725 firms | M (12) | RW |
| Bruneau et al. (2010) | Canada | 1996 | Annual | MD/CS | 5532 firms | M (13) | RW |
| Canizales and Bravo (2011) | Mexico | 2003, 2008 | Annual | AD/CS | 9 States | M (5) | PS |
| Dachraoui and Harchaoui (2004) | Canada | 1981, 1986, 1991, 1996 | Annual | AD/PD | 36 sectors | M, C, and S (36) | TI |
| De Rooy (1974) | USA | 1965 | Annual | MD/CS | 30 firms | Chemical | TI |
| Deyà–Tortella et al. (2016) | Spain | 2007 | Annual | MD/CS | 134 firms | Hotels | PS |
| Dupont and Renzetti (1998) | Canada | 1991 | Annual | MD/CS | 88 firms | Food (3) | TI, RW, WW |
| Dupont and Renzetti (2001) | Canada | 1981, 1986, 1991 | Annual | AD/PD | 58 observations (sector-region) | M | PS, RW |
| Féres et al. (2012) | Brazil | 2002 | Annual | MD/CS | 447 firms | M (6) | RW |
| Féres and Reynaud (2005) | Brazil | 1999 | Annual | MD/CS | 404 firms | M | TI, WW |
| García–Valiñas (2005) | Spain | 1994–2000 | Quarterly | MD/PD | 80 firms | M and S (3) | PS |
| Gómez-Ugalde et al. (2012) | Mexico | 2000–2009 | Bimonthly | AD/TS | Service sector | S | PS |
| Gracia-de-Rentería et al. (2019) | Spain | 1993–2013 | Annual | AD/PD | 187 observations (sector-region) | M (11) | PS |
| Gracia-de-Rentería et al. (2020) | Spain | 2012 | Annual | MD/CS | 2579 firms | M and S (2) | SS |
| Gracia-de-Rentería et al. (2021) | Spain | 1993–2012 | Annual | MD/PD | 8615 firms | M, C, and S (24) | PS |
| Grebenstein and Field (1979) | USA | 1973 | Annual | AD/CS | All SIC two-digit sectors | M | PS |
| Guerrero (2005) | Mexico | 1994 | Annual | MD/CS | 500 firms | M | TI |
| Hussain et al. (2002) | Sri Lanka | 1994–1998 | Monthly | AD/TS | Manufacturing and commercial sectors | M and S (2) | PS |
| Kumar (2006) | India | 1996–1999 | Annual | MD/PD | 92 firms | M (9) | TI |
| Linz and Tsegai (2009) | South Africa | 2004–2009 | Monthly | MD/TS | 5 mines | Mining | TI |
| Lynne (1977) | USA | 1975 | Annual | MD/CS | 156 firms | Retail trade and accommodation (4) | PS |
| Lynne et al. (1978) | USA | 1976 | Monthly | MD/CS | 137–190 firms | Retail trade and accommodation (5) | PS |
| Malla and Gopalakrishnan (1999) | USA | n.s. | Monthly | MD/PD | 13 firms | Energy, food, construction, and retail trade (2) | TI |
| Mitchell et al. (2000) | UK | 1974–1995 | Annual | AD/TS | Non-domestic sector | Non-domestic sector | PS |
| Moeltner and Stoddard (2004) | USA | 1993–2000 | Monthly | MD/PD | 348 firms | S (5) | PS |
| Nahman and De Lange (2012) | South Africa | 2011 | Annual | MD/CS | 58 firms | M (12) | TI |
| Onjala (2001) | Kenia | 1990–2000 | Monthly | MD/PD | 51 firms | M (3) | TI |
| Renzetti (1988) | Canada | 1981 | Annual | MD/CS | 372 firms | M (4) | TI, RW, WW |
| Renzetti (1992) | Canada | 1985 | Annual | MD/CS | 2000 firms | M (7) | TI, RW, WW |
| Renzetti (1993) | Canada | 1985 | Annual | MD/CS | 2000 firms | M (6) | PS, SS |
| Revollo–Fernández et al. (2020) | Mexico | 2013 | Annual | AD/CS | 895 observations (sector-region) | M (15) | TI |
| Reynaud (2003) | France | 1994–1996 | Annual | MD/PD | 51 firms | M and S (8) | PS, SS, WW |
| Scheider and Whitlatch (1991) | USA | 1959–1977 | Annual | MD/PD | 6 firms | M and S (2) | PS |
| Stone and Whittington (1984) | Netherlands | 1974 | Annual | MD/CS | 21 firms | Paper | TI |
| Tobarra–González (2018) | Chile | 2012 | Annual | MD/CS | 2339 firms | M (6) | TI |
| Turnovsky (1969) | USA | 1962, 1965 | Annual | AD/CS | 19 cities | M | PS |
| Vallés and Zárate (2013) | Spain | 2002–2003 | Annual | MD/PD | 87 firms | M and S (10) | PS |
| Vásquez–Lavín et al. (2020) | Chile | 1995–2014 | Annual | MD/PD | 10,528 firms | M (19) | TI |
| Wang and Lall (2002) | China | 1993 | Annual | MD/CS | 2000 firms | M (16) | TI |
| Williams and Suh (1986) | USA | 1976 | Annual | AD/CS | 125–140 cities | M and S | PS |
| Zhou and Tol (2005) | China | 1997–2003 | Annual | AD/PD | 31 regions | M | TI |
| Ziegler and Bell (1984) | USA | n.s. | Annual | MD/CS | 23 firms | Chemical and paper | TI |
| Variable | Specification | References |
|---|---|---|
| Cost or quantity of capital | Value of capital services | Babin et al. (1982), Dachraoui and Harchaoui (2004), Grebenstein and Field (1979) |
| Value of fixed assets | Nahman and De Lange (2012), Revollo-Fernández et al. (2020), Vallés and Zárate (2013), Wang and Lall (2002) | |
| Stock of capital | Gracia-de-Rentería et al. (2019), Kumar (2006), Tobarra-González (2018), Vásquez-Lavín et al. (2020) | |
| FCGF | Canizales and Bravo (2011) | |
| Equity and debt costs | Angulo et al. (2014), Gracia-de-Rentería et al. (2021) | |
| Financial costs | Feres and Reynaud (2005), Linz and Tsegai (2009) | |
| Price of capital | Service price of capital | Babin et al. (1982), Gracia-de-Rentería et al. (2019), Grebenstein and Field (1979) |
| Implicit rental price of capital | Dachraoui and Harchaoui (2004), Dupont and Renzetti (2001) | |
| Interest rate + depreciation rate | Feres et al. (2012), Feres and Reynaud (2005) | |
| Weighted average cost of capital | Angulo et al. (2014), Gracia-de-Rentería et al. (2021) | |
| Cost of capital per output unit | Linz and Tsegai (2009) | |
| Cost or quantity of labour | Staff expenditure | Angulo et al. (2014), Babin et al. (1982), Dachraoui and Harchaoui (2004), Dupont and Renzetti (2001), Feres and Reynaud (2005), Gracia-de-Rentería et al. (2019, 2021), Grebenstein and Field (1979), Guerrero (2005), Kumar (2006), Linz and Tsegai (2009), Reynaud (2003) |
| Number of employees | Arbués et al. (2010), Canizales and Bravo (2011), Nahman and De Lange (2012), Revollo-Fernández et al. (2020), Tobarra-González (2018), Vásquez-Lavín et al. (2020), Wang and Lall (2002) | |
| Price of labour | Average price | Angulo et al. (2014), Babin et al. (1982), Dachraoui and Harchaoui (2004), Dupont and Renzetti (2001), Feres and Reynaud (2005), Gracia-de-Rentería et al. (2019, 2021), Grebenstein and Field (1979), Guerrero (2005), Linz and Tsegai (2009), Reynaud (2003), Vallés and Zárate (2013) |
| Cost or quantity of energy | Expenditure on different energy sources | Canizales and Bravo (2011), Dupont and Renzetti (2001), Feres and Reynaud (2005), Gracia-de-Rentería et al. (2019), Tobarra-González (2018), Vásquez-Lavín et al. (2020) |
| Energy consumption | Nahman and De Lange (2012) | |
| Price of energy | Average price | Feres et al. (2012), Gómez-Ugalde et al. (2012) |
| Weighted average price of different energy sources | Dupont and Renzetti (2001), Feres and Reynaud (2005), Gracia-de-Rentería et al. (2019), Linz and Tsegai (2009) | |
| Cost or quantity of supplies | Supplies expenditure | Angulo et al. (2014), Dachraoui and Harchaoui (2004), Dupont and Renzetti (2001), Feres and Reynaud (2005), Gracia-de-Rentería et al. (2019, 2021), Guerrero (2005), Revollo-Fernández et al. (2020), Tobarra-González (2018), Vallés and Zárate (2013), Vásquez-Lavín et al. (2020) |
| Value of intermediate goods | Canizales and Bravo (2011), Kumar (2006) | |
| Price of supplies | Price index | Dachraoui and Harchaoui (2004), Dupont and Renzetti (2001), Feres and Reynaud (2005) |
| Supplies expenditure per output unit | Guerrero (2005) | |
| Treated as unobservable | Angulo et al. (2014), Gracia-de-Rentería et al. (2019, 2021) | |
| Output | Value of production or revenue firms | Angulo et al. (2014), Dupont and Renzetti (1998, 2001), Feres et al. (2012), Feres and Reynaud (2005), Gracia-de-Rentería et al. (2019, 2020, 2021), Kumar (2006), Renzetti (1992, 1993), Revollo–Fernández et al. (2020), Reynaud (2003), Tobarra–González (2018), Vallés and Zárate (2013), Vásquez–Lavín et al. (2020), Wang and Lall (2002), Williams and Suh (1986) |
| Output quantity | Guerrero (2005), Linz and Tsegai (2009) | |
| Labour force | Bruneau and Renzetti (2014), Bruneau et al. (2010), Hussain et al. (2002), Malla and Gopalakrishnan (1999), Mitchell et al. (2000), Renzetti (1988) | |
| Fiscal category of the street | García Valiñas (2005) | |
| Other regional proxies | Arbués et al. (2010), Canizales and Bravo (2011), Scheider and Whitlatch (1991), Turnovsky (1969), Zhou and Tol (2005) | |
| Price of water | Marginal price | Bruneau and Renzetti (2014), Bruneau et al. (2010), Deyà–Tortella et al. (2016), Dupont and Renzetti (1998, 2001), Gracia-de-Rentería et al. (2021), Lynne (1977), Lynne et al. (1978), Moeltner and Stoddard (2004), Onjala (2001), Renzetti (1988, 1992, 1993), Scheider and Whitlatch (1991), Vallés and Zárate (2013), Williams and Suh (1986), Ziegler and Bell (1984) |
| Average price | Angulo et al. (2014), Babin et al. (1982), Deyà–Tortella et al. (2016), De Rooy (1974), Feres et al. (2012), Feres and Reynaud (2005), García Valiñas (2005), Gómez–Ugalde et al. (2012), Gracia-de-Rentería et al. (2019, 2020, 2021), Grebenstein and Field (1979), Guerrero (2005), Hussain et al. (2002), Linz and Tsegai (2009), Malla and Gopalakrishnan (1999), Mitchell et al. (2000), Renzetti (1988), Reynaud (2003), Stone and Whittington (1984), Turnovsky (1969), Vallés and Zárate (2013), Williams and Suh (1986), Ziegler and Bell (1984), Zhou and Tol (2005) | |
| Perceived price | Arbués et al. (2010) | |
| Shadow price | Kumar (2006), Nahman and De Lange (2012), Revollo–Fernández et al. (2020), Tobarra–González (2018), Vásquez–Lavín et al. (2020), Wang and Lall (2002) |
| Function | Functional Form | Estimation Techniques | Reference | Endogeneity | Sectoral Heterogeneity |
|---|---|---|---|---|---|
| Production function | Translog | LP | Kumar (2006) | - | D |
| n.s. | Revollo–Fernández et al. (2020) | - | S | ||
| Vásquez–Lavín et al. (2020) | - | S | |||
| Wang and Lall (2002) | - | D | |||
| OLS | Cañizales and Bravo (2011) | - | - | ||
| Nahman and De Lange (2012) | - | S | |||
| Tobarra–González (2018) | - | S | |||
| Cost function | Translog | SUR | Angulo et al. (2014) | Lagged price | S |
| Babin et al. (1982) | S | ||||
| Dachraoui and Harchaoui (2004) | Lagged price | D | |||
| Dupont and Renzetti (2001) | IV | - | |||
| Feres and Reynaud (2005) | - | D | |||
| Gracia-de-Rentería et al. (2019) | Lagged price | S | |||
| Gracia-de-Rentería et al. (2021) | Lagged price | S | |||
| Grebenstein and Field (1979) | - | - | |||
| Guerrero (2005) | - | S | |||
| Linz and Tsegai (2009) | - | - | |||
| FGLS | Reynaud (2003) | - | - | ||
| 3SLS | Dupont and Renzetti (1998) | - | - | ||
| Renzetti (1992) | IV | S | |||
| Cobb– Douglas | 2SLS | Renzetti (1988) | IV | S | |
| 3SLS | Onjala (2001) | IV | S | ||
| Demand function | - | Quantile regression | Deyà–Tortella et al. (2016) | Difference variable | Q |
| Exponential | OLS | Ziegler and Bell (1984) | - | D | |
| Lineal | 2SLS | Bruneau and Renzetti (2014) | IV | D | |
| Bruneau et al. (2010) | IV | D | |||
| GLS | Scheider and Whitlatch (1991) | - | - | ||
| GMM | García Valiñas (2005) | - | D | ||
| n.s. | Mitchell et al. (2000) | - | - | ||
| OLS | Gómez–Ugalde et al. (2012) | - | - | ||
| Stone and Whittington (1984) | - | - | |||
| OLS and GLS | Malla and Gopalakrishnan (1999) | - | D | ||
| Log-lineal | 2GLS | Moeltner and Stoddard (2004) | IV | S | |
| n.s. | Lynne (1977) | - | S | ||
| Lynne et al. (1978) | - | S | |||
| OLS | Williams and Suh (1986) | - | - | ||
| Log-log | 2SGMM | Arbués et al. (2010) | - | D | |
| FGLS | Vallés and Zárate (2013) | - | D | ||
| Zhou and Tol (2005) | - | - | |||
| ML | Renzetti (1993) | IV | S | ||
| OLS | De Rooy (1974) | - | - | ||
| Feres et al. (2012) | - | D | |||
| Gracia-de-Rentería et al. (2020) | - | D | |||
| Turnovsky (1969) | - | - | |||
| Linear and log-log | GLS | Hussain et al. (2002) | - | - | |
| Square roots | GLS | Bell and Griffin (2008) | IV | - |
| Particularities of Estimation | Sector | Price Elasticity | Output Elasticity | |||
|---|---|---|---|---|---|---|
| Average | Sector with Max. Value (Elasticity) | Average | Sector with Max. Value (Elasticity) | |||
| Total intake water | ||||||
| De Rooy (1974) | Refrigeration | Chemical | −0.89 | - | 1.21 | - |
| Incorporation to product | −0.35 | - | 1.36 | - | ||
| Steam generation | −0.59 | - | 1.24 | - | ||
| Dupont and Renzetti (1998) | Food | −0.34 | Fruit (−0.38) | 0.46 | Meat (0.50) | |
| Dupont and Renzetti (2001) | M | −0.77 | - | 0.69 | - | |
| Féres et al. (2012) | Recirculation | M | −0.53 | - | 0.66 | - |
| No recirculation | −0.23 | - | 0.53 | - | ||
| Féres and Reynaud (2005) | M | −1.08 | - | 0.91 | - | |
| Guerrero (2005) | M | −0.30 | Beverage (−3.09) | - | - | |
| Kumar (2006) | M | −1.1 | Leather (−0.94) | - | - | |
| Linz and Tsegai (2009) | Mining | −0.85 | - | - | - | |
| Malla and Gopalakrishnan (1999) | OLS | I | - | Food (−0.90*) | - | Other (2.55) |
| GLS | - | Food (−0.37) | - | Food (0.25) | ||
| Nahman and De Lange (2012) | M | −3.0 | Paper (−6.81) | - | - | |
| Onjala (2001) | M | - | Paper (−0.21/−0.37) | - | ||
| Renzetti (1988) | M | −0.54/−0.12 | Light industry | 1.94/0.69 | Light industry | |
| Renzetti (1992) | M | −0.38 * | Paper (−0.59) | - | - | |
| Revollo–Fernández et al. (2020) | M | 0.06 | Chemistry (0.21) | - | - | |
| Stone and Whittington (1984) | Paper | −0.25 | - | - | - | |
| Tobarra–González (2018) | M | −1.1 | Paper (−3.17) | - | - | |
| Vásquez–Lavín et al. (2020) | M | −1.23 | Machinery (−1.50) | - | - | |
| Wang and Lall (2002) | M | −1.03 | Energy (−1.20) | - | - | |
| Zhou and Tol (2005) | M | −0.35 | - | −0.32 | - | |
| Ziegler and Bell (1984) | APW | Chemical and paper | −0.08 | - | - | - |
| MPW | 0.00001 | - | - | - | ||
| Publicly-supplied water | ||||||
| Angulo et al. (2014) | Hotels and restaurants | 0.082 * | Hotels (−0.37) | 0.398 | Hotels (0.64) | |
| Arbués et al. (2010) | Short run | I | −0.25 | 0.195 | ||
| Long run | −0.57 | 0.444 | ||||
| Babin et al. (1982) | M | −0.56 | Paper (−0.66) | - | - | |
| Bell and Griffin (2008) | Short run | M | −0.08 * | - | - | - |
| S | −0.48 * | - | - | |||
| Long run | M | 0.31 * | - | - | - | |
| S | −1.09 | - | - | - | ||
| Canizales and Bravo (2011) | Year 2003 | M | −0.08 | Sugar (−0.07) | - | - |
| Year 2008 | −0.07 | Sugar (−0.05) | - | - | ||
| Deyà–Tortella et al. (2016) | Hotels | −0.02 * | - | - | - | |
| García–Valiñas (2005) | Normal demand | I | −0.12 | - | - | - |
| Peak demand | −0.13 | - | - | - | ||
| Gómez–Ugalde et al. (2012) | S | −1.03 | - | 1.22 | - | |
| Gracia-de-Rentería et al. (2019) | M | −0.66 | Food (−1.69) | 1.07 | Other (1.52) | |
| Gracia-de-Rentería et al. (2021) | APW | I | −0.99 | - | 0.65 | - |
| M | −0.94 | Machinery (−1.22) | 0.19 | Plastic (1.06) | ||
| C | −0.93 | - | −0.10 * | - | ||
| S | −1.00 | Professional activities (−1.08) | 0.74 | Education (1.06) | ||
| MPW | I | −0.86 | - | 0.73 | - | |
| M | −0.52 | Food (−0.62) | −0.37 * | Food (0.65) | ||
| C | −0.58* | - | 2.85 | - | ||
| S | −0.88 | Real estate (−1.24) | 0.83 | Real estate (2.14) | ||
| Grebenstein and Field (1979) | AWWA data | M | −0.33 * | - | - | - |
| MM data | −0.80 | - | - | - | ||
| Hussain et al. (2002) | Log-log | M | −1.34 | - | 0.39 * | - |
| S | −0.17 | - | 0.81 | - | ||
| Linear | M | −1.15 | - | 0.34 * | - | |
| S | −0.17 | - | 0.80 | - | ||
| Lynne (1977) | S | - | Department stores (−1.33) | - | - | |
| Lynne et al. (1978) | S | - | Department stores (−1.07) | - | - | |
| Mitchell et al. (2000) | I | −0.92 | - | 2.85 | - | |
| Moeltner and Stoddard (2004) | S | - | Recreation services (−0.62) | - | - | |
| Renzetti (1993) | M | −0.75 | Food (−2.17) | 0.76 | Food (0.74) | |
| Reynaud (2003) | I | −0.29 | - | 0.34 | - | |
| M | - | Other manufactures (−0.79) | - | - | ||
| S | −0.27 | - | - | - | ||
| Scheider and Whitlatch (1991) | Short run | M | −0.44 * | - | - | - |
| S | −0.23 | - | - | - | ||
| Long run | M | −0.11 * | - | - | - | |
| S | −0.92 | - | - | - | ||
| Turnovsky (1969) | M | −0.5 | - | - | - | |
| Vallés and Zárate (2013) | APW | I | −0.01 | - | 0.301 | - |
| MPW | −0.01 | - | 0.299 | - | ||
| Williams and Suh (1986) | APW | M | −0.73 | 0.20 | ||
| S | −0.36 | 0.17 | ||||
| MPW | M | −0.44 | 0.18 | |||
| S | −0.14 * | 0.18 | ||||
| MTB1 | M | −0.72 | 0.29 | |||
| S | −0.23 * | 0.20 | ||||
| MTB2 | M | −0.97 | 0.27 | |||
| S | −0.34 | 0.20 | ||||
| MTB3 | M | −0.76 | 0.30 | |||
| S | −0.31 | 0.21 | ||||
| Self-supplied water | ||||||
| Gracia-de-Rentería et al. (2020) | M | −0.50 | 0.38 | |||
| Renzetti (1993) | M | −0.31 | Metal (−1.14) | 1.09 | Textile (1.14) | |
| Reynaud (2003) | I | 0.25 * | - | 0.58 | - | |
| M | - | Chemical (−0.06 *) | - | - | ||
| S | −0.05 * | - | - | - | ||
| Recirculated water | ||||||
| Bruneau and Renzetti (2014) | M | −0.24 | 1.04 | |||
| Bruneau et al. (2010) | M | −0.27 | 0.3851 | |||
| Dupont and Renzetti (1998) | Food | −0.82 | Meat (−1.35) | 0.48 | Milk (0.47) | |
| Dupont and Renzetti (2001) | M | −0.69 * | 0.72 | |||
| Renzetti (1988) | M | - | Light industry (−0.77) | - | Chemical (2.48) | |
| Renzetti (1992) | M | −1.83 | Textile (−1.48) | - | ||
| Reference | Elasticity | Water— Capital | Water— Labour | Water— Energy | Water—Supplies |
|---|---|---|---|---|---|
| Total intake water | |||||
| De Rooy (1974) | Cross-price elasticity | S | |||
| Dachraoui and Harchaoui (2004) | ASE | S | S | ||
| Dupont and Renzetti (2001) | Constant output cross-price elasticity | S * | S | S * | C * |
| Féres et al. (2012) | Cross-price elasticity | C | |||
| Féres and Reynaud (2005) | Cross-price elasticity | S * | S * | S | C * |
| Guerrero (2005) | Constant output cross-price elasticity, ASE, and MSE | S * | S * | ||
| Kumar (2006) | Constant output cross-price elasticity and ASE | S | C * | C | |
| MES | C * | ||||
| Linz and Tsegai (2009) | Cross-price elasticity | S | S | C | |
| Revollo–Fernández et al. (2020) | Cross-price elasticity | C * | C * | S | |
| Vásquez–Lavín et al. (2020) | Cross-price elasticity | S | S | C | S* |
| Publicly-supplied water | |||||
| Angulo et al. (2014) | ASE | S | S | S | |
| Babin et al. (1982) | Constant output cross-price elasticity | C | S | ||
| Gómez–Ugalde et al. (2012) | Cross-price elasticity | C | |||
| Gracia-de-Rentería et al. (2019) | Cross-price elasticity | C | C * | C * | S |
| Gracia-de-Rentería et al. (2021) | Cross-price elasticity | S | S | S | |
| Grebenstein and Field (1979) | Constant output cross-price elasticity | C | S | ||
| Vallés and Zárate (2013) | Cross-price elasticity | C | C | C * | |
| Reference | Elasticity | Self-Supplied— Publicly-Supplied | Recirculated—Total Intake |
|---|---|---|---|
| Bruneau et al. (2010) | Cross-price elasticity | - | S |
| Dupont and Renzetti (1998) | ASE | - | S |
| Dupont and Renzetti (2001) | Constant output cross-price elasticity | - | S |
| Féres et al. (2012) | Cross-price elasticity | - | S |
| Gracia-de-Rentería et al. (2020) | Cross-price elasticity | S | - |
| Renzetti (1988) | Constant output cross-price elasticity | - | S |
| Renzetti (1992) | ASE | - | S |
| Reynaud (2003) | Cross-price elasticity and ASE | C * | - |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Gracia-de-Rentería, P.; Barberán, R. Economic Determinants of Industrial Water Demand: A Review of the Applied Research Literature. Water 2021, 13, 1684. https://doi.org/10.3390/w13121684
Gracia-de-Rentería P, Barberán R. Economic Determinants of Industrial Water Demand: A Review of the Applied Research Literature. Water. 2021; 13(12):1684. https://doi.org/10.3390/w13121684
Chicago/Turabian StyleGracia-de-Rentería, Pilar, and Ramón Barberán. 2021. "Economic Determinants of Industrial Water Demand: A Review of the Applied Research Literature" Water 13, no. 12: 1684. https://doi.org/10.3390/w13121684
APA StyleGracia-de-Rentería, P., & Barberán, R. (2021). Economic Determinants of Industrial Water Demand: A Review of the Applied Research Literature. Water, 13(12), 1684. https://doi.org/10.3390/w13121684







