Heterogeneity in Domestic Water Demand: An Application of Multilevel Analysis to the City of Valencia (Spain)
Abstract
:1. Introduction
2. Study Area Description
3. Data and Empirical Model
3.1. Data
- Consumptionitk (Citk): water consumption (in m3) of the household i located in k, in period t.
- BillTAMERitk: billing (in euros) with TAMER tariff included for the household i located in k, in period t.
- Priceitk (Pitk): average price (in euros/m3) paid by household i located in k, in period t.
- Surfaceik (Sik): area of dwelling i located in k
- Individualsik. (Iik): residents of household i located in k.
- Incomek (Rk): income of the neighbourhood k (according to the synthetic income indicator) in the year 2011.
3.2. Empirical Model
3.3. Estimated Model
- The term is the overall average consumption over the whole period of analysis in the city of Valencia and is the average consumption for a given period t, so that the random effect is the difference between the average consumption for the period and the overall average consumption.
- Similarly, the average consumption for neighbourhood k would be , and the random effect is the difference between the average consumption of neighbourhood k and the overall average.
- The average consumption for period t and neighbourhood k is .
- The term is the difference between the observed consumption for unit itk and the predicted consumption for period t and neighbourhood k.
- The coefficient is the average consumption–price elasticity over the analysis period for the city of Valencia.
- Given a time period t, is the average consumption–price elasticity of the city of Valencia for that period.
- Equivalently, for a neighbourhood k, is the average consumption–price elasticity of the neighbourhood for all periods.
- The term is the average elasticity for a household in neighbourhood k in period t.
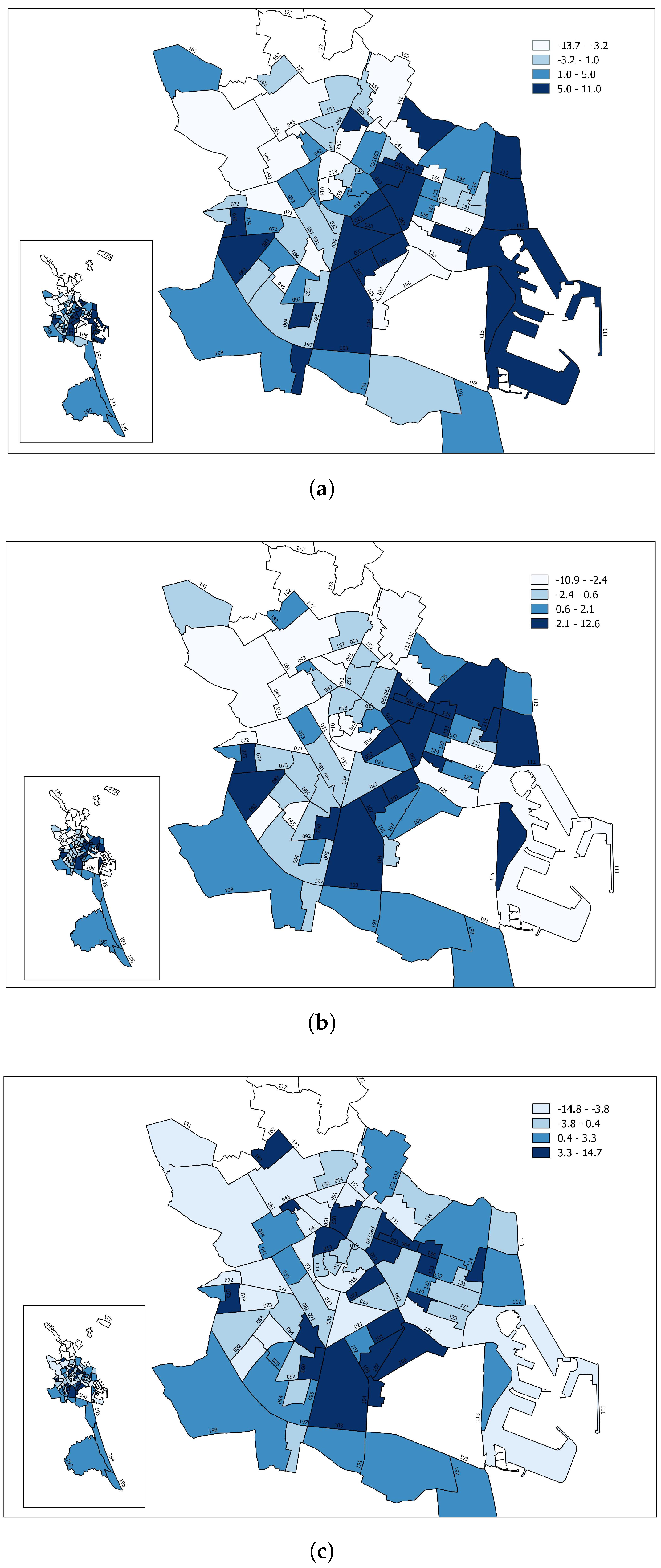
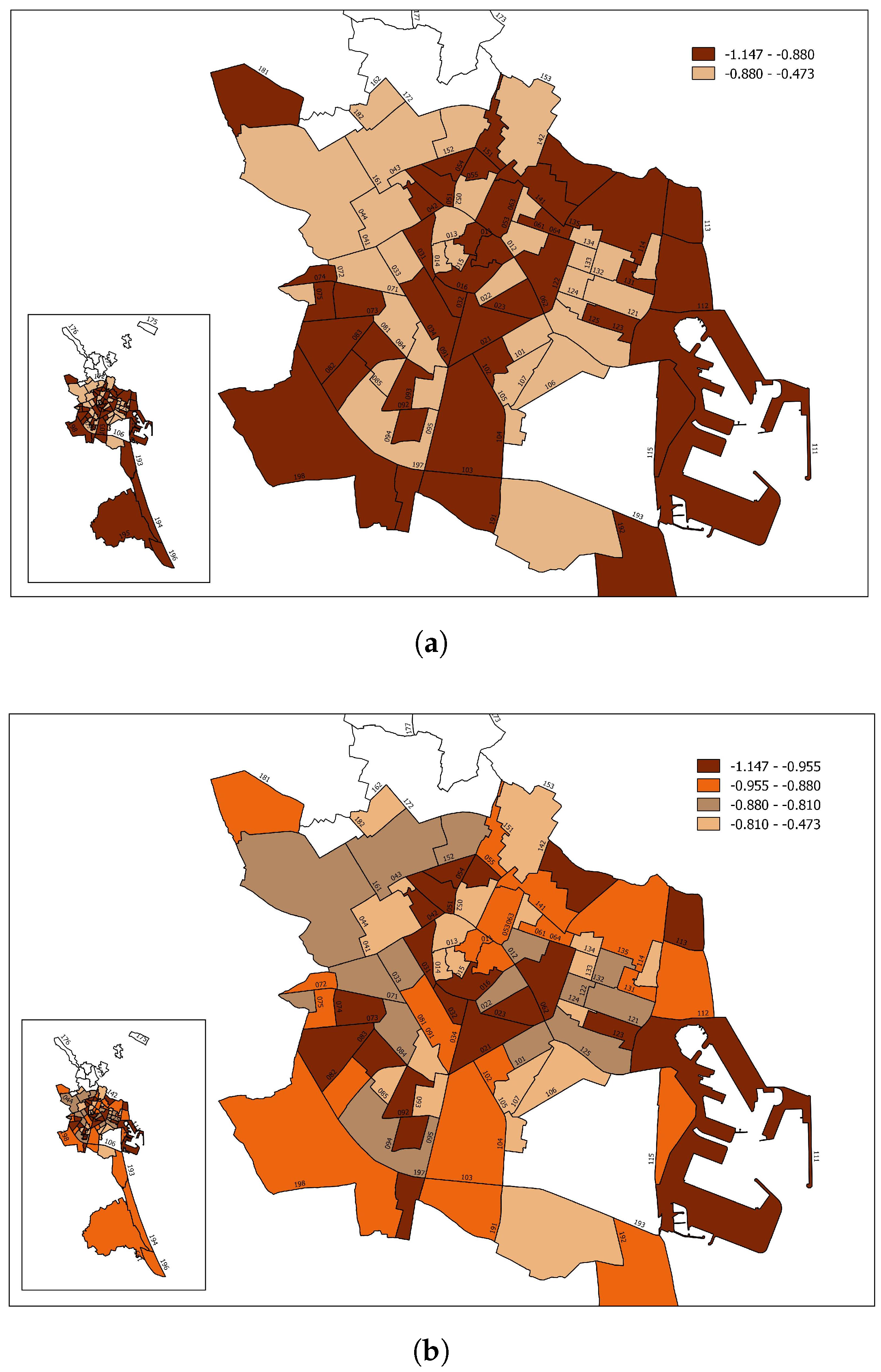
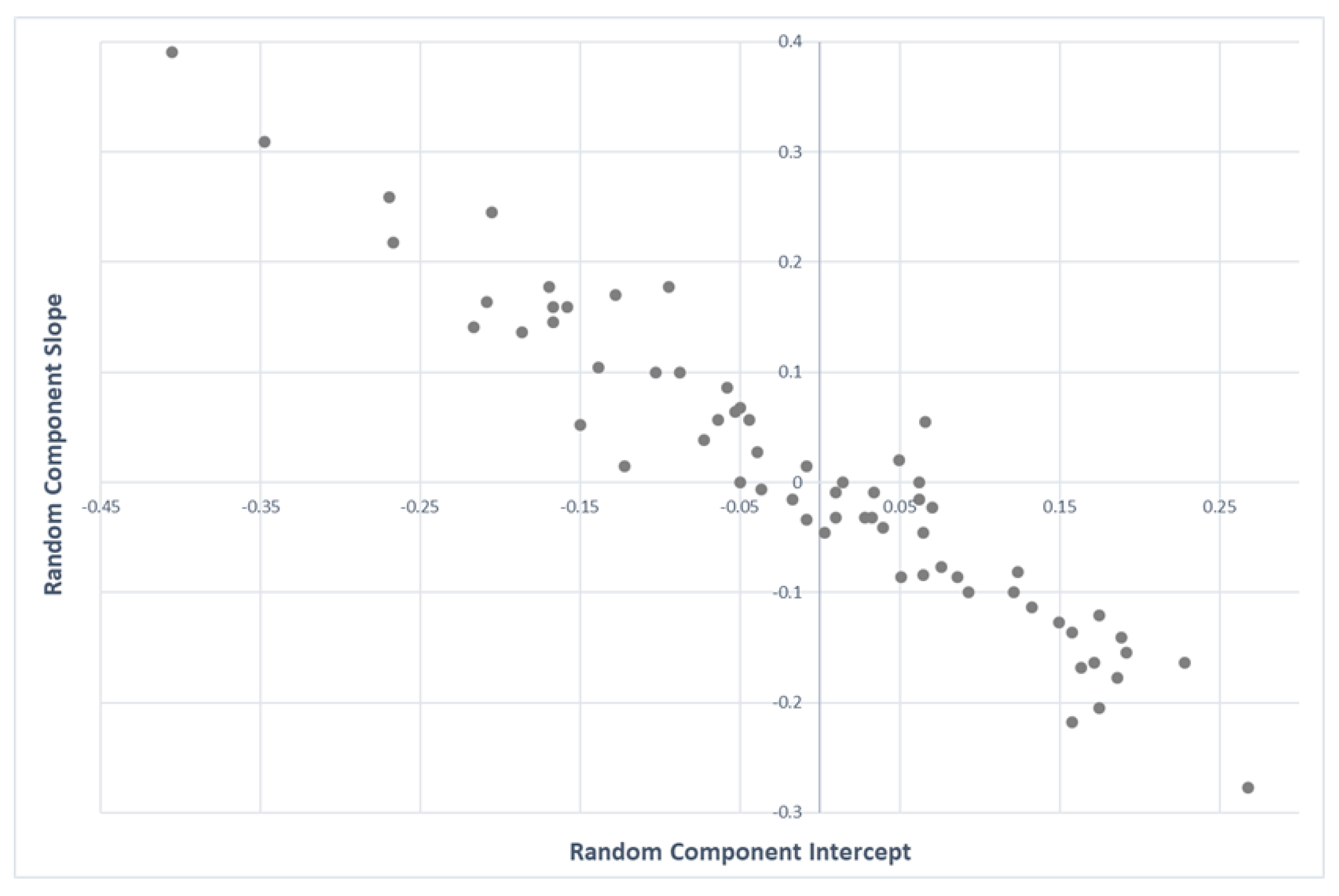
4. Results
- Variance of the random effect neighbourhood:
- Variance of the random effect time:
- Idiosyncratic variance:
5. Discussion and Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Appendix A
| Est. 1 | SE 1 | Est. 2 | SE 2 | Est. 3 | SE 3 | Est. 4 | SE 4 | |
|---|---|---|---|---|---|---|---|---|
| Intercept | 231.323 | 0.0396 | 225.884 | 0.0358 | 230.676 | 0.0376 | 225.227 | 0.0336 |
| log(lagPrice) | −1.8784 | 0.0061 | −1.8886 | 0.0060 | −1.8754 | 0.0061 | −1.8856 | 0.0060 |
| log(Surface) | 0.2463 | 0.0076 | 0.2602 | 0.0068 | 0.2470 | 0.0076 | 0.2608 | 0.0068 |
| Individuals | 0.0724 | 0.0015 | 0.0717 | 0.0015 | 0.0725 | 0.0015 | 0.0719 | 0.0015 |
| Est. 1 | SE 1 | Est. 2 | SE 2 | Est. 3 | SE 3 | Est. 4 | SE 4 | |
|---|---|---|---|---|---|---|---|---|
| Intercept | 232.107 | 0.0497 | 228.217 | 0.0437 | 235.295 | 0.0468 | 231.323 | 0.0396 |
| log(lagPrice) | −1.8685 | 0.0304 | −1.8538 | 0.0185 | −1.8927 | 0.0264 | −1.8784 | 0.0061 |
| log(Surface) | 0.2423 | 0.0076 | 0.2473 | 0.0076 | 0.2412 | 0.0076 | 0.2463 | 0.0076 |
| Individuals | 0.0721 | 0.0015 | 0.0731 | 0.0015 | 0.0713 | 0.0015 | 0.0724 | 0.0015 |
| Intercept | log(lagPrice) | P = 2 | P = 3 | P = 4 | ||
|---|---|---|---|---|---|---|
| 01.el Carme | −1.3500 | 0.3071 | −1.56 | −1.72 | −1.22 | 8.00 |
| 01.el Mercat | −1.1400 | 0.0999 | −1.77 | −1.08 | −1.02 | −1.02 |
| 01.el Pilar | −1.2191 | 0.1406 | −1.73 | −1.17 | −1.45 | −1.23 |
| 01.la Seu | 0.0324 | −1.0333 | −1.90 | 0.93 | −1.42 | −1.42 |
| 01.la Xerea | 0.0659 | −1.0443 | −1.91 | 3.52 | 1.72 | 0.39 |
| 01.Sant Francesc | 0.1639 | −1.1710 | −1.04 | 4.54 | −1.43 | −1.56 |
| 02.Gran Via | 0.1919 | −1.1592 | −1.03 | 8.16 | 1.68 | −1.10 |
| 02.Pla del Remei | 0.0639 | −1.0030 | −1.87 | 6.19 | 6.06 | 5.97 |
| 02.Russafa | 0.1840 | −1.1807 | −1.05 | 5.88 | −1.47 | −1.90 |
| 03.Arrancapins | 0.0414 | −1.0474 | −1.92 | 0.85 | −1.08 | −1.50 |
| 03.el Botanic | 0.1731 | −1.2100 | −1.08 | 2.75 | −1.79 | −1.09 |
| 03.la Petxina | 0.0159 | −1.0044 | −1.87 | 1.28 | 1.11 | 0.97 |
| 03.la Roqueta | 0.1589 | −1.2188 | −1.09 | 0.72 | −1.19 | −1.75 |
| 04.Campanar | −1.2688 | 0.2139 | −1.65 | −1.06 | −1.35 | 3.07 |
| 04.el Calvari | −1.1710 | 0.1718 | −1.70 | −1.20 | 1.79 | 6.95 |
| 04.les Tendetes | 0.0882 | −1.0902 | −1.96 | 2.57 | −1.11 | −1.81 |
| 04.Sant Pau | −1.1517 | 0.0481 | −1.82 | −1.83 | −1.87 | −1.43 |
| 05.Marxalenes | 0.0680 | −1.0870 | −1.96 | 0.78 | −1.76 | −1.37 |
| 05.Morverdre | −1.1700 | 0.1576 | −1.71 | −1.08 | 0.34 | 5.06 |
| 05.Sant Antoni | 0.1698 | −1.1672 | −1.04 | 5.39 | −1.41 | −1.43 |
| 05.Tormos | 0.0543 | −1.0878 | −1.96 | −1.65 | −1.23 | −1.86 |
| 05.T rinitat | 0.0370 | −1.0336 | −1.90 | 1.37 | 0.00 | −1.01 |
| 06.Ciutat Uni. | 0.1117 | −1.0418 | −1.91 | 8.28 | 6.58 | 5.32 |
| 06.Exposicio | 0.0680 | 0.0531 | −1.82 | 10.48 | 12.64 | 13.77 |
| 06.Jaume Roig | −1.0903 | 0.1020 | −1.77 | −1.96 | 2.19 | 5.25 |
| 06.Mestalla | 0.2258 | −1.1667 | −1.04 | 11.03 | 4.25 | −1.75 |
| 07.la Fontsanta | 0.0726 | −1.0269 | −1.90 | 5.40 | 4.30 | 3.50 |
| 07.la Llum | −1.0063 | 0.0109 | −1.86 | 0.13 | 0.58 | 0.91 |
| 07.Nou Moles | −1.0359 | −1.0060 | −1.87 | −1.01 | −1.26 | −1.44 |
| 07.Soternes | 0.0116 | −1.0358 | −1.90 | −1.32 | −1.78 | −1.85 |
| 07.Tres Forques | 0.0976 | −1.1089 | −1.98 | 2.22 | −1.21 | −1.48 |
| 08.Favara | −1.2145 | 0.1616 | −1.71 | −1.25 | −1.68 | 1.17 |
| 08.Patraix | −1.0408 | 0.0285 | −1.84 | −1.11 | −1.95 | −1.09 |
| 08.Safranar | 0.0933 | −1.1016 | −1.97 | 2.29 | −1.85 | −1.90 |
| 08.Sant Isidre | 0.0069 | −1.0449 | −1.91 | −1.42 | −1.25 | −1.60 |
| 08.Vara Quart | 0.1704 | −1.1219 | −1.99 | 8.59 | 3.63 | −1.03 |
| 09.Cami Real | −1.0635 | 0.0554 | −1.81 | −1.51 | −1.26 | 1.41 |
| 09.l’Hort Sanabre | 0.0899 | −1.0875 | −1.96 | 2.92 | −1.64 | −1.27 |
| 09.la Creu Coberta | −1.0591 | 0.0845 | −1.78 | −1.05 | 3.39 | 5.92 |
| 09.la Raiosa | −1.1714 | 0.1459 | −1.72 | −1.03 | −1.91 | 3.28 |
| 09.Sant MArcel-li | 0.1222 | −1.1017 | −1.97 | 5.17 | 1.03 | −1.03 |
| 10.Ciutat Arts | −1.1613 | 0.1604 | −1.71 | −1.01 | 1.51 | 6.33 |
| 10.En Corts | 0.1260 | −1.0865 | −1.95 | 6.61 | 3.09 | 0.50 |
| 10.Fonteta | −1.1035 | 0.0979 | −1.77 | −1.56 | 0.43 | 3.36 |
| 10.Malilla | 0.0643 | −1.0184 | −1.89 | 5.15 | 4.40 | 3.85 |
| 10.Mont-Olivet | 0.0493 | 0.0175 | −1.85 | 6.14 | 6.85 | 7.37 |
| 10.na Rovella | −1.2709 | 0.2597 | −1.61 | −1.09 | 1.48 | 9.27 |
| 11.Betero | −1.1283 | 0.1491 | −1.72 | −1.50 | 3.57 | 8.04 |
| 11.el Cabanyal | 0.0964 | −1.0469 | −1.92 | 6.39 | 4.48 | 3.08 |
| 11.el Grau | 0.2671 | −1.2786 | −1.15 | 7.40 | −1.94 | −1.3 |
| 11.la Malva-rosa | 0.1879 | −1.1518 | −1.02 | 8.27 | 2.09 | −1.47 |
| 11.Natzaret | 0.1007 | −1.0547 | −1.92 | 6.28 | 4.05 | 2.41 |
| 12.Aiora | −1.0731 | 0.0356 | −1.83 | −1.85 | −1.40 | −1.33 |
| 12.Albors | 0.0162 | −1.0011 | −1.87 | 1.55 | 1.50 | 1.47 |
| 12.Cami Fondo | −1.4065 | 0.3952 | −1.47 | −1.27 | 2.82 | 14.67 |
| 12.la Creu del Grau | 0.1348 | −1.1165 | −1.98 | 5.41 | 0.66 | −1.83 |
| 12.Penya- roja | −1.1216 | 0.0113 | −1.86 | −1.37 | −1.91 | −1.57 |
| 13.Ciutat Jardi | −1.0464 | 0.0566 | −1.81 | −1.72 | 1.58 | 3.28 |
| 13.Illa Perduda | 0.0400 | −1.0438 | −1.91 | 0.97 | −1.81 | −1.12 |
| 13.l’Amistat | −1.0951 | 0.1528 | −1.72 | 1.07 | 7.29 | 11.87 |
| 13.la Bega Baixa | −1.2070 | 0.2435 | −1.62 | −1.82 | 6.09 | 13.4 |
| 13.la Carrasca | 0.0384 | −1.0135 | −1.88 | 2.90 | 2.36 | 1.95 |
| 14.Benimaclet | −1.0098 | −1.0339 | −1.90 | −1.33 | −1.71 | −1.73 |
| 14.Cami de Vera | 0.1530 | −1.1306 | −1.00 | 6.25 | 0.94 | −1.98 |
| 15.Orriols | −1.0175 | −1.0172 | −1.89 | −1.94 | −1.64 | −1.16 |
| 15.Sant Lloren −1.1864 | 0.1361 | −1.73 | −1.21 | −1.67 | 0.42 | |
| 15.Torrefiel | 0.0130 | −1.0107 | −1.88 | 0.56 | 0.12 | −1.20 |
| 16.Benicalap | −1.0498 | −1.0008 | −1.87 | −1.04 | −1.07 | −1.09 |
| 16.Ciutat Fallera | −1.0495 | 0.0640 | −1.80 | −1.51 | 2.09 | 4.01 |
| 18.Benimamet | 0.0766 | −1.0833 | −1.95 | 1.89 | −1.49 | −1.01 |
| 19.Castellar | −1.0542 | 0.0593 | −1.81 | −1.31 | 1.10 | 2.88 |
| 19.La Torre | 0.1574 | −1.1383 | −1.01 | 6.16 | 0.53 | −1.61 |
| 19.Otros Pobles Sud | 0.0335 | −1.0115 | −1.88 | 2.56 | 2.09 | 1.75 |
| Intercept | log(lagPrice) | Intercept | log(lagPrice) | |||
|---|---|---|---|---|---|---|
| February 2009 | 0.0753 | −1.0233 | 2010.5 | −1.0005 | −1.1078 | |
| March 2009 | 0.0616 | −1.0350 | 2010.6 | −1.1805 | 0.1553 | |
| April 2009 | 0.0343 | −1.0728 | 2011.1 | 0.0394 | 0.0023 | |
| May 2009 | −1.0448 | −1.0103 | 2011.2 | 0.1669 | −1.0640 | |
| June 2009 | −1.2349 | 0.1814 | 2011.3 | 0.0459 | −1.0495 | |
| January 2010 | −1.1680 | 0.1919 | 2011.4 | 0.1097 | −1.0736 | |
| February 2010 | 0.0279 | −1.0070 | 2011.5 | 0.0782 | −1.1259 | |
| March 2010 | 0.0522 | −1.0142 | 2011.6 | −1.0935 | 0.1106 | |
| April 2010 | 0.0306 | −1.0581 |
References
- Schewe, J.; Heinke, J.; Gerten, D.; Haddeland, I.; Arnell, N.W.; Clark, D.B.; Dankers, R.; Eisner, S.; Fekete, B.M.; Colón-González, F.J.; et al. Multimodel assessment of water scarcity under climate change. Proc. Natl. Acad. Sci. USA 2014, 111, 3245–3250. [Google Scholar] [CrossRef] [Green Version]
- Gosling, S.N.; Arnell, N.W. A global assessment of the impact of climate change on water scarcity. Clim. Chang. 2016, 134, 371–385. [Google Scholar] [CrossRef] [Green Version]
- Field, C.B.; Barros, V.R. Climate change 2014–Impacts, Adaptation and Vulnerability: Regional Aspects; Cambridge University Press: Cambridge, UK, 2014. [Google Scholar]
- He, C.; Liu, Z.; Wu, J.; Pan, X.; Fang, Z.; Li, J.; Bryan, B.A. Future global urban water scarcity and potential solutions. Nat. Commun. 2021, 12, 4667. [Google Scholar] [CrossRef] [PubMed]
- Miller, K.A.; Yates, D.N. Climate Change and Water Resources: A Primer for Municipal Water Providers; American Water Works Association: Washington, DC, USA, 2006. [Google Scholar]
- EEA. Urban Adaptation to Climate Change in Europe; Publications Office of the EU: Luxembourg, 2014. [Google Scholar]
- Garrone, P.; Grilli, L.; Marzano, R. Incentives to water conservation under scarcity: Comparing price and reward effects through stated preferences. J. Clean. Prod. 2020, 244, 118632. [Google Scholar] [CrossRef] [Green Version]
- OECD. Water and Cities; OECD: Paris, France, 2015; p. 180. [Google Scholar] [CrossRef]
- Espey, M.; Espey, J.; Shaw, W.D. Price elasticity of residential demand for water: A meta-analysis. Water Resour. Res. 1997, 33, 1369–1374. [Google Scholar] [CrossRef]
- Dalhuisen, J.M.; Florax, R.J.; De Groot, H.L.; Nijkamp, P. Price and income elasticities of residential water demand: A meta-analysis. Land Econ. 2003, 79, 292–308. [Google Scholar] [CrossRef]
- Sebri, M. A meta-analysis of residential water demand studies. Environ. Dev. Sustain. 2014, 16, 499–520. [Google Scholar] [CrossRef]
- Marzano, R.; Rouge, C.; Garrone, P.; Grilli, L.; Harou, J.J.; Pulido-Velazquez, M. Determinants of the price response to residential water tariffs: Meta-analysis and beyond. Environ. Model. Softw. 2018, 101, 236–248. [Google Scholar] [CrossRef]
- Puri, R.; Maas, A. Evaluating the sensitivity of residential water demand estimation to model specification and instrument choices. Water Resour. Res. 2020, 56, e2019WR026156. [Google Scholar] [CrossRef]
- Hanke, S.H.; Mare, L.D. Residential water demand: A pooled, time series, cross section study of malmö, sweden 1. JAWRA J. Am. Water Resour. Assoc. 1982, 18, 621–626. [Google Scholar] [CrossRef]
- Nieswiadomy, M.L.; Molina, D.J. Comparing residential water demand estimates under decreasing and increasing block rates using household data. Land Econ. 1989, 65, 280–289. [Google Scholar] [CrossRef]
- Hewitt, J.A.; Hanemann, W.M. A discrete/continuous choice approach to residential water demand under block rate pricing. Land Econ. 1995, 71, 173–192. [Google Scholar] [CrossRef]
- Arbúes, F.; Barberan, R.; Villanua, I. Price impact on urban residential water demand: A dynamic panel data approach. Water Resour. Res. 2004, 40. [Google Scholar] [CrossRef] [Green Version]
- García-Valiñas, M.A. Fijación de precios para el servicio municipal de suministro de agua: Un ejercicio de análisis de bienestar. Hacienda Pública Española 2005, 172, 119–142. [Google Scholar]
- Arbues, F.; Villanua, I. Potential for pricing policies in water resource management: Estimation of urban residential water demand in Zaragoza, Spain. Urban Stud. 2006, 43, 2421–2442. [Google Scholar] [CrossRef]
- Olmstead, S.M.; Hanemann, W.M.; Stavins, R.N. Water demand under alternative price structures. J. Environ. Econ. Manag. 2007, 54, 181–198. [Google Scholar] [CrossRef] [Green Version]
- Arbués, F.; Villanúa, I.; Barberán, R. Household size and residential water demand: An empirical approach. Aust. J. Agric. Resour. Econ. 2010, 54, 61–80. [Google Scholar] [CrossRef] [Green Version]
- Deyà-Tortella, B.; Garcia, C.; Nilsson, W.; Tirado, D. Analysis of water tariff reform on water consumption in different housing typologies in Calvià (Mallorca). Water 2017, 9, 425. [Google Scholar] [CrossRef] [Green Version]
- Flores-Arévalo, Y.; Ponce-Oliva, R.D.; Fernández, F.J.; Vásquez-Lavin, F. Sensitivity of Water Price Elasticity Estimates to Different Data Aggregation Levels. Water Resour. Manag. 2021, 35, 2039–2052. [Google Scholar] [CrossRef]
- Maas, A.; Goemans, C.; Manning, D.; Kroll, S.; Arabi, M.; Rodriguez-McGoffin, M. Evaluating the effect of conservation motivations on residential water demand. J. Environ. Manag. 2017, 196, 394–401. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Suárez-Varela, M. Modeling residential water demand: An approach based on household demand systems. J. Environ. Manag. 2020, 261, 109921. [Google Scholar] [CrossRef]
- Hoyos, D.; Artabe, A. Regional differences in the price elasticity of residential water demand in Spain. Water Resour. Manag. 2017, 31, 847–865. [Google Scholar] [CrossRef]
- House-Peters, L.A.; Chang, H. Urban water demand modeling: Review of concepts, methods, and organizing principles. Water Resour. Res. 2011, 47. [Google Scholar] [CrossRef] [Green Version]
- Domene, E.; Saurí, D.; Parés, M. Urbanization and sustainable resource use: The case of garden watering in the metropolitan region of Barcelona. Urban Geogr. 2005, 26, 520–535. [Google Scholar] [CrossRef]
- Domene, E.; Saurí, D. Urbanisation and water consumption: Influencing factors in the metropolitan region of Barcelona. Urban Stud. 2006, 43, 1605–1623. [Google Scholar] [CrossRef]
- March-Corbella, H.; Sauríi Pujol, D. What lies behind domestic water use?: A review essay on the drivers of domestic water consumption. Boletín de la Asociación de Geógrafos Españoles 2009, 50, 297–314. [Google Scholar]
- March, H.; Saurí, D. The suburbanization of water scarcity in the Barcelona metropolitan region: Sociodemographic and urban changes influencing domestic water consumption. Prof. Geogr. 2010, 62, 32–45. [Google Scholar] [CrossRef]
- House-Peters, L.; Pratt, B.; Chang, H. Effects of urban spatial structure, sociodemographics, and climate on residential water consumption in hillsboro, oregon 1. JAWRA J. Am. Water Resour. Assoc. 2010, 46, 461–472. [Google Scholar] [CrossRef]
- March, H.; Perarnau, J.; Saurí, D. Exploring the links between immigration, ageing and domestic water consumption: The case of the Metropolitan Area of Barcelona. Reg. Stud. 2012, 46, 229–244. [Google Scholar] [CrossRef]
- Saurí, D. Water conservation: Theory and evidence in urban areas of the developed world. Annu. Rev. Environ. Resour. 2013, 38, 227–248. [Google Scholar] [CrossRef]
- Domene, E. Cambio en los patrones del consumo de agua en la Barcelona suburbana: Estilos de vida y renta como factores explicativos. Investig. Geogr. 2014, 61, 39–53. [Google Scholar]
- Cavanagh, S.M.; Hanemann, W.M.; Stavins, R.N. Muffled Price Signals: Household Water Demand under Increasing-Block Prices. 2002. Available online: https://ssrn.com/abstract=317924 (accessed on 11 September 2021).
- Mansur, E.T.; Olmstead, S.M. The value of scarce water: Measuring the inefficiency of municipal regulations. J. Urban Econ. 2012, 71, 332–346. [Google Scholar] [CrossRef] [Green Version]
- Balling, R.C., Jr.; Gober, P.; Jones, N. Sensitivity of residential water consumption to variations in climate: An intraurban analysis of Phoenix, Arizona. Water Resour. Res. 2008, 44. [Google Scholar] [CrossRef] [Green Version]
- Breyer, B.; Chang, H.; Parandvash, G.H. Land-use, temperature, and single-family residential water use patterns in Portland, Oregon and Phoenix, Arizona. Appl. Geogr. 2012, 35, 142–151. [Google Scholar] [CrossRef]
- Chang, H.; Parandvash, G.H.; Shandas, V. Spatial variations of single-family residential water consumption in Portland, Oregon. Urban Geogr. 2010, 31, 953–972. [Google Scholar] [CrossRef]
- Polebitski, A.S.; Palmer, R.N. Seasonal residential water demand forecasting for census tracts. J. Water Resour. Plan. Manag. 2010, 136, 27–36. [Google Scholar] [CrossRef]
- Wentz, E.A.; Gober, P. Determinants of small-area water consumption for the city of Phoenix, Arizona. Water Resour. Manag. 2007, 21, 1849–1863. [Google Scholar] [CrossRef]
- Hoffmann, M.; Worthington, A.; Higgs, H. Urban water demand with fixed volumetric charging in a large municipality: The case of Brisbane, Australia. Aust. J. Agric. Resour. Econ. 2006, 50, 347–359. [Google Scholar] [CrossRef]
- Ouyang, Y.; Wentz, E.A.; Ruddell, B.L.; Harlan, S.L. A multi-scale analysis of single-family residential water use in the Phoenix metropolitan area. JAWRA J. Am. Water Resour. Assoc. 2014, 50, 448–467. [Google Scholar] [CrossRef]
- Pint, E.M. Household responses to increased water rates during the California drought. Land Econ. 1999, 75, 246–266. [Google Scholar] [CrossRef]
- Worthington, A.C.; Higgs, H.; Hoffmann, M. Residential water demand modeling in Queensland, Australia: A comparative panel data approach. Water Policy 2009, 11, 427–441. [Google Scholar] [CrossRef] [Green Version]
- Miyawaki, K.; Omori, Y.; Hibiki, A. Panel data analysis of Japanese residential water demand using a discrete/continuous choice approach. Jpn. Econ. Rev. 2011, 62, 365–386. [Google Scholar] [CrossRef] [Green Version]
- Krause, K.; Chermak, J.M.; Brookshire, D.S. The demand for water: Consumer response to scarcity. J. Regul. Econ. 2003, 23, 167–191. [Google Scholar] [CrossRef]
- Pérez-Urdiales, M.; García-Valiñas, M.Á. Efficient water-using technologies and habits: A disaggregated analysis in the water sector. Ecol. Econ. 2016, 128, 117–129. [Google Scholar] [CrossRef]
- Cardoso, M.L.B.D.M.B. Modeling Portuguese Water Demand with Quantile Regression. Ph.D. Thesis, University Institute of Lisbon, Lisbon, Portugal, 2013. [Google Scholar]
- Siddiquee, M.S.H.; Ahamed, R. Exploring Water Consumption in Dhaka City Using Instrumental Variables Regression Approaches. Environ. Process. 2020, 7, 1255–1275. [Google Scholar] [CrossRef]
- Wichman, C.J. Perceived price in residential water demand: Evidence from a natural experiment. J. Econ. Behav. Organ. 2014, 107, 308–323. [Google Scholar] [CrossRef]
- Maldonado-Devis, M.; Almenar-Llongo, V. A Panel Data Estimation of Domestic Water Demand with IRT Tariff Structure: The Case of the City of Valencia (Spain). Sustainability 2021, 13, 1414. [Google Scholar] [CrossRef]
- Rico-Amoros, A.M.; Olcina-Cantos, J.; Saurí, D. Tourist land use patterns and water demand: Evidence from the Western Mediterranean. Land Use Policy 2009, 26, 493–501. [Google Scholar] [CrossRef]
- Saurí, D.; Olcina, J.; Fernando Vera, J.; Martín-Vide, J.; March, H.; Serra-Llobet, A.; Padilla, E. Tourism, climate change and water resources: Coastal Mediterranean Spain as an example. In European Climate Vulnerabilities and Adaptation: A Spatial Planning Perspective; Wiley-Blackwell: Hoboken, NJ, USA, 2013; pp. 231–252. [Google Scholar]
- Morote, Á.F.; Saurí, D.; Hernández, M. Residential tourism, swimming pools, and water demand in the Western Mediterranean. Prof. Geogr. 2017, 69, 1–11. [Google Scholar] [CrossRef] [Green Version]
- Anuario Estadístico del Ayuntamiento de Valencia; Ayuntamiento de Valencia: Valencia, Spain, 2012.
- Arbués, F.; Barberán, R. Tariffs for urban water services in Spain: Household size and equity. Int. J. Water Resour. Dev. 2012, 28, 123–140. [Google Scholar] [CrossRef]
- García-Rubio, M.A.; Ruiz-Villaverde, A.; González-Gómez, F. Urban water tariffs in Spain: What needs to be done? Water 2015, 7, 1456–1479. [Google Scholar] [CrossRef] [Green Version]
- Arbués, F.; Sanaú, J.; Serrano, J.M. El precio del agua en las ciudades: Efectos del modelo de gestión. Papeles Econ. Española 2017, 153, 48–64. [Google Scholar]
- Arbués, F.; García-Valiñas, M. Water tariffs in Spain. In Oxford Research Encyclopedia of Global Public Health; Oxford University Press: Oxford, UK, 2020. [Google Scholar]
- Martínez-Espiñeira, R. An estimation of residential water demand using co-integration and error correction techniques. J. Appl. Econ. 2007, 10, 161–184. [Google Scholar] [CrossRef] [Green Version]
- Foster, H.S.; Beattie, B.R. Urban residential demand for water in the United States: Reply. Land Econ. 1981, 57, 257–265. [Google Scholar] [CrossRef]
- Foster, H.S.; Beattie, B.R. On the specification of price in studies of consumer demand under block price scheduling. Land Econ. 1981, 57, 624–629. [Google Scholar] [CrossRef]
- Nauges, C.; Thomas, A. Privately operated water utilities, municipal price negotiation, and estimation of residential water demand: The case of France. Land Econ. 2000, 76, 68–85. [Google Scholar] [CrossRef]
- Gaudin, S. Effect of price information on residential water demand. Appl. Econ. 2006, 38, 383–393. [Google Scholar] [CrossRef]
- Nieswiadomy, M.L. Estimating urban residential water demand: Effects of price structure, conservation, and education. Water Resour. Res. 1992, 28, 609–615. [Google Scholar] [CrossRef]
- Nieswiadomy, M.; Cobb, S.L. Impact of pricing structure selectivity on urban water demand. Contemp. Econ. Policy 1993, 11, 101–113. [Google Scholar] [CrossRef]
- Billings, R.B.; Agthe, D.E. Price elasticities for water: A case of increasing block rates. Land Econ. 1980, 56, 73–84. [Google Scholar] [CrossRef]
- Howe, C.W. The impact of price on residential water demand: Some new insights. Water Resour. Res. 1982, 18, 713–716. [Google Scholar] [CrossRef]
- Jones, C.V.; Morris, J.R. Instrumental price estimates and residential water demand. Water Resour. Res. 1984, 20, 197–202. [Google Scholar] [CrossRef]
- Martinez-Espineira, R. Estimating water demand under increasing-block tariffs using aggregate data and proportions of users per block. Environ. Resour. Econ. 2003, 26, 5–23. [Google Scholar] [CrossRef]
- Bickel, R. Multilevel Analysis for Applied Research: It’s Just Regression; Guilford Press: New York, NY, USA, 2007. [Google Scholar]
- Hox, J. Multilevel Analysis: Techniques and Applications, 2nd ed.; Routledge: New York, NY, USA, 2010. [Google Scholar]
- Vicèns, J.; Sánchez, B. Regresión Cuantílica: Estimación y Contrastes; Universidad Autónoma de Madrid: Madrid, Spain, 2012. [Google Scholar]
- Arbués, F.; García-Valiñas, M.Á.; Martínez-Espiñeira, R. Estimation of residential water demand: A state-of-the-art review. J. Socio-Econ. 2003, 32, 81–102. [Google Scholar] [CrossRef]
- Worthington, A.C.; Hoffman, M. An empirical survey of residential water demand modelling. J. Econ. Surv. 2008, 22, 842–871. [Google Scholar] [CrossRef] [Green Version]
- García-Valiñas, M.A.; Martínez-Espiñeira, R.; González-Gómez, F. Affordability of residential water tariffs: Alternative measurement and explanatory factors in southern Spain. J. Environ. Manag. 2010, 91, 2696–2706. [Google Scholar] [CrossRef]
- Pérez-Urdiales, M.; García-Valiñas, M.A.; Martínez-Espiñeira, R. Responses to changes in domestic water tariff structures: A latent class analysis on household-level data from Granada, Spain. Environ. Resour. Econ. 2016, 63, 167–191. [Google Scholar] [CrossRef]
- Martínez-Espiñeira, R.; Nauges, C. Is all domestic water consumption sensitive to price control? Appl. Econ. 2004, 36, 1697–1703. [Google Scholar] [CrossRef]
- Baerenklau, K.A.; Schwabe, K.A.; Dinar, A. The residential water demand effect of increasing block rate water budgets. Land Econ. 2014, 90, 683–699. [Google Scholar] [CrossRef] [Green Version]
- Klaiber, H.A.; Smith, V.K.; Kaminsky, M.; Strong, A. Measuring price elasticities for residential water demand with limited information. Land Econ. 2014, 90, 100–113. [Google Scholar] [CrossRef] [Green Version]
- Breyer, E.Y. Household Water Demand and Land Use Context: A Multilevel Approach. Ph.D. Thesis, Portland State University, Portland, OR, USA, 2014. [Google Scholar]
- Hong, C.Y.; Chang, H. Uncovering the influence of household sociodemographic and behavioral characteristics on summer water consumption in the Portland Metropolitan Area. Int. J. Geospat. Environ. Res. 2014, 1, 2. [Google Scholar]
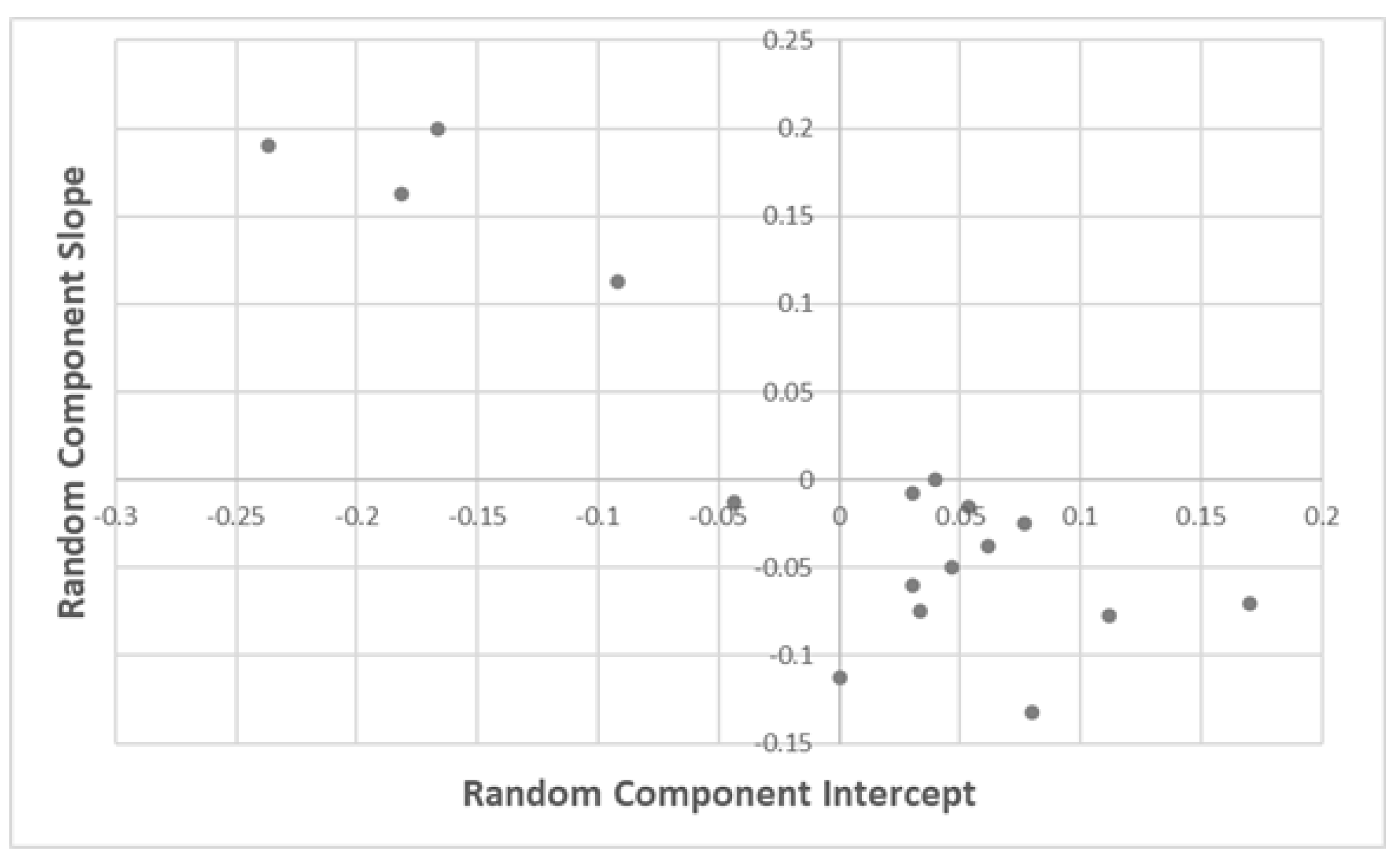
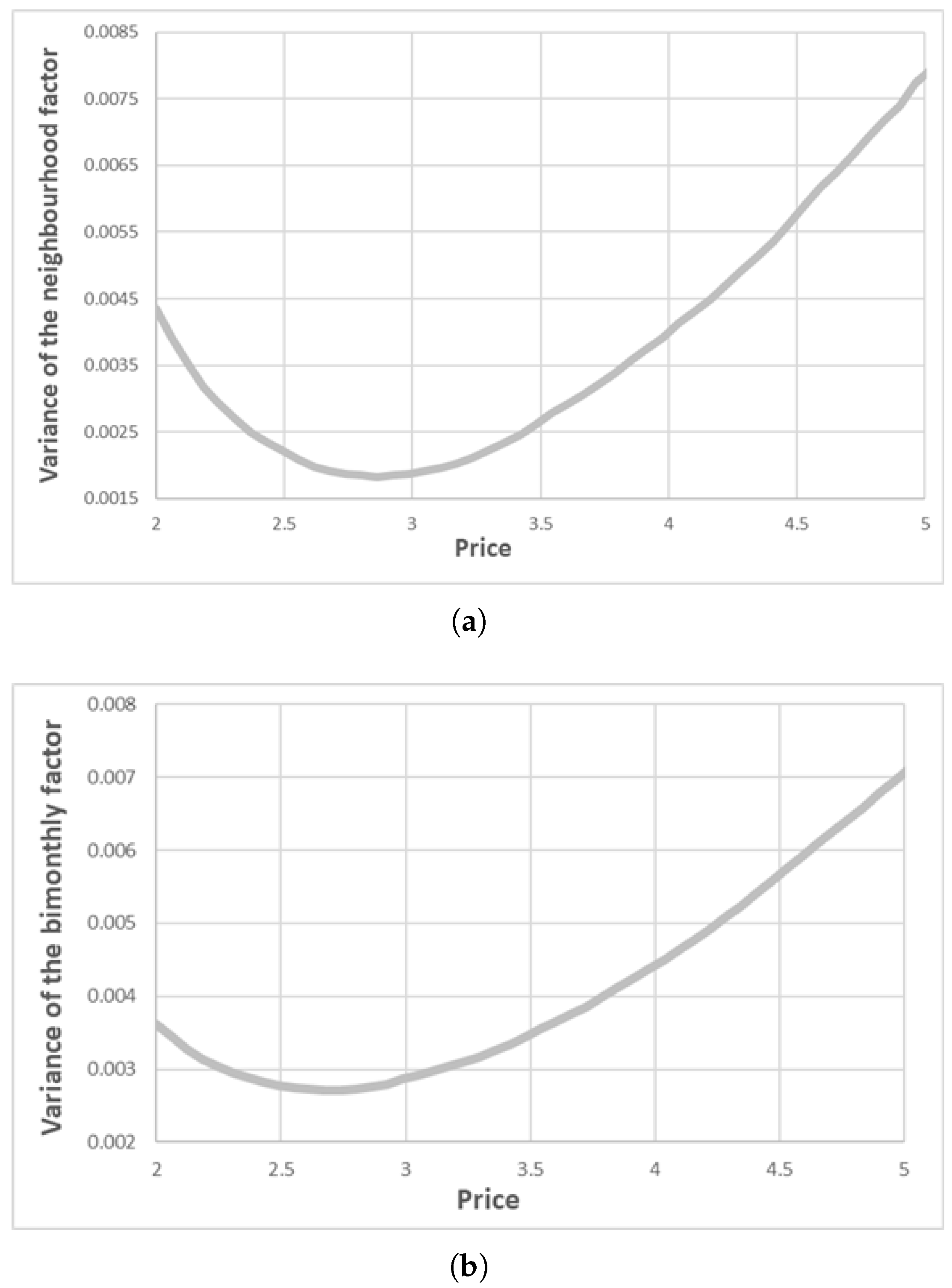
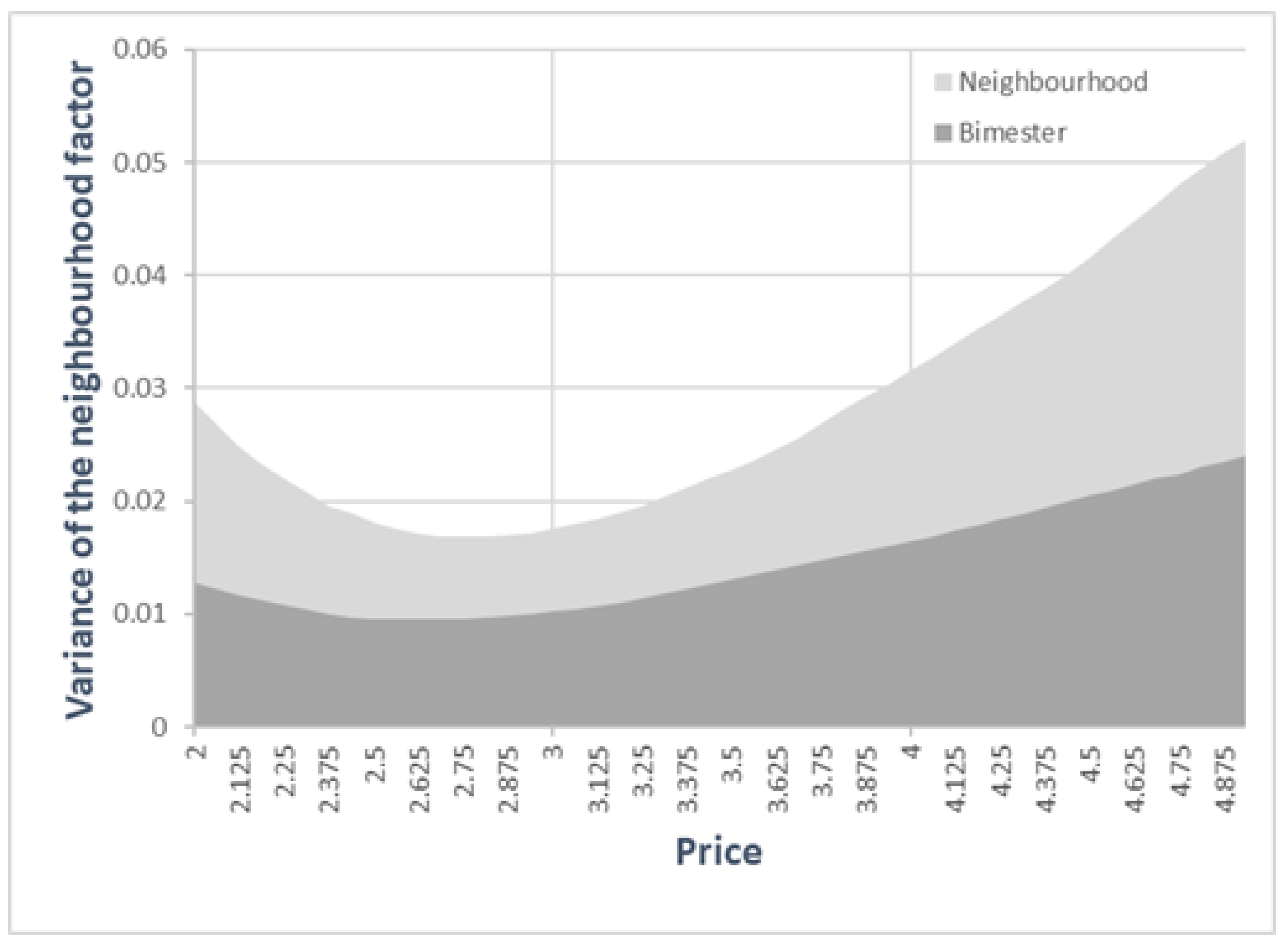
| Random Effects | |||
|---|---|---|---|
| Groups | Name | Variance | Std Dev |
| Neighbourhood | Intercept | 0.02338 | 0.1529 |
| log(lagPrice) | 0.01950 | 0.1397 | |
| Time | Intercept | 0.01264 | 0.1124 |
| log(lagPrice) | 0.01031 | 0.1015 | |
| Residual | 0.26994 | 0.5196 | |
| Fixed effects | |||
| Estimators | Std Err | t-value | |
| Intercept | 2.321.069 | 0.049727 | 46.68 |
| log(lagPrice) | −1.868446 | 0.030420 | −1.55 |
| log(Surface) | 0.242334 | 0.007607 | 31.86 |
| Individuals | 0.072115 | 0.001522 | 47.39 |
| Neighbourhood | ||
|---|---|---|
| Intercept | log(lagPrice) | |
| Intercept | 0.02337705 | −1.02046818 |
| log(lagPrice) | −1.02046818 | 0.01950356 |
| Period | ||
| Intercept | log(lagPrice) | |
| Intercept | 0.01264238 | −1.01011100 |
| log(lagPrice) | −1.01011100 | 0.01031073 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Maldonado-Devis, M.; Almenar-Llongo, V. Heterogeneity in Domestic Water Demand: An Application of Multilevel Analysis to the City of Valencia (Spain). Water 2021, 13, 3400. https://doi.org/10.3390/w13233400
Maldonado-Devis M, Almenar-Llongo V. Heterogeneity in Domestic Water Demand: An Application of Multilevel Analysis to the City of Valencia (Spain). Water. 2021; 13(23):3400. https://doi.org/10.3390/w13233400
Chicago/Turabian StyleMaldonado-Devis, Mónica, and Vicent Almenar-Llongo. 2021. "Heterogeneity in Domestic Water Demand: An Application of Multilevel Analysis to the City of Valencia (Spain)" Water 13, no. 23: 3400. https://doi.org/10.3390/w13233400
APA StyleMaldonado-Devis, M., & Almenar-Llongo, V. (2021). Heterogeneity in Domestic Water Demand: An Application of Multilevel Analysis to the City of Valencia (Spain). Water, 13(23), 3400. https://doi.org/10.3390/w13233400







