Decision Support Model for Ecological Operation of Reservoirs Based on Dynamic Bayesian Network
Abstract
1. Introduction
2. Methods
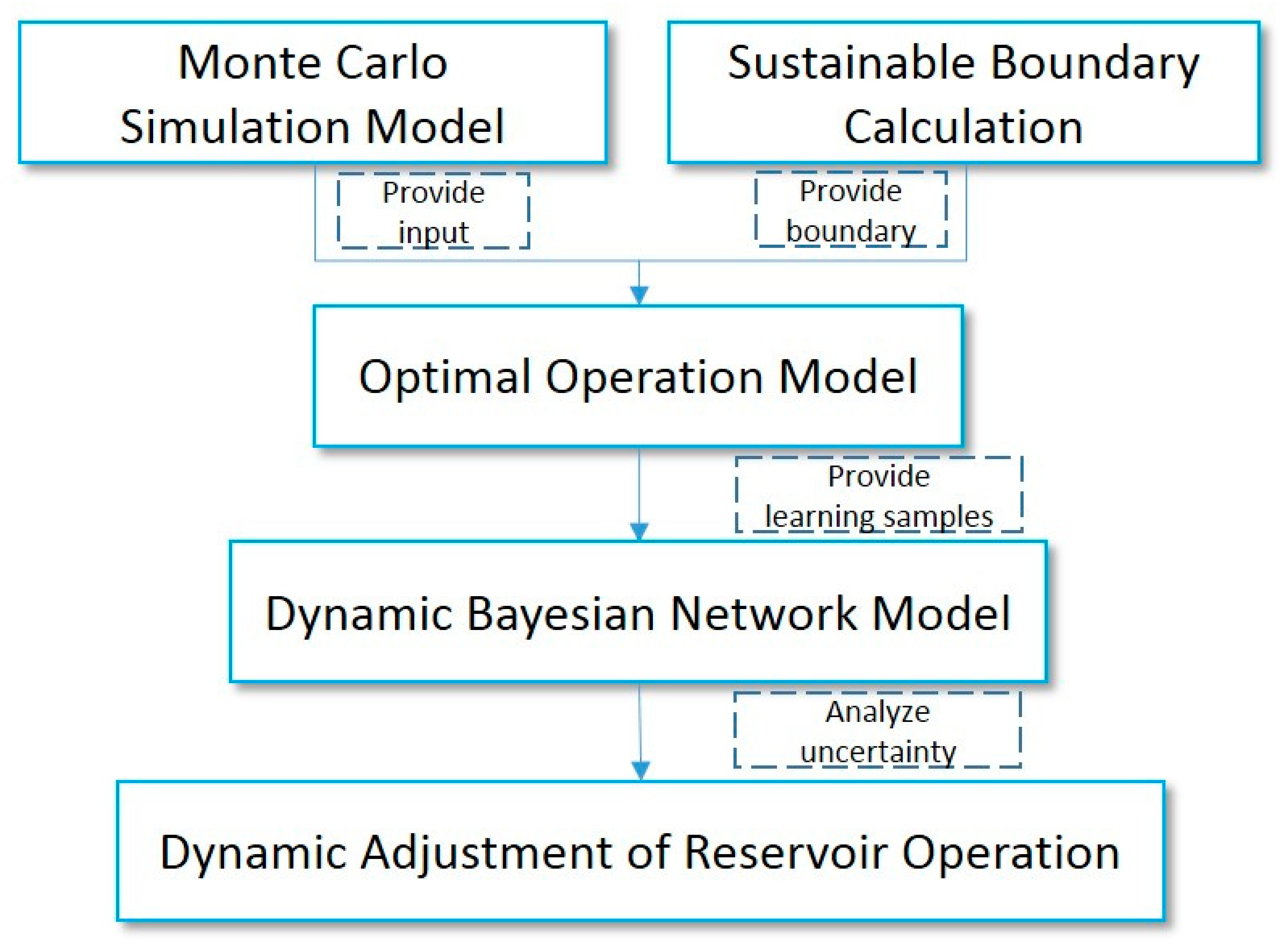
2.1. Methodological Framework
2.2. Formulation of Sustainable Boundaries
2.3. Establishment of an Optimal Operation Model
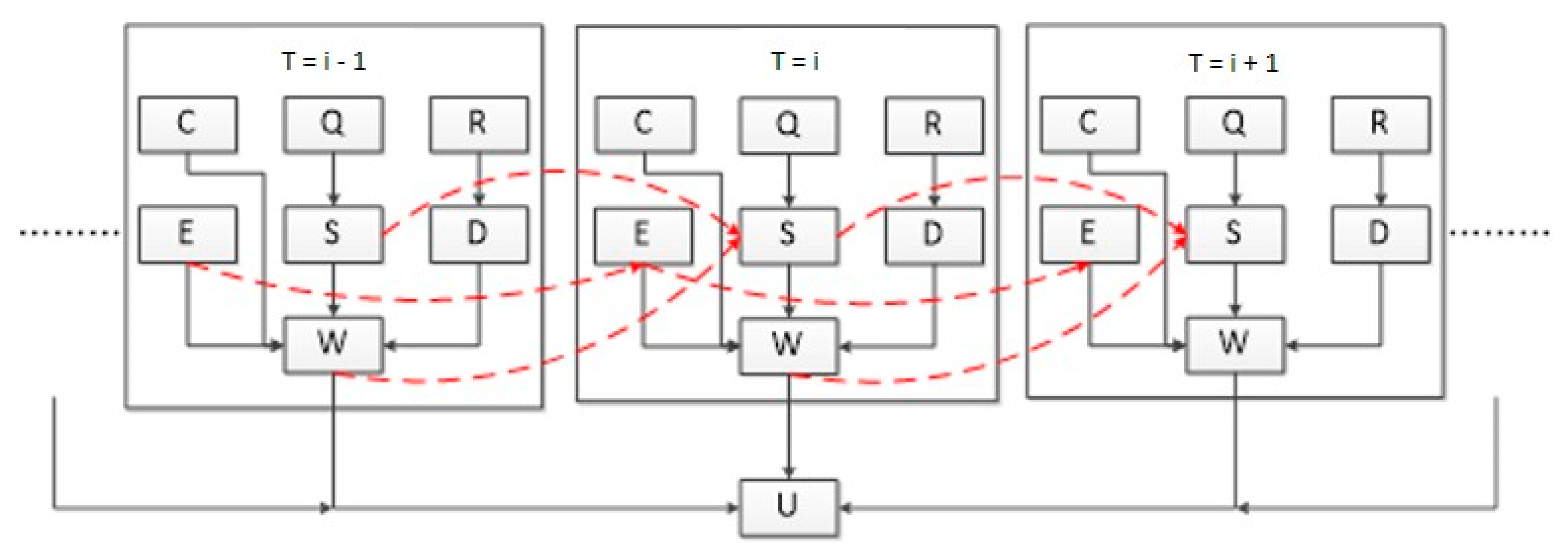
2.4. Establishment of the DBN Model
- (1)
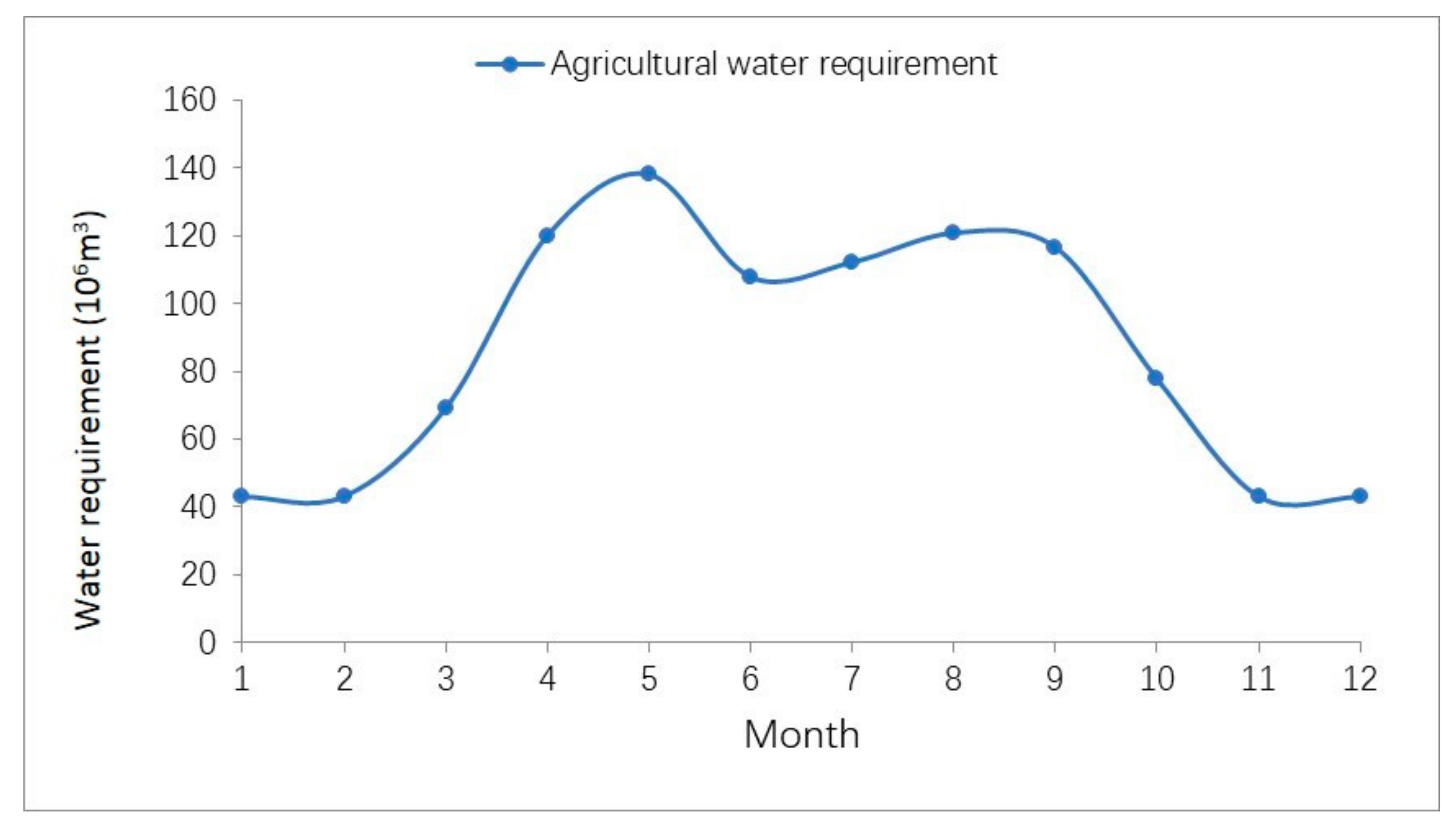
- Select variables. A set of variables that changes over time is taken to represent certain discrete physical data values. To simplify the model, the following parameters of scheduling model are selected: inflow, rainfall, storage of the reservoir, water demand, ecological status, water supply, crop prices and state of objective, which constitute a set of variables affecting the reservoir operation status {Q, R, S, D, E, W, P, U}.
- (2)
- Determination of the causality. The reservoir operation process is described as a causal network among nodes and is a causal relationship between the inflow, rainfall and reservoir water supply. It consists of three parts: the first part is the causal relationship between rainfall and water demand; the second part is the causal relationship between reservoir inflow and storage; the third part is the causal network between water demand, reservoir storage, ecological status and reservoir water supply.
- (3)
- Time spreading. To grasp the time variability of reservoir operation uncertainty, each BN is supplemented with additional nodes for continuous time periods. These additional nodes are only related to the BN in the previous or next time period and have nothing to do with other networks. In this work, the reservoir storage, ecological status and reservoir water supply are used as additional nodes, according to expert knowledge. The ecological state at t has impact on the ecological state at t + 1. Furthermore, the reservoir storage and reservoir water supply at t have impact on the reservoir storage at t + 1.
- (4)
- Parameter learning. The prior probability distributions and the conditional probability distribution tables (CPTs) of the nodes in DBNs are learned from the learning samples achieved in the optimal operation model. However, the lack of data often occurs in real situations. To deal with the incomplete learning samples, the expectation maximization (EM) algorithm [32] is used for the parameter learning in this work, which is largely a kind of maximum likelihood estimation. The mathematical expression of the log-likelihood L(θ|X) function is:where X is the observed samples, Z is the latent variable, θ is the model parameter and P(X, Z|θ) is the marginal probability density function.
2.5. Decision Support Based on Uncertainty Analysis
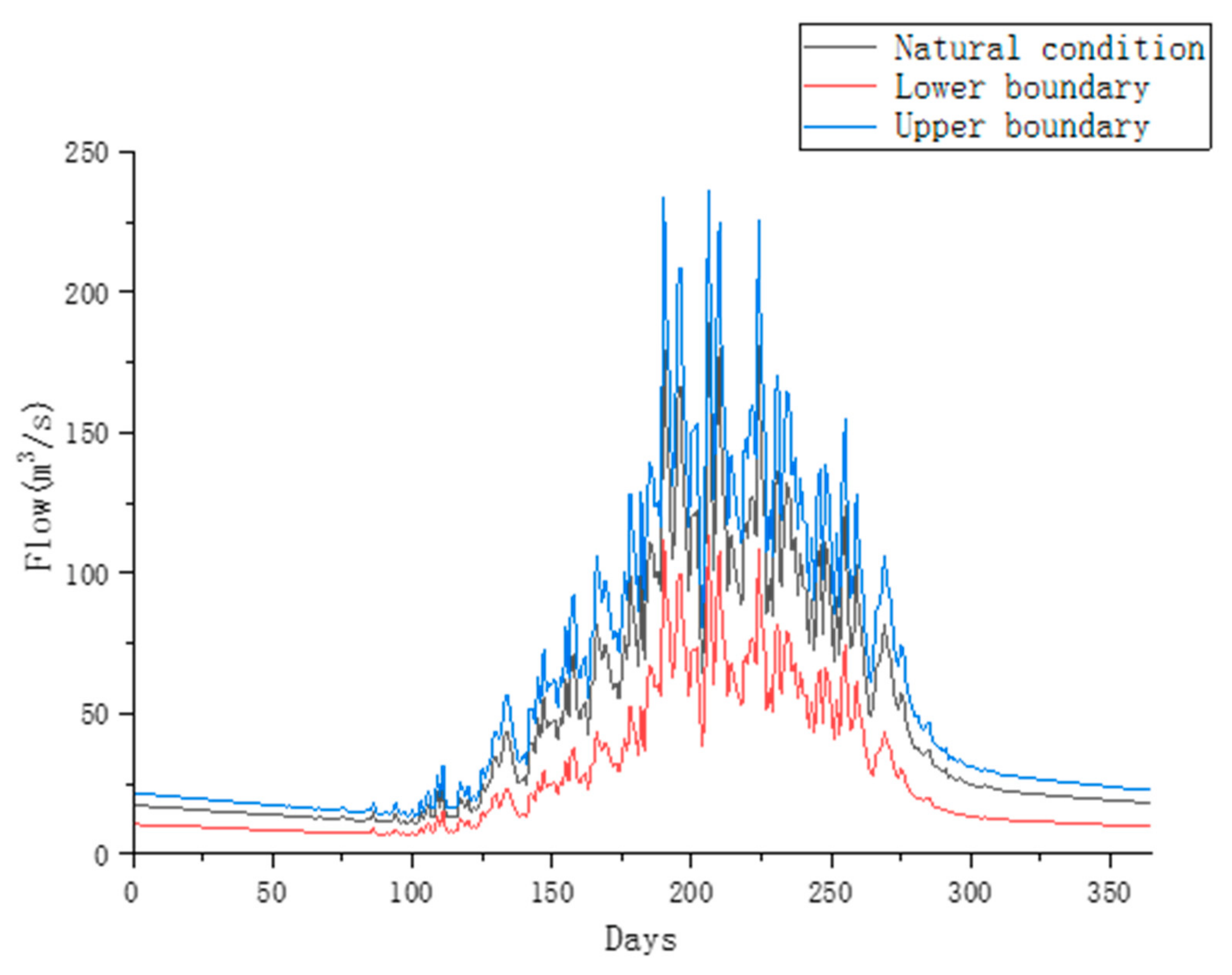
2.5.1. Uncertainty Estimation
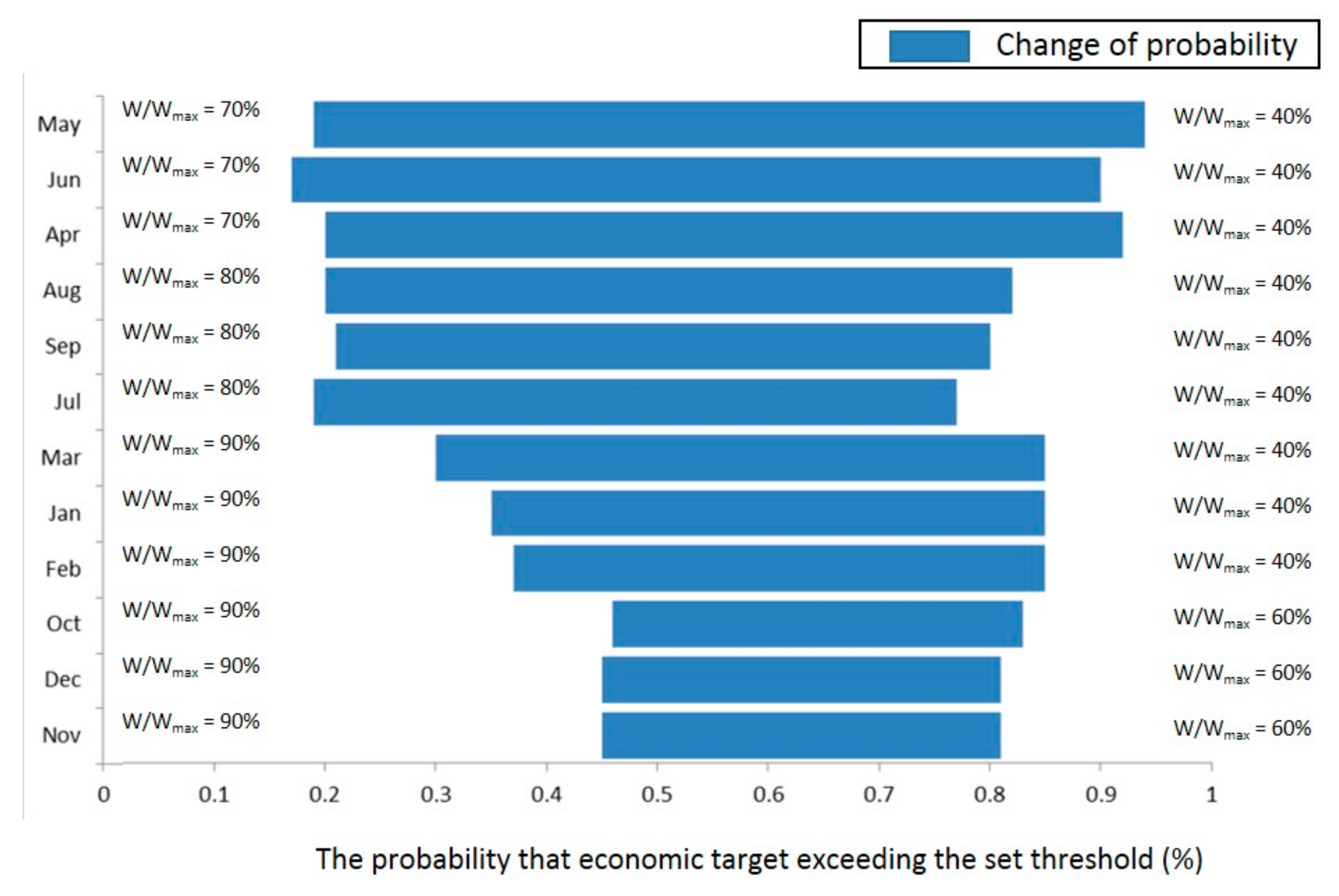
2.5.2. Trade-Off Analysis
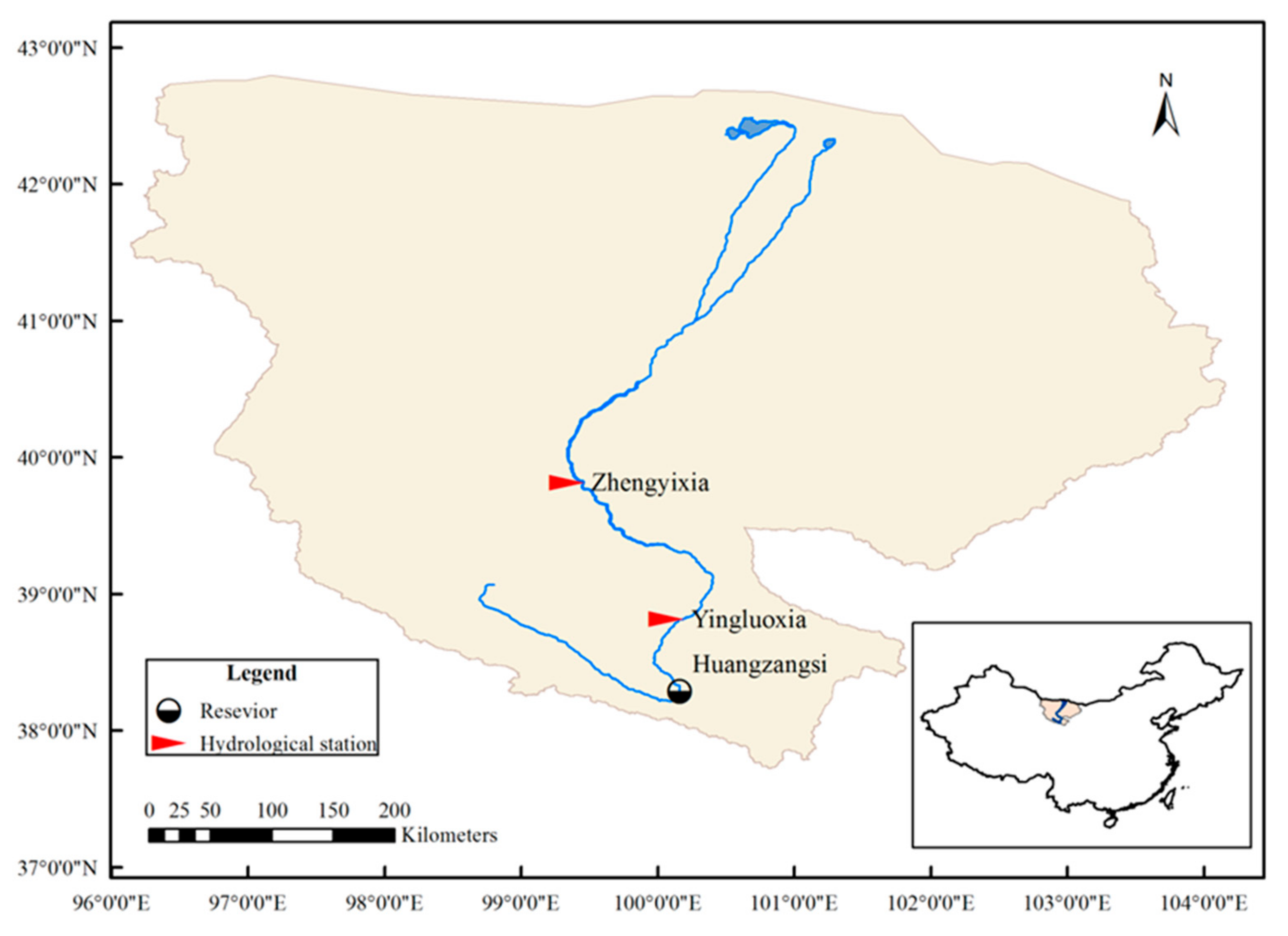
3. Study Area
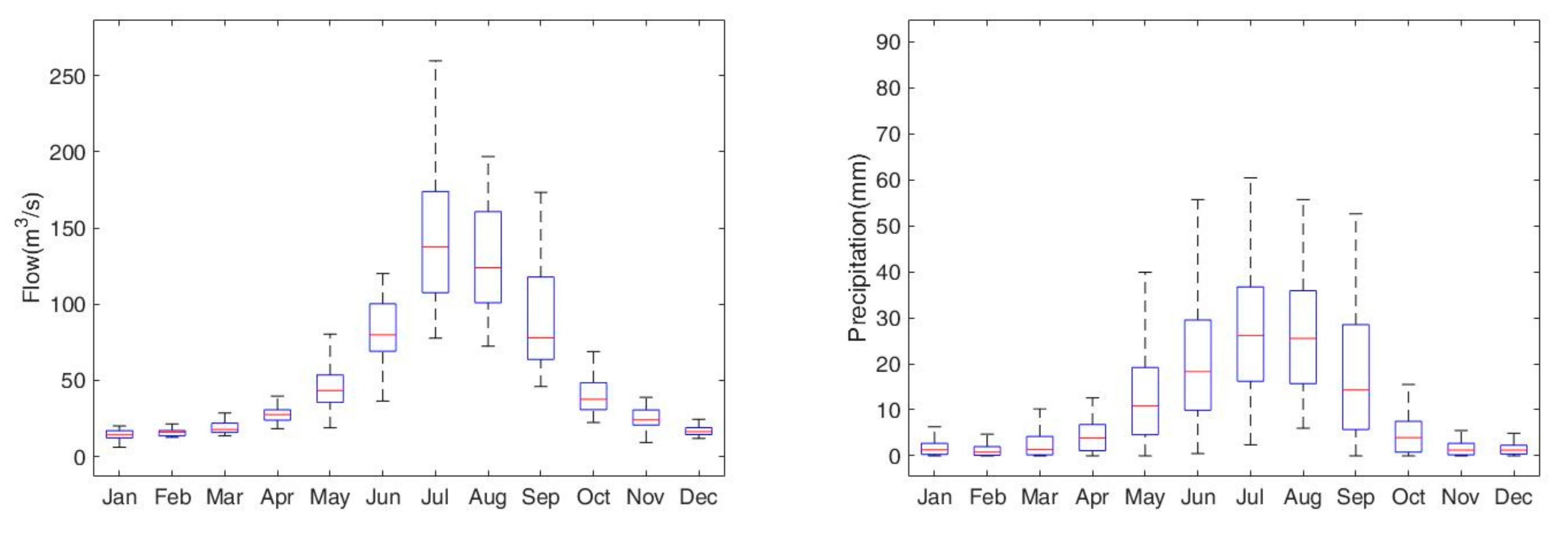
3.1. Description of the Study Area
3.2. Establishment of the Model
4. Result and Discussion
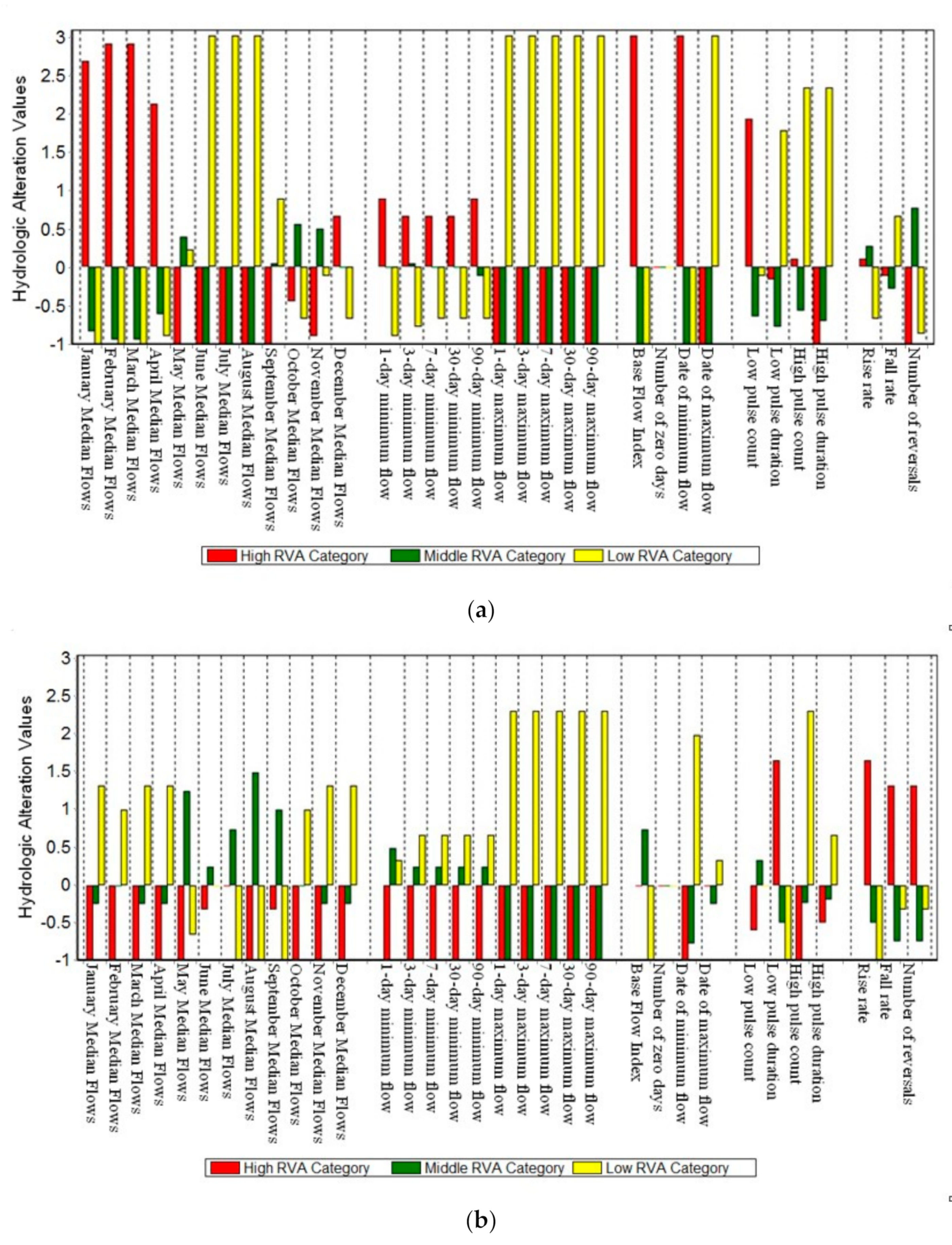
4.1. Determination of Sustainable Boundaries
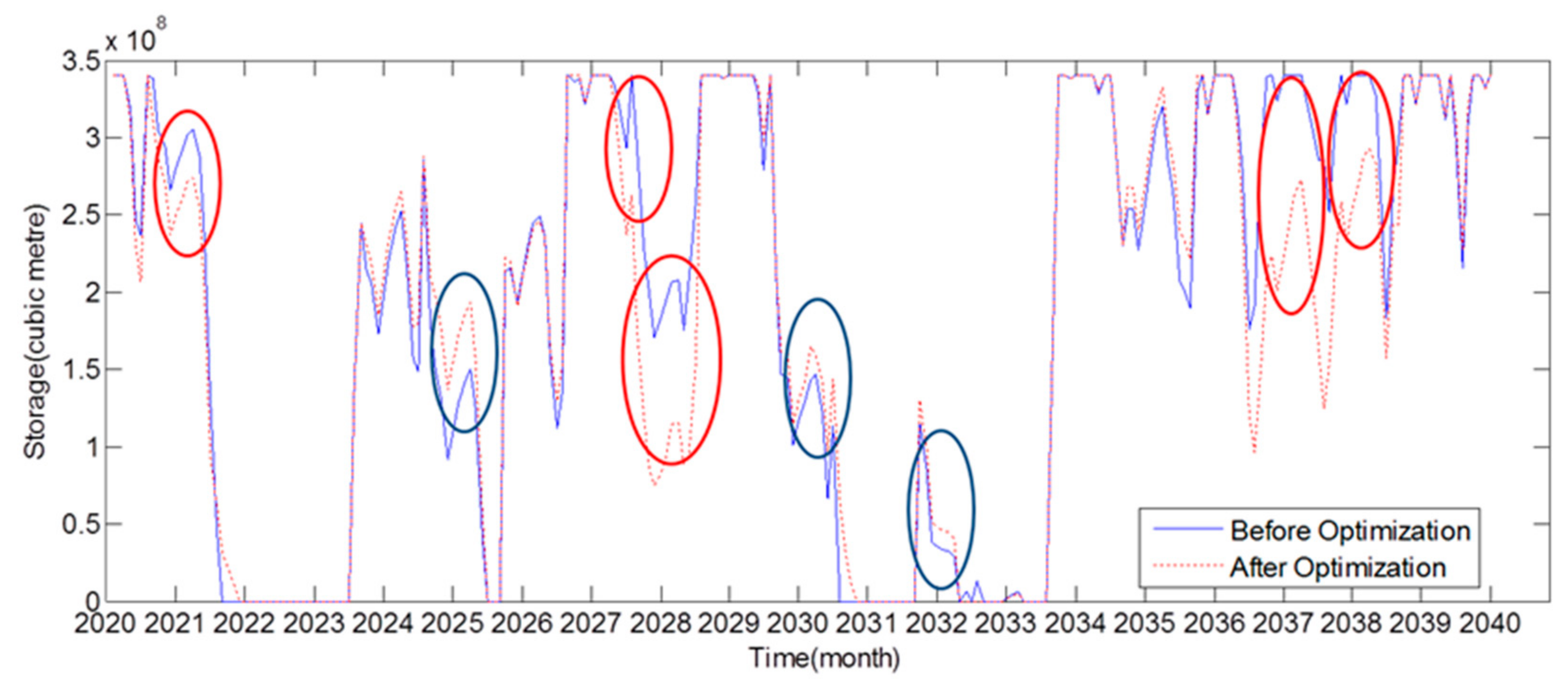
4.2. Dynamic Regulation in Different Time Steps
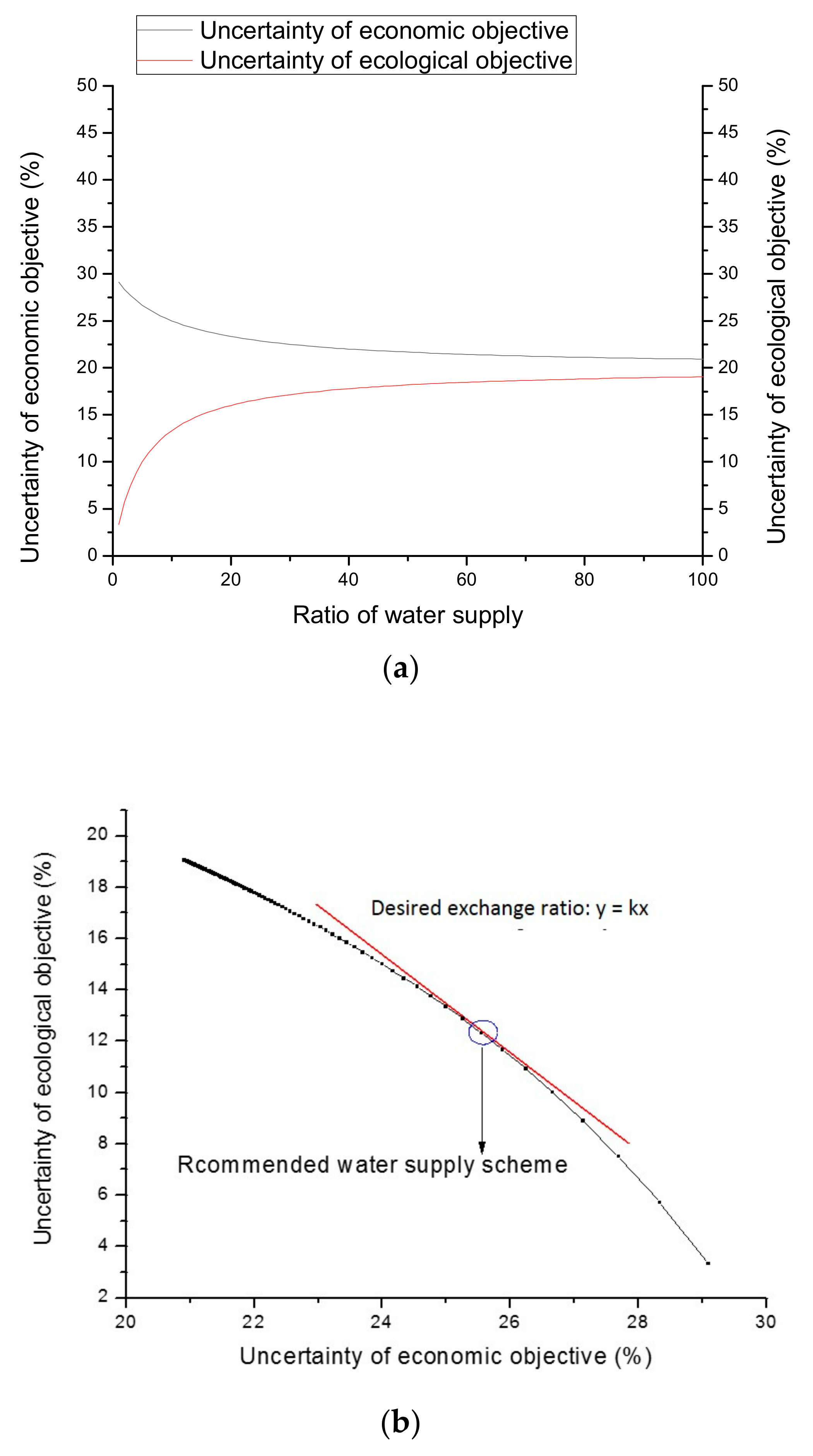
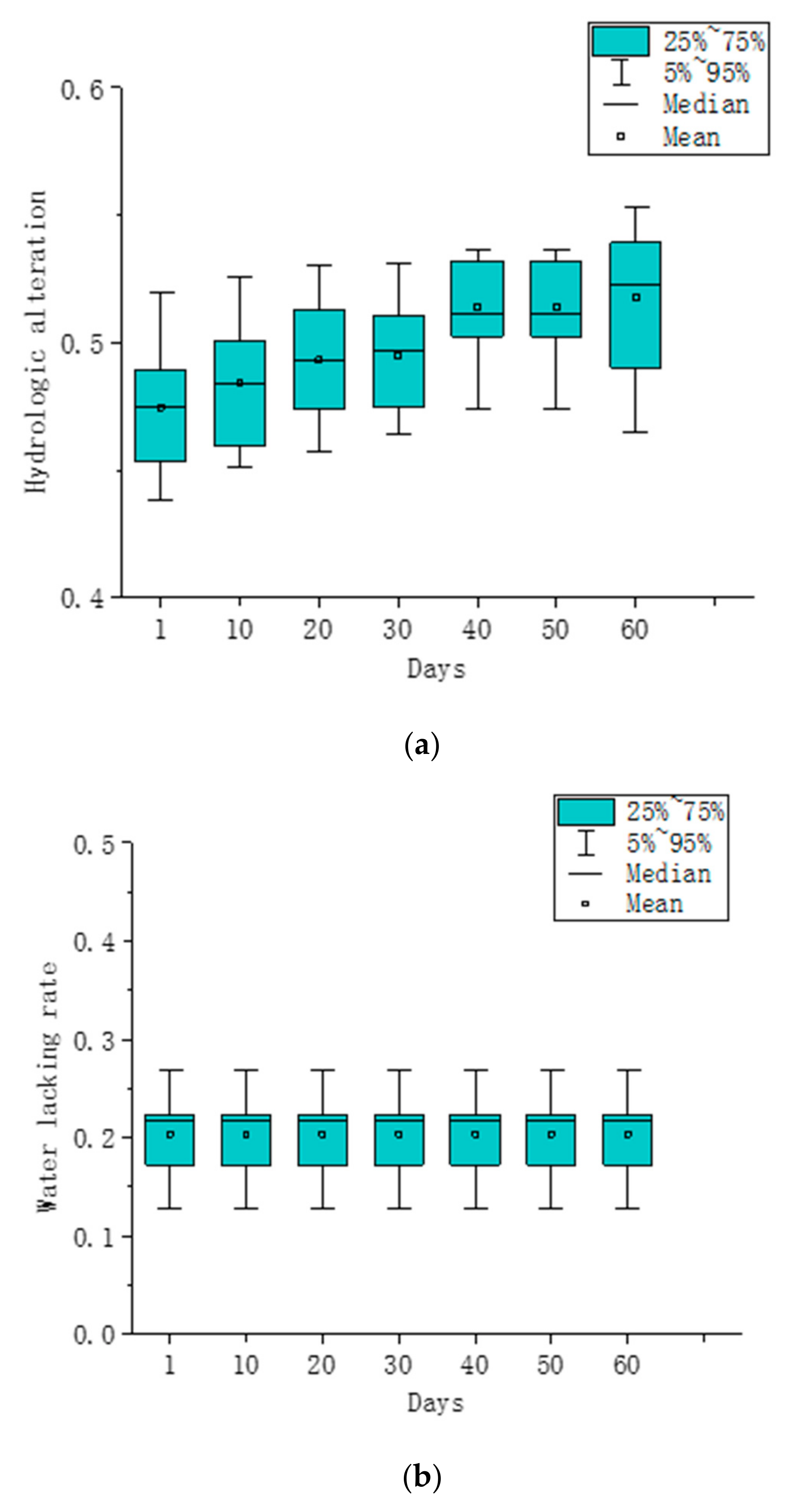
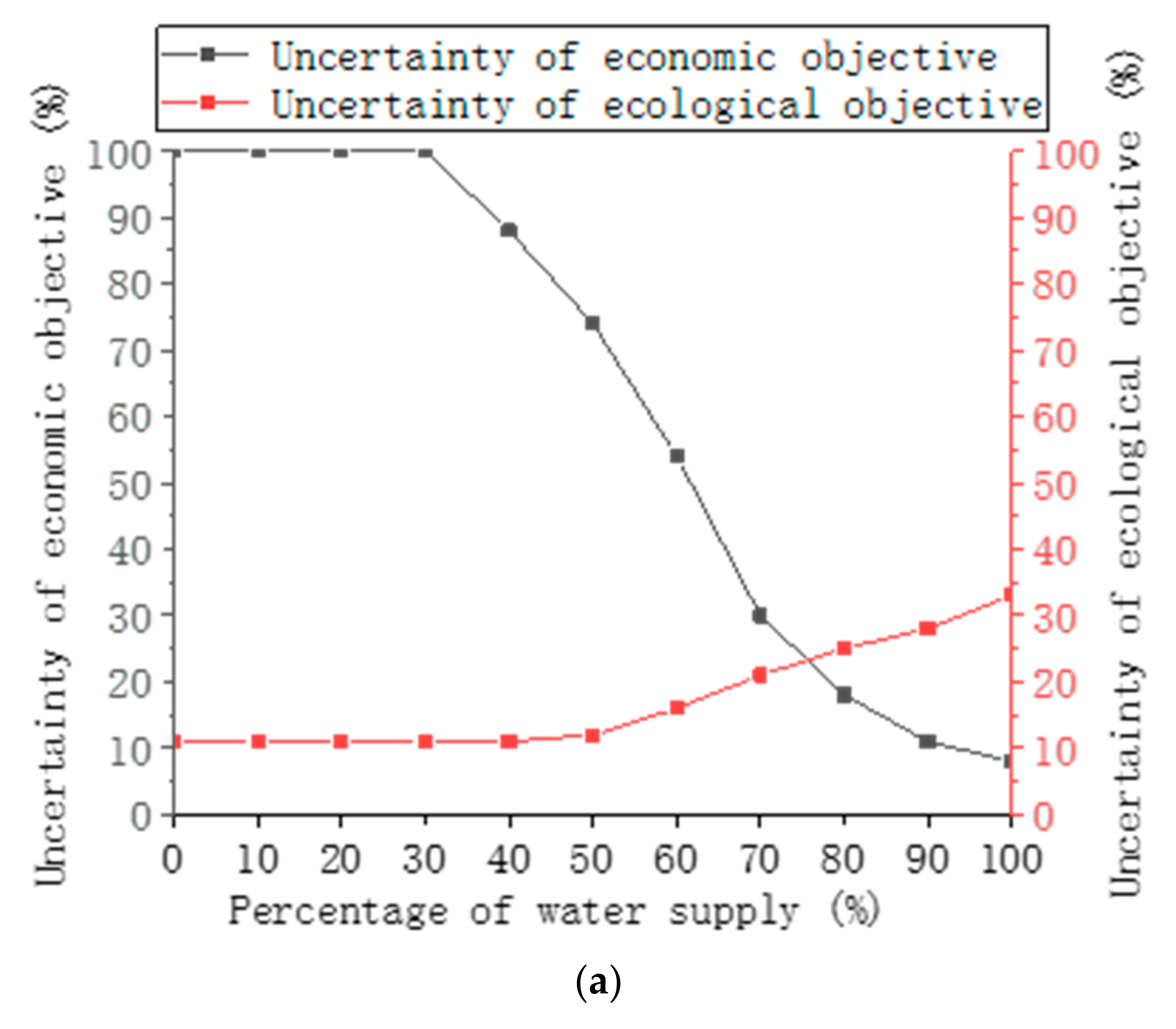
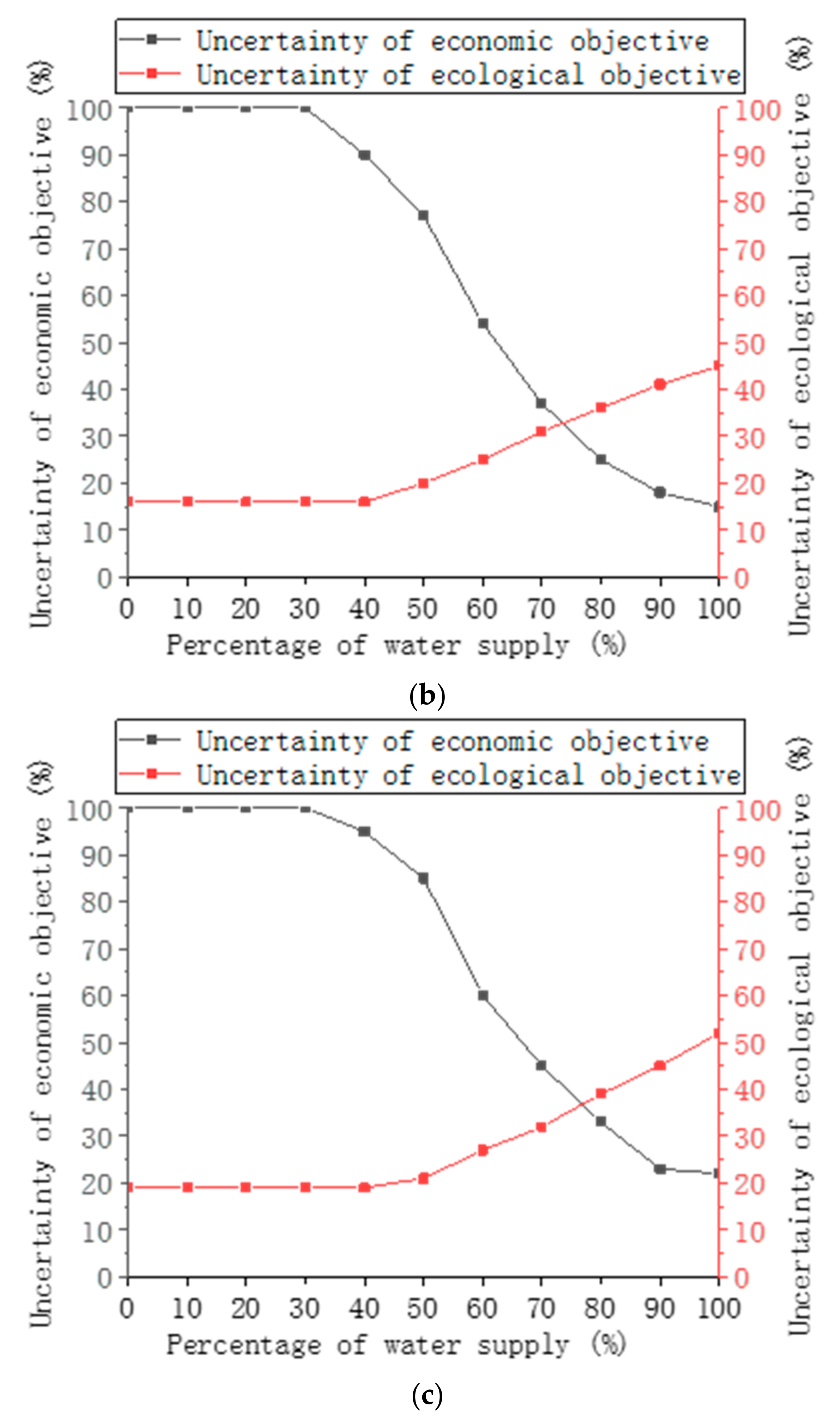
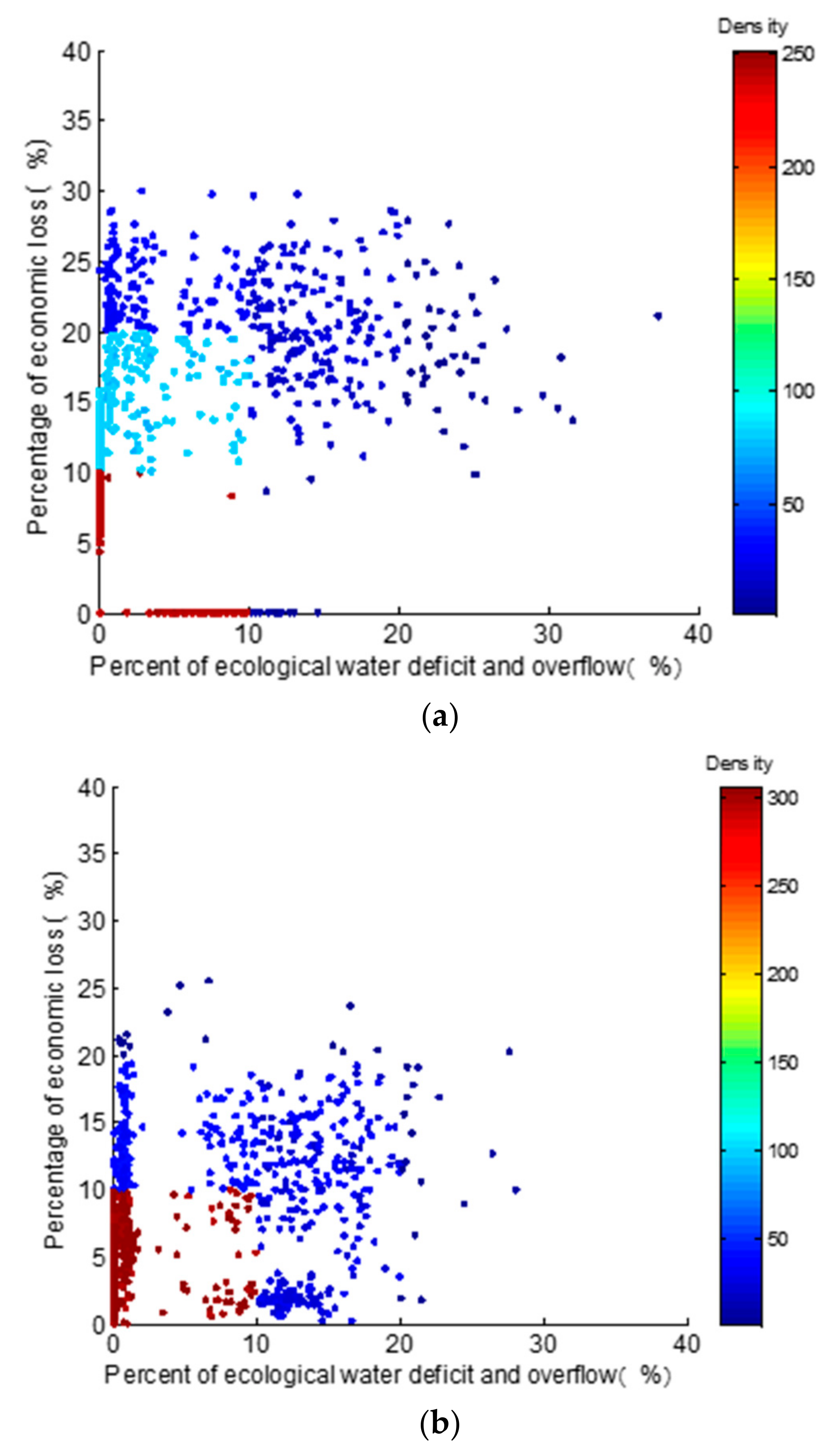
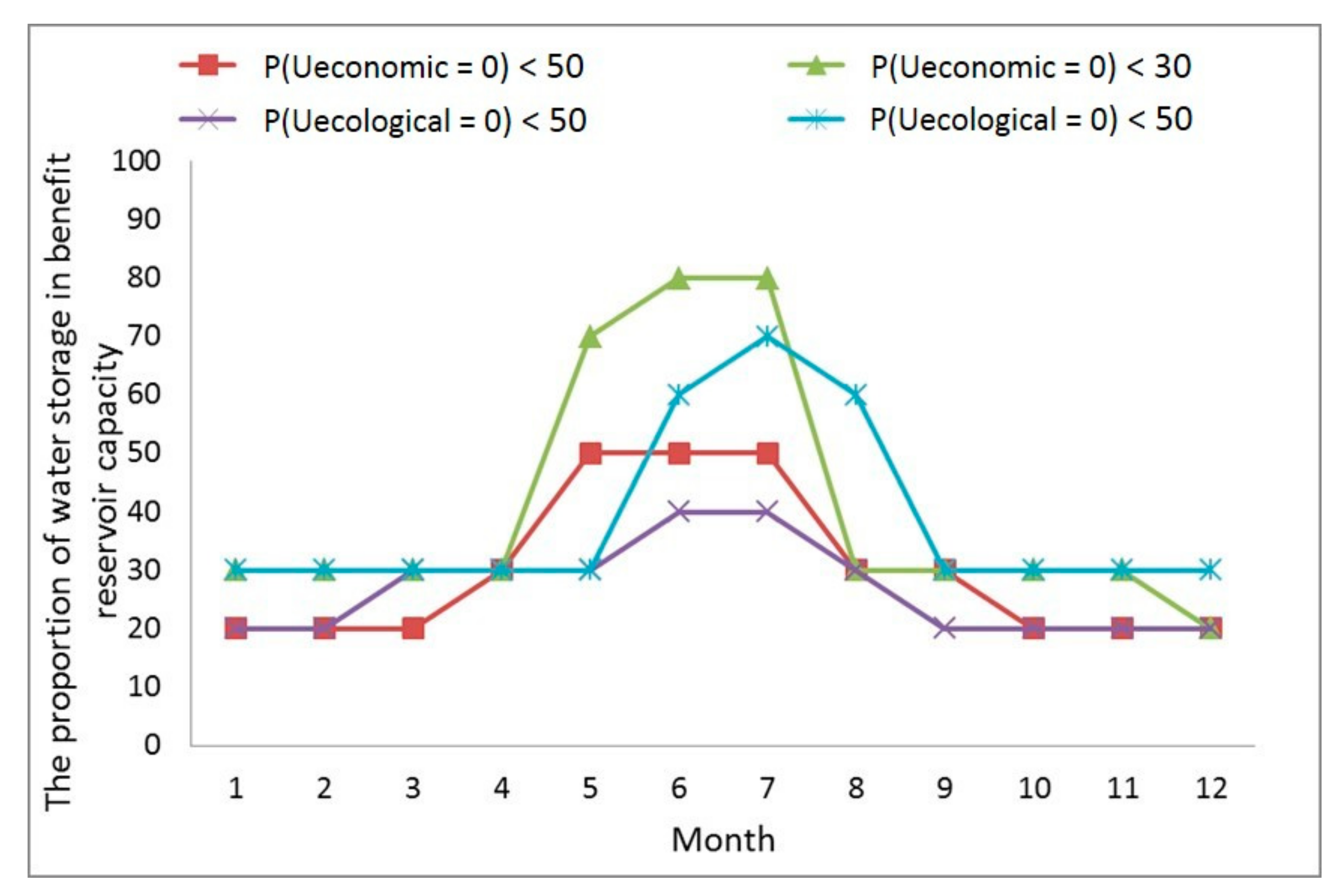
4.3. Uncertainty Analysis of Reservoir Discharge Operation
4.4. Analysis of Model Effectiveness
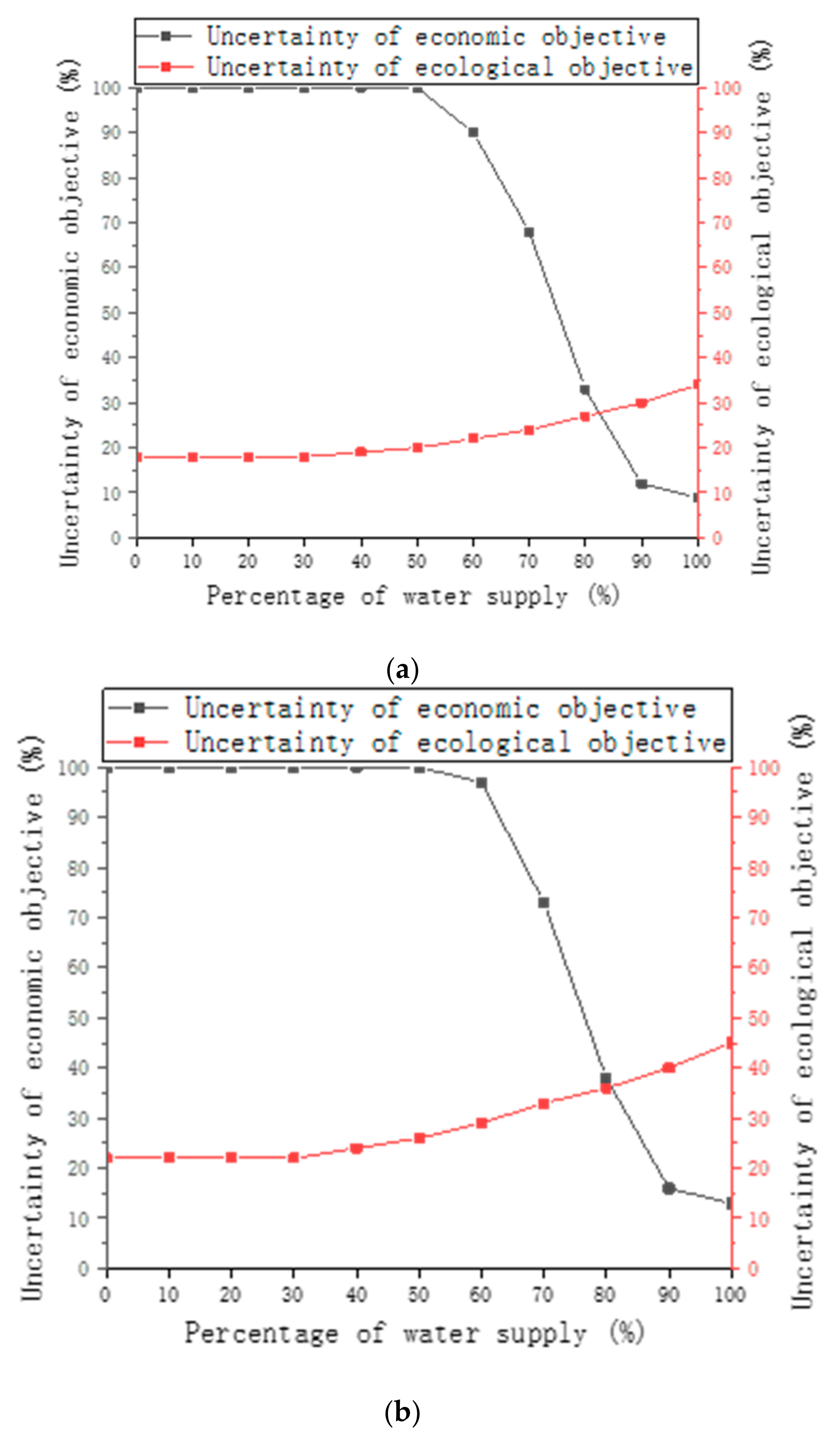
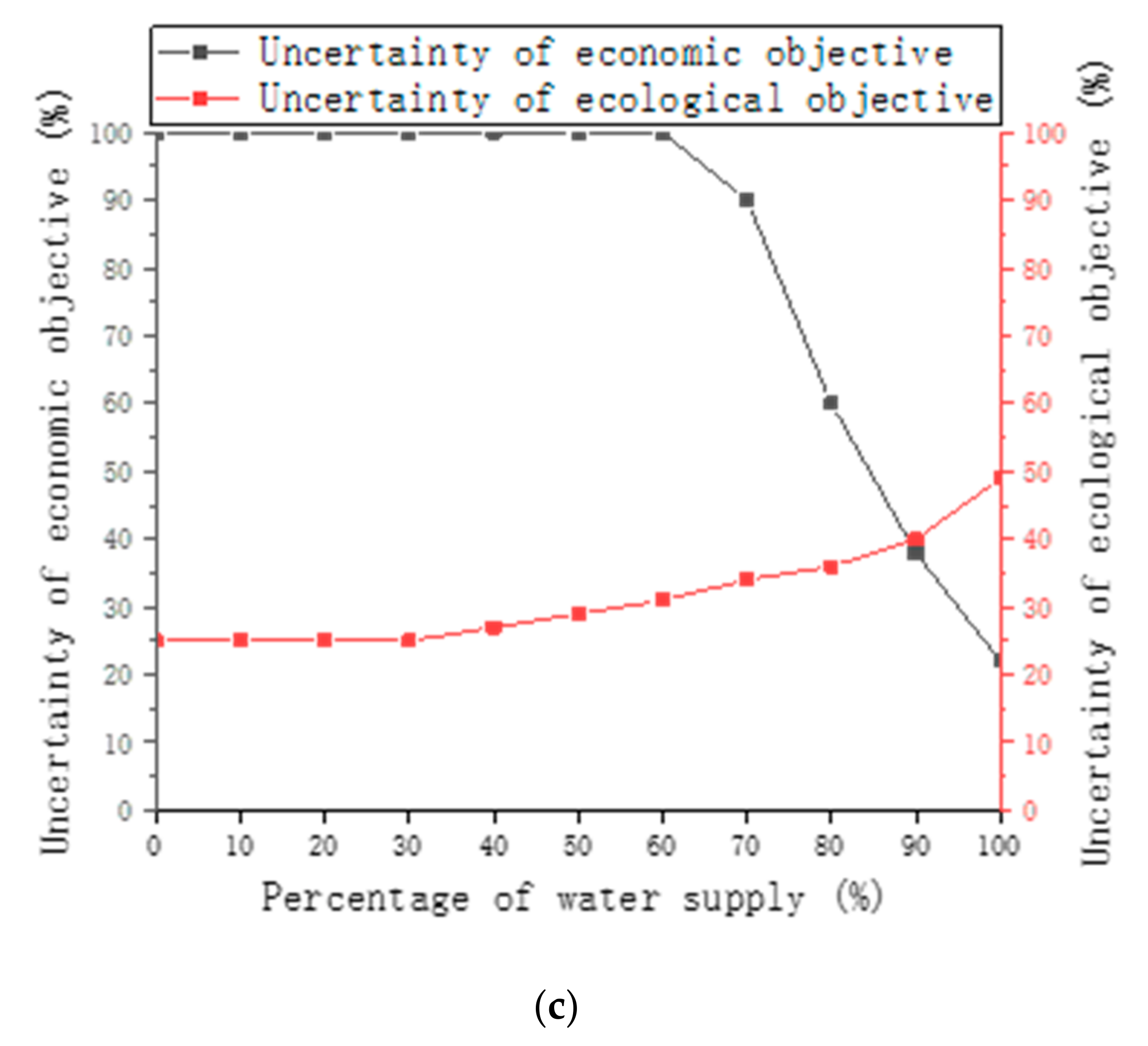
4.5. Response Analysis of Target Uncertainty to Reservoir Storage Available
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Poff, N.L.; Richter, B.D.; Arthington, A.H.; Bunn, S.E.; Naiman, R.J.; Kendy, E.; Acreman, M.; Apse, C.; Bledsoe, B.P.; Freeman, M.C.; et al. The ecological limits of hydrologic alteration (ELOHA): A new framework for developing regional environmental flow standards. Freshw. Biol. 2010, 55, 147–170. [Google Scholar] [CrossRef]
- Richter, B.D. Re-thinking environmental flows: From allocations and reserves to sustainability boundaries. River Res. Appl. 2009, 26, 1052–1063. [Google Scholar] [CrossRef]
- Richter, B.D.; Davis, M.M.; Apse, C.; Konrad, C. A presumptive standard for environmental flow protection. River Res. Appl. 2012, 28, 1312–1321. [Google Scholar] [CrossRef]
- Peñas, F.J.; Barquín, J. Assessment of large-scale patterns of hydrological alteration caused by dams. J. Hydrol. 2019, 572, 706–718. [Google Scholar] [CrossRef]
- De Jalón, S.G.; Del Tánago, M.G.; de Jalón, D.G. A new approach for assessing natural patterns of flow variability and hydrological alterations: The case of the Spanish rivers. J. Environ. Manag. 2019, 233, 200–210. [Google Scholar] [CrossRef] [PubMed]
- Cheng, G.; Li, X.; Zhao, W.; Xu, Z.; Feng, Q.; Xiao, S.; Xiao, H. Integrated study of the water–ecosystem–economy in the Heihe River Basin. Natl. Sci. Rev. 2014, 1, 413–428. [Google Scholar] [CrossRef]
- Wang, Z.; Zhu, J.; Zheng, H. Improvement of Duration-Based Water Rights Management with Optimal Water Intake On/Off Events. Water Resour. Manag. 2015, 29, 2927–2945. [Google Scholar] [CrossRef]
- Yazicigil, H.; Houck, M.H. The effects of risk and reliability on optimal reservoir design. J. Am. Water Resour. Assoc. 1984, 20, 417–424. [Google Scholar] [CrossRef]
- Pearl, J. Probabilistic Reasoning in Intelligent Systems: Networks of Plausible Inference; Morgan Kaufmann Publishers: San Mateo, CA, USA, 1988. [Google Scholar]
- Hanea, A.M.; Gheorghe, M.; Hanea, R.; Ababei, D. Non-parametric Bayesian networks for parameter estimation in reservoir simulation: A graphical take on the ensemble Kalman filter (part I). Comput. Geosci. 2013, 17, 929–949. [Google Scholar] [CrossRef]
- Castelletti, A.; Soncini-Sessa, R. Bayesian Networks and participatory modelling in water resource management. Environ. Model. Softw. 2007, 22, 1075–1088. [Google Scholar] [CrossRef]
- Morrison, R.R.; Stone, M.C. Spatially implemented Bayesian network model to assess environmental impacts of water management. Water Resour. Res. 2014, 50, 8107–8124. [Google Scholar] [CrossRef]
- Brusaferri, A.; Matteucci, M.; Portolani, P.; Vitali, A. Bayesian deep learning based method for probabilistic forecast of day-ahead electricity prices. Appl. Energy 2019, 250, 1158–1175. [Google Scholar] [CrossRef]
- Chen, J.; Zhong, P.A.; An, R.; Zhu, F.; Xu, B. Risk analysis for real-time flood control operation of a multi-reservoir system using a dynamic Bayesian network. Environ. Model. Softw. 2019, 111, 409–420. [Google Scholar] [CrossRef]
- Shin, J.Y.; Kwon, H.H.; Lee, J.H.; Kim, T.W. Probabilistic long-term hydrological drought forecast using Bayesian networks and drought propagation. Meteorol. Appl. 2019, 27, e1827. [Google Scholar] [CrossRef]
- Phan, T.D.; Smart, J.C.; Capon, S.J.; Hadwen, W.L.; Sahin, O. Applications of Bayesian belief networks in water resource management: A systematic review. Environ. Model. Softw. 2016, 85, 98–111. [Google Scholar] [CrossRef]
- Pang, A.; Li, C.; Sun, T.; Yang, W.; Yang, Z. Trade-Off Analysis to Determine Environmental Flows in a Highly Regulated Watershed. Sci. Rep. 2018, 8, 1–11. [Google Scholar] [CrossRef]
- Pang, A.P.; Sun, T. Bayesian networks for environmental flow decision-making and an application in the Yellow River estuary, China. Hydrol. Earth Syst. Sci. 2014, 18, 1641–1651. [Google Scholar] [CrossRef]
- Xue, J.; Gui, D.; Zhao, Y.; Lei, J.; Zeng, F.; Feng, X.; Mao, D.; Shareef, M. A decision-making framework to model environmental flow requirements in oasis areas using Bayesian networks. J. Hydrol. 2016, 540, 1209–1222. [Google Scholar] [CrossRef]
- Marcot, B.G.; Penman, T.D. Advances in Bayesian network modelling: Integration of modelling technologies. Environ. Model. Softw. 2019, 111, 386–393. [Google Scholar] [CrossRef]
- Manoj, K.; Jha, M.A. Dynamic Bayesian Network for Predicting the Likelihood of a Terrorist Attack at Critical Transportation Infrastructure Facilities. J. Infrastruct. Syst. 2009, 15, 31–39. [Google Scholar]
- Kim, S.Y.; Imoto, S.; Miyano, S. Inferring gene networks from time series microarray data using dynamic Bayesian networks. Brief. Bioinform. 2003, 4, 3228–3235. [Google Scholar] [CrossRef] [PubMed]
- Nefian, A.V.; Liang, L.; Pi, X.; Liu, X.; Murphy, K. Dynamic Bayesian Networks for Audio-Visual Speech Recognition. J. Appl. Signal Process. 2002, 11, 1274–1288. [Google Scholar] [CrossRef]
- Robinson, J.W.; Hartemink, A.J. Learning Non-Stationary Dynamic Bayesian Networks. J. Mach. Learn. Res. 2010, 11, 3647–3680. [Google Scholar]
- Richter, B.; Baumgartner, J.; Wigington, R.; Braun, D. How much water does a river need. Freshw. Biol. 1997, 37, 231–249. [Google Scholar] [CrossRef]
- Richter, B.D.; Baumgartner, J.V.; Powell, J.; Braun, D.P. A Method for Assessing Hydrologic Alteration within Ecosystems. Conserv. Biol. 1996, 10, 1163–1174. [Google Scholar] [CrossRef]
- Shiau, J.T.; Wu, F.C. Pareto-optimal solutions for environmental flow schemes incorporating the intra-annual and interannual variability of the natural flow regime. Water Resour. Res. 2007, 43, 1–12. [Google Scholar] [CrossRef]
- Zhou, T.; Dong, Z.; Wu, J.; Lin, M. Study on Joint Regulation of Fenhe Cascade Reservoirs Considering the Ecological Water Demand. Yellow River 2018, 40, 62–65. [Google Scholar]
- Tang, X.; Zhang, Z.; Wei, Y. Quantitative Evaluation of Water Resources Pressure in Heihe River Basin. Bull. Soil Water Conserv. 2014, 34, 219–224. [Google Scholar]
- Stewart, J.I.; Hagan, R.M.; Pruitt, W.O.; Danielson, R.E.; Franklin, W.T.; Hanks, R.J.; Riley, J.P.; Jackson, E.B. Optimizing Crop Production through Control of Water and Salinity Levels in the Soil. Reports. Paper 67. 1977. Available online: https://digitalcommons.usu.edu/water_rep/67 (accessed on 21 March 2021).
- Zhou, T.; Dong, Z.; Wang, W. Study on Multi-Scale Coupled Ecological Dispatching Model Based on the Decomposition-Coordination Principle. Water 2019, 11, 1443. [Google Scholar] [CrossRef]
- Dempster, A.P.; Laird, N.M.; Rubin, D.B. Maximum likelihood from incomplete data via the EM algorithm. J. R. Stat. Soc. 1977, 39, 1–38. [Google Scholar]
- Dong, Z. An interactive method of multi-objective decision making and its application. J. Hydraul. Eng. 1992, 4, 33–38. [Google Scholar]
- Wang, J.; Meng, J.J. Characteristics and Tendencies of Annual Runoff Variations in the Heihe River Basin during the Past 60 years. Sci. Geogr. Sin. 2008, 28, 83–88. [Google Scholar]
- Liu, S.; Xie, Z.; Zeng, Y. Estimation of streamflow in ungauged basins using a combined model of black-box model and semi-distributed model: Case study in the Yingluoxia watershed. J. Beijing Norm. Univ. Nat. Sci. 2016, 52, 393–401. [Google Scholar]
- Yellow River Conservancy Commission. Hydrological Yearbook of the People’s Republic of China; China Water & Power Press: Beijing, China, 2015. [Google Scholar]
- Hao, W. Research on Rational Allocation and Carrying Capacity of Water Resources in Northwest China; Yellow River Water Conservancy Press: Zhengzhou, China, 2003. [Google Scholar]
- Xia, T.; Wang, Z.; Zheng, H. Topography and Data Mining Based Methods for Improving Satellite Precipitation in Mountainous Areas of China. Atmosphere 2015, 8, 983–1005. [Google Scholar] [CrossRef]
- Chen, Y.M. Main Crop Water Requirement and Irrigation of China; Teory and Practice of Rock Mechanics Press: Beijing, China, 1995. [Google Scholar]
- Yu, C.; Yang, Z.; Cai, Y.; Sun, T. A shorter time step for eco-friendly reservoir operation does not always produce better water availability and ecosystem benefits. J. Hydrol. 2016, 540, 900–913. [Google Scholar] [CrossRef]
- Xu, Z.; Loomis, J.; Zhang, Z.; Hamamura, K. Evaluating the performance of different willingness to pay question formats for valuing environmental restoration in rural China. Environ. Dev. Econ. 2006, 11, 585–601. [Google Scholar]
| Crops | January | February | March | April | May | June | July | August | September | October | November | December | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Wheat | ky kc | 0.6 0.5 | 0.6 0.5 | 0.6 0.8 | 1 1.14 | 1 1 | 0.6 0.6 | 0 0 | 0 0 | 0 0 | 0.2 0.5 | 0.2 0.5 | 0.2 0.5 |
| Maize | ky kc | 0 0 | 0 0 | 0 0 | 0 0 | 0 0 | 0.2 0.7 | 0.2 0.8 | 0.2 1 | 0.2 1 | 0 0 | 0 0 | 0 0 |
| Cotton | ky kc | 0 0 | 0 0 | 0 0 | 0.85 0.5 | 0.85 0.5 | 0.5 0.6 | 0.5 1 | 0.5 0.8 | 0.5 0.7 | 0.5 0.8 | 0 0 | 0 0 |
| Nodes | Value Domain | States | Description |
|---|---|---|---|
| Q | (0, 273] | Lowest, very low, low, medium, high, very high, highest | Reservoir inflow (m3/s) |
| R | (0, 98.5] | Low, medium, high | Rainfall (mm) |
| S | [0, 100] | 0, 10, 20, 30, 40, 50, 60, 70, 80, 90, 100 | Percentage of storage in utilizable capacity (%) |
| D | (0, 150] | Low, medium, high | Reservoir water demand (106 m3) |
| E | [0, 100] | Low, medium, high | Ecological status calculated by RVA (%) |
| W | [0, 100] | 0, 10, 20, 30, 40, 50, 60, 70, 80, 90, 100 | The percentage of water supply (%) |
| C | (0, 0.42] (0, 0.35] (0, 2.11] | Low, medium, high Low, medium, high Low, medium, high | Wheat prices (USD/kg) Maize prices (USD/kg) Cotton prices (USD/kg) |
| U | {0,1} | Achieved (keep the flow within the sustainable boundaries and the agricultural loss within threshold value), Not achieved (Can’t keep the flow within the sustainable boundaries nor the agricultural loss within threshold value) | The state of objective |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhou, T.; Dong, Z.; Chen, X.; Ran, Q. Decision Support Model for Ecological Operation of Reservoirs Based on Dynamic Bayesian Network. Water 2021, 13, 1658. https://doi.org/10.3390/w13121658
Zhou T, Dong Z, Chen X, Ran Q. Decision Support Model for Ecological Operation of Reservoirs Based on Dynamic Bayesian Network. Water. 2021; 13(12):1658. https://doi.org/10.3390/w13121658
Chicago/Turabian StyleZhou, Tao, Zengchuan Dong, Xiuxiu Chen, and Qihua Ran. 2021. "Decision Support Model for Ecological Operation of Reservoirs Based on Dynamic Bayesian Network" Water 13, no. 12: 1658. https://doi.org/10.3390/w13121658
APA StyleZhou, T., Dong, Z., Chen, X., & Ran, Q. (2021). Decision Support Model for Ecological Operation of Reservoirs Based on Dynamic Bayesian Network. Water, 13(12), 1658. https://doi.org/10.3390/w13121658







