Effects of Prometryn Exposure Scenarios on Microcystis aeruginosa Growth and Water Qualities in Incubator Experiments
Abstract
1. Introduction
2. Materials and Methods
2.1. Experimental Materials
2.2. Experimental Methods
2.3. Monitoring Indicators and Methods
2.4. Statistical Analysis
3. Theoretical Background
4. Results and Discussion
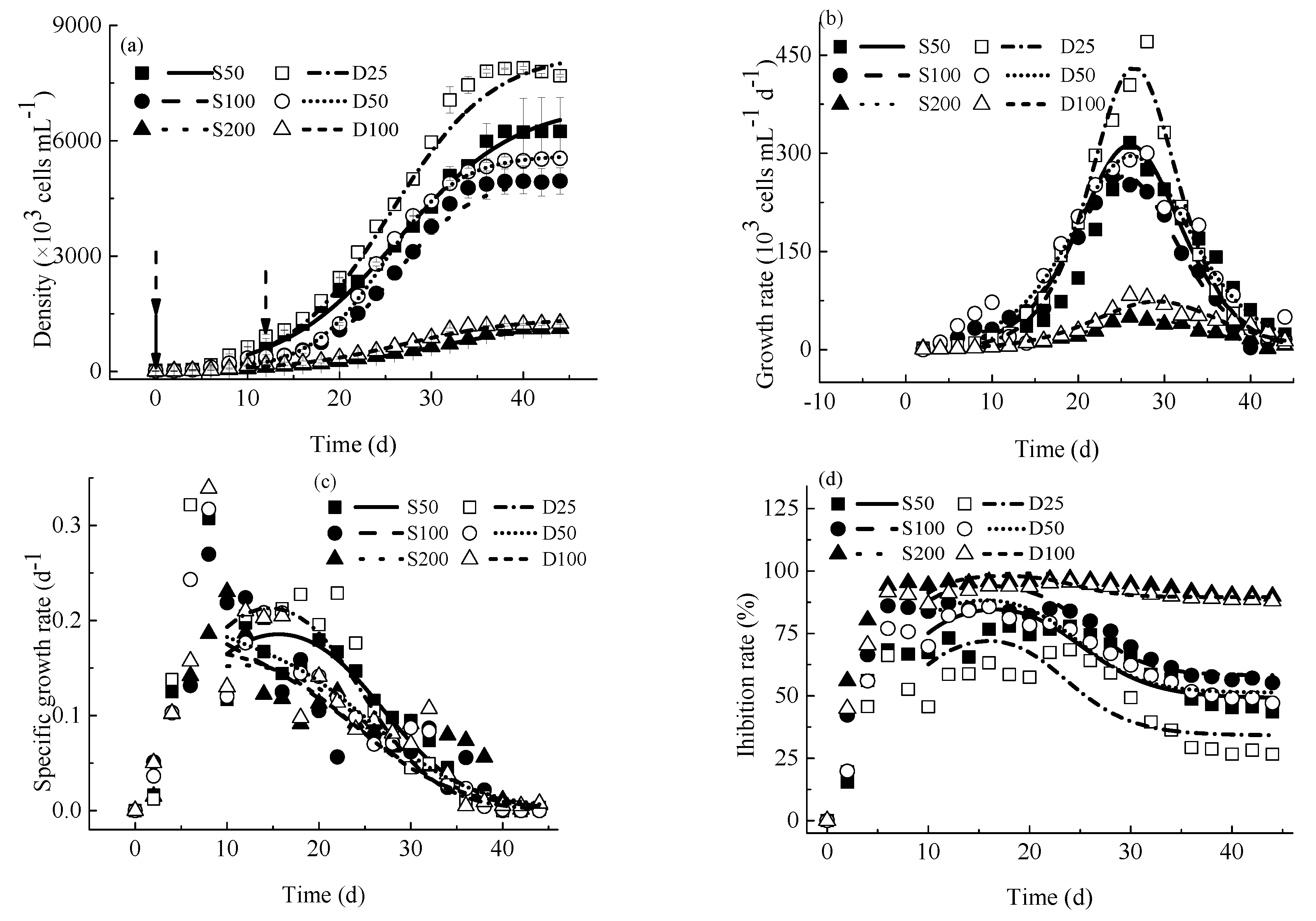
4.1. M. aeruginosa Growth Kinetics
4.1.1. Variations of M. aeruginosa Densities
4.1.2. Growth Rates
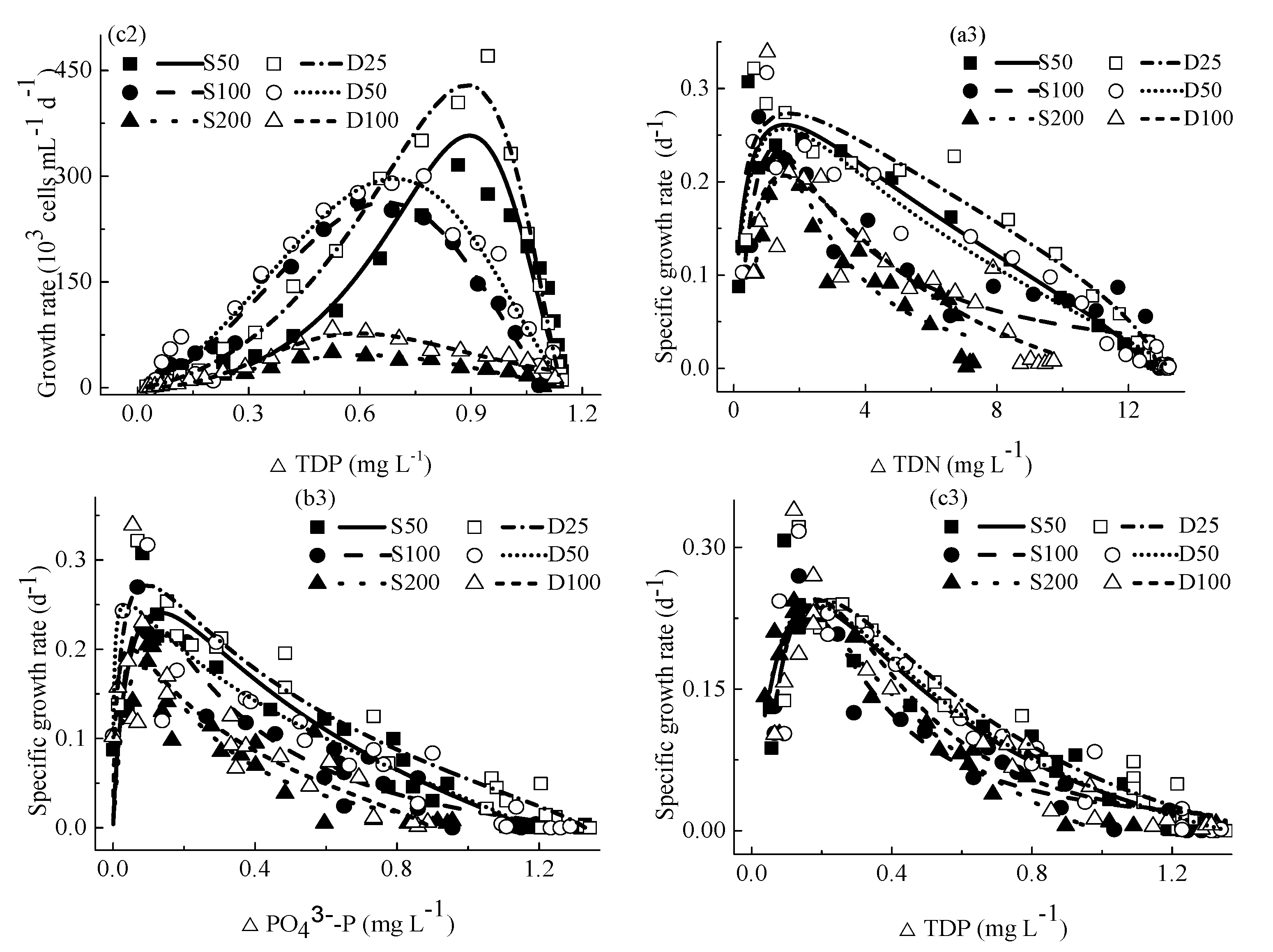
4.1.3. Specific Growth Rates
4.1.4. Inhibition Rates
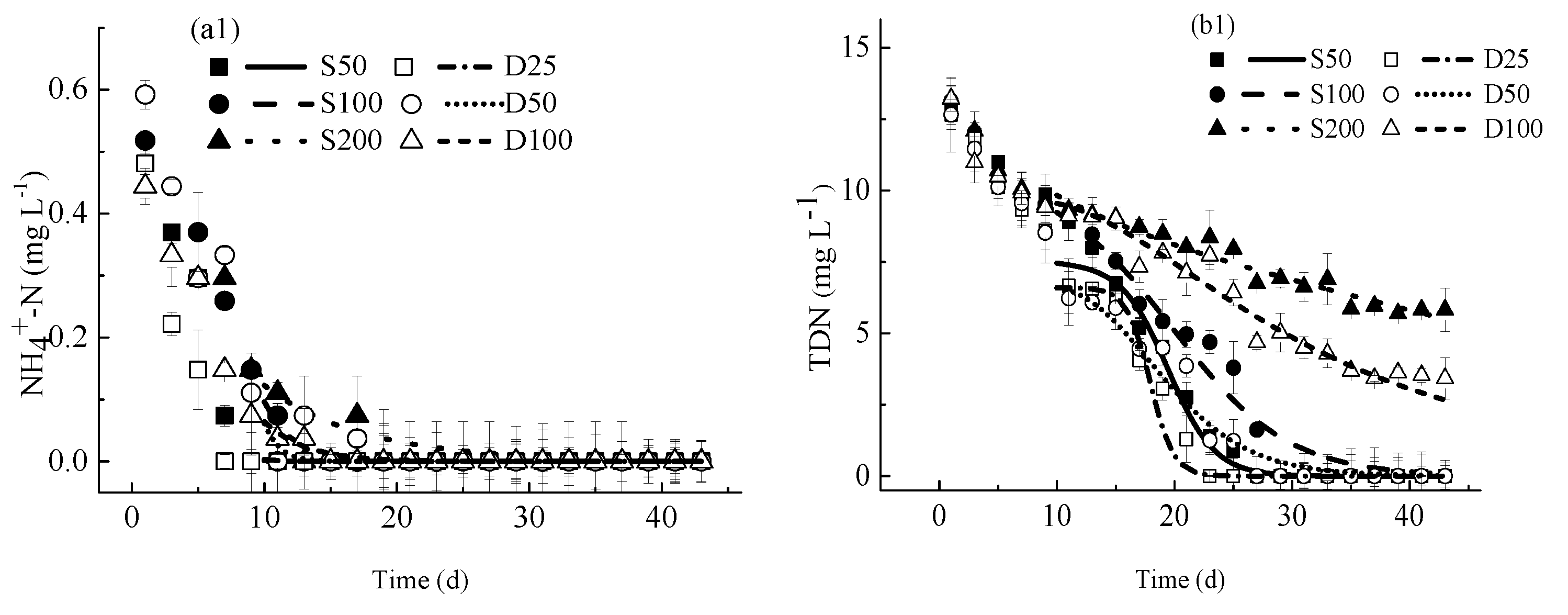
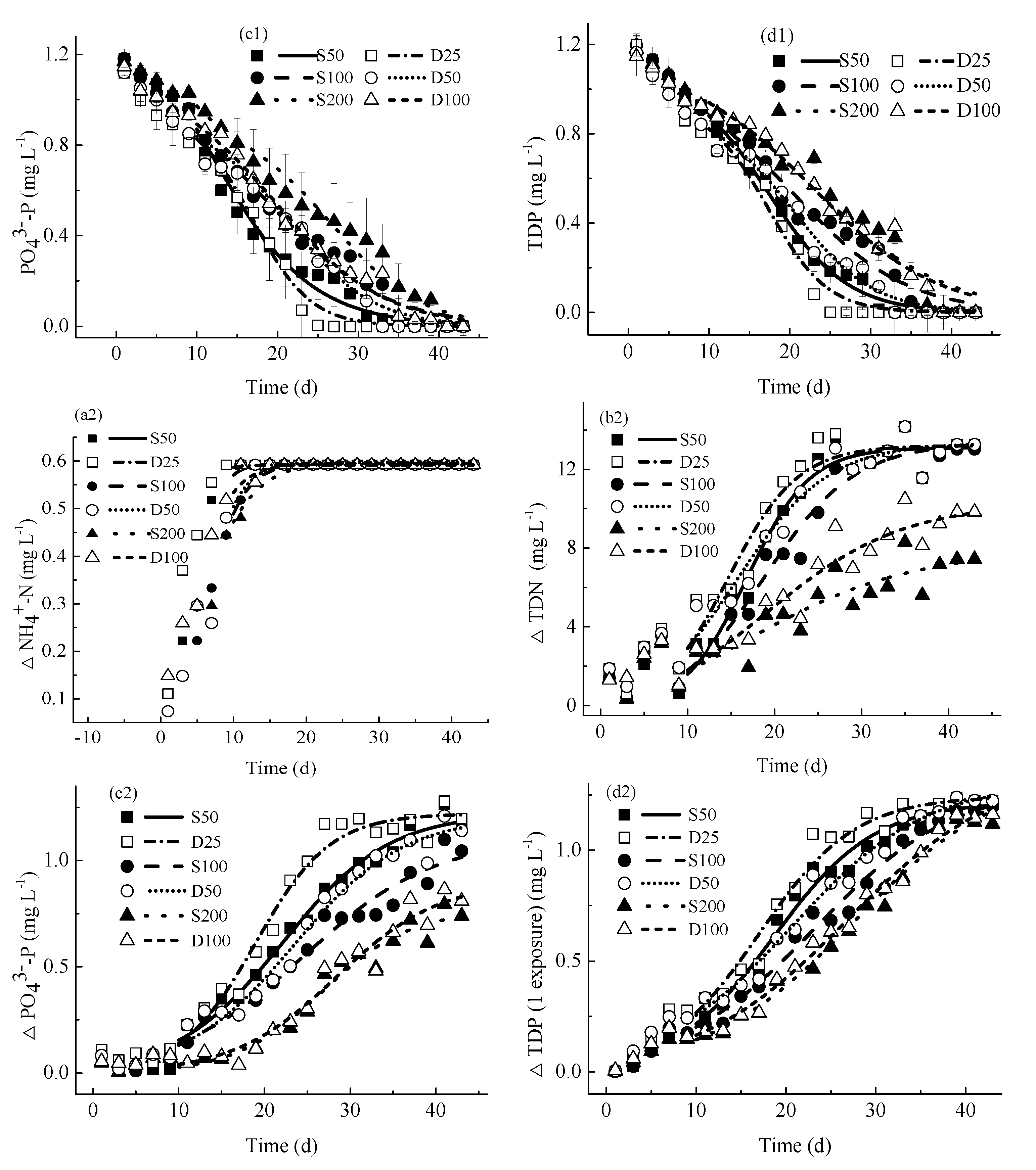
4.2. Nutrients Kinetics
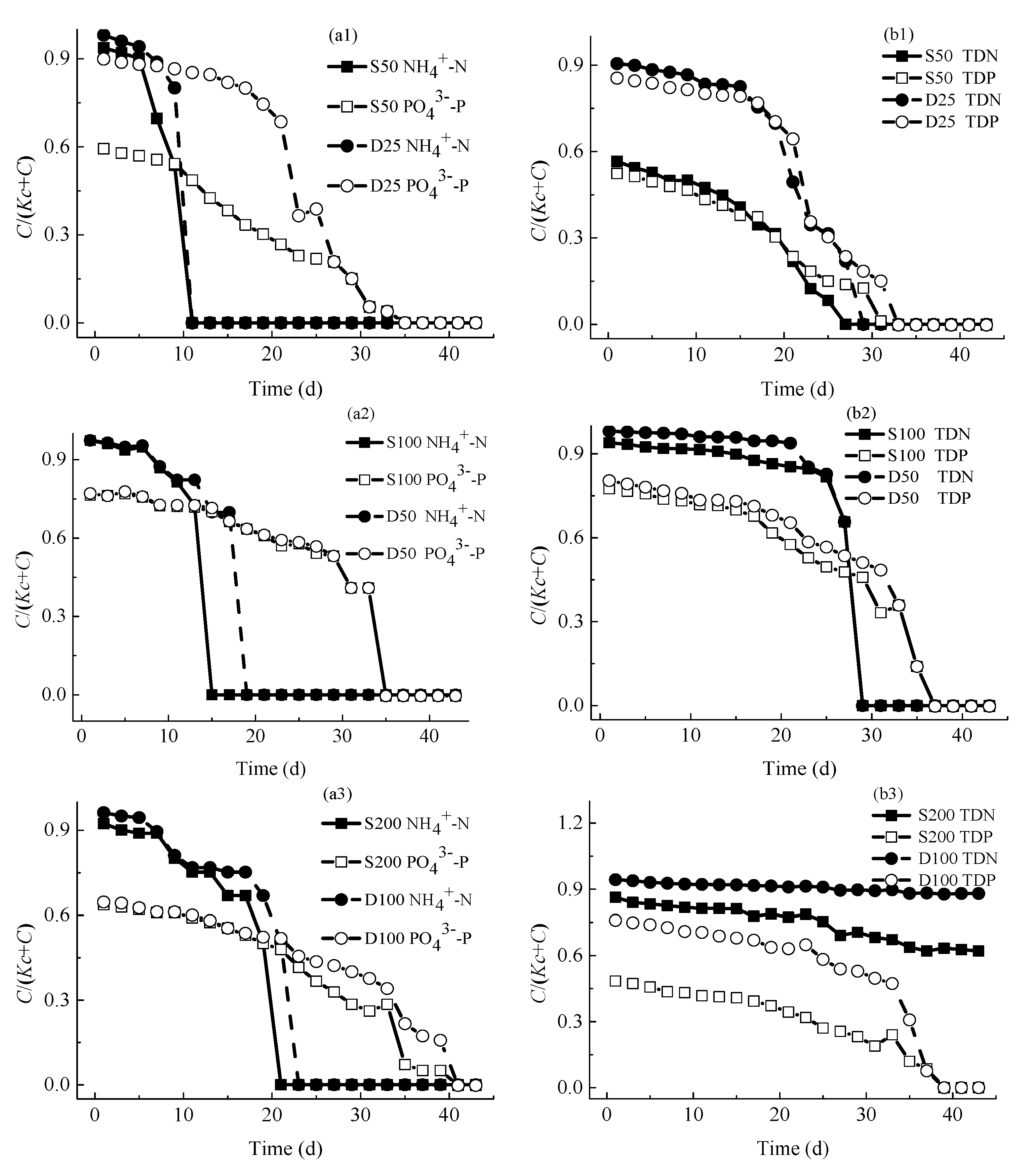
4.2.1. Concentrations of Nutrients
4.2.2. Concentrations of Consumed Nutrients
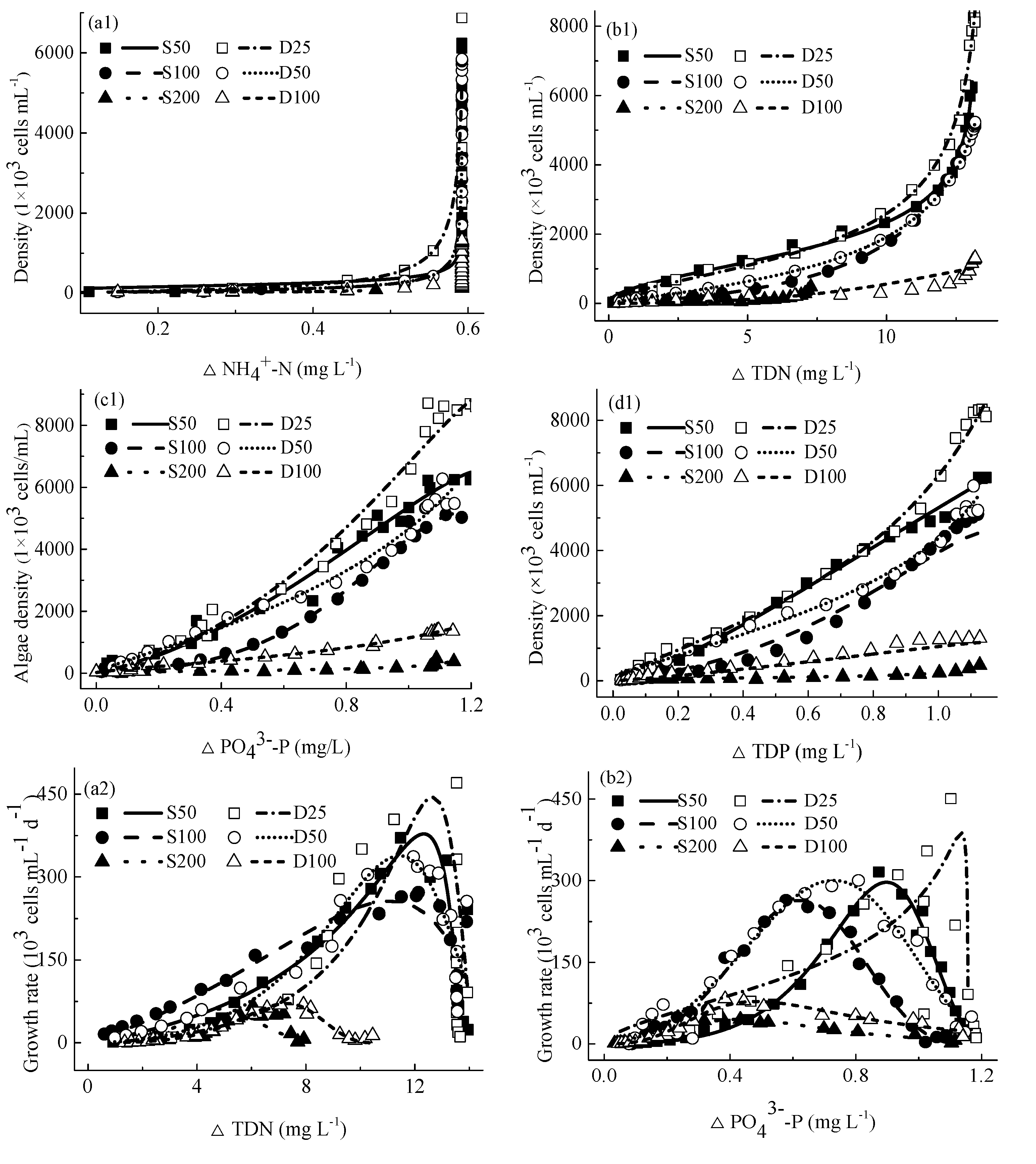
4.3. The Relationship between Specific Growth Rates and Concentrations of Nutrients
4.4. Relationship between M. aeruginosa Growth and Concentrations of Consumed Nutrients
4.4.1. Relationship between M. aeruginosa Densities and Concentrations of Consumed Nutrients
4.4.2. Relationship between M. aeruginosa Growth Rates and Concentrations of Consumed Nutrients
4.4.3. Relationship between M. aeruginosa Specific Growth Rates and Concentrations of Consumed Nutrients
4.5. Discussion on Limiting Nutrients of M. aeruginosa Growth
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Kniss, A.R. Long-term trends in the intensity and relative toxicity of herbicide use. Nat. Commut. 2017, 8, 14865. [Google Scholar] [CrossRef]
- Starr, A.V.; Bargu, S.; Maiti, K.; Delaune, R.D. the effect of atrazine on Louisiana Gulf Coast Estuarine phytoplankton. Arch. Environ. Contam. Toxicol. 2017, 72, 178–188. [Google Scholar] [CrossRef]
- Carlisle, S.M.; Trevors, J.T. Glyphosate in the environment. Water Air Soil Pollut. 1998, 39, 409–420. [Google Scholar]
- Masiá, A.; Campo, J.; Navarro-Ortega, A.; Barcelo, D.; Pico, Y. Pesticide monitoring in the basin of Llobregat River (Catalonia, Spain) and comparison with historical data. Sci. Total Environ. 2015, 503–504, 58–68. [Google Scholar] [CrossRef] [PubMed]
- Cypel, Y.S.; Hines, S.E.; Davey, V.J.; Eber, S.M.; Schneiderman, A. Spirometric pulmonary restriction in herbicide-exposed U.S. Vietnam war veterans. Int. J. Environ. Res. Public Health 2019, 16, 3131. [Google Scholar] [CrossRef] [PubMed]
- Ma, J.; Tong, S.; Wang, P.; Chen, J. Toxicity of seven herbicides to the three cyanobacteria Anabaena flos-aquae, Microcystis flos-aquae and Mirocystis aeruginosa. Int. J. Environ. Res. 2010, 4, 347–352. [Google Scholar]
- Kamrin, M.A. Pesticide Profiles; Lewis Publishers/CRC Press: Boca Raton, FL, USA, 1997; 676p. [Google Scholar]
- Vryzas, Z.; Alexoudis, C.; Vassiliou, G.; Galanis, K.; Papadopoulou-Mourkidou, E. Determination and aquatic risk assessment of pesticide residues in riparian drainage canals in northeastern Greece. Ecotoxicol. Environ. Saf. 2011, 74, 174–181. [Google Scholar] [CrossRef] [PubMed]
- Erickson, W.; Turner, L. Prometryn Analysis of Risks to Endangered and Threatened Salmon and Steelhead; United States Environmental Protection Agency: Washington, DC, USA, 2002; p. 71.
- Zhao, Q.; Zhu, L. Effect of humic acid on prometryn bioaccumulation and the induction of oxidative stress in zebrafish (Danio rerio). RSC Adv. 2016, 6, 16790–16797. [Google Scholar] [CrossRef]
- Zhou, J.; Hu, F.; Jiao, J.; Liu, M.; Li, H. Effects of bacterial-feeding nematodes and prometryne-degrading bacteria on the dissipation of prometryne in contaminated soil. J. Soils Sediments 2012, 12, 576–585. [Google Scholar] [CrossRef]
- Tan, X.; Dai, K.W.; Parajuli, K.; Hang, X.; Duan, Z.; Hu, Y. Effects of phenolic pollution on interspecific competition between Microcystis aeruginosa and Chlorella pyrenoidosa and their photosynthetic responses. Int. J. Environ. Res. Public Health 2019, 16, 3947. [Google Scholar] [CrossRef]
- Bengtson-Nash, S.M.; Quayle, P.A.; Schreiber, U.; Muller, J.F. The selection of a model microalgal species as biomaterial for a novel aquatic phytotoxicity assay. Aquat. Toxicol. 2005, 72, 315–326. [Google Scholar] [CrossRef] [PubMed]
- Nguyen, Q.V.; Tran, T.H.; Pham, T.N.; Thuoc, D.V.; Cao, V.D.; Boo, K.H. Inhibitory effects of Bidens pilosa plant extracts on the growth of the bloom-forming alga Microcystis aeruginosa. Water Air Soil Pollut. 2019, 230, 1–16. [Google Scholar] [CrossRef]
- Zhang, P.; Zhai, C.; Chen, R.; Liu, C.; Xue, R.; Jiang, J. The dynamics of the water bloom-forming Microcystis aeruginosa and its relationship with biotic and abiotic factors in Lake Taihu, China. Ecol. Eng. 2012, 47, 274–277. [Google Scholar] [CrossRef]
- Chalifour, A.; Leblanc, A.; Sleno, L.; Juneau, P. Sensitivity of Scenedesmus obliquus and Microcystis aeruginosa to atrazine: Effects of acclimation and mixed cultures, and their removal ability. Ecotoxicology 2016, 25, 1822–1831. [Google Scholar] [CrossRef] [PubMed]
- Goudar, C.T.; Joeris, K.; Konstantinov, K.B.; Piret, J.M. Logistic equations effectively model mammalian cell batch and fed-batch kinetics by logically constraining the fit. Biotechnol. Prog. 2005, 21, 1109–1118. [Google Scholar] [CrossRef] [PubMed]
- Surendhiran, D.; Vijay, M.; Sivaprakash, B.; Sirajunnisa, A. Kinetic modeling of microalgae growth and lipid synthesis for biodiesel production. 3 Biotech 2015, 5, 663–669. [Google Scholar] [CrossRef] [PubMed]
- Samkhaniyani, F.; Najafpour, G.D.; Ardestani, F. Evaluation of effective nutritional parameters for Scenedesmus sp. microalgae culturing in a photobioreactor for biodiesel production. Int. J. Environ. Sci. Technol. 2017, 14, 1–10. [Google Scholar] [CrossRef]
- Kong, W.W.; Huang, S.L.; Shi, F.F.; Zhou, J.G.; Feng, Y.B.; Xiao, Y. Study on Microcystis aeruginosa growth in incubator experiments by combination of Logistic and Monod functions. Algal Res. 2018, 35, 602–612. [Google Scholar] [CrossRef]
- Gutting, B.W.; Rukhin, A.; Marchette, D.; Mackie, R.S.; Thran, B. Dose-response modeling for inhalational anthrax in rabbits following single or double exposures. Risk Anal. 2016, 36, 2031–2038. [Google Scholar] [CrossRef] [PubMed]
- Lovelace, M.L.; Talbert, R.E.; Scherder, E.F.; Hoagland, R.E. Effects of double applications of simulated quinclorac drift rates on tomato. Weed Sci. 2007, 55, 169–177. [Google Scholar] [CrossRef]
- Schrübbers, L.C.; Valverde, B.E.; Strobel, B.W.; Cedergreen, N. Glyphosate accumulation, translocation, and biological effects in Coffea Arabica after single and double exposures. Eur. J. Agron. 2016, 74, 133–143. [Google Scholar] [CrossRef]
- Waizenegger, J.; Braeuning, A.; Templin, M.; Lampen, A.; Hessel-Pras, S. Structure-dependent induction of apoptosis by hepatotoxic pyrrolizidine alkaloids in the human hepatoma cell line HepaRG: Single versus repeated exposure. Food Chem. Toxicol. 2018, 114, 215–226. [Google Scholar] [CrossRef] [PubMed]
- Arito, H.; Tsuruta, H.; Oguri, M. Changes in sleep and wakefulness following single and repeated exposures to toluene vapor in rats. Arch. Toxicol. 1998, 62, 76–80. [Google Scholar] [CrossRef] [PubMed]
- Huang, S.L.; Kong, W.W.; Yang, Z.J.; Yu, H.; Li, F.Y. Combination of logistic and modified monod functions to study Microcystis aeruginosa growth stimulated by fish feed. Ecotoxicol. Environ. Saf. 2019, 167, 146–160. [Google Scholar] [CrossRef] [PubMed]
- Yao, B.; Xi, B.; Hu, C.; Huo, S.; Su, J.; Liu, H. A model and experimental study of phosphate uptake kinetics in algae: Considering surface adsorption and P-stress. J. Environ. Sci. 2011, 23, 189–198. [Google Scholar] [CrossRef]
- Wu, M.; Huang, S.L.; Zang, C.J.; Du, S.L. Release of nutrient from fish feed and effects on Microcystis aeruginosa growth. Aquac. Res. 2012, 43, 1460–1470. [Google Scholar] [CrossRef]
- Endo, H.; Yoshimura, T.; Kataoka, T.; Suzuki, K. Effects of CO2 and iron availability on phytoplankton and eubacterial community compositions in the northwest subarctic Pacific. J. Exp. Mar. Biol. Ecol. 2013, 439, 160–175. [Google Scholar] [CrossRef]
- Wetzel, R.G.; Likens, G.E. Composition and Biomass of Phytoplanton. Limnological Analyses; Springer: New York, NY, USA, 2000. [Google Scholar]
- Kong, W.; Huang, S.; Yang, Z.; Shi, F.; Feng, Y.; Khatoon, Z. Fish feed quality is a key factor in impacting aquaculture water environment: Evidence from incubator experiments. Sci. Rep. 2020, 10, 187. [Google Scholar] [CrossRef]
- Vörös, L.; Padisák., J. Phytoplankton biomass and chlorophyll-a in some shallow lakes in central Europe. Hydrobiologia 1991, 215, 111–119. [Google Scholar] [CrossRef]
- Hecky, R.E. Nutrient limitation of phytoplankton in freshwater and marine environments: A review of recent evidence on the effects of enrichment. Limnol. Oceanogr. 1988, 33, 796–822. [Google Scholar] [CrossRef]
- Baxter, L.; Brain, R.; Prosser, R.; Solomon, K.; Hanson, M. Sensitivity of a green alga to atrazine is not enhanced by previous acute exposure. Environ. Pollut. 2013, 181, 325–328. [Google Scholar] [CrossRef]
- Li, X.; Hu, H.Y.; Gan, K.; Sun, Y.X. Effects of different nitrogen and phosphorus concentrations on the growth, nutrient uptake, and lipid accumulation of a freshwater microalga Scenedesmus sp. Bioresour. Technol. 2010, 101, 5494–5500. [Google Scholar]
- Qiao, Z.; Yu, H. Effects of stationary phase elongation and initial nitrogen and phosphorus concentrations on the growth and lipid-producing potential of Chlorella sp. HQ. J. Appl. Phycol. 2014, 26, 141–149. [Google Scholar]
- Zhang, H.; Huang, F.; Li, F.; Gu, Z.; Chen, R.; Zhang, Y. An improved logistic model illustrating Microcystis aeruginosa growth under different turbulent mixing conditions. Water 2019, 11, 669. [Google Scholar] [CrossRef]
- Fussmann, G.F.; Ellner, S.P.; Shertzer, K.W.; Hairston, N.G. Crossing the Hopf bifurcation in a live predator-preysystem. Science 2000, 290, 1358–1360. [Google Scholar] [CrossRef]
- Sunda, W.G.; Shertzer, K.W.; Hardison, D.R. Ammonium uptake and growth models in marine diatoms: Monod and Droop revisited. Mar. Ecol. Prog. Ser. 2009, 386, 29–41. [Google Scholar] [CrossRef]
- Kooijman, S.A.L.M.; Hanstveit, A.O.; Oldersma, H. Parametric analyses of population growth in bio-assays. Water Res. 1983, 17, 527–538. [Google Scholar] [CrossRef]
- Tian, F.; Zhou, J.; Sun, Z.; Cai, Z.; Xu, N.; An, M.; Duan, S. Inhibitory effects of Chinese traditional herbs and herb-modified clays on the growth of harmful algae, Phaeocystis globosa and Prorocentrum donghaiense. Harmful Algae 2014, 37, 153–159. [Google Scholar] [CrossRef]
- McGaughy, K.; Hajer, A.A.; Drabold, E.; Bayless, D.; Reza, M.T. Algal remediation of wastewater produced from hydrothermally treated septage. Sustainability 2019, 11, 3454. [Google Scholar] [CrossRef]
- Liebig, M.; Schmidt, G.; Bontje, D.; Kooi, B.W.; Streck, G. Direct and indirect effects of pollutants on algae and algivorous ciliates in an aquatic indoor microcosm. Aquat. Toxicol. 2008, 88, 102–110. [Google Scholar] [CrossRef] [PubMed]
- Ni, L.; Jie, X.; Wang, P.; Li, S.; Wang, G.; Li, Y.; Li, Y. Effect of linoleic acid sustained-release microspheres on Microcystis aeruginosa antioxidant enzymes activity and microcystins production and release. Chemosphere 2018, 121, 110–116. [Google Scholar] [CrossRef]
- Gao, Y.N.; Ge, F.J.; Zhang, L.P.; He, Y.; Lu, Z.; Zhang, Y.Y.; Liu, B.; Zhou, Q.H.; Wu, Z.B. Enhanced toxicity to the cyanobacterium Microcystis aeruginosa by low-dosage repeated exposure to the allelochemical N-phenyl-1-naphthylamine. Chemosphere 2017, 174, 732–738. [Google Scholar] [CrossRef]
- Lee, E.; Jalalizadeh, M.; Zhang, Q. Growth kinetic models for microalgae cultivation: A review. Algal Res. 2015, 12, 497–512. [Google Scholar] [CrossRef]
- Zhu, J.; He, Y.; Wang, J.; Qiao, Z.; Wang, Y.; Li, Z.; Huang, M. Impact of aeration disturbances on endogenous phosphorus fractions and their algae growth potential from malodorous river sediment. Environ. Sci. Pollut. Res. 2017, 24, 8062–8070. [Google Scholar] [CrossRef]
- Liu, X.; Zhan, M.; Ma, Y. Relationship between algal growth and nutritious materials absorbability in the three-gorges valley. Huanjing Kexue 2005, 26, 95–99. (In Chinese) [Google Scholar] [PubMed]
- Ruiz, J.; Arbib, Z.; Alvarez-Diaz, P.D.; Garrido-Pérez, C.; Barragán, J.; Perales, J.A. Photobiotreatment model (PhBT): A kinetic model for microalgae biomass growth and nutrient removal in wastewater. Environ. Technol. 2013, 34, 979–991. [Google Scholar] [CrossRef] [PubMed]
- Cerucci, M.; Jaligama, G.K.; Ambrose, R.B.J. Comparison of the monod and droop methods for dynamic water quality simulations. J. Environ. Eng. 2010, 136, 1009–1019. [Google Scholar] [CrossRef][Green Version]
- Coveney, M.F.; Wetzel, R.G. Biomass, production, and specific growth rate of bacterioplankton and coupling to phytoplankton in an oligotrophic lake. Limnol. Oceanogr. 1995, 40, 1187–1200. [Google Scholar] [CrossRef]
- Li, Y.; Liu, Y.; Zhao, L.; Hastings, A.; Guo, H. Exploring change of internal nutrients cycling in a shallow lake: A dynamic nutrient driven phytoplankton model. Ecol. Model. 2015, 313, 137–148. [Google Scholar] [CrossRef]

| Parameters | S50 | D25 | S100 | D50 | S200 | D100 |
|---|---|---|---|---|---|---|
| Parameters of the modified Logistic equation describing M. aeruginosa growth | ||||||
| a | 4.00 | 4.64 | 5.24 | 5.36 | 4.86 | 4.80 |
| r | 0.15 | 0.19 | 0.24 | 0.26 | 0.20 | 0.20 |
| Nmax | 6982.69 | 8853.65 | 5110.50 | 5857.16 | 1234.29 | 1376.31 |
| Nave | 2973.94 | 4070.76 | 2289.05 | 2802.67 | 470.08 | 640.82 |
| R2 | 0.995 | 0.994 | 0.997 | 0.999 | 0.995 | 0.992 |
| μ′cmax | 261.85 | 420.55 | 306.63 | 380.72 | 61.71 | 68.82 |
| μ′cave | 141.09 | 183.85 | 112.08 | 132.36 | 25.07 | 29.83 |
| Imax | 69.39 | 61.93 | 85.01 | 79.02 | 96.37 | 92.02 |
| Iave | 62.34 | 50.02 | 73.85 | 67.50 | 93.49 | 91.67 |
| μcave | 0.11 | 0.11 | 0.10 | 0.11 | 0.09 | 0.10 |
| Parameters of the Monod equation | ||||||
| NH4+-N | ||||||
| μm | 0.32 | 0.34 | 0.33 | 0.33 | 0.32 | 0.33 |
| Kc | 2.85 × 10−3 | 1.24 × 10−3 | 4.86 × 10−2 | 3.27 × 10−2 | 1.19 × 10−1 | 3.63 × 10−2 |
| R2 | 0.457 | 0.541 | 0.622 | 0.538 | 0.697 | 0.550 |
| TDN | ||||||
| μm | 0.30 | 0.32 | 0.28 | 0.32 | 0.28 | 0.29 |
| Kc | 0.98 | 0.73 | 3.30 | 1.17 | 8.23 | 7.82 |
| R2 | 0.962 | 0.970 | 0.950 | 0.896 | 0.886 | 0.939 |
| PO43−-P | ||||||
| μm | 0.31 | 0.32 | 0.33 | 0.33 | 0.33 | 0.33 |
| Kc | 0.55 | 0.27 | 0.66 | 0.29 | 2.22 | 1.20 |
| R2 | 0.878 | 0.959 | 0.906 | 0.950 | 0.834 | 0.879 |
| TDP | ||||||
| μm | 0.32 | 0.32 | 0.31 | 0.32 | 0.32 | 0.30 |
| Kc | 0.64 | 0.28 | 0.68 | 0.67 | 2.12 | 1.90 |
| R2 | 0.927 | 0.953 | 0.908 | 0.945 | 0.848 | 0.863 |
| Parameters of the Logistic equation describing concentrations of consumed nutrients | ||||||
| ΔNH4+-N | ||||||
| aΔC | 2.30 | 1.81 | 2.46 | 2.78 | 1.41 | 1.55 |
| rΔC | 0.54 | 0.66 | 0.40 | 0.46 | 0.27 | 0.37 |
| ΔCmax | 0.60 | 0.59 | 0.60 | 0.59 | 0.60 | 0.59 |
| R2 | 0.979 | 0.979 | 0.996 | 0.960 | 0.963 | 0.984 |
| ΔCave | 0.54 | 0.55 | 0.51 | 0.51 | 0.52 | 0.53 |
| ΔTDN | ||||||
| aΔC | 3.28 | 2.75 | 2.83 | 2.31 | 1.87 | 2.17 |
| rΔC | 0.20 | 0.19 | 0.14 | 0.15 | 0.08 | 0.09 |
| ΔCmax | 13.65 | 13.62 | 14.43 | 13.88 | 9.49 | 12.06 |
| R2 | 0.949 | 0.934 | 0.948 | 0.939 | 0.795 | 0.893 |
| ΔCave | 8.54 | 9.15 | 7.97 | 8.07 | 4.58 | 5.01 |
| ΔPO43−-P | ||||||
| aΔC | 2.58 | 3.41 | 2.70 | 2.97 | 3.60 | 3.52 |
| rΔC | 0.13 | 0.19 | 0.11 | 0.12 | 0.12 | 0.10 |
| ΔCmax | 1.32 | 1.32 | 1.26 | 1.42 | 1.11 | 1.45 |
| R2 | 0.939 | 0.985 | 0.937 | 0.985 | 0.972 | 0.976 |
| ΔCave | 0.71 | 0.77 | 0.56 | 0.63 | 0.47 | 0.50 |
| ΔTDP | ||||||
| aΔC | 2.78 | 3.01 | 2.74 | 2.76 | 3.19 | 3.03 |
| rΔC | 0.15 | 0.17 | 0.11 | 0.11 | 0.10 | 0.12 |
| ΔCmax | 1.31 | 1.33 | 1.49 | 1.53 | 1.72 | 1.43 |
| R2 | 0.967 | 0.985 | 0.976 | 0.989 | 0.974 | 0.979 |
| ΔCave | 0.75 | 0.80 | 0.67 | 0.70 | 0.57 | 0.65 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yang, Z.; Huang, S.; Huang, X.; Liang, X.; Akram, W.; Khatoon, Z. Effects of Prometryn Exposure Scenarios on Microcystis aeruginosa Growth and Water Qualities in Incubator Experiments. Water 2021, 13, 1346. https://doi.org/10.3390/w13101346
Yang Z, Huang S, Huang X, Liang X, Akram W, Khatoon Z. Effects of Prometryn Exposure Scenarios on Microcystis aeruginosa Growth and Water Qualities in Incubator Experiments. Water. 2021; 13(10):1346. https://doi.org/10.3390/w13101346
Chicago/Turabian StyleYang, Zhenjiang, Suiliang Huang, Xiaowen Huang, Xiaofu Liang, Waseem Akram, and Zobia Khatoon. 2021. "Effects of Prometryn Exposure Scenarios on Microcystis aeruginosa Growth and Water Qualities in Incubator Experiments" Water 13, no. 10: 1346. https://doi.org/10.3390/w13101346
APA StyleYang, Z., Huang, S., Huang, X., Liang, X., Akram, W., & Khatoon, Z. (2021). Effects of Prometryn Exposure Scenarios on Microcystis aeruginosa Growth and Water Qualities in Incubator Experiments. Water, 13(10), 1346. https://doi.org/10.3390/w13101346







