Energy Dissipation in Stilling Basins with Side Jets from Highly Convergent Chutes
Abstract
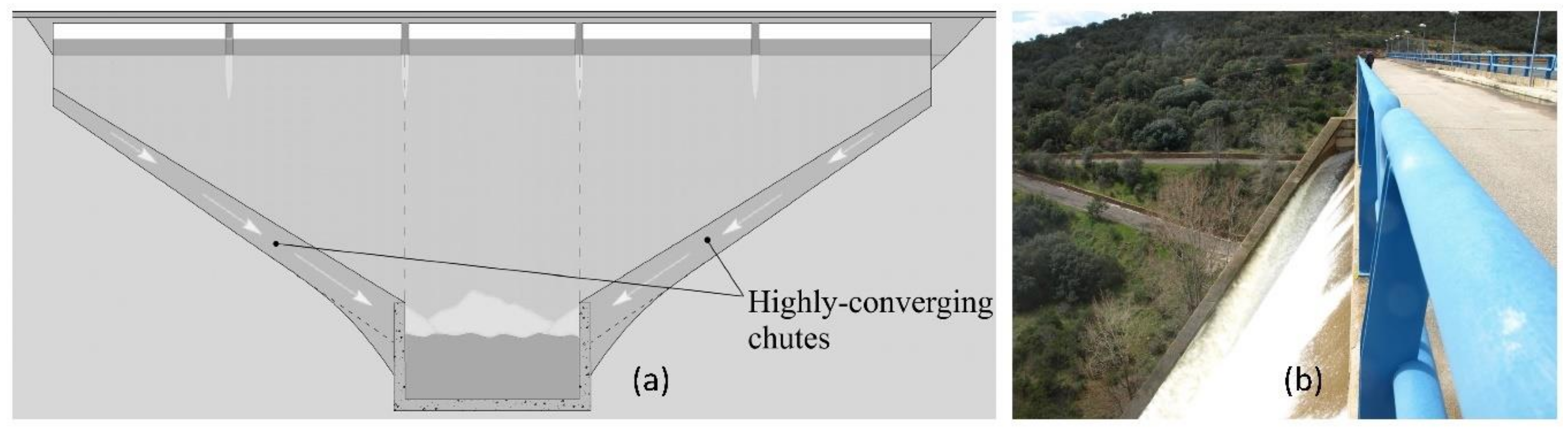
1. Introduction
2. Aim and Scope
- Increasing the spillway capacity.
- Protecting the downstream toe of the dam abutments against potential scour caused by overtopping.
- Enhancing the reservoir storage by increasing the full supply level, preserving the existing freeboards and the former capacity of the spillway.
- To establish objective criteria for the suitable hydraulic conditions of the flow downstream from the stilling basin to enable the appropriate restitution of the flow to the riverbed according to widely accepted technical guidelines.
- To perform a conceptual study of the effect of key HCCs design parameters on the energy dissipation at the stilling basin.
- To assess the design adaptation needs of existing stilling basins depending on the increase in the outlet discharge.
- To obtain experimental data to calibrate and validate numerical models for future research.
3. Methodology
3.1. Experimental Facility
- Maximum length of the weir (Ww): 5 m
- Height of the weir over the bottom of the stilling basin (Hw): 1.5 m
- Vertical upstream slope of the cross-section of the gravity dam
- Downstream slope of the cross-section of the gravity dam: 0.8 H:V
- Width of the stilling basin (Wb): 1 m
- Maximum length of the stilling basin (Lb): 3.7 m
- Maximum height of the sidewalls of the stilling basin (Hb): 0.5 m
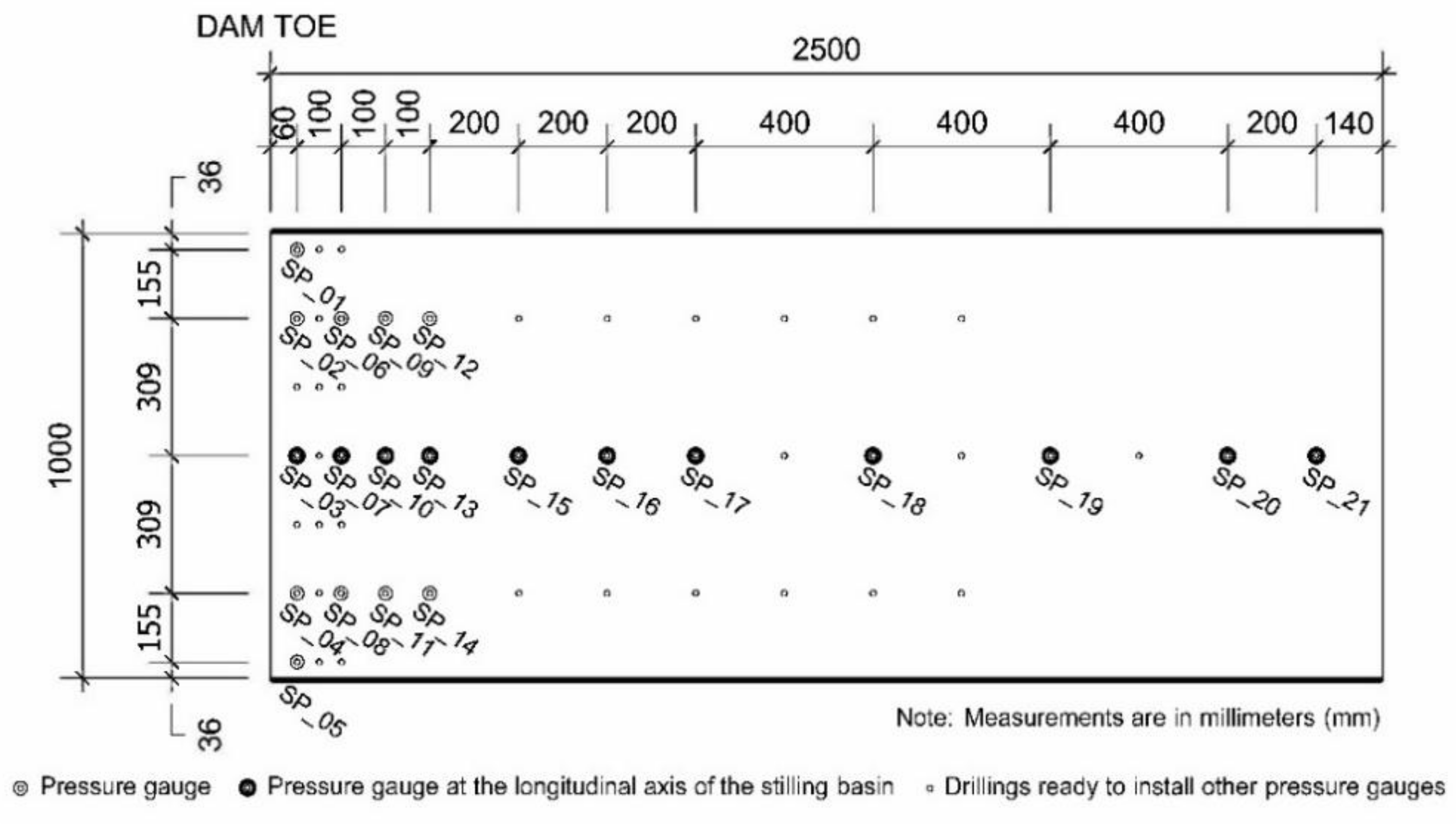
3.2. Instrumentation
- An electromagnetic flowmeter installed at the inlet pipe of the facility. The measured discharge was used as the variable controlling the inlet flow provided by the pumping system.
- An ultrasonic limnimeter for measuring the water level at the inlet tank, placed upstream of the gravity dam.
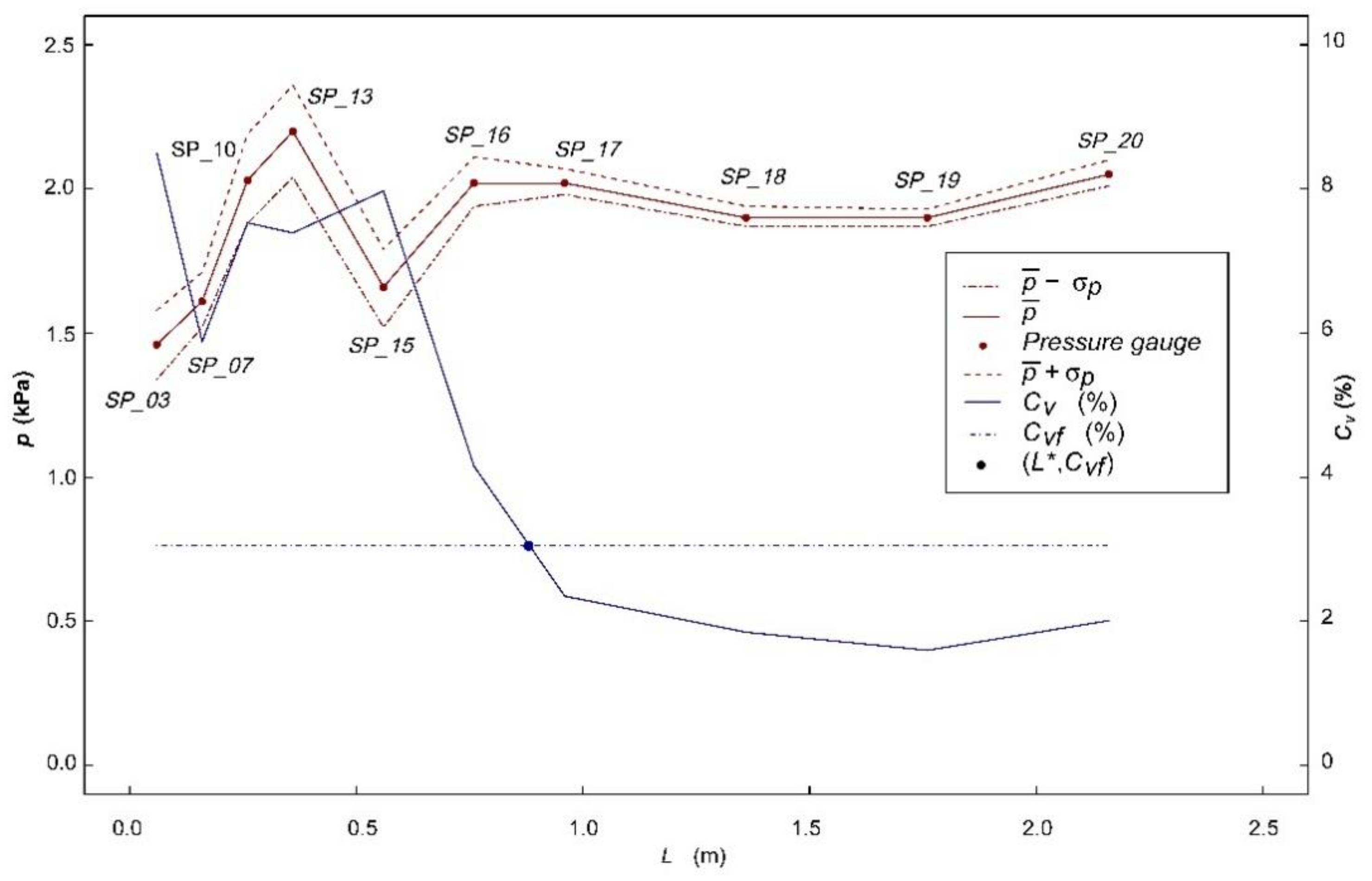
- A total of 21 dynamic pressure gauges located at the bottom of the stilling basin (Figure 4). The measurements analyzed in this study were those obtained from the 11 sensors located along the longitudinal axis of the basin.
- A set of three limnimeters attached to a movable carriage located at the stilling basin, 3.2 m downstream of the dam toe.
- An electronic limnimeter located upstream of the rectangular thin-plate weir at the returning channel, downstream of the model. This sensor provided an indirect measurement of the testing discharge through the calibrated rating curve of the weir.
- Photo and video cameras. The images showed the elapsed time of each test provided by the large chronometer located next to the right sidewall of the experimental facility.
- A self-programmed data acquisition system to gather real-time measurements of the devices. The system included acquisition cards controlled by a laptop computer.
3.3. Research Approach
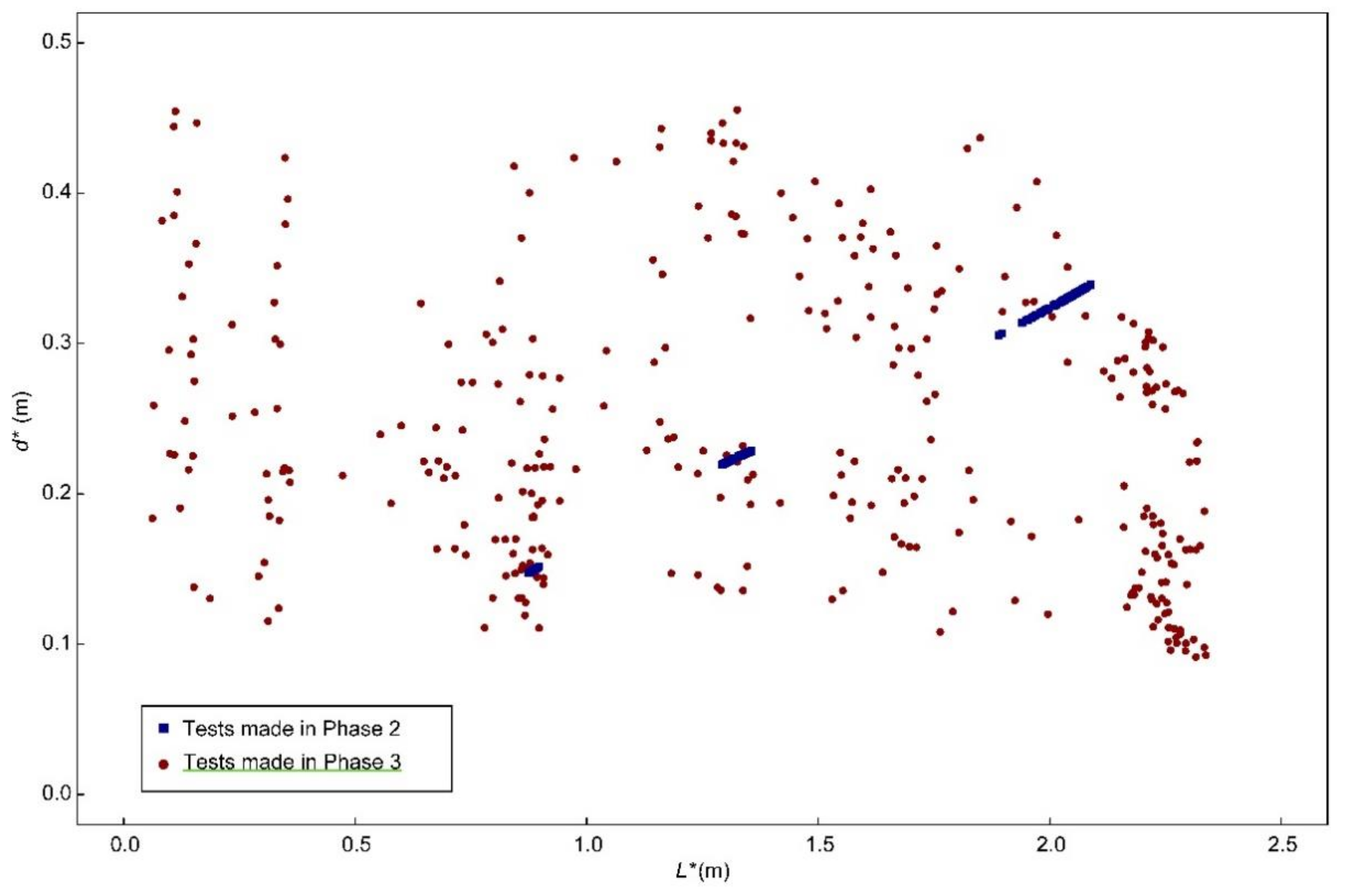
3.3.1. Phase 1: Scope and Selection of Parameters
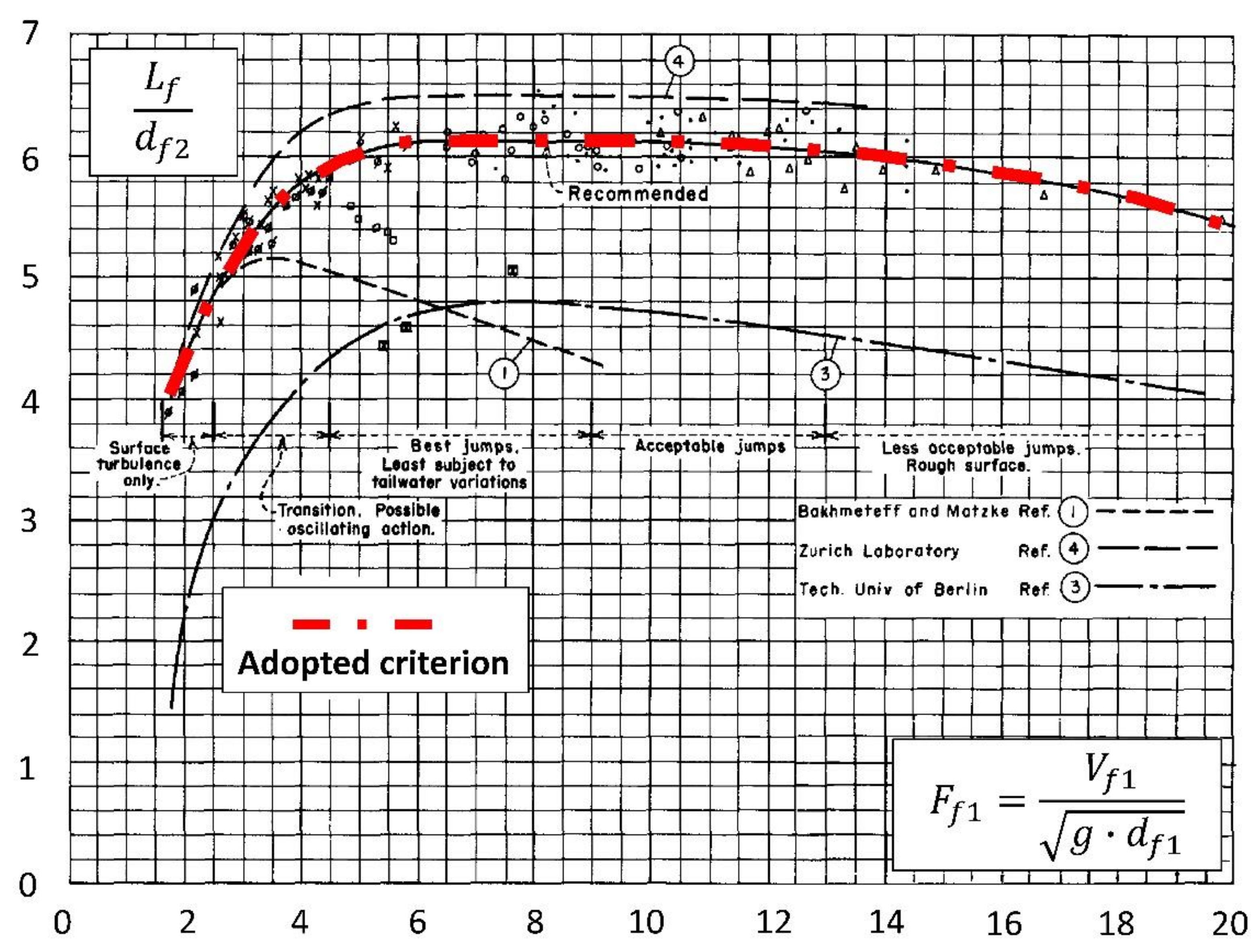
3.3.2. Phase 2: Determination of the Acceptance Criteria for the Energy Dissipation
3.3.3. Phase 3: Core of the Experimental Research
4. Results and Discussion
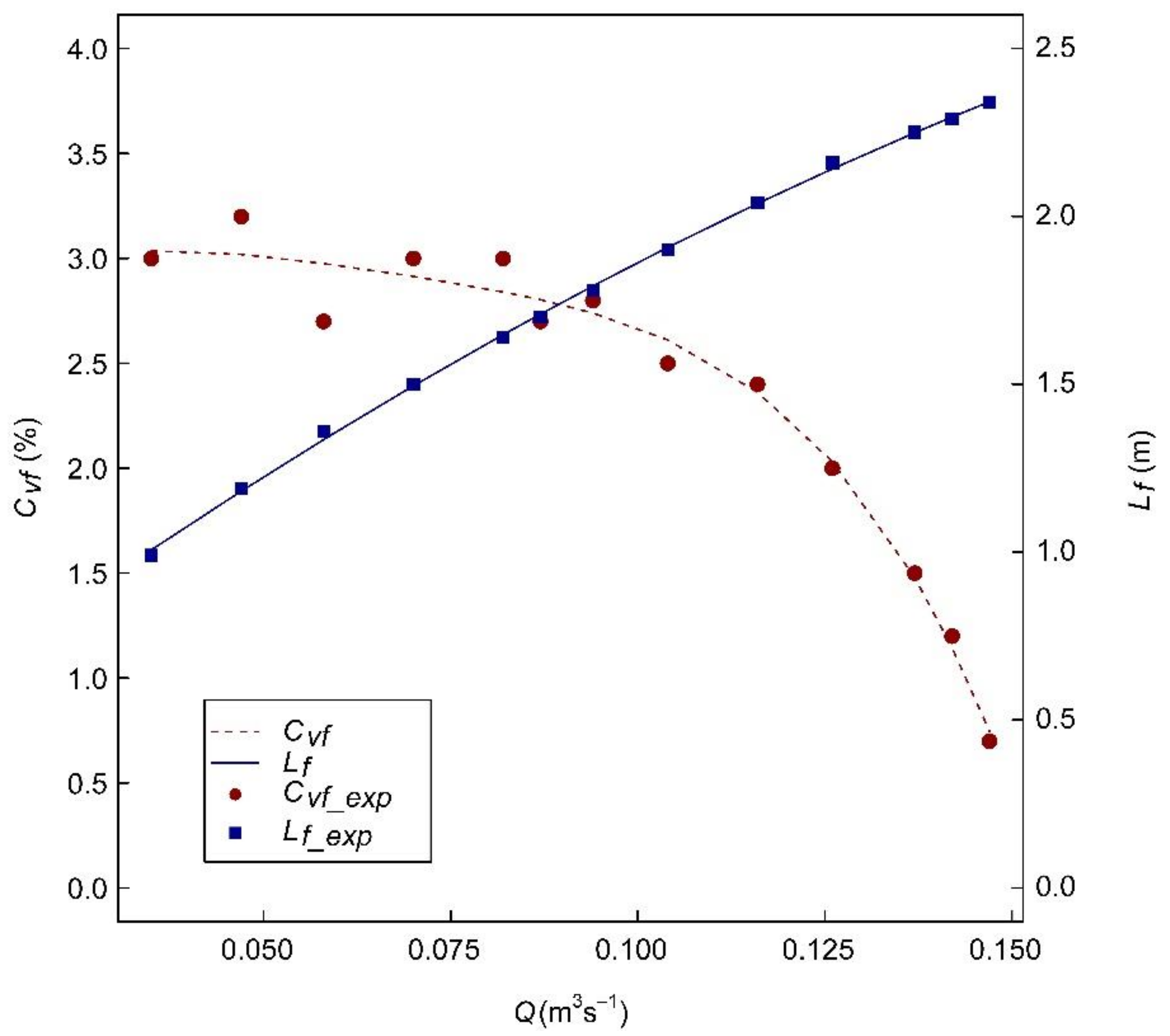
4.1. Energy Dissipation Criteria
4.2. Influence of the Parameters on the Performance of the Stilling Basin
4.2.1. Analysis of the Height of the Bottom of the HCCs over the Bottom of the Basin (P)
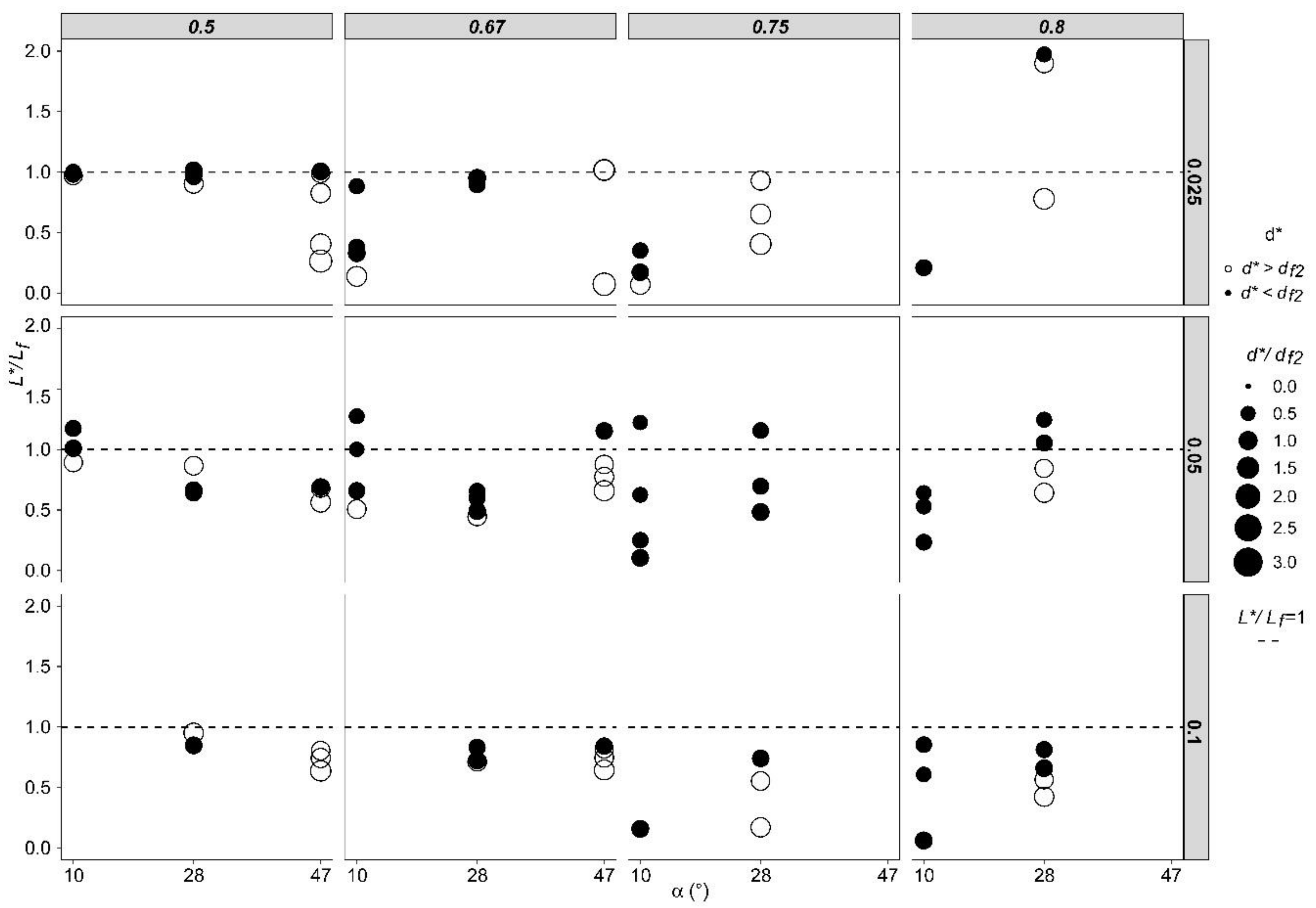
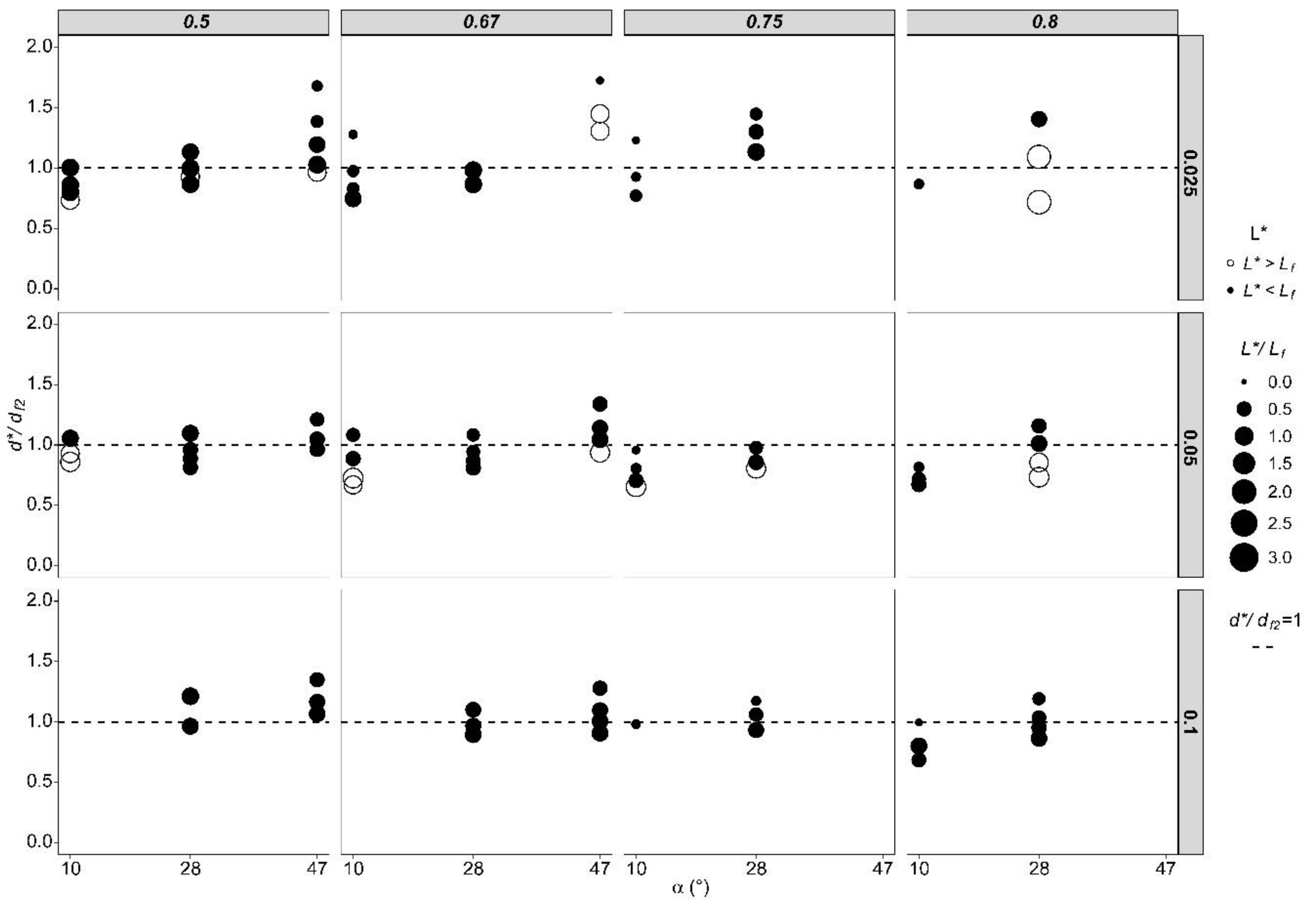
4.2.2. Influence of the Angle between the Bottom of the HCCs with Respect to the Horizontal Plane (α) and the Discharge Rate of the Side Jets (KQ)
4.3. Effect of Submergence on Flow Distribution
5. Conclusions
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Nomenclature
| CV | coefficient of variation of the water pressure, expressed in percentage. |
| CVf | coefficient of variation of the pressure downstream the BOR’s Type I stilling basin, expressed in percentage. |
| df1 | water depth of the flow entering the jump in BOR’s Type I basin. |
| df2 | water depth downstream of the BOR’s Type I basin. |
| d* | water depth downstream of the basin after energy dissipation with side jets discharge. |
| Ff1 | Froude number at the entrance of the hydraulic jump. |
| Ff2 | Froude number downstream the hydraulic jump. |
| Hb | maximum height of the sidewalls of the stilling basin, equals to 0.5 m. |
| Hw | height of the weir over the bottom of the stilling basin, equals to 1.5 m. |
| KQ | discharge rate of the side jets (i.e., Qs/Q). |
| L | horizontal distance from the toe of the dam along the longitudinal axis of the basin. |
| Lb | maximum length of the stilling basin of the experimental facility: 3.7 m. |
| Lf | length of the basin recommended by the BOR criteria for Type I basins. |
| L* | length of the basin required to a suitable energy dissipation with side jets discharge. |
| p | pressure. |
| mean of the pressure values. | |
| P | height of the step from the bottom of the basin to the bottom of the downstream section of the HCCs. |
| Q | total discharge. |
| Qf | frontal discharge. |
| Qs | side discharge from the HCCs inlet. |
| QT | target discharge. |
| Vf1 | velocity of the flow entering the jump in BOR’s Type I basin. |
| Vf2 | velocity of the flow downstream of the BOR’s Type I basin. |
| Wb | width of the stilling basin, equals 1 m. |
| Ww | maximum length of the weir, equals 5 m. |
| α | angle of the bottom of the HCCs with respect the horizontal plane, projected in the front view vertical plane. |
| σp | standard deviation of the pressure values. |
References
- San Mauro, J.; Morera, L.; Salazar, F.; Rossi, R.; Toledo, M.; Morán, R.; Martínez, B.; Caballero, F.; Oñate, E. Modelación Física Y Numérica De Aliviaderos Con Cajeros Altamente Convergentes. In Proceedings of the III Jornadas De Ingeniería Del Agua, Valencia, Spain, 23–24 October 2013. [Google Scholar]
- Larese, A.; Salazar, F.; San Mauro, J.; Oñate, E.; Toledo, M.; Morán, R. Advanced Computational Methods for Dam Protections Against Overtopping. In Proceedings of the Protections 2018 (3rd International Conference on Protection against Overtopping), Grange-over-Sands, UK, 6–8 June 2018. [Google Scholar]
- Mauro, S.; Salazar, F. Mejora De La Seguridad Hidrológica E Incremento De La Capacidad De Embalse De Presas De Fábrica Mediante Aliviaderos Con Cajeros Altamente Convergentes. 2019. Available online: https://www.scipedia.com/public/Peraita_et_al_2019a (accessed on 1 October 2020).
- Lempérière, F.; Vigny, J.; Deroo, L. New Methods and Criteria for Designing Spillways could Reduce Risks and Costs Significantly; Hydropower & Dams: Wallington, UK, 2012; pp. 120–128. [Google Scholar]
- Hunt, S.L. Design of Converging Stepped Spillways. Ph.D. Thesis, Colorado State Univeristy, Fort Collins, CO, USA, 2008. [Google Scholar]
- Hunt, S.L.; Kadavy, K.C.; Abt, S.R.; Temple, D.M. Impact of Converging Chute Walls for Roller Compacted Concrete Stepped Spillways. J. Hydraul. Eng. 2008, 134, 1000–1003. [Google Scholar] [CrossRef]
- Schleiss, A. From Labyrinth to Piano Key Weirs—A Historical Review. In Proceedings of the Labyrinth and Piano Key Weirs; Apple Academic Press: Palm Bay, FL, USA, 2011; pp. 3–15. [Google Scholar]
- Macián-Pérez, J.F.; Vallés-Morán, F.J.; Sánchez-Gómez, S.; De-Rossi-Estrada, M.; García-Bartual, R. Experimental Characterization of the Hydraulic Jump Profile and Velocity Distribution in a Stilling Basin Physical Model. Water 2020, 12, 1758. [Google Scholar] [CrossRef]
- NVE. Guidelines for Embankment Dams. Guideline 4/2012. Norwegian Water Resources and Energy Directorate. 2012. Available online: https://www.nve.no/damsikkerhet-og-kraftforsyningsberedskap/damsikkerhet/regelverk/veileder-for-fyllingsdammer/ (accessed on 1 October 2020).
- Portland Cement Association. Design Manual for RCC Spillways and Overtopping Protection, 1st ed.; Portland Cement Association: Skokie, IL, USA, 2002; p. 100. [Google Scholar]
- FEMA. Technical Manual: Overtopping Protection for Dams; U.S. Department of Homeland Security: Washington, DC, USA, 2014.
- United States Bureau of Reclamation. Design of Small Dams; US Department of the Interior, Bureau of Reclamation: Washington, DC, USA, 1987.
- Morera, L.; San Mauro, J.; Salazar, F.; Toledo, M.Á. Highly-Converging Chutes as an Overtopping Protection for Concrete Dams: Physical and Numerical Modelling; Taylor & Francis Group: London, UK, 2015. [Google Scholar]
- Yang, J. Investigations at Vatnsfell. Int. Water Power Dam. Constr. 2007, 59, 9. [Google Scholar]
- Zaitsoff, M. Overtopping modifications to Tygart Dam. In Proceedings of the National Dam Safety Technical Seminar: Overtopping Protection for Dams, Portland, OR, USA, 13–15 May 2003; pp. 20–21. [Google Scholar]
- Talbot, J.; Robinson, K.; Kadavy, K. Hydraulic Model Study of a Roller Compacted Concrete Stepped Spillway with Converging Chute Walls. In Proceedings of the Association of State Dam Safety Officials Annual Conference, Pittsburg, PA, USA, 7–10 September 1997. [Google Scholar]
- Hunt, S.L.; Temple, D.M.; Abt, S.R.; Kadavy, K.C.; Hanson, G. Converging Stepped Spillways: Simplified Momentum Analysis Approach. J. Hydraul. Eng. 2012, 138, 796–802. [Google Scholar] [CrossRef]
- Hunt, S.L.; Kadavy, K.C.; Abt, S.R.; Temple, D.M. Impact of Converging Chute Walls for RCC Stepped Spillways. Impacts Glob. Clim. Chang. 2005, 1–12. [Google Scholar] [CrossRef]
- Peterka, A.J. Hydraulic Design of Stilling Basins and Energy Dissipators; Department of the Interior, Bureau of Reclamation: Washington, DC, USA, 1978.
- Barjastehmaleki, S. Spillway Stilling Basins and Plunge Pools Lining Design. Ph.D. Thesis, University of Trieste, Trieste, Italy, 2016. [Google Scholar]
- Babaali, H.; Shamsai, A.; Vosoughifar, H. Computational Modeling of the Hydraulic Jump in the Stilling Basin with Convergence Walls using CFD Codes. Arab. J. Sci. Eng. 2015, 40, 381–395. [Google Scholar] [CrossRef]
- Vischer, D.; Hager, W. Energy Dissipators. Oceanogr. Lit. Rev. 1996, 1, 87. [Google Scholar]
- Martín-Vide, J. The Design of Converging Overfall Spillways. Int. J. Hydropower Dams 1995, 2, 87. [Google Scholar]
- Chanson, H. Hydraulics of Open Channel Flow; Elsevier: Amsterdam, The Netherlands, 2004. [Google Scholar]
- San Mauro, J.; Salazar, F.; Morán, R.; Peraita, J.; Toledo, M.Á.; Conde, M.J.; Flórez, V.; Labalde, B.; Alcalde, F. Aliviaderos Con Cajeros Altamente Convergentes. ¿Posible Solución Para La Presa De Oroville? In Proceedings of the V Jornadas de Ingeniería del Agua, A Coruña, Spain, 24–26 October 2017. [Google Scholar]

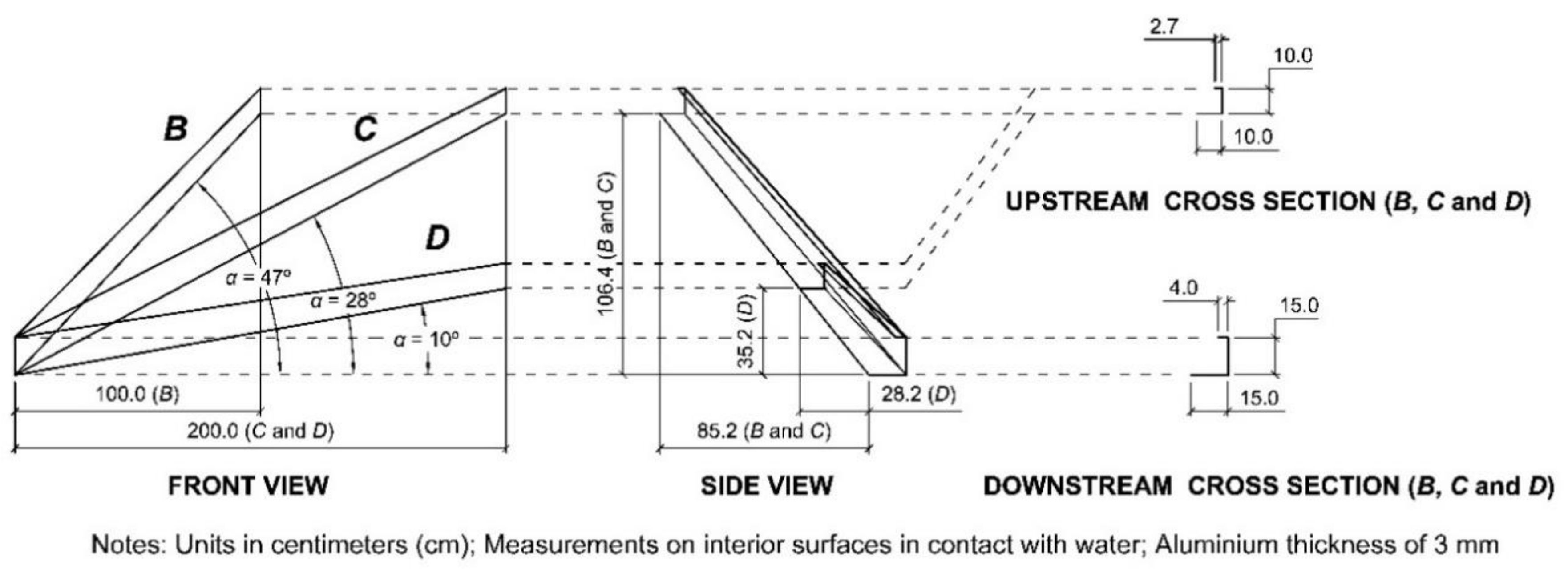

| Configuration | α (°) | KQ (−) | Number of Tests |
|---|---|---|---|
| B | 47 | 0.50 and 0.67 | 132 |
| C | 28 | 0.50, 0.67, 0.75, and 0.80 | 256 |
| D | 10 | 0.50, 0.67, 0.75, and 0.80 | 261 |
| Condition | I (d* < df2) | II (L* < Lf) | I and II | ||||||
|---|---|---|---|---|---|---|---|---|---|
| P (m) | 0.0 | 0.1 | 0.2 | 0.0 | 0.1 | 0.2 | 0.0 | 0.1 | 0.2 |
| QT (m3 s−1) | Number of Tests Fulfilling the Condition/Total Tests for Each P and QT (%) | ||||||||
| 0.010 1 | 21/49 | 15/34 | 10/29 | 8/49 | 8/34 | 6/29 | 0/49 | 0/34 | 0/29 |
| (42.9) | (44.1) | (34.5) | (16.3) | (23.5) | (20.7) | (0.0) | (0.0) | (0.0) | |
| 0.025 | 17/33 | 23/39 | 18/31 | 26/33 | 13/39 | 9/31 | 13/33 | 1/39 | 0/31 |
| (51.5) | (59.0) | (58.1) | (78.8) | (33.3) | (29.0) | (39.4) | (2.6) | (0.0) | |
| 0.050 | 25/36 | 28/40 | 16/34 | 27/36 | 16/40 | 16/34 | 16/36 | 4/40 | 0/34 |
| (69.4) | (70.0) | (47.1) | (75.0) | (40.0) | (47.1) | (44.4) | (10.0) | (0.0) | |
| 0.100 | 11/23 | 25/44 | 22/49 | 23/23 | 27/44 | 30/49 | 11/23 | 8/44 | 4/49 |
| (47.8) | (56.8) | (44.9) | (100) | (61.4) | (61.2) | (47.8) | (18.2) | (8.2) | |
| 0.150 2 | 0/0 | 0/4 | 0/1 | 0/0 | 4/4 | 1/1 | 0/0 | 0/4 | 0/1 |
| (0.0) | (0.0) | (0.0) | (0.0) | (100.0) | (100.0) | (0.0) | (0.0) | (0.0) | |
| All discharges | 74/141 | 91/161 | 66/144 | 84/141 | 68/161 | 61/144 | 40/141 | 13/161 | 4/144 |
| (52.5) | (56.5) | (45.8) | (59.6) | (42.2) | (42.4) | (28.4) | (8.1) | (2.8) | |
| P (m) | 0.0 | 0.1 | 0.2 | |||
|---|---|---|---|---|---|---|
| QT (m3 s−1) | ||||||
| 0.010 1 | 0.85 | 0.51 | 0.83 | 0.43 | 0.76 | 0.49 |
| 0.025 | 0.93 | 1.30 | 0.96 | 0.64 | 0.92 | 0.58 |
| 0.050 | 1.09 | 1.35 | 1.08 | 0.89 | 0.90 | 0.98 |
| 0.100 | 0.97 | 1.54 | 1.02 | 1.24 | 0.94 | 1.18 |
| 0.150 2 | - | - | 0.34 | 1.05 | 0.95 | 1.01 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Moran, R.; Toledo, M.Á.; Peraita, J.; Pellegrino, R. Energy Dissipation in Stilling Basins with Side Jets from Highly Convergent Chutes. Water 2021, 13, 1343. https://doi.org/10.3390/w13101343
Moran R, Toledo MÁ, Peraita J, Pellegrino R. Energy Dissipation in Stilling Basins with Side Jets from Highly Convergent Chutes. Water. 2021; 13(10):1343. https://doi.org/10.3390/w13101343
Chicago/Turabian StyleMoran, Rafael, Miguel Ángel Toledo, Javier Peraita, and Raffaella Pellegrino. 2021. "Energy Dissipation in Stilling Basins with Side Jets from Highly Convergent Chutes" Water 13, no. 10: 1343. https://doi.org/10.3390/w13101343
APA StyleMoran, R., Toledo, M. Á., Peraita, J., & Pellegrino, R. (2021). Energy Dissipation in Stilling Basins with Side Jets from Highly Convergent Chutes. Water, 13(10), 1343. https://doi.org/10.3390/w13101343









