Abstract
The design code Eurocode 7 relies on semi-probabilistic calculation procedures, through utilization of the soil parameters obtained by in situ and laboratory tests, or by the means of transformation models. To reach a prescribed safety margin, the inherent soil parameter variability is accounted for through the application of partial factors to either soil parameters directly or to the resistance. However, considering several sources of geotechnical uncertainty, including the inherent soil variability, measurement error and transformation uncertainty, full probabilistic analyses should be implemented to directly consider the site-specific variability. This paper presents the procedure of developing fragility curves for levee slope stability and piping as failure mechanisms that lead to larger breaches, where a direct influence of the flood event intensity on the probability of failure is calculated. A range of fragility curve sets is presented, considering the variability of levee material properties and varying durations of the flood event, thus providing crucial insight into the vulnerability of the levee exposed to rising water levels. The procedure is applied to the River Drava levee, a site which has shown a continuous trend of increased water levels in recent years.
1. Introduction
As earthen structures constructed for the purpose of flood defence, the levees should be verified for several potential failure modes. According to Wolff [1], these include overtopping, slope stability, external erosion, underseepage and through-seepage, with the latter two being considered as internal erosion mechanisms. These failure modes are conditioned by the levee’s geometrical configuration, its material properties, and overall hydraulic conditions of the site. Based on the examined breach characteristics of hundreds of failures, Özer et al. [2] identified the external erosion as the most frequent for levees, while failures due to internal erosion and instability are less frequent but lead to larger breaches, and as such are emphasized within this study. Of all the internal erosion mechanisms, backward erosion piping is considered to be the primary failure mechanism for levees [3], and even accounts for one-third of all piping failures that occurred in the last century [4]. Various design situations such as rainfall, high water level, seismic peak ground acceleration, etc., can be triggering factors for one or more failure mechanisms, directly or indirectly. Extensive studies have been conducted with various approaches regarding slope stability, Figure 1a, with respect to rainfall [5,6], high water levels [7,8], and peak ground accelerations [9,10], as well as combinations of various events [11]. Regarding the piping failure, Figure 1b, and depending on the mechanism of soil particle removal (e.g., removal of particles by water forces, chemical dispersion of clays, migration of fine material through coarse matrix, etc.), various modes are identified, all pertaining to internal erosion under or through the levee [12,13,14,15].

Figure 1.
Levee failure mechanisms analysed in the study: slope instability (a) and internal erosion (b).
The analysis of different levee failure mechanisms within the Eurocode 7 design code [16] is based on the use of recommended, singular values of partial safety factors (PSFs), with a defined combination of PSFs for action and resistivity (material), depending on the adopted calculation approach for a specific design situation. The code, however, prescribes constant values of PSFs for limit states, with no variation depending on the nature or the duration of the design situation and no recommendation regarding the target reliability values. Du Thinh [17] notes that, during the design process, an engineer must select a set of characteristic values and the corresponding PSFs, hoping to obtain in the end a design that satisfies a prescribed reliability level. On the other hand, the design code Eurocode 0 [18] provides minimum values for the reliability index for three consequence classes, but these are only defined for buildings, not for geotechnical structures. Some other design codes, such as those in [19], acknowledge the uncertain nature of soils, by defining target values of pf and equivalent reliability indices for three consequence levels, based on random finite-element analyses.
Concerning the soil related uncertainties, Phoon and Kulhawy [20] identified three main sources of geotechnical uncertainties: (1) inherent soil variability, which describes the variation of properties from one spatial location to another, (2) measurement error, which implies the scatter of measurements on presumably homogeneous soil volumes, and (3) transformation uncertainty, where, in the process of model characterization, which includes linking the on-site and laboratory test results to the design parameters, some degree of uncertainty is introduced. By implementing a Eurocode 7 semi-probabilistic approach, which utilizes statistical methods to select characteristic values of geotechnical parameters, both spatial correlations between the same parameter sat different sampling points and cross-correlations between different parameters at the same sampling point are neglected [21]. Further, depending on the associated failure mechanisms of levees, different material parameters will control the limit states and different models are necessary to predict the resistance, and thus no uniform reliability level can be obtained with the load and resistance factor design method [22]. The degree of uncertainty involved in calculation of levees is especially high for slope stability [23] and piping mechanisms [24]. Even though the geotechnical community has been more progressive in the implementation of different probability-based methods in analyses of levees, understanding of levee failure mechanisms is still limited [25], while their behaviour during critical conditions mostly remains uncertain.
This paper contributes to the efforts of levee vulnerability evaluations, through the demonstration of a methodology for calculation of fragility curves for relevant failure mechanisms of slope stability and piping. Among the many available probabilistic methods [26], this study adopts the Monte Carlo simulation to determine the levee probability of failure when the hydraulic head rises on the riverside up to the levee crown and over, to simulate overflowing. Even though this method takes the most time to run due to its slow convergence, which is its largest disadvantage, it gives the most accurate results when a sufficient number of runs is chosen. For relatively simple calculations such as the limit equilibrium formulation, the number of runs and computation time to solve the problem are acceptable. Additionally, given that it is applicable to both linear and particularly to nonlinear problems [26,27], with many random variables which may be differently distributed [26], this method is used in this study. The method does not identify the relative contribution of each random variable to the safety factor, as some other methods do (e.g., FOSM), but for this purpose sensitivity analyses were conducted. The demonstrated methodology, applied to the river levee in Croatia, results in sets of fragility curves, which can then be used in risk assessment and categorization of levees [28,29], based on calculated probabilities of failures. This provides a support for the decision making process regarding the optimization of resources for levee reconstructions or maintenance [30]. Furthermore, future design protocols and monitoring activities of levees can be enhanced [31].
2. Methodology for the Development of Fragility Curves
To assess the vulnerability of the levee exposed to raising water levels up to and over the levee crown, with respect to identified failure mechanisms of landside slope stability and piping in the foundation soil, a series of numerical simulations were conducted. Within these simulations, the water level on the riverside is raised until the levee is sure to fail (). Overtopping (i.e., overflow) is usually a result of a high-water event (surge) or it can occur due to wave overtopping. The combined effect of surge and wave overflow is discussed by many authors [32,33,34]. However, if a river levee is considered, only a surge type of overflow is relevant. The results of numerical simulations feed into the proposed methodology of fragility curve development, giving insight into the probability of failure relative to the design event intensity. Sensitivity analyses indicate the influence of certain parameters on the fragility curves’ shapes—i.e., on the variation of the failure probability.
2.1. Slope Stability Evaluation
Slope stability analyses can generally be conducted by limit equilibrium (LEM) and numerical methods incorporated in many commercially available programs, where each method has its own pros and cons [35]. As one of the oldest methods for slope stability calculations, the LEM has been significantly modified, from the introduction of the circular sliding surface [36] to its enhanced versions [37,38], and is still one of the most used methods for slope stability analyses.
Opposite to the deterministic approach which searches and pinpoints a critical slip surface with the lowest factor of safety, many probabilistic studies, such as multivariate adaptive regression splines analysis (Wang et al. [8]), utilize slope stability methods to identify a slip surface with the highest probability of failure. To give an overview of different possibilities and the results they yield, Akbas and Huvaj [39] compared results of probabilistic slope stability analyses by using LEM with integrated Latin Hypercube and Monte Carlo simulation, and by a numerical finite element method (FEM) with integrated Rosenblueth’s point estimate method, as well as random finite element method analyses. They found that FEM analyses resulted in higher probabilities of failure.
This study utilizes LEM and Monte Carlo simulations to conduct series of probabilistic slope stability analyses. The initial total stress state and the pore pressure distribution from steady and transient seepage analyses are modelled separately for each water level increment using FEM, with triangle mesh element sizes of 0.2 m in the body, and 0.5 m elsewhere. The results of both analysis types are tested with different element shapes and sizes, and the resulting distributions are unchanged. Both steady state and transient two-dimensional seepage analyses are governed by a partial differential equation (Equation (1)), where the term on the right-hand side is equal to zero for the steady state.
where is the total head, is the hydraulic conductivity in the i direction, is the applied boundary flux, and is the volumetric water content.
The stress states as well as the water pressures feed into the LEM for slope stability calculation, as shown on the diagram in Figure 2.
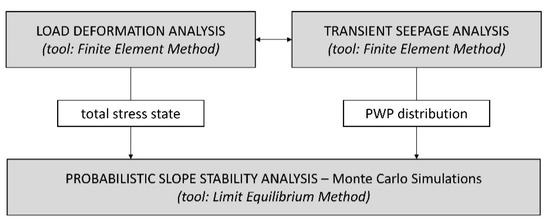
Figure 2.
Workflow of probabilistic analysis of levee slope stability.
A reason for generating a stress state separately is to yield more realistic results by defining a stress state with stress concentrations closer to the levee toe, instead of calculating it as the product of unit weight and depth. The advantages of defining the stress state in this way do not come to fore with a low angle of levee slope where a low stress concentration can be expected; however, a significant difference is evident in the case of levee overflow where shear stress can be applied on the surface of the slope and the stress state adjusted accordingly. Thus, for consistency reasons, all the analyses are conducted using this procedure. Another benefit of separate generation of the stress state is a drastic reduction in calculation time, since the LEM utilizes an iterative procedure to find the interslice forces and thus requires multiple calculations to find the safety factor for just one slip surface. With the imported stress state, the stresses are already defined so the safety factor can be immediately calculated for a trial slip, which is significant considering the number of runs required to conduct a Monte Carlo simulation.
Since the intention of this study is to inspect the probability of failure of the levee due to the water rising, the fragility curves were constructed by incrementally increasing the water level from the levee toe to the levee crown, and over for the case of surge overflow, by calculating the pore pressure distribution from seepage analyses. The overflow was simulated by applying the equivalent shear stress, caused by water flow, along the crown and landside slope, while keeping the water level at the crown height for the free water surface generation through the levee body. When the complete fragility curve was obtained, based on the input of parameters with probabilistic distribution, a sensitivity analysis followed. This included varying the values of parameters, while keeping the other parameters at their means, to assess their influence on the shape of the curve and stability of the levee. The investigated parameters are the statistics of the strength parameters, the permeability, and the duration of the flood. For the latter, additional transient flow analyses were conducted with various water level durations, and the results were then once incorporated into the LEM calculations. The results of these variations are shown as new fragility curves, shifted to the left or right of the ones from the mean analyses.
2.2. Internal Erosion (Piping) Evaluation
The most prominent trigger for internal erosion is the high-water event, and as such this has been subject of many studies. To investigate the erosional behaviour of soil at the microscale (granular) and macroscale (levee), various methods have been used from physical models [40,41]—numerical simulations such as FEM, FDM, DEM [13,14,15,42,43], the material point method [44] and random lattice models [4]. Other tools such as neural networks were also used to help predict soil behaviour under seepage forces based on laboratory and field tests [12,45,46]. Despite many advantages of these advanced tools, the geotechnical community in many cases still relies on the simple empirical or semiempirical rules [47].
Within this study the closed-form analytical Sellmeijer 2-force rule [46], which resulted from a neural network based on field and laboratory tests and numerical analyses, was used for piping analyses. This approach is used in many state-of-the-art levee risk assessment methodologies, such as the VNK2 approach [47,48]. The closed-form solution predicts that for a given head difference a pipe of specific length will form. Once the critical head difference value is reached (), the pipe will start to progress continuously until failure:
In Equation (2), (m) is a seepage path, equal to the width of the levee, and the factors F are the resistance, geometry, and scale term, respectively, and are functions of unit weight, drag force factor, angle of repose, relative density, effective grain size (), kinematic viscosity, coefficient of uniformity and particle angularity. The critical head difference needs to be higher than the actual head difference reduced by the value of (thickness of the top clay layer that covers the aquifer), assuming the levee lays on a clay cover over the underlaying sandy aquifer. The parameter which was used as the random variable is the hydraulic conductivity of the aquifer, while all the other values were kept constant at their measured mean values or suggested mean values for the parameters for which measurements or correlations were not available. To assess the validity of the results obtained by the Sellmeijer’s equation, the levee and the subsoil geometry and parameters should fall within certain limitations for which the rule was developed. The levee should lay on top of a homogeneous sandy aquifer of finite thickness, with horizontal ground surface in the cross-section direction [47]. Some guidelines [31] suggest applying the Sellmeijer method only if the thickness of the aquifer is less than the seepage length. Regarding the range of the parameters, Sellmeijer and Koenders [49] note that the routine is stable over the entire range of practically feasible parameters, while Sellmeijer et al. [42] give ranges for some new parameters introduced in the formula. The ratio of seepage length to hydraulic head difference for which the formula should be applied is .
3. Case Study Example: River Drava Levee
River Drava, with the overall length of 710 km, flows from Italy to eastern Croatia where it merges with Danube, and is historically known for major flood events [50], where prominent events have occurred in the last several years. The case study levee stretches across 6.8 km of the Drava old riverbed, from county Selnica to accumulation lake Dubrava. The levee is fragmented into three segments because of the presence of two smaller rivers, Bednja and Plitvica, flowing perpendicularly to the Drava (Figure 3).
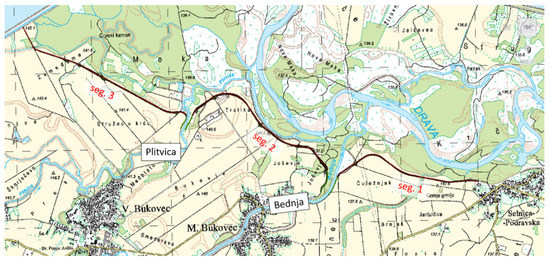
Figure 3.
An overall layout of the Selnica–Dubovica levee with its distinctive segments.
The reach of interest for this study is defined by height and is the starting section of second segment, just after the Bednja river, where the levee’s highest cross-section is present (Figure 4). By the request of the stakeholders, the designed crown level is 0.5 m above the 100-year high water, while the crown is 4.0 m wide. The levee slopes are at 1:3 and the service road is located on the levee’s landside toe.
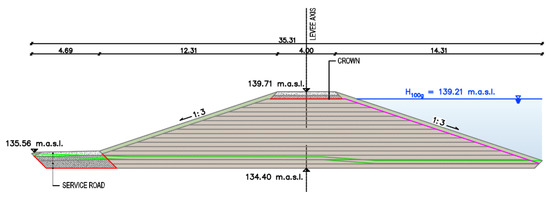
Figure 4.
A cross-section of the case study levee.
3.1. Conducted Investigation Works
To obtain insight into the layering and physical-mechanical characteristics of the subsoil, an extensive geotechnical investigation campaign was conducted, consisting of 12 boreholes at equal spacings along with conduction of Standard Penetration Tests (SPTs), 12 Cone Penetration Tests with pore water measurements (CPTus) and 12 seismic refraction geophysical profiles. Both undisturbed and disturbed samples were taken during the geotechnical drilling, which were tested in a laboratory to determine their physical and mechanical characteristics. In addition to the in situ and laboratory direct test results, transformation models were implemented to relate the on-site and laboratory test results with the design parameters to infer geotechnical properties from indirect measurements. Based on these field and laboratory investigation works, a reliable geotechnical model of the subsoil was formed for the reach of interest regarding stratification and soil parameters to conduct calculations.
The subsoil was divided into a top layer of lower permeability underlined by the thick coarse-grained layer. At the location of the analysed cross-section, the upper low permeability layer was not detected () and only coarse-grained soil was identified. Considering the investigation data scattering because of the mentioned inherent soil variability, measurement error and transformation uncertainty, to develop fragility curves by the means of probabilistic analyses some variation in the soil parameters, need to be considered.
3.2. Probabilistic Characterization of Soil Parameters
Since the soil parameter distributions can vary significantly, they should be limited to keep the values in the realm of possibility for a specific soil, thus avoiding illogical values. Phoon and Kulhawy [20] give a detailed literature review showing the ranges and number of samples for certain obtained statistics. These values for the internal friction angle are taken as guidelines for specifying the limits of their distributions. Since the slope stability of the levee is governed dominantly by the body and berm materials, these materials were probabilistically evaluated. Effective cohesion has seldom been reported in the literature on soil parameters variability, where it is considered as either normally or log-normally distributed, with values similar to those for undrained shear strength reported in the literature [51,52,53]. This study assumes log-normal distribution and the commonly accepted s, thus only the upper limit would be needed. However, as the mean values are already very low, the range for the distribution of is acceptable. Various authors reported that neglecting the correlation coefficient between cohesion and internal friction angle yields conservative results in slope stability calculations if their correlation is actually negative [54,55]. Results from tests conducted by Lumb [54] show a strong negative correlation for the compacted samples, and since the levee in the case study is compacted during construction, a negative correlation, thus a correlation of zero, can be assumed. Some sources suggest using some other value for the correlation coefficient [55,56]. The values and statistics ( as mean value and as coefficient of variation) of each random variable for stability analysis were assumed from the literature [20,27,57] and are shown in Table 1. As the levee was constructed from materials from an undefined borrow site, the mean values of the levee soil parameters were obtained during the deterministic design phase of the levee, such that the stability criteria were met (Table 3) and represent the minimum required values that the materials must have to deterministically ensure slope stability.

Table 1.
Parameters and the statistics used for slope stability analyses.
Two stability design cases (SDCs) were analysed regarding hydraulic conductivity, one where the crown/berm is constructed from a more permeable material, and the other where the whole levee is homogeneous—i.e., the crown/berm and the body have the same conductivity.
Hydraulic conductivities for the subsoil were obtained from correlations with CPTu tests, while the hydraulic conductivities for levee materials were determined from deterministic steady seepage analyses, as minimally required to maintain hydraulic stability of levee in terms of the critical exit hydraulic gradient and free water surface position. To assess the sensitivity of the slope stability to the hydraulic conductivity of the levee body material, an arbitrary value of two orders of magnitude was selected since the range of reported hydraulic conductivity’s CoV is too great to assume a value (30–750%) [26], while the foundation’s and crown/berm’s conductivities were kept the same as those defined for each SDC. For the piping analysis, the statistics of the hydraulic conductivity of the subsoil for case study location were estimated from the correlation with the CPTu test and assumed a log-normal distribution [58,59]. Since the CPTu showed a mixed subsoil profile with lenses of fine-grained soil, the profile was idealized to just one layer with one highly variable hydraulic conductivity. The distribution was described by the median () and the extremely high CoV due to the soil profile idealization by averaging over the whole CPTu profile. However, if it is assumed that the water flows around the fine-grained soil lenses, the conductivity distribution can be defined only for the sandy material, where the median is similar (), but the variation is significantly decreased. Taking this into consideration, the piping calculations were conducted for two piping design cases (PDCs)—first (PDC1), where the subsoil is modelled as a homogeneous soil layer with highly variable hydraulic conductivity estimated from CPTu data for every material in the subsoil, and the second (PDC2), where the hydraulic conductivity of the layer was estimated only from the CPTu data for sand. Parameters chosen for piping analyses are shown in Table 2.

Table 2.
Parameters and their statistics used for piping analyses.
The hydraulic anisotropy ratio, defined as the ratio of the vertical to horizontal conductivity, can vary over a wide range of values [60]. As the levee materials are usually compacted dry of optimum [61], and soils dry of optimum have lower hydraulic anisotropy [62], the used anisotropy ratio values are reduced mean values from the literature [60]. The relative density (Dr) has been obtained via correlation with an SPT test.
The distribution of the hydraulic conductivity was defined through the median instead of the mean value since the parameter values vary over a few orders of magnitude, so the median was more intuitive and simpler to obtain as it is the geometric mean of the available data.
4. The Probabilistic Analyses Background
The methodology for the development of fragility curves for levee stability implies that the proper stress state, as well the proper water pressure state, is established.
To obtain the appropriate stress state for the slope stability analyses, the methodology suggests conduction of the load deformation total stress analyses. Since soil plastification is not relevant to this study, the linear-elastic constitutive model was used, and this required input of soil stiffness and unit weights, as well Poisson’s ratio, whose variation was not considered, even though it may have had some effect on the results [63]. Further, for the design situations, which include water level up to the top of levee crown, numerical analyses were carried out, including commonly used boundary conditions of properly defined hydraulic heads on the riverside and landside. However, if the water level is higher—that is, if surge overflow is considered—the stress analyses should be supplemented with the additional boundary shear stress along the crown and landside slope. Given that this aspect goes beyond standard analyses, a cautious evaluation of these shear stresses is required. The boundaries of both analyses were defined far from the levee region, enough to not affect the results. The constraints of load deformation analyses consisted of fixing movement of lateral soil elements of the model in the horizontal direction, and the bottom elements in two perpendicular directions. Seepage analyses require only hydraulic boundary conditions, which in this case consist of constant or varying hydraulic head values applied on lateral boundaries and on the top boundary of the model, up to the required height. During surge overflow, the water velocity increases down the slope until a terminal velocity is reached at equilibrium between water momentum and slope frictional resistance, after which the flow becomes steady and the velocity can be calculated by the following equation:
where () is the steady flow velocity, is the landside slope angle, is Manning’s coefficient, and is the steady discharge [32]. For supercritical flow which develops on the landside slope, Figure 5, Hewlett et al. [64] proposed a value of Manning’s coefficient of , relevant for slopes of 1:3.
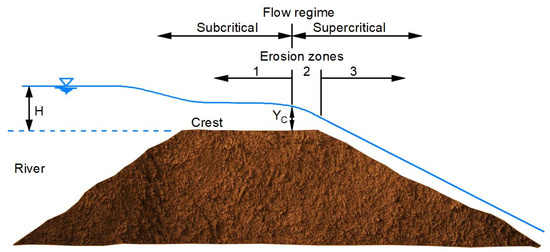
Figure 5.
Flow regimes during overflow of a dam, redrawn from [65].
The discharge over the levee crown can be calculated using the equation for flow over a broad-crown weir, which gives slightly conservative results due to not taking into consideration frictional losses [66]:
where is the gravitational acceleration and () is the upstream head (elevation over the levee crown). If steady flow is assumed, the discharge is constant along the slope. Therefore, the height of water is perpendicular to the slope in the steady, uniform flow area for unit length of the levee and can be calculated from Equations (3) and (4) as:
Finally, when steady, uniform flow is reached, the shear stress from surge overflow is equal to:
where is the unit weight of water. Equation (6) conservatively overestimates results since the resulting pressure is a little bit higher than the pressure in area above the steady flow [34]. Such calculated shear stress is applied along the crown and landside slope, as shown in Figure 6 for the case study numerical model.
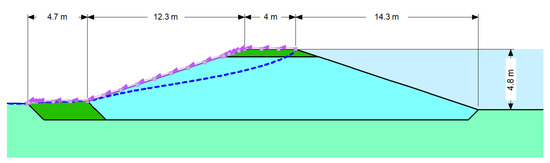
Figure 6.
Numerical model for analyses of case study levee.
With the full stress state properly defined, for all water levels including the surge overflow, stability analyses aim to find the critical slip surface out of the number of generated slip surfaces. To generate several slip surfaces, as well as to evaluate their safety margins, this study adopted a “Grid and Radius” method incorporated into the commercial software GeoStudio [67]. With this method, a grid of slip centres and a grid of slip tangents are created, and these define the number of analysed slip surfaces. However, a larger number of defined slip surfaces yields much longer calculation times, and conducting a single deterministic analysis prior to the probabilistic analyses is recommended. This analysis was conducted with a large grid covering a large area for potential slip surface centres, and a relatively large tangent grid to also cover a large range of possible surface depths. After the critical surface was found, the grid size and number of centre points and tangents were reduced around the critical surface point and tangent, to make smaller, denser grids and possibly find more critical surfaces around the original critical surface, while also minimizing the run time of the probabilistic calculations. This does not guarantee that the critical surface—defined in this case as the surface with maximum probability of failure—will be the same one as the deterministic critical surface, but it is a reasonable starting assumption that it will at least be close to the deterministic surface.
For the probabilistic slope stability analyses, four random variables were assigned, and these include cohesion and angle of internal friction for both levee body material as well the crown road base and berm material. The variability of the soil can generally be modelled by a random field described by the and scale of fluctuation [20]. As opposed to the creation of random fields, the method used in this study sampled a random variable for each material only once and then applied it to all the slices found in the corresponding material. This kind of simulation usually gives conservative results. Within this study, the number of Monte Carlo trials was sufficient to obtain a relatively constant value for each water level, which has been estimated at 15,000.
In regard to piping mechanism, for each hydraulic head difference, 25,000 Monte Carlo simulations were performed using an excel spreadsheet and its built-in random number generator function.
As the aquifer thickness is required for the Sellmeijer rule, two runs were carried out with minimum thickness from soil investigations to values after which further increasing of thickness no longer affected results. Therefore, aquifer thickness in numerical analyses ranged from 5 to 50 m.
5. Results and Discussion
5.1. Fragility Curves for Levee Slope Stability
To serve as a benchmark for the full probability analyses results, results of semi-probabilistic analyses adopted in Eurocode 7 are shown in Table 3. The analysed numerical model included idealized subsoil layering with mean values of both hydraulic and strength parameters, determined from the laboratory and transformation model data. Based on the Eurocode 7 design approach 3 (DA3), the design strength parameters were obtained from characteristic values by applying a prescribed PSFs. Several design situations were analysed by following relevant norms and guidelines for geotechnical design [16,68,69,70], with stability evaluation for both riverside and landslide slopes in drained and undrained conditions. The slope stability was assessed by the means of the LEM utilizing the pore pressure distributions from seepage analyses.

Table 3.
Deterministic safety factors for the case study levee, exposed to various design situations.
Deterministically obtained factors of safety are higher than unity ones, with a safety margin from 10 to 60%, indicating the stable levee slopes for all relevant design situations. However, these analyses neglect the variability of strength parameters as the ones governing the obtained safety values. Therefore, full probabilistic analyses were conducted to develop fragility curves for the levee’s landside slope stability.
Figure 7 shows the fragility curves for the levee’s landside slope stability, through the relation of the hydraulic head on the river side vs. probability of failure. As the case study levee crown also acts as a road base, the crown material, constructed up to 0.5 m above the 100-return period high water, consisted of coarser material mixed with fines. Therefore, the hydraulic conductivity of this layer is higher than levee body material conductivity, so when the water goes over the 100-year water level, the free water surface shifts towards the landside slope yielding a more unfavourable situation. The presented fragility curves were developed for steady seepage and include stability evaluation for levee material conductivity of and for increased conductivity of , while the crown material conductivity was kept constant for each SDC. The curves with higher , marked in blue, refer to the levee constructed with the more permeable crown layer (SDC1), while the curves with lower , marked in red, refer to the crown constructed of same permeability material as the levee body (SDC2). For the 100-year water level event, at 139.21 m a.s.l., there was an abrupt increase in for the case with the more permeable layer on top, while the curve smoothly increased for the case of homogeneous levee. While the curves of SDC1 show an approximate linear trend, the SDC2 fragility curves show a bilinear trend, with the intersection at head value of around 143 m a.s.l. The point of slope change indicates the sudden shift from deeper () to shallower () slip surfaces, which do not exist for SDC1 as there is a slow transition from deeper to shallower surfaces. The increase in the levee body conductivity by two orders of magnitude () at first had a slight positive effect for SDC1 because of the smaller difference in conductivities, but afterwards the negative effect was evident for both design cases.
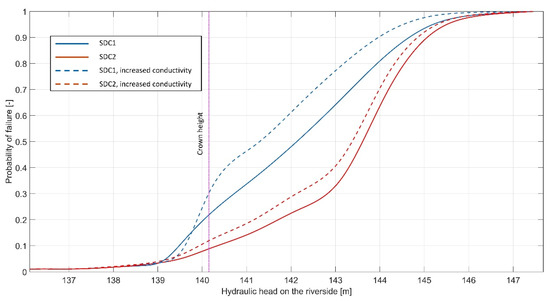
Figure 7.
Fragility curves for landside slope stability with respect to varying hydraulic conductivities.
Further, considering that high-water events are usually of limited duration, preventing the development of a steady seepage, the fragility curves were further evaluated with consideration of transient seepage for a high-water event duration of 5 days. Failure probabilities for transient situations, up to the crown height, are shown in Figure 8. Even though the discrepancy in curves representing different levee conductivities is very low for 5-day high water duration, it should be noted that the time required to numerically reach steady seepage with hydraulic conductivity is higher than 500 days, while for levee conductivity it is less than 50 days.

Figure 8.
Fragility curves for transient seepage of 5-day duration.
The fragility curves for the varied statistics of strength parameters are given for various values obtained by reducing the standard deviation. For both friction angle and cohesion, the s are halved. Figure 9 shows that, by lowering the friction angle’s standard deviations, the stability increased up to a certain hydraulic head value (marked with a point on the curves), after which the stability was reduced when compared to the original case with nonreduced variability. Such behaviour is expected since less variability means less probability of obtaining lower strength values, but also less probability of obtaining higher strength values which increase stability. Thus, for lower head values, when the slope is deterministically stable, less variability is favourable, while for higher head values, when the slope is deterministically unstable (or in equilibrium), less variability is unfavourable. It should be noted that for higher variability the distribution was truncated for a range of realistically possible values, while for lower variability the range was limited by the distribution itself and is lower than the truncated range for higher variability. For cohesion, the curves are practically unchanged, thus no point is marked on the corresponding curves in Figure 9.
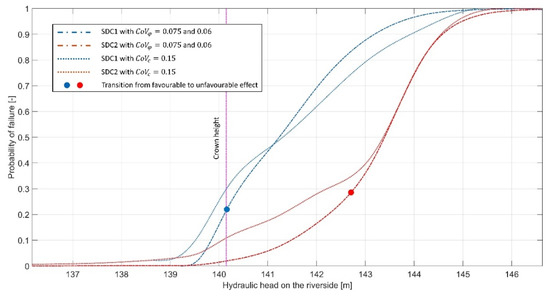
Figure 9.
Fragility curves for variability of reduced strength parameters.
Figure 10 shows the relation between reliability indices and probabilities of failure, for both calculated indices and their theoretical values for normally distributed safety factors. The figure shows results of the analysis with reduced friction angle variability, but all other calculations yielded similar curves. The reliability indices of critical slips were calculated as:
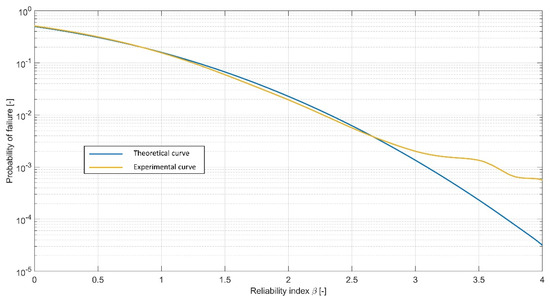
Figure 10.
Probabilities of failure and respective reliability indices for levee slope stability.
The numerically obtained curve shows very good concurrence with the theoretical value up to , which indicates that the safety factor follows a normal distribution. For lower s (higher ), the numerically obtained curve deviates from the theoretical one, which might indicate that for lower probabilities of failure the safety factor no longer follows a normal distribution.
5.2. Fragility Curves for Internal Erosion (Piping)
The piping analyses included hydraulic conductivity as a random variable, whereas simulations were conducted for two piping design cases (PDC1 and PDC2), depending on the procedure used to obtain the hydraulic conductivity distributions and statistics.
Additionally, to investigate the influence of aquifer thickness on the results, piping calculations included the deterministic variations of the thickness, starting from a 5 m value identified by the investigation works, to the value after which further increase does not affect the results (i.e., 50 m for the given analyses). Furthermore, the effective grain size was varied between the minimum and maximum values () which were used for the development of the Sellmeijer’s model [46]. To assess the validity of the results obtained by Sellmeijer’s equation, the levee and the subsoil geometry and parameters should fall within certain limitations for which the procedure is developed. Following the suggestion to apply the Sellmeijer’s procedure only if the thickness of the aquifer is less than the seepage length [31], the maximum aquifer thickness of 35 m should actually be considered for the case study example. The curves in Figure 11 and Figure 12 show the probability of failure for the water rising to the top of the crown for PDC1 and PDC2, respectively; however, for the specified seepage length, the actual hydraulic head for which the formula still applies is around 1 m below the crown.
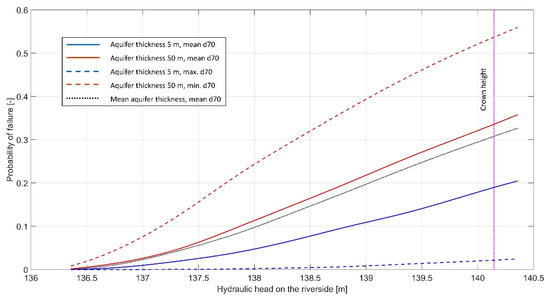
Figure 11.
Probability of piping failure for piping design case 1 (PDC1).
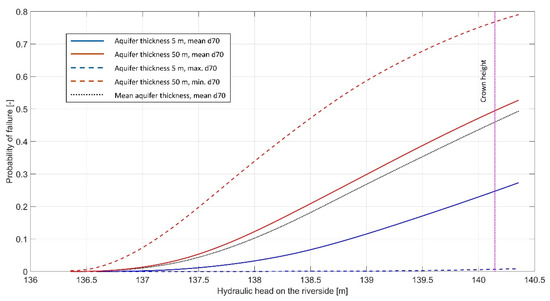
Figure 12.
Probability of piping failure for PDC2.
The “real value” fragility curves for the analysed section are somewhere between the two extreme curves (dashed lines), which vary from of only few percent up to the of 50% for PDC1 and 75% for PDC2. This clearly demonstrates that quantities and quality of in situ and laboratory investigations, required to estimate the key parameters—i.e., aquifer thickness, and hydraulic conductivity are of paramount importance. Otherwise, the for the backward erosion piping failure mechanism cannot be reliably estimated using the Sellmeijer 2-force rule. However, development of the shown curves provides a valuable insight into the effect that certain parameters have on the . By analysing the mean curves for both design cases, as show in Figure 13, it can be expected that for smaller variations of the hydraulic conductivity, the probability of failure decreases in the lower range of hydraulic heads, but afterwards it drastically increases instead. The reason for this is the change in mean value which, even though is very subtle, significantly affects the results and seems to have much more impact on the than the actual variability of the parameter.
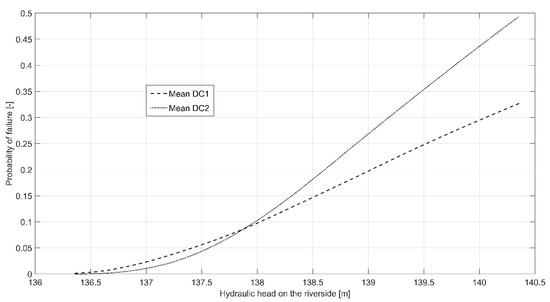
Figure 13.
Mean curves for PDC1 and PDC2.
Overall, by utilizing USACE [28] classification and considering the 100-year flood event (139.21 m a.s.l.), the case study levee fits into the “hazardous” performance regarding piping mechanisms if the mean fragility curves are considered. Regarding the slope stability, for the worst-case scenario of steady seepage, the case study levee fits into the “poor” performance category. If the fragility curves for transient seepage of 5-day duration of the high-water event are analysed, then the probabilities of failure for slope stability indicate the levee have “below average” performances. With a lower variable friction angle, the situation significantly changes in favour of both SDCs, where the levee performance would be classified as “above average”, while for the less variable cohesion the situation remains almost unchanged.
5.3. Discussion on Calculation Assumptions and Recommendations for Future Work
Several assumptions are considered for the sake of calculation simplification and/or because of lack of data. These assumptions, as well their effect on the calculation results, are discussed.
Considering that the levee will be constructed of material of an undefined borrow site, there are no soil investigations to compute its scale of fluctuation, which is therefore assumed as infinite, meaning that all points in the soil region have the same properties. This yields conservative reliability calculations of levee stability. Additionally, the hydraulic conductivity is assumed as constant, and only the effects of its mean value, without inherent variability, are investigated. To consider the variability of hydraulic conductivity, with extremely high range of values as reported by Baecher and Christian [26], a random field seepage analysis should be implemented if Monte Carlo procedure is utilized.
Further, water table on the landside of the levee was fixed at the levee landside toe level and this raised the free water surface inside the levee body during the high-water event. Such a realistic assumption results in higher probabilities of failure. Further, this study considered water to affect slope stability only in terms of pore pressures which lower the shear strength of the material. However, rising and lowering water levels induce cumulative internal erosional effects, eventually leading to levee material degradation. Since this effect is more pronounced with an increasing number of flooding events, numerical models which consider the internal erosion propagation caused by water flow through soil [4,13,15,42,43,44] and its effects on mechanical and hydraulic properties [14] should be implemented in future probabilistic studies of levee stability.
Slope stability analyses were conducted with rising water levels until certain failure was reached. Van der Meer et al. [71] note that levees can endure an overflow of (litre per second) if grass-cover is installed atop the crown and landside slope. However, it is unlikely that the landside slope with a clay and grass-cover will fail at discharges of less than [71]. If the latter is considered as representative for the case-study levee, and by utilizing Equation (4), such discharge occurs at a water height of around 7 cm above the crown, which means the slope would actually fail before reaching the hydraulic heads used for slope stability calculation during the overflow.
This probabilistic study calculates levee slope stability by utilizing finite element and limit equilibrium analyses, coupled with Monte Carlo simulations to determine the probability of failure. For each slip surface, a fixed number of calculations was used (in this case 15,000) with randomly sampled soil parameters according to the assigned distributions, providing the of each slip surface. The slip surface with the highest was then pinpointed as the critical slip surface. However, such a procedure might underestimate the probability of failure of the levee slope, as it considers only specific slip surfaces one by one, without considering the possibility of a different slip surface occurring for each different set of soil parameters. Running the multiple deterministic analysis with variations of soil parameter values will lead to different critical slip surfaces. A combination of shear strength parameters may generate deeper surfaces, while others may generate shallow ones. Thus, imposing a slip surface onto a set of parameters, instead of determining the slip surface based on the parameters, will yield a lower . Combining the various deterministic critical slip surfaces from one Monte Carlo simulation would be a collection of the most critical slip surfaces for each set of random variables realizations and would result in the probability of failure of the levee, instead of a specific slip surface. The quantitative effect of this change in probability calculation procedure could be investigated in future studies.
6. Conclusions
To provide the probabilistic evaluation of stability and piping as a failure mechanism which lead to the larger levee breaches, this study proposes a methodology for the development of fragility curves which give an insight into the probability of failure for identified mechanisms with respect to the riverside water level, including the overflow surge. As the variability of soil parameters, resulting from inherent soil variability, measurement error and transformation uncertainty govern the shape of fragility curves, the necessity for proper selection of each parameter statistic is stresses out. The methodology for development of stability fragility curves is based on the fusion of different types of numerical analyses including the total stress load deformation analysis to obtain a reliable levee stress state and seepage analysis to obtain distribution of pore water pressures. The results of these two analyses feed into the probabilistic LEM analysis. Considering how computationally expensive Monte Carlo simulations are, the presented methodology minimises this disadvantage by combining the numerical analyses with LEM, which has the effect of decreasing the critical failure surface determination time. The necessity of separate stress analysis is additionally emphasized when overflow surge is considered, where equivalent shear stress, caused by water flow, should be applied. For the probabilistic evaluation of piping mechanism, the closed-form analytical Sellmeijer 2-force rule is the one being dominantly used in many state-of-the-art levee risk assessment methodologies.
The methodology was applied to a case study location of River Drava levee, a site which has shown a continuous trend of increased water levels in recent years. From the resulting fragility curves, it can be noted that the permeable crest layer affects stability substantially in cases where the water rises enough to start flowing through it. However, this effect becomes less notable as the ratio of the crown to body conductivities approaches 1. Moreover, if the duration of the high-water event is small enough so that it cannot achieve steady seepage through the levee, the effect also becomes less notable. Considering the soil variability, smaller variability offers increased stability up to a certain point, after which it has unfavourable effects. For the SDC1, this point was found at the crown height, but for SDC2 it was found only at hydraulic heads more than 2 m above the crown.
Regarding piping, even though values for parameters which were not available have been assumed based on correlations and recommendations, meaningful conclusions can still be obtained from the constructed curves. It has been shown how much the results can vary with changes to the investigated parameters—i.e., hydraulic conductivity statistics, effective grain size and aquifer thickness, which emphasizes the importance of gathering relevant data for analyses. Additionally, the reduced variability of the hydraulic conductivity shows a favourable effect until a certain head height which depends on (not exclusively) and aquifer thickness. After that point, the increases. Since the mean value also changed together with the , the effect shown in Figure 13 cannot be completely attributed to the change in variability, but by knowing the amount of change in each statistic their relative contribution is implied.
Since the proposed methodology includes several assumptions for the sake of calculation simplification and/or because of lack of data, this paper discusses them. However, with the lack of reliable data, conservative assumptions were usually made (e.g., higher soil parameter variability, longer flood duration, higher water levels, etc.). When each assumption introduces a small conservative effect, the effects stack and the probability of failure could be overestimated. With more data regarding variability of the levee and foundation soil’s parameters, water levels and their durations, more reliable probabilistic analyses can be conducted.
Author Contributions
Conceptualization, N.R. and M.S.K.; methodology, N.R. and M.S.K.; software, N.R.; validation, N.R., M.B. and M.S.K.; formal analysis, N.R.; investigation, N.R., M.B., M.S.K. and L.L.; writing—original draft preparation, N.R. and M.B.; writing—review and editing, M.S.K. and L.L.; visualization, N.R.; supervision, M.S.K. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by European Union Civil Protection Mechanism, under UCPM-2019-PP-AG call, Grant Agreement Number 874421, oVERFLOw project (Vulnerability assessment of embankments and bridges exposed to flooding hazard).
Conflicts of Interest
The authors declare no conflict of interest. The funders had no role in the design of the study; in the collection, analyses, or interpretation of data; in the writing of the manuscript, or in the decision to publish the results.
References
- Wolff, T.F. Reliability of Levee Systems. In Reliability-Based Design in Geotechnical Engineering; Phoon, K.-K., Ed.; Taylor & Francis: Abingdon, UK, 2008; pp. 448–496. [Google Scholar]
- Özer, I.E.; van Damme, M.; Jonkman, S.N. Towards an International Levee Performance Database (ILPD) and Its Use for Macro-Scale Analysis of Levee Breaches and Failures. Water 2020, 12, 119. [Google Scholar] [CrossRef]
- USACE. Investigation of Underseepage and Its Control, Lower Mississippi River Levees; USACE: Vicksburg, MI, USA, 1956. [Google Scholar]
- Fascetti, A.; Oskay, C. Dual Random Lattice Modeling of Backward Erosion Piping. Comput. Geotech. 2019, 105, 265–276. [Google Scholar] [CrossRef]
- Martinović, K.; Reale, C.; Gavin, K. Fragility Curves for Rainfall-Induced Shallow Landslides on Transport Networks. Can. Geotech. J. 2017, 55, 852–861. [Google Scholar] [CrossRef]
- Doumbouya, L.; Guan, C.S.; Bowa, V.M. Influence of Rainfall Patterns on the Slope Stability of the Lumwana (the Malundwe) Open Pit. Geotech. Geol. Eng. 2020, 38, 1337–1346. [Google Scholar] [CrossRef]
- Far, M.S.; Huang, H. A Hybrid Monte Carlo-Simulated Annealing Approach for Reliability Analysis of Slope Stability Considering the Uncertainty in Water Table Level. Procedia Struct. Integr. 2019, 22, 345–352. [Google Scholar] [CrossRef]
- Wang, L.; Wu, C.; Gu, X.; Liu, H.; Mei, G.; Zhang, W. Probabilistic Stability Analysis of Earth Dam Slope under Transient Seepage Using Multivariate Adaptive Regression Splines. Bull. Eng. Geol. Environ. 2020, 79, 2763–2775. [Google Scholar] [CrossRef]
- Hu, H.; Huang, Y.; Chen, Z. Seismic Fragility Functions for Slope Stability Analysis with Multiple Vulnerability States. Environ. Earth Sci. 2019, 78, 690. [Google Scholar] [CrossRef]
- Pan, Q.; Qu, X.; Wang, X. Probabilistic Seismic Stability of Three-Dimensional Slopes by Pseudo-Dynamic Approach. J. Cent. South Univ. 2019, 26, 1687–1695. [Google Scholar] [CrossRef]
- Xiong, X.; Shi, Z.; Xiong, Y.; Peng, M.; Ma, X.; Zhang, F. Unsaturated Slope Stability around the Three Gorges Reservoir under Various Combinations of Rainfall and Water Level Fluctuation. Eng. Geol. 2019, 261, 105231. [Google Scholar] [CrossRef]
- Kaunda, R.B. A Neural Network Assessment Tool for Estimating the Potential for Backward Erosion in Internal Erosion Studies. Comput. Geotech. 2015, 69, 1–6. [Google Scholar] [CrossRef]
- Robbins, B.A. Numerical Modeling of Backward Erosion Piping. Appl. Numer. Model. Geomech. 2016, 2016, 551–558. [Google Scholar]
- Aboul Hosn, R.; Sibille, L.; Benahmed, N.; Chareyre, B. A Discrete Numerical Model Involving Partial Fluid-Solid Coupling to Describe Suffusion Effects in Soils. Comput. Geotech. 2018, 95, 30–39. [Google Scholar] [CrossRef]
- Yang, J.; Yin, Z.-Y.; Laouafa, F.; Hicher, P.-Y. Analysis of Suffusion in Cohesionless Soils with Randomly Distributed Porosity and Fines Content. Comput. Geotech. 2019, 111, 157–171. [Google Scholar] [CrossRef]
- European Committee for Standardization (CEN). Eurocode 7—Geotechnical Design-Part 1: General Rules; CEN: Brussels, Belgium, 2004. [Google Scholar]
- Thinh, K.D. Probabilistic Approach to the Design of Spread Footings: Application of Eurocode 7. In Proceedings of the 16th International Conference on Soil Mechanics and Geotechnical Engineering, Osaka, Japan, 12–16 September 2005; pp. 2797–2800. [Google Scholar]
- European Committee for Standardization (CEN). Eurocode—Basis of Structural Design; CEN: Brussels, Belgium, 2005. [Google Scholar]
- Canadian Standards Association (CSA). Canadian Highway Bridge Design Code; Canadian Standards Association: Mississauga, ON, Canada, 2014. [Google Scholar]
- Phoon, K.-K.; Kulhawy, F.H. Characterization of Geotechnical Variability. Can. Geotech. J. 1999, 36, 612–624. [Google Scholar] [CrossRef]
- Low, B.K.; Phoon, K.-K. Reliability-Based Design and Its Complementary Role to Eurocode 7 Design Approach. Comput. Geotech. 2015, 65, 30–44. [Google Scholar] [CrossRef]
- Fenton, G.A.; Naghibi, F.; Dundas, D.; Bathurst, R.J.; Griffiths, D.V. Reliability-Based Geotechnical Design in the 2014 Canadian Highway Bridge Design Code. Can. Geotech. J. 2016, 53, 236–251. [Google Scholar] [CrossRef]
- Hamedifar, H.; Bea, R.G.; Pestana-Nascimento, J.M.; Roe, E.M. Role of Probabilistic Methods in Sustainable Geotechnical Slope Stability Analysis. Procedia Earth Planet. Sci. 2014, 9, 132–142. [Google Scholar] [CrossRef]
- Mazzoleni, M.; Bacchi, B.; Barontini, S.; Di Baldassarre, G.; Pilotti, M.; Ranzi, R. Flooding Hazard Mapping in Floodplain Areas Affected by Piping Breaches in the Po River, Italy. J. Hydrol. Eng. 2014, 19, 717–731. [Google Scholar] [CrossRef]
- Schweckendiek, T.; Vrouwenvelder, A.C.W.M.; Calle, E.O.F. Updating Piping Reliability with Field Performance Observations. Struct. Saf. 2014, 47, 13–23. [Google Scholar] [CrossRef]
- Baecher, G.B.; Christian, J.T. Reliability and Statistics in Geotechnical Engineering; Wiley: Hoboken, NJ, USA, 2003. [Google Scholar]
- Nadim, F. Tools and Strategies for Dealing with Uncertainty in Geotechnics. In Probabilistic Methods in Geotechnical Engineering; Griffiths, D.V., Fenton, G.A., Eds.; CISM Courses and Lectures; Springer: Berlin/Heidelberg, Germany, 2007. [Google Scholar]
- USACE. Introduction to Probability and Reliability Methods for Use in Geotechnical Engineering; Engineering and Design; USACE: Washington, DC, USA, 1997. [Google Scholar]
- Santamarina, J.C.; Altschaeffl, A.G.; Chameau, J.L. Reliability of Slopes: Incorporating Qualitative Information. In Rockfall Prediction and Control and Landslide Case Histories; Transportation Research Record; Transportation Research Board: Washigton, DC, USA, 1992; pp. 1–5. ISBN 0-309-05206-8. [Google Scholar]
- Simm, J.; Tarrant, O. Development of Fragility Curves to Describe the Performance of UK Levee Systems. In Proceedings of the Twenty-Sixth International Congress on Large Dams, Vienna, Austria, 1–7 July 2018. [Google Scholar]
- TAW/ENW. Technical Report on Sand Boils (Piping); Hydraulic Engineering Reports; Rijkswaterstaat: Amsterdam, The Netherlands, 1999. [Google Scholar]
- Hughes, S.A.; Nadal, N.C. Laboratory Study of Combined Wave Overtopping and Storm Surge Overflow of a Levee. Coast. Eng. 2009, 56, 244–259. [Google Scholar] [CrossRef]
- Hughes, S.A.; Shaw, J.M.; Howard, I.L. Earthen Levee Shear Stress Estimates for Combined Wave Overtopping and Surge Overflow. J. Waterw. Port Coast. Ocean Eng. 2012, 138, 267–273. [Google Scholar] [CrossRef]
- Xu, Y.; Li, L.; Amini, F. Slope Stability of Earthen Levee Strengthened by Roller-Compacted Concrete under Hurricane Overtopping Flow Conditions. Geomech. Geoengin. 2013, 8, 76–85. [Google Scholar] [CrossRef]
- Kaur, A.; Sharma, D.R.K. Slope stability analysis techniques: A review. Int. J. Eng. Appl. Sci. Technol. 2016, 1, 52–57. [Google Scholar]
- Petterson, K.E. The Early History of Circular Sliding Surfaces. Géotechnique 1955, 5, 275–296. [Google Scholar] [CrossRef]
- Morgenstern, N.R.; Price, V.E. The Analysis of the Stability of General Slip Surfaces. Géotechnique 1965, 15, 79–93. [Google Scholar] [CrossRef]
- Spencer, E. A Method of Analysis of the Stability of Embankments Assuming Parallel Inter-Slice Forces. Géotechnique 1967, 17, 11–26. [Google Scholar] [CrossRef]
- Akbas, B.; Huvaj, N. Probabilistic Slope Stability Analyses Using Limit Equilibrium and Finite Element Methods; IOS Press: Rotterdam, The Netherlands, 2015. [Google Scholar]
- Planès, T.; Mooney, M.A.; Rittgers, J.B.R.; Parekh, M.L.; Behm, M.; Sneider, R. Time-Lapse Monitoring of Internal Erosion in Earthen Dams and Levees Using Ambient Seismic Noise. Géotechnique 2016, 66, 301–312. [Google Scholar] [CrossRef]
- Hunter, R.P.; Bowman, E.T. Visualisation of Seepage-Induced Suffusion and Suffosion within Internally Erodible Granular Media. Géotechnique 2018, 68, 918–930. [Google Scholar] [CrossRef]
- El Shamy, U.; Aydin, F. Multiscale Modeling of Flood-Induced Piping in River Levees. J. Geotech. Geoenviron. Eng. 2008, 134, 1385–1398. [Google Scholar] [CrossRef]
- Liang, Y.; Jim Yeh, T.-C.; Wang, Y.-L.; Liu, M.; Wang, J.; Hao, Y. Numerical Simulation of Backward Erosion Piping in Heterogeneous Fields. Water Resour. Res. 2017, 53, 3246–3261. [Google Scholar] [CrossRef]
- Yerro, A.; Rohe, A.; Soga, K. Modelling Internal Erosion with the Material Point Method. Procedia Eng. 2017, 175, 365–372. [Google Scholar] [CrossRef]
- Sellmeijer, J.B. Numerical Computation of Seepage Erosion below Dams (Piping). In Proceedings of the 3rd International Conference on Scour and Erosion (ICSE-3), Amsterdam, The Netherlands, 1–3 November 2006. [Google Scholar]
- Sellmeijer, H.; de la Cruz, J.L.; van Beek, V.M.; Knoeff, H. Fine-Tuning of the Backward Erosion Piping Model through Small-Scale, Medium-Scale and IJkdijk Experiments. Eur. J. Environ. Civ. Eng. 2011, 15, 1139–1154. [Google Scholar] [CrossRef]
- Kramer, R. Piping Under Transient Conditions. Master’s Thesis, University of Twente, Enschede, The Netherlands, 9 October 2014. [Google Scholar]
- VNK2 Project Office Flood Risk in the Netherlands. VNK2: The Method in Brief; VNK2: Utrecht, The Netherlands, 2012. [Google Scholar]
- Sellmeijer, J.B.; Koenders, M.A. A Mathematical Model for Piping. Appl. Math. Model. 1991, 15, 646–651. [Google Scholar] [CrossRef]
- Krušelj, Ž. Katastrofalne Poplave u Koprivničkoj i Đurđevačkoj Podravini 1965., 1966. i 1972. godine. Podrav. Časopis za Multidiscip. Istraživanja 2017, 16, 5–35. [Google Scholar]
- Schneider, H.R. Definition and Determination of Characteristic Soil Properties; Balkema: Hamburg, Germany, 1997. [Google Scholar]
- Ahmed, A.; Soubra, A.-H. Extension of Subset Simulation Approach for Uncertainty Propagation and Global Sensitivity Analysis. Georisk 2012, 6, 162–176. [Google Scholar] [CrossRef][Green Version]
- Andreev, S.; Zhivkov Zhelyazkov, A. Probability of Failure of an Embankment Dam Due to Slope Instability and Overtopping: First Order Second Moment Method for Assessment of Uncertainty. In Proceedings of the 13th International Benchmark Workshop on Numerical Analysis of Dams, Lausanne, Switzerland, 9–11 September 2015; pp. 207–215. [Google Scholar]
- Lumb, P. Safety Factors and the Probability Distribution of Soil Strength. Can. Geotech. J. 1970, 7, 225–242. [Google Scholar] [CrossRef]
- Wolff, T.F. Analysis and Design of Embankment Dam Slopes: A Probabilistic Approach. Ph.D. Thesis, Purdue University, West Laffayete, IN, USA, 6 May 1985. [Google Scholar]
- Correlation Coefficient (Cohesion and Friction Angle) in an SWedge Probabilistic. Available online: https://www.rocscience.com/help/swedge/swedge/Correlation_Coefficient.htm (accessed on 18 May 2020).
- Phoon, K.-K.; Kulhawy, F.H. Evaluation of Geotechnical Property Variability. Can. Geotech. J. 1999, 36, 625–639. [Google Scholar] [CrossRef]
- Fenton, G.A.; Griffiths, D.V. Statistics of Free Surface Flow through Stochastic Earth Dam. J. Geotech. Eng. 1996, 122, 427–436. [Google Scholar] [CrossRef]
- Griffiths, D.V.; Fenton, G.A. The Random Finite Element Method (RFEM) in Stead Seepage Analysis. In Probabilistic Methods in Geotechnical Engineering; CISM Courses and Lectures; Springer: Berlin/Heidelberg, Germany, 2007; pp. 225–241. [Google Scholar]
- Chapuis, R.P.; Gill, D.E. Hydraulic Anisotropy of Homogeneous Soils and Rocks: Influence of the Densification Process. Bull. Int. Assoc. Eng. Geol. 1989, 39, 75–86. [Google Scholar] [CrossRef]
- Budhu, M. Soil Mechanics and Foundations, 3rd ed.; John Wiley & Sons, Inc.: Hoboken, NJ, USA, 2011. [Google Scholar]
- Rahardjo, H.; Satyanaga, A.; Choon, L.E. Hydraulic Anisotropy Behavior of Compacted Soil. In Proceedings of the 19th International Conference on Soil Mechanics and Geotechnical Engineering, Seoul, Korea, 17–21 September 2017. [Google Scholar]
- Fredlund, D.G.; Scoular, R.E.G. Using Limit Equilibrium Concepts in Finite Element Slope Stability Analysis. In Proceedings of the International Symposium on Slope Stability Engineering, IS-Shikoku ’99, Matsuyama, Shikoku, Japan, 8–11 November 1999; pp. 31–47. [Google Scholar]
- Hewlett, H.W.M.; Boorman, L.A.; Bramley, M.E. Design of Reinforced Grass Waterways; Construction and Industry Research and Information Association: London, UK, 1987; p. 116. [Google Scholar]
- Powledge, G.R.; Ralston, D.C.; Miller, P.; Chen, Y.H.; Clopper, P.E.; Temple, D.M. Mechanics of Overflow Erosion on Embankments. II: Hydraulic and Design Considerations. J. Hydraul. Eng. 1989, 115, 1056–1075. [Google Scholar] [CrossRef]
- Hughes, S.A. Combined Wave and Surge Overtopping of Levees: Flow Hydrodynamics and Articulated Concrete Mat. Stability; USACE, Engineer Research and Developement Center, Coastal and Hydraulics Laboratory: Washington, DC, USA, 2008. [Google Scholar]
- GEO-SLOPE. Stability Modeling with GeoStudio; GEO-SLOPE International Ltd.: Calgary, AB, Canada, 2017. [Google Scholar]
- European Committee for Standardization (CEN). Eurocode 8—Design of Structures for Earthquake Resistance–Part. 1: General Rules, Seismic Actions and Rules for Buildings; CEN: Brussels, Belgium, 2004. [Google Scholar]
- European Committee for Standardization (CEN). Eurocode 8–Design of Structures for Earthquake Resistance–Part. 5: Foundations, Retaining Structures and Geotechnical Aspects; CEN: Brussels, Belgium, 2004. [Google Scholar]
- Pickles, A.; Sandham, R. Application of Eurocode 7 to the Design of Flood Embankments (C749); CIRIA: London, UK, 2014; ISBN 978-0-86017-754-8. [Google Scholar]
- Van der Meer, J.W.; ter Horst, W.L.A.; van Valzen, E.H. Calculation of Fragility Curves for Flood Defence Assets. In Flood Risk Management: Research and Practice; Taylor & Francis Group: London, UK, 2009; pp. 567–573. [Google Scholar]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).