Modeling Surface Processes on Debris-Covered Glaciers: A Review with Reference to the High Mountain Asia
Abstract
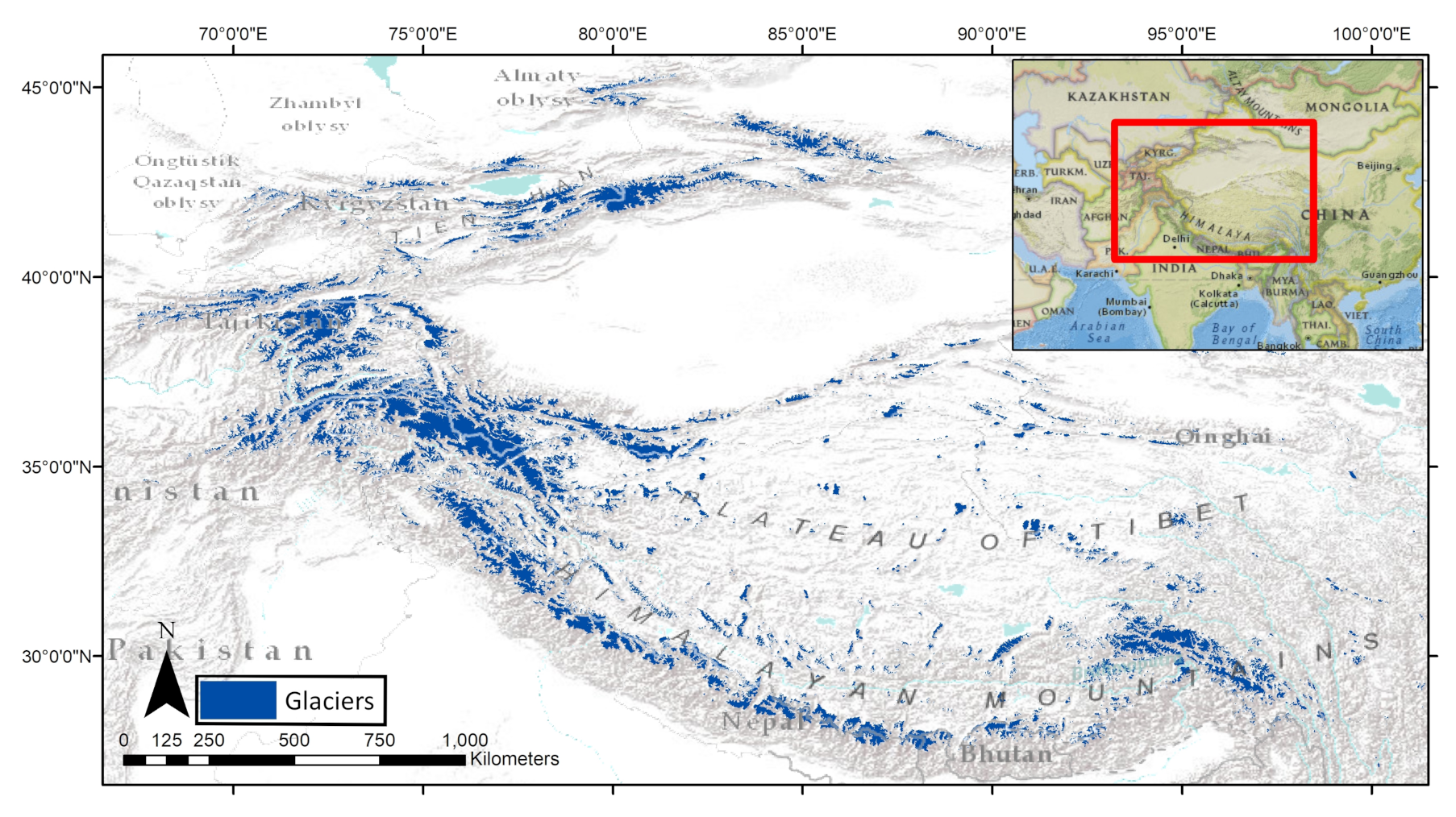
1. Introduction
2. Supraglacial Debris
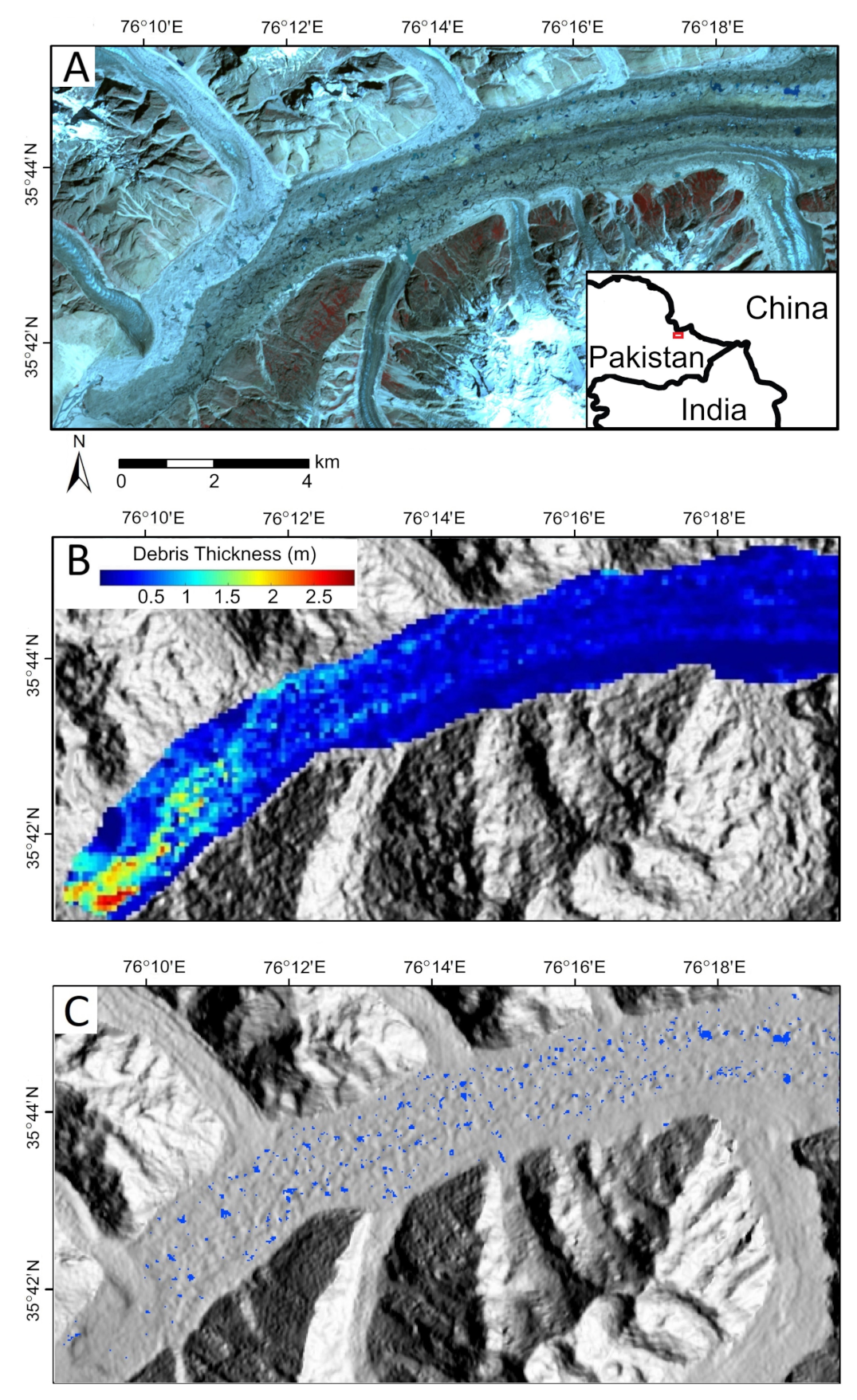
2.1. Properties of Supraglacial Debris
2.2. Transport of Supraglacial Debris
3. Surface Ablation
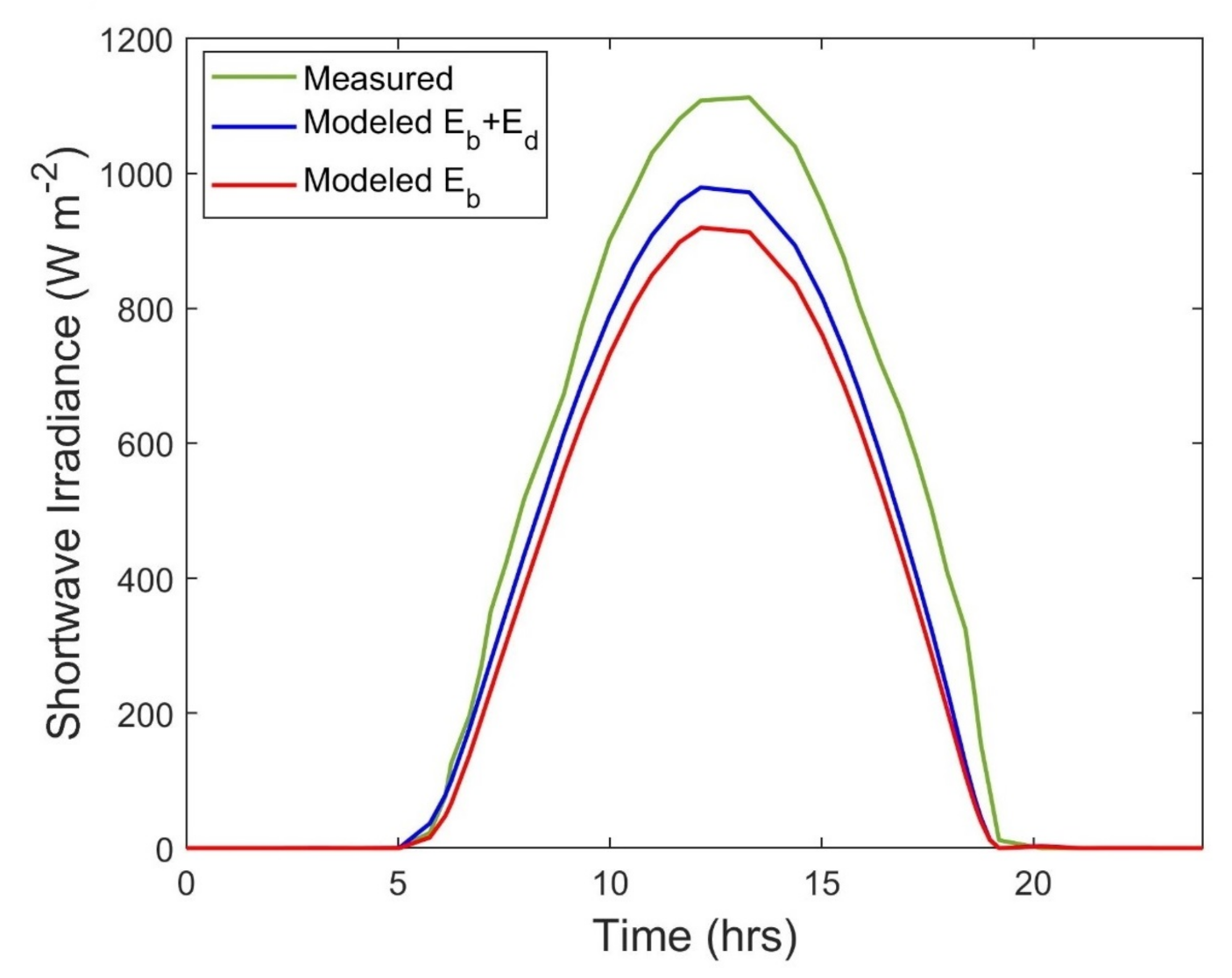
3.1. Surface Energy Balance
3.2. Ablation Dynamics
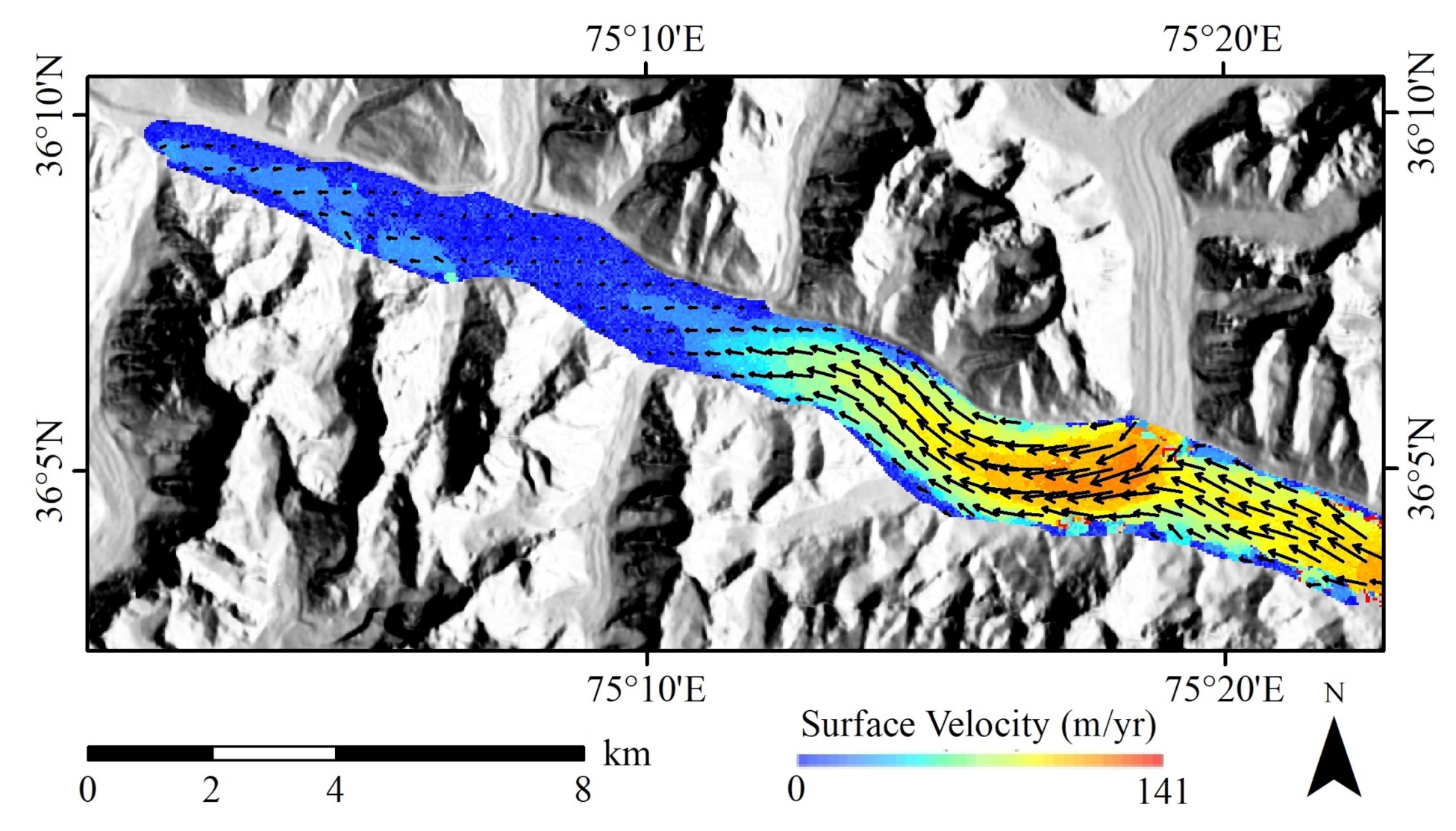
4. Surface Ice-Flow
5. Supraglacial Water Bodies
5.1. Supraglacial Ponds, Lakes, and Ice Cliffs
5.2. Supraglacial Drainage and Ponding
6. Feedback and System Couplings
7. Model Inputs and Validation
7.1. Meteorological Data and Ablation Rate
7.2. Remote Sensing of Glacier Surface
8. Issues and Research Directions
9. Conclusions
- The properties and transport of supraglacial debris.
- Surface energy balance and ablation dynamics.
- Supraglacial water bodies and ice-cliffs.
- Surface ice-flow.
- Systems couplings and feedbacks between debris load, ablation, water bodies, and topographic conditions.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Seong, Y.B.; Owen, L.A.; Yi, C.; Finkel, R.C. Quaternary glaciation of Muztag Ata and Kongur Shan: Evidence for glacier response to rapid climate changes throughout the Late Glacial and Holocene in westernmost Tibet. Geol. Soc. Am. Bull. 2009, 121, 348–365. [Google Scholar] [CrossRef]
- Immerzeel, W.W.; Van Beek, L.P.; Bierkens, M.F. Climate change will affect the Asian water towers. Science 2010, 328, 1382–1385. [Google Scholar] [CrossRef] [PubMed]
- Benn, D.; Bolch, T.; Hands, K.; Gulley, J.; Luckman, A.; Nicholson, L.; Quincey, D.; Thompson, S.; Toumi, R.; Wiseman, S. Response of debris-covered glaciers in the Mount Everest region to recent warming, and implications for outburst flood hazards. Earth-Sci. Rev. 2012, 114, 156–174. [Google Scholar] [CrossRef]
- Scherler, D.; Bookhagen, B.; Strecker, M.R. Spatially variable response of Himalayan glaciers to climate change affected by debris cover. Nat. Geosci. 2011, 4, 156–159. [Google Scholar] [CrossRef]
- Miles, E.S.; Willis, I.; Buri, P.; Steiner, J.F.; Arnold, N.S.; Pellicciotti, F. Surface pond energy absorption across four Himalayan glaciers accounts for 1/8 of total catchment ice loss. Geophys. Res. Lett. 2018, 45, 10–464. [Google Scholar] [CrossRef]
- Bush, A.B.; Bishop, M.P.; Huo, D.; Chi, Z.; Tiwari, U. Issues in Climate Analysis and Modeling for Understanding Mountain Erosion Dynamics. In Reference Module in Earth Systems and Environmental Sciences; Elsevier: Amsterdam, The Netherlands, 2020. [Google Scholar] [CrossRef]
- Bolch, T.; Kulkarni, A.; Kääb, A.; Huggel, C.; Paul, F.; Cogley, J.G.; Frey, H.; Kargel, J.S.; Fujita, K.; Scheel, M.; et al. The state and fate of Himalayan glaciers. Science 2012, 336, 310–314. [Google Scholar] [CrossRef]
- Fujita, K.; Sakai, A. Modelling runoff from a Himalayan debris-covered glacier. Hydrol. Earth Syst. Sci 2014, 18, 2679–2694. [Google Scholar] [CrossRef]
- Rowan, A.V.; Egholm, D.L.; Quincey, D.J.; Glasser, N.F. Modelling the feedbacks between mass balance, ice flow and debris transport to predict the response to climate change of debris-covered glaciers in the Himalaya. Earth Planet. Sci. Lett. 2015, 430, 427–438. [Google Scholar] [CrossRef]
- Anderson, L.S.; Anderson, R.S. Modeling debris-covered glaciers: Response to steady debris deposition. Cryosphere 2016, 10, 1105. [Google Scholar] [CrossRef]
- Dobreva, I.D.; Bishop, M.P.; Bush, A.B. Climate-glacier dynamics and topographic forcing in the Karakoram Himalaya: Concepts, issues and research directions. Water 2017, 9, 405. [Google Scholar] [CrossRef]
- Östrem, G. Ice melting under a thin layer of moraine, and the existence of ice cores in moraine ridges. Geogr. Ann. 1959, 41, 228–230. [Google Scholar] [CrossRef]
- Adhikary, S.; Masayoshi, N.; Seko, K.; Shakya, B. Dust Influence on the Melting Process of Glacier Ice: Experimental Results from Lirung Glacier, Nepal Himalayas; IAHS Publication: Wallingford, UK, 2000; pp. 43–52. [Google Scholar]
- Kayastha, R.B.; Takeuchi, Y.; Nakawo, M.; Ageta, Y. Practical prediction of ice melting beneath various thickness of debris cover on Khumbu Glacier, Nepal, using a positive degree-day factor. IAHS-AISH P 2000, 264, 71–81. [Google Scholar]
- Nicholson, L.; Benn, D.I. Calculating ice melt beneath a debris layer using meteorological data. J. Glaciol. 2006, 52, 463–470. [Google Scholar] [CrossRef]
- Reid, T.D.; Brock, B.W. An energy-balance model for debris-covered glaciers including heat conduction through the debris layer. J. Glaciol. 2010, 56, 903–916. [Google Scholar] [CrossRef]
- Pratap, B.; Dobhal, D.; Mehta, M.; Bhambri, R. Influence of debris cover and altitude on glacier surface melting: A case study on Dokriani Glacier, central Himalaya, India. Ann. Glaciol. 2015, 56, 9–16. [Google Scholar] [CrossRef]
- Brock, B.W.; Mihalcea, C.; Kirkbride, M.P.; Diolaiuti, G.; Cutler, M.E.; Smiraglia, C. Meteorology and surface energy fluxes in the 2005–2007 ablation seasons at the Miage debris-covered glacier, Mont Blanc Massif, Italian Alps. J. Geophys. Res. Atmos. 2010, 115. [Google Scholar] [CrossRef]
- Collier, E.; Nicholson, L.; Brock, B.; Maussion, F.; Essery, R.; Bush, A. Representing moisture fluxes and phase changes in glacier debris cover using a reservoir approach. Cryosphere 2014, 8, 1429–1444. [Google Scholar] [CrossRef]
- MacGregor, K.R.; Anderson, R.S.; Waddington, E.D. Numerical modeling of glacial erosion and headwall processes in alpine valleys. Geomorphology 2009, 103, 189–204. [Google Scholar] [CrossRef]
- Benn, D.; Evans, D.J. Glaciers and Glaciation; Routledge: Abingdon, UK, 2014. [Google Scholar]
- Kääb, A.; Berthier, E.; Nuth, C.; Gardelle, J.; Arnaud, Y. Contrasting patterns of early twenty-first-century glacier mass change in the Himalayas. Nature 2012, 488, 495–498. [Google Scholar] [CrossRef]
- Immerzeel, W.; Pellicciotti, F.; Bierkens, M. Rising river flows throughout the twenty-first century in two Himalayan glacierized watersheds. Nat. Geosci. 2013, 6, 742–745. [Google Scholar] [CrossRef]
- Salerno, F.; Thakuri, S.; Tartari, G.; Nuimura, T.; Sunako, S.; Sakai, A.; Fujita, K. Debris-covered glacier anomaly? Morphological factors controlling changes in the mass balance, surface area, terminus position, and snow line altitude of Himalayan glaciers. Earth Planet. Sci. Lett. 2017, 471, 19–31. [Google Scholar] [CrossRef]
- Sakai, A.; Takeuchi, N.; Fujita, K.; Nakawo, M. Role of Supraglacial Ponds in the Ablation Process of a Debris-covered Glacier in the Nepal Himalayas; IAHS Publication: Wallingford, UK, 2000; pp. 119–132. [Google Scholar]
- Wessels, R.L.; Kargel, J.S.; Kieffer, H.H. ASTER measurement of supraglacial lakes in the Mount Everest region of the Himalaya. Ann. Glaciol. 2002, 34, 399–408. [Google Scholar] [CrossRef]
- Miles, E.S.; Steiner, J.; Willis, I.; Buri, P.; Immerzeel, W.W.; Chesnokova, A.; Pellicciotti, F. Pond dynamics and supraglacial-englacial connectivity on debris-covered Lirung Glacier, Nepal. Front. Earth Sci. 2017, 5, 69. [Google Scholar] [CrossRef]
- Benn, D.I.; Thompson, S.; Gulley, J.; Mertes, J.; Luckman, A.; Nicholson, L. Structure and evolution of the drainage system of a Himalayan debris-covered glacier, and its relationship with patterns of mass loss. Cryosphere 2017, 11, 2247–2264. [Google Scholar] [CrossRef]
- Gibson, M.J.; Glasser, N.F.; Quincey, D.J.; Mayer, C.; Rowan, A.V.; Irvine-Fynn, T.D. Temporal variations in supraglacial debris distribution on Baltoro Glacier, Karakoram between 2001 and 2012. Geomorphology 2017, 295, 572–585. [Google Scholar] [CrossRef]
- Zhang, Y.; Fujita, K.; Liu, S.; Liu, Q.; Nuimura, T. Distribution of debris thickness and its effect on ice melt at Hailuogou glacier, southeastern Tibetan Plateau, using in situ surveys and ASTER imagery. J. Glaciol. 2011, 57, 1147–1157. [Google Scholar] [CrossRef]
- Steiner, J.F.; Buri, P.; Miles, E.S.; Ragettli, S.; Pellicciotti, F. Supraglacial ice cliffs and ponds on debris-covered glaciers: Spatio-temporal distribution and characteristics. J. Glaciol. 2019, 65, 617–632. [Google Scholar] [CrossRef]
- Farinotti, D.; Immerzeel, W.W.; de Kok, R.J.; Quincey, D.J.; Dehecq, A. Manifestations and mechanisms of the Karakoram glacier Anomaly. Nat. Geosci. 2020, 13, 8–16. [Google Scholar] [CrossRef]
- Reid, T.; Brock, B. Assessing ice-cliff backwasting and its contribution to total ablation of debris-covered Miage glacier, Mont Blanc massif, Italy. J. Glaciol. 2014, 60, 3–13. [Google Scholar] [CrossRef]
- Miles, K.E.; Hubbard, B.; Quincey, D.J.; Miles, E.S.; Irvine-Fynn, T.D.; Rowan, A.V. Surface and subsurface hydrology of debris-covered Khumbu Glacier, Nepal, revealed by dye tracing. Earth Planet. Sci. Lett. 2019, 513, 176–186. [Google Scholar] [CrossRef]
- Steiner, J.F.; Pellicciotti, F.; Buri, P.; Miles, E.S.; Immerzeel, W.W.; Reid, T.D. Modelling ice-cliff backwasting on a debris-covered glacier in the Nepalese Himalaya. J. Glaciol. 2015, 61, 889–907. [Google Scholar] [CrossRef]
- Buri, P.; Miles, E.S.; Steiner, J.F.; Immerzeel, W.W.; Wagnon, P.; Pellicciotti, F. A physically based 3-D model of ice cliff evolution over debris-covered glaciers. J. Geophys. Res. Earth Surf. 2016, 121, 2471–2493. [Google Scholar] [CrossRef]
- Cuffey, K.M.; Paterson, W.S.B. The Physics of Glaciers; Academic Press: Cambridge, MA, USA, 2010. [Google Scholar]
- Miles, E.S.; Pellicciotti, F.; Willis, I.C.; Steiner, J.F.; Buri, P.; Arnold, N.S. Refined energy-balance modelling of a supraglacial pond, Langtang Khola, Nepal. Ann. Glaciol. 2016, 57, 29–40. [Google Scholar] [CrossRef]
- Huo, D.; Bishop, M.P.; Young, B.W.; Chi, Z.; Haritashya, U.K. Numerical Modeling Issues for Understanding Complex Debris-Covered Glaciers. In Reference Module in Earth Systems and Environmental Sciences; Elsevier: Amsterdam, The Netherlands, 2020. [Google Scholar]
- Juen, M.; Mayer, C.; Lambrecht, A.; Han, H.; Liu, S. Impact of varying debris cover thickness on ablation: A case study for Koxkar Glacier in the Tien Shan. Cryosphere 2014, 8, 377. [Google Scholar] [CrossRef]
- Rounce, D.; Quincey, D.; McKinney, D. Debris-covered energy balance model for Imja-Lhotse Shar Glacier in the Everest region of Nepal. Cryosphere Discuss 2015, 9, 3503–3540. [Google Scholar] [CrossRef]
- Bolch, T.; Buchroithner, M.F.; Peters, J.; Baessler, M.; Bajracharya, S. Identification of glacier motion and potentially dangerous glacial lakes in the Mt. Everest region/Nepal using spaceborne imagery. Nat. Hazards Earth Syst. Sci. 2008, 8, 1329–1340. [Google Scholar] [CrossRef]
- Shukla, A.; Gupta, R.; Arora, M. Estimation of debris cover and its temporal variation using optical satellite sensor data: A case study in Chenab basin, Himalaya. J. Glaciol. 2009, 55, 444–452. [Google Scholar] [CrossRef]
- Sakai, A.; Nakawo, M.; Fujita, K. Distribution characteristics and energy balance of ice cliffs on debris-covered glaciers, Nepal Himalaya. Arct. Antarct. Alp. Res. 2002, 34, 12–19. [Google Scholar] [CrossRef]
- Rounce, D.R.; King, O.; McCarthy, M.; Shean, D.E.; Salerno, F. Quantifying debris thickness of debris-covered glaciers in the Everest Region of Nepal through inversion of a subdebris melt model. J. Geophys. Res. Earth Surf. 2018, 123, 1094–1115. [Google Scholar] [CrossRef]
- Mihalcea, C.; Mayer, C.; Diolaiuti, G.; D’agata, C.; Smiraglia, C.; Lambrecht, A.; Vuillermoz, E.; Tartari, G. Spatial distribution of debris thickness and melting from remote-sensing and meteorological data, at debris-covered Baltoro glacier, Karakoram, Pakistan. Ann. Glaciol. 2008, 48, 49–57. [Google Scholar] [CrossRef]
- Huang, L.; Li, Z.; Han, H.; Tian, B.; Zhou, J. Analysis of thickness changes and the associated driving factors on a debris-covered glacier in the Tienshan Mountain. Remote Sens. Environ. 2018, 206, 63–71. [Google Scholar] [CrossRef]
- Zhang, Y.; Hirabayashi, Y.; Fujita, K.; Liu, S.; Liu, Q. Heterogeneity in supraglacial debris thickness and its role in glacier mass changes of the Mount Gongga. Sci. China Earth Sci. 2016, 59, 170–184. [Google Scholar] [CrossRef]
- Quincey, D.; Copland, L.; Mayer, C.; Bishop, M.; Luckman, A.; Belo, M. Ice velocity and climate variations for Baltoro Glacier, Pakistan. J. Glaciol. 2009, 55, 1061–1071. [Google Scholar] [CrossRef]
- Jouvet, G.; Picasso, M.; Rappaz, J.; Huss, M.; Funk, M. Modelling and numerical simulation of the dynamics of glaciers including local damage effects. Math. Model. Nat. Phenom. 2011, 6, 263–280. [Google Scholar] [CrossRef][Green Version]
- Reid, T.; Carenzo, M.; Pellicciotti, F.; Brock, B. Including debris cover effects in a distributed model of glacier ablation. J. Geophys. Res. Atmos. 2012, 117. [Google Scholar] [CrossRef]
- Anderson, R.S. A model of ablation-dominated medial moraines and the generation of debris-mantled glacier snouts. J. Glaciol. 2000, 46, 459–469. [Google Scholar] [CrossRef]
- Benn, D.I.; Owen, L.A. Himalayan glacial sedimentary environments: A framework for reconstructing and dating the former extent of glaciers in high mountains. Quat. Int. 2002, 97, 3–25. [Google Scholar] [CrossRef]
- van Woerkom, T.; Steiner, J.F.; Kraaijenbrink, P.D.; Miles, E.; Immerzeel, W.W. Sediment supply from lateral moraines to a debris-covered glacier in the Himalaya. Earth Surf. Dyn. 2019, 7, 411–427. [Google Scholar] [CrossRef]
- Benn, D.I.; Lehmkuhl, F. Mass balance and equilibrium-line altitudes of glaciers in high-mountain environments. Quat. Int. 2000, 65, 15–29. [Google Scholar] [CrossRef]
- Wirbel, A.; Jarosch, A.H.; Nicholson, L. Modelling debris transport within glaciers by advection in a full-Stokes ice flow model. Cryosphere 2018, 12, 189–204. [Google Scholar] [CrossRef]
- Owen, L.A.; Derbyshire, E. The Karakoram glacial depositional system. Z. Geomorphol. 1989, 76, 33–73. [Google Scholar]
- Mattson, L. Ablation on debris covered glaciers: An example from the Rakhiot Glacier, Punjab, Himalaya. Intern. Assoc. Hydrol. Sci. 1993, 218, 289–296. [Google Scholar]
- Reznichenko, N.; Davies, T.; Shulmeister, J.; McSaveney, M. Effects of debris on ice-surface melting rates: An experimental study. J. Glaciol. 2010, 56, 384–394. [Google Scholar] [CrossRef]
- Hambrey, M.J.; Quincey, D.J.; Glasser, N.F.; Reynolds, J.M.; Richardson, S.J.; Clemmens, S. Sedimentological, geomorphological and dynamic context of debris-mantled glaciers, Mount Everest (Sagarmatha) region, Nepal. Quat. Sci. Rev. 2008, 27, 2361–2389. [Google Scholar] [CrossRef]
- Kirkbride, M.P.; Deline, P. The formation of supraglacial debris covers by primary dispersal from transverse englacial debris bands. Earth Surf. Process. Landforms 2013, 38, 1779–1792. [Google Scholar] [CrossRef]
- Thakuri, S.; Salerno, F.; Smiraglia, C.; Bolch, T.; D’Agata, C.; Viviano, G.; Tartari, G. Tracing glacier changes since the 1960s on the south slope of Mt. Everest (central Southern Himalaya) using optical satellite imagery. Cryosphere 2014, 8, 1297–1315. [Google Scholar] [CrossRef]
- Anderson, L.S.; Anderson, R.S. Debris thickness patterns on debris-covered glaciers. Geomorphology 2018, 311, 1–12. [Google Scholar] [CrossRef]
- Pelto, M.S. Mass Balance of Adjacent Debris-Covered and Clean Glacier Ice in the North Cascades, Washington; IAHS Publication: Wallingford, UK, 2000; pp. 35–42. [Google Scholar]
- Mertes, J.R.; Thompson, S.S.; Booth, A.D.; Gulley, J.D.; Benn, D.I. A conceptual model of supra-glacial lake formation on debris-covered glaciers based on GPR facies analysis. Earth Surf. Process. Landforms 2017, 42, 903–914. [Google Scholar] [CrossRef]
- Mihalcea, C.; Mayer, C.; Diolaiuti, G.; Lambrecht, A.; Smiraglia, C.; Tartari, G. Ice ablation and meteorological conditions on the debris-covered area of Baltoro glacier, Karakoram, Pakistan. Ann. Glaciol. 2006, 43, 292–300. [Google Scholar] [CrossRef]
- Nakawo, M.; Young, G.J. Field experiments to determine the effect of a debris layer on ablation of glacier ice. Ann. Glaciol. 1981, 2, 85–91. [Google Scholar] [CrossRef]
- Fyffe, C.L.; Reid, T.D.; Brock, B.W.; Kirkbride, M.P.; Diolaiuti, G.; Smiraglia, C.; Diotri, F. A distributed energy-balance melt model of an alpine debris-covered glacier. J. Glaciol. 2014, 60, 587–602. [Google Scholar] [CrossRef]
- Bird, R.E.; Riordan, C. Simple solar spectral model for direct and diffuse irradiance on horizontal and tilted planes at the earth’s surface for cloudless atmospheres. J. Clim. Appl. Meteorol. 1986, 25, 87–97. [Google Scholar] [CrossRef]
- Reda, I.; Konings, J.; Xie, Y. A method to measure the broadband longwave irradiance in the terrestrial direct solar beam. J. Atmos. Sol.-Terr. Phys. 2015, 129, 23–29. [Google Scholar] [CrossRef][Green Version]
- Chavez, P.S. Image-based atmospheric corrections-revisited and improved. Photogramm. Eng. Remote Sens. 1996, 62, 1025–1035. [Google Scholar]
- Jacobson, M.Z.; Jacobson, M.Z. Fundamentals of Atmospheric Modeling; Cambridge University: Cambridge, UK, 2005. [Google Scholar]
- Gueymard, C. SMARTS2: A Simple Model of the Atmospheric Radiative Transfer of Sunshine: Algorithms and Performance Assessment; Florida Solar Energy Center: Cocoa, FL, USA, 1995. [Google Scholar]
- de Kok, R.J.; Steiner, J.F.; Litt, M.; Wagnon, P.; Koch, I.; Azam, M.F.; Immerzeel, W.W. Measurements, models and drivers of incoming longwave radiation in the Himalaya. Int. J. Climatol. 2020, 40, 942–956. [Google Scholar] [CrossRef]
- Dozier, J.; Frew, J. Rapid calculation of terrain parameters for radiation modeling from digital elevation data. IEEE Trans. Geosci. Remote Sens. 1990, 28, 963–969. [Google Scholar] [CrossRef]
- Proy, C.; Tanre, D.; Deschamps, P. Evaluation of topographic effects in remotely sensed data. Remote Sens. Environ. 1989, 30, 21–32. [Google Scholar] [CrossRef]
- Bishop, M.P.; Young, B.W.; Colby, J.D.; Furfaro, R.; Schiassi, E.; Chi, Z. Theoretical Evaluation of Anisotropic Reflectance Correction Approaches for Addressing Multi-Scale Topographic Effects on the Radiation-Transfer Cascade in Mountain Environments. Remote Sens. 2019, 11, 2728. [Google Scholar] [CrossRef]
- Steiner, J.F.; Pellicciotti, F. Variability of air temperature over a debris-covered glacier in the Nepalese Himalaya. Ann. Glaciol. 2016, 57, 295–307. [Google Scholar] [CrossRef]
- Dadic, R.; Mott, R.; Lehning, M.; Burlando, P. Wind influence on snow depth distribution and accumulation over glaciers. J. Geophys. Res. Earth Surf. 2010, 115, F1. [Google Scholar] [CrossRef]
- Braithwaite, R.J.; Olesen, O.B. Response of the energy balance on the margin of the Greenland ice sheet to temperature changes. J. Glaciol. 1990, 36, 217–221. [Google Scholar] [CrossRef][Green Version]
- Khan, M.I. Ablation on Barpu Glacier, Karakoram Himalaya, Pakistan a Study of Melt Processes on a Faceted, Debris-Covered Ice Surface. Master’s Thesis, Wilfrid Laurier University, Waterloo, ON, Canada, 1989. [Google Scholar]
- Minora, U.; Senese, A.; Bocchiola, D.; Soncini, A.; D’agata, C.; Ambrosini, R.; Mayer, C.; Lambrecht, A.; Vuillermoz, E.; Smiraglia, C.; et al. A simple model to evaluate ice melt over the ablation area of glaciers in the Central Karakoram National Park, Pakistan. Ann. Glaciol. 2015, 56, 202–216. [Google Scholar] [CrossRef]
- Kellerer-Pirklbauer, A. The supraglacial debris system at the Pasterze Glacier, Austria: Spatial distribution, characteristics and transport of debris. Z. Geomorphol. Suppl. Issues 2008, 52, 3–25. [Google Scholar] [CrossRef]
- Collier, E.; Mölg, T.; Maussion, F.; Scherer, D.; Mayer, C.; Bush, A. High-resolution interactive modelling of the mountain glacier-atmosphere interface: An application over the Karakoram. Cryosphere 2013, 7, 779. [Google Scholar] [CrossRef]
- Morland, L.; Johnson, I. Steady motion of ice sheets. J. Glaciol. 1980, 25, 229–246. [Google Scholar] [CrossRef][Green Version]
- Herman, F.; Braun, J. Evolution of the glacial landscape of the Southern Alps of New Zealand: Insights from a glacial erosion model. J. Geophys. Res. Earth Surf. 2008, 113. [Google Scholar] [CrossRef]
- Bueler, E.; Brown, J. Shallow shelf approximation as a “sliding law” in a thermomechanically coupled ice sheet model. J. Geophys. Res. Earth Surf. 2009, 114. [Google Scholar] [CrossRef]
- Egholm, D.L.; Knudsen, M.F.; Clark, C.D.; Lesemann, J.E. Modeling the flow of glaciers in steep terrains: The integrated second-order shallow ice approximation (iSOSIA). J. Geophys. Res. Earth Surf. 2011, 116. [Google Scholar] [CrossRef]
- Copland, L.; Pope, S.; Bishop, M.P.; Shroder, J.F.; Clendon, P.; Bush, A.; Kamp, U.; Seong, Y.B.; Owen, L.A. Glacier velocities across the central Karakoram. Ann. Glaciol. 2009, 50, 41–49. [Google Scholar] [CrossRef]
- Quincey, D.; Braun, M.; Glasser, N.F.; Bishop, M.; Hewitt, K.; Luckman, A. Karakoram glacier surge dynamics. Geophys. Res. Lett. 2011, 38. [Google Scholar] [CrossRef]
- Dehecq, A.; Gourmelen, N.; Trouvé, E. Deriving large-scale glacier velocities from a complete satellite archive: Application to the Pamir-Karakoram-Himalaya. Remote Sens. Environ. 2015, 162, 55–66. [Google Scholar] [CrossRef]
- Dehecq, A.; Gourmelen, N.; Gardner, A.S.; Brun, F.; Goldberg, D.; Nienow, P.W.; Berthier, E.; Vincent, C.; Wagnon, P.; Trouvé, E. Twenty-first century glacier slowdown driven by mass loss in High Mountain Asia. Nat. Geosci. 2019, 12, 22–27. [Google Scholar] [CrossRef]
- Gardner, A.S.; Moholdt, G.; Scambos, T.; Fahnstock, M.; Ligtenberg, S.; van den Broeke, M.; Nilsson, J. Increased West Antarctic and unchanged East Antarctic ice discharge over the last 7 years. Cryosphere 2012, 12, 521–547. [Google Scholar] [CrossRef]
- Wendleder, A.; Friedl, P.; Mayer, C. Impacts of climate and supraglacial lakes on the surface velocity of Baltoro Glacier from 1992 to 2017. Remote Sens. 2018, 10, 1681. [Google Scholar] [CrossRef]
- Rankl, M.; Kienholz, C.; Braun, M. Glacier changes in the Karakoram region mapped by multimission satellite imagery. Cryosphere 2014, 8, 977–989. [Google Scholar] [CrossRef]
- Leprince, S.; Barbot, S.; Ayoub, F.; Avouac, J.P. Automatic and precise orthorectification, coregistration, and subpixel correlation of satellite images, application to ground deformation measurements. IEEE Trans. Geosci. Remote Sens. 2007, 45, 1529–1558. [Google Scholar] [CrossRef]
- Watson, C.S.; Quincey, D.J.; Carrivick, J.L.; Smith, M.W.; Rowan, A.V.; Richardson, R. Heterogeneous water storage and thermal regime of supraglacial ponds on debris-covered glaciers. Earth Surf. Process. Landforms 2017, 43, 229–241. [Google Scholar] [CrossRef]
- Thompson, S.; Benn, D.I.; Mertes, J.; Luckman, A. Stagnation and mass loss on a Himalayan debris-covered glacier: Processes, patterns and rates. J. Glaciol. 2016, 62, 467–485. [Google Scholar] [CrossRef]
- Reynolds, J.M. On the Formation of Supraglacial Lakes on Debris-Covered Glaciers; IAHS Publication: Wallingford, UK, 2000; pp. 153–164. [Google Scholar]
- Immerzeel, W.; Kraaijenbrink, P.; Shea, J.; Shrestha, A.; Pellicciotti, F.; Bierkens, M.; De Jong, S. High-resolution monitoring of Himalayan glacier dynamics using unmanned aerial vehicles. Remote Sens. Environ. 2014, 150, 93–103. [Google Scholar] [CrossRef]
- Gulley, J.; Benn, D. Structural control of englacial drainage systems in Himalayan debris-covered glaciers. J. Glaciol. 2007, 53, 399–412. [Google Scholar] [CrossRef]
- Watson, C.S.; Quincey, D.J.; Carrivick, J.L.; Smith, M.W. The dynamics of supraglacial ponds in the Everest region, central Himalaya. Glob. Planet. Chang. 2016, 142, 14–27. [Google Scholar] [CrossRef]
- Richardson, S.D.; Reynolds, J.M. An overview of glacial hazards in the Himalayas. Quat. Int. 2000, 65, 31–47. [Google Scholar] [CrossRef]
- Lüthje, M.; Pedersen, L.; Reeh, N.; Greuell, W. Modelling the evolution of supraglacial lakes on the West Greenland ice-sheet margin. J. Glaciol. 2006, 52, 608–618. [Google Scholar] [CrossRef]
- Benn, D.; Wiseman, S.; Hands, K. Growth and drainage of supraglacial lakes on debris-mantled Ngozumpa Glacier, Khumbu Himal, Nepal. J. Glaciol. 2001, 47, 626–638. [Google Scholar] [CrossRef]
- Quincey, D.J.; Glasser, N.F. Morphological and ice-dynamical changes on the Tasman Glacier, New Zealand, 1990–2007. Glob. Planet. Chang. 2009, 68, 185–197. [Google Scholar] [CrossRef]
- Lüthje, M.; Feltham, D.; Taylor, P.; Worster, M. Modeling the summertime evolution of sea-ice melt ponds. J. Geophys. Res. Ocean. 2006, 111. [Google Scholar] [CrossRef]
- Mernild, S.H.; Hasholt, B. Climatic control on river discharge simulations, Mittivakkat Glacier catchment, Ammassalik Island, SE Greenland. Hydrol. Res. 2006, 37, 327–346. [Google Scholar] [CrossRef]
- Arnold, N.S.; Rees, W.G.; Hodson, A.J.; Kohler, J. Topographic controls on the surface energy balance of a high Arctic valley glacier. J. Geophys. Res. Earth Surf. 2006, 111. [Google Scholar] [CrossRef]
- Garg, P.K.; Shukla, A.; Jasrotia, A.S. Influence of topography on glacier changes in the central Himalaya, India. Glob. Planet. Chang. 2017, 155, 196–212. [Google Scholar] [CrossRef]
- Takeuchi, N.; Li, Z. Characteristics of surface dust on Ürümqi glacier No. 1 in the Tien Shan mountains, China. Arct. Antarct. Alp. Res. 2008, 40, 744–750. [Google Scholar] [CrossRef]
- Yue, X.; Zhao, J.; Li, Z.; Zhang, M.; Fan, J.; Wang, L.; Wang, P. Spatial and temporal variations of the surface albedo and other factors influencing Urumqi Glacier No. 1 in Tien Shan, China. J. Glaciol. 2017, 63, 899–911. [Google Scholar] [CrossRef]
- Pritchard, M.S.; Bush, A.B.; Marshall, S.J. Neglecting ice-atmosphere interactions underestimates ice sheet melt in millennial-scale deglaciation simulations. Geophys. Res. Lett. 2008, 35. [Google Scholar] [CrossRef]
- Brown, G.H. Glacier meltwater hydrochemistry. Appl. Geochem. 2002, 17, 855–883. [Google Scholar] [CrossRef]
- Salerno, F.; Rogora, M.; Balestrini, R.; Lami, A.; Tartari, G.A.; Thakuri, S.; Godone, D.; Freppaz, M.; Tartari, G. Glacier Melting Increases the Solute Concentrations of Himalayan Glacial Lakes. Environ. Sci. Technol. 2016, 50, 9150–9160. [Google Scholar] [CrossRef] [PubMed]
- Colombo, N.; Salerno, F.; Martin, M.; Malandrino, M.; Giardino, M.; Serra, E.; Godone, D.; Said-Pullicino, D.; Fratianni, S.; Paro, L.; et al. Influence of permafrost, rock and ice glaciers on chemistry of high-elevation ponds (NW Italian Alps). Sci. Total Environ. 2019, 685, 886–901. [Google Scholar] [CrossRef] [PubMed]
- Bøggild, C.E.; Olesen, O.B.; Andreas, P.A.; Jørgensen, P. Automatic glacier ablation measurements using pressure transducers. J. Glaciol. 2004, 50, 303–304. [Google Scholar] [CrossRef][Green Version]
- Reggiani, P.; Coccia, G.; Mukhopadhyay, B. Predictive uncertainty estimation on a precipitation and temperature reanalysis ensemble for Shigar Basin, Central Karakoram. Water 2016, 8, 263. [Google Scholar] [CrossRef]
- Bishop, M.P.; Bonk, R.; Kamp, U., Jr.; Shroder, J.F., Jr. Terrain analysis and data modeling for alpine glacier mapping. Polar Geogr. 2001, 25, 182–201. [Google Scholar] [CrossRef]
- Berthier, E.; Vadon, H.; Baratoux, D.; Arnaud, Y.; Vincent, C.; Feigl, K.; Remy, F.; Legresy, B. Surface motion of mountain glaciers derived from satellite optical imagery. Remote Sens. Environ. 2005, 95, 14–28. [Google Scholar] [CrossRef]
- Burgess, E.W.; Forster, R.R.; Larsen, C.F. Flow velocities of Alaskan glaciers. Nat. Commun. 2013, 4, 2416. [Google Scholar] [CrossRef]
- Raup, B.H.; Andreassen, L.M.; Bolch, T.; Bevan, S. Remote sensing of glaciers. In Remote Sensing of the Cryosphere; John Wiley & Sons: Hoboken, NJ, USA, 2015; pp. 123–156. [Google Scholar]
- Fahnestock, M.; Scambos, T.; Moon, T.; Gardner, A.; Haran, T.; Klinger, M. Rapid large-area mapping of ice flow using Landsat 8. Remote Sens. Environ. 2016, 185, 84–94. [Google Scholar] [CrossRef]
- Sidjak, R. Glacier mapping of the Illecillewaet icefield, British Columbia, Canada, using Landsat TM and digital elevation data. Int. J. Remote Sens. 1999, 20, 273–284. [Google Scholar] [CrossRef]
- Albert, T.H. Evaluation of remote sensing techniques for ice-area classification applied to the tropical Quelccaya Ice Cap, Peru. Polar Geogr. 2002, 26, 210–226. [Google Scholar] [CrossRef]
- Paul, F.; Huggel, C.; Kääb, A. Combining satellite multispectral image data and a digital elevation model for mapping debris-covered glaciers. Remote Sens. Environ. 2004, 89, 510–518. [Google Scholar] [CrossRef]
- Brenning, A. Benchmarking classifiers to optimally integrate terrain analysis and multispectral remote sensing in automatic rock glacier detection. Remote Sens. Environ. 2009, 113, 239–247. [Google Scholar] [CrossRef]
- Karimi, N.; Farokhnia, A.; Karimi, L.; Eftekhari, M.; Ghalkhani, H. Combining optical and thermal remote sensing data for mapping debris-covered glaciers (Alamkouh Glaciers, Iran). Cold Reg. Sci. Technol. 2012, 71, 73–83. [Google Scholar] [CrossRef]
- Scherler, D.; Bookhagen, B.; Strecker, M.R. Hillslope-glacier coupling: The interplay of topography and glacial dynamics in High Asia. J. Geophys. Res. Earth Surf. 2011, 116. [Google Scholar] [CrossRef]
- Fujita, K.; Sakai, A.; Nuimura, T.; Yamaguchi, S.; Sharma, R.R. Recent changes in Imja Glacial Lake and its damming moraine in the Nepal Himalaya revealed by in situ surveys and multi-temporal ASTER imagery. Environ. Res. Lett. 2009, 4, 045205. [Google Scholar] [CrossRef]
- Rippin, D.M.; Pomfret, A.; King, N. High resolution mapping of supra-glacial drainage pathways reveals link between micro-channel drainage density, surface roughness and surface reflectance. Earth Surf. Process. Landforms 2015, 40, 1279–1290. [Google Scholar] [CrossRef]
- Gibson, M.; Glasser, N.; Quincey, D.J.; Rowan, A.V.; Irvine-Fynn, T. Changes in glacier surface cover on Baltoro glacier, Karakoram, north Pakistan, 2001–2012. J. Maps 2017, 13, 100–108. [Google Scholar] [CrossRef]
- Xie, Z.; Haritashya, U.K.; Asari, V.K.; Young, B.W.; Bishop, M.P.; Kargel, J.S. GlacierNet: A Deep-Learning Approach for Debris-Covered Glacier Mapping. IEEE Access 2020, 8, 83495–83510. [Google Scholar] [CrossRef]
- Liu, L.; Jiang, L.; Sun, Y.; Wang, H.; Yi, C.; Hsu, H. Morphometric controls on glacier mass balance of the Puruogangri ice field, central Tibetan Plateau. Water 2016, 8, 496. [Google Scholar] [CrossRef]
- Scambos, T.A.; Dutkiewicz, M.J.; Wilson, J.C.; Bindschadler, R.A. Application of image cross-correlation to the measurement of glacier velocity using satellite image data. Remote Sens. Environ. 1992, 42, 177–186. [Google Scholar] [CrossRef]
- Bindschadler, R.; Fahnestock, M.; Skvarca, P.; Scambos, T. Surface-velocity field of the northern Larsen Ice Shelf, Antarctica. Ann. Glaciol. 1994, 20, 319–326. [Google Scholar] [CrossRef]
- Frezzotti, M.; Capra, A.; Vittuari, L. Comparison between glacier ice velocities inferred from GPS and sequential satellite images. Ann. Glaciol. 1998, 27, 54–60. [Google Scholar] [CrossRef]
- Evans, A.N. Glacier surface motion computation from digital image sequences. IEEE Trans. Geosci. Remote Sens. 2000, 38, 1064–1072. [Google Scholar] [CrossRef]
- Kääb, A. Combination of SRTM3 and repeat ASTER data for deriving alpine glacier flow velocities in the Bhutan Himalaya. Remote Sens. Environ. 2005, 94, 463–474. [Google Scholar] [CrossRef]
- Ayoub, F.; Leprince, S.; Avouac, J.P. Co-registration and correlation of aerial photographs for ground deformation measurements. ISPRS J. Photogramm. Remote Sens. 2009, 64, 551–560. [Google Scholar] [CrossRef]
- Chi, Z. Investigation of Glacial Dynamics in the Lambert Glacier-Amery Ice Shelf System (LAS) Using Remote Sensing. Ph.D. Thesis, Texas A&M University, College Station, TX, USA, 2012. [Google Scholar]
- Kumar, V.; Venkataramana, G.; Høgda, K.A. Glacier surface velocity estimation using SAR interferometry technique applying ascending and descending passes in Himalayas. Int. J. Appl. Earth Obs. Geoinf. 2011, 13, 545–551. [Google Scholar] [CrossRef]
- Spedding, N. Hydrological Controls on Sediment Transport Pathways: Implications for Debris-Covered Glaciers; IAHS Publication: Wallingford, UK, 2000; pp. 133–142. [Google Scholar]



| Model Reviewed | Model Type | Model Highlights |
|---|---|---|
| Nakawo and Young [67] | Surface Ablation | Classic model accounts for debris temperature, thickness, and thermal conductivity. |
| Nicholson and Benn [15] | Surface Ablation | Improved debris thermal conductivity calculation affected by pore-space and moisture. |
| Reid and Brock [16] | Surface Ablation | Supports the calculation of thermal conductivity and internal temperature profiles within debris. |
| Fyffe et al. [68] | Surface Ablation | Distributed model highlights differential ablation under heterogeneous surface cover conditions. |
| Rounce et al. [41] | Surface Ablation | Sensitivity tests on debris thermal conductivity, albedo, and surface roughness. |
| Zhang et al. [30] | Surface Ablation | Estimation of debris surface thermal resistance using remote sensing approaches. |
| Fujita et al. [8] | Surface Ablation | Accounts for ablation due to precipitation, more accurate estimates of wind speed and albedo. |
| Minora et al. [82] | Surface Ablation | Sensitivity tests on ablation-air temperature relationship. |
| Collier et al. [84] | Glacier–Atmosphere | Accounts for glacier–atmosphere interactive coupling. |
| Anderson [52] | Debris Transport | Diffusive debris flux from medial moraines. |
| Anderson and Anderson [10] | Debris Transport | 2D supraglacial and englacial debris advection governed by ice dynamics. |
| Wirbel et al. [56] | Debris Transport | 3D englacial debris advection and diffusion governed by ice dynamics. |
| Sakai et al. [25] | Supraglacial Pond | One of the first energy and mass balance model for supraglacial ponds. |
| Miles et al. [38] | Supraglacial Pond | Improved version of Sakai et al. [25]’s model, more accurate computation of energy and mass fluxes. |
| Steiner et al. [35] | Ice-cliff | Energy balance on ice-cliffs affected by complex terrain. |
| Buri et al. [36] | Ice-cliff | 3D ice-cliff evolution model accounting for water-caused ablation at cliff base. |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Huo, D.; Chi, Z.; Ma, A. Modeling Surface Processes on Debris-Covered Glaciers: A Review with Reference to the High Mountain Asia. Water 2021, 13, 101. https://doi.org/10.3390/w13010101
Huo D, Chi Z, Ma A. Modeling Surface Processes on Debris-Covered Glaciers: A Review with Reference to the High Mountain Asia. Water. 2021; 13(1):101. https://doi.org/10.3390/w13010101
Chicago/Turabian StyleHuo, Da, Zhaohui Chi, and Andong Ma. 2021. "Modeling Surface Processes on Debris-Covered Glaciers: A Review with Reference to the High Mountain Asia" Water 13, no. 1: 101. https://doi.org/10.3390/w13010101
APA StyleHuo, D., Chi, Z., & Ma, A. (2021). Modeling Surface Processes on Debris-Covered Glaciers: A Review with Reference to the High Mountain Asia. Water, 13(1), 101. https://doi.org/10.3390/w13010101