Optimization of Irrigation and Leaching Depths Considering the Cost of Water Using WASH_1D/2D Models
Abstract
:1. Introduction
2. Methods
2.1. Virtual Net Income
2.2. Numerical Model of Root Water Uptake and Crop Growth
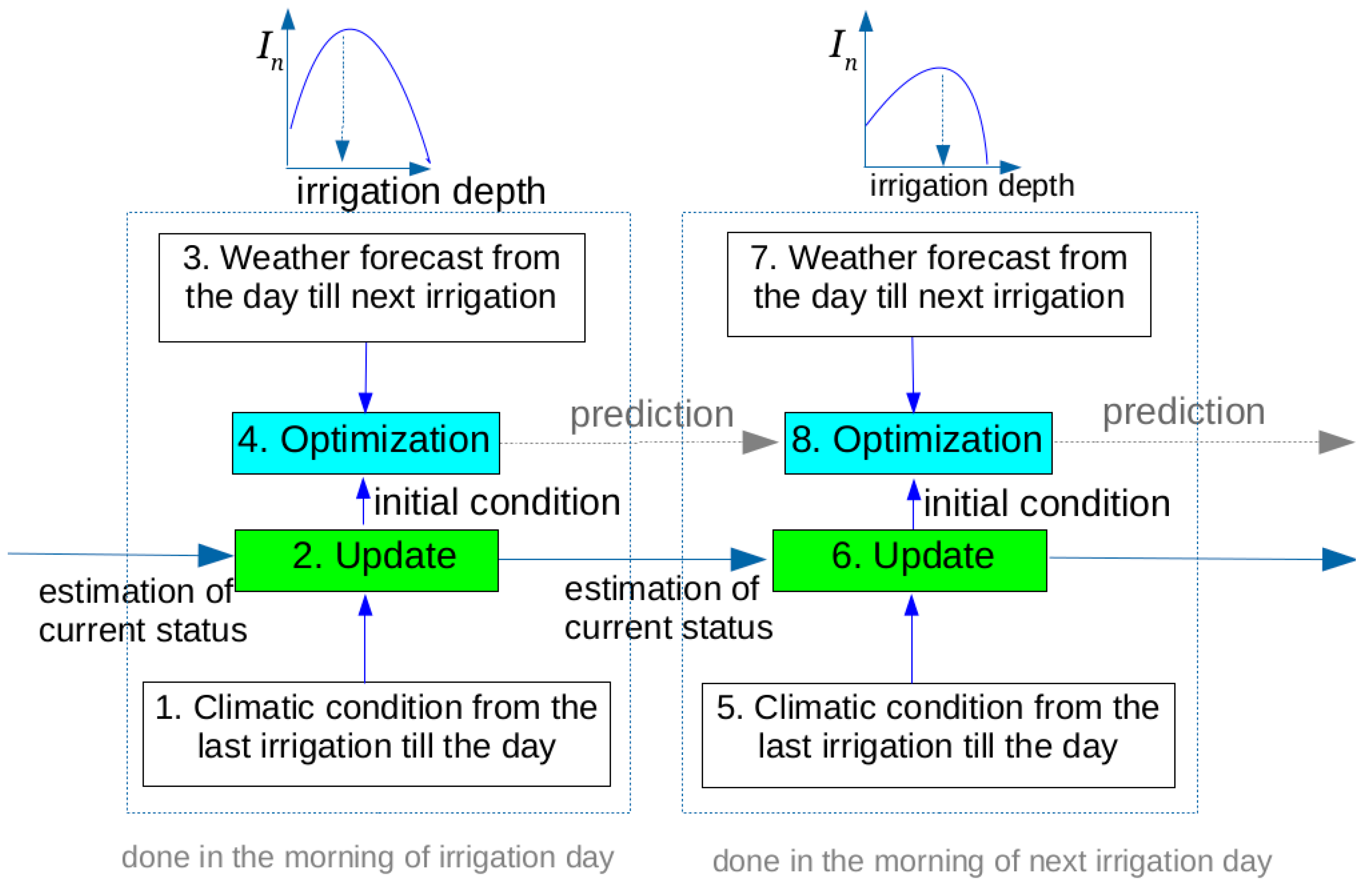
2.3. Optimized Irrigation
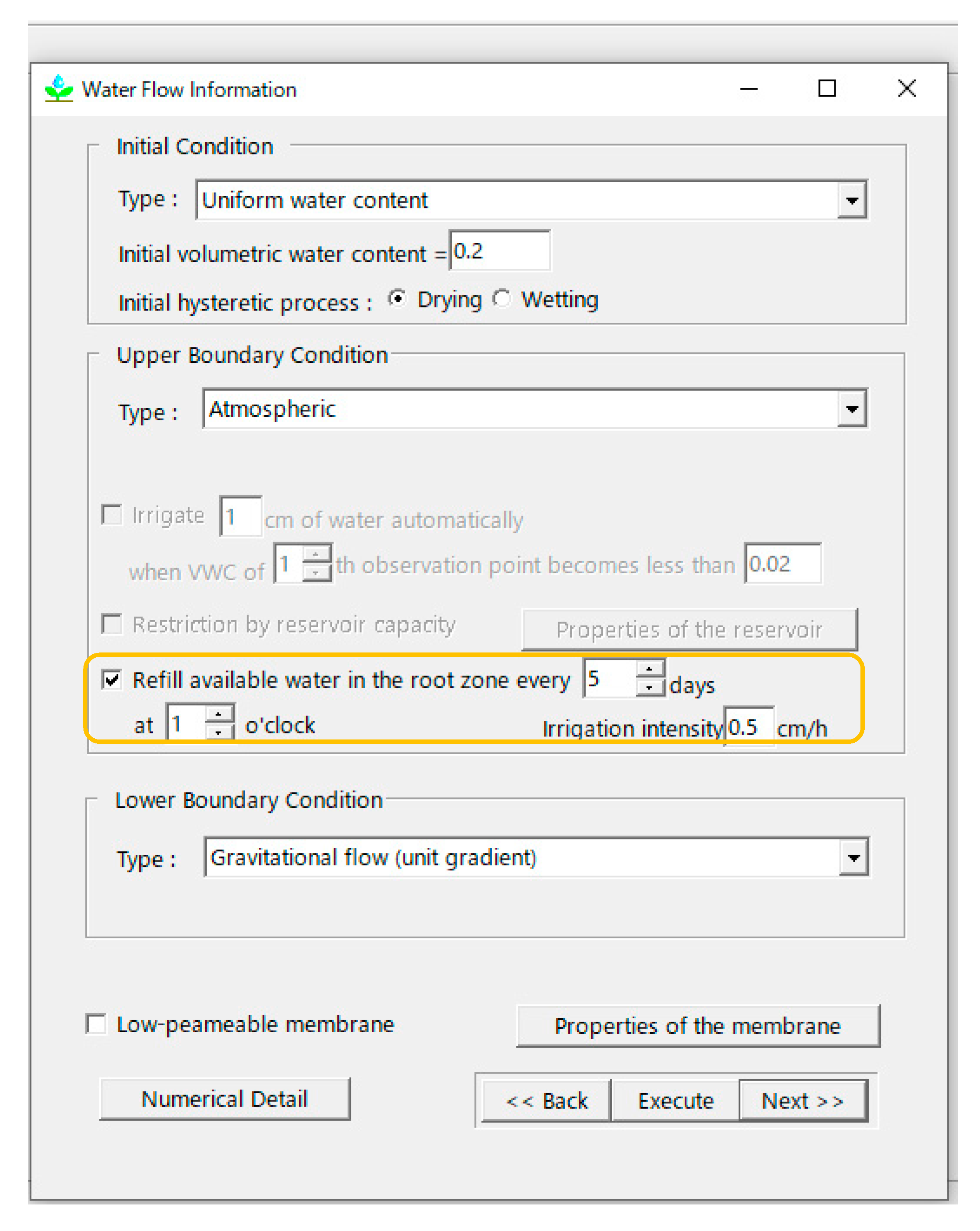
2.4. Refilling Irrigation
2.5. Optimized Leaching
2.6. Conditions for the Numerical Experiment
- S1.
- Refilling irrigation using freshwater (0.17 g/L of NaCl) at every 5 days.
- S2.
- Refilling irrigation in the root zone is refilled using saline water (1.7 g/L of NaCl) at every 5 days.
- S3.
- Optimized irrigation on a weekly basis using fresh water.
- S4.
- Optimized irrigation on a weekly basis using saline water.
- S5.
- Same as S2 except for optimized leaching is carried out at the middle of the growing season.
3. Results and Discussion
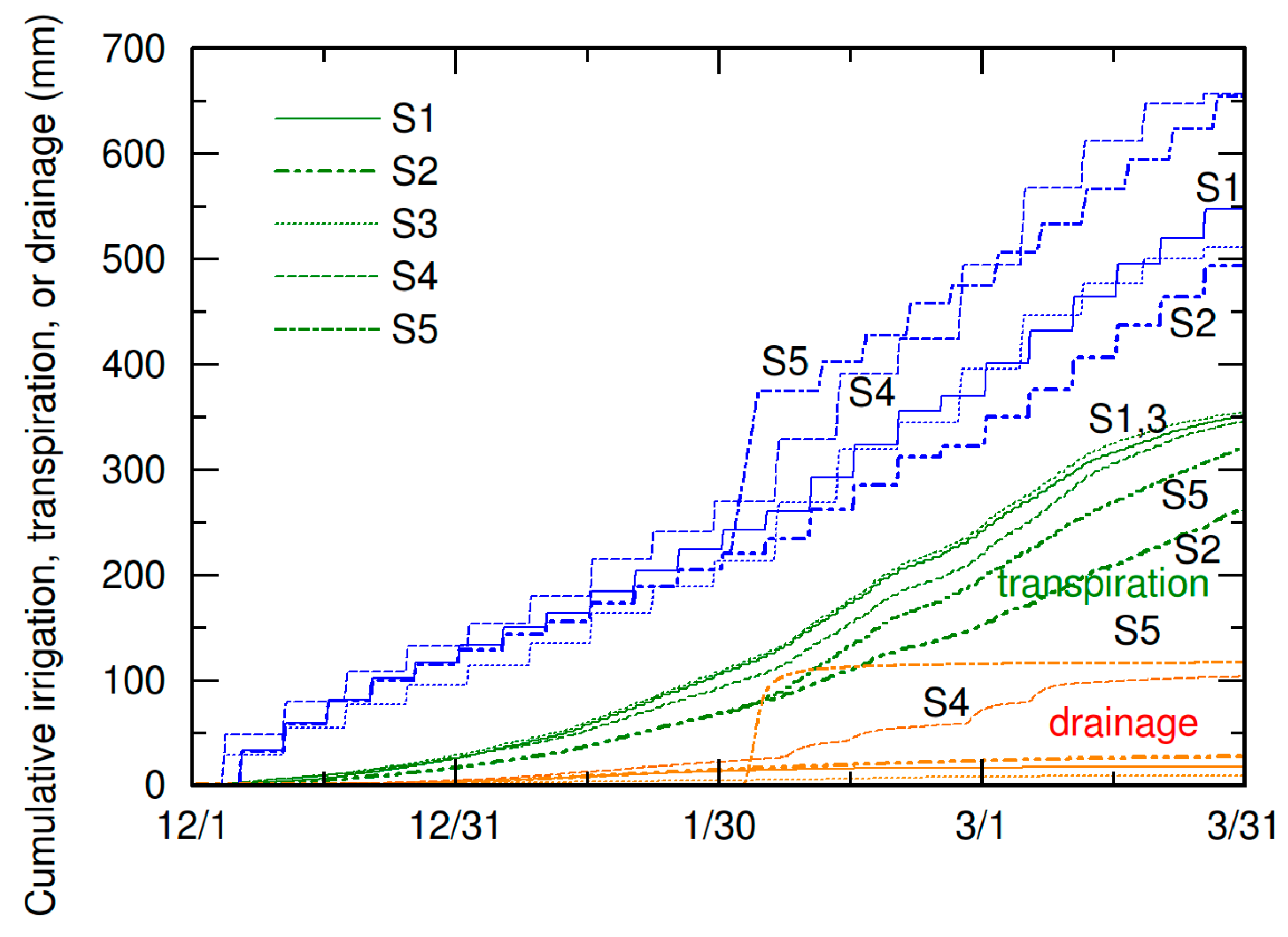
3.1. Cumulative Irrigation, Transpiration, and Drainage
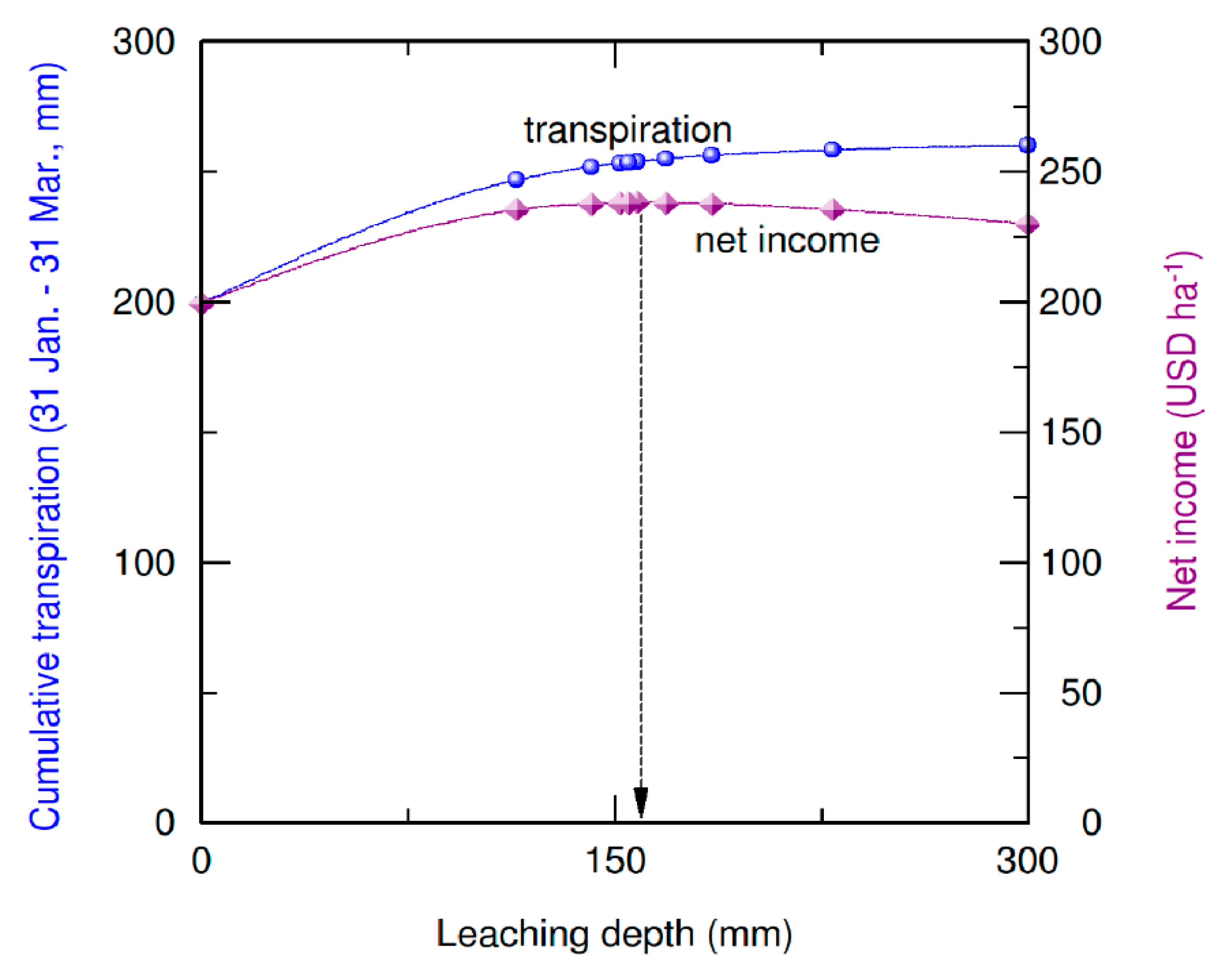
3.2. Disadvantages and Advantages of the Proposed Leaching Scheme
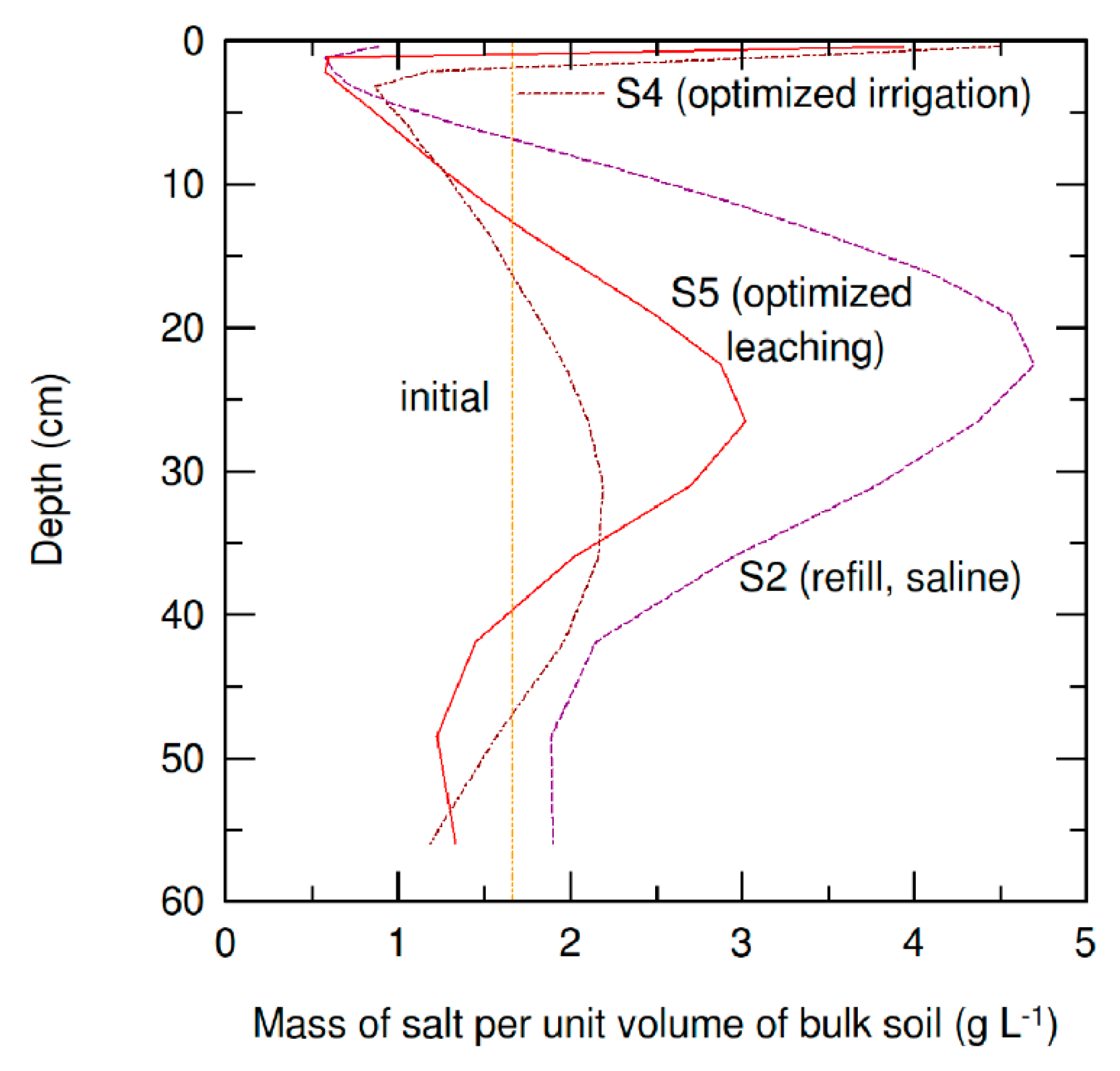
3.3. Soil Salt Content
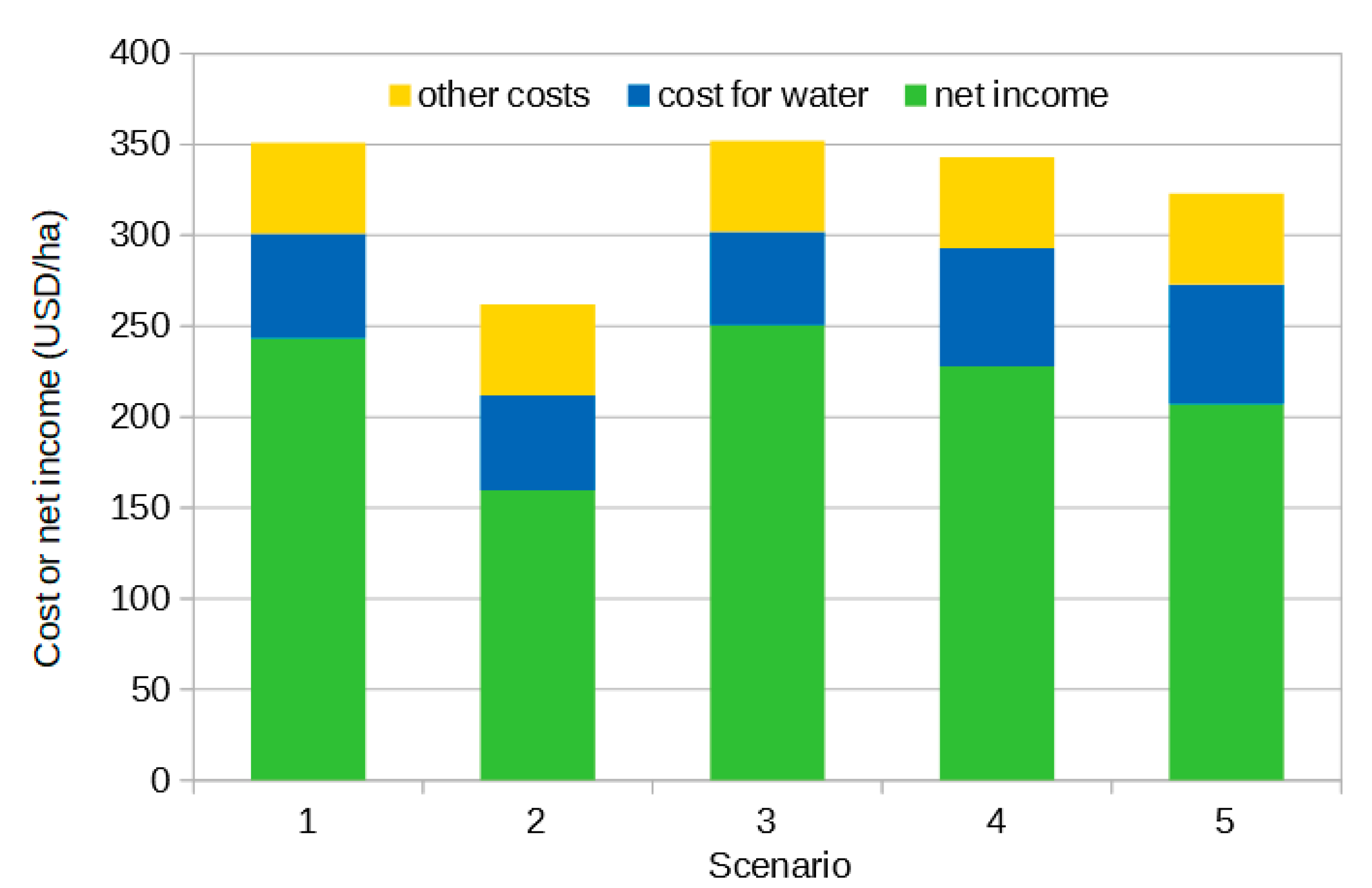
3.4. Net Income
4. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Shani, U.; Dudley, L.M. Field studies of crop response to drought and salt stress. Soil Sci. Soc. Am. J. 2001, 65, 1522–1528. [Google Scholar] [CrossRef]
- Mohammadi, M.; Ghahraman, B.; Davary, K.; Ansari, H.; Shahidi, A.; Bannayan, M. Nested Validation of Aquacrop Model for Simulation of Winter Wheat Grain Yield, Soil Moisture and Salinity Profiles under Simultaneous Salinity and Water Stress. Irrig. Drain. 2016, 65, 112–128. [Google Scholar] [CrossRef]
- Phogat, V.; Pitt, T.; Cox, J.; Šimůnek, J.; Skewes, M.A. Soil water and salinity dynamics under sprinkler irrigated almond exposed to a varied salinity stress at different growth stages. Agric. Water Manag. 2018, 201, 70–82. [Google Scholar] [CrossRef] [Green Version]
- FAO. Facts and Figures about Irrigation Areas, Irrigated Crops, Environment. Food and Agriculture Organization of the United Nations (FAO). 2014. Available online: http://www.fao.org/nr/water/aquastat/didyouknow/print3.stm (accessed on 28 March 2020).
- Qadir, M.; Quillérou, E.; Nangia, V.; Murtaza, G.; Singh, M.; Thomas, R.; Drechsel, P.; Noble, A. Economics of salt-induced land degradation and restoration. Nat. Resour. Forum 2014, 38, 282–295. [Google Scholar] [CrossRef]
- Phogat, V.; Mallants, D.; Cox, J.; Šimůnek, J.; Oliver, D.; Awad, J. Management of soil salinity associated with irrigation of protected crops. Agric. Water Manag. 2020, 227, 105845. [Google Scholar] [CrossRef]
- Ayers, R.S.; Westcot, D.W. Water Quality for Agriculture; FAO Irrigation and Drainage Paper No. 29, Revision 1; FAO: Rome, Italy, 1985. [Google Scholar]
- Letey, J.; Feng, G. Dynamic versus steady-state approaches to evaluate irrigation management of saline waters. Agric. Water Manag. 2007, 91, 1–10. [Google Scholar] [CrossRef]
- Corwin, D.L.; Rhoades, J.D.; Simunek, J. Leaching requirement for soil salinity control: Steady-state versus transient models. Agric. Water Manag. 2007, 90, 165–180. [Google Scholar] [CrossRef]
- Hanson, B.R.; Hopmans, J.W.; Simunek, J. Leaching with Subsurface Drip Irrigation under Saline, Shallow Groundwater Conditions. Vadose Zone J. 2008, 7, 810–818. [Google Scholar] [CrossRef] [Green Version]
- Ramos, T.B.; Šimunek, J.; Gonçalves, M.C.; Martins, J.; Prazeres, A.; Castanheira, N.L.; Pereira, L.S. Field evaluation of a multicomponent solute transport model in soils irrigated with saline waters. J. Hydrol. 2011, 407, 129–144. [Google Scholar] [CrossRef]
- Isidoro, D.; Grattan, S.R. Predicting soil salinity in response to different irrigation practices, soil types and rainfall scenarios. Irrig. Sci. 2010, 29, 197–211. [Google Scholar] [CrossRef] [Green Version]
- Qureshi, A.S.; Ahmad, W.; Ahmad, A.-F.A. Optimum groundwater table depth and irrigation schedules for controlling soil salinity in central Iraq. Irrig. Drain. 2013, 62, 414–424. [Google Scholar] [CrossRef]
- Van Dam, J.C.; Huygen, J.; Wesseling, J.G.; Feddes, R.A.; Kabat, P.; Van Walsum, P.E.V. Simulation of Transport Processes in the Soil–Water–Air–Plant Environment. In SWAP Users Manual; DLO-Winand String Center: Wageningen, The Netherlands, 1997. [Google Scholar]
- Corwin, D.L.; Grattan, S.R. Are existing irrigation salinity leaching requirement guidelines overly conservative or obsolete? J. Irrig. Drain. Eng. 2018, 144, 02518001. [Google Scholar] [CrossRef] [Green Version]
- Fujimaki, H.; Tokumoto, I.; Saito, T.; Inoue, M.; Shibata, M.; Okazaki, T.; Nagaz, K.; El Mokh, F. Determination of irrigation depths using a numerical model and quantitative weather forecast and comparison with an experiment. In Practical Applications of Agricultural System Models to Optimize the Use of Limited Water; Ahuja, L.R., Ma, L., Lascano, R.J., Eds.; ACSESS: Madison, WI, USA, 2014; Volume 5, pp. 209–235. [Google Scholar] [CrossRef] [Green Version]
- Abd El Baki, H.M.; Fujimaki, H.; Tokumoto, I.; Saito, T. Determination of irrigation depths using a numerical model of crop growth and quantitative weather forecast and evaluation of its effect through a field experiment for potato. J. Jpn. Soc. Soil Phys. 2017, 136, 15–24. [Google Scholar]
- El Baki, H.M.A.; Fujimaki, H.; Tokumoto, I.; Saito, T. A new scheme to optimize irrigation depth using a numerical model of crop response to irrigation and quantitative weather forecasts. Comput. Electron. Agric. 2018, 150, 387–393. [Google Scholar] [CrossRef]
- El Baki, H.M.A.; Raoof, M.; Fujimaki, H. Determining Irrigation Depths for Soybean Using a Simulation Model of Water Flow and Plant Growth and Weather Forecasts. Agronomy 2020, 10, 369. [Google Scholar] [CrossRef] [Green Version]
- Allen, R.; Pereira, L.; Raes, D.; Smith, M. Crop Evapotranspiration: Guidelines for Computing Crop Water Requirements; FAO Irrigation and Drainage Paper No. 56; FAO: Rome, Italy, 1998. [Google Scholar]
- Press, W.H.; Flannery, B.P.; Teukolsky, S.A.; Vetterling, W.T. Numerical Recipes in Pascal--The Art of Scientific Computing. Math. Comput. 1991, 56, 396. [Google Scholar] [CrossRef]
- Fujimaki, H.; Yanagawa, A. Application of Evaporation Method Using Two Tensiometers for Determining Unsaturated Hydraulic Conductivity beyond Tensiometric Range. Eurasian Soil Sci. 2019, 52, 405–413. [Google Scholar] [CrossRef]
- Mirás-Avalos, J.M.; Asensio-Rubio, J.S.; Ramírez-Cuesta, J.; Maestre-Valero, J.F.; Intrigliolo, D.S. Irrigation-Advisor—A Decision Support System for Irrigation of Vegetable Crops. Water 2019, 11, 2245. [Google Scholar] [CrossRef] [Green Version]
- Wang, Z.; Liao, R.; Lin, H.; Jiang, G.; He, X.; Wu, W.; Zhangzhong, L. Effects of drip irrigation levels on soil water, salinity and wheat growth in North China. Int. J. Agric. Biol. Eng. 2018, 11, 146–156. [Google Scholar] [CrossRef]
- He, K.; Yang, Y.; Yang, Y.; Chen, S.; Hu, Q.; Liu, X.; Gao, F. HYDRUS Simulation of Sustainable Brackish Water Irrigation in a Winter Wheat-Summer Maize Rotation System in the North China Plain. Water 2017, 9, 536. [Google Scholar] [CrossRef] [Green Version]
- Peragón, J.M.; Pérez-Latorre, F.J.; Delgado, A.; Tóth, T. Best management irrigation practices assessed by a GIS-based decision tool for reducing salinization risks in olive orchards. Agric. Water Manag. 2018, 202, 33–41. [Google Scholar] [CrossRef]
- Domínguez, A.; Tarjuelo, J.; De Juan, J.; Mata, E.L.; Breidy, J.; Karam, F. Deficit irrigation under water stress and salinity conditions: The MOPECO-Salt Model. Agric. Water Manag. 2011, 98, 1451–1461. [Google Scholar] [CrossRef]
- Raes, D.; Steduto, P.; Hsiao, T.C.; Fereres, E. Aquacrop Reference Manual; FAO: Rome, Italy, 2009; Available online: http://www.fao.org/nr/water/aquacrop.html (accessed on 8 August 2020).

| Parameter | Unit | Value | Equation |
|---|---|---|---|
| λ | cm | 0.36 | Equation (11) Equation (12) |
| as | - | 0.26 | |
| bs | - | 16 | |
| cs | - | 3 | |
| ds | - | 0.27 | |
| ah | W cm−2 s−1 | 0.0078 | Equation (13) |
| bh | W cm−2 s−1 | 0.0052 | |
| ch | - | 18,041 | |
| dh | W cm−2 s−1 | 0.0011 | |
| eh | - | 5.96 | |
| αmax | - | 0.27 | Equation (14) |
| αmin | - | 0.18 | |
| al | - | 12 | |
| bl | - | 5.2 |
| Parameter | Unit | Value | Equation |
|---|---|---|---|
| akc | - | 1.19 | Equation (5) |
| bkc | - | −0.32 | |
| ckc | - | 0.1 | |
| dkc | - | 0.00000112 | |
| ekc | - | 3.9 | |
| brt | - | 1 | Equation (7) |
| zr0 | cm | 2 | |
| adrt | cm | 55 | Equation (8) |
| bdrt | - | −0.05 | |
| cdrt | cm | 5 | |
| Ψ50 | cm | −4000 | Equation (9) |
| Ψo50 | cm | −8000 | |
| P | - | 3 |
| Parameter | Description | Unit | Value |
|---|---|---|---|
| Pc | Price of crop | USD kg−1 | 0.05 |
| ε | Transpiration productivity | - | 0.002 |
| Pw | Price of water | USD m−3 | 0.01 |
| Cot | Other costs | USD ha−1 | 50 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Fujimaki, H.; Abd El Baki, H.M.; Mohamad Mahdavi, S.; Ebrahimian, H. Optimization of Irrigation and Leaching Depths Considering the Cost of Water Using WASH_1D/2D Models. Water 2020, 12, 2549. https://doi.org/10.3390/w12092549
Fujimaki H, Abd El Baki HM, Mohamad Mahdavi S, Ebrahimian H. Optimization of Irrigation and Leaching Depths Considering the Cost of Water Using WASH_1D/2D Models. Water. 2020; 12(9):2549. https://doi.org/10.3390/w12092549
Chicago/Turabian StyleFujimaki, Haruyuki, Hassan M. Abd El Baki, Seyed Mohamad Mahdavi, and Hamed Ebrahimian. 2020. "Optimization of Irrigation and Leaching Depths Considering the Cost of Water Using WASH_1D/2D Models" Water 12, no. 9: 2549. https://doi.org/10.3390/w12092549






