Effect of Fluvial Discharges and Remote Non-Tidal Residuals on Compound Flood Forecasting in San Francisco Bay
Abstract
1. Introduction
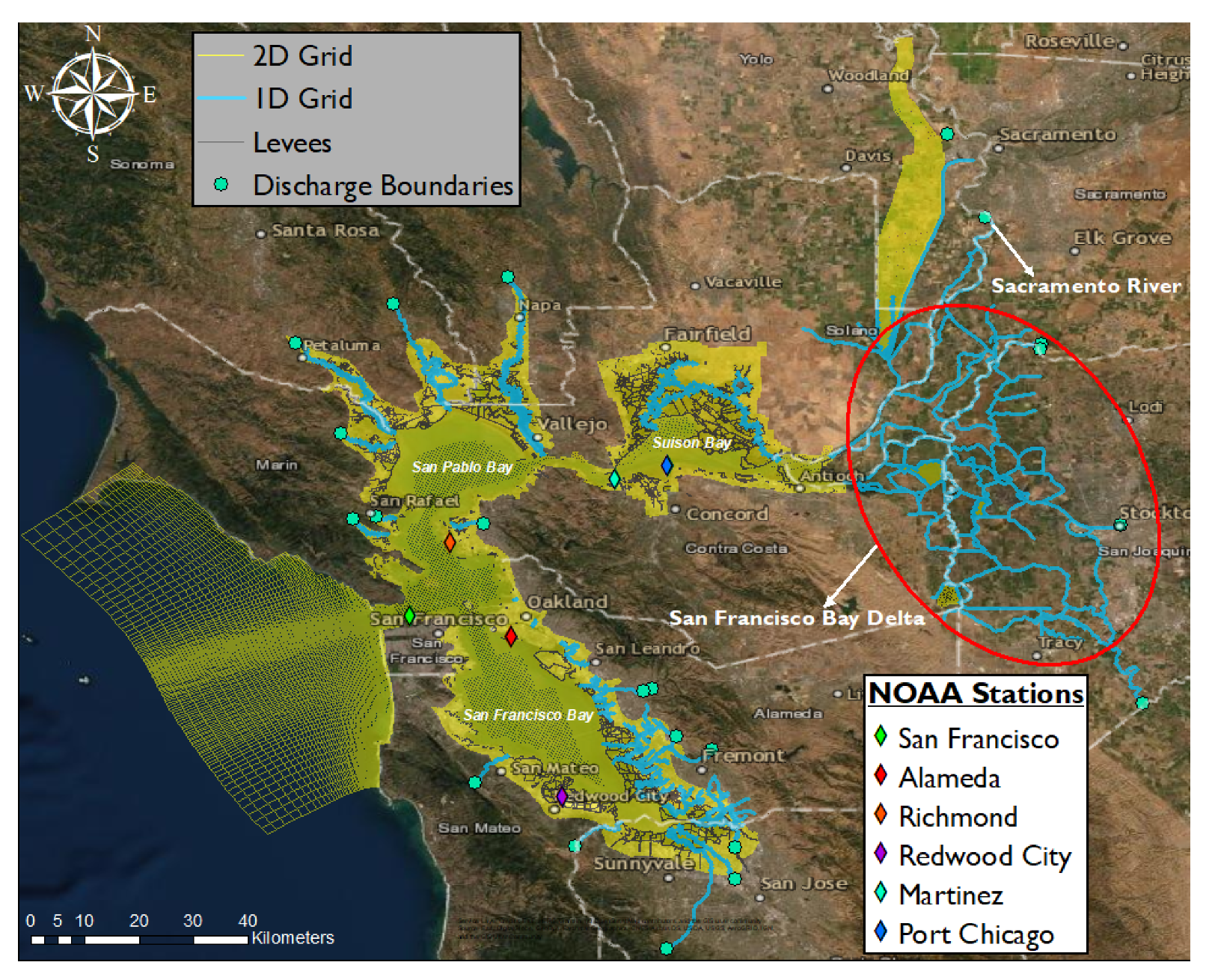
2. Study Area and Model Description
2.1. Offshore Boundaries
2.1.1. Tides
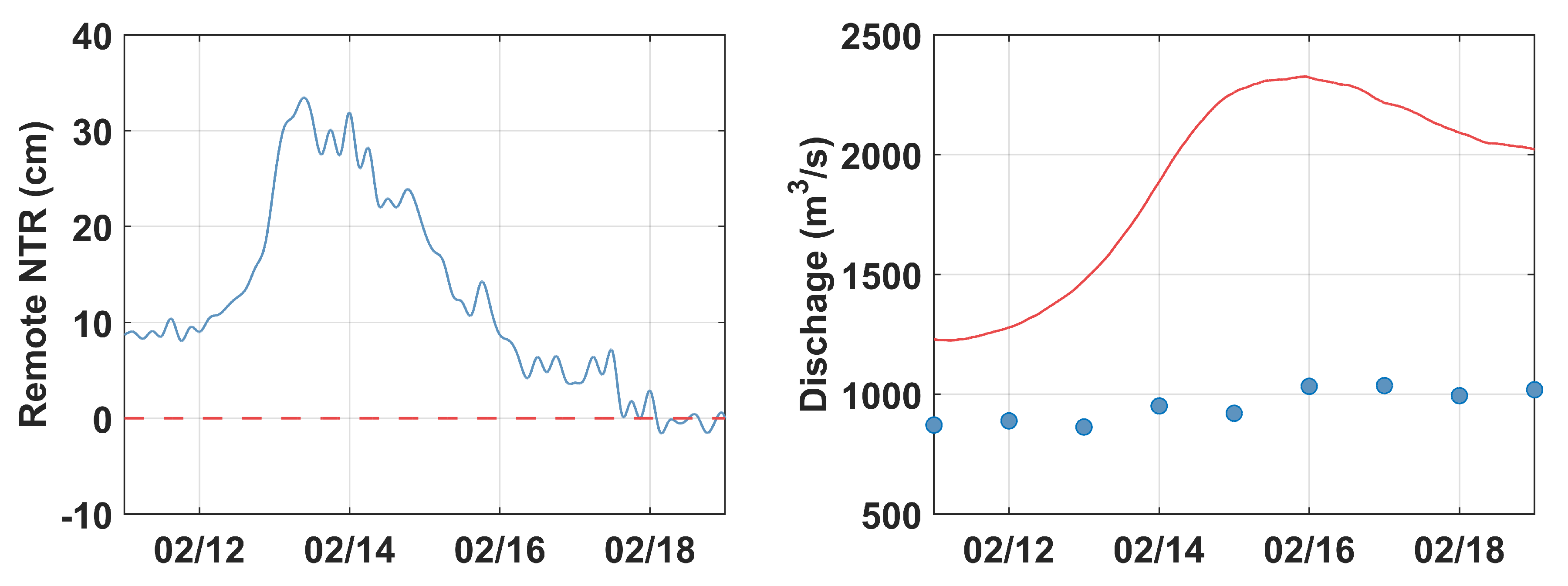
2.1.2. Remote Non-Tidal Residuals
2.2. Discharge Boundaries
2.3. Atmospheric Inputs
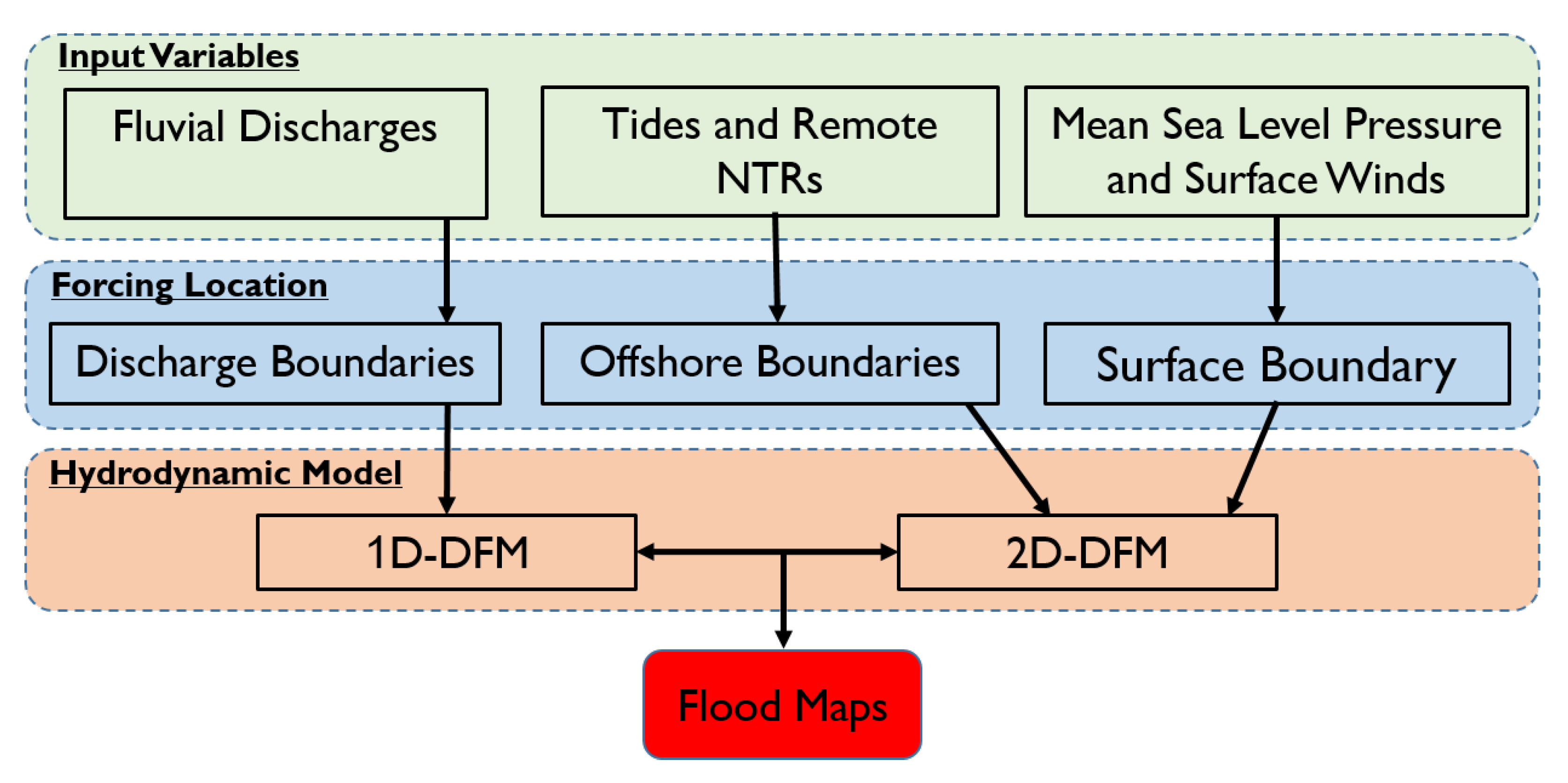
2.4. Integrated System
3. February 2019 Storm
3.1. Model Setup for Storm Experiments
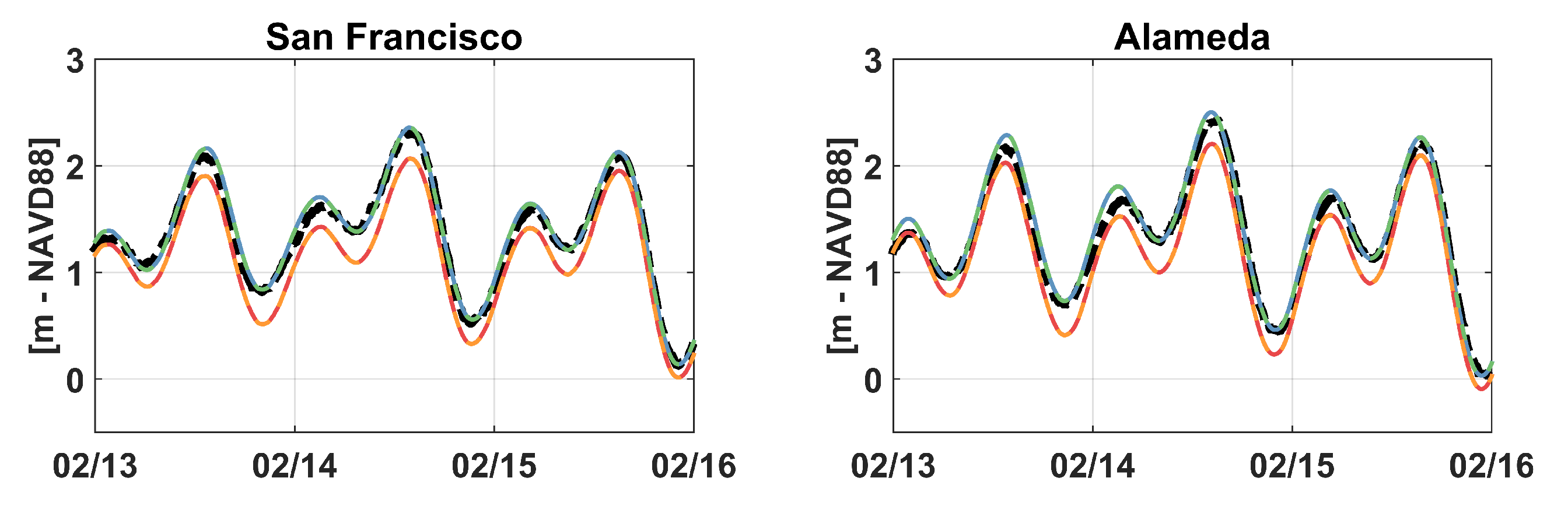
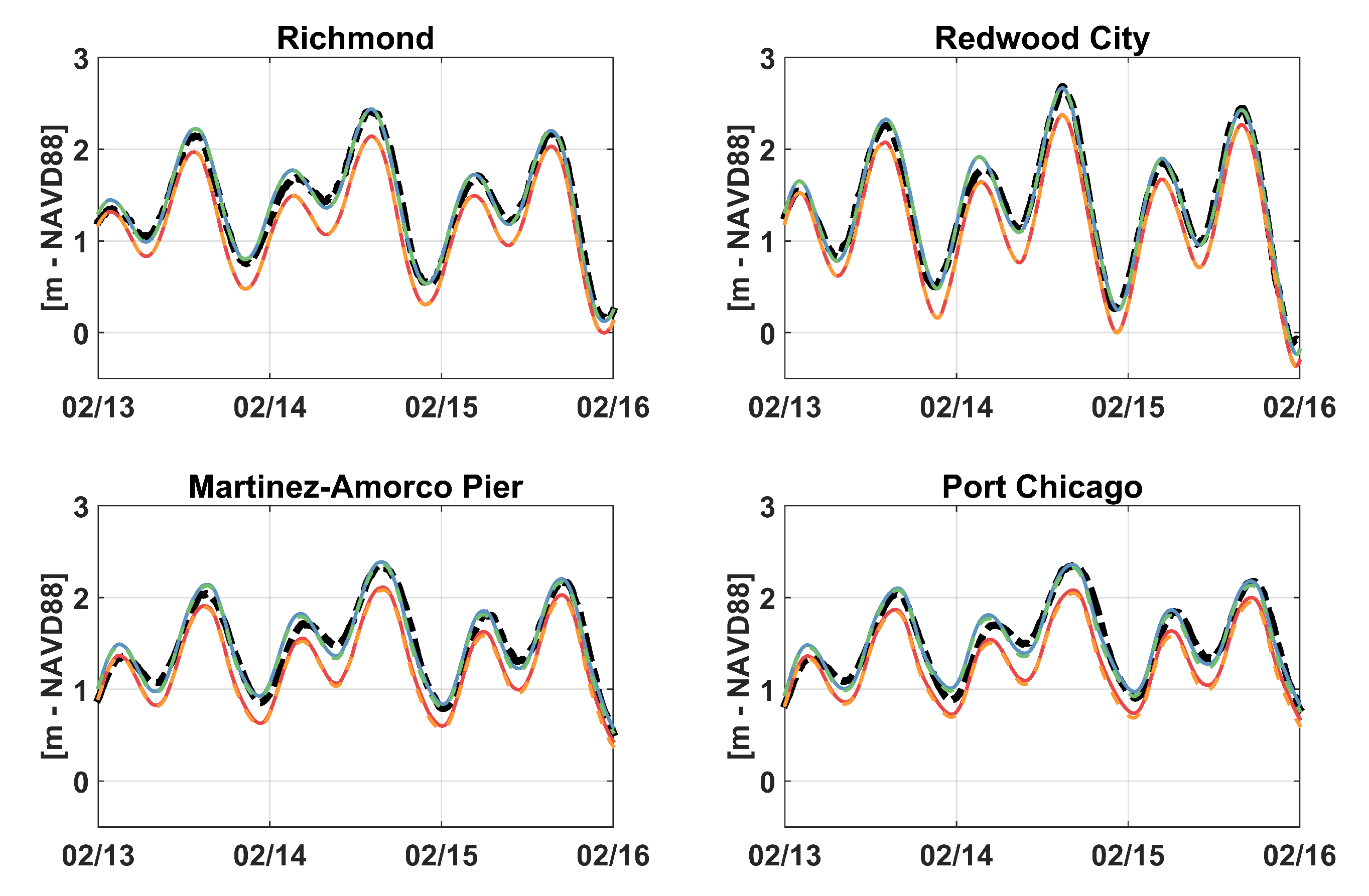
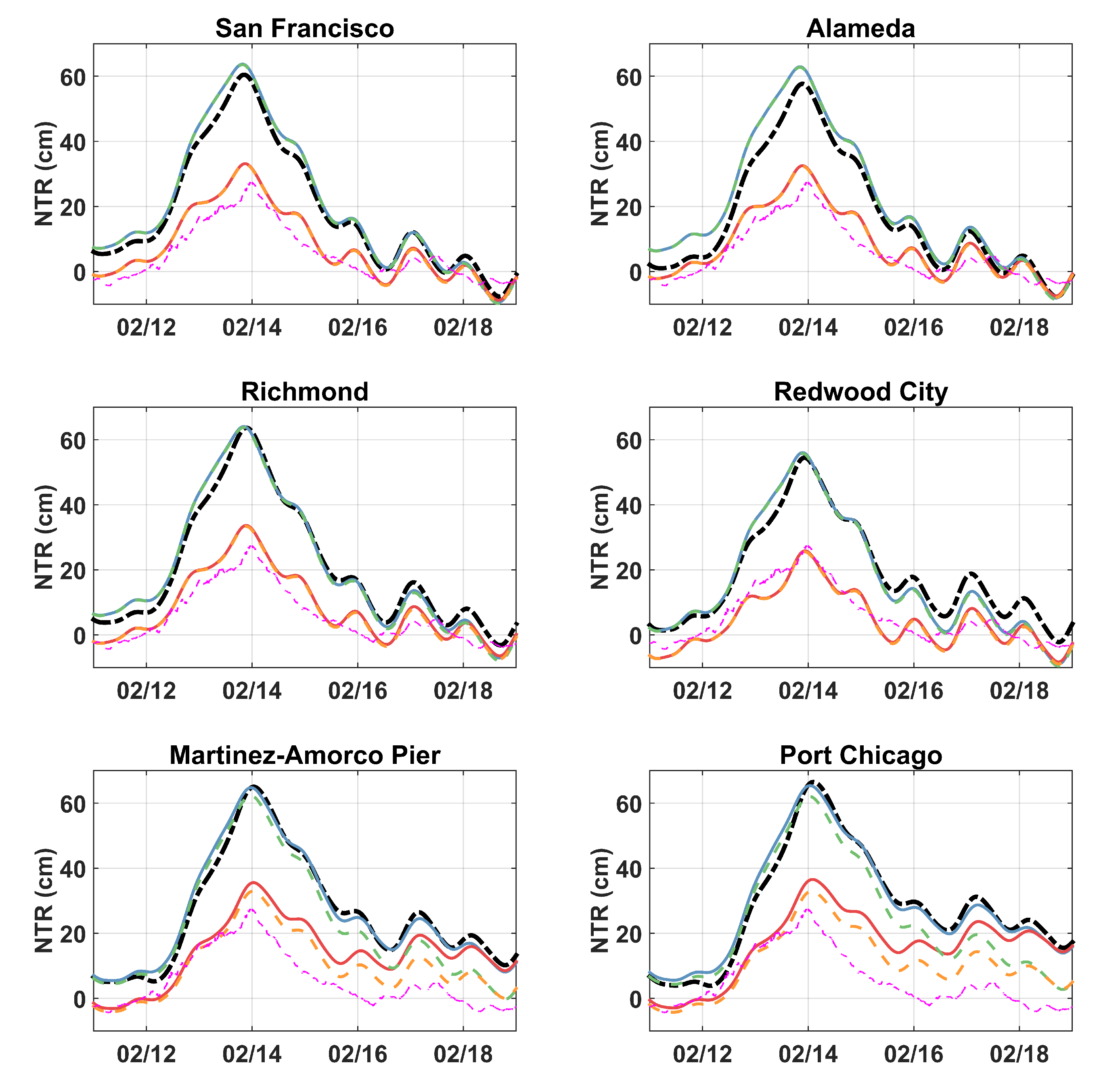
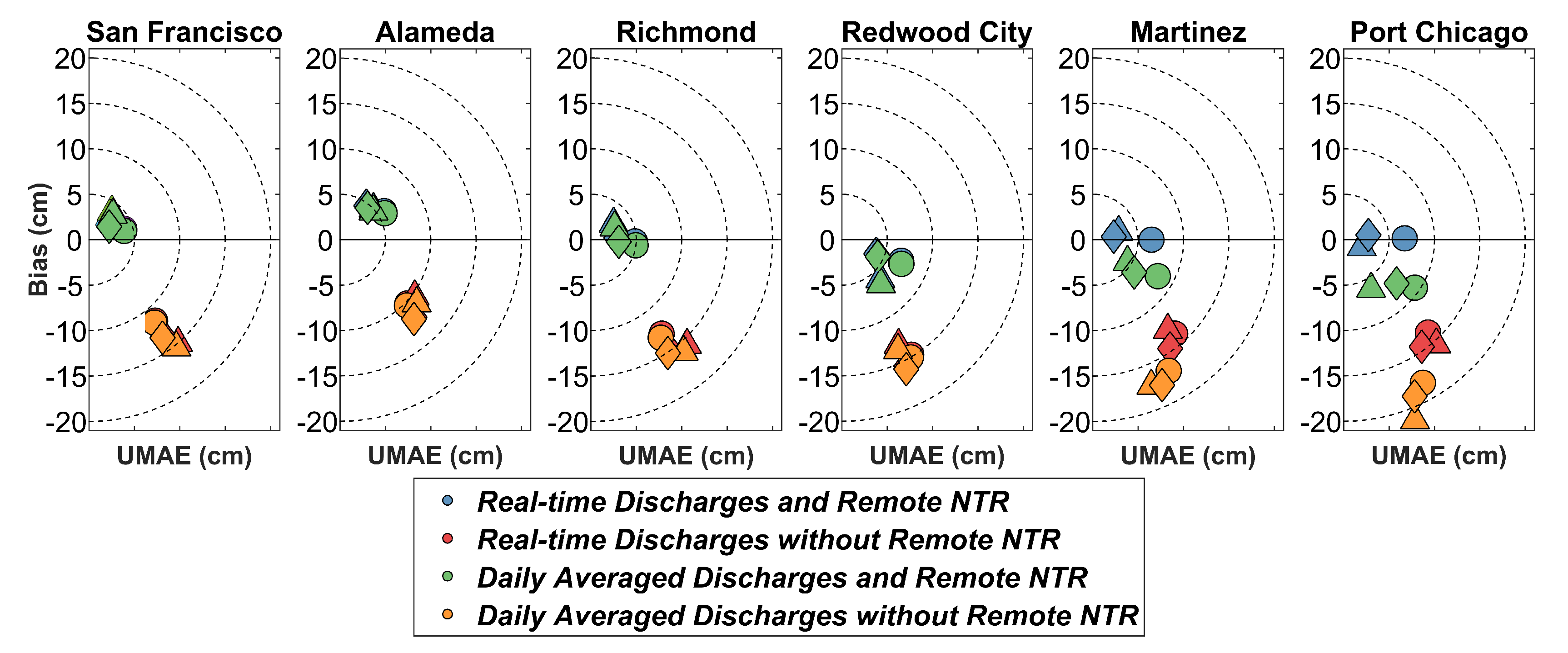
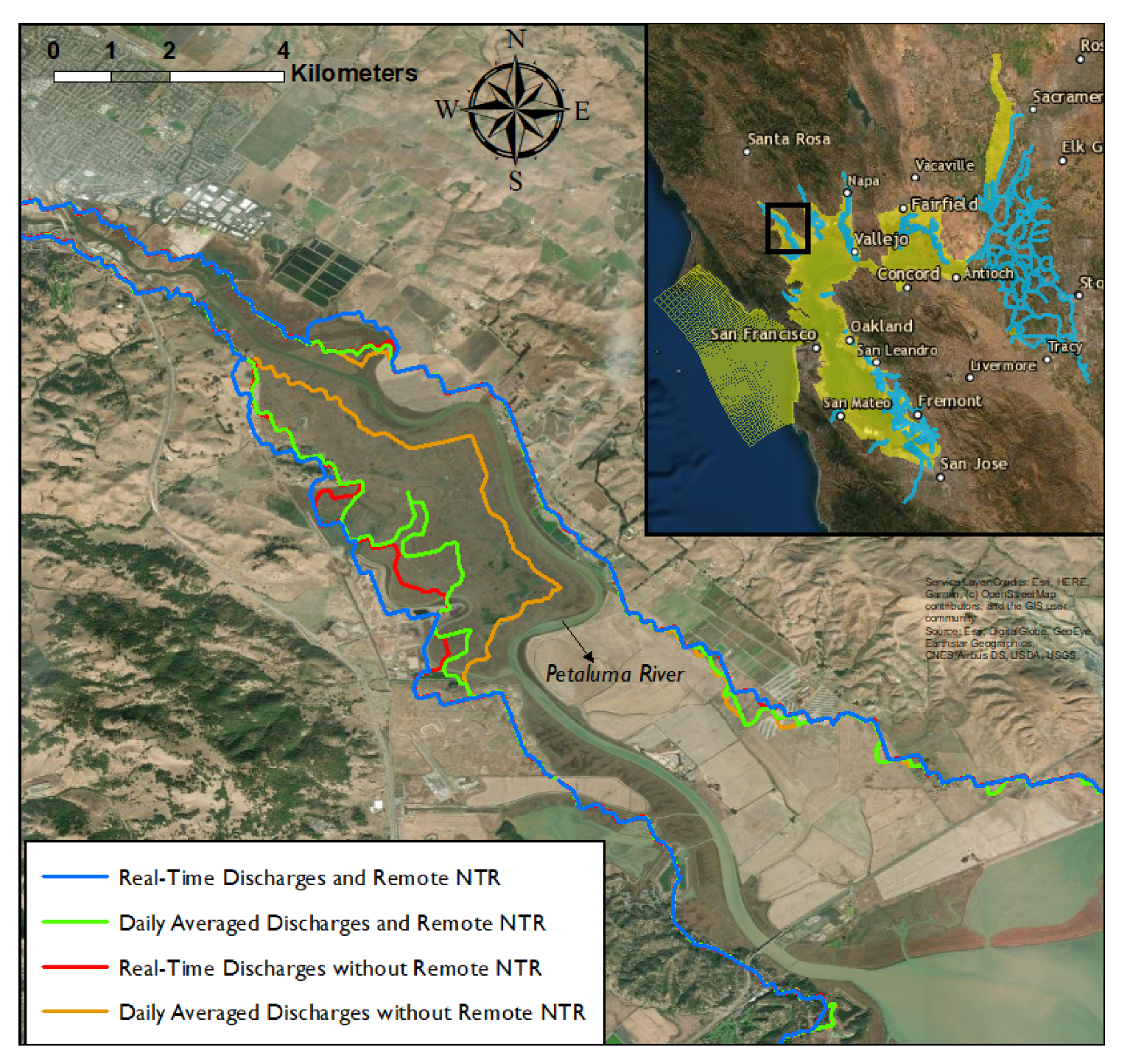
3.2. Results
4. Discussion
5. Summary and Future Developments
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Abbreviations
| AQPI | Advanced Quantitative Precipitation Information |
| CoSMoS | Coastal Storm Modeling System |
| DFM | Delft3D Flexible Mesh |
| HRRR | High-Resolution Rapid Refresh |
| HYCOM | HYbrid Coordinate Ocean Model |
| IBE | Inverse Barometric Effect |
| NOAA | National Oceanic and Atmospheric Administration |
| NTR | Non-Tidal Residual |
| NWM | National Water Model |
| MAE | Mean Averaged Error |
| SLR | Sea-Level Rise |
| USGS | United States Geological Survey |
| WCOFS | West Coast Operational Forecast System |
References
- Vitousek, S.; Barnard, P.L.; Fletcher, C.H.; Frazer, N.; Erikson, L.; Storlazzi, C.D. Doubling of coastal flooding frequency within decades due to sea-level rise. Sci. Rep. 2017, 7, 1–9. [Google Scholar] [CrossRef] [PubMed]
- Taherkhani, M.; Vitousek, S.; Barnard, P.L.; Frazer, N.; Anderson, T.R.; Fletcher, C.H. Sea-level rise exponentially increases coastal flood frequency. Sci. Rep. 2020, 10, 1–17. [Google Scholar] [CrossRef] [PubMed]
- Church, J.A.; White, N.J. Sea-level rise from the late 19th to the early 21st century. Surv. Geophys. 2011, 32, 585–602. [Google Scholar] [CrossRef]
- Hay, C.C.; Morrow, E.; Kopp, R.E.; Mitrovica, J.X. Probabilistic reanalysis of twentieth-century sea-level rise. Nature 2015, 517, 481–484. [Google Scholar] [CrossRef]
- Leuliette, E.W.; Willis, J.K. Balancing the sea level budget. Oceanography 2011, 24, 122–129. [Google Scholar] [CrossRef]
- Vermeer, M.; Rahmstorf, S. Global sea level linked to global temperature. Proc. Natl. Acad. Sci. USA 2009, 106, 21527–21532. [Google Scholar] [CrossRef]
- Sweet, W.V.; Park, J. From the extreme to the mean: Acceleration and tipping points of coastal inundation from sea level rise. Earth’s Future 2014, 2, 579–600. [Google Scholar] [CrossRef]
- Wuebbles, D.J.; Fahey, D.W.; Hibbard, K.A. Climate Science Special Report; Fourth National Climate Assessment; US Global Change Research Program: Washington, DC, USA, 2017; Volume I. [Google Scholar]
- Zscheischler, J.; Westra, S.; Van Den Hurk, B.J.; Seneviratne, S.I.; Ward, P.J.; Pitman, A.; AghaKouchak, A.; Bresch, D.N.; Leonard, M.; Wahl, T. Future climate risk from compound events. Nat. Clim. Chang. 2018, 8, 469–477. [Google Scholar] [CrossRef]
- Wahl, T.; Jain, S.; Bender, J.; Meyers, S.D.; Luther, M.E. Increasing risk of compound flooding from storm surge and rainfall for major US cities. Nat. Clim. Chang. 2015, 5, 1093–1097. [Google Scholar] [CrossRef]
- Santiago-Collazo, F.L.; Bilskie, M.V.; Hagen, S.C. A comprehensive review of compound inundation models in low-gradient coastal watersheds. Environ. Model. Softw. 2019, 119, 166–181. [Google Scholar] [CrossRef]
- Chassignet, E.P.; Hurlburt, H.E.; Smedstad, O.M.; Halliwell, G.R.; Hogan, P.J.; Wallcraft, A.J.; Baraille, R.; Bleck, R. The HYCOM (hybrid coordinate ocean model) data assimilative system. J. Mar. Syst. 2007, 65, 60–83. [Google Scholar] [CrossRef]
- Kurapov, A.; Pelland, N.; Rudnick, D. Seasonal and interannual variability in along-slope oceanic properties off the US West Coast: Inferences from a high-resolution regional model. J. Geophys. Res. Oceans 2017, 122, 5237–5259. [Google Scholar] [CrossRef]
- Durski, S.M.; Kurapov, A.L.; Allen, J.S.; Kosro, P.M.; Egbert, G.D.; Shearman, R.K.; Barth, J.A. Coastal ocean variability in the US Pacific Northwest region: Seasonal patterns, winter circulation, and the influence of the 2009-2010 El Niño. Ocean Dyn. 2015, 65, 1643–1663. [Google Scholar] [CrossRef]
- Gochis, D.; Barlage, M.; Dugger, A.; FitzGerald, K.; Karsten, L.; McAllister, M.; McCreight, J.; Mills, J.; RafieeiNasab, A.; Read, L.; et al. The WRF-Hydro modeling system technical description (Version 5.0). NCAR Tech. Note 2018, 107. Available online: https://ral.ucar.edu/sites/default/files/public/WRFHydroV5TechnicalDescription.pdf (accessed on 2 September 2020).
- Kim, J.; Han, H.; Johnson, L.E.; Lim, S.; Cifelli, R. Hybrid machine learning framework for hydrological assessment. J. Hydrol. 2019, 577, 123913. [Google Scholar] [CrossRef]
- Kim, J.; Read, L.; Johnson, L.E.; Gochis, D.; Cifelli, R.; Han, H. An experiment on reservoir representation schemes to improve hydrologic prediction: Coupling the National Water Model with the HEC-ResSim. Hydrol. Sci. J. 2020, 1–15. [Google Scholar] [CrossRef]
- Han, H.; Kim, J.; Chandrasekar, V.; Choi, J.; Lim, S. Modeling streamflow enhanced by precipitation from atmospheric river using the NOAA national water model: A case study of the Russian river basin for February 2004. Atmosphere 2019, 10, 466. [Google Scholar] [CrossRef]
- Salas, F.R.; Somos-Valenzuela, M.A.; Dugger, A.; Maidment, D.R.; Gochis, D.J.; David, C.H.; Yu, W.; Ding, D.; Clark, E.P.; Noman, N. Towards real-time continental scale streamflow simulation in continuous and discrete space. JAWRA J. Am. Water Resour. Assoc. 2018, 54, 7–27. [Google Scholar] [CrossRef]
- Viterbo, F.; Mahoney, K.; Read, L.; Salas, F.; Bates, B.; Elliott, J.; Cosgrove, B.; Dugger, A.; Gochis, D.; Cifelli, R. A Multiscale, Hydrometeorological forecast evaluation of National Water Model forecasts of the May 2018 Ellicott City, Maryland, Flood. J. Hydrometeorol. 2020, 21, 475–499. [Google Scholar] [CrossRef]
- Benjamin, S.G.; Weygandt, S.S.; Brown, J.M.; Hu, M.; Alexander, C.R.; Smirnova, T.G.; Olson, J.B.; James, E.P.; Dowell, D.C.; Grell, G.A.; et al. A North American hourly assimilation and model forecast cycle: The Rapid Refresh. Mon. Weather. Rev. 2016, 144, 1669–1694. [Google Scholar] [CrossRef]
- English, J.M.; Turner, D.D.; Marquis, M.; James, E.; Alcott, T.; Moninger, W.R.; Bytheway, J.L.; Wang, H. AQPI: RAP/HRRR Model Forecasts of Atmospheric River Events over the San Francisco Bay Area. AGUFM 2019, 2019, H33P–2238. [Google Scholar]
- Zhu, Y.; Newell, R.E. Atmospheric rivers and bombs. Geophys. Res. Lett. 1994, 21, 1999–2002. [Google Scholar] [CrossRef]
- Corringham, T.W.; Ralph, F.M.; Gershunov, A.; Cayan, D.R.; Talbot, C.A. Atmospheric rivers drive flood damages in the western United States. Sci. Adv. 2019, 5, eaax4631. [Google Scholar] [CrossRef]
- Herdman, L.; Erikson, L.; Barnard, P. Storm surge propagation and flooding in small tidal rivers during events of mixed coastal and fluvial influence. J. Mar. Sci. Eng. 2018, 6, 158. [Google Scholar] [CrossRef]
- NOAA Office for Coastal Management, NOAA Sea Level Rise Viewer. 2020. Available online: https://coast.noaa.gov/slr/ (accessed on 15 June 2020).
- Barnard, P.L.; Schoellhamer, D.H.; Jaffe, B.E.; McKee, L.J. Sediment transport in the San Francisco Bay coastal system: An overview. Mar. Geol. 2013, 345, 3–17. [Google Scholar] [CrossRef]
- Cifelli, R.; Pratt, G.; Johnson, L. AQPI: Collaborative science to improve precipitation, streamflow, and coastal flooding forecasts in the San Francisco Bay Area. AGUFM 2018, 2018, PA41D–1343. [Google Scholar]
- Chen, H.; Cifelli, R.; Chandrasekar, V. Integrating multi-scale data for seamless QPE in the AQPI system. AGUFM 2019, 2019, A53L–3065. [Google Scholar]
- Godt, J.W.; Arnal, C.H.; Baum, R.L.; Brien, D.; Coe, J.A.; De Mouthe, J.; Ellis, J.W.G.; Graymer, R.W.; Harp, E.L.; Hillhouse, J.W.; et al. Maps Showing Locations of Damaging Landslides Caused by El Nino Rainstorms, Winter Season 1997–1998, San Francisco Bay Region, California. USGS. 1999. Available online: http://pubs.usgs.gov/mf/1999/mf-2325 (accessed on 15 June 2020).
- Sallenger, A.H., Jr.; Krabill, W.; Brock, J.; Swift, R.; Manizade, S.; Stockdon, H. Sea-cliff erosion as a function of beach changes and extreme wave runup during the 1997–1998 El Niño. Mar. Geol. 2002, 187, 279–297. [Google Scholar] [CrossRef]
- Winter Storm Dumps 230 mm of Rain in California. 2019. Available online: http://floodlist.com/america/usa/winter-storm-california-february-2019 (accessed on 15 June 2020).
- Achete, F.; van der Wegen, M.; Roelvink, D.; Jaffe, B. A 2-D process-based model for suspended sediment dynamics: A first step towards ecological modeling. Hydrol. Earth Syst. Sci. 2015, 19, 2837. [Google Scholar] [CrossRef]
- Achete, F.; Van der Wegen, M.; Roelvink, J.A.; Jaffe, B. How can climate change and engineered water conveyance affect sediment dynamics in the San Francisco Bay-Delta system? Clim. Chang. 2017, 142, 375–389. [Google Scholar] [CrossRef]
- Martyr-Koller, R.; Kernkamp, H.; van Dam, A.; van der Wegen, M.; Lucas, L.; Knowles, N.; Jaffe, B.; Fregoso, T. Application of an unstructured 3D finite volume numerical model to flows and salinity dynamics in the San Francisco Bay-Delta. Estuarine Coast. Shelf Sci. 2017, 192, 86–107. [Google Scholar] [CrossRef]
- Vroom, J.; van der Wegen, M.; Martyr-Koller, R.; Lucas, L. What determines water temperature dynamics in the San Francisco Bay-Delta System? Water Resour. Res. 2017, 53, 9901–9921. [Google Scholar] [CrossRef]
- Buffington, K.; Thorne, K. LEAN-Corrected San Francisco Bay Digital Elevation Model; Geological Survey Data Release: Santa Cruz, CA, USA, 2019. [Google Scholar] [CrossRef]
- Doehring, C.; Beagle, J.; Lowe, J.; Grossinger, R.; Salomon, M.; Kauhanen, P.; Nakata, S.; Askevold, R.; Bezalel, S. San Francisco Bay Shore Inventory: Mapping for Sea Level Rise Planning; Technical Report; San Francisco Estuary Institute: Richmond, CA, USA, 2016. [Google Scholar]
- Barnard, P.L.; Hanes, D.M.; Lescinski, J.; Elias, E. Monitoring and modeling nearshore dredge disposal for indirect beach nourishment, Ocean Beach, San Francisco. Coast. Eng. 2006, 5, 4192–4204. [Google Scholar]
- Nederhoff, K.; Tehranirad, B.; Herman, L.; Erikson, L.; Barnard, P.; van der Wegen, M.; Saleh, R. What drives high water levels in the San Francisco Bay? Coast. Eng. 2020, in press. [Google Scholar]
- Stacey, M.T.; Fram, J.P.; Chow, F.K. Role of tidally periodic density stratification in the creation of estuarine subtidal circulation. J. Geophys. Res. Oceans 2008, 113, C8. [Google Scholar] [CrossRef]
- Egbert, G.D.; Erofeeva, S.Y. Efficient inverse modeling of barotropic ocean tides. J. Atmos. Oceans Technol. 2002, 19, 183–204. [Google Scholar] [CrossRef]
- Cosgrove, B.; Gochis, D.; Graziano, T.M.; Clark, E.P.; Flowers, T. The evolution of NOAA’s National Water Model: An overview of version 2.1 and future operational plans. AGUFM 2019, 2019, H51D-01. [Google Scholar]
- Dhondia, J.F.; Riley, D.; Herr, H.; Lee, P.; Tubbs, C.; Bickel, J.; Maestre, A.; Brown, J.; Flowers, T. Near real-Time hydrologic operational evaluation of National Water Model (NWM) streamflow short-and medium-range forecasts. AGUFM 2019, 2019, H43I-2140. [Google Scholar]
- Khanal, S.; Ridder, N.; de Vries, H.; Terink, W.; van den Hurk, B. Storm surge and extreme river discharge: A compound event analysis using ensemble impact modeling. Front. Earth Sci. 2019, 7, 224. [Google Scholar] [CrossRef]
- Couasnon, A.; Eilander, D.; Muis, S.; Veldkamp, T.; Haigh, I.; Wahl, T.; Winsemius, H.; Ward, P. Measuring compound flood potential from river discharge and storm surge extremes at the global scale. Nat. Hazards Earth Syst. Sci. Discuss. 2020, 20, 489–504. [Google Scholar] [CrossRef]
- Dusterhoff, S.; Beagle, J.; Collins, J.; Doehring, C. Initial Protocol to Identify and Delineate the Head of Tide Zone; San Francisco Estuary Institute: Richmond, CA, USA, 2014. [Google Scholar]
- Gary, Q. Highway 37 Needs A Lasting Flood Fix. Could This Deal Be It? 2020. Available online: https://www.northbaybusinessjournal.com/article/article/oft-flooded-highway-37-in-northern-california-eyed-for-locally-directed-lon/?artslide=0> (accessed on 19 June 2020).
- Dettinger, M. Fifty-two years of “pineapple-express” storms across the West Coast of North America. In US Geological Survey; PIER Project Rep. CEC-500-2005-004; Scripps Institution of Oceanography for the California Energy Commission: La Jolla, CA, USA, 2004; Volume 20. [Google Scholar]
- Dettinger, M.D. Atmospheric rivers as drought busters on the US West Coast. J. Hydrometeorol. 2013, 14, 1721–1732. [Google Scholar] [CrossRef]
- Lamjiri, M.A.; Ralph, F.M.; Dettinger, M.D. Recent Changes in United States Extreme 3-Day Precipitation Using the R-CAT Scale. J. Hydrometeorol. 2020, 21, 1207–1221. [Google Scholar] [CrossRef]
- Hatchett, B.J.; Cao, Q.; Dawson, P.B.; Ellis, C.J.; Hecht, C.W.; Kawzenuk, B.; Lancaster, J.T.; Osborne, T.; Wilson, A.M.; Anderson, M.L.; et al. Observations of an extreme atmospheric river storm with a diverse sensor network. Earth Space Sci. 2020, e2020EA001129. [Google Scholar] [CrossRef]
- USGS. Available online: https://waterservices.usgs.gov/rest/Statistics-Service.html#Daily (accessed on 15 June 2020).
- Engstrom, W.N. The California storm of January 1862. Q. Res. 1996, 46, 141–148. [Google Scholar] [CrossRef]
- Porter, K.; Sue Wing, I. Overview of the ARkStorm Scenario; Open File Report: 2010-1312; USGS: Reston, VA, USA, 2011. [Google Scholar]
- Bromirski, P.D.; Flick, R.E. Storm surge in the San Francisco Bay/Delta and nearby coastal locations. Shore Beach 2008, 76, 29–37. [Google Scholar]
- Wang, R.Q.; Herdman, L.M.; Erikson, L.; Barnard, P.; Hummel, M.; Stacey, M.T. Interactions of estuarine shoreline infrastructure with multiscale sea level variability. J. Geophys. Res. Oceans 2017, 122, 9962–9979. [Google Scholar] [CrossRef]
- Holleman, R.C.; Stacey, M.T. Coupling of sea level rise, tidal amplification, and inundation. J. Phys. Oceanogr. 2014, 44, 1439–1455. [Google Scholar] [CrossRef]
| Data | Forecast Model | Forecast Time |
|---|---|---|
| Wind and Atmospheric Pressure | HRRR | 18 h |
| Fluvial Discharges | NWM | 18 h |
| Remote Non-Tidal Residuals | HYCOM | 180 h |
| Coastal Model | Hydro-CoSMoS | 16 h |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Tehranirad, B.; Herdman, L.; Nederhoff, K.; Erikson, L.; Cifelli, R.; Pratt, G.; Leon, M.; Barnard, P. Effect of Fluvial Discharges and Remote Non-Tidal Residuals on Compound Flood Forecasting in San Francisco Bay. Water 2020, 12, 2481. https://doi.org/10.3390/w12092481
Tehranirad B, Herdman L, Nederhoff K, Erikson L, Cifelli R, Pratt G, Leon M, Barnard P. Effect of Fluvial Discharges and Remote Non-Tidal Residuals on Compound Flood Forecasting in San Francisco Bay. Water. 2020; 12(9):2481. https://doi.org/10.3390/w12092481
Chicago/Turabian StyleTehranirad, Babak, Liv Herdman, Kees Nederhoff, Li Erikson, Robert Cifelli, Greg Pratt, Michael Leon, and Patrick Barnard. 2020. "Effect of Fluvial Discharges and Remote Non-Tidal Residuals on Compound Flood Forecasting in San Francisco Bay" Water 12, no. 9: 2481. https://doi.org/10.3390/w12092481
APA StyleTehranirad, B., Herdman, L., Nederhoff, K., Erikson, L., Cifelli, R., Pratt, G., Leon, M., & Barnard, P. (2020). Effect of Fluvial Discharges and Remote Non-Tidal Residuals on Compound Flood Forecasting in San Francisco Bay. Water, 12(9), 2481. https://doi.org/10.3390/w12092481







