Physical Modelling of Arctic Coastlines—Progress and Limitations
Abstract
1. Introduction
2. Current State of the Art
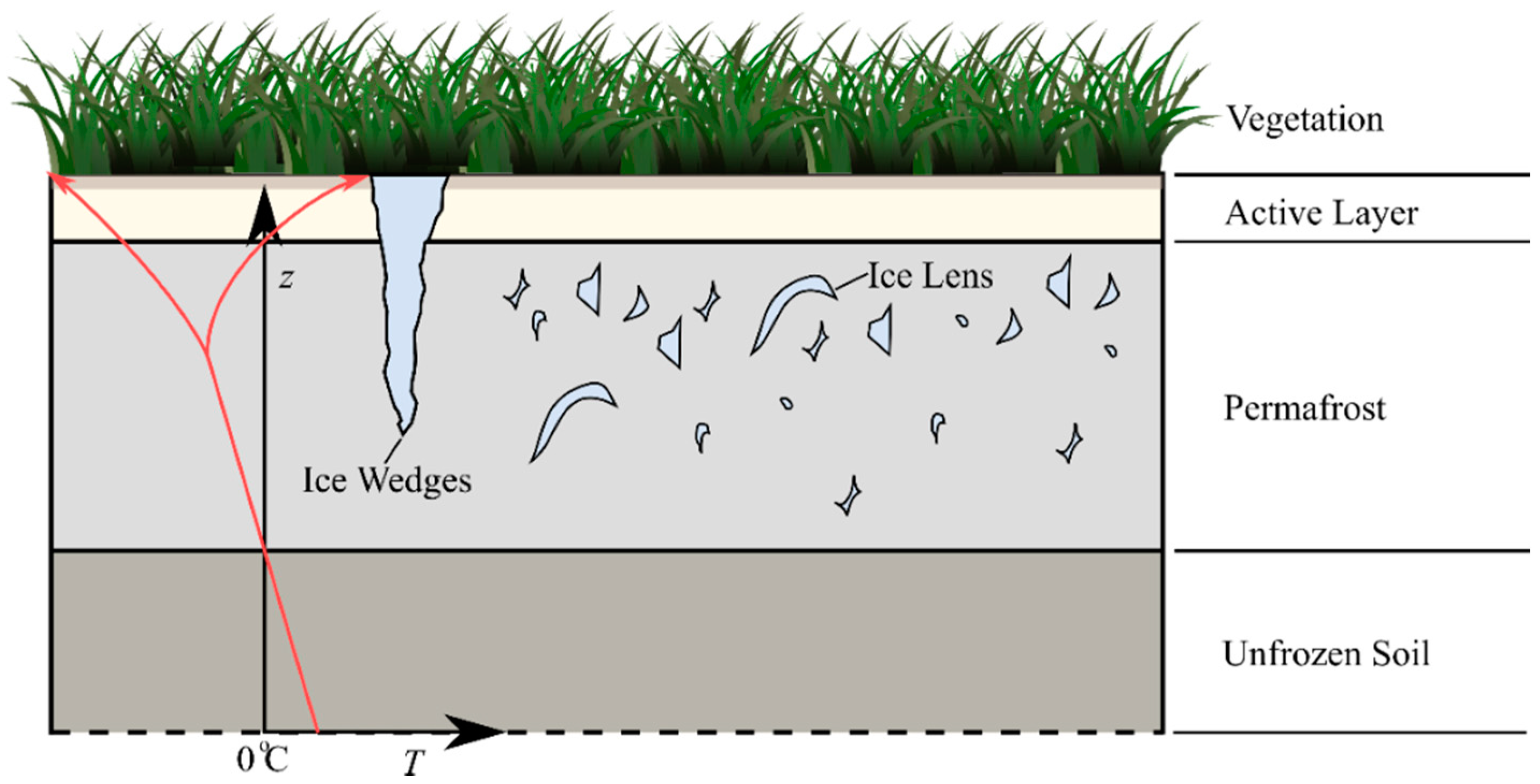
2.1. Permafrost
2.2. Recession of Coastlines
2.2.1. General Approach to Erosion in Coastal Engineering
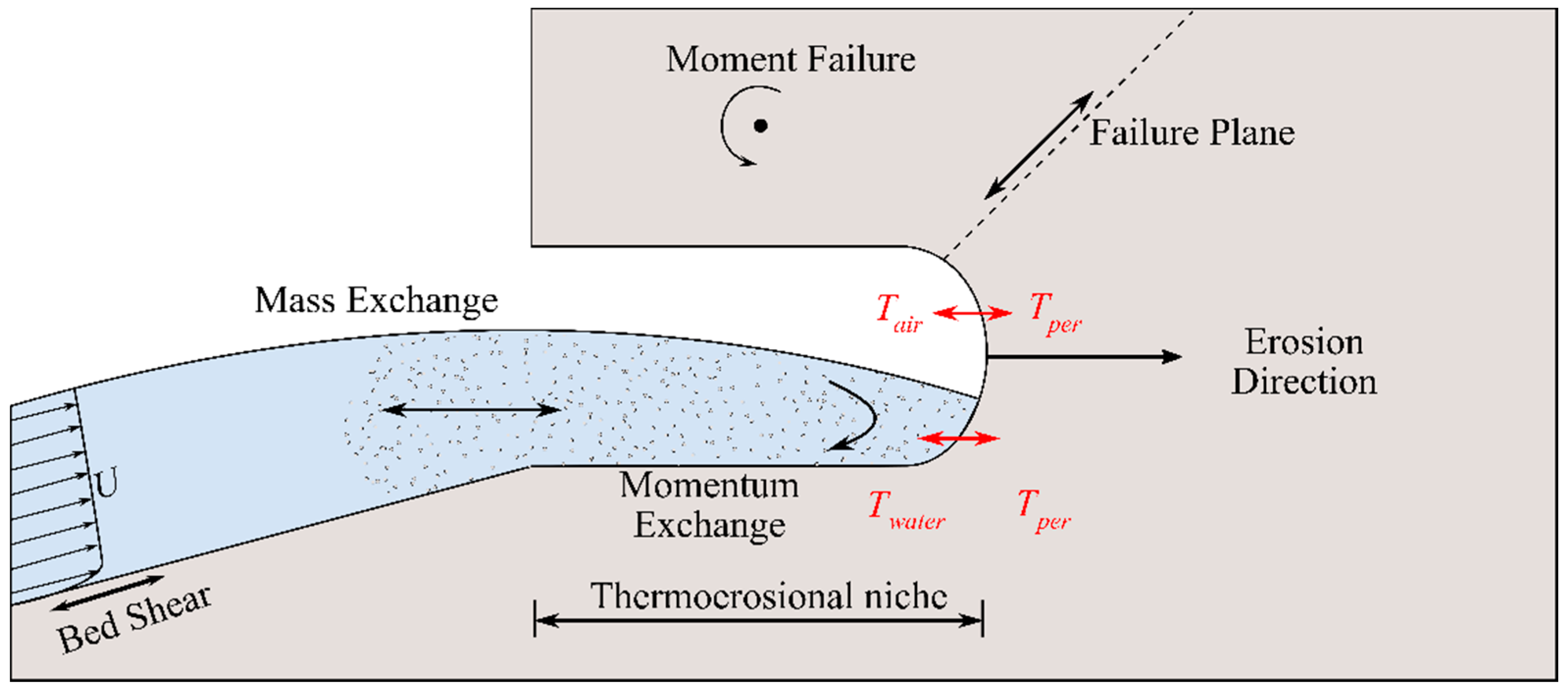
2.2.2. Thermomechanical Erosion
2.3. Analytical and Observational Models
2.4. Research Needs
3. Modelling Complexity in Permafrost Coastlines
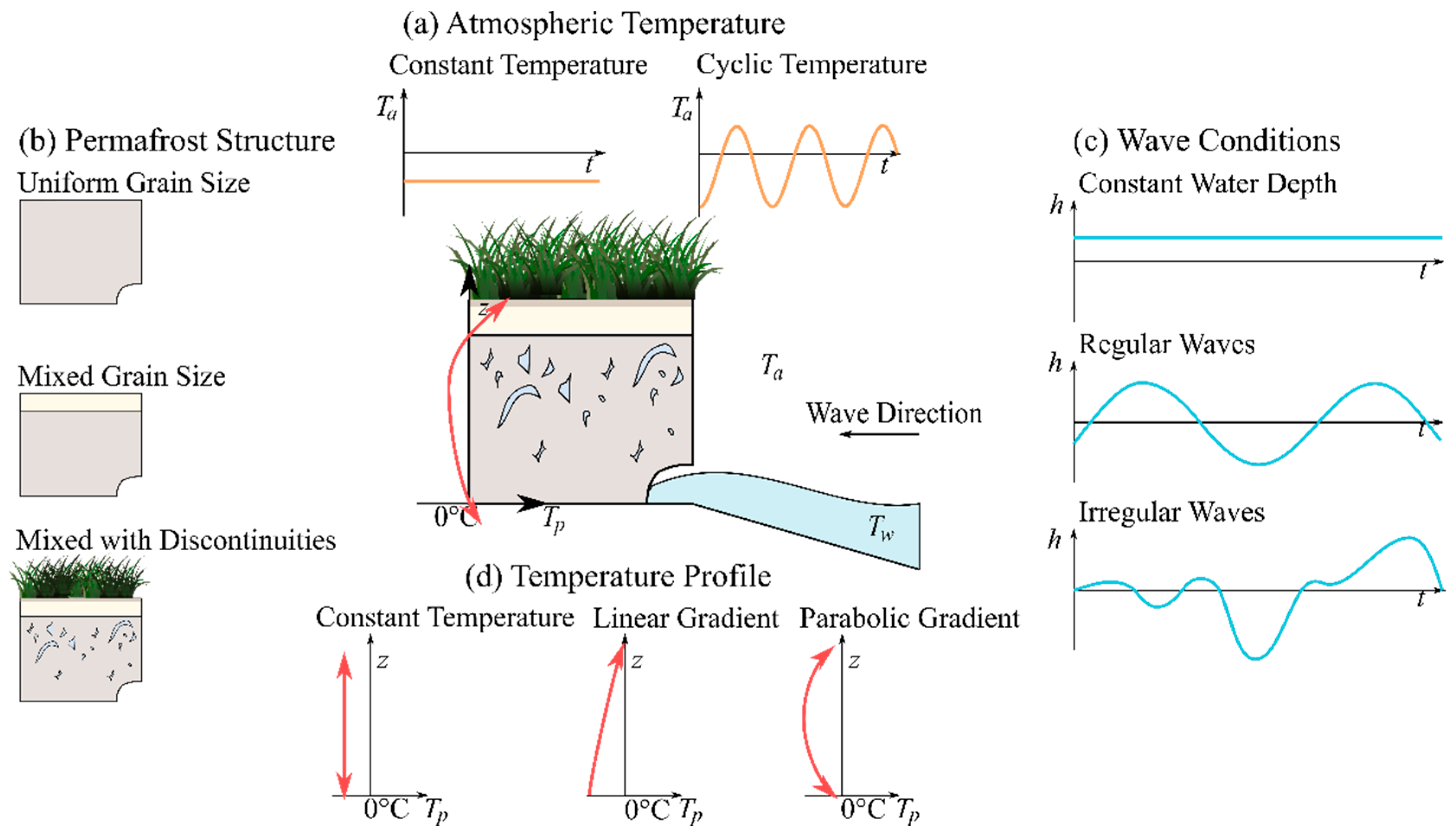
3.1. Scaling Considerations
3.2. Physical Model Complexity and Challenges
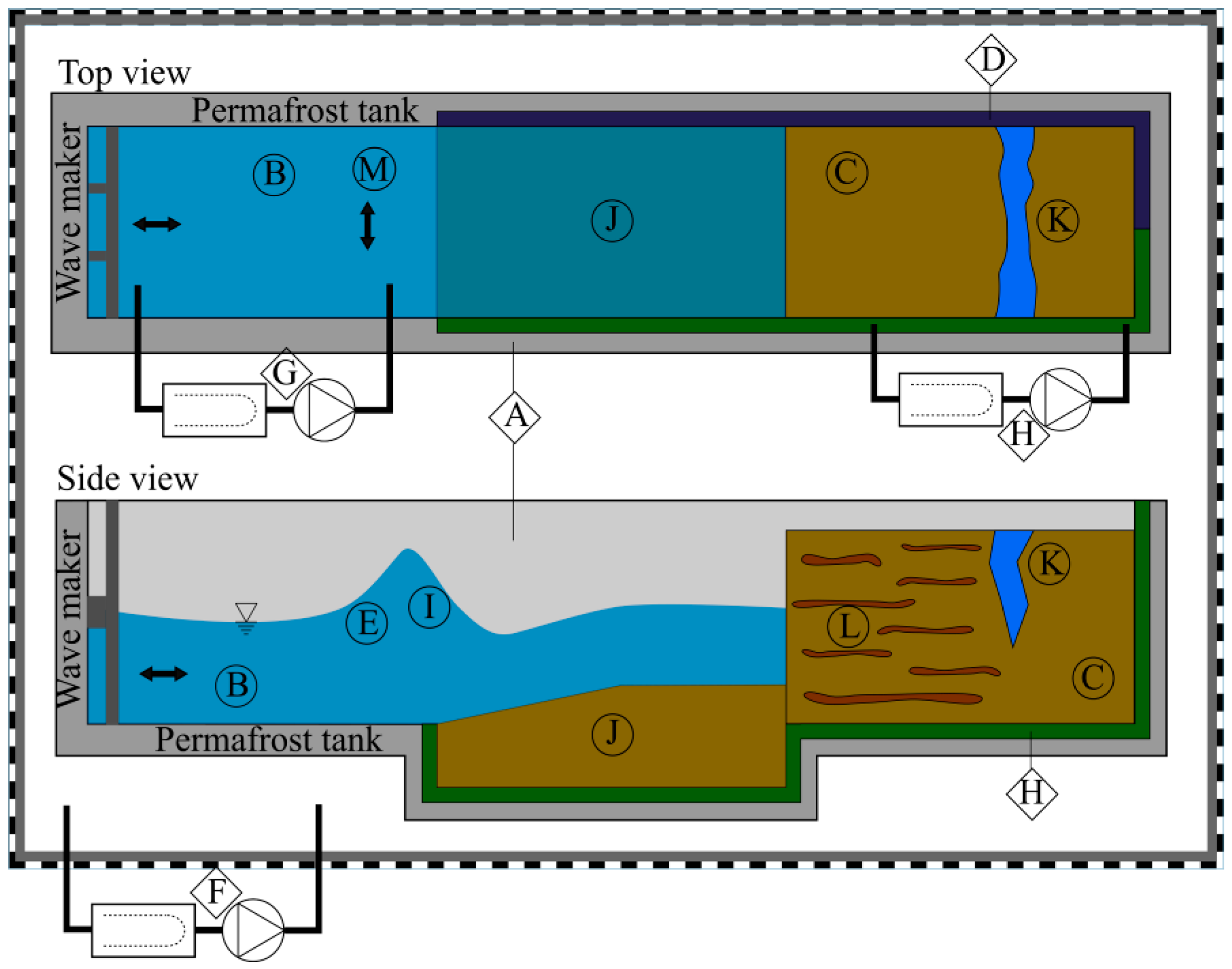
3.3. Technological Aspects of Experimentation
4. Zeroth- and First-Generation Modelling
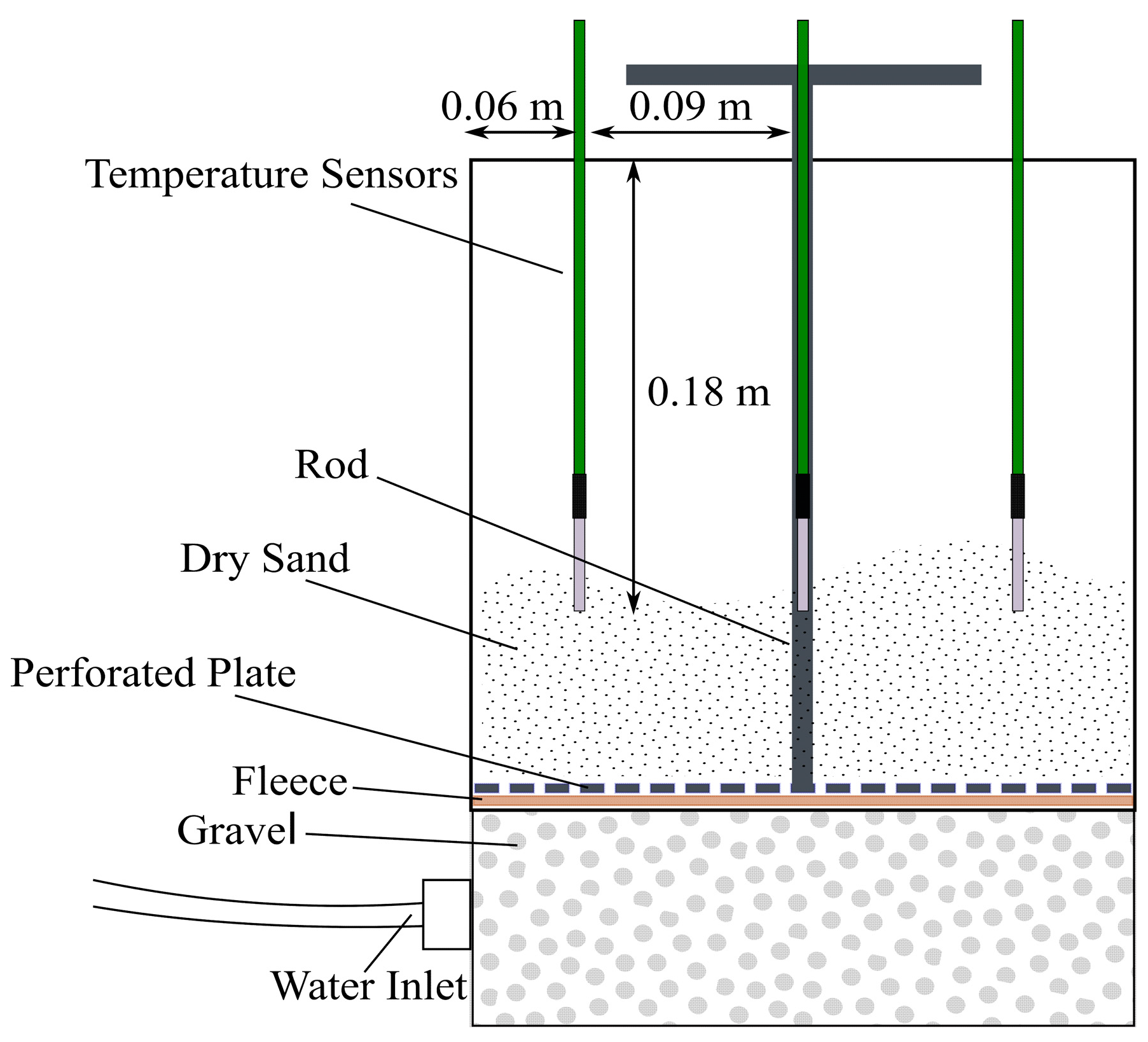
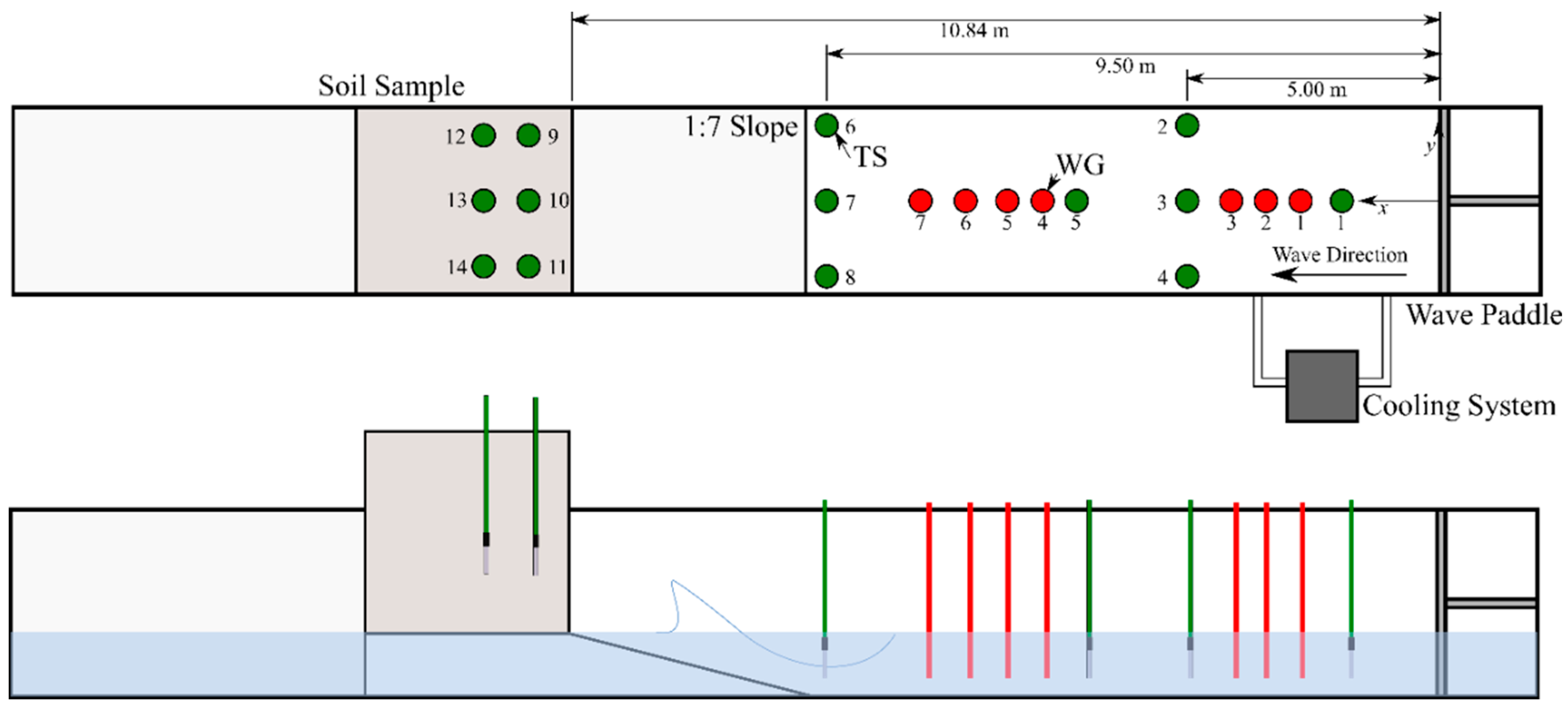
4.1. Development of Permafrost Sample
4.2. Wave Tests
4.3. Experimental Program
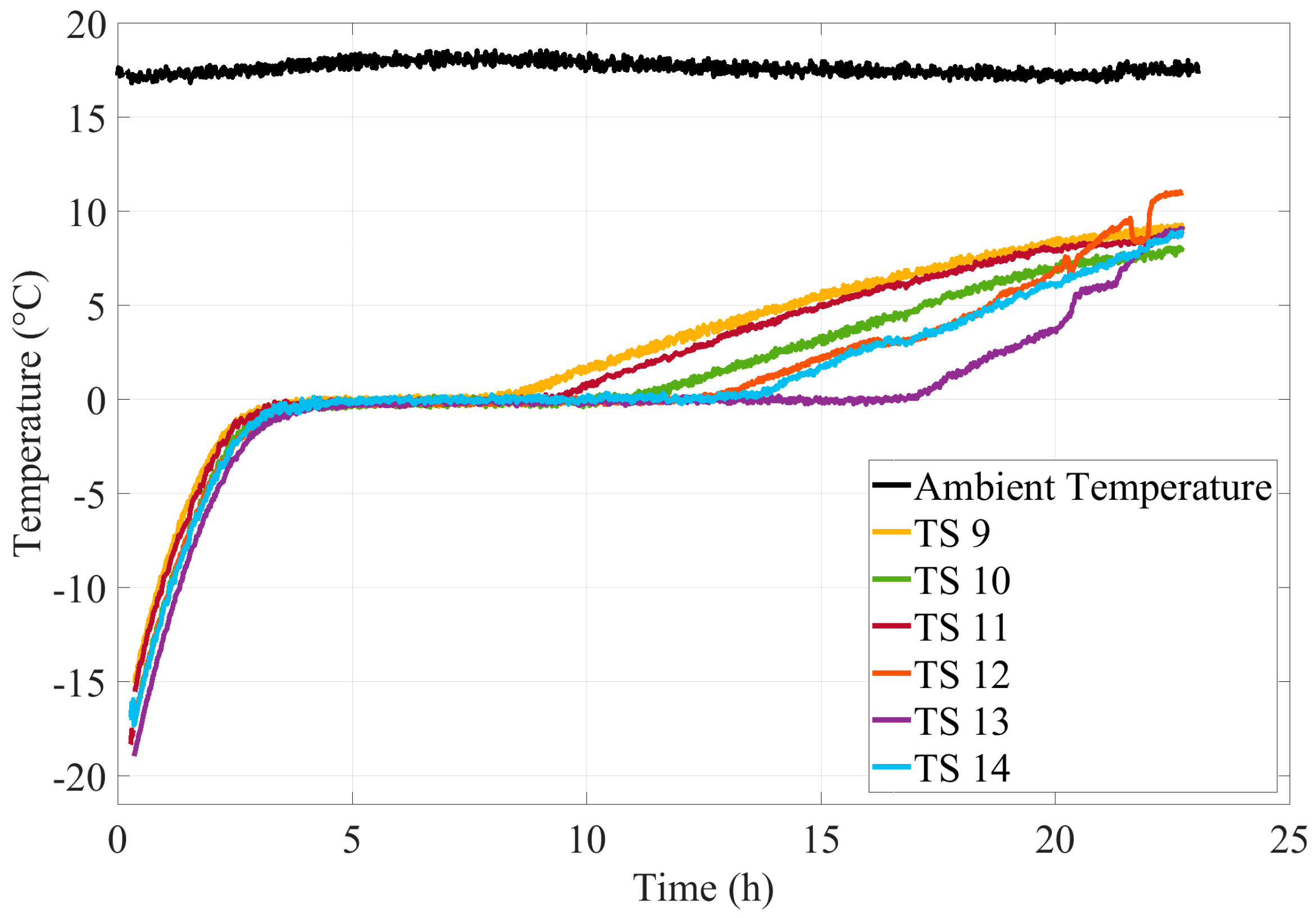
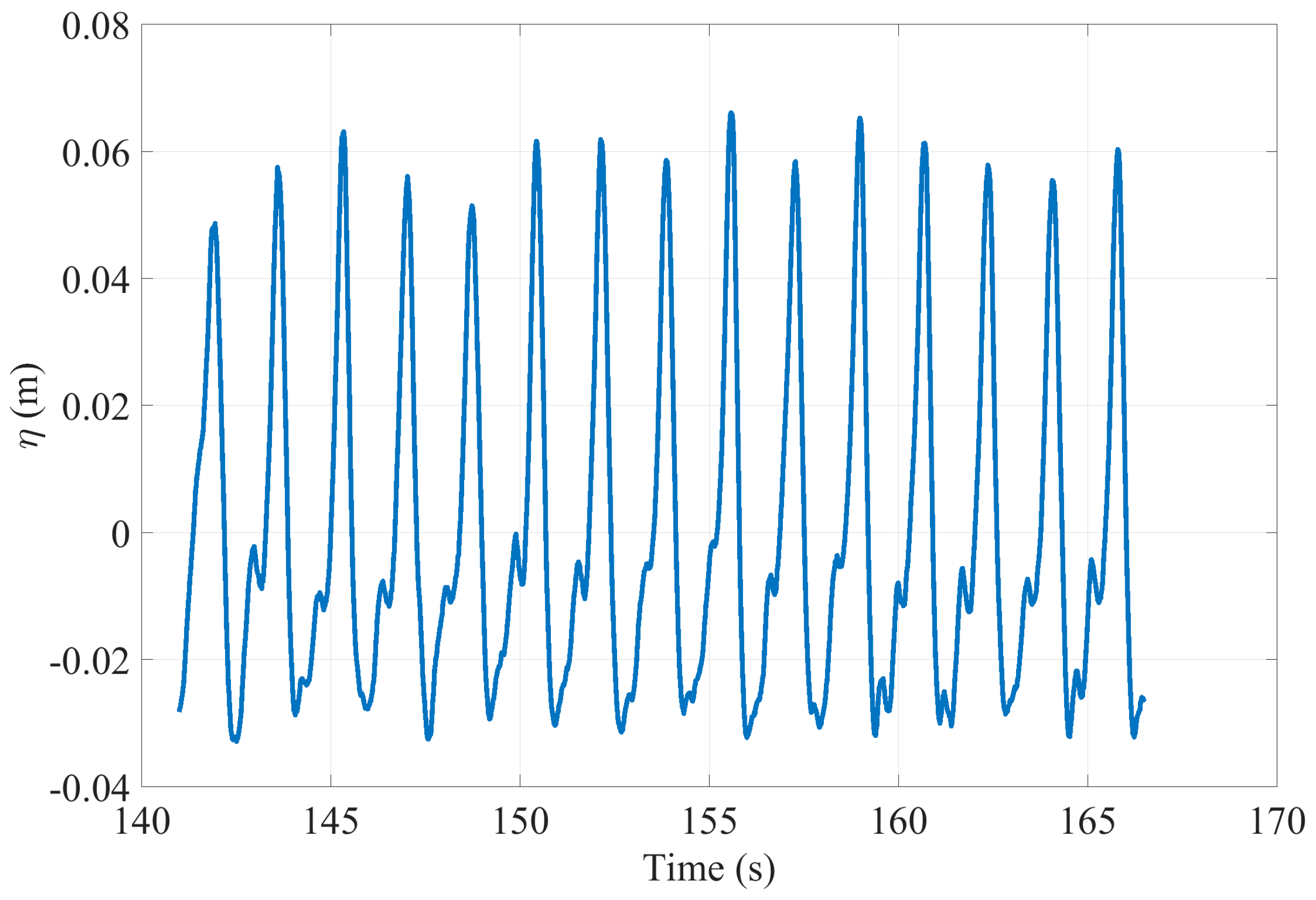
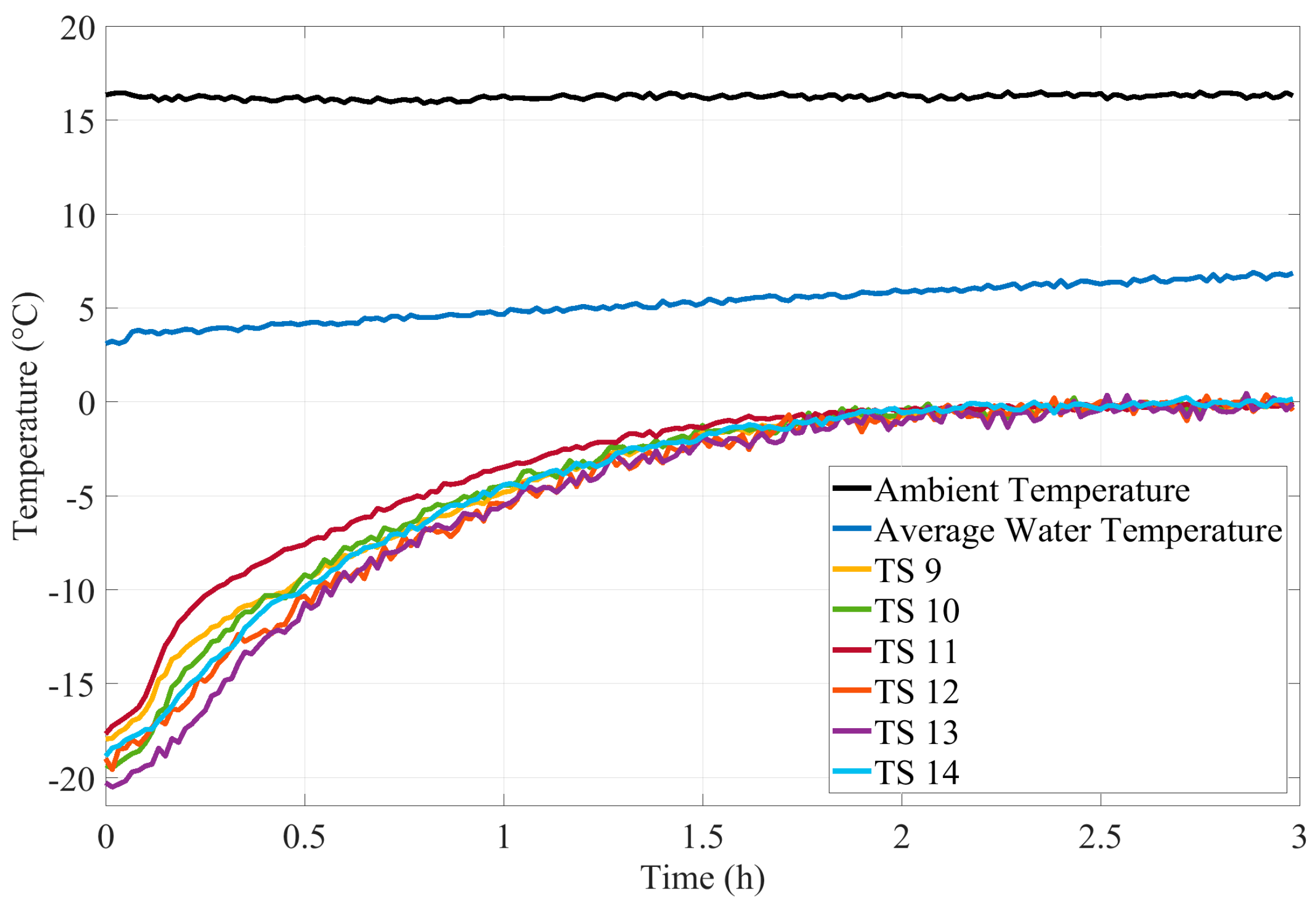
5. Results and Discussion
6. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Cai, L.; Alexeev, V.A.; Arp, C.D.; Jones, B.M.; Romanovsky, V.E. Modelling the impacts of projected sea ice decline on the low atmosphere and near-surface permafrost on the North Slope of Alaska. Int. J. Climatol. 2018, 38, 5491–5504. [Google Scholar] [CrossRef]
- Coch, C.; Lamoureux, S.F.; Knoblauch, C.; Eischeid, I.; Fritz, M.; Obu, J.; Lantuit, H. Summer rainfall dissolved organic carbon, solute, and sediment fluxes in a small Arctic coastal catchment on Herschel Island (Yukon Territory, Canada). Arct. Sci. 2018, 4, 750–780. [Google Scholar] [CrossRef]
- Biskaborn, B.K.; Smith, S.L.; Noetzli, J.; Matthes, H.; Vieira, G.; Streletskiy, D.A.; Schoeneich, P.; Romanovsky, V.E.; Lewkowicz, A.G.; Abramov, A.; et al. Permafrost is warming at a global scale. Nat. Commun. 2019, 10, 264. [Google Scholar] [CrossRef] [PubMed]
- Lemmen, D.; James, T.; Warren, F.; Clarke, C. Canada’s Marine Coasts in a Changing Climate; Government of Canada: Ottawa, ON, Canada, 2016.
- Macdonald, R.W.; Harner, T.; Fyfe, J. Recent climate change in the Arctic and its impact on contaminant pathways and interpretation of temporal trend data. Sci. Total Environ. 2005, 342, 5–86. [Google Scholar] [CrossRef] [PubMed]
- Lantuit, H.; Overduin, P.P.; Couture, N.; Wetterich, S.; Aré, F.; Atkinson, D.; Brown, J.; Cherkashov, G.; Drozdov, D.; Forbes, D.L. The Arctic coastal dynamics database: A new classification scheme and statistics on Arctic permafrost coastlines. Estuaries Coasts 2012, 35, 383–400. [Google Scholar] [CrossRef]
- Harris, S.; French, H.; Heginbottom, J.; Johnston, G.; Ladanyi, B.; Sego, D.; van Everdingen, R. Glossary of Permafrost and Related Ground-Ice Terms; National Research Council: Ottawa, ON, Canada, 1988; ISBN 0-660-125404. [Google Scholar]
- Lantuit, H.; Pollard, W.H. Fifty years of coastal erosion and retrogressive thaw slump activity on Herschel Island, southern Beaufort Sea, Yukon Territory, Canada. Geomorphology 2008, 95, 84–102. [Google Scholar] [CrossRef]
- Lantuit, H.; Atkinson, D.; Paul Overduin, P.; Grigoriev, M.; Rachold, V.; Grosse, G.; Hubberten, H.-W. Coastal erosion dynamics on the permafrost-dominated Bykovsky Peninsula, North Siberia, 1951–2006. Polar Res. 2011, 30, 7341. [Google Scholar] [CrossRef]
- Irrgang, A.M.; Lantuit, H.; Manson, G.K.; Günther, F.; Grosse, G.; Overduin, P.P. Variability in rates of coastal change along the Yukon Coast, 1951 to 2015. J. Geophys. Res. 2018, 123, 779–800. [Google Scholar] [CrossRef]
- Lantuit, H.; Overduin, P.P.; Wetterich, S. Recent progress regarding permafrost coasts. Permafr. Periglac. Process. 2013, 24, 120–130. [Google Scholar] [CrossRef]
- Jones, B.M.; Arp, C.D.; Jorgenson, M.T.; Hinkel, K.M.; Schmutz, J.A.; Flint, P.L. Increase in the rate and uniformity of coastline erosion in Arctic Alaska. Geophys. Res. Lett. 2009, 36, 1–5. [Google Scholar] [CrossRef]
- Cunliffe, A.M.; Tanski, G.; Radosavljevic, B.; Palmer, W.F.; Sachs, T.; Lantuit, H.; Kerby, J.T.; Myers-Smith, I.H. Rapid retreat of permafrost coastline observed with aerial drone photogrammetry. Cryosphere 2019, 13, 1513–1528. [Google Scholar] [CrossRef]
- Ford, J.D.; Smit, B. A framework for assessing the vulnerability of communities in the Canadian Arctic to risks associated with climate change. Arctic 2004, 57, 389–400. [Google Scholar] [CrossRef]
- Pearce, T.; Smit, B. Vulnerability and adaptation to climate change in the Canadian Arctic. Clim. Vulnerability 2013, 4, 293–303. [Google Scholar] [CrossRef]
- Irrgang, A.M.; Lantuit, H.; Gordon, R.R.; Piskor, A.; Manson, G.K. Impacts of past and future coastal changes on the Yukon coast—Threats for cultural sites, infrastructure, and travel routes. Arct. Sci. 2019, 5, 107–126. [Google Scholar] [CrossRef]
- Yoon, J.-R.; Kim, Y.-D. Reviews on natural resources in the Arctic: Petroleum, gas, gas hydrates and minerals. Ocean Polar Res. 2001, 23, 51–62. [Google Scholar]
- Tolvanen, A.; Eilu, P.; Juutinen, A.; Kangas, K.; Kivinen, M.; Markovaara-Koivisto, M.; Naskali, A.; Salokannel, V.; Tuulentie, S.; Similä, J. Mining in the Arctic environment–A review from ecological, socioeconomic and legal perspectives. J. Environ. Manag. 2019, 233, 832–844. [Google Scholar] [CrossRef]
- Lantuit, H.; Rachold, V.; Pollard, W.H.; Steenhuisen, F.; Ødegård, R.; Hubberten, H.-W. Towards a calculation of organic carbon release from erosion of Arctic coasts using non-fractal coastline datasets. Mar. Geol. 2009, 257, 1–10. [Google Scholar] [CrossRef]
- Vonk, J.E.; Sánchez-García, L.; van Dongen, B.E.; Alling, V.; Kosmach, D.; Charkin, A.; Semiletov, I.P.; Dudarev, O.V.; Shakhova, N.; Roos, P. Activation of old carbon by erosion of coastal and subsea permafrost in Arctic Siberia. Nature 2012, 489, 137. [Google Scholar] [CrossRef]
- Couture, N.J.; Irrgang, A.; Pollard, W.; Lantuit, H.; Fritz, M. Coastal erosion of permafrost soils along the Yukon Coastal plain and fluxes of organic carbon to the Canadian Beaufort Sea. J. Geophys. Res. Biogeosci. 2018, 123, 406–422. [Google Scholar] [CrossRef]
- Ramage, J.L.; Irrgang, A.M.; Morgenstern, A.; Lantuit, H. Increasing coastal slump activity impacts the release of sediment and organic carbon into the Arctic Ocean. Biogeosciences 2018, 15, 1483–1495. [Google Scholar] [CrossRef]
- Klein, K.P.; Lantuit, H.; Heim, B.; Fell, F.; Doxaran, D.; Irrgang, A.M. Long-term high-resolution sediment and sea surface temperature spatial patterns in Arctic nearshore waters retrieved using 30-year landsat archive imagery. Remote Sens. 2019, 11, 2791. [Google Scholar] [CrossRef]
- Outridge, P.M.; Macdonald, R.W.; Wang, F.; Stern, G.A.; Dastoor, A.P. A mass balance inventory of mercury in the Arctic Ocean. Environ. Chem. 2008, 5, 89–111. [Google Scholar] [CrossRef]
- Are, F.E. Thermal Abrasion of Seacoasts; Nauka Press: Moscow, Russia, 1988; ISBN 0273-8457. [Google Scholar]
- Wobus, C.; Anderson, R.; Overeem, I.; Matell, N.; Clow, G.; Urban, F. Thermal erosion of a permafrost coastline: Improving process-based models using time-lapse photography. Arct. Antarct. Alp. Res. 2011, 43, 474–484. [Google Scholar] [CrossRef]
- Manson, G.K.; Solomon, S.M.; Forbes, D.L.; Atkinson, D.E.; Craymer, M. Spatial variability of factors influencing coastal change in the western Canadian Arctic. Geo-Mar. Lett. 2005, 25, 138–145. [Google Scholar] [CrossRef]
- Overeem, I.; Anderson, R.S.; Wobus, C.W.; Clow, G.D.; Urban, F.E.; Matell, N. Sea ice loss enhances wave action at the Arctic coast. Geophys. Res. Lett. 2011, 38, 1–6. [Google Scholar] [CrossRef]
- Kobayashi, N.; Vidrine, J.C.; Nairn, R.B.; Soloman, S.M. Erosion of frozen cliffs due to storm surge on Beaufort Sea Coast. J. Coast. Res. 1999, 15, 332–344. [Google Scholar]
- Lantuit, H.; Pollard, W.H. Temporal stereophotogrammetric analysis of retrogressive thaw slumps on Herschel Island, Yukon Territory. Nat. Hazards Earth Syst. Sci. 2005, 5, 413–423. [Google Scholar] [CrossRef]
- Lantuit, H.; Pollard, W.H.; Couture, N.; Fritz, M.; Schirrmeister, L.; Meyer, H.; Hubberten, H.-W. Modern and late Holocene retrogressive thaw slump activity on the Yukon coastal plain and Herschel Island, Yukon Territory, Canada. Permafr. Periglac. Process. 2012, 23, 39–51. [Google Scholar] [CrossRef]
- Hoque, M.A.; Pollard, W.H. Stability of permafrost dominated coastal cliffs in the Arctic. Polar Sci. 2016, 10, 79–88. [Google Scholar] [CrossRef]
- Guégan, E.B.M.; Christiansen, H.H. Seasonal Arctic coastal bluff dynamics in Adventfjorden, Svalbard. Permafr. Periglac. Process. 2017, 28, 18–31. [Google Scholar] [CrossRef]
- Hughes, S.A. Physical Models and Laboratory Techniques in Coast. Eng.; World Scientific: Singapore, 1993; ISBN 981021541X. [Google Scholar]
- Tsytovich, N. The Mechanics of Frozen Ground (Translated); Scripta Book Company: Lansing, MI, USA, 1975. [Google Scholar]
- Osterkamp, T.; Burn, C. Permafrost, 1st ed.; Academic Press: Cambridge, MA, USA, 2003. [Google Scholar]
- Cannone, N.; Wagner, D.; Hubberten, H.W.; Guglielmin, M. Biotic and abiotic factors influencing soil properties across a latitudinal gradient in Victoria Land, Antarctica. Geoderma 2008, 144, 50–65. [Google Scholar] [CrossRef]
- Zhang, T.; Osterkamp, T.E.; Stamnes, K. Effects of climate on the active layer and permafrost on the north slope of Alaska, USA. Permafrost Periglac. Process. 1997, 8, 45–67. [Google Scholar] [CrossRef]
- Deprez, M.; de Kock, T.; de Schutter, G.; Cnudde, V. A review on freeze-thaw action and weathering of rocks. Earth-Sci. Rev. 2020, 203, 103143. [Google Scholar] [CrossRef]
- Harry, D.G.; Gozdzik, J.S. Ice wedges: Growth, thaw transformation, and palaeoenvironmental significance. J. Quat. Sci. 1988, 3, 39–55. [Google Scholar] [CrossRef]
- Yang, Z.; Still, B.; Ge, X. Mechanical properties of seasonally frozen and permafrost soils at high strain rate. Cold Reg. Sci. Technol. 2015, 113, 12–19. [Google Scholar] [CrossRef]
- Callaghan, D.P.; Nielsen, P.; Short, A.; Ranasinghe, R. Statistical simulation of wave climate and extreme beach erosion. Coast. Eng. 2008, 55, 375–390. [Google Scholar] [CrossRef]
- Larson, M.; Erikson, L.; Hanson, H. An analytical model to predict dune erosion due to wave impact. Coast. Eng. 2004, 51, 675–696. [Google Scholar] [CrossRef]
- McCall, R.T.; van Thiel de Vries, J.S.M.; Plant, N.G.; van Dongeren, A.R.; Roelvink, J.A.; Thompson, D.M.; Reniers, A.J.H.M. Two-dimensional time dependent hurricane overwash and erosion modeling at Santa Rosa Island. Coast. Eng. 2010, 57, 668–683. [Google Scholar] [CrossRef]
- Roelvink, D.; Reniers, A.; van Dongeren, A.; van Thiel de Vries, J.; McCall, R.; Lescinski, J. Modelling storm impacts on beaches, dunes and barrier islands. Coast. Eng. 2009, 56, 1133–1152. [Google Scholar] [CrossRef]
- van Thiel de Vries, J.S.M.; van Gent, M.R.A.; Walstra, D.J.R.; Reniers, A.J.H.M. Analysis of dune erosion processes in large-scale flume experiments. Coast. Eng. 2008, 55, 1028–1040. [Google Scholar] [CrossRef]
- Holthuijsen, L.H. Waves in Oceanic and Coastal Waters; Cambridge University Press: Cambridge, MA, USA, 2007; ISBN 9780511618536. [Google Scholar]
- Madsen, O.S.; Grant, W.D. Quantitative description of sediment transport by waves. Coast. Eng. 1976, 15, 1092–1112. [Google Scholar] [CrossRef]
- Hanley, M.E.; Hoggart, S.P.G.; Simmonds, D.J.; Bichot, A.; Colangelo, M.A.; Bozzeda, F.; Heurtefeux, H.; Ondiviela, B.; Ostrowski, R.; Recio, M.; et al. Shifting sands? Coastal protection by sand banks, beaches and dunes. Coast. Eng. 2014, 87, 136–146. [Google Scholar] [CrossRef]
- Bruun, P. Coastal Erosion and the Development of Beach Profiles; Technical Memorandum No. 44, U.S. Beach Erosion Board; US Army Engineer Research and Development Center (ERDC): Vicksburg, MS, USA, 1954. [Google Scholar]
- Trenhaile, A.S. Modeling the erosion of cohesive clay coasts. Coast. Eng. 2009, 56, 59–72. [Google Scholar] [CrossRef]
- Ogorodov, S.A.; Baranskaya, A.V.; Belova, N.G.; Kamalov, A.M.; Kuznetsov, D.E.; Overduin, P.P.; Shabanova, N.N.; Vergun, A.P. Coastal dynamics of the Pechora and Kara Seas under changing climatic conditions and human disturbances. Geogr. Environ. Sustain. 2016, 9, 53–73. [Google Scholar] [CrossRef]
- Hoque, M.A.; Pollard, W.H. Arctic coastal retreat through block failure. Can. Geotech. J. 2009, 46, 1103–1115. [Google Scholar] [CrossRef]
- Forbes, D.L.; Taylor, R.B. Ice in the shore zone and the geomorphology of cold coasts. Prog. Phys. Geogr. 1994, 18, 59–89. [Google Scholar] [CrossRef]
- Kovacs, A.; Sodhi, D.S. Ice pile-up and ride-up on arctic and subarctic beaches. Coast. Eng. 1981, 5, 247–273. [Google Scholar] [CrossRef]
- Ettema, R. Review of alluvial-channel responses to river ice. J. Cold Reg. Eng. 2002, 16, 191–217. [Google Scholar] [CrossRef]
- Ettema, R.; Baker, J.L.; Howlett, G.; Hudson, B. Ice-floe impact with a rubble-mound causeway at the port of nome, alaska. J. Cold Reg. Eng. 2019, 33, 5019001. [Google Scholar] [CrossRef]
- Ettema, R.; Zabilansky, L. Ice influences on channel stability: Insights from missouri’s fort peck reach. J. Hydraul. Eng. 2004, 130, 279–292. [Google Scholar] [CrossRef]
- Balmer, R.T. Modern Engineering Thermodynamics-Textbook with Tables Booklet; Academic Press: Cambridge, MA, USA, 2011; ISBN 0123850738. [Google Scholar]
- Costard, F.; Dupeyrat, L.; Gautier, E.; Carey-Gailhardis, E. Fluvial thermal erosion investigations along a rapidly eroding river bank: Application to the Lena River (central Siberia). Earth Surf. Process. Landf. 2003, 28, 1349–1359. [Google Scholar] [CrossRef]
- Veuille, S.; Fortier, D.; Verpaelst, M.; Grandmont, K.; Charbonneau, S. Heat advection in the active layer of permafrost: Physical modelling to quantify the impact of subsurface flow on soil thawing. In Proceedings of the 7th Canadian Conference on Permafrost and 68th Canadian Conference on Geotechnic, Quebec City, QC, Canada, 21–23 September 2015 ; pp. 20–23. [Google Scholar]
- Manson, G.K.; Solomon, S.M. Past and future forcing of beaufort sea coastal change. Atmosphere-Ocean 2007, 45, 107–122. [Google Scholar] [CrossRef]
- Budetta, P.; Galietta, G.; Santo, A. A methodology for the study of the relation between coastal cliff erosion and the mechanical strength of soils and rock masses. Eng. Geol. 2000, 56, 243–256. [Google Scholar] [CrossRef]
- Dean, R.G. Physical modelling of littoral processes. Phys. Model. Coast. Eng. 1985, 1, 119–139. [Google Scholar]
- Are, F.; Reimnitz, E. The a and m coefficients in the Bruun/Dean equilibrium profile equation seen from the Arctic. J. Coast. Res. 2008, 2, 243–249. [Google Scholar] [CrossRef]
- Kobayashi, N. Formation of thermoerosional niches into frozen bluffs due to storm surges on the Beaufort Sea coast. J. Geophys. Res. 1985, 90, 11983–11988. [Google Scholar] [CrossRef]
- Pogojeva, M.; Yakushev, E.; Ilinskaya, A.; Polukhin, A.; Braaten, H.-F.; Kristiansen, T. Experimental study of the influence of thawing permafrost on the chemical properties of sea water. Russ. J. Earth Sci. 2018, 18. [Google Scholar] [CrossRef]
- Stettner, S.; Beamish, A.; Bartsch, A.; Heim, B.; Grosse, G.; Roth, A.; Lantuit, H. Monitoring inter- and intra-seasonal dynamics of rapidly degrading ice-rich permafrost riverbanks in the Lena delta with TerraSAR-X time series. Remote Sens. 2018, 10, 51. [Google Scholar] [CrossRef]
- Obu, J.; Lantuit, H.; Grosse, G.; Günther, F.; Sachs, T.; Helm, V.; Fritz, M. Coastal erosion and mass wasting along the Canadian Beaufort Sea based on annual airborne LiDAR elevation data. Geomorphology 2017, 293, 331–346. [Google Scholar] [CrossRef]
- Holthuijsen, L.H.; Booij, N.; Herbers, T.H.C. A prediction model for stationary, short-crested waves in shallow water with ambient currents. Coast. Eng. 1989, 13, 23–54. [Google Scholar] [CrossRef]
- Afzal, M.S.; Bihs, H.; Kamath, A.; Arntsen, Ø.A. Three-dimensional numerical modeling of pier scour under current and waves using level-set method. J. Offshore Mech. Arct. Eng. 2015, 137. [Google Scholar] [CrossRef]
- Ahmad, N.; Bihs, H.; Myrhaug, D.; Kamath, A.; Arntsen, Ø.A. Numerical modeling of breaking wave induced seawall scour. Coast. Eng. 2019, 150, 108–120. [Google Scholar] [CrossRef]
- Sumer, B.M.; Whitehouse, R.J.S.; Tørum, A. Scour around coastal structures: A summary of recent research. Coast. Eng. 2001, 44, 153–190. [Google Scholar] [CrossRef]
- Hall, J.W.; Meadowcroft, I.C.; Lee, E.M.; van Gelder, P.H.A.J.M. Stochastic simulation of episodic soft coastal cliff recession. Coast. Eng. 2002, 46, 159–174. [Google Scholar] [CrossRef]
- Russell-Head, D.S. The melting of free-drifting icebergs. Ann. Glaciol. 1980, 1, 119–122. [Google Scholar] [CrossRef]
- White, F.M.; Spaulding, M.L.; Gominho, L. Theoretical Estimates of the Various Mechanisms Involved in Iceberg Deterioration in the Open Ocean Environment; Rhode Island University: Kingston, RI, USA, 1980. [Google Scholar]
- Barnhart, K.R.; Anderson, R.S.; Overeem, I.; Wobus, C.; Clow, G.D.; Urban, F.E. Modeling erosion of ice-rich permafrost bluffs along the Alaskan Beaufort Sea coast. J. Geophys. Res. 2014, 119, 1155–1179. [Google Scholar] [CrossRef]
- Ahmad, N.; Bihs, H.; Chella, M.A.; Kamath, A.; Arntsen, Ø.A. CFD modeling of arctic coastal erosion due to breaking waves. ISOPE-19-29-1-033 2019, 29, 33–41. [Google Scholar] [CrossRef]
- Kobayashi, N.; Aktan, D. Thermoerosion of frozen sediment under wave action. J. Waterw. Port Coast. Ocean Eng. 1986, 112, 140–158. [Google Scholar] [CrossRef]
- Dupeyrat, L.; Costard, F.; Randriamazaoro, R.; Gailhardis, E.; Gautier, E.; Fedorov, A. Effects of ice content on the thermal erosion of permafrost: Implications for coastal and fluvial erosion. Permafr. Periglac. Process. 2011, 22, 179–187. [Google Scholar] [CrossRef]
- Overduin, P.P.; Schneider von Deimling, T.; Miesner, F.; Grigoriev, M.N.; Ruppel, C.; Vasiliev, A.; Lantuit, H.; Juhls, B.; Westermann, S. Submarine permafrost map in the arctic modeled using 1-D transient heat flux (SuPerMAP). J. Geophys. Res. 2019, 124, 3490–3507. [Google Scholar] [CrossRef]
- MacMahan, J.; Thornton, E.; Koscinski, J.; Wang, Q. Field observations and modeling of surfzone sensible heat flux. J. Appl. Meteorol. Climatol. 2018, 57, 1371–1383. [Google Scholar] [CrossRef]
- Sinnett, G.; Feddersen, F. The competing effects of breaking waves on surfzone heat fluxes: Albedo versus wave heating. J. Geophys. Res. 2018, 123, 7172–7184. [Google Scholar] [CrossRef]
- Heller, V. Scale effects in physical hydraulic engineering models. J. Hydraul. Res. 2011, 49, 293–306. [Google Scholar] [CrossRef]
- Kamphuis, J.W. Physical modelling. In Herbich, Herbich (Hg.) 1991–Handbook of Coastal and Ocean Engineering; Gulf professional Publishing: Houston, TX, USA, 1992. [Google Scholar]
- Davies, M.C.R.; Hamza, O.; Harris, C. Physical modelling of permafrost warming in rock slopes. In Proceedings of the 8th International Conference on Permafrost, Lisse, The Netherlands, 21–25 July 2003; pp. 169–173. [Google Scholar]
- Dong, Y.; Lu, N.; McCartney, J.S. Scaling shear modulus from small to finite strain for unsaturated soils. J. Geotech. Geoenviron. Eng. 2018, 144, 4017110. [Google Scholar] [CrossRef]
- Timco, G.W.; Weeks, W.F. A review of the engineering properties of sea ice. Cold Reg. Sci. Technol. 2010, 60, 107–129. [Google Scholar] [CrossRef]
- Hopkins, M.A. Onshore ice pile-up: A comparison between experiments and simulations. Cold Reg. Sci. Technol. 1997, 26, 205–214. [Google Scholar] [CrossRef]
- Zhou, L.; Riska, K.; von Bock und Polach, R.; Moan, T.; Su, B. Experiments on level ice loading on an icebreaking tanker with different ice drift angles. Cold Reg. Sci. Technol. 2013, 85, 79–93. [Google Scholar] [CrossRef]
- Hirdaris, S.E.; Bai, W.; Dessi, D.; Ergin, A.; Gu, X.; Hermundstad, O.A.; Huijsmans, R.; Iijima, K.; Nielsen, U.D.; Parunov, J. Loads for use in the design of ships and offshore structures. Ocean Eng. 2014, 78, 131–174. [Google Scholar] [CrossRef]
- Gao, P.; Le Person, S.; Favre-Marinet, M. Scale effects on hydrodynamics and heat transfer in two-dimensional mini and microchannels. Int. J. Therm. Sci. 2002, 41, 1017–1027. [Google Scholar] [CrossRef]
- Incropera, F.P.; Lavine, A.S.; Bergman, T.L.; DeWitt, D.P. Fundamentals of Heat and Mass Transfer; Wiley: Hoboken, NJ, USA, 2007; ISBN 0471457280. [Google Scholar]
- Rapp, B.E. Microfluidics. Modeling, Mechanics, and Mathematics; William Andrew: Kidlington, UK, 2017; ISBN 9781455731411. [Google Scholar]
- Black, R.F. Permafrost: A review. Geol. Soc. Am. Bull. 1954, 65, 839–856. [Google Scholar] [CrossRef]
- Dean, R.G.; Dalrymple, R.A. Water Wave Mechanics for Engineers and Scientists; World Scientific Publishing Company: Singapore, 1991; ISBN 9814365696. [Google Scholar]
- Schäffer, H.A.; Klopman, G. Review of multidirectional active wave absorption methods. J. Waterw. Port Coast. Ocean Eng. 2000, 126, 88–97. [Google Scholar] [CrossRef]
- Spinneken, J.; Swan, C. The operation of a 3D wave basin in force control. Ocean Eng. 2012, 55, 88–100. [Google Scholar] [CrossRef]
- Mathisen, P.P.; Madsen, O.S. Waves and currents over a fixed rippled bed: 2. Bottom and apparent roughness experienced by currents in the presence of waves. J. Geophys. Res. 1996, 101, 16543–16550. [Google Scholar] [CrossRef]
- Welzel, M.; Schendel, A.; Hildebrandt, A.; Schlurmann, T. Scour development around a jacket structure in combined waves and current conditions compared to monopile foundations. Coast. Eng. 2019, 152, 103515. [Google Scholar] [CrossRef]
- Font, M.; Lagarde, J.-L.; Amorese, D.; Coutard, J.-P.; Dubois, A.; Guillemet, G.; Ozouf, J.-C.; Vedie, E. Physical modelling of fault scarp degradation under freeze–thaw cycles. Earth Surface Process. Landf. 2006, 31, 1731–1745. [Google Scholar] [CrossRef]
- Vedie, E.; Lagarde, J.-L.; Font, M. Physical modelling of rainfall-and snowmelt-induced erosion of stony slope underlain by permafrost. E Earth Surface Process. Landf. 2011, 36, 395–407. [Google Scholar] [CrossRef]
- Védie, E.; Costard, F.; Font, M.; Lagarde, J.L. Laboratory simulations of Martian gullies on sand dunes. Geophys. Res. Lett. 2008, 35. [Google Scholar] [CrossRef]
- Rivière, A.; Jost, A.; Gonçalvès, J.; Font, M. Pore water pressure evolution below a freezing front under saturated conditions: Large-scale laboratory experiment and numerical investigation. Cold Regions Sci. Technol. 2019, 158, 76–94. [Google Scholar] [CrossRef]
- Thomas, H.R.; Cleall, P.; Li, Y.-C.; Harris, C.; Kern-Luetschg, M. Modelling of cryogenic processes in permafrost and seasonally frozen soils. Geotechnique 2009, 59, 173–184. [Google Scholar] [CrossRef]
- Randriamazaoro, R.; Dupeyrat, L.; Costard, F.; Gailhardis, E.C. Fluvial thermal erosion: Heat balance integral method. Earth Surface Process. Landf. 2007, 32, 1828–1840. [Google Scholar] [CrossRef]
- Cataño-Lopera, Y.A.; García, M.H. Geometry and migration characteristics of bedforms under waves and currents. Part 1: Sandwave morphodynamics. Coast. Eng. 2006, 53, 767–780. [Google Scholar] [CrossRef]
- Song, A.J.; Lever, J.H.; Bates, S.W. Modeling Relevant to Safe Operations of US Navy Vessels in Arctic Conditions: Physical Modeling of Ice Loads; US Army Engineer Research and Development Center (ERDC): Vicksburg, MS, USA, 2016. [Google Scholar]
- DIN. Soil, Investigation and Testing—Determination of Density of Non-Cohesive Soils for Maximum and Minimum Compactness; Deutsches Institut für Normung e.V: Berlin, Germany, 1996. [Google Scholar]




| Generation | |||||||
|---|---|---|---|---|---|---|---|
| Parameter Space | 2D | 3D | |||||
| Parameter Category | Parameter | 0 | 1 | 2 | 3 | 4 | 5 |
| Permafrost Soil Model | Vertical Structure of Permafrost | × | × | ||||
| Horizontal Structure of Permafrost | × | × | × | ||||
| Soil Grain Size | × | × | × | × | × | × | |
| Water/Ice Content | × | × | × | × | × | × | |
| Organic Content | × | × | |||||
| Temperature Profile | × | × | × | × | |||
| Hydrodynamic Boundary Conditions | Water Level (Tides, Sea Level Rise) | × | × | × | × | × | × |
| Regular Waves | × | × | |||||
| Irregular Waves | × | × | × | ||||
| Currents | × | × | × | ||||
| Wave Direction | × | × | |||||
| Ambient Environment | Air Temperature (passive/active) | × | × | × | × | × | × |
| Cyclical Time Series | × | × | |||||
| Water Properties/Chemistry | Salinity | × | × | ||||
| Water Temperature | × | × | × | × | × | × | |
| Sediment Concentration | × | × | |||||
| Experiment | Water (Yes/No) | Water Level | Wave Height/Period | Water Volume |
|---|---|---|---|---|
| (-) | (-) | (m) | (m)/(s) | (L) |
| Exp. 1 | No | -/- | -/- | -/- |
| Exp. 2 | Yes | 0.20–0.265 | -/- | 650–862 |
| Exp. 3 | Yes | 0.20 | 0.085/1.7 | 650 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Korte, S.; Gieschen, R.; Stolle, J.; Goseberg, N. Physical Modelling of Arctic Coastlines—Progress and Limitations. Water 2020, 12, 2254. https://doi.org/10.3390/w12082254
Korte S, Gieschen R, Stolle J, Goseberg N. Physical Modelling of Arctic Coastlines—Progress and Limitations. Water. 2020; 12(8):2254. https://doi.org/10.3390/w12082254
Chicago/Turabian StyleKorte, Sophia, Rebekka Gieschen, Jacob Stolle, and Nils Goseberg. 2020. "Physical Modelling of Arctic Coastlines—Progress and Limitations" Water 12, no. 8: 2254. https://doi.org/10.3390/w12082254
APA StyleKorte, S., Gieschen, R., Stolle, J., & Goseberg, N. (2020). Physical Modelling of Arctic Coastlines—Progress and Limitations. Water, 12(8), 2254. https://doi.org/10.3390/w12082254







