Flood Mapping Uncertainty from a Restoration Perspective: A Practical Case Study
Abstract
1. Introduction
2. Materials and Methods
2.1. Site Location
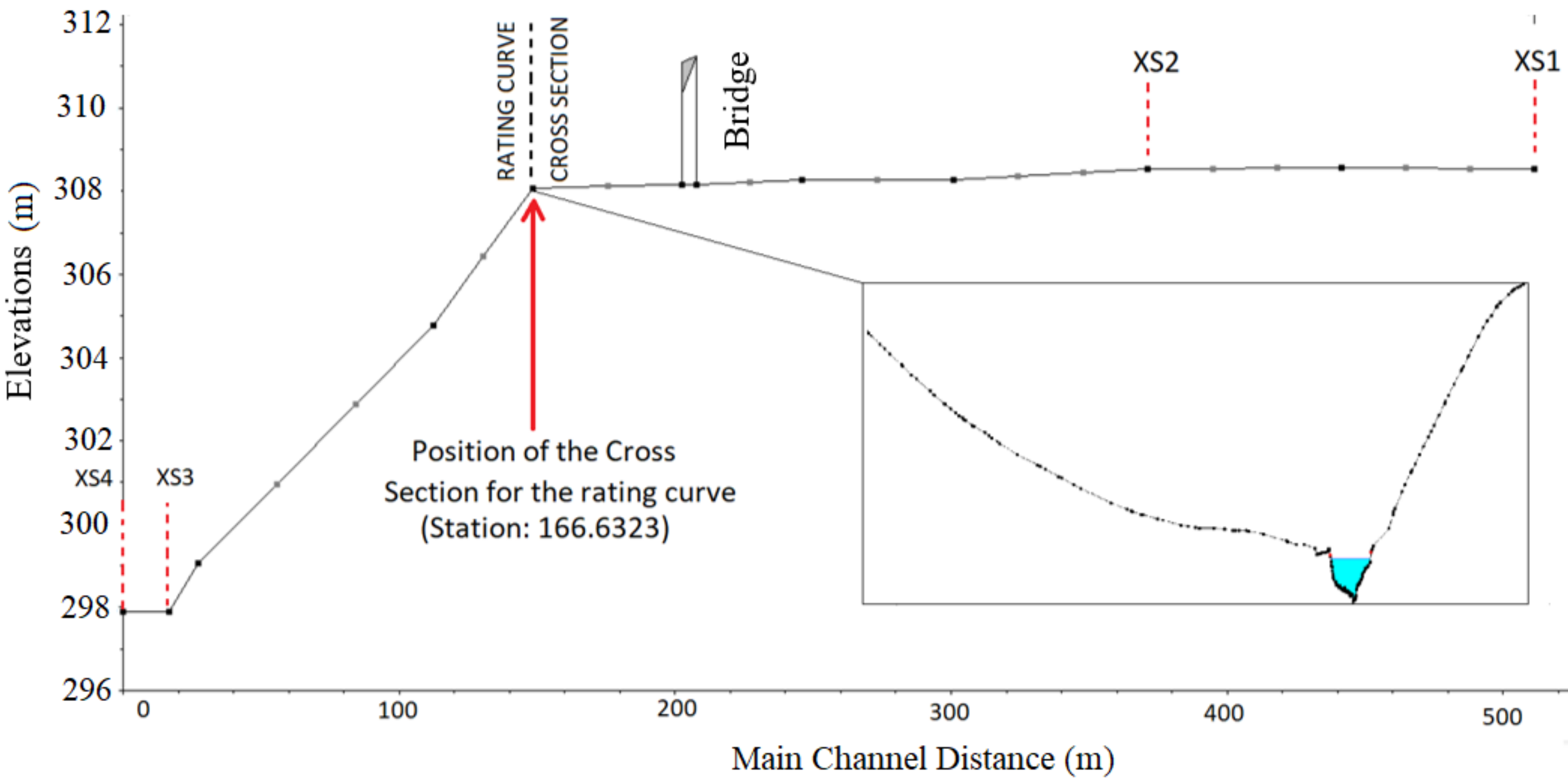
2.2. Digital Elevation Model
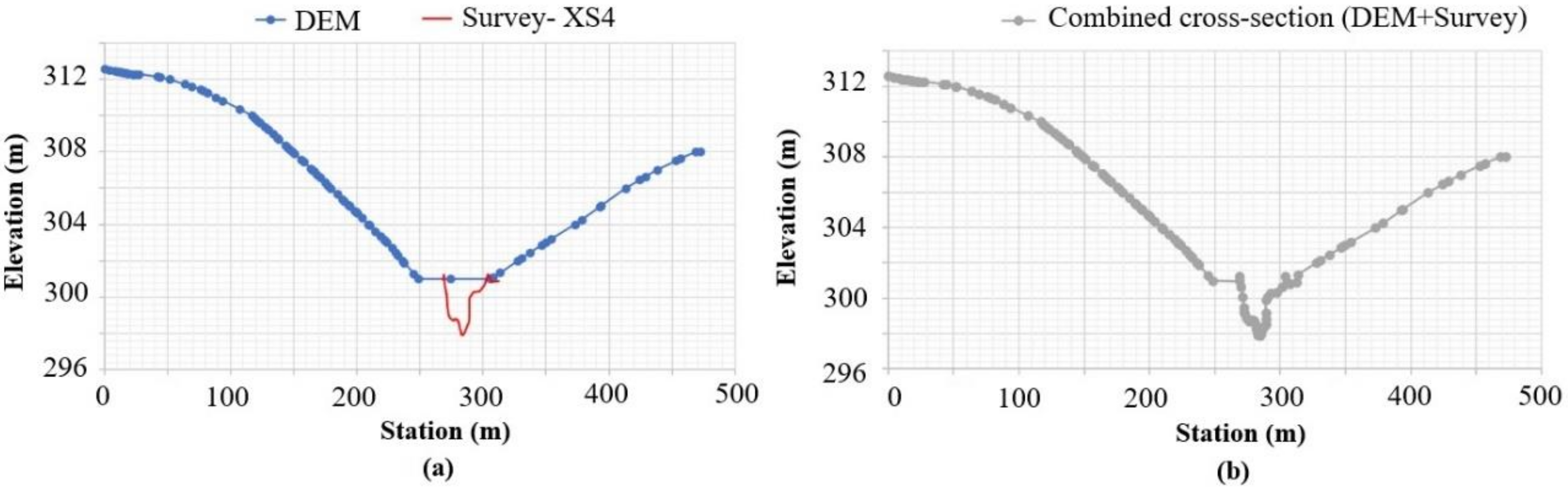
2.3. Bathymetric Adjustments
2.4. Rating Curve
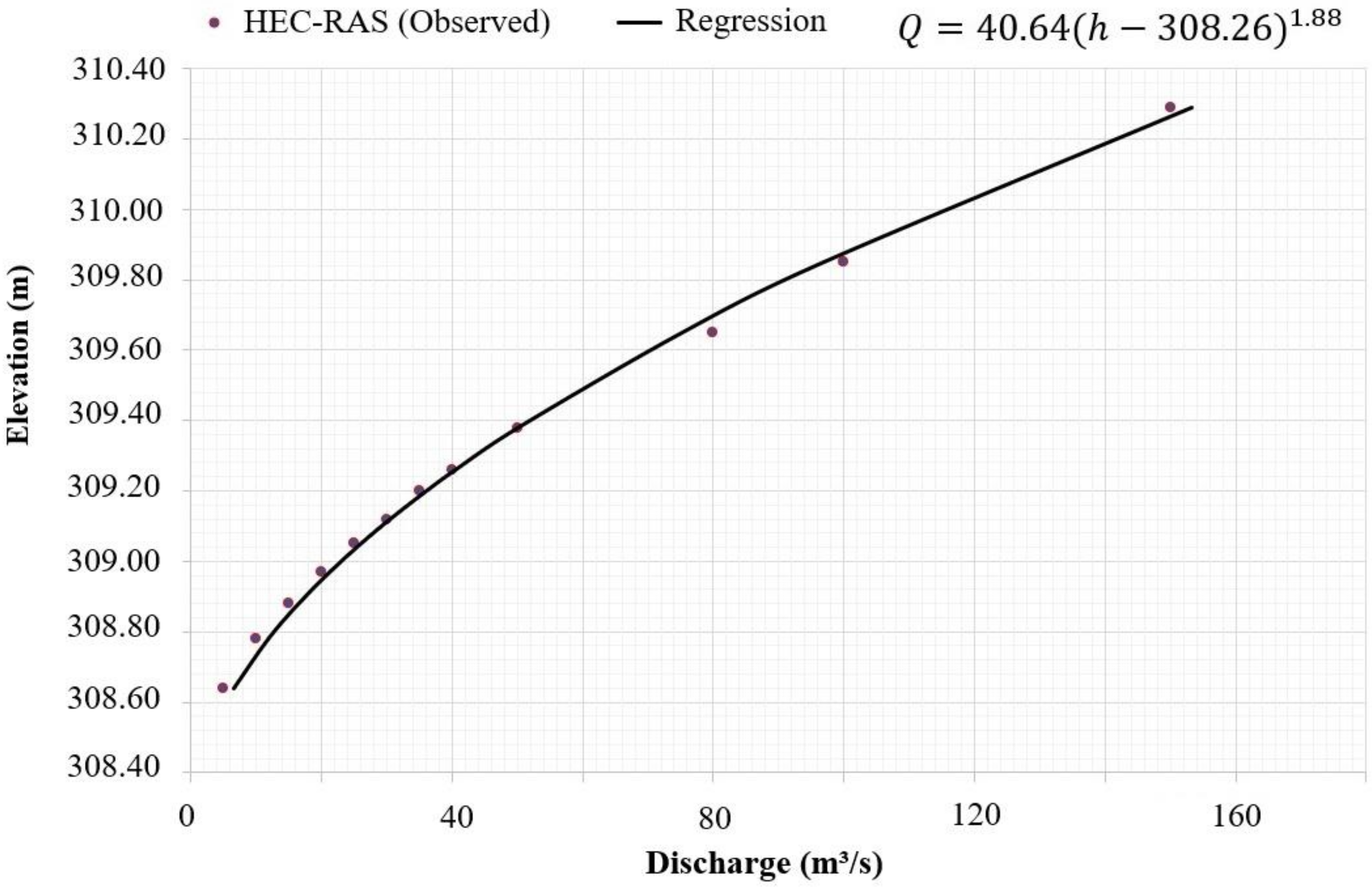
2.4.1. Rating Curve Function
2.4.2. Synthetic Stage–Discharge Data
2.5. Frequency Analysis
2.5.1. Generalized Extreme Values (GEV) Function
2.5.2. Extreme Flow Data and Drainage Area Correction Factor
2.6. Bayesian Model
2.6.1. Bayesian Rating Curve Model
2.6.2. Fully Bayesian Model
2.6.3. Markov Chain Monte Carlo Simulations
2.7. HEC-RAS Model Set-Up
3. Results
3.1. Results of the Synthetic Rating Curve
3.2. Results of the Extreme Data Time Series at the Study Site
3.3. Results of the Bayesian Approach
4. Discussion
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Appendix A
| Q USGS (m3/s) | Q Site (m3/s) | Hmax (m) | Year | Q USGS (m3/s) | Q Site (m3/s) | Hmax (m) | Year |
|---|---|---|---|---|---|---|---|
| 196.24 | 66.40 | 309.56 | 1924 | 81.27 | 27.50 | 309.08 | 1961 |
| 194.25 | 65.73 | 309.56 | 1925 | 81.84 | 27.69 | 309.08 | 1962 |
| 129.41 | 43.79 | 309.30 | 1926 | 110.15 | 37.27 | 309.22 | 1963 |
| 138.75 | 46.95 | 309.34 | 1927 | 92.03 | 31.14 | 309.13 | 1964 |
| 107.60 | 36.41 | 309.21 | 1928 | 40.21 | 13.61 | 308.82 | 1965 |
| 104.21 | 35.26 | 309.19 | 1929 | 78.15 | 26.45 | 309.06 | 1966 |
| 156.59 | 52.99 | 309.42 | 1930 | 100.24 | 33.92 | 309.17 | 1967 |
| 77.59 | 26.25 | 309.06 | 1931 | 114.40 | 38.71 | 309.24 | 1968 |
| 113.55 | 38.42 | 309.23 | 1932 | 136.20 | 46.09 | 309.33 | 1969 |
| 144.70 | 48.96 | 309.37 | 1933 | 94.01 | 31.81 | 309.14 | 1970 |
| 65.41 | 22.13 | 308.99 | 1934 | 70.23 | 23.76 | 309.02 | 1971 |
| 66.83 | 22.61 | 309.00 | 1935 | 155.18 | 52.51 | 309.41 | 1972 |
| 201.05 | 68.03 | 309.58 | 1936 | 110.15 | 37.27 | 309.22 | 1973 |
| 147.81 | 50.02 | 309.38 | 1937 | 89.76 | 30.37 | 309.12 | 1974 |
| 221.72 | 75.03 | 309.65 | 1938 | 71.92 | 24.34 | 309.02 | 1975 |
| 85.80 | 29.03 | 309.10 | 1939 | 88.63 | 29.99 | 309.11 | 1976 |
| 112.70 | 38.14 | 309.23 | 1940 | 138.19 | 46.76 | 309.34 | 1977 |
| 105.91 | 35.84 | 309.20 | 1941 | 92.03 | 31.14 | 309.13 | 1978 |
| 101.09 | 34.21 | 309.18 | 1942 | 186.89 | 63.24 | 309.53 | 1979 |
| 100.81 | 34.11 | 309.17 | 1943 | 106.19 | 35.93 | 309.20 | 1980 |
| 96.28 | 32.58 | 309.15 | 1944 | 108.45 | 36.70 | 309.21 | 1981 |
| 141.02 | 47.72 | 309.35 | 1945 | 147.53 | 49.92 | 309.38 | 1982 |
| 53.52 | 18.11 | 308.91 | 1946 | 171.88 | 58.16 | 309.47 | 1983 |
| 146.96 | 49.73 | 309.38 | 1947 | 150.65 | 50.98 | 309.39 | 1984 |
| 232.20 | 78.57 | 309.68 | 1948 | 66.54 | 22.52 | 308.99 | 1985 |
| 123.18 | 41.68 | 309.28 | 1949 | 74.19 | 25.10 | 309.04 | 1986 |
| 96.28 | 32.58 | 309.15 | 1950 | 159.14 | 53.85 | 309.43 | 1987 |
| 146.96 | 49.73 | 309.38 | 1951 | 163.95 | 55.48 | 309.44 | 1988 |
| 106.47 | 36.03 | 309.20 | 1952 | 110.15 | 37.27 | 309.22 | 1989 |
| 163.67 | 55.38 | 309.44 | 1953 | 104.49 | 35.36 | 309.19 | 1990 |
| 127.14 | 43.02 | 309.29 | 1954 | 98.83 | 33.44 | 309.17 | 1991 |
| 111.00 | 37.56 | 309.22 | 1955 | 113.27 | 38.33 | 309.23 | 1992 |
| 118.65 | 40.15 | 309.26 | 1956 | 159.99 | 54.14 | 309.43 | 1993 |
| 186.89 | 63.24 | 309.53 | 1957 | 119.78 | 40.53 | 309.26 | 1994 |
| 180.66 | 61.13 | 309.51 | 1958 | 104.21 | 35.26 | 309.19 | 1995 |
| 121.20 | 41.01 | 309.27 | 1959 | 131.96 | 44.65 | 309.31 | 1996 |
| 125.73 | 42.54 | 309.29 | 1960 | 175.85 | 59.50 | 309.49 | 1997 |
References
- Wohl, E.; Lane, S.N.; Wilcox, A.C. The science and practice of river restoration. Water Resour. Res. 2015, 51, 5974–5997. [Google Scholar] [CrossRef]
- Wohl, E. What should these rivers look like? Historical range of variability and human impacts in the Colorado Front Range, USA. Earth Surf. Process. Landf. 2011, 36, 1378–1390. [Google Scholar] [CrossRef]
- Nardini, A.; Pavan, S. River restoration: Not only for the sake of nature but also for saving money while addressing flood risk. A decision-making framework applied to the Chiese River (Po basin, Italy). J. Flood Risk Manag. 2012, 5, 111–133. [Google Scholar] [CrossRef]
- Araújo, P.V.N.; Amaro, V.E.; Silva, R.M.; Lopes, A.B. Delimitation of flood areas based on a calibrated a DEM and geoprocessing: Case study on the Uruguay River, Itaqui, southern Brazil. Nat. Hazards Earth Syst. Sci. 2019, 19, 237–250. [Google Scholar] [CrossRef]
- Mondragón-Monroy, R.; Honey-Rosés, J. Urban River Restoration and Planning in Latin America: A systematic review. Univ. Br. Columbia 2016, 1–29. [Google Scholar] [CrossRef]
- Stephens, T.A.; Bledsoe, B.P. Probabilistic mapping of flood hazards: Depicting uncertainty in streamflow, land use, and geomorphic adjustment. Anthropocene 2020, 29, 100231. [Google Scholar] [CrossRef]
- Teng, J.; Jakeman, A.J.; Vaze, J.; Croke, B.F.W.; Dutta, D.; Kim, S. Flood inundation modelling: A review of methods, recent advances and uncertainty analysis. Environ. Model. Softw. 2017, 90, 201–216. [Google Scholar] [CrossRef]
- Domeneghetti, A.; Vorogushyn, S.; Castellarin, A.; Merz, B.; Brath, A. Probabilistic flood hazard mapping: Effects of uncertain boundary conditions. Hydrol. Earth Syst. Sci. 2013, 17, 3127–3140. [Google Scholar] [CrossRef]
- Highfield, W.E.; Norman, S.A.; Brody, S.D. Examining the 100-Year Floodplain as a Metric of Risk, Loss, and Household Adjustment. Risk Anal. 2013, 33, 186–191. [Google Scholar] [CrossRef]
- Brody, S.D.; Sebastian, A.; Blessing, R.; Bedient, P.B. Case study results from southeast Houston, Texas: identifying the impacts of residential location on flood risk and loss. J. Flood Risk Manag. 2018, 11, S110–S120. [Google Scholar] [CrossRef]
- Tyler, J.; Sadiq, A.A.; Noonan, D.S. A review of the community flood risk management literature in the USA: lessons for improving community resilience to floods. Nat. Hazards 2019, 96, 1223–1248. [Google Scholar] [CrossRef]
- Freeze, R.A.; James, B.; Massmann, J.; Sperling, T.; Smith, L. Hydrogeological Decision Analysis: 4. The Concept of Data Worth and Its Use in the Development of Site Investigation Strategies. Ground Water 1992, 30, 574–588. [Google Scholar] [CrossRef]
- Merz, B.; Thieken, A.H. Separating natural and epistemic uncertainty in flood frequency analysis. J. Hydrol. 2005, 309, 114–132. [Google Scholar] [CrossRef]
- Apel, H.; Aronica, G.T.; Kreibich, H.; Thieken, A.H. Flood risk analyses—How detailed do we need to be? Nat. Hazards 2009, 49, 79–98. [Google Scholar] [CrossRef]
- Liu, Y.; Gupta, H.V. Uncertainty in hydrologic modeling: Toward an integrated data assimilation framework. Water Resour. Res. 2007, 43. [Google Scholar] [CrossRef]
- Bates, P.D.; Horritt, M.S.; Aronica, G.; Beven, K. Bayesian updating of flood inundation likelihoods conditioned on flood extent data. Hydrol. Process. 2004, 18, 3347–3370. [Google Scholar] [CrossRef]
- Abily, M.; Bertrand, N.; Delestre, O.; Gourbesville, P.; Duluc, C.M. Spatial Global Sensitivity Analysis of High Resolution classified topographic data use in 2D urban flood modelling. Environ. Model. Softw. 2016, 77, 183–195. [Google Scholar] [CrossRef]
- Savage, J.T.S.; Bates, P.; Freer, J.; Neal, J.; Aronica, G. When does spatial resolution become spurious in probabilistic flood inundation predictions? Hydrol. Process. 2016, 30, 2014–2032. [Google Scholar] [CrossRef]
- Stephens, E.M.; Bates, P.D.; Freer, J.E.; Mason, D.C. The impact of uncertainty in satellite data on the assessment of flood inundation models. J. Hydrol. 2012, 414–415, 162–173. [Google Scholar] [CrossRef]
- Neal, J.; Keef, C.; Bates, P.; Beven, K.; Leedal, D. Probabilistic flood risk mapping including spatial dependence. Hydrol. Process. 2013, 27, 1349–1363. [Google Scholar] [CrossRef]
- Vaze, J.; Viney, N.; Stenson, M.; Renzullo, L.; van Dijk, A.; Dutta, D.; Crosbie, R.; Lerat, J.; Penton, D.; Vleeshouwer, J.; et al. The Australian water resource assessment modelling system (AWRA). In Proceedings of the 20th International Congress on Modelling and Simulation, MODSIM 2013, Adelaide, Australia, 1–6 December 2013; pp. 3015–3021. [Google Scholar]
- Beven, K. Facets of uncertainty: Epistemic uncertainty, non-stationarity, likelihood, hypothesis testing, and communication. Hydrol. Sci. J. 2016, 61, 1652–1665. [Google Scholar] [CrossRef]
- Osorio, A.L.N.A.; Rampinelli, C.G.; Reis, D.S. A Bayesian Approach to Incorporate Imprecise Information on Hydraulic Knowledge in a River Reach and Assess Prediction Uncertainties in Streamflow Data. In Proceedings of the World Environmental and Water Resources Congress, Minneapolis, Minnesota, 3–7 June 2018. [Google Scholar]
- Osorio, A.L.N.A. Modelo Bayesiano Completo para análise de frequência de cheias com incorporação do conhecimento hidráulico na modelagem das incertezas na curva- chave. In Dissertação de Mestrado em Tecnologia Ambiental e Recursos Hídricos; Publicação PTARH.DM-196/17; Departamento de Engenharia Civil e Ambiental, Universidade de Brasília: Brasília, Brazil, 2017. [Google Scholar]
- Le Coz, J.; Renard, B.; Bonnifait, L.; Branger, F.; Le Boursicaud, R. Combining hydraulic knowledge and uncertain gaugings in the estimation of hydrometric rating curves: A Bayesian approach. J. Hydrol. 2014, 509, 573–587. [Google Scholar] [CrossRef]
- Pappenberger, F.; Matgen, P.; Beven, K.J.; Henry, J.B.; Pfister, L.; Fraipont, P. Influence of uncertain boundary conditions and model structure on flood inundation predictions. Adv. Water Resour. 2006, 29, 1430–1449. [Google Scholar] [CrossRef]
- Liu, Z.; Merwade, V.; Jafarzadegan, K. Investigating the role of model structure and surface roughness in generating flood inundation extents using one- and two-dimensional hydraulic models. J. Flood Risk Manag. 2019, 12. [Google Scholar] [CrossRef]
- Dimitriadis, P.; Tegos, A.; Oikonomou, A.; Pagana, V.; Koukouvinos, A.; Mamassis, N.; Koutsoyiannis, D.; Efstratiadis, A. Comparative evaluation of 1D and quasi-2D hydraulic models based on benchmark and real-world applications for uncertainty assessment in flood mapping. J. Hydrol. 2016, 534, 478–492. [Google Scholar] [CrossRef]
- Georgakakos, K.P.; Seo, D.J.; Gupta, H.; Schaake, J.; Butts, M.B. Towards the characterization of streamflow simulation uncertainty through multimodel ensembles. J. Hydrol. 2004, 298, 222–241. [Google Scholar] [CrossRef]
- Zarzar, C.M.; Hosseiny, H.; Siddique, R.; Gomez, M.; Smith, V.; Mejia, A.; Dyer, J. A Hydraulic MultiModel Ensemble Framework for Visualizing Flood Inundation Uncertainty. J. Am. Water Resour. Assoc. 2018, 54, 807–819. [Google Scholar] [CrossRef]
- Horritt, M.S. A methodology for the validation of uncertain flood inundation models. J. Hydrol. 2006, 326, 153–165. [Google Scholar] [CrossRef]
- Papaioannou, G.; Vasiliades, L.; Loukas, A.; Aronica, G.T. Probabilistic flood inundation mapping at ungauged streams due to roughness coefficient uncertainty in hydraulic modelling. Adv. Geosci. 2017, 44, 23–34. [Google Scholar] [CrossRef]
- Pappenberger, F.; Beven, K.; Horritt, M.; Blazkova, S. Uncertainty in the calibration of effective roughness parameters in HEC-RAS using inundation and downstream level observations. J. Hydrol. 2005, 302, 46–69. [Google Scholar] [CrossRef]
- Werner, M.G.F.; Hunter, N.M.; Bates, P.D. Identifiability of distributed floodplain roughness values in flood extent estimation. J. Hydrol. 2005, 314, 139–157. [Google Scholar] [CrossRef]
- Call, B.C.; Belmont, P.; Schmidt, J.C.; Wilcock, P.R. Changes in floodplain inundation under nonstationary hydrology for an adjustable, alluvial river channel. Water Resour. Res. 2017, 53, 3811–3834. [Google Scholar] [CrossRef]
- Aronica, G.T.; Franza, F.; Bates, P.D.; Neal, J.C. Probabilistic evaluation of flood hazard in urban areas using Monte Carlo simulation. Hydrol. Process. 2012, 26, 3962–3972. [Google Scholar] [CrossRef]
- Wu, X.Z. Probabilistic solution of floodplain inundation equation. Stoch. Environ. Res. Risk Assess. 2016, 30, 47–58. [Google Scholar] [CrossRef]
- Pedrozo-Acuña, A.; Rodríguez-Rincón, J.P.; Arganis-Juárez, M.; Domínguez-Mora, R.; González Villareal, F.J. Estimation of probabilistic flood inundation maps for an extreme event: Pánuco River, México. J. Flood Risk Manag. 2015, 8, 177–192. [Google Scholar] [CrossRef]
- Di Baldassarre, G.; Schumann, G.; Bates, P.D.; Freer, J.E.; Beven, K.J. Flood-plain mapping: a critical discussion of deterministic and probabilistic approaches. Hydrol. Sci. J. 2010, 55, 364–376. [Google Scholar] [CrossRef]
- Romanowicz, R.; Beven, K. Estimation of flood inundation probabilities as conditioned on event inundation maps. Water Resour. Res. 2003, 39, 1–12. [Google Scholar] [CrossRef]
- Reitan, T.; Petersen-Øverleir, A. Bayesian power-law regression with a location parameter, with applications for construction of discharge rating curves. Stoch. Environ. Res. Risk Assess. 2008, 22, 351–365. [Google Scholar] [CrossRef]
- Reitan, T.; Petersen-Øverleir, A. Bayesian methods for estimating multi-segment discharge rating curves. Stoch. Environ. Res. Risk Assess. 2009, 23, 627–642. [Google Scholar] [CrossRef]
- Coles, S.G.; Tawn, J.A. Modelling Extremes of the Areal Rainfall Process. J. Royal Stat. Soc. 1996, 58, 329–347. [Google Scholar] [CrossRef]
- Kuczera, G. Comprehensive at-site flood frequency analysis using Monte Carlo Bayesian inference. Water Resour. Res. 1999, 35, 1551–1557. [Google Scholar] [CrossRef]
- Reis, D.S.; Stedinger, J.R. Bayesian MCMC flood frequency analysis with historical information. J. Hydrol. 2005, 313, 97–116. [Google Scholar] [CrossRef]
- O’Connell, D.R.H. Nonparametric Bayesian flood frequency estimation. J. Hydrol. 2005, 313, 79–96. [Google Scholar] [CrossRef]
- Neppel, L.; Renard, B.; Lang, M.; Ayral, P.A.; Coeur, D.; Gaume, E.; Jacob, N.; Payrastre, O.; Pobanz, K.; Vinet, F. Flood frequency analysis using historical data: Accounting for random and systematic errors. Hydrol. Sci. J. 2010, 55, 192–208. [Google Scholar] [CrossRef]
- Paiva, R.C.D.; Collischonn, W.; Tucci, C.E.M. Large scale hydrologic and hydrodynamic modeling using limited data and a GIS based approach. J. Hydrol. 2011, 406, 170–181. [Google Scholar] [CrossRef]
- Winter, B.; Schneeberger, K.; Huttenlau, M.; Stötter, J. Sources of uncertainty in a probabilistic flood risk model. Nat. Hazards 2018, 91, 431–446. [Google Scholar] [CrossRef]
- Koivumäki, L.; Alho, P.; Lotsari, E.; Käyhkö, J.; Saari, A.; Hyyppä, H. Uncertainties in flood risk mapping: A case study on estimating building damages for a river flood in Finland. J. Flood Risk Manag. 2010, 3, 166–183. [Google Scholar] [CrossRef]
- GIS.NY.GOV. New York Government GIS Data Set. Available online: http://gis.ny.gov/gisdata/inventories/details.cfm?DSID=1336 (accessed on 28 March 2020).
- USACE HEC-GeoRAS 10.2. Available online: https://www.hec.usace.army.mil/software/hec-georas/ (accessed on 20 March 2020).
- US Army Corps of Engineers Hydrologic Engineering Center—River Analysis System-HEC-RAS 5.0.7. Available online: https://www.hec.usace.army.mil/software/hec-ras/ (accessed on 20 December 2019).
- Eberhart, R.; Kennedy, J. A new optimizer using particle swarm theory. Proc. Int. Symp. Micro Mach. Hum. Sci. 1995, 39–43. [Google Scholar] [CrossRef]
- Griffis, V.W.; Stedinger, J.R. Log-pearson type distribution and its application in flood frequency analysis. I: Distribution characteristics. J. Hydrol. Eng. 2007, 12, 482–491. [Google Scholar] [CrossRef]
- Hosking, J.R.M. L-Moments; R Package, Version 2.8. Available online: https://cran.r-project.org/web/packages/Lmoments (accessed on 22 December 2019).
- Vrugt, J.A.; ter Braak, C.J.F.; Clark, M.P.; Hyman, J.M.; Robinson, B.A. Treatment of input uncertainty in hydrologic modeling: Doing hydrology backward with Markov chain Monte Carlo simulation. Water Resour. Res. 2008, 44, 1–15. [Google Scholar] [CrossRef]
- Vrugt, J.A.; Ter Braak, C.J.F.; Diks, C.G.H.; Robinson, B.A.; Hyman, J.M.; Higdon, D. Accelerating Markov chain Monte Carlo simulation by differential evolution with self-adaptive randomized subspace sampling. Int. J. Nonlinear Sci. Numer. Simul. 2009, 10, 273–290. [Google Scholar] [CrossRef]
- Vrugt, J.A. Markov chain Monte Carlo simulation using the DREAM software package: Theory, concepts, and MATLAB implementation. Environ. Model. Softw. 2016, 75, 273–316. [Google Scholar] [CrossRef]
- Guillaume, J.; Andrews, F. DiffeRentialEvolution Adaptive Metropolis; R Packge Version 0.4-2. Available online: https://rdrr.io/rforge/dream/man/dream.html (accessed on 15 December 2019).



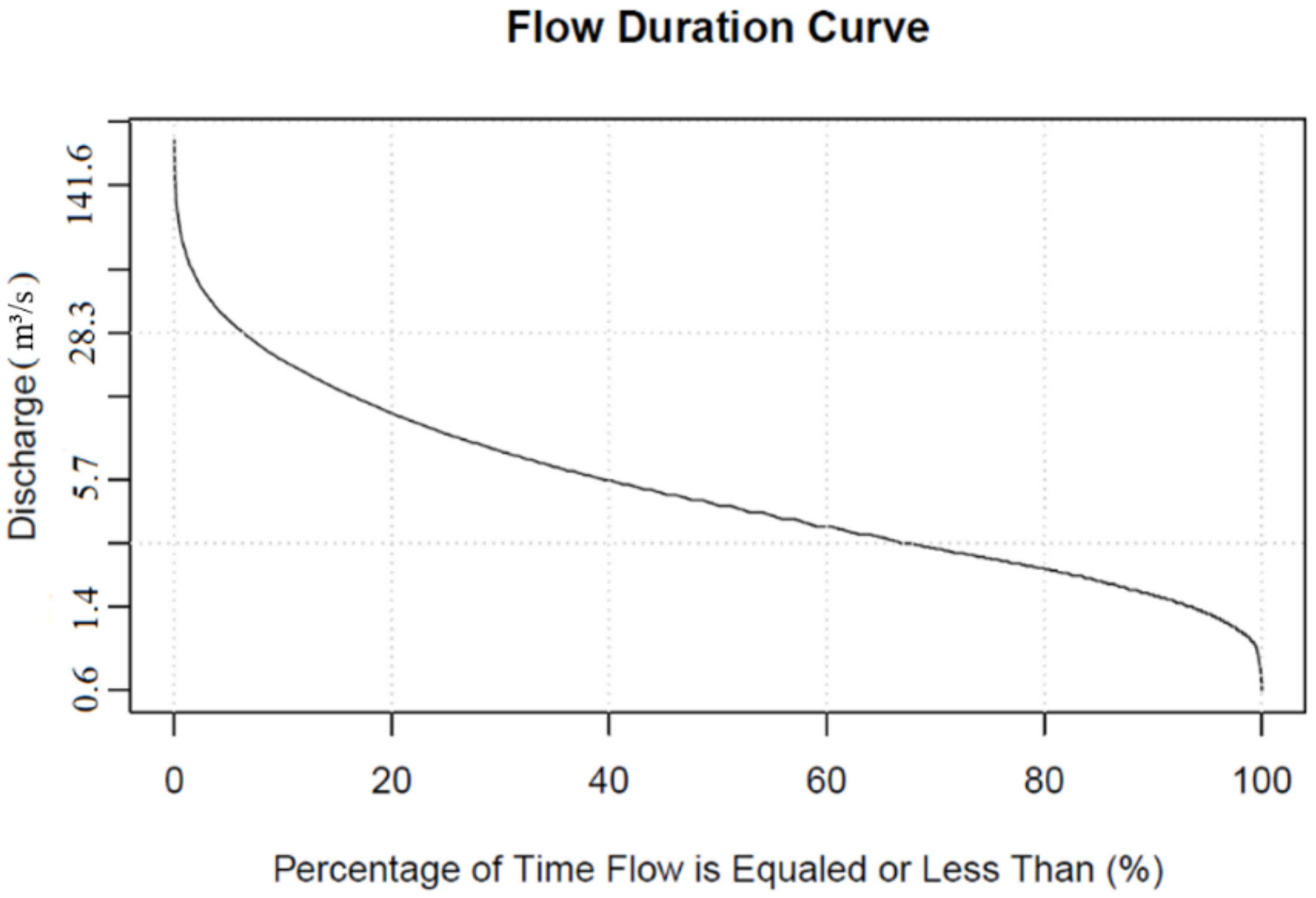
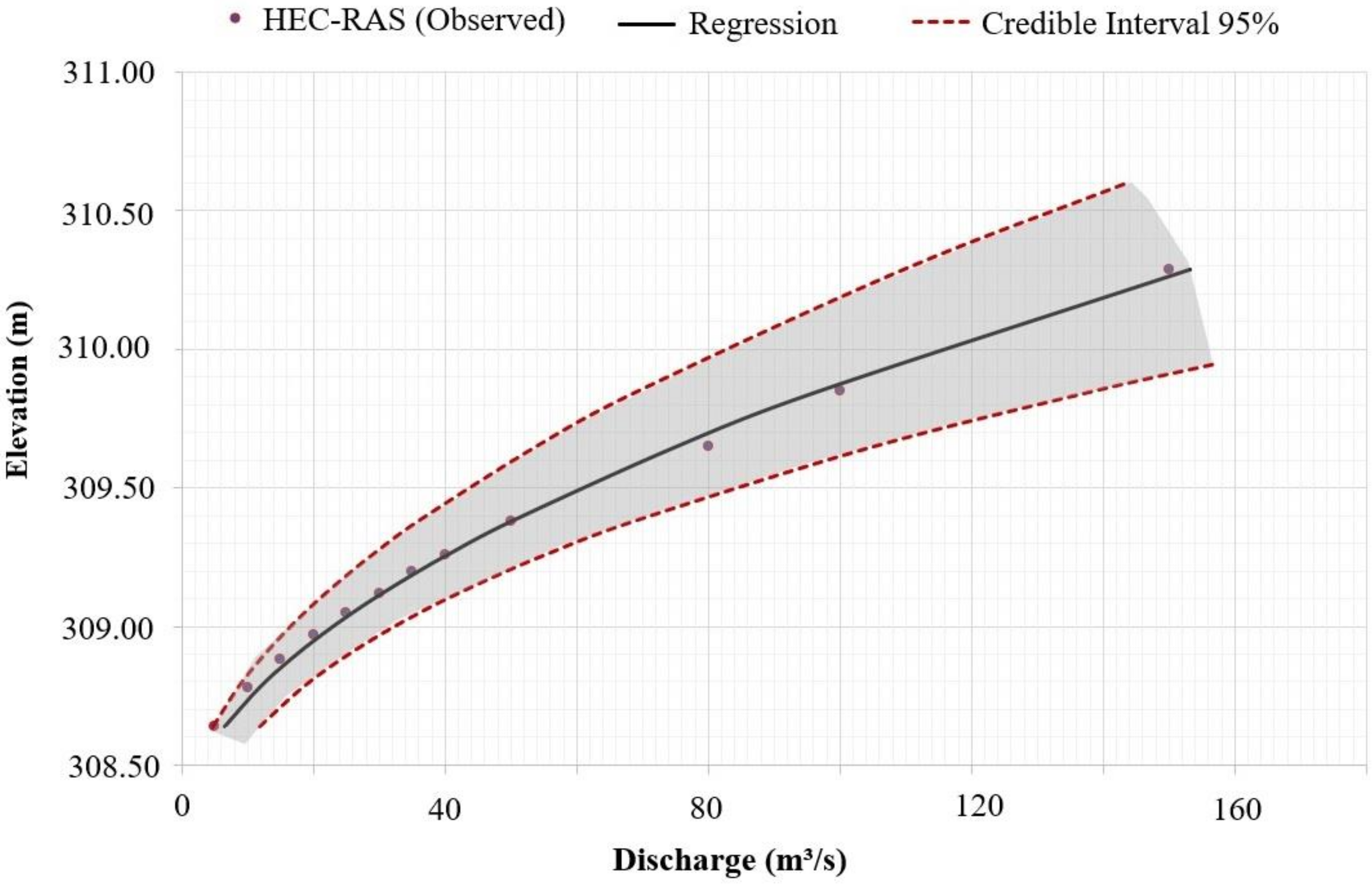


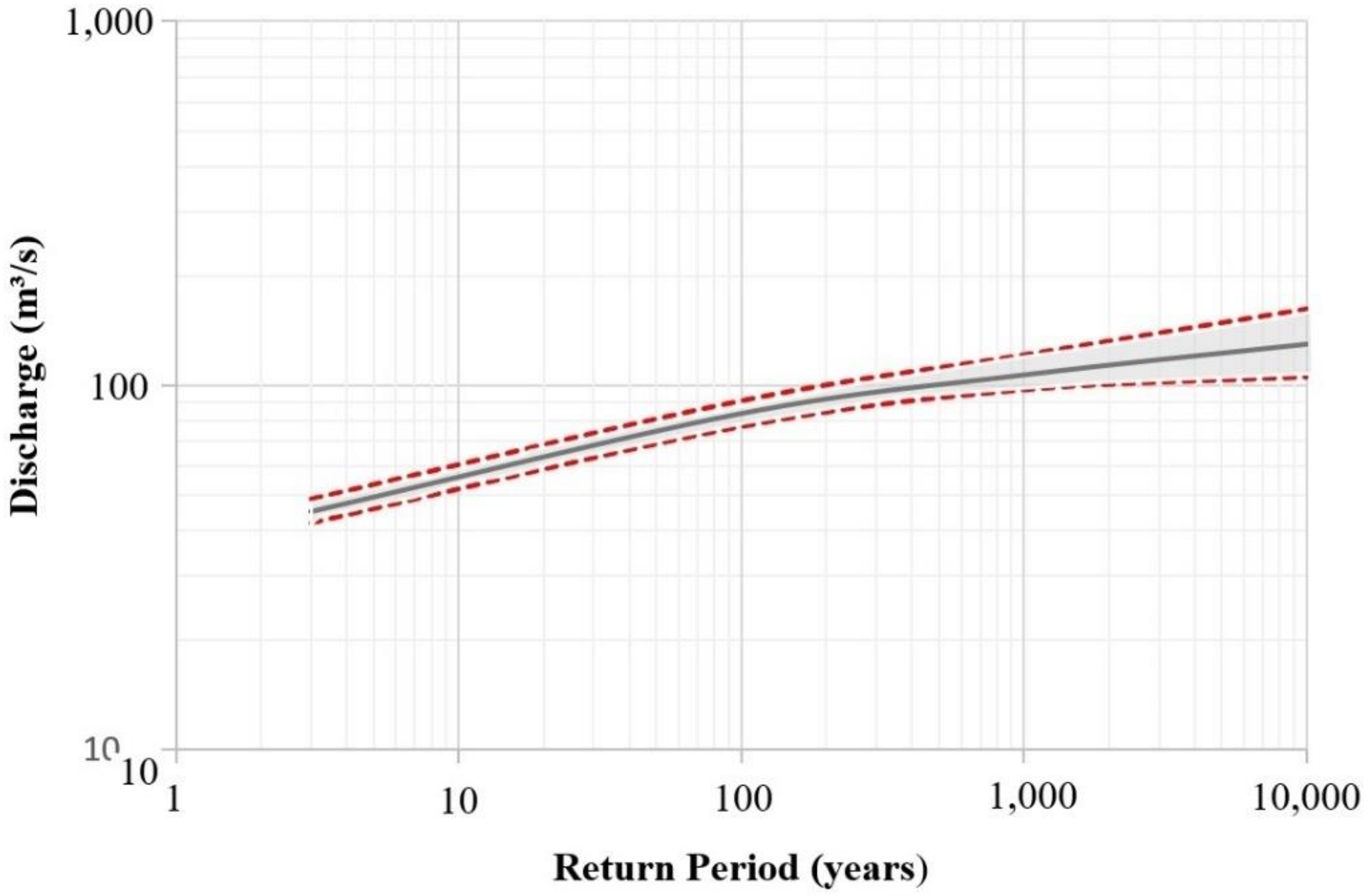

| RP | Q (m3/s) 2.5% | Q (m3/s) Med | Q (m3/s) 97.5% |
|---|---|---|---|
| 3 | 41.78 | 44.97 | 48.57 |
| 100 | 77 | 83.61 | 90.47 |
| 1000 | 97.22 | 106.76 | 120.98 |
| 10000 | 105.53 | 129.67 | 161.72 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Rampinelli, C.G.; Knack, I.; Smith, T. Flood Mapping Uncertainty from a Restoration Perspective: A Practical Case Study. Water 2020, 12, 1948. https://doi.org/10.3390/w12071948
Rampinelli CG, Knack I, Smith T. Flood Mapping Uncertainty from a Restoration Perspective: A Practical Case Study. Water. 2020; 12(7):1948. https://doi.org/10.3390/w12071948
Chicago/Turabian StyleRampinelli, Cássio G., Ian Knack, and Tyler Smith. 2020. "Flood Mapping Uncertainty from a Restoration Perspective: A Practical Case Study" Water 12, no. 7: 1948. https://doi.org/10.3390/w12071948
APA StyleRampinelli, C. G., Knack, I., & Smith, T. (2020). Flood Mapping Uncertainty from a Restoration Perspective: A Practical Case Study. Water, 12(7), 1948. https://doi.org/10.3390/w12071948






