An Artificial Compressibility Method for 1D Simulation of Open-Channel and Pressurized-Pipe Flow

Abstract

Piping systems (e.g., storm sewers) that transition between free-surface flow and surcharged flow are challenging to model in one-dimensional (1D) networks as the continuity equation changes from hyperbolic to elliptic as the water surface reaches the pipe ceiling. Previous network models are known to have poor mass conservation or unpredictable convergence behavior at such transitions. To address this problem, a new algorithm is developed for simulating unsteady 1D flow in closed conduits with both free-surface and surcharged flow. The shallow-water (hydrostatic) approximation is used as the governing equations. The artificial compressibility (AC) method is implemented as a dual-time-stepping discretization for a finite-volume solver with timescale interpolation used for face reconstruction. A new formulation for the AC celerity parameter is proposed such that the AC celerity matches the equivalent gravity wave speed for the local hydraulic head—which has some similarities to the classic Preissmann Slot used to approximate pressurized flow in conduits. The new approach allows the AC celerity to be set locally by the flow (i.e., non-uniform in space) and removes it as a free parameter of the AC solution method. The derivation of the AC method provides for only a minor change in the form of the solution equations when a computational element switches from free-surface to surcharged. The new solver is tested for both unsteady free-surface (supercritical, subcritical) and surcharged flow transitions in a circular pipe and is implemented in an open-source Python code available under the name “PipeAC.” The results are compared to laboratory experiments that include rapid flow changes due to opening/closing of gates. Results show that the new algorithm is satisfactory for 1D representation of unsteady transition behavior with two caveats: (i) sufficient grid resolution must be applied, and (ii) the shallow-water equation approximations (hydrostatic, single-fluid) limit the accuracy of the solution with regards to the celerity of the turbulent unsteady bore that propagates upstream. This research might benefit any piping network model that must smoothly handle unsteady transitions from free surface to surcharged flow.

1. Introduction

There is an ongoing need for city-wide models of stormwater networks to facilitate real-time modeling and operational control [1,2,3], design for urban growth [4,5,6], low-impact development [7,8,9], flood mitigation [10,11,12], runoff water quality [13], and address impacts of the changing climate [14,15]. Such models must be computationally efficient to allow a large number of simulations for calibration [16], design optimization [17,18], Monte-Carlo uncertainty analysis [19], and simulation of stochastic rainstorms instead of a single design storm [20,21]; however, the models must also be detailed and comprehensive is their treatment of the piping system for an entire city [22]. Two major challenges for system-wide modeling of municipal stormwater networks are: (i) numerical stability near a pressure celerity shock occurring at the transition between open-channel and surcharged flow [23,24], and (ii) efficient parallel computation for large systems [25,26]. This paper focuses on the modeling the transitions, with best practices for parallel computation considered in the algorithm design. The efficacy of a new method for simulating one-dimensional (1D) unsteady transitions between supercritical, subcritical, and surcharged flows is presented in detail herein. Analyses of parallel performance reserved for future work.

The new algorithm uses the concept of “Artificial Compressibility” (AC) whose roots are in Chorin’s classic approaches for treating the combined hyperbolic/elliptic nature of the incompressible Navier-Stokes equations [27,28]. The AC method has been demonstrated as effective for parallel solution of two-dimensional (2D) and three-dimensional (3D) incompressible flow (e.g., [29,30]). The present work appears to be the first providing an AC method for solving 1D closed-conduit water flow. Beyond this new application, other novel contributions include (i) use of the recent “timescale face reconstruction” method [31] applied to surcharged pipe flow, (ii) a formulation of the artificial compressibility parameter that varies in space to ensure pressure celerity is at gravity-wave speeds, (iii) an implicit time-linearized friction term built into the Runge-Kutta 4th-order (RK4) time-march that ensures flow reversals have friction opposing the end-of-step flow direction, and (iv) the ability to handle unsteady transitions between open-channel and surcharged sections with minimal changes in the numerical solution algorithm.

The algorithm developed herein is called “PipeAC,” and is based on a 1D finite-volume formulation of the shallow-water and incompressible flow equations with added artificial compressibility terms. A 3-level backwards implicit stencil is used for real-time discretization [32]. Runge-Kutta 4th-order explicit time-stepping is used for time-marching in pseudo-time. A timescale spatial discretization is applied for interpolations from finite-volume elements to faces [31]. The present code is tested for circular pipes with open channel (subcritical, supercritical) and surcharged flow, but the underlying algorithm is not strictly limited to pipe flow. PipeAC is coded in Python (v3.7) and is available as public domain software [33]. Investigation of the practical implementation of the method in a large network requires further development of an efficient compiled code, which is an ongoing project of the NCIMM research team in developing a new computational engine for the widely-used Storm Water Management Model (SWMM) [31,34].

This paper provides a background on modeling in Section 2, which motivates using artificial compressibility for pipe network simulation. In Section 3, the governing equations for finite-volume artificial compressibility are derived. The numerical approach of PipeAC is described in Section 4. Conditions for unsteady flow test cases developed from the experiments of Trajkovic Ivetic et al. [35] are outlined in Section 5. Results and discussion are provided in Section 6 and Section 7, respectively. Conclusions in Section 8 summarize the present findings.

2. Background

2.1. Challenges of Surcharged Pipe in a Stormwater Drainage Network

Stormwater systems are generally designed to carry the hydrological runoff from a “design storm” as a gravity-driven flow with a free surface. Design conditions requiring a full pipe, i.e., pressurized or “surcharged,” are usually reserved for a few locations where pipes are either deeply buried or the pipe size for free-surface flow is impractical. However, the spatial and temporal variability of many real-world storms will exceed the design storm and cause surcharged conditions at a variety of locations across a system. Surcharged pressures can lead to water levels that back up through the curb inlets and cause flooding on the street, so modeling the occurrence and system behaviors for the transitions between free-surface and surcharged flow is critical to many of the stormwater modeling applications discussed in Section 1, above.

Where storm sewers flow with an unpressurized free surface the hydrostatic Saint-Venant equations provide the relationships between mass and momentum transport. In contrast, closed conduit flow (i.e., surcharged pipe) can be considered either compressible flow for transient analysis [36,37] or as a series of quasi-steady incompressible flow solutions as in the gradient algorithms used in the widely-used EPANET code for water distribution systems [38,39]. A challenge for large-scale network modeling is that rapid events can be significant to operations [40,41,42], but are difficult to represent in system-wide models [43,44,45]. Modeling pressure transients in a surcharged pipe moving at acoustic velocities requires numerical methods that are stable at large Courant-Friedrichs-Lewy (CFL) numbers or use very small time steps [46,47]. Such transient solvers have yet to be demonstrated capable of solving large stormwater networks, so efficiently handling the incompressibility approximation—as in the widely-used SWMM code [48]—remains an ongoing challenge. The problem with incompressibility is that it treats the pressure celerity as infinite rather than as an acoustic speed. To maintain mass conservation throughout a system the pressure wave indicating that mass moves into a surcharged pipe section must be instantaneously transmitted through all the connected surcharged sections. In effect, the use of the incompressibility constraint neglects nonlinear advection for 1D equations in the surcharged pipe; i.e., $u\partial u/\partial x=0$ for velocity ($u)$ in a uniform diameter pipe with incompressible flow.

2.2. Hyperbolic (Free Surface) vs. Elliptic (Surcharged) Continuity Equations

Stormwater network models must be able to handle both surcharged and free-surface flows. Invoking the incompressibility constraint at the boundary between a section of free-surface flow and a section of surcharged pipe flow has the mathematical effect of changing the continuity equation from hyperbolic to elliptic, which can be readily illustrated with two common 3D forms of mass conservation:

$$\begin{array}{c}\hfill \mathsf{h}\mathsf{y}\mathsf{p}\mathsf{e}\mathsf{r}\mathsf{b}\mathsf{o}\mathsf{l}\mathsf{i}\mathsf{c}:\frac{\partial \eta }{\partial t}+u\frac{\partial \eta }{\partial x}+v\frac{\partial \eta }{\partial y}=w,\mathsf{e}\mathsf{l}\mathsf{l}\mathsf{i}\mathsf{p}\mathsf{t}\mathsf{i}\mathsf{c}:\frac{\partial u}{\partial x}+\frac{\partial v}{\partial y}+\frac{\partial w}{\partial z}=0,\end{array}$$

where u,v,w are Cartesian velocities in x,y,z directions and $\eta$ is a free surface elevation. The hyperbolic form is derived from continuity and the kinematic boundary condition (integrated over depth) [49]. In contrast, the elliptic form (without a free surface) arises from requiring a divergence-free velocity field for an incompressible flow [50]. The hyperbolic equation is prognostic as it can be integrated forward in time from some known past state to predict a future state. In contrast, the elliptic equation is diagnostic in that it is a constraint that must be instantaneously satisfied everywhere at every instant in time; i.e., it cannot be simply integrated forward in time but is inherently both a local and (integrated) global constraint on the fluid behavior. In contrast to continuity, the conservation of momentum is inherently prognostic for both free surface and surcharged flows; thus, coupling the hyperbolic free surface continuity with momentum provides an equation set that is marched forward in time for both velocity and volume, whereas coupling the elliptic incompressible continuity with momentum requires solution of a time-marching equation for velocity with a local/global volume constraint.

The distinction between hyperbolic and elliptic forms is important as numerical solution methods for hyperbolic problems generally perform poorly on elliptic problems and vice-versa. The hyperbolic equation can be thought of as providing “local” solutions, where effects at point x propagate some limited distance $\Delta x$ in time step $\Delta t$ based on celerity $\mathcal{C}$, whereas the elliptic equation are “non-local” requiring any change at x must instantaneously affect the entire domain. There are two canonical approaches to this problem for stormwater systems: (i) introduction of an approximate hyperbolic equation for the incompressible pipe flow, and (ii) switching the governing equations to the incompressible form at the boundaries between free-surface and surcharged flow. The “Preissmann Slot” [51,52] is an example of the former approach and the head perturbation equation for surcharged flow in SWMM5 is an example of the latter (see Equations (3)–(25) in Rossman [48]).

2.3. The Preissmann Slot: A Hyperbolic Approximation of Incompressible Surcharged Pipe

The Preissmann Slot approximates a surcharged closed conduit as a pipe with narrow, longitudinal slot at the crown that has walls extending infinitely high on either side. This imaginary pipe-slot combination can never be surcharged. Instead, there will always be a free surface somewhere in the slot whose gradients provide the driving force in the surcharged pipe. An advantage of this approach is that the Saint-Venant equations apply in both free-surface and surcharged sections [53,54], which theoretically allows a smooth solution across the transition. However, a pressure celerity shock at the transition may still exist if (i) the hydrostatic pressure rises rapidly in the surcharged section, or (ii) the transition from open to surcharged includes a hydraulic jump. Furthermore, the slot alters local mass conservation by allowing a small amount of water to be stored/transported in the slot volume above the pipe; however, global mass conservation can be sustained if the underlying algorithm is mass conservative. The key algorithmic point is that pressure celerity in the Saint-Venant solution will be at a wave speed that is slower than the acoustic velocity. As noted in Cunge and Wegner [51], the wave speed for the Preissmann Slot is a function of gravity, the pipe cross-sectional area, and the slot width.

Numerical approaches that directly use the incompressibility constraint might seem less ad hoc than the Preissmann Slot, but that viewpoint is arguable. Incompressibility replaces the very fast (but finite) real-world pressure celerity with an infinite celerity—an instantaneous transmission of information that is clearly non-physical. The Preissmann Slot treats the pressure celerity by slowing it down below the acoustic speed—while clearly not the correct speed it is, at least, a plausible physical speed. In effect, the incompressibility approximation imagines the water as a solid that can be pushed through a pipe without deformation whereas the Preissmann Slot imagines the fluid as somewhat more compressible than water. Thus, incompressibility and the Preissmann Slot are merely alternative approximations of the true pressure celerity. Neither is correct, and whether a slower celerity or an infinite celerity is preferable depends on the problem being investigated, the numerical algorithm, and the types of errors that are acceptable. Interestingly, the Artificial Compressibility (AC) method provides some insights into the relationship between the Preissmann Slot and incompressible flow methods, as discussed below.

2.4. Artificial Compressibility for a Hyperbolic Continuity Solution That Is Exactly Incompressible

Chorin [27] proposed the Artificial Compressibility (AC) method as a way to change the form of the steady incompressible equations from elliptic to hyperbolic for a more tractable numerical solution while still solving the incompressible equations. Chorin’s innovation was to see that artificial unsteady terms could be added to the steady-state incompressible continuity and momentum equations to create equations that could be time-marched in pseudo-time, $\tau$, i.e., adding terms of the form $\partial \mathrm{\Psi }/\partial \tau$, where $\mathrm{\Psi }$ is merely a place-holder for solution variables in the present exposition. The steady-state incompressible solution is recovered by marching the AC momentum and continuity equations forward in pseudo-time until $\partial \mathrm{\Psi }/\partial \tau =0$. Thus, the AC approach creates a prognostic equation for continuity in pseudo-time that will satisfy the diagnostic constraint of incompressibility when converged to the pseudo-time steady state.

The steady-state incompressible AC method of Chorin [27] was later extended to both compressible and unsteady flows [55,56,57]. For unsteady flows the AC method is sometimes known as a “dual time-stepping” approach [58] as it includes a time-march in real-time and a separate time-march in pseudo-time. The “outer-loop” solution over real-time step $\Delta t$ for step n to $n+1$ requires some number of “inner-loop” iterations in $\Delta \tau$, where these inner-loop iterations are a consistent set of hyperbolic equations that are not subtime steps of $\Delta t$. That is, $\sum \Delta \tau >\Delta t$ is allowed (although not required). For a fully-converged solution, the AC method is theoretically equivalent (to machine precision and numerical truncation error) to any other numerical solution of the incompressible flow equations—which is not true for the Preissmann Slot.

Both the Preissmann Slot and AC methods use solutions of hyperbolic equations for time-marching, the difference is that the AC method can be converged to ensure local mass-conservation (through inner iterations) whereas the Preissmann Slot will be locally non-conservative with a single step due to the change in storage in the slot. However, if inner-loop iterations are cut off when $\partial \mathrm{\Psi }/\partial \tau >0$, mass will not be exactly conserved in the AC method. Interestingly, an argument can be made that the Preissmann Slot is effectively the first $\Delta \tau$ step of an AC method where the AC parameter is tuned to the same celerity implied by the Preissmann Slot width. Alternatively, one might propose an inner iteration of the Preissmann Slot to obtain a method similar to AC. This speculative idea revisited in the discussion in Section 7.3 as it perhaps is easier to see after the new ideas for the AC celerity parameter are presented in Section 3.3.

2.5. The Relationship between the Artificial Compressibility Method and Elliptic Solvers

The AC method is an alternative to requiring an elliptic solver for the coupled diagnostic continuity and prognostic momentum equations of unsteady incompressible flow. The approaches are mathematically distinct but share some similarities [59,60]. The elliptic problem implies a matrix inversion over the entire domain, which requires some inner-loop iterations in a time-marching solution. Similar to the AC pseudo-time stepping, each inner-loop iteration in an elliptic solver is an approximate solution with some error that is characterized by failure to exactly conserve mass (i.e., a residual). Both AC and elliptic methods can theoretically converge to conservation at machine accuracy, but typically inner-loop iterations are stopped when the solution reaches some acceptable measure of the global residual. The key difference between the methods is that an elliptic solver uses the characteristics of the matrix to determine the solution perturbation at each iteration whereas the AC approach propagates information through the domain as artificial pressure waves. It can be argued that the artificial pressure waves are more tractable for the mathematically stiff systems of stormwater networks where (i) surcharging is variable in both space and time, and (ii) identifying well-posed boundary conditions at each open-channel/surcharge interface can be a problem.

The AC approach is appealing because it is (i) simple to code, (ii) can use widely-tested hyperbolic numerical schemes, (iii) does not require a matrix inversion, and (iv) is stable as long as the artificial compressibility parameter is chosen carefully and the pseudo-time-stepping satisfies a CFL condition. However, the AC method can require small steps in pseudo-time, which can be computationally expensive—especially in an unsteady scheme with dual time-stepping. In general, over some interested real-time duration $t_1$ to $t_2$ an AC method will require more total outer and inner-loop iterations than an elliptic solver (hence more floating point operations) to reach a desired convergence norm. In the 1980s, elliptic solvers for the incompressible flow equations received a boost from Patankar’s SIMPLE algorithm [61], which has roots in Chorin’s projection method [28] as a splitting form of incompressible solution. Adoption of efficient elliptic solvers was supported by the LINPACK and later LAPACK software libraries for matrix solutions. While AC methods never entirely disappeared from the literature, their advancement for incompressible flow was overwhelmed by advances in elliptic solvers through the 1990s and early 2000s. Nevertheless, the overall simplicity and hyperbolicity of AC schemes saw their continued use well into the 1990s in adaptive multigrid [62] and unsteady flows [63,64,65].

2.6. Recent Development of the Artificial Compressibility Method

It appears that Sotiropolous in the late 1990s was the first to note that AC methods hold particular promise for vector and parallel computing of incompressible flows [30]; an idea that was further developed in a series of papers over a decade [66,67,68]. For parallel computing, the advantage of AC is that it replaces the global solution of an elliptic matrix inversion with local hyperbolic wave propagation. This “local” limitation means that communication between processors is readily predicted and controlled—A critical issue today because the death of Moore’s law for computer clock speed [69] implies that high-performance computing on large problems is limited by the communication bandwidth between processors rather than the number of floating point operations [70]. Indeed, The rapid increase in parallel computing has also seen a resurgence of interest in AC methods since 2004, e.g., [71,72,73]. Research has included multifluid flows [74,75], compressible flow [76], incompressible flow [77], shear-thickening and shear-thinning fluids [78], and a link-wise discretization similar to Lattice-Boltzmann methods [79]. Foundations for characteristic-based methods were developed as an an early part of this work [80,81,82], and have been studied for higher accuracy discretizations [83,84]. A relatively new addition has been an entropically-damped formulation [85], which substitutes a thermodynamic approximation for the simple artificial compressibility of Chorin [27].

Indeed, from these rather modest foundations the research using AC methods has exploded over the last five years. More than 200 papers were retrieved by database searches for 2015–2020 using the terms artificial compressibility, pseudo compressibility, and dual time stepping. These studies include analysis of the relationships between AC and fractional step methods [86,87], studies of turbulent flow [88,89,90], development of discontinuous Galerkin methods [91,92,93], parallel solution of large-scale problems [94,95,96], multi-fluid simulations [97], further advances to entropically-damped AC methods [98,99,100], implementation high-order numerical schemes [101,102,103], use of characteristic methods [104,105,106], application for non-hydrostatic effects [107,108], magneto-hydrodynamic simulations [109,110,111], solution with lattice Boltzmann methods [112], and solution by smoothed particle hydrodynamics [113,114]. Note the above are examples and should not be considered an exhaustive list of recent work. For those seeking deeper theoretical understanding, the mathematical foundations of AC are derived in detail by Lemarie-Rieusset [115].

In summary, the AC method is an established numerical approach with a long history in 2D and 3D incompressible flow simulation. Arguably, the AC method holds potential for being efficient for solution of large 1D pipe networks solved on massively-parallel computers. However, only a single work, that of Bassi et al. [116], uses the AC method in a 1D model, and none of the applications in the literature consider the use of AC for transitions between free-surface and pressurized flow (as studied herein).

The remainder of this paper demonstrates that the AC method can be effectively used to model the unsteady transitions between supercritical, subcritical, and surcharged flows that commonly occur in stormwater systems.

3. Governing Equations

3.1. Finite-Volume Continuity and Momentum

To avoid the complexities of dealing with the short time and space scales of non-hydrostatic pressure [117], models for free surface flows commonly use the “shallow water” equations that include the Boussinesq, hydrostatic, and incompressibility approximations, e.g., [118]. Following the approach of Hodges [119], the incompressible, hydrostatic, 1D equations for mass and momentum conservation can be written for a finite volume with a free surface as

$$\begin{array}{cc}\hfill L_e\frac{\partial A_e}{\partial t}& =Q_u-Q_d+q_e{L}_e,\hfill \end{array}$$

(1)

$$\begin{array}{cc}\hfill L_e\frac{\partial Q_e}{\partial t}& ={\beta }_u{Q}_u{U}_u-{\beta }_d{Q}_d{U}_d+g{A}_u{\eta }_u-g{A}_d{\eta }_d+g\left(A_d-A_u\right){\int }_L\eta \left(x\right)\lambda \left(x\right)\mathrm{d}x-g{V}_e{S}_{f\left(e\right)},\hfill \end{array}$$

(2)

where Q is a flow rate, U is a corresponding average velocity, A is a cross-sectional flow area, $\eta$ is the water surface elevation, g is gravity, L is an element length, q is a leakage inflow per unit length along a volume, and subscripts $e,u,d$ represent the finite-volume element, the nominal upstream face, and the nominal downstream face, respectively. The coefficient $\beta$ is the standard nonlinear velocity integration coefficient (e.g., [119]). A uniform approximation of $\beta =1$ is typically used for 1D models, and is adopted herein so that $\beta$ can be dropped from subsequent equations. The term $S_f$ in Equation (2) is the friction slope that represents the normalized energy dissipation rate over the finite-volume element. The $\eta \left(x\right)\lambda \left(x\right)$ term is a quadrature function introduced by Hodges [119] that represents the nonlinear effects of spatial variability of both the free surface and the conduit or channel shape on the integrated piezometric pressure over a finite-volume element. By definition, $\lambda$ is a weighting function that must satisfy

$$\begin{array}{c}\hfill {\int }_L\lambda \left(x\right)\mathrm{d}x=1.\end{array}$$

The choice of different $\eta \lambda$ discretizations leads to different approximations of the effects of spatially-varying piezometric pressure over a control volume. Derivation of the above is presented in detail by Hodges [119].

The above are a finite-volume form of the Saint-Venant equations for free-surface flow, but they can be readily converted to equations for pressurized pipe flow if we neglect non-hydrostatic pressure and consider a piezometric pressure defined as $P\equiv \rho gH$. Thus, by simply substituting $\eta =H$ we arrive at an equivalent set of equations that apply to a finite volume of pressurized pipe with piezometric head H.

3.2. Artificial Compressibility for Continuity

The AC method introduced by Chorin [27] can be represented as a pseudo-time derivative of density added to the governing equations. For continuity this becomes:

$$\begin{array}{cc}\hfill \frac{1}{{\rho }_0}\frac{\partial }{\partial \tau }{\int }_V\tilde{\rho }\mathrm{d}V+L_e\frac{\partial A_e}{\partial t}& =Q_u-Q_d+q_e{L}_e\hfill \end{array}$$

(3)

where ${\rho }_0$ is the reference or “incompressible” density of the fluid, $\tilde{\rho }$ is an artificial density, and $\tau$ is pseudo-time. A more recent alternative approach is the “entropically-damped artificial compressibility” (EDAC) formulation that adds a scaled Laplacian of pressure to continuity [85,98,99]. For simplicity, the present work will use the classic AC approaches of Chorin [27] and Rogers et al. [32] that are consistent with Equation (3).

The AC method requires that as $\tau \to \infty$ there must be a steady-state (in pseudo-time) such that $\partial /\partial \tau \to 0$ and incompressible continuity, Equation (1), is recovered. As described in Breuer and Hänel [120], we introduce an artificial equation of state $\tilde{p}={\gamma }^2\tilde{\rho }$, where $\tilde{p}$ is a pressure and $\gamma$ is the artificial speed of sound (units of LT${}^{-1}$), i.e., the propagation speed of a pressure disturbance across pseudo-time $\tau$. Note that the literature generally uses $\beta$ instead of $\gamma$ in the artificial equation of state, but we reserve $\beta$ for the momentum coefficient in Equation (2), which is common nomenclature for 1D open-channel flows. It follows that the pseudo-time derivative in Equation (3) can be written as

$$\begin{array}{c}\hfill \frac{1}{{\rho }_0{\gamma }^2}\frac{\partial }{\partial \tau }{\int }_V\tilde{p}\mathrm{d}V.\end{array}$$

As $\partial /\partial \tau \to 0$ we require $\tilde{p}\to p+c$, where p is the true pressure and c is a constant, which implies spatial gradients are preserved, i.e., $\partial \tilde{p}/\partial x=\partial p/\partial x$. Note that $c=0$ will generally be obtained when the boundary conditions for $\tilde{p}$ are Dirichlet. Consistent with the open-channel Saint-Venant equations, the combination of hydrostatic pressure and potential energy can be represented as piezometric pressure (i.e., $\rho g\eta$), so an artificial piezometric pressure can be defined as $\tilde{P}\equiv \tilde{p}+{\rho }_{0}gz$ where z is the vertical elevation above the baseline $z=0$. It follows that $\tilde{p}=\tilde{P}-{\rho }_{0}gz$. In general, it will be convenient to work in terms of an artificial piezometric head (i.e., the equivalent static water elevation, or $\eta$, in a free surface flow), i.e., $\tilde{H}\equiv \tilde{P}{\left({\rho }_{0}g\right)}^{-1}$. With the above, Equation (3) for continuity becomes

$$\begin{array}{cc}\hfill \frac{g{L}_e}{{\gamma }^2}\frac{\partial }{\partial \tau }\left({\tilde{H}}_e{A}_e\right)+L_e\frac{\partial A_e}{\partial t}& =Q_u-Q_d+q_e{L}_e\hfill \end{array}$$

(4)

Although the above was originally derived for an open-channel flow, it becomes an equation for a closed-conduit flow by requiring $\partial A_e/\partial t=0$.

3.3. Choosing an Artificial Speed of Sound

The choice of $\gamma$, the artificial speed-of-sound (or pressure celerity), in Equation (4) plays a role in the robustness of an AC method. Typically $\gamma$ is taken as a uniform, constant parameter (e.g., [32,60,66,121]). Indeed, a global $\gamma =1$ is often a default in artificial compressibility studies (e.g., [30,56,122,123]), although higher values are also found (e.g., [62,78,124]). A wide range of studies fail to document the values used for $\gamma$; likely because it formally controls convergence rates rather than accuracy (e.g., [73,77,81,83,120])—although it can also affect the simulation result for upwind schemes [124]. Methods have been developed to select an optimum global $\gamma$ based on flow characteristics and/or model time step (e.g., [63,64,125,126,127]), or using mesh spacing [72], or as a preconditioning parameter for a solution matrix [128]. For the present purposes, a key observation is that from a mathematical standpoint $\gamma$ is a coefficient of the $\partial /\partial \tau$ term that is an ad hoc addition to continuity; thus, $\gamma$ is not related to any gradients in space and can be considered an arbitrary and independent value for any control volume. Although not expressly stated, this idea is implicit in [74] where $\gamma$ is a local dynamic function of the flow for an “artificial fluid” with “pseudotime stretching.” For the present work, it is useful to follow [74] in treating $\gamma$ as a local function of space and pseudo-time, which we will represent as ${\gamma }_e$ for a finite-volume element.

Let us introduce a length scale ℓ that is a local function of the flow geometry and pressure head (as described further below) and hence denoted as ${\ell }_e$ for a finite-volume element. Multiplying continuity, Equation (4), by ${\ell }_e/L_e$, provides

$$\begin{array}{cc}\hfill \frac{g{\ell }_e}{{\gamma }_e^2}\frac{\partial }{\partial \tau }\left({\tilde{H}}_e{A}_e\right)& ={\ell }_e\left\{-\frac{\partial A_e}{\partial t}+\frac{Q_u-Q_d}{L_e}+q_e\right\}.\hfill \end{array}$$

(5)

Although ${\ell }_e$ is arguably arbitrary, defining it as a modified hydraulic depth (varying with both pseudo-time and location) has some particular advantages. We will let ${\ell }_e$ represent the hydraulic depth associated with an imagined free surface flow for $\eta =\tilde{H}$ where the closure of the conduit is neglected. To elaborate, let $z_{\left(c\right)e}$ be the crown height of a closed-conduit element (i.e., the elevation of the top inside that is representative of the entire element). Define $B_{\left(m\right)e}$ as the maximum breadth of the conduit, which occurs at some elevation $z_{\left(m\right)}$ near the conduit midpoint. Let $B_e$ be the actual breadth (topwidth) at the free surface when ${\tilde{H}}_e<z_{\left(c\right)e}$. Furthermore, let $A_{\left(m\right)e}$ represent the cross-sectional area of the conduit below the location of maximum breadth, $z_{\left(m\right)}$. It follows that a modified hydraulic depth can be defined as

$$\begin{array}{c}\hfill {\ell }_e\equiv \{\begin{array}{cc}{A}_e{B}_e^{-1}\hfill & {\tilde{H}}_e<z_{\left(m\right)e}\\ \left[\left({\tilde{H}}_e-z_{\left(m\right)e}\right)B_{\left(m\right)}+A_{\left(m\right)e}\right]B_{\left(m\right)e}^{-1}\hfill & {\tilde{H}}_e\ge z_{\left(m\right)e}\end{array}\end{array}$$

(6)

The above assigns ${\ell }_e$ for a free surface flow below the maximum conduit width using the traditional definition of hydraulic depth. However, for a free surface flow above the maximum conduit width and for any closed conduit flow, ${\ell }_e$ is the hydraulic depth as imagined for a flow with free surface ${\eta }_e={\tilde{H}}_e$ in an open channel with vertical sidewalls beginning at the widest elevation of the conduit. The purpose of this approach is that we can define a local non-dimensional number ${\mathcal{F}}_e$ for each element as

$$\begin{array}{c}\hfill {\mathcal{F}}_e\equiv \frac{{\gamma }_e}{\sqrt{g{\ell }_e}}\end{array}$$

(7)

where ${\mathcal{F}}_e$ is a form of Froude number relating the AC pressure celerity (${\gamma }_e$) to the gravity wave speed at hydraulic depth ${\ell }_e$. We can now write the AC continuity equation as

$$\begin{array}{cc}\hfill \frac{\partial }{\partial \tau }\left({\tilde{H}}_e{A}_e\right)& ={\ell }_e{\mathcal{F}}_e^2\left\{-\frac{\partial A_e}{\partial t}+\frac{Q_u-Q_d}{L_e}+q_e\right\}.\hfill \end{array}$$

(8)

In dealing with liquid flow in a pipe, it is reasonable to take ${\mathcal{F}}_e=1$, which is equivalent to ${\gamma }_e=\sqrt{g{\ell }_e}$. That is, the AC pressure celerity is selected to locally slow the speed of acoustic pressure waves in pseudo-time to the speed of an equivalent gravity wave on hydraulic depth ${\ell }_e$. The advantage of this approach is it automates the selection of ${\gamma }_e$ and ensures a local value that is consistent with the value ${\tilde{H}}_e$, which thus allows smooth transition from open-channel flow to surcharged flow. This approach also makes it trivial to choose a pseudo time-step size that satisfies the local CFL condition for the artificial pressure wave.

3.4. Artificial Compressibility for Momentum

Derivation of the AC equation for momentum is simpler as it requires adding only a pseudo-time derivative of the integrated momentum, $Q_e{L}_e$, to Equation (2) and replacing the piezometric head ($\eta$) with the AC head ($\tilde{H}$). The integrated piezometric pressure term involving quadrature of $\eta$ and $\lambda$ can be represented by the $T_{(2,0)}$ approach of Hodges [119], which approximates the piezometric pressure distribution across a finite-volume element by a parabola with a uniform $\lambda \left(x\right)=L_e^{-1}$. This approximation modifies the coefficient of the $gA\tilde{H}$ terms in Equation (2) and provides a source term of

$$\begin{array}{c}\hfill K_e\equiv \frac{g}{6}\left[A_d\left({\tilde{H}}_u+4{\tilde{H}}_e\right)-A_u\left({\tilde{H}}_d+4{\tilde{H}}_e\right)\right].\end{array}$$

(9)

The friction term $\left(gV{S}_f\right)$ from Equation (2) is represented by a model for the friction slope of $S_f=FU\left|U\right|$ or $gV{S}_f=gFLQ\left|U\right|$ where F is a dimensional friction coefficient that depends on the type of turbulence model applied. Basic friction models are

$$\begin{array}{cc}\hfill F& \equiv \{\begin{array}{ccc}\frac{{\tilde{n}}^2}{R_h^{4/3}}& :& \mathrm{Chezy-Manning}\mathrm{model}\\ \frac{f_P}{2g{D}_h}& :& \mathrm{Darcy-Weisbach}\mathrm{model}\end{array}\hfill \end{array}$$

(10)

where $\tilde{n}$ is the Gauckler-Strickler-Manning open-channel friction coefficient, $R_h$ is the hydraulic radius, $f_P$ is the Darcy friction factor for pipe flow, and $D_h$ is the hydraulic diameter. For the present version of PipeAC, only the Chezy-Manning model is used.

With the above substitutions, Equation (2) can be written as

$$\begin{array}{cc}\hfill \frac{\partial Q_e}{\partial \tau }=& -\frac{\partial Q_e}{\partial t}+\frac{1}{L_e}\left\{Q_u{U}_u-Q_d{U}_d+\frac{5}{6}g{A}_u{\tilde{H}}_u-\frac{5}{6}g{A}_d{\tilde{H}}_d+K_e-g{F}_e{L}_e{Q}_e\left|U_e\right|\right\}\hfill \end{array}$$

(11)

where $\beta =1$ is implied. The 5/6 coefficient for the $g{A}_u{H}_u$ and $g{A}_d{H}_d$ terms—as compared to unity implied by Equation (2)—arise from the $T_{(2,0)}$ approximation of the $\int \eta \lambda \mathrm{d}x$ term of Equation (2), which is consistent with the $K_e$ source term of Equation (9). The detailed derivation is presented by Hodges [119].

3.5. Solution Variables

For the present work, it is convenient to take $Q_e$ and either $A_e$ or $H_e$ as the principal solution variables, (as discussed in Section 4.2, below) with the provision that the element velocity is recovered by $U_e=Q_e{A}_e^{-1}$ and the element volume by $V_e=A_e{L}_e$. Furthermore, as $\partial /\partial \tau \to 0$ we have $\tilde{H}\to H+c$, where H is the true piezometric head and c is a constant. If physical Dirichlet boundary conditions on $\tilde{H}$ are provided we will have $c=0$ and $\tilde{H}=H$. Thus, in the discrete equations it is convenient to replace $\tilde{H}$ with H, keeping in mind that H only represents the true piezometric head at convergence to a pseudo steady-state. For simplicity, PipeAC is confined to fixed geometry where $L_e$ and geometry relationships of $A_e\left(z\right)$ are static.

4. Numerical Method

4.1. Overview

The new PipeAC numerical method is designed to solve the dual time-stepping, finite-volume, 1D problem posed by Equations (8) and (11) for both free-surface and surcharged flow in a closed conduit. In the following, the semi-discrete form of these prognostic equations is presented in Section 4.2, the discrete form for auxiliary terms in Section 4.3, interpolation of element values to faces in Section 4.4, handling of hydraulic jumps in Section 4.5 and a Runge-Kutta 4th order (RK4) time-marching scheme is presented in Section 4.6. Details of the linearized friction term in the RK4 are presented in Appendix A).

4.2. Semi-Discrete Governing Equations

The real-time derivatives in continuity, Equation (8), and momentum, Equation (11), for an AC method can be approximated with a semi-discrete stencil of the general form

$$\begin{array}{c}\hfill \frac{\partial \varphi }{\partial t}=\frac{1}{\Delta t}\left(a_1{\varphi }^{n+1}+a_2{\varphi }^n+a_3{\varphi }^{n-1}+...\right)\end{array}$$

(12)

where superscripts indicate discrete time levels. Using $a_j\in \left\{3/2,-2,1/2,0,0,...\right\}$ provides a 3-level backwards stencil as applied by Rogers et al. [32]. Similarly, a 2-level backwards stencil is defined as $a_j\in \left\{1/2,-1/2,0,0,...\right\}$. Using a general backwards stencil of $N_B$ terms the pseudo-time semi-discrete finite-volume formulation of Equation (11) can be written as

$$\begin{array}{c}\hfill \frac{\partial Q_e}{\partial \tau }=-\frac{a_1}{\Delta t}{Q}_e^{n+1}-\frac{1}{\Delta t}\sum _{j=2,N_B}{a}_j{Q}_e^{n+2-j}-gF{Q}_e\left|U_e\right|+S_e\end{array}$$

(13)

where the source term is

$$\begin{array}{cc}\hfill S_e& \equiv \frac{1}{L_e}\left\{Q_u{U}_u-Q_d{U}_d+\frac{5}{6}g\left[A_u{H}_u-A_d{H}_d\right]+K_e\right\}.\hfill \end{array}$$

(14)

Note that the friction term $gF{Q}_e\left|U_e\right|$ is separated from the $S_e$ source term in this nomenclature as friction is handled implicitly within the pseudo-time marching (as discussed in Section 4.6 below and derived in Appendix A) whereas $S_e$ is strictly the explicit source term. PipeAC is coded with both 2-level and 3-level implicit stencils, but only the 3-point stencil was used in the present work.

The semi-discrete form of continuity, Equation (8), can be manipulated into different forms for open-channel versus surcharged conduits. Open-channel continuity presents a challenge as $H_e=f\left(A_e\right)$, which implies a nonlinear term in the $\partial /\partial \tau$ on the LHS of Equation (8) that will depend on conduit geometry. For simplicity, in open-channel flows we seek an artificial compressibility equation of the form $\partial A_e/\partial \tau =S$. The reason for using $A_e$ rather than $H_e$ as the solution variable for open-channel flow is that small changes in $H_e$ can cause relatively large changes in $A_e$ (depending on conduit shape). In contrast, small changes in $A_e$ will always result in small changes in $H_e$ for any practical conduit cross-section. Using the chain rule and product rule for differentiation, it can be shown that

$$\begin{array}{c}\hfill \frac{\partial HA}{\partial \tau }=G\frac{\partial A}{\partial \tau }\mathsf{w}\mathsf{h}\mathsf{e}\mathsf{r}\mathsf{e}G\equiv A\frac{\partial H}{\partial A}+H.\end{array}$$

The semi-discrete form of Equation (8) for an open channel using a general backwards stencil is then

$$\begin{array}{c}\hfill \frac{\partial A_e}{\partial \tau }=\frac{{\ell }_e{\mathcal{F}}_e^2}{G_e}\left\{-\frac{a_1}{\Delta t}{A}_e^{n+1}-\frac{1}{\Delta t}\sum _{j=2,N_B}{a}_k{A}_e^{n+2-j}+\frac{Q_u-Q_d}{L_e}+q_e\right\}\end{array}$$

(15)

where G is considered a geometric coefficient that can be treated explicitly in the time-marching scheme.

For a surcharged conduit, continuity is simpler as $A_e$ is constant and hence is factored out of the $\partial /\partial \tau$ term in Equation (8). Furthermore, the real-time derivative of $A_e$ is also identically zero in a closed conduit. The resulting surcharged conduit artificial compressibility equation is

$$\begin{array}{c}\hfill \frac{\partial H_e}{\partial \tau }=\frac{{\ell }_e{\mathcal{F}}_e^2}{A_e}\left\{\frac{Q_u-Q_d}{L_e}+q_e\right\}.\end{array}$$

(16)

Equations (13), (15) and (16) constitute the dual-time marching system of PipeAC that is applicable in a system with mixed open-channel and surcharged conduits. From any discrete time step n in real time we take pseudo-time steps $m=\left\{1,2,3...\right\}$ until we reach a pseudo-time steady-state $(\partial /\partial \tau =0)$, at which point we will have converged to the discrete real-time march equations for the unknown $n+1$ step:

$$\begin{array}{cc}\hfill \mathsf{m}\mathsf{o}\mathsf{m}\mathsf{e}\mathsf{n}\mathsf{t}\mathsf{u}\mathsf{m}:& Q_e^{n+1}=\frac{1}{a_1}\left\{\sum _{j=2,N_B}{a}_k{Q}_e^{n+2-j}-\Delta tgF{Q}_e\left|U\right|+\Delta t{S}_e\right\},\hfill \end{array}$$

(17)

$$\begin{array}{cc}\hfill \mathsf{o}\mathsf{p}\mathsf{e}\mathsf{n} \mathsf{c}\mathsf{h}\mathsf{a}\mathsf{n}\mathsf{n}\mathsf{e}\mathsf{l}:& A_e^{n+1}=\frac{1}{a_1}\left\{\sum _{j=2,N_B}{a}_k{A}_e^{n+2-j}+\frac{\Delta t}{L_e}\left(Q_u-Q_d\right)+\Delta t{q}_e\right\},\hfill \end{array}$$

(18)

$$\begin{array}{cc}\hfill \mathsf{s}\mathsf{u}\mathsf{r}\mathsf{c}\mathsf{h}\mathsf{a}\mathsf{r}\mathsf{g}\mathsf{e}\mathsf{d} \mathsf{c}\mathsf{o}\mathsf{n}\mathsf{d}\mathsf{u}\mathsf{i}\mathsf{t}:& 0=Q_u^{n+1}-Q_d^{n+1}+q_e^{n+1}{L}_e.\hfill \end{array}$$

(19)

Equation (17) is the converged, real-time, unsteady momentum solution that applies to every element (both open and surcharged). In contrast only one of Equations (18) or (19) is the converged, real-time, unsteady continuity solution on a computational element. In PipeAC, an element is evaluated as being either “open-channel” or “surcharged” for selecting the governing continuity equation at the beginning of each pseudo-time step. Thus, an element cannot change status during substeps of the RK4 advance (Section 4.6) but can change status during at the end of a $\Delta \tau$ step of the pseudo-time march.

4.3. Discrete Equations, Other Terms

To complete the set of semi-discrete, pseudo-time marching Equations (13), (15) and (16) requires geometric definitions and interpolations of finite-volume element values (subscript e) to face values (subscripts $d,u$). The interpolation approach is discussed in Section 4.4, below. A summary of the geometrical relationships used on elements to close the equation set are:

$$\begin{array}{c}\hfill \begin{array}{ccc}H=f\left(A\right)\hfill & :& \mathrm{open}\mathrm{channel}\mathrm{geometry},\hfill \\ B=f\left(A\right)\hfill & :& \mathrm{open}\mathrm{channel}\mathrm{top}\mathrm{width},\hfill \\ L_w=f\left(A\right)\hfill & :& \mathrm{open}\mathrm{channel}\mathrm{wetted}\mathrm{perimeter},\hfill \\ L_c=f\left(\mathrm{shape}\right)\hfill & :& \mathrm{surcharged}\mathrm{conduit}\mathrm{circumference},\hfill \\ R_h=A{L}_w^{-1}\hfill & :& \mathrm{hydraulic}\mathrm{radius},\hfill \\ D_h=A{L}_c^{-1}\hfill & :& \mathrm{hydraulic}\mathrm{diameter},\hfill \\ \partial H/\partial A=f\left(A\right)\hfill & :& \mathrm{open}\mathrm{channel}\mathrm{head}-\mathrm{geometry}\mathrm{relationship},\hfill \\ \ell =\mathrm{see}\mathrm{Equation}\left(6\right)\hfill & :& \mathrm{modified}\mathrm{hydraulic}\mathrm{depth},\hfill \\ U=Q{A}^{-1}\hfill & :& \mathrm{average}\mathrm{velocity}.\hfill \end{array}\end{array}$$

(20)

Geometry definitions for the finite-volume elements in PipeAC are considered characteristic values; e.g., the value of $A_e$ for a finite-volume element is considered an average for the volume rather than the value precisely at the element center. Thus, the volume of water in an element is recovered with $L_e{A}_e$ without reference to the slope of the pipe element or the slope of the free surface.

4.4. Timescale Interpolation from Finite-Volume Elements to Faces

Face values for a finite volume, e.g., $Q_u$, $A_d$, are determined by interpolation from the finite-volume element values. Here we follow the “timescale” approach [31], where the celerities of information from the cell center to the upstream and downstream faces are defined for each element and used for face interpolation. To briefly explain, it is convenient to temporarily abandon the $e,u,d$ subscripting that provides an element-centered view of the discretization and adopt the conventional i subscript as the index for a element center, with $i-1$ as an adjacent upstream element and $i+1$ as a downstream element. For the i element with the $i-1/2$ face in the upstream direction, the information celerity ($\mathcal{C}$) from the cell center to the upstream face is

$$\begin{array}{c}\hfill {\mathcal{C}}_{i-1/2[+]}\equiv U_i-\sqrt{g{\ell }_i}\end{array}$$

(21)

where the $[+]$ indicates the information approaching the $i-1/2$ face is from the $[+]$ downstream side and $\sqrt{g\ell }$ is the effective wave propagation speed at modified hydraulic depth ℓ. Similarly, the information speed from the i face to the $i+1/2$ face is given by

$$\begin{array}{c}\hfill {\mathcal{C}}_{i+1/2[-]}\equiv U_i+\sqrt{g{\ell }_i}.\end{array}$$

(22)

where the $[-]$ indicates information approaching the $i+1/2$ face from the $[-]$ upstream side. The provisional timescale of information transit from the i cell to a face is given by, e.g.,

$$\begin{array}{cc}\hfill {\mathcal{T}}_{i+1/2[-]}& =\frac{L_i}{2{\mathcal{C}}_{i+1/2[-]}}\hfill \end{array}$$

(23)

which is subject to limiters ${\mathcal{T}}_{\max }$ and ${\mathcal{T}}_{\min }$ such that where $\mathcal{T}<{\mathcal{T}}_{\min }$ the computed $\mathcal{T}$ is replaced by ${\mathcal{T}}_{\min }$. Similarly, where $\mathcal{T}>{\mathcal{T}}_{\max }$ we apply $\mathcal{T}={\mathcal{T}}_{\max }$. These limiters prevent negative, zero, or infinite timescales. With the above, the timescale interpolation of any variable ($\varphi$) from element values ${\varphi }_i$ and ${\varphi }_{i+1}$ to the face value ${\varphi }_{i+1/2}$ is given by linear weighting in timescales:

$$\begin{array}{c}\hfill {\varphi }_{i+1/2}=\left(\frac{{\mathcal{T}}_{i+1/2[+]}}{{\mathcal{T}}_{i+1/2[+]}+{\mathcal{T}}_{i+1/2[-]}}\right){\varphi }_i+\left(\frac{{\mathcal{T}}_{i+1/2[-]}}{{\mathcal{T}}_{i+1/2[+]}+{\mathcal{T}}_{i+1/2[-]}}\right){\varphi }_{i+1}.\end{array}$$

(24)

Timescale interpolation is used for $\varphi \in \left\{Q,A,T\right\}$ whereas H interpolation to the cell face uses conventional linear spatial interpolation based on the adjacent element lengths, e.g., $L_{i-1}$ and $L_i$ for the $L_{i-1/2}$ face. Face velocities are consistent with the interpolated flowrate and areas as $U_{i+1/2}=Q_{i+1/2}{A}_{i+1/2}^{-1}$. The timescale approach is advantageous as it smoothly switches between upwind weighted interpolation in supercritical flow to more centrally-weighted interpolation in subcritical flow. The spatial interpolation for H to the faces (rather than timescale interpolation) follows recommendations in Hodges and Liu [31], where it was noted that use of timescale interpolation for water surface elevation led to numerical instabilities that could not be readily controlled. The linear spatial interpolation for H ameliorates the problem, but still has a tendency to propagate energy to the subgrid scale causing V-shaped grid scale oscillations—which are annoying but not necessarily destabilizing. This problem is ameliorated in free-surface flows with a flowrate oscillation damping filter (Q-filter), which does not affect mass conservation but merely acts to dissipate momentum that is being passed down into grid-scale oscillations [31]. The Q-filter was used in the present work, but it was discovered that a similar damping filter was also needed for the surcharged pressure head in pipes. An equivalent H-filter can be derived by simply replacing Q with H in the flowrate oscillation damping filter presented in Hodges and Liu [31]—see their Equations (18)–(22). Herein, the H-filter only applies to surcharged cells and does not alter mass conservation.

4.5. Hydraulic Jumps

The PipeAC numerical method follows Hodges and Liu [31] in handling hydraulic jump conditions in an open channel. Briefly, a jump occurs when an upstream element i is supercritical and the downstream element $i+1$ is subcritical. When this occurs the face $i+1/2$ is characterized by two values of A and two values of H. The H on the supercritical side is the sum of the upstream flow depth and the conduit invert at the $i+1/2$ face. The subcritical side extrapolates the downstream element H to the jump face. In steeply sloping geometry it is possible to have a jump occur where the upstream $H_{i+1/2}$ would be higher than the downstream $H_{i+1/2}$; in such cases the jump is simply neglected and the standard interpolation approach is used. A limiter is invoked on the downstream jump elevation when the effective jump height would cause the downstream total energy head to exceed the upstream total energy head. This condition can occur as an occasional numerical artifact of simple extrapolation from the downstream H to the subcritical jump face. In this approach a hydraulic jump will always occur on a face, and each finite-volume element is either fully subcritical or fully supercritical. More sophisticated jump approaches are discussed and implemented in the SvePy open-channel code [129], but have not been investigated with PipeAC.

4.6. The RK4 Pseudo-Time March

The semi-discrete equations are marched forward in pseudo-time with a 3-level backwards implicit stencil in real time, similar to Rogers et al. [32]. A unique addition is the use of an implicit treatment of the linearized friction term in momentum, as described in Appendix A. The implicit friction treatment ensures that dissipation is always opposite the direction of the flow in any substep of the RK4, which ensures stability in reversing flows. The general RK4 approach for a step from m to $m+1$ in pseudo-time interval $\Delta \tau$ can be presented as

$$\begin{array}{c}\hfill {\varphi }^{m+1}={\varphi }^m+\frac{\Delta \tau }{6}\left(k^{\left(1\right)}+2k^{\left(2\right)}+2k^{\left(3\right)}+k^{\left(4\right)}\right)\end{array}$$

(25)

where

$$\begin{array}{cc}\hfill k^{\left(1\right)}& =C\mathrm{\Lambda }\left[S\left({\varphi }^m\right)+\mathrm{\Gamma }{\varphi }^m\right],\hfill \end{array}$$

(26)

$$\begin{array}{cc}\hfill k^{\left(2\right)}& =C\mathrm{\Lambda }\left[S\left({\varphi }^m+\frac{\Delta \tau }{2}{k}^{\left(1\right)}\right)+\mathrm{\Gamma }{\varphi }^m\right],\hfill \end{array}$$

(27)

$$\begin{array}{cc}\hfill k^{\left(3\right)}& =C\mathrm{\Lambda }\left[S\left({\varphi }^m+\frac{\Delta \tau }{2}{k}^{\left(2\right)}\right)+\mathrm{\Gamma }{\varphi }^m\right],\hfill \end{array}$$

(28)

$$\begin{array}{cc}\hfill k^{\left(4\right)}& =C\mathrm{\Lambda }\left[S\left({\varphi }^m+\Delta \tau k^{\left(3\right)}\right)+\mathrm{\Gamma }{\varphi }^m\right].\hfill \end{array}$$

(29)

The RK4 terms have different definitions for the time-evolution equations for flow (Q), open-channel area $\left(A\right)$ and surcharged-conduit head $\left(H\right)$. For clarity in the following the e subscripts that indicate values at the element center are omitted, and thus are implied for any term without a u or d subscript. The $\mathrm{\Gamma }$ coefficients for the linear implicit terms are

$$\begin{array}{c}\hfill {\mathrm{\Gamma }}_Q=-\frac{a_1}{\Delta t}-gF\left|U\right|;{\mathrm{\Gamma }}_A=-\frac{a_1}{\Delta t};{\mathrm{\Gamma }}_H=0\end{array}$$

where $a_1$ is the weighting of the $n+1$ term in the backwards real-time stencil of Equation (12). The $\mathrm{\Lambda }$ weighting coefficients are

$$\begin{array}{cc}\hfill {\mathrm{\Lambda }}_{\left(r\right)}& \equiv \frac{1}{1-\Delta \tau {\mathrm{\Gamma }}_{\left(r\right)}}forr\in \left\{A,H,Q\right\}.\hfill \end{array}$$

The C represents the AC coefficients, which are given as

$$\begin{array}{c}\hfill C_Q=1;C_A=\frac{\ell {\mathcal{F}}^2}{G};C_H=\frac{\ell {\mathcal{F}}^2}{A}\end{array}$$

where $\mathcal{F}=1$ is used for the present work, as discussed after Equation (8). Finally, the source terms are

$$\begin{array}{cc}\hfill S_Q& =-\frac{1}{\Delta t}\sum _{j=2,N_B}{a}_j{Q}^{n+2-j}+\frac{1}{L}\left\{Q_u{U}_u-Q_d{U}_d+\frac{5}{6}g\left[A_u{H}_u-A_d{H}_d\right]+K_e\right\},\hfill \end{array}$$

(30)

$$\begin{array}{cc}\hfill S_A=& -\frac{1}{\Delta t}\sum _{j=2,N_B}{a}_j{A}^{n+2-j}+\frac{Q_u-Q_d}{L}+q_e,\hfill \end{array}$$

(31)

$$\begin{array}{cc}\hfill S_H& =\frac{Q_u-Q_d}{L}+q_e.\hfill \end{array}$$

(32)

The $a_j$ are the backwards real-time stencil weights that are coefficient for the known real-time n and $n-1$ values of Q and A, respectively. In the present work, lateral leakage fluxes ($q_e$) are set to zero throughout.

5. Test Case

5.1. Geometry of Test Setup

To test the new algorithm, we compare PipeAC performance to laboratory experiments reported by Trajkovic et al. [35] for unsteady flows transitioning between open-channel flow and surcharged-pipe flow. These data were also use by Leon et al. [130] for model validation. The data from Trajkovic et al. [35] figures for Type A and Type D experiments have been digitized for the present comparisons (available for download as provided in Hodges [33]). Their experimental apparatus is a ∼10 m pipe with 0.1 m inside diameter. An undershot gate at the upstream pipe end is used to control flow from a constant-head tank. The downstream end uses either a supercritical overflow to another tank (Case A), or a pressurized reservoir to surcharge the downstream end of the pipe (Case D). Pressure taps along the length of the pipe are used to measure flow head. A summary of the pipe geometry and pressure measurement locations through the test section between gates is provided in

Table 1. Distance (m) from upstream gate (G1) to pressure measurement taps P2–P8 and downstream gate (G2) in Trajkovic et al. [35] experiments.

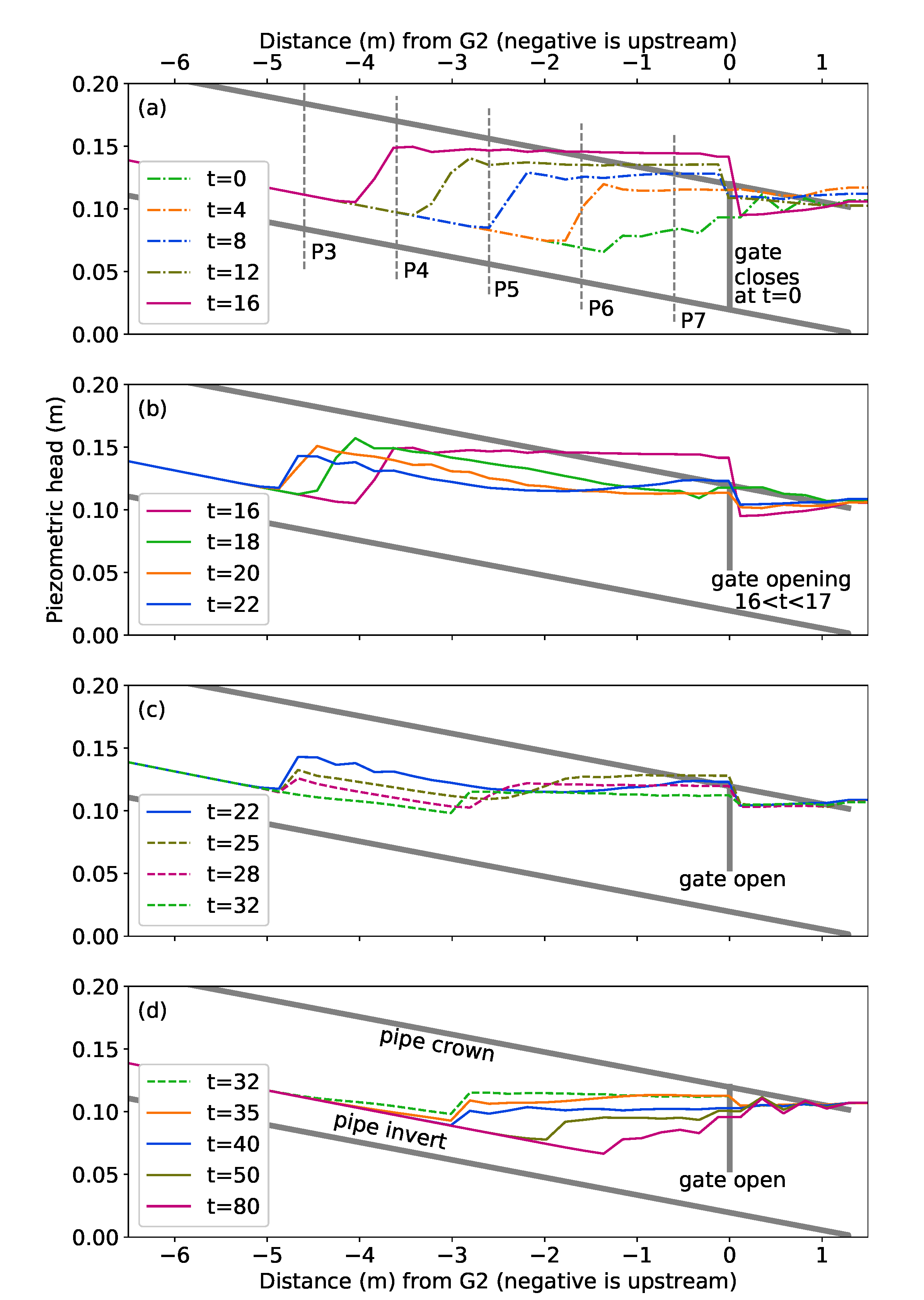
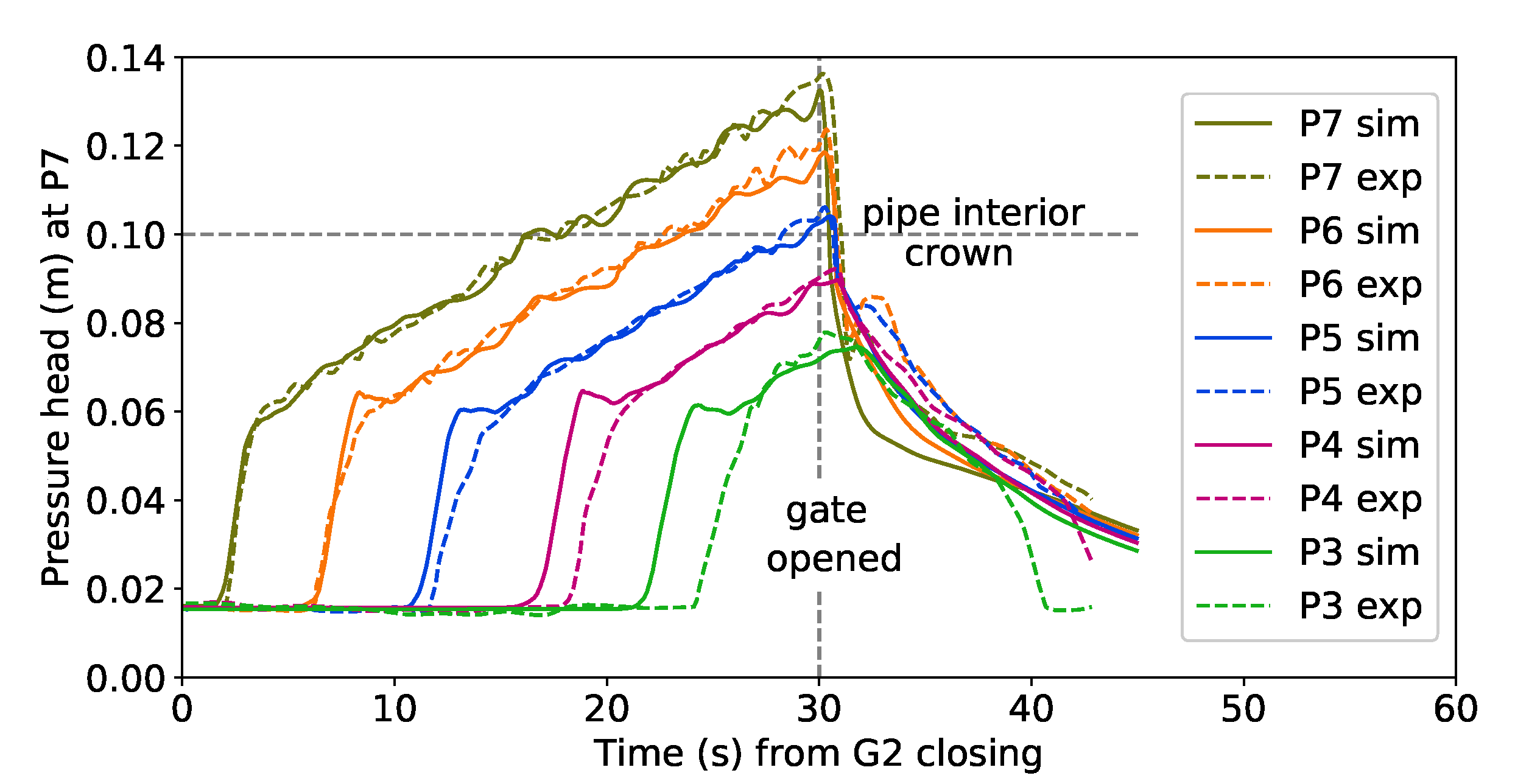
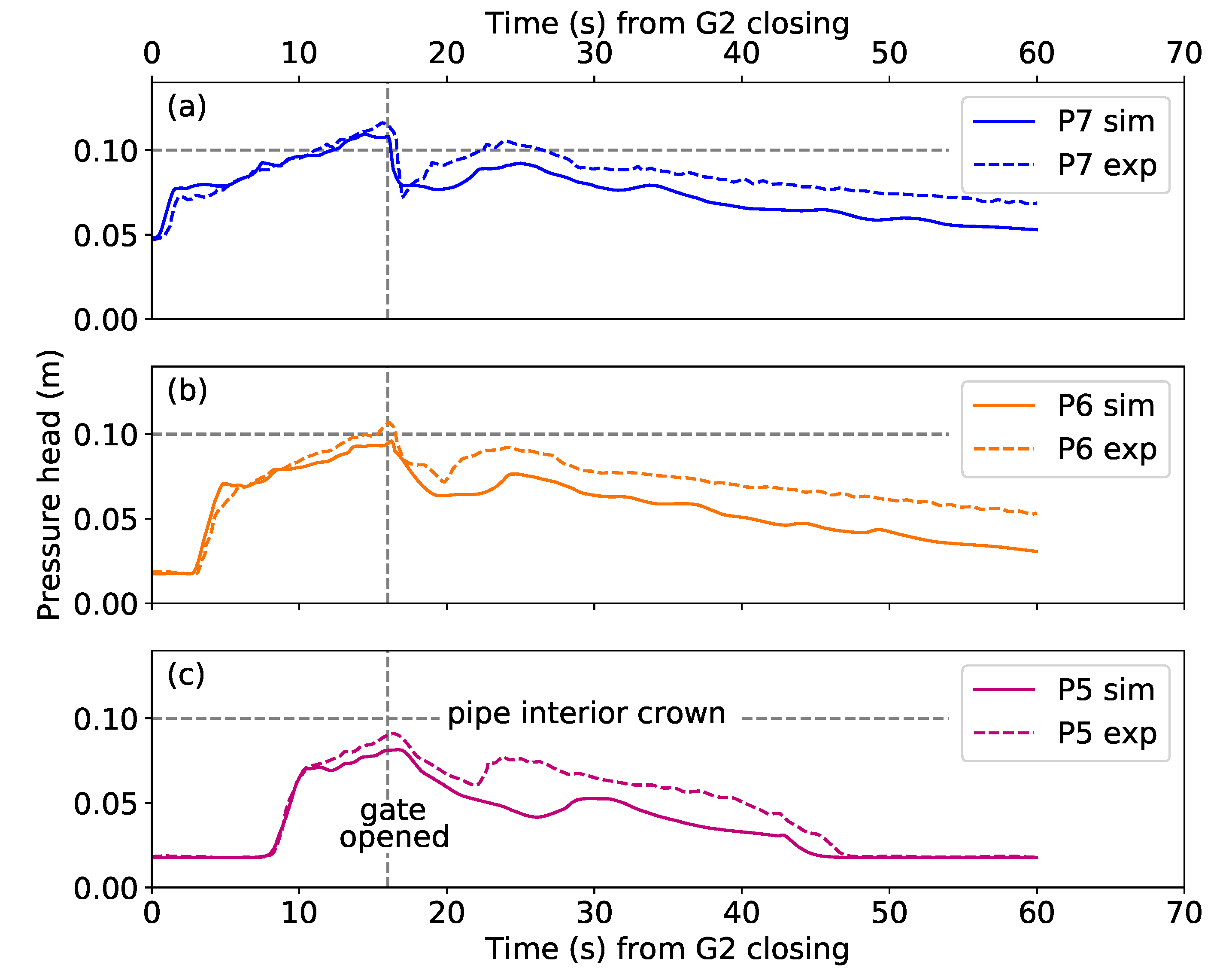
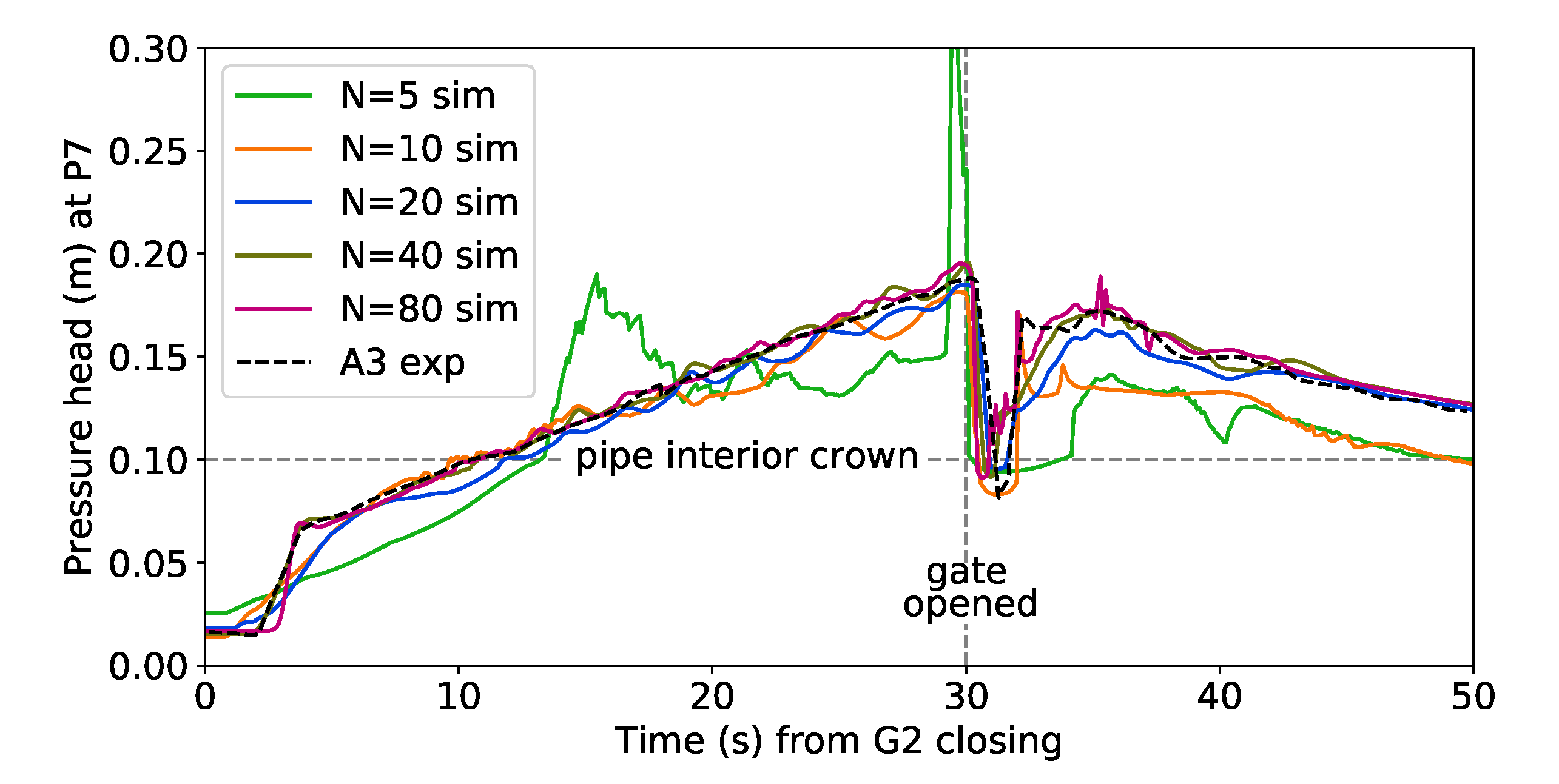
G1	P2	P3	P4	P5	P6	P7	P8	G2
0	2.5	3.7	4.7	5.7	6.7	7.7	8.2	8.3

.

Unfortunately, geometry details in Trajkovic et al. [35] were insufficient to exactly replicate their downstream boundary conditions, so the present work extended the pipe by 1.0 m and added a 5.0 m buffer domain consisting of a 0.5 m diameter pipe whose crown was coincident with the crown of the downstream end of the experimental pipe. The buffer domain has zero slope and with the larger diameter it allows subcritical flow conditions at the numerical model outlet, which ensures a fixed head boundary condition can be readily applied. The Gauckler-Strickler-Manning friction coefficient in the test section was 0.008, following that reported by Trajkovic et al. [35]. The buffer domain used a friction coefficient of 0.016 to help damp wave reflections off the downstream boundary. By using the buffer domain, the supercritical flow cases had downstream H boundary conditions that did not affect flow through the downstream gate G2.

5.2. Flow Conditions for Tests

The Trajkovic et al. [35] Type A and D experiments were originally conducted by establishing a baseline flowrate in the system with gate G1 (upstream) at a fixed opening for the duration of the experiments and gate G2 (downstream) set at an initial height to establish a steady flow over an interval of time. Once the stable flow is obtained, G2 was closed “instantaneously,” held closed for some duration, and then reopened to a height that varied by experiment. A truly instantaneous gate closing/opening is impossible in the real world and can cause numerical problems in a simulation, so an arbitrary gate closing speed of 0.1 m/s was used in the simulations. This allows the G2 gate to fully open or close in 1.0 s. Quantitative conditions for the test cases are provided in

Table 2. Type A and Type D experiments reported in [35], as tested with PipeAC. Model downstream H is measured above the lowest point in the test pipe (not including buffer domain). * See discussion in text as how values for Q and bed slope were obtained for Case A4.

Type	Bed Slope	Upstream Q (m3 s${}^{-1}$)	Downstream H (m)	G1 Height (m)	G2 Initial Height (m)	Initial Interval of Steady Flow (s)	G2 Closed Interval (s)	G2 Reopen Height (m)
A1	0.027	0.0013	0.03	0.014	0.100	120	30.0	0.008
A2	0.027	0.0013	0.03	0.014	0.100	120	30.0	0.015
A3	0.027	0.0013	0.03	0.014	0.100	120	30.0	0.028
A4	0.014 *	0.0013 *	0.03	0.014	0.100	120	30.0	0.100
D1	0.014	0.0015	0.107	0.015	0.033	240	16.0	0.033

. For further details of the experimental apparatus and testing conditions please see Trajkovic et al. [35].

The numerical simulations use fixed Q upstream boundary conditions to match the measured values from the experiments of Trajkovic et al. [35]. The downstream H boundary conditions are enforced at the end of the buffer domain.

Note that for Case A4 the experimental Q and $S_0$ were not provided in Trajkovic et al. [35], but from their reported data it is clear that one of these was not the same as those used in Cases A1–A3. The peak pressure at gauge P7 in Trajkovic et al. [Figure 3—is different from the peak pressure at the same gauge in their Figure 4. Such a discrepancy is only possible if the experiments used different flow rates and/or slopes. As shown in Section 6 below, the present simulations provide reasonable estimates of peak pressures and the rate of pressure increase at P7 for Cases A1–A3, so several simulations at varying flow rates and slopes were conducted to examine the likely flow rate and slope used in Case A4. The simulation that matched the experimental results most closely used the same Q as Cases A1–A3 with the bed slope of Case D1, as presented in Section 6, below. It seems likely that these are the correct values for Case A4 and were simply omitted in Trajkovic et al. [35].

5.3. Consistent Data Comparisons

The data analyses in Trajkovic et al. [35] are reported in terms of the pressure head measured from the sloping bottom of the pipe at individual sensors. For the numerical model, we use $H_e-z_{b\left(e\right)}-{\delta }_e$ where $H_e$ is the simulated piezometric head on the computational element containing the reported sensor location, $z_{b\left(e\right)}$ is the inside bottom elevation of pipe at that location, and ${\delta }_e$ is a sensor head offset shown in

Table 3. Sensor head adjustment, ${\delta }_e$, between the model and experimental sensors for different bed slopes. Values for P3—P7 are in meters of head.

Cases	Slope	P3	P4	P5	P6	P7
A1, A2, A3	0.027	–	–	0.0050	–	0.0060
A4, D1	0.014	0.0100	0.0095	0.0095	0.0095	0.0090

. The ${\delta }_e$ accounts for the fact that the computational cell centers were not exactly at the sensor location and thus there is an offset of the baseline along the sloping pipe. Rather than attempting to estimate the geometry effect of the displacement, the small values of ${\delta }_e$ were obtained by minimizing the difference between the simulation and the experiments at the end of the steady-flow ramp-up period.

5.4. Calibration of Drag Model for Undershot Gate

The test cases use two undershot gates to control the flow conditions. From the data in Trajkovic et al. [35] it is impossible to reconstruct an accurate estimation of the frictional losses through these gates. Lacking any other data, these are modeled using a standard discharge equation following Crane Co. [131] and Brater et al. [132]:

$$\begin{array}{cc}\hfill Q=C_v{A}_g\sqrt{2g\Delta H}\mathsf{w}\mathsf{h}\mathsf{e}\mathsf{r}\mathsf{e}{C}_v& \equiv C_d{\left(1-C_d^2\frac{A_g^2}{A_1^2}\right)}^{-1/2}\hfill \end{array}$$

Here $A_g$ is the open cross sectional area under the gate, $A_1$ is the upstream cross-sectional area approaching the gate, $\Delta H$ is the change in piezometric head across the gate, $C_v$ is the effective discharge coefficient that includes effect of approach velocity and $C_d$ is the gate discharge coefficient when approach velocity is negligible. For simplicity, a closed gate is modeled as a gate with leakage through a minimal area of ${10}^{-5}$ m${}^2$. The only calibration in the model was in adjustment of $C_D$. Tested values of $C_D$ were $\left\{0.66,0.76,0.86\right\}$. The differences between the results were relatively small, but 0.76 was deemed superior and used in the present work. There did not seem to be any value in further refining the estimate.

5.5. Grid Refinement Test Setup

The baseline discretization used in the simulations was 40 cells over the 8.3 m between gates G1 and G2. Grid refinement behavior was tested with Case A3 using 5, 10, 20, and 80 cells in the test section. The discretization of all sections for different simulations are provide in

Table 4. Discretization of simulations. N is the number of cells in the section, $\Delta x$ is the length of each cell.

Cases	Upstream of G1	Test Section G1 to G2	Downstream of G2	Buffer
	N:$\Delta \mathbf{x}$ (m)	N:$\Delta \mathbf{x}$ (m)	N:$\Delta \mathbf{x}$ (m)	N:$\Delta \mathbf{x}$ (m)
A3a	2:0.750	5:1.66000	2:0.7000	5:1.000
A3b	2:0.750	10:0.83000	2:0.7000	5:1.000
A3c	3:0.500	20:0.41500	3:0.4667	10:0.500
A1, A2, A3, A4, D1	6:0.250	40:0.20750	6:0.2333	20:0.250
A3e	12:0.125	80:0.10375	12:0.1167	40:0.125

. Simulations with more than 80 cells in the test section were not conducted as a cell length less than the pipe diameter (0.1 m) inherently violates the hydrostatic approximation of the Saint-Venant equations that requires horizontal length scales to be greater than vertical lengths scales. Results from the grid refinement study are found in Section 6.5, below.

6. Results

6.1. Temporal Evolution of Piezometric Head

The test cases described in Section 5 have been simulated in the PipeAC finite-volume code. The general progression of the piezometric head in the simulations follows the illustrations in Figure 1 and Figure 2 for Case A3 and D1, respectively. An initial steady supercritical flow through upstream gate G1 is achieved ($t<0)$ with gate G2 being fully open (Cases A1–A4) or partially open (Case D1, see Table 2). With gate G2 fully open the initial steady flow is supercritical throughout the entire test section of the pipe (i.e., between the gates), as shown in Figure 1a in the $t=0$ s line. For gate G2 partially open (Case D1) the gate partially restricts the flow forming a transitional steady-state profile, as shown for the $t=0$ line in Figure 2a. At $t=0$ gate G2 is rapidly closed. A bore subsequently propagates upstream until the gate is re-opened, as shown by the piezometric head profiles in Figure 1a for $0<t\le 30$ s and in Figure 2a for $0<t\le 16$ s. In Case A3 the gate G2 re-opens to 0.028 m at time $t=30$ s, and for Case D1 the gate re-opening is to 0.033 m at time $t=16$ s. There is a first transitional phase from $30<t<31$ s in Case A3 (Figure 1b) in which the upstream bore holds position and there is a rapid decrease in the surcharge pressure moving up the channel. In Case D1, Figure 2b, this transition phase is longer—from $16<t<22$ s—and shows the bore continuing to move slightly upstream with the surcharge pressure rapidly depleted and the water surface elevation dropping relatively evenly along the channel between the bore and gate G2. In the second transition phase, for Case A3, Figure 1c, the water surface elevation drops below surcharge and a secondary bore that crosses into surcharge forms and propagates up the channel. Note that the original upstream bore appears to hold its position and slowly decline in magnitude. The effect is similar in for Case D1, Figure 2c, except that the secondary bore is not surcharged. By $t=36$ s in Case A3 and $t=32$ s in D1 (Figure 1d and Figure 2d, respectively), both systems transition into a simple drawdown to the steady-state conditions with their respective gate restrictions at G2. Unfortunately, the experimental results reported in Trajkovic et al. [35] do not have sufficient detail to re-create the evolution of the piezometric profiles illustrated in Figure 1 and Figure 2.

6.2. Comparison of Simulations and Experiments for Cases A1–A3

We can make direct comparisons between simulations and experiments at sensors where data were reported in Trajkovic et al. [35]. For the A1–A3 experiments, a comparison of the experimentally- measured and simulated head at gauge P7, which is 0.6 m upstream of gate G2 (see Table 3), is shown in Figure 3. The simulations track well with the filling of the pipe, including the magnitude of the sudden pressure drop and subsequent recovery shortly after the gate is opened.

Results further upstream in the pipe, at pressure gauge P5, are shown in Figure 4. It can be seen that the bore at the leading edge of the pressure signal in the simulations moves upstream slightly faster than that measured in the experiment. Note that the A1–A3 numerical simulations are identical prior to $t=30$ as they all use identical initial conditions (supercritical steady flow with gate G1 at 0.014 m) and have gate G2 closed at exactly the same time. The differences between simulations after $t=30$ are due to different re-opening heights for gate G2 (see Table 2). For Cases A1 and A2, the pressure-drop magnitude and duration at the gate opening are well-represented in the simulation. In contrast Case A3 has a good representation only for the pressure-drop magnitude, but shows an exaggerated duration for the pressure reduction after the abrupt opening of the gate. The increased duration is related to the propagation of the secondary bore through P5 for $31<t<34$ as shown in Figure 1c. There we see a rapid change from surcharge (lines $t=31$ s to $t=32$ s), followed by the secondary bore propagating upstream (lines $t=32$ s to $t=34$ s). The implication of the discrepancy between the observations and the model is that the secondary bore in the experiments moves more rapidly upstream than the model can represent—hence the longer duration of the opening pulse at P5 in the model.

6.3. Comparison of Simulations and Experiments for Case A4

For Case A4, the bed slope is about half that of Cases A1–A3 (see Table 2). In Figure 5, the bore at P6 and P7 (near to G2) are well-represented, but as the bore propagates upstream sequentially through P5, P4, and P3 there is an increasing phase error—the simulation bore propagates upstream faster than the experiment. It can also be observed that the simulation bore has a sharper front in the simulations than the experiments—a discrepancy that is small at P7 but increases moving upstream from P6 to P3.

6.4. Comparison of Simulations and Experiments for Case D1

Case D1 is quite different from Cases A1–A4 as the pipe downstream of the gate and in the buffer zone are surcharged in D1, versus the supercritical drawdown into the buffer domain in A1–A4. Unfortunately, Trajkovic et al. [35] did not give a measurement of the surcharged head in the downstream end of the pipe. A number of test cases were conducted and compared to the experimental data. As shown in Figure 6, the results at the reported sensors in Trajkovic et al. [35] is quite reasonable for a downstream head that is only slightly greater than the pipe crown elevation at the downstream end of the pipe (see Downstream H in Table 2). For this experiment the downstream gate G2 is initially partially open, which provides a standing hydraulic jump as the initial condition (see $t=0$ line in Figure 2a). The gate is then rapidly closed for only 16 seconds before being re-opened to its initial height. It can be seen that the model provides reasonable representation of the bore propagating upstream prior to the gate opening. The drawdown after the gate opened shows the model emptying the upstream test section faster than the observed system—which might be attributable to the drag coefficient used for the gate. The gate $C_D$ calibration study (Section 5.4) was conducted using data for Cases A1–A3, which have a steeper pipe slope and a greater pressure drop across the gate than Case D1.

6.5. Grid Refinement Results

A grid refinement study (Section 5.5) was conducted to compare with the experimental results at P7 and P5 for Case A3, similar to Figure 3 and Figure 4. Results of the grid refinement study are shown in Figure 7 and Figure 8. It can be seen that results from N = 20 to N = 80 are reasonably similar—although the bore front for N = 20 is less steep. The N = 10 simulation is significantly degraded in quality, but still shows the same basic flow features. The coarse N = 5 simulation is unable to represent the sharp bore front at P7 but instead has a pressure spike when the pipe transitions to surcharged at P7, and another pressure spike when gate is opened. Note that these coarse-grid simulations never show the correct surcharged conditions at P5.

7. Discussion

7.1. Interpretation of Results

Overall, the results presented in Figure 3, Figure 4, Figure 5 and Figure 6 show reasonable agreement between the PipeAC model and the experiment. Perfect agreement is not expected as Trajkovic et al. [35] reported trapped air pockets and multiphase bubbly regions in these dynamic flows. It is likely that the present simulations are at the limit of what can be captured for pipe flow undergoing rapid unsteady changes across supercritical, subcritical, and surcharged regimes when the simulation model assumes a single liquid that is governed by the hydrostatic approximation.

From the grid refinement study in Figure 7 and Figure 8, it appears that it takes at least N = 20 grid cells to get a reasonable representation of the unsteady dynamics of associated with the gate rapidly closing and opening. From Table 4, N = 20 corresponds to an element length slightly more than $4\times$ the pipe diameter of 0.1 m. At coarser resolutions, PipeAC remains stable but the dynamics are poorly represented. It is not surprising that the N = 5 simulation does quite poorly. As noted in Section 4.5 and discussed in detail in Hodges and Liu [31], the hydraulic jump discretization used herein will force a supercritical-to-subcritical condition to occur on the face of a finite-volume. This simplifies the numerical method as an entire computational cell is either subcritical or supercritical—there are no “transitional” elements. With sufficiently fine grid resolution, forcing the jump to occur on a cell face has marginal effect on the results. However, at coarse grid resolution this approach can be troublesome. In the present simulations, with N = 5 there are only 4 locations where jumps are allowed: $x=\left\{-6.64,-4.98,-3.32,-1.67\right\}$ as measured from the downstream gate G2 and used in Figure 1. Thus, it is impossible for location P7 (at $x=-0.6$ m from G2) to see a hydraulic jump in the N = 5 simulation.

The behavior at the bore front as it moves upstream is particularly interesting. In Figure 3, Figure 5 and Figure 6a it can be seen that at P7, only 0.6 m upstream from gate G2, the steep bore seen in the experiments is well-represented by the simulation. As the bore moves upstream—i.e., at P5 in Figure 4 and in the evolution across sensors shown in Figure 5—the experimental data shows the sharp corner of the bore progressively erodes, and the observed bore propagation speed is slower than that in the simulation. To understand these phenomena, it is useful to consider the bore propagation shown in the grid refinement tests of Figure 7 and Figure 8 for sensors P7 and P5, respectively. At P7, we see the sharp experimental front is well-represented by tests N = $\left\{40,80\right\}$, but the N = $\left\{5,10,20\right\}$ show a shallower slope at the front. However, moving upstream to P5 we see the experimental front has a shallower slope—which is well-represented by the N = 20 simulations but not by the finer N = $\left\{40,80\right\}$ simulations. Indeed, at P5 there it is clear that the coarser N = 20 simulation is “better” than the finer resolution simulations. This “better” agreement at coarser resolution is consistent with prior analysis of a hydrostatic model in representing non-hydrostatic waves [133]. Briefly—the real waves in the experiment are inherently non-hydrostatic and include dispersion, whereas the hydrostatic simulation neglects dispersion but includes nonlinear steepening. At coarse grid resolution, numerical dispersion and numerical dissipation can act similar to physical dispersion in modifying the wave, hence the excellent N = 20 results from about $14<t<30$ in Figure 8 are serendipitous. Numerical error at a particular grid scale can approximate the missing non-hydrostatic physics—giving the “right answer for the wrong reason.” At finer resolution, numerical dissipation is decreased and the wave front becomes steeper, as seen in Figure 8. Furthermore, Figure 4 and Figure 5 also show that the hydrostatic model has a slightly faster wave speed as the bore propagates upstream, which is expected in a low-order hydrostatic model.

The behavior of Case A3 at sensor P5, as shown in Figure 4 and Figure 8, illustrates the limitations of the PipeAC algorithm for rapid changes with the flow near the surcharge threshold. The experimental data for Case A3 at sensor P5 show the opening of the gate causes a rapid pressure drop at P5 such that the head drops below surcharged. We do not have information from the experiments as to whether or not the pressure drop actually allowed air to enter the head space at P5, or if the pipe remained full with a slightly negative pressure. The PipeAC model effectively assumes that air can move into the head space whenever the piezometric pressure drops below pipe crown elevation, which is an inherent limitation of the present single-fluid model. Future work should consider implementation of approaches that correctly handle sub-atmospheric pressure [134,135,136]. However, from the point of view of large-scale network models, the abrupt transient and pressure drops are handled reasonably—causing neither catastrophic instabilities nor degrading the simulation quality after the abrupt transient. Note that the model handles the abrupt transient better at sensor P7, as shown in Figure 3, where the pressure drop is only slightly below surcharge in Case A3.

A final feature that can be noted in the simulation results are oscillations after the return to surcharge at sensor P5 for Case A3. Incipient oscillations for the N = 40 resolution are seen in the Case A3 line in Figure 4 for $33<t<37$ after the abrupt return to surcharge. The oscillations are also visible in the N = 80 grid refinement test, as shown Figure 8. The N = 20 test only briefly crosses to surcharged after the gate opens at P5 and shows no oscillations. For the N = $\left\{40,80\right\}$ tests, the oscillations persist for only a few seconds and are likely an artifact of the impulse that occurs when the solution crosses rapidly from free-surface flow to surcharged. That these oscillations occur only when the flow abruptly crosses to weakly surcharged is an indication that these are likely induced by the change of the continuity solution from A to H, i.e., as in Equations (15) and (16), respectively. It seems that some form of smoothing for the transition between these equation forms could be useful in reducing these oscillations.

7.2. Implications for Large-Scale Network Models

The algorithm developed for numerical simulation in PipeAC is a step towards large-scale 1D modeling of stormwater networks. Consistent with this goal, the method uses “no-neighbour” spatial interpolation, which ensures that a computational element only needs to know values on its adjacent faces and the faces only need to know the adjacent elements; i.e., the discretization of an element does not include a neighbour element and the discretization of a face does not include a neighbour face [31]. The no-neighbour approach inherently limits a code to 1st and 2nd-order spatial discretizations, but reduces the communication burden associated with decomposing a system for parallel computing [70]. Arguably, the PipeAC method could be improved in its ability to handle abrupt transitions by inclusion of higher-order discretization methods, but that would increase the communication burden in the parallel network model that is under development.

At this point, it is not clear that the PipeAC algorithm will be suitable for the entire solution of a city-scale stormwater network. The NCIMM research team’s working hypothesis (which remains to be demonstrated) is that it will be more effective to use a standard Saint-Venant solver—such as SvePy [31,129]—for all cells $H<z_c-{\delta }_H$, where $z_c$ is the elevation of the inside crown of the pipe and ${\delta }_H$ is a small length scale. That is, the standard hyperbolic solver for the Saint-Venant equations should be used up until the flow is about to transition to surcharge, and then the dual time-stepping AC method is invoked. However, this idea remains speculative and there remain a number of issues associated with artificial shocks and oscillations that might be produced when switching the solution algorithm.

7.3. Possible Approaches Melding Artificial Compressibility and the Preissmann Slot

Another area that should be investigated is the use of the AC method with limited pseudo-time stepping. In the present work, the inner loop (RK4 pseudo-time stepping) is iterated until L${}_1$, L${}_2$ and L${}_{\infty }$ norms for $\Delta Q$ and $\Delta H$ are all below cutoff values of $\left\{5\times {10}^{-8},{10}^{-8},{10}^{-7}\right\}$, respectively, or the number of iterations reaches 100 (details are available in Hodges [33]). For the simulations herein the relative error in volume conservation is $O\left({10}^{-6}\right)$ or better. However, the importance of this level of mass conservation is questionable. Note that a single time step of a Preissmann Slot method (Section 2.3) is similar to the first iteration of an AC method (Section 2.4) in that it solves a hyperbolic continuity equation using an artificial wave speed. Indeed, as shown in Section 3.3, the novel representation of the AC pressure celerity $\gamma$ using the hydraulic depth (${\ell }_e$) and the Froude number ${\mathcal{F}}_e=1$ ensures the AC pressure celerity is exactly a gravity wave speed. Hence, the first AC iteration in the PipeAC method is effectively a Preissmann Slot approximation where the slot width is set to obtain the gravity wave speed for the local piezometric head, H. Further investigation is needed to understand the relationship between the number of AC iterations (or the norms used for convergence), the selection of ${\mathcal{F}}_e$, and how permutations in these affect the results in a large-scale network simulation. Limiting the number of AC pseudo time-steps has the potential for making the solver much faster—albeit by losing some mass conservation. This idea has previously been investigated for coastal ocean flows [71], but has not been considered in 1D network modeling.

8. Conclusions

This paper presents a new approach to an old numerical method—the artificial compressibility (AC) approach of Chorin. It is demonstrated that a dual-timestepping AC approach can be used with the 1D Saint-Venant equations and 1D incompressible flow closed-conduit equations to solve unsteady flows that transition between supercritical, subcritical, and surcharged regimes. The formulation of the AC governing equations allow the transition from open-channel flow to surcharged-pipe flow to be made with only small changes in the numerical algorithm—i.e, switching from solution of cross-sectional area to piezometric head as the solution variable for continuity. Satisfactory comparisons are made to previously published experimental measurements of unsteady transitional flows in a circular pipe.

The new finite-volume model, PipeAC, uses a low-order numerical scheme (timescale interpolation) to translate cell-centered values to faces—which makes the algorithm a building block towards efficient large-scale computation of city-wide stormwater networks. Two numerical contributions that have wider implications are: (i) demonstration that the artificial compressibility parameter—which has previously been considered a somewhat arbitrary value associated with solution convergence rates—can be formulated in terms of an equivalent gravity-wave speed and hence the first iteration is mathematically equivalent (for surcharged pipe) to a Preissmann Slot time step; (ii) a dual time-stepping method using a Runge-Kutta time advance in pseudo time can be implemented with an implicit treatment of the friction term to ensure the correct direction of friction (opposing velocity) in each substep of the RK advance.

The known limitations of the present work are (i) the underlying equations are hydrostatic, single-fluid, and 1D, which inherently cannot exactly represent multi-fluid interactions of air and water at the front of an unsteady bore or its correct celerity, and (ii) sufficient grid resolution must be applied to reasonably capture the shock front of a bore. The overall computational efficiency of the new method remains an unknown issue to be further investigated. It is speculated that artificial compressibility will be most useful as a technique that is selectively used in closed-conduit flow for surcharged pipe and where pipe sections are nearing surcharge.

The benefit of this research is that it provides a simple, consistent, and mass conservative approach to handling the switch between hyperbolic and elliptic equations that occurs when the free-surface flow in a pipe becomes constrained by the pipe ceiling. This issue has previously been a challenge to stormwater modeling that causes either loss of mass conservation or slow convergence of the solution.