B-Spline Method of Lines for Simulation of Contaminant Transport in Groundwater
Abstract
1. Introduction
2. Governing Equations
3. B-Spline Method of Lines
3.1. Spatial Discretization
3.2. Temporal Discretization
4. Numerical Applications
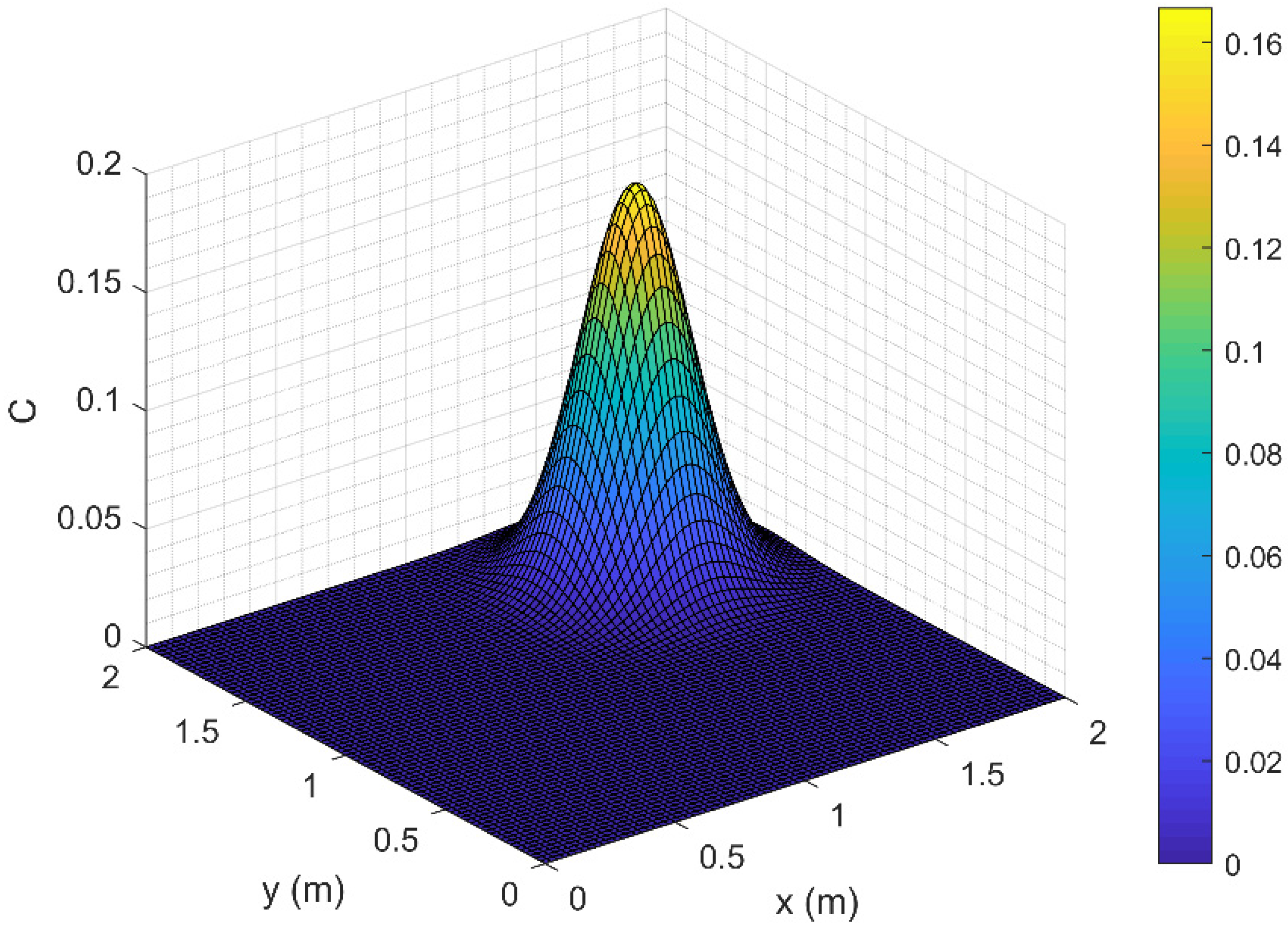
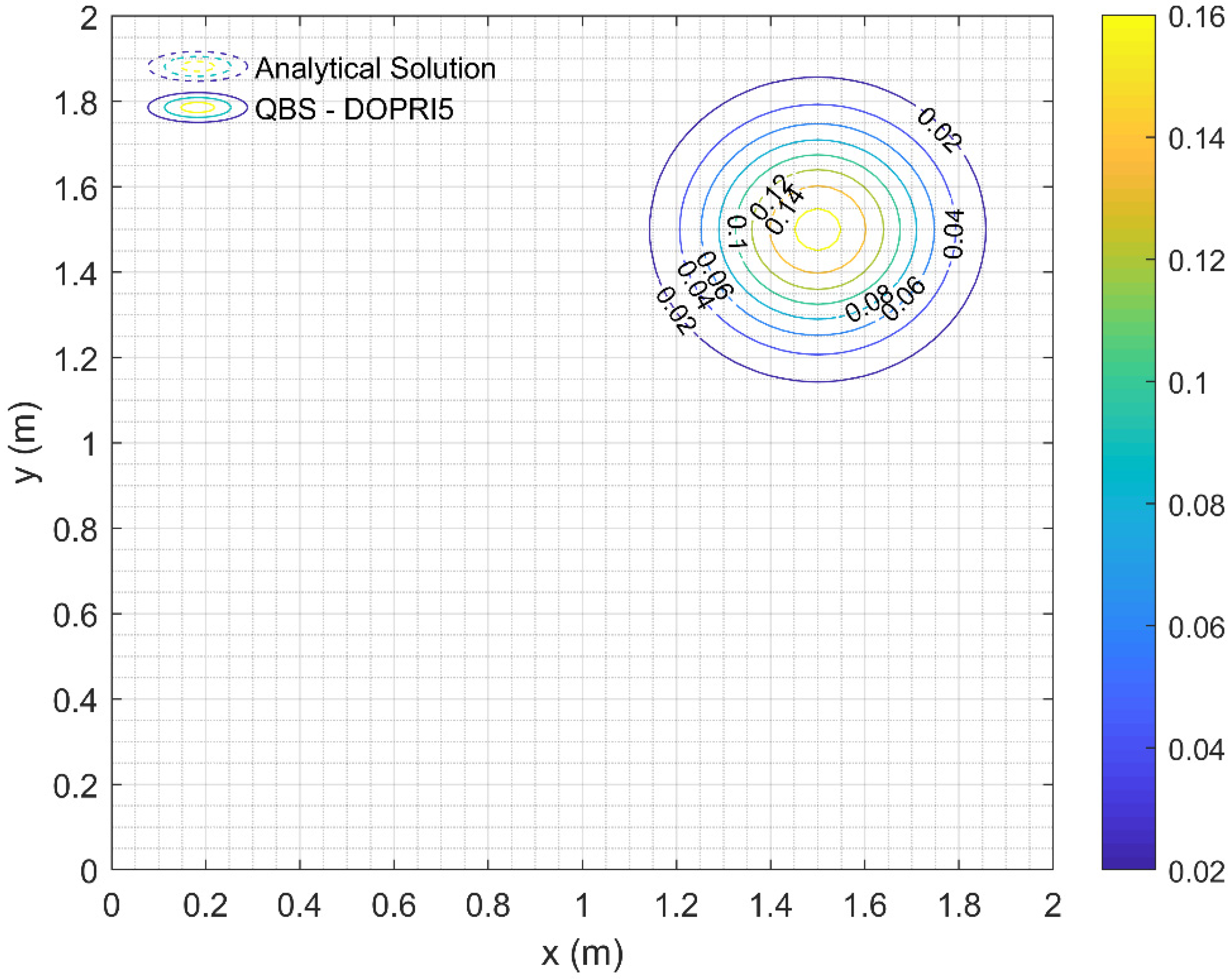
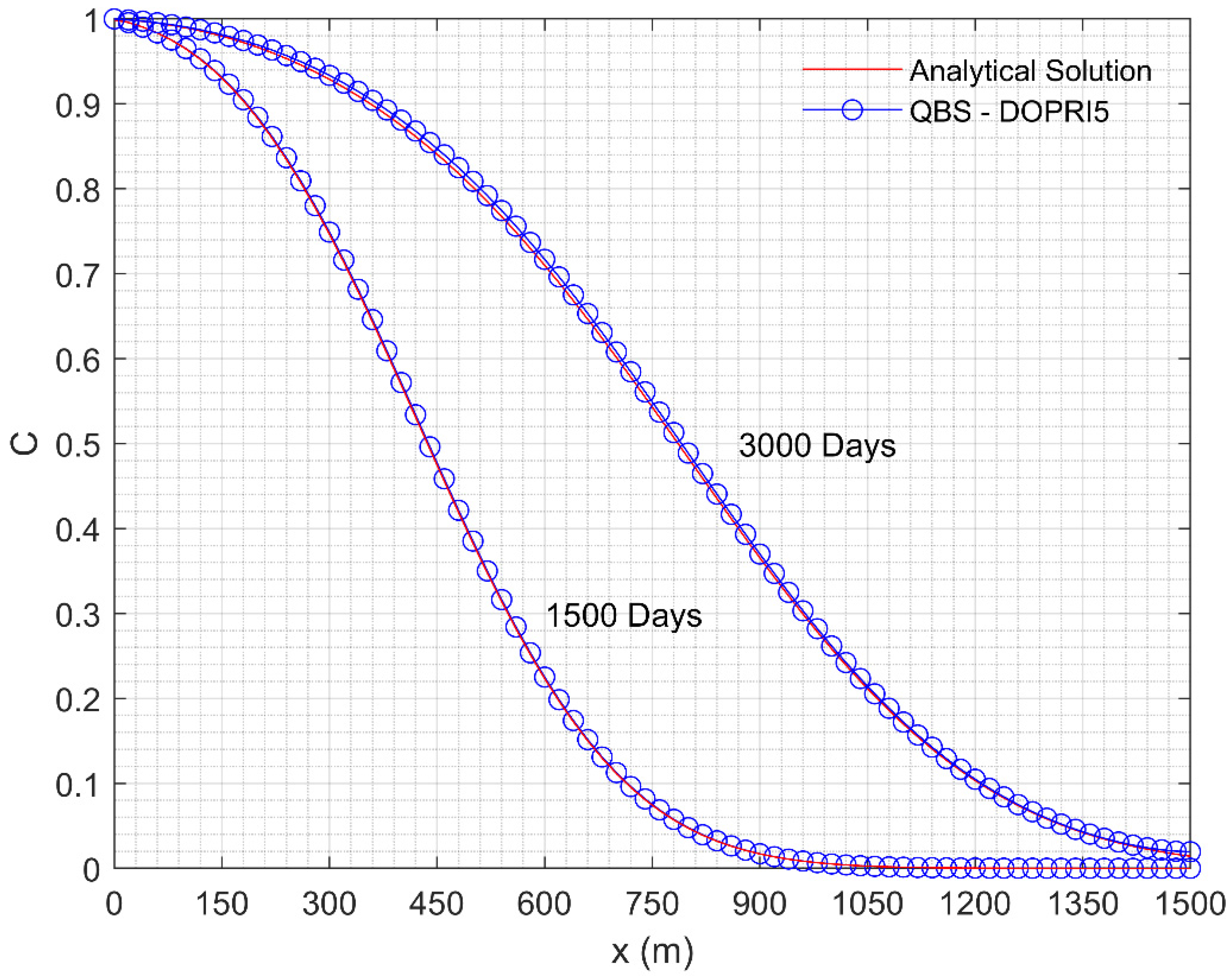
4.1. Example 1
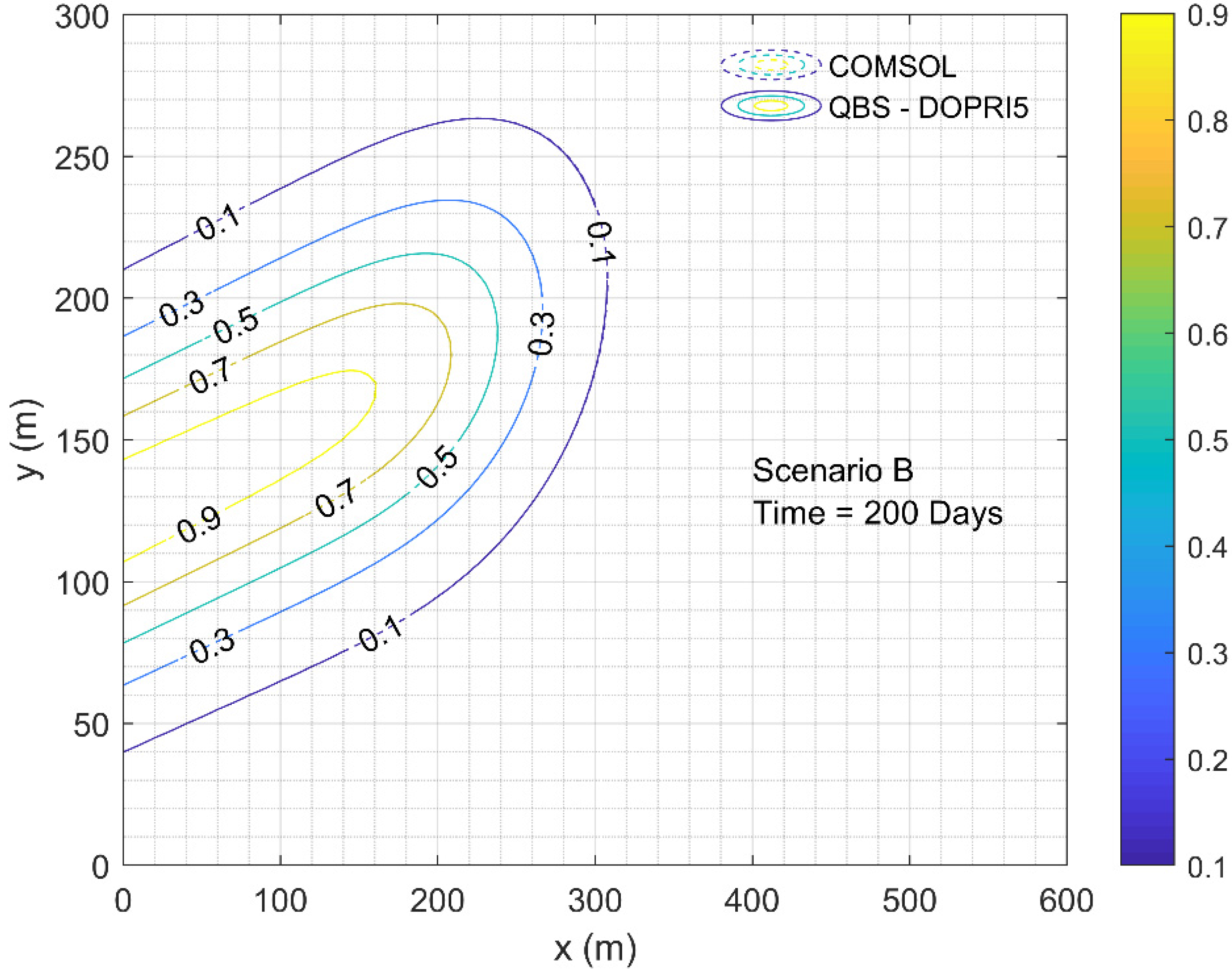
4.2. Example 2
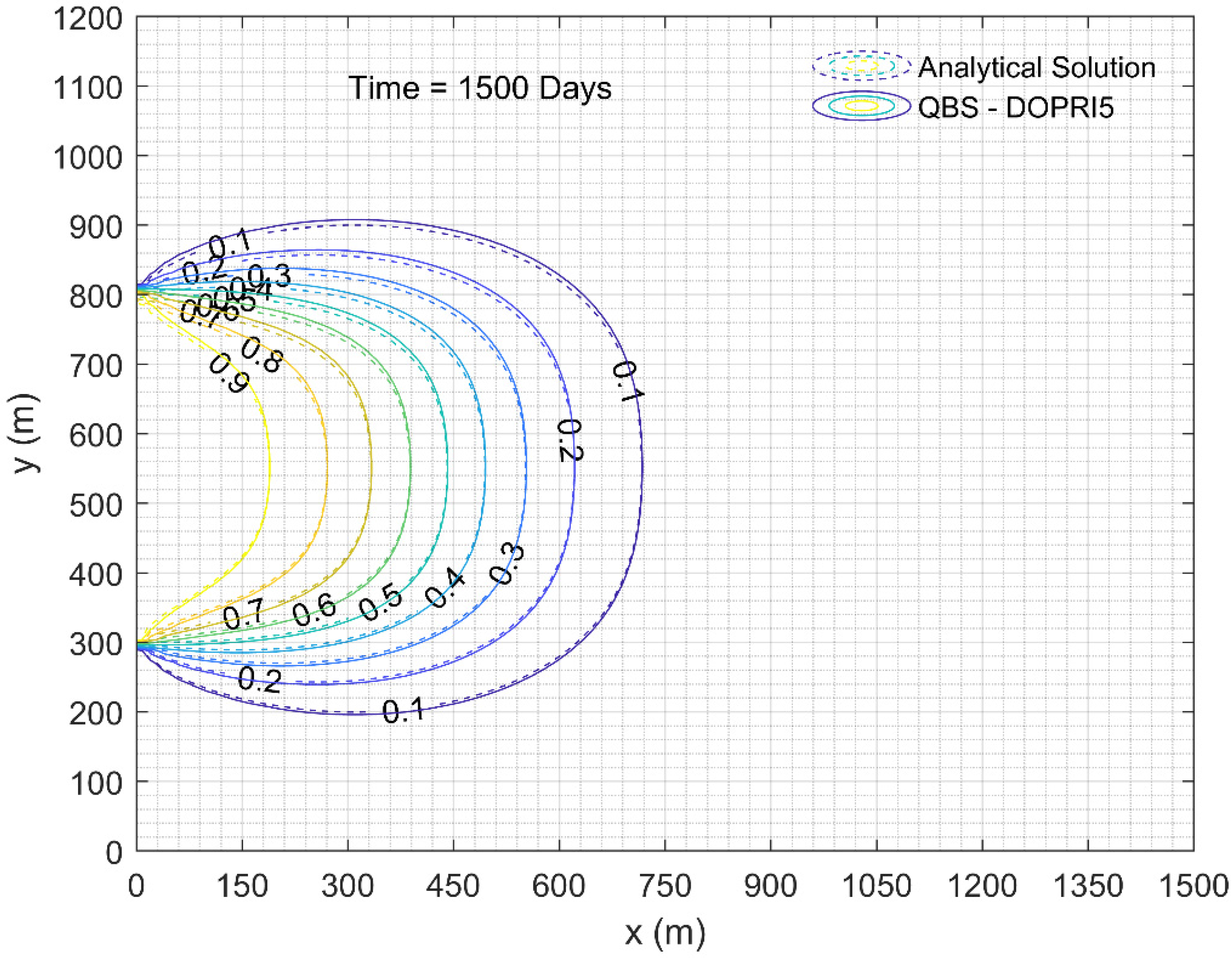
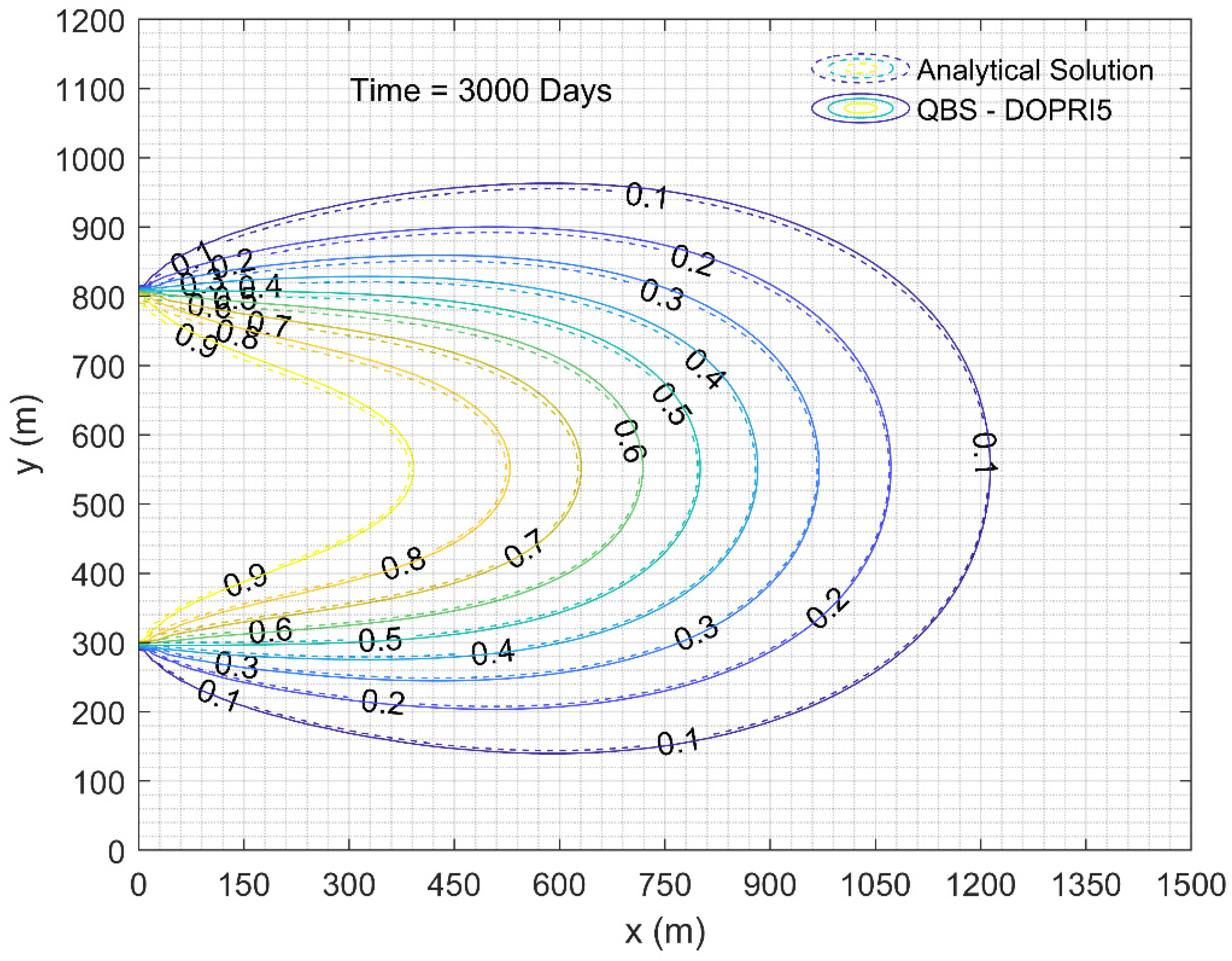
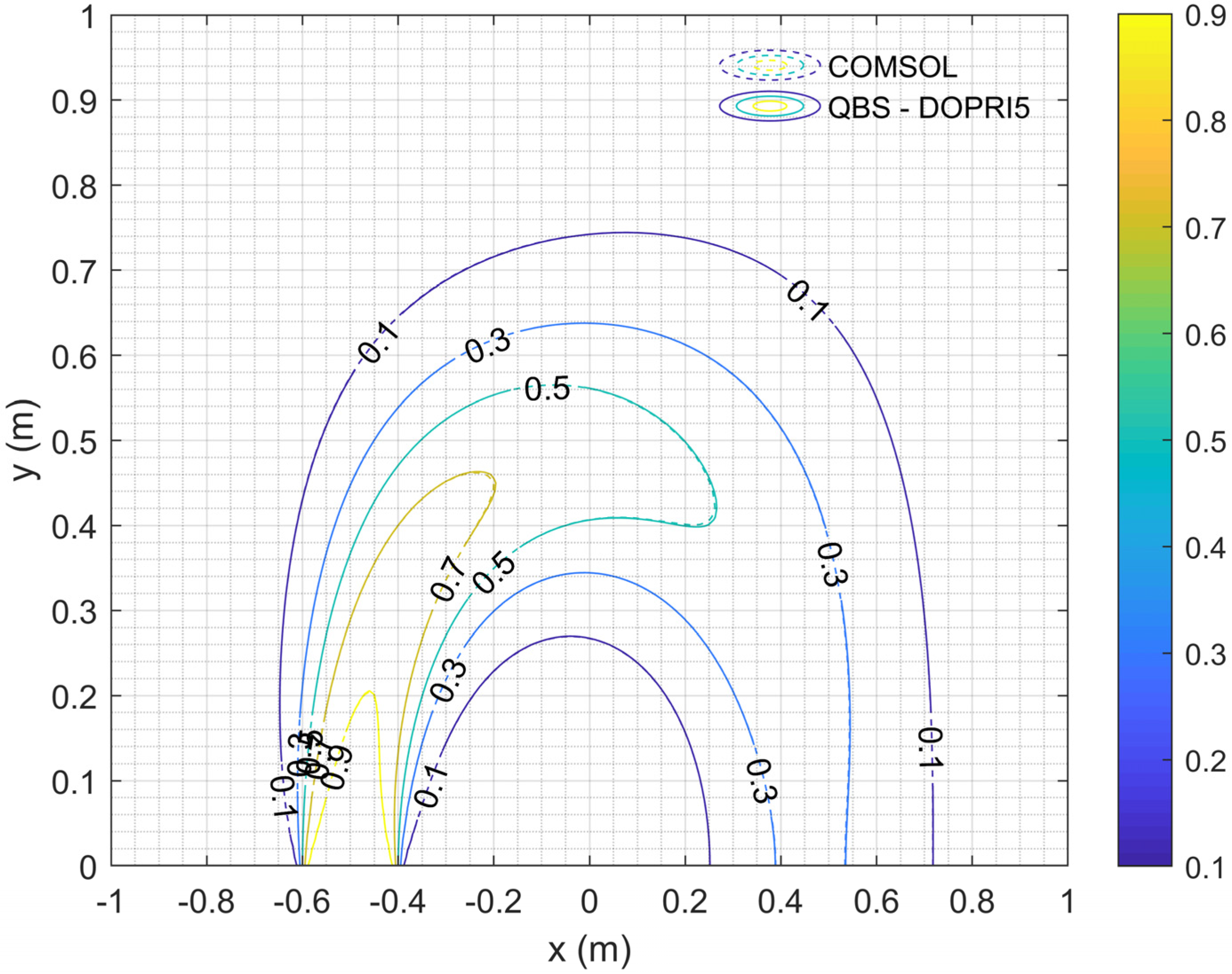
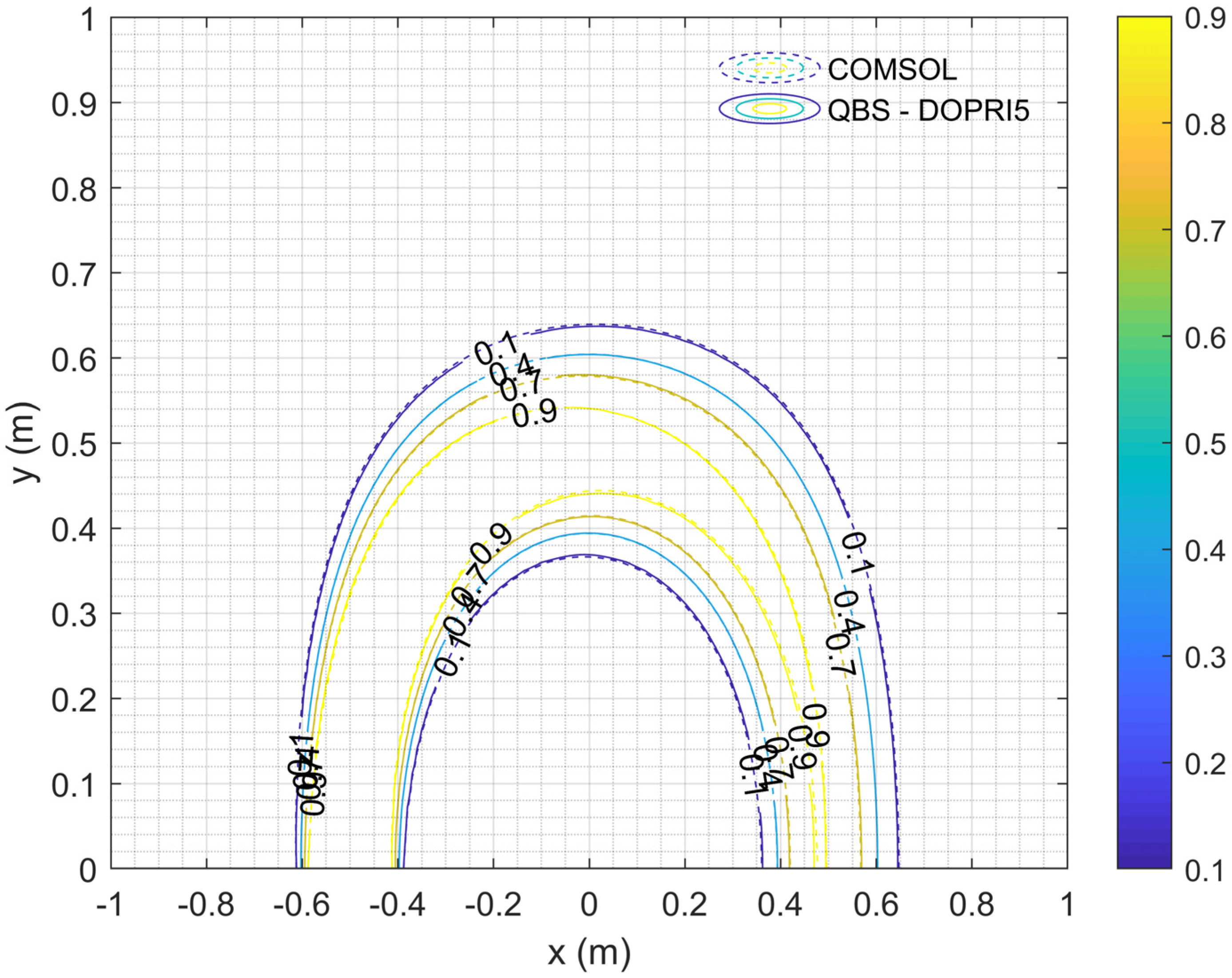
4.3. Example 3
4.4. Example 4
5. Conclusions
Supplementary Materials
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Appendix A
References
- Sun, N.Z. Mathematical Modeling of Groundwater Pollution; Springer: New York, NY, USA, 1996. [Google Scholar] [CrossRef]
- Wang, H.F.; Anderson, M.P. Introduction to Groundwater Modeling: Finite Difference and Finite Element Methods; Academic Press: San Diego, CA, USA, 1982. [Google Scholar] [CrossRef]
- Tatalovich, M.E.; Lee, K.Y.; Chrysikopoulos, C.V. Modeling the transport of contaminants originating from the dissolution of DNAPL pools in aquifers in the presence of dissolved humic substances. Transp. Porous Media 2000, 38, 93–115. [Google Scholar] [CrossRef]
- Noye, B.; Tan, H. Finite difference methods for solving the two-dimensional advection–diffusion equation. Int. J. Numer. Methods Fluids 1989, 9, 75–98. [Google Scholar] [CrossRef]
- Ataie-Ashtiani, B.; Lockington, D.A.; Volker, R.E. Numerical correction for finite-difference solution of the advection—Dispersion equation with reaction. J. Contam. Hydrol. 1996, 23, 149–156. [Google Scholar] [CrossRef]
- Dehghan, M. Weighted finite difference techniques for the one-dimensional advection-diffusion equation. Appl. Math. Comput. 2004, 147, 307–319. [Google Scholar] [CrossRef]
- Sheu, T.W.H.; Chen, Y.H. Finite element analysis of contaminant transport in groundwater. Appl. Math. Comput. 2002, 127, 23–43. [Google Scholar] [CrossRef]
- Badrot-Nico, F.; Brissaud, F.; Guinot, V. A finite volume upwind scheme for the solution of the linear advection-diffusion equation with sharp gradients in multiple dimensions. Adv. Water Resour. 2007, 30, 2002–2025. [Google Scholar] [CrossRef]
- Eldho, T.I.; Vasudeva Rao, B. Simulation of two-dimensional contaminant transport with dual reciprocity boundary elements. Eng. Anal. Bound. Elem. 1997, 20, 213–228. [Google Scholar] [CrossRef]
- Mittal, R.C.; Jain, R.K. Numerical solution of convection-diffusion equation using cubic B-splines collocation methods with Neumann’ s boundary conditions. Int. J. Appl. Math. Comput. 2012, 4, 115–127. [Google Scholar]
- Boddula, S.; Eldho, T.I. A moving least squares based meshless local petrov-galerkin method for the simulation of contaminant transport in porous media. Eng. Anal. Bound. Elem. 2017, 78, 8–19. [Google Scholar] [CrossRef]
- Meenal, M.; Eldho, T.I. Two-dimensional contaminant transport modeling using meshfree point collocation method (PCM). Eng. Anal. Bound. Elem. 2012, 36, 551–561. [Google Scholar] [CrossRef]
- Bahar, E.; Gürarslan, G. Numerical solution of advection-diffusion equation using operator splitting method. Int. J. Eng. Appl. Sci. 2017, 9, 76–88. [Google Scholar] [CrossRef][Green Version]
- Gurarslan, G.; Karahan, H.; Alkaya, D.; Sari, M.; Yasar, M. Numerical solution of advection-diffusion equation using a sixth-order compact finite difference method. Math. Probl. Eng. 2013, 2013, 672936. [Google Scholar] [CrossRef]
- Gurarslan, G. Accurate simulation of contaminant transport using high-order compact finite difference schemes. J. Appl. Math. 2014, 2014, 396738. [Google Scholar] [CrossRef]
- Zhou, J.G. A lattice boltzmann method for solute transport. Int. J. Numer. Methods Fluids 2009, 61, 848–863. [Google Scholar] [CrossRef]
- Perko, J. A single-relaxation-time lattice Boltzmann model for anisotropic advection-diffusion equation based on the diffusion velocity flux formulation. Comput. Geosci. 2018, 22, 1423–1432. [Google Scholar] [CrossRef]
- Korkmaz, A.; Dağ, İ. Cubic B-spline differential quadrature methods for the advection-diffusion equation. Int. J. Numer. Methods Heat Fluid Flow 2012, 22, 1021–1036. [Google Scholar] [CrossRef]
- Irk, D.; Dağ, İ.; Tombul, M. Extended cubic B-spline solution of the advection-diffusion equation. KSCE J. Civ. Eng. 2015, 19, 929–934. [Google Scholar] [CrossRef]
- Dhawan, S.; Kapoor, S.; Kumar, S. Numerical method for advection diffusion equation using FEM and B-splines. J. Comput. Sci. 2012, 3, 429–437. [Google Scholar] [CrossRef]
- Korkmaz, A.; Dağ, I. Quartic and quintic B-spline methods for advection–diffusion equation. Appl. Math. Comput. 2016, 274, 208–219. [Google Scholar] [CrossRef]
- Nazir, T.; Abbas, M.; Izani, A.; Abd, A. The numerical solution of advection—Diffusion problems using new cubic trigonometric B-splines approach. Appl. Math. Model. 2016, 40, 4586–4611. [Google Scholar] [CrossRef]
- Mohammadi, R. Exponential B-Spline solution of convection-diffusion equations. Appl. Math. 2013, 4, 33152. [Google Scholar] [CrossRef]
- Mittal, R.C.; Tripathi, A. Numerical solutions of two-dimensional unsteady convection–diffusion problems using modified bi-cubic B-spline finite elements. Int. J. Comput. Math. 2017, 94, 1–21. [Google Scholar] [CrossRef]
- Rohila, R.; Mittal, R.C. An efficient Bi-cubic B-spline ADI method for numerical solutions of two-dimensional unsteady advection diffusion equations. Int. J. Numer. Methods Heat Fluid Flow 2018, 28, 2620–2649. [Google Scholar] [CrossRef]
- Shukla, H.S.; Tamsir, M. An exponential cubic B-spline algorithm for multi-dimensional convection-diffusion equations. Alexandria Eng. J. 2018, 57, 1999–2006. [Google Scholar] [CrossRef]
- Dormand, J.R.; Prince, P.J. A family of embedded Runge-Kutta formulae. J. Comput. Appl. Math. 1980, 6, 19–26. [Google Scholar] [CrossRef]
- Bear, J.; Cheng, A.H.-D. Modeling Groundwater Flow and Contaminant Transport; Springer: Berlin, Germany, 2010. [Google Scholar] [CrossRef]
- Mittal, R.C.; Arora, G. Quintic B-spline collocation method for numerical solution of the Kuramoto-Sivashinsky equation. Commun. Nonlinear Sci. Numer. Simul. 2010, 15, 2798–2808. [Google Scholar] [CrossRef]
- Hamdi, S.; Schiesser, W.; Griffiths, G. Method of lines. Scholarpedia 2007, 2, 2859. [Google Scholar] [CrossRef]
- Fehlberg, E. Low Order Classical Runge Kutta Formulas with Stepwise Control and Their Application to Some Heat Transfer Problems. 1969. Available online: https://ntrs.nasa.gov/search.jsp?R=19690021375 (accessed on 1 June 2020).
- Shampine, L.F. Some practical Runge-Kutta formulas. Math. Comput. 1986, 46, 135–150. [Google Scholar] [CrossRef]
- Butcher, J.C. Implicit runge-kutta processes. Math. Comput. 1964, 18, 50–64. [Google Scholar] [CrossRef]
- Kalita, J.C.; Dalal, D.C.; Dass, A.K. A class of higher order compact schemes for the unsteady two-dimensional convection-diffusion equation with variable convection coefficients. Int. J. Numer. Methods Fluids 2002, 38, 1111–1131. [Google Scholar] [CrossRef]
- Dehghan, M.; Mohebbi, A. High-order compact boundary value method for the solution of unsteady convection-diffusion problems. Math. Comput. Simul. 2008, 79, 683–699. [Google Scholar] [CrossRef]
- Karaa, S.; Zhang, J. High order ADI method for solving unsteady convection-diffusion problems. J. Comput. Phys. 2004, 198, 1–9. [Google Scholar] [CrossRef]
- Tian, Z.F.; Ge, Y.B. A fourth-order compact ADI method for solving two-dimensional unsteady convection-diffusion problems. J. Comput. Appl. Math. 2007, 198, 268–286. [Google Scholar] [CrossRef]
- Wexler, E.J. Analytical Solutions for One-, Two-, and Three-Dimensional Solute Transport in Ground-Water Systems with Uniform Flow; United State Goverment Printing Office: Washington, DC, USA, 1992.

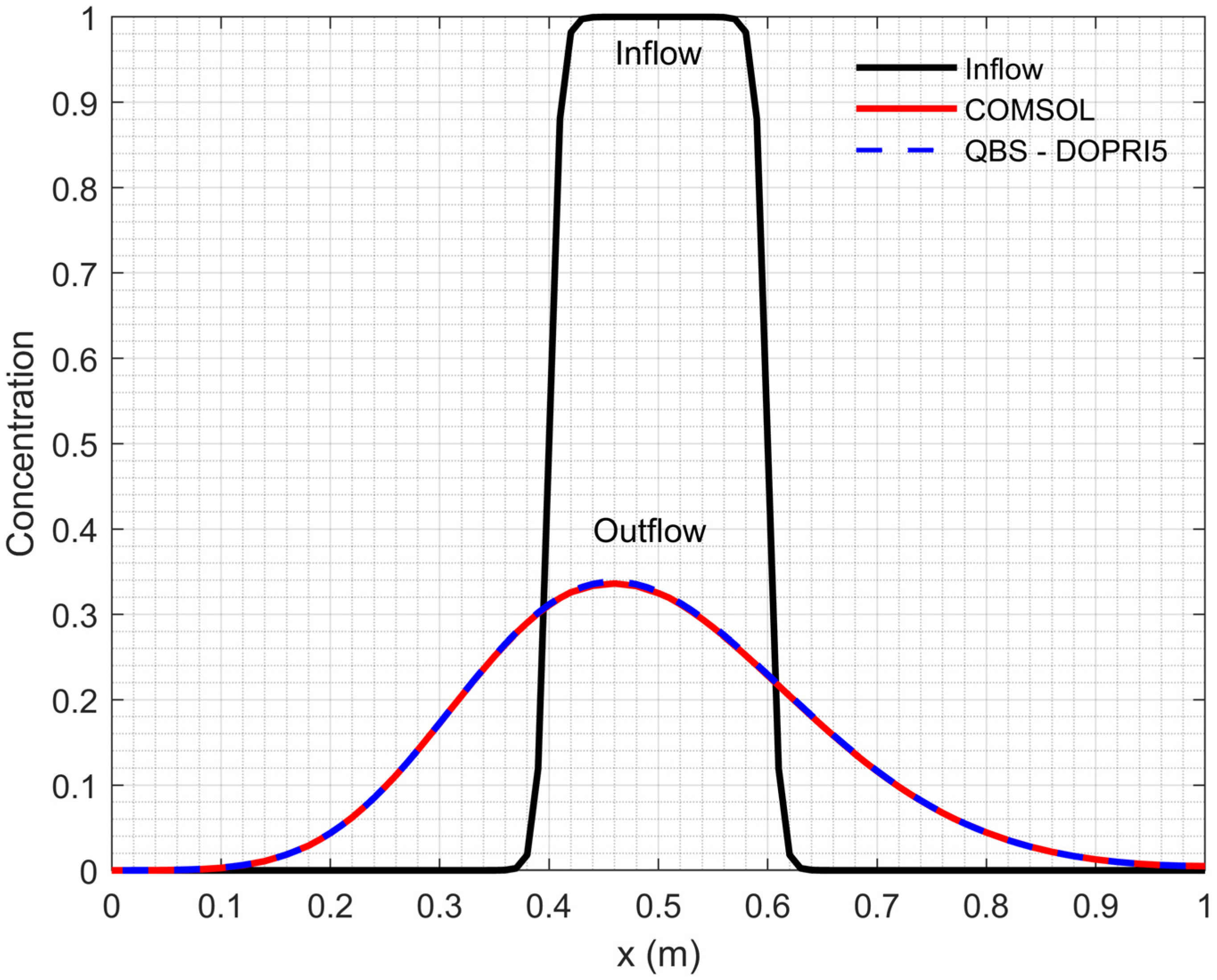
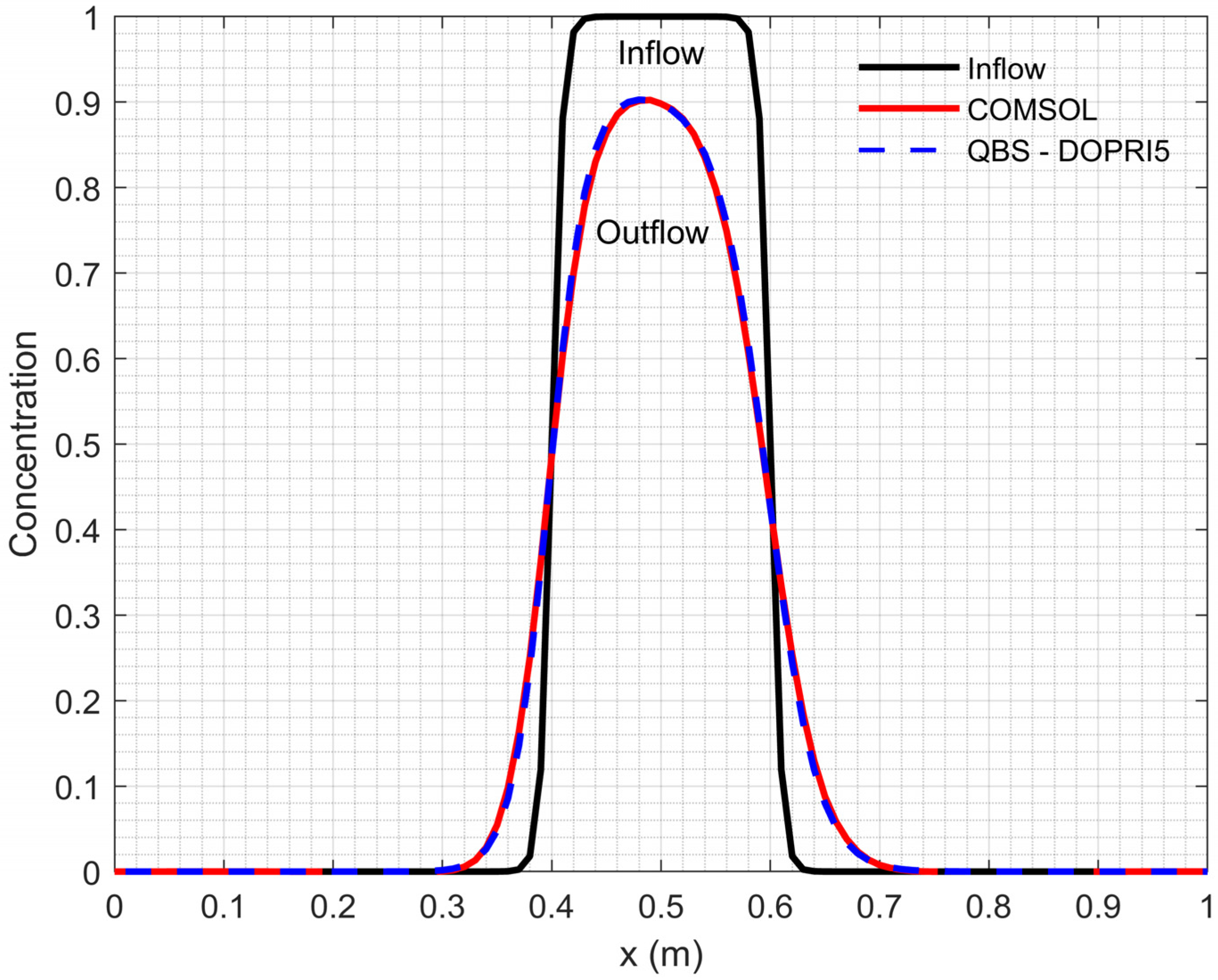
| 0 | |||||||
| 0 | |||||||
| 0 | |||||||
| 0 | |||||||
| 0 | |||||||
| Dehghan and Mohebbi [35] | Mittal and Tripathi [24] | QBS-DOPRI5 | |
|---|---|---|---|
| 0.04 | |||
| 0.02 | |||
| 0.01 |
| References | ||||
|---|---|---|---|---|
| Average Error | Maximum Error | Average Error | Maximum Error | |
| Noye and Tan [4] | - | - | ||
| Kalita et al. [34] | - | - | ||
| Karaa and Zhang [36] | - | - | ||
| Tian and Ge [37] | - | - | ||
| Dehghan and Mohebbi [35] | - | - | ||
| Shukla and Tamsir [26] | - | - | ||
| Gurarslan MC-CD6 [15] | - | - | ||
| Gurarslan RK4-CD6 [15] | - | - | ||
| Mittal and Tripathi [24] | ||||
| QBS-DOPRI5 | ||||
| Location | BEM [9] | MLPG-MLS [11] | MLPG-MLS [11] | QBS-DOPRI5 | QBS-DOPRI5 | Reference Solution |
|---|---|---|---|---|---|---|
| 0.774 | 0.771 | 0.771 | 0.767 | 0.768 | 0.768 | |
| 0.797 | 0.794 | 0.795 | 0.824 | 0.833 | 0.833 | |
| 0.362 | 0.361 | 0.361 | 0.391 | 0.389 | 0.389 | |
| 0.057 | 0.056 | 0.056 | 0.058 | 0.052 | 0.052 |
| Method | CPU | |||||
|---|---|---|---|---|---|---|
| QBS-DOPRI5 | 0.767 | 0.824 | 0.391 | 0.058 | 0.57 | |
| 0.768 | 0.831 | 0.389 | 0.053 | 1.40 | ||
| 0.768 | 0.833 | 0.389 | 0.052 | 19.57 | ||
| 0.768 | 0.833 | 0.389 | 0.052 | 278.17 | ||
| 0.768 | 0.833 | 0.389 | 0.052 | 9041.92 | ||
| FDM-DOPRI5 | 0.815 | 0.867 | 0.421 | 0.074 | 0.31 | |
| 0.779 | 0.845 | 0.397 | 0.057 | 0.38 | ||
| 0.771 | 0.836 | 0.391 | 0.053 | 1.05 | ||
| 0.769 | 0.834 | 0.390 | 0.052 | 8.38 | ||
| 0.769 | 0.833 | 0.389 | 0.052 | 84.04 | ||
| 0.768 | 0.833 | 0.389 | 0.052 | 1302.46 | ||
| Reference Solution | 0.768 | 0.833 | 0.389 | 0.052 | 8399.55 | |
| Method | CPU | |||||
|---|---|---|---|---|---|---|
| QBS-DOPRI5 | 0.779 | 0.852 | 0.336 | 0.026 | 0.76 | |
| 0.781 | 0.861 | 0.331 | 0.023 | 1.97 | ||
| 0.782 | 0.864 | 0.330 | 0.022 | 26.08 | ||
| 0.782 | 0.864 | 0.330 | 0.022 | 479.95 | ||
| FDM-DOPRI5 | 0.844 | 0.895 | 0.378 | 0.045 | 0.37 | |
| 0.804 | 0.880 | 0.345 | 0.027 | 0.47 | ||
| 0.791 | 0.871 | 0.337 | 0.023 | 1.25 | ||
| 0.786 | 0.867 | 0.334 | 0.022 | 10.08 | ||
| 0.784 | 0.866 | 0.332 | 0.022 | 97.03 | ||
| 0.783 | 0.865 | 0.331 | 0.022 | 1532.50 | ||
| 0.782 | 0.864 | 0.330 | 0.022 | 27691.71 | ||
| Reference Solution | 0.782 | 0.864 | 0.330 | 0.022 | 174576.14 | |
| Scenario A | Scenario B | |||
|---|---|---|---|---|
| QBS-DOPRI5 | COMSOL | QBS-DOPRI5 | COMSOL | |
| 0.003 | 0.003 | 0.000 | 0.000 | |
| 0.044 | 0.043 | 0.000 | 0.000 | |
| 0.173 | 0.172 | 0.002 | 0.000 | |
| 0.251 | 0.251 | 0.048 | 0.055 | |
| 0.312 | 0.311 | 0.485 | 0.486 | |
| 0.338 | 0.335 | 0.875 | 0.864 | |
| 0.327 | 0.325 | 0.898 | 0.898 | |
| 0.286 | 0.285 | 0.806 | 0.799 | |
| 0.229 | 0.228 | 0.426 | 0.426 | |
| 0.170 | 0.169 | 0.080 | 0.088 | |
| 0.117 | 0.116 | 0.008 | 0.008 | |
| 0.044 | 0.044 | 0.000 | -0.001 | |
| 0.013 | 0.013 | 0.000 | 0.000 | |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Bahar, E.; Gurarslan, G. B-Spline Method of Lines for Simulation of Contaminant Transport in Groundwater. Water 2020, 12, 1607. https://doi.org/10.3390/w12061607
Bahar E, Gurarslan G. B-Spline Method of Lines for Simulation of Contaminant Transport in Groundwater. Water. 2020; 12(6):1607. https://doi.org/10.3390/w12061607
Chicago/Turabian StyleBahar, Ersin, and Gurhan Gurarslan. 2020. "B-Spline Method of Lines for Simulation of Contaminant Transport in Groundwater" Water 12, no. 6: 1607. https://doi.org/10.3390/w12061607
APA StyleBahar, E., & Gurarslan, G. (2020). B-Spline Method of Lines for Simulation of Contaminant Transport in Groundwater. Water, 12(6), 1607. https://doi.org/10.3390/w12061607





