Tsunami Propagation and Flooding in Sicilian Coastal Areas by Means of a Weakly Dispersive Boussinesq Model
Abstract
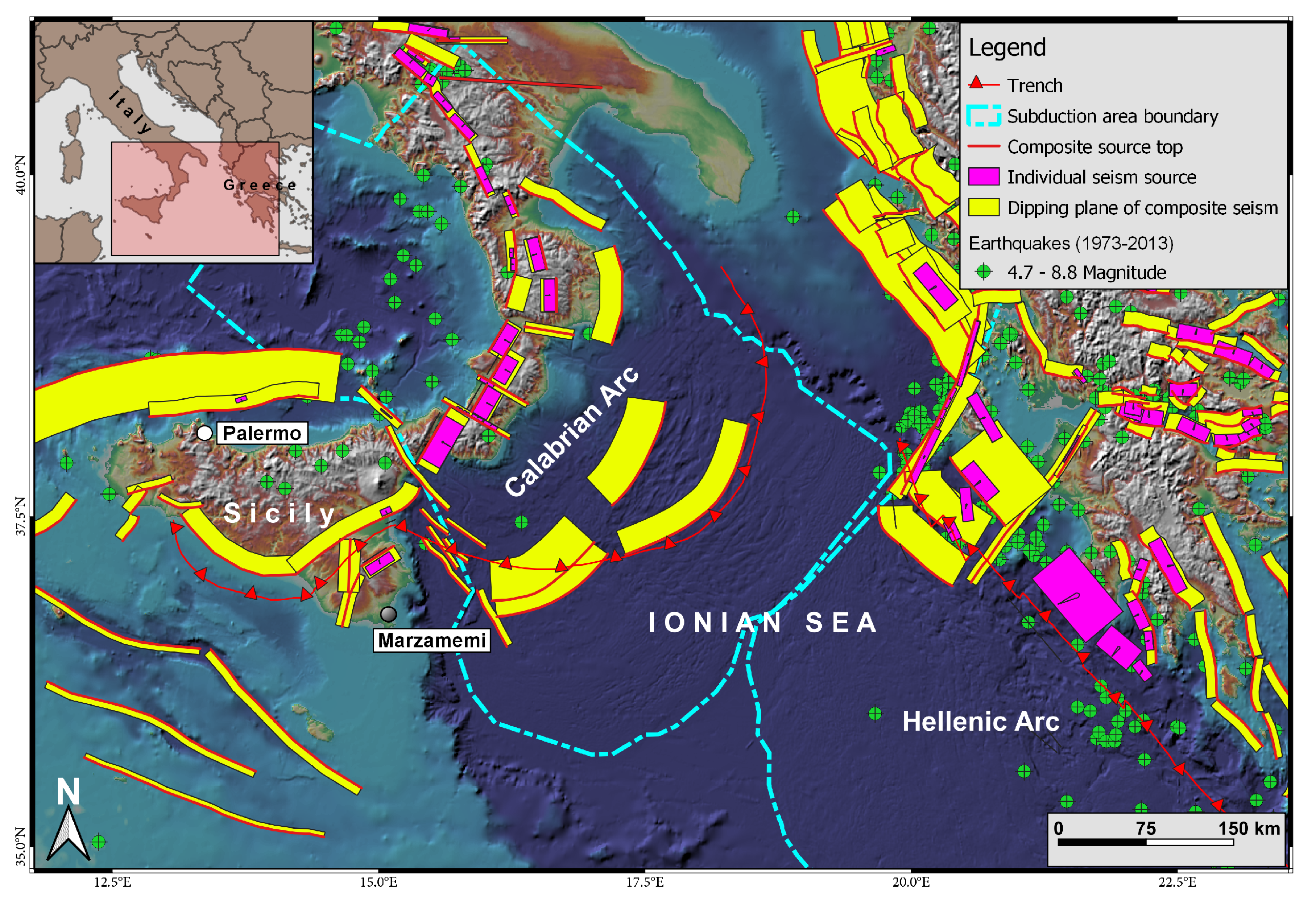
1. Introduction
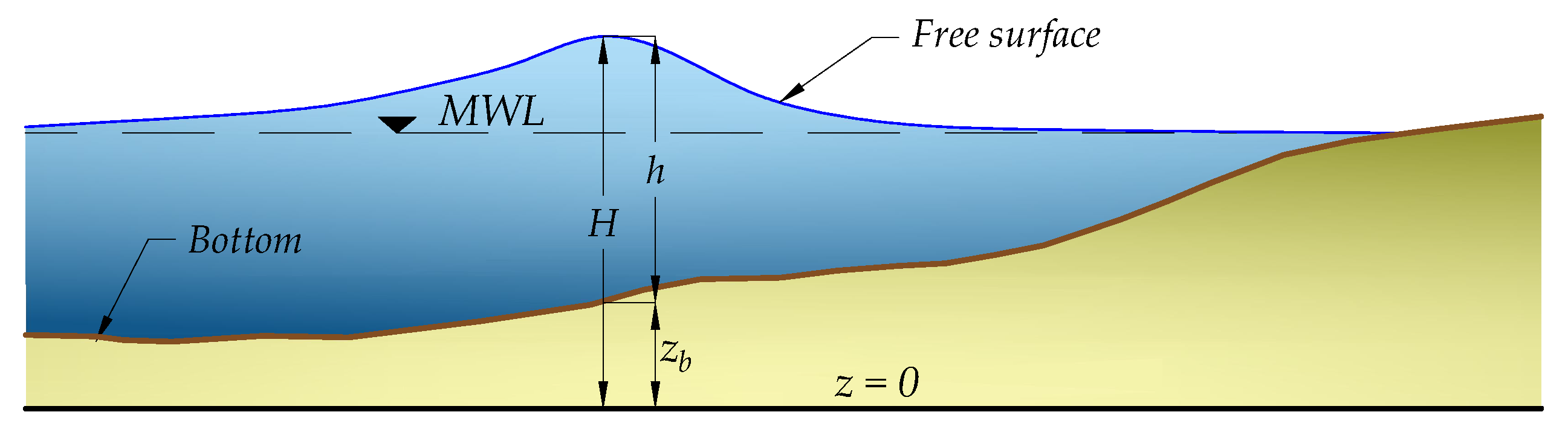
2. Materials and Methods
2.1. The Numerical Model
3. Validation of the Numerical Model
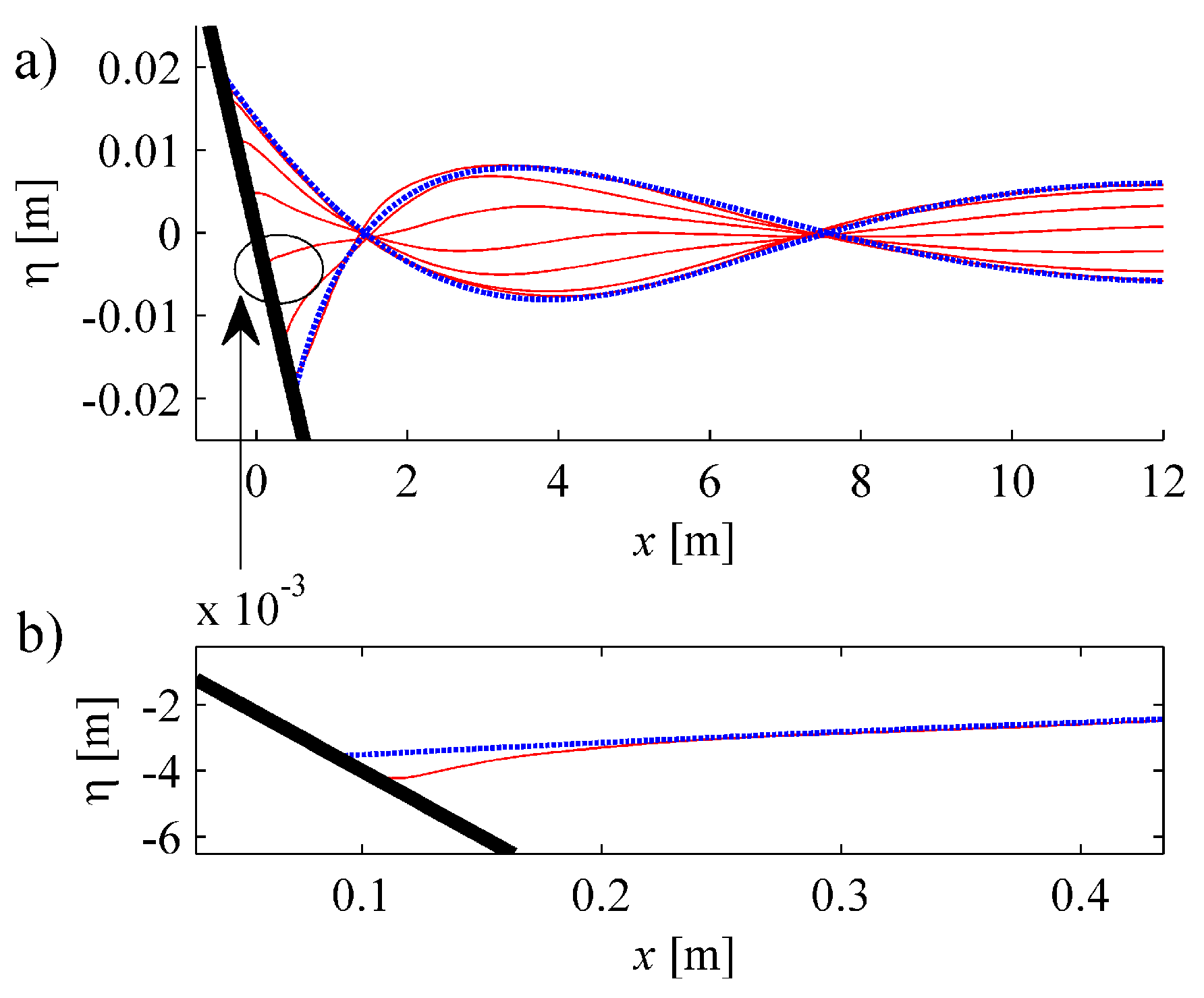
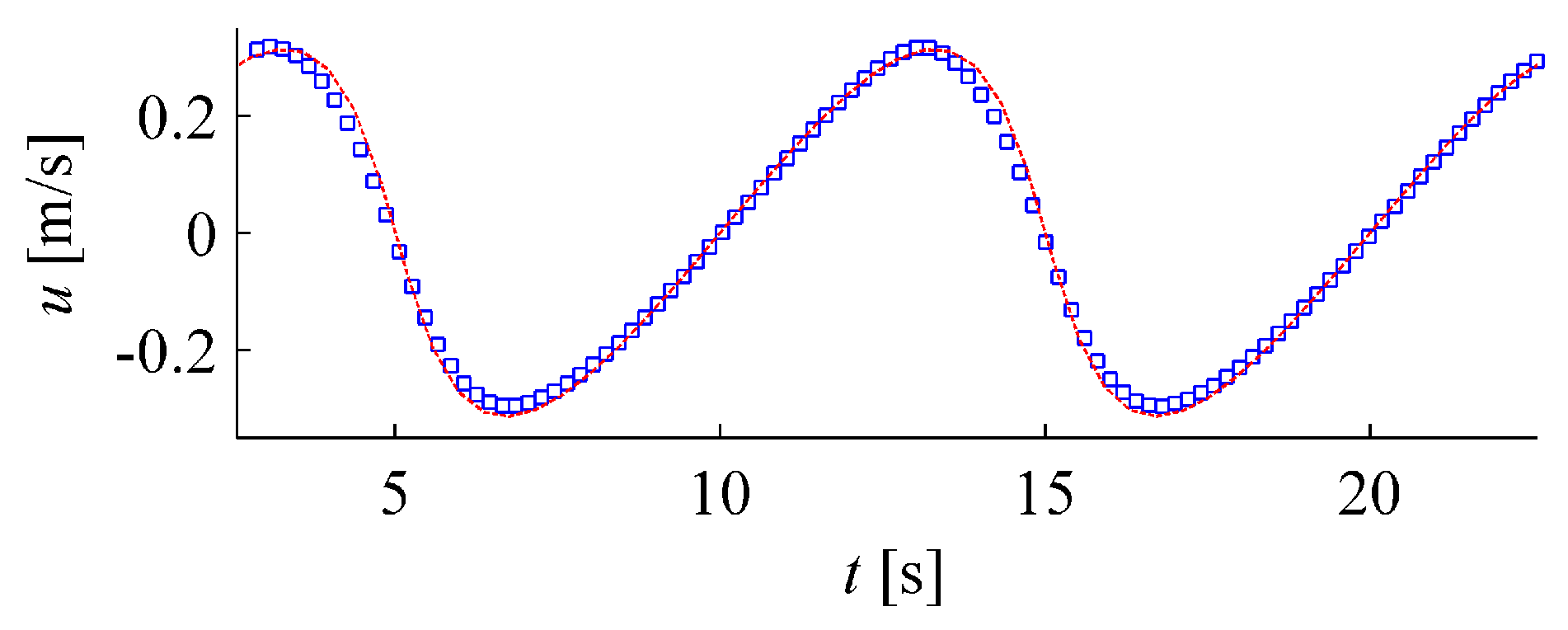
3.1. The Carrier and Greenspan Numerical Solution
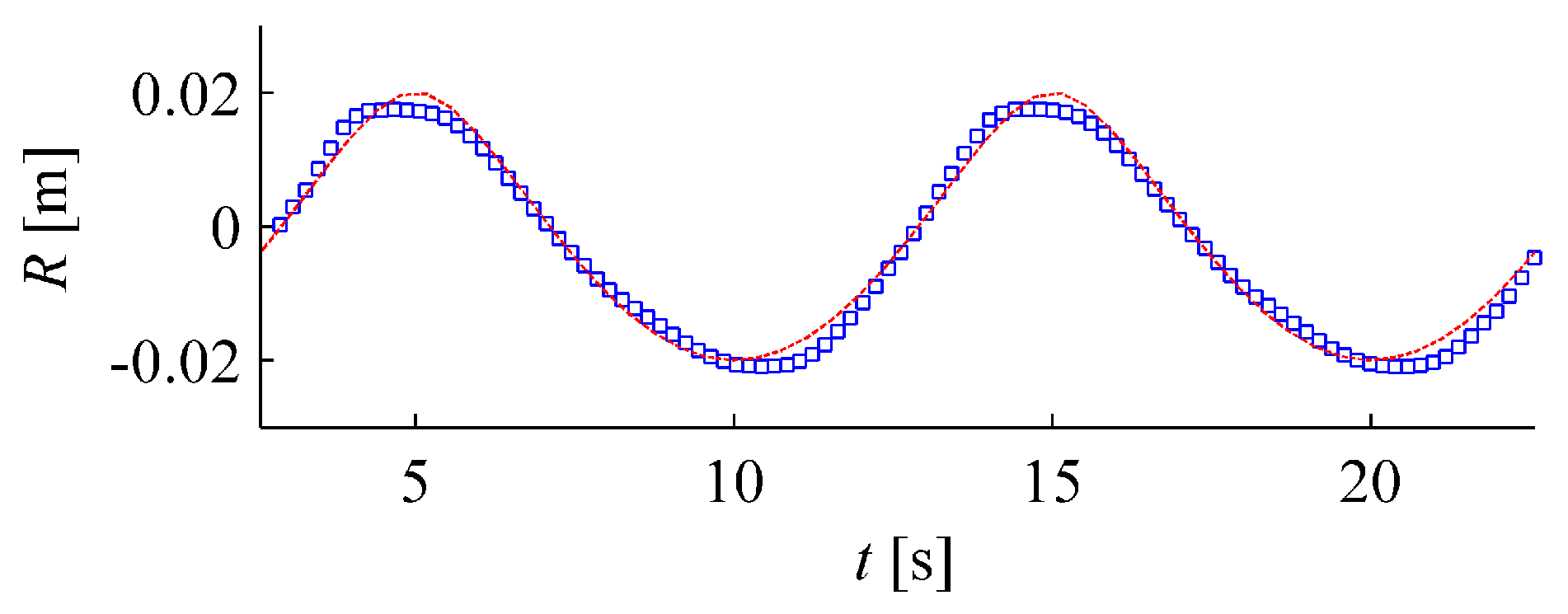
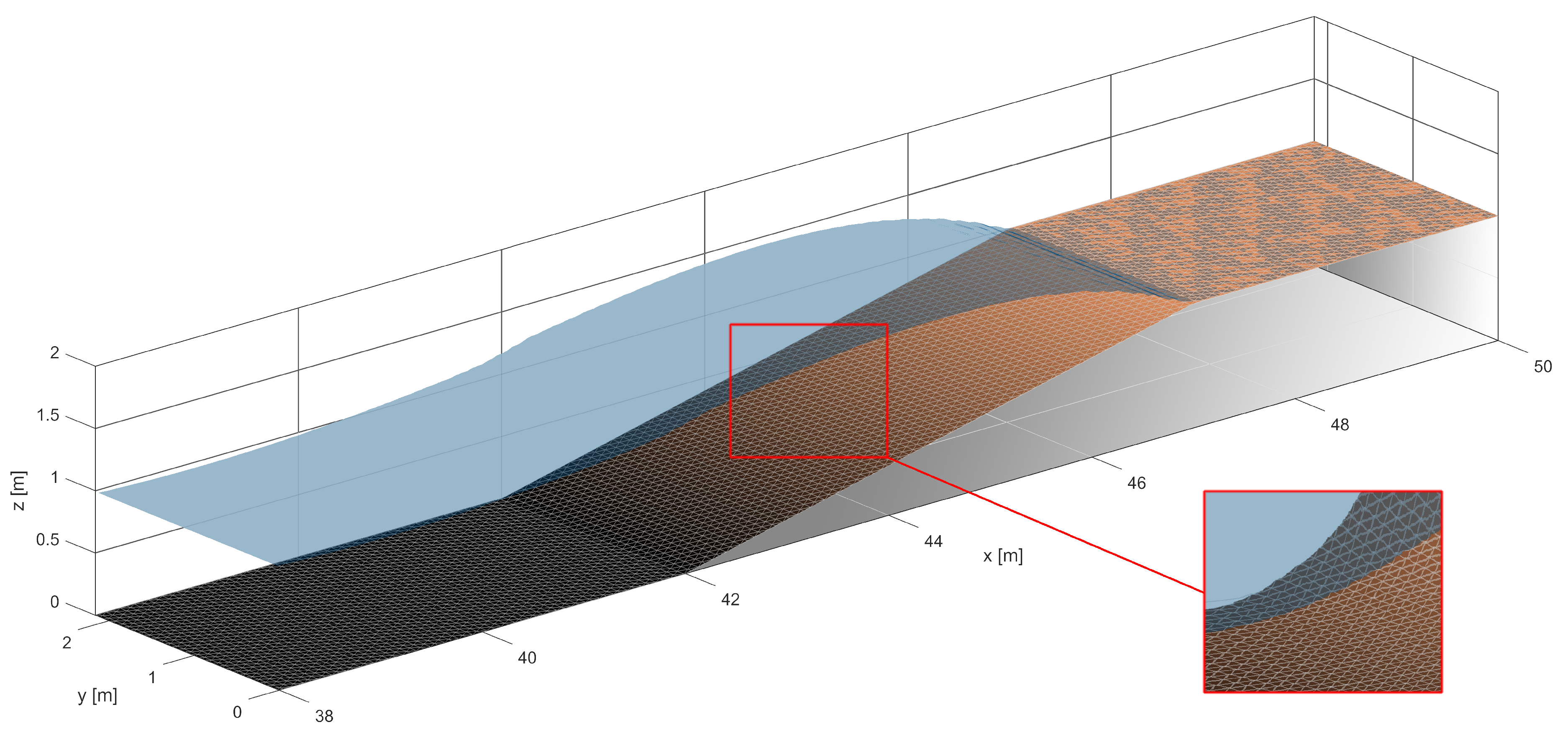
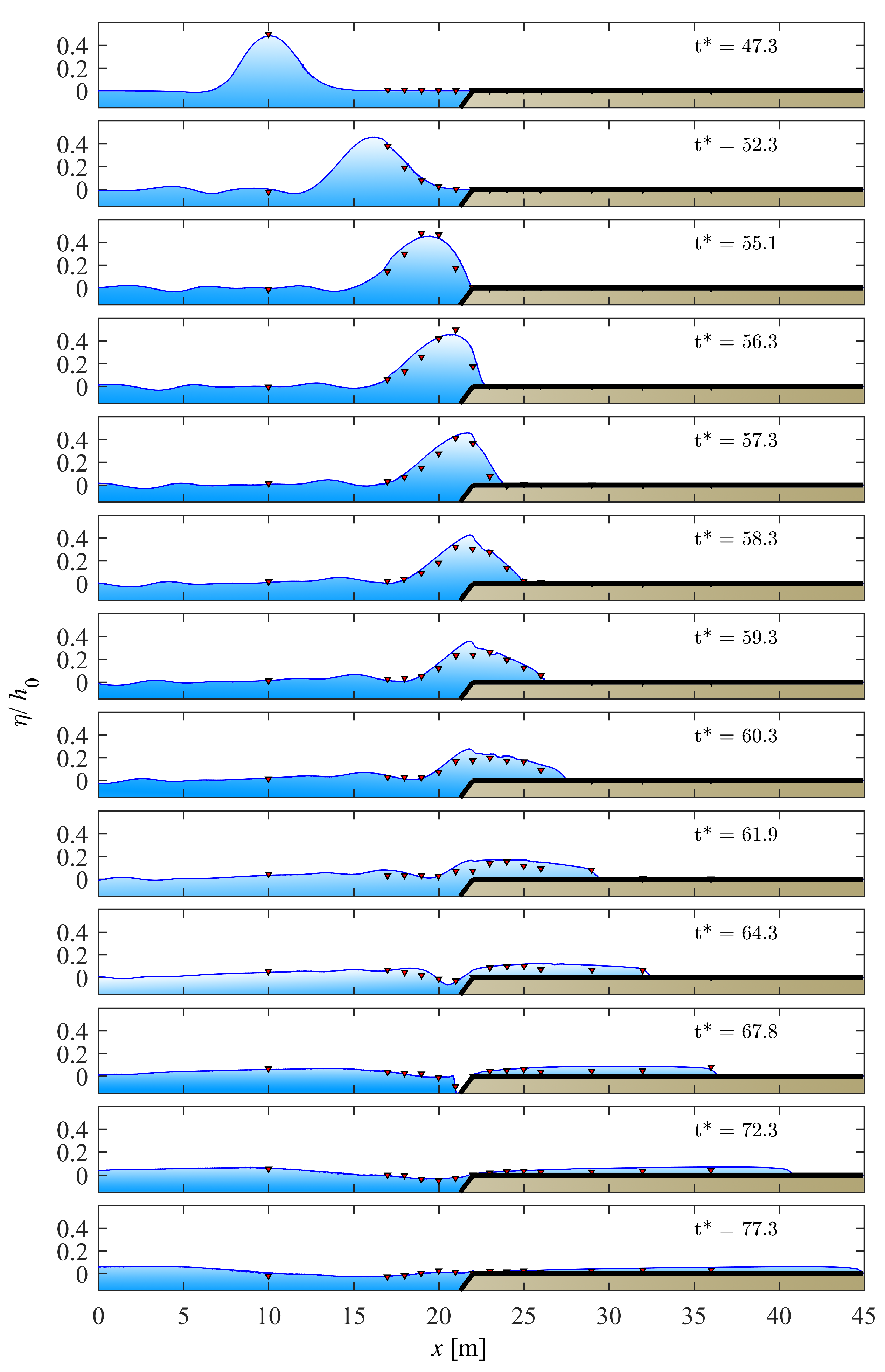
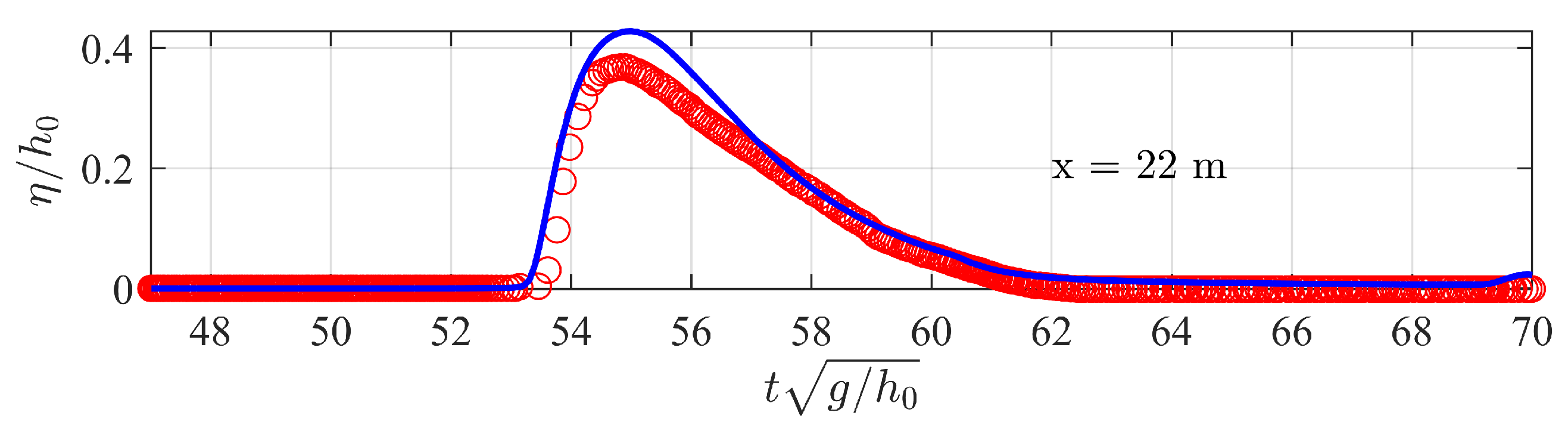
3.2. The Fringing Reef Experiment
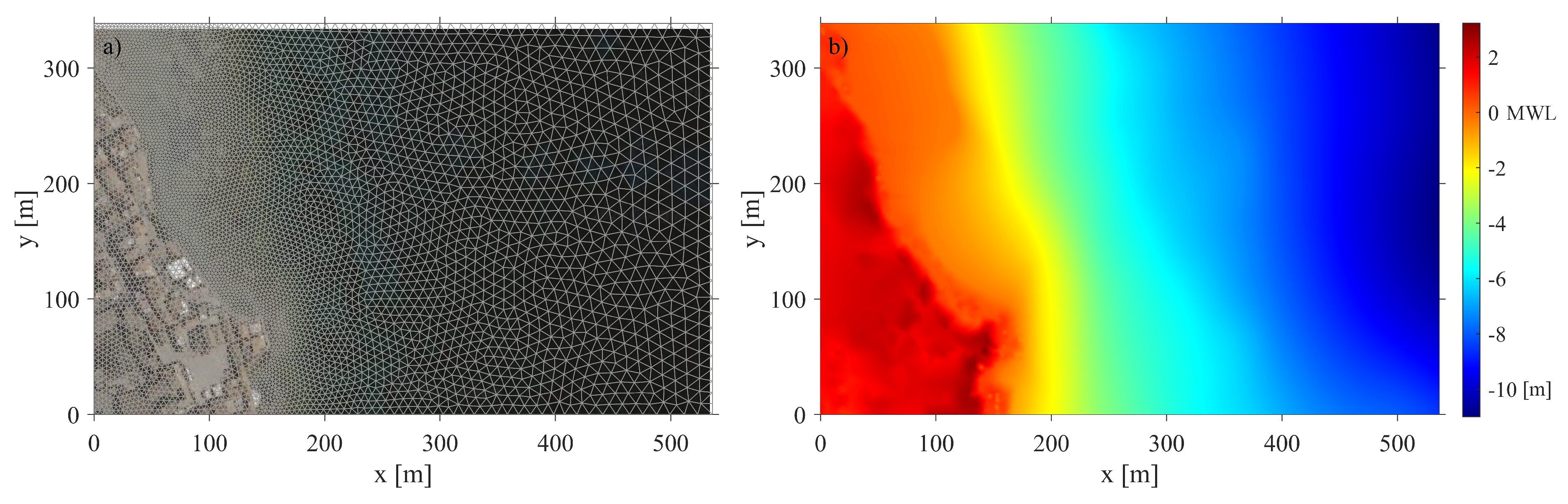
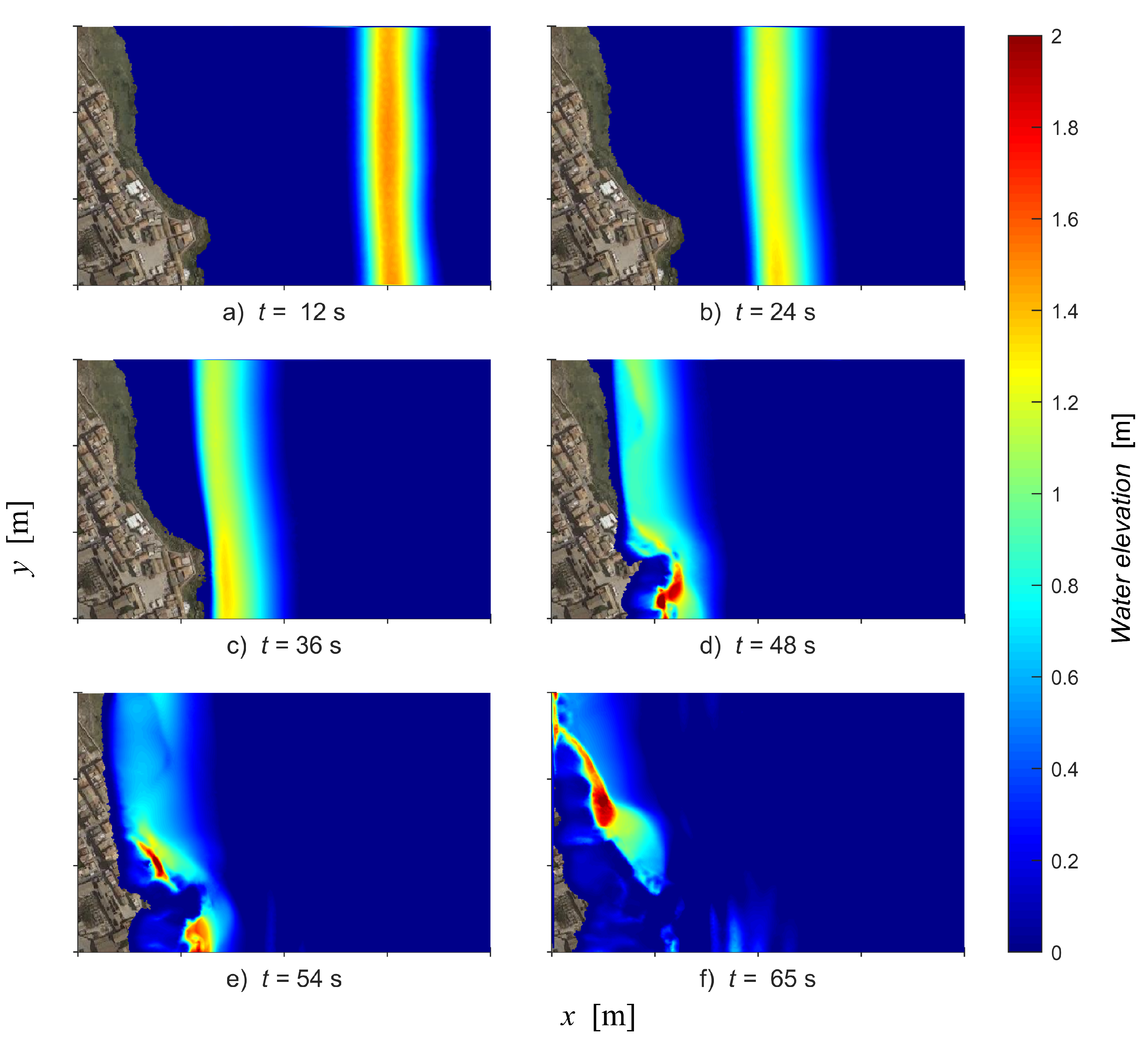
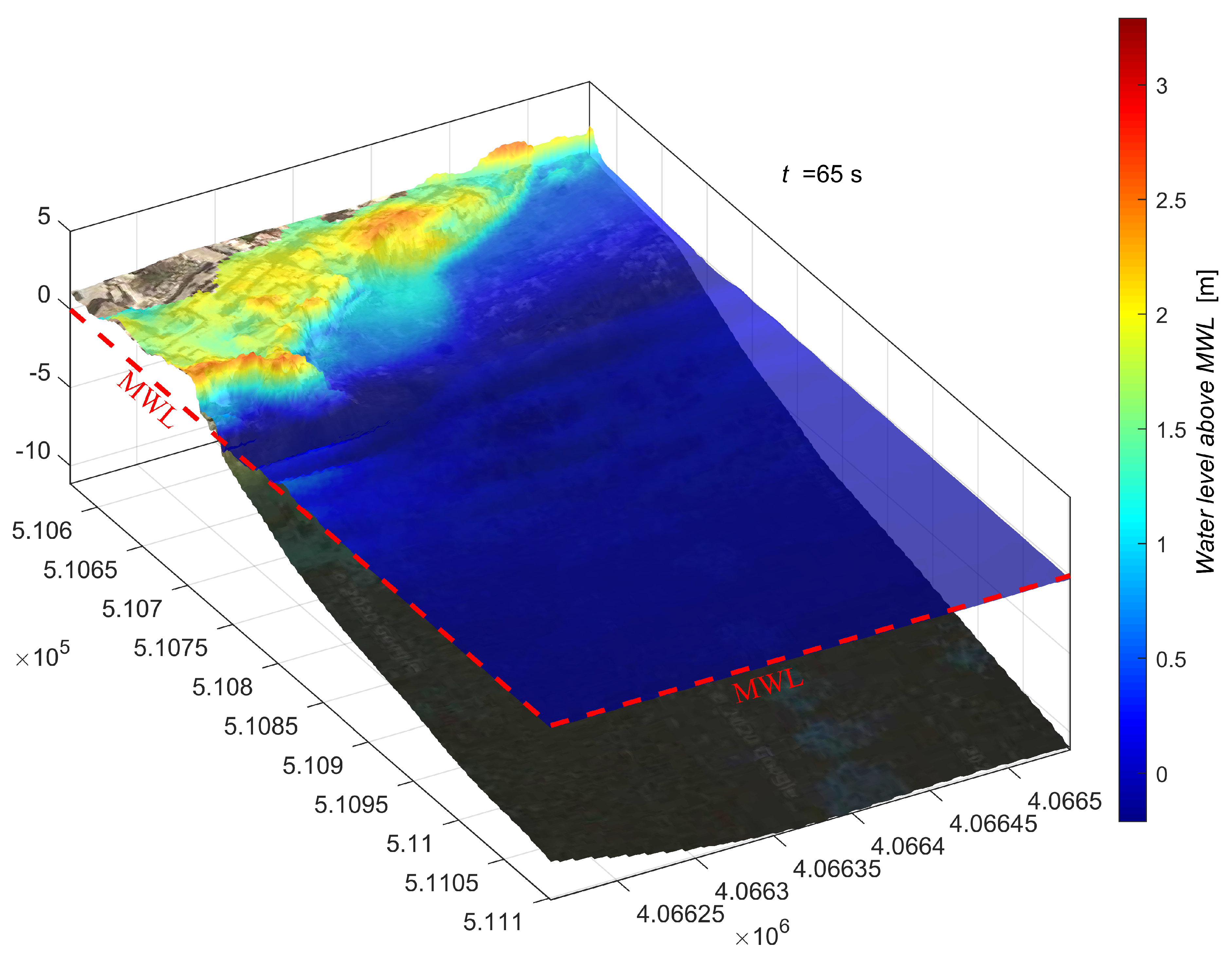
4. Results and Discussions of a Real Case of Tsunami Propagation
5. Concluding Remarks
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Molina, R.; Manno, G.; Lo Re, C.; Anfuso, G.; Ciraolo, G. Storm Energy Flux Characterization along the Mediterranean Coast of Andalusia (Spain). Water 2019, 11, 509. [Google Scholar] [CrossRef]
- Molina, R.; Manno, G.; Lo Re, C.; Anfuso, G.; Ciraolo, G. A Methodological Approach to Determine Sound Response Modalities to Coastal Erosion Processes in Mediterranean Andalusia (Spain). J. Mar. Sci. Eng. 2020, 8, 154. [Google Scholar] [CrossRef]
- Manno, G.; Lo Re, C.; Ciraolo, G. Uncertainties in shoreline position analysis: The role of run-up and tide in a gentle slope beach. Ocean Sci. 2017, 13, 661–671. [Google Scholar] [CrossRef]
- Lo Re, C.; Musumeci, R.E.; Foti, E. A shoreline boundary condition for a highly nonlinear Boussinesq model for breaking waves. Coast. Eng. 2012, 60, 41–52. [Google Scholar] [CrossRef]
- Roeber, V.; Cheung, K.F.; Kobayashi, M.H. Shock-capturing Boussinesq-type model for nearshore wave processes. Coast. Eng. 2010, 57, 407–423. [Google Scholar] [CrossRef]
- Roeber, V.; Cheung, K.F. Boussinesq-type model for energetic breaking waves in fringing reef environments. Coast. Eng. 2012, 70, 1–20. [Google Scholar] [CrossRef]
- Zhang, H.; Zhang, M.; Ji, Y.; Wang, Y.; Xu, T. Numerical study of tsunami wave run-up and land inundation on coastal vegetated beaches. Comput. Geosci. 2019, 132, 9–22. [Google Scholar] [CrossRef]
- Marivela, R.; Weiss, R.; Synolakis, C. The Temporal and Spatial Evolution of Momentum, Kinetic Energy and Force in Tsunami Waves during Breaking and Inundation. arXiv 2016, arXiv:1611.04514. [Google Scholar]
- Manoj Kumar, G.; Sriram, V.; Didenkulova, I. A hybrid numerical model based on FNPT-NS for the estimation of long wave run-up. Ocean Eng. 2020, 202, 107181. [Google Scholar] [CrossRef]
- Wei, Z.; Dalrymple, R.A.; Rustico, E.; Hérault, A.; Bilotta, G. Simulation of Nearshore Tsunami Breaking by Smoothed Particle Hydrodynamics Method. J. Waterway Port Coast. Ocean Eng. 2016, 142, 05016001. [Google Scholar] [CrossRef]
- Qin, X.; Motley, M.; LeVeque, R.; Gonzalez, F.; Mueller, K. A comparison of a two-dimensional depth-averaged flow model and a three-dimensional RANS model for predicting tsunami inundation and fluid forces. Nat. Hazards Earth Syst. Sci. 2018, 18, 2489–2506. [Google Scholar] [CrossRef]
- Qu, K.; Ren, X.; Kraatz, S. Numerical investigation of tsunami-like wave hydrodynamic characteristics and its comparison with solitary wave. Appl. Ocean Res. 2017, 63, 36–48. [Google Scholar] [CrossRef]
- Arico, C.; Lo Re, C. A non-hydrostatic pressure distribution solver for the nonlinear shallow water equations over irregular topography. Adv. Water Resour. 2016, 98, 47–69. [Google Scholar] [CrossRef]
- Presti, V.L.; Antonioli, F.; Auriemma, R.; Ronchitelli, A.; Scicchitano, G.; Spampinato, C.; Anzidei, M.; Agizza, S.; Benini, A.; Ferranti, L.; et al. Millstone coastal quarries of the Mediterranean: A new class of sea level indicator. Quat. Int. 2014, 332, 126–142. [Google Scholar] [CrossRef]
- Samaras, A.; Karambas, T.V.; Archetti, R. Simulation of tsunami generation, propagation and coastal inundation in the Eastern Mediterranean. Ocean Sci. 2015, 11, 643–655. [Google Scholar] [CrossRef]
- Schambach, L.; Grilli, S.T.; Kirby, J.T.; Shi, F. Landslide Tsunami Hazard Along the Upper US East Coast: Effects of Slide Deformation, Bottom Friction, and Frequency Dispersion. Pure Appl. Geophys. 2019, 176, 3059–3098. [Google Scholar] [CrossRef]
- Mueller, C.; Micallef, A.; Spatola, D.; Wang, X. The Tsunami Inundation Hazard of the Maltese Islands (Central Mediterranean Sea): A Submarine Landslide and Earthquake Tsunami Scenario Study. Pure Appl. Geophys. 2020, 177, 1617–1638. [Google Scholar] [CrossRef]
- Suardana, A.M.A.P.; Sugianto, D.N.; Helmi, M. Study of Characteristics and the Coverage of Tsunami Wave Using 2D Numerical Modeling in the South Coast of Bali, Indonesia. Int. J. Oceans Oceanogr. 2019, 13, 237–250. [Google Scholar]
- Papadopoulos, G.A.; Fokaefs, A. Strong tsunamis in the Mediterranean Sea: A re-evaluation. ISET J. Earthq. Technol. 2005, 42, 159–170. [Google Scholar]
- DISS Working Group. Database of Individual Seismogenic Sources (DISS). In A Compilation of Potential Sources for Earthquakes Larger than M 5.5 in Italy and Surrounding Areas; Istituto Nazionale di Geofisica e Vulcanologia: Rome, Italy, 2018. [Google Scholar] [CrossRef]
- Caputo, R.; Pavlides, S. The Greek Database of Seismogenic Sources (GreDaSS), version 2.0.0: A Compilation of Potential Seismogenic Sources (Mw > 5.5) in the Aegean Region; University of Ferrara: Ferrara, Italy, 2013. [Google Scholar] [CrossRef]
- Gutscher, M.A.; Roger, J.; Baptista, M.A.; Miranda, J.M.; Tinti, S. Source of the 1693 Catania earthquake and tsunami (southern Italy): New evidence from tsunami modeling of a locked subduction fault plane. Geophys. Res. Lett. 2006, 33, L08309. [Google Scholar] [CrossRef]
- Catalano, R.; Doglioni, C.; Merlini, S. On the mesozoic Ionian basin. Geophys. J. Int. 2001, 144, 49–64. [Google Scholar] [CrossRef]
- Papadopoulos, G.A.; Daskalaki, E.; Fokaefs, A.; Giraleas, N. Tsunami hazard in the Eastern Mediterranean sea: Strong earthquakes and tsunamis in the west Hellenic arc and trench system. J. Earthq. Tsunami 2010, 4, 145–179. [Google Scholar] [CrossRef]
- LeVeque, R.J. Numerical Methods for Conservation Laws; Birkhäuser Boston: Basel, Switzerland, 2013. [Google Scholar]
- Toro, E.F. Riemann Solvers and Numerical Methods for Fluid Dynamics: A Practical Introduction; Springer Science & Business Media: New York, NY, USA, 2013. [Google Scholar]
- Stelling, G.S.; Duinmeijer, S.P.A. A staggered conservative scheme for every Froude number in rapidly varied shallow water flows. Int. J. Numer. Methods Fluids 2003, 43, 1329–1354. [Google Scholar] [CrossRef]
- Carrier, G.; Greenspan, H. Water waves of finite amplitude on a sloping beach. J. Fluid Mech. 1958, 4, 97–109. [Google Scholar] [CrossRef]
- Roeber, V. Boussinesq-Type Model for Nearshore Wave Processes in Fringing Reef Environment. Ph.D. Thesis, University of Hawaii at Manoa, Honolulu, HI, USA, December 2010. [Google Scholar]
- Engwirda, D. Locally-Optimal Delaunay-Refinement and Optimisation-Based Mesh Generation. Ph.D. Thesis, The University of Sydney, Sydney, Australia, 2014. [Google Scholar]
- Basili, R.; Brizuela, B.; Herrero, A.; Iqbal, S.; Lorito, S.; Maesano, F.E.; Murphy, S.; Perfetti, P.; Romano, F.; Scala, A.; et al. NEAM Tsunami Hazard Model 2018 (NEAMTHM18): Online Data of the Probabilistic Tsunami Hazard Model for the NEAM Region from the TSUMAPS-NEAM Project; Istituto Nazionale di Geofisica e Vulcanologia (INGV): Roma, Italy, 2018. [Google Scholar] [CrossRef]

© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lo Re, C.; Manno, G.; Ciraolo, G. Tsunami Propagation and Flooding in Sicilian Coastal Areas by Means of a Weakly Dispersive Boussinesq Model. Water 2020, 12, 1448. https://doi.org/10.3390/w12051448
Lo Re C, Manno G, Ciraolo G. Tsunami Propagation and Flooding in Sicilian Coastal Areas by Means of a Weakly Dispersive Boussinesq Model. Water. 2020; 12(5):1448. https://doi.org/10.3390/w12051448
Chicago/Turabian StyleLo Re, Carlo, Giorgio Manno, and Giuseppe Ciraolo. 2020. "Tsunami Propagation and Flooding in Sicilian Coastal Areas by Means of a Weakly Dispersive Boussinesq Model" Water 12, no. 5: 1448. https://doi.org/10.3390/w12051448
APA StyleLo Re, C., Manno, G., & Ciraolo, G. (2020). Tsunami Propagation and Flooding in Sicilian Coastal Areas by Means of a Weakly Dispersive Boussinesq Model. Water, 12(5), 1448. https://doi.org/10.3390/w12051448






