Developing THMs’ Predictive Models in Two Water Supply Systems in Greece
Abstract
1. Introduction
2. Disinfection Methods and Effects
3. DBP Predictive Models—A Review
4. Case Studies—THM Formation Models
4.1. General Data
4.2. Statistical Analysis
4.3. Multiple Regression Analysis
5. Results and Discussion
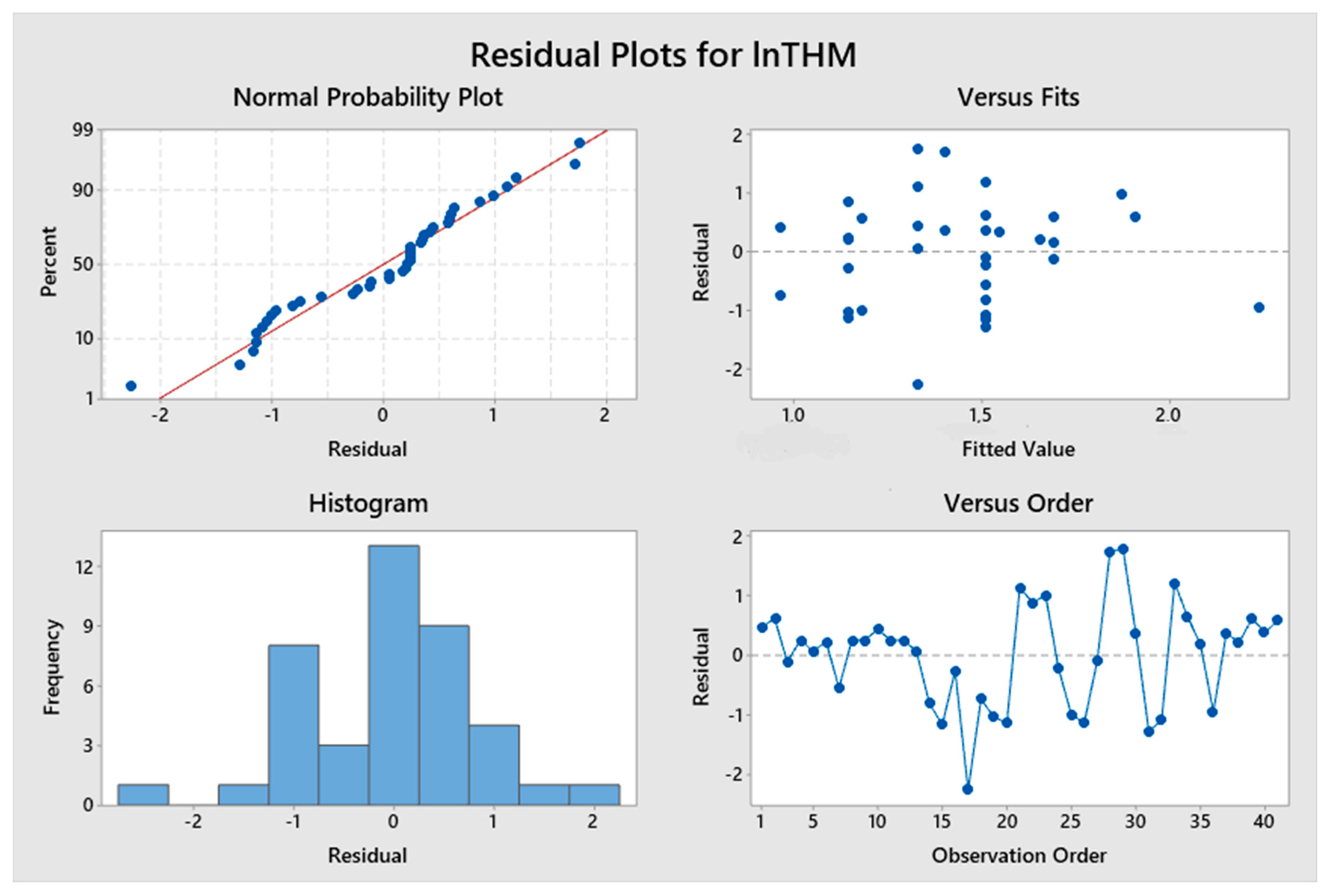
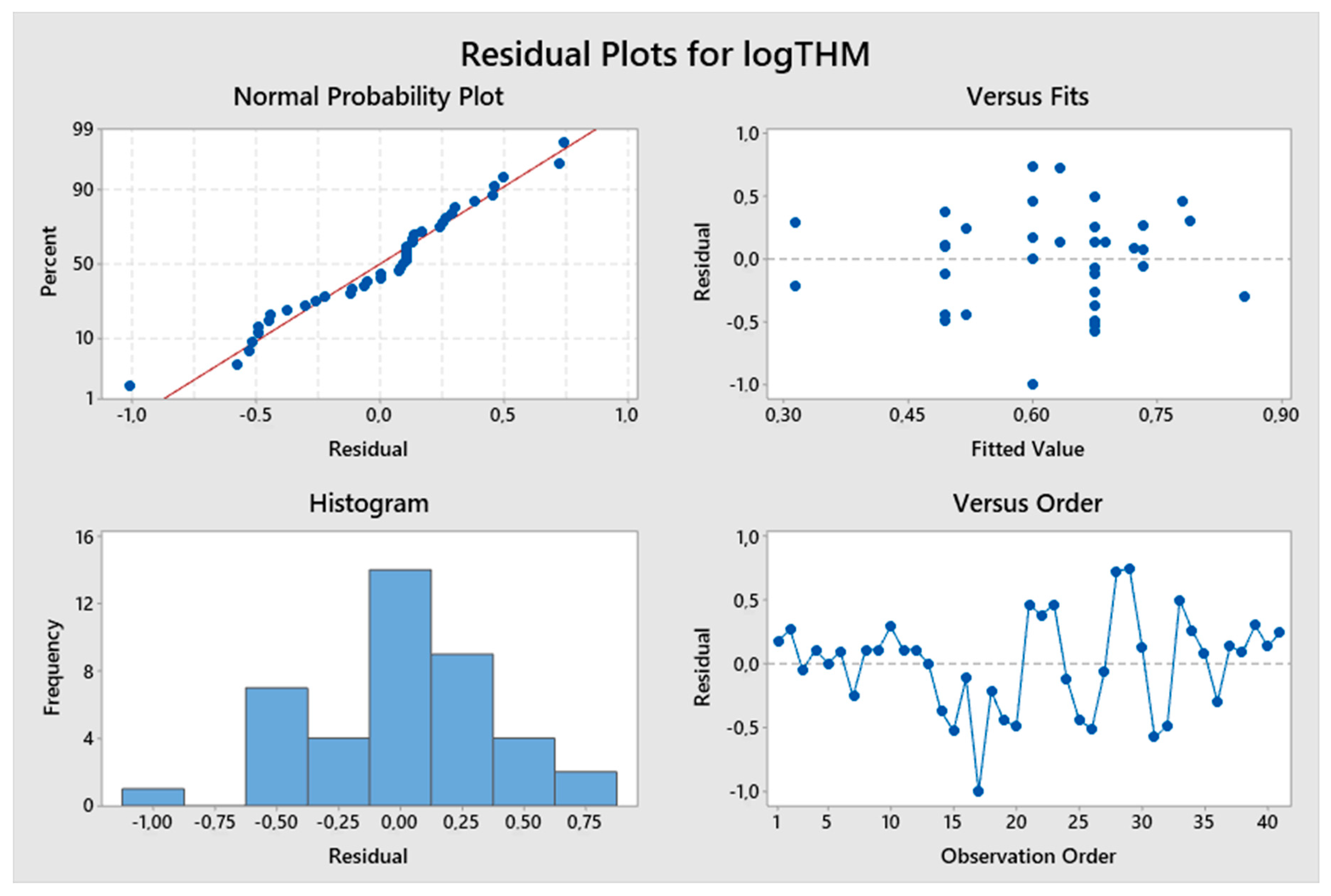
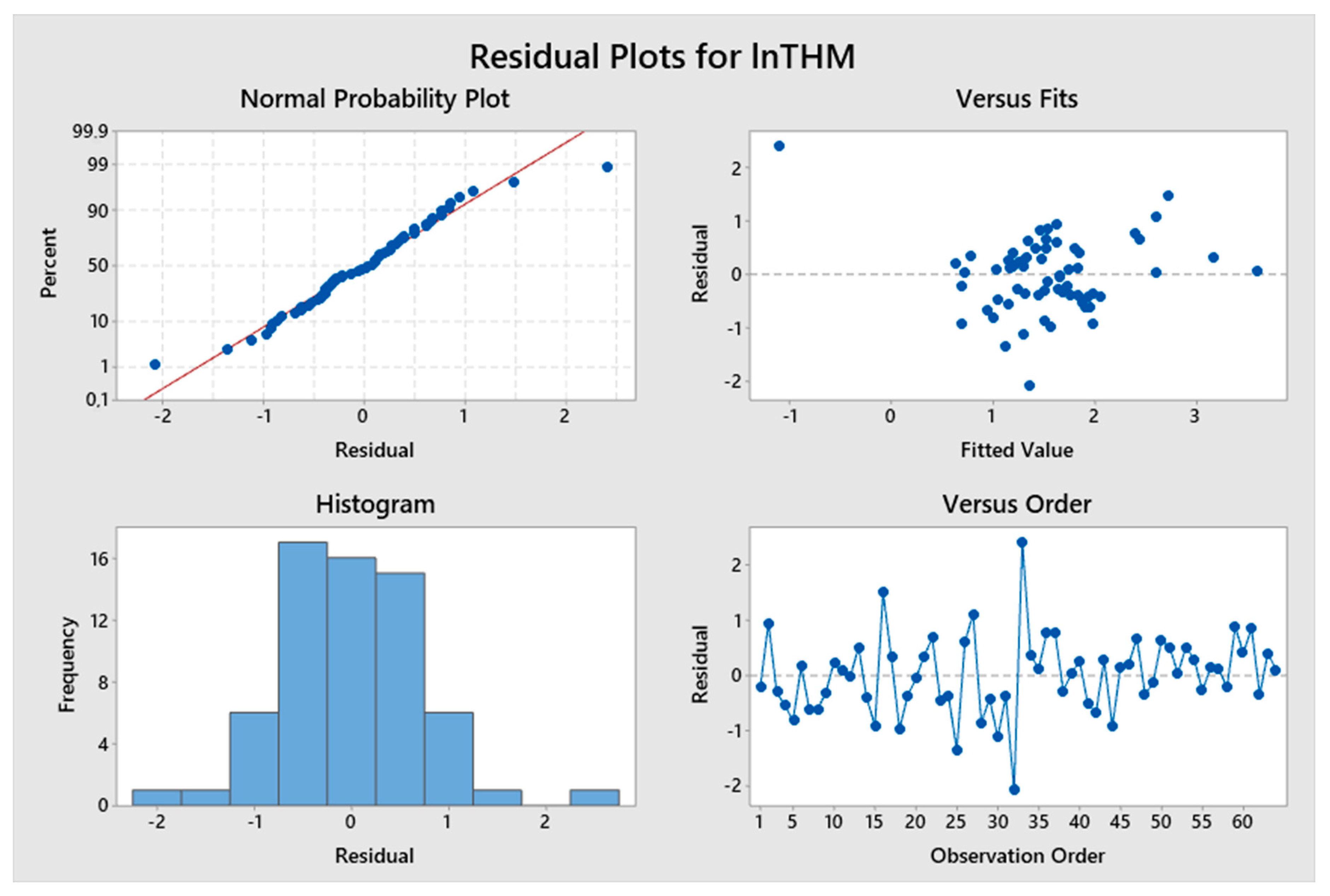
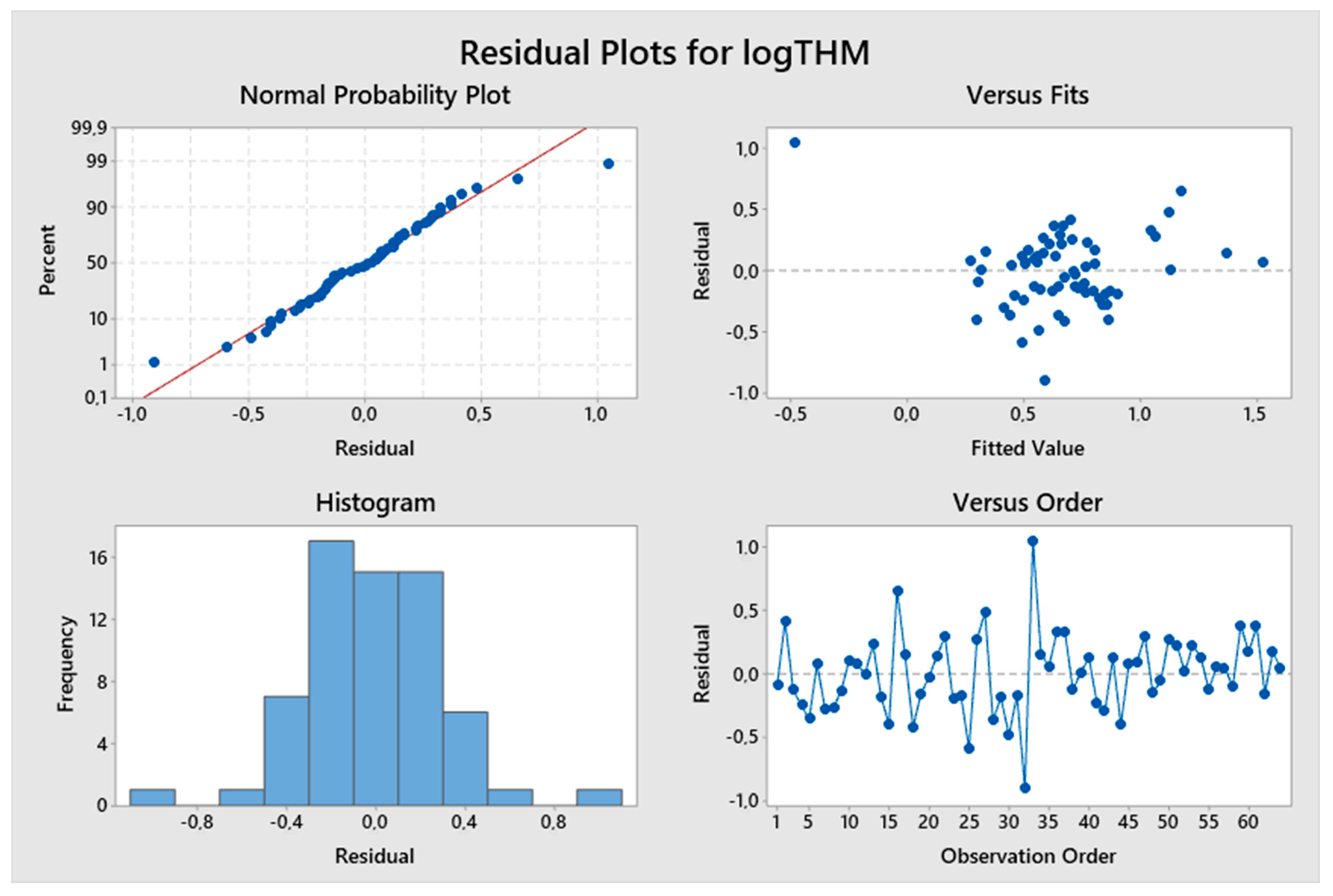
5.1. Model Development
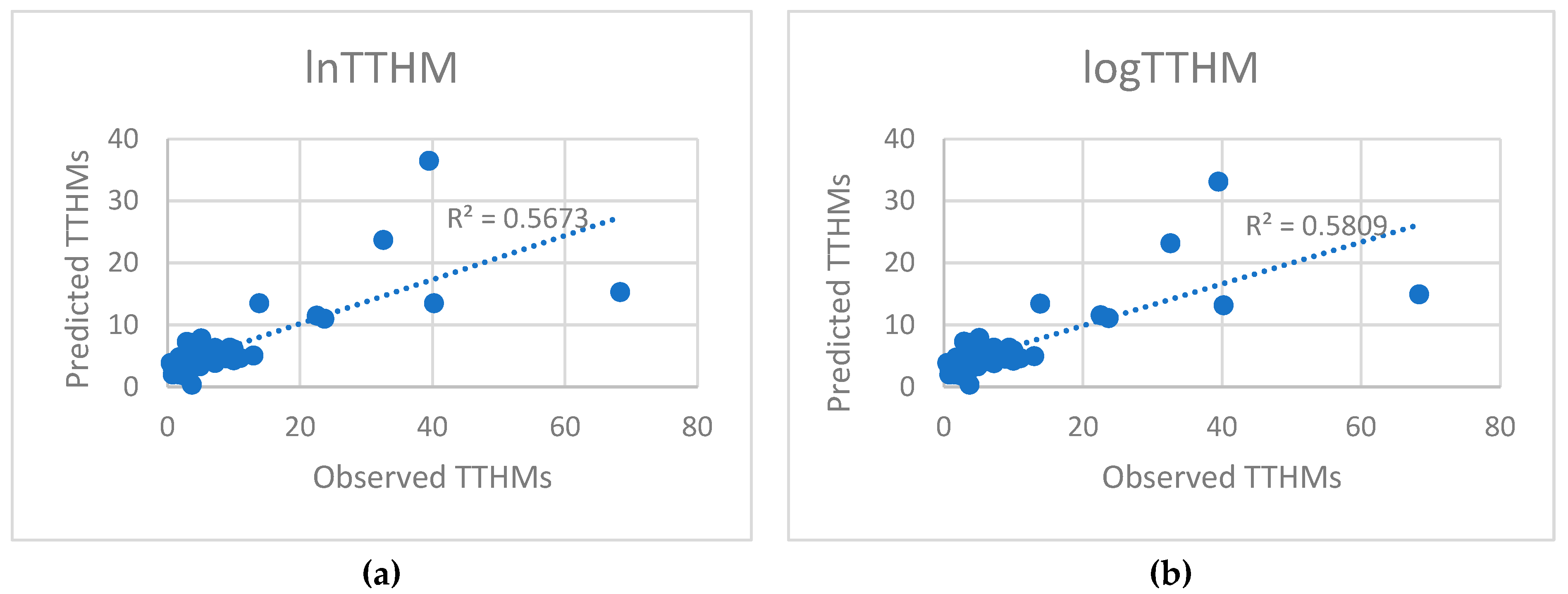
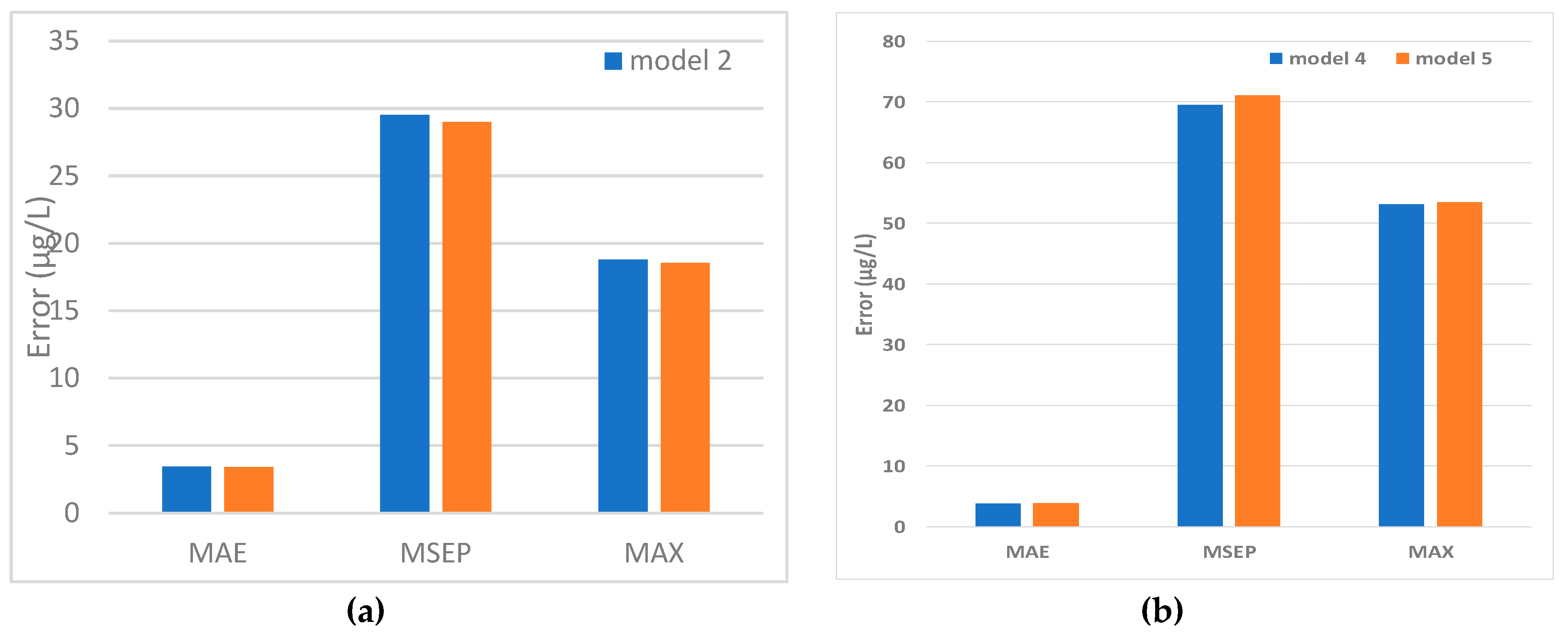
5.2. Predicted and Observed Values Comparison
6. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Kanakoudis, V.; Tsitsifli, S. Potable water security assessment – a review on monitoring, modelling and optimization techniques, applied to water distribution networks. Destil. Water Treat. 2017, 99, 18–26. [Google Scholar] [CrossRef]
- Richardson, S.D.; Plewa, M.J.; Wagner, E.D.; Schoeny, R.; DeMarini, D.M. Occurrence, genotoxicity, and carcinogenicity of regulated and emerging disinfection by-products in drinking water: A review and roadmap for research. Mutat. Res. Mutat. Res. 2007, 636, 178–242. [Google Scholar] [CrossRef] [PubMed]
- Ohanian, E.V.; Mullin, C.S.; Orme, J. Health effects of disinfectants and disinfection by-products: A regulatory perspective. Water Chlorin. Chem. Environ. Impact Health Effects 1989, 6, 75–86. [Google Scholar]
- Environmental Protection Agency. Water Treatment Manual: Disinfection; Environmental Protection Agency: Wexford, Ireland, 2011. [Google Scholar]
- Tsitsifli, S.; Kanakoudis, V. Disinfection Impacts to Drinking Water Safety—A Review. Proceedings 2018, 2, 603. [Google Scholar] [CrossRef]
- Rook, J.J. Formation of haloforms during chlorination of natural waters. Water Treat Exam 1974, 23, 234–243. [Google Scholar]
- Bellar, T.; Lichtenberg, J.; Kroner, R. The Occurrence of Organohalides in Chlorinated Drinking Waters. J. Am. Water Work. Assoc. 1974, 66, 703–706. [Google Scholar] [CrossRef]
- Sadiq, R.; Rodríguez, M.J. Disinfection by-products (DBPs) in drinking water and predictive models for their occurrence: a review. Sci. Total. Environ. 2004, 321, 21–46. [Google Scholar] [CrossRef]
- King, W.D.; Marrett, L.D. Case-control study of bladder cancer and chlorination by-products in treated water (Ontario, Canada). Cancer Causes Control. 1996, 7, 596–604. [Google Scholar] [CrossRef]
- Boorman, G.A.; Dellarco, V.; Dunnick, J.K.; Chapin, R.E.; Hunter, S.; Hauchman, F.; Gardner, H.; Cox, M.; Sills, R.C. Drinking water disinfection byproducts: review and approach to toxicity evaluation. Environ. Health Perspect. 1999, 107, 207–217. [Google Scholar]
- Chowdhury, S.; Champagne, P.; McLellan, P.J. Models for predicting disinfection byproduct (DBP) formation in drinking waters: A chronological review. Sci. Total. Environ. 2009, 407, 4189–4206. [Google Scholar] [CrossRef]
- Nikolaou, A.D.; Arhonditsis, G.B.; Golfinopoulos, S.K.; Lekkas, T.D. Predicting the formation of trihalomethanes and haloacetic in surface waters by linear regression models. Epidemiology 2002, 13, 172. [Google Scholar]
- Li, B.; Qu, J.; Liu, H.; Zhao, X. Formation and distribution of disinfection by-products during chlorine disinfection in the presence of bromide ion. Sci. Bull. 2008, 53, 2717–2723. [Google Scholar] [CrossRef]
- Sohn, J.; Amy, G.; Yoon, Y. Bromide Ion Incorporation Into Brominated Disinfection By-Products. Water Air Soil Pollut. 2006, 174, 265–277. [Google Scholar] [CrossRef]
- Ye, B.; Wang, W.; Yang, L.; Wei, J.; E, X. Factors influencing disinfection by-products formation in drinking water of six cities in China. J. Hazard. Mater. 2009, 171, 147–152. [Google Scholar] [CrossRef]
- Abokifa, A.A.; Yang, Y.J.; Lo, C.S.; Biswas, P. Investigating the role of biofilms in trihalomethane formation in water distribution systems with a multicomponent model. Water Res. 2016, 104, 208–219. [Google Scholar] [CrossRef]
- Minear, R.; Morrow, C.M. Raw Water Bromide in Finished Drinking Water. Research Report 9; Water Resources Research Center, University of Tennessee: Knoxville, TN, USA, 1983. [Google Scholar]
- Ozekin, K. Modelling Bromate Formation During Ozonation and Assessing its Control. Ph.D. Thesis, University of Colorado, Denver, CO, USA, 1994. [Google Scholar]
- Gibbs, M.S.; Morgan, N.; Maier, H.R.; Dandy, G.C.; Holmes, M.; Nixon, J.B. Use of artificial neural networks for modeling chlorine residuals in water distribution systems. In Proceedings of the International Congress on Modeling and Simulation; Modeling and Simulation Society of Australia and New Zealand Inc.: Townsville, Australia, 2003; Volume 2, pp. 789–794. [Google Scholar]
- Rodriguez, M.J.; West, J.R.; Powell, J.; Sérodes, J.B. Application of two approaches to model chlorine residuals in Severn Trent Water Ltd (STW) distribution systems. Water Sci. Technol. 1997, 36, 317–324. [Google Scholar] [CrossRef]
- Sérodes, J.B.; Rodriguez, M.J.; Ponton, A. Chlorcast (c): A methodology for developing decision-making tools for chlorine disinfection control. Environ. Modell Softw. 2001, 16, 53–62. [Google Scholar] [CrossRef]
- Elshorbagy, W. Simulation of THM species in water distribution systems. Water Res. 2000, 34, 3431–3439. [Google Scholar] [CrossRef]
- Abdullah, P.; Yew, C.; Bin Ramli, M.S. Formation, modeling and validation of trihalomethanes (THM) in Malaysian drinking water: a case study in the districts of Tampin, Negeri Sembilan and Sabak Bernam, Selangor, Malaysia. Water Res. 2003, 37, 4637–4644. [Google Scholar] [CrossRef]
- Amy, G.L.; Chadik, P.A.; Chowdhury, Z.K. Developing Models for Predicting Trihalomethane Formation Potential and Kinetics. J. - Am. Water Work. Assoc. 1987, 79, 89–97. [Google Scholar] [CrossRef]
- Uyak, V.; Ozdemir, K.; Toroz, I. Multiple linear regression modeling of disinfection by-products formation in Istanbul drinking water reservoirs. Sci. Total. Environ. 2007, 378, 269–280. [Google Scholar] [CrossRef] [PubMed]
- Singer, P.C. Control of Disinfection By-Products in Drinking Water. J. Environ. Eng. 1994, 120, 727–744. [Google Scholar] [CrossRef]
- Pourmoghaddas, H.; Stevens, A.A. Relationship between trihalomethanes and haloacetic acids with total organic halogen during chlorination. Water Res. 1995, 29, 2059–2062. [Google Scholar] [CrossRef]
- Nikolaou, A.D.; Lekkas, T.D. The role of natural organic materials during formation of chlorination by-products: a review. Acta Hydrochim. Hydrobiol. 2001, 2, 63–77. [Google Scholar] [CrossRef]
- Nikolaou, A.D.; Golfinopoulos, S.K.; Kostopoulou, M.N.; Lekkas, T.D. Decomposition of dihaloacetonitriles in water solutions and fortified drinking water samples. Chemosphere 2000, 41, 1149–1154. [Google Scholar] [CrossRef]
- Golfinopoulos, S.K.; Nikolaou, A.D. Formation of DBPs in the drinking water of Athens, Greece: A ten-year study. Glob. Nest J. 2005, 7, 106–118. [Google Scholar]
- Golfinopoulos, S.K.; Arhonditsis, G.B. Multiple regression models: A methodology for evaluating trihalomethane concentrations in drinking water from raw water characteristics. Chemosphere 2002, 47, 1007–1018. [Google Scholar] [CrossRef]
- Farmaki, E.G.; Samios, S.A.; Thomaidis, N.S.; Golfinopoulos, S.; Efstathiou, C.E.; Lekkas, T.D. Artificial neural networks predictive models. A case study: carbon and bromine concentrations prediction based on chlorination time. Global Nest J. 2012, 14, 10–17. [Google Scholar]
- Nikolaou, A.; Lekkas, T.; Golfinopoulos, S. Kinetics of the formation and decomposition of chlorination by-products in surface waters. Chem. Eng. J. 2004, 100, 139–148. [Google Scholar] [CrossRef]
- Zar, J.H. Biostatistical Analysis, 2nd ed.; PrenticeHall: Englewood Cliffs, NJ, USA, 1984. [Google Scholar]
- Ott, L. An Introduction to Statistical Methods and Data Analysis, 3rd ed.; PWS-Kent Publising Company: Boston, MA, USA, 1988. [Google Scholar]
- Golfinopoulos, S.K.; Xilourgidis, N.K.; Kostopoulou, M.N.; Lekkas, T.D. Use of a multiple regression model for predicting trihalomethane formation. Water Res. 1998, 32, 2821–2829. [Google Scholar] [CrossRef]
- Uyak, V.; Toroz, I. Modeling the Formation of Chlorination By-Products During Enhanced Coagulation. Environ. Monit. Assess. 2006, 121, 503–517. [Google Scholar] [CrossRef] [PubMed]
- Sprent, P.; Draper, N.R.; Smith, H. Applied Regression Analysis. Biom. JSTOR 1981, 37, 863. [Google Scholar] [CrossRef]

| Parameter | Units | |
|---|---|---|
| Br- | Bromide ion | mg/L |
| Cl2 | Initial chlorine concentration | |
| pH | pH | |
| T | temperature | °C |
| NVTOC | Non-volatile organic carbon | mg/L |
| TOC | Total organic carbon | mg/L |
| D | Chlorine dose | mg/L |
| t | Reaction time | hrs |
| UV | UV absorbance at 254 nm | cm−1 |
| ΤΤHΜο | Initial total THM concentration | |
| Flu | fluorescence | % |
| Co | Residual chlorine at the treatment plant after chlorination | mg/L |
| α | Parameter depending on location which chloroform is predicted | |
| ε | Random error | |
| Ch-a | Chlorophyll-a | mg/m3 |
| DOC | Dissolved organic carbon | mg/L |
| WDN A | WDN B | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| Parameter | N | AV | SD | MIN | MAX | Parameter | N | AV | SD | MIN | MAX |
| pH | 41 | 7.6707 | 0.1677 | 7.00 | 8.00 | pH | 64 | 7.6895 | 0.3931 | 6.92 | 8.90 |
| T | 41 | 20.122 | 3.816 | 13.0 | 30.0 | Conductivity | 64 | 715.5 | 179.3 | 419.0 | 1141.0 |
| Conductivity | 41 | 485.4 | 75.7 | 259.0 | 686.0 | Turbidity | 64 | 0.1983 | 0.3157 | 0.01 | 2.45 |
| Turbidity | 41 | 0.3993 | 0.138 | 0.21 | 0.82 | TOC | 64 | 5.227 | 7.52 | 0.01 | 39.5 |
| Residual Chlorine | 41 | 0.17 | 0.0729 | 0.05 | 0.40 | Residual Chlorine | 63 | 0.3313 | 0.1192 | 0.16 | 0.80 |
| TTHMs | 41 | 5.866 | 5.382 | 0.39 | 22.84 | TTHMs | 64 | 8.07 | 11.36 | 0.48 | 68.35 |
| WDN A | WDN B | ||
|---|---|---|---|
| Parameter | K-S | Parameter | K-S |
| pH | 0.228 | pH | 0.077 |
| T (οC) | 0.165 | Conductivity | 0.099 |
| Conductivity | 0.212 | Turbidity | 0.275 |
| Turbidity | 0.225 | TOC | 0.244 |
| Residual Chlorine | 0.145 | Residual Chlorine | 0.120 |
| TTHMs | 0.224 | TTHMs | 0.282 |
| ln (TTHMs) | 0.153 | Log turbidity | 0.181 |
| Log (TTHMs) | 0.127 | ||
| WDN A | WDN B | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| Parameter | pH | T | Residual Chlorine | Turbidity | Conductivity | Parameter | TTHMs | pH | Conductivity | TOC |
| T | −0.158 | pH | 0.465 | |||||||
| Res.chlorine | 0.252 | −0.362 | Conductivity | −0.316 | −0.397 | |||||
| Turbidity | −0.524 | 0.105 | −0.299 | Turbidity | 0.553 | 0.074 | −0.173 | |||
| Conductivity | −0.136 | −0.108 | −0.307 | 0.049 | TOC | 0.049 | 0.097 | 0.145 | 0.115 | |
| TTHMs | −0.009 | −0.125 | 0.266 | −0.003 | −0.406 | Res. chlorine | 0.301 | 0.218 | −0.042 | 0.498 |
| Term | Coef | t-Value | p-Value | Model | R2 | Durbin Watson |
|---|---|---|---|---|---|---|
| Constant | 0.781 | 2.23 | 0.032 | lnTTHMs = 0.781 + 3.64 ResChl | 8.63% | 1.19478 |
| ResChl | 6.64 | 1.92 | 0.062 | |||
| Constant | 1.096 | 4.33 | 0.000 | logTTHMs = 1.096 + 0.602 logResChl | 9.13% | 1.23129 |
| logResChl | 0.602 | 1.98 | 0.055 | |||
| Constant | −3.2 | −1.79 | 0.079 | lnTTHMs = −3.2 + 1.072 pH – 3.658 (TOC)−0.1 | 46.90% | 2.14728 |
| pH | 1.072 | 4.59 | 0.000 | |||
| (TOC)−0.1 | −3.658 | −6.42 | 0.000 | |||
| Constant | −5.04 | −3.18 | 0.002 | logTTHMs = −5.04 + 8.17 logpH – 1.595 (TOC)−0.1 | 46.34% | 2.14778 |
| logpH | 8.17 | 4.50 | 0.000 | |||
| (TOC)−0.1 | −1.595 | −6.40 | 0.000 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Tsitsifli, S.; Kanakoudis, V. Developing THMs’ Predictive Models in Two Water Supply Systems in Greece. Water 2020, 12, 1422. https://doi.org/10.3390/w12051422
Tsitsifli S, Kanakoudis V. Developing THMs’ Predictive Models in Two Water Supply Systems in Greece. Water. 2020; 12(5):1422. https://doi.org/10.3390/w12051422
Chicago/Turabian StyleTsitsifli, Stavroula, and Vasilis Kanakoudis. 2020. "Developing THMs’ Predictive Models in Two Water Supply Systems in Greece" Water 12, no. 5: 1422. https://doi.org/10.3390/w12051422
APA StyleTsitsifli, S., & Kanakoudis, V. (2020). Developing THMs’ Predictive Models in Two Water Supply Systems in Greece. Water, 12(5), 1422. https://doi.org/10.3390/w12051422






