Comparison of Methods for Imputing Non-Wetting Storm Surge to Improve Hazard Characterization
Abstract
:1. Introduction
2. Methods
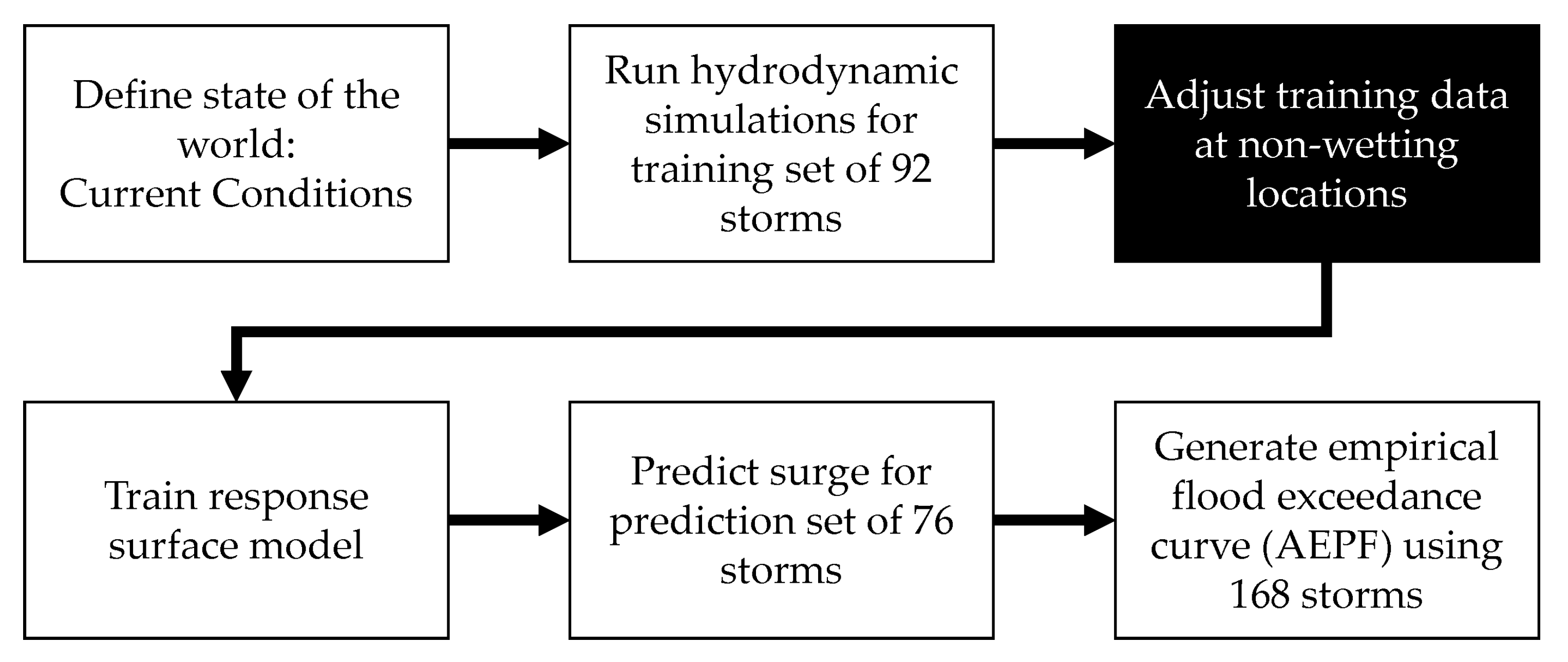
2.1. Experimental Design
2.2. Technical Context
- (1)
- Conditionally Parametric Locally Weighted Regression (CPARLWR) [19] with full model specification (the local weighting of observations from nearby grid points is limited to points within regions of similar hydrology, i.e., the same watershed):
- (2)
- Point-level ordinary least squares regression with full model specification.
- (3)
- Point-level ordinary least squares regression with a reduced-form model:
- (4)
- Point- and track-level ordinary least squares regression with reduced-form model:
- (5)
- Step function assigning equal surge elevation and wave heights to any synthetic storms more extreme than wetting storms from the simulation set.
2.3. Training and Prediction Storms
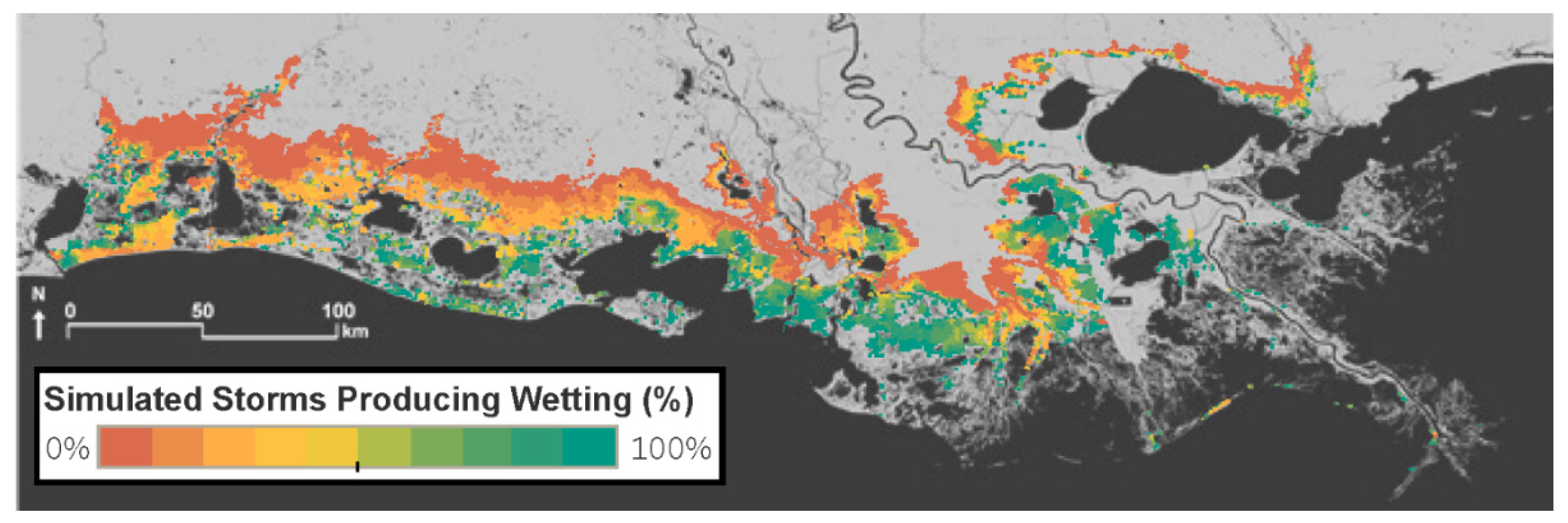
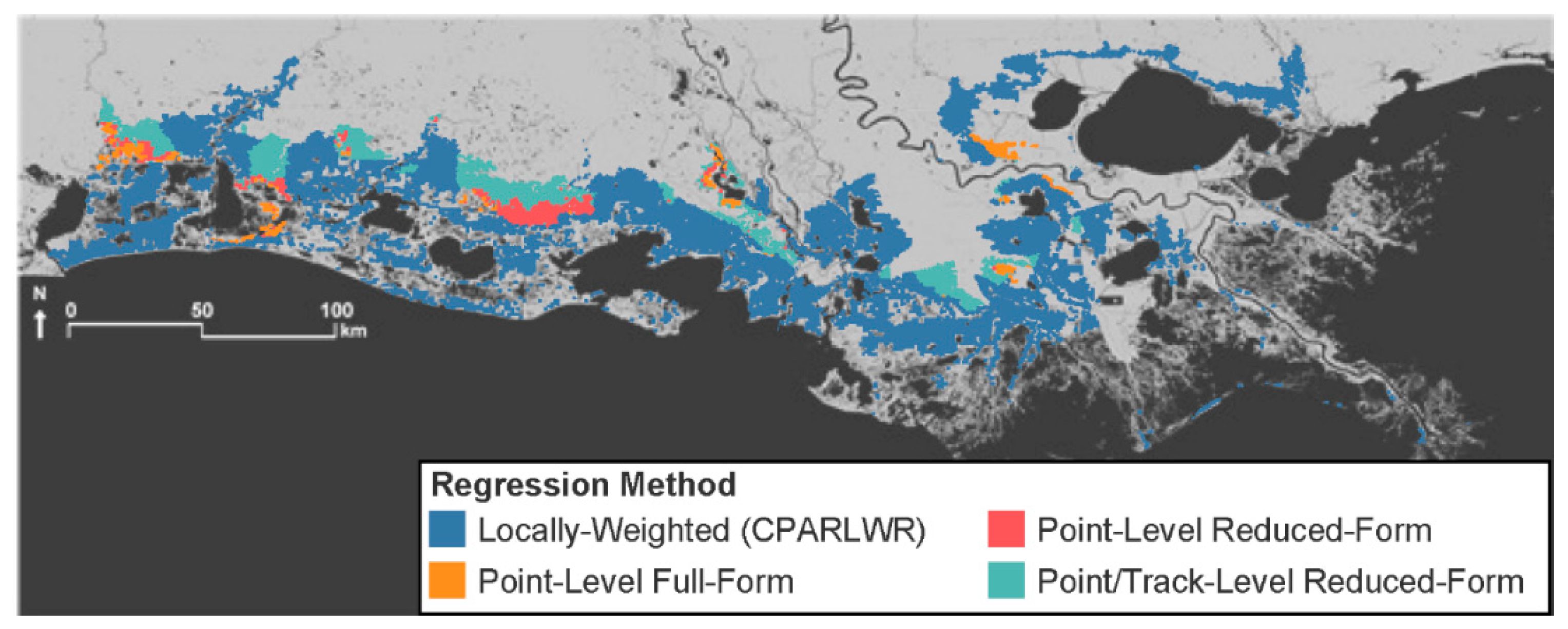
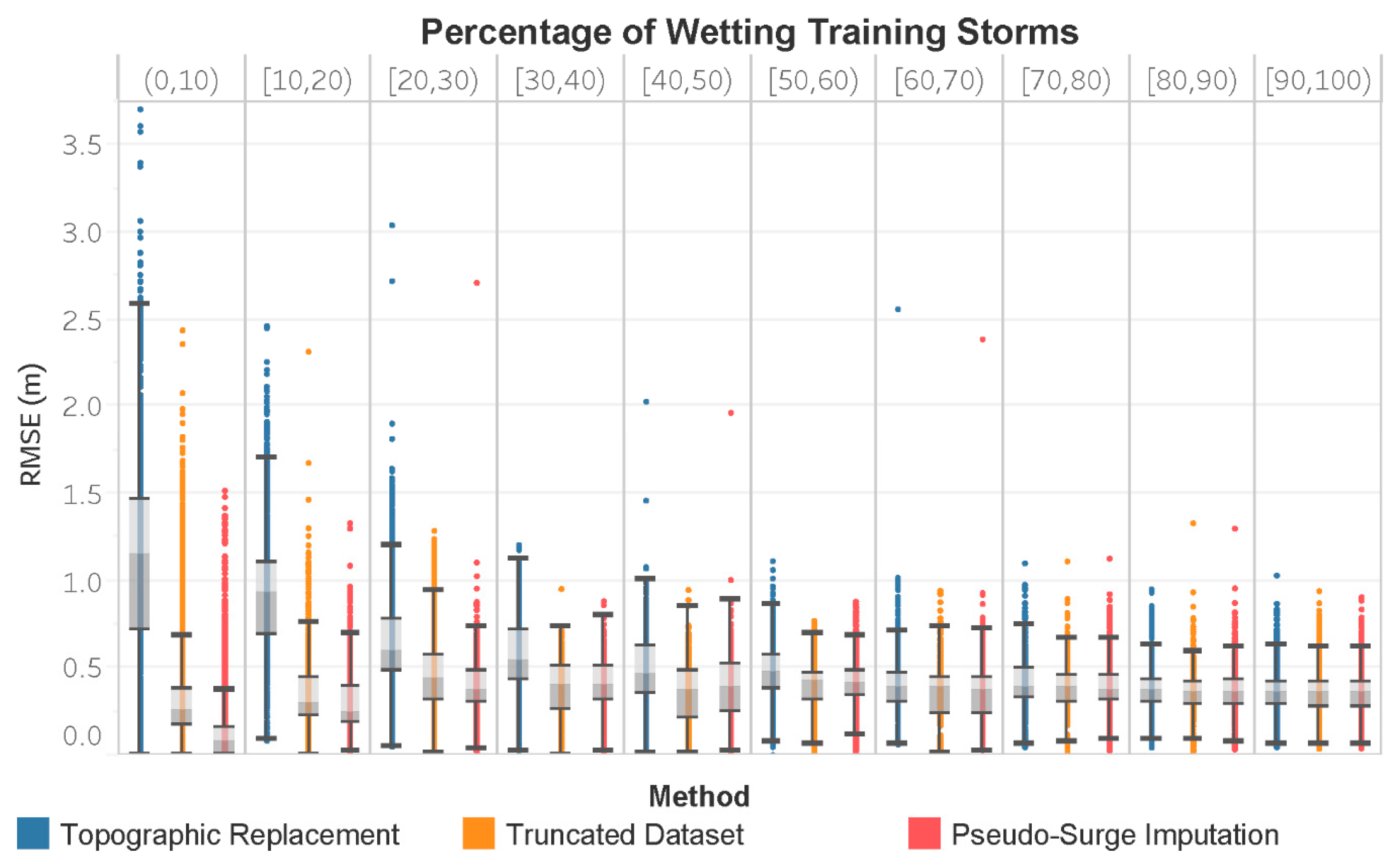
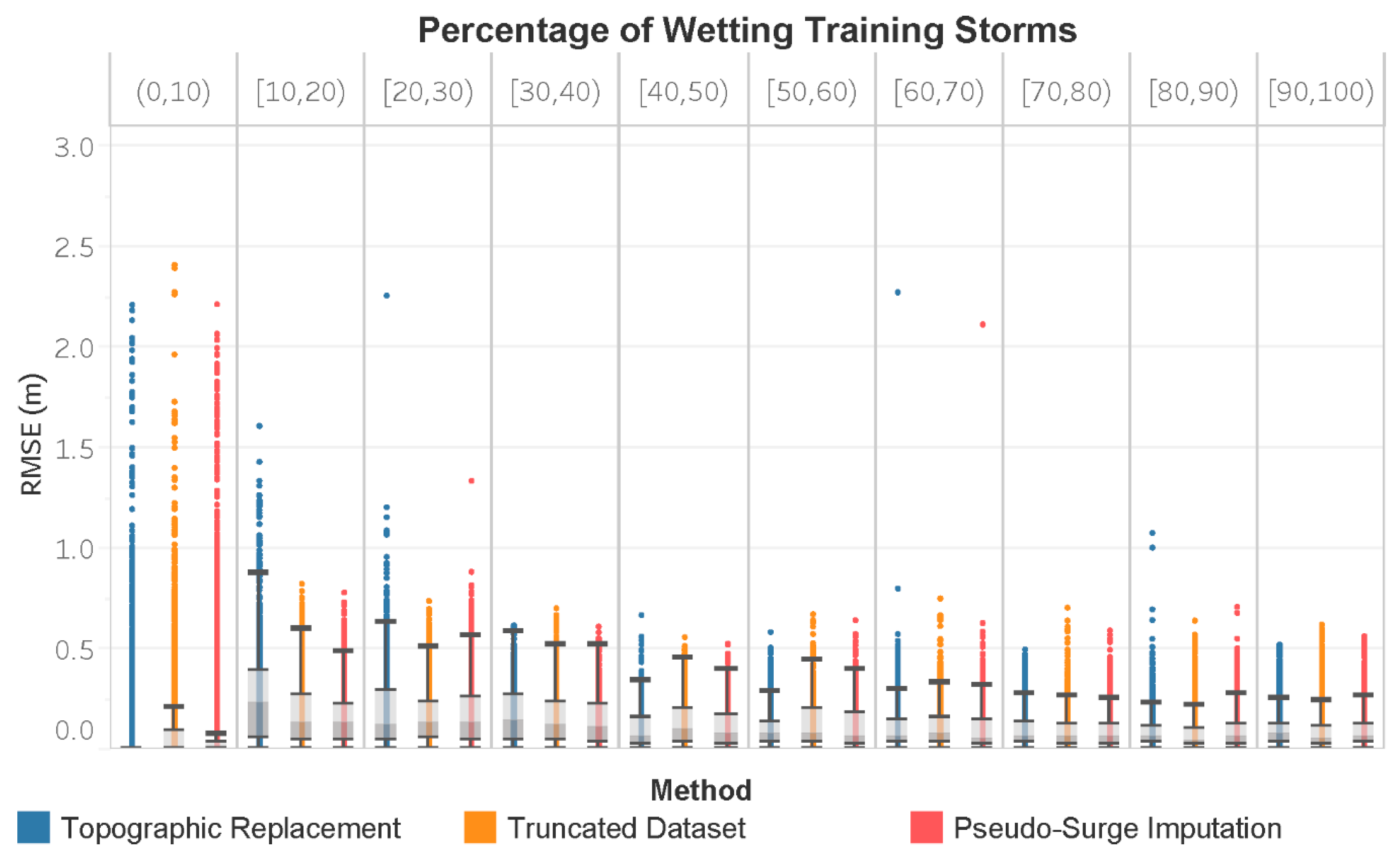
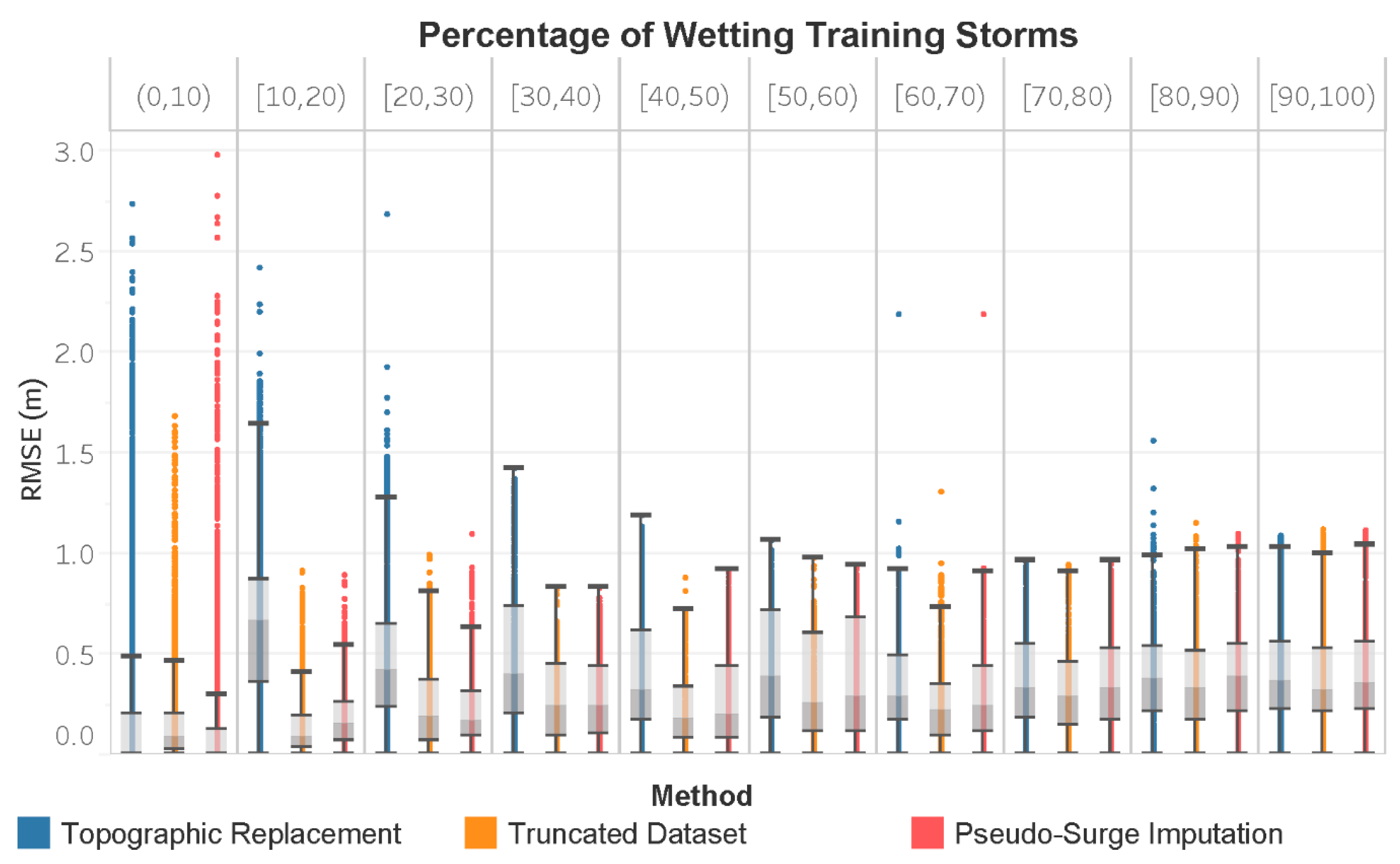
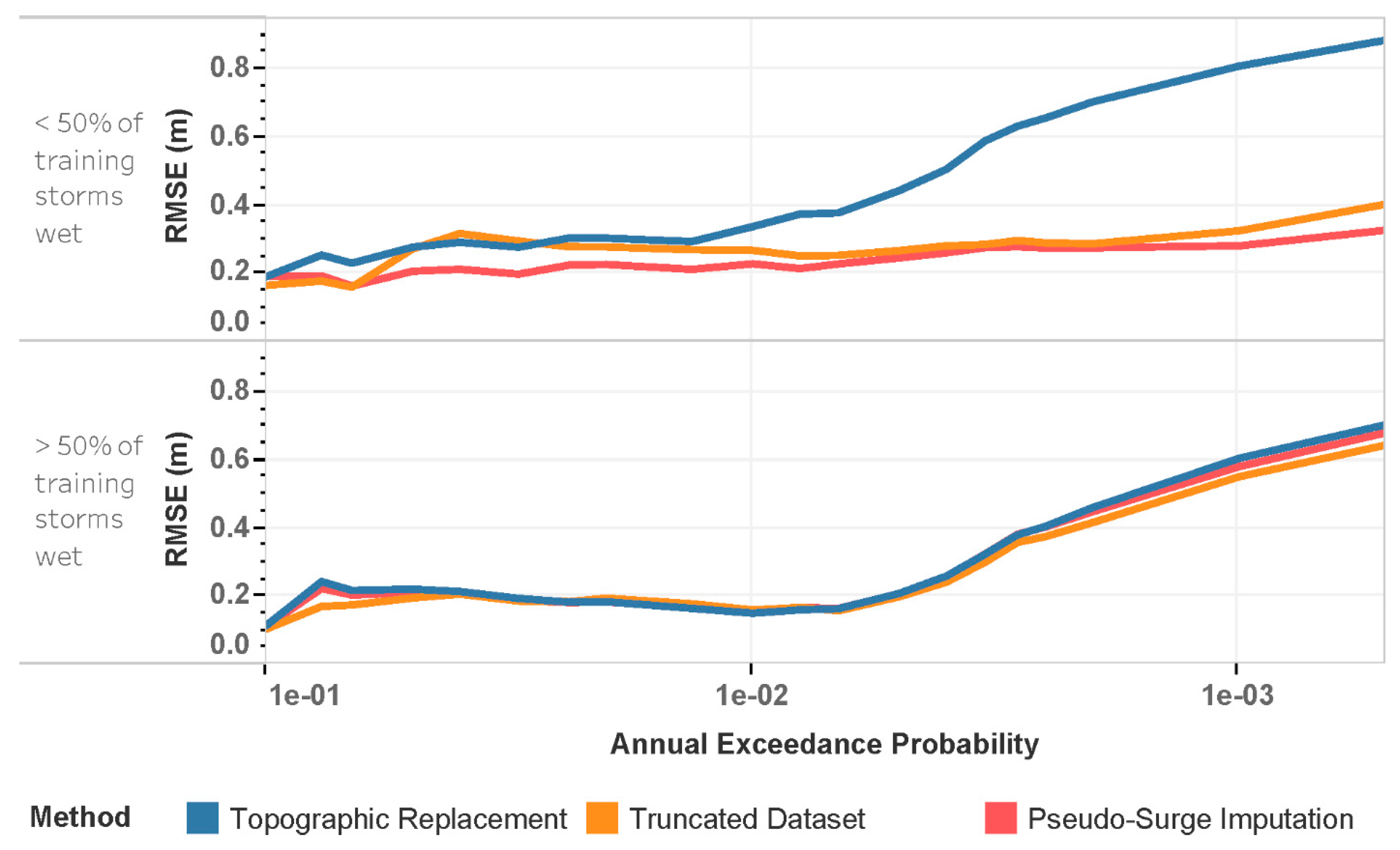
3. Results
4. Discussion
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
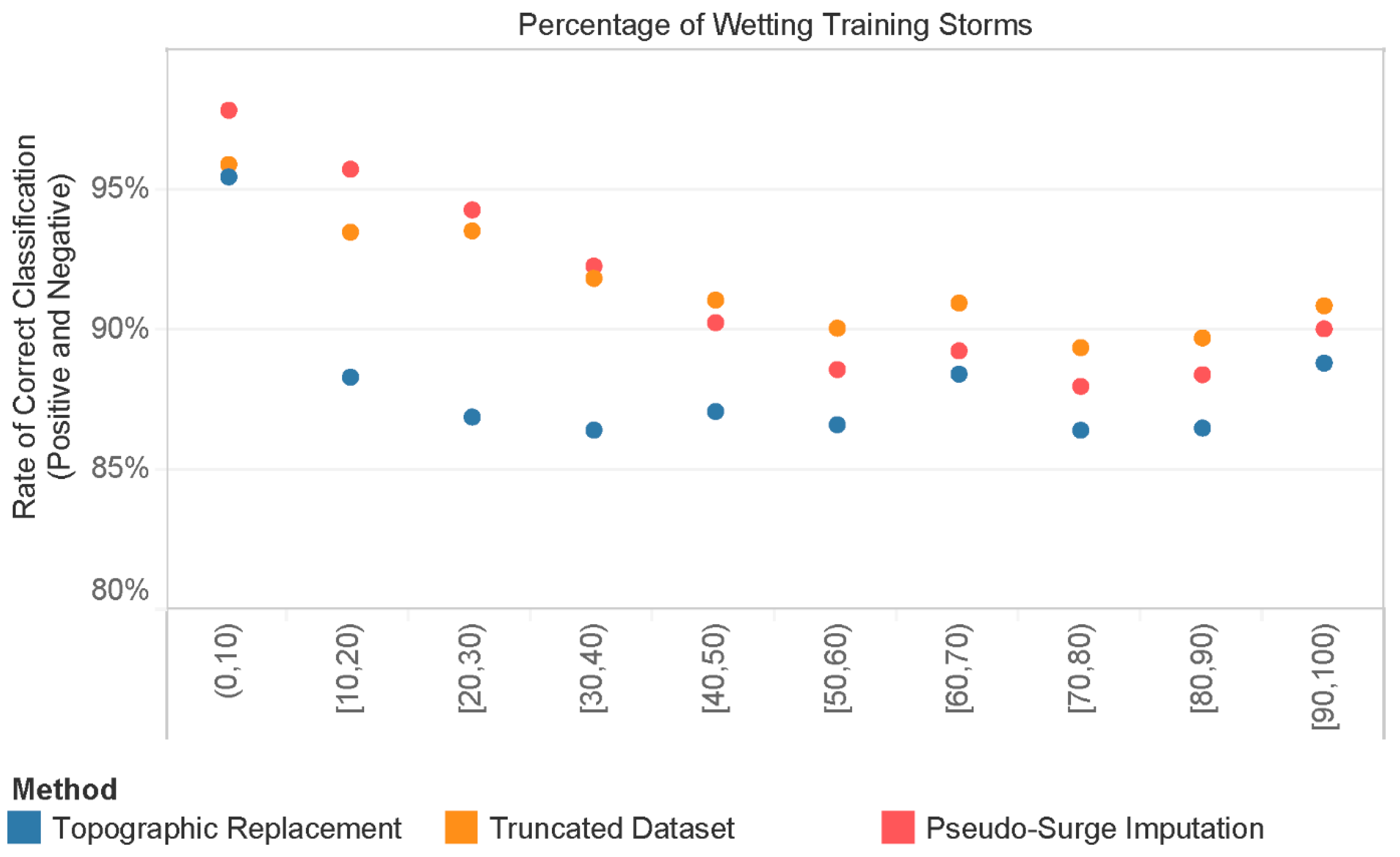
Appendix A. Identifying the Optimal Pseudo-Surge Values
| Set | Description | Relationships |
|---|---|---|
| All locations | - | |
| All storms | - | |
| All location–storm pairs | ||
| Location–storm pairs where the storm is wetting | ||
| Location–storm pairs where the storm is non-wetting | , , | |
| Simulation set location–storm pairs | ||
| Wetting simulation set location–storm pairs | ||
| Non-wetting simulation set location–storm pairs | , , | |
| Prediction set location–storm pairs | , , | |
| Wetting prediction set location–storm pairs | ||
| Non-wetting prediction set location–storm pairs | , , |
Pointwise Selection of Optimal Pseudo-surge
Appendix B. Table of Storm Parameters
| ID | cp | rmax | vf | x | Training | |
|---|---|---|---|---|---|---|
| 1 | 960 | 11 | 11 | 0 | −91.211 | Yes |
| 2 | 960 | 21 | 11 | 0 | −91.211 | No |
| 3 | 960 | 35.6 | 11 | 0 | −91.211 | Yes |
| 4 | 930 | 8 | 11 | 0 | −91.211 | No |
| 5 | 930 | 17.7 | 11 | 0 | −91.211 | Yes |
| 6 | 930 | 25.8 | 11 | 0 | −91.211 | No |
| 7 | 900 | 6 | 11 | 0 | −91.211 | Yes |
| 8 | 900 | 14.9 | 11 | 0 | −91.211 | No |
| 9 | 900 | 21.8 | 11 | 0 | −91.211 | Yes |
| 10 | 960 | 11 | 11 | 0 | −90.451 | Yes |
| 11 | 960 | 21 | 11 | 0 | −90.451 | No |
| 12 | 960 | 35.6 | 11 | 0 | −90.451 | Yes |
| 13 | 930 | 8 | 11 | 0 | −90.451 | No |
| 14 | 930 | 17.7 | 11 | 0 | −90.451 | Yes |
| 15 | 930 | 25.8 | 11 | 0 | −90.451 | No |
| 16 | 900 | 6 | 11 | 0 | −90.451 | Yes |
| 17 | 900 | 14.9 | 11 | 0 | −90.451 | No |
| 18 | 900 | 21.8 | 11 | 0 | −90.451 | Yes |
| 19 | 960 | 11 | 11 | 0 | −89.848 | Yes |
| 20 | 960 | 21 | 11 | 0 | −89.848 | No |
| 21 | 960 | 35.6 | 11 | 0 | −89.848 | Yes |
| 22 | 930 | 8 | 11 | 0 | −89.848 | No |
| 23 | 930 | 17.7 | 11 | 0 | −89.848 | Yes |
| 24 | 930 | 25.8 | 11 | 0 | −89.848 | No |
| 25 | 900 | 6 | 11 | 0 | −89.848 | Yes |
| 26 | 900 | 14.9 | 11 | 0 | −89.848 | No |
| 27 | 900 | 21.8 | 11 | 0 | −89.848 | Yes |
| 28 | 960 | 11 | 11 | 0 | −89.276 | Yes |
| 29 | 960 | 21 | 11 | 0 | −89.276 | No |
| 30 | 960 | 35.6 | 11 | 0 | −89.276 | Yes |
| 31 | 930 | 8 | 11 | 0 | −89.276 | No |
| 32 | 930 | 17.7 | 11 | 0 | −89.276 | Yes |
| 33 | 930 | 25.8 | 11 | 0 | −89.276 | No |
| 34 | 900 | 6 | 11 | 0 | −89.276 | Yes |
| 35 | 900 | 14.9 | 11 | 0 | −89.276 | No |
| 36 | 900 | 21.8 | 11 | 0 | −89.276 | Yes |
| 37 | 960 | 11 | 11 | 0 | −88.647 | Yes |
| 38 | 960 | 21 | 11 | 0 | −88.647 | No |
| 39 | 960 | 35.6 | 11 | 0 | −88.647 | Yes |
| 40 | 930 | 8 | 11 | 0 | −88.647 | No |
| 41 | 930 | 17.7 | 11 | 0 | −88.647 | Yes |
| 42 | 930 | 25.8 | 11 | 0 | −88.647 | No |
| 43 | 900 | 6 | 11 | 0 | −88.647 | Yes |
| 44 | 900 | 14.9 | 11 | 0 | −88.647 | No |
| 45 | 900 | 21.8 | 11 | 0 | −88.647 | Yes |
| 46 | 960 | 18.2 | 11 | −45 | −91.368 | Yes |
| 47 | 960 | 24.6 | 11 | −45 | −91.368 | Yes |
| 48 | 900 | 12.5 | 11 | −45 | −91.368 | No |
| 49 | 900 | 18.4 | 11 | −45 | −91.368 | No |
| 50 | 960 | 18.2 | 11 | −45 | −90.724 | Yes |
| 51 | 960 | 24.6 | 11 | −45 | −90.724 | Yes |
| 52 | 900 | 12.5 | 11 | −45 | −90.724 | No |
| 53 | 900 | 18.4 | 11 | −45 | −90.724 | No |
| 54 | 960 | 18.2 | 11 | −45 | −89.921 | Yes |
| 55 | 960 | 24.6 | 11 | −45 | −89.921 | Yes |
| 56 | 900 | 12.5 | 11 | −45 | −89.921 | No |
| 57 | 900 | 18.4 | 11 | −45 | −89.921 | No |
| 58 | 960 | 18.2 | 11 | −45 | −89.105 | Yes |
| 59 | 960 | 24.6 | 11 | −45 | −89.105 | Yes |
| 60 | 900 | 12.5 | 11 | −45 | −89.105 | No |
| 61 | 900 | 18.4 | 11 | −45 | −89.105 | No |
| 66 | 960 | 18.2 | 11 | 45 | −90.994 | Yes |
| 67 | 960 | 24.6 | 11 | 45 | −90.994 | Yes |
| 68 | 900 | 12.5 | 11 | 45 | −90.994 | No |
| 69 | 900 | 18.4 | 11 | 45 | −90.994 | No |
| 70 | 960 | 18.2 | 11 | 45 | −90.214 | Yes |
| 71 | 960 | 24.6 | 11 | 45 | −90.214 | Yes |
| 72 | 900 | 12.5 | 11 | 45 | −90.214 | No |
| 73 | 900 | 18.4 | 11 | 45 | −90.214 | No |
| 74 | 960 | 18.2 | 11 | 45 | −89.638 | Yes |
| 75 | 960 | 24.6 | 11 | 45 | −89.638 | Yes |
| 76 | 900 | 12.5 | 11 | 45 | −89.638 | No |
| 77 | 900 | 18.4 | 11 | 45 | −89.638 | No |
| 78 | 960 | 18.2 | 11 | 45 | −89.047 | Yes |
| 79 | 960 | 24.6 | 11 | 45 | −89.047 | Yes |
| 80 | 900 | 12.5 | 11 | 45 | −89.047 | No |
| 81 | 900 | 18.4 | 11 | 45 | −89.047 | No |
| 201 | 960 | 11 | 11 | 0 | −94.22 | Yes |
| 202 | 960 | 21 | 11 | 0 | −94.22 | No |
| 203 | 960 | 35.6 | 11 | 0 | −94.22 | Yes |
| 204 | 930 | 8 | 11 | 0 | −94.22 | No |
| 205 | 930 | 17.7 | 11 | 0 | −94.22 | Yes |
| 206 | 930 | 25.8 | 11 | 0 | −94.22 | No |
| 207 | 900 | 6 | 11 | 0 | −94.22 | Yes |
| 208 | 900 | 14.9 | 11 | 0 | −94.22 | No |
| 209 | 900 | 21.8 | 11 | 0 | −94.22 | Yes |
| 210 | 960 | 11 | 11 | 0 | −93.558 | Yes |
| 211 | 960 | 21 | 11 | 0 | −93.558 | No |
| 212 | 960 | 35.6 | 11 | 0 | −93.558 | Yes |
| 213 | 930 | 8 | 11 | 0 | −93.558 | No |
| 214 | 930 | 17.7 | 11 | 0 | −93.558 | Yes |
| 215 | 930 | 25.8 | 11 | 0 | −93.558 | No |
| 216 | 900 | 6 | 11 | 0 | −93.558 | Yes |
| 217 | 900 | 14.9 | 11 | 0 | −93.558 | No |
| 218 | 900 | 21.8 | 11 | 0 | −93.558 | Yes |
| 219 | 960 | 11 | 11 | 0 | −92.964 | Yes |
| 220 | 960 | 21 | 11 | 0 | −92.964 | No |
| 221 | 960 | 35.6 | 11 | 0 | −92.964 | Yes |
| 222 | 930 | 8 | 11 | 0 | −92.964 | No |
| 223 | 930 | 17.7 | 11 | 0 | −92.964 | Yes |
| 224 | 930 | 25.8 | 11 | 0 | −92.964 | No |
| 225 | 900 | 6 | 11 | 0 | −92.964 | Yes |
| 226 | 900 | 14.9 | 11 | 0 | −92.964 | No |
| 227 | 900 | 21.8 | 11 | 0 | −92.964 | Yes |
| 228 | 960 | 11 | 11 | 0 | −92.317 | Yes |
| 229 | 960 | 21 | 11 | 0 | −92.317 | No |
| 230 | 960 | 35.6 | 11 | 0 | −92.317 | Yes |
| 231 | 930 | 8 | 11 | 0 | −92.317 | No |
| 232 | 930 | 17.7 | 11 | 0 | −92.317 | Yes |
| 233 | 930 | 25.8 | 11 | 0 | −92.317 | No |
| 234 | 900 | 6 | 11 | 0 | −92.317 | Yes |
| 235 | 900 | 14.9 | 11 | 0 | −92.317 | No |
| 236 | 900 | 21.8 | 11 | 0 | −92.317 | Yes |
| 237 | 960 | 11 | 11 | 0 | −91.654 | Yes |
| 238 | 960 | 21 | 11 | 0 | −91.654 | No |
| 239 | 960 | 35.6 | 11 | 0 | −91.654 | Yes |
| 240 | 930 | 8 | 11 | 0 | −91.654 | No |
| 241 | 930 | 17.7 | 11 | 0 | −91.654 | Yes |
| 242 | 930 | 25.8 | 11 | 0 | −91.654 | No |
| 243 | 900 | 6 | 11 | 0 | −91.654 | Yes |
| 244 | 900 | 14.9 | 11 | 0 | −91.654 | No |
| 245 | 900 | 21.8 | 11 | 0 | −91.654 | Yes |
| 401 | 975 | 11 | 11 | 0 | −94.22 | No |
| 402 | 975 | 21 | 11 | 0 | −94.22 | Yes |
| 403 | 975 | 35.6 | 11 | 0 | −94.22 | No |
| 404 | 975 | 11 | 11 | 0 | −93.558 | No |
| 405 | 975 | 21 | 11 | 0 | −93.558 | Yes |
| 406 | 975 | 35.6 | 11 | 0 | −93.558 | No |
| 407 | 975 | 11 | 11 | 0 | −92.964 | No |
| 408 | 975 | 21 | 11 | 0 | −92.964 | Yes |
| 409 | 975 | 35.6 | 11 | 0 | −92.964 | No |
| 410 | 975 | 11 | 11 | 0 | −92.317 | No |
| 411 | 975 | 21 | 11 | 0 | −92.317 | Yes |
| 412 | 975 | 35.6 | 11 | 0 | −92.317 | No |
| 413 | 975 | 11 | 11 | 0 | −91.654 | No |
| 414 | 975 | 21 | 11 | 0 | −91.654 | Yes |
| 415 | 975 | 35.6 | 11 | 0 | −91.654 | No |
| 501 | 975 | 11 | 11 | 0 | −91.211 | No |
| 502 | 975 | 21 | 11 | 0 | −91.211 | Yes |
| 503 | 975 | 35.6 | 11 | 0 | −91.211 | No |
| 504 | 975 | 11 | 11 | 0 | −90.451 | No |
| 505 | 975 | 21 | 11 | 0 | −90.451 | Yes |
| 506 | 975 | 35.6 | 11 | 0 | −90.451 | No |
| 507 | 975 | 11 | 11 | 0 | −89.848 | No |
| 508 | 975 | 21 | 11 | 0 | −89.848 | Yes |
| 509 | 975 | 35.6 | 11 | 0 | −89.848 | No |
| 510 | 975 | 11 | 11 | 0 | −89.276 | No |
| 511 | 975 | 21 | 11 | 0 | −89.276 | Yes |
| 512 | 975 | 35.6 | 11 | 0 | −89.276 | No |
| 513 | 975 | 11 | 11 | 0 | −88.647 | No |
| 514 | 975 | 21 | 11 | 0 | −88.647 | Yes |
| 515 | 975 | 35.6 | 11 | 0 | −88.647 | No |
| 516 | 975 | 18.2 | 11 | −45 | −91.368 | Yes |
| 517 | 975 | 24.6 | 11 | −45 | −91.368 | Yes |
| 518 | 975 | 18.2 | 11 | −45 | −90.724 | Yes |
| 519 | 975 | 24.6 | 11 | −45 | −90.724 | Yes |
| 520 | 975 | 18.2 | 11 | −45 | −89.921 | Yes |
| 521 | 975 | 24.6 | 11 | −45 | −89.921 | Yes |
| 522 | 975 | 18.2 | 11 | −45 | −89.105 | Yes |
| 523 | 975 | 24.6 | 11 | −45 | −89.105 | Yes |
| 524 | 975 | 18.2 | 11 | 45 | −90.994 | Yes |
| 525 | 975 | 24.6 | 11 | 45 | −90.994 | Yes |
| 526 | 975 | 18.2 | 11 | 45 | −90.214 | Yes |
| 527 | 975 | 24.6 | 11 | 45 | −90.214 | Yes |
| 528 | 975 | 18.2 | 11 | 45 | −89.638 | Yes |
| 529 | 975 | 24.6 | 11 | 45 | −89.638 | Yes |
| 530 | 975 | 18.2 | 11 | 45 | −89.047 | Yes |
| 531 | 975 | 24.6 | 11 | 45 | −89.047 | Yes |
References
- Louisiana Coastal Protection and Restoration Authority. Louisiana’s Comprehensive Master Plan for a Sustainable Coast; Louisiana Coastal Protection and Restoration Authority: Baton Rouge, LA, USA, 2017. [Google Scholar]
- Fischbach, J.R.; Johnson, D.R.; Ortiz, D.S.; Bryant, B.P.; Hoover, M.; Ostwald, J. Coastal Louisiana Risk Assessment Model: Technical Description and 2012 Coastal Master Plan Analysis Results; RAND Corporation: Santa Monica, CA, USA, 2012. [Google Scholar]
- Johnson, D.R. Improving Flood Risk Estimates and Mitigation Policies in Coastal Louisiana under Deep Uncertainty; Pardee RAND Graduate School: Santa Monica, CA, USA, 2013. [Google Scholar]
- Johnson, D.R.; Fischbach, J.R.; Ortiz, D.S. Estimating Surge-Based Flood Risk with the Coastal Louisiana Risk Assessment Model. J. Coast. Res. 2013, 67, 109–126. [Google Scholar] [CrossRef]
- Toro, G.R.; Resio, D.T.; Divoky, D.; Niedoroda, A.W.; Reed, C. Efficient joint-probability methods for hurricane surge frequency analysis. Ocean Eng. 2010, 37, 125–134. [Google Scholar] [CrossRef]
- Resio, D.T.; Irish, J.L.; Cialone, M.A. A surge response function approach to coastal hazard assessment. Part 1: Basic concepts. Natural Hazards 2009, 51, 163–182. [Google Scholar] [CrossRef]
- Hsu, C.H.; Olivera, F.; Irish, J.L. A hurricane surge risk assessment framework using the joint probability method and surge response functions. Nat. Hazards 2018, 91, 7–28. [Google Scholar] [CrossRef]
- Condon, A.J.; Sheng, Y.P. Optimal storm generation for evaluation of the storm surge inundation threat. Ocean Eng. 2012, 43, 13–22. [Google Scholar] [CrossRef]
- Ho, F.P.; Myers, V.A. Joint Probability Method of Tide Frequency Analysis Applied to Apalachicola Bay and St. George Sound, Florida; National Oceanic and Atmospheric Administration: Washington, DC, USA, 1975.
- Fischbach, J.R.; Johnson, D.R.; Kuhn, K. Bias and efficiency tradeoffs in the selection of storm suites used to estimate flood risk. J. Mar. Sci. Eng. 2016, 4, 10. [Google Scholar] [CrossRef] [Green Version]
- Zhang, J.; Taflanidis, A.A.; Nadal-Caraballo, N.C.; Melby, J.A.; Diop, F. Advances in surrogate modeling for storm surge prediction: Storm selection and addressing characteristics related to climate change. Nat. Hazards 2018, 94, 1225–1253. [Google Scholar] [CrossRef]
- Johnson, D.R.; Geldner, N.B. Contemporary decision methods for agricultural, environmental, and resource management and policy. Annu. Rev. Resour. Econ. 2019, 11, 19–41. [Google Scholar] [CrossRef]
- Kwakkel, J.H.; Haasnoot, M. Supporting DMDU: A taxonomy of approaches and tools. In Decision Making under Deep Uncertainty; Springer: Cham, Switzerland, 2019; pp. 355–374. [Google Scholar]
- U.S. Army Corps of Engineers. Louisiana Coastal Protection and Restoration Final Technical Report, Hydraulics and Hydrology Appendix; U.S. Army Corps of Engineers: New Orleans, LA, USA, 2009.
- Interagency Performance Evaluation Taskforce. Performance Evaluation of the New Orleans and Southeast Louisiana Hurricane Protection System, Appendix 8: Hazard Analysis; U.S. Army Corps of Engineers: New Orleans, LA, USA, 2009.
- Fischbach, J.R.; Johnson, D.R.; Kuhn, K.; Pollard, M.; Stelzner, C.; Costello, R.; Molina-Perez, E.; Sanchez, R.; Roberts, H.J.; Cobell, Z. 2017 Coastal Master Plan Attachment C3-25: Storm Surge and Risk Assessment; Louisiana Coastal Protection and Restoration Authority: Baton Rouge, LA, USA, 2017; p. 219. [Google Scholar]
- Meselhe, E.; White, E.; Reed, D. 2017 Coastal Master Plan: Appendix C: Modeling Chapter 2—Future Scenarios; Louisiana Coastal Protection and Restoration Authority: Baton Rouge, LA, USA, 2017; p. 32. [Google Scholar]
- Roberts, H.J.; Cobell, Z. 2017 Coastal Master Plan Attachment C3-25.1: Storm Surge; Louisiana Coastal Protection and Restoration Authority: Baton Rouge, LA, USA, 2017; p. 110. [Google Scholar]
- Cleveland, W.S.; Devlin, S.J. Locally weighted regression: An approach to regression analysis by local fitting. J. Am. Stat. Assoc. 1988, 83, 596–610. [Google Scholar] [CrossRef]
- Resio, D.T. White Paper on Estimating Hurricane Inundation Probabilities; U.S. Army Corps of Engineers: New Orleans, LA, USA, 2007.
- Selby, B.; Kockelman, K.M. Spatial prediction of traffic levels in unmeasured locations: Applications of universal kriging and geographically weighted regression. J. Transp. Geogr. 2013, 29, 24–32. [Google Scholar] [CrossRef]
- Meng, Q. Regression kriging versus geographically weighted regression for spatial interpolation. Int. J. Adv. Remote Sens. GIS 2014, 3, 606–615. [Google Scholar]
- Mosavi, A.; Ozturk, P.; Chau, K.W. Flood prediction using machine learning models: Literature review. Water 2018, 10, 1536. [Google Scholar] [CrossRef] [Green Version]
- Nocedal, J.; Wright, S. Numerical Optimization; Springer Science & Business Media: New York, NY, USA, 2006. [Google Scholar]
- Rosasco, L.; Vito, E.D.; Caponnetto, A.; Piana, M.; Verri, A. Are loss functions all the same? Neural Comput. 2004, 16, 1063–1076. [Google Scholar] [CrossRef] [PubMed] [Green Version]


| Covariate | Variable | Units | Description |
|---|---|---|---|
| Central pressure | Mbars 1 | Minimum atmospheric central pressure | |
| Radius of max windspeed | nm | Lateral size of the storm | |
| Forward velocity | knots | Movement speed | |
| Landfall location | degrees | Longitudinal location of storm landfall 2 | |
| Landfall angle | degrees | Angle at which the storm makes landfall 3 | |
| Distance | nm | Distance from grid point to landfall | |
| Azimuthal angle | degrees | Angle between storm track and grid point |
| Decile Bin | Grid Points |
|---|---|
| 21,219 | |
| 3395 | |
| 2355 | |
| 1199 | |
| 809 | |
| 1052 | |
| 1064 | |
| 1058 | |
| 1229 | |
| 1650 | |
| Total | 35,050 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Shisler, M.P.; Johnson, D.R. Comparison of Methods for Imputing Non-Wetting Storm Surge to Improve Hazard Characterization. Water 2020, 12, 1420. https://doi.org/10.3390/w12051420
Shisler MP, Johnson DR. Comparison of Methods for Imputing Non-Wetting Storm Surge to Improve Hazard Characterization. Water. 2020; 12(5):1420. https://doi.org/10.3390/w12051420
Chicago/Turabian StyleShisler, Matthew P., and David R. Johnson. 2020. "Comparison of Methods for Imputing Non-Wetting Storm Surge to Improve Hazard Characterization" Water 12, no. 5: 1420. https://doi.org/10.3390/w12051420
APA StyleShisler, M. P., & Johnson, D. R. (2020). Comparison of Methods for Imputing Non-Wetting Storm Surge to Improve Hazard Characterization. Water, 12(5), 1420. https://doi.org/10.3390/w12051420





