Experimental Analysis of Velocity Distribution in a Coarse-Grained Debris Flow: A Modified Bagnold’s Equation
Abstract
:1. Introduction
2. Material and Methods
2.1. Pertinent Aspects of Bagnold’s Theory and Its Application to Debris Flow
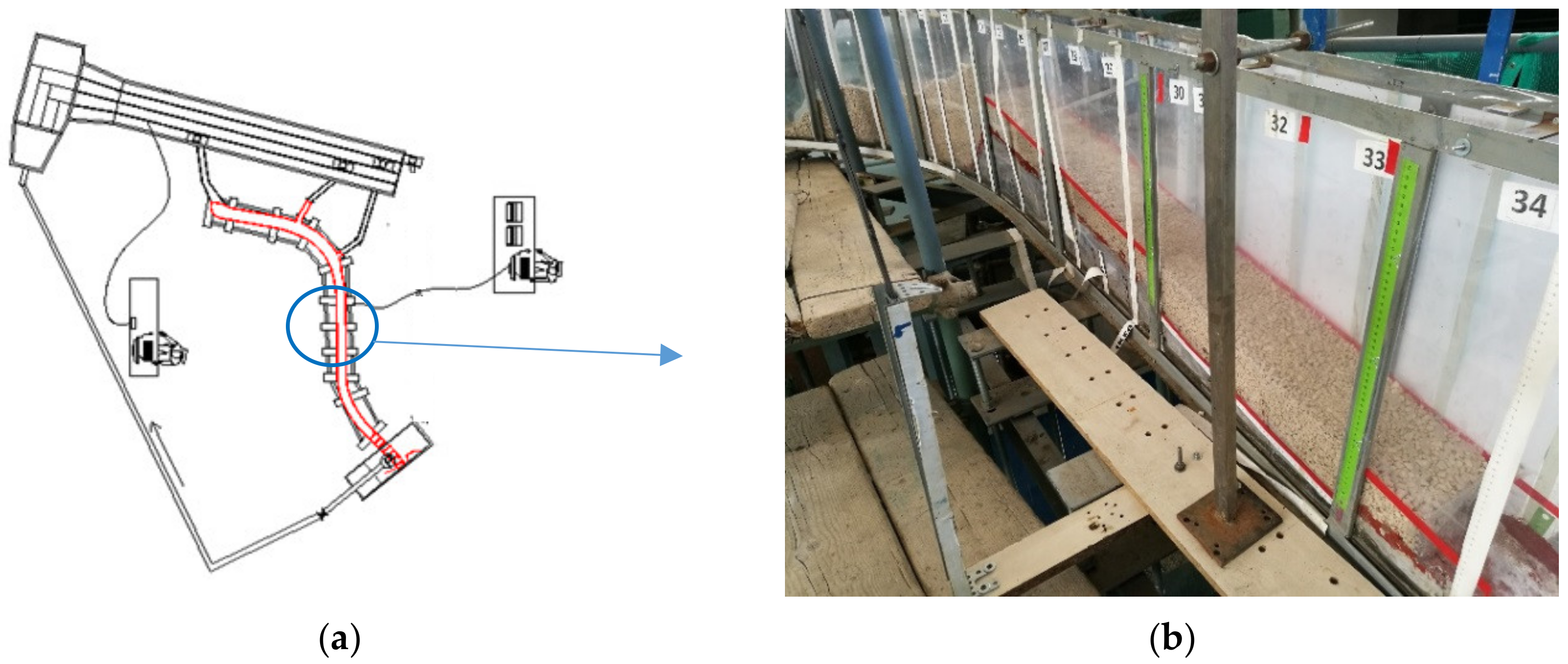
2.2. Experimental Apparatus and Procedure
3. Results
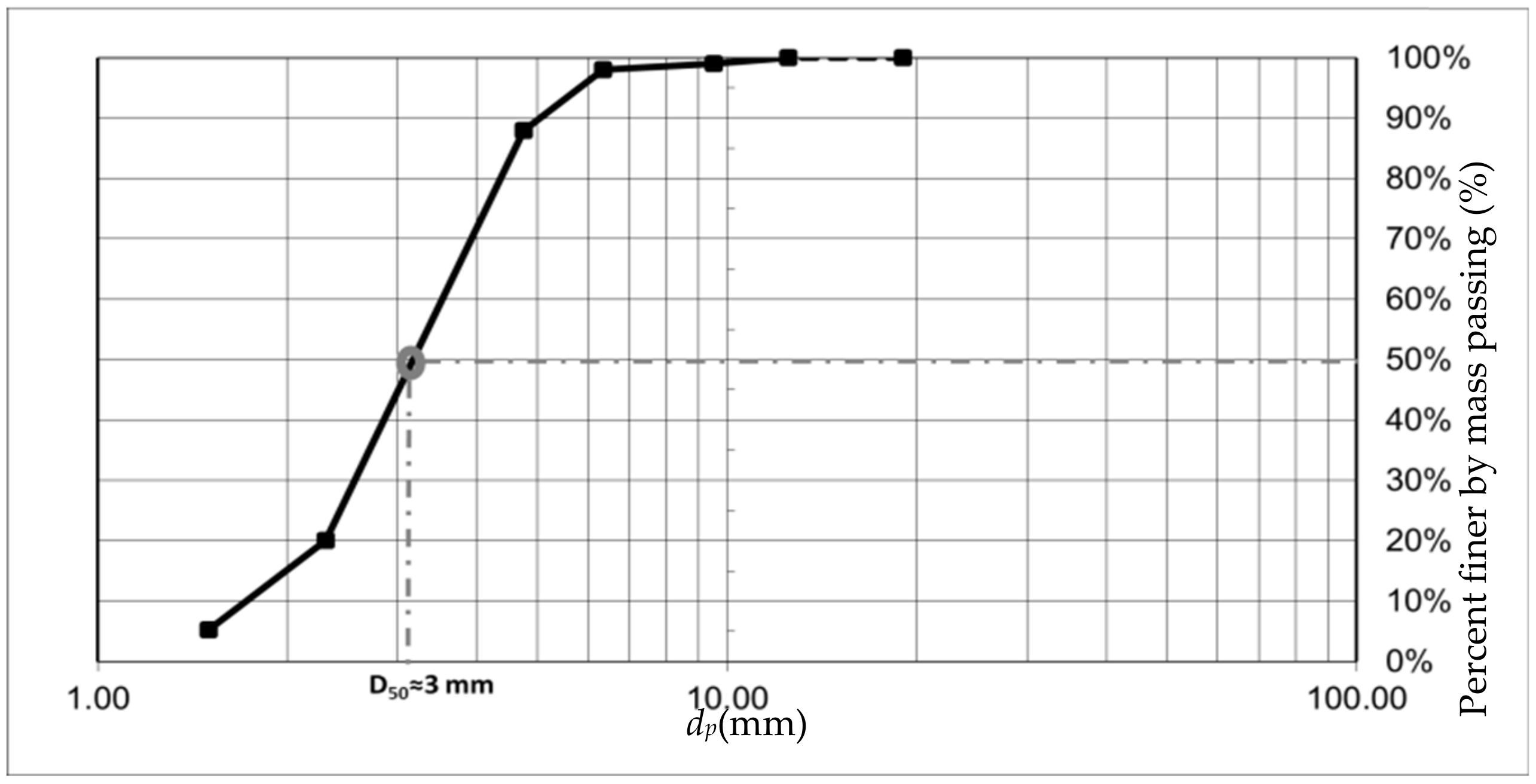
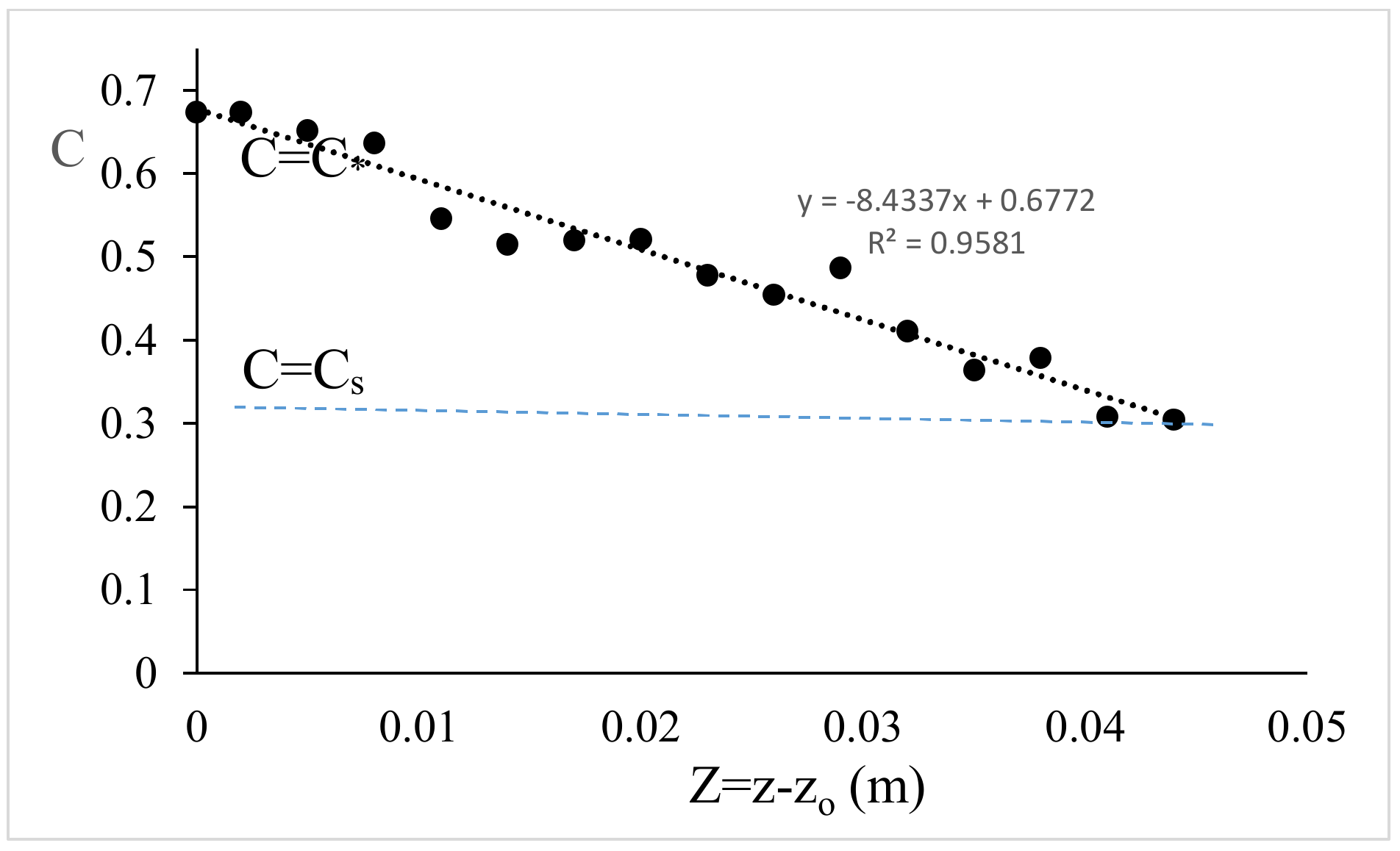
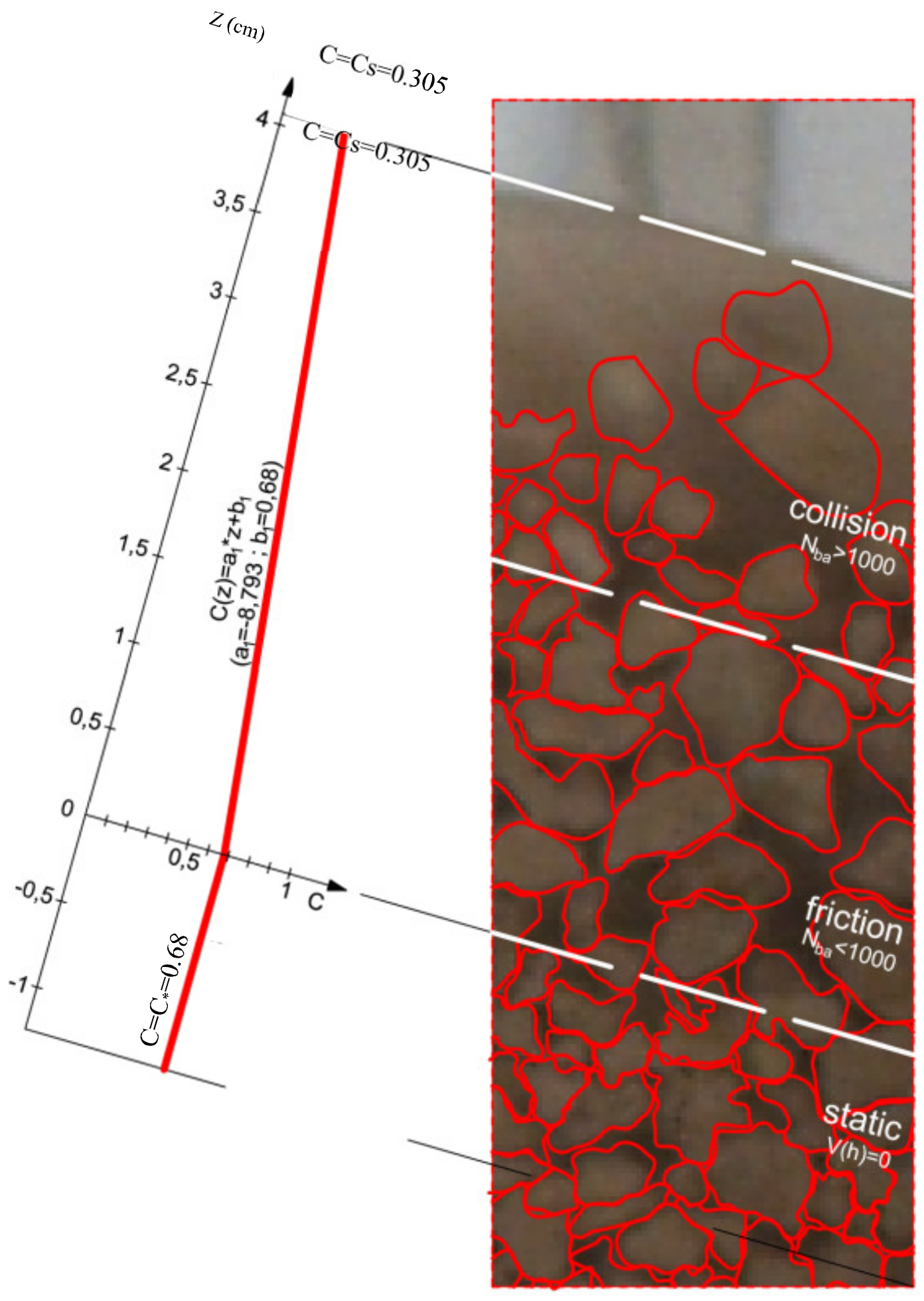
3.1. Grains Concentration Distribution
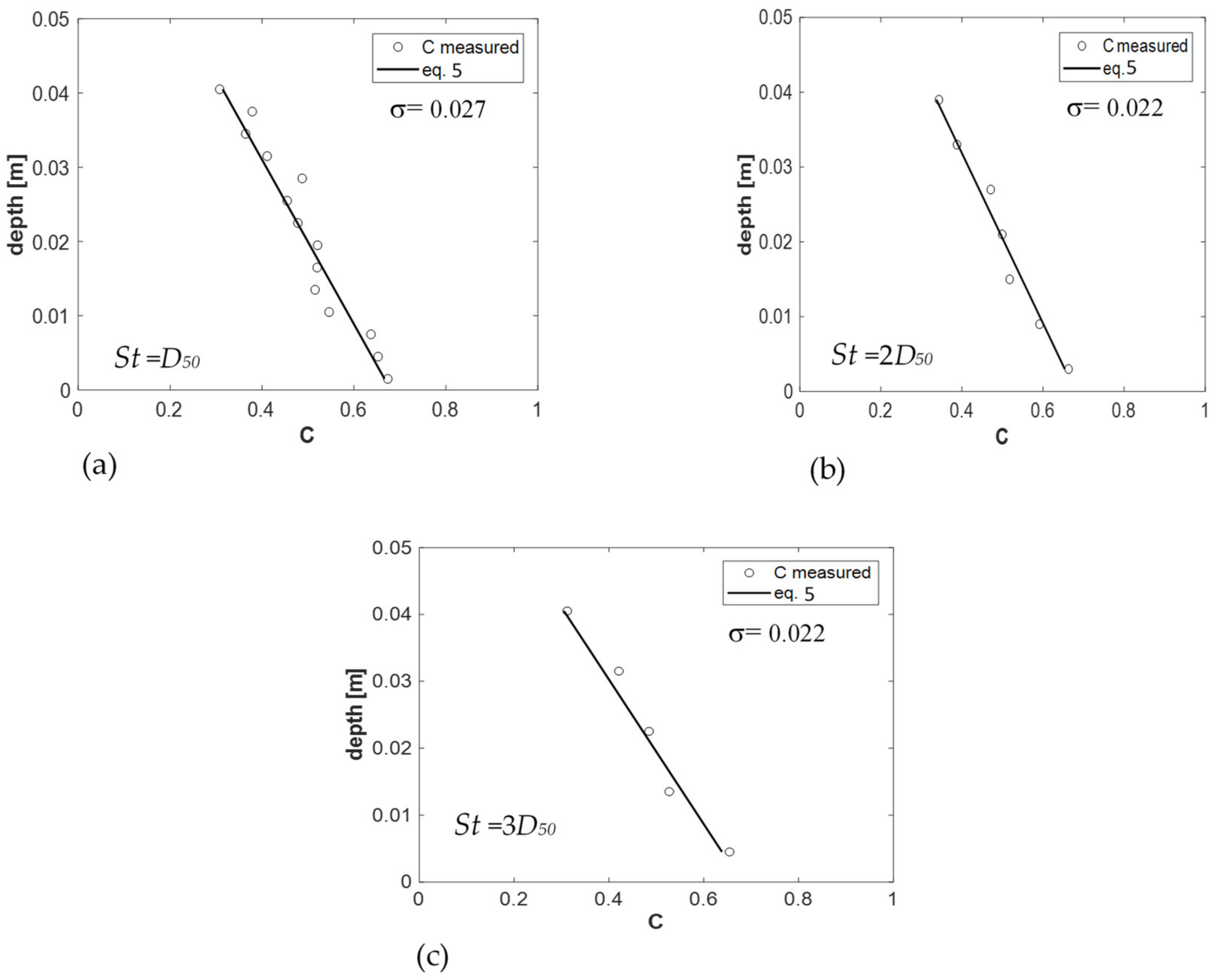
3.2. Modified Bagnold’s Equation Applied to Debris Flow
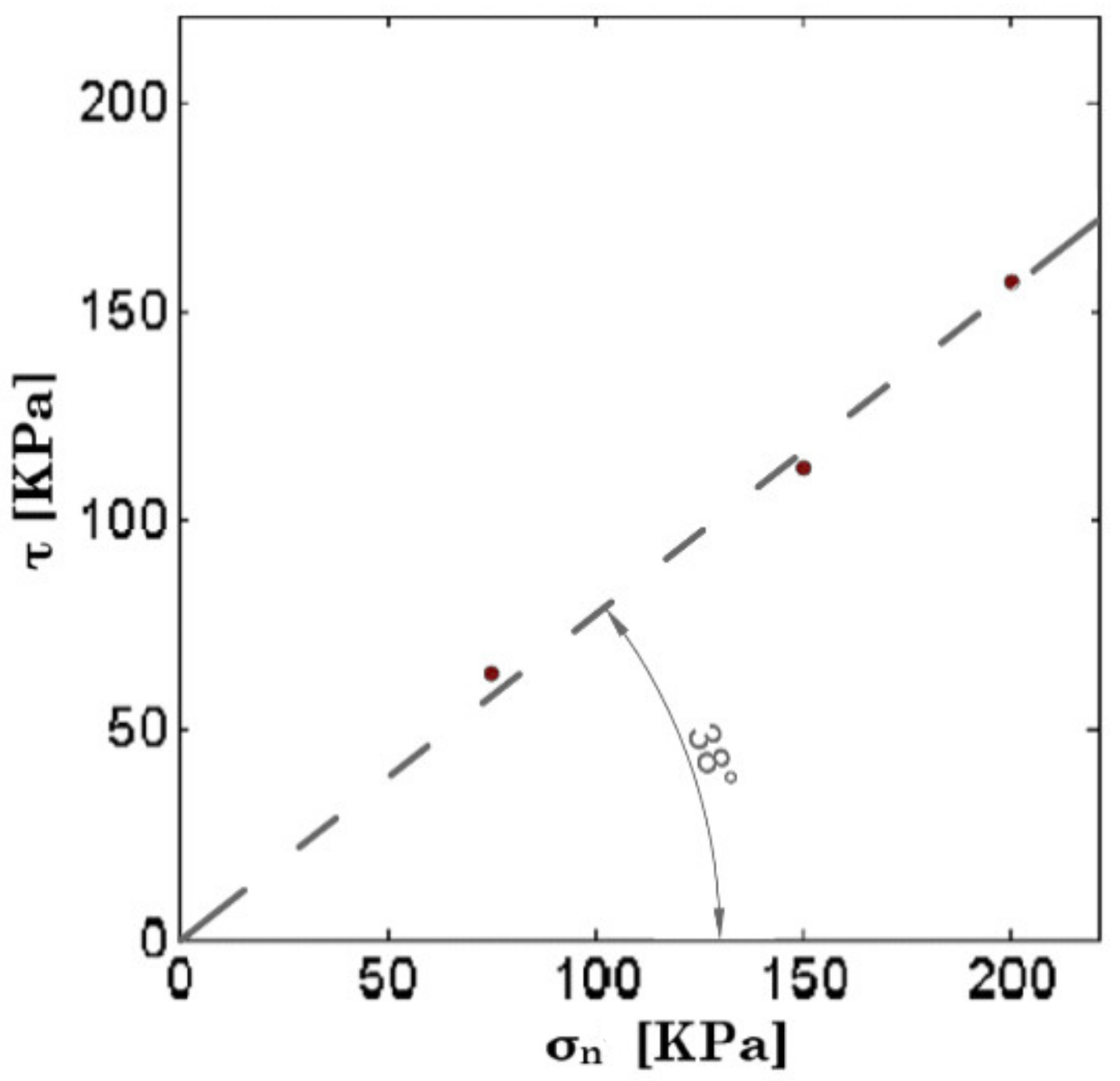
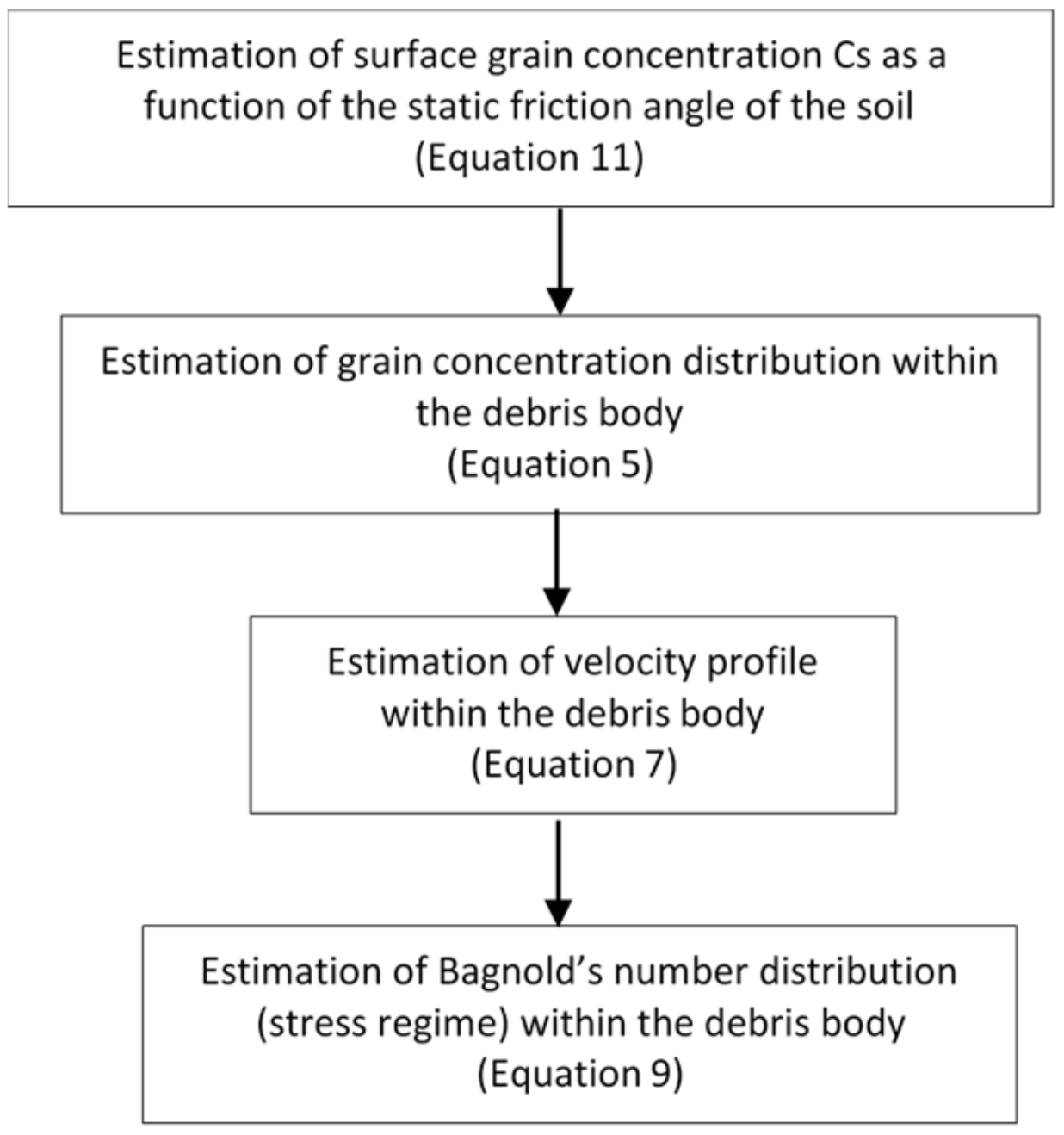
3.3. Free Surface Grains Concentration and Procedure for Its Estimation
4. Discussion
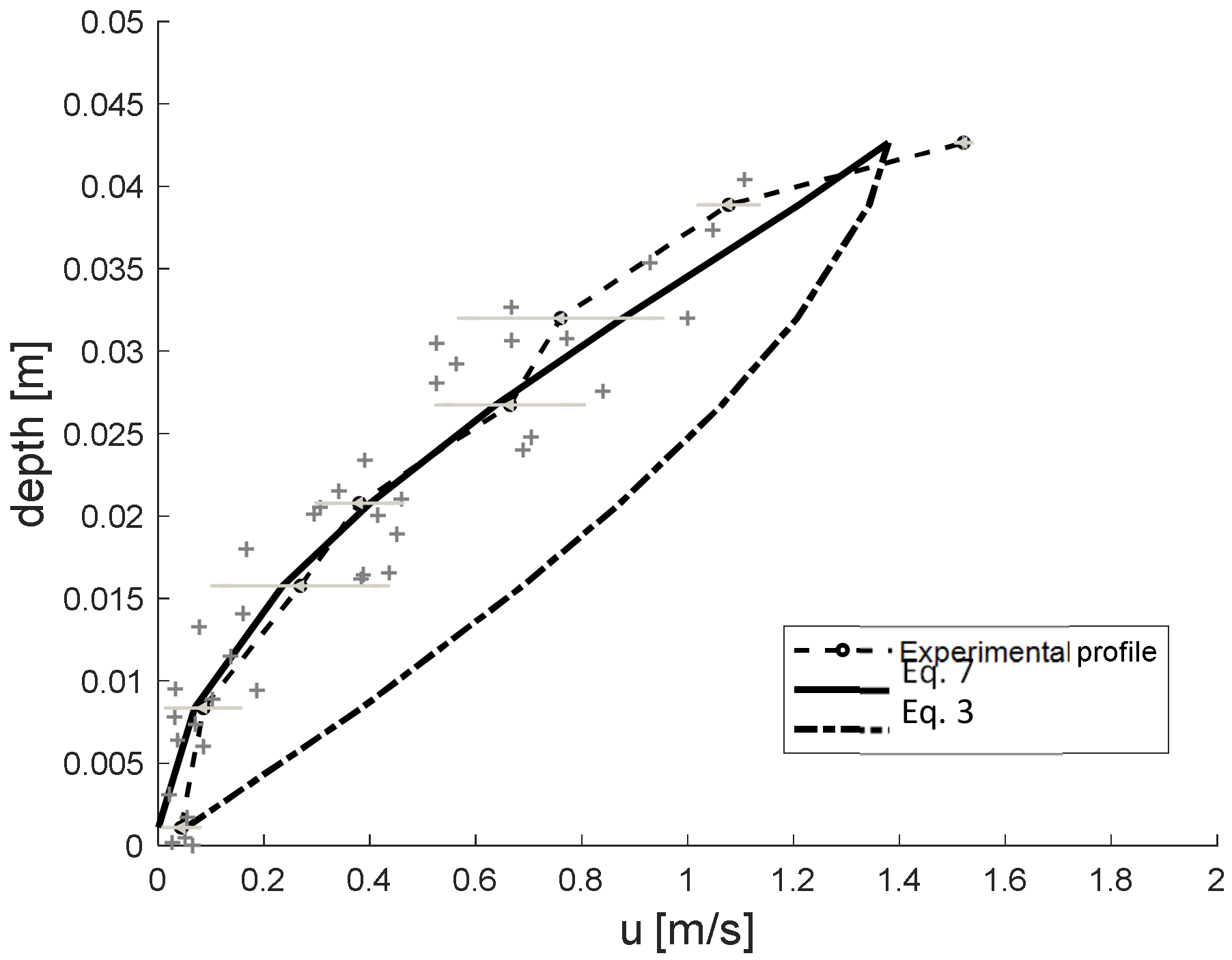
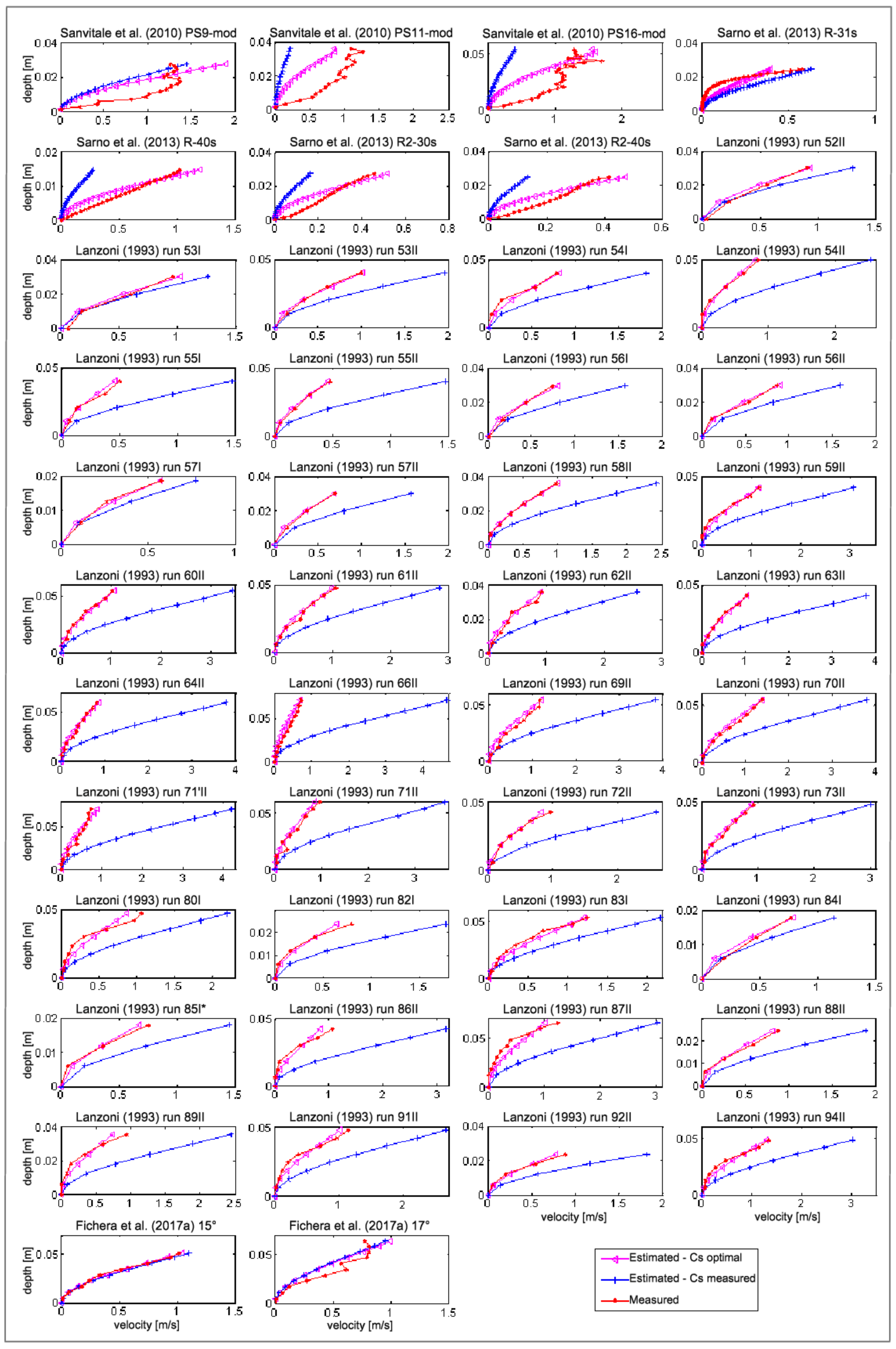
4.1. Velocity Profiles and Comparisons with Literature Data
4.2. Main Aspects Derived by the Proposed Modified Expressions and Procedure
5. Conclusions
- (1)
- the distribution of the grain concentration can be interpreted by a linear law obtained between the value of the maximum package value, C*, at the bed and the value of the free surface concentration, Cs;
- (2)
- by removing the hypothesis of uniform grain concentration along the entire depth, modified expressions of Bagnold’s number and of the longitudinal velocity, which take into account the variation of the grain concentration in the entire depth, are presented. The expression of the velocity profile includes two parameters: the maximum package value, C*, which could be determined by using either experimental data appositely collected or physically-based literature data, and the value of the free surface concentration, Cs;
- (3)
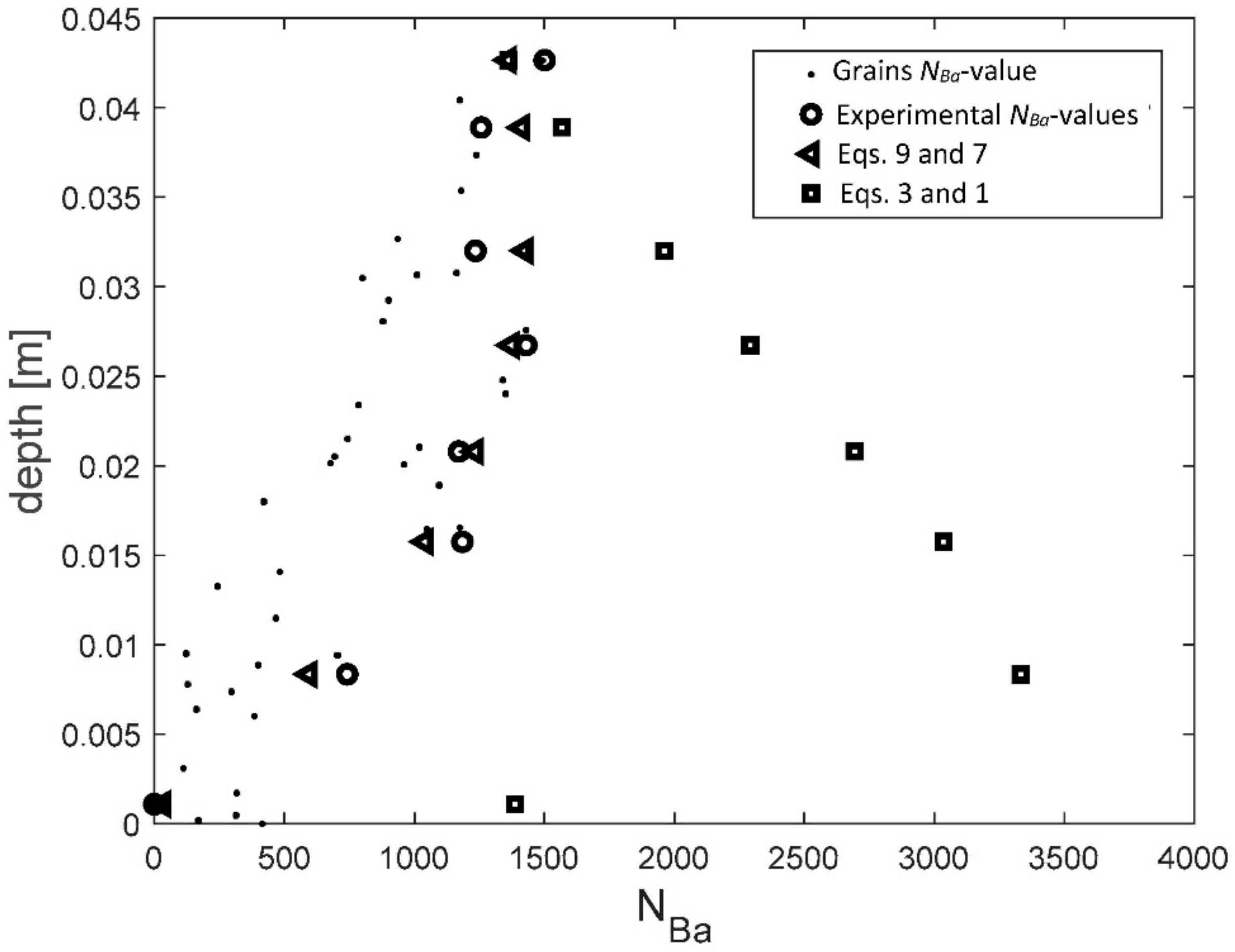
- by using the modified expression of Bagnold’s number, it has been verified that a varying stress regime can develop within the debris flow. The NBa-values are strongly lower than 1000 when close to the bed (frictional regime) and are greater than 1000 (collisional-inertial regime) when close to the free surface;
- (4)
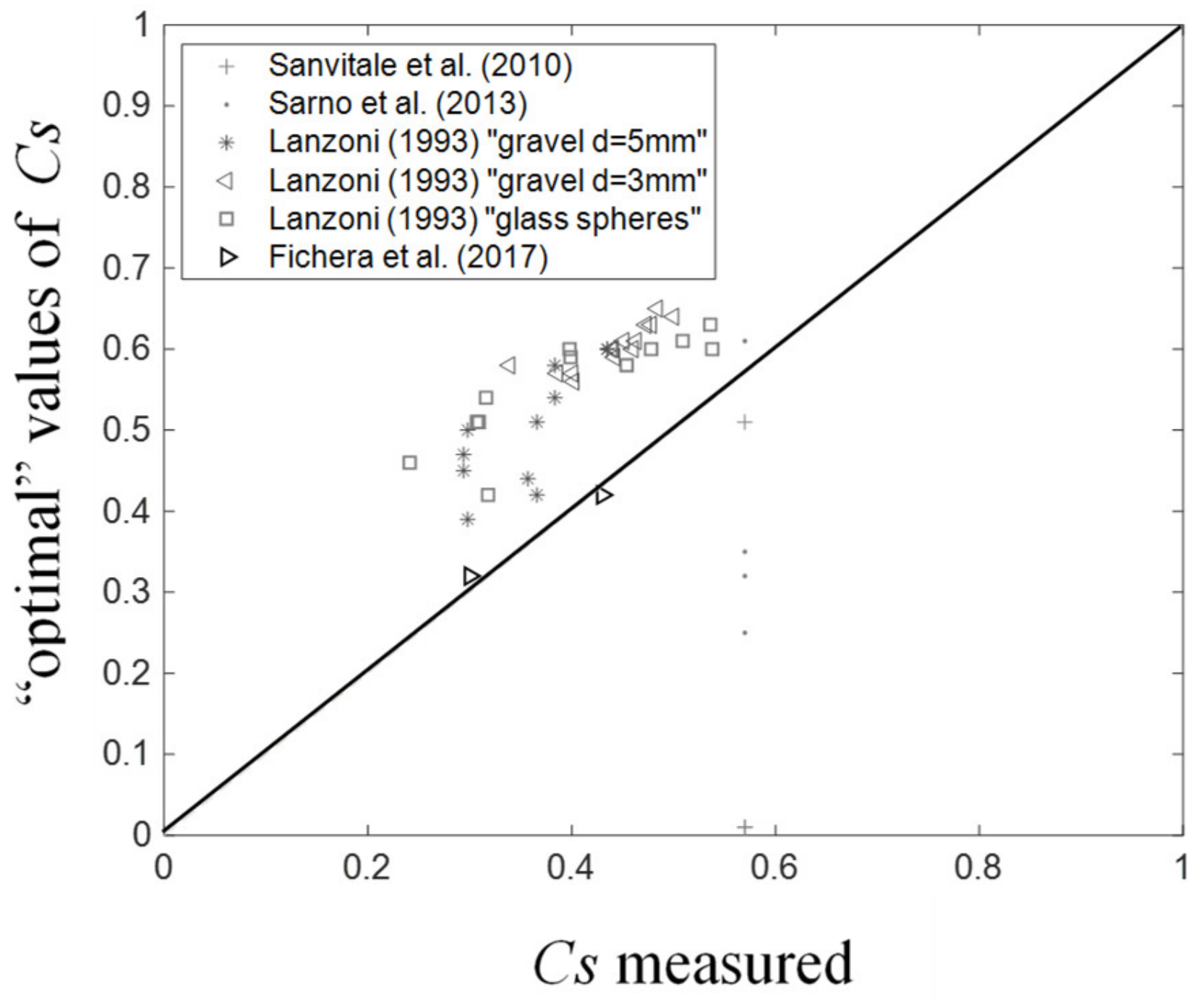
- it has been verified that, in the first approximation, surface concentration Cs can be estimated as a function of the static friction angle of the material, which can be determined by simple shear tests.
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Takahashi, T. Debris flow. Annu. Rev. Fluid Mech. 1981, 13, 57–77. [Google Scholar] [CrossRef]
- Cannon, S.; Gartner, J.; Wilson, R.C.; Bowers, J.C.; Laber, J. Storm rainfall conditions for floods and debris flows from recently burned areas in south western Colorado and southern California. Geomorphology 2008, 96, 250–269. [Google Scholar] [CrossRef]
- Theule, J.I.; Liébault, F.; Laigle, D.; Loye, A.; Jaboyedoff, M. Channel scour and fill by debris flows and bedload transport. Geomorphology 2015, 243, 92–105. [Google Scholar] [CrossRef]
- Iverson, R.M. The physics of debris flows. Rev. Geophys. 1997, 35, 245–296. [Google Scholar] [CrossRef] [Green Version]
- Kaitna, R.; Rickenmann, D.; Schatzmann, M. Experimental study on rheologic behaviour of debris-flow material. Acta Geotech. 2007, 2, 71–85. [Google Scholar] [CrossRef]
- Armanini, A. Granular flows driven by gravity. J. Hydraul. Res. 2013, 51, 111–120. [Google Scholar] [CrossRef]
- Van Rijn, L.C. Sediment transport, part I: Bed load transport. J. Hydraul. Eng. 1984, 110, 1431–1456. [Google Scholar] [CrossRef] [Green Version]
- Van Rijn, L.C. Sediment transport, part II: Suspended load transport. J. Hydraul. Eng. 1984, 110, 1613–1641. [Google Scholar] [CrossRef]
- Joshi, S.; Xu, Y.J. Assessment of suspended sand availability under different flow conditions of the Lowermost Mississippi River at Tarbert Landing during 1973–2013. Water 2015, 7, 7022–7044. [Google Scholar] [CrossRef]
- Joshi, S.; Xu, Y.J. Bedload and suspended load transport in the 140-km reach downstream of the Mississippi River avulsion to the Atchafalaya River. Water 2017, 9, 716. [Google Scholar] [CrossRef] [Green Version]
- Campbell, C.S. Granular shear flows at the elastic limit. J. Fluid Mech. 2002, 465, 261–291. [Google Scholar] [CrossRef]
- Campbell, C.S. Stress-controlled elastic granular shear flows. J. Fluid Mech. 2005, 539, 273–297. [Google Scholar] [CrossRef] [Green Version]
- Kaitna, R.; Dietrich, W.E.; Hsu, L. Surface slopes, velocity profiles and fluid pressure in coarse-grained debris flows saturated with water and mud. J. Fluid Mech. 2014, 7, 377–403. [Google Scholar] [CrossRef]
- Takahashi, T. Debris Flows: Mechanics, prediction and countermeasures. Balkema-Proc and Monogr. In Eng., Water and Earth Sc.; Taylor and Francis: New York, NY, USA, 2007. [Google Scholar]
- Bonnet-Staub, I. Definition d’une typologie des deposits de laves torrentielles et identification de critres granulomtriques et geotechniques concernant les zones sources. J. Bull. Eng. Geol. Environ. 1999, 57, 359–367. [Google Scholar] [CrossRef]
- Bagnold, R.A. Experiments on a gravity-free dispersion of large solid spheres in a Newtonian fluid under shear. Proc. R. Soc. Lond. A 1954, 225, 49–63. [Google Scholar]
- Hunt, M.; Zenit, R.; Campbell, C.S.; Brennen, C.E. Revisiting the 1954 suspension experiments of RA Bagnold. J. Fluid Mech. 2002, 452, 1–24. [Google Scholar] [CrossRef] [Green Version]
- Bagnold, R.A. The shearing and dilation of dry sand and the ‘singing’ mechanism. Proc. R. Soc. Lond. A 1966, 295, 219–232. [Google Scholar]
- Bagnold, R.A. An empirical correlation of bedload transport rates in flumes and natural rivers. Proc. R. Soc. Lond. A 1980, 372, 453–473. [Google Scholar]
- Egashira, S.; Miyamoto, K.; Itoh, T. Constitutive equations of debris flow and their applicability. In Proceedings of the 1st International Conference on Debris-Flow Hazards Mitigation: Mechanics, Prediction, and Assessment, San Francisco, CA, USA, 7–9 August 1997; pp. 340–349. [Google Scholar]
- Iverson, R.M.; Denlinger, R.P. Flow of variably fluidized granular masses across three-dimensional terrain: Coulomb mixture theory. J. Geophys. Res. 2001, 106, 537–552. [Google Scholar] [CrossRef]
- Iverson, R.M. Elementary theory of bed-sediment entrainment by debris flows and avalanches. J. Geophys. Res. 2012, 117, F03006. [Google Scholar] [CrossRef]
- Iverson, R.M.; Ouyang, C. Entrainment of bed material by Earth-surface mass flows: Review and reformulation of depth-integratedtheory. Rev. Geophys. 2015, 53, 27–58. [Google Scholar] [CrossRef]
- Hungr, O.; McDougall, S.; Bovis, M. Entrainment of material by Debris flows. In Debris-Flow Hazards and Related Phenomena; Jakob, M., Hungr, O., Eds.; Springer: Berlin/Heidelberg, Germany, 2005; pp. 135–158. [Google Scholar]
- Scheidl, C.; Rickenmann, D. Empirical prediction of debris-flow mobility and deposition on fans. Earth Surf. Process. Landf. 2009, 35, 157–173. [Google Scholar] [CrossRef]
- Berger, C.; McArdell, B.W.; Schlunegger, F. Direct measurement of channel erosion by debris flows, Illgraben, Switzerland. J. Geophys. Res. 2011, 116, F01002. [Google Scholar] [CrossRef] [Green Version]
- Chiodi, F.; Claudin, P.; Andreotti, B. A two-phase flow model of sediment transport: Transition from bedload to suspended load. J. Fluid Mech. 2014, 755, 561–581. [Google Scholar] [CrossRef] [Green Version]
- Thibaud, R.; Chauchat, J. A two-phase model for sheet flow regime based on dense granular flow rheology. J. Geophys. Res. Am. Geophys. Union 2013, 118, 619–634. [Google Scholar]
- Chapman, S.; Cowling, T.G. The Mathematical Theory of Non-Uniform Gases, 3rd ed.; Cambridge University Press: Cambridge, UK, 1971. [Google Scholar]
- Jenkins, J.T.; Savage, S.B. A theory for rapid flow of identical, smooth, nearly elastic, spherical particles. J. Fluid Mech. 1983, 130, 186–202. [Google Scholar] [CrossRef]
- Lun, C.K.K.; Savage, S.B.; Jeffrey, D.J.; Chepurniy, N. Kinetic theories for granular flow: Inelastic particles in Couette flow and slightly in elastic particles in a general flow field. J. Fluid Mech. 1984, 140, 223–256. [Google Scholar] [CrossRef]
- Jenkins, J.T.; Richman, M.W. Kinetic theory for plane flows of a dense gas of identical, rough, inelastic, circular disks. Phys. Fluids 1985, 28, 3485–3494. [Google Scholar] [CrossRef]
- Lanzoni, S. Meccanica di miscugli solio-liquido in regime granulo-inerziale. Ph.D. Thesis, University of Padova, Padua, Italy, 1993. [Google Scholar]
- Armanini, A.; Capart, H.; Fraccarollo, L.; Larcher, M. Rheological stratification in experimental free-surface flows of granular-liquid mixtures. J. Fluid Mech. 2005, 532, 269–319. [Google Scholar] [CrossRef] [Green Version]
- Sanvitale, N.; Bowman, E.T.; Genevois, R. Experimental measurements of velocity through granular-liquid flows. Ital. J. Eng. Geol. Environ. Book Casa Editrice Università La Sapienza 2010. [Google Scholar] [CrossRef]
- Iverson, R.M.; Logan, M.; Lahusen, R.G.; Berti, M. The perfect debris flow? Aggregated results from 28 large-scale experiments. J. Geophys. Res. 2010, 115, F03005. [Google Scholar]
- Sarno, L.; Papa, M.N.; Tai, Y.C.; Carravetta, A.; Martino, R. A reliable PIV approach for measuring velocity profiles of highly sheared granular flows. In Latest Trends in Engineering Mechanics, Structures, Engineering Geology. 2013. ISBN: 978-960-474-376-6. Available online: https://www.researchgate.net/publication/278961892_A_reliable_PIV_approach_for_measuring_velocity_profiles_of_highly_sheared_granular_flows (accessed on 13 May 2020).
- Hsu, L.; Dietrich, W.E.; Sklar, L.S. Experimental study of bedrock erosion by granular flows. J. Geophys. Res. 2008, 113, F02001. [Google Scholar] [CrossRef]
- Fichera, A.; Stancanelli, L.M.; Lanzoni, S.; Foti, E. Stony Debris Flow Debouching in a River Reach: Energy Dissipative Mechanisms and Deposit Morphology. In Proceedings of the Workshop on World Landslide Forum, Ljubljana, Slovenia, 9 May–2 June 2017; Springer: Cham, Switzerland, 2017; pp. 377–383. [Google Scholar]
- Marchi, L.; Dalla Fontana, G. GIS morphometric indicators for the analysis of sediment dynamics in mountain basins. Environ. Geol. 2005, 48, 218–228. [Google Scholar] [CrossRef]
- Gruber, S.; Huggel, C.; Pike, R. Modelling mass movements and landslide susceptibility. In Geomorphometry; Hengl, T., Reuter, H.I., Eds.; Elsevier: Amsterdam, The Netherlands, 2008; pp. 527–550. Available online: http://www.zora.uzh.ch/id/eprint/6475/ (accessed on 13 May 2020).
- Takahashi, T. Mechanical characteristics of debris flow. J. Hydraulics Div. ASCE 1978, 104, 1153–1169. [Google Scholar]
- Takahashi, T. Debris flow on prismatic open channel. J. Hydraulics Div. ASCE 1980, 106, 1153–1169. [Google Scholar]
- Gregoretti, C.; Dalla Fontana, G. The triggering of debris flows due to channel-bed failure in some alpine headwater basins of Dolomites: Analyses of critical runoff. Hydrological Process. 2008, 22, 2248–2263. [Google Scholar] [CrossRef]
- Berti, M.; Genevois, R.; Simoni, A.; Tecca, P.R. Field observations of a debris flow event in the Dolomites. Geomorphology 1999, 29, 256–274. [Google Scholar] [CrossRef]
- Moscariello, A.; Marchi, L.; Maraga, F.; Mortara, G. Alluvial fans in the Italian Alps: Sedimentary facies and processes. In Flood & Megaflood Processes and Deposits—Recent and Ancient Example; Martini, P., Baker, V.R., Garzon, G., Eds.; Blackwell Science: Oxford, UK, 2002; pp. 141–166. [Google Scholar]
- Savage, S.B.; Lun, C.K.K. Particle size segregation in inclined chute flow of dry cohesionless granular solids. J. Fluid Mech. 1988, 189, 311–335. [Google Scholar] [CrossRef]
- Aharonov, E.; Sparks, D. Rigidity phase transition in granular packings. Phys. Rev. E 1999, 60, 6890–6896. [Google Scholar] [CrossRef]
- Takahashi, T. An occurrence mechanism of mud-debris flows, and their characteristics in motion. Annu. DPRI 1977, 20, 405–435. [Google Scholar]
- Tsai, Y.F.; Tsai, H.K.; Ch, Y.L. Study on the configurations of debris-flow fans. IJEGE 2011, 2011, 03.B-032. [Google Scholar]
- Lanzoni, S.; Gregoretti, C.; Stancanelli, L.M. Coarse-grained debris flow dynamics on erodible beds. J. Geophys. Res. Earth Surf. 2017, 122, 596–614. [Google Scholar] [CrossRef]
- Chen, S.C.; An, S. Flume experiment of debris flow confluence formed alluvial fan in the main channel. In River, Coastal and Estuarine Morphodynamics: RCEM 2007; Dohmen-Janssen, C.M., Hulscher, S.J.M.H., Eds.; Taylor and Francis: London, UK, 2007; pp. 829–835. [Google Scholar]
- Fichera, A. Analisi e caratterizzazione del comportamento di una colata detritica. Ph.D. Thesis, University of Enna “KORE”, Italy, Kore, 2017. [Google Scholar]
- Lanzoni, S.; Tubino, M. Rheometric experiments on mature debris flows. In Proceedings of the XXV International Association for Hydro-Environment, Tokyo, Japan, 30 August–3 September 1993. Editor: Japan Society of Civil Engineers, Local Organizing Committee of the XXV Congress, IAHR, 1993. [Google Scholar]
- ASM International Handbook Committee. Engineered Materials Handbook; Desk Edition 1995; ASM International: Novelty, OH, USA, 1995; ISBN 0-87170-283-5. [Google Scholar]
- Zhao, Y.; Liu, Z. Study of Material Composition Effects on the Mechanical Properties of Soil-Rock Mixtures. Hindawi. Adv. Civil Eng. 2018, 2018, 3854727. [Google Scholar] [CrossRef]



© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Termini, D.; Fichera, A. Experimental Analysis of Velocity Distribution in a Coarse-Grained Debris Flow: A Modified Bagnold’s Equation. Water 2020, 12, 1415. https://doi.org/10.3390/w12051415
Termini D, Fichera A. Experimental Analysis of Velocity Distribution in a Coarse-Grained Debris Flow: A Modified Bagnold’s Equation. Water. 2020; 12(5):1415. https://doi.org/10.3390/w12051415
Chicago/Turabian StyleTermini, Donatella, and Antonio Fichera. 2020. "Experimental Analysis of Velocity Distribution in a Coarse-Grained Debris Flow: A Modified Bagnold’s Equation" Water 12, no. 5: 1415. https://doi.org/10.3390/w12051415




