CFD Modelling of Particle-Driven Gravity Currents in Reservoirs
Abstract
1. Introduction
2. Materials and Methods
2.1. Governing Equations and Model Setup
2.1.1. Hydrodynamic Model
2.1.2. Sediment Transport Model
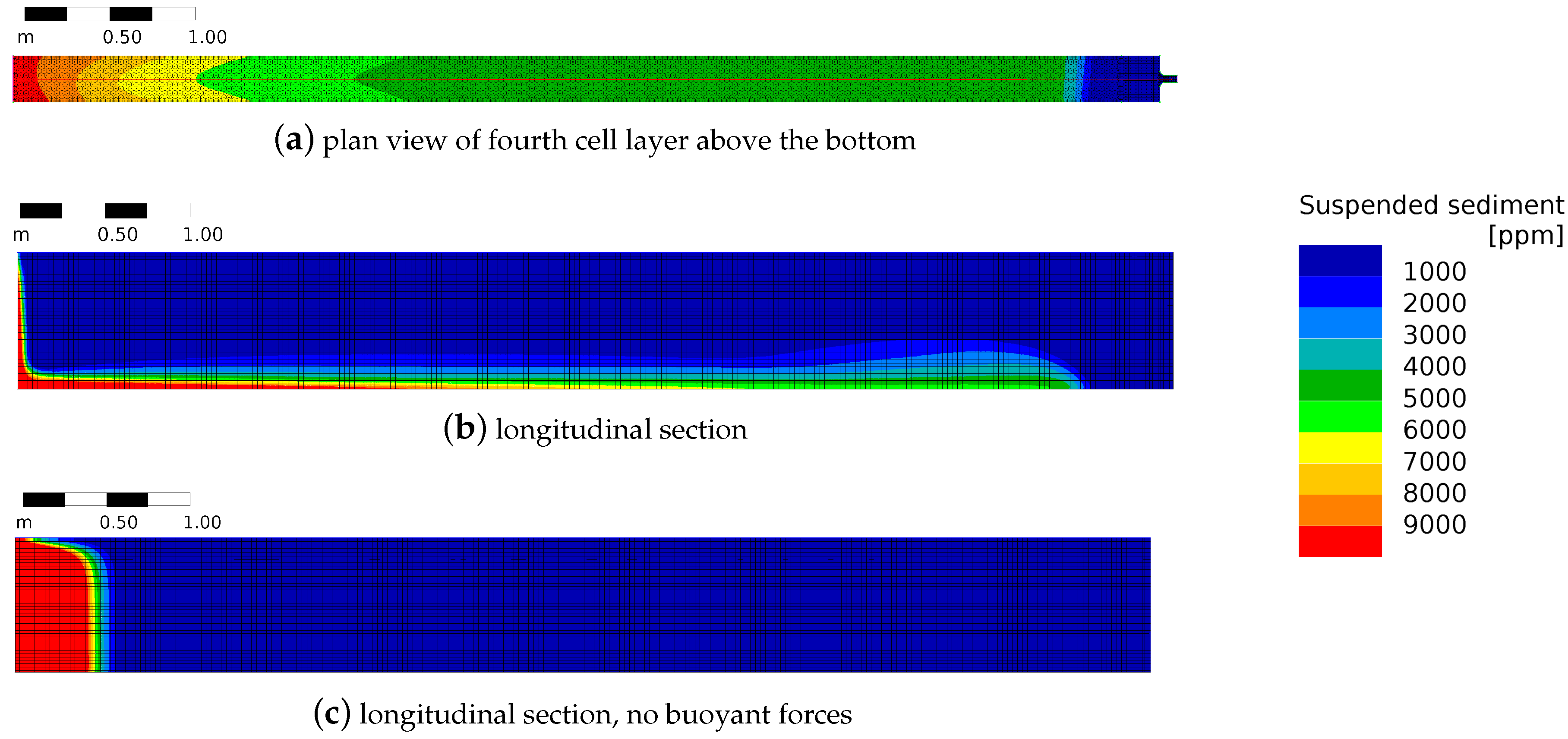
2.1.3. Buoyant Forces
2.1.4. Discretization
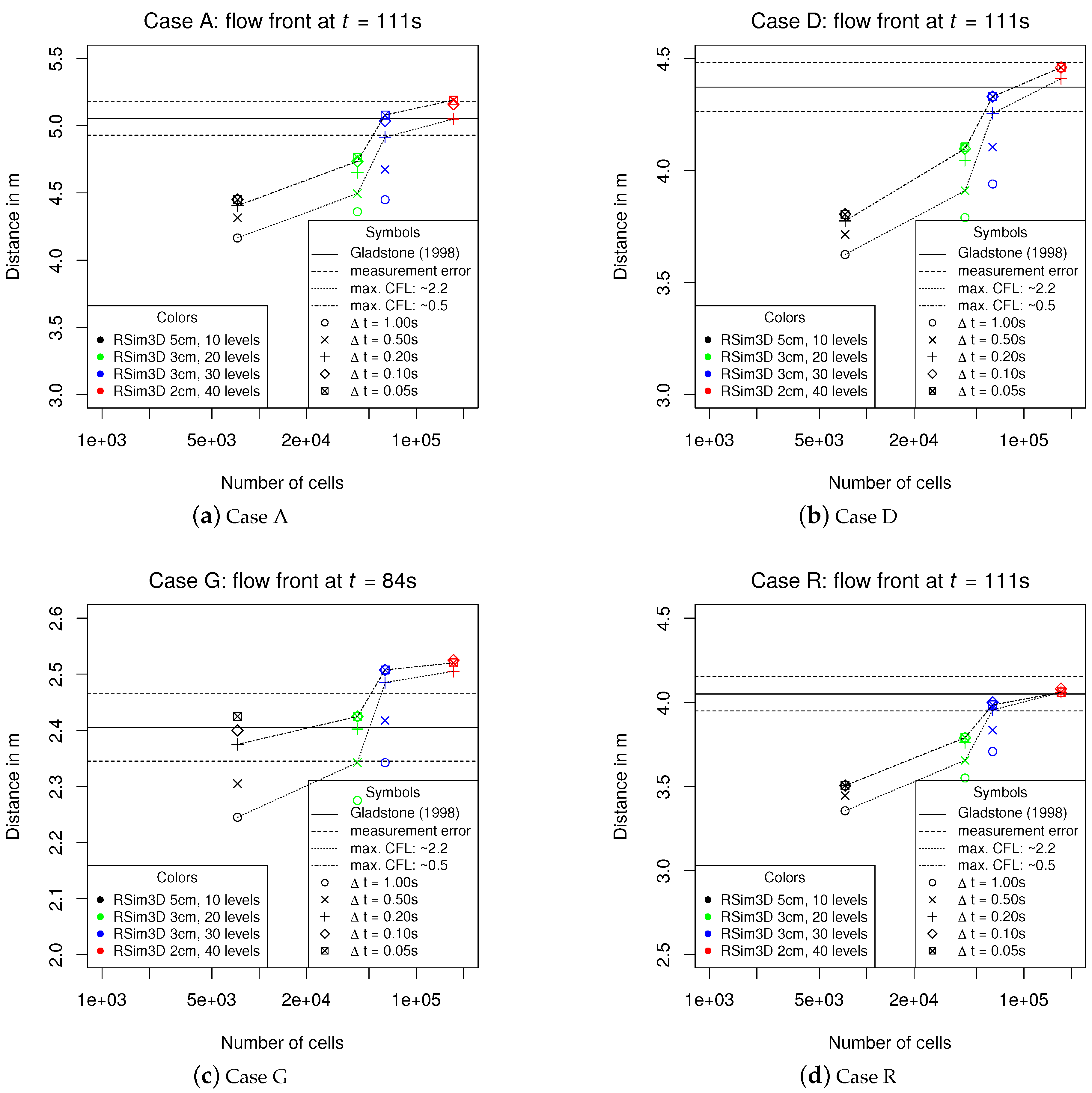
2.2. Code Validation and Mesh Sensitivity Analysis
- Case A: one grain fraction with = 25 µm and = 0.8 mm s−1.
- Case D: two grain fractions to equal amounts with = 25 µm and = 69 µm and = 0.8 mm s−1 and = 5.8 mm s−1, respectively.
- Case G: one grain fraction with = 69 µm and = 5.8 mm s−1.
- Case R: five grain fractions to equal amounts with = 17 µm, = 37 µm, = 63 µm, = 88 µm and = 105 µm and = 0.3 mm s−1, = 1.7 mm s−1, = 4.8 mm s−1, = 9.4 mm s−1 and = 11.3 mm s−1, respectively.
2.3. Test Case for the Study of Turbidity Current Venting Efficiency
3. Results
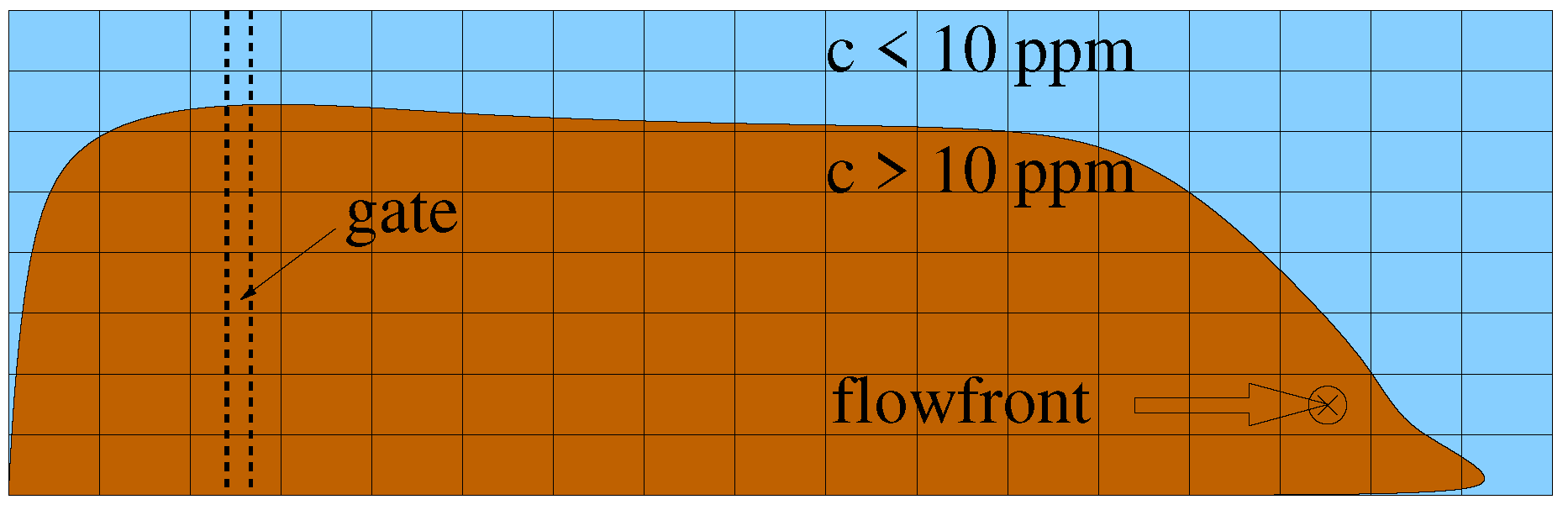
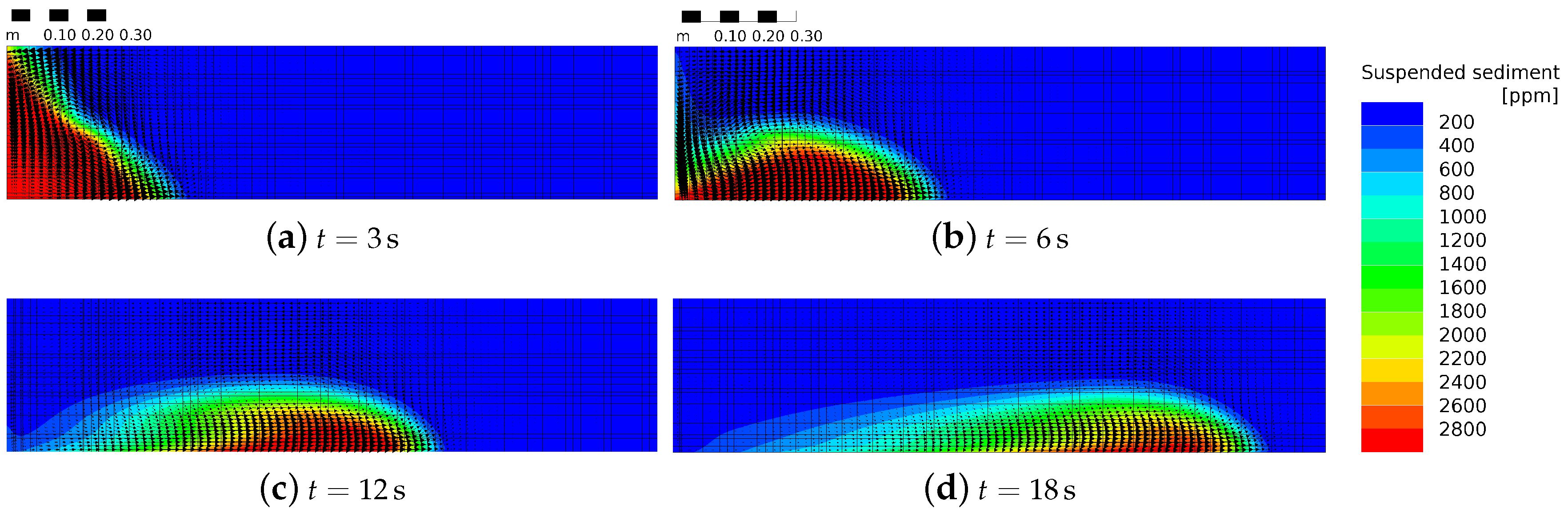
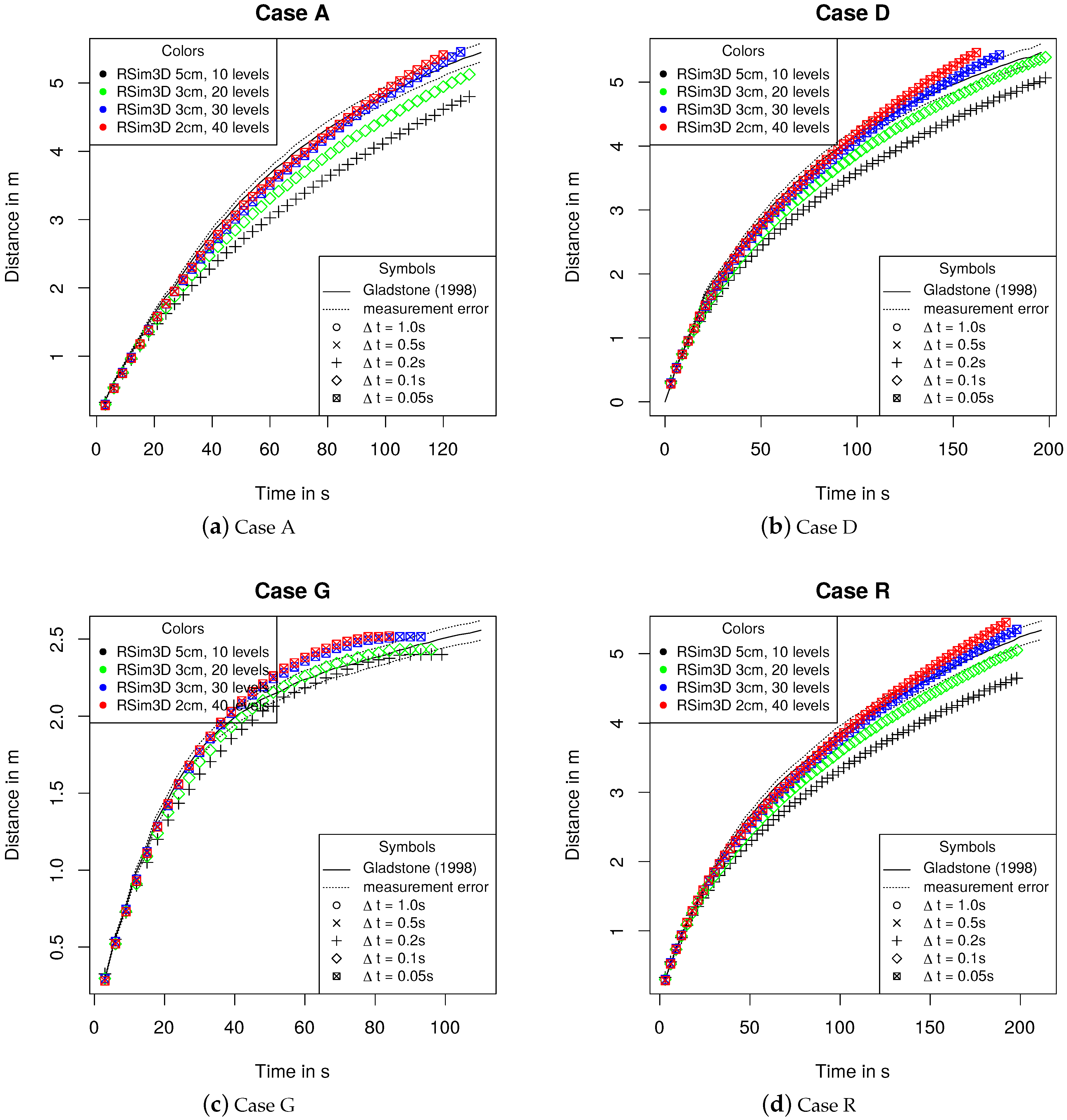
3.1. Flow Front Advance in Lock Exchange Experiments
3.2. Computational Effort of the Numerical Models of the Lock Exchange Experiments
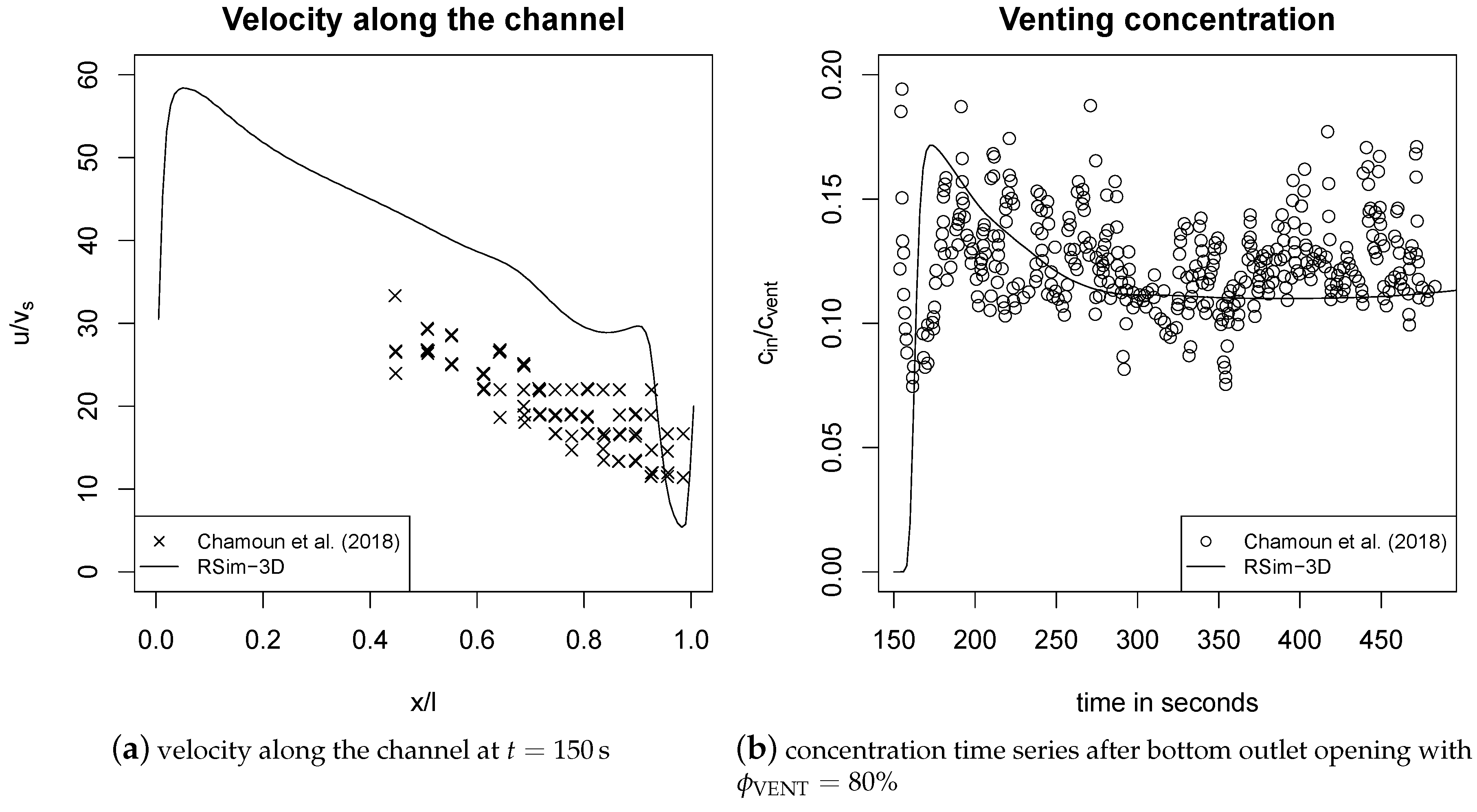
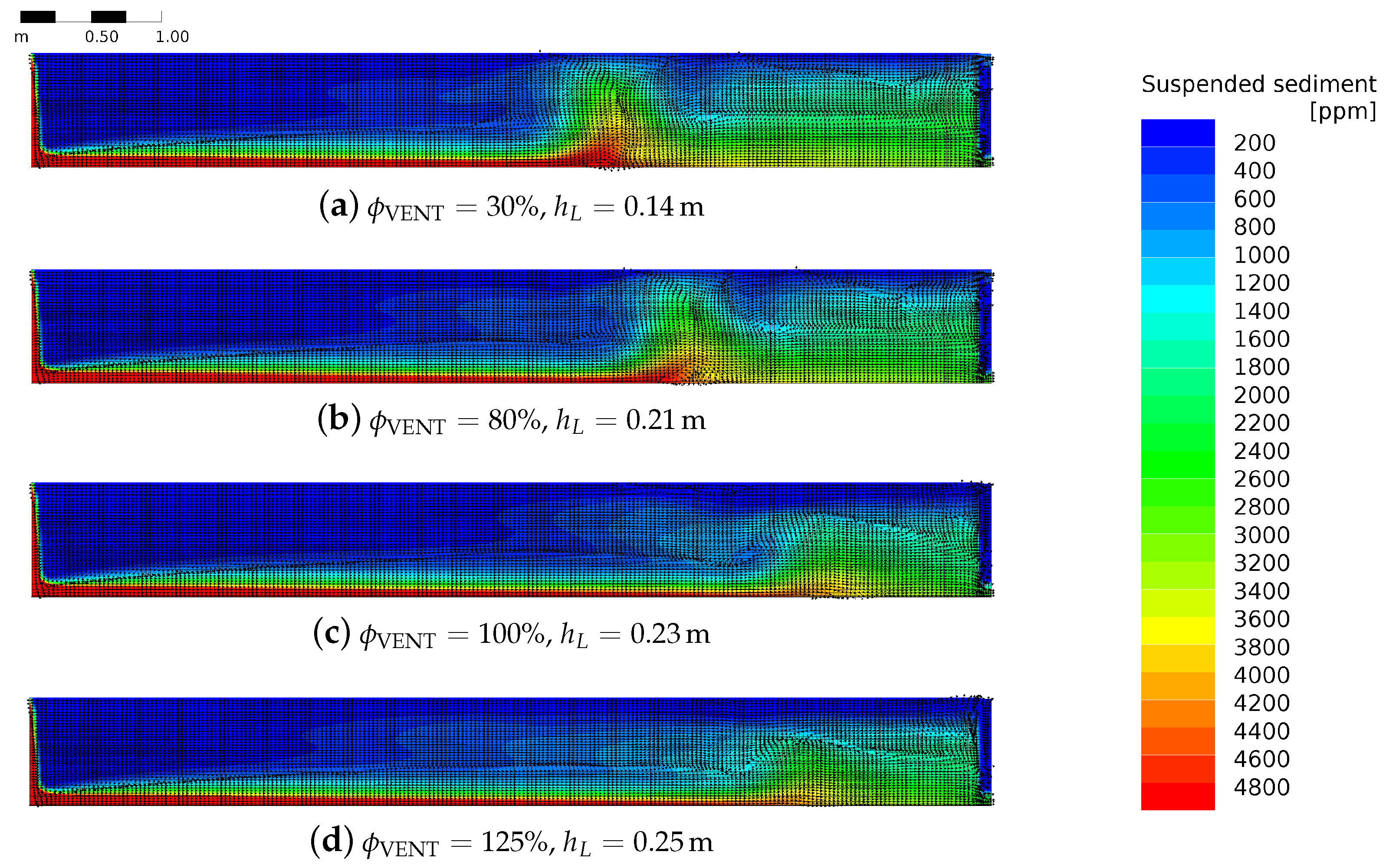
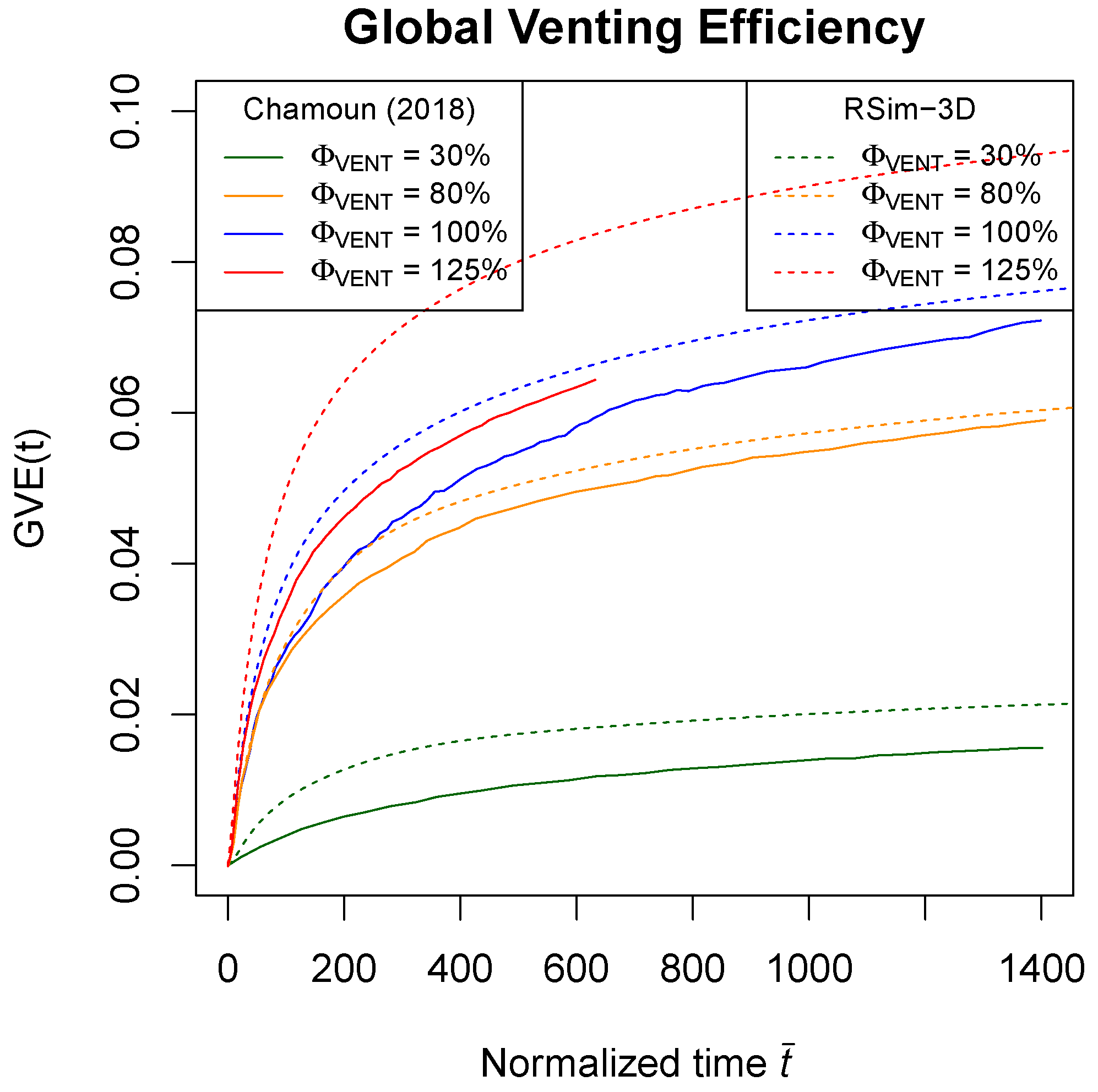
3.3. Venting
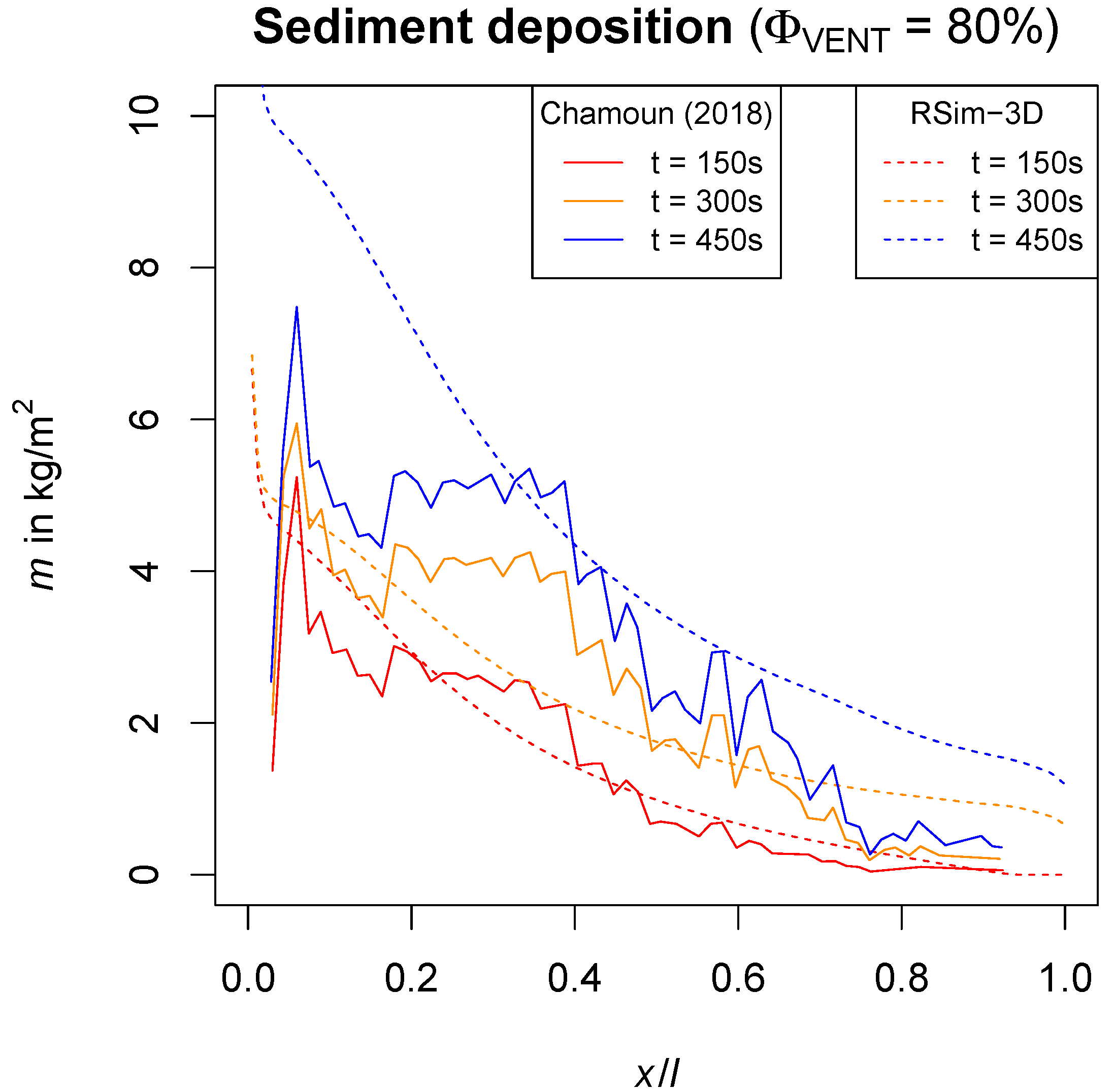
3.4. Sediment Deposition Along the Channel
4. Discussion
4.1. Code Verification and Validation
4.2. Mesh Sensitivity Analysis and Quantitative Error Analysis
4.3. Venting
4.4. Applicability of the Code to Real Reservoirs
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Abbreviations
| CFD | computational fluid dynamics |
| GVE | global venting efficiency |
| VENT | venting |
References
- Hauer, C.; Wagner, B.; Aigner, J.; Holzapfel, P.; Flödl, P.; Liedermann, M.; Tritthart, M.; Sindelar, C.; Pulg, U.; Klösch, M.; et al. State of the art, shortcomings and future challenges for a sustainable sediment management in hydropower: A review. Renew. Sustain. Energy Rev. 2018, 98, 40–55. [Google Scholar] [CrossRef]
- Esmaeili, T.; Sumi, T.; Kantoush, S.A.; Kubota, Y.; Haun, S.; Ruther, N. Three-Dimensional Numerical Study of Free-Flow Sediment Flushing to Increase the Flushing Efficiency: A Case-Study Reservoir in Japan. Water 2017, 9, 900. [Google Scholar] [CrossRef]
- Chamoun, S.; De Cesare, G.; Schleiss, A.J. Managing reservoir sedimentation by venting turbidity currents: A review. Int. J. Sediment Res. 2016, 31, 195–204. [Google Scholar] [CrossRef]
- Boes, R.; Auel, C.; Müller-Hagmann, M.; Albayrak, I. Sediment bypass tunnels to mitigate reservoir sedimentation and restore sediment continuity. In Reservoir Sedimentation; Taylor & Francis Group: London, UK, 2014; pp. 221–228. [Google Scholar] [CrossRef]
- Habersack, H.; Bogner, K.; Schneider, J.; Brauner, M. Catchment-Wide Analysis of the Sediment Regime with Respect to Reservoir Sedimentation. Int. J. Sediment Res. 2000, 16, 159–169. [Google Scholar]
- Omelan, M.; Visscher, J.; Rüther, N.; Stokseth, S. Sediment management for sustainable hydropower development. In Proceedings of the 13th International Symposium on River Sedimentation (ISRS 2016), Stuttgart, Germany, 19–22 September 2016; Wieprecht, S., Haun, S., Weber, K., Noack, M., Terheiden, K., Eds.; CRC Press Taylor & Francis Group: London, UK, 2017; pp. 1132–1140. [Google Scholar]
- De Cesare, G.; Schleiss, A.; Hermann, F. Impact of turbidity currents on reservoir sedimentation. J. Hydraul. Eng. 2001, 127, 6–16. [Google Scholar] [CrossRef]
- Necker, F.; Härtel, C.; Kleiser, L.; Meiburg, E. High-resolution simulations of particle-driven gravity currents. Int. J. Multiph. Flow 2002, 28, 279–300. [Google Scholar] [CrossRef]
- Georgoulas, A.; Angelidis, P.; Panagiotidis, T.; Kotsovinos, N. 3D Numerical modelling of turbidity currents. Environ. Fluid Mech. 2010, 10, 603–635. [Google Scholar] [CrossRef]
- Huang, C.C.; Lin, W.C.; Ho, H.C.; Tan, Y.C. Estimation of Reservoir Sediment Flux through Bottom Outlet with Combination of Numerical and Empirical Methods. Water 2019, 11, 1353. [Google Scholar] [CrossRef]
- Lee, F.Z.; Lai, J.S.; Tan, Y.C.; Sung, C.C. Turbid density current venting through reservoir outlets. KSCE J. Civ. Eng. 2014, 18, 694–705. [Google Scholar] [CrossRef]
- Liu, L.; Wang, Y. Modelling Reservoir Turbidity Using Landsat 8 Satellite Imagery by Gene Expression Programming. Water 2019, 11, 1479. [Google Scholar] [CrossRef]
- Huppert, H.E.; Simpson, J.E. The slumping of gravity currents. J. Fluid Mech. 1980, 99, 785–799. [Google Scholar] [CrossRef]
- La Rocca, M.; Adduce, C.; Sciortino, G.; Pinzon, A. Experimental and numerical simulation of three-dimensional gravity currents on smooth and rough bottom. Phys. Fluids 2008, 20, 106603. [Google Scholar] [CrossRef]
- Musumeci, R.; Viviano, A.; Foti, E. Influence of Regular Surface Waves on the Propagation of Gravity Currents: Experimental and Numerical Modeling. J. Hydraul. Eng. 2017, 143. [Google Scholar] [CrossRef]
- Stancanelli, L.M.; Musumeci, R.E.; Foti, E. Dynamics of Gravity Currents in the Presence of Surface Waves. J. Geophys. Res. Ocean. 2018, 123, 2254–2273. [Google Scholar] [CrossRef]
- Fan, J.H. Experimental studies on density currents. Sci. Sin. 1960, 4, 275–303. [Google Scholar]
- Bonnecaze, R.T.; Huppert, H.E.; Lister, J.R. Particle-driven gravity currents. J. Fluid Mech. 1993, 250, 339–369. [Google Scholar] [CrossRef]
- Gladstone, C.; Phillips, J.C.; Sparks, R.S.J. Experiments on bidisperse, constant-volume gravity currents: Propagation and sediment deposition. Sedimentology 1998, 45, 833–843. [Google Scholar] [CrossRef]
- De Rooij, F.; Dalziel, S.B. Time- and Space-Resolved Measurements of Deposition under Turbidity Currents. In Particulate Gravity Currents; Blackwell Science Ltd.: Oxford, UK, 2001; pp. 207–215. [Google Scholar] [CrossRef]
- Baas, J.H.; Van Kesteren, W.; Postma, G. Deposits of depletive high-density turbidity currents: A flume analogue of bed geometry, structure and texture. Sedimentology 2004, 51, 1053–1088. [Google Scholar] [CrossRef]
- Sequeiros, O.; Naruse, H.; Endo, N.; Garcia, M.; Parker, G. Experimental study on self-accelerating turbidity currents. J. Geophys. Res. Ocean. 2009, 114. [Google Scholar] [CrossRef]
- Sequeiros, O.; Spinewine, B.; Beaubouef, R.; Sun, T.; Garcia, M.; Parker, G. Bedload transport and bed resistance associated with density and turbidity currents. Sedimentology 2010, 57, 1463–1490. [Google Scholar] [CrossRef]
- Chamoun, S.; De Cesare, G.; Schleiss, A.J. Venting of turbidity currents approaching a rectangular opening on a horizontal bed. J. Hydraul. Res. 2018, 56, 44–58. [Google Scholar] [CrossRef]
- Chamoun, S.; De Cesare, G.; Schleiss, A.J. Management of turbidity current venting in reservoirs under different bed slopes. J. Environ. Manag. 2017, 204, 519–530. [Google Scholar] [CrossRef] [PubMed]
- Chamoun, S.; De Cesare, G.; Schleiss, A.J. Influence of Operational Timing on the Efficiency of Venting Turbidity Currents. J. Hydraul. Eng. 2018, 144. [Google Scholar] [CrossRef]
- La Rocca, M.; Adduce, C.; Sciortino, G.; Pinzon, A.; Boniforti, M. A two-layer, shallow-water model for 3D gravity currents. J. Hydraul. Res. 2012, 50, 208–217. [Google Scholar] [CrossRef]
- La Rocca, M.; Prestininzi, P.; Adduce, C.; Sciortino, G.; Hinkelmann, R. Lattice Boltzmann simulation of 3D gravity currents around obstacles. Int. J. Offshore Polar Eng. 2013, 23, 178–185. [Google Scholar]
- An, S.; Julien, P.Y.; Venayagamoorthy, S.K. Numerical simulation of particle-driven gravity currents. Environ. Fluid Mech. 2012, 12, 495–513. [Google Scholar] [CrossRef]
- Stancanelli, L.; Musumeci, R.; Foti, E. Computational Fluid Dynamics for Modeling Gravity Currents in the Presence of Oscillatory Ambient Flow. Water 2018, 10, 635. [Google Scholar] [CrossRef]
- Cantero, M.I.; Balachandar, S.; García, M.H. An Eulerian–Eulerian model for gravity currents driven by inertial particles. Int. J. Multiph. Flow 2008, 34, 484–501. [Google Scholar] [CrossRef]
- An, S.; Julien, P.Y. Three-Dimensional Modeling of Turbid Density Currents in Imha Reservoir, South Korea. J. Hydraul. Eng. 2014, 140, 05014004. [Google Scholar] [CrossRef]
- Deltares. Delft3D-FLOW; Deltares: Delft, The Netherlands, 2014. [Google Scholar]
- Shields, A. Anwendung der Ähnlichkeitsmechanik und der Turbulenzforschung auf die Geschiebebewegung. In Mitteilungen der Preußischen Versuchsanstalt für Wasser- Erd- und Schiffbau; Preußische Versuchsanstalt für Wasser- Erd- und Schiffbau: Berlin, Germany, 1936. [Google Scholar]
- Cantero, M.; García, M.; Balachandar, S. Effect of particle inertia on the dynamics of depositional particulate density currents. Comput. Geosci. 2008, 34, 1307–1318. [Google Scholar] [CrossRef]
- Lavelli, A.; Boillat, J.J.; De Cesare, G. Numerical 3D modelling of the vertical mass exchange induced by turbidity currents in Lake Lugano (Switzerland). In Proceedings of the 5th International Conference on Hydro-Science and- Engineering (ICHE-2002), Warsaw, Poland, 18–21 September 2002. [Google Scholar]
- Hillebrand, G.; Klassen, I.; Olsen, N.R.B. 3D CFD modelling of velocities and sediment transport in the Iffezheim hydropower reservoir. Hydrol. Res. 2017, 48, 147–159. [Google Scholar] [CrossRef]
- NTNU—Norwegian University of Science and Technology. SSIIM. 2019. Available online: http://folk.ntnu.no/nilsol/ssiim/ (accessed on 18 January 2020).
- Olsen, N.R.B. SSIIM; Norwegian University of Science and Technology: Trondheim, Norway, 2018. [Google Scholar]
- Lai, Y.G. Two-Dimensional Depth-Averaged Flow Modeling with an Unstructured Hybrid Mesh. J. Hydraul. Eng. 2010, 136, 12–23. [Google Scholar] [CrossRef]
- Rouse, H. Modern conceptions of the mechanics of fluid turbulence. Trans. Am. Soc. Civ. Eng. 1937, 102, 463–505. [Google Scholar]
- Tritthart, M. Three-dimensional numerical modelling of turbulent river flow using polyhedral finite volumes. In Wiener Mitteilungen; Vienna University of Technology: Vienna, Austria, 2005; Volume 193. [Google Scholar]
- Tritthart, M.; Schober, B.; Liedermann, M.; Habersack, H. Development of an integrated sediment transport model and its application to the Danube River. In Proceedings of the 33rd IAHR Congress, Vancouver, BC, Canada, 9–14 August 2009; pp. 876–883. [Google Scholar]
- Tritthart, M.; Schober, B.; Habersack, H. Non-uniformity and layering in sediment transport modelling 1: Flume simulations. J. Hydraul. Res. 2011, 49, 325–334. [Google Scholar] [CrossRef]
- Tritthart, M.; Gutknecht, D. Three-Dimensional Simulation of Free-Surface Flows Using Polyhedral Finite Volumes. Eng. Appl. Comput. Fluid Mech. 2007, 1, 1–14. [Google Scholar] [CrossRef]
- Farhadi, A.; Mayrhofer, A.; Tritthart, M.; Glas, M.; Habersack, H. Accuracy and comparison of standard k-E with two variants of k- turbulence models in fluvial applications. Eng. Appl. Comput. Fluid Mech. 2018, 12, 216–235. [Google Scholar] [CrossRef]
- Launder, B.; Spalding, D. The numerical computation of turbulent flows. Comput. Methods Appl. Mech. Eng. 1974, 3, 269–289. [Google Scholar] [CrossRef]
- Atkinson, J.F.; Chakraborti, R.K.; VanBenschoten, J.E. Effects of Floc Size and Shape in Particle Aggregation. In Flocculation in Natural and Engineered Environmental Systems, 1st ed.; CRC Press: Boca Raton, FL, USA, 2004; Chapter 5; pp. 95–120. [Google Scholar]
- Van Rijn, L.C. Sediment Transport, Part II: Suspended Load Transport. J. Hydraul. Eng. 1984, 110, 1613–1641. [Google Scholar] [CrossRef]
- Tritthart, M.; Hauer, C.; Haimann, M.; Habersack, H. Three dimensional variability of suspended load transport in rivers and its ecological implications in terms of reservoir flushing and reservoir drawdown. In Proceedings of the 38th IAHR World Congress, Panama City, FL, USA, 1–6 September 2019; pp. 3568–3575. [Google Scholar] [CrossRef]
- Thonon, I.; Perk, M. Measuring suspended sediment characteristics using a LISST-ST in an embanked flood plain of the River Rhine. IAHS-AISH Publ. 2003, 283, 37–44. [Google Scholar]
- Glock, K.; Tritthart, M.; Habersack, H.; Hauer, C. Comparison of Hydrodynamics Simulated by 1D, 2D and 3D Models Focusing on Bed Shear Stresses. Water 2019, 11, 226. [Google Scholar] [CrossRef]
- Tritthart, M.; Liedermann, M.; Habersack, H. Modelling spatio-temporal flow characteristics in groyne fields. River Res. Appl. 2009, 25, 62–81. [Google Scholar] [CrossRef]
- Tritthart, M.; Liedermann, M.; Schober, B.; Habersack, H. Non-uniformity and layering in sediment transport modelling 2: River application. J. Hydraul. Res. 2011, 49, 335–344. [Google Scholar] [CrossRef]
- Haimann, M.; Hauer, C.; Tritthart, M.; Prenner, D.; Leitner, P.; Moog, O.; Habersack, H. Monitoring and modelling concept for ecological optimized harbour dredging and fine sediment disposal in large rivers. Hydrobiologia 2018, 814, 89–107. [Google Scholar] [CrossRef]
- Glas, M.; Glock, K.; Tritthart, M.; Liedermann, M.; Habersack, H. Hydrodynamic and morphodynamic sensitivity of a river’s main channel to groyne geometry. J. Hydraul. Res. 2018, 56, 714–726. [Google Scholar] [CrossRef]
- Tritthart, M.; Haimann, M.; Habersack, H.; Hauer, C. Spatio-temporal variability of suspended sediments in rivers and ecological implications of reservoir flushing operations. River Res. Appl. 2019, 35, 918–931. [Google Scholar] [CrossRef]
- Roache, P.J. Fundamentals of Verification and Validation; Hermosa Publishers: Socorro, NM, USA, 2009. [Google Scholar]
- Slater, J.W. Examining Spatial (Grid) Convergence. 2008. Available online: https://www.grc.nasa.gov/www/wind/valid/tutorial/spatconv.html (accessed on 20 December 2019).

| Δt | Meshes | 5vl10 | 3vl20 | 3vl30 | 2vl40 |
|---|---|---|---|---|---|
| horizontal spacing in cm | 5 | 3 | 3 | 2 | |
| s | number of vertical layers | 10 | 20 | 30 | 40 |
| total number of cells | 7280 | 42,160 | 63,240 | 172,200 | |
| 1.00 | max. Courant number | 2.2 | 4.7 | 7.2 | – |
| 0.50 | 1.2 | 2.5 | 3.9 | – | |
| 0.20 | 0.5 | 1.1 | 1.7 | 2.2 | |
| 0.10 | 0.3 | 0.5 | 0.8 | 1.1 | |
| 0.05 | 0.1 | 0.3 | 0.4 | 0.6 |
| Grain Size in µm | 67 | 80 | 90 | 110 | 140 | 150 | 160 | 214 |
|---|---|---|---|---|---|---|---|---|
| Stokes fall velocity Equation (2) in mm s−1 | 0.4 | 0.6 | 0.7 | 0.9 | 1.5 | 1.7 | 2.0 | 3.5 |
| volumetric fraction at inflow in ppm | 2328 | 2328 | 2328 | 4655 | 4655 | 2328 | 2328 | 2328 |
| share of total sediment in % | 10 | 10 | 10 | 20 | 20 | 10 | 10 | 10 |
| Δt | Meshes | 5vl10 | 3vl20 | 3vl30 | 2vl40 |
|---|---|---|---|---|---|
| horizontal spacing in cm | 5 | 3 | 3 | 2 | |
| s | number of vertical layers | 10 | 20 | 30 | 40 |
| total number of cells | 7280 | 42,160 | 63,240 | 172,200 | |
| 1.00 | Computation time in h | 0.5 | 12.8 | 17.0 | – |
| 0.50 | 0.6 | 10.8 | 17.7 | – | |
| 0.20 | 0.7 | 11.5 | 17.0 | 57.0 | |
| 0.10 | 0.7 | 12.1 | 17.5 | 60.7 | |
| 0.05 | 0.8 | 13.4 | 18.0 | 67.0 |
| Δts | 5vl10 | 3vl20 | 3vl30 | 2vl40 | 5vl10 | 3vl20 | 3vl30 | 2vl40 |
|---|---|---|---|---|---|---|---|---|
| Case | A | Case | D | |||||
| 1.00 | 0.515 | 0.315 | 0.224 | – | 0.405 | 0.245 | 0.128 | – |
| 0.50 | 0.396 | 0.216 | 0.110 | – | 0.309 | 0.145 | 0.049 | – |
| 0.20 | 0.318 | 0.127 | 0.035 | 0.017 | 0.237 | 0.072 | 0.017 | 0.021 |
| 0.10 | 0.282 | 0.091 | 0.018 | 0.011 | 0.213 | 0.051 | 0.013 | 0.024 |
| 0.05 | 0.273 | 0.077 | 0.013 | 0.011 | 0.230 | 0.049 | 0.011 | 0.022 |
| Case | G | Case | R | |||||
| 1.00 | 0.026 | 0.018 | 0.006 | – | 0.348 | 0.186 | 0.080 | – |
| 0.50 | 0.014 | 0.006 | 0.002 | – | 0.276 | 0.107 | 0.028 | – |
| 0.20 | 0.008 | 0.003 | 0.004 | 0.007 | 0.221 | 0.056 | 0.010 | 0.020 |
| 0.10 | 0.006 | 0.002 | 0.006 | 0.010 | 0.210 | 0.045 | 0.008 | 0.021 |
| 0.05 | 0.005 | 0.002 | 0.007 | 0.010 | 0.229 | 0.047 | 0.007 | 0.016 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wildt, D.; Hauer, C.; Habersack, H.; Tritthart, M. CFD Modelling of Particle-Driven Gravity Currents in Reservoirs. Water 2020, 12, 1403. https://doi.org/10.3390/w12051403
Wildt D, Hauer C, Habersack H, Tritthart M. CFD Modelling of Particle-Driven Gravity Currents in Reservoirs. Water. 2020; 12(5):1403. https://doi.org/10.3390/w12051403
Chicago/Turabian StyleWildt, Daniel, Christoph Hauer, Helmut Habersack, and Michael Tritthart. 2020. "CFD Modelling of Particle-Driven Gravity Currents in Reservoirs" Water 12, no. 5: 1403. https://doi.org/10.3390/w12051403
APA StyleWildt, D., Hauer, C., Habersack, H., & Tritthart, M. (2020). CFD Modelling of Particle-Driven Gravity Currents in Reservoirs. Water, 12(5), 1403. https://doi.org/10.3390/w12051403








