Evaluation of Uncertainty Intervals for Daily, Statistically Derived Streamflow Estimates at Ungaged Basins across the Continental U.S.
Abstract
:1. Introduction
2. Materials and Methods
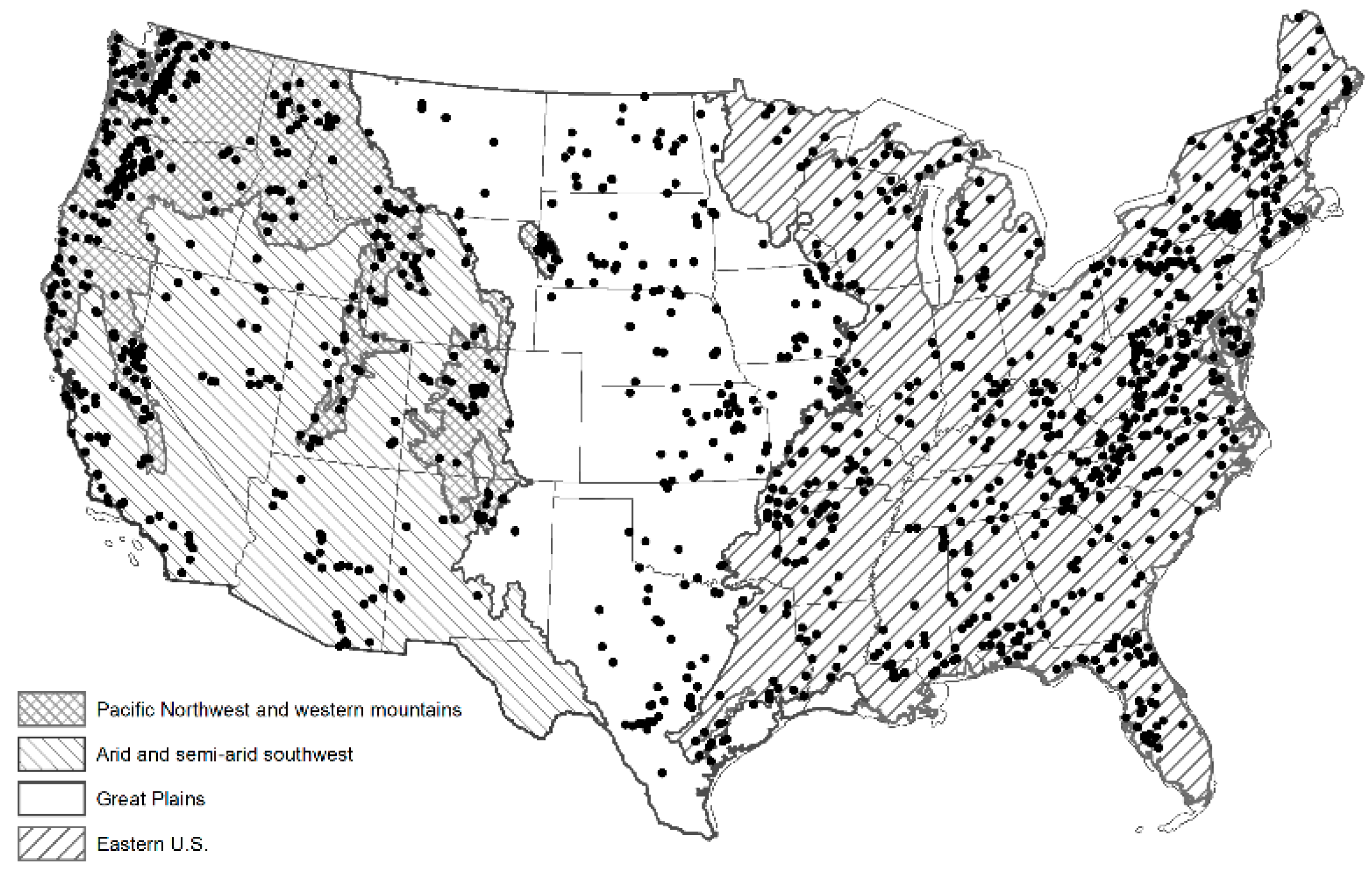
2.1. Study Area
2.2. Streamflow Estimation Methods
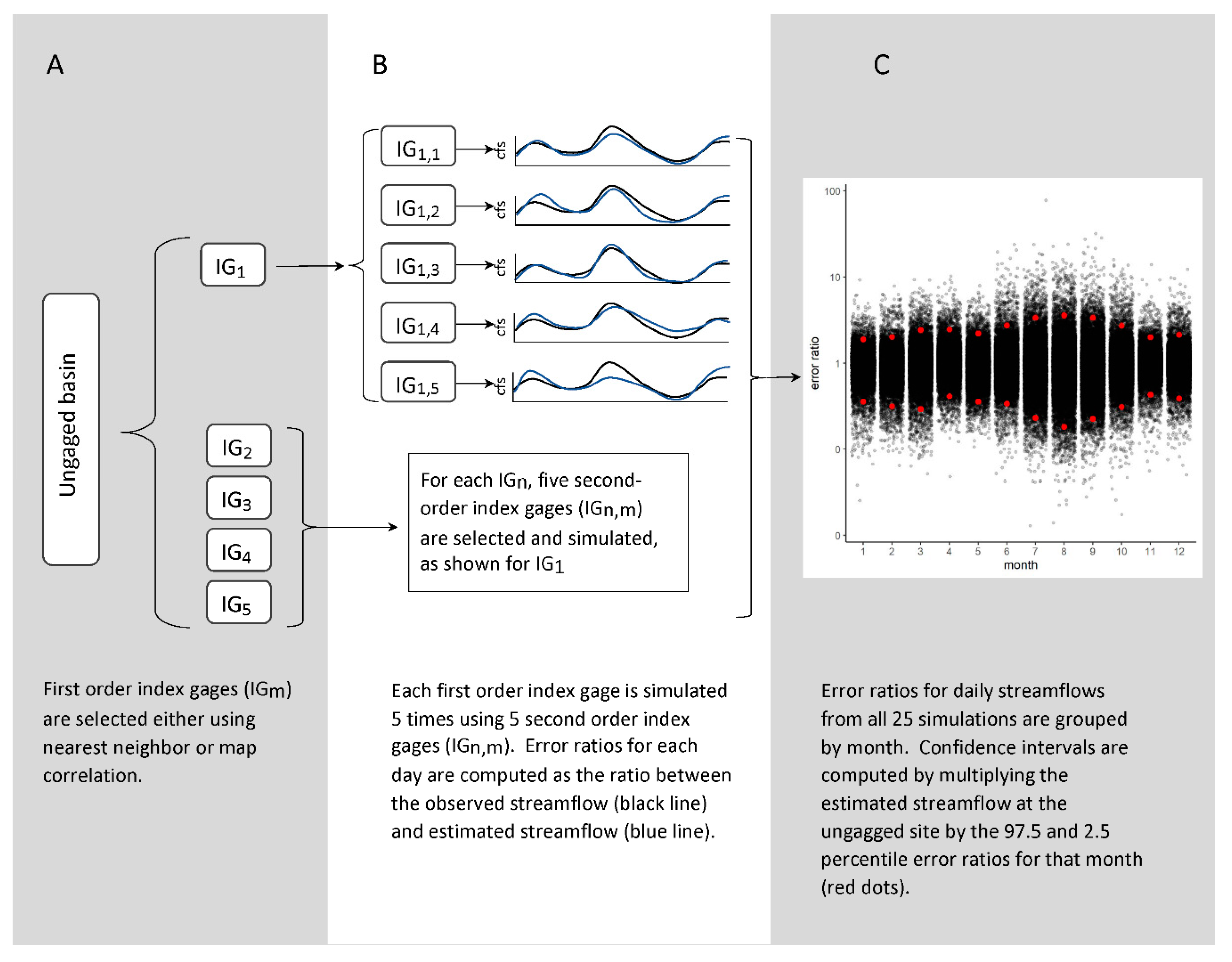
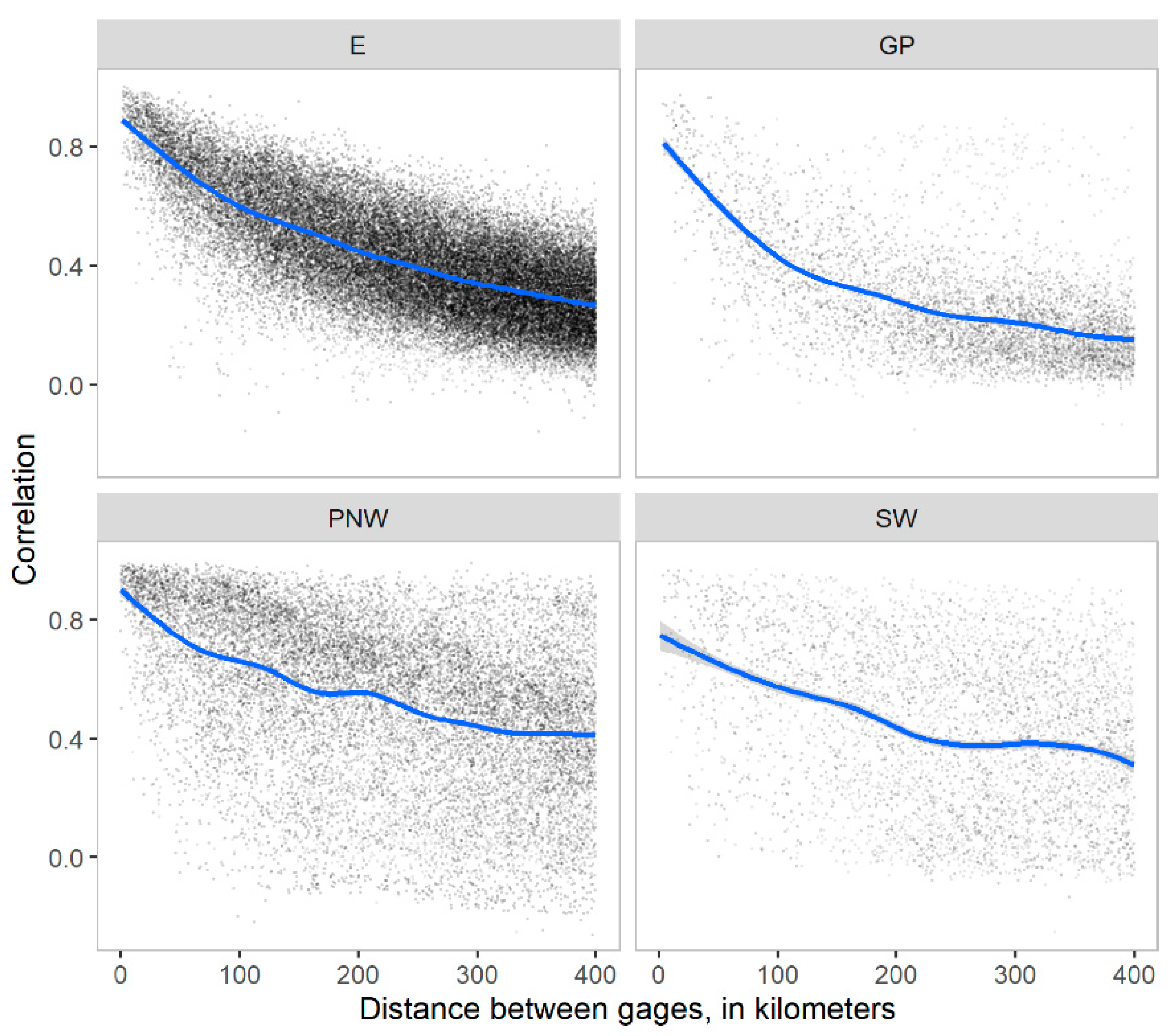
2.3. Index Gage Selection Methods
2.4. Uncertainty Characterization
2.5. Evaluation of Uncertainty Intervals
3. Results and Discussion
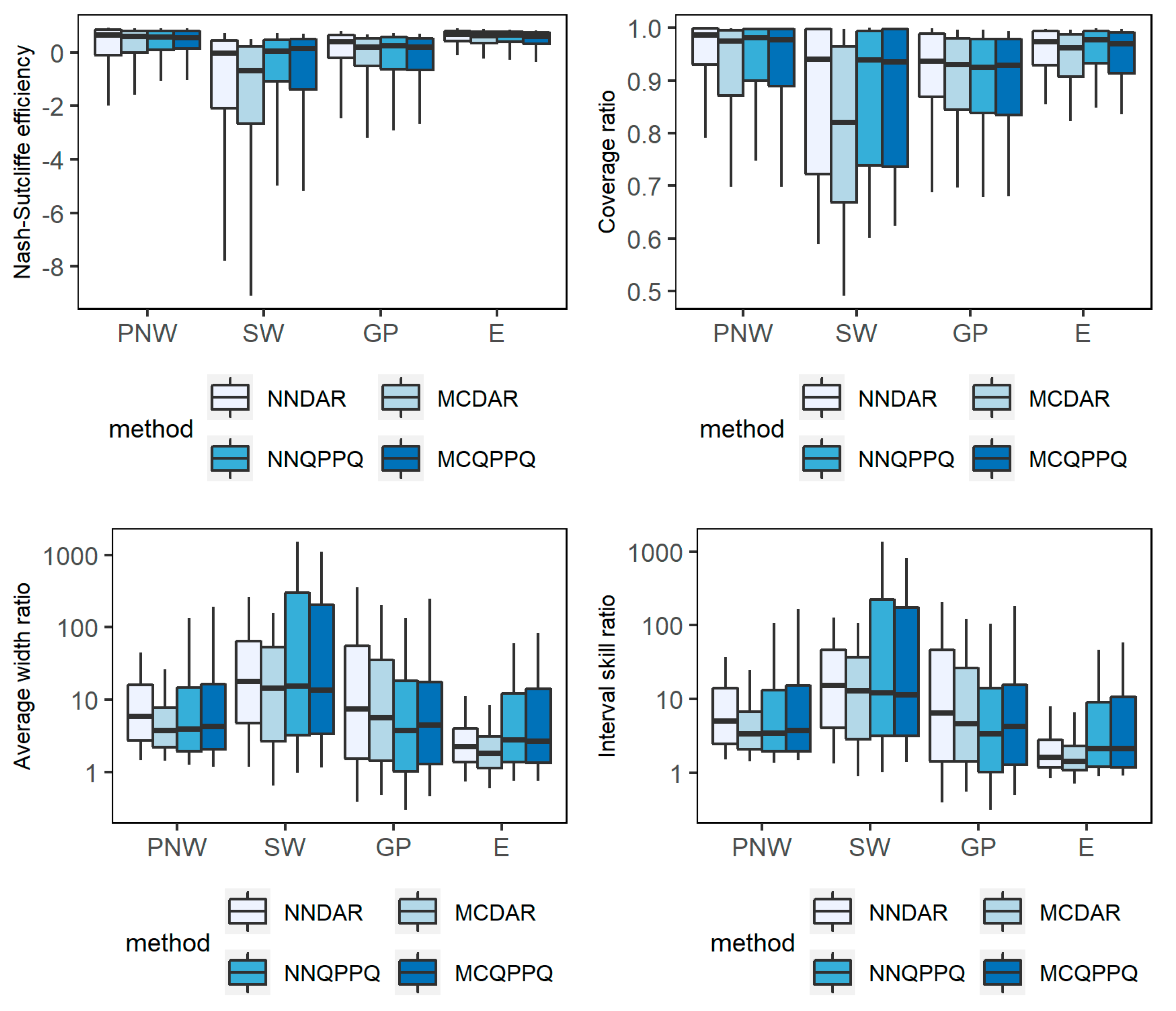
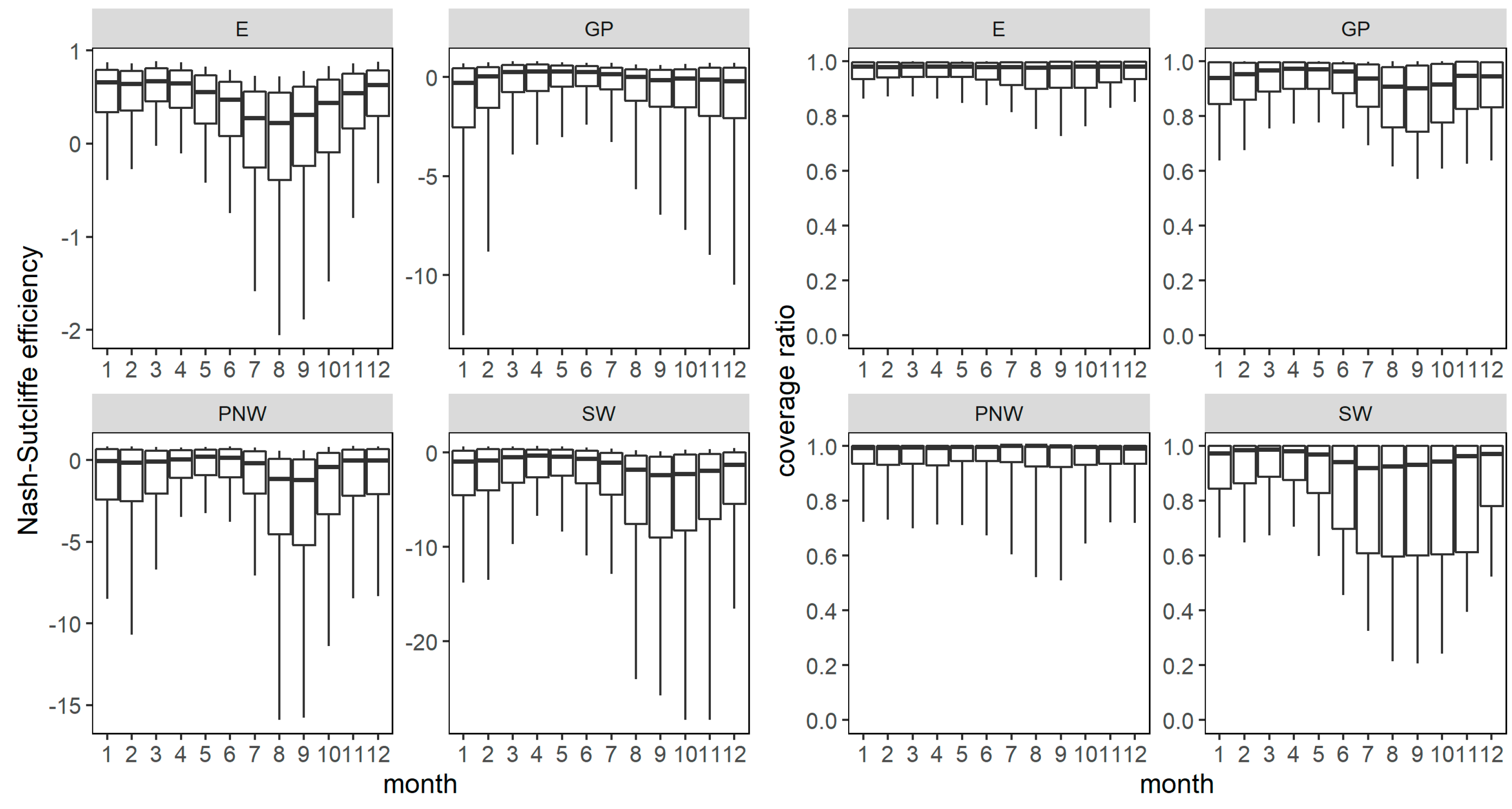
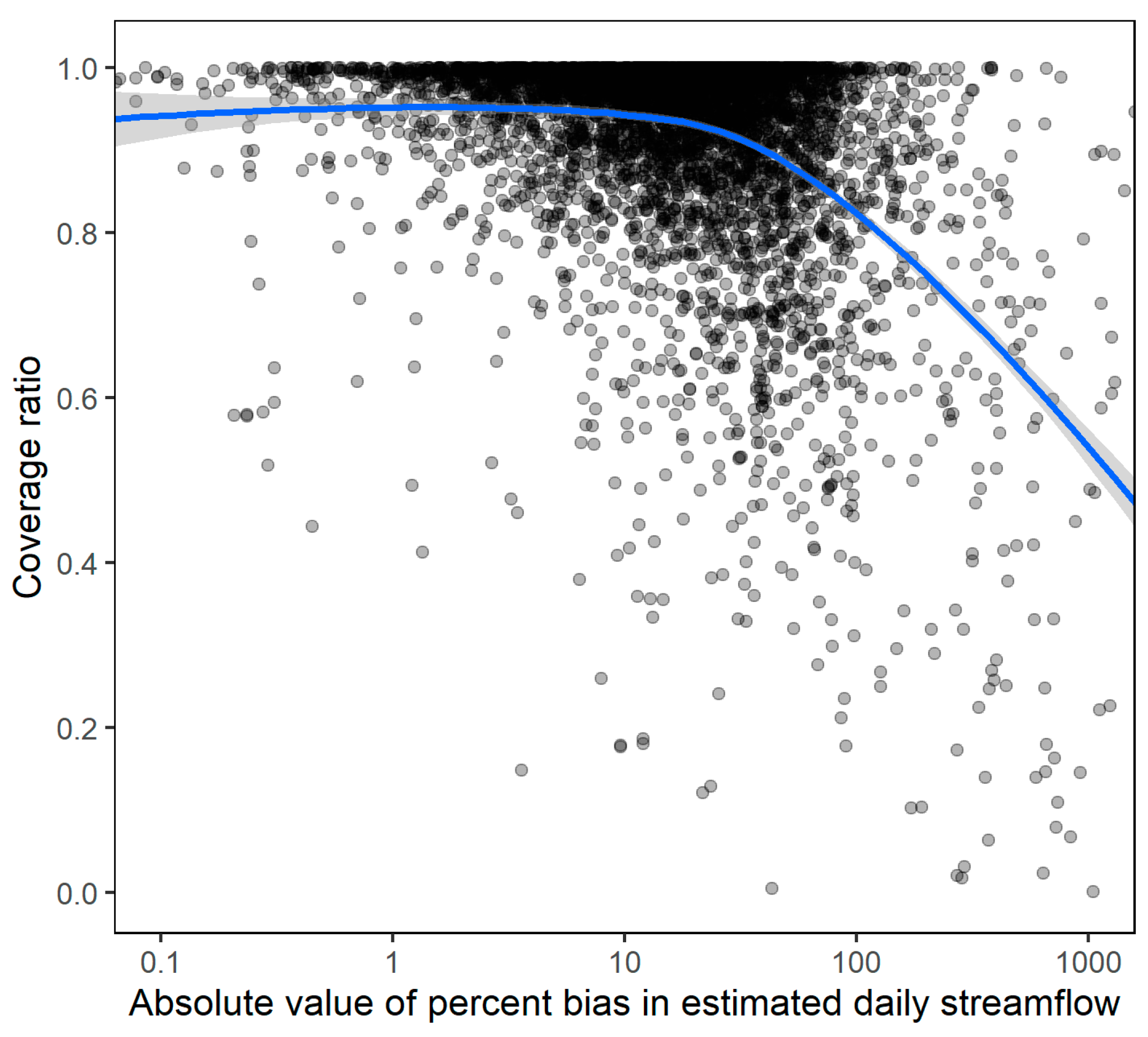
3.1. Reliability of Empirical Uncertainty Intervals
3.2. Interval Sharpness
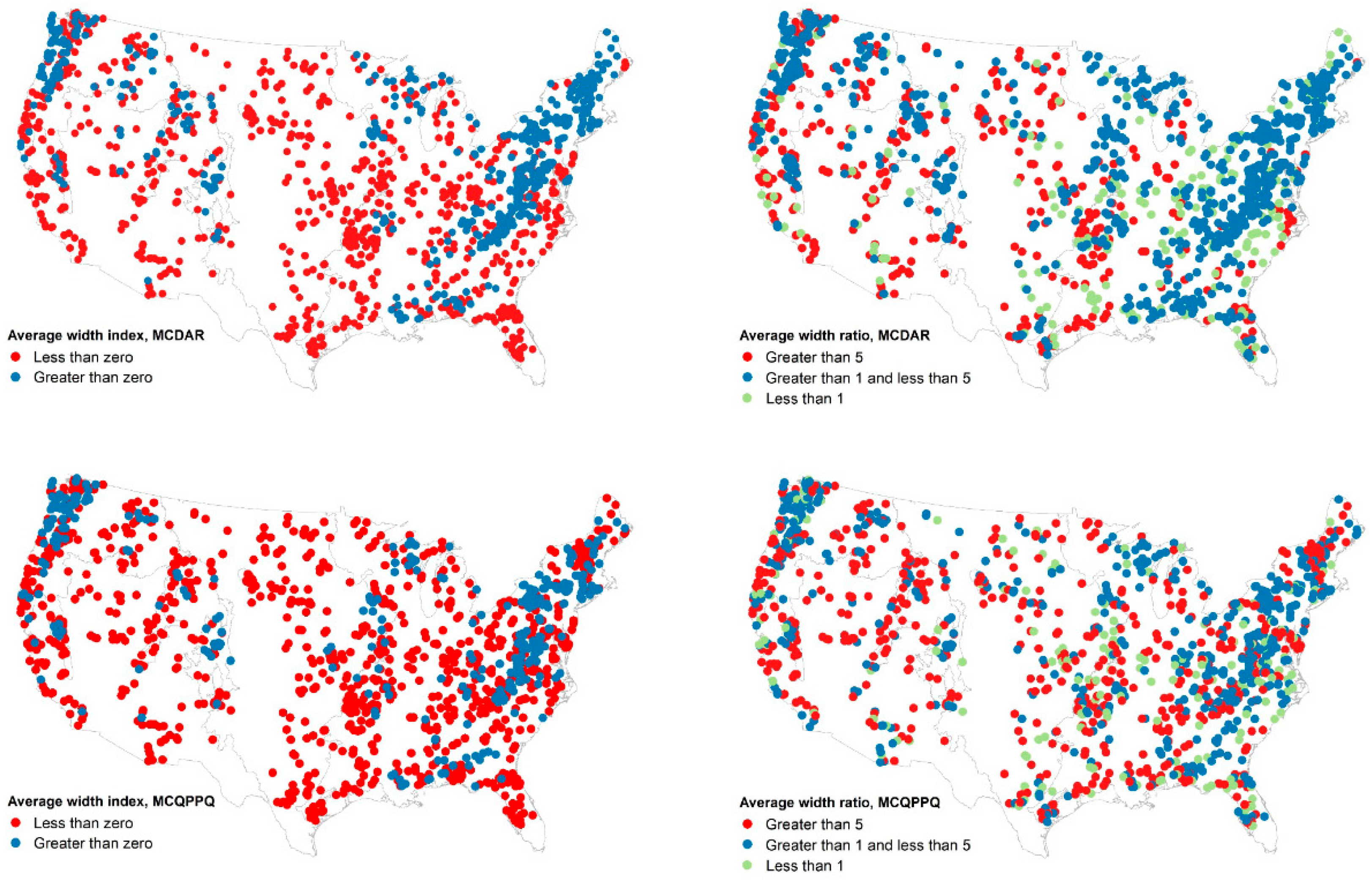
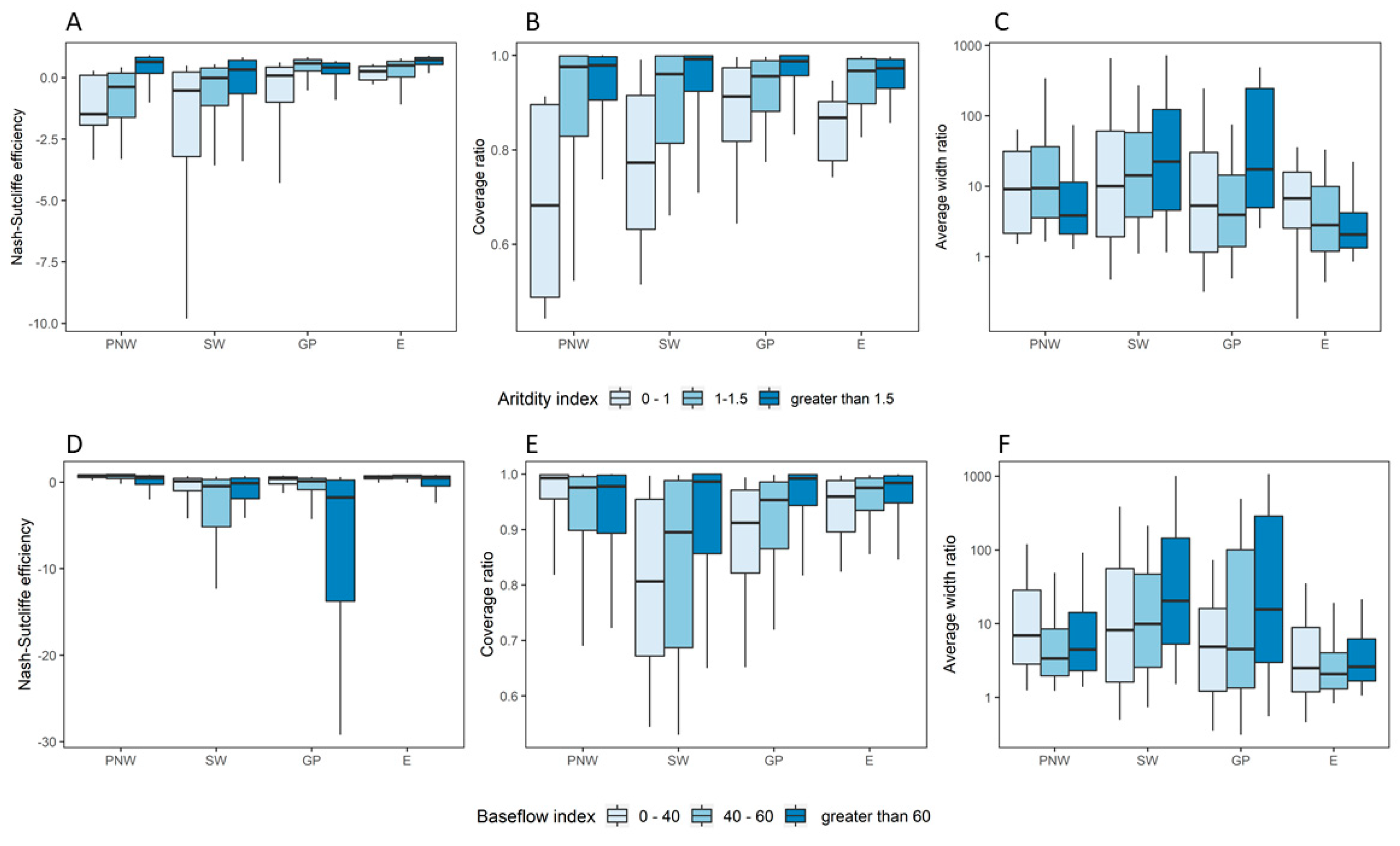
3.3. Sensitivity to Regional Factors
4. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Kennedy, K.; Lutz, K.; Hatfield, C.; Martin, L.; Barker, T.; Kennedy, K.; Palmer, R.; Detwiler, L.; Anleitner, J.; Hickey, J. The Connecticut River Flow Restoration Study: A Watershed-Scale Assessment of the Potential for Flow Restoration Through Dam Re-Operation; The Nature Conservancy, U.S. Army Corps of Engineers, and University of Massachusetts: Northampton, MA, USA, 2018. [Google Scholar]
- Poff, N.L.; Richter, B.D.; Arthington, A.H.; Bunn, S.E.; Naiman, R.J.; Kendy, E.; Acreman, M.; Apse, C.; Bledsoe, B.P.; Freeman, M.C.; et al. The ecological limits of hydrologic alteration (ELOHA): A new framework for developing regional environmental flow standards: Ecological limits of hydrologic alteration. Freshw. Biol. 2010, 55, 147–170. [Google Scholar] [CrossRef] [Green Version]
- Richter, B.D.; Mathews, R.; Harrison, D.L.; Wigington, R. Ecologically sustainable water management: Managing river flows for ecological integrity. Ecol. Appl. 2003, 13, 206–224. [Google Scholar] [CrossRef]
- Weiskel, P.K.; Brandt, S.L.; DeSimone, L.A.; Ostiguy, L.J.; Archfield, S.A. Indicators of Streamflow Alteration, Habitat Fragmentation, Impervious Cover, and Water Quality for Massachusetts Stream Basins; Scientific Investigagions Report 2009-5272; U.S. Geological Survey: Reston, VA, USA, 2009. [Google Scholar]
- Shu, C.; Ouarda, T.B.M.J. Improved methods for daily streamflow estimates at ungauged sites. Water Resour. Res. 2012, 48. [Google Scholar] [CrossRef]
- Hirsch, R.M. An evaluation of some record reconstruction techniques. Water Resour. Res. 1979, 15, 1781–1790. [Google Scholar] [CrossRef]
- Gianfagna, C.C.; Johnson, C.E.; Chandler, D.G.; Hofmann, C. Watershed area ratio accurately predicts daily streamflow in nested catchments in the Catskills, New York. J. Hydrol. Reg. Stud. 2015, 4, 583–594. [Google Scholar] [CrossRef] [Green Version]
- Asquith, W.H.; Roussel, M.C.; Vrable, J. Statewide Analysis of the Drainage-Area Ratio Method for 34 Streamflow Percentile Ranges in Texas; Scientific Investigations Report 2006-5286; U.S. Geological Survey: Reston, VA, USA, 2006; p. 34. [Google Scholar]
- Emerson, D.G.; Vecchia, A.V.; Dahl, A.L. Evaluation of Drainage Area Ratio Method Used to Estimate Streamflow for the Red River of the North Basin, North Dakota and Minnesota; Scientific Investigations Report; U.S. Geological Survey: Reston, VA, USA, 2005; p. 13. [Google Scholar]
- Ries III, K.G.; Friesz, P.J. Methods for Estimating Low-Flow Statistics for Massachusetts Streams; Water-Resources Investigations Report 00-4135; U.S. Geological Survey: Reston, VA, USA, 2000. [Google Scholar]
- Fennessey, N.M. A Hydro-Climatological Model of Daily Streamflow for the Northeast United States. Ph.D. Thesis, Tufts University, Medford, MA, USA, 1994. [Google Scholar]
- Smakhtin, V.Y. Generation of natural daily flow time-series in regulated rivers using a non-linear spatial interpolation technique. Regul. Rivers Res. Manag. 1999, 15, 311–323. [Google Scholar] [CrossRef]
- Mohamoud, Y.M. Prediction of daily flow duration curves and streamflow for ungauged catchments using regional flow duration curves. Hydrol. Sci. J. 2008, 53, 706–724. [Google Scholar] [CrossRef]
- Archfield, S.A.; Vogel, R.M.; Steeves, P.A.; Brandt, S.L.; Weiskel, P.K.; Garabedian, S.P. The Massachusetts Sustainable-Yield Estimator: A Decision-Support Tool to Assess Water Availability at Ungaged Stream Locations in Massachusetts; Scientific Investigations Report 2009-5227; U.S. Geological Survey: Reston, VA, USA, 2010. [Google Scholar]
- Lorenz, D.L.; Ziegeweid, J.R. Methods to Estimate Historical Daily Streamflow for Ungaged Stream Locations in Minnesota; Scientific Investigations Report 2015-5181; U.S. Geological Survey: Reston, VA, USA, 2016. [Google Scholar]
- Gazoorian, C.L. Estimation of Unaltered Daily Mean Streamflow at Ungaged Streams of New York, Excluding Long Island, Water Years 1961–2010; Scientific Investigations Rerpot 2014-5220; U.S. Geological Survey: Reston, VA, USA, 2015; p. 29. [Google Scholar]
- Stuckey, M.H.; Koerkle, E.H.; Ulrich, J.E. Estimation of Baseline Daily Mean Streamflows for Ungaged Locations on Pennsylvania Streams, Water Years 1960-2008; Scientific Investigations Report; U.S. Geological Survey: Reston, VA, USA, 2012; p. 68. [Google Scholar]
- Nash, J.E.; Sutcliffe, J.V. River flow forecasting through conceptual models part I—A discussion of principles. J. Hydrol. 1970, 10, 282–290. [Google Scholar] [CrossRef]
- Fry, L.M.; Hunter, T.S.; Phanikumar, M.S.; Fortin, V.; Gronewold, A.D. Identifying streamgage networks for maximizing the effectiveness of regional water balance modeling: Identifying Gage Networks. Water Resour. Res. 2013, 49, 2689–2700. [Google Scholar] [CrossRef]
- Bourgin, F.; Andréassian, V.; Perrin, C.; Oudin, L. Transferring global uncertainty estimates from gauged to ungauged catchments. Hydrol. Earth Syst. Sci. 2015, 19, 2535–2546. [Google Scholar] [CrossRef]
- Farmer, W.H.; Levin, S. Characterizing Uncertainty in Daily Streamflow Estimates at Ungauged Locations for the Massachusetts Sustainable Yield Estimator. J. Am. Water Resour. Assoc. 2018, 54, 198–210. [Google Scholar] [CrossRef]
- Falcone, J.A.U.S. Geological Survey GAGES-II Time Series Data from Consistent Sources of Land Use, Water Use, Agriculture, Timber Activities, Dam Removals, and Other Historical Anthropogenic Influences; U.S. Geological Survey: Reston, VA, USA, 2017. [Google Scholar]
- Levin, S.B. Performance Metrics for 95-Percent Confidence Intervals of Estimated Daily Streamflow Using Four Transfer-Based Simulation Methods Across the Continental U.S.; U.S. Geological Survey Data Release. Available online: https://www.sciencebase.gov/catalog/item/5e861895e4b01d50927fb74a (accessed on 1 May 2020).
- Over, T.M.; Farmer, W.H.; Russell, A.M. Refinement of a Regression-Based Method for Prediction of Flow-Duration Curves of Daily Streamflow in the Conterminous United States; Scientific Investigations Report 2018-5072; U.S. Geological Survey: Reston, VA, USA, 2018; p. 44. [Google Scholar]
- Archfield, S.A.; Vogel, R.M. Map correlation method: Selection of a reference streamgage to estimate daily streamflow at ungaged catchments. Water Resour. Res. 2010, 46. [Google Scholar] [CrossRef]
- Andréassian, V.; Lerat, J.; Le Moine, N.; Perrin, C. Neighbors: Nature’s own hydrological models. J. Hydrol. 2012, 414–415, 49–58. [Google Scholar]
- Bock, A.R.; Farmer, W.H.; Hay, L.E. Quantifying uncertainty in simulated streamflow and runoff from a continental-scale monthly water balance model. Adv. Water Resour. 2018, 122, 166–175. [Google Scholar] [CrossRef]
- Gneiting, T.; Raftery, A.E. Strictly Proper Scoring Rules, Prediction, and Estimation. J. Am. Stat. Assoc. 2007, 102, 359–378. [Google Scholar] [CrossRef]
- US Environmental Protection Agency, Office of Research and Development. Ecoregions of North America. Available online: https://www.epa.gov/eco-research/ecoregions-north-america (accessed on 16 March 2020).
- Moriasi, D.N.; Arnold, J.G.; Van Liew, M.W.; Bingner, R.L.; Harmel, R.D.; Veith, T.L. Model Evaluation Guidelines for Systematic Quantification of Accuracy in Watershed Simulations. Trans. ASABE 2007, 50, 885–900. [Google Scholar] [CrossRef]
- Adams, D.K.; Comrie, A.C. The North American Monsoon. Bull. Am. Meteorol. Soc. 1997, 78, 2197–2214. [Google Scholar] [CrossRef] [Green Version]
- Patil, S.; Stieglitz, M. Controls on hydrologic similarity: Role of nearby gauged catchments for prediction at an ungauged catchment. Hydrol. Earth Syst. Sci. 2012, 16, 551–562. [Google Scholar] [CrossRef] [Green Version]
- Singh, R.; Archfield, S.A.; Wagener, T. Identifying dominant controls on hydrologic parameter transfer from gauged to ungauged catchments—A comparative hydrology approach. J. Hydrol. 2014, 517, 985–996. [Google Scholar] [CrossRef]
- Middleton, N.; Thomas, D. World Atlas of Desertification; UNEP: Nairobi, Kenya, 1997; ISBN 0340691662. [Google Scholar]
| Metric | Region | Number of Sites | Quantiles of Metrics for NNDAR | Quantiles of Metrics for MCDAR | ||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 1% | 5% | 25% | 50% | 75% | 95% | 99% | 1% | 5% | 25% | 50% | 75% | 95% | 99% | |||
| NSE | PNW | 319 | −10 | −4.2 | −0.14 | 0.65 | 0.85 | 0.94 | 0.98 | −10 | −3.5 | −0.01 | 0.59 | 0.80 | 0.94 | 0.97 |
| SW | 123 | −44 | −16 | −2.2 | −0.02 | 0.46 | 0.82 | 0.91 | −63 | −21 | −2.7 | −0.68 | 0.23 | 0.72 | 0.82 | |
| GP | 161 | −25 | −8.7 | −0.19 | 0.40 | 0.66 | 0.84 | 0.86 | −81 | −11 | −0.52 | 0.21 | 0.53 | 0.78 | 0.85 | |
| E | 728 | −7.8 | −0.99 | 0.43 | 0.68 | 0.81 | 0.93 | 0.97 | −5.9 | −1.1 | 0.34 | 0.63 | 0.77 | 0.90 | 0.94 | |
| CR | PNW | 319 | 0.44 | 0.64 | 0.93 | 0.99 | 1.0 | 1.0 | 1.0 | 0.10 | 0.49 | 0.87 | 0.97 | 1.0 | 1.0 | 1.0 |
| SW | 123 | 0.15 | 0.46 | 0.72 | 0.94 | 1.0 | 1.0 | 1.0 | 0.11 | 0.35 | 0.67 | 0.82 | 0.96 | 1.0 | 1.0 | |
| GP | 161 | 0.25 | 0.58 | 0.87 | 0.94 | 0.99 | 1.0 | 1.0 | 0.11 | 0.60 | 0.85 | 0.93 | 0.98 | 1.0 | 1.0 | |
| E | 728 | 0.64 | 0.79 | 0.93 | 0.97 | 0.99 | 1.0 | 1.0 | 0.57 | 0.75 | 0.91 | 0.96 | 0.99 | 1.0 | 1.0 | |
| AWR | PNW | 319 | 0.16 | 0.91 | 2.7 | 5.8 | 16 | 93 | 1760 | 0.32 | 1.1 | 2.2 | 3.7 | 7.8 | 107 | 626 |
| SW | 123 | 0.18 | 0.68 | 4.7 | 18 | 65 | 528 | 2080 | 0.05 | 0.25 | 2.7 | 14 | 54 | 449 | 6850 | |
| GP | 161 | 0.02 | 0.23 | 1.1 | 7.4 | 55 | 558 | 3110 | 0.02 | 0.24 | 1.4 | 5.6 | 35 | 781 | 17,100 | |
| E | 728 | 0.08 | 0.33 | 1.4 | 2.2 | 4.0 | 25 | 186 | 0.07 | 0.20 | 1.1 | 1.8 | 3.1 | 18 | 113 | |
| ISR | PNW | 319 | 0.30 | 1.2 | 2.4 | 5.1 | 14 | 65 | 1470 | 0.63 | 1.2 | 2.06 | 3.3 | 6.7 | 82 | 559 |
| SW | 123 | 0.31 | 0.83 | 4.0 | 15 | 47 | 317 | 1930 | 0.06 | 0.38 | 2.8 | 13 | 38 | 304 | 5070 | |
| GP | 161 | 0.02 | 0.23 | 1.4 | 6.5 | 46 | 484 | 1950 | 0.02 | 0.24 | 1.4 | 4.6 | 26 | 492 | 2840 | |
| E | 728 | 0.08 | 0.36 | 1.2 | 1.6 | 2.8 | 19 | 104 | 0.07 | 0.23 | 1.1 | 1.4 | 2.3 | 14 | 51 | |
| AWI | PNW | 319 | −434 | −40 | −5.8 | −1.1 | 0.25 | 0.64 | 0.75 | −287 | −59 | −1.6 | −0.22 | 0.40 | 0.69 | 0.79 |
| SW | 123 | −1590 | −714 | −75 | −18 | −5.7 | 0.07 | 0.36 | −9000 | −1480 | −62 | −13 | −1.7 | 0.34 | 0.69 | |
| GP | 161 | −3380 | −819 | −121 | −24 | −6.6 | −1.1 | 0.43 | −21,800 | −1510 | −103 | −28 | −6.7 | −0.28 | 0.63 | |
| E | 728 | −104 | −35 | −2.4 | −0.12 | 0.3 | 0.55 | 0.64 | −99 | −35 | −2.1 | −0.02 | 0.39 | 0.62 | 0.70 | |
| ISS | PNW | 319 | −340 | −27 | −3.5 | −0.45 | 0.39 | 0.70 | 0.78 | −211 | −36 | −1.4 | 0.06 | 0.49 | 0.74 | 0.79 |
| SW | 123 | −1100 | −204 | −27 | −9.2 | −2.5 | 0.23 | 0.51 | −3280 | −388 | −23 | −5.3 | −1.1 | 0.35 | 0.62 | |
| GP | 161 | −1960 | −413 | −46 | −8.8 | −1.9 | 0.13 | 0.53 | −3830 | −607 | −32 | −10 | −1.9 | 0.28 | 0.66 | |
| E | 728 | −48 | −14 | −0.81 | 0.30 | 0.55 | 0.69 | 0.75 | −49 | −16 | −0.77 | 0.28 | 0.56 | 0.72 | 0.77 | |
| NSE | PNW | 319 | −9.1 | −2.6 | 0.08 | 0.57 | 0.80 | 0.92 | 0.95 | −9.3 | −3.1 | 0.15 | 0.56 | 0.81 | 0.91 | 0.96 |
| SW | 123 | −18 | −9.5 | −1.2 | 0.06 | 0.49 | 0.83 | 0.87 | −16 | −9.6 | −1.5 | 0.14 | 0.49 | 0.80 | 0.84 | |
| GP | 161 | −47 | −7.2 | −0.63 | 0.26 | 0.57 | 0.82 | 0.86 | −29 | −7.6 | −0.66 | 0.20 | 0.53 | 0.76 | 0.84 | |
| E | 728 | −4.0 | −0.97 | 0.40 | 0.64 | 0.78 | 0.89 | 0.93 | −3.9 | −1.2 | 0.33 | 0.61 | 0.75 | 0.87 | 0.92 | |
| CR | PNW | 319 | 0.38 | 0.62 | 0.90 | 0.98 | 1.0 | 1.0 | 1.0 | 0.26 | 0.54 | 0.89 | 0.98 | 1.0 | 1.0 | 1.0 |
| SW | 123 | 0.34 | 0.51 | 0.73 | 0.94 | 0.99 | 1.0 | 1.0 | 0.45 | 0.57 | 0.73 | 0.94 | 1.0 | 1.0 | 1.0 | |
| GP | 161 | 0.39 | 0.64 | 0.84 | 0.92 | 0.98 | 1.0 | 1.0 | 0.42 | 0.60 | 0.84 | 0.93 | 0.98 | 1.0 | 1.0 | |
| E | 728 | 0.41 | 0.79 | 0.93 | 0.98 | 0.99 | 1.0 | 1.0 | 0.38 | 0.75 | 0.91 | 0.97 | 0.99 | 1.0 | 1.0 | |
| AWR | PNW | 319 | 0.45 | 0.88 | 1.9 | 3.9 | 15 | 788 | 5380 | 0.42 | 0.82 | 2.03 | 4.2 | 17 | 1400 | 37,600 |
| SW | 123 | 0.22 | 0.38 | 3.1 | 15 | 373 | 3200 | 27,400 | 0.17 | 0.46 | 3.23 | 14 | 220 | 3260 | 32,800 | |
| GP | 161 | 0.06 | 0.15 | 1.0 | 3.7 | 18 | 739 | 26,900 | 0.03 | 0.30 | 1.3 | 4.5 | 18 | 1090 | 22,400 | |
| E | 728 | 0.11 | 0.41 | 1.34 | 2.7 | 12 | 217 | 966 | 0.15 | 0.45 | 1.3 | 2.7 | 14 | 247 | 815 | |
| ISR | PNW | 319 | 0.93 | 1.2 | 2.0 | 3.4 | 14 | 647 | 3820 | 0.93 | 1.2 | 2.0 | 3.7 | 15 | 1170 | 29,000 |
| SW | 123 | 0.23 | 0.44 | 3.1 | 12 | 228 | 1890 | 26,500 | 0.20 | 0.49 | 3.1 | 11 | 186 | 1870 | 26,100 | |
| GP | 161 | 0.09 | 0.20 | 1.0 | 3.4 | 14 | 637 | 23,700 | 0.04 | 0.32 | 1.23 | 4.3 | 15 | 892 | 5750 | |
| E | 728 | 0.12 | 0.51 | 1.2 | 2.1 | 9.0 | 128 | 809 | 0.20 | 0.61 | 1.2 | 2.1 | 11 | 192 | 612 | |
| AWI | PNW | 319 | −1540 | −482 | −4.8 | −0.55 | 0.35 | 0.67 | 0.75 | −13,100 | −826 | −6.3 | −0.69 | 0.35 | 0.69 | 0.79 |
| SW | 123 | −29,200 | −3360 | −414 | −22 | −3.8 | 0.29 | 0.51 | −15,000 | −3800 | −371 | −30 | −5.8 | 0.09 | 0.63 | |
| GP | 161 | −45,700 | −2260 | −88 | −16 | −3.9 | −0.22 | 0.60 | −42,000 | −2060 | −127 | −27 | −4.7 | 0.15 | 0.70 | |
| E | 728 | −635 | −138 | −9.6 | −0.96 | 0.22 | 0.57 | 0.67 | −621 | −216 | −13 | −1.1 | 0.18 | 0.58 | 0.66 | |
| ISS | PNW | 319 | −1090 | −281 | −3.3 | −0.13 | 0.45 | 0.71 | 0.76 | −8670 | −508 | −4.2 | −0.32 | 0.43 | 0.70 | 0.77 |
| SW | 123 | −23,800 | −1500 | −151 | −9.0 | −1.6 | 0.61 | 0.70 | −12,000 | −1270 | −134 | −17 | −1.7 | 0.43 | 0.60 | |
| GP | 161 | −20,900 | −576 | −31 | −5.6 | −0.84 | 0.43 | 0.56 | −9300 | −824 | −45 | −9.9 | −1.2 | 0.40 | 0.55 | |
| E | 728 | −316 | −73 | −4.8 | −0.17 | 0.49 | 0.69 | 0.75 | −286 | −111 | −6.3 | −0.25 | 0.44 | 0.68 | 0.75 | |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Levin, S.B.; Farmer, W.H. Evaluation of Uncertainty Intervals for Daily, Statistically Derived Streamflow Estimates at Ungaged Basins across the Continental U.S. Water 2020, 12, 1390. https://doi.org/10.3390/w12051390
Levin SB, Farmer WH. Evaluation of Uncertainty Intervals for Daily, Statistically Derived Streamflow Estimates at Ungaged Basins across the Continental U.S. Water. 2020; 12(5):1390. https://doi.org/10.3390/w12051390
Chicago/Turabian StyleLevin, Sara B., and William H. Farmer. 2020. "Evaluation of Uncertainty Intervals for Daily, Statistically Derived Streamflow Estimates at Ungaged Basins across the Continental U.S." Water 12, no. 5: 1390. https://doi.org/10.3390/w12051390
APA StyleLevin, S. B., & Farmer, W. H. (2020). Evaluation of Uncertainty Intervals for Daily, Statistically Derived Streamflow Estimates at Ungaged Basins across the Continental U.S. Water, 12(5), 1390. https://doi.org/10.3390/w12051390





