1. Introduction
A number of engineering activities on geological formations (e.g., enhanced oil recovery, soil remediation, drilling operations) involve the use of chemical solutions and mixtures of liquids and solid particles. Nature is rich in fluids with complex constituent laws, for example, slush and marshes around river beds, animal and natural secretions, blood and lava, and Newtonian fluids are an exception. A good understanding of flows of complex fluids can benefit industrial and environmental applications by reducing costs, reducing impact and promoting innovative and design optimization techniques.
Foams and sludge, as well as heavy oil, stimulant fluids and cement mixtures, have particular rheological behavior: they can resemble yield-stress fluids for very low shear rates, and generally show shear-thinning or shear-thickening behavior. In particular, drilling muds, which are ubiquitous in underground applications, are mixtures of water emulsified with oil, clay, weighting material, small amounts of salts and polymeric fluids, and at low cutting speed have a very high apparent viscosity [
1], resembling Bingham fluids. Recently, a renewed interest towards aqueous foams and their flow in porous media, has stimulated the investigation of non-Newtonian fluids in heterogeneous media [
2]. Foams, which can be modeled as shear-thinning fluids, are often used in hydraulic fracturing to saturate fractures, and allow the generation of high-gradient pressure to divert the flow to less permeable regions. Experimental evidence [
3] showed that foam viscosity, as well as bubble morphology, is strongly affected by aperture heterogeneity. The structure of foams or the particular physical composition of aqueous solutions inevitably implies a non-Newtonian relationship between shear-stress and shear-rate, and the flow of these fluids in complex geometries is not yet fully described and experimentally validated. Even the numerical effort required, when a complex rheology is coupled with natural geometries, results in a demanding task.
In formations of the low permeability matrix, the fluids predominantly flow through fracture networks; in particular, across the single fracture, the flux tends to concentrate along the path of least resistance, where the space between walls is wider. Both artificial and natural fractures show a high degree of variability of the aperture, which can be described by a log-normal or gamma distribution [
3,
4]. Spatial correlation is usually introduced according to two approaches: a traditional one dating back to the 1980s consists in reproducing the fracture aperture as a 2D random spatial function, assuming a certain correlation function; a second one reproduces the fracture walls as two self-like fractal surfaces and generates the aperture by coupling the walls, imposing a separation between the two middle planes. The latter better represents fractures according to experimental evidence [
5]. In fact, considering a fracture generated by shearing, the aperture field along the slip direction appears constant at a scale larger than the slip length, while at a smaller scale it exhibits the same self-affine behavior as that of the wall roughness.
The flow of Newtonian fluids in fractures has been studied for decades and numerous analytical and numerical models have been proposed. A traditional approach, initially proposed by Dagan [
6] for statistically homogeneous porous formations and extended by Zimmerman [
7] to rock fractures, allows a reasonably accurate prediction of hydraulic conductivity and flow rate. According to Beran [
8], given the frequency distribution of the conductance, an upper and a lower bound can be defined, corresponding to an arrangement in series (SA) and in parallel (PA) of the individual conductive elements [
6].
Many field and laboratory experiments on Newtonian fluid flow in fractures are available in the literature. The experimental data have been used to demonstrate that it is possible to make accurate predictions of hydraulic conductivity based only on the first two moments of the aperture distribution function and the proportion of the contact area (see Zimmerman [
7]). The same authors conducted further experiments on the non-linear regimes of flow in rock fractures [
9]. Silliman [
10] analyzed field data to understand the reason why hydraulic and tracer tests provide different estimates of fracture aperture. He noted that the maximum difference between aperture estimates occurs when the variance of the aperture distribution is large. In the same paper, it is suggested that the relative variation of the aperture estimates may provide a means whereby the orientation of anisotropy or channeling may be identified. It is clear that an accurate quantification of rock fracture aperture is important in investigating hydro-mechanical properties of rock fractures [
11]. More recently, laboratory experiments have been carried out to directly observe the fluid flow in a rough-walled fractures [
12], and micro-particle image velocimetry (PIV) was used to asses the evolution of non-Fickian tailing when eddies developed at large fluid velocities. These experimental results contradict results from numerous previous studies based upon simulations in 2-D fracture geometries and highlight the need for caution when using 2-D simulations to understand 3-D transport processes.
In comparison to Newtonian fluid, little has been produced on the flow of non-Newtonian fluids in fractures. The early approaches to the study of complex rheology fluid flows in a single fracture consisted in the introduction of a simplified geometry, for example generating a 1D fracture by coupling two sinusoidal walls [
13], or assuming an aperture distribution a conceptualizing a fracture as a series of channels [
14,
15]. These analytical or semi-analytical models allow us to qualitatively asses the influence of rheological and geometric properties estimators (e.g., statistical moments, wavelength, amplitude) on fluid flow. Literature shows also a serious lack of research on fracture flows of non-Newtonian fluids especially regarding yield-stress fluids [
16], generally classified as Herschel–Bulkley (HB) fluids, but also with power-law fluids (Ostwald–deWaele fluids). One of the reasons is the complexity in handling functions relating to shear-stress and shear rate-showing singularities, as happens about the yield-stress value. Rodríguez de Castro and Radilla [
17] proposed a method to predict the pressure drop in a rough-walled fracture at a given injection flow rate by only using the shear rheology of the fluid, the hydraulic aperture of the fracture, and the inertial coefficients as inputs, valid with HB and Carreau fluids. Experiments with non-Newtonian fluids are even more challenging, also due to the needs of accurate measurements and interpretations of rheological properties of the fluids, with a continuous effort to correctly quantify uncertainties [
18]. Recently, Chiapponi et al. [
19] studied theoretically and experimentally the back-flow of Ostwald–deWaele fluids from a disk-shaped elastic fracture, highlighting the different efficiency of the process in the presence of shear-thinning fluids. In a slightly different context, with gravity currents of HB fluids instead of pressurized flows, the experiments documented in Di Federico et al. [
20] validated a general analytical solution based on the perturbation of a self-similar solution. The agreement between theory and experiments was encouraging on the correctness of the conceptual model and of the analytical details. With additional complexities due to the presence of thermal effects (temperature is a very sensitive parameter in the rheological properties of non-Newtonian fluids), the onset of thermal convection of Ostwald–deWaele fluids in a Hele–Shaw cell was modeled and reproduced experimentally in Petrolo et al. [
21]. In that case, a special attention was paid in determining the rheological properties of the fluids, in a regime with very small shear-rate values.
In this paper we present experimental results on Ostwald–deWaele fluids, to validate the available models of power-law fluids in statistically varying fractures, including the recent extension to truncated power-law fluids recently proposed in Felisa et al. [
15]. The paper is organized as follows. The theory is presented in
Section 2. The numerical model is detailed in
Section 3, while the experimental setup and the procedure is described in
Section 4. Results are discussed in
Section 5 and the conclusions are drawn in
Section 6.
2. Theory
We consider the schematic in
Figure 1. The simplest case refers to a lubrication model and is represented by the flow of a non-Newtonian power-law fluid between two smooth parallel plates separated by a distance
b, the fracture aperture, with upper and lower plates at
and
, respectively. Assuming a uniform pressure gradient
in the
y direction, the shear stress profile is given by (see [
22,
23]):
where
is the shear stress in the
plane,
is the reduced pressure,
p is the pressure,
g is the acceleration due to gravity, and
is the fluid density. For a purely viscous power-law fluid with shear in a single plane, results
where
is the velocity component collinear with the gradient pressure,
m is the consistency index, and
n is the flow behaviour index. For
, the model describes a shear-thinning (pseudo-plastic) behavior, whereas
describes a shear-thickening behavior. Substituting Equation (
2) into Equation (
1) and integrating, with the no-slip condition at the wall,
, and assuming null vertical velocity, yields the velocity profile
The total volumetric flux through the fracture for a width
in the
y direction (parallel to the pressure gradient) is derived by integrating Equation (
3) from
to
:
In the present paper, we consider the case of a variable aperture fracture, with flow due to a pressure gradient perpendicular to constant aperture channels, according to the scheme shown in
Figure 2. The fracture model is discretized into
N cells of width
in series, with the
i-th cell having an aperture
. By virtue of mass conservation, volumetric flux
through each cell is constant, and assuming that the flow law given by Equation (
4) holds locally, the pressure gradient in each cell is given by
The total pressure gradient is the sum of pressure gradients, with a mean value
and taking the limit as
, under ergodicity it results
where
is the probability density function (PDF) for the fracture aperture. In literature, several studies proposed either a log-normal [
24,
25,
26] or a gamma [
27,
28] PDF; moreover, fracture wall topographies have been measured as Gaussian [
29], suggesting that the aperture should present a similar distribution. Here, a log-normal PDF is considered with the following expression
where
is the geometric mean,
is the arithmetic mean (expected value), and
the variance of the natural logarithm of
b. Utilizing Equation (
6) with Equation (
7) provides the following expressions of volumetric flow rate and equivalent aperture:
Further details on the derivation of formulas and on the implications of the results in the analysis, can be found in [
14].
3. Numerical Model
A 1D numerical model based on the lubrication model [
30] is adopted to estimate the flow rate through the synthetic fracture described in
Section 4 and represented in
Figure 2. In order to solve the problem via the finite difference method, pressure boundary conditions are considered at the two dashed sides of
Figure 2b: a source pressure
at the upstream boundary
and a sink pressure
at the downstream boundary
. No-flow conditions are imposed on the two vertical (solid) boundaries (at
and
). The lubrication model (Equation (
3)) has been demonstrated satisfactory if the following conditions are satisfied [
31]:
the Reynolds number is sufficiently low, so that no recirculation regions are produced between asperities;
the fracture is sufficiently smooth. The ratio between the standard deviation of the aperture, , and the shortest wavelength of the aperture variation, , must be below 1/5 ().
The one dimensional mass conservation is
where
is the specific flow rate. For a power-law fluid, given the expression of the flow rate (Equation (
4)), the governing equation can be written as:
Equation (
10) can be expressed in a finite differences scheme, resulting in a non-linear system of equations:
where the unknowns are the values of pressure
, having assumed a regular array of cells with constant
. A staggered grid has been adopted, with value of aperture
evaluated at the mid points. The system of Equation (
11), with additional equations arising from the boundary conditions, has been solved iteratively, with sequential sweeps through the grid until convergence is reached, according to the method described in Patankar [
32]. Several tests were performed for grid independence, and iterations were stopped upon reaching a mean quadratic error below a fixed threshold.
4. Experiments
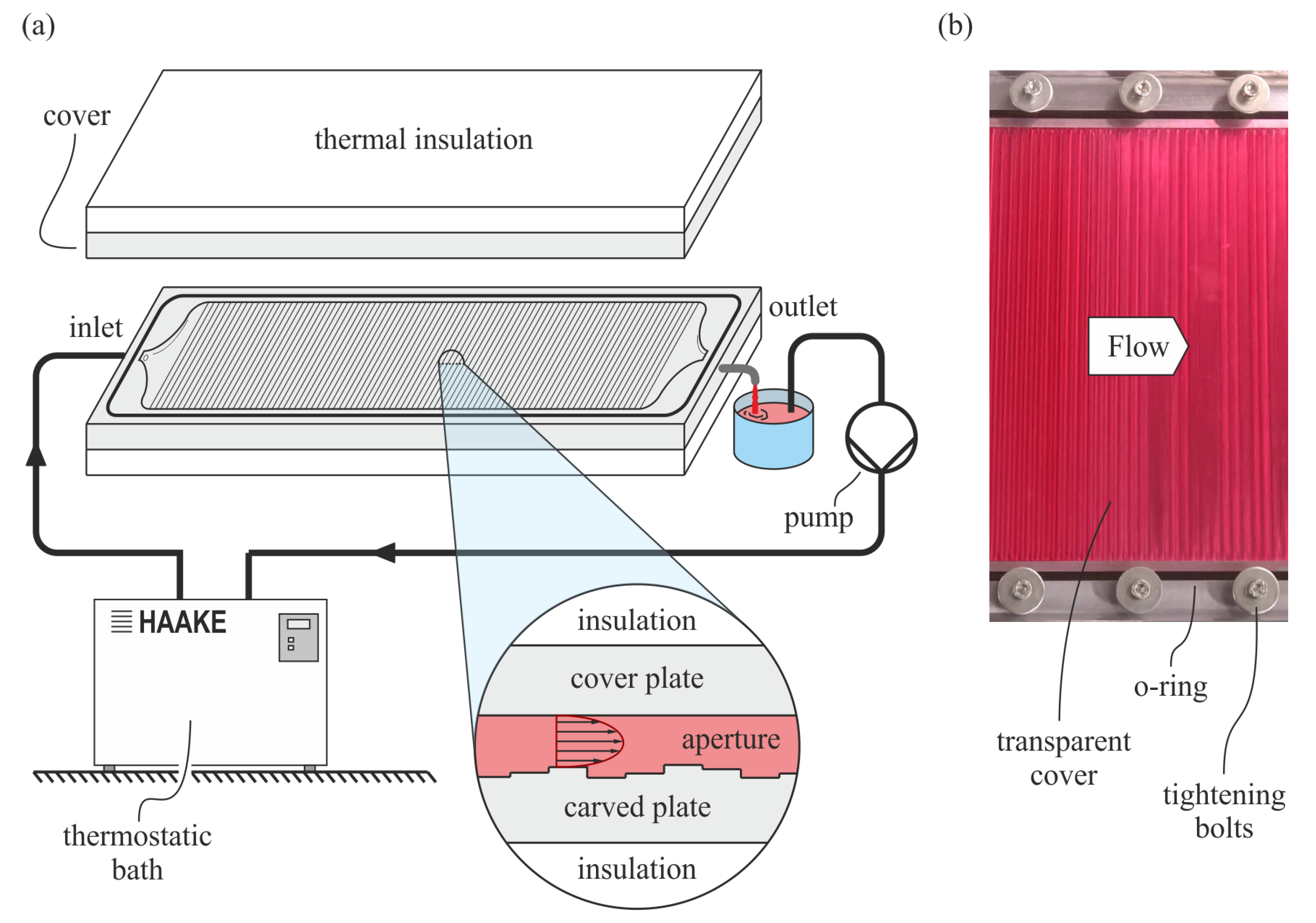
Validation of the theoretical results has required the setup of a series of experiments conducted in the Hydraulic Laboratory of Parma University.
A plate of Aluminum and thick was machined with a computer numerical control (CNC) tool in order to shape the lower surface of the variable aperture fracture. Such a surface consists of a sequence of 200 faces long and wide, each milled at a different height. A top cover provides the flat upper surface of the aperture. Both a transparent polycarbonate ( thick) cover and a steel ( thick) cover were realized, with the sealing between the Aluminum plate and the cover guaranteed by a diameter o-ring. The transparent cover was used for some preliminary tests and it was useful to understand the qualitative behavior of the apparatus (e.g., to verify the absence of air entrapment), whereas the steel cover, used for the final tests, has a high stiffness and suffers minimal deformations due to the pressures of the fluid into the aperture. The inlet and the outlet have a divergent shape, designed to avoid head losses and to ensure a uniform distribution of the fluid velocity at the ends of the fracture.
Figure 3 shows an exploded view of the apparatus, the details of the sealing, and a photo of the assembly during a preliminary test.
The geometry of the fracture was controlled using a dial indicator with an accuracy equal to
.
Figure 4a shows the actual value of the distance between the two plates,
b, as a function of the longitudinal abscissa
y. The average value of the aperture
is equal to
(with a maximum equal to
and a minimum of
), while the standard deviation of the natural logarithm of the aperture is
. The dial indicator was also used to measure the increase in aperture due to the internal pressure of the fluid, and it was found that for pressure gradient up to
the variation of the aperture is of the order of
. Increasing flow rate requires a larger pressure gradient which, in turn, increases the mean value of
b. We remind that the flow rate varies with the third power of
b, hence such a variation of the aperture (
) results in a variation in Q up to ≈8%.
Figure 4b shows the quantile-quantile (Q-Q) plot that compares the actual distribution of
to the Gaussian distribution. The agreement is fairly good especially in the range
, while slight deviations from the theoretical distribution occur in both the left and right tails.
A palette pump controlled by an electronic inverter was used to recirculate the fluid through a closed circuit consisting of (i) a small tank containing the fluid; (ii) a suction pipe; (iii) the pump; (iv) a discharge pipe including a heat exchanger and (v) the fracture that ends with an outlet, at atmospheric pressure. The heat exchanger was immersed in a thermal bath (HAAKE DC5), which made it possible to control the temperature of the fluid; in addition, for the purpose of minimizing heat losses, the plates in their final assembly were thermally insulated with a thick polystyrene coat. Two thermocouples were installed in contact with the carved plate, one close to the inlet and the other just upstream of the outlet, in order to check that no thermal gradient was present along the aperture during tests and to measure the actual temperature of the fluid during the experiment.
The pressure gradient was measured with a Honeywell 420DP differential pressure transducer (full scale ), with an upstream pressure tap at and a downstream pressure tap at , (). Data were acquired with a National Instruments DAQ system with a data rate equal to .
4.1. Test Schedule
The experimental fluid was obtained by mixing pure glycerol and water, for tests with a Newtonian fluid, and water and E415 (or Carbomer), for tests with non-Newtonian power-law fluid. The mass density was measured with a pycnometer. The rheological parameters were measured with a Ubbeholde viscometer, for the Newtonian fluids, and in a parallel-plate rheometer by Anton Paar, at the same temperature of the experiments, for the non-Newtonian mixtures. The rheological parameters of the power-law fluid are listed in
Table 1 and were estimated according to the techniques detailed in [
18,
19,
33].
4.2. Uncertainty Quantification
The absolute uncertainty of the dial indicator was , while the time uncertainty was taken to be equal to (human error on using stopwatch). We also assumed an uncertainty and in measuring the fluid behavior index and the consistency index, including the effects of a possible thermal shift between the experimental conditions and the rheometer measurements. Mass density was estimated with an absolute uncertainty of , hence . The accuracy of the thermocouples was , and the uncertainty in pressure measurement was .
5. Results and Discussion
Figure 5a–e shows the experimental data and the theoretical analytical and numerical curves for discharge
Q as a function of pressure gradient
for Newtonian fluids. The results match fairly well for all combinations of parameters tested, with a tendency of the theoretical curve to slightly overestimate experimental and numerical results. For the experimental data, the percentage deviation from the theory is shown in
Figure 6a, with values below
. No general trend can be observed, also considering that any variation with the flow rate is much smaller than the amplitude of the error bars. The deviation of the numerical results is almost invariant with the flow rate, and is generally below
. This is probably due to the finite length of the fracture, which makes it not completely accurate to describe the fracture itself through the Equation (
7). In the case of a longer fracture, it would be possible to obtain more consistent (statistical) estimators, with a better modelling of the geometry and maybe with a greater agreement between numerical results and theory.
Figure 5f,g shows the comparison for non-Newtonian fluids, with less agreement between experiments and theory, especially for some combinations of the tested parameters (test 7 and 8). Two of the three tests show a fairly good agreement between the numerical model and analytical derivation, both underestimating the experiments. A third experiment gives better results, with both the numerical model and experiments well reproducing the analytical results, see
Figure 5f. It should be noted that the fluid used in test 6 is characterized by the presence of a non-negligible yield stress, which is more or less unavoidable for shear-thinning fluid with high values of fluid consistency.
Figure 6b shows the difference between the experimental and numerical results and the theory for the three experiments with non-Newtonian power-law fluid.
The discrepancy between experiments and theory can be attributed to rheological parameter estimation methodologies, which are much more sensitive for non-Newtonian fluids. The flow field in the fracture is characterized by the value of the shear stress ranging from 0 (in the mid-plane of the fracture,
) up to a maximum value (per unit width)
at
. For the maximum gradient pressure it results in shear rates of
, which are beyond the range of measurements of the instrumentation currently available; moreover, the estimates of both
n and
m are strongly influenced by the range of rheological measurements, since the power-law model rarely describes the rheological properties of experimental fluids for large ranges of variation of the shear-rate. In this respect, future research should focus on the implementation of rheology measurements coherent with the characteristics of each test. For example, the present experimental setup could be improved by adding a second circuit in series with the fracture, consisting of two parallel plates and working under a pressure gradient similar to the pressure gradient between the inlet and the outlet sections of the fracture, and with the same fluid at the same temperature. With a gap between the plates equal to the average gap of the fracture, also the shear rate range should be similar. Such a new apparatus should give an integral and more reliable estimate of the parameters.
A second source of discrepancy between experimental results and theory can be attributed to the presence of slip at the walls. The slip phenomenon has been observed and studied in several cases related to the flow of shear-thinning fluids [
34,
35,
36], with a decreasing viscosity and a shear rate increase. This feature is demonstrated to cause a non-linear velocity profile leading to the apparent slip [
37]. The last aspect is ageing of the experimental fluids, which results in a progressive evolution of the rheological parameters due to continuous high shear-rates. This last aspect is equivalent to a time-dependency of the process, often without a recovery of the initial properties of the fluid. Further investigation for a deep understanding of these aspects is required and left for future work.
6. Conclusions
This work presents a novel experimental device used to reproduce the flow of both Newtonian and non-Newtonian power-law fluids in a variable aperture fracture. The fracture aperture was designed to represent a spatially homogeneous and correlated random field with a log-normal distribution. Experimental tests were conducted with Newtonian and shear-thinning fluids and different combinations of parameters to validate theoretical and numerical models.
In the case of a Newtonian fluid, experimental, numerical and theoretical results match fairly well for all combinations of the tested parameters, with a tendency of the theoretical curve to slightly overestimate experimental results. The results of the numerical model are generally between the two.
In the case of non-Newtonian power-law (shear-thinning) fluid, experimental and theoretical analytical results show a less good agreement for some combinations of the parameters, with the theoretical curve underestimating the experimental results. Such discrepancies could be attributed (i) to a limited accuracy of the power-law model for large values of the shear rates, and (ii) to the possible presence of slip at the boundaries. Although only three tests are available, a significantly wide range of consistency index and fluid behavior index has been reproduced.
Overall, the experiments correctly reproduce the flowrate-gradient pressure relations, with better agreement for Newtonian one-parameter fluids than for two-parameter power-law fluids.
Future improvements in the current analysis are based on more appropriate measurements of rheological parameters, with special rheometers designed to reproduce as much as possible the geometry of the flow field in the fracture and the resulting strain tensor, and working in the same range of shear rate values. This is a classic problem in rheometry, with most commercial and experimental rheometers only approximating a pure viscometric flow (characterized by a single component of the strain rate tensor), with unavoidable interference from the other components. We bear in mind that the lubrication model used to derive the analytical expression, then implemented in the numerical finite-differences model, limits the strain rate tensor to a pure shear rate in a single plane, which can be a working hypothesis that is not fully representative of the process.