River Channel Forms in Relation to Bank Steepness: A Theoretical Investigation Using a Variational Analytical Method
Abstract
:1. Introduction
2. Basic Flow Relations in an Open Channel with Bedload Transport
3. Variational Analysis of the Effect of Channel-Form Adjustment on Bedload Transport
4. Effects of Riverbank Steepness on Equilibrium Channel Geometry
4.1. Equilibrium Channel Relations at the Lower Threshold
4.2. Averaged Equilibrium Channel Relations
5. Comparison of Theoretical Results with Previous Studies
5.1. Equilibrium Channel Relations at the Lower Threshold
5.2. Averaged Equilibrium Channel Relations
6. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Blench, T. Mobile Bed Fluviology; University of Alberta Press: Edmonton, AB, Canada, 1969; 164p. [Google Scholar]
- Mackin, J. Concept of the graded river. GSA Bull. 1948, 59, 463. [Google Scholar] [CrossRef] [Green Version]
- Huang, H.Q.; Chang, H.H.; Nanson, G.C. Minimum energy as the general form of critical flow and maximum flow efficiency and for explaining variations in river channel pattern. Water Resour. Res. 2004, 40, 13. [Google Scholar] [CrossRef]
- Nanson, G.C.; Huang, H.Q. Least action principle, equilibrium states, iterative adjustment and the stability of alluvial channels. Earth Surf. Process. Landf. 2008, 33, 923–942. [Google Scholar] [CrossRef] [Green Version]
- Nanson, G.C.; Huang, H.Q. Self-adjustment in rivers: Evidence for least action as the primary control of alluvial-channel form and process. Earth Surf. Process. Landf. 2017, 42, 575–594. [Google Scholar] [CrossRef]
- Nanson, G.C.; Huang, H.Q. A philosophy of rivers: Equilibrium states, channel evolution, teleomatic change and least action principle. Geomorphology 2018, 302, 3–19. [Google Scholar] [CrossRef]
- Lane, E.W. The design of stable channels. Transactions 1955, 120, 1234–1279. [Google Scholar]
- Lane, E.W. A Study of the Shape of Channels Formed by Natural Streams Flowing in Eroding Material, M R D Sediment Series; U.S. Army Engineer Division, Missouri River, Corps of Engineers: Omaha, NE, USA, 1957. [Google Scholar]
- Schumm, S.A. Fluvial Geomorphology: The historical perspective. In River Mechanics; Shen, H.W., Ed.; Box 606: Fort Collins, CO, USA, 1971. [Google Scholar]
- Andrews, E.D. Bed-material entrainment and hydraulic geometry of gravel-bed rivers in Colorado. GSA Bull. 1984, 95, 371. [Google Scholar] [CrossRef]
- Hey, R.D.; Thorne, C.R. Stable channels with mobile gravel beds. J. Hydraul. Eng. 1986, 112, 671–689. [Google Scholar] [CrossRef]
- Huang, H.Q.; Nanson, G.C. Vegetation and channel variation; A case study of four small streams in southeastern Australia. Geomorphology 1997, 18, 237–249. [Google Scholar] [CrossRef]
- Huang, H.Q.; Nanson, G.C. The influence of bank strength on channel geometry: An integrated analysis of some observations. Earth Surf. Process. Landf. 1998, 23, 865–876. [Google Scholar] [CrossRef]
- Lacey, G. Stable channels in alluvium. Min. Proc. Inst. Civ. Eng. 1930, 229, 259–292. [Google Scholar] [CrossRef]
- Leopold, L.B.; Maddock, T. The hydraulic geometry of stream channels and some physiographic implications. Prof. Paper 1953, 252. [Google Scholar] [CrossRef] [Green Version]
- Leopold, L.B.; Wolman, M.G. River Channel Patterns: Braided, Meandering and Straight, US Geological Survey Professional Paper; US Government Printing Office: Washington, DC, USA, 1957.
- Schumm, S.A. The Shape of Alluvial Channels in Relation to Sediment Type, Erosion and Sedimentation in a Semiarid Enviroment, US Geological Survey Professional Paper; US Government Printing Office: Washington, DC, USA, 1960; pp. 17–30.
- Schumm, S.A. Geomorphic Thresholds and the Complex Response of Drainage System, Fluvial Geomorphology; Publications of Geomorphology, State University of New York: New York, NY, USA, 1973; pp. 299–310. [Google Scholar]
- Schumm, S.A. The Fluvial System; A Wiley-Interscience Publication: Hoboken, NJ, USA, 1977. [Google Scholar]
- Schumm, S.A. Experimental Fluvial Geomorphology; John Wiley & Sons: Hoboken, NJ, USA, 1987. [Google Scholar]
- Schumm, S.A.; Khan, H.R. Experimental study of channel patterns. GSA Bull. 1972, 83, 1755. [Google Scholar] [CrossRef]
- Henderson, F.M. Open Channel Flow; Macmillan Pub, Co.: New York, NY, USA, 1966. [Google Scholar]
- Ikeda, S.; Parker, G.; Kimura, Y. Stable width and depth of straight gravel rivers with heterogeneous bed materials. Water Resour. Res. 1988, 24, 713–722. [Google Scholar] [CrossRef]
- Parker, G. Self-Formed Straight Rivers with Equilibrium Banks and Mobile Bed. 1. Sand-Silt River. J. Fluid Mech. 1978, 89, 109–125. [Google Scholar] [CrossRef]
- Parker, G. Self-Formed Straight Rivers with Equilibrium Banks and Mobile Bed. 2. Gravel River. J. Fluid Mech. 1978, 89, 127–146. [Google Scholar] [CrossRef]
- Eaton, B.; Millar, R. Predicting gravel bed river response to environmental change: The strengths and limitations of a regime-based approach. Earth Surf. Process. Landf. 2016, 42, 994–1008. [Google Scholar] [CrossRef]
- Chang, H.H. Geometry of rivers in regime. J. Hydraul. Div. ASCE 1979, 105, 691–706. [Google Scholar]
- Chang, H.H. Minimum stream power and river channel patterns. J. Hydrol. 1979, 41, 303–327. [Google Scholar] [CrossRef]
- Chang, H.H. Geometry of gravel streams. J. Hydraul. Div. ASCE 1980, 106, 1443–1456. [Google Scholar]
- Chang, H.H. Stable alluvial canal design. J. Hydraul. Div. ASCE 1980, 106, 873–891. [Google Scholar]
- Chang, H.H. Mathematical-model for erodible channels. J. Hydraul. Div. ASCE 1982, 108, 678–689. [Google Scholar]
- Chang, H.H. Analysis of river meanders. J. Hydraul. Div. ASCE 1984, 110, 37–50. [Google Scholar] [CrossRef]
- Chang, H.H. Modeling of river channel changes. J. Hydraul. Div. ASCE 1984, 110, 157–172. [Google Scholar] [CrossRef]
- Chang, H.H. River morphology and thresholds. J. Hydraul. Div. ASCE 1985, 111, 503–519. [Google Scholar] [CrossRef]
- Mengoni, B.; Paris, E.; Bettess, R. Analytical approach to river regime. J. Hydraul. Div. ASCE 1982, 108, 1179–1193. [Google Scholar]
- Yang, C.T. Unit stream power and sediment transport. J. Hydraul. Div. ASCE 1974, 100, 1269–1272. [Google Scholar]
- Yang, C.T. Minimum unit stream power and fluvial hydraulics. J. Hydraul. Div. ASCE 1976, 102, 919–934. [Google Scholar]
- Yang, C.T. Minimum unit stream power and fluvial hydraulics. J. Hydraul. Div. ASCE 1978, 104, 122–125. [Google Scholar]
- Yang, C.T. Unit stream power equations for total load. J. Hydrol. 1979, 40, 123–138. [Google Scholar] [CrossRef]
- Yang, C.T. Unit stream power equation for gravel. J. Hydraul. Div. ASCE 1984, 110, 1783–1797. [Google Scholar] [CrossRef]
- Yang, C.T.; Molinas, A. Sediment transport and unit stream power function. J. Hydraul. Div. ASCE 1982, 108, 774–793. [Google Scholar]
- Yang, C.T.; Song, C.C.S. Theory of minimum rate of energy-dissipation. J. Hydraul. Div. ASCE 1979, 105, 769–784. [Google Scholar]
- Yang, C.T.; Song, C.C.S.; Woldenberg, M.J. Hydraulic geometry and minimum rate of energy-dissipation. Water Resour. Res. 1981, 17, 1014–1018. [Google Scholar] [CrossRef]
- Yang, C.T.; Stall, J.B. Applicability of unit stream power equation-closure. J. Hydraul. Div. ASCE 1978, 104, 1095–1103. [Google Scholar]
- Yang, C.T.; Stall, J.B. Applicability of unit stream power equation. J. Hydraul. Div. ASCE 1978, 104, 289–297. [Google Scholar]
- Ferguson, R.I. Hydraulics and hydraulic geometry. Prog. Phys. Geogr. Earth Environ. 1986, 10, 1–31. [Google Scholar] [CrossRef]
- Griffiths, G.A. Extremal Hypotheses for River Regime: An Illusion of Progress. Water Resour. Res. 1984, 20, 113–118. [Google Scholar] [CrossRef]
- Chang, H.H. Comment on “Extremal hypotheses for river regime: An illusion of progress” by George A. Griffiths. Water Resour. Res. 1984, 20, 1767–1768. [Google Scholar] [CrossRef]
- Eaton, B.C.; Millar, R.G. Optimal alluvial channel width under a bank stability constraint. Geomorphology 2004, 62, 35–45. [Google Scholar] [CrossRef]
- Song, C.C.S.; Yang, C.T. Comment on “Extremal hypotheses for river regime:An illsion of progress” by George A. Griffiths. Water Resour. Res. 1986, 22, 993–994. [Google Scholar] [CrossRef]
- Millar, R.G. Theoretical regime equations for mobile gravel-bed rivers with stable banks. Geomorphology 2005, 64, 207–220. [Google Scholar] [CrossRef]
- Huang, H.Q.; Chang, H.H. Scale independent linear behavior of alluvial channel flow. J. Hydraul. Div. ASCE 2006, 132, 722–730. [Google Scholar] [CrossRef] [Green Version]
- Huang, H.Q.; Nanson, G.C. Hydraulic geometry and maximum flow efficiency as products of the principle of least action. Earth Surf. Process. Landf. 2000, 25, 1–16. [Google Scholar] [CrossRef]
- Huang, Q.H.; Nanson, G.C. Alluvial channel-form adjustment and the variational principle of least action. In Proceedings of the Congress-International Association for Hydraulic Research, Beijing, China, 16–21 September 2001; pp. 402–408. [Google Scholar]
- Huang, H.Q.; Nanson, G.C. A stability criterion inherent in laws governing alluvial channel flow. Earth Surf. Process. Landforms 2002, 27, 929–944. [Google Scholar] [CrossRef]
- Huang, H.Q.; Nanson, G.C. Why some alluvial rivers develop an anabranching pattern. Water Resour. Res. 2007, 43, 12. [Google Scholar] [CrossRef]
- Millar, R.G. An Optimization Model for the Development and Response of Alluvial River Channels. Ph.D. Thesis, University of British Columbia, Vancouver, BC, Canada, 1994. [Google Scholar]
- Millar, R.G. Influence of bank vegetation on alluvial channel patterns. Water Resour. Res. 2000, 36, 1109–1118. [Google Scholar] [CrossRef]
- Millar, R.G.; Quick, M.C. Effect of bank stability on geometry of gravel rivers. J. Hydraul. Eng. 1993, 119, 1343–1363. [Google Scholar] [CrossRef]
- Millar, R.G.; Quick, M.C. Stable width and depth of gravel-bed rivers with cohesive banks. J. Hydraul. Div. ASCE 1998, 124, 1005–1013. [Google Scholar] [CrossRef]
- Chien, N. Meyer-Peter Formula for Bed Load Transport Aniond Einstein Bed Load Function; University of California: Berkeley, CA, USA, 1954. [Google Scholar]
- Huang, H.Q. Reformulation of the bed load equation of Meyer-Peter and Muller in light of the linearity theory for alluvial channel flow. Water Resour. Res. 2010, 46, 09533. [Google Scholar] [CrossRef]
- Meyer-Peter, E.; Muller, R. Formulas for Bed-Load Transport. InIAHSR 2nd Meeting, Stockholm, Appendix 2; IAHR: Madrid, Spain, 1948. [Google Scholar]
- Einstein, H.A. Formula for transportation of bed load. Trans. ASEC 1942, 107, 561–597. [Google Scholar]
- Einstein, H.A. The Bed Load Function for Sediment Transportation in Open Channel Flows; S. Department of Agriculture, Technical Bulletion: Washington, DC, USA, 1950; p. 71. [Google Scholar]
- Lane, E.W. Progress Report on Results of Studies on Design of Stable Channels; Hydraulic laboratory Report Hyd-352; US Bureau of Reclamation: Washington, DC, USA, 1952.
- Nanson, R.A.; Nanson, G.C.; Huang, H.Q. The hydraulic geometry of narrow and deep channels: Evidence for flow optimisation and controlled peatland growth. Geomorphology 2010, 117, 143–154. [Google Scholar] [CrossRef] [Green Version]
- Rhodes, D.D. The b-f-m diagram for downstream hydraulic geometry. Geogr. Ann. Ser. A Phys. Geogr. 1987, 69, 147. [Google Scholar] [CrossRef]
- Huang, H.Q. The multivariate controls of hydraulic geometry: A causal investigation in terms of boundary shear distribution. Earth Surf. Process. Landforms 1995, 20, 115–130. [Google Scholar] [CrossRef]

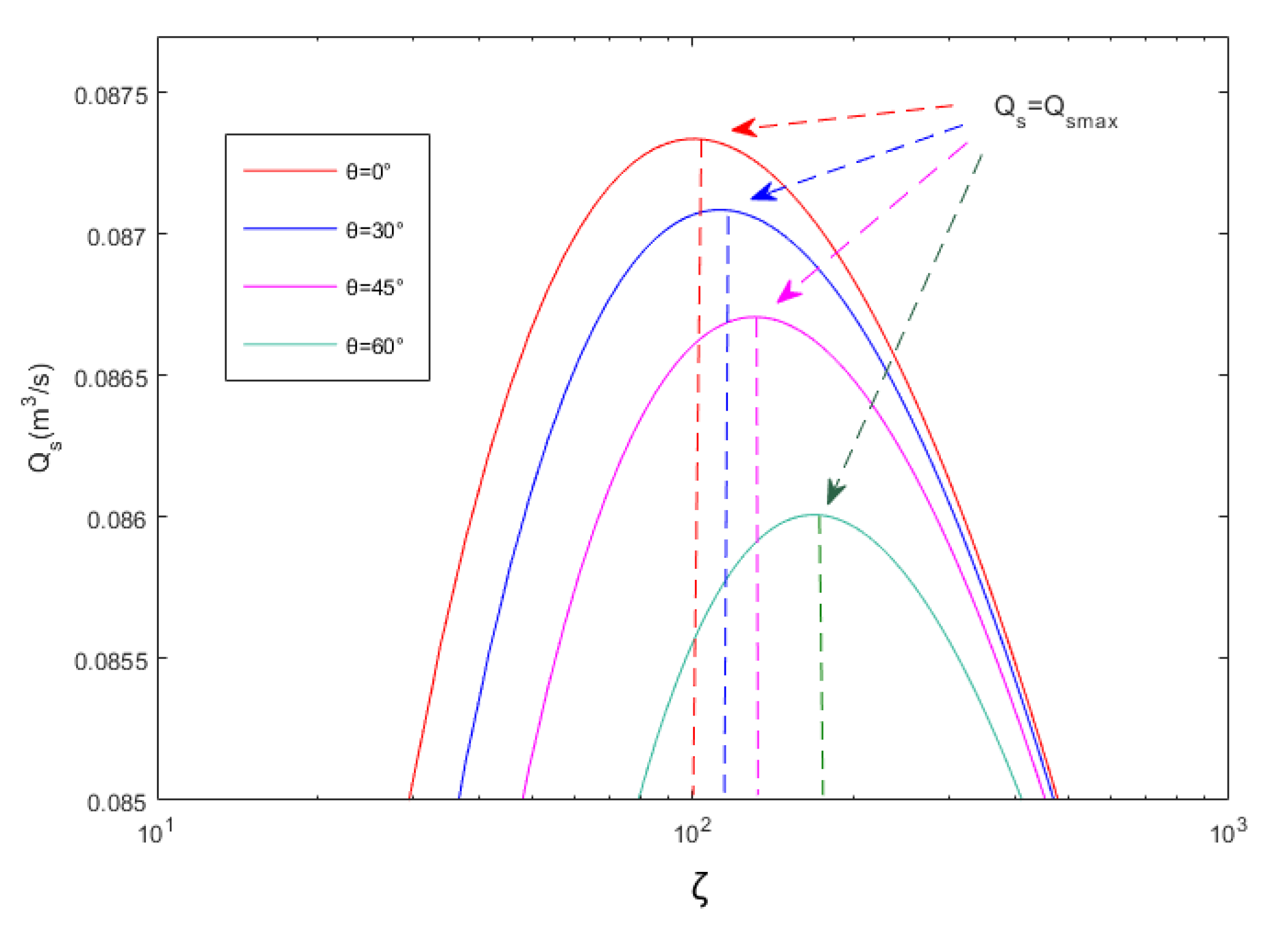
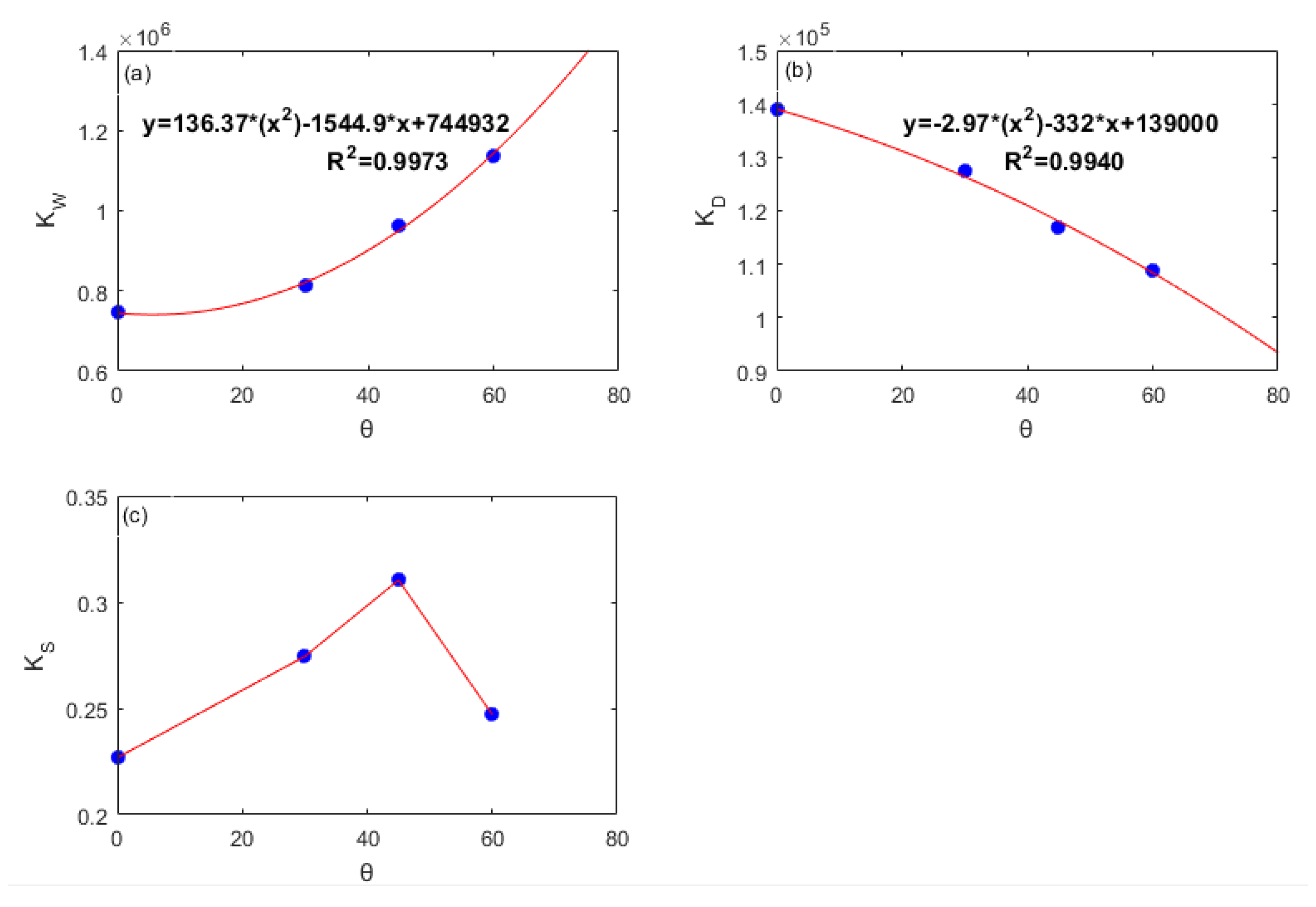
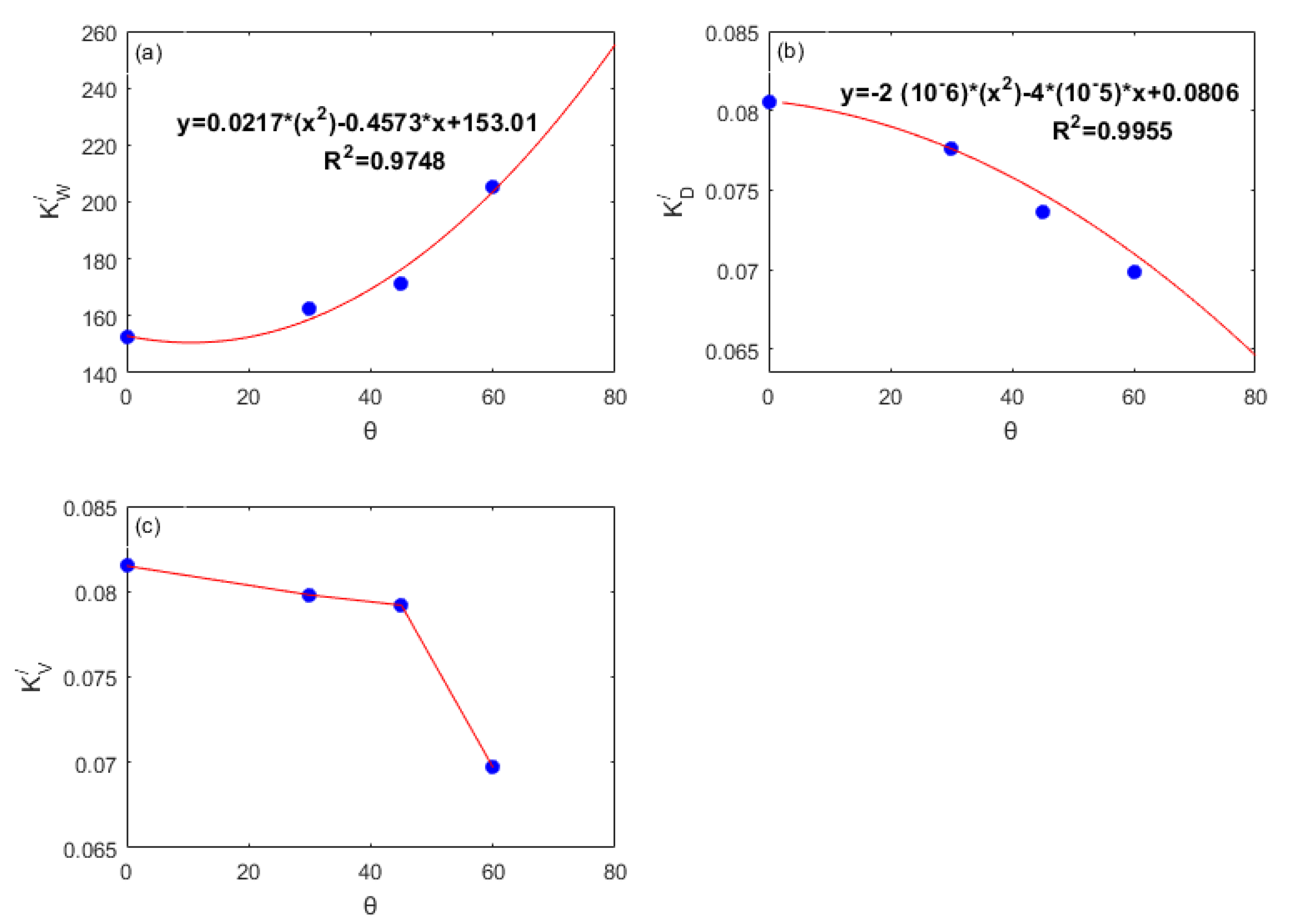
| (m3/s) | ||||
|---|---|---|---|---|
| 0° | 101 | −10.62 | 0.08733 | 0.29 |
| 30° | 113 | 0 | 0.08708 | 0 |
| 45° | 128.7 | 13.89 | 0.08670 | −0.44 |
| 60° | 168.5 | 49.12 | 0.08601 | −1.23 |
| Values of the Coefficients in Equation (22) | ||
|---|---|---|
| 0° | 2 | |
| 30° | 2.31 | |
| 45° | 2.83 | |
| 60° | 4 |
| Potential Varying Range of | ||
|---|---|---|
| 0° | 625 | 3–625 |
| 30° | 749.8 | 3–749 |
| 45° | 878.2 | 3–878 |
| 60° | 1000 | 5–1000 |
| Averaged Equilibrium Channel Relations | ||
|---|---|---|
| 0° | ||
| 30° | ||
| 45° | ||
| 60° |
| Averaged Hydraulic Geometry Relations | ||
|---|---|---|
| 0° | ||
| 30° | ||
| 45° | ||
| 60° |
| Channel Geometry Factors | This Study | Threshold Theory (Lane, 1952) [66] |
|---|---|---|
| Width () | ||
| Depth () | ||
| Slope () | ||
| Width/depth ratio () | 2–4 | 7.05–8.61* |
| Hydraulic Geometry Factors | This Study | Hydraulic Geometry Model (Rhodes, 1987) [68] | Huang and Warner (1995) [69] |
|---|---|---|---|
| Width () | |||
| Depth () | |||
| Velocity () |
| Theoretical Results of this Study | Results of Huang and Nanson (1998) [13] | ||||
|---|---|---|---|---|---|
| Bank angle | Channel width change (%) | Channel depth change (%) | Bank type | Channel width change (%) | Channel depth change (%) |
| 0° | 0 | 0 | Cohesive sand or gravels | 0 | 0 |
| 30° | 8.8 | −8.3 | |||
| 45° | 29.1 | −15.9 | |||
| 60° | 52.6 | −21.6 | Noncohesive sand | 62.2 | −26.7 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Fan, J.; Huang, H.; Yu, G.; Su, T. River Channel Forms in Relation to Bank Steepness: A Theoretical Investigation Using a Variational Analytical Method. Water 2020, 12, 1250. https://doi.org/10.3390/w12051250
Fan J, Huang H, Yu G, Su T. River Channel Forms in Relation to Bank Steepness: A Theoretical Investigation Using a Variational Analytical Method. Water. 2020; 12(5):1250. https://doi.org/10.3390/w12051250
Chicago/Turabian StyleFan, Jinsheng, Heqing Huang, Guoan Yu, and Teng Su. 2020. "River Channel Forms in Relation to Bank Steepness: A Theoretical Investigation Using a Variational Analytical Method" Water 12, no. 5: 1250. https://doi.org/10.3390/w12051250
APA StyleFan, J., Huang, H., Yu, G., & Su, T. (2020). River Channel Forms in Relation to Bank Steepness: A Theoretical Investigation Using a Variational Analytical Method. Water, 12(5), 1250. https://doi.org/10.3390/w12051250





