Abstract
Unit hydrographs (UHs) remain widely used in hydrologic modeling to predict the stormflow that is produced at a basin outlet in response to runoff generated throughout the basin. Numerous studies have demonstrated that a basin’s UH depends on its geomorphic properties, and several methods estimate synthetic UHs using such properties. However, previous studies have not examined whether the channel network type (such as dendritic, parallel, pinnate, rectangular, and trellis) impacts the UH shape. The objectives of this study were to determine: (1) whether those five network types exhibit distinct UHs, and (2) whether knowledge of the network type is sufficient to replace the actual flow path structure in UH estimation. To achieve these objectives, a UH framework is developed based on kinematic wave theory. The framework allows the impacts of the network structure on the UH to be isolated into two random variables, which facilitates comparisons between network types. The framework is applied to 10 basins of each type. The results show that the five network types exhibit distinct instantaneous UHs, but the type allows accurate UH determination only for pinnate basins.
1. Introduction
A common task in hydrologic modeling is predicting the stormflow that occurs at a basin outlet in response to the runoff produced throughout the basin. Many hydrologic models, such as HEC-HMS [1] and SWAT [2], transform runoff into stormflow using a unit hydrograph (UH). The UH concept goes back to Sherman [3], who defined it as the stormflow hydrograph resulting from one unit of average excess rainfall [4]. The UH is known to depend on the basin morphology [5,6,7], and various methods estimate the UH from such characteristics [8]. Traditional synthetic UH methods consider only limited aspects of the basin morphology. For example, the original SCS method uses a single dimensionless UH for all watersheds [9], but that UH is rescaled using the watershed area, mainstream length, and average slope. The original SCS method has been updated so that the dimensionless UH shape can vary based on a selected peaking factor [10,11] that estimates the UH based on the distribution of travel times to the outlet and a linear reservoir that describes the effects of storage within the watershed. Originally, the travel time distribution was based on hypothetical basin configurations, but the method in [11] has been updated to use the actual flow path configuration for the watershed of interest [12,13,14].
UHs have also been generated using probability density functions (PDFs); given their similar mathematical properties, the authors of [8,15] modeled the basin as a series of linear reservoirs, producing a UH with a gamma distribution. This model is usually classified as “conceptual” [15], in contrast to the earliest synthetic UH methods, which rely on some degree of subjectivity in fitting rainfall‒runoff data. For instance, the authors of [16,17] list several PDFs that have been successfully used to fit the UH, including incomplete [18] and two-parameter gamma distributions [19,20], chi-squared [21], beta [22], and Weibull [23] distributions.
The Geomorphologic Instantaneous UH (GIUH) estimates the UH from the PDF of travel times to the outlet, and the PDF is estimated using Horton’s ratios, which describe the network structure. The authors of [5,24,25] proposed a similar UH based on channel links instead of [26] stream orders, and [27] extended the GIUH approach to consider the effects of hillslope travel times. The GIUH approach has also been generalized to allow a nonlinear relationship between runoff and stormflow [28]. The breadth of the GIUH approach can accommodate much variability within and between basins—for instance, partitioning a basin into units where each unit has a different parametrization [29].
UH methods have also been developed using the width function, as determined from a digital elevation model (DEM), which is the distribution of flow lengths to the outlet [30]. Thus, they explicitly consider the flow path structure for any basin of interest. They also use a spatial representation of the flow speed or flood-wave celerity along the flow paths to determine the travel times [31]. Different representations for the celerity have been proposed, including using two velocities representing hillslope and channel flows (e.g., [31,32,33]) or two velocities representing surface and subsurface flows [34]. Spatially distributed travel time (SDTT) or spatially distributed UH methods are similar, but they use a celerity that varies continuously in space throughout the watershed [35,36]. Some SDTT methods also relax the linearity assumption of traditional UH methods because their travel times vary in time (e.g., [37,38,39,40,41,42]).
As these previous studies demonstrate, the UH is known to depend on the channel network structure. However, it is not known whether the channel network type affects the UH. Watersheds can exhibit distinct channel network structures depending on the geomorphic conditions under which they developed, and these differences have led to the use of network types such as dendritic, parallel, pinnate, rectangular, and trellis (Figure 1). Dendritic networks are tree-like, with channels oriented in many directions and tributaries forming acute angles at confluences. This network type develops when few lithologic or topographic constraints are present [43]. Parallel networks have major channels that are aligned with each other and develop when the region has a pre-existing slope [43,44,45,46,47]. Pinnate networks tend to be feather-like, with a single main channel and many tributaries joining the main channel at acute angles, but the origin of this network type is unclear [43,46,47,48]. Rectangular networks have channels with right-angle bends and tributaries that merge at right-angles. They form when the channels exploit orthogonal jointing in the bedrock [45]. Trellis networks resemble a garden trellis with numerous short tributaries joining irregular main streams. This network type develops in fold-and-thrust belts like the Appalachian Mountains [43,48]. Additional network types have also been identified for regions with very high relief [49]. Networks can often be classified by inspection because their differences are readily apparent to the eye, but quantitative methods have also been developed to ensure objectivity [49,50,51,52,53]. The network type has been shown to affect the time of concentration of a watershed [54], but its impact on the UH remains unexplored.
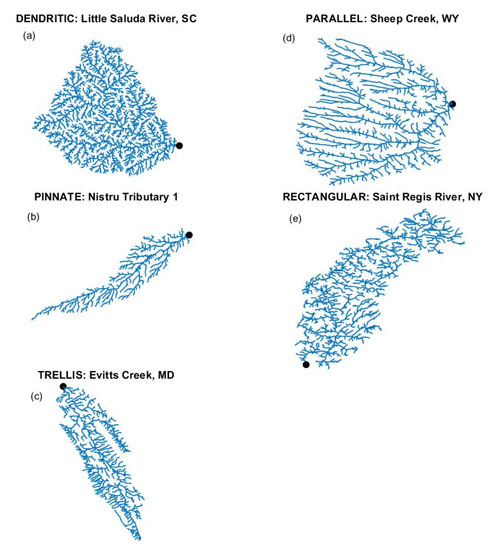
Figure 1.
An example channel network from the (a) dendritic, (b) pinnate, (c) trellis, (d) parallel, and (e) rectangular types. Black dots indicate the basin outlets.
The objectives of this study are to determine: (1) whether the dendritic, parallel, pinnate, rectangular, and trellis network types exhibit distinct UHs, and (2) whether knowledge of the type provides enough information to replace explicit consideration of a basin’s structure in UH determination. To accomplish these goals, 10 basins of each type are extracted from DEMs. Each grid cell within a basin is considered to be either a hillslope or a channel, and the flood wave travel time within each cell is calculated using the kinematic wave approximation. The required cell characteristics (e.g., channel slope and width) are estimated using approximations that are applied throughout the watershed. The UH is then determined as the PDF of total travel times from each cell to the basin outlet. This approach is an extension of the SDTT method proposed by [40] and relaxes the linearity assumption of traditional UH theory because the resulting UHs can vary with the rate of runoff production. More importantly, this approach isolates the effects of the flow path network into two random variables (one for the hillslopes and one for the channels). The distributions for these random variables are compared among network types without requiring specification of large numbers of basin characteristics. The distributions are also estimated from either the actual flow paths of each basin (following existing SDTT methods), the network type (which is the simplification being explored), or from average conditions among all basins (which is similar to traditional synthetic UH methods). Thus, the benefit of considering the network type in UH estimation can be evaluated. Finally, these different UH approaches are applied to an example storm to examine the impacts on the resulting hydrographs.
2. Materials and Methods
2.1. Hillslope Travel Time Distribution
The flood wave travel time within a hillslope cell is based on an expression derived by [55], who applied the kinematic wave approach to a sloping plane where flow enters from the upslope and is generated locally by runoff. That derivation assumes that the duration of runoff exceeds the cell’s time of concentration. If this expression is combined with Manning’s equation and written for a hillslope cell at location j, it becomes:
where is the travel time for hillslope cell j, is Manning’s roughness coefficient, is the flow length in the cell, is the slope, is the ratio of the flow entering from upslope to the flow that is produced within the plane, and is the runoff rate. Although [55] calls the net rainfall intensity, it is called runoff here because it could also represent the rate at which old water is released by the addition of new water (rainfall) in the cell. Whether the runoff is old or new water, it is assumed that any infiltration has already been removed, the runoff is spatially uniform, and the runoff travels on the ground surface.
The authors of [40] and [56] modified this expression for use in a SDTT method. The authors of [56] allowed the runoff to vary in time, but constrained it to be homogeneous in space, so it becomes where i is an index for time. Thus, the possibility of partial area runoff production [57] is neglected. Because the runoff rate varies in time, the travel time varies in time and becomes . In reality, also varies in time, but [56] made the approximation that , where is the total area that is upslope of the grid cell and is the area of the grid cell itself. This assumption has been made by others (e.g., [28,58]) and was evaluated in detail by [56], who found it to be a good approximation of full kinematic wave routing on hillslopes. Using these approximations, Equation (1) becomes:
Even though every grid cell has the same area , can vary between grid cells depending on whether flow occurs in the diagonal or cardinal directions of the DEM.
An expression can then be written for the total hillslope travel time () for flow that starts at any cell k in the basin and moves to the basin outlet:
where the summation includes all hillslope cells on the path between cell k and the basin outlet. The total hillslope travel time is also equivalent to the time that the flood wave takes to move from point k to the channel network. Equation (3) indicates that the hillslope travel time depends on a variety of local characteristics. To simplify the model and isolate the impact of the flow path structure, three approximations are implemented. First, variation in the local flow length is neglected by replacing with , which is an effective flow length in the cell. Assuming that flow directions are equally likely to occur in all cardinal and diagonal directions, that effective length is the average of the cardinal and diagonal flow lengths of the grid cells (). Second, all hillslope cells are assumed to have the same roughness , which is frequently assumed when applying similar models due to data limitations (e.g., [40,56,59]). Third, all hillslope cells are assumed to have the same effective slope . In reality, most basins tend to have convex-up hillslopes due to slope-dependent transport processes such as rain splash, bioturbation, and soil creep [60,61,62]. However, planar hillslopes are a common assumption in many similar models (e.g., [40,59]). Using these approximations, the total hillslope travel time becomes:
To simplify the notation, the constant basin properties are collected into a single hillslope coefficient . In addition, the summation in Equation (4) is defined as where the subscript k is included because each location has a different path to the outlet and thus a different value for that summation. Substituting these variables into Equation (4), it becomes:
One can consider as the outcome (for location k) of a random variable . The variable probabilistically describes the collection of values that occurs within the basin. The meaning of can be elucidated by considering a simplified case. If one neglects the contribution of upslope cells (i.e., in Equation (4)), then the distribution of reduces to the distribution of hillslope travel distances in the basin. In the more general case, the distribution of is a hillslope travel distance distribution that is modified to account for upslope flow contributions.
It is assumed that the random variable is described by the Johnson Special Bounded (SB) distribution (this assumption is evaluated later). This distribution is related to the normal distribution, which is associated with sums [63,64], and is a sum as shown in Equation (4). The Johnson SB PDF is written as:
where is a shape parameter that primarily controls the skewness, and is a second shape parameter that primarily controls the kurtosis. and are the location and scale parameters, respectively. If the network type impacts the UH (the central hypothesis of this study), then the distribution parameters , , , and depend on the network type. It is also expected that they depend on maximum upslope area that is observed among all hillslope cells (i.e., the size of the hillslopes). These assumptions and the nature of any such dependence are examined later.
2.2. Channel Travel Time Distribution
A similar approach is used for the travel time distribution for the channels. The flood wave travel time in a channel cell is based on an expression derived by [65], who considered a wide rectangular channel with flow entering from both upstream and laterally under the kinematic wave approximation. If the equation in [65] is applied to a channel cell at location j, it can be written as:
where is the travel time in the channel cell j, is the length of the channel in the cell, is Manning’s roughness coefficient, is the channel width, is the flow at the downstream end of the cell, and is the flow that is contributed to the cell from upstream. It is unlikely that the entire upstream area simultaneously contributes flow to a channel cell for storms with realistic durations (unlike hillslopes, which drain relatively small areas). Following [66], it is assumed that only a constant fraction r of the upstream area contributes flow simultaneously. Thus, and if runoff is spatially homogeneous. In reality, r is expected to vary in time during a storm [38]. An expression can then be written for the total channel travel time from a cell k in the basin to the outlet :
where the summation includes all channel cells on the path between cell k and the outlet.
Several approximations are implemented to isolate the effect of the network structure. Local variations in cell flow lengths are again neglected by replacing with , and all channel cells are assumed to have the same roughness . In addition, the channel slope is assumed to depend on the contributing area according to a power function where b and θ are constants that can vary among basins [67,68,69,70,71]. The coefficient b is related to the vertical relief of the basin, while θ describes the concavity of the longitudinal profiles of the channels. The slope‒area relationship describes the average slope at a given contributing area, but much variation typically occurs around this average value [70,72,73]. In addition, deviations from a power function can also occur [74]. Such complexities are neglected here. Finally, the channel width is also assumed to depend on the contributing area according to a power function where d and e are constants that can vary between basins. Such a dependence has been observed empirically [68,75,76,77] and has been used in other models [38]. Using these simplifications in Equation (8), one obtains:
To simplify the notation, the constants in front of the summation are collected into a single channel coefficient , and the summation in Equation (9) is defined as . Using these definitions, Equation (9) can be written:
The variable is viewed as the outcome for location k of a random variable . If upstream flows were neglected (i.e., in Equation (9)), then the distribution of would describe the distribution of channel travel distances within the basin, which is essentially the basin’s width function. Thus, the distribution of can be viewed as a modified width function that accounts for upstream flow.
It is assumed that is described by the Johnson SB distribution, which can be written as:
where and are the shape parameters, is the location parameter, and is the scale parameter. If the network type affects the UH, then the parameters , , , and depend on the network type. These parameters are also expected to depend on the maximum upstream area for any channel cell (i.e., the size of the basin). The choice of distribution and any dependence of the parameters on the network type will be evaluated later.
2.3. Total Travel Time Distribution
The total travel time from an arbitrary point k to the outlet () is the sum of the hillslope and channel travel times from that point, so one can write:
To simplify the notation, the time-invariant portion of the overall travel time is defined as . The PDF for X can be determined by a convolution assuming that and are independent. The hillslope size is typically similar irrespective of the hillslope’s position in the basin [78], so the hillslope and channel travel times from a point to the outlet are expected to be independent [4]. Because an analytical solution for this convolution is not known, the convolution is performed numerically:
where n is the number of discrete increments of X used in the numerical evaluation, ΔX is the size of the increment, and l is an index for those increments. Finally, the instantaneous UH (IUH) associated with runoff rate can be found from the PDF of , which is:
The IUH varies in time because varies in time. The UH for runoff rate can then be calculated as [40]:
where is the runoff time step. Stormflow hydrographs can then be calculated by a convolution of the runoff values and the associated UHs, as described by [41].
In summary, this modeling approach isolates the effect of the drainage network structure into the random variables and , which are modifications of the travel distance distributions that also account for the effects of upstream flow on the travel times. For a given basin, the PDFs for and can be calculated without prior specification of most basin characteristics (L, θ, and e are required). Thus, within the presented framework, they allow the most direct and general assessment of impact of the network structure on the IUH (with as few confounding effects as possible). We have hypothesized that the parameters that determine the PDFs for and can be found based on the network type as well as and . The distributions of and can be transformed into a time-varying IUH using the following basin properties as inputs:, , , r, b, d, θ, and e.
2.4. Application
The presented UH framework is applied to 10 basins from each of the five network types. Based on inspection of satellite photos and available imperviousness data (see Supplementary Materials), all the basins have little human development and no obvious human alteration of the channel network. Nearly all the basins were originally processed by [53]. They chose each outlet to ensure that the associated basin exhibits a single network type (i.e., the outlets do not correspond to stream gauge locations). In their collection, however, Buckeye Run, WV (dendritic) and Stony Run, WV (trellis) are sub-basins within other included basins. Furthermore, Hill Creek, UT (parallel) does not strongly exhibit parallel characteristics. Thus, these three basins were replaced with Rockcastle Creek, KY (dendritic), Penn’s Creek, PA (trellis), and Mancos River Tributary, CO (parallel). The new basins were selected from regions where the networks had been previously classified with a quantitative method [54]. The new basins were processed in the manner used by [53] for the other basins. Specifically, the TauDEM toolbox for ArcGIS was used to fill pits, determine flow directions (according to the D8 algorithm), and calculate upslope/upstream areas and slopes [79,80,81]. The computed travel time can be infinite in a cell if the local slope is zero. Thus, any zero slope was replaced by the lesser of (1) the resolution of the calculated slope (which is estimated as 1 m divided by the DEM grid cell length) or (2) 0.8 times the minimum nonzero slope present in the processed DEM.
A cell is considered to contain a channel if the contributing area exceeds a selected threshold. Montgomery [82] divided the slope‒area plot into five geomorphic zones (hillslopes, valley heads, colluvial channels, bedrock channels, and alluvial channels), and we evaluated two thresholds based on these zones. The first threshold separates the valley heads and colluvial channels, and the second distinguishes the colluvial and bedrock channels. The presented results use the second threshold because it avoids producing unrealistic adjacent, parallel channels at small contributing areas (the results when the first threshold is used are discussed later).
Basic characteristics for the 50 basins are summarized in Table 1. Additional general properties of the basins are provided in the Supplementary Materials. The pinnate basins tend to be larger than the other types with an average area of 1014 km2. The parallel and rectangular basins are the smallest with average areas of 217 km2 and 254 km2, respectively. The DEM resolution depends on the DEM source. It is coarsest (on average 76.4 m) for pinnate basins in Ukraine and Moldova, for which the Shuttle Radar Topography Mission (SRTM) provided data at a resolution of 3 arc seconds. The other network types have an average resolution of 27 m. The channel threshold area (which also determines ) is largest for pinnate basins (on average 688,560 m2) and smallest for dendritic and parallel basins (on average 53,720 m2 and 76,850 m2, respectively).

Table 1.
Basin areas and channel threshold areas for the 50 analyzed basins. The thresholds are identified between the colluvial and bedrock channel segments in the slope‒area plots.
3. Results
3.1. Distributions of Ash and Asc
In order to calculate values within any basin, values must be selected for the flow length in each DEM cell L, the width‒area exponent e, and the slope‒area exponent . was set based on the DEM resolution of each basin under consideration, and was assigned a typical value of 0.5 for all basins [82]. Because might depend in part on the network type, it was calculated from the slope‒area plot of each basin. The value of for each basin is provided in the Supplementary Materials. has averages of 0.37, 0.43, 0.35, 0.38, and 0.39 for the dendritic, parallel, pinnate, rectangular, and trellis types, respectively.
Before comparing the distributions of and between network types, it is necessary to examine whether the Johnson SB distribution is appropriate. Twenty-four theoretical distributions were identified as candidates to describe and based on their general properties (e.g., the existence of a lower bound). The parameters of each distribution were estimated for each basin using Easyfit version 5.6, which selects the parameter estimation method (method of moments, L-moments, maximum likelihood, or least squares) according to the distribution type. The fit of each distribution was then measured using the Kolmogorov‒Smirnov (K‒S) statistic, which is the maximum deviation between the sample cumulative distribution function (CDF) (i.e., determined directly from the DEMs) and the theoretical CDF [83,84]. The K‒S statistic is not compared to a critical value in a hypothesis test because the observations of and are not independent due to the nested structure of the drainage networks. Thus, they violate the assumptions required to perform such a test [83,85]. Because the candidate distributions have different numbers of parameters, the Akaike Information Criterion (AIC), as formulated by [86], was also used to assess the fit of each distribution while accounting for the number of parameters and possible overfitting.
The K‒S statistics for the four best-fitting distributions for and are plotted for all basins in Figure 2. The four best-fitting distributions for are the generalized extreme value, three-parameter Weibull, four-parameter generalized gamma, and Johnson SB (Figure 2a). Overall, the Johnson SB distribution fits the observations of best with an average K‒S statistic of 0.014. Among the considered distributions, it also produces the lowest average K‒S statistic for each type except rectangular. Furthermore, the Johnson SB distribution produces the best AIC values for 31 of the 50 basins. The Weibull distribution produces the best AIC values for the remaining basins. Overall, these results suggest that the Johnson SB distribution is the best choice for representing and that the use of a four-parameter distribution is warranted.
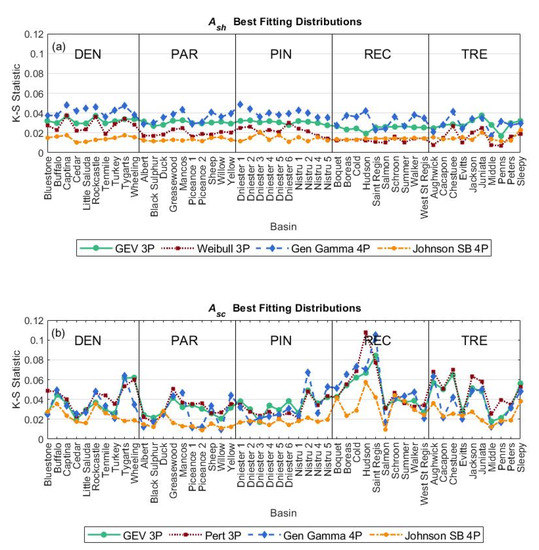
Figure 2.
Kolmogorov‒Smirnov (K‒S) statistics for the four best fitting distributions for (a) and (b) . DEN denotes dendritic, PAR denotes parallel, PIN denotes pinnate, REC denotes rectangular, and TRE denotes trellis.
The four best-fitting distributions for are the generalized extreme value, PERT, four-parameter generalized gamma, and Johnson SB distributions (Figure 2b). On average, the Johnson SB distribution fits the observed CDFs of best with an average K‒S statistic of 0.023. The Johnson SB distribution also exhibits the best average performance for each network type. The Johnson SB distribution produces the best AIC values for 26 of the 50 basins (the four-parameter generalized gamma distribution produces the best AIC values for many of the remaining basins). Overall, these results suggest that the Johnson SB distribution is also the best choice for representing .
Figure 3 compares the distributions of and for an example basin of each type. The distributions always have positive skewness, but the degree of peakedness and skewness varies between the network types. Specifically, the rectangular and trellis basins have more apparent peaks and skewness than the other types. In all cases, the Johnson SB distribution fits the histograms well. The distributions also differ substantially between the five basins. Notably, the distribution has negative skewness for the dendritic and parallel basins. It is nearly symmetrical for the trellis basin and has positive skewness for the pinnate and rectangular basins. The Johnson SB distribution fits histograms well, but it misses local fluctuations in some of the histograms.
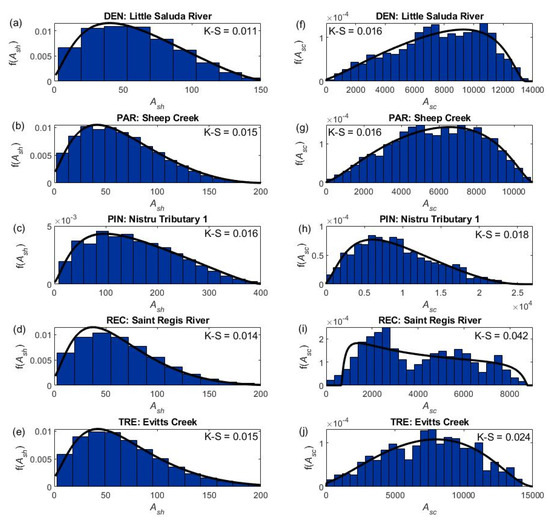
Figure 3.
Histograms and fitted Johnson SB distributions for (a–e) and (f–j) for an example basin of each type. The basins are the same as those in Figure 1.
Figure 4 plots the calibrated Johnson SB distribution parameters for against for all 50 basins. The shape parameters and and the location parameter appear to be independent of and relatively constant within each type. However, differences are observed in the parameter values for different types. For example, rectangular and trellis basins tend to have higher and values than the other network types. Higher values produce more peaked distributions, and higher values produce greater skewness. Thus, these results confirm that the differences observed earlier for the example basins are typical for the network types. The scale parameter depends on (Figure 4), and this dependence appears to differ between types. Most notably, the pinnate and trellis basins have steeper relationships than the other types. The relationships can be approximated by power functions (a power function is preferable to a linear function because it always passes through the origin as expected for both and ). The dependence of the distribution parameters on network type is interesting because the type is based on the channel network structure not the hillslope flow paths. These results suggest a connection between the flow path structure on the hillslopes and the channels.
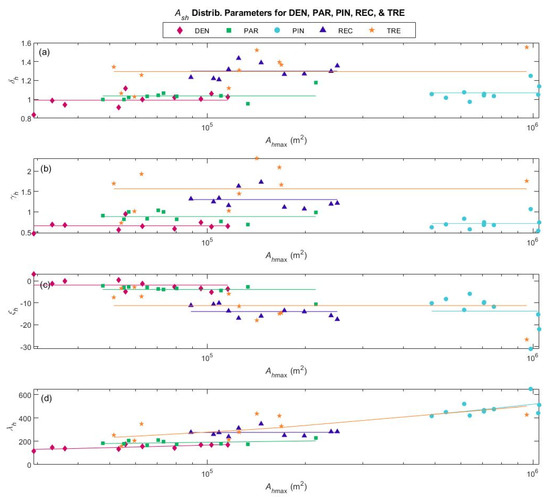
Figure 4.
Parameters (a) , (b) , (c) , and (d) of the Johnson SB distribution for plotted against the maximum hillslope area . The symbols show the calibrated parameter values for each basin. The horizontal lines in (a–c) show the average parameter value for each network type. The lines in (d) show power functions fitted to the values for each network type.
Figure 5 plots the Johnson SB parameters for against . The shape parameters and and the location parameter appear to be independent of . does not appear to differ between the network types, but the skewness-related parameter appears to differ. Dendritic and parallel basins have negative values, while pinnate basins have positive values (which is consistent with the example basins in Figure 3). The scale parameter varies with , and the observed relationships can be approximated with power functions. The power functions may differ between certain network types. Specifically, the power function for pinnate basins is much higher than the power function for rectangular basins.
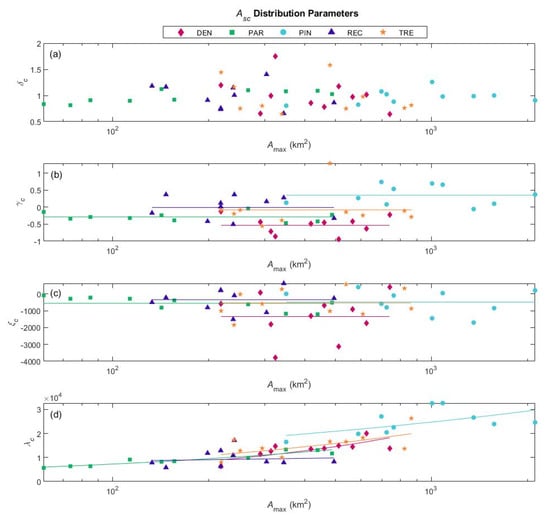
Figure 5.
Parameters (a) , (b) , (c) , and (d) of the Johnson SB distribution for plotted against the maximum upstream area . The symbols show the calibrated parameter values for each basin. The horizontal lines in (b–c) show the average parameter value for each network type. The lines in (d) show power functions fitted to the values for each network type.
To determine whether the differences in the distribution parameters for and are statistically significant, an analysis of variance (ANOVA) was employed for the parameters that are independent of and . Specifically, a one-way ANOVA method was used for unadjusted pairwise comparisons between network types [87] with a 90% confidence interval (p-value = 0.1). Similarly, an analysis of covariance (ANCOVA) was used to determine whether the coefficients and exponents of the power functions are significantly different between types [88]. For , the power function is:
where and are the fitted coefficient and exponent, respectively. The power function for is the same but uses the coefficient and exponent . The ANCOVA analysis was performed by first taking the logarithms of the variables involved and examining whether the intercepts and slopes of the resulting linear relationships are different.
For , all 10 pairs of network types have at least one parameter that is significantly different (Table 2). Thus, the differences that were identified visually in Figure 4 are consistent enough between types to be significant. For , eight out of 10 pairs of network types have at least one parameter that is significantly different (Table 2). Most commonly, the different parameter is , which is associated with skewness. In contrast, never differs between types. Fewer parameters are significantly different for than because the parameters for tend to be more variable within a given network type. Overall, these results confirm that the distributions for and are different between the five network types.

Table 2.
Distribution parameters that exhibit significant differences between the network types based on the analysis of variance (ANOVA) and analysis of covariance (ANCOVA) tests. For each pairing of network types, the top row reports parameters for , and the bottom row reports parameters for .
Table 3 provides the average values of , , and for each network type (and average values for all basins combined). It also provides the coefficient and exponent of the power function that estimates from for each type (and a fitted power function for all basins combined). Equivalent information is provided for , , and , but only an overall average value is provided for because this parameter does not vary significantly between types.

Table 3.
Estimated parameters of the Johnson SB distribution for (left) and (right).
We next evaluate the reliability of estimating the distributions for and from the network type (as well as and ). To make this assessment, the K‒S statistic is calculated when the distributions for and are estimated by three methods. In Method 1, the distribution parameters are determined directly from the and distributions for each basin (i.e., using the values shown in Figure 4 and Figure 5). In Method 2, they are estimated from the network type (using the values for each type in Table 3). In Method 3, they are estimated without consideration of the network type (using the values for all basins combined in Table 3).
Comparing Methods 3 and 2 for , 44 of the 50 basins have improved accuracy (lower K‒S statistics) when the network type is included (Figure 6a). The average K‒S statistic across all basins is 0.095 for Method 3 and 0.037 for Method 2. The improvement occurs for all types but is smallest for trellis networks. Thus, considering the network type provides much better estimates of the distribution than neglecting the network type. Comparing Methods 2 and 1 for , the K‒S statistics are relatively similar (the average K‒S statistic is 0.014 for Method 1). However, Method 1 provides better K‒S statistics for trellis basins. Thus, the network type provides adequate information for estimating the distribution of for most types, but explicit consideration of the individual basins is needed for trellis networks.
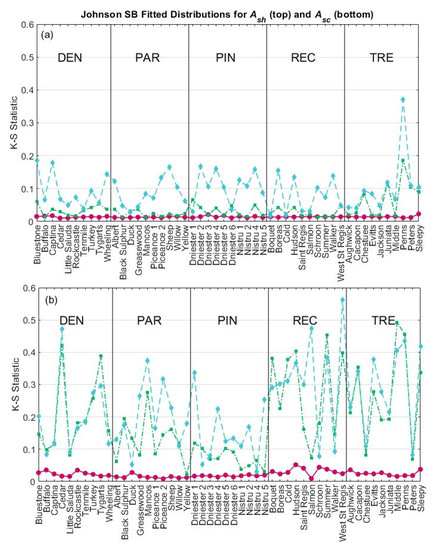
Figure 6.
Kolmogorov‒Smirnov (K‒S) statistics for the Johnson SB distribution for (a) and (b) when the distribution parameters are estimated separately for each network (Method 1), based on network type (Method 2), and neglecting network type (Method 3).
For , 31 of the 50 basins have improved accuracy (lower K‒S statistics) when the network type is included (comparing Methods 3 and 2), but the overall improvement is small (Figure 6b). The average K‒S statistic is 0.231 for Method 3 and 0.190 for Method 2. The improvement is greatest for parallel and pinnate basins. Using Method 2 for parallel basins, the K‒S value is reduced by a third, while the value is halved for pinnate basins. For dendritic basins, almost no improvement is observed. Dendritic basins are expected to exhibit the highest degree of variability in their network structures because they develop without strong topographic or lithologic constraints. The K‒S statistics for Method 1 are typically much lower than those of Method 2 (the average K‒S statistic for Method 1 is 0.023). The only case where the distribution of can be accurately estimated from the network type instead of the individual network is pinnate.
3.2. IUHs
Four cases are used to compare the IUHs between network types and between different estimation methods. Case 1 explicitly considers the individual cell slopes and the actual flow paths for each basin (i.e., the travel times are based on Equations (3) and (8)). This method is equivalent to a pre-existing nonlinear SDTT method [41] and is considered the best estimate of the IUH for each basin. Case 2 replaces the individual cell slopes with (for hillslopes) and the slope‒area relationship (for channels), and it replaces the actual distributions of and with a theoretical distribution that is calibrated for each basin (i.e., the travel times are based on Equations (4) and (9)). The case continues to use the distribution parameters that were obtained from each individual basin. This case evaluates the assumptions that allow the network structure to be isolated in the variables and . Case 3 instead estimates the distribution parameters based on the network type. This is a synthetic UH method that uses the network type to infer the flow path configuration. Case 4 estimates the parameters of the theoretical distributions irrespective of the network type. This case is analogous to traditional synthetic UH methods that neglect consideration of an individual basin’s network structure.
For this comparison, most of the parameters were set to constant values for all 50 basins (Table 4). This approach reduces confounding effects under the assumption that these parameters are independent of the network type. The selected roughness for the hillslopes corresponds to short-grass prairie [89], and the roughness for channels corresponds to a low-slope stream with weeds and stones or a mountain stream with cobbles and boulders [90]. The fraction of area contributing flow falls within the range for humid to arid climates (0.2 to 0.5) [66]. The width‒area coefficient is a typical value [82]. The value varies between basins and might be associated with the network type, so it is estimated from the slope‒area plot from each basin’s DEM. For Cases 2 through 4, was estimated as the average hillslope slope from the DEM of each basin because it might also depend on the network type. For consistency, was set based on the DEM resolution of each basin under consideration. The values of , , and for each basin are provided in the Supplementary Materials.

Table 4.
Model parameters used in the development of the instantaneous unit hydrographs. Parameters that vary are determined from the digital elevation model for each basin.
The IUHs from Case 1 exhibit notable differences between the example basins of each type (Figure 7). The IUH for the dendritic basin is negatively skewed, the IUH for the pinnate basin is positively skewed, and the IUHs for the other basins are approximately symmetrical. Comparing Figure 7 to the right column in Figure 3, one sees that the IUH shapes are almost identical to the distributions of for the same basins. The distributions play a much larger role than the distributions in determining the IUHs because 80% or more of the total travel time occurs in the channels.
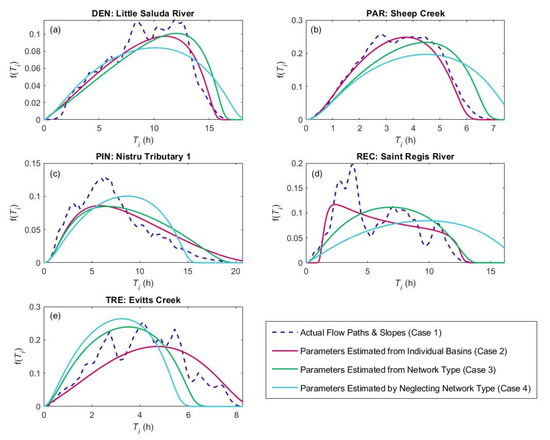
Figure 7.
Instantaneous unit hydrographs (IUHs) estimated by the four methods described in the legend for an example basin of the (a) dendritic, (b) parallel, (c) pinnate, (d) rectangular, and (e) trellis types. The basins are the same as those in Figure 1.
When the slopes are approximated and the theoretical distribution is used (Case 2), the IUHs remain similar to Case 1, but the local fluctuations in the IUHs are lost (Figure 7). For the pinnate and trellis basins, the IUHs for Case 2 also shift to the right. The travel times depend nonlinearly on slope, so using the average slope for a given contributing area is not equivalent to using the distribution of slopes for that contributing area. When the network type is used to estimate the IUH (Case 3), the IUH for the pinnate basin remains very close to Case 2 while the other basins deviate more. This result is consistent with the earlier results that showed the distributions of are best estimated from the network type for the pinnate case. Case 4, which neglects the network type, has approximately zero skewness and is a poor match for the IUHs from Case 1 for all basins shown.
Four metrics are used to quantify the difference in performance between the network-type-based method (Case 3) and the case that neglects the type (Case 4) for all 50 basins (Figure 8). The first metric is the Root Mean Squared Error (RMSE) [91,92] where Case 1 is considered the observed IUH (Figure 8a). The second metric is the Nash‒Sutcliffe Coefficient of Efficiency (NSCE) [93]. Because larger NSCE values indicate better performance (in contrast with the other metrics), Figure 8b instead shows 1-NSCE so that lower values indicate better performance. The third metric is the absolute error in the IUH peak value (Figure 8c), and the fourth metric is the absolute error in the time of the IUH peak (Figure 8d).
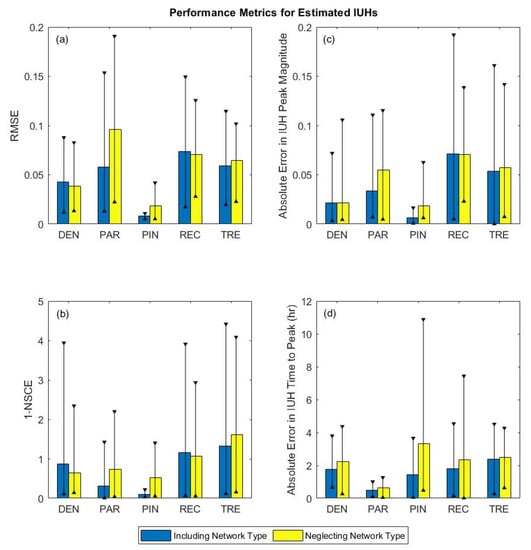
Figure 8.
Performance metrics when the instantaneous unit hydrographs are estimated by either including or neglecting the network type as indicated in the legend. Column heights indicate the average performance and black bars indicate the range of performance for each case.
By most measures, considering the network type provides little improvement in the estimated IUH. For time to peak, however, considering the type improves the average performance for all types and reduces the range in performance for all types except trellis. This improvement occurs because the network type helps determine the skewness of the IUH as seen in Figure 7. Considering the type also provides an improvement in performance by all measures for parallel and pinnate basins. However, by most measures, pinnate has lower errors when the type is considered than the other network types. This result occurs because the pinnate type is an adequate substitute for the individual flow path network when estimating the distributions of and .
The RMSEs for Case 3 were also calculated when the assumed parameter values were varied from those in Table 4 (not shown). Overall, the RMSE decreases when the hillslope roughness increases, the channel roughness increases, the width‒area coefficient d increases, the slope‒area coefficient b decreases, the fraction of area contributing flow r decreases, the runoff decreases, and the linear reservoir constant K increases. It remains almost unchanged as the average hillslope slope changes. These results are explained in depth by [94,95].
3.3. Hydrographs
In this section, we consider whether the differences in the IUHs that were observed in the previous section produce meaningful differences in the response to a storm. Specifically, a 6-h SCS Type II storm with a total depth of 12.7 mm and an 18-min time step (5% of the storm duration) was applied to the example basins. For simplicity, all rainfall was assumed to become runoff (no losses were considered). The hydrologic response was then generated using the four IUH methods (i.e., Cases 1–4). To facilitate comparison between basins, the resulting discharge hydrographs were normalized by each basin’s area to produce hydrographs for specific discharge q (Figure 9). Overall, the hydrographs exhibit visual differences between the five basins, which suggests that the differences in the and distributions (and IUHs) between the network types can produce differences in the generated hydrographs. The results also suggest that the different IUH methods can produce visibly different hydrographs, including differences in the timing and magnitude of the peak value. If Case 1 is again considered the most accurate case, the IUH method that uses the network type (Case 3) usually provides a better approximation than the method that neglects any consideration of network structure (Case 4). However, the use of the actual flow paths (Case 2) provides a noteworthy improvement in the hydrograph over Case 3 in all cases except pinnate. Overall, these results are consistent with the IUH results presented earlier and demonstrate that the IUH differences produce meaningful differences in the storm hydrographs.
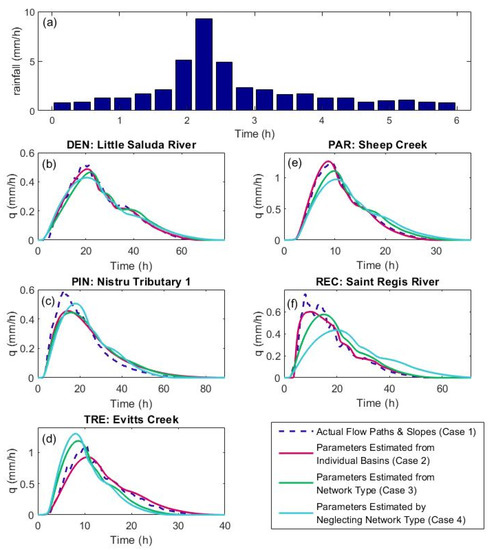
Figure 9.
(a) Rainfall intensity for a 6-h SCS Type II storm and the resulting specific discharge hydrographs for an example basin of the (b) dendritic, (c) pinnate, (d) trellis, (e) parallel, and (f) rectangular types when the IUH is determined using the four methods described in the legend. The basins are the same as those in Figure 1.
4. Discussion and Conclusions
This study considered whether the dendritic, parallel, pinnate, rectangular, and trellis networks exhibit distinct UHs and whether knowledge of the network type provides sufficient information about the network structure for synthetic UH determination. Flood wave travel times were calculated based on a kinematic wave approach, and approximations were implemented to isolate the effects of the network structure into two random variables ( and ). The distribution of is similar to the distribution of hillslope travel lengths, but it accounts for the effects of upslope flow contributions on the travel time. The distribution of is similar to the width function, but it also includes the effects of upstream flow.
The distributions of are significantly different between the five network types. Because the types are determined from the channel network structure, this result suggests that the flow path structure on the hillslopes (which determines ) is somehow associated with the channel network type. It is possible that the flow path structure on the hillslopes depends on the channel network configuration into which they flow or perhaps that the dominant hillslope processes are associated with the network types and control the hillslope flow paths.
The distributions of are also significantly different between the five network types. Most notably, the parameter that controls the skewness of the distribution differs between types. Dendritic and parallel basins have negative skewness (i.e., many large values), which is associated with abundant locations in the basin that are distant from the outlet (see examples in Figure 1). In contrast, pinnate basins have positive skewness (i.e., few large values), which is associated fewer locations in the basin that are far from the outlet (see Figure 1). The other network types tend to have more symmetrical distributions for . The differences in the distributions are also observed in the associated IUHs. Overall, the results suggest that dendritic, parallel, pinnate, rectangular, and trellis networks have distinct UHs as hypothesized.
Using the network type produces better estimates of the distributions for individual basins than neglecting the type. For all types aside from trellis, the network type provides sufficient information to determine the distributions. For trellis, considering the type provides only modest improvements over neglecting it. Using the network type also produces better estimates of the distributions for individual basins than neglecting it. However, for all types except pinnate, knowledge of the type does not provide sufficient information to accurately estimate the distributions.
The proposed synthetic UH method, which estimates the distributions of and based on the network type, provides better estimates of the IUH time to peak than a method that neglects the type. This improvement occurs because the time to peak is affected by the skewness of the and distributions, which is different among the types. However, other measures of performance such as RMSE and NSCE usually show little improvement when network type is considered. The exceptions are parallel and pinnate, which show noteworthy improvement in all measures when the type is considered. By most measures, pinnate networks have lower errors than the other types.
Although not discussed in detail in this paper, the analyses were repeated for a medium and small sub-basin within each of the 50 large basins [95]. Those results suggest that the distinctions between the network types become less clear at small scales, so the value of the network type in UH determination decreases. We also repeated the analysis when the IUH is coupled with a linear reservoir similar to the Clark method. After applying the linear reservoir, all UHs became positively skewed. The distinctions between network types remained but became smaller. Finally, we repeated the analysis using a smaller area threshold for identifying the channel cells and found that the same qualitative conclusions hold.
Overall, the results suggest that considering network type provides some benefits over neglecting it. Thus, considering the network type may help hydrologists better understand the hydrologic behavior of a particular basin in comparison to other basins that have different network types. The distinctive hydrologic response a given network type may also help explain the geomorphic evolution of that network type. However, knowledge of the type is an adequate substitute for the actual flow path configuration only for pinnate basins. Thus, the results do not support the hypothesis that the network type can provide sufficient information about the flow path structure for synthetic UH determination, except for pinnate networks. For pinnate networks, the typical network structure may provide enough information to make a detailed consideration of an individual network’s structure unnecessary.
This research could be extended along several paths. First, the effects of misclassifying a network on the synthetic UH performance could be investigated because it might be difficult to classify some networks in practice. Second, the effect of the DEM resolution on the results could be studied. It is expected that finer resolutions would better characterize each network and thus may provide clearer differences between network types. Third, further examination of the hillslope travel time distributions is warranted. For example, it might be possible to relate the dominant hillslope processes to the travel time distributions on the hillslopes. The hillslope travel times are expected to become more important when smaller basins are modeled. Fourth, the assumption that a constant fraction of upstream area simultaneously contributes flow to channels could be further analyzed. A relationship between this fraction and the overall basin size could be considered. Similarly, the effects of other simplifying assumptions (the constant hillslope slope, the constant area threshold to distinguish hillslopes and channels, the power law slope‒area relationship for the channels, etc.) could be examined because they might impact the results. Fifth, the assumption that runoff occurs uniformly across the basin and that the flow occurs on the ground surface could be relaxed to consider partial area runoff production and the distinction of old and new water. This change may affect the resulting hydrographs. Sixth, the impacts on urbanization on the hydrologic response of different network types could be examined. It is expected that impervious areas would change both the pattern of runoff production and the roughness, and the introduction of gutter and pipe systems might reduce the differences between the network types. Finally, the IUHs from the proposed method were evaluated by comparing to a pre-existing SDTT model that explicitly represents the slopes and flow paths within the basin. For pinnate basins where a network-type-based synthetic UH may be viable, future research should compare the results from the synthetic UH to observed hydrographs. Comparisons should also be made to UHs inferred from streamflow data. Such comparisons would also allow for testing other assumptions in the UH method, including the use of kinematic wave theory.
Supplementary Materials
The following are available online at https://www.mdpi.com/2073-4441/12/3/669/s1, Table S1: Summary of geomorphic properties for the 50 analyzed basins, Table S2: Summary of general properties for the 50 analyzed basins.
Author Contributions
Conceptualization, J.D.N. and J.G.; methodology, J.D.N.; software, K.C., D.M., A.A., S.H.; validation, K.C., D.M., A.A., S.H.; formal analysis, D.M.; writing—original draft preparation, K.C., D.M., and J.D.N.; writing—review and editing, J.D.N. and J.G.; supervision, J.D.N. and J.G.; project administration, J.D.N.; funding acquisition, J.D.N. and J.G. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by Mountain-Plains Consortium grant number MPC-481, FONDECYT 1161439, and ANID/FONDAP/15110017.
Acknowledgments
The authors thank Michael Coleman for his help generating preliminary results for this study and Tomas Bunster for assistance in generating the hydrograph results. The authors also thank the two anonymous reviewers for their suggestions of how to improve the manuscript.
Conflicts of Interest
The authors declare no conflict of interest. The funders had no role in the design of the study; in the collection, analyses, or interpretation of data; in the writing of the manuscript, or in the decision to publish the results.
References
- Feldman, A.D. Hydrologic Modeling System HEC-HMS; U.S. Army Corps of Engineers Technical Reference Manual: Davis, CA, USA, 2000.
- Arnold, J.G.; Fohrer, N. SWAT2000: Current capabilities and research opportunities in applied watershed modelling. Hydrol. Process. 2005, 19, 563–572. [Google Scholar] [CrossRef]
- Sherman, L.K. Streamflow from rainfall by the unit hydrograph method. Engl. News Record. 1932, 108, 501–505. [Google Scholar]
- Cudennec, C.; Fouad, Y.; Sumarjo Gatot, I.; Duchesne, J. A geomorphological explanation of the unit hydrograph concept. Hydrol. Process. 2004, 18, 603–621. [Google Scholar] [CrossRef]
- Rodríguez-Iturbe, I.; Valdes, J.B. The geomorphologic structure of hydrologic response. Water Resour. Res. 1979, 15, 1409–1420. [Google Scholar] [CrossRef]
- Rinaldo, A.; Vogel, G.K.; Rigon, R.; Rodriguez-Iturbe, I. Can one gauge the shape of a basin? Water Resour. Res. 1995, 31, 1119–1127. [Google Scholar] [CrossRef]
- Robinson, J.S.; Sivapalan, M.; Snell, J.D. On the relative roles of hillslope processes, channel routing and network geomorphology in the hydrologic response of natural catchments. Water Resour. Res. 1995, 31, 3089–3101. [Google Scholar] [CrossRef]
- Singh, P.K.; Mishra, S.K.; Jain, M.K. A review of the synthetic unit hydrograph: From the empirical UH to advanced geomorphological methods. Hydrol. Sci. J. 2014, 59, 239–261. [Google Scholar] [CrossRef]
- SCS. Section 4 Hydrology. In National Engineering Handbook; Soil Conservation Service: Washington DC, USA, 1972. [Google Scholar]
- NRCS. Hydrographs. In National Engineering Handbook; U.S. Department of Agriculture: Washington, DC, USA, 2007; 16p. [Google Scholar]
- Clark, C.O. Storage and the Unit Hydrograph. Proc. Am. Soc. Civ. Eng. 1945, 69, 1333–1360. [Google Scholar]
- Kull, D.W.; Feldman, A.D. Evolution of Clark’s unit graph method to spatially distributed runoff. J. Hydrol. Eng. 1998, 3, 9–19. [Google Scholar] [CrossRef]
- Peters, J.C.; Easton, D.J. Runoff simulation using radar rainfall data. J. Am. Water Resour. Assoc. 1996, 32, 753–760. [Google Scholar] [CrossRef]
- Saghafian, B.; Julien, P.Y.; Rajaie, H. Runoff hydrograph simulation based on time variable isochrone technique. J. Hydrol. 2002, 261, 193–203. [Google Scholar] [CrossRef]
- Nash, J.E. The form of the instantaneous unit hydrograph. In Comptes Rendus et Rapports; IASH–IUGG: Toronto, ON, Canada, 1957; pp. 114–118. [Google Scholar]
- Snyder, F.F. Synthetic unit-graphs. Trans. Am. Geophys. Union 1938, 19, 447–454. [Google Scholar] [CrossRef]
- Bhunya, P.K.; Berndtsson, R.; Ojha, C.S.P.; Mishra, S.K. Suitability of Gamma, Chi-square, Weibull, and Beta distributions as synthetic unit hydrographs. J. Hydrol. 2007, 334, 28–38. [Google Scholar] [CrossRef]
- Gray, D.M. Synthetic unit hydrographs for small drainage areas. J. Hydraul. Div. 1961, 87, 33–54. [Google Scholar]
- Bhunya, P.K.; Mishra, S.K.; Berndtsson, R. Simplified two-parameter gamma distribution for derivation of synthetic unit hydrograph. J. Hydrol. Eng. 2003, 8, 226–230. [Google Scholar] [CrossRef]
- Croley, T.E., II. Gamma synthetic hydrographs. J. Hydrol. 1980, 47, 41–52. [Google Scholar] [CrossRef]
- Bhunya, P.K.; Singh, P.K.; Mishra, S.K. Fréchet and chi-square parametric expressions combined with Horton ratios to derive a synthetic unit hydrograph. Hydrol. Sci. J. 2009, 54, 274–286. [Google Scholar] [CrossRef]
- Bhunya, P.K.; Mishra, S.K.; Ojha, C.S.P.; Berndtsson, R. Parameter estimation of beta distribution for unit hydrograph derivation. J. Hydrol. Eng. 2004, 9, 325–332. [Google Scholar] [CrossRef]
- Koutsoyiannis, D.; Xanthopoulos, T. On the parametric approach to unit hydrograph identification. Water Resour. Manag. 1989, 3, 107–128. [Google Scholar] [CrossRef]
- Gupta, V.K.; Waymire, E.; Wang, C.T. A representation of an instantaneous unit hydrograph from geomorphology. Water Resour. Res. 1980, 16, 855–862. [Google Scholar] [CrossRef]
- Gupta, V.K.; Waymire, E. On the formulation of an analytical approach to hydrologic response and similarity at the basin scale. J. Hydrol. 1983, 65, 95–123. [Google Scholar] [CrossRef]
- Strahler, A.N. Quantitative analysis of watershed geomorphology. Eos. Trans. Am. Geophys. Union 1957, 38, 913–920. [Google Scholar] [CrossRef]
- Van der Tak, L.D.; Bras, R.L. Incorporating hillslope effects into the geomorphologic instantaneous unit hydrograph. Water Resour. Res. 1990, 26, 2393–2400. [Google Scholar] [CrossRef]
- Rodríguez-Iturbe, I.; González-Sanabria, M.; Bras, R.L. A geomorphoclimatic theory of the instantaneous unit hydrograph. Water Resour. Res. 1982, 18, 877–886. [Google Scholar] [CrossRef]
- Rigon, R.; Bancheri, M.; Formetta, G.; de Lavenne, A. The geomorphological unit hydrograph from a historical-critical perspective. Earth Surf. Proc. Land. 2016, 41, 27–37. [Google Scholar] [CrossRef]
- Kirkby, M. Tests of the random network model, and its application to basin hydrology. Earth Surf. Process. 1976, 1, 197–212. [Google Scholar] [CrossRef]
- Botter, G.; Rinaldo, A. Scale effect on geomorphologic and kinematic dispersion. Water Resour. Res. 2003, 39, 1286. [Google Scholar] [CrossRef]
- D’Odorico, P.; Rigon, R. Hillslope and channel contributions to the hydrologic response. Water Resour. Res. 2003, 39, 1–9. [Google Scholar] [CrossRef]
- Nicótina, L.; Alessi Celegon, E.; Rinaldo, A.; Marani, M. On the impact of rainfall patterns on the hydrologic response. Water Resour. Res. 2008, 44, 1–14. [Google Scholar] [CrossRef]
- Biswal, B.; Singh, R. Incorporating channel network information in hydrologic response modelling: Development of a model and inter-model comparison. Adv. Water Resour. 2017, 100, 168–182. [Google Scholar] [CrossRef]
- Lee, K.T.; Chen, N.-C.; Chung, Y.-R. Derivation of variable IUH corresponding to time-varying rainfall intensity during storms. Hydrol. Sci. J. 2008, 53, 323–337. [Google Scholar] [CrossRef]
- Maidment, D.R. GIS and hydrological modeling, Environmental Modeling within GIS; Oxford: University Press: New York, NY, USA, 1993. [Google Scholar]
- Bunster, T.; Gironás, J.; Niemann, J.D. On the influence of upstream flow contributions in spatially distributed travel time models for hydrograph prediction. Water Resour. Res. 2019, 55, 1–21. [Google Scholar] [CrossRef]
- Du, J.; Xie, H.; Hu, Y.; Xu, Y.; Xu, C.Y. Development and testing of a new storm runoff routing approach based on time variant spatially distributed travel time method. J. Hydrol. 2009, 369, 44–54. [Google Scholar] [CrossRef]
- Foda, R.F.; Awadallah, A.G.; Gad, M.A. A Fast semi distributed rainfall runoff model for engineering applications in arid and semi-arid regions. Water Resour. Manag. 2017, 31, 4941–4955. [Google Scholar] [CrossRef]
- Gironás, J.; Niemann, J.D.; Roesner, L.A.; Rodriguez, F.; Andrieu, H. A morpho-climatic instantaneous unit hydrograph model for urban catchments based on the kinematic wave approximation. J. Hydrol. 2009, 377, 317–334. [Google Scholar] [CrossRef]
- Lee, K.T.; Yen, B.C. Geomorphology and kinematic-wave-based hydrograph derivation. J. Hydraul. Eng. 1997, 123, 73–80. [Google Scholar] [CrossRef]
- Muzik, I. Flood modelling with GIS-derived distributed unit hydrographs. Hydrol. Process. 1996, 10, 1401–1409. [Google Scholar] [CrossRef]
- Zernitz, E.R. Drainage Patterns and Their Significance. J. Geol. 1932, 40, 498–521. [Google Scholar] [CrossRef]
- Castelltort, S.; Simpson, G.; Darrioulat, A. Slope-control on the aspect ratio of river basins. Terra Nov. 2009, 21, 265–270. [Google Scholar] [CrossRef]
- Howard, A.D. Drainage analysis in geologic interpretation: A summation. Am. Assoc. Pet. Geol. Bull. 1967, 51, 2246–2259. [Google Scholar] [CrossRef]
- Jung, K.; Niemann, J.D.; Huang, X. Under what conditions do parallel river networks occur? Geomorphology 2011, 132, 260–271. [Google Scholar] [CrossRef]
- Phillips, L.F.; Schumm, S.A. Effect of regional slope on drainage networks. Geology 1987, 15, 813–816. [Google Scholar] [CrossRef]
- Parvis, M. Drainage pattern significance in airphoto identification of soils and bedrocks. Photogramm. Eng. 1950, 16, 375–409. [Google Scholar]
- Pereira-Claren, A.; Gironás, J.; Niemann, J.D.; Passalacqua, P.; Mejia, A.; Escauriaza, C. Planform geometry and relief characterization of drainage networks in high-relief environments: An analysis of Chilean Andean basins. Geomorphology 2019, 341, 46–64. [Google Scholar] [CrossRef]
- Argialas, D.; Lyon, J.; Mintzer, O. Quantitative description and classification of drainage patterns. Photogramm. Eng. Remote Sens. 1988, 54, 505–509. [Google Scholar]
- Hadipriono, F.C.; Lyon, J.G.; Li, T. The development of a knowledge based expert system for analysis of drainage patterns. Photogramm. Eng. Remote Sens. 1990, 56, 905–909. [Google Scholar]
- Ichoku, C.; Chorowicz, J. A numerical approach to the analysis and classification of channel network patterns types. Water Resour. Res. 1994, 30, 161–174. [Google Scholar] [CrossRef]
- Mejía, A.I.; Niemann, J.D. Identification and characterization of dendritic, parallel, pinnate, rectangular, and trellis networks based on deviations from planform self-similarity. J. Geophys. Res. 2008, 113, 1–21. [Google Scholar] [CrossRef]
- Jung, K.; Marpu, P.R.; Ouarda, T.B.M.J. Impact of river network type on the time of concentration. Arab. J. Geosci. 2017, 10, 1–17. [Google Scholar] [CrossRef]
- Wong, T.S.W. Time of concentration formulae for planes with upstream inflow. Hydrol. Sci. J. 1995, 40, 663–666. [Google Scholar] [CrossRef]
- Zuazo, V.; Gironás, J.; Niemann, J.D. Assessing the impact of travel time formulations on the performance of spatially distributed travel time methods applied to hillslopes. J. Hydrol. 2014, 519, 1315–1327. [Google Scholar] [CrossRef]
- Dunne, T.; Black, R.D. Partial area contributions to storm runoff in a small New England watershed. Water Resour. Res. 1970, 6, 1296–1311. [Google Scholar] [CrossRef]
- Melesse, A.M.; Graham, W.D. Storm runoff prediction based on a spatially distributed travel time method utilizing remote sensing and GIS. J. Am. Water Resour. Assoc. 2004, 40, 863–879. [Google Scholar] [CrossRef]
- Robinson, J.J.S.; Sivapalan, M. Instantaneous response functions of overland flow and subsurface stormflow for catchment models. Hydrol. Process. 1996, 10, 845–862. [Google Scholar] [CrossRef]
- Gilbert, G.K. The convexity of hilltops. J. Geol. 1909, 17, 344–350. [Google Scholar] [CrossRef]
- Roering, J.J.; Kirchner, J.W.; Dietrich, W.E. Hillslope evolution by nonlinear, slope-dependent transport: Steady state morphology and equilibrium adjustment timescales. J. Geophys. Res. 2001, 106, 16499–16513. [Google Scholar] [CrossRef]
- Tucker, G.E.; Bras, R.L. Hillslope processes, drainage density, and landscape morphology. Water Resour. Res. 1998, 34, 2751–2764. [Google Scholar] [CrossRef]
- George, F.; Ramachandran, K.M. Estimation of parameters of Johnson’s system of distributions. J. Mod. Appl. Stat. Methods 2011, 10, 494–504. [Google Scholar] [CrossRef]
- Kottegoda, N.T. Fitting Johnson SB curve by the method of maximum likelihood to annual maximum daily rainfalls. Water Resour. Res. 1987, 23, 728–732. [Google Scholar] [CrossRef]
- Wong, T.S.W. Formulas for time of travel in channel with upstream inflow. J. Hydrol. Eng. 2001, 6, 416–422. [Google Scholar] [CrossRef]
- Iacobellis, V.; Fiorentino, M. Derived distribution of floods based on the concept of partial area coverage with a climatic appeal. Water Resour. Res. 2000, 36, 469–482. [Google Scholar] [CrossRef]
- Flint, J.J. Stream gradient as a function of order, magnitude, and discharge. Water Resour. Res. 1974, 10, 969–973. [Google Scholar] [CrossRef]
- Hack, J.T. Studies of Longitudinal Stream Profiles in Virginia and Maryland; Geological Survey Professional Paper 294-B; United States Government Printing Office: Washington, DC, USA, 1957.
- Sklar, L.; Dietrich, W.E. River Longitudinal profiles and bedrock incision models: Stream power and the influence of sediment supply. In Rivers Over Rock: Fluvial Processes in Bedrock Channels; American Geophysical Union: Washington, DC, USA, 2013. [Google Scholar] [CrossRef]
- Tarboton, D.G.; Bras, R.L.; Rodriguez-Iturbe, I. Scaling and elevation in river networks. Water Resour. Res. 1989, 25, 2037–2051. [Google Scholar] [CrossRef]
- Willgoose, G.; Bras, R.L.; Rodriguez-Iturbe, I. A physical explanation of an observed link area-slope relationship. Water Resour. Res. 1991, 27, 1697–1702. [Google Scholar] [CrossRef]
- Cohen, S.; Willgoose, G.; Hancock, G. A methodology for calculating the spatial distribution of the area-slope equation and the hypsometric integral within a catchment. J. Geophys. Res. Earth Surf. 2008, 113, 1–13. [Google Scholar] [CrossRef]
- Niemann, J.D.; Bras, R.L.; Veneziano, D.; Rinaldo, A. Impacts of surface elevation on the growth and scaling properties of simulated river networks. Geomorphology 2001, 40, 37–55. [Google Scholar] [CrossRef]
- Ijjasz-Vasquez, E.J.; Bras, R.L. Scaling regimes of local slope versus contributing area in digital elevation models. Geomorphology 1995, 12, 299–311. [Google Scholar] [CrossRef]
- Leopold, L.B.; Maddock, T.J. The Hydraulic Geometry of Stream Channels and Some Physiographic Implications, Geological Survey Professional Paper 252; United States Geological Service: Washington, DC, USA, 1953. [CrossRef]
- Montgomery, D.R.; Gran, K.B. Downstream variations in the width of bedrock channels. Water Resour. Res. 2001, 37, 1841–1846. [Google Scholar] [CrossRef]
- Wolman, M.G. The Natural Channel of Brandywine Creek Pennsylvania, Geological Survey Professional Paper 271; United States Government Printing Office: Washington, DC, USA, 1955; 56p.
- Tucker, G.E.; Catani, F.; Rinaldo, A.; Bras, R.L. Statistical analysis of drainage density from digital terrain data. Geomorphology 2001, 36, 187–202. [Google Scholar] [CrossRef]
- O’Callaghan, J.F.; Mark, D.M. The extraction of drainage networks from digital elevation data. Comput. Vision Graph. Image Process. 1984, 28, 323–344. [Google Scholar] [CrossRef]
- Tarboton, D.G. Terrain Analysis Using Digital Elevation Models (TauDEM, ver. 5.3.5). In Proceedings of the 23rd ESRI International Users Conference, San Diego, CA, USA, 7–11 July 2003. [Google Scholar]
- Tarboton, D.G.; Bras, R.L.; Rodriguez-Iturbe, I. On the extraction of channel networks from digital elevation data. Hydrol. Process. 1991, 5, 81–100. [Google Scholar] [CrossRef]
- Montgomery, D.R. Slope distributions, threshold hillslopes, and steady-state topography. Am. J. Sci. 2001, 301, 432–454. [Google Scholar] [CrossRef]
- D’Agostino, R.B.; Stephens, M.A. (Eds.) Goodness-of-Fit Techniques; Marcel Dekker, Inc.: New York, NY, USA, 1986. [Google Scholar] [CrossRef]
- Weber, M.D.; Leemis, L.M.; Kincaid, R.K. Minimum Kolmogorov-Smirnov test statistic parameter estimates. J. Stat. Comput. Simul. 2006, 76, 195–206. [Google Scholar] [CrossRef]
- Jogesh Babu, G.; Rao, C.R. Goodness-of-fit tests when parameters are estimated. Indian J. Stat. 2004, 66, 63–74. [Google Scholar]
- Anderson, D.R.; Burnham, K.P.; Thompson, W.L. Null hypothesis testing: Problems, prevalence, and an alternative. J. Wildl. Manag. 2000, 64, 912–923. [Google Scholar] [CrossRef]
- Cohen, Y.; Cohen, J.Y. Analysis of Variance. In Statistics and Data with R; John Wiley & Sons, Ltd.: Chichester, UK, 2008; pp. 463–509. [Google Scholar] [CrossRef]
- Maxwell, S.; Delaney, H. Designing Experiments and Analyzing Data: A Model Comparison Perspective, Briefings in Functional Genomics Proteomics; Taylor & Fancis Group, LLC.: New York, NY, USA, 2004. [Google Scholar] [CrossRef]
- McCuen, R.H.; Johnson, P.A.; Ragan, R.M. Highway Hydrology: Hydraulic Design Series No. 2; Federal Highway Administration: Arlington, VA, USA, 2002.
- Chow, V.T. Open-Channel Hydraulics; McGraw-Hill: New York, NY, USA, 1959. [Google Scholar]
- Moriasi, D.N.; Arnold, J.G.; Van Liew, M.W.; Bingner, R.L.; Harmel, R.D.; Veith, T.L. Model evaluation uidelines for systematic quantification of accuracy in watershed simulations. Trans. ASABE 2007, 50, 885–900. [Google Scholar] [CrossRef]
- Singh, J.; Knapp, H.V.; Arnold, J.G.; Demissie, M. Hydrological modeling of the Iroquois River watershed using HSPF and SWAT. J. Am. Water Resour. Assoc. 2005, 41, 343–360. [Google Scholar] [CrossRef]
- Nash, J.E.; Sutcliffe, J.V. River flow forecasting through conceptual models part I—A discussion of principles. J. Hydrol. 1970, 10, 282–290. [Google Scholar] [CrossRef]
- Czyzyk, K.A. A Nonlinear Synthetic Unit Hydrograph Method that Accounts for Channel Network Type. Master’s Thesis, Colorado State University, Fort Collins, CO, USA, 2018. [Google Scholar]
- Mirossi, D. Is Channel Network Classification Beneficial for More Accurately Estimating the Instantaneous Unit Hydrograph? Master’s Thesis, University of Trento, Trento, Italy, 2019. [Google Scholar]
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).