Time Variant Sensitivity Analysis of Hydrological Model Parameters in a Cold Region Using Flow Signatures
Abstract
1. Introduction
2. Materials and Methods
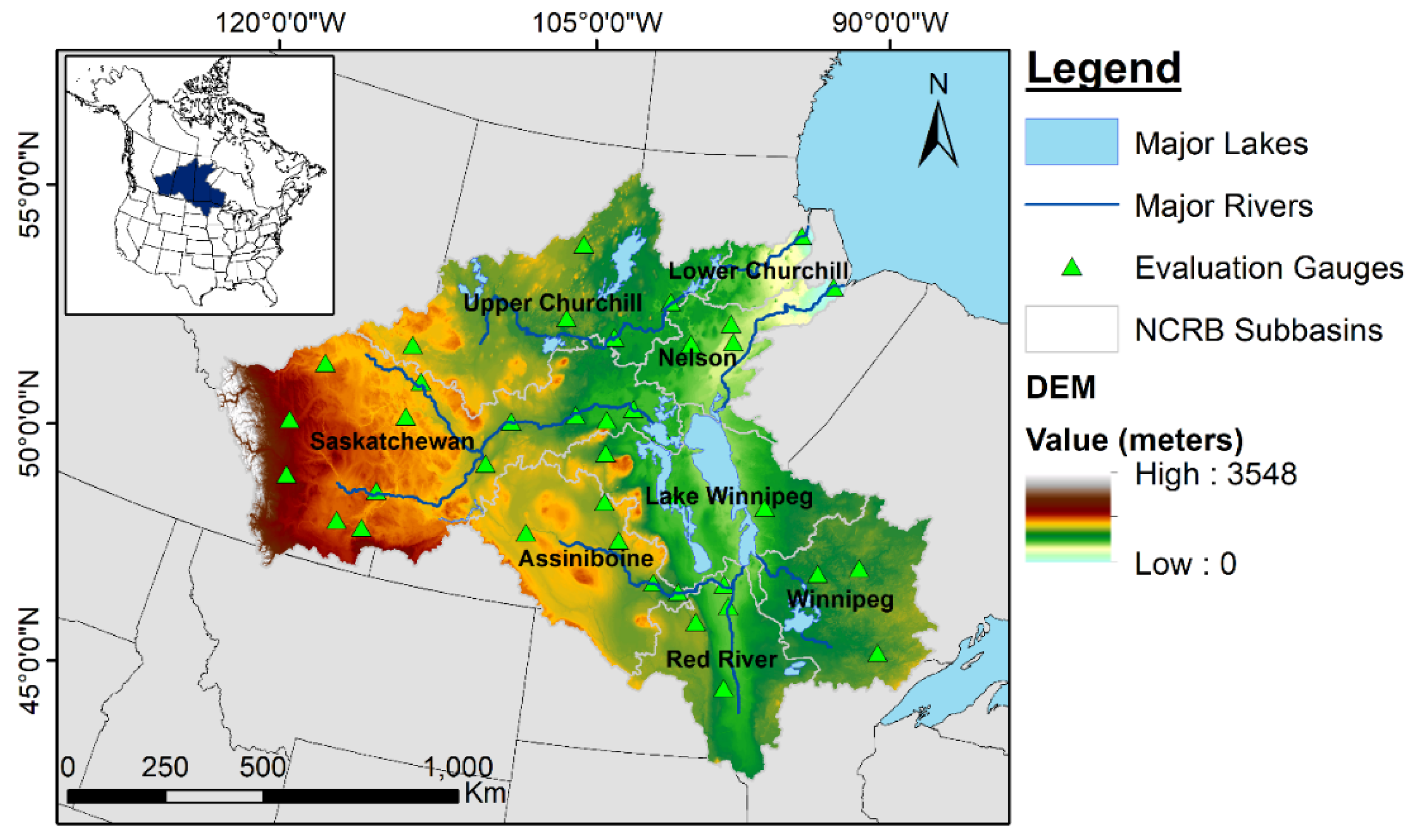
2.1. Study Area
2.2. Hydrological Modeling
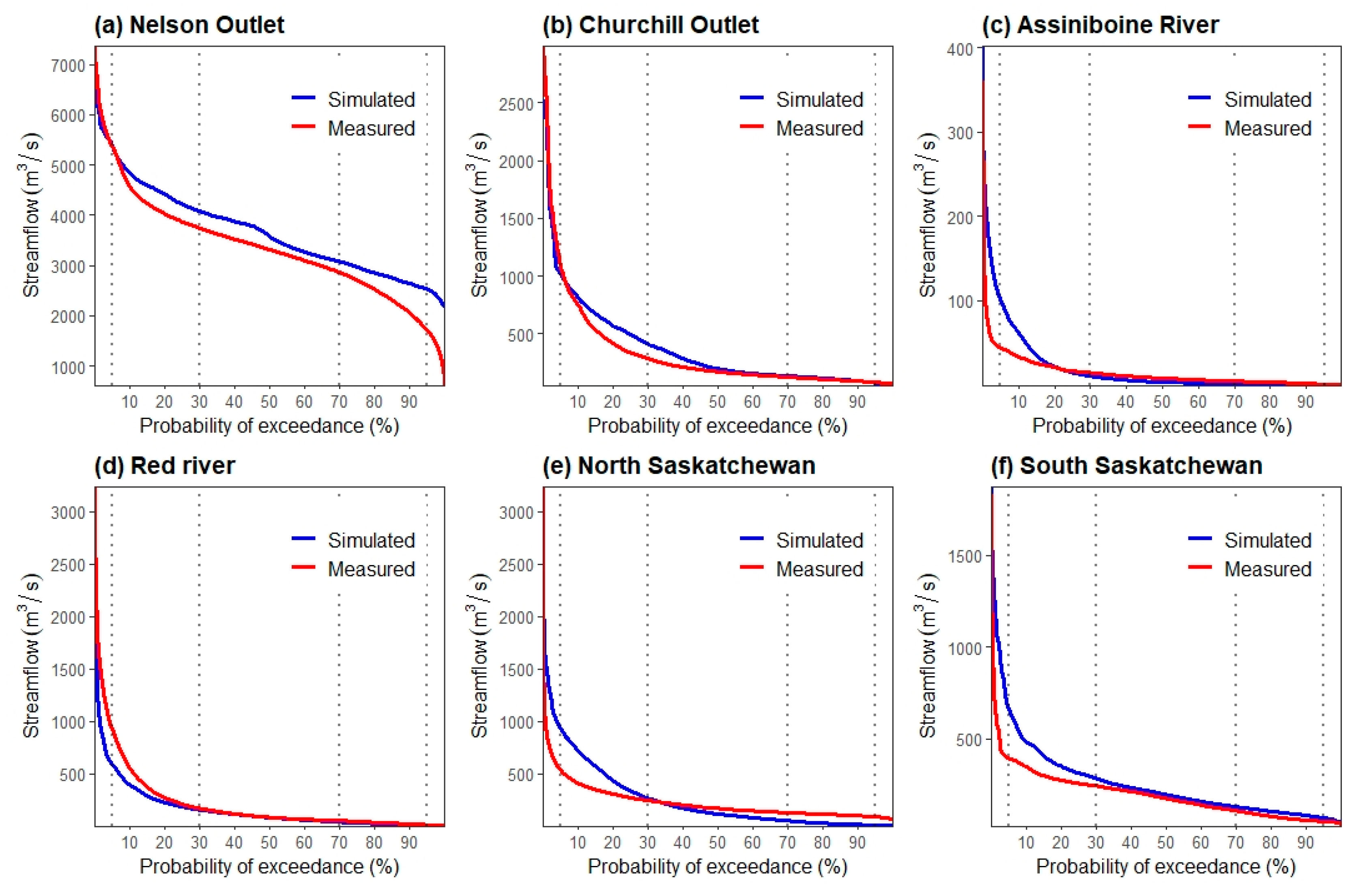
2.3. Evaluation Criteria
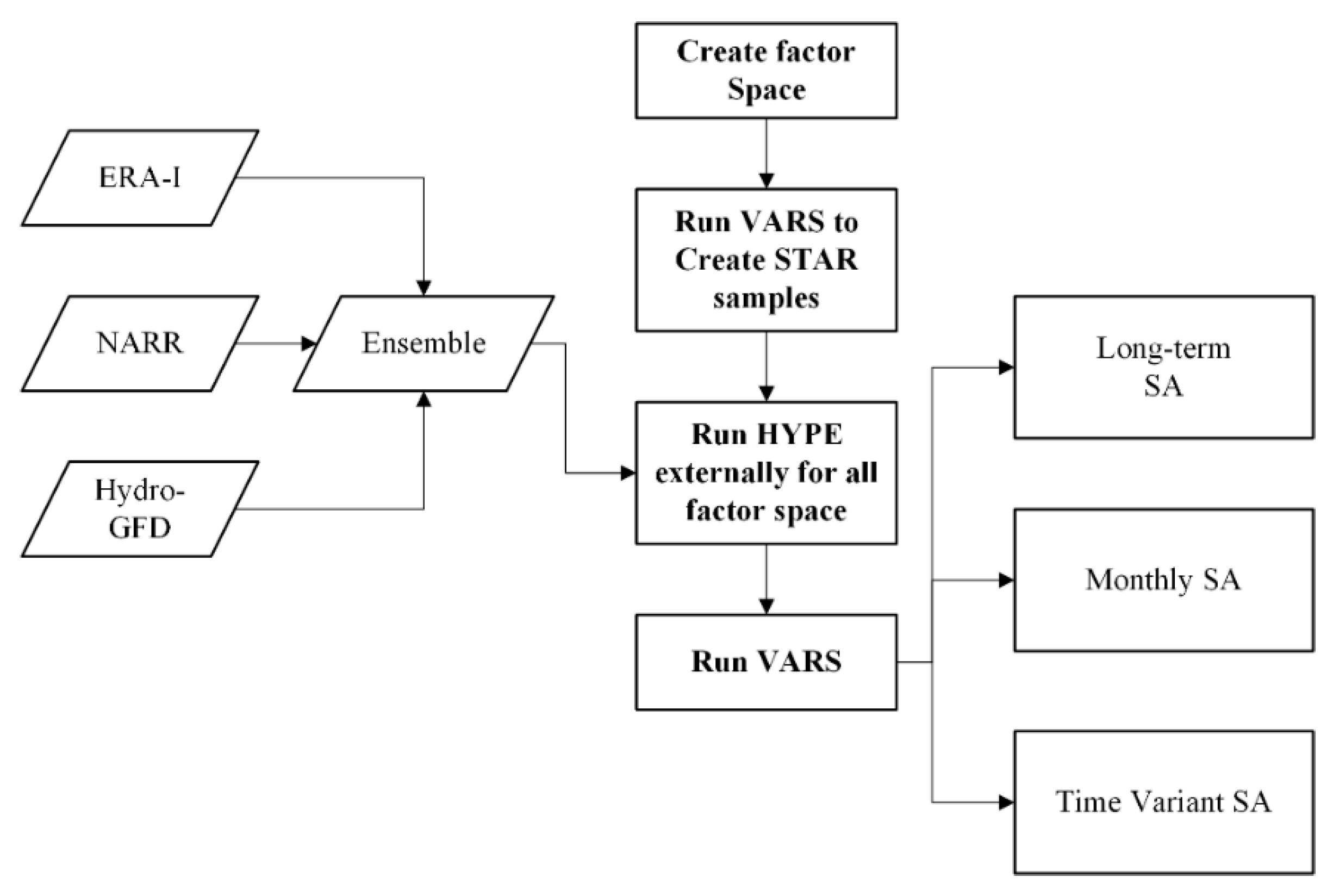
2.4. Sensitivity Analysis Using VARS
2.4.1. Long-Term SA
2.4.2. Monthly SA
2.4.3. Time Variant Sensitivity Analysis
3. Results and Discussion
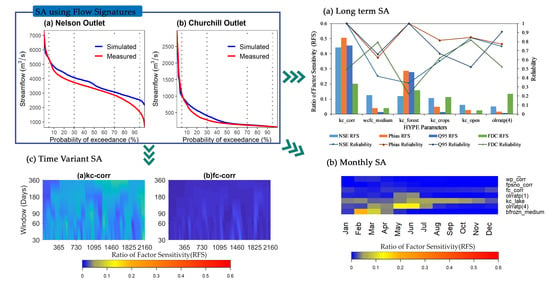
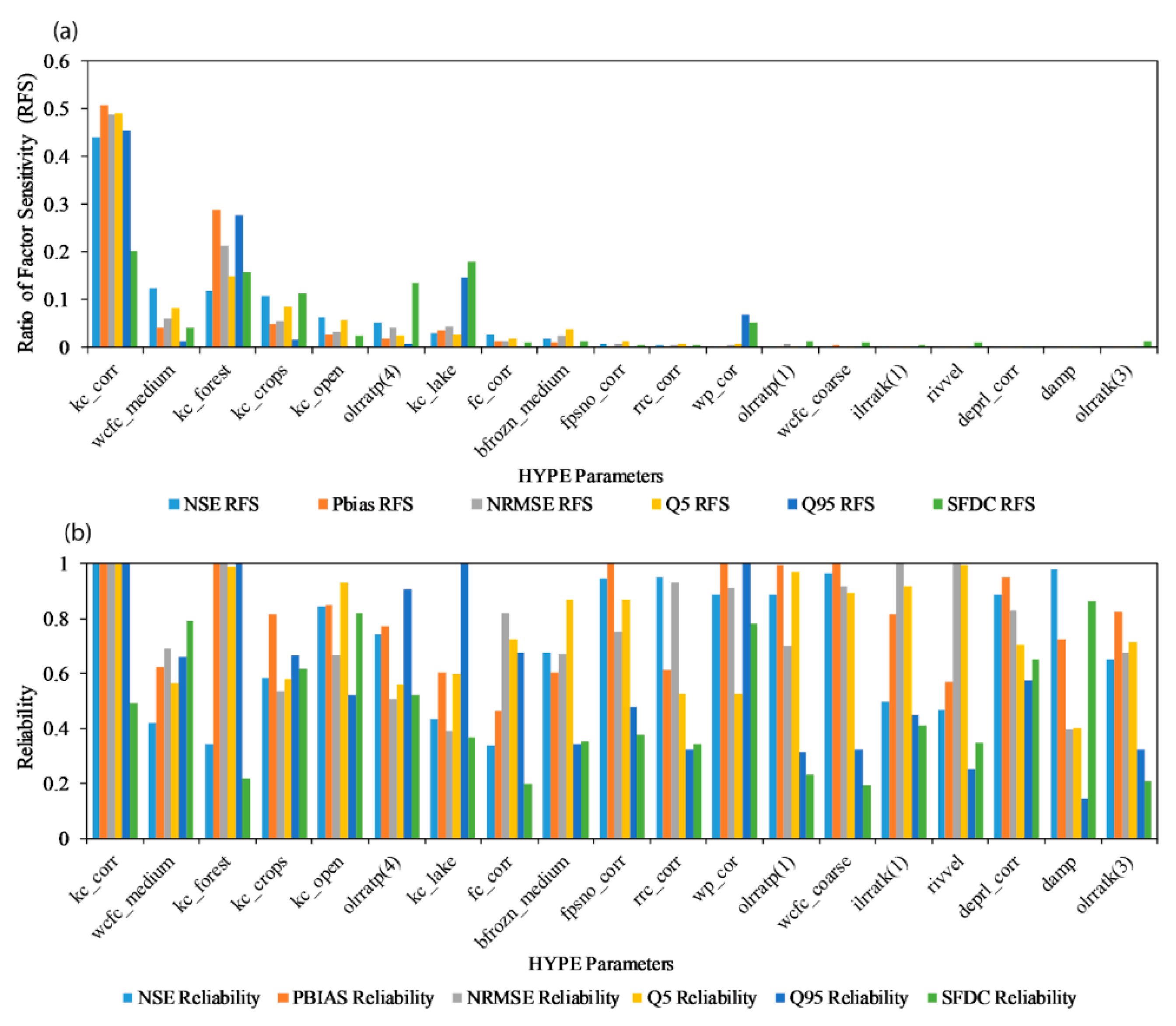
3.1. Long-Term SA
3.2. Monthly SA
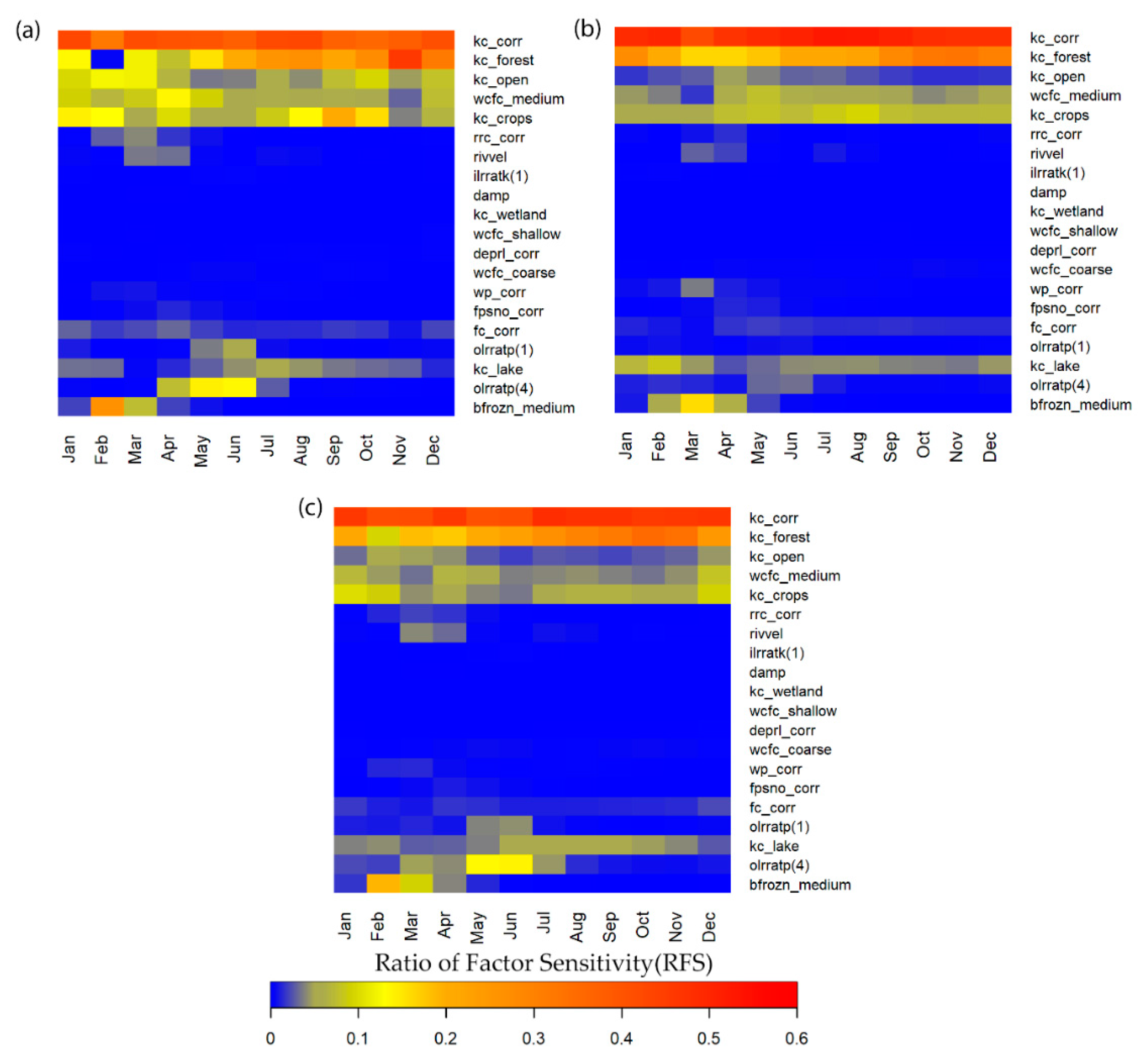
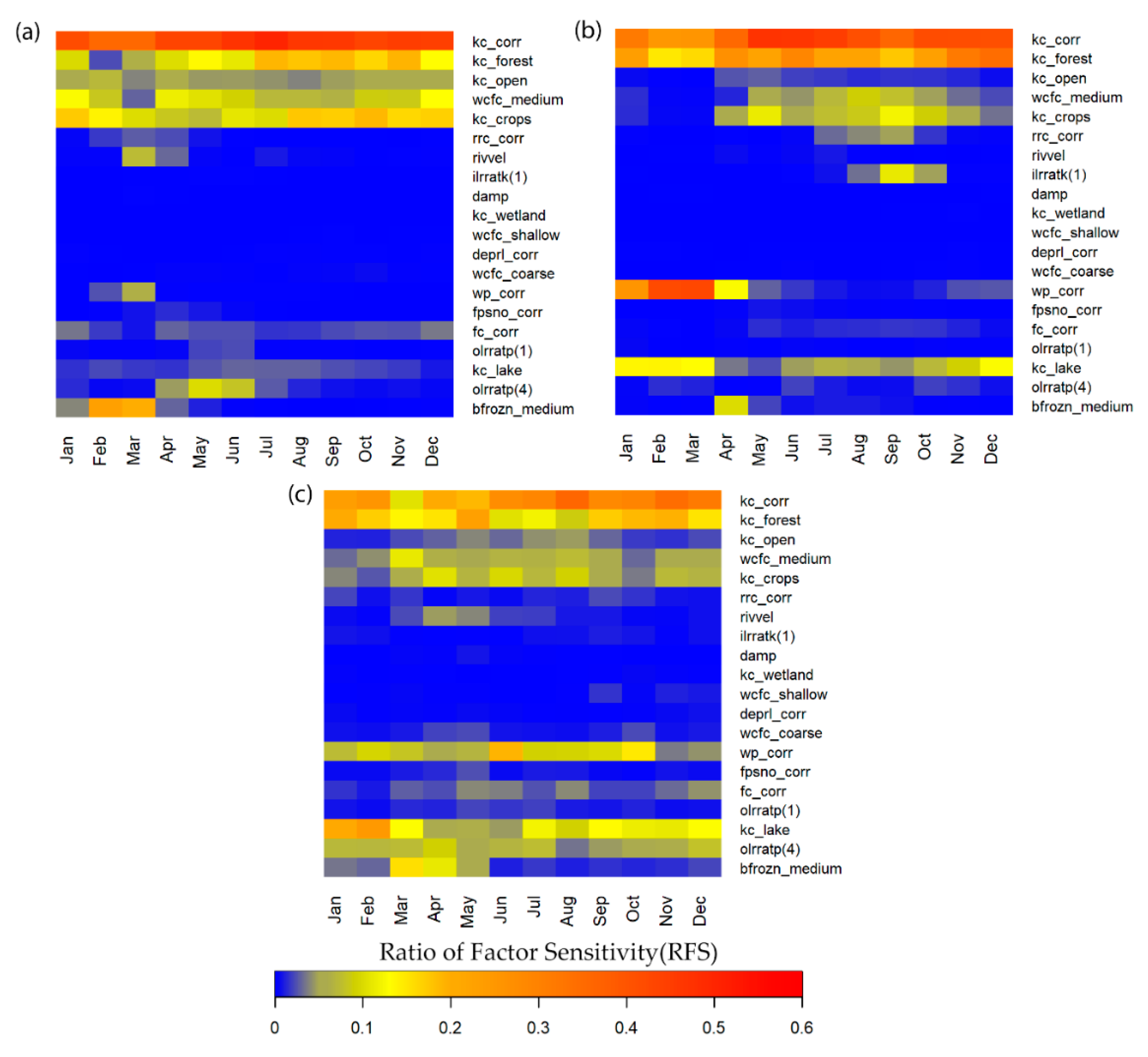
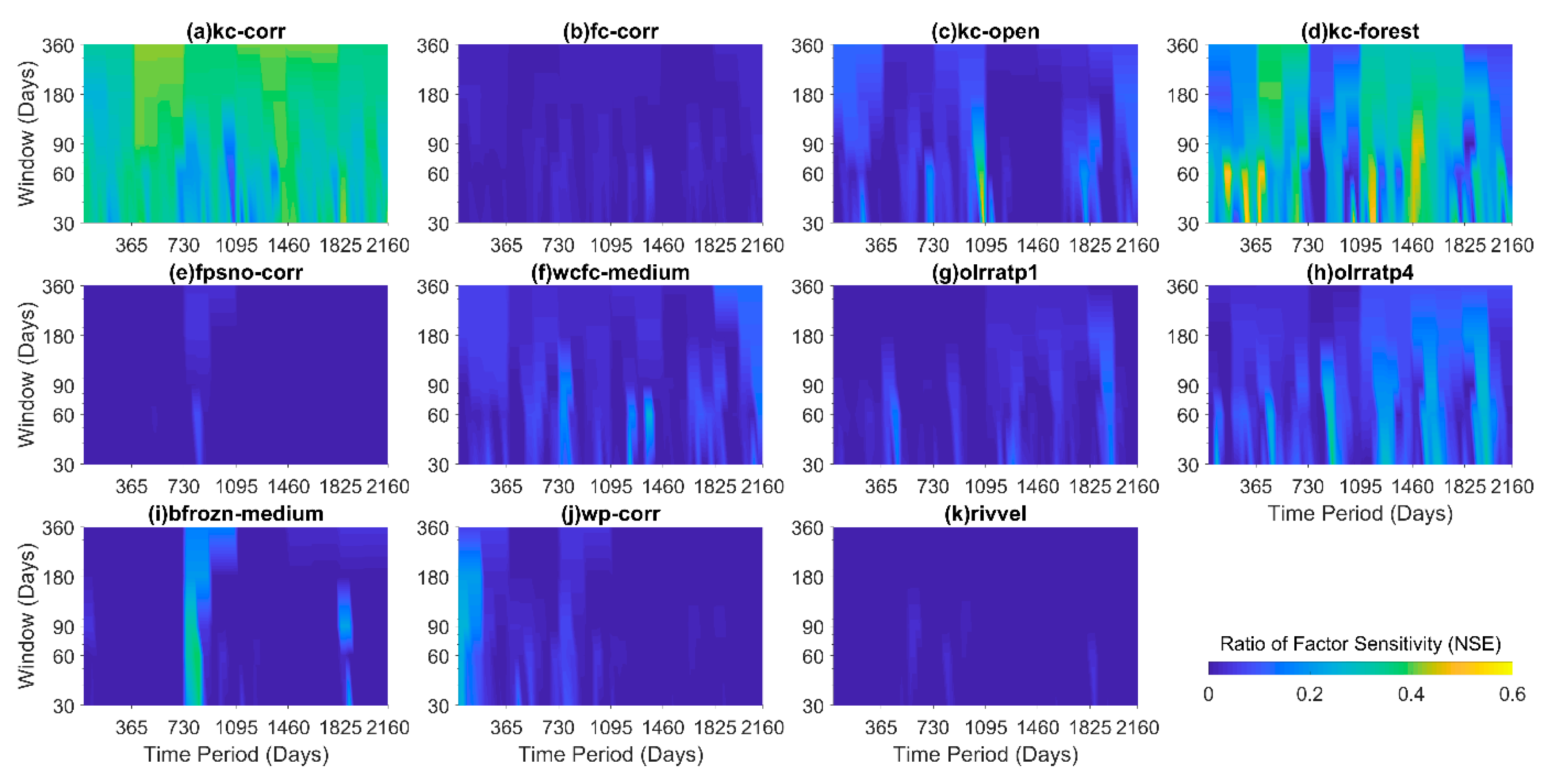
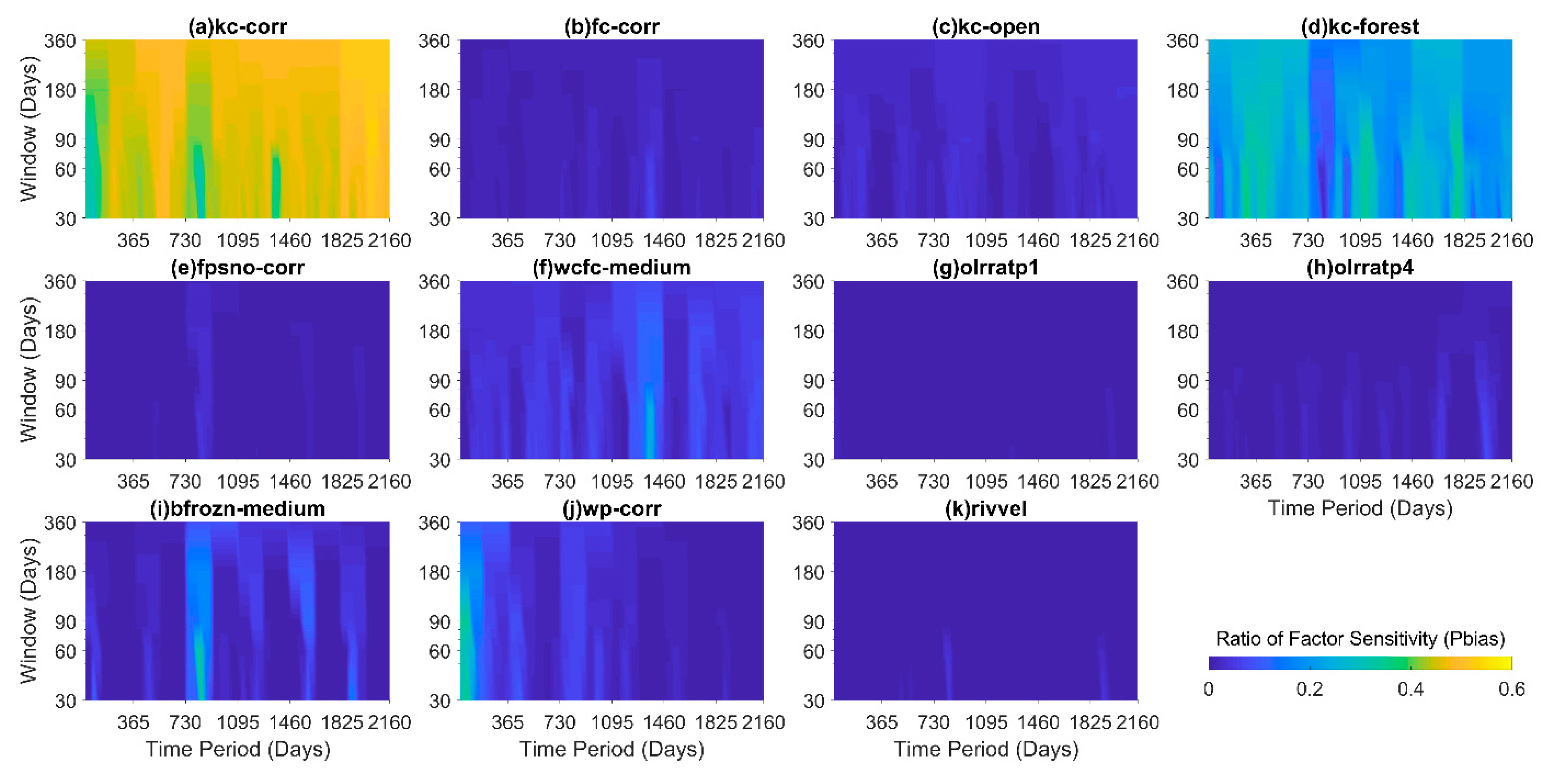
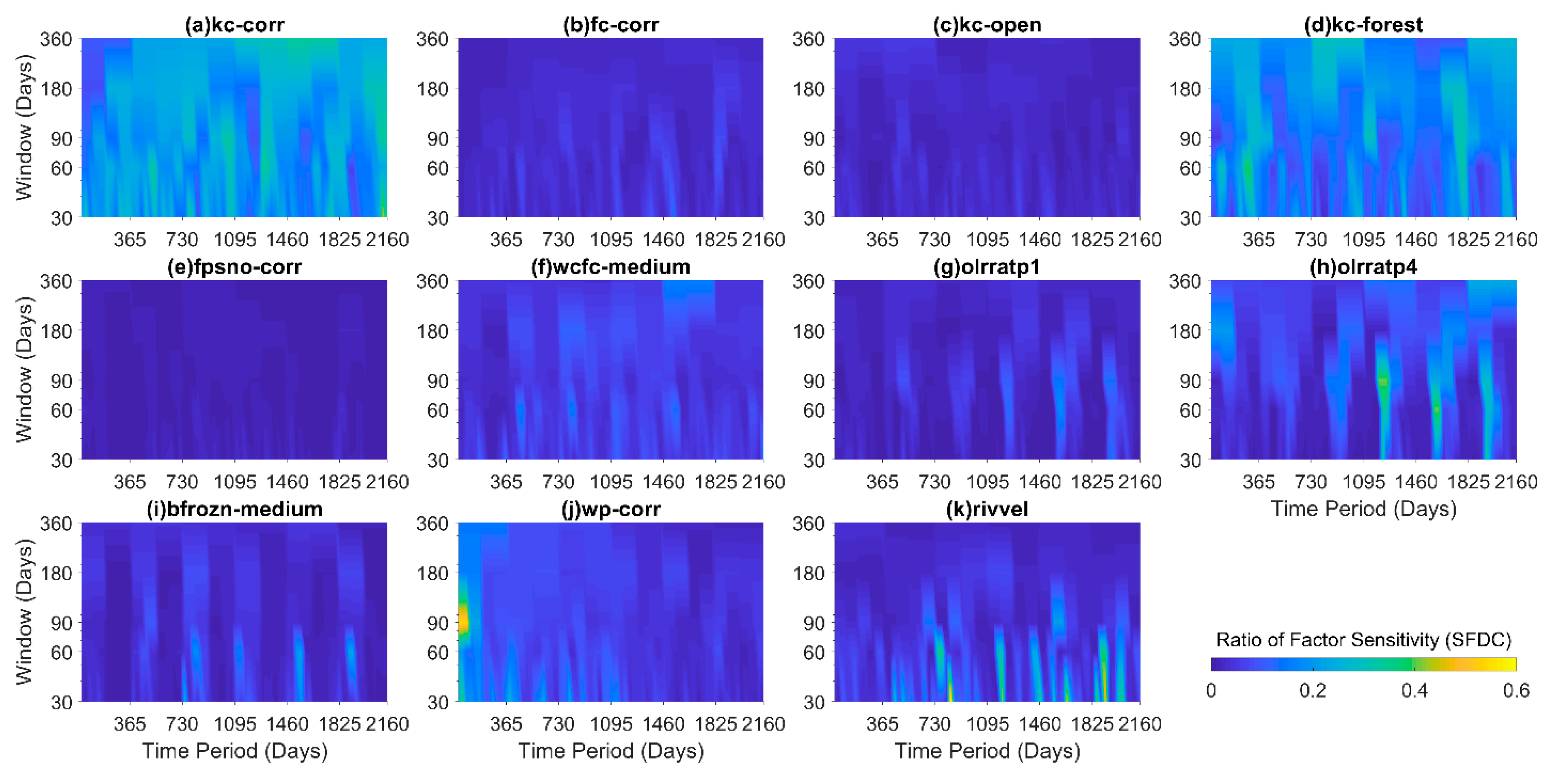
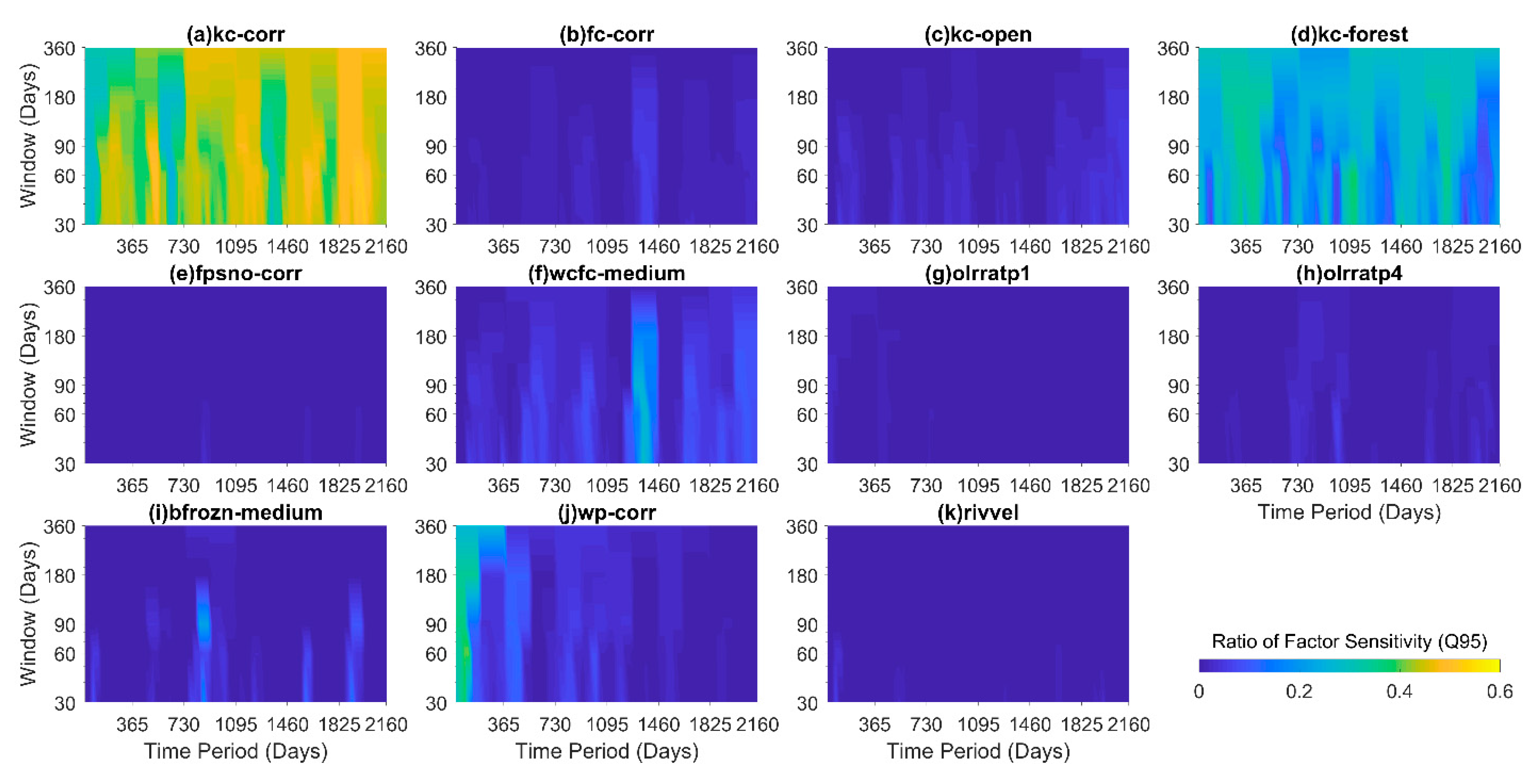
3.3. Time Variant Sensitivity Analysis
3.4. Impact of the Choice of Evaluation Metrics
4. Conclusions
Supplementary Materials
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Benke, K.K.; Lowell, K.E.; Hamilton, A.J. Parameter uncertainty, sensitivity analysis and prediction error in a water-balance hydrological model. Math. Comput. Model. 2008, 47, 1134–1149. [Google Scholar] [CrossRef]
- Shen, Z.Y.; Chen, L.; Chen, T. Analysis of parameter uncertainty in hydrological and sediment modeling using GLUE method: A case study of SWAT model applied to Three Gorges Reservoir Region, China. Hydrol. Earth Syst. Sci. 2012, 16, 121–132. [Google Scholar] [CrossRef]
- Feyen, L.; Kalas, M.; Vrugt, J.A. Semi-distributed parameter optimization and uncertainty assessment for large-scale streamflow simulation using global optimization/Optimisation de paramètres semi-distribués et évaluation de l’incertitude pour la simulation de débits à grande échelle pa. Hydrol. Sci. J. 2008, 53, 293–308. [Google Scholar] [CrossRef]
- van Zelm, R.; Huijbregts, M.A.J. Quantifying the Trade-off between Parameter and Model Structure Uncertainty in Life Cycle Impact Assessment. Environ. Sci. Technol. 2013, 47, 9274–9280. [Google Scholar] [CrossRef] [PubMed]
- Pianosi, F.; Wagener, T. Understanding the time-varying importance of different uncertainty sources in hydrological modelling using global sensitivity analysis. Hydrol. Process. 2016, 30, 3991–4003. [Google Scholar] [CrossRef]
- Höllering, S.; Wienhöfer, J.; Ihringer, J.; Samaniego, L.; Zehe, E. Regional analysis of parameter sensitivity for simulation of streamflow and hydrological fingerprints. Hydrol. Earth Syst. Sci. 2018, 22, 203. [Google Scholar] [CrossRef]
- Razavi, S.; Gupta, H.V. What do we mean by sensitivity analysis? The need for comprehensive characterization of “global” sensitivity in Earth and Environmental systems models. Water Resour. Res. 2015, 51, 3070–3092. [Google Scholar] [CrossRef]
- Tian, W. A review of sensitivity analysis methods in building energy analysis. Renew. Sustain. Energy Rev. 2013, 20, 411–419. [Google Scholar] [CrossRef]
- Sobol, I.M. Global sensitivity indices for nonlinear mathematical models and their Monte Carlo estimates. Math. Comput. Simul. 2001, 55, 271–280. [Google Scholar] [CrossRef]
- Morris, M.D. Factorial sampling plans for preliminary computational experiments. Technometrics 1991, 32, 161–174. [Google Scholar] [CrossRef]
- Rosolem, R.; Gupta, H.V.; Shuttleworth, W.J.; Zeng, X.; De Gonçalves, L.G.G. A fully multiple-criteria implementation of the Sobol’ method for parameter sensitivity analysis. J. Geophys. Res. Atmos. 2012, 117, D07103. [Google Scholar] [CrossRef]
- Baroni, G.; Tarantola, S. A General Probabilistic Framework for uncertainty and global sensitivity analysis of deterministic models: A hydrological case study. Environ. Model. Softw. 2014, 51, 26–34. [Google Scholar] [CrossRef]
- Razavi, S.; Gupta, H. A new framework for comprehensive, robust, and efficient global sensitivity analysis: 1. Theory. Water Resour. Res. 2016, 8324, 423–439. [Google Scholar] [CrossRef]
- Razavi, S.; Tolson, B.A.; Burn, D.H. Review of surrogate modeling in water resources. Water Resour. Res. 2012, 48, W07401. [Google Scholar] [CrossRef]
- Zhan, C.S.; Song, X.M.; Xia, J.; Tong, C. An efficient integrated approach for global sensitivity analysis of hydrological model parameters. Environ. Model. Softw. 2013, 41, 39–52. [Google Scholar] [CrossRef]
- Song, X.; Zhang, J.; Zhan, C.; Xuan, Y.; Ye, M.; Xu, C. Global sensitivity analysis in hydrological modeling: Review of concepts, methods, theoretical framework, and applications. J. Hydrol. 2015, 523, 739–757. [Google Scholar] [CrossRef]
- Asher, M.J.; Croke, B.F.W.; Jakeman, A.J.; Peeters, L.J.M. A review of surrogate models and their application to groundwater modeling. Water Resour. Res. 2015, 51, 5957–5973. [Google Scholar] [CrossRef]
- Lilhare, R.; Pokorny, S.; Déry, S.J.; Stadnyk, T.A.; Koenig, K.A. Sensitivity Analysis and Uncertainty Assessment in Water Budget Simulated by the Variable Infiltration Capacity Model across the Lower Nelson River Basin, Manitoba, Canada. Hydrol. Process. 2020. [Google Scholar] [CrossRef]
- Liang, X.; Lettenmaier, D.P.; Wood, E.F.; Burges, S.J. A simple hydrologically based model of land surface water and energy fluxes for general circulation models. J. Geophys. Res. 1994, 99, 14115–14128. [Google Scholar] [CrossRef]
- Rasouli, K.; Pomeroy, J.W.; Janowicz, J.R.; Carey, S.K.; Williams, T.J. Hydrological sensitivity of a northern mountain basin to climate change. Hydrol. Process. 2014, 28, 4191–4208. [Google Scholar] [CrossRef]
- Fang, X.; Pomeroy, J.W. Snowmelt runoff sensitivity analysis to drought on the Canadian prairies. Hydrol. Process. 2007, 19, 2594–2609. [Google Scholar] [CrossRef]
- Loucks, D.P.; van Beek, E.; Stedinger, J.R.; Dijkman, J.P.M.; Villars, M.T. Model Sensitivity and Uncertainty Analysis. Water Resour. Syte. Plan. Manage. 2005, 255–290. [Google Scholar]
- Muleta, M.K.; Nicklow, J.W. Sensitivity and uncertainty analysis coupled with automatic calibration for a distributed watershed model. J. Hydrol. 2005, 306, 127–145. [Google Scholar] [CrossRef]
- Kannan, N.; White, S.M.; Worrall, F.; Whelan, M.J. Sensitivity analysis and identification of the best evapotranspiration and runoff options for hydrological modelling in SWAT-2000. J. Hydrol. 2007, 332, 456–466. [Google Scholar] [CrossRef]
- Xie, H.; Shen, Z.; Chen, L.; Qiu, J.; Dong, J. Time-varying sensitivity analysis of hydrologic and sediment parameters at multiple timescales: Implications for conservation practices. Sci. Total Environ. 2017, 598, 353–364. [Google Scholar] [CrossRef]
- Razavi, S.; Gupta, H.V. A multi-method Generalized Global Sensitivity Matrix approach to accounting for the dynamical nature of earth and environmental systems models. Environ. Model. Softw. 2019, 114, 1–11. [Google Scholar] [CrossRef]
- Viglione, A.; Parajka, J.; Rogger, M.; Salinas, J.L.; Laaha, G.; Sivapalan, M.; Blöschl, G. Comparative assessment of predictions in ungauged basins—Part 3: Runoff signatures in Austria. Hydrol. Earth Syst. Sci. 2013, 17, 2263. [Google Scholar] [CrossRef]
- Shafii, M.; Tolson, B.A. Optimizing hydrological consistency by incorporating hydrological signatures into model calibration objectives. Water Resour. Res. 2015, 51, 3796–3814. [Google Scholar] [CrossRef]
- Donnelly, C.; Andersson, J.C.M.; Arheimer, B. Using flow signatures and catchment similarities to evaluate the E-HYPE multi-basin model across Europe. Hydrol. Sci. J. 2016, 61, 255–273. [Google Scholar] [CrossRef]
- Pan, S.; Fu, G.; Chiang, Y.M.; Ran, Q.; Xu, Y.P. A two-step sensitivity analysis for hydrological signatures in Jinhua River Basin, East China. Hydrol. Sci. J. 2017, 62, 2511–2530. [Google Scholar] [CrossRef]
- Lindström, G.; Pers, C.; Rosberg, J.; Strömqvist, J.; Arheimer, B. Development and testing of the HYPE (Hydrological Predictions for the Environment) water quality model for different spatial scales. Hydrol. Res. 2010, 41, 295–319. [Google Scholar] [CrossRef]
- Zubrycki, K.; Roy, D.; Osman, H.; Lewtas, K.; Gunn, G.; Grosshans, R. Large Area Planning in the Nelson-Churchill River Basin (NCRB): Laying a Foundation in Northern Manitoba; International Institute for Sustainable Development: Winnipeg, MB, Canada, 2016. [Google Scholar]
- Manitoba Hydro. Climate Change Report Fiscal Year 2014–2015. Available online: https://www.hydro.mb.ca/environment/pdf/climate_change_report_2014_15.pdf (accessed on 15 June 2019).
- Gray, D.M.; Toth, B.; Zhao, L.; Pomeroy, J.W.; Granger, R.J. Estimating areal snowmelt infiltration into frozen soils. Hydrol. Process. 2001, 15, 3095–3111. [Google Scholar] [CrossRef]
- Zhang, T.; Barry, R.G.; Knowles, K.; Heginbottom, J.A.; Brown, J. Statistics and characteristics of permafrost and ground ice distribution in the Northern Hemisphere. Polar Geogr. 1999, 23, 132–154. [Google Scholar] [CrossRef]
- Smith, M.W.; Riseborough, D.W. Climate and the limits of permafrost: A zonal analysis. Permafr. Periglac. Process. 2002, 13, 1–15. [Google Scholar] [CrossRef]
- Kurz, D.; Alfaro, M.; Graham, J. Thermal conductivities of frozen and unfrozen soils at three project sites in northern Manitoba. Cold Reg. Sci. Technol. 2017, 140, 30–38. [Google Scholar] [CrossRef]
- Carey, S.K.; Pomeroy, J.W. Progress in Canadian snow and frozen ground hydrology, 2003–2007. Can. Water Resour. J. 2009, 34, 127–138. [Google Scholar] [CrossRef]
- Tefs, A.A.G.; MacDonald, M.K.; Stadnyk, T.A.; Koenig, K.A.; Hamilton, M.; Slota, P.; Crawford, J. Simulating effects of Nelson-Churchill River regulation controls on reservoir performance in HYPE. Unpublished work. 2019. [Google Scholar]
- MacDonald, M.K.; Stadnyk, T.A.; Dery, S.; Gustafsson, D.; Isberg, K. Improved high-latitude water storage for hydrological modelling of the Hudson Bay Drainage Basin. Unpublished work. 2019. [Google Scholar]
- Déry, S.J.; Stadnyk, T.A.; MacDonald, M.K.; Gauli-Sharma, B. Recent trends and variability in river discharge across northern Canada. Hydrol. Earth Syst. Sci. 2016, 20, 4801–4818. [Google Scholar] [CrossRef]
- Sabarly, F.; Essou, G.; Lucas-Picher, P.; Poulin, A.; Brissette, F. Use of Four Reanalysis Datasets to Assess the Terrestrial Branch of the Water Cycle over Quebec, Canada. J. Hydrometeorol. 2016, 17, 1447–1466. [Google Scholar] [CrossRef]
- Nash, J.E.; Sutcliffe, J.V. River flow forecasting through conceptual models part I—A discussion of principles. J. Hydrol. 1970, 10, 282–290. [Google Scholar] [CrossRef]
- Gupta, H.V.; Sorooshian, S.; Yapo, P.O. Status of Automatic Calibration for Hydrologic Models: Comparison with Multilevel Expert Calibration. J. Hydrol. Eng. 1999, 4, 135–143. [Google Scholar] [CrossRef]
- U.S. Environmental Protection Agency. EPA’s Report on the Environment (ROE) (2008 Final Report); U.S. Environmental Protection Agency: Washington, DC, USA, 2008.
- Demirel, M.C.; Booij, M.J.; Hoekstra, A.Y. Effect of different uncertainty sources on the skill of 10 day ensemble low flow forecasts for two hydrological models. Water Resour. Res. 2013, 49, 4035–4053. [Google Scholar] [CrossRef]
- Jiang, S. Hydrological Water Quality Modelling of Nested Meso Scale Catchments. Doctoral Thesis, Technical University of Braunschweig, Braunschweig, Germany, 2014. [Google Scholar]
- Arheimer, B.; Pimentel, R.; Isberg, K.; Crochemore, L.; Andersson, J.C.M.; Hasan, A.; Pineda, L. Global catchment modelling using World-Wide HYPE (WWH), open data and stepwise parameter estimation. Hydrol. Earth Syst. Sci. Discuss. 2019, 2, 535–559. [Google Scholar] [CrossRef]
- Gelfan, A.; Gustafsson, D.; Motovilov, Y.; Arheimer, B.; Kalugin, A.; Krylenko, I.; Lavrenov, A. Climate change impact on the water regime of two great Arctic rivers: Modeling and uncertainty issues. Clim. Chang. 2017, 141, 499–515. [Google Scholar] [CrossRef]
- Razavi, S.; Gupta, H. A new framework for comprehensive, robust, and efficient global sensitivity analysis: 2. Application. Water Resour. Res. 2016, 1, 440–455. [Google Scholar] [CrossRef]
- Castaings, W.; Dartus, D.; Le Dimet, F.X.; Saulnier, G.M. Sensitivity analysis and parameter estimation for distributed hydrological modeling: Potential of variational methods. Hydrol. Earth Syst. Sci. 2009, 13, 503–517. [Google Scholar] [CrossRef]
- Gonzaga, M.; Oliveira, A.D.; Netto, D.A.; Joaquim, R.; Neves, D.J.; Nascimento, A.; Almeida, C. Sensitivity Analysis and Calibration of Hydrological Modeling of the Watershed Northeast Brazil. J. Environ. Prot. 2015, 6, 837–850. [Google Scholar]
- Rosenberg, L.; Hammer, T.; Shaw, J. Software metrics and reliability. In Proceedings of the 9th International Symposium on Software Reliability Engineering, Paderborn, Germany, 4–7 November 1998. [Google Scholar]
- Razavi, S.; Sheikholeslami, R.; Gupta, H.V.; Haghnegahdar, A. VARS-TOOL: A toolbox for comprehensive, efficient, and robust sensitivity and uncertainty analysis. Environ. Model. Softw. 2019, 112, 95–107. [Google Scholar] [CrossRef]
- Zhao, Y.; Nan, Z.; Yu, W.; Zhang, L. Calibrating a hydrological model by stratifying frozen ground types and seasons in a cold alpine basin. Water 2019, 11, 985. [Google Scholar] [CrossRef]
- Ghasemizade, M.; Baroni, G.; Abbaspour, K.; Schirmer, M. Combined analysis of time-varying sensitivity and identifiability indices to diagnose the response of a complex environmental model. Environ. Model. Softw. 2017, 88, 22–34. [Google Scholar] [CrossRef]
- Massmann, C.; Wagener, T.; Holzmann, H. A new approach to visualizing time-varying sensitivity indices for environmental model diagnostics across evaluation time-scales. Environ. Model. Softw. 2014, 51, 190–194. [Google Scholar] [CrossRef]
- Hong, Y. Actual evapotranspiration estimation for different land use and land cover in urban regions using Landsat 5 data. J. Appl. Remote Sens. 2010, 4, 041873. [Google Scholar] [CrossRef]
- Verstraeten, W.W.; Muys, B.; Feyen, J.; Veroustraete, F.; Minnaert, M.; Meiresonne, L.; De Schrijver, A. Comparative analysis of the actual evapotranspiration of Flemish forest and cropland, using the soil water balance model WAVE. Hydrol. Earth Syst. Sci. Discuss. 2010, 9, 225–241. [Google Scholar] [CrossRef]
- Klyatis, L.M.; Anderson, E. Reliability Prediction and Testing Textbook; Wiley: Hoboken, NJ, USA, 2018. [Google Scholar]
- Campos, C.A.; Hernández, M.E.; Moreno-Casasola, P.; Cejudo Espinosa, E.; Robledo, R.A.; Infante Mata, D. Soil water retention and carbon pools in tropical forested wetlands and marshes of the Gulf of Mexico. Hydrol. Sci. J. 2011, 56, 1388–1406. [Google Scholar] [CrossRef]
- Gray, D.M.; Landine, P.G.; Granger, R.J. Simulating infiltration into frozen Prairie soils in streamflow models. Can. J. Earth Sci. 1985, 22, 464–472. [Google Scholar] [CrossRef]
- Watanabe, K.; Kito, T.; Dun, S.; Wu, J.Q.; Greer, R.C.; Flury, M. Water Infiltration into a Frozen Soil with Simultaneous Melting of the Frozen Layer. Vadose Zone J. 2013, 12, 1–7. [Google Scholar] [CrossRef]
- Wang, S.; Fu, B.J.; Gao, G.Y.; Yao, X.L.; Zhou, J. Soil moisture and evapotranspiration of different land cover types in the Loess Plateau, China. Hydrol. Earth Syst. Sci. 2012, 16, 2883–2892. [Google Scholar] [CrossRef]
- Jones, N.E.; Petreman, I.C.; Schmidt, B.J. High Flows and Freshet Timing in Canada: Observed Trends; Ontario Ministry of Natural Resources and Forestry: Peterborough, ON, Canada, 2015. [Google Scholar]
- Fang, X.; Minke, A.; Pomeroy, J.W.; Brown, T.; Westbrook, C.; Guo, X.; Guangul, S. A Review of Canadian Priarie Hydrology: Principles, Modelling and Response to Land Use and Drainage Change; University of Saskatchewan: Saskatoon, SK, Canada, 2007. [Google Scholar]
- Unduche, F.; Tolossa, H.; Senbeta, D.; Zhu, E. Evaluation of four hydrological models for operational flood forecasting in a Canadian Prairie watershed. Hydrol. Sci. J. 2018, 63, 1133–1149. [Google Scholar] [CrossRef]
- Price, K.; Purucker, S.T.; Kraemer, S.R.; Babendreier, J.E. Tradeoffs among watershed model calibration targets for parameter estimation. Water Resour. Res. 2012, 48, W10542. [Google Scholar] [CrossRef]
- Lawford, R.G.; Prowse, T.D.; Hogg, W.D.; Warkentin, A.A.; Pilon, P.J. Hydrometeorological aspects of flood hazards in Canada. Atmos. Ocean 1995, 33, 303–328. [Google Scholar] [CrossRef]
- Environment Canada. Causes of Flooding. Available online: https://www.canada.ca/en/environment-climate-change/services/water-overview/quantity/causes-of-flooding.html (accessed on 2 February 2020).
- Van Der Linden, S.; Virtanen, T.; Oberman, N.; Kuhry, P. Sensitivity analysis of discharge in the Arctic USA basin, East-European Russia. Clim. Chang. 2003, 57, 139–161. [Google Scholar] [CrossRef]
- Zahmatkesh, Z.; Kumar Jha, S.; Coulibaly, P.; Stadnyk, T. An overview of river flood forecasting procedures in Canadian watersheds. Can. Water Resour. J. 2019, 44, 213–229. [Google Scholar] [CrossRef]
- Schöber, J.; Achleitner, S.; Kirnbauer, R.; Schöberl, F.; Schönlaub, H. Hydrological modelling of glacierized catchments focussing on the validation of simulated snow patterns—Applications within the flood forecasting system of the Tyrolean river Inn. Adv. Geosci. 2010, 27, 99–109. [Google Scholar] [CrossRef]
- Cordeiro, M.R.C.; Wilson, H.F.; Vanrobaeys, J.; Pomeroy, J.W.; Fang, X. Simulating cold-region hydrology in an intensively drained agricultural watershed in Manitoba, Canada, using the Cold Regions Hydrological Model. Hydrol. Earth Syst. Sci. 2017, 21, 3483–3506. [Google Scholar] [CrossRef]
- Bhuiyan, H.A.K.M.; McNairn, H.; Powers, J.; Merzouki, A. Application of HEC-HMS in a cold region watershed and use of RADARSAT-2 soil moisture in initializing the model. Hydrology 2017, 4, 9. [Google Scholar] [CrossRef]
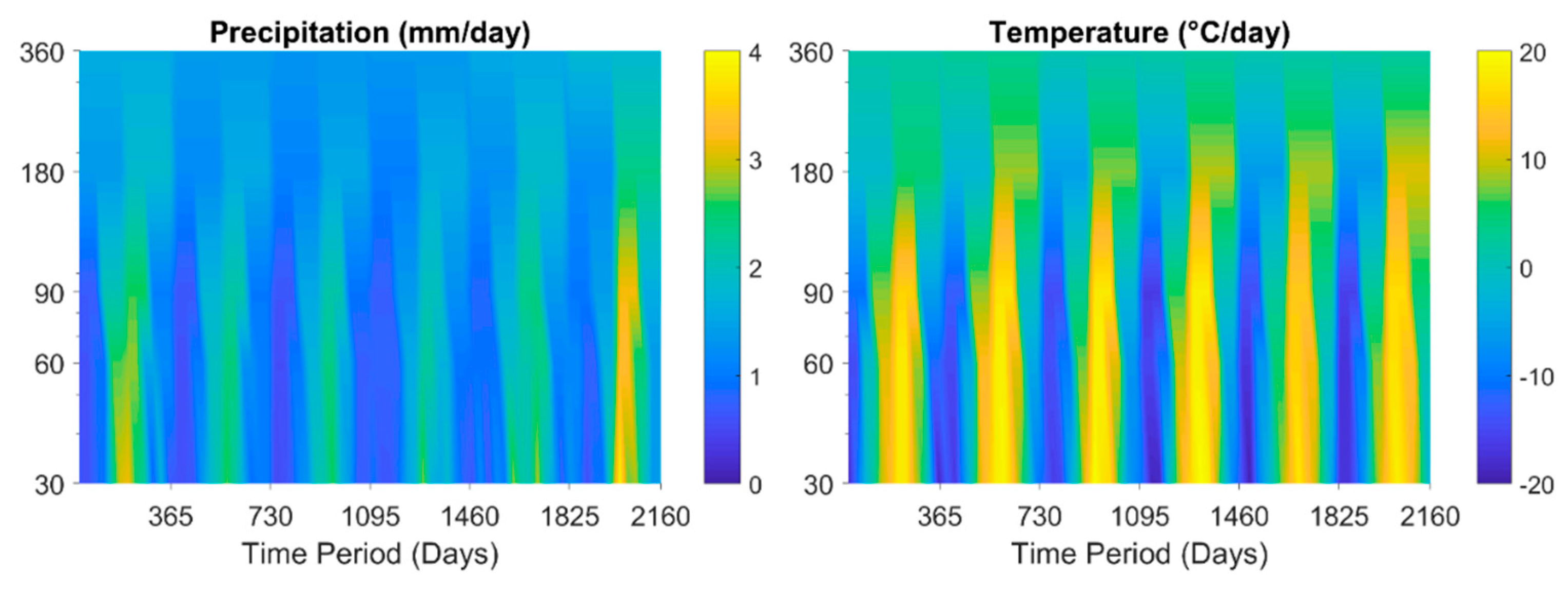
| Characteristic/Data Type | Information/Product | Source |
|---|---|---|
| Topography (routing and watershed delineation) | Hydro1K | United States Geological Survey (USGS) |
| Soil characteristics | Harmonized World Soil Database (HWSD) V1.2 | Food and Agricultural Organization (FAO) [32] |
| Land use characteristics | ESA CCI Land Cover 2010 V1.4 | ESA Climate Change Initiative—Land cover project 2014 |
| Lakes and wetlands | Global Lakes and Wetlands Database | WWF and the Center for Environmental Systems Research |
| Reservoirs | Global reservoir and Dam database (GRanD) V1.1 | Socioeconomic Data and Applications Center (SEDAC) [33] |
| Discharge | (i) HYDAT | (i) Environment Canada |
| (ii) USGS | (ii) https://waterdata.usgs.gov/nwis | |
| (iii) Dery et al [41] | (iii) Nelson and Churchill Outlets only | |
| Precipitation and near-surface air temperature | (i) ERA-Interim | (i)European Centre for Medium Range Weather Forecasts (ECMWF) [34] |
| (ii) NARR | (ii) National Centers for Environmental Prediction (NCEP) [35] | |
| (iii) Hydro-GFD | (iii) Swedish Meteorological and Hydrological Institute (SMHI) [36] | |
| Snow | GlobSnow | Finnish Meteorological Institute (FMI) |
| Glacier fluctuations | Fluctuations of Glaciers (FoG) | World Glacier Monitoring Service (WGMS) [37] |
| Evapotranspiration | FLUXNET | fluxnet.ornl.gov |
| S.N. | Parameters | Description | Dependency | Lower Limit | Upper Limit |
|---|---|---|---|---|---|
| 1 | rrc_corr | Correction factor for recession coefficients | Soil type | 0.9 | 1.2 |
| 2 | kc_corr | Correction factor for Crop Coefficient for PET model | Land use | 0.9 | 1.4 |
| 3 | fc_corr | Correction factor for fraction of soil available for ET | Soil type | 0.8 | 1.3 |
| 4 | wp_corr | Correction factor for wilting point | Soil type | 0.8 | 1.1 |
| 5 | deprl_corr | Correction factor for depth relation for soil temperature memory | Soil type | 0.6 | 1.6 |
| 6 | fpsno_corr | Correction factor for snow sublimation | Land use | 0.8 | 1.2 |
| 7 | kc_lake | Crop coefficient factor for lake type land use | Land use | 0.7 | 1.3 |
| 8 | kc_wetland | Crop coefficient factor for wetland type land use | Land use | 0.4 | 0.9 |
| 9 | kc_crops | Crop coefficient factor for crop type land use | Land use | 0.7 | 1.3 |
| 10 | kc_forest | Crop coefficient factor for forest type land use | Land use | 0.4 | 0.9 |
| 11 | kc_open | Crop coefficient factor for open type land use | Land use | 0.7 | 1.3 |
| 12 | wcfc_coarse | Fraction of soil (coarse) available for ET | Soil type | 0.05 | 0.25 |
| 13 | wcfc_medium | Fraction of soil (medium) available for ET | Soil type | 0.1 | 0.3 |
| 14 | wcfc_fine | Fraction of soil (fine) available for ET | Soil type | 0.1 | 0.3 |
| 15 | wcfc_organic | Fraction of soil (organic) available for ET | Soil type | 0.3 | 0.5 |
| 16 | wcfc_shallow | Fraction of soil (shallow) available for ET | Soil type | 0.05 | 0.15 |
| 17 | ilrratp(3) | Parameter of rating curve for ilake (cluster 3) outflow (exponent) | Ilake region | 1 | 2 |
| 18 | ilrratk(1) | Parameter of rating curve for ilake (cluster 1) outflow (rate) | Ilake region | 50 | 70 |
| 19 | ilrratk(3) | Parameter of rating curve for ilake (cluster 3) outflow (rate) | Ilake region | 2 | 30 |
| 20 | olrratp(1) | Parameter of rating curve for outlet lake (cluster 1) outflow (exponent) | Olake region | 3 | 4 |
| 21 | olrratp(4) | Parameter of rating curve for outlet lake (cluster 4) outflow (exponent) | Olake region | 1 | 2 |
| 22 | olrratk(3) | Parameter of rating curve for outlet lake (cluster 3) outflow (rate) | Olake region | 60 | 100 |
| 23 | damp | Fraction of delay in the watercourse | Routing | 0.4 | 0.7 |
| 24 | rivvel | Celerity of flood in watercourse | Routing | 0.5 | 1.5 |
| 25–29 | bfrozn_(Soil-Type) | Soil dependent infiltration parameter | Frozen soil | 1 | 4 |
| 30–34 | bcosby_(Soil-Type) | Shape coefficient of soil water potential moisture curve | Frozen soil | 2 | 15 |
| Parameters | NSE | PBIAS | Q95 | SFDC | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| IVARS10 | IVARS30 | IVARS50 | IVARS10 | IVARS30 | IVARS50 | IVARS10 | IVARS30 | IVARS50 | IVARS10 | IVARS30 | IVARS50 | |
| kc_corr | 34 | 34 | 34 | 34 | 34 | 34 | 34 | 34 | 34 | 34 | 34 | 34 |
| wcfc_medium | 33 | 33 | 33 | 30 | 31 | 31 | 29 | 29 | 29 | 28 | 28 | 28 |
| kc_crops | 32 | 31 | 31 | 31 | 32 | 32 | 28 | 30 | 30 | 30 | 30 | 30 |
| kc_forest | 31 | 32 | 32 | 33 | 33 | 33 | 33 | 33 | 33 | 33 | 33 | 32 |
| kc_open | 30 | 30 | 30 | 28 | 29 | 29 | 24 | 26 | 26 | 26 | 27 | 27 |
| olrratp(4) | 29 | 29 | 29 | 32 | 28 | 28 | 30 | 28 | 28 | 32 | 31 | 31 |
| fc_corr | 28 | 27 | 27 | 27 | 27 | 27 | 25 | 27 | 27 | 25 | 24 | 23 |
| kc_lake | 27 | 28 | 28 | 29 | 30 | 30 | 32 | 32 | 32 | 31 | 32 | 33 |
| bfrozn_medium | 26 | 26 | 26 | 26 | 26 | 26 | 22 | 23 | 25 | 21 | 23 | 26 |
| fpsno_corr | 25 | 25 | 25 | 22 | 24 | 24 | 18 | 18 | 19 | 19 | 19 | 19 |
| rrc_corr | 24 | 24 | 24 | 18 | 18 | 18 | 20 | 20 | 23 | 18 | 18 | 20 |
| wp_cor | 23 | 23 | 23 | 24 | 23 | 23 | 31 | 31 | 31 | 29 | 29 | 29 |
| olrratp(1) | 22 | 22 | 22 | 23 | 22 | 22 | 21 | 22 | 24 | 24 | 25 | 25 |
| wcfc_coarse | 21 | 21 | 21 | 25 | 25 | 25 | 14 | 15 | 15 | 23 | 22 | 22 |
| ilrratk(1) | 20 | 20 | 20 | 17 | 17 | 15 | 23 | 21 | 20 | 20 | 20 | 18 |
| rivvel | 19 | 19 | 19 | 21 | 20 | 19 | 27 | 25 | 22 | 22 | 21 | 21 |
| deprl_corr | 18 | 18 | 18 | 19 | 19 | 21 | 19 | 19 | 18 | 17 | 17 | 17 |
| damp | 17 | 17 | 17 | 20 | 21 | 20 | 26 | 24 | 21 | 16 | 16 | 16 |
| ilrratk(3) | 16 | 16 | 16 | 13 | 13 | 13 | 11 | 11 | 11 | 11 | 12 | 13 |
| wcfc_fine | 15 | 14 | 14 | 16 | 14 | 14 | 15 | 13 | 13 | 13 | 11 | 11 |
| wcfc_shallow | 14 | 13 | 13 | 14 | 16 | 17 | 10 | 10 | 10 | 15 | 15 | 15 |
| wcfc_organic | 13 | 15 | 15 | 12 | 12 | 12 | 17 | 17 | 16 | 12 | 13 | 12 |
| kc_wetland | 12 | 12 | 12 | 15 | 15 | 16 | 13 | 14 | 14 | 14 | 14 | 14 |
| olrratk(3) | 11 | 11 | 10 | 11 | 11 | 11 | 16 | 16 | 17 | 27 | 26 | 24 |
| ilrratp(3) | 10 | 10 | 11 | 7 | 8 | 9 | 9 | 9 | 9 | 6 | 7 | 9 |
| bfrozn_coarse | 9 | 9 | 9 | 9 | 10 | 10 | 8 | 7 | 7 | 7 | 8 | 8 |
| bfrozn_organic | 8 | 8 | 8 | 10 | 9 | 8 | 12 | 12 | 12 | 10 | 10 | 10 |
| bfrozn_shallow | 7 | 6 | 6 | 8 | 6 | 6 | 6 | 6 | 6 | 9 | 6 | 6 |
| bfrozn_fine | 6 | 7 | 7 | 6 | 7 | 7 | 7 | 8 | 8 | 8 | 9 | 7 |
| bcosby_organic | 5 | 5 | 4 | 4 | 4 | 5 | 3 | 3 | 3 | 4 | 2 | 4 |
| bcosby_shallow | 4 | 4 | 5 | 5 | 5 | 4 | 5 | 5 | 5 | 2 | 1 | 1 |
| bcosby_medium | 3 | 3 | 3 | 1 | 2 | 2 | 4 | 4 | 4 | 1 | 3 | 2 |
| bcosby_coarse | 2 | 2 | 2 | 3 | 1 | 1 | 1 | 1 | 1 | 3 | 4 | 3 |
| bcosby_fine | 1 | 1 | 1 | 2 | 3 | 3 | 2 | 2 | 2 | 5 | 5 | 5 |

| Parameters | TVSA for a 30-Day Window Period | Monthly SA | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| NSE | PBIAS | NRMSE | Q5 | Q95 | SFDC | NSE | PBIAS | NRMSE | Q5 | Q95 | SFDC | |
| kc_corr | 31 | 34 | 33 | 34 | 34 | 33 | 33 | 34 | 34 | 34 | 34 | 34 |
| wcfc-medium | 28 | 30 | 27 | 30 | 30 | 25 | 29 | 29 | 29 | 30 | 27 | 29 |
| kc_forest | 34 | 33 | 34 | 32 | 32 | 29 | 34 | 33 | 33 | 32 | 32 | 32 |
| kc_crops | 33 | 28 | 28 | 28 | 28 | 27 | 31 | 31 | 30 | 31 | 30 | 28 |
| kc_open | 32 | 24 | 25 | 23 | 24 | 20 | 28 | 28 | 27 | 27 | 25 | 25 |
| olrratp(4) | 30 | 27 | 30 | 26 | 25 | 31 | 30 | 26 | 31 | 29 | 24 | 27 |
| kc_lake | 26 | 29 | 29 | 27 | 29 | 26 | 26 | 30 | 28 | 24 | 31 | 33 |
| fc_corr | 19 | 26 | 23 | 25 | 26 | 22 | 23 | 24 | 24 | 25 | 23 | 24 |
| bfrozn_medium | 29 | 32 | 32 | 33 | 27 | 28 | 32 | 32 | 32 | 33 | 28 | 30 |
| fpsno_corr | 24 | 25 | 24 | 24 | 20 | 16 | 22 | 22 | 21 | 21 | 21 | 23 |
| rrc_corr | 22 | 21 | 20 | 21 | 23 | 23 | 25 | 23 | 23 | 23 | 26 | 21 |
| wp_cor | 27 | 31 | 31 | 29 | 33 | 32 | 21 | 27 | 22 | 26 | 33 | 31 |
| olrratp(1) | 25 | 20 | 26 | 22 | 21 | 24 | 27 | 21 | 26 | 22 | 20 | 20 |
| wcfc_coarse | 17 | 19 | 21 | 18 | 18 | 21 | 20 | 20 | 20 | 20 | 19 | 22 |
| ilrratk(1) | 21 | 22 | 19 | 19 | 31 | 19 | 19 | 19 | 19 | 17 | 29 | 18 |
| rivvel | 20 | 23 | 22 | 31 | 22 | 34 | 24 | 25 | 25 | 28 | 22 | 26 |
| deprl_corr | 15 | 17 | 15 | 17 | 17 | 18 | 18 | 18 | 18 | 19 | 18 | 16 |
| damp | 14 | 16 | 16 | 15 | 19 | 14 | 16 | 14 | 16 | 16 | 14 | 17 |
| ilrratk(3) | 13 | 9 | 11 | 9 | 10 | 10 | 14 | 10 | 13 | 11 | 9 | 10 |
| wcfc_organic | 11 | 13 | 13 | 12 | 12 | 13 | 11 | 12 | 11 | 12 | 11 | 13 |
| wcfc_fine | 12 | 10 | 10 | 11 | 11 | 11 | 12 | 9 | 10 | 13 | 17 | 11 |
| wcfc_shallow | 23 | 18 | 14 | 20 | 15 | 30 | 17 | 17 | 15 | 18 | 13 | 19 |
| kc_wetland | 16 | 14 | 17 | 13 | 16 | 17 | 13 | 15 | 14 | 14 | 16 | 14 |
| ilrratp(3) | 8 | 8 | 8 | 8 | 6 | 7 | 10 | 8 | 8 | 8 | 8 | 6 |
| olrratk(3) | 18 | 15 | 18 | 16 | 14 | 12 | 15 | 16 | 17 | 15 | 12 | 15 |
| bfrozn_coarse | 7 | 11 | 9 | 10 | 9 | 9 | 8 | 11 | 9 | 10 | 7 | 8 |
| bfrozn_organic | 9 | 12 | 12 | 14 | 13 | 15 | 9 | 13 | 12 | 9 | 10 | 12 |
| bfrozn_fine | 6 | 7 | 7 | 7 | 8 | 8 | 6 | 7 | 7 | 7 | 15 | 9 |
| bfrozn_shallow | 10 | 6 | 6 | 6 | 7 | 6 | 7 | 6 | 6 | 6 | 6 | 7 |
| bcosby_shallow | 4 | 5 | 5 | 5 | 3 | 5 | 5 | 5 | 5 | 4 | 5 | 4 |
| bcosby_organic | 5 | 4 | 4 | 4 | 5 | 4 | 4 | 3 | 4 | 5 | 4 | 2 |
| bcosby_medium | 2 | 3 | 3 | 3 | 2 | 3 | 3 | 2 | 3 | 2 | 3 | 5 |
| bcosby_coarse | 3 | 1 | 1 | 1 | 4 | 1 | 1 | 1 | 1 | 1 | 1 | 1 |
| bcosby_fine | 1 | 2 | 2 | 2 | 1 | 2 | 2 | 4 | 2 | 3 | 2 | 3 |

© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Bajracharya, A.; Awoye, H.; Stadnyk, T.; Asadzadeh, M. Time Variant Sensitivity Analysis of Hydrological Model Parameters in a Cold Region Using Flow Signatures. Water 2020, 12, 961. https://doi.org/10.3390/w12040961
Bajracharya A, Awoye H, Stadnyk T, Asadzadeh M. Time Variant Sensitivity Analysis of Hydrological Model Parameters in a Cold Region Using Flow Signatures. Water. 2020; 12(4):961. https://doi.org/10.3390/w12040961
Chicago/Turabian StyleBajracharya, Ajay, Hervé Awoye, Tricia Stadnyk, and Masoud Asadzadeh. 2020. "Time Variant Sensitivity Analysis of Hydrological Model Parameters in a Cold Region Using Flow Signatures" Water 12, no. 4: 961. https://doi.org/10.3390/w12040961
APA StyleBajracharya, A., Awoye, H., Stadnyk, T., & Asadzadeh, M. (2020). Time Variant Sensitivity Analysis of Hydrological Model Parameters in a Cold Region Using Flow Signatures. Water, 12(4), 961. https://doi.org/10.3390/w12040961