1. Introduction
The design of offshore structures, ships, and coastal works is based on an estimate of the extreme values of sea state parameters such as the significant wave height (SWH). Such an estimate is naturally a function of the probability of the extreme events, and it is normally carried out by fitting appropriate extreme value distribution curves to experimental data series. Data, whenever possible, are provided by in situ wave meters (buoys, or sometimes pressure gauges or wave stacks) and more recently by satellite altimeter data.
However, while the advantage of using experimental data are obvious, only very few wave meters sites are available all over the world, and even less have been kept long enough to provide a reliable historical series. The problem of evaluating extreme events in locations where no data are available remains therefore open.
The best available solution to this problem is nowadays provided by simulated data: during the last 20 years, many state and international meteorological centres, as well as some research institutions and private companies have started systematically running global and regional wave spectral generation and propagation models. Such simulation systems (henceforth indicated as “model”) are in turn driven by meteorological forecasting systems and constantly validated through the acquisition (“assimilation”) of measured data from both wave meters and satellite altimeters at fixed steps in time. Both forecast and analysis data are published in near real time, thus providing long time series of simulated data, also often indicated as “synthetic data”, which are nowadays an important source of information for statistical analyses, to the point that the use of wave data produced by such model chains has now become commonplace. Estimating the extreme values of SWH for high return times through synthetic data raises however various issues: apart from the obvious problem of reliability of the model chains of both the atmospheric and the sea wave parts, an important aspect is the way through which ground truth wave data are assimilated into the analysis. Most of the assimilation procedures are carried out with satellite altimeter data, which are scattered in time (at many hours’ intervals) and wide apart in space (tens or hundreds of kilometers), so extreme SWH values may often be missed. It is also worth noting that the sampling time of the models, i.e., the time interval at which data are stored and released, is often higher than the standard sampling time of buoys, thus causing a negative bias on the estimated extreme values [
1,
2,
3].
In order to overcome these problems, an integrated procedure [
4] was been proposed by some of the authors of the present paper whereby the curves of extreme SWH as a function of the return time T
R (in the following: SWH(T
R)) deriving from synthetic data are compared and calibrated with the similar curves computed from buoy data in different locations. This provides a way of deriving SWH(T
R) curves for sites where no experimental data are available.
The present paper presents an extension of the same technique and provides an experimental authentication of the methodology based on a new large set of reliable data along the coasts of the USA.
The determination of the probability of extreme SWH is one of the main problems of coastal, offshore, and marine engineering, so that the relevant literature is not only extensive, but also increasing with time as the technology improves and the requirements become more stringent. Therefore, in the following, only contributions which are connected to the aims of this paper will be considered.
All the procedures are substantially based on fitting Extreme Value Probability Distributions (in the following: EVPD) to buoy recorded time series of SWH; references on the general problem date back to many years ago [
5], however Goda’s textbook [
6] is still the most common reference for maritime engineering, even though many authors have improved the approach by considering various methods in various parts of the word: for instance in the Arab-Persian Gulf [
7], in the North Atlantic [
8,
9], in the Korean Seas [
10], in the Gulf of Mexico [
11,
12], in Malaysia [
13] and in the Black Sea [
14]. Much work has also gone on the special case of estimating extreme SWH for special applications such as offshore power plants [
15,
16,
17,
18].
As per the use of model data for the evaluation of wave climate, a recent and very useful contribution is the work by Lin-Ye et al. [
14] who combine the results from a SWAN model with a non-stationary multivariate statistical approach. An interesting sensitivity study of high return period SWH, based on a SWAN model driven by a combination of the ECMWF (European Centre for Medium-Range Weather Forecasts) reanalysis wind and the Holland hurricane model, is also reported in [
19]. The previously mentioned work by Niroomandi et al. [
9] makes use of wave hindcast from the NCEP’s Climate Forecast System and a SWAN wave model validated with buoy measurement, to characterize their temporal and spatial variabilities of extreme SWH. Applications of wave models to risk assessment have been reported, among others, in [
20,
21].
Other useful results are provided in [
22], where a 44-year long wave hindcast data base built up with a WAVEWATCH-III model were used to produce statistics on extreme SWH and compared with buoy data in the Biscay bay. In [
23], data produced by SWAVE wave model driven by ECMWF ERA-Interim wind data were used to compute SWH 100 years extreme values in various locations. Joint distribution of the extreme wave height and wind speed are considered in [
24].
Another important aspect, which has been tackled by many researchers, and which has significant connection with the present paper, is the influence of various factors on the accuracy of EVPD estimates, especially when synthetic rather than experimental data are used: You et al. [
25] found that the uncertainty is caused mainly by short wave record, missing storm wave data, different methods, high or too low thresholds. The effect of threshold values on the estimates of extreme wave heights is considered in [
26,
27,
28,
29]. It is also interesting in this context to note that Beyá et al. [
30], in carrying out a 35-year wave hindcast and calibration, found that the accuracy is lower for the highest wave heights.
Since the use of synthetic data is the only available possibility in locations where no wave meters are available, it is clear that there is ample room for improvement; the present paper seeks to provide and test a methodology which integrates of synthetic and experimental data in order to yield SWH(TR) curves for such locations.
2. Methods
In order to overcome the problems described in
Section 1 to estimate SWH extreme values and return times from model data, a new procedure—in the following indicated as “integrated”—was proposed [
4].
2.1. Integrated Procedure
The basic idea is that that the parameters of any SWH(T
R) function, which links SWH with its return time T
R, are themselves randomly distributed and that the distribution of such parameters can be estimated by integrating the data from the model with those from the buoys in the area. A somewhat similar approach with rainfall data is reported in [
31].
Thus, if SWH
m(T
R, X, Y) is the significant wave height for the generic location X Y and for a given T
R estimated from a wave spectral generation and propagation, it can be assumed that the “true” value of SWH
b is given by the following Equation (1):
In the Equation (1), E represents the error originating from many sources, but mostly due to the meteorological uncertainty. It should here be remembered that model data derive from a chain made up of two parts: a wave model which takes explicitly into account the physical aspects of the wave formation and propagation, which is basically a deterministic algorithm; and a meteorological part, which provides the input winds and involves necessarily a higher degree of randomness.
It should be made clear here that the value SWH
b is “true” in a purely conventional sense, and it is assumed here to be the value computed from buoy recorded data, i.e., the value that would be used for design or research purposes if experimental data were available. Additionally, the procedure proposed here is independent from the particular form of extreme value distribution SWH(T
R), which is adopted and fitted to the data: there are indeed many alternatives, and the relevant state of the research on the field has been briefly discussed in
Section 1.
In particular, according to current ocean engineering, the Weibull distribution was adopted (Equation (2)) with the Peak Over Threshold (POT) method in the form described for instance in [
6].
where H
P are the peak values of SWH while A, B and k are the distribution parameters also respectively known as scale, position, and shape parameters. While A and B can be computed with the least square method, the shape parameter k, following the usual practise as indicated in [
6,
32], is chosen with the best fit criterion among the following 4 values (0.75; 1.00; 1.40 and 2.00).
In any case, since the present paper is not aimed at evaluating, discussing or recommending one particular form of SWH(TR) or any particular procedure to estimate its parameters, the only requirement is that such form and procedure should be uniform throughout the whole analysis.
Once the distribution parameters are known in a given location, the SWH return value for a return period T
R (in years) is computed by making use of Equation (3):
where λ is mean frequency of the recorded extreme events: it is given by ratio between the total number of events N
T and the length n of the observation period expressed in years.
The same operation is carried out in each available buoy location with both the historical experimental direct datasets SWH
b(T
R) and with the model data series SWH
m(T
R); since however most of the times the buoy positions do not exactly coincide with model grid points, a spatial bi-linear interpolation procedure (co-location) is used, as described in [
33].
Assuming then the error E in Equation (1) to be represented by an appropriate probability distribution E(μ, σ), which is of course unknown, the problem is reduced to the search of the appropriate parameters; i.e., the average μ and the root mean square σ of its distribution. They can be estimated, again for each T
R, by taking into account the “true” values SWH
bi(T
R) computed at the locations i where the wave buoys are available. E
i(T
R), again for each location i is thus evaluated as:
The relative error e
i at location i is then given by Equation (5):
Its expected value μ(T
R) in the area can then be estimated as:
and its root mean square σ(T
R) as:
where the sums over the index i being extended to N
b wave buoys considered in the region. Therefore, for a generic location t where no buoy data are available, an estimated SWH
st of the “true” SWH
bt, can be obtained from SWH
mt(T
R) by following Equation (8)
where SWH
mt(T
R) is evaluated by using model recorded data at location t.
The integrated procedure, is thus schematically illustrated in
Figure 1 for a general test location.
The computational cost of the method is not very high, since it amounts to computing 2Nb + 1 EVPD, an easily standardized and commonly available algorithm, as opposed to a single one, as it would be needed for a conventional procedure based on model data only. The estimation of Ei(TR), ei(TR) and SWHst(TR) is straightforward and can be carried out in a single EXCEL® file.
2.2. Validation
In order to verify the soundness of the procedure and the reliability of the results in a given test location, enough historical data must be available to estimate the experimental true value of the SWHb(TR) with a given TR return time in order to compare it with the estimated value. It is worth recalling that, as stated above, “true” means the value that would be computed from an experimental time series.
In order to do so, the spatial distribution parameters have to be evaluated by making use of a number of wave meters that should not include the test location.
Assuming then that in a given area there are N
b buoys available, the procedure is applied by taking one of them to provide the “true” values at the test location t, while the remaining N
a = N
b − 1 series are used to estimate the relative error distribution e(T
R) according to Equation (5). The procedure highlighted in
Figure 1 can thus be applied N
b times, each time choosing in rotation one of the available data series to be taken as test location. Such a methodology, normally called “jackknife” is well known and has been tested in various application [
34,
35].
For each of the N
b available test locations a corrected estimated return time curve (SWH
st) is thus obtained, and it can be compared with the “true” SWH
bt curve. The following
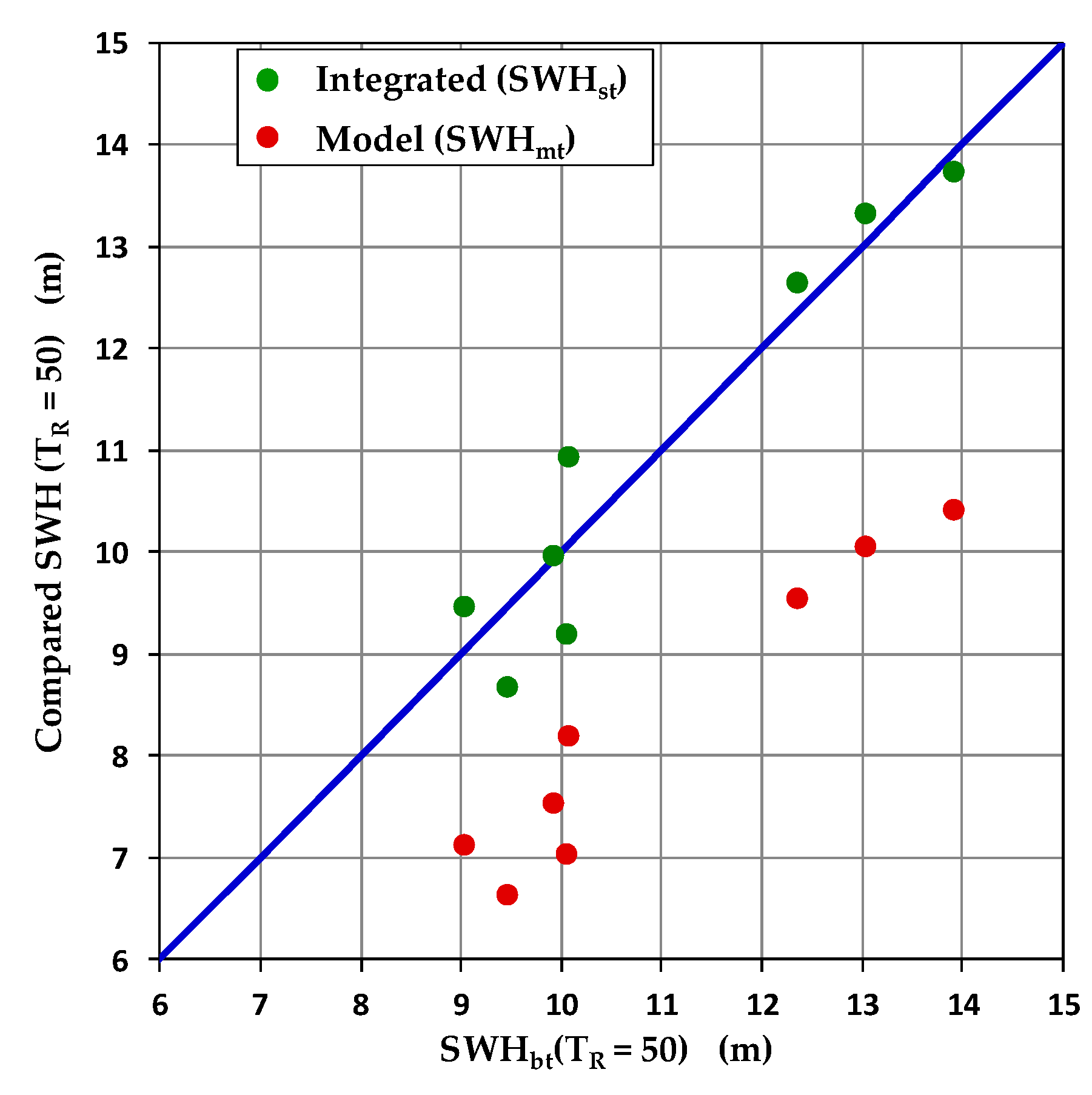
Figure 2 reports an example of the results for NOAA buoy 46014 located along the US Pacific Coast. Here N
b = 8 and therefore N
a = 7.
In
Figure 2, the estimated SWH
st is much closer to the buoy value SWH
bt than the model SWH
mt, thus providing a better and safer evaluation of the sea state design value. The same computation can be carried out by rotating the test position among the N
b available buoy locations: this kind of analysis is performed over three test areas described in
Section 2.2.
For each test location t the model error (ERM) and the integrated procedure error (ERS), both normalized with the buoy value and indicated as “relative errors”, are computed and defined respectively as:
ERM = (Model − Buoy)/Buoy = (SWHmt − SWHbt)/SWHbt;
ERS = (Integrated − Buoy)/Buoy = (SWHst − SWHbt)/SWHbt;
Improvement = abs(ERM) − abs(ERS).
Improvement, which is the difference between the absolute relative errors, will show how accurate the integrated procedure is compared to the simple application of the model data; all values will be reported in percentage.
2.3. Study Sites
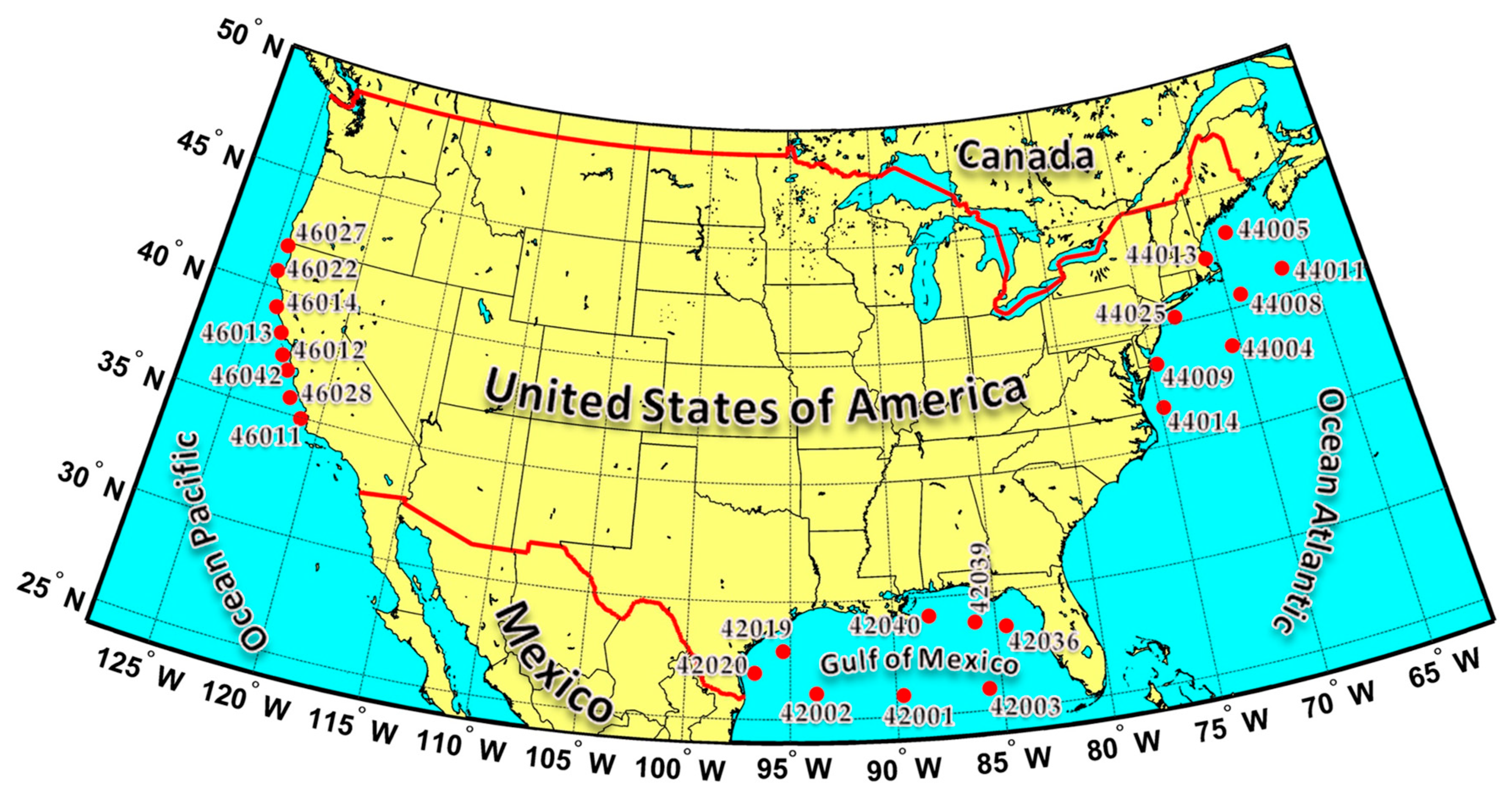
Three areas have been considered for this work: the West (Pacific) Coast and the East (Atlantic) Coast of the United States and the Gulf of Mexico, indicated in the following respectively as PC, AC and GoM. The reason for this choice is the availability of long and good quality wave buoy records given by NOAA (National Oceanic and Atmospheric Administration) National Data Buoy Center (NDBC) [
36].
Figure 3 reports the areas considered with the geographical location of the buoys, and their relative NOAA-NDBC identification code number. All the data records are approximately 30 years long and the sampling rate is one hour.
Model data are obtained from the climate forecast system (CFS), run by NOAA National Center for Environmental Prediction (NCEP) [
37], which produced the CFS Reanalysis (CFSR) dataset, i.e., a reanalysis of the sea and atmosphere state for the period of 1979 to 2009, on all grid points and with a 3-hourly time resolution. For this study we used the two following 10’ × 10’ nested grid data sets:
The integrated procedure had already been applied for some of the GoM area buoys in [
4], but here for the first time a jackknife validation as described in
Section 2.2 is carried out. The model data have also been updated to the most recent version (Phase 2) of CFSR dataset, which was not yet available at the time.
4. Discussion
In considering the results, it should be borne in mind that the object of the investigation is inherently stochastic, since the formation of waves is a natural process driven by meteorological phenomena. The unknown functions SWH(TR) are the outcome of a statistical elaboration on extreme wave data, and as such they are unavoidably affected by random variations.
The following
Table 7, which summarises the main results of
Section 3, shows that the SWH
mt values, computed through the simple use of model data are systematically affected by an error that is never lower in absolute value than 9.70%, and on average of the order of 20%. Besides, the errors are always negative, i.e., the SWH
mt present a negative bias over the buoy values, so that using model results as design parameters would seriously put any coastal or offshore construction at risk.
It also appears that, as remarked in
Section 3.1, the model errors are consistent between the 50 and 100 years return times, since the SWH(T
R) curves portray a similar behaviour for the high values of T
R, which are of interest in practical applications.
A further consideration is that, while the average extreme SWH in the three areas are not too far apart from each other, the model errors are relatively lower in the GoM—most likely reflecting a slightly better performance of the NOAA modelling system in the meteorological conditions of that area.
By applying the integrated procedure, the error ERS decreases to about 0.3–0.5%—a drastic and consistent improvement—even though there are some variations between the various test sites. Only one location (buoy 42002 in GoM, see
Table 5 and
Table 6) shows a negative improvement, i.e., an error of the integrated procedure which is, in absolute value, slightly (4%) greater than the model error. Additionally, in this case however, the resulting error has a positive value, i.e., the SWH computed with the integrated procedure is higher than the buoy-based value—certainly a safer result.
An inherent negative bias in the model has thus been completely removed. It is worth mentioning that the presence of such a negative bias confirms what had been highlighted in previous work [
1,
3,
25,
38], i.e., that the weather/wave models underestimate the extremes despite the constant assimilation of satellite measurement, which due to their coarse temporal and spatial resolution are likely to miss the strongest peaks of the storms.
Considering the inherently stochastic nature of the problem, the results are more than satisfying.
Applying the integrated methodology to any given location requires of course the handling of a considerable amount of data. Simply using model data only requires downloading a single series from one of the available weather/wave systems, such as NOAA [
37] or ECMWF [
39]; integrating it, if N
b wave buoy are available, requires downloading N
b extra model data series as well as N
b buoy data series. On the other hand, the computational effort is not particularly heavy since the extreme value fitting procedures, briefly recalled in
Section 2.1, are nowadays fully standardized.
5. Conclusions
A new procedure, based on integrating wave model data with those obtained with experimental wave data series, has been proposed and tested to evaluate SWH values for a given return time TR in a given location.
Extreme SWH values derived from model time series are integrated with the corresponding extreme value series from available buoys in the same geographical area.
While of course the calibration or the assimilation of measured wave data with weather/wave model results is nothing new, this is the first time that an integration is carried out to determine the parameters of the SWH extreme value distributions. Such parameters are themselves randomly distributed and they have been estimated by making use of the differences between the SWH obtained from the model and those computed from the in-situ data. In other words, the model data are used as indicators, and the buoy data are used for the correction of biases and the evaluation of uncertainties.
By making use of a jackknife procedure, 24 tests have been carried out on three areas along the coasts of the United States, where long records of good quality buoy data are available. It has been shown that the use of model data always causes a relevant undervaluation of the SWH values for a given return time TR and that a considerable improvement in accuracy is gained by making use of this integrated procedure in place of using model data.
In a location where there are no buoy wave meters, or where the data series are not long enough for a correct estimate, the integration of the buoy data in the area with model archive data provides a useful and general design tool to derive the extreme value SWH.
Compared with the simple application of a model on the location of interest, the integrated procedure requires a much heavier amount of data, since it implies accessing many time series rather than a single one; on the other hand, the computational burden is not excessive, since it only requires well known and widely accepted procedures for EVPD.
Extension of the method to any other area in the world is certainly possible, provided that a number of wave meter data series in the general area are accessible: while model data are available all over the world, how to identify and evaluate the relevant wave meter buoys is a matter of specific investigation, which should be carried out along the lines outlined here.