Machine Learning Approaches for Predicting Health Risk of Cyanobacterial Blooms in Northern European Lakes
Abstract
:1. Introduction
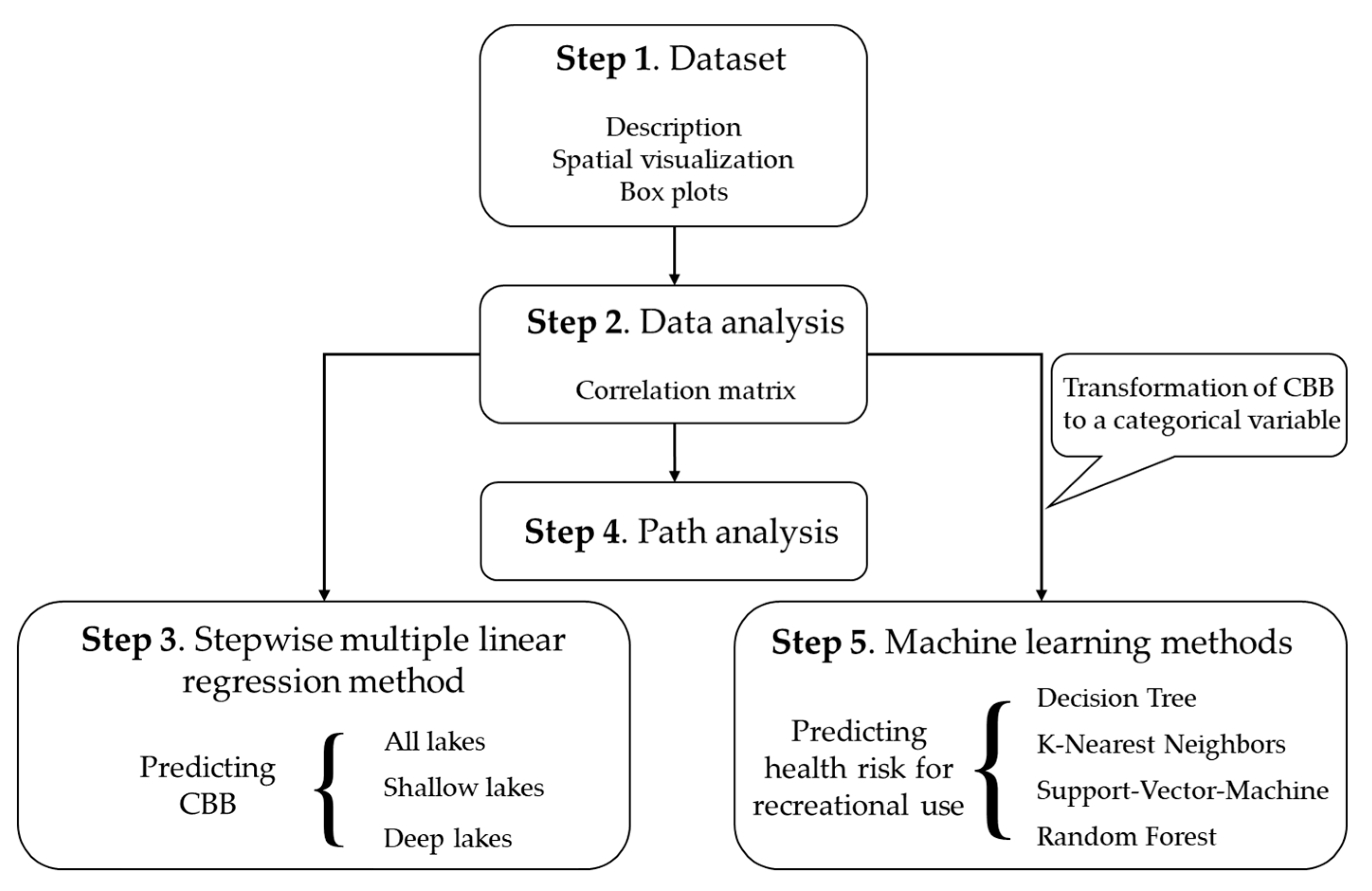
2. Materials and Methods
2.1. Dataset
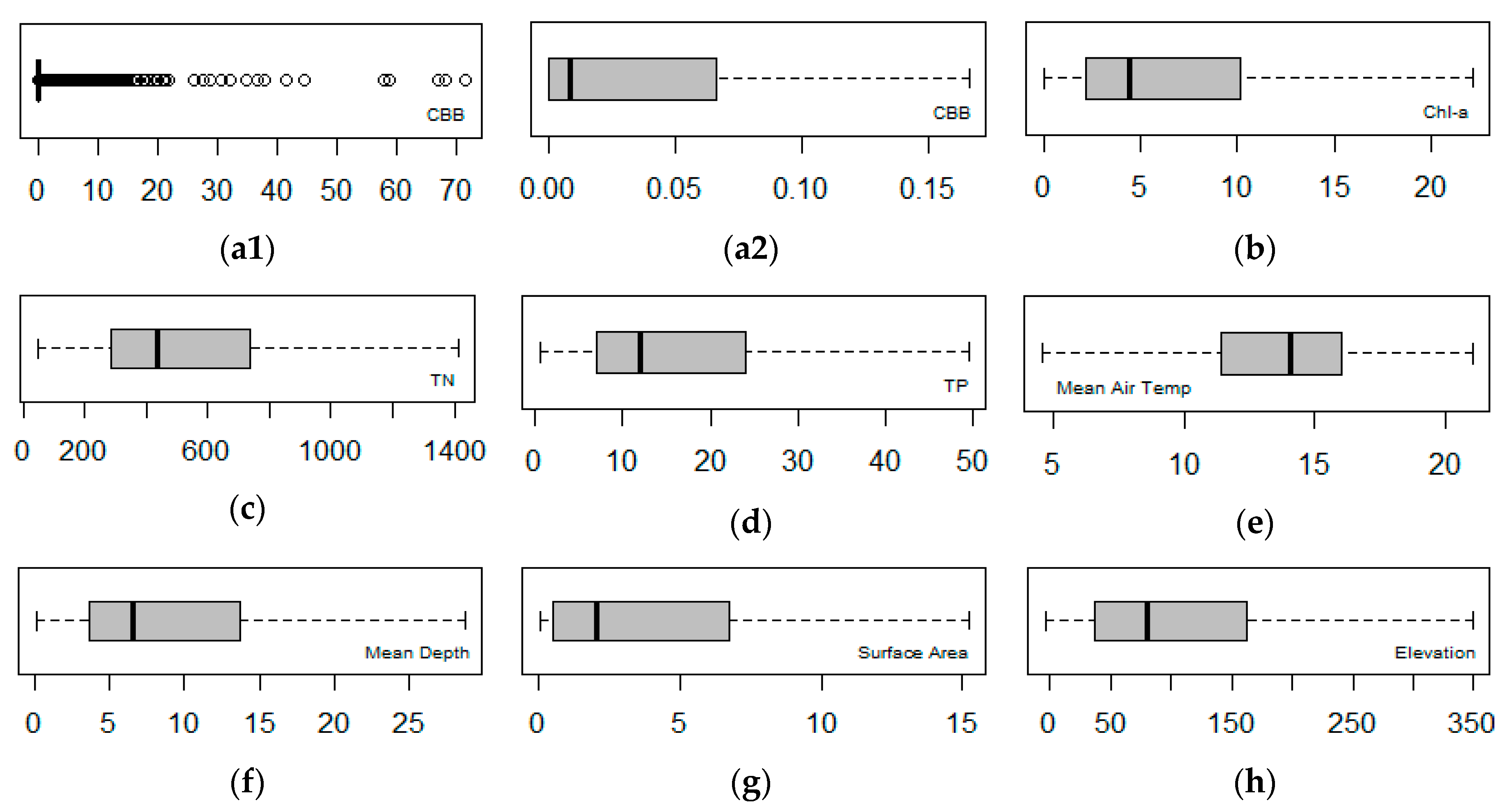
2.2. Explorative Analysis
2.3. Stepwise Multiple Linear Regression
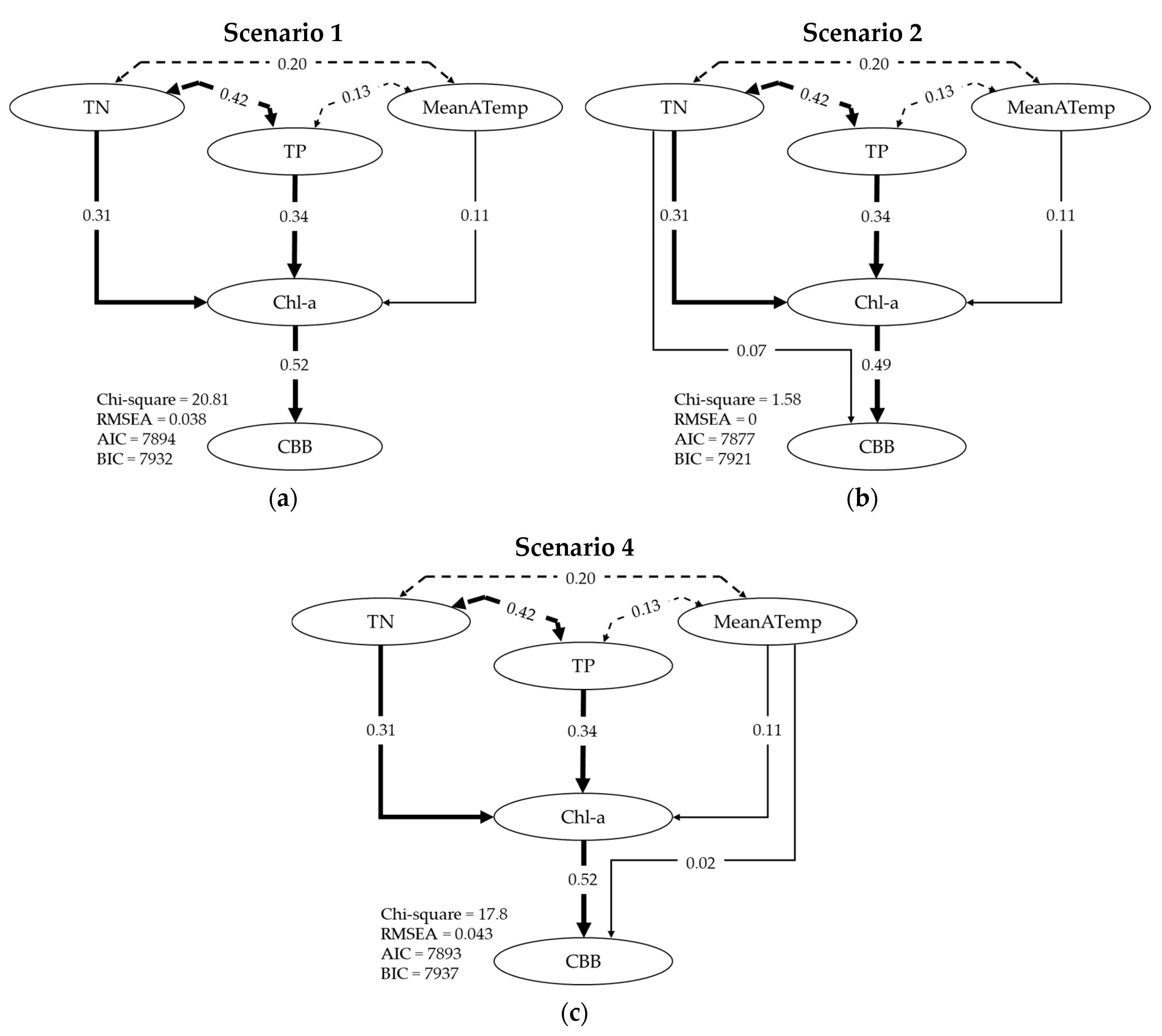
2.4. Path Analysis
2.5. Machine Learning Methods
- DT is a supervised machine learning technique for inducing a decision tree from training data. A decision tree, also referred to as a classification tree, is a flowchart-like diagram that shows the various outcomes from a series of decisions. Practically, it is the mapping of observations about an item to conclusions about its target value [51].
- k-NN is a relatively simple approach to classification that is completely nonparametric. Given a point x0 that one wishes to classify into one of the K groups, the algorithm finds the k observed data points that are nearest to x0. The classification rule is to assign x0 to the population that has the most observed data points out of the k-nearest neighbors. Points for which there is no majority are either classified to one of the majority populations at random or left unclassified [52].
- SVM is an algorithm that classifies data by determining the optimal hyperplane that separates observations according to their class labels. The central concept of this method is to accommodate classes that are separable by linear and non-linear class boundaries [53].
- RF is a classifier algorithm that evolved from decision trees. It collects the classifications and chooses the most voted prediction as the result. RFs sample data from the original dataset and a subset of features is randomly selected from the optional features to grow the tree at each node. The strength of the RFs relies on the capability to enable a large number of weak or weakly correlated classifiers to form a strong classifier [54].
3. Results and Discussion
3.1. Identifying Variables Explaining CBB Variation
3.2. Describing Dependent Relationships among Variables
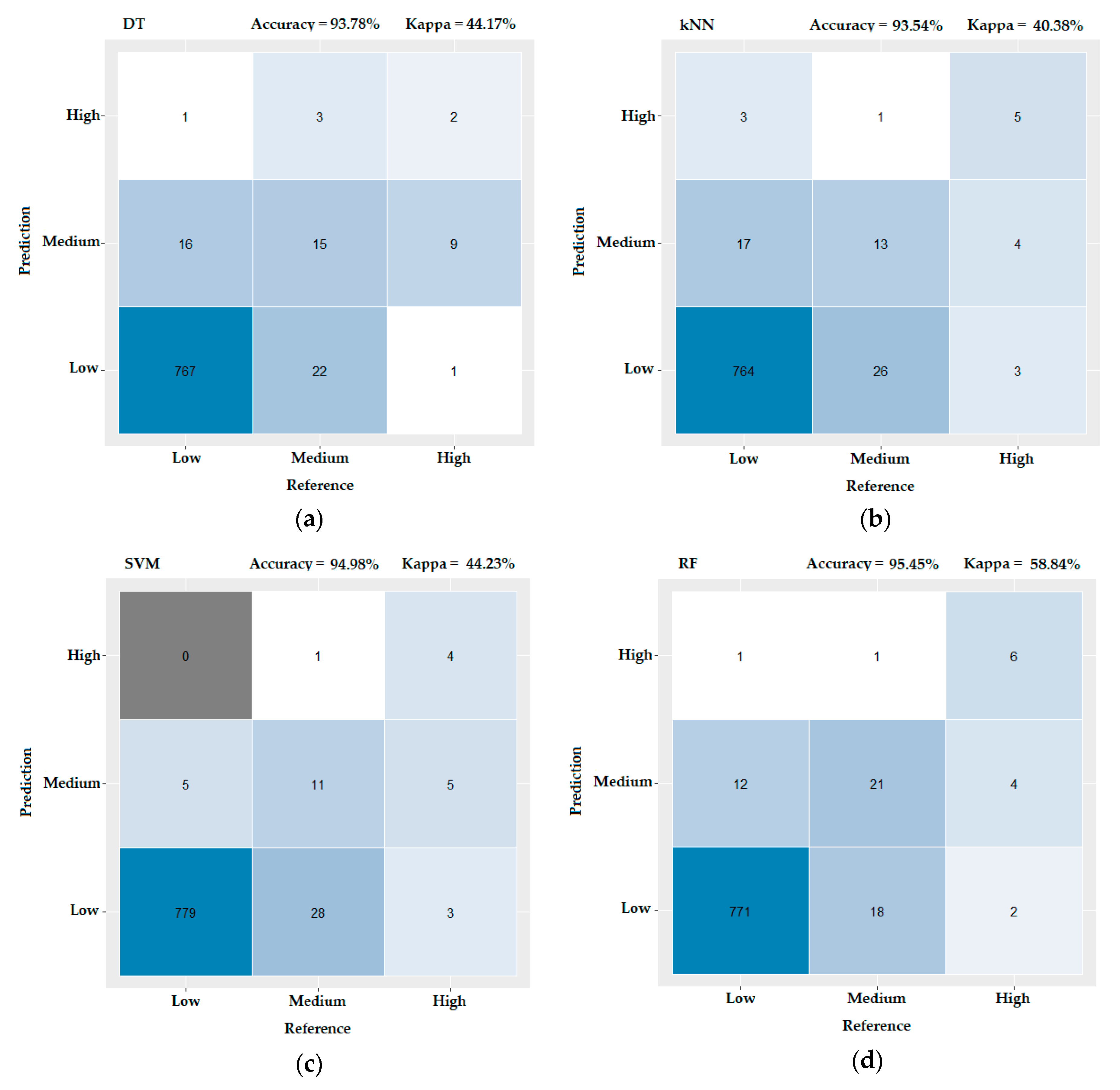
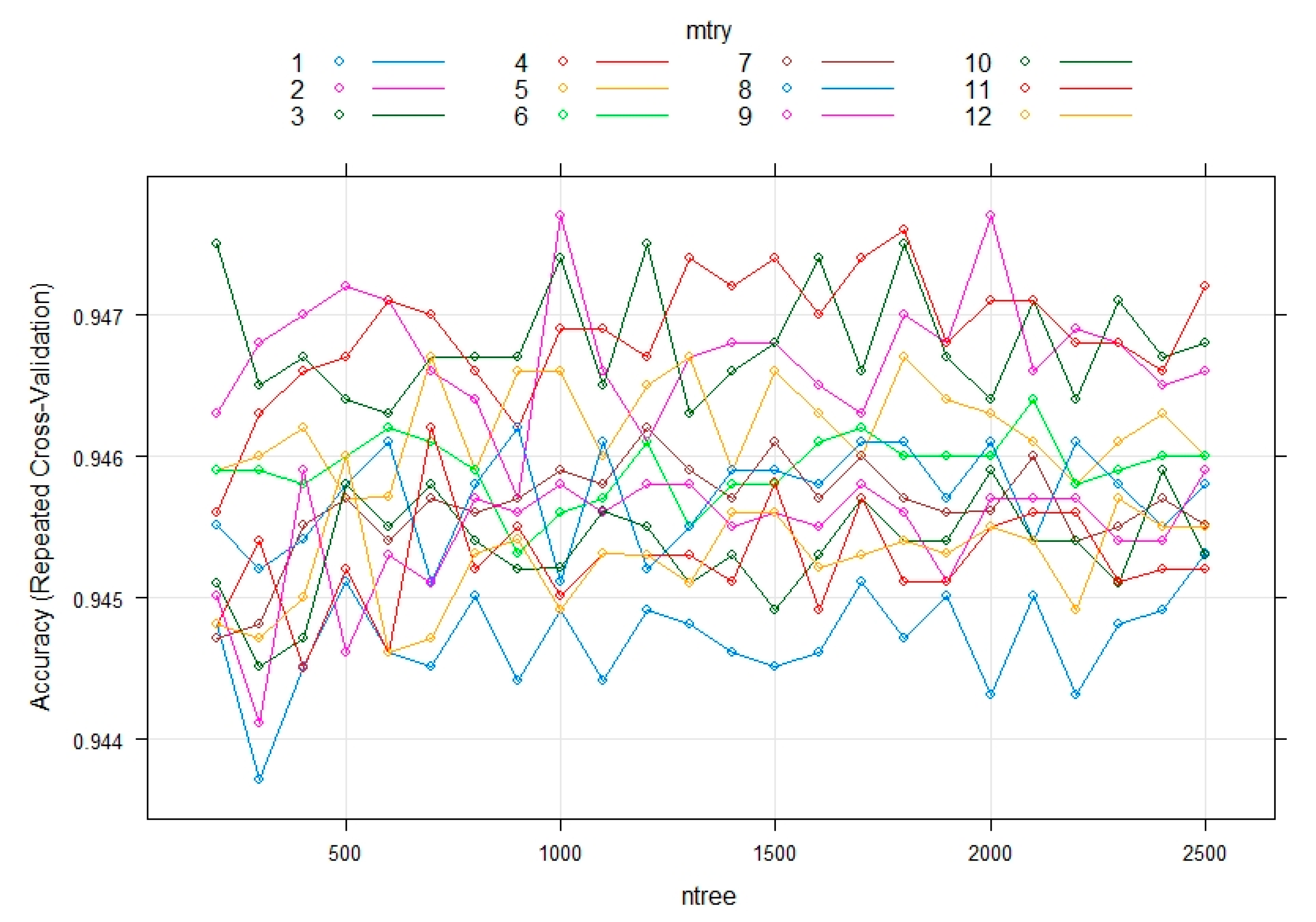
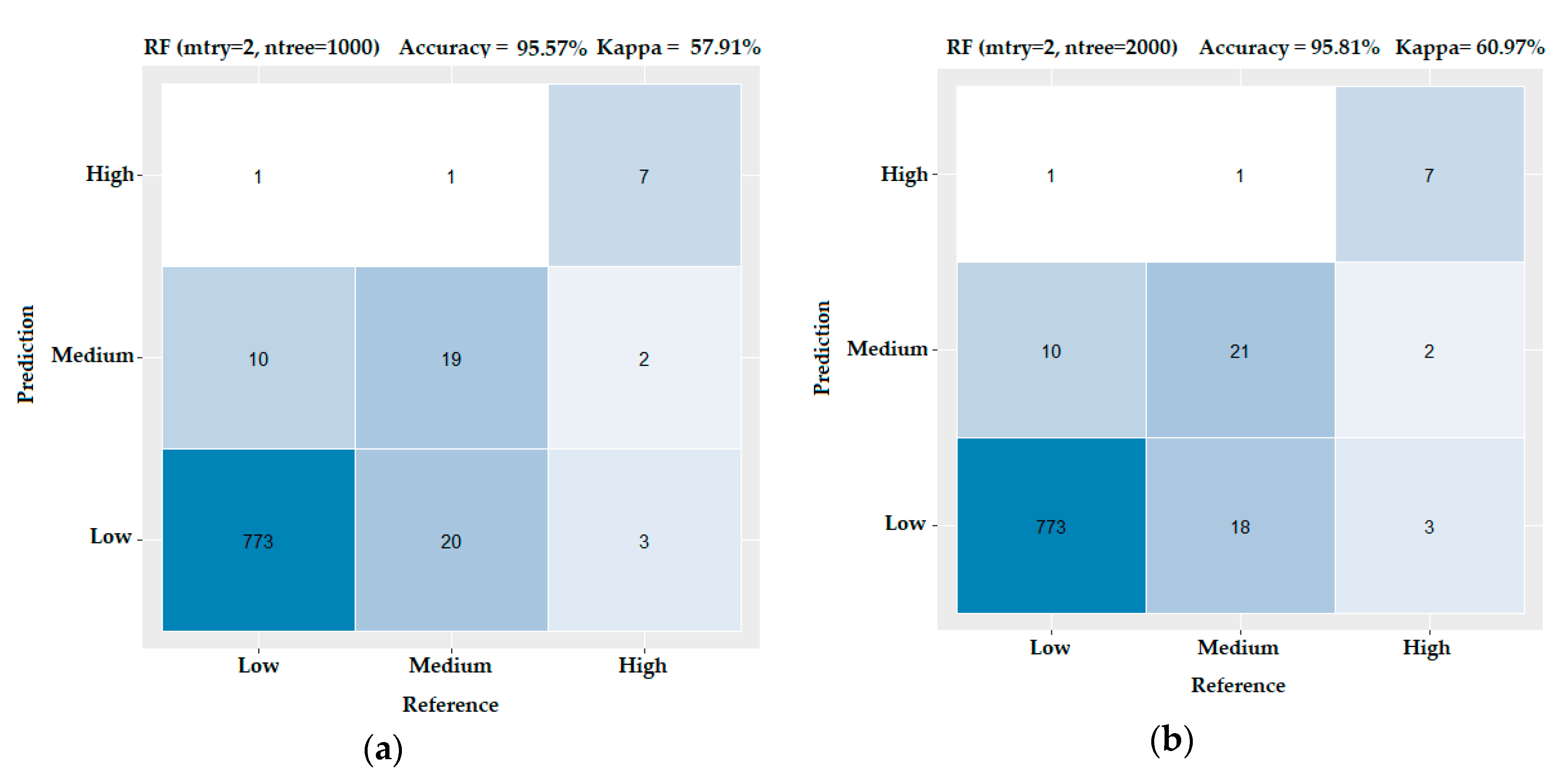
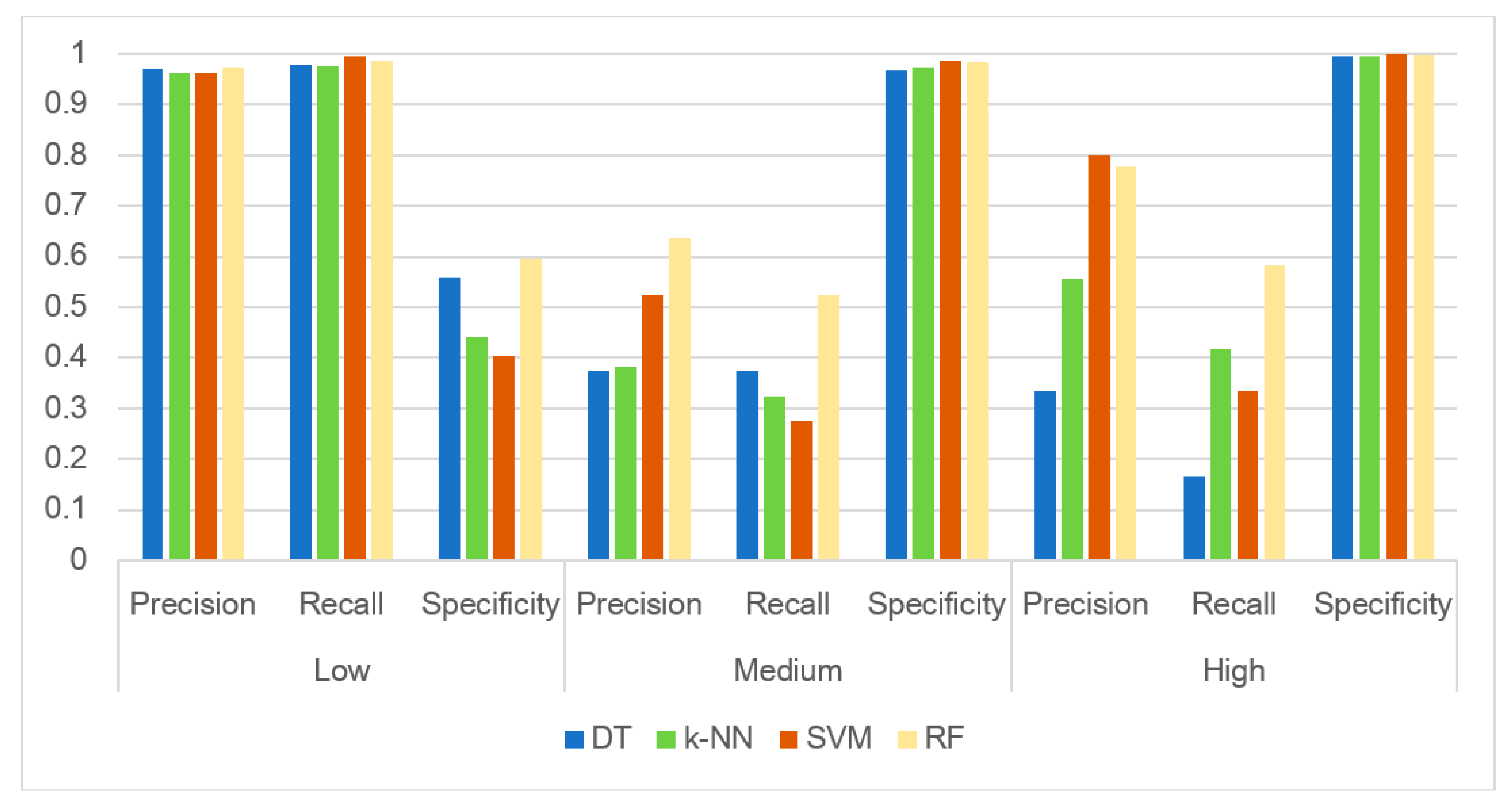
3.3. Evaluating the Performance of the Machine Learning Methods
4. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Carmichael, W. A world overview—One-hundred-twenty-seven years of research on toxic cyanobacteria—Where do we go from here? In Cyanobacterial Harmful Algal Blooms: State of the Science and Research Needs; Hudnell, H.K., Ed.; Springer: New York, NY, USA, 2008; Volume 619, pp. 105–125. [Google Scholar]
- Paerl, H.W.; Huisman, J. Blooms like it hot. Science 2008, 320, 57–58. [Google Scholar] [CrossRef] [Green Version]
- O’Neil, J.M.; Davis, T.W.; Burford, M.A.; Gobler, C.J. The rise of harmful cyanobacteria blooms: The potential roles of eutrophication and climate change. Harmful Algae 2012, 14, 313–334. [Google Scholar] [CrossRef]
- Carmichael, W.W.; Boyer, G.L. Health impacts from cyanobacteria harmful algae blooms: Implications for the North American Great Lakes. Harmful Algae 2016, 54, 194–212. [Google Scholar] [CrossRef] [PubMed]
- Mellios, N.; Papadimitriou, T.; Laspidou, C. Predictive modeling of microcystin concentrations in a hypertrophic lake by means of Adaptive Neuro Fuzzy Inference System (ANFIS). Eur. Water 2016, 55, 91–103. [Google Scholar]
- Lévesque, B.; Gervais, M.-C.; Chevalier, P.; Gauvin, D.; Anassour-Laouan-Sidi, E.; Gingras, S.; Fortin, N.; Brisson, G.; Greer, C.; Bird, D. Prospective study of acute health effects in relation to exposure to cyanobacteria. Sci. Total Environ. 2014, 466, 397–403. [Google Scholar] [CrossRef]
- Hamilton, D.P.; Wood, S.A.; Dietrich, D.R.; Puddick, J. Costs of harmful blooms of freshwater cyanobacteria. In Cyanobacteria: An Economic Perspective; Sharma, N.K., Rai, A.K., Stal, L.J., Eds.; John Wiley & Sons: Chichester, UK, 2013; Volume 1, pp. 245–256. [Google Scholar]
- Solheim, A.L.; Rekolainen, S.; Moe, S.J.; Carvalho, L.; Philips, G.; Ptacnik, R.; Penning, W.E.; Tóth, L.G.; O’Toole, C.; Schartau, A.K.; et al. Ecological threshold responses in European lakes and their applicability for the Water Framework Directive (WFD) implementation: Synthesis of lakes results from the REBECCA project. Aquat. Ecol. 2008, 42, 317–334. [Google Scholar] [CrossRef]
- Francis, G. Poisonous Australian Lake. Nature 1878, 18, 11–12. [Google Scholar] [CrossRef] [Green Version]
- Carpenter, S.R.; Stanley, E.H.; Vander Zanden, M.J. State of the world’s freshwater ecosystems: Physical, chemical, and biological changes. Annu. Rev. Environ. Resour. 2011, 36, 75–99. [Google Scholar] [CrossRef] [Green Version]
- Elliott, J.A. The seasonal sensitivity of cyanobacteria and other phytoplankton to changes in flushing rate and water temperature. Glob. Chang. Biol. 2010, 16, 864–876. [Google Scholar] [CrossRef]
- Paerl, H.W.; Otten, T.G. Harmful cyanobacterial blooms: Causes, consequences, and controls. Microb. Ecol. 2013, 65, 995–1010. [Google Scholar] [CrossRef]
- Wells, M.L.; Trainer, V.L.; Smayda, T.J.; Karlson, B.S.O.; Trick, C.G.; Kudela, R.M.; Ishikawa, A.; Bernard, S.; Wulff, A.; Anderson, D.M.; et al. Harmful algal blooms and climate change: Learning from the past and present to forecast the future. Harmful Algae 2015, 49, 68–93. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Laspidou, C.; Kofinas, D.; Mellios, N.; Latinopoulos, D.; Papadimitriou, T. Investigation of factors affecting the trophic state of a shallow Mediterranean reconstructed lake. Ecol. Eng. 2017, 103, 154–163. [Google Scholar] [CrossRef]
- Mellios, N.; Kofinas, D.; Laspidou, C.; Papadimitriou, T. Mathematical modeling of trophic state and nutrient flows of Lake Karla using the PCLake model. Environ. Process. 2015, 2, 85–100. [Google Scholar] [CrossRef] [Green Version]
- Richardson, J.; Feuchtmayr, H.; Miller, C.; Hunter, P.D.; Maberly, S.C.; Carvalho, L. Response of cyanobacteria and phytoplankton abundance to warming, extreme rainfall events and nutrient enrichment. Glob. Chang. Biol. 2019, 25, 3365–3380. [Google Scholar] [CrossRef] [Green Version]
- Beaulieu, M.; Pick, F.; Gregory-Eaves, I. Nutrients and water temperature are significant predictors of cyanobacterial biomass in a 1147 lakes data set. Limnol. Oceanogr. 2013, 58, 1736–1746. [Google Scholar] [CrossRef]
- Moe, S.J.; Couture, R.M.; Haande, S.; Lyche Solheim, A.; Jackson-Blake, L. Predicting lake quality for the next generation: Impacts of catchment management and climatic factors in a probabilistic model framework. Water 2019, 11, 1767. [Google Scholar] [CrossRef] [Green Version]
- Romo, S.; Soria, J.; Fernandez, F.; Ouahid, Y.; Baron-Sola, A. Water residence time and the dynamics of toxic cyanobacteria. Freshw. Biol. 2013, 58, 513–522. [Google Scholar] [CrossRef]
- Paerl, H.W.; Fulton, R.S.; Moisander, P.H.; Dyble, J. Harmful freshwater algal blooms, with an emphasis on cyanobacteria. Sci. World J. 2001, 1, 76–113. [Google Scholar] [CrossRef]
- Wood, S.A.; Prentice, M.J.; Smith, K.; Hamilton, D.P. Low dissolved inorganic nitrogen and increased heterocyte frequency: Precursors to Anabaena planktonica blooms in a temperate, eutrophic reservoir. J. Plankton Res. 2010, 32, 1315–1325. [Google Scholar] [CrossRef] [Green Version]
- Noges, T.; Laugaste, R.; Noges, P.; Tonno, I. Critical N: P ratio for cyanobacteria and N 2-fixing species in the large shallow temperate lakes Peipsi and Võrtsjärv, North-East Europe. Hydrobiologia 2008, 599, 77–86. [Google Scholar] [CrossRef]
- Havens, K.E.; Phlips, E.J.; Cichra, M.F.; Li, B.L. Light availability as a possible regulator of cyanobacteria species composition in a shallow subtropical lake. Freshw. Biol. 1998, 39, 547–556. [Google Scholar] [CrossRef]
- Scheffer, M.; Rinaldi, S.; Gragnani, A.; Mur, L.R.; Van Nes, E.H. On the dominance of filamentous cyanobacteria in shallow, turbid lakes. Ecology 1997, 78, 272–282. [Google Scholar] [CrossRef]
- Carey, C.C.; Ibelings, B.W.; Hoffmann, E.P.; Hamilton, D.P.; Brookes, J.D. Eco-physiological adaptations that favour freshwater cyanobacteria in a changing climate. Water Res. 2012, 46, 1394–1407. [Google Scholar] [CrossRef] [PubMed]
- Brookes, J.D.; Carey, C.C. Resilience to blooms. Science 2011, 334, 46–47. [Google Scholar] [CrossRef]
- Kosten, S.; Huszar, V.L.; Bécares, E.; Costa, L.S.; Van Donk, E.; Hansson, L.A.; Jeppesen, E.; Kruk, C.; Lacerot, G.; Mazzeo, N.; et al. Warmer climates boost cyanobacterial dominance in shallow lakes. Glob. Chang. Biol. 2012, 18, 118–126. [Google Scholar] [CrossRef]
- Richardson, J.; Miller, C.; Maberly, S.C.; Taylor, P.; Globevnik, L.; Hunter, P.; Jeppesen, E.; Mischke, U.; Moe, S.J.; Pasztaleniec, A.; et al. Effects of multiple stressors on cyanobacteria abundance vary with lake type. Glob. Chang. Biol. 2018, 24, 5044–5055. [Google Scholar] [CrossRef] [Green Version]
- Psilovikos, A. Water Resources; Tziolas: Thessaloniki, Greece, 2020; ISBN 978-960-602-0. (In Greek) [Google Scholar]
- Karamoutsou, L.; Psilovikos, A. The use of Artificial Neural Network in Water Quality Prediction in Lake Kastoria, Greece. In Proceedings of the 14th Conference of the Hellenic hydrotechnical Association (HHA), Volos, Greece, 16–17 May 2019; pp. 882–889. [Google Scholar]
- Rigosi, A.; Carey, C.C.; Ibelings, B.W.; Brookes, J.D. The interaction between climate warming and eutrophication to promote cyanobacteria is dependent on trophic state and varies among taxa. Limnol. Oceanogr. 2014, 59, 99–114. [Google Scholar] [CrossRef] [Green Version]
- Taranu, Z.E.; Zurawell, R.W.; Pick, F.; Gregory-Eaves, I. Predicting cyanobacterial dynamics in the face of global change: The importance of scale and environmental context. Glob. Chang. Biol. 2012, 18, 3477–3490. [Google Scholar] [CrossRef]
- Wei, B.; Sugiura, N.; Maekawa, T. Use of artificial neural network in the prediction of algal blooms. Water Res. 2001, 35, 2022–2028. [Google Scholar] [CrossRef]
- Recknagel, F.; French, M.; Harkonen, P.; Yabunaka, K.I. Artificial neural network approach for modelling and prediction of algal blooms. Ecol. Model. 1997, 96, 11–28. [Google Scholar] [CrossRef]
- World Health Organization. Guidelines for Safe Recreational Waters: Coastal and Fresh Waters; Chapter 8; WHO Publishing: Geneva, Switzerland, 2003; Volume 1, pp. 136–158. [Google Scholar]
- Bláha, L.; Babica, P.; Maršálek, B. Toxins produced in cyanobacterial water blooms-toxicity and risks. Interdiscip. Toxicol. 2009, 2, 36–41. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Moe, S.J.; Schmidt-Kloiber, A.; Dudley, B.J.; Hering, D. The WISER way of organising ecological data from European rivers, lakes, transitional and coastal waters. Hydrobiologia 2013, 704, 11–28. [Google Scholar] [CrossRef] [Green Version]
- Hering, D.; Borja, A.; Carvalho, L.; Feld, C.K. Assessment and recovery of European water bodies: Key messages from the WISER project. Hydrobiologia 2013, 704, 1–9. [Google Scholar] [CrossRef]
- Schmidt-Kloiber, A.; Moe, S.J.; Dudley, B.; Strackbein, J.; Vogl, R. The WISER metadatabase: The key to more than 100 ecological datasets from European rivers, lakes and coastal waters. Hydrobiologia 2013, 704, 29–38. [Google Scholar] [CrossRef] [Green Version]
- Jordan, M.I.; Mitchell, T.M. Machine learning: Trends, perspectives, and prospects. Science 2015, 349, 255–260. [Google Scholar] [CrossRef] [PubMed]
- Revelle, W. psych: Procedures for Personality and Psychological Research, Northwestern University, Evanston, Illinois, USA. 2017. Available online: https://CRAN.R-project.org/package=psych/ (accessed on 25 November 2019).
- Team, R.C. R: A Language and Environment for Statistical Computing. R Foundation for Statistical Computing, Vienna, Austria. Available online: https://www.R-project.org/ (accessed on 20 November 2019).
- Carvalho, L.; McDonald, C.; De Hoyos, C.; Mischke, U.; Phillips, G.; Borics, G.; Poikane, S.; Skjelbred, B.; Solheim, A.L.; Van Wichelen, J.; et al. Sustaining recreational quality of European lakes: Minimizing the health risks from algal blooms through phosphorus control. J. Appl. Ecol. 2013, 50, 315–323. [Google Scholar] [CrossRef] [Green Version]
- Ghaffar, S.; Stevenson, R.J.; Khan, Z. Cyanobacteria Dominance in Lakes and Evaluation of Its Predictors: A Study of Southern Appalachians Ecoregion, USA. In MATEC Web of Conferences. EDP Sci. 2016, 60, 02001. [Google Scholar]
- Wickham, H.; Averick, M.; Bryan, J.; Chang, W.; D’Agostino McGowan, L.; François, R.; Grolemund, G.; Hayes, A.; Henry, L.; Hester, J.; et al. Welcome to the Tidyverse. J. Open Source Softw. 2019, 4, 1686. [Google Scholar] [CrossRef]
- Kuhn, M.; Wing, J.; Wenston, S.; Williams, A.; Keefer, C.; Engelhardt, A.; Cooper, T.; Mayer, Z.; Kenkel, B.; Team, R.C.; et al. Caret: Classification and regression training. R Package Version 2016, 6, 78. [Google Scholar]
- Lumley, T.; Miller, A. Leaps: Regression subset selection. R Package Vesion 2009, 2, 2366. [Google Scholar]
- Venables, B.D.; Ripley, W.N. Modern Applied Statistics with S, 4th ed.; Springer: New York, NY, USA, 2008; pp. 1–496. [Google Scholar]
- Rosseel, Y. Lavaan: An R package for structural equation modeling and more. Version 0.5–12 (BETA). J. Stat. Softw. 2012, 48, 1–36. [Google Scholar] [CrossRef] [Green Version]
- Rokach, L. Ensemble-based classifiers. Artif. Intell. Rev. 2010, 33, 1–39. [Google Scholar] [CrossRef]
- Rokach, L.; Maimon, O. Top-down induction of decision trees classifiers-a survey. IEEE Trans. Syst. ManCybern. Part C 2005, 35, 476–487. [Google Scholar] [CrossRef] [Green Version]
- Neath, R.C.; Johnson, M.S. Discrimination and Classification. In International Encyclopedia of Education, 3rd ed.; Baker, E., McGaw, B., Peterson, P., Eds.; Elsevier Ltd.: London, UK, 2010; Volume 1, pp. 135–141. [Google Scholar]
- Hsu, C.W.; Lin, C.J. A comparison of methods for multiclass support vector machines. IEEE Trans. Neural Netw. 2002, 13, 415–425. [Google Scholar] [PubMed] [Green Version]
- Mao, W.; Wang, F.Y. Cultural Modeling for Behavior Analysis and Prediction. In New Advances in Intelligence and Security Informatics, 1st ed.; Academic Press: Waltham, MA, USA, 2012; pp. 91–102. [Google Scholar]
- Wickham, H. ggplot2: Elegant Graphics for Data Analysis, 1st ed.; Springer: New York, NY, USA, 2016. [Google Scholar]
- Therneau, T.; Atkinson, B.; Ripley, B. Rpart: Recursive Partitioning and Regression Trees, R Package Version 4.1-13. 2018. Available online: https://CRAN.R-project.org/package=rpart/ (accessed on 10 January 2020).
- Meyer, D.; Dimitriadou, E.; Hornik, K.; Weingessel, A.; Leisch, F. e1071: Misc Functions of the Department of Statistics, Probability Theory Group (Formerly: E1071), TU Wien. R Package Version 1.7-3. 2019. Available online: https://CRAN.R-project.org/package=e1071 (accessed on 10 January 2020).
- Auguie, B. gridExtra: Miscellaneous Functions for "Grid" Graphics. R Package Version 2.3. 2017. Available online: https://CRAN.R-project.org/package=gridExtra (accessed on 10 January 2020).
- Liaw, A.; Wiener, M. Classification and regression by randomForest. R News 2002, 2, 18–22. [Google Scholar]
- Dolman, A.M.; Rücker, J.; Pick, F.R.; Fastner, J.; Rohrlack, T.; Mischke, U.; Wiedner, C. Cyanobacteria and cyanotoxins: The influence of nitrogen versus phosphorus. PLoS ONE 2012, 7, e38757. [Google Scholar] [CrossRef]
- Shakhari, S.; Banerjee, I. A multi-class classification system for continuous water quality monitoring. Heliyon 2019, 5, e01822. [Google Scholar] [CrossRef] [Green Version]
- Leisch, F.; Dimitriadou, E. mlbench: Machine Learning. Benchmark Problems. R Package Version 2.1-1. 2010. Available online: https://cran.r-project.org/web/packages/mlbench/index.html (accessed on 15 January 2020).
- Hastie, T.; Tibshirani, R.; Friedman, J. The Elements of Statistical Learning: Data Mining, Inference, and Prediction, 2nd ed.; Springer Science & Business Media: New York, NY, USA, 2017. [Google Scholar]
- Landis, J.R.; Koch, G.G. An application of hierarchical kappa-type statistics in the assessment of majority agreement among multiple observers. Biometrics 1977, 33, 363–374. [Google Scholar] [CrossRef]

| Country | Number of Lakes | Median/Mean No. of Observations Per Lake | Sampling Month | Time Period |
|---|---|---|---|---|
| UK | 81 | 3/3.39 | June to October | 2007–2008 |
| Denmark | 20 | 19/17.06 | June to September | 1989–2012 |
| Norway | 408 | 4/5.41 | May to October | 1988–2009 |
| Sweden | 77 | 4.5/6.71 | May to October | 2001–2009 |
| Finland | 217 | 1/3.42 | May to October | 1993–2009 |
| Lithuania | 19 | 1/2.47 | June to September | 2011–2012 |
| Variable | Minimum | Maximum | Median | Mean |
|---|---|---|---|---|
| Latitude | 50.078 | 69.897 | 59.866 | 60.341 |
| Elevation (m a.s.l.) | −4 | 1057 | 126 | 79.9 |
| Surface area (km2) | 0.019 | 1377 | 39.1 | 2.1 |
| Mean depth (m) | 0.096 | 239 | 12.1 | 6.6 |
| Max depth (m) | 1 | 516 | 35.79 | 22 |
| Mean air temperature (°C) | −0.3 | 21.1 | 13.6 | 14.1 |
| Max air temperature (°C) | 9.8 | 34.1 | 23.58 | 23.8 |
| Total nitrogen (μg/L) | 47 | 6841.7 | 656.9 | 435 |
| Total phosphorus (μg/L) | 0.5 | 1270 | 28.86 | 12 |
| TN/TP | 0.92 | 565 | 34.5 | 43.3 |
| Chlorophyll-a (μg/L) | 0 | 310.1 | 10.89 | 4.4 |
| Cyanobacteria biomass (mg/L) | 0 | 71.5 | 0.642 | 0.00844 |
| Risk Category | Limits According to Cyanobacterial Biomass |
|---|---|
| Low | CBB ≤ 2 mg/L |
| Medium | 2 mg/L< CBB ≤ 10 mg/L |
| High | CBB > 10 mg/L |
| Linear Model | R2 | BIC | AIC | RMSE |
|---|---|---|---|---|
| All lakes | ||||
| CBB = −0.32 + 27.33 × Chl-a | 0.33 | 20,662 | 20,643 | 2.698 |
| CBB = −0.45 + 25.71 × Chl-a + 2.1 × TN | 0.33 | 20,651 | 20,626 | 2.697 |
| Shallow lakes | ||||
| CBB = 0.03 + 24.99 × Chla | 0.28 | 4704 | 4690 | 5.667 |
| CBB = −0.56 + 21.44 × Chl-a + 5.83 × TN | 0.27 | 4698 | 4680 | 5.676 |
| CBB = −2.26 + 21.86 × Chl-a + 6.16 × TN + 250.2×MeanDep | 0.27 | 4695 | 4672 | 5.648 |
| CBB = −2.64 + 22.26 × Chl-a + 9.63 × TN + 268.13 × MeanDep – 18.13 × TN/TP | 0.27 | 4694 | 4669 | 5.643 |
| Deep Lakes | ||||
| CBB = −0.4 + 29.48 × Chl-a | 0.43 | 11,695 | 11,676 | 1.294 |
| CBB = −0.4 + 26.98 × Chl-a + 35.67 × TN/TP | 0.43 | 11,598 | 11,568 | 1.291 |
| CBB = −0.21 + 26.2 × Chl-a – 3.47 × TN + 86.68 × TN/TP | 0.44 | 11,594 | 11,565 | 1.278 |
| Scenario | z-Value | Pr (>|z|) |
|---|---|---|
| 1 | ||
| Chl-a ~ TN | 21.985 | 0.000 |
| Chl-a ~ TP | 24.122 | 0.000 |
| Chl-a ~ MeanATemp | 8.346 | 0.000 |
| CBB ~ Chl-a | 39.611 | 0.000 |
| 2 | ||
| Chl-a ~ TN, TP, MeanATemp | As in Scenario 1 | |
| CBB ~ Chl-a | 32.946 | 0.000 |
| CBB ~ TN | 4.389 | 0.000 |
| 3 | ||
| Chl-a ~ TN, TP, MeanATemp | As in Scenario 1 | |
| CBB ~ Chl-a | 34.31 | 0.000 |
| CBB ~ TP | 0.929 | 0.353 |
| 4 | ||
| Chl-a ~ TN, TP, MeanATemp | As in Scenario 1 | |
| CBB ~ Chl-a | 38.327 | 0.000 |
| CBB ~ MeanATemp | 1.736 | 0.083 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Mellios, N.; Moe, S.J.; Laspidou, C. Machine Learning Approaches for Predicting Health Risk of Cyanobacterial Blooms in Northern European Lakes. Water 2020, 12, 1191. https://doi.org/10.3390/w12041191
Mellios N, Moe SJ, Laspidou C. Machine Learning Approaches for Predicting Health Risk of Cyanobacterial Blooms in Northern European Lakes. Water. 2020; 12(4):1191. https://doi.org/10.3390/w12041191
Chicago/Turabian StyleMellios, Nikolaos, S. Jannicke Moe, and Chrysi Laspidou. 2020. "Machine Learning Approaches for Predicting Health Risk of Cyanobacterial Blooms in Northern European Lakes" Water 12, no. 4: 1191. https://doi.org/10.3390/w12041191
APA StyleMellios, N., Moe, S. J., & Laspidou, C. (2020). Machine Learning Approaches for Predicting Health Risk of Cyanobacterial Blooms in Northern European Lakes. Water, 12(4), 1191. https://doi.org/10.3390/w12041191






