The Influence of Pool-Riffle Morphological Features on River Mixing
Abstract
:1. Introduction
2. Materials and Methods
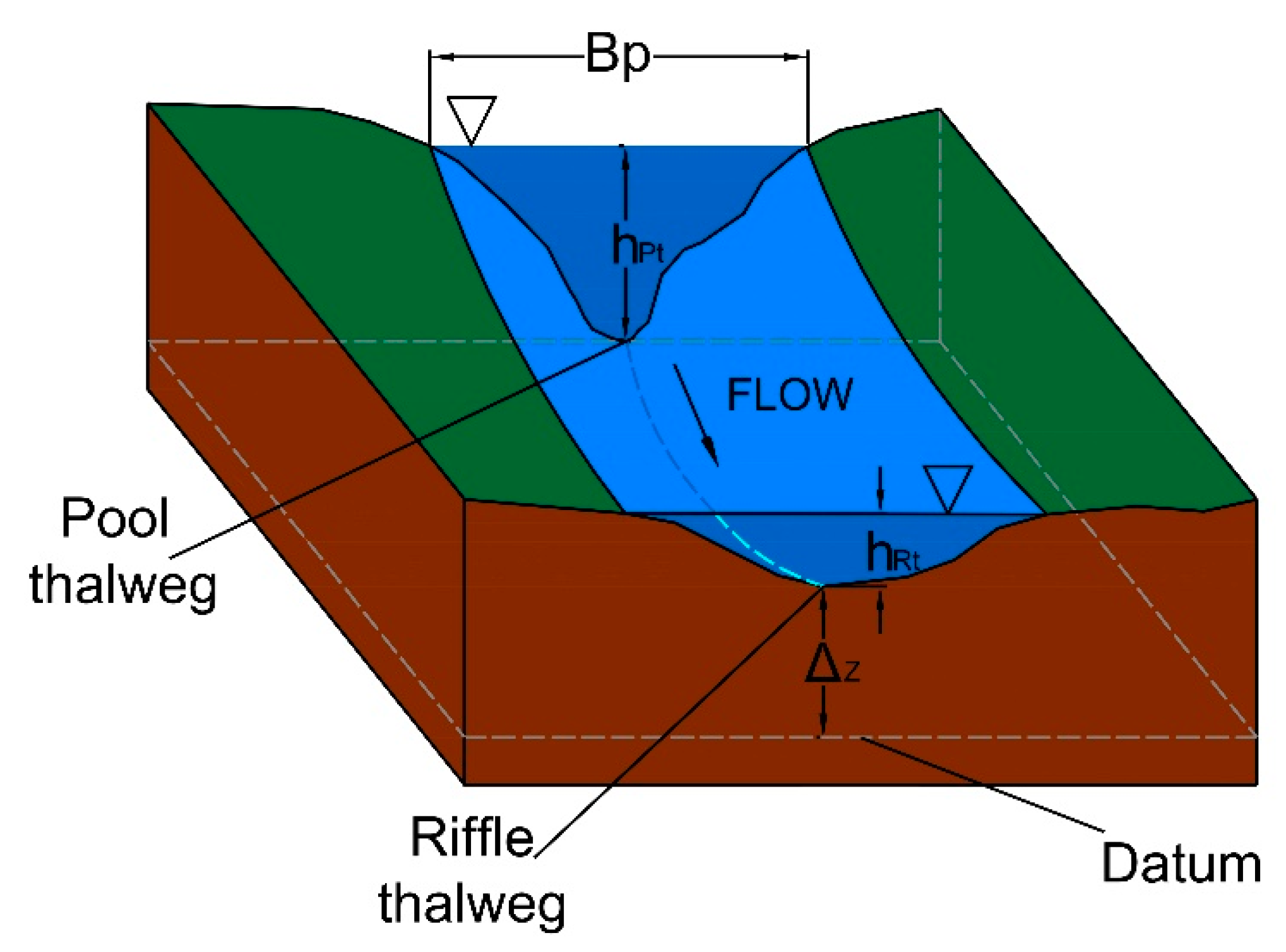
2.1. Syntethic Pool-Riffle Generation
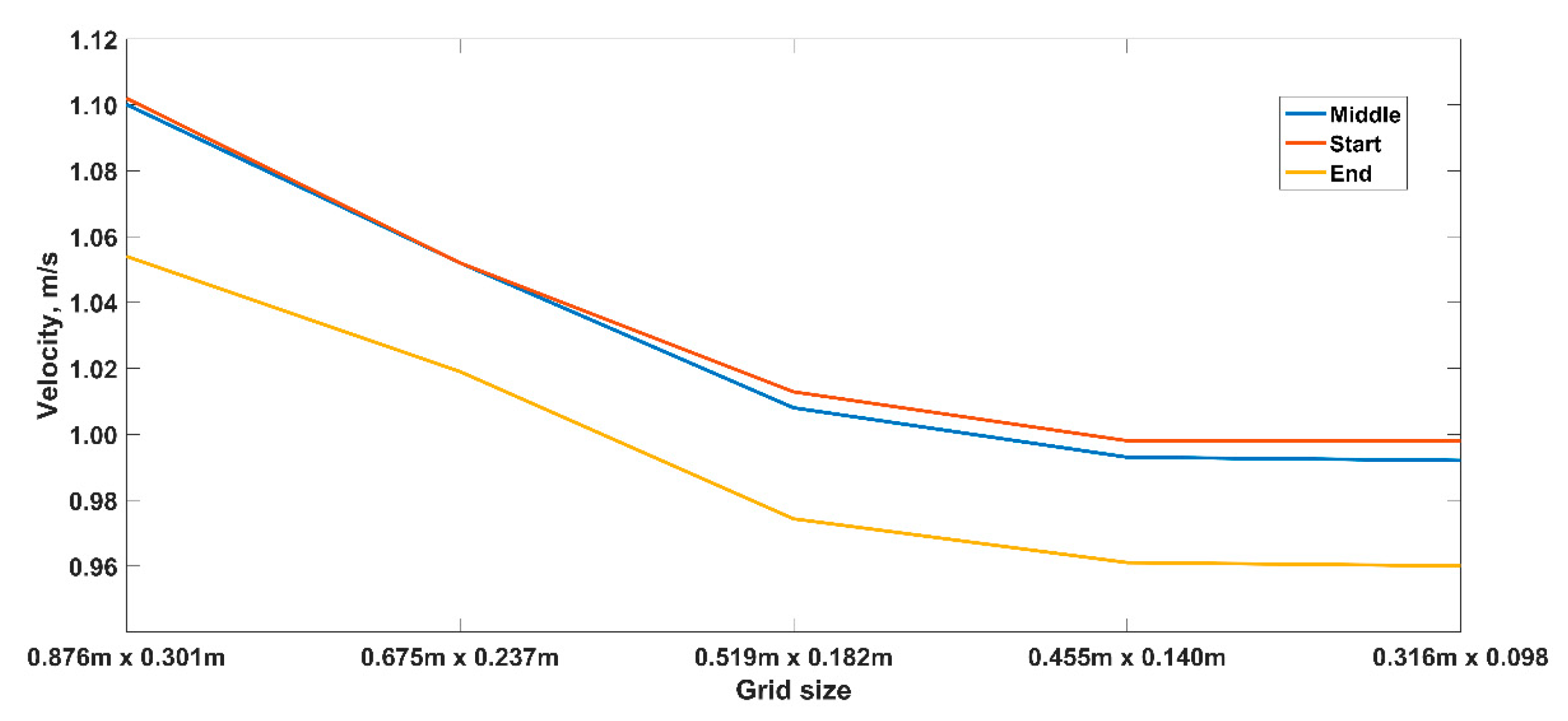
2.2. Numerical Modelling: Hydrodinamic and Transport Simulations
2.3. Dimensional Analysis
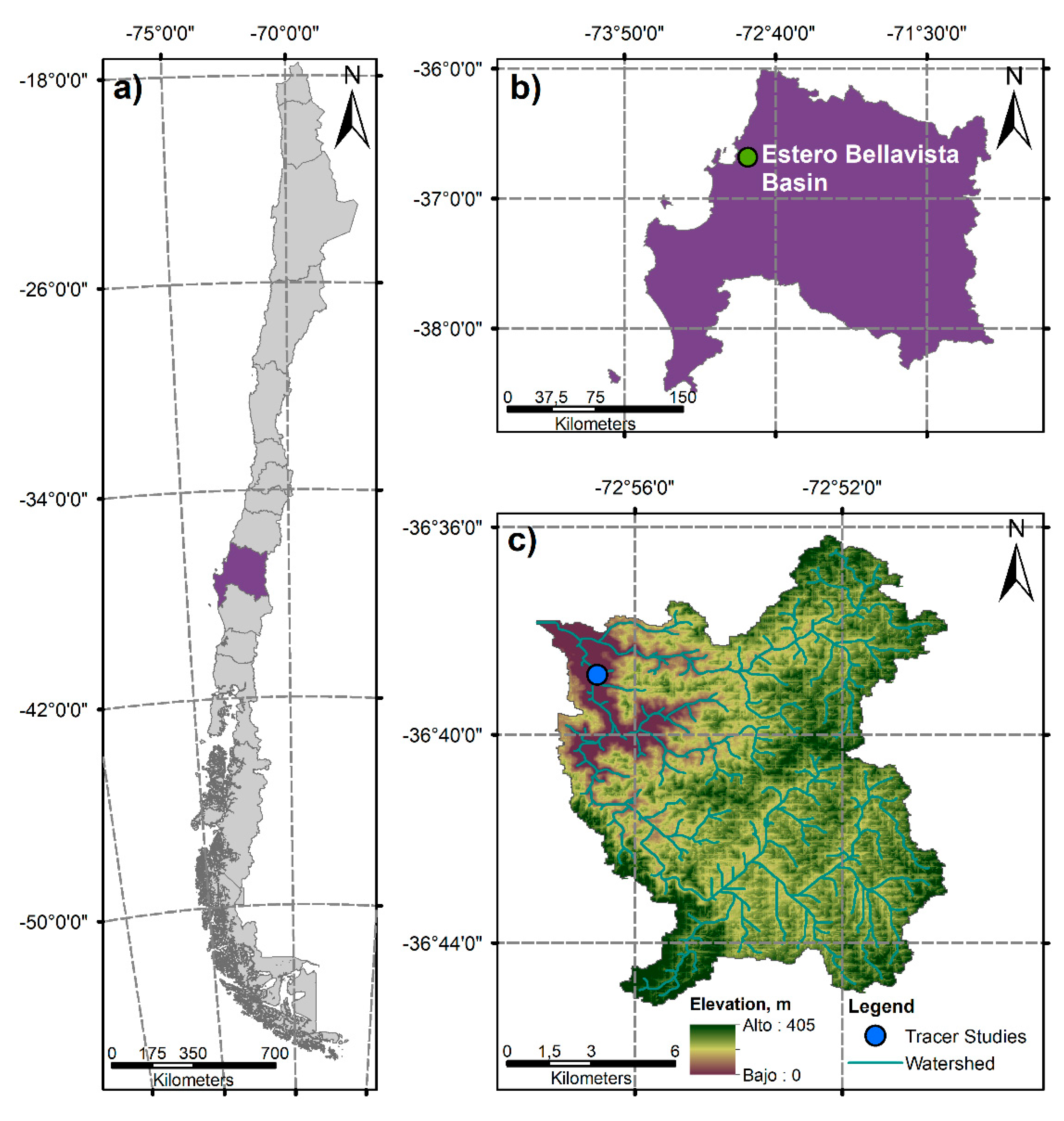
2.4. Validation: Numerical and Field Experiments
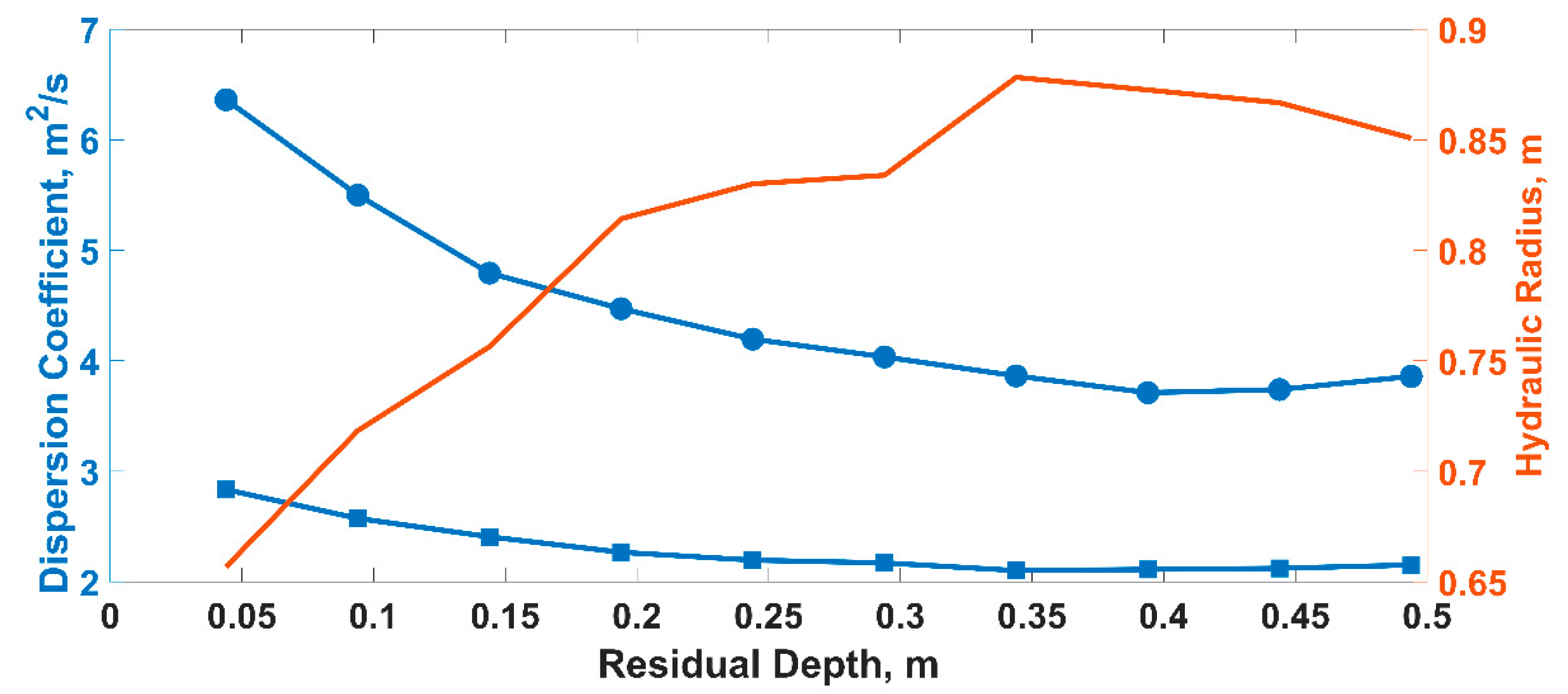
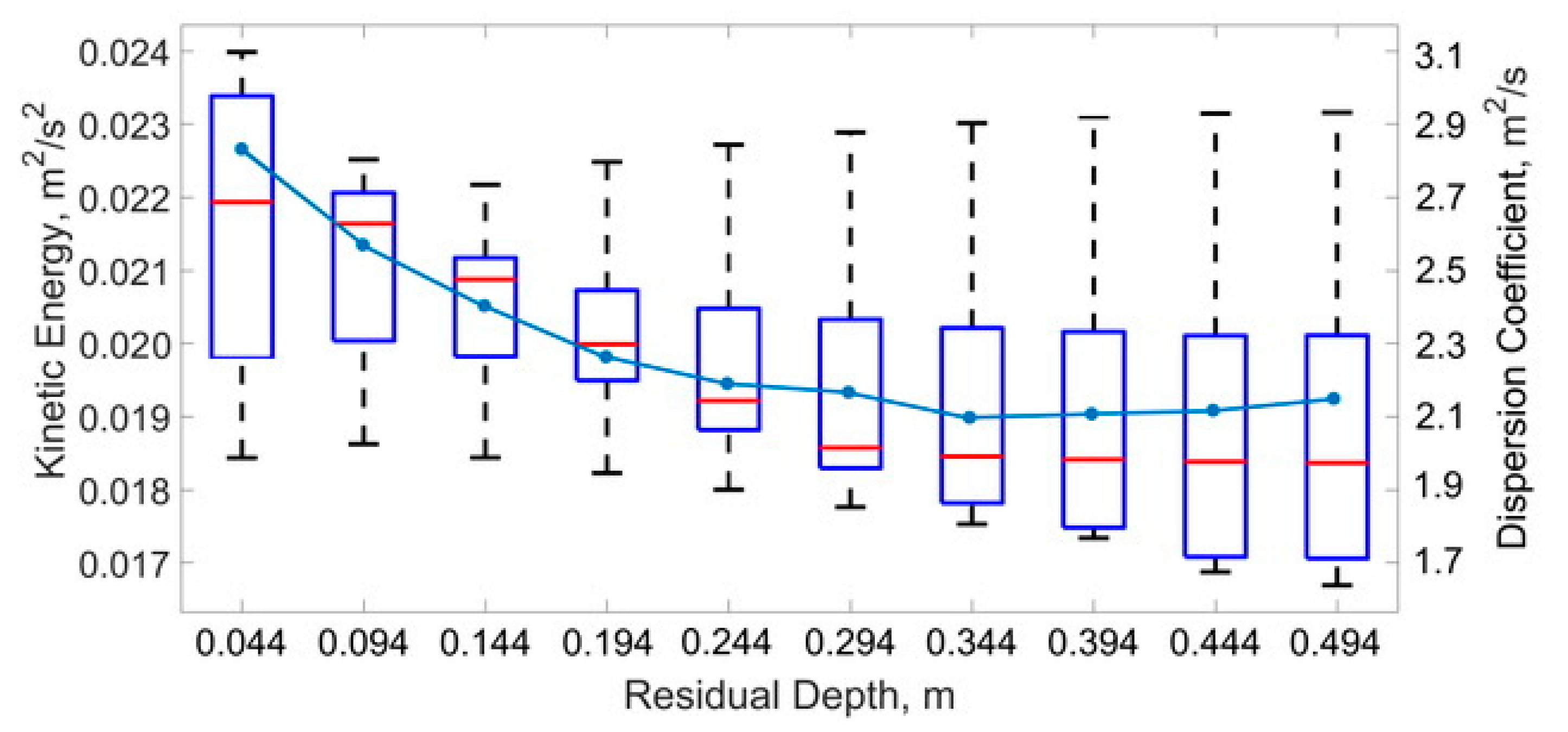
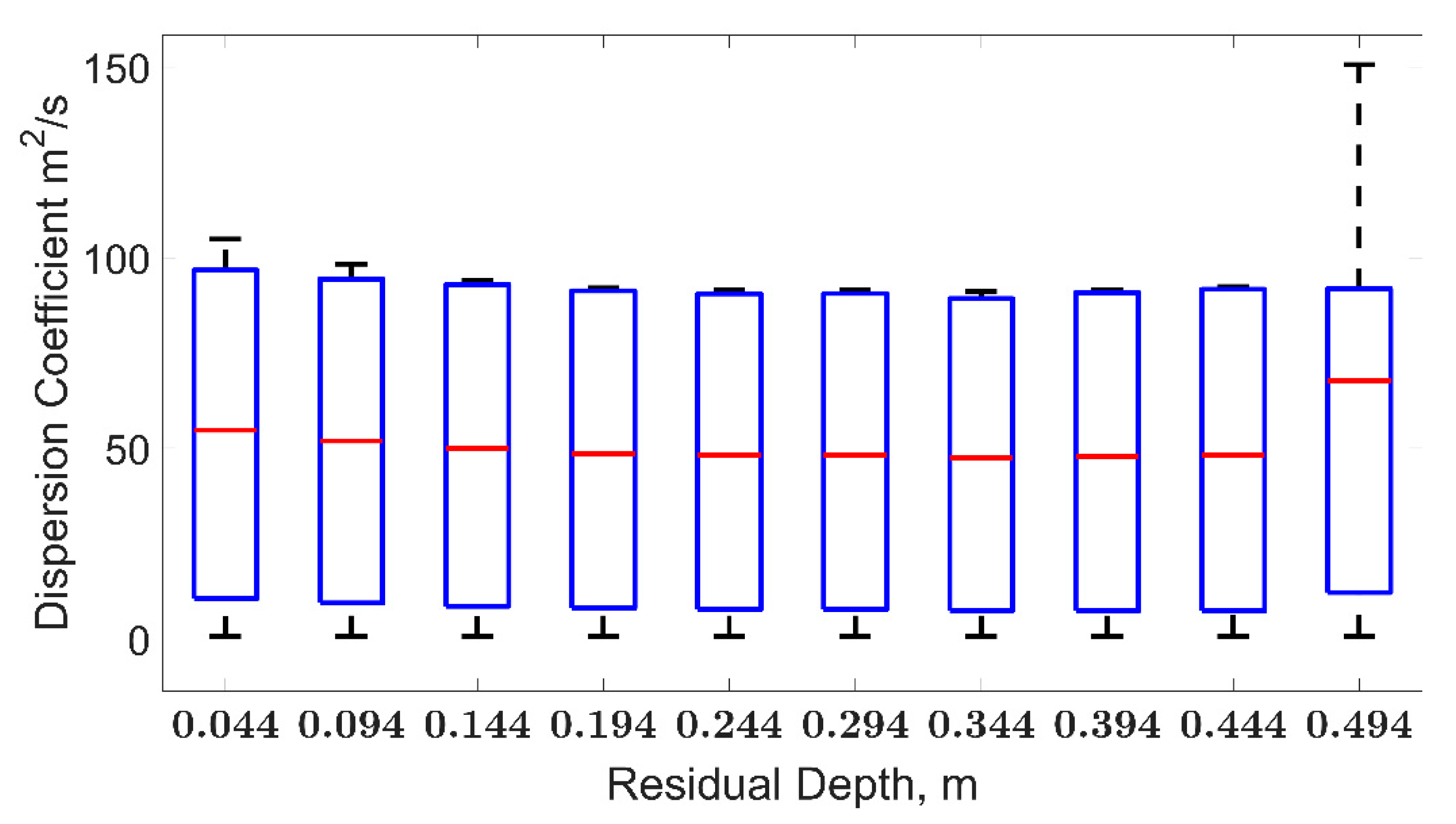
3. Results
4. Discussion
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Jackson, T.R.; Haggerty, R.; Apte, S.; O’Connor, B. A mean residence time relationship for lateral cavities in gravel-bed rivers and streams: Incorporating streambed roughness and cavity shape. Water Resour. Res. 2013, 49, 3642–3650. [Google Scholar] [CrossRef]
- Wang, Z.Y.; Lee, J.H.; Melching, C.S. River Dynamics and Integrated River Management; Springer Science & Business: Berlin, Germany, 2014. [Google Scholar]
- Altunkaynak, A. Prediction of longitudinal dispersion coefficient in natural streams by prediction map. J. Hydro-Environ. Res. 2016, 12, 105–116. [Google Scholar] [CrossRef]
- Lanzoni, S.; Ferdousi, A.; Tambroni, N. River banks and channel axis curvature: effects on the longitudinal dispersion in alluvial rivers. Adv. Water Resour. 2018, 113, 55–72. [Google Scholar] [CrossRef] [Green Version]
- Huai, W.; Haoran, S.; Song, S.; Shaoqiang, N. A simplified method for estimating the longitudinal dispersion coefficient in ecological channels with vegetation. Ecol. Indic. 2018, 92, 91–98. [Google Scholar] [CrossRef]
- Rutherford, J. River Mixing; John Wiley & Sons: Chichester, UK, 1994. [Google Scholar]
- Baek, K.O.; Seo, W. Routing procedures for observed dispersion coefficients in two-dimensional river mixing. Adv. Water Resour. 2010, 33, 1551–1559. [Google Scholar] [CrossRef]
- Baek, K.O.; Seo, W. On the methods for determining the transverse dispersion coefficient in river mixing. Adv. Water Resour. 2016, 90, 1–9. [Google Scholar] [CrossRef]
- Han, L.; Mignot, E.; Riviere, N. Shallow Mixing Layer Downstream from a Sudden Expansion. J. Hydraul. Eng. 2016, 143, 04016105. [Google Scholar] [CrossRef] [Green Version]
- Mignot, E.; Cai, W.; Polanco, J.; Escauriaza, C.; Riviere, N. Measurement of mass exchange processes and coefficients in a simplified open-channel lateral cavity connected to a main stream. Environ. Fluid Mech. 2017, 17, 429–448. [Google Scholar] [CrossRef]
- Shucksmith, J.; Boxall, J.; Guymer, I. Effects of emergent and submerged natural vegetation on longitudinal mixing in open channel flow. Water Resour. Res. 2010, 46. [Google Scholar] [CrossRef]
- Tenebe, I.T.; Ogbiye, A.S.; Omole, D.O.; Emenike, P.C. Estimation of longitudinal dispersion co-efficient: A review. Cogent. Eng. 2016, 3. [Google Scholar] [CrossRef]
- Etermad-Shadidi, A.; Taghipour, M. Predicting longitudinal dispersion coefficient in natural streams using M5′ model tree. J. Hydraul. Eng. 2012, 138, 542–554. [Google Scholar] [CrossRef]
- Sokáč, M.; Velísková, Y.; Gualtieri, C. An approximate method for 1-D simulation of pollution in streams with dead zones. J. Hydrol. Hydromech. 2018, 66, 437–447. [Google Scholar] [CrossRef]
- Perucca, E.; Comporeale, C.; Ridolfi, L. Estimation of the dispersion coefficient in rivers with riparian vegetation. Adv. Water Res. 2009, 32, 78–87. [Google Scholar] [CrossRef]
- Wallis, S.G.; Manson, J.R. Methods for predicting dispersion coefficients in rivers. P. I. Civil Eng.-Wat M. 2004, 157, 131–141. [Google Scholar] [CrossRef]
- Deng, Z.; Singh, V.; Bengtsson, L. Longitudinal Dispersion Coefficient in Straight Rivers. J. Hydraul. Eng. 2001, 127, 919–927. [Google Scholar] [CrossRef]
- Toprak, Z.; Cigizoglu, H. Predicting longitudinal dispersion coefficient in natural streams by artificial intelligence methods. Hydrol. Process. 2008, 22, 4106–4129. [Google Scholar] [CrossRef]
- Sahay, R. Prediction of longitudinal dispersion coefficients in natural rivers using artificial neural network. Environ. Fluid Mech. 2010, 11, 247–261. [Google Scholar] [CrossRef]
- Martin, J. Application of Two-Dimensional Water Quality Model. J. Environ. Eng. 1988, 114, 317–336. [Google Scholar] [CrossRef]
- Kannel, P.; Lee, S.; Kanel, S.; Lee, Y.; Ahn, K. Application of QUAL2Kw for water quality modeling and dissolved oxygen control in the river Bagmati. Environ. Monit. Assess. 2006, 125, 201–217. [Google Scholar] [CrossRef]
- Chen, Q.; Tan, K.; Zhu, C.; Li, R. Development and application of a two-dimensional water quality model for the Daqinghe River Mouth of the Dianchi Lake. J. Environ. Sci. 2009, 21, 313–318. [Google Scholar] [CrossRef]
- Wang, Q.; Zhao, X.; Yang, M.; Zhao, Y.; Liu, K.; Ma, Q. Water quality model establishment for middle and lower reaches of Hanshui River, China. Chinese Geogr. Sci. 2011, 21, 646–655. [Google Scholar] [CrossRef]
- Deus, R.; Brito, D.; Mateus, M.; Kenov, I.; Fornaro, A.; Neves, R.; Alves, C. Impact evaluation of a pisciculture in the Tucuruí reservoir (Pará, Brazil) using a two-dimensional water quality model. J. Hydrol. 2013, 487, 1–12. [Google Scholar] [CrossRef]
- Choi, H.; Han, K. Development and applicability assessment of 1-D water quality model in Nakdong river. KSCE J. Civ. Eng. 2014, 18, 2234–2243. [Google Scholar] [CrossRef]
- Seo, I.; Cheong, T. Predicting longitudinal dispersion coefficient in natural streams. J. Hydraul. Eng. 1998, 124, 25–32. [Google Scholar] [CrossRef]
- Palancar, M.; Aragón, J.; Sánchez, F.; Gil, R. The determination of longitudinal dispersion coefficients in rivers. Water Environ. Res. 2003, 75, 324–335. [Google Scholar] [CrossRef]
- Elder, J. The dispersion of a marked fluid in turbulent shear flow. J. Fluid Mech. 1959, 5, 544–560. [Google Scholar] [CrossRef]
- Fischer, H. Discussion of simple method for prediction of dispersion in streams by R.S. McQuivey and T.N. Keefer. J. Environ. Eng. 1975, 504, 453–455. [Google Scholar]
- Huber, J. Robust Statistics; John Wiley & Sons, Inc.: New York, NY, USA, 1981. [Google Scholar]
- Kashefipour, S.; Falconer, F. Longitudinal dispersion coefficients in natural channels. Water Resour. 2002, 36, 1596–1608. [Google Scholar] [CrossRef]
- Fischer, H. Dispersion Predictions in Natural Streams. J. Sanitary Eng. Div. 1968, 94, 927–943. [Google Scholar]
- McQuivey, R.; Keefer, T. Simple method for predicting dispersion in streams. J. Environ. Eng. 1974, 100, 997–1011. [Google Scholar]
- Zeng, Y.; Huai, W. Estimation of longitudinal dispersion coefficient in rivers. J. Hydro-Environ. Res. 2014, 8, 2–8. [Google Scholar] [CrossRef]
- Sahin, S. An Empirical Approach for Determining Longitudinal Dispersion Coefficients in Rivers. Environ. Process. 2014, 1, 277–285. [Google Scholar] [CrossRef] [Green Version]
- Yotsukura, N.; Fischer, H.; Sayre, W. Measurement of Mixing Characteristics of the Missouri River between Sioux City, Iowa, and Plattsmouth, Nebraska; U.S. Government Publishing Office: Washington, DC, USA, 1970. [Google Scholar]
- Nordin, C.; Sabol, G. Empirical Data on Longitudinal Dispersion in Rivers; U.S. Geological Survey: Lakewood, CO, USA, 1974; pp. 20–74. [Google Scholar]
- Ho, D.; Schlosser, P.; Caplow, T. Determination of longitudinal dispersion coefficient and net advection in the tidal Hudson River with a large-scale, high resolution SF6 tracer release experiment. Environ. Sci. Tech. 2002, 36, 3234–3241. [Google Scholar] [CrossRef] [PubMed]
- Chau, S.; Witcher, J. Longitudinal tracer studies: Research methodology of the middle range. Br. J. Manag. 2005, 16, 343–355. [Google Scholar] [CrossRef] [Green Version]
- Ho, D.; Engel, C.; Variano, E.; Schmieder, P.; Condon, M. Tracer studies of sheet flow in the Florida Everglades. Geophys. Res. Lett. 2009, 36. [Google Scholar] [CrossRef] [Green Version]
- Disley, T.; Gharabaghi, B.; Mahboubi, A.; McBean, E. Predictive equation for longitudinal dispersion coefficient. Hydrol. Process. 2015, 29, 161–172. [Google Scholar] [CrossRef]
- Seo, I.; Baek, K. Estimation of the Longitudinal Dispersion Coefficient Using the Velocity Profile in Natural Streams. J. Hydraul. Eng. 2004, 130, 227–236. [Google Scholar] [CrossRef]
- El Kadi Abderrezzak, K.; Ata, R.; Zaoui, F. One-dimensional numerical modelling of solute transport in streams: The role of longitudinal dispersion coefficient. J. Hydrol. 2015, 527, 978–989. [Google Scholar] [CrossRef]
- Brown, R.; Pasternack, G. Hydrologic and topographic variability modulate channel change in mountain rivers. J. Hydrol. 2014, 510, 551–564. [Google Scholar] [CrossRef] [Green Version]
- Brown, R.; Pasternack, G.; Lin, T. The Topographic Design of River Channels for Form-Process Linkages. Environ. Manag. 2015, 57, 929–942. [Google Scholar] [CrossRef] [Green Version]
- Deutsch, C.; Wang, L. Hierarchical object-based stochastic modeling of fluvial reservoirs. Math. Geol. 1996, 28, 857–880. [Google Scholar] [CrossRef]
- Caamaño, D.; Goodwin, P.; Buffington, J.; Liou, J.; Daley-Laursen, S. Unifying Criterion for the Velocity Reversal Hypothesis in Gravel-Bed Rivers. J. Hydraul. Eng. 2009, 135, 66–70. [Google Scholar] [CrossRef] [Green Version]
- Deltares. Delft3D Flexible Mesh Suite: D-Flow User Manual, 1st ed.; Deltares: Delft, The Netherlands, 2016. [Google Scholar]
- Deltares. Delft3D Flexible Mesh Suite: D-Flow Technical Reference Manual, 1st ed.; Deltares: Delft, The Netherlands, 2016. [Google Scholar]
- Lee, W.; Choi, H. Characteristics of bankfull discharge and its estimation using hydraulic geometry in the Han River basin. J. Civ. Eng. 2017, 22, 2290–2299. [Google Scholar] [CrossRef]
- Deltares. Delft3D Flexible Mesh Suite: D-Water Quality User Manual, 1st ed.; Deltares: Delft, The Netherlands, 2016. [Google Scholar]
- Xu, C.; Zhang, J.; Bi, X.; Xu, Z.; He, Y.; Gin, K. Developing an integrated 3D-hydrodynamic and emerging contaminant model for assessing water quality in a Yangtze Estuary Reservoir. Chemosphere 2017, 188, 218–230. [Google Scholar] [CrossRef]
- Saad, Y.; Schulz, M. GMRES: A generalized minimal residual algorithm for solving nonsymmetric linear systems. SIAM J. Sci. Statis. Comput. 1986, 7, 856–869. [Google Scholar] [CrossRef] [Green Version]
- Thomann, R.; Mueller, J. Principles of Surface Water Quality Modeling and Control; Harper & Row Publishers: New York, NY, USA, 1987. [Google Scholar]
- Fischer, H.; List, E.; Koh, R.; Imberger, J.; Brooks, N. Mixing in Inland and Coastal Waters; Academic Press: London, UK, 1979. [Google Scholar]
- Demetracopoulos, A. Computation of Transverse Mixing in Streams. J. Environ. Eng. 1994, 120, 699–706. [Google Scholar] [CrossRef]
- Singh, S.; Beck, M. Dispersion Coefficient of Streams from Tracer Experiment Data. J. Environ. Eng. 2003, 129, 539–546. [Google Scholar] [CrossRef]
- Baek, K.O.; Seo, W.; Jeong, J. Evaluation of dispersion coefficients in meandering channels from transient tracer tests. J. Hydraul. Eng. 2006, 132, 1021–1032. [Google Scholar] [CrossRef]
- Buckingham, E. On Physically Similar Systems; Illustrations of the Use of Dimensional Equations. Phys. Rev. 1914, 4, 345–376. [Google Scholar] [CrossRef]
- Comina, C.; Lasagna, M.; De Luca, D.; Sambuelli, L. Discharge measurement with salt dilution method in irrigation canals: direct sampling and geophysical controls. Hydrol. Earth Syst. Sci. Dis. 2013, 10, 10035–10060. [Google Scholar] [CrossRef] [Green Version]
- Lancaster, J.; Hildrew, A. Characterizing In-stream Flow Refugia. Can. J. Fish. Aquat. Sci. 1993, 50, 1663–1675. [Google Scholar] [CrossRef]
- Wilson, D.; Labadz, J.; Butcher, D. Variation in Time of Travel in UK River Systems: A Comparative Study; Wiley: Chichester, UK, 2000. [Google Scholar]
- Montgomery, D.R.; Buffington, J.M. Channel processes, classification and response. River Ecol. Manag. 1998, 112, 1250–1263. [Google Scholar]
- Buffington, J.M.; Montgomery, D.R. Geomorphic Classification of Rivers. In Treatise on Geomorphology; Academic Press: San Diego, CA, USA, 2013; pp. 730–762. [Google Scholar]
- Antonopoulos, V.Z.; Georgiou, P.E.; Antonopoulos, Z.V. Dispersion coefficient prediction using empirical models and ANNs. Environ. Process. 2015, 2, 379–394. [Google Scholar] [CrossRef] [Green Version]
- Stoesser, T.; Kara, S.; MacVicar, B.; Best, J. Turbulent Flow over a mildly sloped pool-riffle sequence. In Proceedings of the IAHR River Flow Conference, Bundesanstalt, Germany, 8–10 September 2010. [Google Scholar]
- Cowan, W.L. Estimating hydraulic roughness coefficients. Agric. Eng. 1956, 37, 473–475. [Google Scholar]
- Wilcox, A.C.; Nelson, J.M.; Wohl, E.E. Flow resistance dynamics in step-pool channels: 2. Partitioning between grain, spill, and woody debris resistance. Water Resour. Res. 2006, 42. [Google Scholar] [CrossRef] [Green Version]
- Yager, E.M.; Kirchner, J.W.; Dietrich, W.E. Calculating bed load transport in steep boulder bed channels. Water Resour. Res. 2007, 43. [Google Scholar] [CrossRef]
- Yager, E.M.; Dietrich, W.E.; Kirchner, J.W.; McArdell, B.W. Prediction of sediment transport in step-pool channels. Water Resour. Res. 2012, 48. [Google Scholar] [CrossRef] [Green Version]


| Reference | Formula | Simplifications |
|---|---|---|
| Elder [28] | Uniform flow in an infinitely wide channel. | |
| Fischer [29] | Validated using measurements in straight prismatic channels of various regular cross-sectional shapes. | |
| Seo and Cheong [26] | Developed using dimensional analysis and the one-step Huber method [30]. | |
| Kashefipour and Falconer [31] | Calibrated and validated using data from 30 streams in USA; previously used by Fischer [32], McQuivey and Keefer [33], and Seo and Cheong [26]. | |
| Zeng and Huai [34] | Calibrated and validated using data from 50 rivers in the USA. | |
| Sahin [35] | Developed using dimensional analysis. This equation includes the hydraulic radius and the shape of the cross-section |
| Bathymetry Scenario | Residual Pool Depth, m |
|---|---|
| 1 | 0.494 |
| 2 | 0.444 |
| 3 | 0.394 |
| 4 | 0.344 |
| 5 | 0.294 |
| 6 | 0.244 |
| 7 | 0.194 |
| 8 | 0.154 |
| 9 | 0.094 |
| 10 | 0.044 |
| Combination | Correlation |
|---|---|
| 0.8383 | |
| 0.8909 | |
| 0.9205 | |
| 0.8304 | |
| 0.8798 | |
| 0.9495 | |
| 0.8556 | |
| 0.8304 | |
| 0.8096 | |
| 0.8798 | |
| 0.9532 | |
| 0.9065 | |
| 0.9065 | |
| 0.9624 | |
| 0.8556 | |
| 0.9499 | |
| 0.9590 | |
| 0.8556 |
| Variable | Bathymetry Scenario | ||||
|---|---|---|---|---|---|
| Bellavista 1 | Bellavista 2 | Bellavista 3 | Bellavista 4 | Bellavista 5 | |
| 0.48 | 1.17 | 0.39 | 0.81 | 0.57 | |
| 0.14 | 0.09 | 0.14 | 0.07 | 0.05 | |
| 0.21 | 0.96 | 0.12 | 0.57 | 0.39 | |
| 15.81 | 11.30 | 14.97 | 8.10 | 11.82 | |
| 8.61 | 6.46 | 16.40 | 5.20 | 12.00 | |
| 7.25 | 5.80 | 15.10 | 4.50 | 8.22 | |
| 0.16 | 0.26 | 0.15 | 0.30 | 0.21 | |
| 0.38 | 0.51 | 0.42 | 0.26 | 0.30 | |
| 0.008 | 0.010 | 0.008 | 0.020 | 0.010 | |
| 0.086 | 0.058 | 0.086 | 0.086 | 0.319 | |
| Initial Dispersion Coefficient | Estimated Dispersion Coefficient (Method of Moments) | Difference |
|---|---|---|
| 0.0 | 0.437 | 0.437 |
| 0.5 | 1.707 | 1.207 |
| 0.6 | 1.789 | 1.189 |
| 0.7 | 1.872 | 1.172 |
| 0.8 | 1.963 | 1.163 |
| 0.9 | 2.055 | 1.155 |
| 1.0 | 2.150 | 1.150 |
| 1.1 | 2.229 | 1.129 |
| 1.2 | 2.307 | 1.107 |
| 1.3 | 2.385 | 1.085 |
| 1.4 | 2.463 | 1.063 |
| 1.5 | 2.541 | 1.041 |
| 1.6 | 2.619 | 1.019 |
| 1.7 | 2.697 | 0.997 |
| 1.8 | 2.776 | 0.976 |
| 1.9 | 2.854 | 0.954 |
| 2.0 | 2.932 | 0.932 |
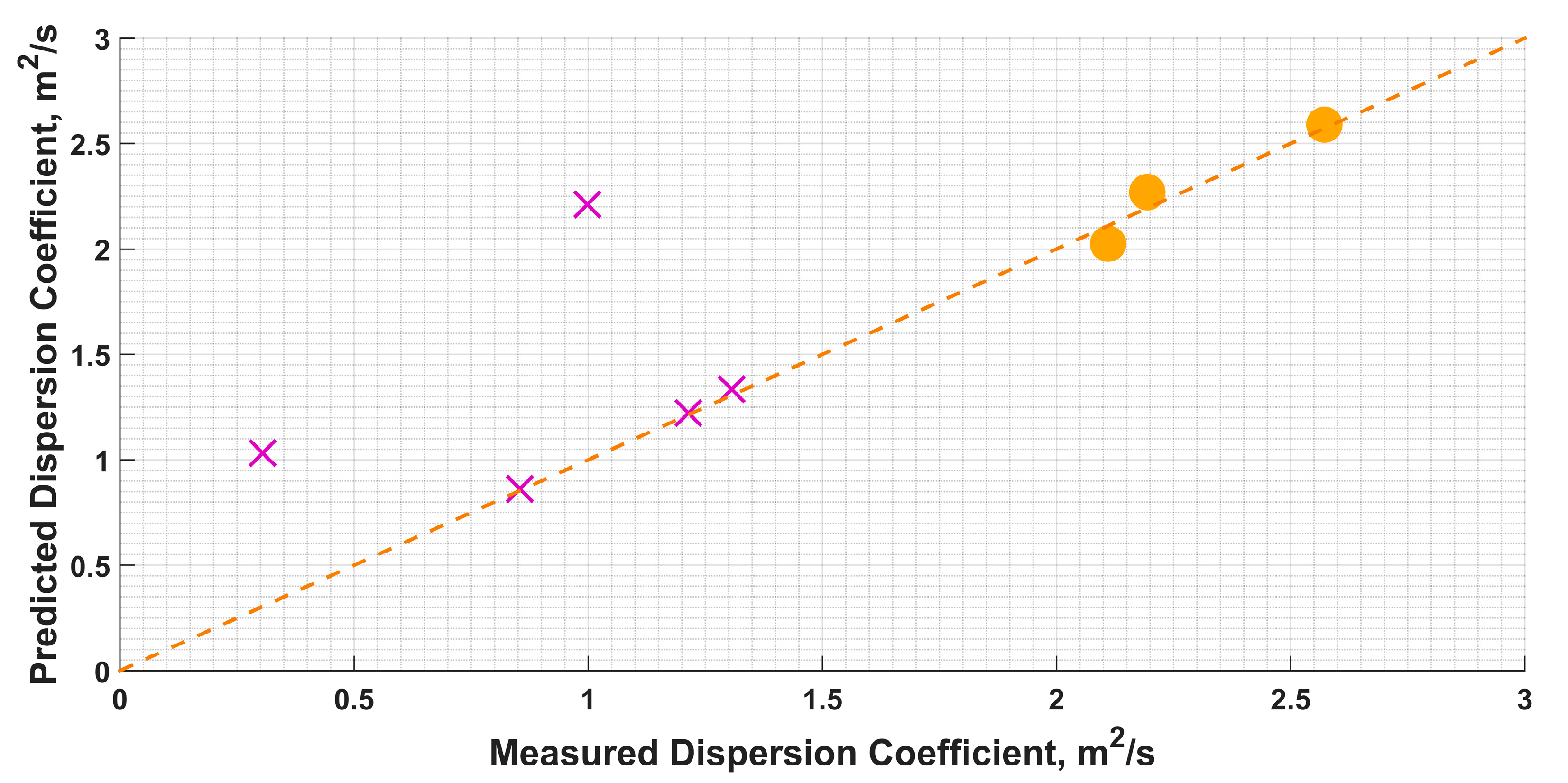
| Bathymetry Scenarios | ||
|---|---|---|
| 3 | 2.110 | 2.025 |
| 6 | 2.194 | 2.270 |
| 9 | 2.572 | 2.589 |
| Bellavista 1 (Tracer experiments) | 1.214 | 1.222 |
| Bellavista 2 (Tracer experiments) | 0.305 | 1.032 |
| Bellavista 3 (Tracer experiments) | 0.998 | 2.212 |
| Bellavista 4 (Tracer experiments) | 0.854 | 0.862 |
| Bellavista 5 (Tracer experiments) | 1.306 | 1.335 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Fuentes-Aguilera, P.; Caamaño, D.; Alcayaga, H.; Tranmer, A. The Influence of Pool-Riffle Morphological Features on River Mixing. Water 2020, 12, 1145. https://doi.org/10.3390/w12041145
Fuentes-Aguilera P, Caamaño D, Alcayaga H, Tranmer A. The Influence of Pool-Riffle Morphological Features on River Mixing. Water. 2020; 12(4):1145. https://doi.org/10.3390/w12041145
Chicago/Turabian StyleFuentes-Aguilera, Patricio, Diego Caamaño, Hernán Alcayaga, and Andrew Tranmer. 2020. "The Influence of Pool-Riffle Morphological Features on River Mixing" Water 12, no. 4: 1145. https://doi.org/10.3390/w12041145
APA StyleFuentes-Aguilera, P., Caamaño, D., Alcayaga, H., & Tranmer, A. (2020). The Influence of Pool-Riffle Morphological Features on River Mixing. Water, 12(4), 1145. https://doi.org/10.3390/w12041145





