Spatial Forecasting of Dissolved Oxygen Concentration in the Eastern Black Sea Basin, Turkey
Abstract
:1. Introduction
2. Materials and Methods
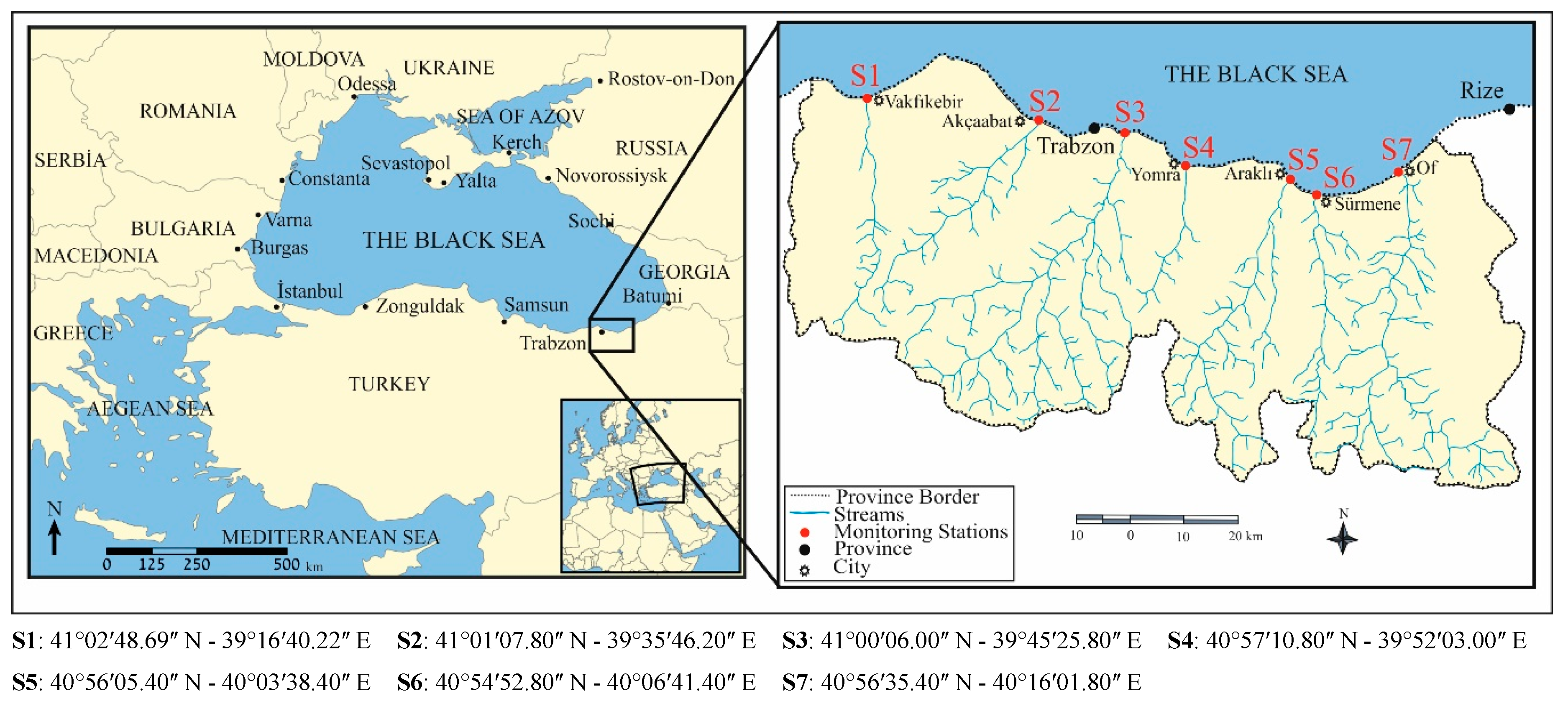
2.1. Study Area
2.2. The Stream Gauging
2.3. Stream Water Quality Monitoring
2.4. Modeling Variables
2.5. Multivariate Adaptive Regression Splines (MARS) Method
2.6. Teaching–Learning Based Optimization (TLBO) Algorithm
2.7. Model Development Applications
3. Results and Discussion
3.1. Stream Water-Quality Assessment
3.1.1. Flow Rate
3.1.2. Water Temperature
3.1.3. pH
3.1.4. Luminescent Dissolved Oxygen Concentration
3.1.5. Luminescent Dissolved Oxygen Saturation
3.1.6. Total Dissolved Solids
3.1.7. Electrical Conductivity
3.2. Stream Water-Quality Modeling
3.2.1. MARS Modeling Results
3.2.2. TLBO Algorithm and CRA Modeling Results
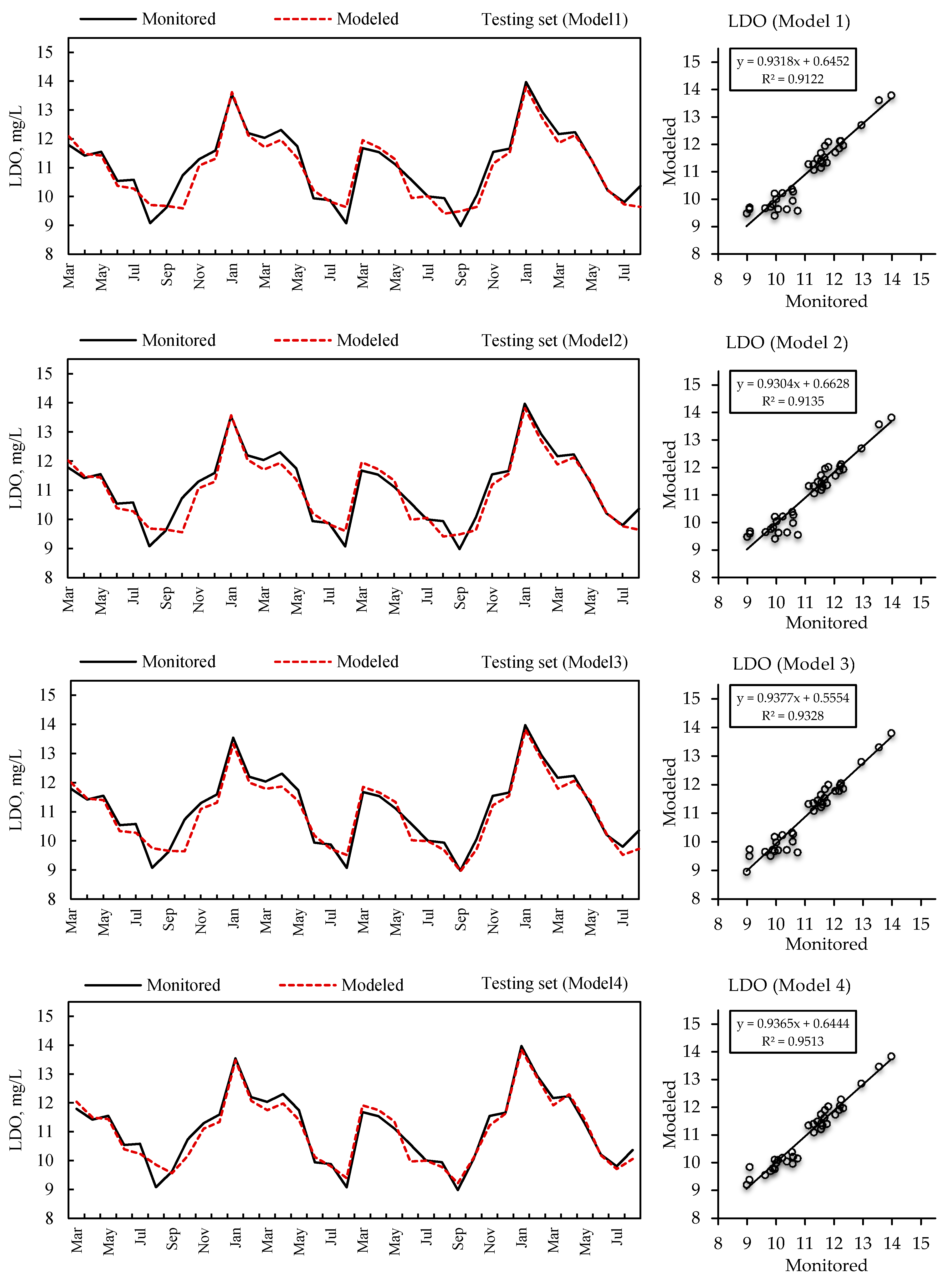
3.2.3. Comparison of the MARS, TLBO, and CRA Modeling Results
4. Conclusions
- On a seasonal basis, all streams showed the same trend in that the higher LDO concentrations were observed in the winter months with the coldest WT values, while the lower LDO concentrations appeared in the summer months with the warmest WT values. Interstational correlation coefficients up to R = 0.968 for the stream LDO concentrations and R = 0.992 for the stream WT values supported this trend.
- Autumns, which presented higher TDS concentrations brought about higher EC values, while springs, which presented the lower TDS concentrations gave rise to lower EC values. It was concluded that the higher TDS concentrations were due to the lower flow rates, by taking the negative but strong or moderate correlations into consideration.
- The MARS method produced much better results than the TLBO and CRA methods, for both training and testing the data sets for all models, especially for Model 4, which included all input variables.
- The LDO concentrations predicted by the MARS method were almost near the LDO concentrations measured by a portable field meter. It was concluded that the DO concentration could be successfully predicted by the MARS method in any stream, where WT, pH, and EC, or SC were measured but the DO concentration was not monitored, in case of similar watershed characteristics with the studied streams.
- In the TLBO and CRA methods, lower RMSE and MAE, as well as higher NSCE values were obtained by an exponential function for all models. The LDO concentrations predicted by the TLBO method were almost near the LDO concentrations predicted by the CRA method, that is, the TLBO method could not perform any improvement compared to the CRA method.
- It was concluded that the involvement of the pH variable, which is a parameter commonly used for modeling the DO concentration, the independent variables significantly increased the prediction performance.
- Although the history of the MARS method dates back to the pioneering work of Friedman [49], there is a limited availability of its application in the modeling of DO concentration [44,46]. Therefore, the use of this method is encouraged and recommended for studies related to water resources and environment since the proposed MARS method yielded successful results for this study.
- It is expected that the present study will make a significant contribution to the national literature as part of the stream water-quality monitoring and to the international literature as part of the stream water-quality modeling.
- This study will be continued for one and a half year follow up with a monthly frequency, due to limited economic opportunities. For temporal forecasting, a long-term study covering more frequent monitoring is strongly recommended.
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Sarkar, A.; Pandey, P. River water quality modelling using artificial neural network technique. Aquat. Proced. 2015, 4, 1070–1077. [Google Scholar] [CrossRef]
- Cox, B.A. A review of dissolved oxygen modelling techniques for lowland rivers. Sci. Total Environ. 2003, 314, 303–334. [Google Scholar] [CrossRef]
- Heddam, S. Use of optimally pruned extreme learning machine (OP-ELM) in forecasting dissolved oxygen concentration (DO) Several hours in advance: A case study from the Klamath River, Oregon, USA. Environ. Process. 2016, 3, 909–937. [Google Scholar] [CrossRef]
- Spanou, M.; Chen, D. An object-oriented tool for the control of point-source pollution in river systems. Environ. Model. Softw. 2000, 15, 35–54. [Google Scholar] [CrossRef]
- Mulholland, P.J.; Houser, J.N.; Maloney, K.O. Stream diurnal dissolved oxygen profiles as indicators of in-stream metabolism and disturbance effects: Fort Benning as a case study. Ecol. Indic. 2005, 5, 243–252. [Google Scholar] [CrossRef]
- Sanchez, E.; Colmenarejo, M.F.; Vicente, J.; Rubio, A.; Garcia, M.G.; Travieso, L.; Borja, R. Use of the water quality index and dissolved oxygen deficit as simple indicators of watersheds pollution. Ecol. Indic. 2007, 7, 315–328. [Google Scholar] [CrossRef]
- Rajwa, A.; Rowinski, P.M.; Bialik, R.J.; Karpinski, M. Stream diurnal profiles of dissolved oxygen-case studies. In Proceedings of the 3rd IAHR Europe Congress, Porto, Portugal, 14–16 April 2014. [Google Scholar]
- Lewis, M.E. Dissolved Oxygen, Version 2.0, Chapter A6, Section 6.2. In Techniques of Water-Resources Investigations, Book 9; US Geological Survey: Washington, DC, USA, 2006. [Google Scholar]
- Bayram, A.; Onsoy, H.; Komurcu, M.I.; Tufekci, M. Reciprocal influence of Kurtun Dam and wastewaters from the settlements on water quality in the stream Harsit, NE Turkey. Environ. Earth Sci. 2014, 72, 2849–2860. [Google Scholar] [CrossRef]
- Gultekin, F.; Ersoy, A.F.; Hatipoglu, E.; Celep, S. Determination of water quality parameters in wet season of surface water in Trabzon. Ekoloji 2012, 21, 77–88. [Google Scholar] [CrossRef]
- Bayram, A. Water quality of the Değirmendere stream, drinking water source of Trabzon Province, Turkey. Desalin. Water Treat. 2017, 62, 120–139. [Google Scholar] [CrossRef]
- Koralay, N.; Kara, O.; Kezik, U. Effects of run-of-the-river hydropower plants on the surface water quality in the Solakli stream watershed, Northeastern Turkey. Water Environ. J. 2018, 32, 412–421. [Google Scholar] [CrossRef]
- Cox, B.A. A review of currently available in-stream water-quality models and their applicability for simulating dissolved oxygen in lowland rivers. Sci. Total Environ. 2003, 314, 335–377. [Google Scholar] [CrossRef]
- Rankovic, V.; Radulovic, J.; Radojevic, I.; Ostojic, A.; Comic, L. Neural network modeling of dissolved oxygen in the Gruza reservoir, Serbia. Ecol. Modell. 2010, 221, 1239–1244. [Google Scholar] [CrossRef]
- Soyupak, S.; Karaer, F.; Gürbüz, H.; Kivrak, E.; Sentürk, E.; Yazici, A. A neural network-based approach for calculating dissolved oxygen profiles in reservoirs. Neural Comput. Appl. 2003, 12, 166–172. [Google Scholar] [CrossRef]
- Sengorur, B.; Dogan, E.; Koklu, R.; Samandar, A. Dissolved oxygen estimation using artificial neural network for water quality control. Fresenius Environ. Bull. 2006, 15, 1064–1067. [Google Scholar]
- Kanda, E.K.; Kosgei, J.R.; Kipkorir, E.C. Simulation of organic carbon loading using MIKE 11 model: A case of River Nzoia, Kenya. Water Pract. Technol. 2015, 10, 298–304. [Google Scholar] [CrossRef]
- Najah, A.; El-Shafie, A.; Karim, O.A.; El-Shafie, A.H. Performance of ANFIS versus MLP-NN dissolved oxygen prediction models in water quality monitoring. Environ. Sci. Pollut. Res. 2014, 21, 1658–1670. [Google Scholar] [CrossRef] [PubMed]
- Ay, M.; Kisi, O. Estimation of dissolved oxygen by using neural networks and neuro fuzzy computing techniques. KSCE J. Civ. Eng. 2017, 21, 1631–1639. [Google Scholar] [CrossRef]
- Singh, K.P.; Malik, A.; Mohan, D.; Sinha, S. Multivariate statistical techniques for the evaluation of spatial and temporal variations in water quality of Gomti River (India)—A case study. Water Res. 2004, 38, 3980–3992. [Google Scholar] [CrossRef]
- Zhang, Q.; Li, Z.; Zeng, G.; Li, J.; Fang, Y.; Yuan, Q.; Wang, Y.; Ye, F. Assessment of surface water quality using multivariate statistical techniques in red soil hilly region: A case study of Xiangjiang watershed, China. Environ. Monit. Assess. 2009, 152, 123–131. [Google Scholar] [CrossRef]
- Bu, H.; Tan, X.; Li, S.; Zhang, Q. Water quality assessment of the Jinshui River (China) using multivariate statistical techniques. Environ. Earth Sci. 2010, 60, 1631–1639. [Google Scholar] [CrossRef]
- Panepinto, D.; Genon, G. Modeling of Po River water quality in Torino (Italy). Water Resour. Manag. 2010, 24, 2937–2958. [Google Scholar] [CrossRef]
- Akbal, F.; Gurel, L.; Bahadir, T.; Guler, I.; Bakan, G.; Buyukgungor, H. Multivariate statistical techniques for the assessment of surface water quality at the mid-black sea coast of Turkey. Water Air Soil Pollut. 2011, 216, 21–37. [Google Scholar] [CrossRef]
- DSİ. General Directorate of State Hydraulic Works (Devlet Su İşleri Genel Müdürlüğü, in Turkish). DSİ 2016 Yılı Resmi Su Kaynakları İstatistikleri, Havzalara Göre Yillik Ortalama Yüzeysuyu Su Potansiyeli, 2013–2016. Available online: http://www.dsi.gov.tr/dsi-resmi-istatistikler/resmi-i-statistikler-2016/2016-y%C4%B1l%C4%B1-verileri (accessed on 6 March 2020).
- TÜİK. Turkish Statistical Institute (Türkiye İstatistik Kurumu, in Turkish). Nüfus ve Demografi, Yıllara Göre İl Nüfusları. Available online: http://tuik.gov.tr/UstMenu.do?metod=temelist (accessed on 6 March 2020).
- TÜİK. (Turkish Statistical Institute (Türkiye İstatistik Kurumu, in Turkish)). Municipal population served by the sewerage system. Available online: https://biruni.tuik.gov.tr/medas/?kn=120&locale=en (accessed on 6 March 2020).
- DSİ. General Directorate of State Hydraulic Works (Devlet Su İşleri Genel Müdürlüğü, in Turkish). 2015 Akım Gözlem Yıllığı. Available online: http://www.dsi.gov.tr/docs/agi-yıllık-dsi/dsi_2015.pdf?sfvrsn=2 (accessed on 6 March 2020).
- Diamantopoulou, M.J.; Antonopoulos, V.Z.; Papamichail, D.M. Cascade correlation artificial neural networks for estimating missing monthly values of water quality parameters in rivers. Water Resour. Manag. 2007, 21, 649–662. [Google Scholar] [CrossRef]
- Chen, L.H.; Li, L. Evaluation of dissolved oxygen in water by artificial neural network and sample optimization. J. Cent. South Univ. Technol. 2008, 15, 416–420. [Google Scholar] [CrossRef]
- Singh, K.P.; Basant, A.; Malik, A.; Jain, G. Artificial neural network modeling of the river water quality—A case study. Ecol. Model. 2009, 220, 888–895. [Google Scholar] [CrossRef]
- Ay, M.; Kisi, O. Modeling of dissolved oxygen concentration using different neural network techniques in Foundation Creek, El Paso County, Colorado. J. Environ. Eng. 2011, 138, 654–662. [Google Scholar] [CrossRef]
- Wen, X.; Fang, J.; Diao, M.; Zhang, C. Artificial neural network modeling of dissolved oxygen in the Heihe River, Northwestern China. Environ. Monit. Assess. 2013, 185, 4361–4371. [Google Scholar] [CrossRef] [PubMed]
- Antanasijevic, D.; Pocajt, V.; Povrenovic, D.; Peric-Grujic, A.; Ristic, M. Modelling of dissolved oxygen content using artificial neural networks: Danube River, North Serbia, case study. Environ. Sci. Pollut. Res. 2013, 20, 9006–9013. [Google Scholar] [CrossRef]
- Kisi, O.; Akbari, N.; Sanatipour, M.; Hashemi, A.; Teimourzadeh, K.; Shiri, J. Modeling of dissolved oxygen in river water using artificial intelligence techniques. J. Environ. Inf. 2013, 22, 92–101. [Google Scholar] [CrossRef]
- Heddam, S. Modeling hourly dissolved oxygen concentration (DO) using two different adaptive neuro-fuzzy inference systems (ANFIS): A comparative study. Environ. Monit. Assess. 2014, 186, 597–619. [Google Scholar] [CrossRef]
- Evrendilek, F.; Karakaya, N. Monitoring diel dissolved oxygen dynamics through integrating wavelet denoising and temporal neural networks. Environ. Monit. Assess. 2014, 186, 1583–1591. [Google Scholar] [CrossRef] [PubMed]
- Heddam, S. Generalized regression neural network-based approach for modelling hourly dissolved oxygen concentration in the Upper Klamath River, Oregon, USA. Environ. Technol. 2014, 35, 1650–1657. [Google Scholar] [CrossRef]
- Heddam, S. Modelling hourly dissolved oxygen concentration (DO) using dynamic evolving neural-fuzzy inference system (DENFIS)-based approach: Case study of Klamath River at Miller Island Boat Ramp, OR, USA. Environ. Sci. Pollut. Res. 2014, 21, 9212–9227. [Google Scholar] [CrossRef] [PubMed]
- Nemati, S.; Fazelifard, M.H.; Terzi, O.; Ghorbani, M.A. Estimation of dissolved oxygen using data-driven techniques in the Tai Po River, Hong Kong. Environ. Earth Sci. 2015, 74, 4065–4073. [Google Scholar] [CrossRef]
- Bayram, A.; Kankal, M. Artificial Neural Network Modeling of Dissolved Oxygen Concentration in a Turkish Watershed. Pol. J. Environ. Stud. 2015, 24, 1507–1515. [Google Scholar]
- Kanda, E.K.; Kipkorir, E.C.; Kosgei, J.R. Dissolved oxygen modelling using artificial neural network: A case of River Nzoia, Lake Victoria basin, Kenya. J. Water Sec. 2016, 2. [Google Scholar] [CrossRef] [Green Version]
- Olyaie, E.; Abyaneh, H.Z.; Mehr, A.D. A comparative analysis among computational intelligence techniques for dissolved oxygen prediction in Delaware River. Geosci. Front. 2017, 8, 517–527. [Google Scholar] [CrossRef] [Green Version]
- Heddam, S.; Kisi, O. Modelling daily dissolved oxygen concentration using least square support vector machine, multivariate adaptive regression splines and M5 model tree. J. Hydrol. 2018, 559, 499–509. [Google Scholar] [CrossRef]
- Elkiran, G.; Nourani, V.; Abba, S.I.; Abdullahi, J. Artificial intelligence-based approaches for multi-station modelling of dissolve oxygen in river. Glob. J. Environ. Sci. Manag. 2018, 4, 439–450. [Google Scholar]
- Yaseen, Z.M.; Ehteram, M.; Sharafati, A.; Shahid, S.; Al-Ansari, N.; El-Shafie, A. The integration of nature-inspired algorithms with least square support vector regression models: Application to modeling river dissolved oxygen concentration. Water 2018, 10, 1124. [Google Scholar] [CrossRef] [Green Version]
- Csabragi, A.; Molnar, S.; Tanos, P.; Kovacs, J.; Molnar, M.; Szabo, I.; Hatvani, I.G. Estimation of dissolved oxygen in riverine ecosystems: Comparison of differently optimized neural networks. Ecol. Eng. 2019, 138, 298–309. [Google Scholar] [CrossRef]
- Kisi, O.; Alizamir, M.; Gorgij, A.D. Dissolved oxygen prediction using a new ensemble method. Environ. Sci. Pollut. Res. 2020, 27, 9589–9603. [Google Scholar] [CrossRef] [PubMed]
- Friedman, J.H. Multivariate adaptive regression splines. Ann. Statist. 1991, 19, 79–141. [Google Scholar] [CrossRef]
- Zhang, W.; Goh, A.T. Multivariate adaptive regression splines and neural network models for prediction of pile drivability. Geosci. Front. 2016, 7, 45–52. [Google Scholar] [CrossRef] [Green Version]
- Kisi, O.; Parmar, K.S. Application of least square support vector machine and multivariate adaptive regression spline models in long term prediction of river water pollution. J. Hydrol. 2016, 534, 104–112. [Google Scholar] [CrossRef]
- Tiryaki, S.; Tan, H.; Bardak, S.; Kankal, M.; Nacar, S.; Peker, H. Performance evaluation of multiple adaptive regression splines, teaching–learning based optimization and conventional regression techniques in predicting mechanical properties of impregnated wood. Eur. J. Wood Wood Prod. 2019, 77, 645–659. [Google Scholar] [CrossRef]
- Suman, S. Prediction of Pile Capacity Parameters Using Functional Networks and Multivariate Adaptive Regression Splines. Master’s Thesis, National Institute of Technology, Odisha, India, 2015. [Google Scholar]
- Samui, P. Multivariate adaptive regression spline (Mars) for prediction of elastic modulus of jointed rock mass. Geotech. Geol. Eng. 2013, 31, 249–253. [Google Scholar] [CrossRef]
- Khuntia, S.; Mujtaba, H.; Patra, C.; Farooq, K.; Sivakugan, N.; Das, B.M. Prediction of compaction parameters of coarse grained soil using multivariate adaptive regression splines (MARS). Int. J. Geotech. Eng. 2015, 9, 79–88. [Google Scholar] [CrossRef]
- Dey, P.; Das, A.K. Application of multivariate adaptive regression spline-assisted objective function on optimization of heat transfer rate around a cylinder. Nucl. Eng. Technol. 2016, 48, 1315–1320. [Google Scholar] [CrossRef] [Green Version]
- Rao, R.V.; Savsani, V.J.; Vakharia, D.P. Teaching–learning-based optimization: A novel method for constrained mechanical design optimization problems. Comput. Aided Des. 2011, 43, 303–315. [Google Scholar] [CrossRef]
- Rao, R.V.; Savsani, V.J.; Vakharia, D.P. Teaching–learning-based optimization: An optimization method for continuous non-linear large scale problems. Inf. Sci. 2012, 183, 1–15. [Google Scholar] [CrossRef]
- Dede, T. Optimum design of grillage structures to LRFD-AISC with teaching-learning based optimization. Struct. Multidiscip. Optim. 2013, 48, 955–964. [Google Scholar] [CrossRef]
- Togan, V. Design of pin jointed structures using teaching-learning based optimization. Struct. Eng. Mech. 2013, 47, 209–225. [Google Scholar] [CrossRef]
- Csabragi, A.; Molnar, S.; Tanos, P.; Kovacs, J. Application of artificial neural networks to the forecasting of dissolved oxygen content in the Hungarian section of the river Danube. Ecol. Eng. 2017, 100, 63–72. [Google Scholar] [CrossRef]
- Palani, S.; Liong, S.Y.; Tkalich, P. An ANN application for water quality forecasting. Mar. Pollut. Bull. 2008, 56, 1586–1597. [Google Scholar] [CrossRef] [PubMed]
- Bayram, A.; Kankal, M.; Onsoy, H. Estimation of suspended sediment concentration from turbidity measurements using artificial neural networks. Environ. Monit. Assess. 2012, 184, 4355–4365. [Google Scholar] [CrossRef]
- Fetene, B.N.; Shufen, R.; Dixit, U.S. FEM-based neural network modeling of laser-assisted bending. Neural Comput. Appl. 2018, 29, 69–82. [Google Scholar] [CrossRef]
- Nacar, S.; Hinis, M.A.; Kankal, M. Forecasting daily streamflow discharges using various neural network models and training algorithms. KSCE J. Civ. Eng. 2018, 22, 3676–3685. [Google Scholar] [CrossRef]
- Dawson, C.W.; Wilby, R. An artificial neural network approach to rainfall-runoff modelling. Hydrol. Sci. J. 1998, 43, 47–66. [Google Scholar] [CrossRef]
- Legates, D.R.; McCabe, G.J. Evaluating the use of “goodness-of-fit” measures in hydrologic and hydroclimatic model validation. Water Resour. Res. 1999, 35, 233–241. [Google Scholar] [CrossRef]
- Uluer, O.; Kirmaci, V.; Atas, S. Using the artificial neural network model for modeling the performance of the counter flow vortex tube. Expert Syst. Appl. 2009, 36, 12256–12263. [Google Scholar] [CrossRef]
- TWPCR. Turkish Water Pollution Control Regulation; The Official Gazette No.: 25687; (Su Kirliligi Kontrolü Yönetmeliği, in Turkish); The Official Gazette of the Republic of Turkey: Ankara, Turkey, 2004. [Google Scholar]
- Yesilnacar, M.I.; Uyanik, S. Investigation of water quality of the world’s largest irrigation tunnel system, the Sanliurfa tunnels in Turkey. Fresenius Environ. Bull. 2005, 14, 300–306. [Google Scholar]
- Bulut, V.N.; Bayram, A.; Gundogdu, A.; Soylak, M.; Tufekci, M. Assessment of water quality variables in the stream Galyan, Trabzon, Turkey. Environ. Monit. Assess. 2010, 165, 1–13. [Google Scholar] [CrossRef] [PubMed]
- TSWQMR. Turkish Superficial Water Quality Management Regulation; The Official Gazette No.: 28483; (Yüzeysel Su Kalitesi Yönetimi Yönetmeliği, in Turkish); The Official Gazette of the Republic of Turkey: Ankara, Turkey, 2012. [Google Scholar]
- TSWQR. Turkish Surface Water Quality Regulation; The Official Gazette No.: 29327; (Yüzeysel Su Kalitesi Yönetimi Yönetmeliğinde Değişiklik Yapılmasına Dair Yönetmelik, in Turkish); The Official Gazette of the Republic of Turkey: Ankara, Turkey, 2015. [Google Scholar]
- Bayram, A. Rebuttal to ‘Evaluation of surface water quality and heavy metal pollution of Coruh River Basin (Turkey) by multivariate statistical methods’ by Bilgin and Konanc (Environ. Earth Sci. 2016, 75, 1029). Environ. Earth Sci. 2017, 76, 700. [Google Scholar] [CrossRef]
- TSWQR. Turkish Surface Water Quality Regulation; The Official Gazette No.: 29797; (Yerüstü Su Kalitesi Yönetmeliğinde Değişiklik Yapılmasına Dair Yönetmelik, in Turkish); The Official Gazette of the Republic of Turkey: Ankara, Turkey, 2016. [Google Scholar]
- Satilmis, U. A Study on Spatial and Temporal Variation of Surface Water Quality in the Stream Değirmendere Watershed (Trabzon). Master’s Thesis, Karadeniz Technical University, Trabzon, Turkey, 2015. (In Turkish with English abstract). [Google Scholar]
- TS 266. Water Intended for Human Consumption; (Sular-İnsani Tüketim Amaçlı Sular, in Turkish); Türk Standartları Enstitüsü (TSE): Ankara, Turkey, 2005. [Google Scholar]
- EU 1998 Official Journal of European Communities, Council Directive 98/83/EC of 3 November 1998 on the Quality of Water Intended for Human Consumption. Available online: http://eurlex.europa.eu/LexUriServ/LexUriServ.do?uri=OJ:L:1998:330:0032:0054:EN:PDF (accessed on 29 February 2020).
- WHO. Guidelines for Drinking-Water Quality, 4th ed.; World Health Organization: Geneva, Switzerland, 2011. [Google Scholar]
- US EPA. Drinking Water Standards and Health Advisories; United States Environmental Protection Agency: Washington, DC, USA, 2009. Available online: http://water.epa.gov/action/advisories/drinking/upload/dwstandards2009.pdf (accessed on 29 February 2020).
- Nacar, S.; Bayram, A.; Satilmis, U.; Baki, O.T. The surface water quality monitoring and assessment of the Eastern Black Sea Basin (Trabzon Province) Streams, Turkey. In Proceedings of the 12th International Congress on Advances in Civil Engineering, İstanbul, Turkey, 21–23 September 2016; Turan, Ö., Hilmi, L., Eds.; p. 111, (Full text in CD). [Google Scholar]


| Stream | Gauging Station | Coordinates | Drainage Area (km2) | Operating Altitude (m) | Gauging (2015–2016) |
|---|---|---|---|---|---|
| Foldere | Şerifli | 39°17’06’’ E – 41°00’59’’ N | 181.30 | 60 | Yes |
| Kalenima | Doğanköy | 39°28’10’’ E – 40°54’10’’ N | 129.40 | 410 | No |
| Değirmendere | Öğütlü | 41°11’00’’ E – 40°51’50’’ N | 728.40 | 160 | Yes |
| Yomra | Taşdelen | 39°51’23’’ E – 40°51’14’’ N | 68.85 | 385 | Yes |
| Karadere | Ağnas | 40°00’25’’ E – 40°50’58’’ N | 635.70 | 78 | Yes |
| Manahoz | Ortaköy | 40°07’00’’ E – 40°51’00’’ N | 174.00 | 150 | No |
| Solaklı | Ulucami | 40°15’20’’ E – 40°45’00’’ N | 576.80 | 275 | No |
| Author(s) | Year | Reference Number | Input Variables | |||||||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Q | WT | pH | EC | SC | WD | TS | TA | WH | AT | NO2− | NO3− | NH4+ | PO43− | TP | COD | SO42− | Na+ | K+ | Ca2+ | Cl− | BOD | |||
| Diamantopoulou et al. | 2007 | [29] | * | * | * | * | * | * | * | * | * | |||||||||||||
| Chen and Li | 2008 | [30] | * | * | * | |||||||||||||||||||
| Singh et al. | 2009 | [31] | * | * | * | * | * | * | * | * | * | * | * | |||||||||||
| Ay and Kisi | 2011 | [32] | * | * | * | * | ||||||||||||||||||
| Wen et al. | 2013 | [33] | * | * | * | * | * | * | * | * | ||||||||||||||
| Antanasijevic et al. | 2013 | [34] | * | * | * | * | ||||||||||||||||||
| Kisi et al. | 2013 | [35] | * | * | * | * | ||||||||||||||||||
| Heddam | 2014 | [36] | * | * | * | * | ||||||||||||||||||
| Evrendilek and Karakaya | 2014 | [37] | * | * | * | * | ||||||||||||||||||
| Heddam | 2014 | [38] | * | * | * | * | ||||||||||||||||||
| Heddam | 2014 | [39] | * | * | * | * | ||||||||||||||||||
| Nemati et al. | 2015 | [40] | * | * | * | * | * | * | * | * | ||||||||||||||
| Bayram and Kankal | 2015 | [41] | * | * | ||||||||||||||||||||
| Kanda et al. | 2016 | [42] | * | * | * | * | ||||||||||||||||||
| Olyaie et al. | 2017 | [43] | * | * | * | * | ||||||||||||||||||
| Heddam and Kisi | 2018 | [44] | * | * | * | * | ||||||||||||||||||
| Elkiran et al. | 2018 | [45] | * | * | * | |||||||||||||||||||
| Yaseen et al. | 2018 | [46] | * | * | * | * | ||||||||||||||||||
| Csabragi et al. | 2019 | [47] | * | * | * | * | ||||||||||||||||||
| Kisi et al. | 2020 | [48] | * | * | * | |||||||||||||||||||
| Stream | Training Group | Testing Group |
|---|---|---|
| Foldere | ● | |
| Kalenima | ● | |
| Değirmendere | ▲ | |
| Yomra | ● | |
| Karadere | ● | |
| Manahoz | ▲ | |
| Solaklı | ● |
| Water-Quality Indicators | Training Data Set | Testing Data Set | ||||||
|---|---|---|---|---|---|---|---|---|
| Min | Mean | Max | SD | Min | Mean | Max | SD | |
| LDO, mg/L | 8.25 | 10.89 | 15.08 | 1.38 | 8.98 | 11.08 | 13.97 | 1.20 |
| WT, °C | 0.93 | 14.16 | 27.35 | 6.37 | 3.30 | 13.43 | 23.70 | 5.53 |
| pH | 7.62 | 8.37 | 9.68 | 0.37 | 7.41 | 8.26 | 8.98 | 0.37 |
| EC, µS/cm | 58.11 | 165.34 | 792.53 | 108.42 | 55.71 | 125.97 | 280.60 | 57.43 |
| Water-Quality Indicators | Water Quality Classes, TWPCR [69] | Water Quality Classes, TSWQMR [72] | ||||||
|---|---|---|---|---|---|---|---|---|
| I | II | III | IV | I | II | III | IV | |
| WT, °C | 25 | 25 | 30 | >30 | ≤25 | ≤25 | ≤30 | >30 |
| pH | 6.5–8.5 | 6.5–8.5 | 6.0–9.0 | <6.0 to >9.0 | 6.5–8.5 | 6.5–8.5 | 6.0–9.0 | <6.0 to >9.0 |
| DO, mg/L | 8 | 6 | 3 | <3 | >8 | 6–8 | 3–6 | <3 |
| DO, % | 90 | 70 | 40 | <40 | 90 | 70–90 | 40–70 | <40 |
| TDS, mg/L | 500 | 1500 | 5000 | >5000 | – | – | – | – |
| EC, µS/cm | – | – | – | – | <400 | 400–1000 | 1001–3000 | >3000 |
| Water-Quality | Water Quality Classes, TSWQR [73] | Water Quality Classes, TSWQR [75] | ||||||
| Indicators | I | II | III | IV | I | II | III | IV |
| WT, °C | ≤25 | ≤25 | ≤30 | >30 | – | – | – | – |
| pH | 6.5–8.5 | 6.5–8.5 | 6.0–9.0 | <6.0 to >9.0 | 6–9 | 6–9 | 6–9 | 6–9 |
| DO, mg/L | >8 | 6 | 3 | <3 | >8 | 6 | 3 | <3 |
| DO, % | >90 | 70 | 40 | <40 | – | – | – | – |
| TDS, mg/L | – | – | – | – | – | – | – | – |
| EC, µS/cm | <400 | 1000 | 3000 | >3000 | <400 | 1000 | 3000 | >3000 |
| Stations | Water-Quality Indicators (One-year period from March 2015 to February 2016) [81] | |||||||||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| WT, °C | pH | LDO, mg/L | LDO Saturation, % | TDS, mg/L | EC, µS/cm | |||||||||||||||||||
| Min | Mean | Max | SD | Min | Mean | Max | SD | Min | Mean | Max | SD | Min | Mean | Max | SD | Min | Mean | Max | SD | Min | Mean | Max | SD | |
| S1 | 2.12 | 13.74 | 27.33 | 7.22 | 8.14 | 8.37 | 9.19 | 0.30 | 8.62 | 11.08 | 14.48 | 1.60 | 99.82 | 104.21 | 113.70 | 4.22 | 67.74 | 104.39 | 164.55 | 37.16 | 105.28 | 178.16 | 352.47 | 92.57 |
| S2 | 0.93 | 14.58 | 27.03 | 7.68 | 8.31 | 8.56 | 9.12 | 0.26 | 9.03 | 10.89 | 14.45 | 1.49 | 97.63 | 104.79 | 130.76 | 9.52 | 108.65 | 157.21 | 211.67 | 38.81 | 168.03 | 265.25 | 424.53 | 98.00 |
| S3 | 3.79 | 12.89 | 21.20 | 5.46 | 8.33 | 8.48 | 8.63 | 0.10 | 9.08 | 11.16 | 13.54 | 1.18 | 98.68 | 103.91 | 120.68 | 5.71 | 60.55 | 107.47 | 159.35 | 33.21 | 94.92 | 172.40 | 280.60 | 58.94 |
| S4 | 3.14 | 14.72 | 26.05 | 7.09 | 8.09 | 8.54 | 9.50 | 0.40 | 8.25 | 10.43 | 13.53 | 1.60 | 97.46 | 100.18 | 102.79 | 1.84 | 50.11 | 78.56 | 134.68 | 25.06 | 87.21 | 136.03 | 268.93 | 61.75 |
| S5 | 3.09 | 13.66 | 24.09 | 6.91 | 8.08 | 8.39 | 8.86 | 0.27 | 8.91 | 11.19 | 15.08 | 1.65 | 98.26 | 105.25 | 122.74 | 6.62 | 44.97 | 113.02 | 420.07 | 101.86 | 68.78 | 194.80 | 792.53 | 201.36 |
| S6 | 3.30 | 13.45 | 23.70 | 6.64 | 7.74 | 8.21 | 8.98 | 0.40 | 8.98 | 11.16 | 13.97 | 1.38 | 98.74 | 104.79 | 117.93 | 5.57 | 36.03 | 54.67 | 82.58 | 14.72 | 55.71 | 91.48 | 157.87 | 34.82 |
| S7 | 3.39 | 12.70 | 22.21 | 5.86 | 7.74 | 8.30 | 8.71 | 0.27 | 9.42 | 11.14 | 14.00 | 1.33 | 96.14 | 102.91 | 110.03 | 3.89 | 41.01 | 71.22 | 97.70 | 17.86 | 67.85 | 115.31 | 184.05 | 37.43 |
| Stations | Water-Quality Indicators (One-year period from September 2015 to August 2016) | |||||||||||||||||||||||
| WT, °C | pH | LDO, mg/L | LDO Saturation, % | TDS, mg/L | EC, µS/cm | |||||||||||||||||||
| Min | Mean | Max | SD | Min | Mean | Mean | SD | Min | Mean | Max | SD | Min | Mean | Max | SD | Min | Mean | Max | SD | Min | Mean | Max | SD | |
| S1 | 2.12 | 13.74 | 27.35 | 7.22 | 7.65 | 8.29 | 8.29 | 0.47 | 9.64 | 11.32 | 14.48 | 1.41 | 101.39 | 106.90 | 130.44 | 8.09 | 39.59 | 97.44 | 164.55 | 37.44 | 65.42 | 165.18 | 317.00 | 85.74 |
| S2 | 0.93 | 14.67 | 26.81 | 7.72 | 7.94 | 8.49 | 8.49 | 0.32 | 8.84 | 11.01 | 14.45 | 1.47 | 99.97 | 105.95 | 130.76 | 8.56 | 50.70 | 149.90 | 211.67 | 46.08 | 83.43 | 253.67 | 424.53 | 104.53 |
| S3 | 3.79 | 13.27 | 21.20 | 5.79 | 7.96 | 8.39 | 8.39 | 0.26 | 9.07 | 11.16 | 13.54 | 1.33 | 100.43 | 104.54 | 120.68 | 5.40 | 60.55 | 107.47 | 159.35 | 31.10 | 96.35 | 174.44 | 280.60 | 57.84 |
| S4 | 3.14 | 14.48 | 26.05 | 7.06 | 7.69 | 8.56 | 8.56 | 0.59 | 8.25 | 10.65 | 13.53 | 1.58 | 99.39 | 101.71 | 102.89 | 1.79 | 56.63 | 75.16 | 134.68 | 23.38 | 87.21 | 128.90 | 268.93 | 56.61 |
| S5 | 3.09 | 13.37 | 24.09 | 6.77 | 7.76 | 8.34 | 8.34 | 0.36 | 9.70 | 11.45 | 15.08 | 1.63 | 100.41 | 106.92 | 122.74 | 6.01 | 57.87 | 110.25 | 420.07 | 100.03 | 69.60 | 187.82 | 792.53 | 195.86 |
| S6 | 3.30 | 13.14 | 22.53 | 6.39 | 7.41 | 7.98 | 7.98 | 0.39 | 8.98 | 11.27 | 13.97 | 1.44 | 100.91 | 104.93 | 115.03 | 4.23 | 39.83 | 55.40 | 82.58 | 14.98 | 56.76 | 91.94 | 157.87 | 34.14 |
| S7 | 3.39 | 12.55 | 20.20 | 5.95 | 7.62 | 8.19 | 8.19 | 0.30 | 9.56 | 11.33 | 14.00 | 1.43 | 100.99 | 104.23 | 110.03 | 2.85 | 38.54 | 69.06 | 97.70 | 16.25 | 58.11 | 111.50 | 184.05 | 34.97 |
| Stations | Water Temperature, °C | pH | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| S2 | S3 | S4 | S5 | S6 | S7 | S2 | S3 | S4 | S5 | S6 | S7 | |
| S1 | 0.989 b 0.000 | 0.944 b 0.000 | 0.949 b 0.000 | 0.922 b 0.000 | 0.948 b 0.000 | 0.913 b 0.000 | 0.824 b 0.000 | 0.219 0.383 | 0.300 0.227 | 0.309 0.211 | 0.725 b 0.001 | 0.472 a 0.048 |
| S2 | 0.954 b 0.000 | 0.970 b 0.000 | 0.935 b 0.000 | 0.951 b 0.000 | 0.920 b 0.000 | − | 0.003 0.990 | 0.584 a 0.011 | 0.202 0.421 | 0.542 a 0.020 | 0.346 0.159 | |
| S3 | 0.961 b 0.000 | 0.979 b 0.000 | 0.980 b 0.000 | 0.970 b 0.000 | − | 0.121 0.633 | 0.550 a 0.018 | 0.498 a 0.035 | 0.556 a 0.014 | |||
| S4 | 0.971 b 0.000 | 0.973 b 0.000 | 0.935 b 0.000 | 0.117 0.643 | 0.130 0.608 | 0.165 0.513 | ||||||
| S5 | 0.992 b 0.000 | 0.986 b 0.000 | 0.432 0.074 | 0.758 b 0.000 | ||||||||
| S6 | 0.981 b 0.000 | 0.500 a 0.035 | ||||||||||
| Stations | Luminescent dissolved oxygen, mg/L | Luminescent dissolved oxygen, % | ||||||||||
| S2 | S3 | S4 | S5 | S6 | S7 | S2 | S3 | S4 | S5 | S6 | S7 | |
| S1 | 0.935 b 0.000 | 0.883 b 0.000 | 0.933 b 0.000 | 0.933 b 0.000 | 0.911 b 0.000 | 0.896 b 0.000 | 0.588 a 0.010 | 0.206 0.411 | 0.289 0.245 | 0.433 0.073 | 0.695 b 0.001 | 0.689 b 0.002 |
| S2 | 0.894 b 0.000 | 0.914 b 0.000 | 0.885 b 0.000 | 0.863 b 0.000 | 0.837 b 0.000 | 0.716 b 0.001 | 0.312 0.208 | 0.441 0.067 | 0.612 b 0.007 | 0.736 b 0.000 | ||
| S3 | 0.882 b 0.000 | 0.922 b 0.000 | 0.906 b 0.000 | 0.937 b 0.000 | 0.307 0.215 | 0.338 0.170 | 0.205 0.414 | 0.527 a 0.025 | ||||
| S4 | 0.891 b 0.000 | 0.908 b 0.000 | 0.873 b 0.000 | 0.286 0.250 | 0.178 0.480 | 0.428 0.077 | ||||||
| S5 | 0.839 b 0.000 | 0.967 b 0.000 | 0.340 0.167 | 0.650 b 0.004 | ||||||||
| S6 | 0.968 b 0.000 | 0.812 b 0.000 | ||||||||||
| Stations | Total dissolved solids, mg/L | Electrical conductivity, µS/cm | ||||||||||
| S2 | S3 | S4 | S5 | S6 | S7 | S2 | S3 | S4 | S5 | S6 | S7 | |
| S1 | 0.882 b 0.000 | 0.670 b 0.002 | 0.875 b 0.000 | 0.595 b 0.009 | 0.624 b 0.006 | 0.610 b 0.007 | 0.964 b 0.000 | 0.791 b 0.000 | 0.941 b 0.000 | 0.658 b 0.003 | 0.791 b 0.000 | 0.765 b 0.000 |
| S2 | 0.755 b 0.000 | 0.745 b 0.000 | 0.405 0.095 | 0.435 0.071 | 0.579 a 0.012 | 0.788 b 0.000 | 0.887 b 0.000 | 0.578 a 0.012 | 0.672 b 0.002 | 0.689 b 0.002 | ||
| S3 | 0.601 b 0.008 | 0.536 a 0.022 | 0.623 b 0.006 | 0.910 b 0.000 | 0.749 b 0.000 | 0.707 b 0.001 | 0.731 b 0.001 | 0.907 b 0.000 | ||||
| S4 | 0.798 b 0.000 | 0.767 b 0.000 | 0.602 b 0.008 | 0.816 b 0.000 | 0.855 b 0.000 | 0.762 b 0.000 | ||||||
| S5 | 0.741 b 0.000 | 0.662 b 0.003 | 0.777 b 0.000 | 0.782 b 0.000 | ||||||||
| S6 | 0.740 b 0.000 | 0.856 b 0.000 | ||||||||||
| MARS Model 1 | MARS Model 2 | MARS Model 3 | MARS Model 4 | ||||
|---|---|---|---|---|---|---|---|
| Basic | Equations | Basic | Equations | Basic | Equations | Basic | Equations |
| Functions | Functions | Functions | Functions | ||||
| BF02 | max (0.501816 − WT) | BF02 | max (0.501816 − WT) | BF01 | max (WT − 0.501816) | BF01 | max (WT − 0.501816) |
| BF03 | max (WT − 0.890111) | BF04 | max (0.315742 − WT) | BF02 | max (0.501816 − WT) | BF02 | max (0.501816 − WT) |
| BF04 | max (0.890111 − WT) | BF06 | max (0.595661 − WT) | BF03 | max (pH − 0.724264) × BF01 | BF03 | max (pH − 0.724264) × BF01 |
| BF06 | max (0.326452 − WT) | BF08 | max (0.463269 − WT) | BF05 | max (pH − 0.613074) × BF01 | BF04 | max (0.724264 − pH) × BF01 |
| BF08 | max (0.595661 − WT) | BF10 | max (0.441271 − WT) | BF07 | max (pH − 0.500589) × BF02 | BF05 | max (pH − 0.613074) × BF01 |
| BF09 | max (WT − 0.16559) | BF12 | max (0.762159 − WT) | BF09 | max (pH − 0.70212) × BF01 | BF07 | max (pH − 0.500589) × BF02 |
| BF10 | max (0.16559 − WT) | BF13 | max (WT − 0.828759) | BF11 | max (pH − 0.538634) × BF01 | BF08 | max (0.500589 − pH) × BF02 |
| BF11 | max (WT − 0.828759) | BF14 | max (0.828759 − WT) | BF12 | max (0.538634 − PH) × BF01 | BF09 | max (pH − 0.70212) × BF01 |
| BF14 | max (0.79445 − WT) | BF16 | max (0.791625 − WT) | BF13 | max (pH − 0.590224) × BF01 | BF11 | max (pH − 0.538634) × BF01 |
| BF16 | max (0.860646 − WT) | BF18 | max (0.677397 − WT) | BF15 | max (pH − 0.600353) × BF01 | BF13 | max (pH − 0.590224) × BF01 |
| BF18 | max (0.801312 − WT) | BF19 | max (WT − 0.284057) | BF17 | max (WT − 0.321796) | BF15 | max (pH − 0.600353) × BF01 |
| BF20 | max (0.791625 − WT) | BF20 | max (0.284057 − WT) | BF18 | max (0.321796 − WT) | BF17 | max (WT − 0.321796) |
| BF22 | max (0.466095 − WT) | BF21 | max (WT − 0.374672) | BF19 | max (pH − 0.581743) × BF18 | BF18 | max (0.321796 − WT) |
| BF24 | max (0.340767 − WT) | BF24 | max (0.650151 − WT) | BF20 | max (0.581743 − pH) × BF18 | BF19 | max (pH − 0.581743) × BF18 |
| BF26 | max (0.671342 − WT) | BF26 | max (0.622906 − WT) | BF25 | max (pH − 0.175147) × BF17 | BF20 | max (0.581743 − pH) × BF18 |
| BF28 | max (0.444299 − WT) | BF28 | max (0.694753 − WT) | BF21 | max (pH − 0.437102) × BF01 | ||
| BF30 | max (0.431181 − WT) | BF30 | max (0.716347 − WT) | BF33 | max (pH − 0.551355) × BF01 | ||
| BF34 | max (0.650151 − WT) | BF31 | max (WT − 0.417053) | ||||
| BF36 | max (0.630575 − WT) | BF32 | max (0.417053 − WT) | ||||
| BF38 | max (0.615439 − WT) | BF34 | max (0.340767 − WT) | ||||
| BF40 | max (0.683451 − WT) | BF36 | max (0.55449 − WT) | ||||
| BF38 | max (EC − 0.252423) | ||||||
| BF39 | max (0.252423 − EC) | ||||||
| LDO Model 1 = | 0.254679 + 0.0886742 × BF02 + 2.15867 × BF03 + 0.0444198 × BF04 + 0.165892 × BF06 + 0.0705814 × BF08 − 0.0450666 × BF09 − 0.0228572 × BF10 − 0.257149 × BF11 + 0.0483375 × BF14 + 0.0454513 × BF16 + 0.0475508 × BF18 + 0.0485729 × BF20 + 0.0990403 × BF22 + 0.148585 × BF24 + 0.0579245 × BF26 + 0.103979 × BF28 + 0.108156 × BF30 + 0.0612519 × BF34 + 0.0641136 × BF36 + 0.0669608 × BF38 + 0.0565882 × BF40 | ||||||
| LDO Model 2 = | 0.284243 + 0.0871611 × BF02 + 0.161665 × BF04 + 0.0680995 × BF06 + 0.0992744 × BF08 + 0.104501 × BF10 + 0.0476524 × BF12 − 0.162201 × BF13 + 0.0423067 × BF14 + 0.0453071 × BF16 + 0.0542304 × BF18 − 0.0407528 × BF19 + 0.177219 × BF20 − 0.0414545 × BF21 + 0.0584495 × BF24 + 0.0628739 × BF26 + 0.0526291 × BF28 + 0.0508015 × BF30 − 0.0426374 × BF31 + 0.111746 × BF32 + 0.141249 × BF34 + 0.0754296 × BF36 + 0.0194781 × BF38 + 0.065239 × BF39 | ||||||
| LDO Model 3 = | 0.433206 + 0.534022 × BF02 − 5.03225 × BF03 + 1.63042 × BF05 + 2.18339 × BF07 + 2.44452 × BF20 − 0.46187 × BF25 − 3.45894 × BF09 − 0.166635 × BF11 − 1.8866 × BF12 + 1.39271 × BF13 + 1.48764 × BF15 − 0.263369 × BF17 + 0.474985 × BF18 + 24.5231 × BF19 | ||||||
| LDO Model 4 = | 0.31183 − 1.13213 × BF01 + 1.2448 × BF02 + 4.33683 × BF03+ 0.730011 × BF04 + 22.2679 × BF05 + 0.783317 × BF07 + 0.3346 × BF08 − 19.1624 × BF09 − 33.0927 × BF11 + 41.9666 × BF13 − 47.8018 × BF15 + 0.253183 × BF17 + 29.2467 × BF19 + 0.706642 × BF20 + 6.09 × BF21 + 19.8123 × BF23 | ||||||
| Models | Methods | Functions | Coefficients | ||||
|---|---|---|---|---|---|---|---|
| Model 1 | TLBO | 0.0848 | 0.0683 | −2.6255 | |||
| CRA | 0.0848 | 0.0683 | −2.6255 | ||||
| TLBO | 0.2357 | −0.6627 | |||||
| CRA | 0.2357 | −0.6627 | |||||
| TLBO | 0.7912 | −0.7633 | |||||
| CRA | 0.7912 | −0.7633 | |||||
| Model 2 | TLBO | 0.0941 | 0.0844 | −2.6933 | −0.0895 | ||
| CRA | 0.0938 | 0.0841 | −2.6912 | −0.0883 | |||
| TLBO | 0.1681 | −0.6621 | −0.1991 | ||||
| CRA | 0.1681 | −0.6621 | −0.1991 | ||||
| TLBO | 0.7808 | −0.8414 | 0.2261 | ||||
| CRA | 0.7808 | −0.8414 | 0.2261 | ||||
| Model 3 | TLBO | 0.0781 | 0.0362 | −2.5699 | 0.0697 | ||
| CRA | 0.0780 | 0.0360 | −2.5700 | −0.0700 | |||
| TLBO | 0.2210 | −0.6639 | −0.0711 | ||||
| CRA | 0.2210 | −0.6640 | −0.0710 | ||||
| TLBO | 0.7323 | −0.8097 | 0.1869 | ||||
| CRA | 0.7320 | −0.8100 | 0.1870 | ||||
| Model 4 | TLBO | 0.0886 | 0.0512 | −2.6432 | −0.0997 | 0.0747 | |
| CRA | 0.0886 | 0.0512 | 0.6432 | −0.0997 | 0.0747 | ||
| TLBO | 0.1695 | −0.6606 | −0.2135 | 0.0351 | |||
| CRA | 0.1695 | −0.6605 | 0.2135 | 0.0351 | |||
| TLBO | 0.7365 | −0.8600 | 0.1737 | 0.1481 | |||
| CRA | 0.7365 | −0.8600 | 0.1737 | 0.1481 | |||
| Models | Methods | Functions | Training | Testing | ||||
|---|---|---|---|---|---|---|---|---|
| RMSE | MAE | NSCE | RMSE | MAE | NSCE | |||
| MARS | 0.4109 | 0.3056 | 0.9111 | 0.3718 | 0.2844 | 0.9033 | ||
| TLBO | Exponential | 0.4177 | 0.3038 | 0.9082 | 0.3770 | 0.2834 | 0.9005 | |
| TLBO | Power | 0.5736 | 0.4460 | 0.8269 | 0.4634 | 0.3840 | 0.8497 | |
| Model 1 | TLBO | Linear | 0.5703 | 0.4042 | 0.8289 | 0.4418 | 0.3391 | 0.8634 |
| CRA | Exponential | 0.4177 | 0.3038 | 0.9082 | 0.3770 | 0.2834 | 0.9005 | |
| CRA | Power | 0.5736 | 0.4460 | 0.8269 | 0.4636 | 0.3843 | 0.8496 | |
| CRA | Linear | 0.5703 | 0.4041 | 0.8289 | 0.4418 | 0.3391 | 0.8634 | |
| MARS | 0.4123 | 0.3069 | 0.9106 | 0.3686 | 0.2813 | 0.9049 | ||
| TLBO | Exponential | 0.4175 | 0.3051 | 0.9083 | 0.3747 | 0.2805 | 0.9017 | |
| TLBO | Power | 0.5188 | 0.4110 | 0.8584 | 0.4362 | 0.3563 | 0.8668 | |
| Model 2 | TLBO | Linear | 0.5387 | 0.3772 | 0.8473 | 0.4534 | 0.3316 | 0.8561 |
| CRA | Exponential | 0.4175 | 0.3050 | 0.9083 | 0.3748 | 0.2805 | 0.9017 | |
| CRA | Power | 0.5188 | 0.4110 | 0.8584 | 0.4362 | 0.3563 | 0.8669 | |
| CRA | Linear | 0.5387 | 0.3771 | 0.8473 | 0.4535 | 0.3316 | 0.8560 | |
| MARS | 0.3134 | 0.2475 | 0.9483 | 0.3382 | 0.2637 | 0.9199 | ||
| TLBO | Exponential | 0.4170 | 0.3059 | 0.9085 | 0.3783 | 0.2884 | 0.8998 | |
| TLBO | Power | 0.5684 | 0.4375 | 0.8300 | 0.4533 | 0.3774 | 0.8562 | |
| Model 3 | TLBO | Linear | 0.5360 | 0.3862 | 0.8488 | 0.4397 | 0.3432 | 0.8647 |
| CRA | Exponential | 0.4170 | 0.3060 | 0.9085 | 0.3787 | 0.2888 | 0.8996 | |
| CRA | Power | 0.5684 | 0.4375 | 0.8300 | 0.4533 | 0.3773 | 0.8562 | |
| CRA | Linear | 0.5361 | 0.3863 | 0.8488 | 0.4405 | 0.3434 | 0.8642 | |
| MARS | 0.2599 | 0.2125 | 0.9645 | 0.2709 | 0.2126 | 0.9487 | ||
| TLBO | Exponential | 0.4167 | 0.3068 | 0.9086 | 0.3753 | 0.2845 | 0.9014 | |
| TLBO | Power | 0.5176 | 0.4135 | 0.8590 | 0.4322 | 0.3540 | 0.8693 | |
| Model 4 | TLBO | Linear | 0.5180 | 0.3799 | 0.8588 | 0.4561 | 0.3609 | 0.8544 |
| CRA | Exponential | 0.4167 | 0.3068 | 0.9086 | 0.3753 | 0.2845 | 0.9014 | |
| CRA | Power | 0.5176 | 0.4135 | 0.8590 | 0.4322 | 0.3540 | 0.8693 | |
| CRA | Linear | 0.5180 | 0.3799 | 0.8588 | 0.4561 | 0.3609 | 0.8544 | |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Nacar, S.; Bayram, A.; Baki, O.T.; Kankal, M.; Aras, E. Spatial Forecasting of Dissolved Oxygen Concentration in the Eastern Black Sea Basin, Turkey. Water 2020, 12, 1041. https://doi.org/10.3390/w12041041
Nacar S, Bayram A, Baki OT, Kankal M, Aras E. Spatial Forecasting of Dissolved Oxygen Concentration in the Eastern Black Sea Basin, Turkey. Water. 2020; 12(4):1041. https://doi.org/10.3390/w12041041
Chicago/Turabian StyleNacar, Sinan, Adem Bayram, Osman Tugrul Baki, Murat Kankal, and Egemen Aras. 2020. "Spatial Forecasting of Dissolved Oxygen Concentration in the Eastern Black Sea Basin, Turkey" Water 12, no. 4: 1041. https://doi.org/10.3390/w12041041
APA StyleNacar, S., Bayram, A., Baki, O. T., Kankal, M., & Aras, E. (2020). Spatial Forecasting of Dissolved Oxygen Concentration in the Eastern Black Sea Basin, Turkey. Water, 12(4), 1041. https://doi.org/10.3390/w12041041





