Interplay between Fingering Instabilities and Initial Soil Moisture in Solute Transport through the Vadose Zone
Abstract
1. Introduction
2. Materials and Methods
2.1. Mathematical Model of Unsaturated Flow in Porous Media
2.2. Transport of a Passive Solute
2.3. Finite Element Implementation
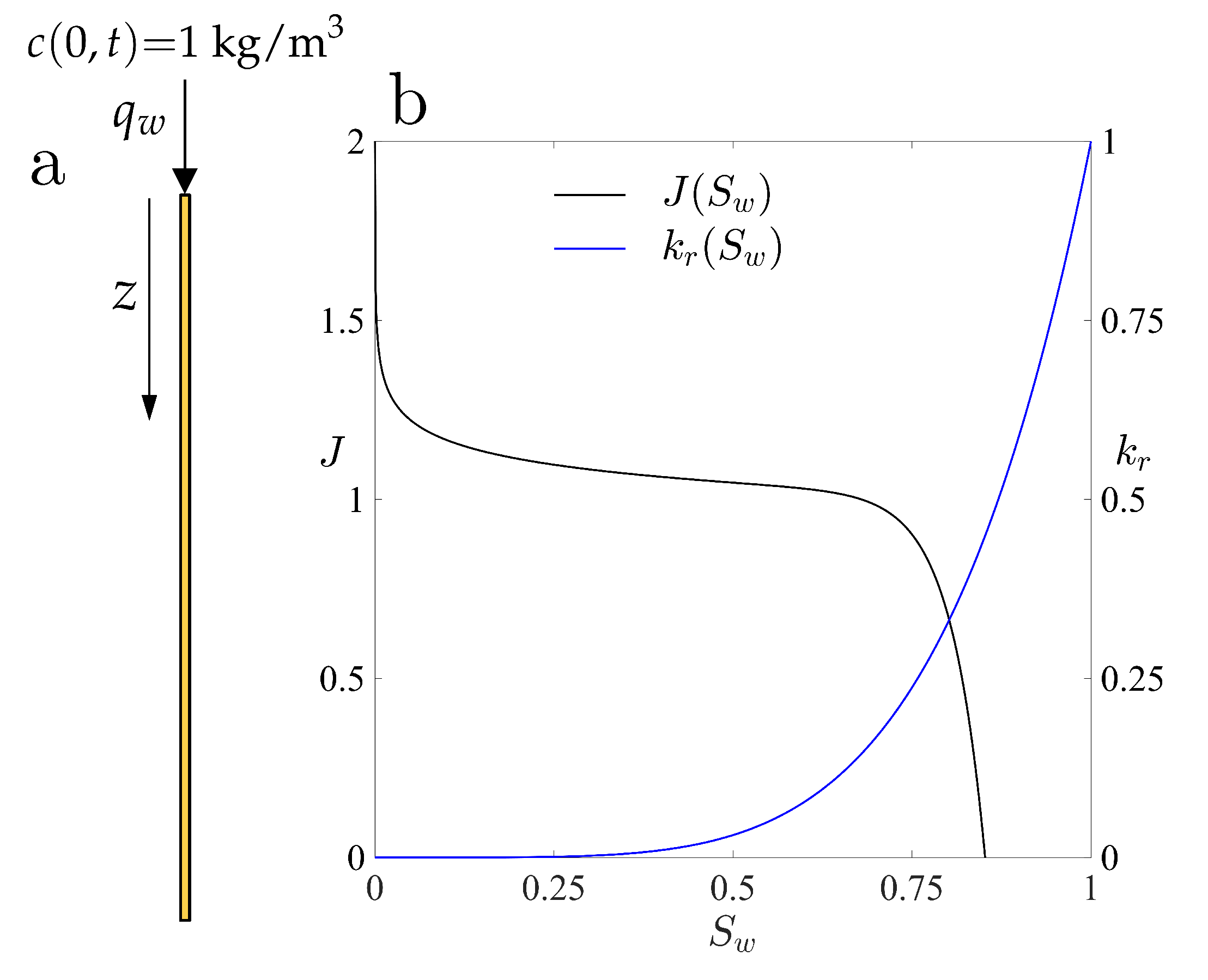
3. Results: One-Dimensional Infiltration Fronts
3.1. Problem Set-Up
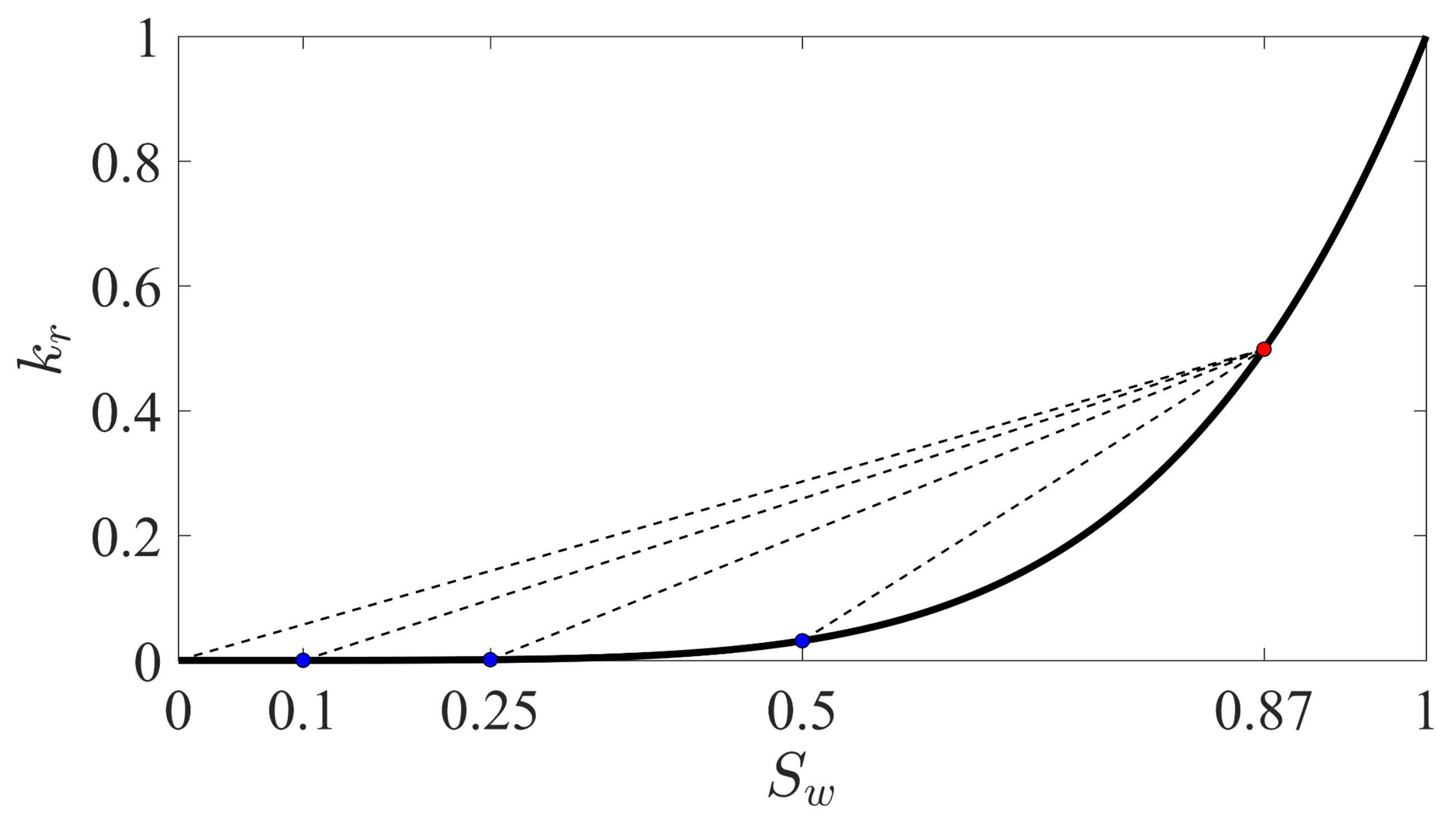
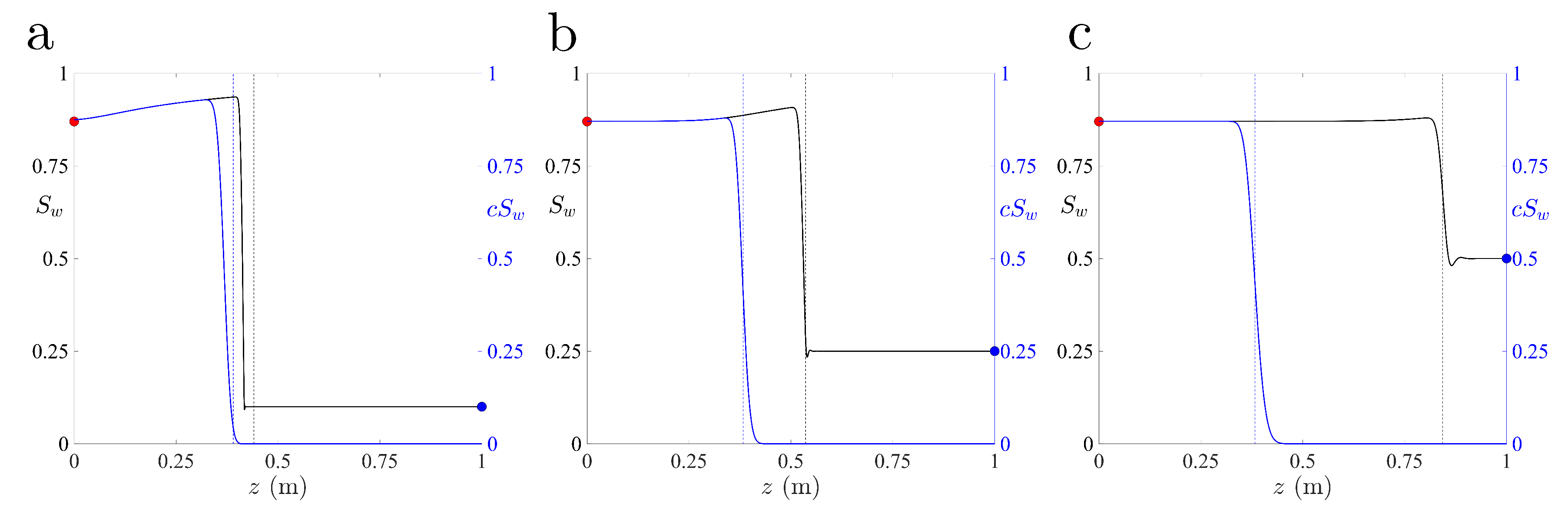
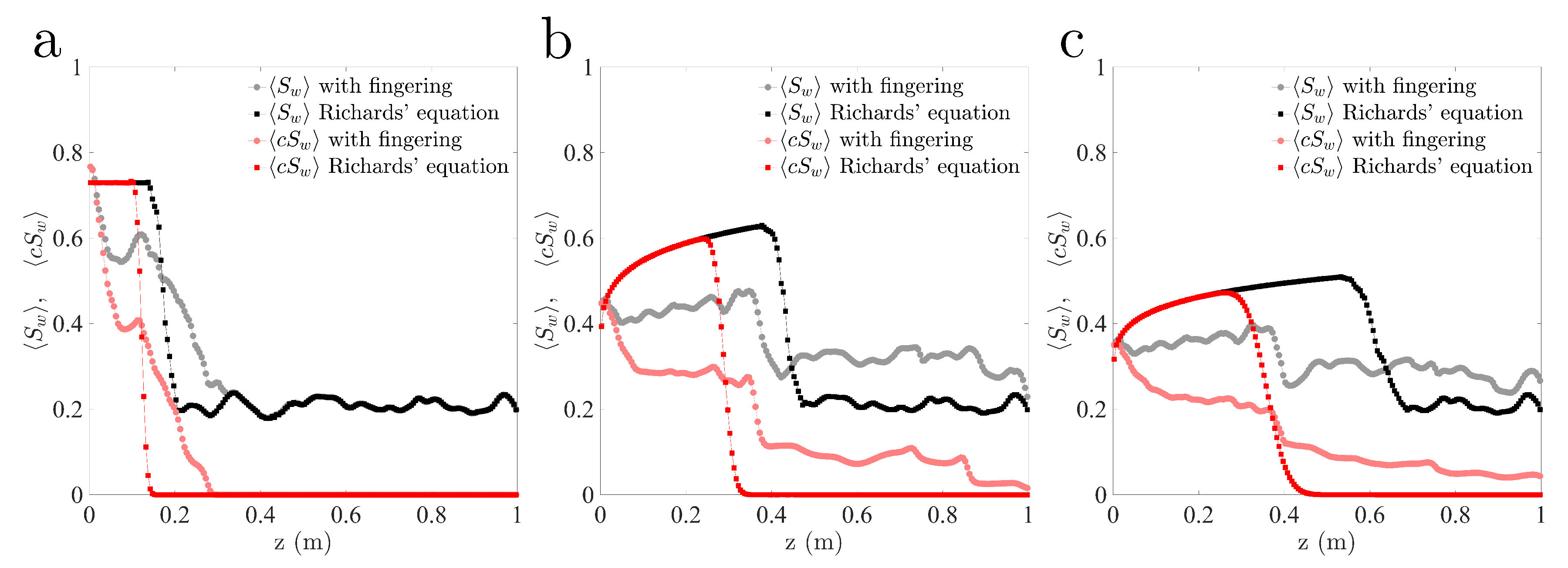
3.2. Impact of the Initial Saturation on Solute Transport
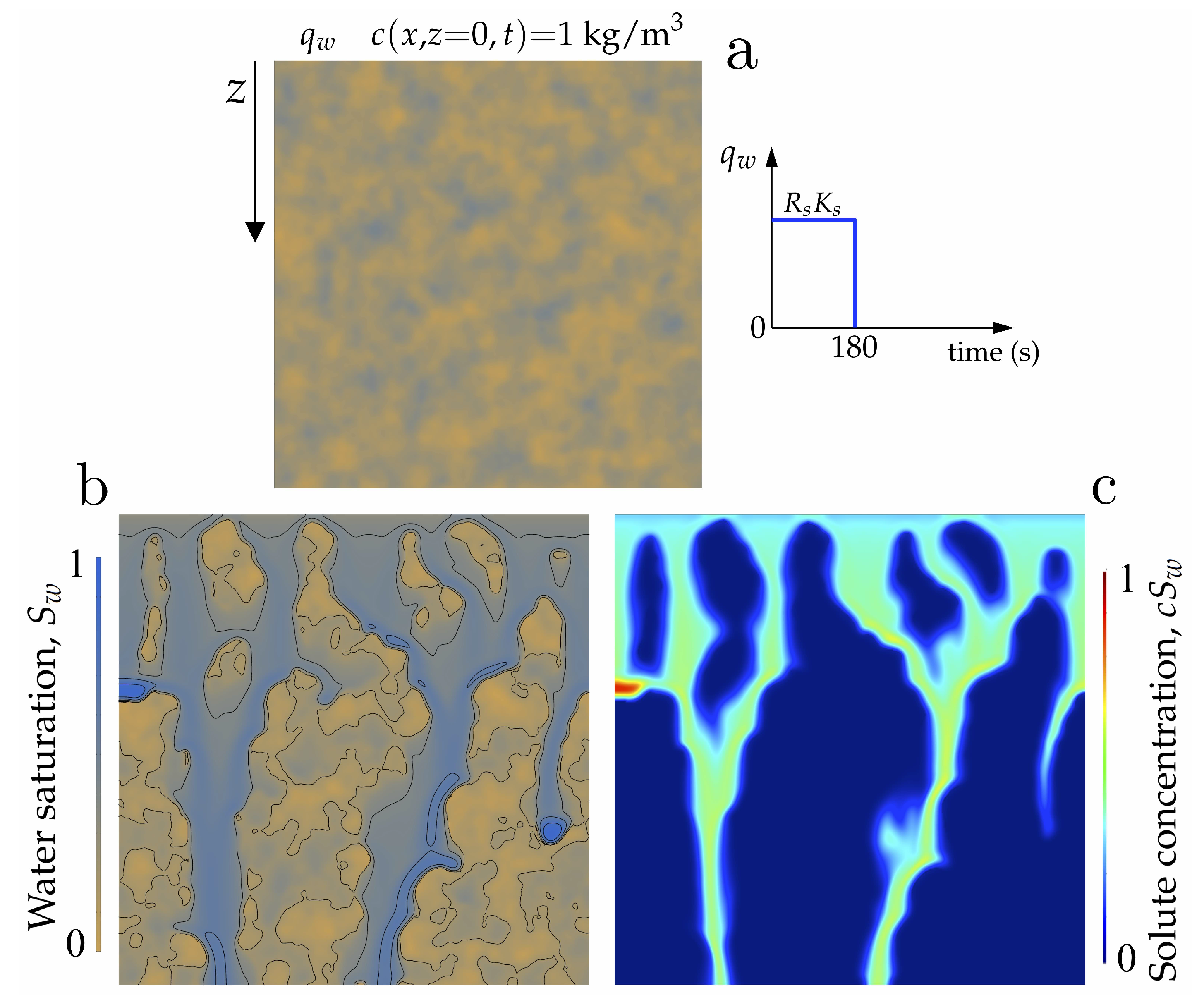
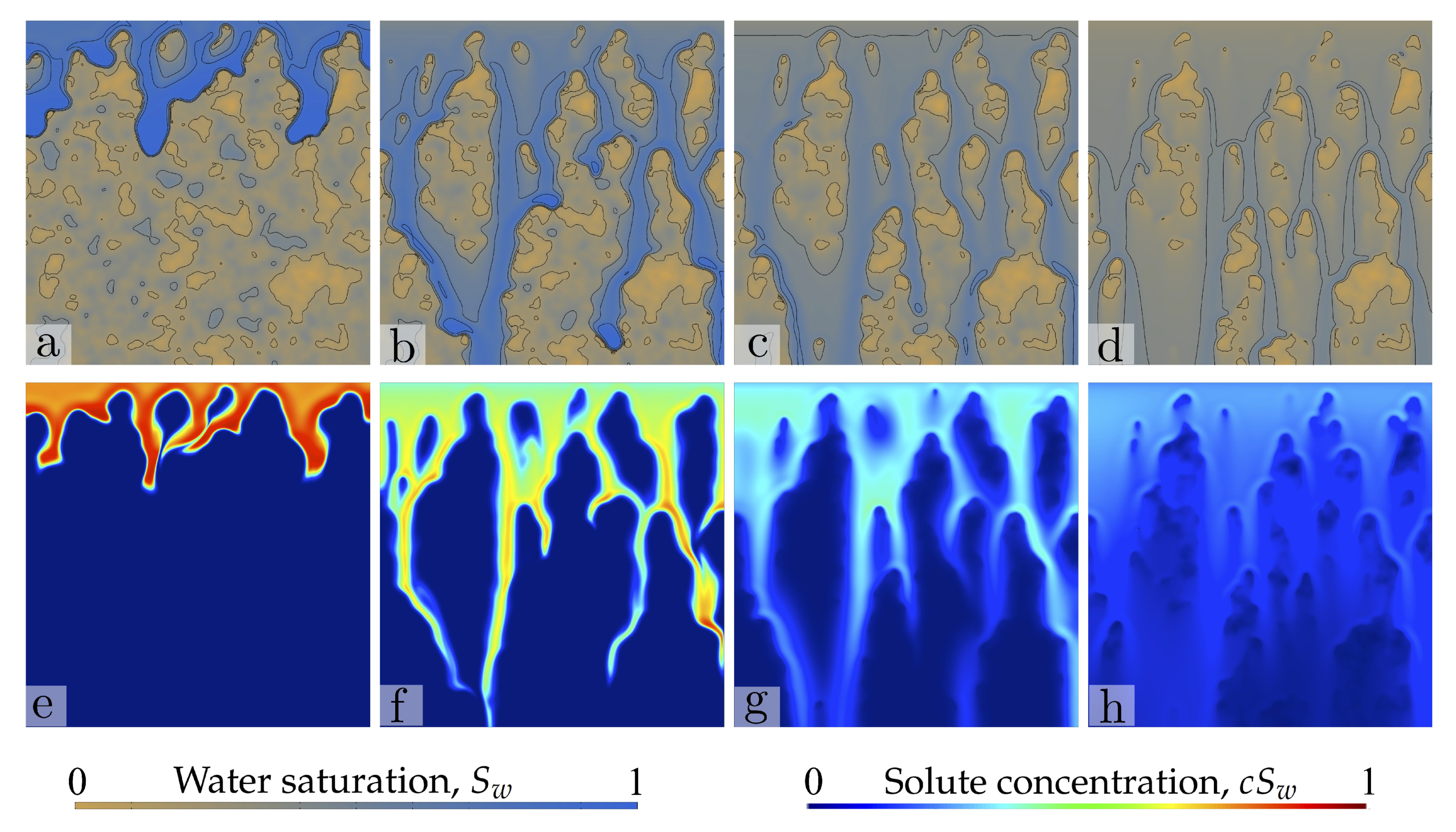
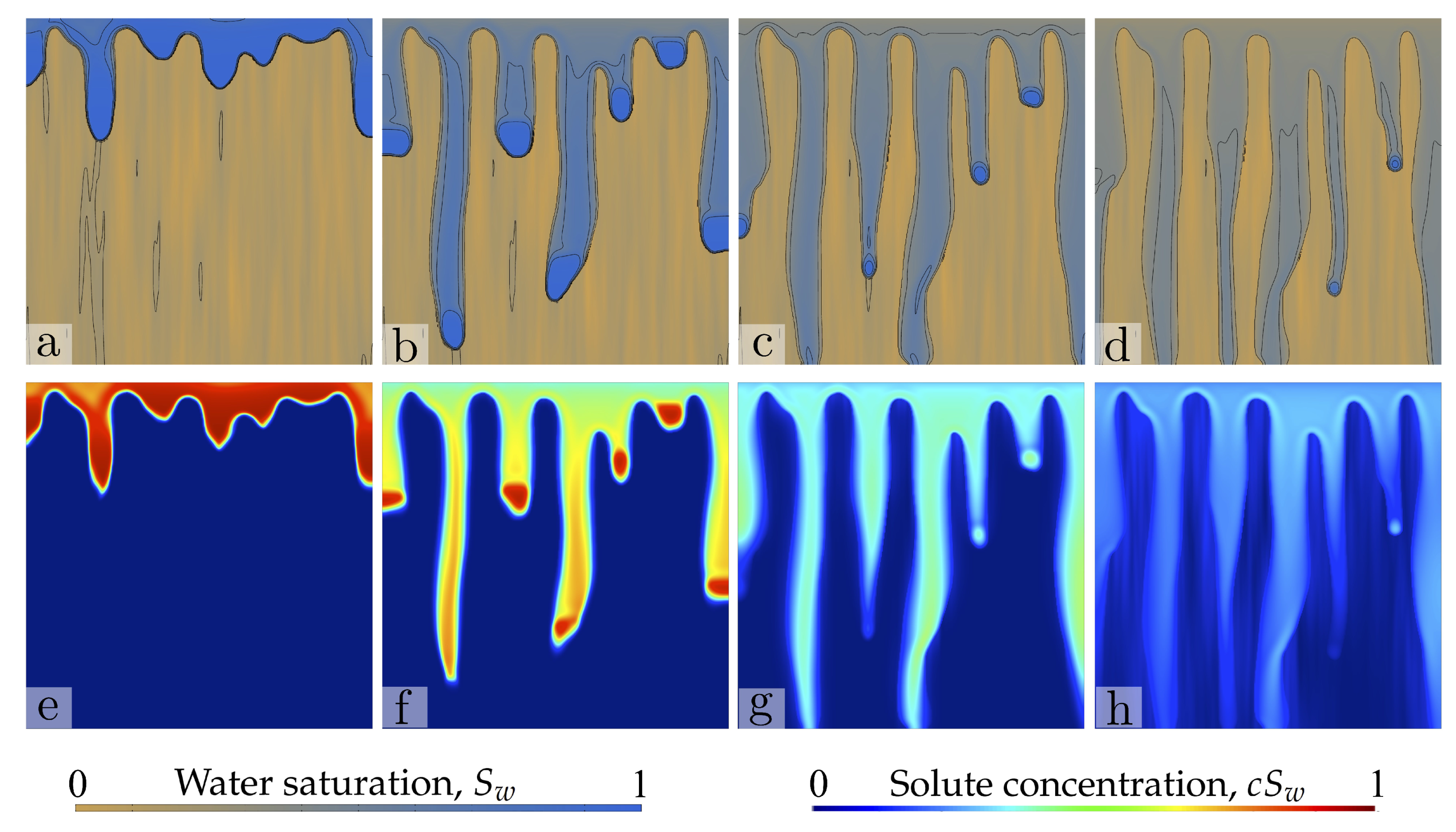
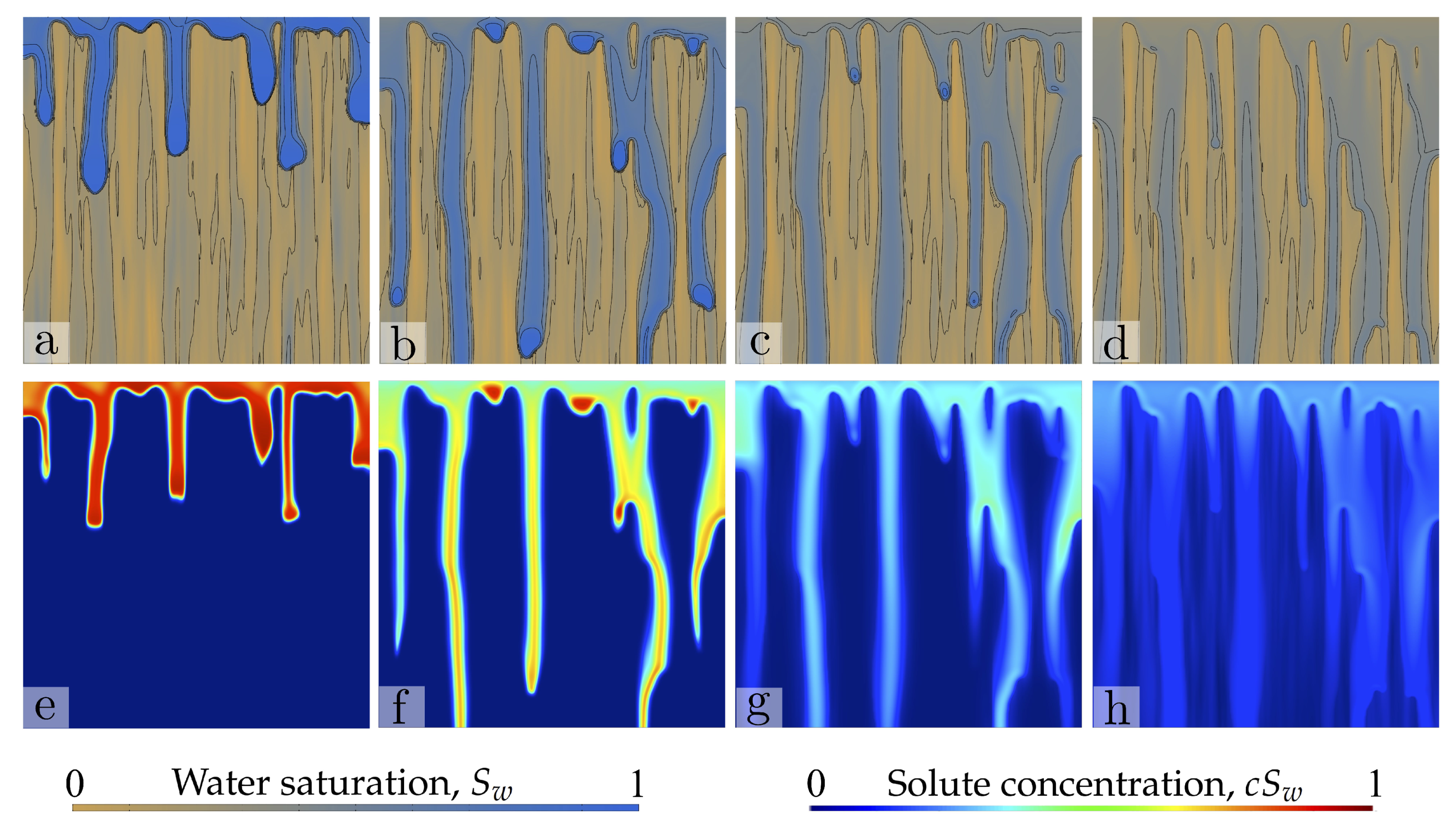
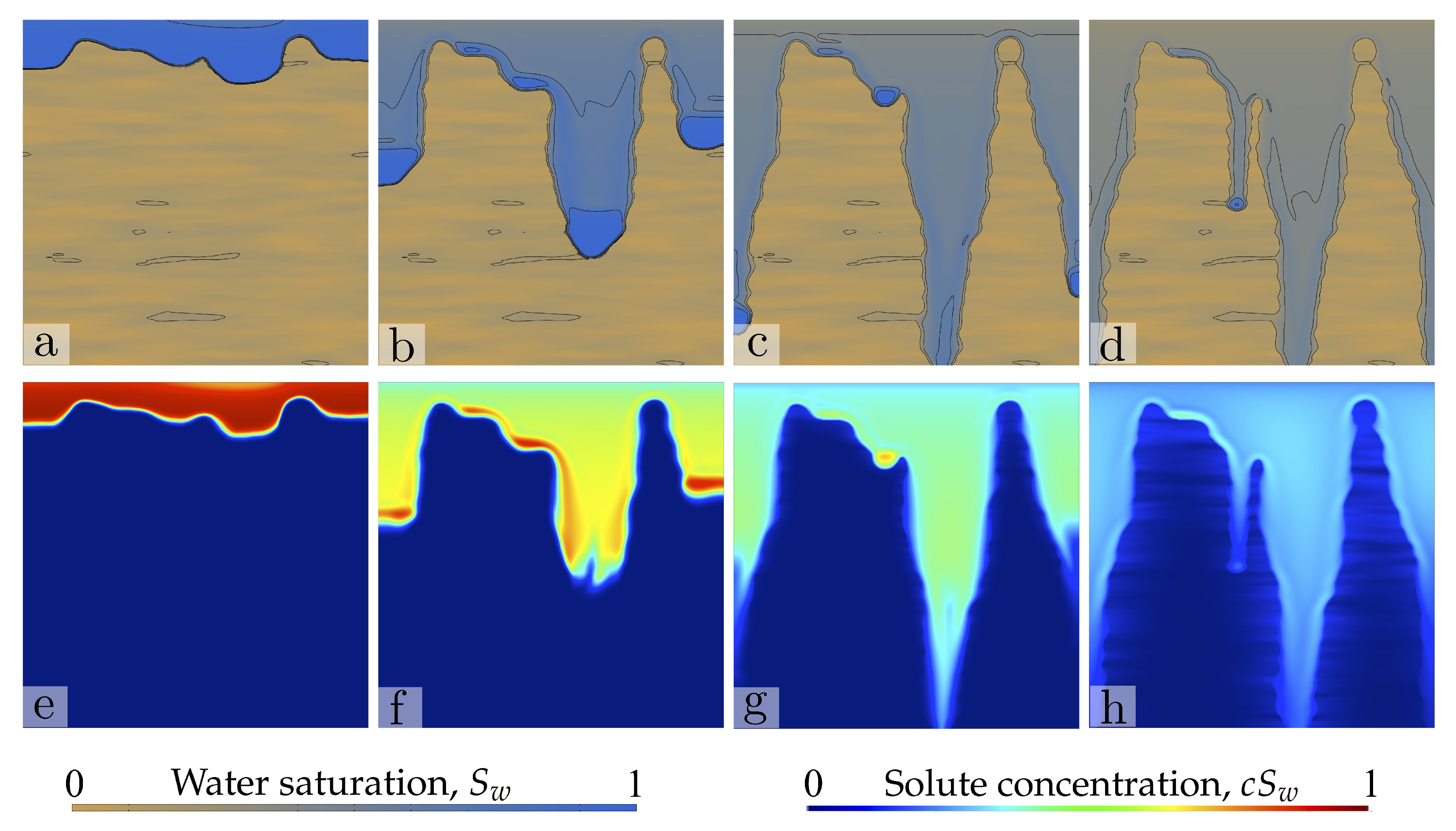
4. Results: Two-Dimensional Infiltration Patterns
4.1. Problem Set-Up
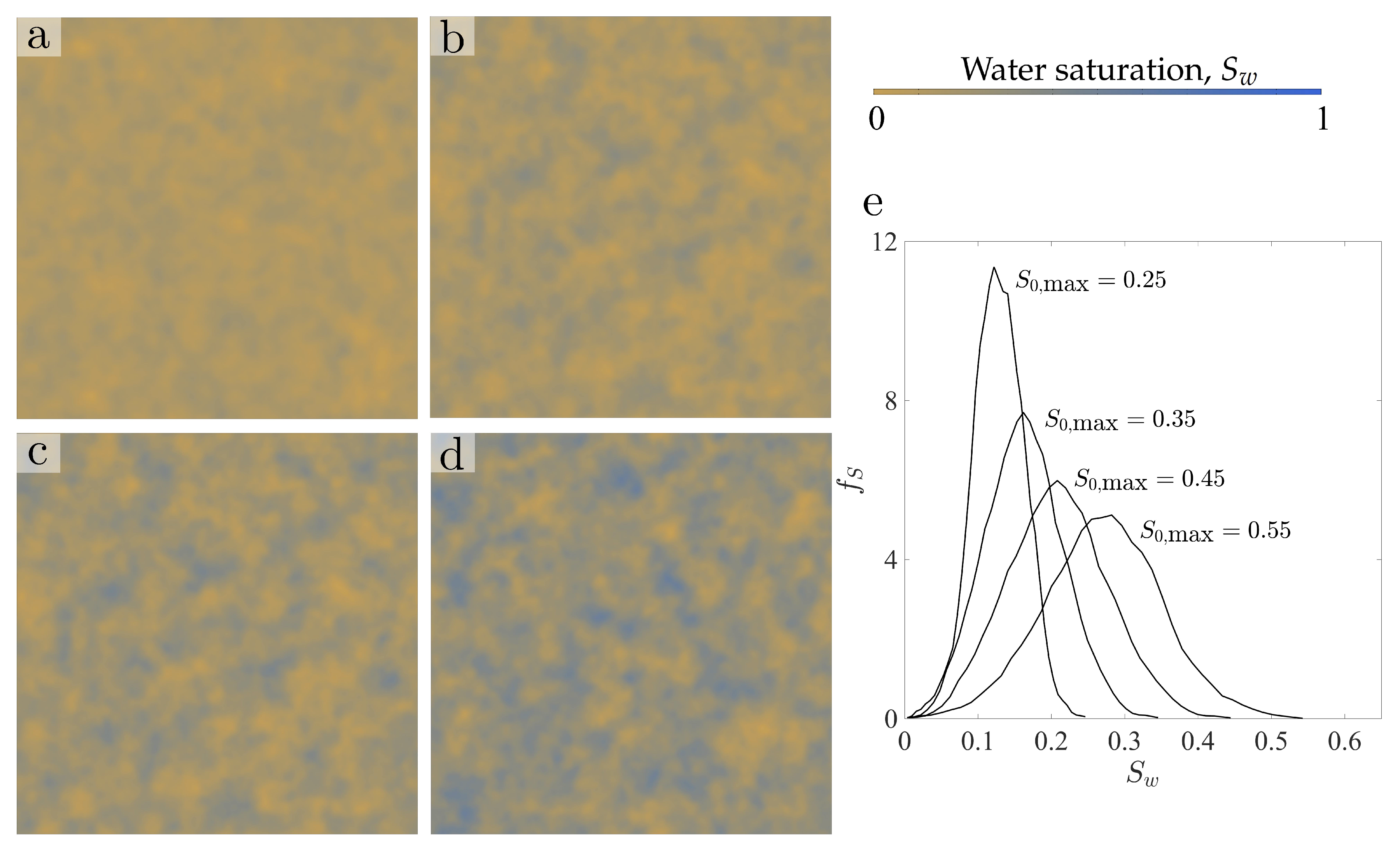
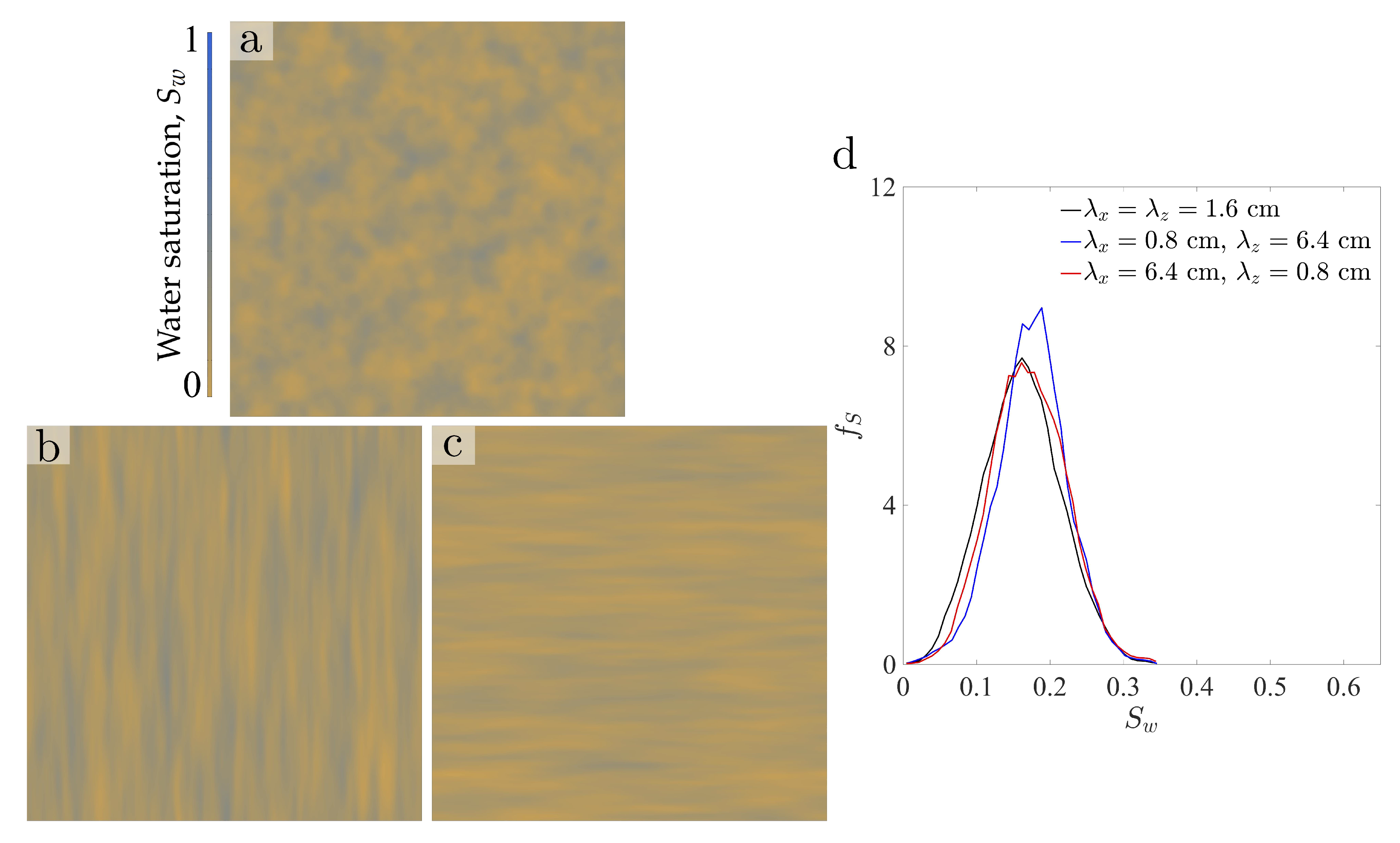
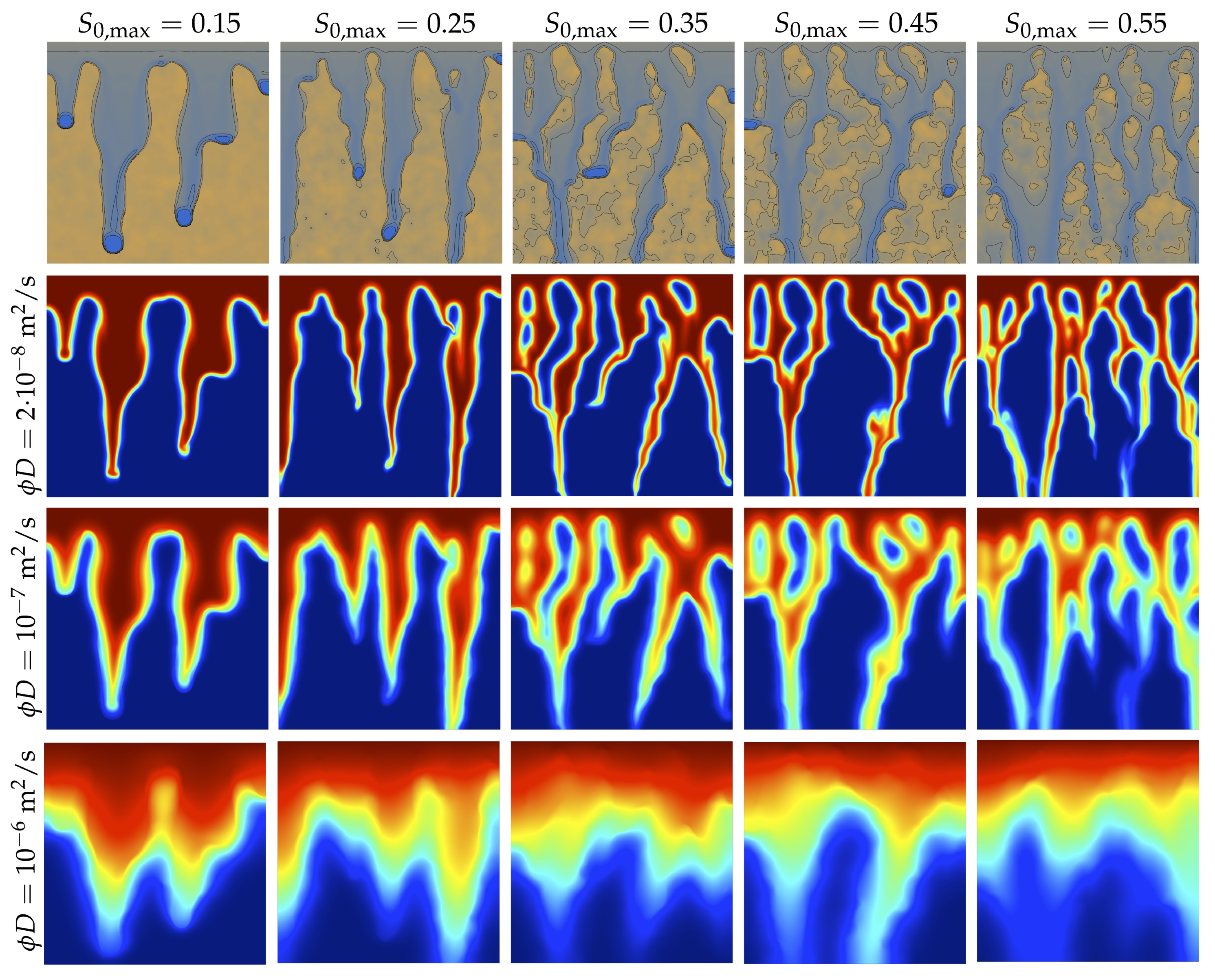
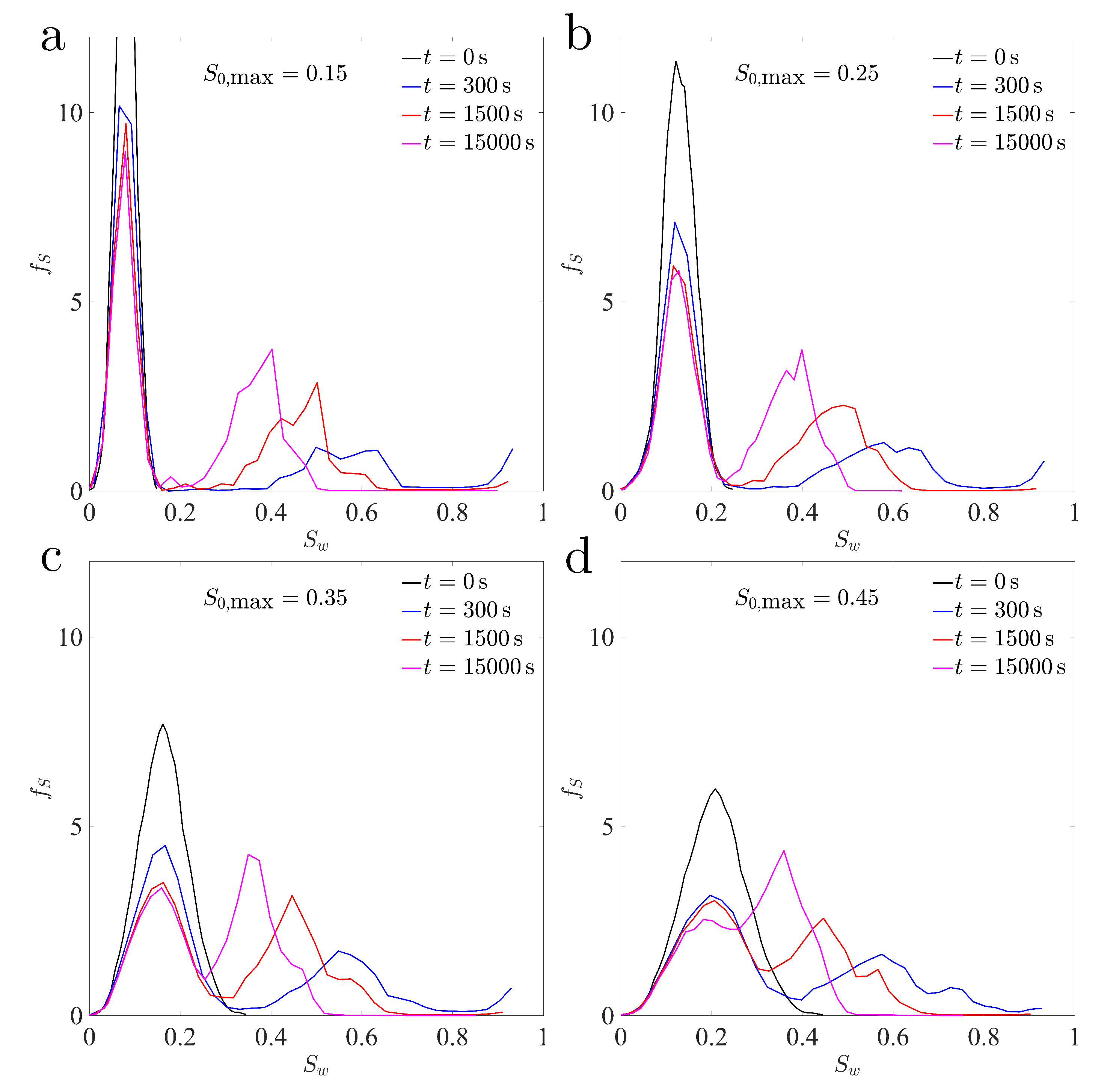
4.2. Statistics of the Initial Water Saturation Fields
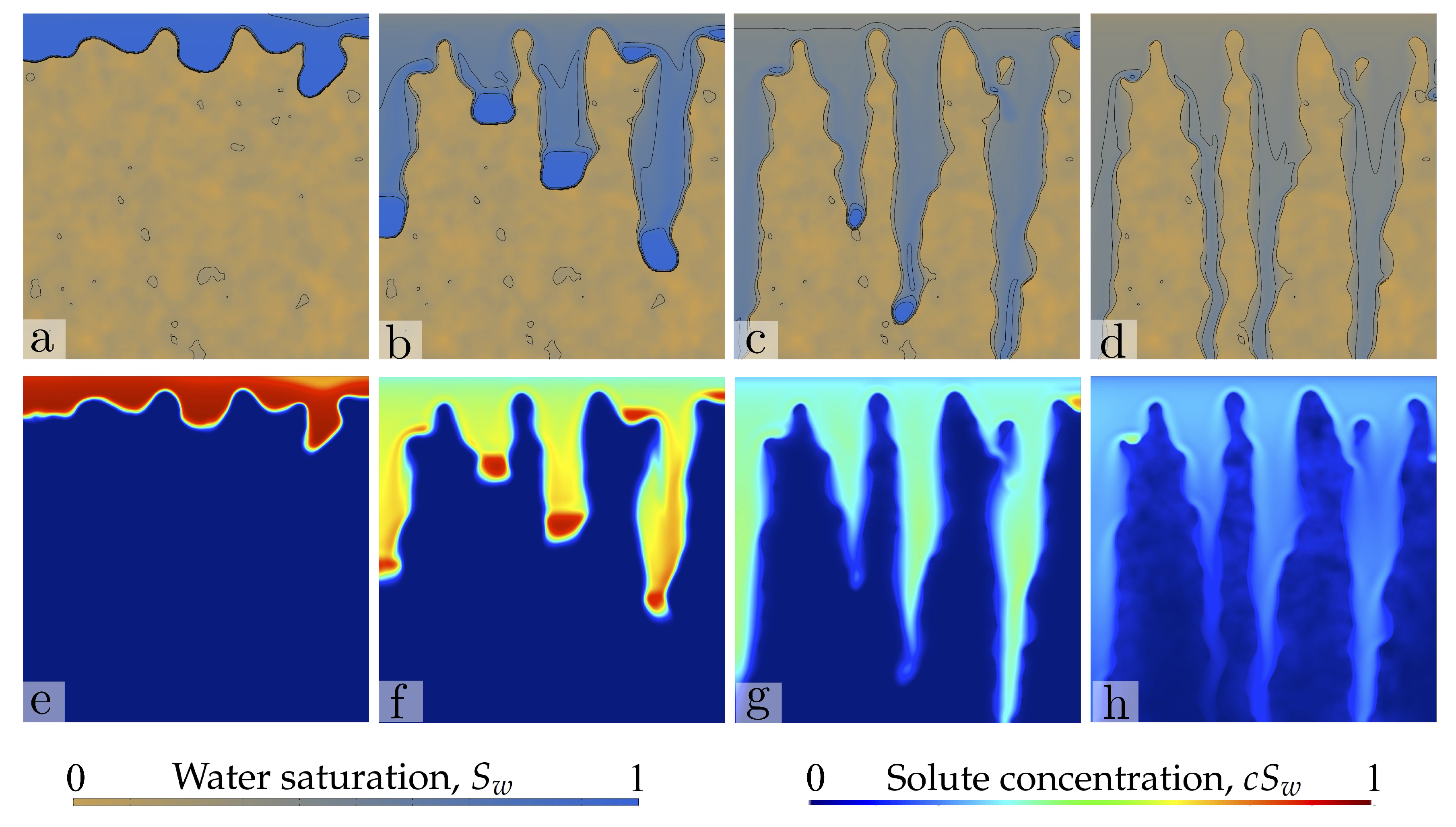
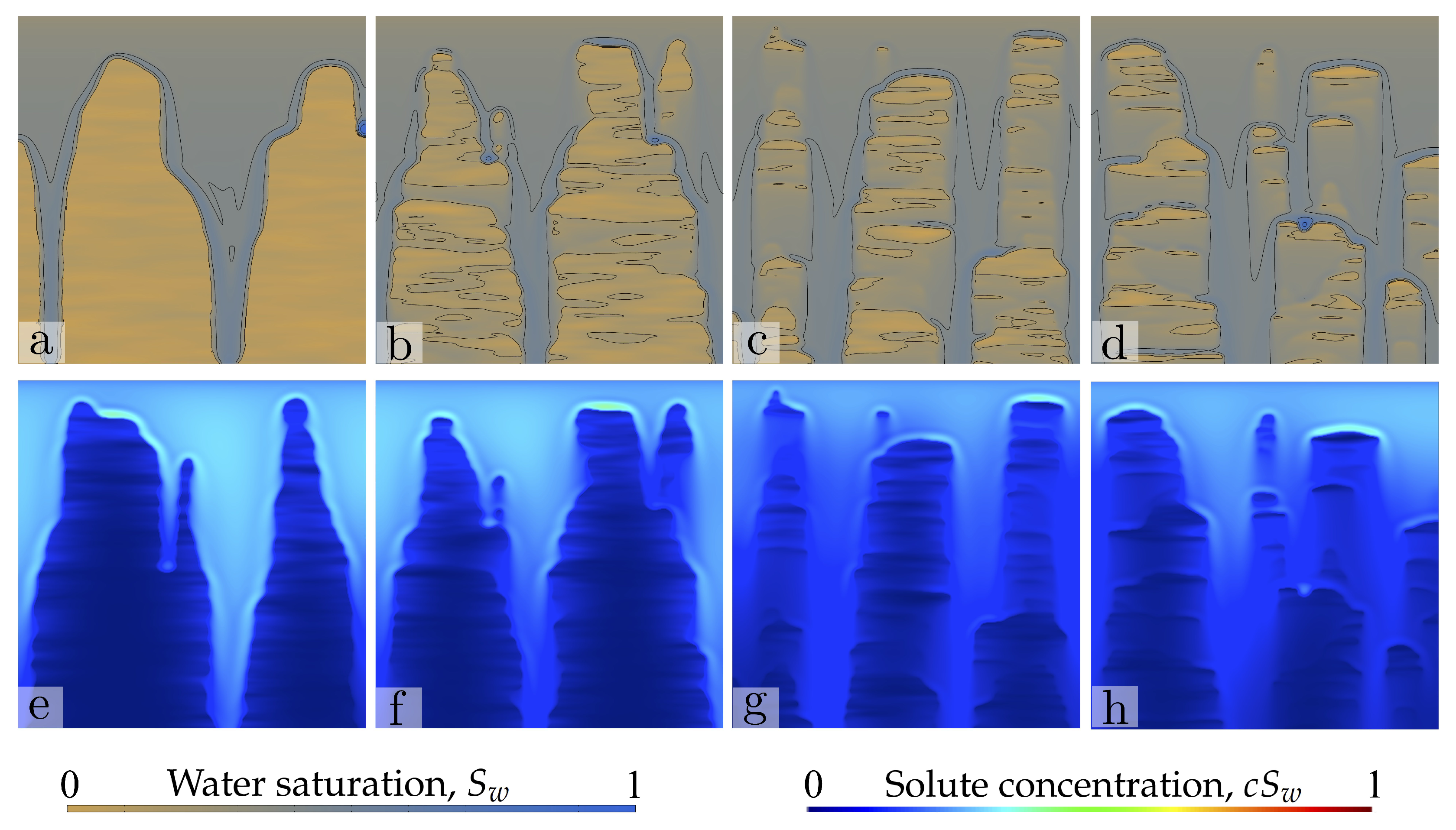
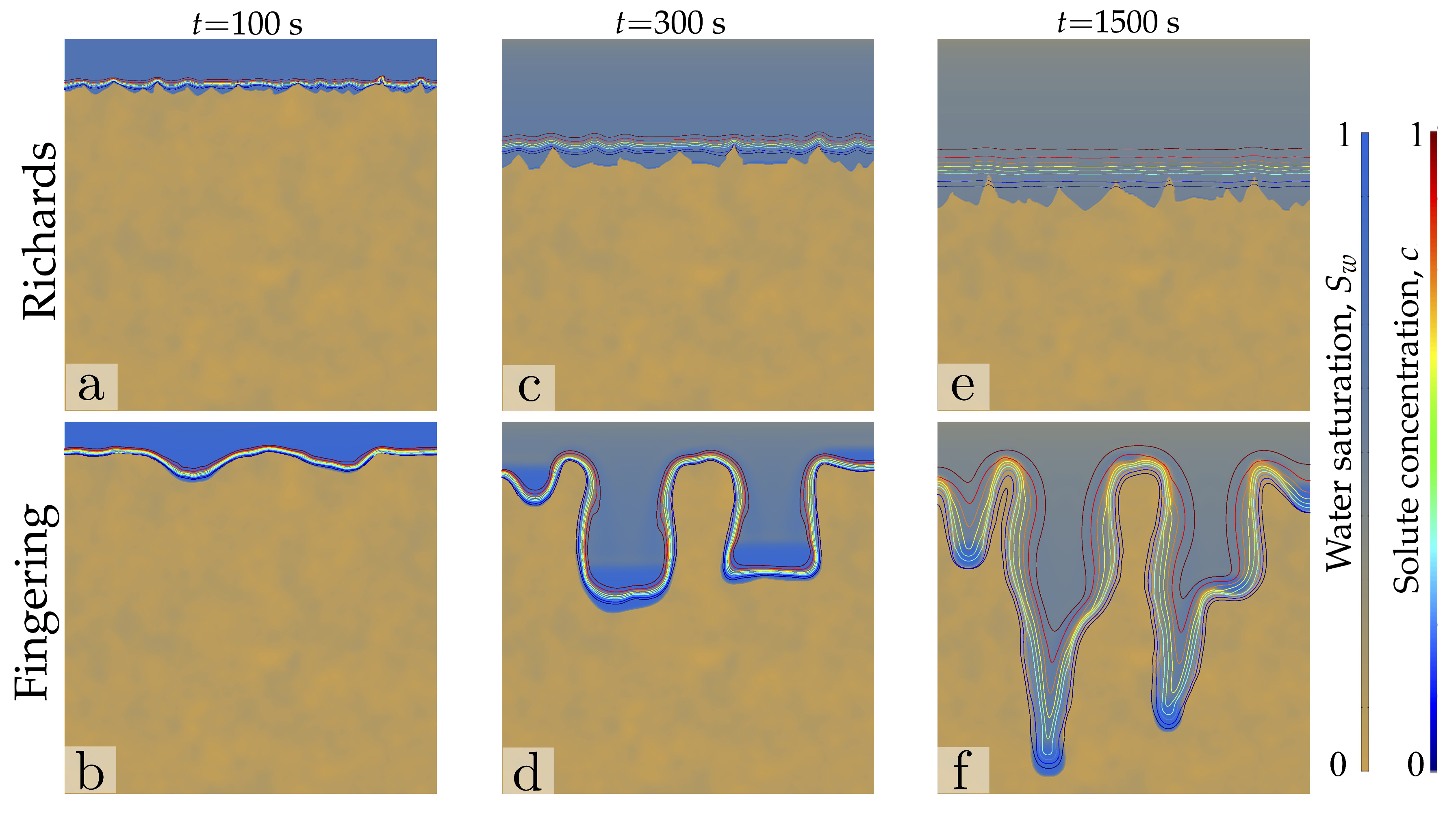
4.3. Sample Two-Dimensional Simulations
4.4. Analysis: Impact of the Spatial Structure of the iNitial Saturation Field on Water and Solute Transport
4.5. Analysis: Impact of the Solute Diffusivity/Dispersivity on the Effective Solute Dilution
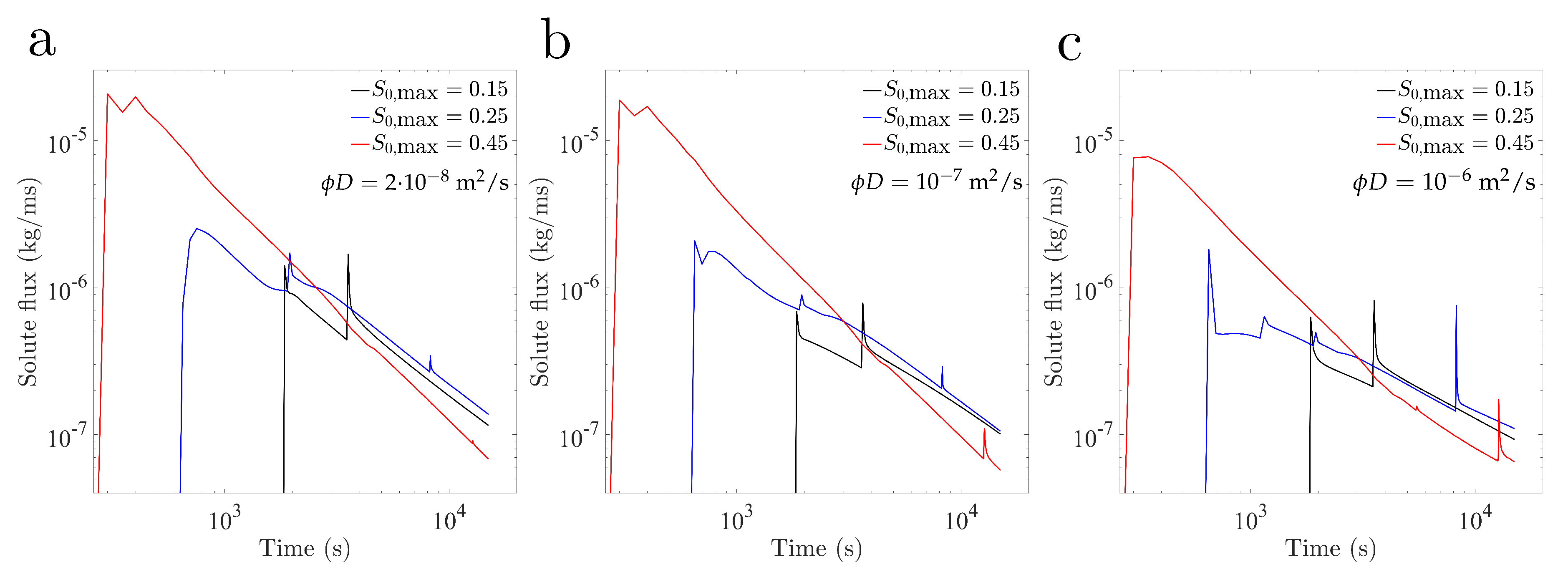
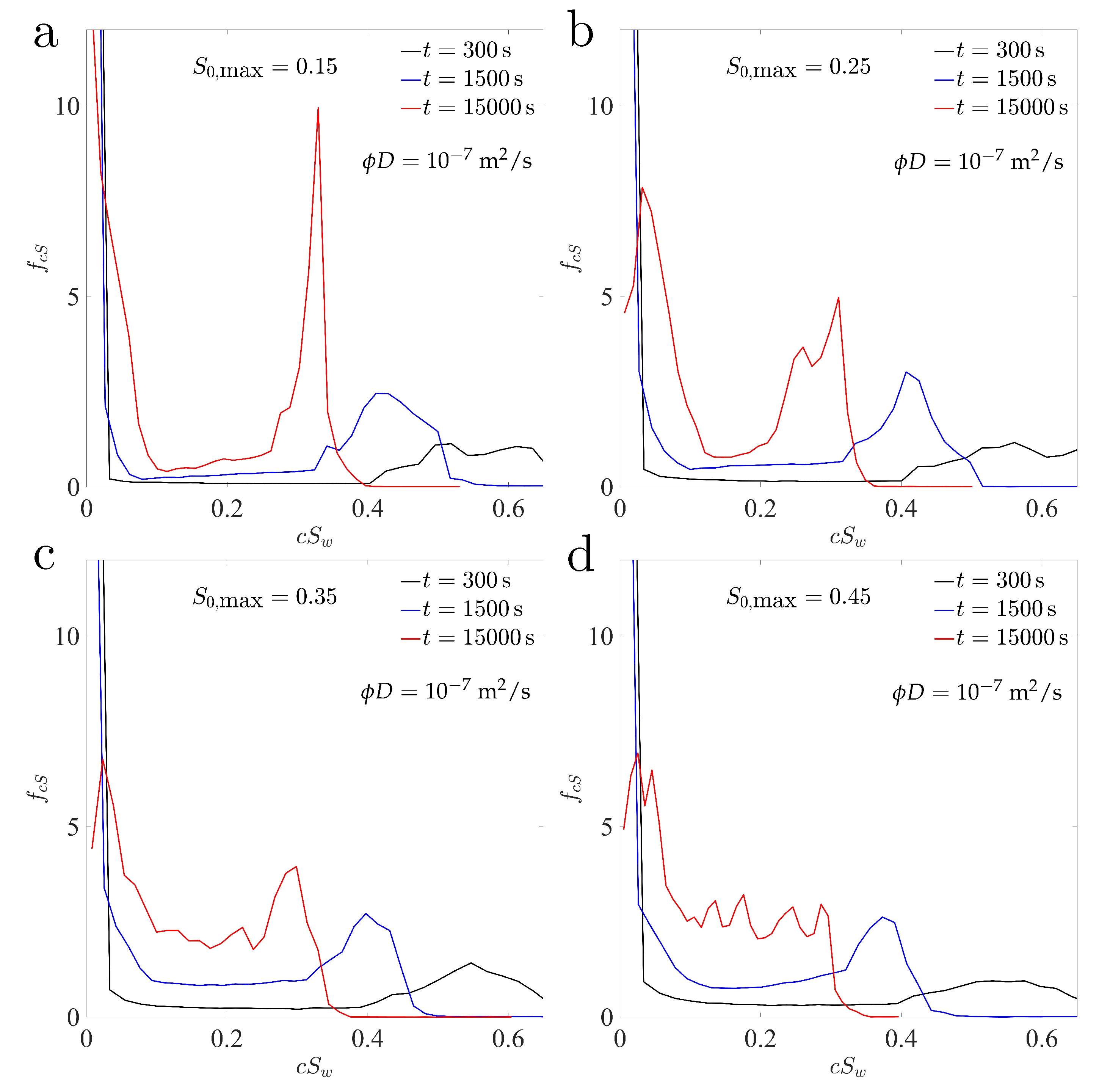
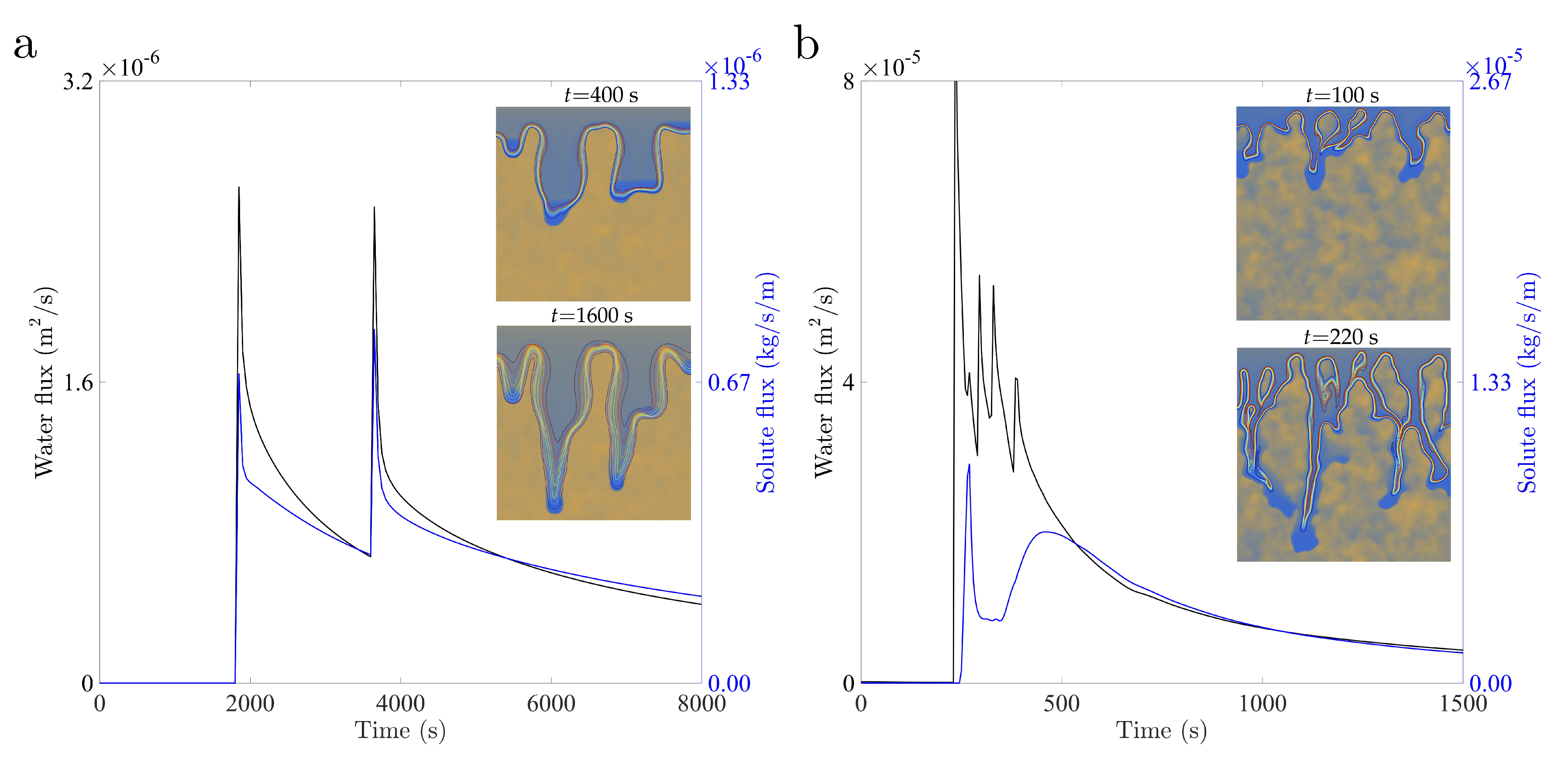
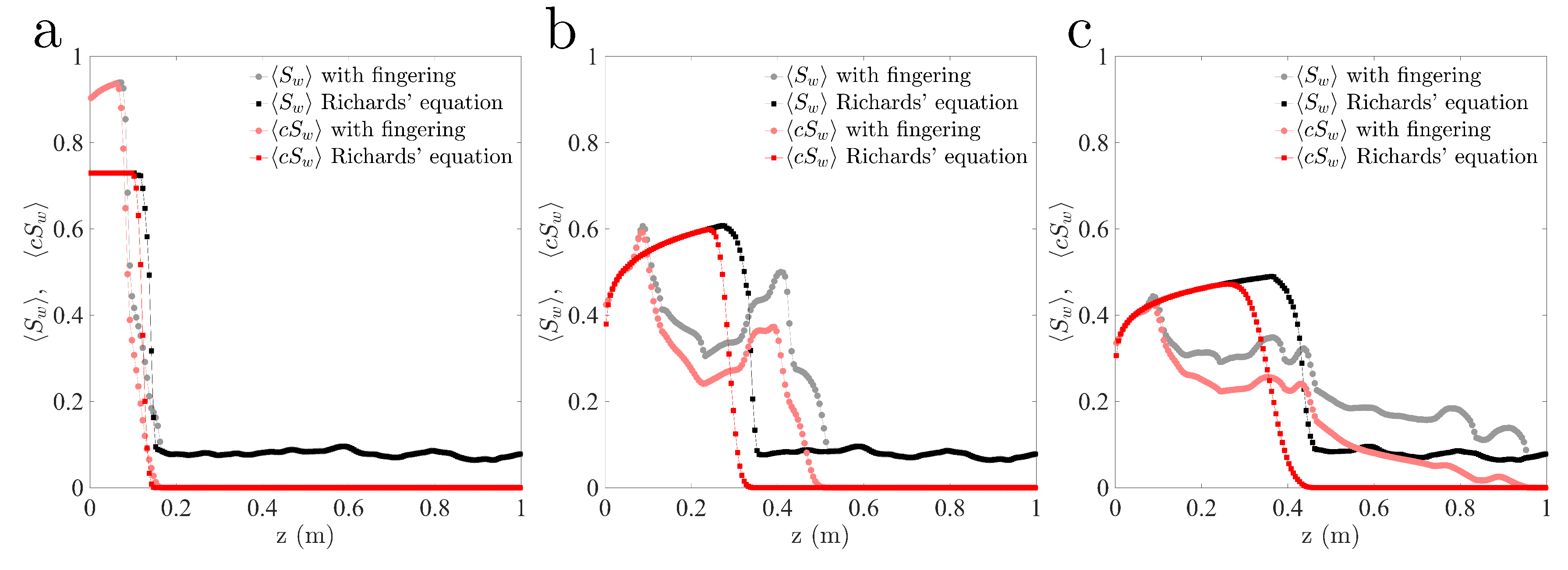
4.6. Analysis: Solute Fluxes and Overall Statistics of the Concentration and Saturation Fields
4.7. Solute Transport in Stable and Unstable Infiltration Fronts
5. Conclusions
- To the best of our knowledge, these are the first numerical simulations of solute transport during unstable infiltration into soil. We show that the patterns of water flow and solute transport arising from unstable infiltration are very different from those obtained using Richards’ equation, which predicts compact, stable front of water saturation and solute concentration.
- The initial water content and its spatial distribution play a key role in the patterns of water infiltration and solute transport in unsaturated coarse soil. The structure of initial freshwater saturation controls solute transport through two mechanisms: (1) the interplay between the fingering instability and the increased conductivity at the wet patches; (2) the lateral dilution of solute into the ambient water. The extent to which the former mechanism controls transport is related to the anisotropy of the initial water saturation field and to the maximum saturations at the water pockets. Isotropic distributions of low initial water saturation lead to the classical straight, downward-moving fingers, with finger sizes and spacing controlled by the internal hydrodynamic length scales. Isotropic fields with large saturation lead to complex infiltration patterns, with finger meandering and efficient solute dilution into the ambient water. Anisotropic fields with preferentially vertical correlation, combined with the fingering instability, promote focused transport and reduce mixing to the extent of lateral dilution due to solute diffusion/dispersion. Water pockets of lenticular shape thicken the finger size and induce lateral mixing of the solute. Lateral mixing becomes very efficient as the horizontal correlation length increases.
- The effective diffusivity/dispersivity of solute is particularly important for solute dilution in dry soils, or in those where the initial water saturation field induces flow focusing (vertical correlation). When the initial saturation field leads to complex infiltration patterns (the presence of water lenses or isotropic fields with large saturation), the flow field is complex and enhances mixing, leading to more efficient dilution.
- The integrated solute fluxes at the outlet (bottom of the domain) are consistent with the one-dimensional prediction of a delayed arrival of the solute when the soil is initially wet.
Author Contributions
Funding
Conflicts of Interest
References
- Nielsen, D.R.; van Genuchten, M.T.; Biggar, J.W. Water Flow and Solute Transport Processes in the Unsaturated Zone. Water Resour. Res. 1986, 22, 89S–108S. [Google Scholar] [CrossRef]
- Candela, L.; Caballero, J.; Ronen, D. Glyphosate transport through weathered granite soils under irrigated and non-irrigated conditions—Barcelona, Spain. Sci. Total Environ. 2010, 408, 2509–2516. [Google Scholar] [CrossRef]
- Botros, F.E.; Onsoy, Y.S.; Ginn, T.R.; Harter, T. Richards Equation-Based Modeling to Estimate Flow and Nitrate Transport in a Deep Alluvial Vadose Zone. Vadose Zone J. 2012, 11, 4–20. [Google Scholar] [CrossRef]
- Silber, A.; Israeli, Y.; Elingold, I.; Levi, M.; Levkovitch, I.; Russo, D.; Assouline, S. Irrigation with desalinated water: A step toward increasing water saving and crop yields. Water Resour. Res. 2015, 51, 450–464. [Google Scholar] [CrossRef]
- Valdes-Abellan, J.; Jiménez-Martínez, J.; Candela, L.; Jacques, D.; Kohfahl, C.; Tamoh, K. Reactive transport modelling to infer changes in soil hydraulic properties induced by non-conventional water irrigation. J. Hydrol. 2017, 549, 114–124. [Google Scholar] [CrossRef]
- Zhuang, J.; Tyner, J.S.; Perfect, E. Colloid transport and remobilization in porous media during infiltration and drainage. J. Hydrol. 2009, 377, 112–117. [Google Scholar] [CrossRef]
- Torkzaban, S.; Hassanizadeh, S.; Schijven, J.F.; de Bruin, A.M.; de Roda Husman, A.M. Virus transport in saturated and unsaturated sand columns. Vadose Zone J. 2006, 5, 877–885. [Google Scholar] [CrossRef]
- Zhang, Q.; Hassanizadeh, S.M.; Raoof, A.; van Genuchten, M.T.; Roels, S.M. Modeling Virus Transport and Remobilization during Transient Partially Saturated Flow. Vadose Zone J. 2012, 11. [Google Scholar] [CrossRef]
- Jiménez-Martínez, J.; de Anna, P.; Tabuteau, H.; Turuban, R.; Borgne, T.L.; Méheust, Y. Pore-scale mechanisms for the enhancement of mixing in unsaturated porous media and implications for chemical reactions. Geophys. Res. Lett. 2015, 42, 5316–5324. [Google Scholar] [CrossRef]
- Jiménez-Martínez, J.; Borgne, T.L.; Tabuteau, H.; Méheust, Y. Impact of saturation on dispersion and mixing in porous media: Photobleaching pulse injection experiments and shear-enhanced mixing model. Water Resour. Res. 2017, 53, 1457–1472. [Google Scholar] [CrossRef]
- Jiménez-Martínez, J.; Porter, M.L.; Hyman, J.D.; Carey, J.W.; Viswanathan, H.S. Mixing in a three-phase system: Enhanced production of oil-wet reservoirs by CO2 injection. Geophys. Res. Lett. 2016, 43, 196–205. [Google Scholar] [CrossRef]
- Russo, D.; Zaidel, J.; Laufer, A. Numerical analysis of flow and transport in a three–dimensional partially saturated heterogeneous soil. Water Resour. Res. 1998, 34, 1451–1468. [Google Scholar] [CrossRef]
- Starr, J.L.; Parlange, J.Y.; Frink, C.R. Water and chloride movement through a layered field soil. Soil Sci. Soc. Am. J. 1994, 50, 1384–1390. [Google Scholar] [CrossRef]
- Steenhuis, T.S.; Parlange, J.Y.; Andreini, M.S. A Numerical Model for Preferential Solute Movement in Structured Soils. Geoderma 1990, 46, 193–208. [Google Scholar] [CrossRef]
- Snow, V.O.; Clothier, B.E.; Scotter, D.R.; White, R.E. Solute transport in a layered field soil: Experiments and modelling using the convection-dispersion approach. J. Contaminant Hydrol. 1994, 16, 339–358. [Google Scholar] [CrossRef]
- Koestel, J.; Larsbo, M. Imaging and quantification of preferential solute transport in soil macropores. Water Resour. Res. 2014, 50, 4357–4378. [Google Scholar] [CrossRef]
- Jiménez-Martínez, J.; Tamoh, K.; Candela, L.; Elorza, F.; Hunkeler, D. Multiphase Transport of Tritium in Unsaturated Porous Media—Bare and Vegetated Soils. Math. Geosci. 2012, 44, 187–208. [Google Scholar] [CrossRef]
- Russo, D. Alternating irrigation water quality as a method to control solute concentrations and mass fluxes below irrigated fields: A numerical study. Water Resour. Res. 2016, 52, 3440–3456. [Google Scholar] [CrossRef]
- Russo, D. Effect of pulse release date and soil characteristics on solute transport in a combined vadose zone-groundwater flow system: Insights from numerical simulations. Water Resour. Res. 2011, 47, W05532. [Google Scholar] [CrossRef]
- Richards, L.A. Capillary conduction of liquids through porous mediums. Physics 1931, 1, 318–333. [Google Scholar] [CrossRef]
- Horton, R.E. The role of infiltration in the hydrologic cycle. Trans. Am. Geophys. Union 1933, 14, 446–460. [Google Scholar] [CrossRef]
- Philip, J.R. The theory of infiltration 1. The infiltration equation and its solution. Soil Sci. 1957, 83, 345–357. [Google Scholar] [CrossRef]
- Philip, J.R. Theory of infiltration. In Advances in Hydroscience; Chow, V.T., Ed.; Academic Press: New York, NY, USA, 1969; pp. 215–296. [Google Scholar]
- Jiménez-Martínez, J.; Skaggs, T.; van Genuchten, M.; Candela, L. A root zone modelling approach to estimating groundwater recharge from irrigated areas. J. Hydrol. 2009, 367, 138–149. [Google Scholar] [CrossRef]
- Jiménez-Martínez, J.; Candela, L.; Molinero, J.; Tamoh, K. Groundwater recharge in irrigated semi-arid areas: quantitative hydrological modelling and sensitivity analysis. Hydrogeol. J. 2010, 18, 1811–1824. [Google Scholar] [CrossRef]
- Šimůnek, J.; Jarvis, N.J.; van Genuchten, M.T.; Gärdenäs, A. Review and comparison of models for describing non-equilibrium and preferential flow and transport in the vadose zone. J. Hydrol. 2003, 272, 14–35. [Google Scholar] [CrossRef]
- Russo, D.; Laufer, A.; Gerstl, Z.; Ronen, D.; Weisbrod, N.; Zentner, E. On the mechanism of field-scale solute transport: Insights from numerical simulations and field observations. Water Resour. Res. 2014, 50, 7484–7504. [Google Scholar] [CrossRef]
- Šimůnek, J.; van Genuchten, M.T. Modeling Nonequilibrium Flow and Transport Processes Using HYDRUS. Vadose Zone J. 2008, 7, 782–797. [Google Scholar] [CrossRef]
- Raoof, A.; Hassanizadeh, S.M.; Leijnse, A. Upscaling Transport of Adsorbing Solutes in Porous Media: Pore-Network Modeling. Vadose Zone J. 2010, 9, 624–636. [Google Scholar] [CrossRef]
- Raoof, A.; Hassanizadeh, S.M. Saturation-dependent solute dispersivity in porous media: Pore-scale processes. Water Resour. Res. 2013, 49, 1943–1951. [Google Scholar] [CrossRef]
- de Vries, E.T.; Raoof, A.; van Genuchten, M.T. Multiscale modelling of dual-porosity porous media; a computational pore-scale study for flow and solute transport. Adv. Water Resour. 2017, 105, 82–95. [Google Scholar] [CrossRef]
- Szymkiewicz, A.; Gumuła-Kawęcka, A.; Potrykus, D.; Jaworska-Szulc, B.; Pruszkowska-Caceres, M.; Gorczewska-Langner, W. Estimation of Conservative Contaminant Travel Time through Vadose Zone Based on Transient and Steady Flow Approaches. Water 2018, 10, 1417. [Google Scholar] [CrossRef]
- Hill, D.E.; Parlange, J.Y. Wetting front instability in layered soils. Soil Sci. Soc. Am. J. 1972, 36, 697–702. [Google Scholar] [CrossRef]
- Glass, R.J.; Parlange, J.Y.; Steenhuis, T.S. Wetting front instability, 2. Experimental determination of relationships between system parameters and two-dimensional unstable flow field behaviour in initially dry porous media. Water Resour. Res. 1989, 25, 1195–1207. [Google Scholar] [CrossRef]
- Ritsema, C.J.; Dekker, L.W.; Nieber, J.L.; Steenhuis, T.S. Modeling and field evidence of finger formation and finger recurrence in a water repellent sandy soil. Water Resour. Res. 1998, 34, 555–567. [Google Scholar] [CrossRef]
- DiCarlo, D.A. Stability of gravity-driven multiphase flow in porous media: 40 years of advancements. Water Resour. Res. 2013, 49, 4531–4544. [Google Scholar] [CrossRef]
- Xiong, Y. Flow of water in porous media with saturation overshoot: A review. J. Hydrol. 2014, 510, 353–362. [Google Scholar] [CrossRef]
- Glass, R.J.; Oosting, G.H.; Steenhuis, T.S. Preferential solute transport in layered homogeneous sands as a consequence of wetting front instability. J. Hydrol. 1989, 110, 87–105. [Google Scholar] [CrossRef]
- Muskat, M.; Meres, M.W. The flow of heterogeneous fluids through porous media. Physics 1936, 7, 346–363. [Google Scholar] [CrossRef]
- Muskat, M. Physical Principles of Oil Production; McGraw-Hill: New York, NY, USA, 1949. [Google Scholar]
- Bear, J. Dynamics of Fluids in Porous Media; Elsevier: New York, NY, USA, 1972. [Google Scholar]
- Cueto-Felgueroso, L.; Juanes, R. Nonlocal interface dynamics and pattern formation in gravity-driven unsaturated flow through porous media. Phys. Rev. Lett. 2008, 101, 244504. [Google Scholar] [CrossRef]
- Cueto-Felgueroso, L.; Juanes, R. A phase-field model of unsaturated flow. Water Resour. Res. 2009, 45, W10409. [Google Scholar] [CrossRef]
- Sciarra, G. Phase field modeling of partially saturated deformable porous media. J. Mech. Phys. Solids 2016, 94, 230–256. [Google Scholar] [CrossRef]
- Beljadid, A.; Cueto-Felgueroso, L.; Juanes, R. A continuum model of unstable infiltration in porous media endowed with an entropy function. Adv. Water Resour. 2019. in review. [Google Scholar]
- Leverett, M.C. Capillary behavior of porous solids. Petrol. Trans. AIME 1941, 142, 152–169. [Google Scholar] [CrossRef]
- Aavatsmark, I. Capillary energy and the entropy condition for the Buckley-Leverett equation. In Current Progress in Hyperbolic Systems: Riemann Problems and Computations; Contemporary Mathematics; Lindquist, W.B., Ed.; American Mathematical Society: Providence, RI, USA, 1989; Volume 100, pp. 21–25. [Google Scholar]
- Aavatsmark, I. Kapillarenergie als Entropiefunktion. Z. Angew. Math. Mech. 1989, 69, 319–327. [Google Scholar] [CrossRef]
- COMSOL. COMSOL Multiphysics Structural Mechanics Module User’s Guide v5.2a; Comsol: Stockholm, Sweden, 2016. [Google Scholar]
- Brooks, R.H.; Corey, A.T. Properties of porous media affecting fluid flow. J. Irrig. Drain. Div. Proc. Am. Soc. Civ. Eng. 1966, IR2, 61–88. [Google Scholar]
- van Genuchten, M.T. A closed-form equation for predicting the hydraulic conductivity of unsaturated soils. Soil Sci. Soc. Am. J. 1980, 44, 892–898. [Google Scholar] [CrossRef]
- Gelhar, L.W.; Axness, C.L. Three-Dimensional Stochastic Analysis of Macrodispersion in Aquifers. Water Resour. Res. 1983, 19, 161–180. [Google Scholar] [CrossRef]
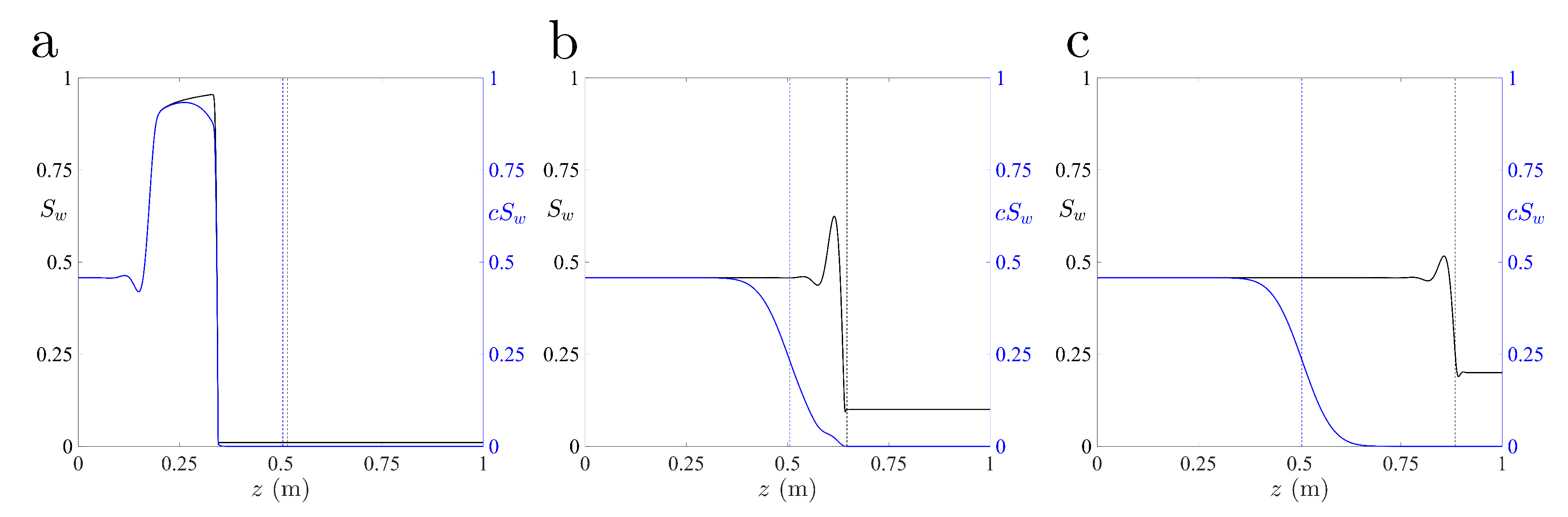



| Name | Value | Unit | Description |
|---|---|---|---|
| 0.3 | – | Soil porosity | |
| 1000 | kg/m | Water density | |
| 0.001 | Pa·s | Water viscosity | |
| g | 9.81 | m/s | Acceleration of gravity |
| 0.01 | – | Minimum initial water saturation | |
| – | Maximum initial water saturation | ||
| [0.8,6.4] | cm | Horizontal correlation length | |
| [0.8,12.8] | cm | Vertical correlation length | |
| m | Capillary height | ||
| 40 | cm/min | Saturated hydraulic conductivity | |
| – | Effective water saturation | ||
| 0.1 | – | Irreducible water saturation | |
| – | Flux ratio (top boundary) | ||
| – | Relative permeability function | ||
| J | – | Leverett J-function | |
| m | Gradient energy multiplier | ||
| m | Characteristic gradient energy length | ||
| a | 7 | – | Exponent of relative permeability function |
| 10 | – | Parameter of the Leverett J-function | |
| 40 | – | Parameter of the Leverett J-function | |
| 1 | – | Parameter of the Leverett J-function | |
| 2· | m/s | Effective solute diffusivity/dispersivity |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Cueto-Felgueroso, L.; Suarez-Navarro, M.J.; Fu, X.; Juanes, R. Interplay between Fingering Instabilities and Initial Soil Moisture in Solute Transport through the Vadose Zone. Water 2020, 12, 917. https://doi.org/10.3390/w12030917
Cueto-Felgueroso L, Suarez-Navarro MJ, Fu X, Juanes R. Interplay between Fingering Instabilities and Initial Soil Moisture in Solute Transport through the Vadose Zone. Water. 2020; 12(3):917. https://doi.org/10.3390/w12030917
Chicago/Turabian StyleCueto-Felgueroso, Luis, María José Suarez-Navarro, Xiaojing Fu, and Ruben Juanes. 2020. "Interplay between Fingering Instabilities and Initial Soil Moisture in Solute Transport through the Vadose Zone" Water 12, no. 3: 917. https://doi.org/10.3390/w12030917
APA StyleCueto-Felgueroso, L., Suarez-Navarro, M. J., Fu, X., & Juanes, R. (2020). Interplay between Fingering Instabilities and Initial Soil Moisture in Solute Transport through the Vadose Zone. Water, 12(3), 917. https://doi.org/10.3390/w12030917





