Studying Unimodal, Bimodal, PDI and Bimodal-PDI Variants of Multiple Soil Water Retention Models: II. Evaluation of Parametric Pedotransfer Functions Against Direct Fits
Abstract
1. Introduction
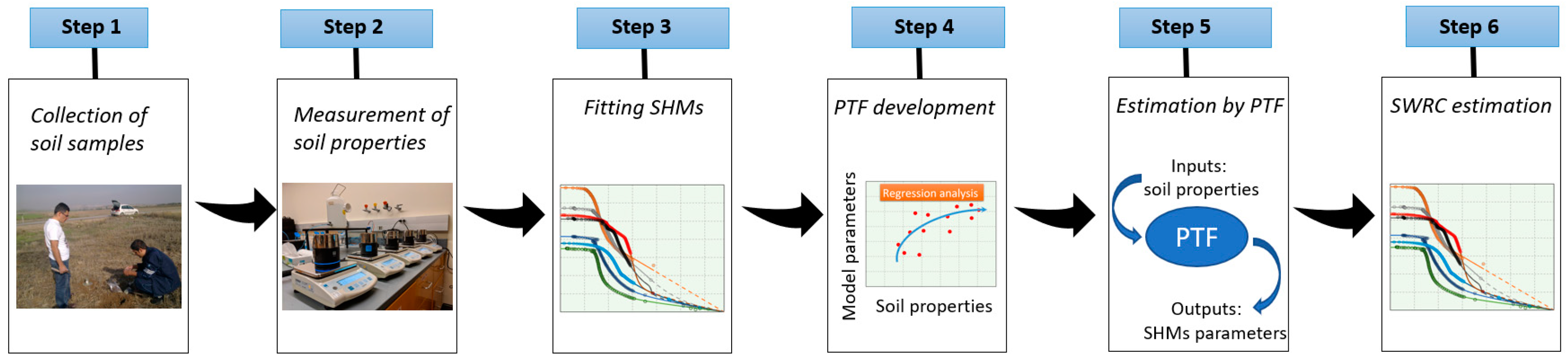
2. Materials and Methods
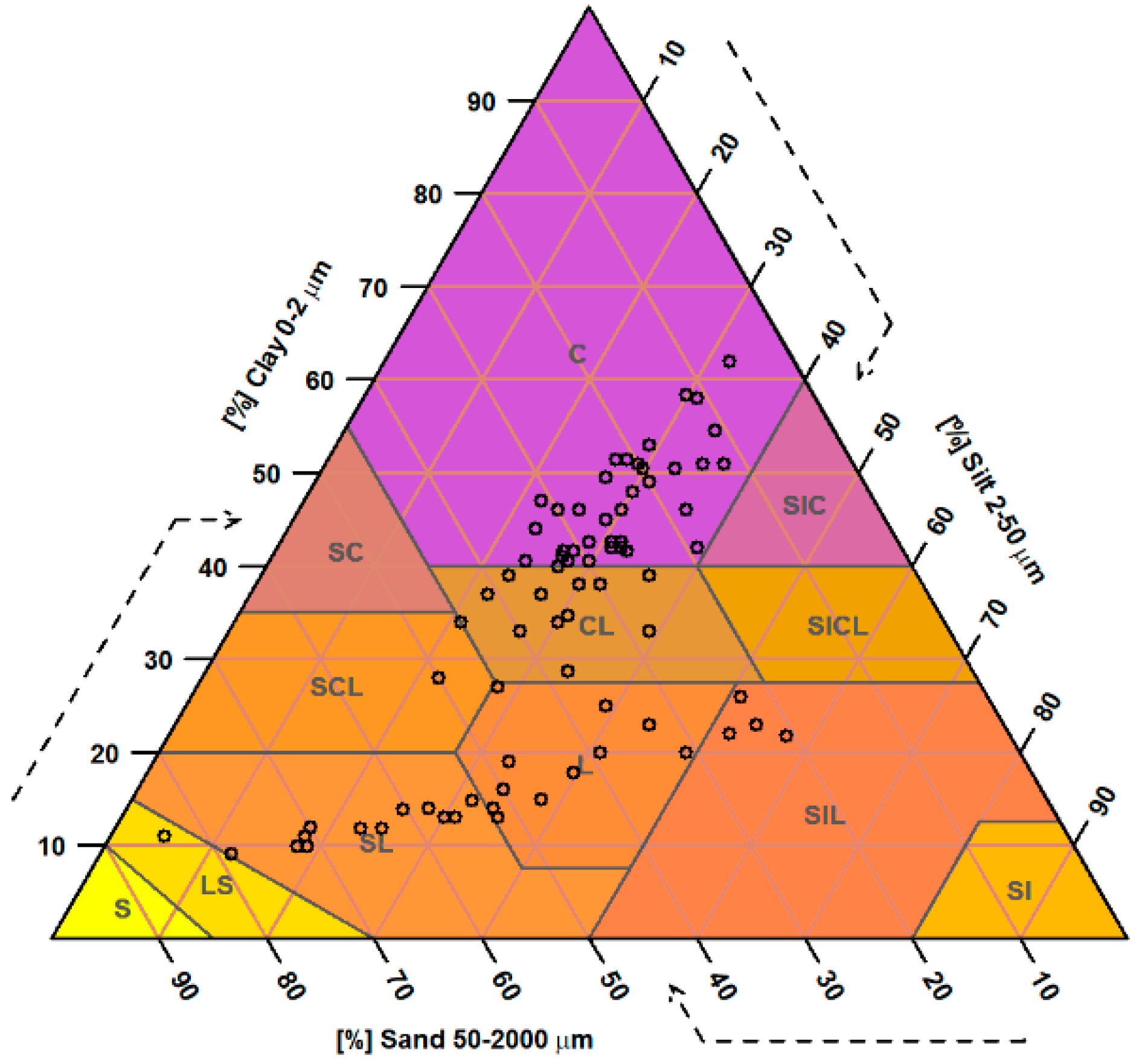
2.1. Data Collection and Laboratory Analyses
2.2. SWRC Parametrization
2.3. Developing Parametric Pedotransfer Functions
2.4. Evaluation Criteria
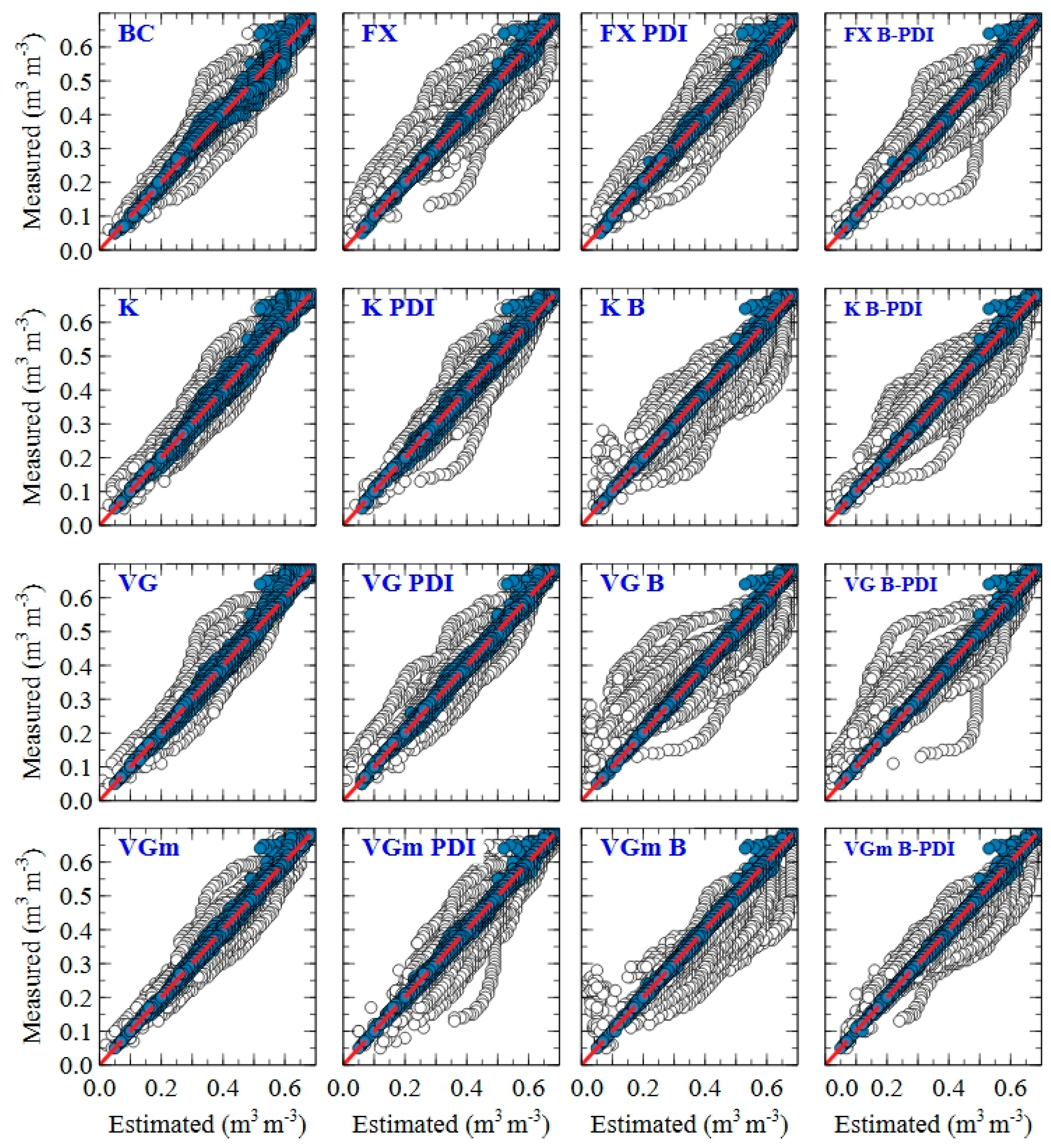
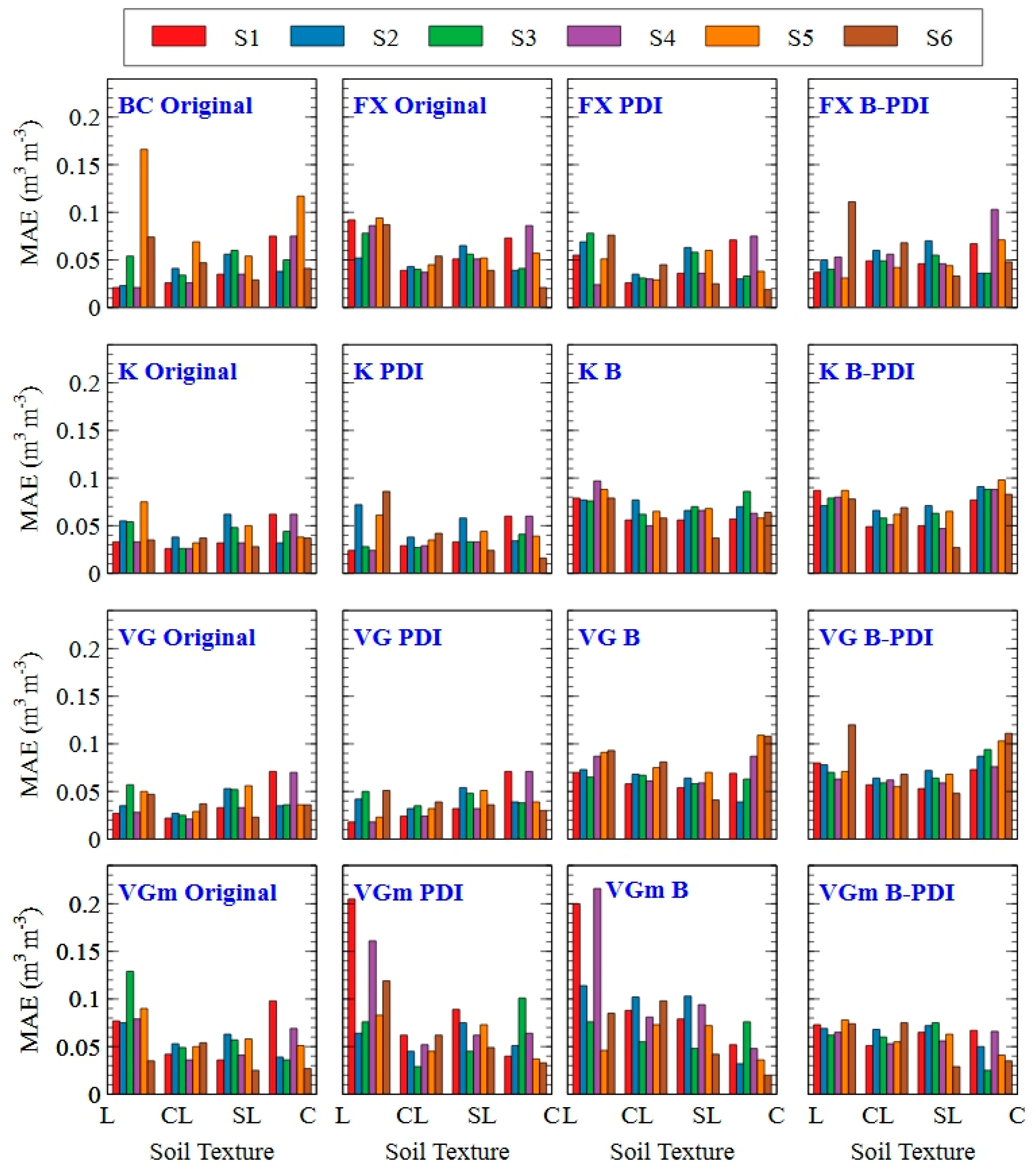
3. Results
3.1. Overall Performance of the Models
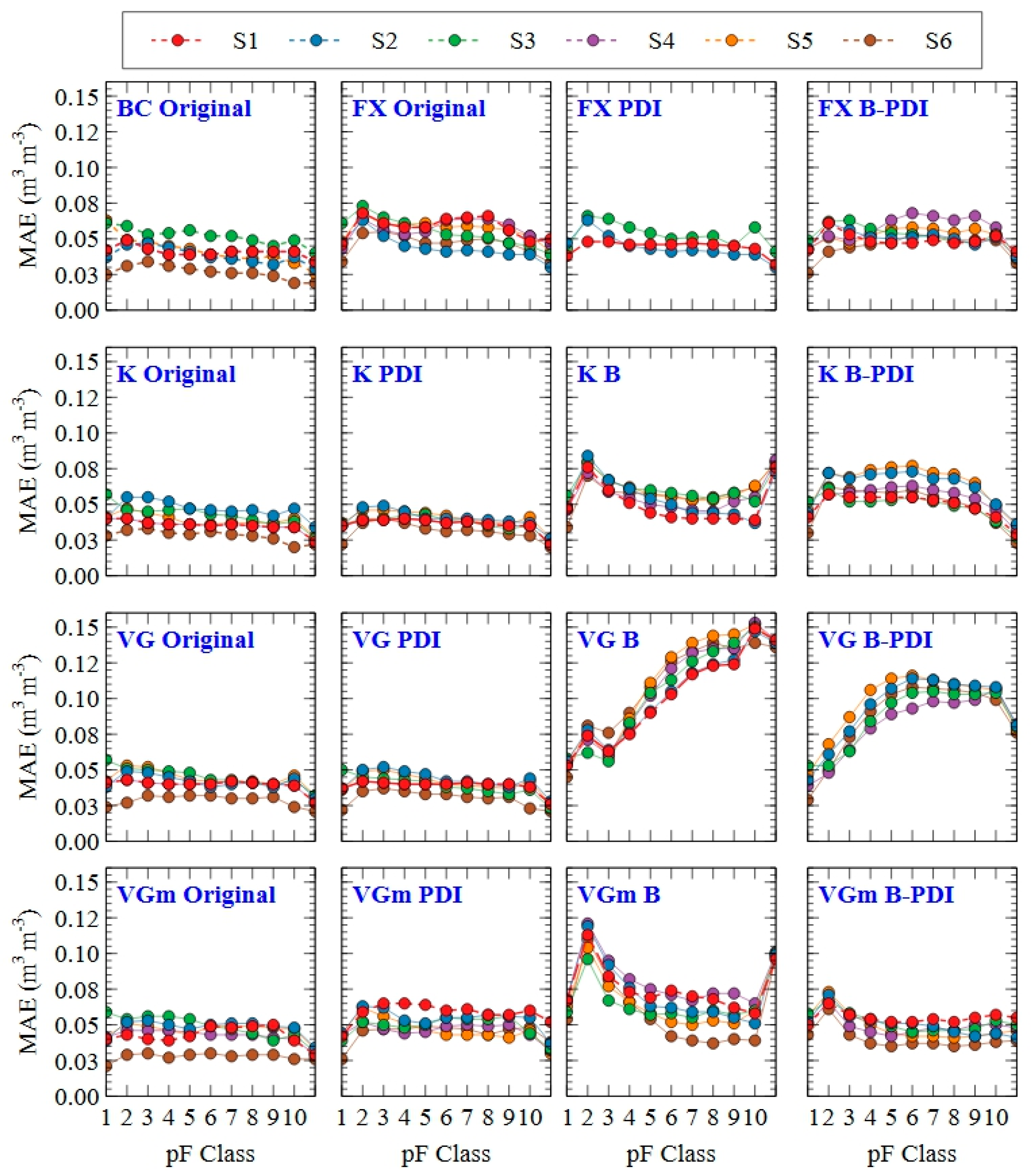
3.2. Performance across Textural and Tension Classes
4. Discussion
4.1. Overall Performance of the Parametric PTFs
4.2. Performance Across Soil Textures and Tension Classes
4.3. Importance of the Input Parameters
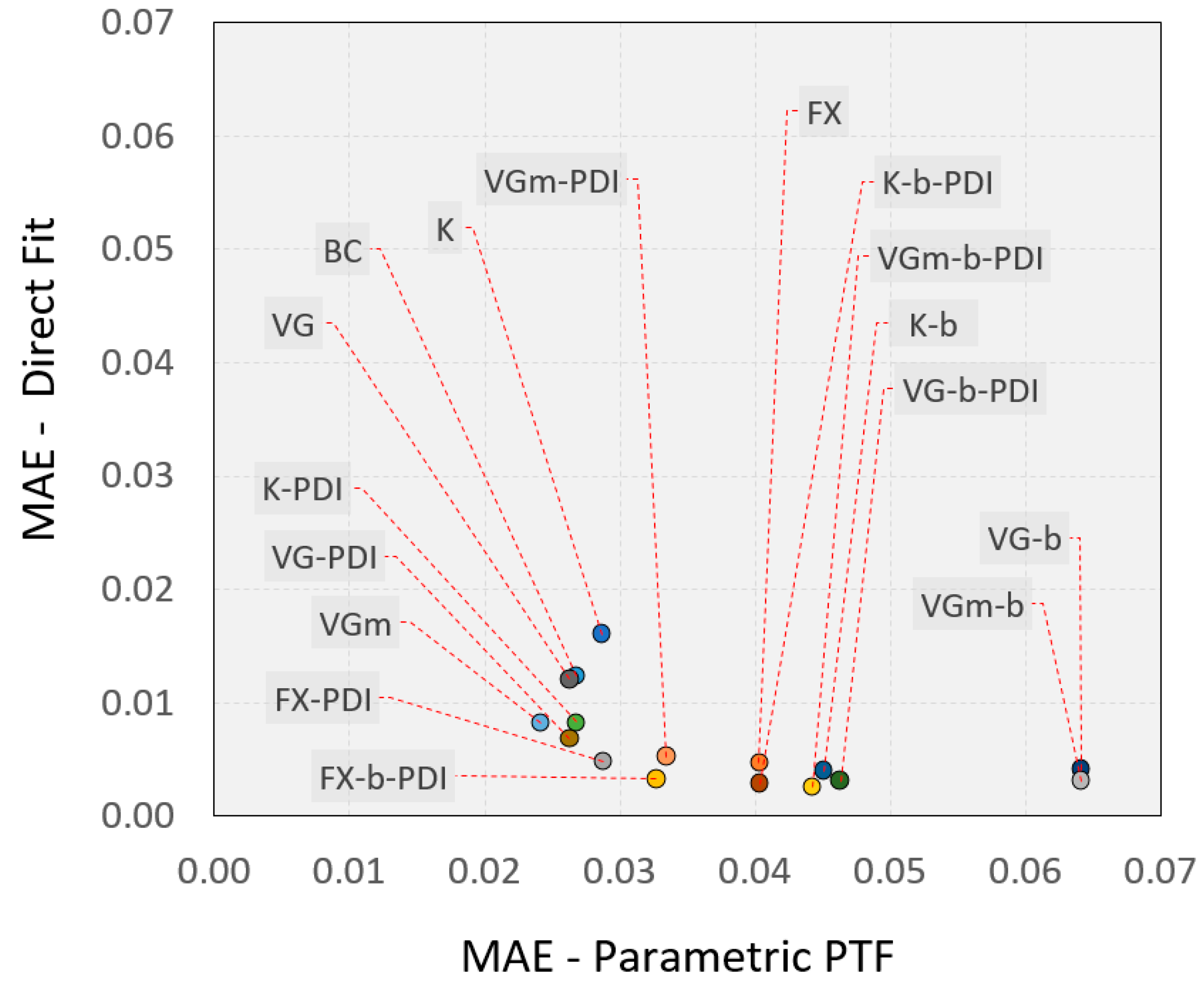
4.4. Fitted versus Parametric PTF Estimated SWRC
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
Appendix A
Appendix A.1. Unimodal Expressions:
Appendix A.2. PDI Expressions:
Appendix A.3. Bimodal Expressions:
Appendix A.4. Bimodal-PDI Expressions:
Appendix B
| par | Equation | |
|---|---|---|
| BC | log(α) | S1, S2, S4→ −0.959 − 4.542(Silt) − 2.868(Clay2) + 11.817(Clay)(Silt) S3→ −1.009 − 4.614(Silt) + 0.050(SOM) − 2.838(Clay2) + 11.885(Clay)(Silt) S5→ −0.663 − 1.940(Silt) − 0.321(BD2) + 1.402(Clay2) + 0.063(BD)(SOM) − 0.133(Clay)(SOM) S6→ −1.273 − 3.199(Silt2) − 2.670(Clay2) − 1.419(BD)(Silt) + 9.453(Clay)(Silt) |
| λ | S1, S4→ 0.398 + 0.003(Silt) + 0.682(Clay)(Silt) S2→ 0.506 + 0.477(Clay) − 0.777(BD)(Clay) − 0.086(BD)(Silt) S3→ 0.371 − 0.113(Clay)(SOM) + 0.004(Silt)(SOM) S5→ 0.501 + 0.561(Clay) + 0.001(SA) − 1.84 × 10 − 5(SA2) − 0.833(BD)(Clay) − 0.086 (Silt)(SOM) S6→ 0.983 − 0.754(BD)(θS) − 0.284(BD)(Clay) | |
| θr | S1, S3, & S4→ 0.028 − 0.194(Silt2) + 0.434(Clay2) S2 & S5→ 0.308 − 0.109(BD2) − 0.055(Clay2) − 0.165(BD)(Silt) S6→ 0.068 + 0.640(θS2) − 0.283(BD)(θS) − 0.066(Silt)(SOM) | |
| θs | S1 & S4→ 0.446 + 1.358(Clay)(Silt) S2→ 0.781 − 0.135(BD2) + 0.124(Clay2) S3→ 0.305 + 1.319(Silt) − 1.895(Silt2) + 0.178(Clay)(SOM) S5→ 0.694 + 0.085(SOM) − 0.157(BD2) + 7.06 × 10−6(SA2) + 0.264(BD)(Clay) − 0.187(Clay)(SOM) − 0.001(Silt)(SA) | |
| FX | Log(α) | S1, S4→ −2.036 − 6.063(Silt2) − 1.077(Clay2) + 9.015(Clay)(Silt) S2→ −1.856 + 1.671(BD)(Clay) − 1.764(BD)(Silt) S3→ −1.894 − 4.431(Silt2) − 1.573(Clay2) + 9.542(Clay)(Silt) − 0.773(Silt)(SOM) S5→ −1.769 − 5.589(Silt2) − 1.268(Clay2) − 0.149(BD)(SOM) + 8.405(Clay)(Silt) S6→ −1.555 − 8.899(Silt2) − 0.121(BD)(SOM) − 5.501(θS)(Clay) + 18.627(Clay)(Silt) |
| Log(n) | S1, S3→ 0.319 − 0.758(Silt2) + 1.533(Clay2) S2→ 1.051 + 4.176(Silt2) − 2.709(BD)(Silt) S4→ 0.475 − 0.541(Silt) + 0.012(Clay)(SA) S5, S6→ 0.767 + 0.454(SOM) − 0.587(BD)(Silt) − 0.426(BD)(SOM) | |
| Log(hr) | S1, S3→ 2.661 − 1.679(Clay) − 0.094(Silt) + 2.013(Clay2) S2→ −1.420(Clay) + 1.426(Clay2) − 0.400(BD)(Silt) S4→ 2.090 + 0.023(SA) + 3.378(Silt2) + 0.176(Clay2) − 5.061(Clay)(Silt) − 0.032(Silt)(SA) S5→ 2.775 − 1.420(Clay) + 1.426(Clay2) − 0.400(BD)(Silt) S6→ 2.666 − 0.007(SA) − 0.059(SOM2) + 3.59 × 10 −4(SA2) − 2.656(θS)(Clay) + 0.610(Clay)(SOM) − 0.016(Silt)(SA) | |
| θs | S1, S4→ 0.455 + 1.322(Clay)(Silt) S2→ 0.792 − 0.136(BD2) + 0.093(Clay2) S3→ 0.311 + 1.296(Silt) − 1.818(Silt2) + 0.175(Clay)(SOM) S5→ 0.811 + 0.036(SOM) − 0.163(BD2) − 0.020(Clay)(SOM) | |
| m | S1, S3, S4→ 0.231 + 3.236(Silt) + 2.688(Clay2) − 10.96(Clay)(Silt) S2, S5→ 0.584 − 2.013(Clay) + 1.452(BD)(Silt) + 3.685(Clay2) − 4.835(Clay)(Silt) S6→ 2.133 − 3.130(θS) + 0.453(Silt)(SOM) | |
| FX-PDI | Log(α) | S1, S2, S4→ −1.071 − 5.543(Silt) − 3.691(Clay2) + 14.613(Clay)(Silt) S3→ 1.111 − 5.497(Silt) − 3.501(Clay2) + 0.015(SOM2) + 14.331(Clay)(Silt) S5→ −1.128 − 5.638(Silt) − 3.652(Clay2) + 0.039(BD)(SOM) + 14.814(Clay)(Silt) S6→ −0.618 − 0.391(BD2) − 2.088(Silt) + 1.788(Clay2) + 0.113(SOM2) + 0.071(BD)(SOM) − 0.629(θS)(SOM) |
| Log(n) | S1, S2, S4, S5→ 0.471 − 1.489(Silt) + 3.278(Clay)(Silt) S3→ 0.526 − 1.219(Silt) − 0.011(SOM) + 2.456(Clay)(Silt) + 0.189(Clay)(SOM) S6→ 0.343 − 0.043(BD)(SOM) + 1.399(θS)(Clay) − 1.192(θS)(Silt) | |
| θr | S1, S3→ 0.023 + 0.210(Silt) − 0.610(Silt2) + 1.125(Clay2) S2, S5→ 0.641 − 0.226(BD2) − 0.016(Silt2) − 0.282(BD)(Silt) S4→ 0.060 + 1.015(Clay)(SA) − 0.007(Silt)(SA) S6→ − 0.546 + 1.363(θS) − 0.605(θS)(Silt) − 0.098(Clay)(SOM) + 0.005(Clay)(SA) | |
| θs | S1, S4→ 0.453 + 1.315(Clay)(Silt) S2→ 0.786 − 0.135(BD2) + 0.098(Clay2) S3→ 0.309 + 1.299(Silt) − 1.831(Silt2) + 0.174(Clay)(SOM) S5→ 0.819 − 0.171(BD2) + 0.026(BD)(SOM) − 0.007(Clay)(SOM) | |
| m | S1→ 1.179 − 3.118(Clay) + 3.144(Clay2) S2→ −0.158 + 0.574(BD) S3→ 0.791 − 0.605(Clay)(SOM) S4→ 0.931 − 1.199(Clay) + 2.20 × 10 −5(SA2) S5→ 0.922 − 0.012(SA) + 1.23 × 10 −4(SA2) − 0.442(Clay)(SOM) S6→ 1.824 − 1.461(BD)(θS) − 0.562(Clay)(SOM) | |
| FX-b-PDI | Log(α1) | S1→ −1.926 − 2.231(Silt2) + 2.225(Clay2) S2→ −1.609 + 1.772(Clay2) − 1.275(BD)(Silt) S3→ −1.240 − 0.808(SOM) − 2.723(Silt2) + 0.102(SOM2) + 1.103(Clay)(SOM) S4→ −1.939 + 0.001(SA) − 2.198(Silt2) + 2.117(Clay2) S5→ −1.140 + 0.016(SOM) −0.022(SOM2) −1.806(BD)(Silt) S6→ −1.470 − 0.048(SOM) − 0.009(SOM2) − 1.896(BD)(Silt) + 0.116(θS)(SOM) + 3.515(Clay)(Silt) − 0.001(SOM)(SA) |
| Log(n1) | S1, S4→ 0.389 + 1.006(Clay)(Silt) S2, S5→ 0.587 − 0.083(BD2) + 0.346(Clay)(Silt) S3→ 0.375 + 0.478(Clay)(Silt) + 0.206(Clay)(SOM) S6→ 0.310 + 0.385(θs2) + 0.445(Clay)(Silt) | |
| θr | S1→ −0.020 + 1.849(Clay)(Silt) S2→ 0.365 − 0.180(BD2) + 0.217(BD)(Clay) S3→ −0.012 + 1.811(Clay)(Silt) S4→ 0.020 + 0.456(Clay)(Silt) + 0.008(Clay)(SA) S5→ 0.421 − 0.177(BD2) − 0.023(BD)(SOM) + 0.002(BD)(SA) + 1.25 × 10−4(SOM)(SA) S6→ 0.163 − 0.184(BD2) + 0.382(BD)(θs) + 0.005(Clay)(SA) − 0.079(θS)(SOM) + 0.014(BD)(SOM) | |
| θs | S1→ 0.454 + 1.316(Clay)(Silt) S2→ 0.788 − 0.135(BD2) + 0.096(Clay2) S3→ 0.313 + 1.343(Silt) − 1.871(Silt2) + 0.159(Clay)(SOM) S4→ 0.454 + 1.316(Clay)(Silt) S5→ 0.779 − 0.157(BD2) + 0.029(BD)(SOM) − 0.022(Clay)(SOM) + 0.002(Silt)(SA) | |
| Log(α2) | S1→ −0.988 − 8.727(Silt) + 8.774(Silt2) + 0.324(Clay2) + 7.864(Clay)(Silt) S2→ −2.414 + 0.448(BD) − 2.047(BD)(Silt) + 6.947(Clay)(Silt) S3→ −1.271 − 6.954(Silt) + 6.438(Silt2) + 8.284(Clay)(Silt) S4→ −1.190 − 5.734(Silt) + 5.603(Silt2) − 1.41 × 10 −4(SA2) + 0.072(Silt)(SA) S5→ −0.334 − 1.015(BD) − 0.438(SOM) + 0.006(SOM)(SA) S6→ −0.460 + 1.843(θs) − 3.923(BD)(θs) + 0.008(BD)(SA) | |
| Log(n2) | S1→ 0.422 + 0.396(Clay2) S2→ 1.058 − 0.396(BD) − 0.272(Clay) S3→ 0.400 + 0.541(Clay2) S4→ 0.491 − 0.002(Silt)(SA) S5→ 1.314 − 0.538(BD) − 0.218(BD)(Clay) − 0.010(Silt)(SA) S6→ 0.526 − 0.287(θs2) + 0.136(BD)(Clay) | |
| w2 | S1→ 0.186 + 2.909(Clay) + 3.093(Silt2) − 9.554(Clay)(Silt) S2→ 0.651 − 0.125(BD) − 0.017(Silt) S3→ 0.887 − 1.552(Silt) − 0.183(SOM) + 0.787(Silt)(SOM) S4→ 0.453 + 0.006(SA) + 0.264(Silt2) + 0.905(Clay)(Silt) − 0.029(Silt)(SA) S5→ 0.590 − 0.623(Silt) − 0.051(SOM) + 0.407(Silt)(SOM) S6→ 0.510 + 0.657(Clay)(Silt) + 0.009(Silt)(SA) | |
| m1 | S1, S4→ 0.980 − 1.234(Clay) S2, S5, S6→ −0.319 + 0.711(BD) S3→ 1.059 − 1.471(Clay) | |
| m2 | S1, S2→ 0.617 − 0.061(Silt) S3→ 0.631 − 0.117(Silt)(SOM) S4→ 0.894 − 0.022(SA) + 2.88 × 10−4(SA2) S5→ 0.647 − 0.129(Silt)(SOM) S6→ 0.868 − 1.471(θs)(Silt) | |
| K | Log(hm) | S1, S3, S4→ 1.731 + 3.860(Silt) + 1.527(Clay2) − 7.986(Clay)(Silt) S2→ 2.289 + 4.692(Silt2) + 0.691(Clay2) − 5.440(Clay)(Silt) S5→ 1.275 + 0.674(BD) + 0.573(Clay2) + 3.978(Silt2) − 2.841(Clay)(Silt) S6→ 1.110 + 1.202(θS) − 0.048(SOM) − 0.395(Silt2) + 1.269(Clay2) + 2.803(BD)(Silt) − 6.360(Clay)(Silt) |
| σ | S1, S2, S4→ 1.767 − 1.021(Clay) − 0.814(Silt) + 5.650(Clay)(Silt) S3→ 1.520 − 0.015(Silt) + 1.929(Clay)(Silt) + 0.105(Clay)(SOM) S5→ 1.537 − 0.185(BD)(Silt) + 2.142(Clay)(Silt) + 0.180(Silt)(SOM) S6→ 0.473 + 0.714(Clay) + 0.416(Silt2) + 1.393(BD)(θS) | |
| θr | S1, S4→ −0.002 + 0.397(Clay) + 0.366(Silt) − 0.797(Silt2) S2→ 0.418 − 0.139(BD2) − 0.367(Silt2) S3→ −0.019 + 0.421(Clay) + 0.330(Silt) − 0.766(Silt2) + 0.009(SOM2) S5→ 0.285 − 0.106(BD2) − 0.356(Silt2) + 0.008(SOM2) + 0.164(BD)(Clay) S6→ −0.019 − 0.134(BD2) − 0.526(Silt2) + 0.570(BD)(θS) + 0.333(Clay)(Silt) | |
| θs | S1→ 0.454 + 1.418(Clay)(Silt) S2→ 0.800 − 0.139(BD2) + 0.138(Clay2) S3→ 0.307 + 1.368(Silt) − 1.956(Silt2) + 0.187(Clay)(SOM) S4→ 0.454 + 1.418(Clay)(Silt) S5→ 0.838 − 0.175(BD2) + 0.022(BD)(SOM) + 0.009(Clay)(SOM) | |
| K-PDI | Log(hm) | S1, S3, S4, S5→ 1.520 + 4.933(Silt) + 2.512(Clay2) − 12.216(Clay)(Silt) S2→ 1.644 + 0.389(BD) + 5.851(Silt2) + 1.656(Clay2) − 8.069(Clay)(Silt) S6→ 2.046 + 0.805(θS2) − 0.001(SOM) + 6.834(Silt2) + 2.045(Clay2) − 11.538(Clay)(Silt) |
| σ | S1, S4→ 1.092 + 1.998(Silt) − 4.733(Clay)(Silt) S2→ 0.824 + 1.809(Silt) + 0.131(BD2) − 3.559(Clay)(Silt) S3→ 0.973 + 1.738(Silt) + 0.070(SOM2) − 4.104(Clay)(Silt) S5→ 0.448 + 1.915(Silt) + 0.220(BD2) + 0.097(SOM2) − 2.226(Clay)(Silt) − 0.308(Silt)(SOM) S6→ 0.847 + 1.353(BD)(Silt) + 1.178(θS)(Silt) − 5.227(Clay)(Silt) + 0.005(SOM)(SA) | |
| θr | S1, S4→ −0.007 + 0.692(Clay) + 0.507(Silt) − 1.087(Silt2) S2→ 0.337 − 0.088(BD2) − 0.930(Silt2) + 1.604(Clay)(Silt) S3→ −0.019 + 0.708(Clay) + 0.483(Silt) − 1.066(Silt2) + 0.006(SOM2) S5→ 0.305 + 0.054(SOM) − 0.093(BD2) − 1.135(Silt2) + 2.046(Clay)(Silt) − 0.128(Clay)(SOM) S6→ −0.362 + 1.084(θS) − 0.477(Silt2) + 0.003(Clay)(SA) | |
| θs | S1, S4→ 0.456 + 1.315(Clay)(Silt) S2→ 0.784 − 0.133(BD2) + 0.108(Clay2) S3→ 0.360 + 0.658(Silt) − 0.808(Silt2) + 0.641(Clay2) + 0.013(SOM2) S5→ 0.457 + 0.219(SOM) + 0.240(BD)(Clay) − 0.159(BD)(SOM) + 0.009(Silt)(SOM) + 3.01 × 10 −4(SOM)(SA) | |
| K-b | Log(hm1) | S1, S2, S3→ 2.582 + 0.456(Clay2) S4, S5→ 2.750 − 0.008(Clay)(SA) S6→ 4.154 − 1.922(BD)(θS) − 0.010(Clay)(SA) |
| σ1 | S1, S2, S3, S4, S5, S6→ 1.356 + 0.635(Silt) | |
| θr | S1, S4→ 0.057 − 0.161(Clay)(Silt) S2→ 0.160 − 0.058(BD) − 0.054(Silt2) − 0.107(BD)(Clay) S3→ 0.044 + 0.005(SOM2) − 0.128(Clay)(Silt) S5→ 0.184 − 0.090(BD) − 0.126(Clay) + 0.026(Silt)(SOM) S6→ −0.025 + 0.268(θS2) − 0.001(Silt2) + 0.032(BD)(Clay) + 0.220(θS)(Silt) − 0.799(Clay)(Silt) | |
| θs | S1, S4→ 0.455 + 1.330(Clay)(Silt) S2→ 0.792 − 0.136(BD2) + 0.098(Clay2) S3→ 0.317 + 1.269(Silt) − 1.786(Silt2) + 0.176(Clay)(SOM) S5→ 0.813 + 0.035(SOM) − 0.164(BD2) − 0.019(Clay)(SOM) | |
| Log(hm2) | S1→ 3.348 − 4.328(Silt) + 5.114(Silt2) + 2.456(Clay)(Silt) S2→ 2.229 − 5.031(Clay) − 0.415(Silt) + 6.065(BD)(Clay) S3→ 2.631 − 0.516(Silt2) + 0.524(Clay)(SOM) + 0.023(Silt)(SOM) S4→ 2.766 + 2.57 × 10 −4(SA2) − 0.875(Clay) S5→ 2.480 + 0.009(SOM)(SA) S6→ 2.470 − 1.440(θS2) − 0.002(SOM)(SA) + 0.521(θS)(SOM) + 0.018(SA) | |
| σ2 | S1→ 1.417 + 1.936(Clay2) S2→ 0.944 − 0.990(Clay2) + 2.205(BD)(Clay) S3→ 1.304 + 0.953(Clay)(SOM) S4→ 1.416 + 1.936(Clay2) S5, S6→ 1.306 + 0.010(SOM)(SA) | |
| w2 | S1, S2, S3, S4→ 0.495 + 0.030(Clay) S5→ 0.486 − 0.079(Clay) + 0.001(BD)(SA) S6→ 0.607 + 0.215(Clay) + 0.009(Silt2) − 0.264(BD)(Clay) − 0.188(BD)(Silt) | |
| K-b-PDI | Log(hm1) | S1, S2, S3, S4→ 2.346 − 0.715(Clay2) S5→ 2.328 − 0.812(Clay2) + 0.001(SOM)(SA) S6→ 2.219 − 2.759(Clay2) + 1.885(θS)(Clay) + 2.99 × 10−4(SOM)(SA) |
| σ1 | S1, S2, S3, S4, S5→ 1.107 + 1.719(Clay)(Silt) S6→ 1.501 − 3.464(Clay) − 5.711(θS)(Silt) + 0.516(θS)(SOM) + 15.642(Clay)(Silt) | |
| θr | S1, S3, S4→ 0.180 − 0.546(Silt) + 2.256(Clay)(Silt) S2, S5→ 0.929 − 0.534(BD) − 0.220(Silt2) S6→ −0.342 + 0.933(θS) − 0.001(SOM) − 0.012(SOM2) + 0.514(θS)(Clay) − 0.460(Clay)(Silt) | |
| θs | S1, S4→ 0.455 + 1.315(Clay)(Silt) S2→ 0.787 − 0.134(BD2) + 0.100(Clay2) S3→ 0.312 + 1.293(Silt) − 1.822(Silt2) + 0.173(Clay)(SOM) S5→ 0.808 + 0.034(SOM) − 0.161(BD2) − 0.017(Clay)(SOM) | |
| Log(hm2) | S1, S2→ 2.499 − 1.642(Clay2) S3→ 2.367 + 0.240(SOM) − 1.705(Clay2) − 0.080(SOM2) S4→ 2.422 − 0.012(Clay)(SA) S5→ 2.265 − 0.063(SOM2) + 0.163(BD)(SOM) − 0.010(Clay)(SA) S6→ 1.038 + 1.894(BD)(θS) − 0.010(Clay)(SA) | |
| σ2 | S1, S2, S3→ 1.247 + 0.343(Clay)(Silt) S4, S5→ 1.327 + 0.003(SA) − 1.469(Silt2) S6→ −0.448 + 2.731(BD)(θS) − 0.319(θS)(SOM) | |
| w2 | S1→ 0.534 + 0.077(Clay) − 0.410(Clay)(Silt) S2→ 0.618 − 0.055(BD) − 0.099(Clay) S3→ 0.342 + 0.245(SOM) − 0.065(SOM2) S4→ 0.537 - 0.194(Clay)(Silt) S5→ 0.492 + 0.116(Clay) + 0.029(SOM) − 0.480(Clay)(Silt) S6→ 0.337 + 0.130(SOM) - 0.059(SOM2) + 0.078(BD)(SOM) + 0.002(Silt)(SA) | |
| VG | α | S1, S2, S4→ −1.186 − 4.644(Silt) − 3.038(Clay2) + 12.213(Clay)(Silt) S3→ −1.241 − 4.723(Silt) + 0.055(SOM) − 3.005(Clay2) + 12.287(Clay)(Silt) S5→ −1.462 − 3.087(Silt) + 0.080(SOM) − 0.019(BD)(SOM) + 5.604(Clay)(Silt) S6→ −1.344 − 0.469(θS2) − 2.131(BD)(Silt) + 0.061(BD)(SOM) + 4.481(Clay)(Silt) |
| n | S1→ 0.216 − 0.100(Silt) − 0.109(Clay)(Silt) S2→ 0.279 − 0.030(BD2) − 0.040(BD)(Silt) − 0.417(Clay)(Silt) S3→ 0.222 − 0.088(Silt) − 0.007(SOM) − 0.127(Clay)(Silt) S4→ 0.192 + 0.109(Clay) − 0.020(Silt) − 0.472(Clay)(Silt) S5→ 0.221 − 0.059(BD)(Silt) − 0.172(Clay)(Silt) − 0.017(Silt)(SOM) S6→ 0.443 − 0.320(BD)(θS) − 0.048(BD)(Silt) − 0.238(Clay)(Silt) + 0.009(Silt)(SOM) | |
| θr | S1→ 0.016 + 0.411(Clay) − 0.372(Silt2) S2→ 0.296 + 0.115(Clay) − 0.111(BD2) − 0.440(Silt2) S3→ 0.043 − 0.939(Silt2) + 0.015(SOM2) + 1.691(Clay)(Silt) − 0.088(Clay)(SOM) S4→ 0.017 + 0.411(Clay) − 0.013(Silt) − 0.354(Silt2) S5→ 0.125 + 0.308(Clay) + 0.029(SOM2) − 0.174(BD)(Silt) − 0.068(BD)(SOM) S6→ −0.100 − 0.385(Silt2) + 0.174(BD)(θS) + 0.624(θS)(Clay) | |
| θs | S1, S4→ 0.456 + 1.357(Clay)(Silt) S2→ 0.781 − 0.131(BD2) + 0.143(Clay2) S3→ 0.335 + 1.182(Silt) − 1.706(Silt2) + 0.183(Clay)(SOM) S5→ 0.815 + 0.033(SOM) − 0.163(BD2) − 0.009(Clay)(SOM) | |
| VG-PDI | α | S1, S2, S4→ −1.241 − 4.335(Silt) − 2.919(Clay2) + 11.276(Clay)(Silt) S3→ −1.509 − 2.870(Silt) + 0.031(SOM2) + 5.128(Clay)(Silt) S5→ −1.545 − 2.947(Silt) + 0.064(BD)(SOM) + 5.326(Clay)(Silt) S6→ −1.442 + 0.013(BD2) + 0.088(SOM2) − 1.826(BD)(Silt) − 0.015(BD)(SOM) − 0.286(θS)(SOM) + 3.633(Clay)(Silt) |
| n | S1, S2, S4→ 0.311 − 0.556(Silt) + 1.207(Clay)(Silt) S3, S5→ 0.340 − 0.501(Silt) − 0.031(SOM) + 1.125(Clay)(Silt) S6→ 0.390 − 0.140(θS2) − 0.369(BD)(Silt) − 0.021(BD)(SOM) + 0.922(Clay)(Silt) | |
| θr | S1, S4→ 0.018 + 0.875(Clay) − 0.029(Silt) − 0.539(Silt2) S2→ 0.260 + 0.613(Clay) − 0.098(BD2) − 0.640(Silt2) S3→ 0.016 + 0.840(Clay) − 0.539(Silt2) + 0.032(Clay)(SOM) − 0.021(Silt)(SOM) S5→ 0.256 + 0.618(Clay) − 0.100(BD2) − 0.653(Silt2) + 0.005(BD)(SOM) S6→ −0.100 − 0.140(BD2) − 1.342(Silt2) + 0.716(BD)(θS) + 1.828(Clay)(Silt) | |
| θs | S1, S4→ 0.454 + 1.328(Clay)(Silt) S2→ 0.787 − 0.135(BD2) + 0.108(Clay2) S3→ 0.312 + 1.289(Silt) − 1.834(Silt2) + 0.178(Clay)(SOM) S5→ 0.746 − 0.141(BD2) + 0.173(Clay2) + 0.027(BD)(SOM) | |
| VG-b | Log(α1) | S1, S2, S4→ −2.389 + 0.456(Silt2) S3→ −2.225 − 0.062(SOM2) S5→ −2.218 − 0.083(BD)(SOM) S6→ − 0.015 − 3.238(BD)(θS) |
| Log(n1) | S1, S2, S4→ 0.378 − 0.676(Clay)(Silt) S3, S5→ 0.410 + 0.008(SOM) − 0.017(SOM2) − 0.772(Clay)(Silt) S6→ 0.643 − 0.588(θS) − 0.034(SOM2) + 0.131(θS)(SOM) − 0.170(Clay)(Silt) | |
| θr | S1, S4→ 0.003 + 0.119(Silt2) S2, S5→ 0.015-0.025(Silt2) − 0.057(BD)(Clay) + 0.066(BD)(Silt) S3→ 0.002 + 0.118(Silt2) + 4.51 × 10−4(SOM2) S6→ 0.002 + 0.227(Silt) + 0.065(Silt2) − 0.346(θS)(Silt) | |
| θs | S1, S4→ 0.456 + 1.320(Clay)(Silt) S2→ 0.780 − 0.130(BD2) + 0.115(Clay2) S3→ 0.327 + 1.193(Silt) − 1.670(Silt2) + 0.177(Clay)(SOM) S5→ 0.803 + 0.034(SOM) − 0.159(BD2) − 0.011(Clay)(SOM) | |
| Log(α2) | S1, S3→ −1.298–3.945(Clay) − 5.678(Silt2) + 9.879(Clay)(Silt) S2→ −1.316 − 0.070(BD2) − 2.675(Silt2) − 1.388(BD)(Clay) + 0.583(Clay)(Silt) S4→ −2.135 − 0.006(Silt)(SA) S5→ −2.246 + 0.002(BD)(SA) S6→ −1.235 − 1.756(BD)(θS) + 0.205(BD)(SOM) | |
| Log(n2) | S1, S2, S3, S4, S5, S6→ 0.228 + 0.367(Silt) | |
| w2 | S1, S2, S3, S4, S5, S6→ 0.496 − 0.220(Silt) + 0.582(Silt2) | |
| VG-b-PDI | Log(α1) | S1, S4→ −1.576 − 4.139(Clay) − 4.883(Silt2) + 13.717(Clay)(Silt) S2→ −1.908 − 0.443(BD)(Silt) + 0.250(Clay)(Silt) S3→ −2.014 + 0.236(Clay2) − 0.179(Silt)(SOM) S5→ −1.844 − 0.086(BD2) − 0.191(Silt)(SOM) S6→ −1.064 − 0.311(BD2) − 1.289(θS2) − 0.105(Silt)(SOM) |
| Log(n1) | S1→ 0.502 − 0.080(Silt) + 0.025(Clay2) − 1.172(Clay)(Silt) S2→ 0.697 − 1.143(Silt) + 1.216(Silt2) − 0.283(BD)(Clay) S3→ 0.487 + 0.230(Silt2) + 0.389(Clay2) − 1.974(Clay)(Silt) S4→ 0.448 − 0.003(SA) − 0.425(Silt2) + 4.06 × 10−5(SA2) S5→ 0.361 − 0.297(Silt2) − 3.57 × 10−5(SA2) + 0.002(BD)(SA) S6→ 0.320 − 0.310(Silt2) − 3.35 × 10 −5(SA2) + 0.062(BD)(θS) + 0.002(BD)(SA) | |
| θr | S1, S3, S4→ 0.025 + 1.200(Clay)(Silt) S2→ 0.501 − 0.262(BD) + 0.631(Silt2) − 0.243(BD)(Silt) S5→ 0.203 + 1.532(Silt2) + 2.97 × 10−5(SA2) − 0.651(BD)(Silt) S6→ −0.195 + 0.590(θS) − 0.317(Silt) + 0.660(Silt2) − 0.001(SOM2) + 2.19 × 10−5(SA2) | |
| θs | S1, S4→ 0.454 + 1.321(Clay)(Silt) S2→ 0.787 − 0.135(BD2) + 0.100(Clay2) S3→ 0.310 + 1.301(Silt) − 1.828(Silt2) + 0.173(Clay)(SOM) S5→ 0.773 + 0.041(SOM) − 0.150(BD2) + 5.26 × 10−6(SA2) − 0.040(Clay)(SOM) + 0.001(Silt)(SA) | |
| Log(α2) | S1, S3→ −2.307 + 2.306(Clay2) S2→ −2.012 − 0.141(BD2) + 1.759(Clay2) S4→ −2.278 − 1.677(Clay) + 0.017(SA) + 6.323(Clay2) − 0.042(Clay)(SA) S5→ −2.269 + 0.008(BD)(SA) S6→ 0.685 − 0.327(BD2) − 3.022(BD)(θS) + 1.94 × 10−4(SOM)(SA) | |
| Log(n2) | S1, S3→ 0.336 − 0.486(Clay)(Silt) S2→ −0.057 + 0.175(BD2) + 0.180(BD)(Clay) S4→ 0.343 − 0.006(Silt)(SA) S5→ −0.726 + 0.680(BD) + 1.658(Clay)(Silt) S6→ 0.332 + 0.006(SA) − 0.019(θS)(SA) + 0.015(Silt)(SA) | |
| w2 | S1, S3, S4→ 0.673 − 1.012(Clay)(Silt) S2, S5, S6→ 0.722 − 0.020(BD2) − 1.174(Clay)(Silt) | |
| VGm | Log(α) | S1, S2→ −1.803 − 10.338(Silt2) − 4.471(Clay2) + 17.146(Clay)(Silt) S3→ −0.728 − 7.770(Silt) − 5.066(Clay2) + 0.019(SOM2) + 20.084(Clay)(Silt) S4→ −0.680 − 7.826(Silt) − 5.296(Clay2) + 20.425(Clay)(Silt) S5→ −1.597 + 0.036(SOM) − 0.111(BD2) − 10.071(Silt2) − 4.335(Clay2) + 15.972(Clay)(Silt) S6→ −1.488 + 3.123(Clay) + 0.021(SOM2) − 2.398(BD)(Silt) − 1.847(θS)(Clay) |
| Log(n) | S1, S2, S3, S4, S5→ 0.611 − 1.993(Silt) + 4.257(Clay)(Silt) S6→ 0.618 − 2.008(Silt) + 4.349(Clay)(Silt) − 0.032(Clay)(SOM) | |
| θr | S1, S3→ 0.025 + 0.185(Silt) − 0.386(Silt2) + 0.355(Clay2) S2→ 0.436 − 0.249(BD) + 0.002(Silt2) − 0.099(BD)(Silt) S4→ 0.018 + 0.274(Silt) − 0.500(Silt2) + 0.003(Clay)(SA) S5→ 0.445 − 0.271(BD) − 0.190(Silt2) S6→ −0.306 + 0.777(θS) + 1.99 × 10−5(SA2) − 0.184(θS)(Silt) − 0.025(Clay)(SOM) − 0.005(Silt)(SA) | |
| θs | S1, S4→ 0.457 + 1.303(Clay)(Silt) S2→ 0.778 − 0.129(BD2) + 0.116(Clay2) S3→ 0.341 + 1.112(Silt) − 1.571(Silt2) + 0.177(Clay)(SOM) S5→ 0.808 + 0.039(SOM) − 0.162(BD2) − 0.025(Clay)(SOM) | |
| Log(m) | S1, S4→ −0.394 − 4.345(Clay) + 1.782(Silt) + 3.577(Clay2) S2→ −0.648 − 1.738(BD)(Clay) + 1.337(BD)(Silt) S3→ −0.393 − 4.326(Clay) + 1.782(Silt) + 3.543(Clay2) − 0.001(SOM2) S5, S6→ −0.635 − 0.005(SOM2) − 1.750(BD)(Clay) + 1.342(BD)(Silt) | |
| VGm-PDI | Log(α) | S1, S4→ −1.927 − 8.150(Silt2) − 3.484(Clay2) + 14.055(Clay)(Silt) S2→ −1.819 − 10.975(Silt2) − 4.945(Clay2) + 16.931(Clay)(Silt) S3→ −2.063 − 7.678(Silt2) − 2.788(Clay2) + 0.035(SOM2) + 13.143(Clay)(Silt) S5, S6→ −1.900 − 10.393(Silt2) − 4.004(Clay2) + 0.040(SOM2) + 15.146(Clay)(Silt) |
| Log(n) | S1→ 0.089 + 1.372(Clay) − 1.150(Silt2) S2→ 0.563 + 0.586(Clay) − 1.228(BD)(Silt) S3→ 0.217 − 2.416(Silt2) + 0.009(SOM2) + 4.377(Clay)(Silt) − 0.035(Silt)(SOM) S4→ 0.194 + 0.016(SA) − 0.026(Silt)(SA) S5→ 0.564 − 1.097(BD)(Silt) + 0.004(SOM)(SA) S6→ −0.191 + 2.172(θS) − 0.009(BD)(SA) − 4.590(θS)(Silt) + 3.475(Clay)(Silt) − 0.559(Clay)(SOM) + 0.009(SOM)(SA) | |
| θr | S1, S3, S4→ 0.152 − 0.557(Silt2) + 1.119(Clay2) S2, S5→ 0.243 − 0.705(Silt2) + 0.617(Clay2) S6→ −0.359 − 2.393(Silt2) + 1.391(BD)(θS) − 0.628(BD)(Clay) + 3.541(Clay)(Silt) | |
| θs | S1, S4→ 0.552 − 0.313(Silt) + 1.347(Clay)(Silt) S2→ 0.740 + 0.223(Silt) − 0.268(BD2) − 0.276(Clay2) S3→ 0.438 + 1.279(Clay)(Silt) + 0.046(Silt)(SOM) S5→ 0.750 + 0.095(SOM) − 0.279(BD2) − 0.205(Clay)(SOM) | |
| Log(m) | S1→ 0.062 − 5.386(Silt) + 9.343(Silt2) S2→ −0.877 + 0.486(BD2) S3→ −0.622 + 0.614(SOM) − 0.226(SOM2) − 2.088(Clay2) S4→ −0.328 − 0.352(Clay) + 6.84 × 10−5(SA2) − 0.021(Clay)(SA) S5→ −0.849 + 0.483(BD2) − 0.144(SOM2) + 0.705(Silt)(SOM) S6→ −0.146 − 1.321(θS)(SOM) + 1.542(Silt)(SOM) | |
| VGm-b | Log(α1) | S1, S2, S3→ −1.356 − 6.170(Silt) − 7.060(Clay2) + 17.793(Clay)(Silt) S4→ −2.806 + 0.037(SA) − 0.053(Clay)(SA) S5→ −2.536-0.011(BD)(SA) S6→ −1.834 − 1.551(BD)(θS) |
| Log(n1) | S1→ 0.237 + 2.284(Silt2) − 0.922(Clay2) S2→ −0.319 + 2.216(BD)(Silt) S3→ −0.005 + 1.693(Silt) − 0.447(Clay)(SOM) S4→ 0.237 + 2.284(Silt2) − 0.922(Clay2) S5→ 0.097 + 0.499(BD)(Silt) + 0.499(Silt)(SOM) S6→ −0.440 + 0.753(θS) + 1.259(BD)(Silt) | |
| θr | S1, S4→ 0.019 + 0.859(Silt2) − 0.285(Clay2) S2→ 0.120 + 2.141(Silt2) − 1.078(Clay2) + 0.533(BD)(Clay) − 0.968(BD)(Silt) S3→ 0.001 + 0.835(Silt2) − 0.257(Clay2) + 0.009(SOM2) S5→ −0.010 − 0.260(Silt2) − 0.114(Clay2) + 0.154(BD)(Silt) + 3.57 × 10−4(SOM)(SA) S6→ 0.027 − 0.177(Clay2) + 0.031(θS)(Silt) + 3.06 × 10−4(SOM)(SA) | |
| θs | S1, S4→ 0.378 + 0.281(Silt) + 0.463(Clay)(Silt) S2→ 0.743 + 0.215(Silt) − 0.267(BD2) − 0.282(Clay2) S3→ 0.396 + 0.582(Clay)(Silt) + 0.147(Silt)(SOM) S5→ 0.836 + 0.050(SOM) − 0.183(BD2) − 0.057(Clay)(SOM) | |
| Log(α2) | S1→ −1.936 − 2.545(Silt2) + 2.001(Clay)(Silt) S2→ −1.271 − 0.517(BD) − 2.025(Silt2) S3→ −2.122 − 0.053(SOM2) + 0.628(Clay)(SOM) S4→ −2.448 + 0.032(SA) + −3.84 × 10−4(SA2) S5→ −2.161 − 0.086(SOM2) − 0.016(Clay)(SA) + 0.010(SOM)(SA) S6→ −1.126 − 1.653(BD)(θs) + 0.003(SOM)(SA) | |
| Log(n2) | S1→ 0.409 + 0.149(Clay) − 0.096(Silt) S2→ 2.146 − 1.477(BD) − 2.658(Clay)(Silt) S3→ 0.302 + 0.161(Clay) − 0.084(SOM) + 0.469(Silt)(SOM) S4→ 0.307 + 0.051(Clay) − 1.79 × 10 −4(SA2) + 0.037(Silt)(SA) S5→ 0.938 − 0.423(BD) − 0.560(Clay)(Silt) S6→ 0.154 + 0.559(θs2) | |
| w2 | S1, S2, S4→ 0.391 + 0.602(Silt2) S3→ 0.451 − 0.062(SOM) + 0.736(Silt2) S5, S6→ 0.585 − 0.563(Silt2) + 0.022(BD)(SOM) | |
| Log(m1) | S1→ −0.618 + 0.238(Clay)(Silt) S2→ −0.552 + 0.456(BD) + 5.074(Silt2) − 3.362(BD)(Silt) S3→ −0.468 + 0.127(Clay) − 0.494(SOM) + 0.083(SOM2) + 0.680(Silt)(SOM) S4→ −0.483 − 0.014(SA) + 0.037(Silt)(SA) S5→ 0.433 − 0.773(BD) − 9.964(Silt2) + 3.258(BD)(Silt) S6→ −0.418 − 0.645(θs2) + 0.025(θs)(SA) − 0.014(Clay)(SA) | |
| Log(m2) | S1, S3→ −0.275 − 2.238(Clay)(Silt) S2→ −1.630 + 1.152(BD) S4→ −0.318 − 0.021(Silt)(SA) S5, S6→ −1.101 + 0.569(BD) | |
| VGm-b-PDI | Log(α1) | S1 − 5→ −2.475 + 0.556(Clay) S6→ 0.635 − 4.245(BD)(θs) + 0.329(BD)(Clay) |
| Log(n1) | S1→ 0.226 + 3.283(Silt2) − 0.629(Silt) − 0.469(Clay)(Silt) S2→ 0.125 + 2.711(Silt2) − 0.222(BD)(Silt) S3, S5, S6→ 0.127 + 0.155(Clay)(Silt) + 0.457(Silt)(SOM) S4→ 0.134 + 2.418(Silt2) − 0.600(Clay)(Silt) | |
| θr | S1, S3, S4→ 0.061 + 0.810(Clay)(Silt) S2, S5→ 0.026 + 0.261(BD)(Clay) + 0.149(Clay)(Silt) S6→ 0.114 − 0.516(θs)(Silt) + 1.199(Clay)(Silt) | |
| θs | S1, S4→ 0.455 + 1.313(Clay)(Silt) S2→ 0.787 − 0.134(BD2) + 0.099(Clay2) S3→ 0.312 + 1.294(Silt) − 1.821(Silt2) + 0.172(Clay)(SOM) S5→ 0.773 + 0.042(SOM) − 0.150(BD2) + 5.86 × 10 −6(SA2) − 0.042(Clay)(SOM) + 0.001(Silt)(SA) | |
| Log(α2) | S1→ −1.571 − 2.743(Silt) − 2.793(Clay2) + 8.305(Clay)(Silt) S2→ −1.675 − 1.160(Silt) − 0.050(BD2) + 1.709(Clay)(Silt) S3, S4→ −1.778 − 1.233(Silt) + 2.161(Clay)(Silt) S5→ −1.861 + 0.070(BD) − 1.604(Silt) + 2.594(Clay)(Silt) + 0.171(Silt)(SOM) S6→ −1.687 − 0.465(θs2) + 0.028(SOM2) − 0.948(BD)(Silt) + 2.175(Clay)(Silt) | |
| Log(n2) | S1, S3, S4→ 0.525 − 0.494(Silt2) S2, S5→ 0.778 − 0.638(Silt2) − 0.598(BD)(Clay) S6→ 0.412 − 0.706(Silt2) + 0.514(BD)(θs) − 0.590(BD)(Clay) | |
| w2 | S1→ 0.229 + 0.587(Silt) + 0.399(Clay2) S2, S5→ 0.386 + 0.209(BD)(Silt) S3, S4→ 0.267 + 0.450(Clay) + 1.009(Silt2) − 0.558(Clay)(Silt) S6→ 0.583 − 0.164(BD)(θs) | |
| Log(m1) | S1→ −0.458 − 1.166(Silt2) S2→ −1.113 + 0.347(BD2) S3→ −0.175 − 1.331(Clay2) − 0.097(Clay)(SOM) − 0.465(Silt)(SOM) S4→ −0.384 − 0.021(Silt)(SA) S5→ 0.001 − 1.293(Silt) − 0.005(BD)(SA) S6→ 0.382 − 1.509(θs) − 0.051(SOM) | |
| Log(m2) | S1, S3→ − 0.307 + 0.736(Clay) − 1.272(Silt) S2→ −0.401 − 1.273(Silt) + 0.868(BD)(Clay) S4→ −0.079 − 1.255(Silt) + 0.001(SA) S5→ −0.010 − 1.325(Silt) − 0.001(BD)(SA) S6→ −0.448 − 1.374(Silt) + 0.688(BD)(θs) − 0.021(BD)(SOM) − 0.001(BD)(SA) |
References
- Bouma, J.; van Lanen, H.A.J. Transfer functions and threshold values: From soil characteristics to land qualities. In Proceedings of the International Workshop on Quantified Land Evaluation Procedures, Washington, DC, USA, 27 April–2 May 1987. [Google Scholar]
- Cornelis, W.M.; Ronsyn, J.; Van Meirvenne, M.; Hartmann, R. Evaluation of pedotransfer functions for predicting the soil moisture retention curve. Soil Sci. Soc. Am. J. 2001, 65, 638–648. [Google Scholar] [CrossRef]
- Haghverdi, A.; Leib, B.G.; Cornelis, W.M. A simple nearest-neighbor technique to predict the soil water retention curve. Trans. ASABE 2015, 58, 697–705. [Google Scholar]
- Haghverdi, A.; Cornelis, W.; Ghahraman, B. A pseudo-continuous neural network approach for developing water retention pedotransfer functions with limited data. J. Hydrol. 2012, 442, 46–54. [Google Scholar] [CrossRef]
- Haghverdi, A.; Öztürk, H.; Cornelis, W. Revisiting the pseudo continuous pedotransfer function concept: Impact of data quality and data mining method. Geoderma 2014, 226, 31–38. [Google Scholar] [CrossRef]
- Schindler, U.; Durner, W.; von Unold, G.; Mueller, L.; Wieland, R. The evaporation method: Extending the measurement range of soil hydraulic properties using the air-entry pressure of the ceramic cup. J. Plant Nutr. Soil Sci. 2010, 173, 563–572. [Google Scholar] [CrossRef]
- Schindler, U.; Durner, W.; von Unold, G.; Müller, L. Evaporation method for measuring unsaturated hydraulic properties of soils: Extending the measurement range. Soil Sci. Soc. Am. J. 2010, 74, 1071–1083. [Google Scholar] [CrossRef]
- Peters, A.; Durner, W. Simplified evaporation method for determining soil hydraulic properties. J. Hydrol. 2008, 356, 147–162. [Google Scholar] [CrossRef]
- Peters, A.; Iden, S.C.; Durner, W. Revisiting the simplified evaporation method: Identification of hydraulic functions considering vapor, film and corner flow. J. Hydrol. 2015, 527, 531–542. [Google Scholar] [CrossRef]
- Wösten, J.; Pachepsky, Y.A.; Rawls, W. Pedotransfer functions: Bridging the gap between available basic soil data and missing soil hydraulic characteristics. J. Hydrol. 2001, 251, 123–150. [Google Scholar] [CrossRef]
- Vereecken, H.; Weynants, M.; Javaux, M.; Pachepsky, Y.; Schaap, M.G.; van Genuchten, M.T. Using pedotransfer functions to estimate the van Genuchten–Mualem soil hydraulic properties: A review. Vadose Zone J. 2010, 9, 795–820. [Google Scholar] [CrossRef]
- Fields, J.S.; Owen, J.S., Jr.; Zhang, L.; Fonteno, W.C. Use of the evaporative method for determination of soilless substrate moisture characteristic curves. Sci. Hortic. 2016, 211, 102–109. [Google Scholar] [CrossRef]
- Grath, S.M.; Ratej, J.; Jovičić, V.; Curk, B.C. Hydraulic characteristics of alluvial gravels for different particle sizes and pressure heads. Vadose Zone J. 2015, 14. [Google Scholar] [CrossRef][Green Version]
- Herbrich, M.; Gerke, H.H. Scales of water retention dynamics observed in eroded Luvisols from an arable postglacial soil landscape. Vadose Zone J. 2017, 16. [Google Scholar] [CrossRef]
- Schindler, U.; Mueller, L.; da Veiga, M.; Zhang, Y.; Sandro, S.; Hu, C. Comparison of water-retention functions obtained from the extended evaporation method and the standard methods sand/kaolin boxes and pressure plate extractor. J. Plant Nutr. Soil Sci. 2012, 175, 527–534. [Google Scholar] [CrossRef]
- Schwen, A.; Zimmermann, M.; Bodner, G. Vertical variations of soil hydraulic properties within two soil profiles and its relevance for soil water simulations. J. Hydrol. 2014, 516, 169–181. [Google Scholar] [CrossRef]
- Zhuang, L.; Bezerra Coelho, C.R.; Hassanizadeh, S.M.; van Genuchten, T.H. Analysis of the hysteretic hydraulic properties of unsaturated soil. Vadose Zone J. 2017, 16, 1–9. [Google Scholar] [CrossRef]
- Haghverdi, A.; Öztürk, H.S.; Durner, W. Measurement and estimation of the soil water retention curve using the evaporation method and the pseudo continuous pedotransfer function. J. Hydrol. 2018, 563, 251–259. [Google Scholar] [CrossRef]
- Nemes, A.; Schaap, M.; Wösten, J. Functional evaluation of pedotransfer functions derived from different scales of data collection. Soil Sci. Soc. Am. J. 2003, 67, 1093–1102. [Google Scholar] [CrossRef]
- Schaap, M.G.; Leij, F.J.; Van Genuchten, M.T. Neural network analysis for hierarchical prediction of soil hydraulic properties. Soil Sci. Soc. Am. J. 1998, 62, 847–855. [Google Scholar] [CrossRef]
- Tomasella, J.; Pachepsky, Y.; Crestana, S.; Rawls, W.J. Comparison of two techniques to develop pedotransfer functions for water retention. Soil Sci. Soc. Am. J. 2003, 67, 1085–1092. [Google Scholar] [CrossRef]
- Vereecken, H.; Maes, J.; Feyen, J.; Darius, P. Estimating the soil moisture retention characteristic from texture, bulk density, and carbon content. Soil Sci. 1989, 148, 389–403. [Google Scholar] [CrossRef]
- Hodnett, M.; Tomasella, J. Marked differences between van Genuchten soil water-retention parameters for temperate and tropical soils: A new water-retention pedo-transfer functions developed for tropical soils. Geoderma 2002, 108, 155–180. [Google Scholar] [CrossRef]
- Van Genuchten, M.T. A closed-form equation for predicting the hydraulic conductivity of unsaturated soils 1. Soil Sci. Soc. Am. J. 1980, 44, 892–898. [Google Scholar] [CrossRef]
- Haghverdi, A.; Öztürk, H.S.; Durner, W. Studying Unimodal, Bimodal, PDI and Bimodal-PDI Variants of Multiple Soil Water Retention Models: I. Direct Model Fit Using the Extended Evaporation and Dewpoint Methods. Water 2020, 12. (in press).
- Jackson, M.L. Soil Chemical Analysis: Advanced Course; UW-Madison Libraries Parallel Press: Madison, WI, USA, 2005. [Google Scholar]
- Gee, G.W.; Bauder, J.W. Particle-size analysis. Methods Soil Anal. Part 1 Phys. Miner. Methods 1986, 5, 383–411. [Google Scholar]
- Kemper, W.; Rosenau, R. Aggregate stability and size distribution. Methods Soil Anal. Part 1 Phys. Miner. Methods 1986, 5, 425–442. [Google Scholar]
- Blake, G.R.; Hartge, K. Bulk density. Methods Soil Anal. Part 1 Phys. Miner. Methods 1986, 5, 363–375. [Google Scholar]
- Iden, S.C.; Durner, W. Comment on “Simple consistent models for water retention and hydraulic conductivity in the complete moisture range” by A. Peters. Water Resour. Res. 2014, 50, 7530–7534. [Google Scholar] [CrossRef]
- Peters, A. Simple consistent models for water retention and hydraulic conductivity in the complete moisture range. Water Resour. Res. 2013, 49, 6765–6780. [Google Scholar] [CrossRef]
- Durner, W. Hydraulic conductivity estimation for soils with heterogeneous pore structure. Water Resour. Res. 1994, 30, 211–223. [Google Scholar] [CrossRef]
- Romano, N.; Nasta, P.; Severino, G.; Hopmans, J.W. Using bimodal lognormal functions to describe soil hydraulic properties. Soil Sci. Soc. Am. J. 2011, 75, 468–480. [Google Scholar] [CrossRef]
- Brooks, R.; Corey, T. HYDRAU uc properties of porous media. Hydrol. Pap. Colo. State Univ. 1964, 24, 37. [Google Scholar]
- Fredlund, D.G.; Xing, A. Equations for the soil-water characteristic curve. Can. Geotech. J. 1994, 31, 521–532. [Google Scholar] [CrossRef]
- Kosugi, K.I. Lognormal distribution model for unsaturated soil hydraulic properties. Water Resour. Res. 1996, 32, 2697–2703. [Google Scholar] [CrossRef]
- Base SAS 9.4 Procedures Guide; SAS Institute: Carrie, NC, USA, 2015.
- Minasny, B.; McBratney, A. The neuro-m method for fitting neural network parametric pedotransfer functions. Soil Sci. Soc. Am. J. 2002, 66, 352–361. [Google Scholar] [CrossRef]
| Basic Soil Properties | HYPROP Measured Data | ||||||||
|---|---|---|---|---|---|---|---|---|---|
| Sand (%) | Silt (%) | Clay (%) | BD (Mg m−3) | SOM (%) | SA (%) | pF (-) | SWC (cm3 cm−3) | θs (m3 cm−3) | |
| Mean | 35.20 | 30.67 | 34.13 | 1.23 | 1.18 | 30.72 | 1.77 | 0.47 | 0.59 |
| SD | 17.38 | 8.68 | 15.05 | 0.18 | 0.59 | 18.91 | 0.78 | 0.12 | 0.07 |
| Max. | 83.60 | 57.60 | 62.20 | 1.66 | 3.07 | 75.40 | 3.91 | 0.69 | 0.69 |
| Min. | 5.90 | 5.20 | 9.40 | 0.91 | 0.01 | 1.50 | −2.00 | 0.05 | 0.40 |
| Model 1 | Parameters | Source |
|---|---|---|
| BC | α, λ, θr, θs | [34] |
| FX | α, n, hr, θs, m | [8,30,31,32,33,35] |
| FX-PDI | α, n, θr, θs, m | |
| FX-b-PDI | α1, n1, θr, θs, α2, n2, w2, m1, m2 | |
| K | hm, σ, θr, θs | [9,30,31,32,33,36] |
| K-PDI | hm, σ, θr, θs | |
| K-b | hm1, σ1, θr, θs, hm2, σ2, w2 | |
| K-b-PDI | hm1, σ1, θr, θs, hm2, σ2, w2 | |
| VG | α, n, θr, θs | [8,24,30,31,32,33] |
| VG-PDI | α, n, θr, θs | |
| VG-b | α1, n1, θr, θs, α2, n2, w2 | |
| VG-b-PDI | α1, n1, θr, θs, α2, n2, w2 | |
| VGm | α, n, θr, θs, m | |
| VGm-PDI | α, n, θr, θs, m | |
| VGm-b | α1, n1, θr, θs, m1, α2, n2, m2, w2 | |
| VGm-b-PDI | α1, n1, θr, θs, m1, α2, n2, m2, w2 |
| Scenario | Input Parameters 1 | Regression Terms Considered |
|---|---|---|
| S1 | Silt, Clay | Silt, Clay, Silt2, Clay2, Clay × Silt |
| S2 | Silt, Clay, BD | BD, Clay, Silt, BD2, Silt2, Clay2, BD × Clay, BD × Silt, Clay × Silt |
| S3 | Silt, Clay, SOM | Clay, Silt, SOM, Silt2, Clay2, SOM2, Clay × Silt, Clay × SOM, Silt × SOM |
| S4 | Silt, Clay, SA | Clay, Silt, SA, Silt2, Clay2, SA2, Clay × Silt, Clay × SA, Silt × SA |
| S5 | Silt, Clay, SA, BD, SOM | BD, Clay, Silt, SOM, SDA, BD2, Silt2, Clay2, SOM2, SA2, BD × Clay, BD × Silt, BD × SOM, BD × SA, Clay × Silt, Clay × SOM, Clay × SA, Silt × SOM, Silt × SA, SOM × SA |
| S6 | Silt, Clay, SA, BD, SOM, θs | BD, θs, Clay, Silt, OM, SA, BD2, θs2, Silt2, Clay2, SOM2, SA2, BD × θs, BD × Clay, BD × Silt, BD × SOM, BD × SA, θs × Clay, θs × Silt, θs × OM, θs × SA, Clay × Silt, Clay × SOM, Clay × SA, Silt × SOM, Silt × SA, SOM × SA |
| Models | S1 | S2 | S3 | S4 | S5 | S6 | |
|---|---|---|---|---|---|---|---|
| BC | RMSE | 0.054 | 0.051 | 0.069 | 0.054 | 0.074 | 0.037 |
| MAE | 0.042 | 0.039 | 0.059 | 0.042 | 0.056 | 0.027 | |
| r | 0.91 | 0.92 | 0.84 | 0.91 | 0.83 | 0.96 | |
| MBE | −0.006 | −0.006 | −0.007 | −0.006 | −0.005 | −0.002 | |
| FX | RMSE | 0.07 | 0.063 | 0.077 | 0.063 | 0.074 | 0.057 |
| MAE | 0.052 | 0.049 | 0.062 | 0.049 | 0.053 | 0.040 | |
| r | 0.85 | 0.88 | 0.81 | 0.88 | 0.86 | 0.91 | |
| MBE | 0.009 | 0.007 | 0.003 | 0.007 | −0.005 | 0.007 | |
| K | RMSE | 0.048 | 0.055 | 0.063 | 0.048 | 0.051 | 0.038 |
| MAE | 0.039 | 0.044 | 0.053 | 0.039 | 0.041 | 0.029 | |
| r | 0.92 | 0.90 | 0.86 | 0.92 | 0.91 | 0.96 | |
| MBE | −0.005 | −0.006 | −0.006 | −0.005 | −0.006 | −0.012 | |
| VG | RMSE | 0.051 | 0.052 | 0.064 | 0.051 | 0.056 | 0.036 |
| MAE | 0.041 | 0.041 | 0.054 | 0.041 | 0.045 | 0.026 | |
| r | 0.91 | 0.91 | 0.86 | 0.91 | 0.90 | 0.96 | |
| MBE | −0.009 | −0.009 | −0.01 | −0.009 | −0.009 | −0.012 | |
| VGm | RMSE | 0.054 | 0.056 | 0.069 | 0.053 | 0.056 | 0.034 |
| MAE | 0.041 | 0.043 | 0.056 | 0.042 | 0.044 | 0.024 | |
| r | 0.90 | 0.90 | 0.84 | 0.91 | 0.89 | 0.96 | |
| MBE | −0.003 | −0.002 | −0.004 | −0.005 | −0.001 | −0.002 | |
| FX-PDI | RMSE | 0.052 | 0.065 | 0.07 | 0.055 | 0.065 | 0.042 |
| MAE | 0.041 | 0.049 | 0.06 | 0.043 | 0.05 | 0.029 | |
| r | 0.91 | 0.87 | 0.84 | 0.90 | 0.87 | 0.95 | |
| MBE | −0.008 | −0.009 | −0.007 | −0.007 | −0.007 | −0.006 | |
| K-PDI | RMSE | 0.045 | 0.049 | 0.046 | 0.045 | 0.049 | 0.038 |
| MAE | 0.036 | 0.039 | 0.037 | 0.036 | 0.039 | 0.027 | |
| r | 0.93 | 0.92 | 0.93 | 0.93 | 0.92 | 0.95 | |
| MBE | −0.003 | −0.003 | −0.004 | −0.003 | −0.006 | −0.003 | |
| VG-PDI | RMSE | 0.048 | 0.052 | 0.056 | 0.048 | 0.051 | 0.038 |
| MAE | 0.038 | 0.041 | 0.047 | 0.038 | 0.04 | 0.026 | |
| r | 0.92 | 0.91 | 0.89 | 0.92 | 0.92 | 0.96 | |
| MBE | −0.008 | −0.008 | −0.007 | −0.008 | −0.008 | −0.006 | |
| VGm-PDI | RMSE | 0.067 | 0.064 | 0.056 | 0.058 | 0.061 | 0.048 |
| MAE | 0.049 | 0.049 | 0.043 | 0.045 | 0.048 | 0.033 | |
| r | 0.84 | 0.87 | 0.89 | 0.89 | 0.88 | 0.92 | |
| MBE | 0.011 | 0.006 | 0.002 | 0.011 | 0.006 | 0.006 |
| Models | S1 | S2 | S3 | S4 | S5 | S6 | |
|---|---|---|---|---|---|---|---|
| K-b | RMSE | 0.067 | 0.071 | 0.074 | 0.066 | 0.072 | 0.063 |
| MAE | 0.052 | 0.055 | 0.060 | 0.052 | 0.057 | 0.045 | |
| r | 0.88 | 0.87 | 0.84 | 0.88 | 0.86 | 0.90 | |
| MBE | 0.030 | 0.030 | 0.028 | 0.029 | 0.030 | 0.026 | |
| VG-b | RMSE | 0.083 | 0.085 | 0.085 | 0.085 | 0.089 | 0.085 |
| MAE | 0.065 | 0.067 | 0.067 | 0.067 | 0.070 | 0.064 | |
| r | 0.88 | 0.87 | 0.86 | 0.86 | 0.85 | 0.88 | |
| MBE | 0.016 | 0.017 | 0.010 | 0.015 | 0.016 | 0.014 | |
| VGm-b | RMSE | 0.098 | 0.099 | 0.085 | 0.100 | 0.092 | 0.086 |
| MAE | 0.076 | 0.077 | 0.065 | 0.079 | 0.070 | 0.064 | |
| r | 0.81 | 0.80 | 0.85 | 0.80 | 0.82 | 0.88 | |
| MBE | 0.056 | 0.059 | 0.047 | 0.059 | 0.048 | 0.059 | |
| FX-b-PDI | RMSE | 0.059 | 0.059 | 0.066 | 0.06 | 0.06 | 0.047 |
| MAE | 0.046 | 0.047 | 0.052 | 0.048 | 0.046 | 0.033 | |
| r | 0.90 | 0.90 | 0.87 | 0.90 | 0.91 | 0.94 | |
| MBE | 0.002 | 0.004 | 0.002 | 0.007 | 0.003 | 0.004 | |
| K-b-PDI | RMSE | 0.058 | 0.069 | 0.065 | 0.061 | 0.071 | 0.056 |
| MAE | 0.046 | 0.053 | 0.053 | 0.048 | 0.055 | 0.04 | |
| r | 0.89 | 0.86 | 0.86 | 0.89 | 0.85 | 0.92 | |
| MBE | 0.012 | 0.013 | 0.012 | 0.011 | 0.012 | 0.014 | |
| VG-b-PDI | RMSE | 0.063 | 0.076 | 0.074 | 0.064 | 0.081 | 0.066 |
| MAE | 0.050 | 0.058 | 0.060 | 0.050 | 0.063 | 0.046 | |
| r | 0.91 | 0.88 | 0.86 | 0.91 | 0.87 | 0.92 | |
| MBE | −0.007 | −0.005 | −0.009 | −0.008 | −0.007 | −0.007 | |
| VGm-b-PDI | RMSE | 0.065 | 0.069 | 0.071 | 0.065 | 0.071 | 0.059 |
| MAE | 0.053 | 0.055 | 0.058 | 0.052 | 0.057 | 0.044 | |
| r | 0.89 | 0.89 | 0.86 | 0.90 | 0.88 | 0.93 | |
| MBE | 0.031 | 0.030 | 0.029 | 0.030 | 0.031 | 0.030 |
| Models | par | S1 | S2 | S3 | S4 | S5 | S6 |
|---|---|---|---|---|---|---|---|
| BC | α | 0.73 | 0.73 | 0.74 | 0.73 | 0.63 | 0.73 |
| λ | 0.15 | 0.28 | 0.10 | 0.15 | 0.36 | 0.59 | |
| θr | 0.57 | 0.76 | 0.57 | 0.57 | 0.76 | 0.82 | |
| θs | 0.73 | 0.81 | 0.61 | 0.73 | 0.41 | ||
| FX | α | 0.70 | 0.64 | 0.63 | 0.70 | 0.64 | 0.49 |
| n | 0.49 | 0.45 | 0.49 | 0.28 | 0.55 | 0.55 | |
| hr | −0.18 | −0.15 | −0.18 | −0.09 | −0.15 | −0.09 | |
| θs | 0.72 | 0.79 | 0.61 | 0.72 | 0.82 | ||
| m | 0.65 | 0.65 | 0.66 | 0.66 | 0.53 | 0.77 | |
| FX-PDI | α | 0.71 | 0.71 | 0.72 | 0.71 | 0.71 | 0.62 |
| n | 0.73 | 0.73 | 0.73 | 0.73 | 0.73 | 0.74 | |
| θr | 0.79 | 0.84 | 0.79 | 0.77 | 0.84 | 0.89 | |
| θs | 0.72 | 0.80 | 0.62 | 0.72 | 0.83 | ||
| m | 0.35 | 0.17 | 0.30 | 0.33 | 0.25 | 0.34 | |
| FX-b-PDI | α1 | 0.14 | 0.14 | 0.14 | 0.12 | −0.04 | 0.06 |
| n1 | −0.06 | −0.12 | 0.11 | −0.06 | −0.12 | −0.08 | |
| θr | 0.62 | 0.80 | 0.64 | 0.74 | 0.80 | 0.82 | |
| θs | 0.73 | 0.80 | 0.68 | 0.73 | 0.84 | ||
| α2 | 0.46 | 0.47 | 0.51 | 0.19 | 0.43 | 0.31 | |
| n2 | −0.14 | −0.19 | 0.06 | −0.21 | −0.09 | −0.32 | |
| w2 | 0.04 | −0.28 | 0.20 | −0.18 | −0.11 | −0.12 | |
| m1 | 0.36 | 0.21 | 0.42 | 0.36 | 0.21 | 0.21 | |
| m2 | −0.34 | −0.34 | 0.09 | 0.20 | −0.21 | 0.05 | |
| K | hm | 0.84 | 0.85 | 0.84 | 0.84 | 0.85 | 0.81 |
| σ | 0.27 | 0.27 | 0.18 | 0.27 | 0.17 | 0.33 | |
| θr | 0.77 | 0.79 | 0.78 | 0.77 | 0.81 | 0.90 | |
| θs | 0.73 | 0.81 | 0.61 | 0.73 | 0.83 | ||
| K-PDI | hm | 0.83 | 0.86 | 0.83 | 0.83 | 0.83 | 0.86 |
| σ | 0.53 | 0.51 | 0.57 | 0.53 | 0.42 | 0.47 | |
| θr | 0.87 | 0.89 | 0.88 | 0.87 | 0.89 | 0.95 | |
| θs | 0.72 | 0.80 | 0.77 | 0.72 | 0.78 | ||
| K-b | hm1 | −0.04 | −0.04 | −0.04 | −0.27 | −0.27 | −0.10 |
| σ1 | −0.23 | −0.23 | −0.23 | −0.23 | −0.23 | −0.21 | |
| θr | 0.03 | −0.03 | 0.11 | 0.03 | 0.06 | 0.31 | |
| θs | 0.72 | 0.80 | 0.61 | 0.72 | 0.82 | ||
| hm2 | 0.08 | 0.17 | 0.13 | 0.24 | 0.29 | 0.26 | |
| σ2 | 0.10 | 0.13 | 0.13 | 0.10 | 0.22 | 0.23 | |
| w2 | −0.39 | −0.39 | −0.39 | −0.39 | −0.17 | −0.26 | |
| K-b-PDI | hm1 | −0.08 | −0.08 | −0.08 | −0.08 | −0.23 | −0.24 |
| σ1 | −0.18 | −0.18 | −0.18 | −0.18 | −0.18 | −0.13 | |
| θr | 0.80 | 0.80 | 0.80 | 0.80 | 0.80 | 0.88 | |
| θs | 0.73 | 0.80 | 0.62 | 0.73 | 0.83 | ||
| hm2 | 0.08 | 0.08 | 0.01 | 0.06 | −0.04 | 0.07 | |
| σ2 | −0.34 | −0.34 | −0.34 | −0.06 | −0.06 | −0.03 | |
| w2 | −0.40 | −0.49 | 0.08 | −0.34 | −0.24 | 0.02 | |
| VG | α | 0.67 | 0.67 | 0.68 | 0.67 | 0.59 | 0.64 |
| n | 0.13 | 0.18 | 0.10 | 0.10 | 0.14 | 0.40 | |
| θr | 0.74 | 0.80 | 0.69 | 0.73 | 0.79 | 0.78 | |
| θs | 0.73 | 0.81 | 0.60 | 0.73 | 0.82 | ||
| VG-PDI | α | 0.65 | 0.65 | 0.66 | 0.65 | 0.64 | 0.50 |
| n | 0.55 | 0.55 | 0.56 | 0.55 | 0.56 | 0.55 | |
| θr | 0.89 | 0.89 | 0.88 | 0.89 | 0.89 | 0.94 | |
| θs | 0.72 | 0.80 | 0.62 | 0.72 | 0.83 | ||
| VG-b | α1 | −0.36 | −0.36 | 0.08 | −0.36 | −0.01 | −0.04 |
| n1 | 0.05 | 0.05 | 0.04 | 0.05 | 0.04 | 0.07 | |
| θr | 0.10 | 0.30 | 0.06 | 0.10 | 0.30 | 0.22 | |
| θs | 0.73 | 0.80 | 0.61 | 0.73 | 0.83 | ||
| α2 | 0.16 | 0.08 | 0.16 | −0.14 | −0.25 | 0.14 | |
| n2 | −0.02 | −0.02 | −0.02 | −0.02 | −0.02 | −0.02 | |
| w2 | −0.21 | −0.21 | −0.21 | −0.21 | −0.21 | −0.21 | |
| VG-b-PDI | α1 | −0.07 | −0.26 | −0.27 | −0.07 | −0.28 | −0.17 |
| n1 | −0.01 | −0.09 | −0.03 | −0.29 | −0.32 | −0.32 | |
| θr | 0.41 | 0.39 | 0.41 | 0.41 | 0.38 | 0.40 | |
| θs | 0.73 | 0.81 | 0.62 | 0.73 | 0.84 | ||
| α2 | −0.03 | −0.05 | −0.03 | −0.02 | −0.08 | 0.08 | |
| n2 | −0.06 | 0.19 | −0.06 | 0.06 | 0.20 | 0.05 | |
| w2 | 0.10 | 0.03 | 0.10 | 0.10 | 0.03 | 0.03 | |
| VGm | α | 0.71 | 0.71 | 0.71 | 0.71 | 0.70 | 0.70 |
| n | 0.60 | 0.60 | 0.60 | 0.60 | 0.60 | 0.58 | |
| θr | 0.44 | 0.65 | 0.44 | 0.41 | 0.66 | 0.63 | |
| θs | 0.72 | 0.79 | 0.59 | 0.72 | 0.82 | ||
| m | 0.73 | 0.75 | 0.71 | 0.73 | 0.74 | 0.74 | |
| VGm-PDI | α | 0.64 | 0.64 | 0.69 | 0.64 | 0.69 | 0.69 |
| n | 0.54 | 0.55 | 0.49 | 0.26 | 0.27 | 0.42 | |
| θr | 0.83 | 0.83 | 0.83 | 0.83 | 0.83 | 0.88 | |
| θs | 0.70 | 0.79 | 0.69 | 0.70 | 0.82 | ||
| m | 0.27 | 0.34 | 0.51 | 0.34 | 0.43 | 0.42 | |
| VGm-b | α1 | −0.08 | −0.08 | −0.08 | 0.05 | 0.05 | −0.04 |
| n1 | 0.20 | 0.21 | 0.07 | 0.20 | 0.11 | 0.17 | |
| θr | 0.31 | 0.32 | 0.31 | 0.31 | 0.42 | 0.38 | |
| θs | 0.69 | 0.78 | 0.67 | 0.69 | 0.81 | ||
| α2 | 0.02 | −0.16 | 0.04 | −0.09 | 0.34 | 0.15 | |
| n2 | −0.33 | −0.22 | −0.29 | −0.19 | −0.22 | −0.18 | |
| w2 | −0.24 | −0.24 | −0.20 | −0.24 | −0.17 | −0.15 | |
| m1 | −0.18 | 0.07 | 0.03 | 0.20 | 0.07 | 0.20 | |
| m2 | 0.04 | 0.05 | 0.04 | −0.08 | 0.05 | 0.05 | |
| VGm-b-PDI | α1 | −0.16 | −0.16 | −0.16 | −0.16 | −0.16 | 0.37 |
| n1 | 0.17 | 0.22 | 0.26 | 0.26 | 0.26 | 0.26 | |
| θr | 0.27 | 0.25 | 0.27 | 0.27 | 0.25 | 0.31 | |
| θs | 0.73 | 0.81 | 0.62 | 0.73 | 0.84 | ||
| α2 | −0.33 | −0.35 | −0.31 | −0.31 | −0.36 | −0.28 | |
| n2 | −0.27 | 0.13 | −0.27 | −0.27 | 0.13 | 0.27 | |
| w2 | 0.14 | −0.04 | 0.08 | 0.08 | −0.04 | −0.21 | |
| m1 | −0.19 | 0.31 | 0.19 | 0.21 | 0.12 | 0.14 | |
| m2 | 0.11 | 0.16 | 0.11 | 0.00 | −0.02 | −0.04 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Haghverdi, A.; Öztürk, H.S.; Durner, W. Studying Unimodal, Bimodal, PDI and Bimodal-PDI Variants of Multiple Soil Water Retention Models: II. Evaluation of Parametric Pedotransfer Functions Against Direct Fits. Water 2020, 12, 896. https://doi.org/10.3390/w12030896
Haghverdi A, Öztürk HS, Durner W. Studying Unimodal, Bimodal, PDI and Bimodal-PDI Variants of Multiple Soil Water Retention Models: II. Evaluation of Parametric Pedotransfer Functions Against Direct Fits. Water. 2020; 12(3):896. https://doi.org/10.3390/w12030896
Chicago/Turabian StyleHaghverdi, Amir, Hasan Sabri Öztürk, and Wolfgang Durner. 2020. "Studying Unimodal, Bimodal, PDI and Bimodal-PDI Variants of Multiple Soil Water Retention Models: II. Evaluation of Parametric Pedotransfer Functions Against Direct Fits" Water 12, no. 3: 896. https://doi.org/10.3390/w12030896
APA StyleHaghverdi, A., Öztürk, H. S., & Durner, W. (2020). Studying Unimodal, Bimodal, PDI and Bimodal-PDI Variants of Multiple Soil Water Retention Models: II. Evaluation of Parametric Pedotransfer Functions Against Direct Fits. Water, 12(3), 896. https://doi.org/10.3390/w12030896





