A New Framework to Model Hydraulic Bank Erosion Considering the Effects of Roots
Abstract
1. Introduction
2. Material and Methods
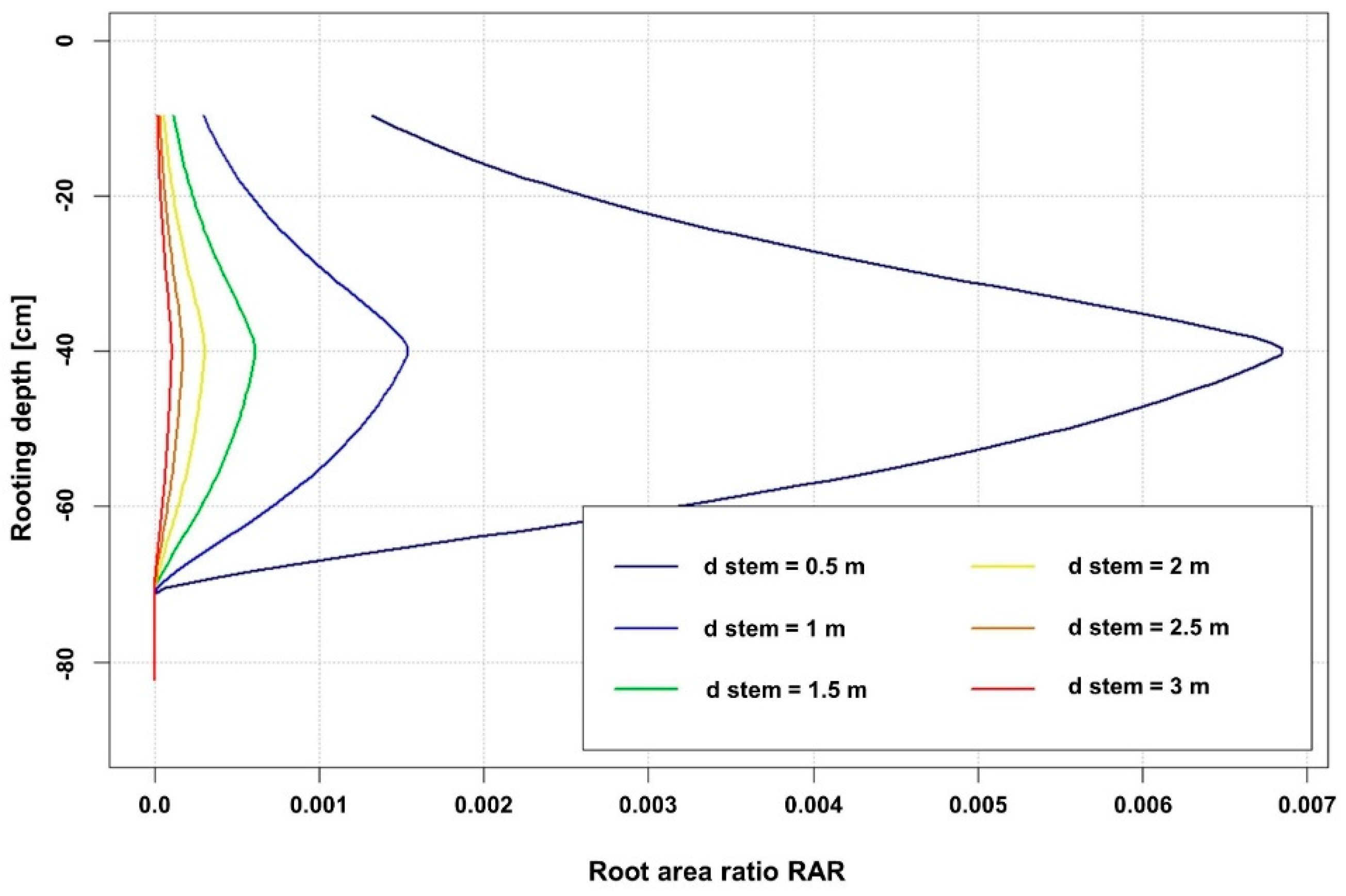
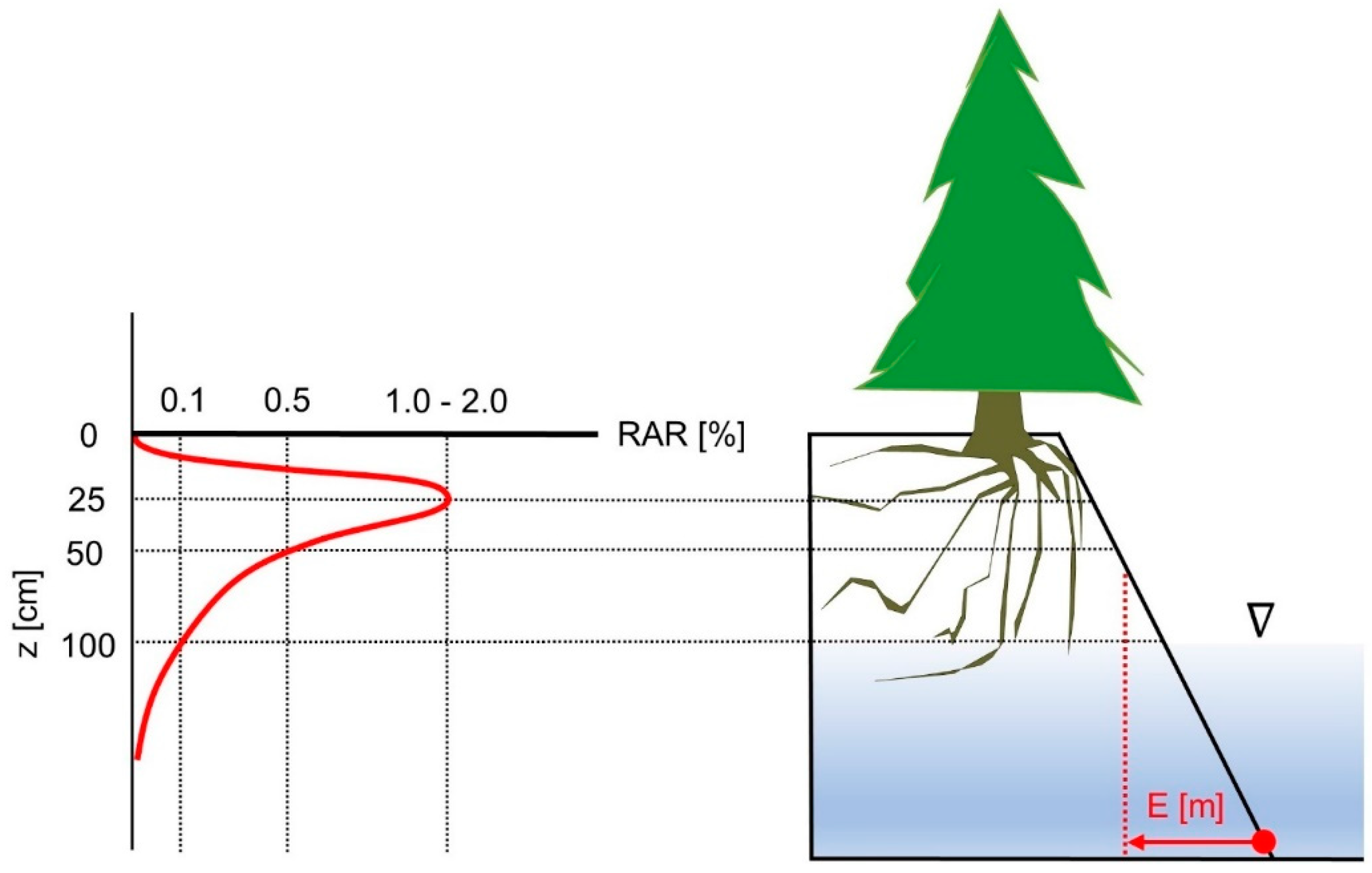
2.1. Description of the Framework
2.2. Case Studies
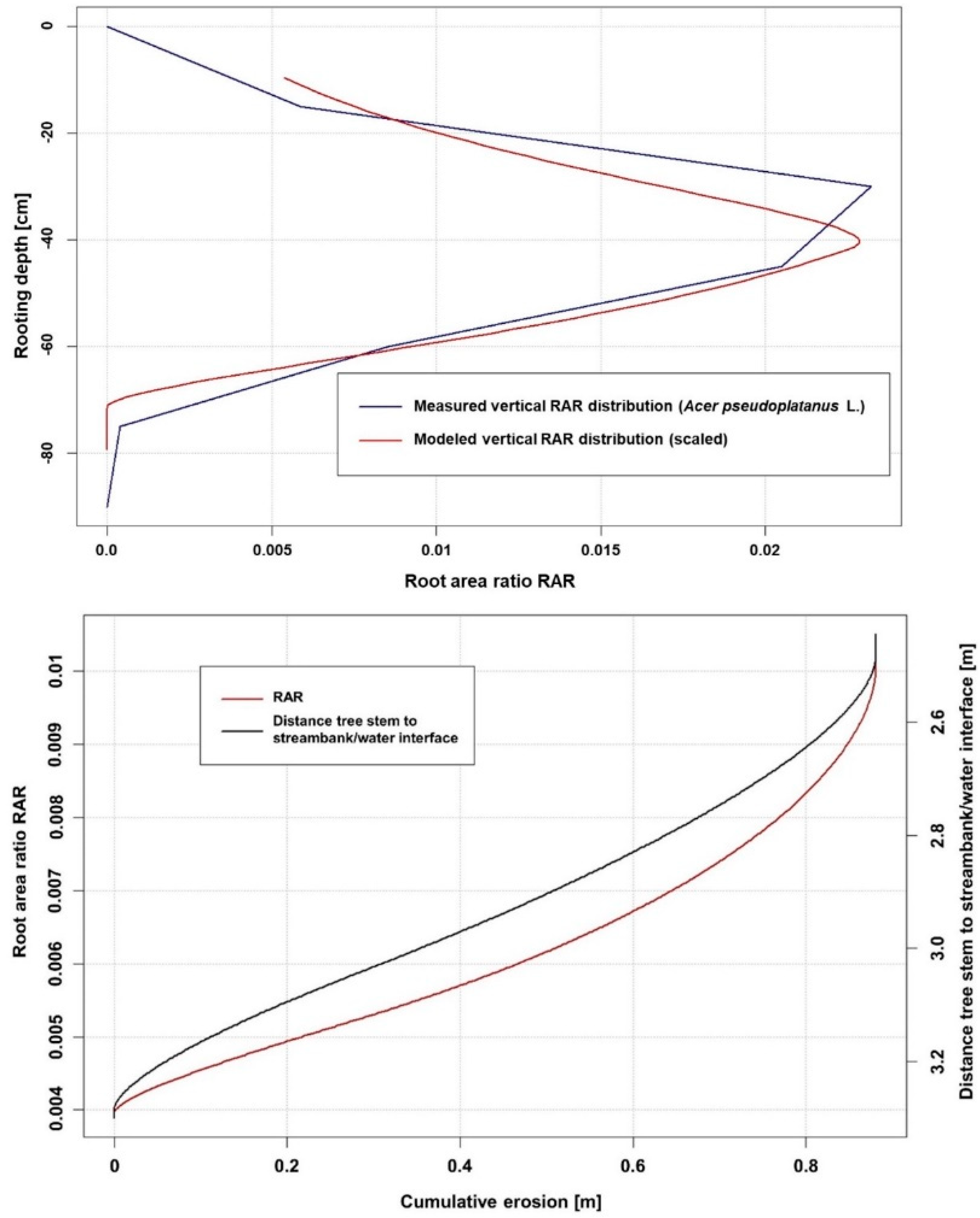
2.2.1. The Selwyn/Waikirikiri River Catchment
2.2.2. The Thur River Catchment
2.2.3. The Sulzigraben Catchment
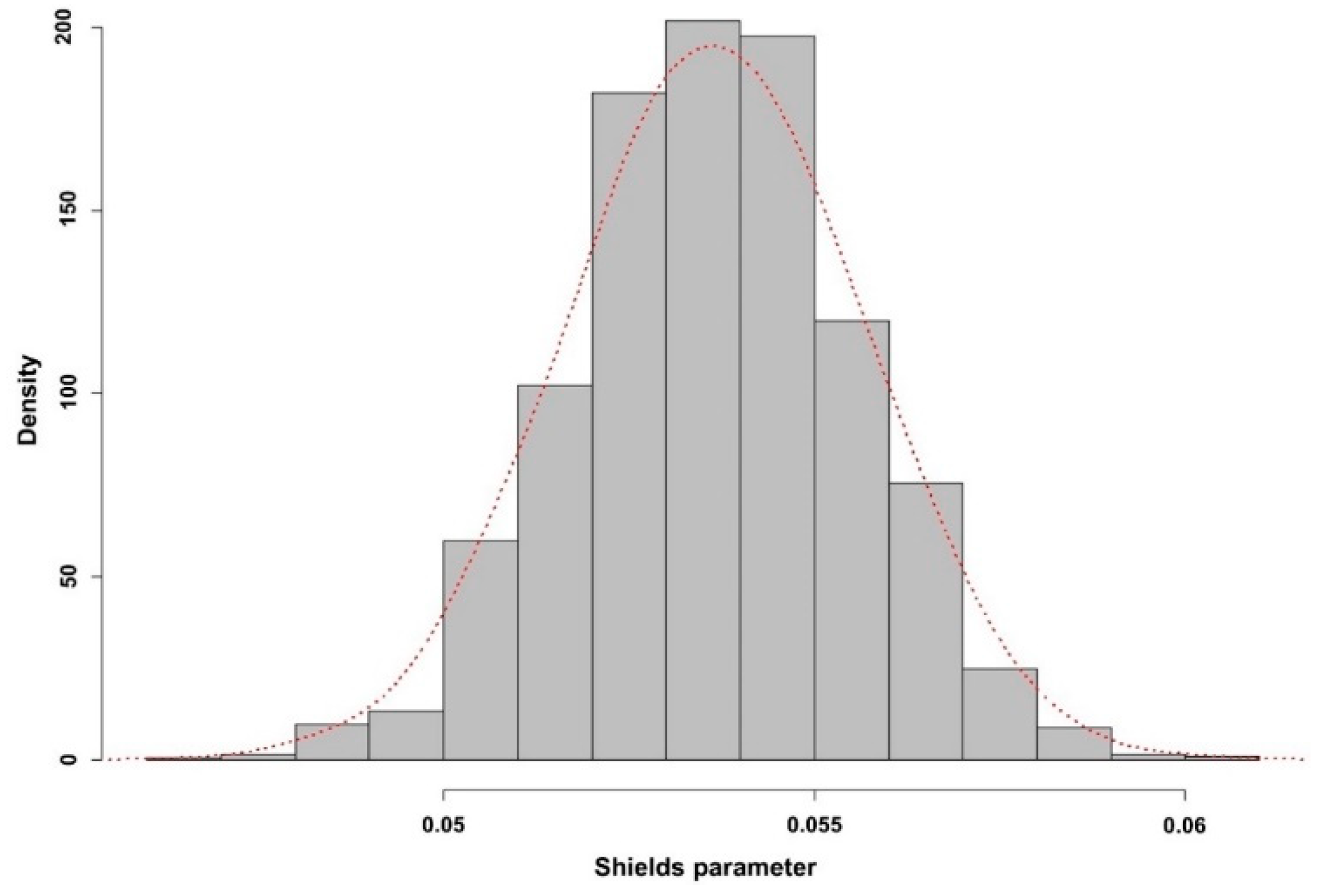
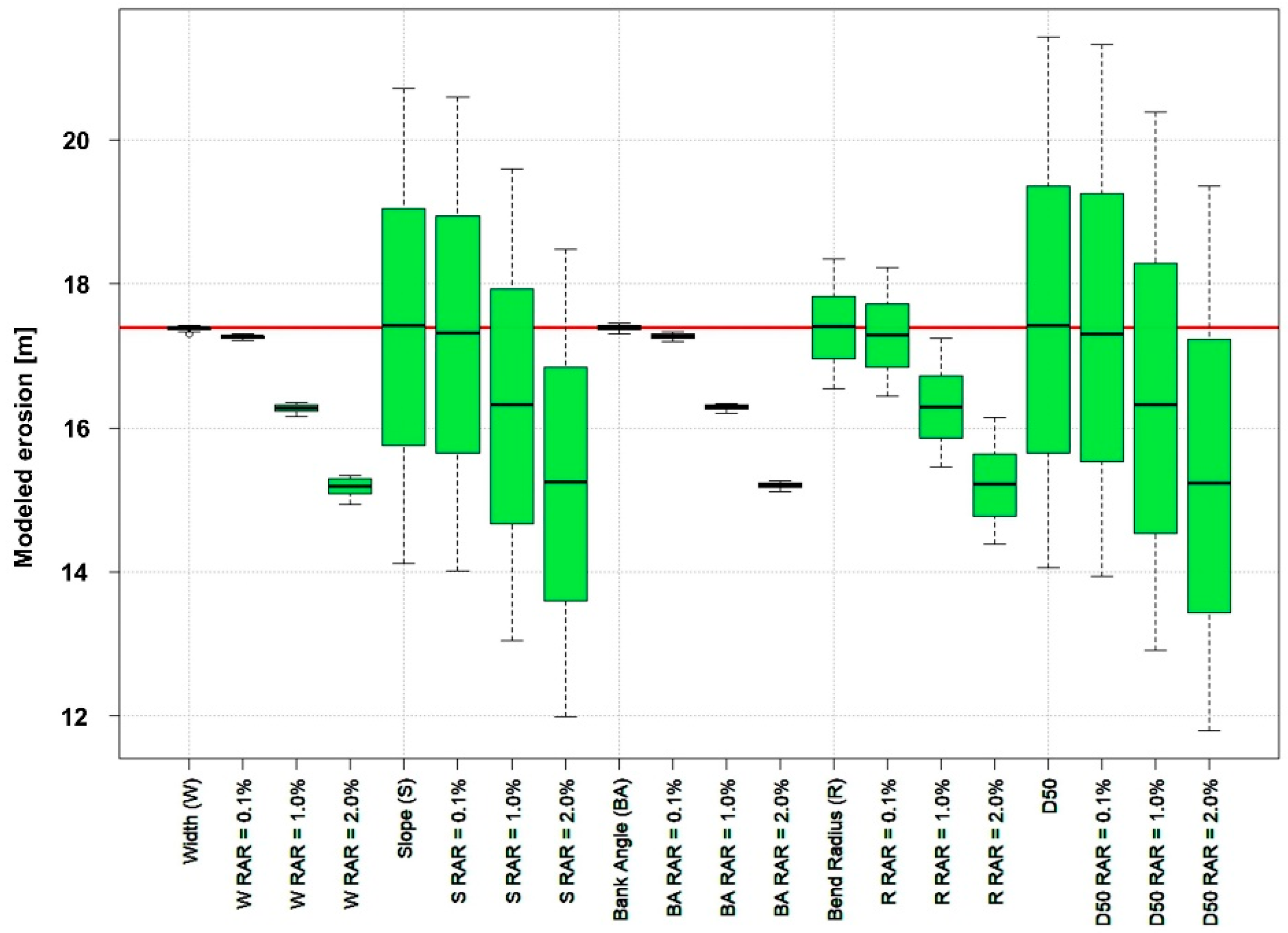
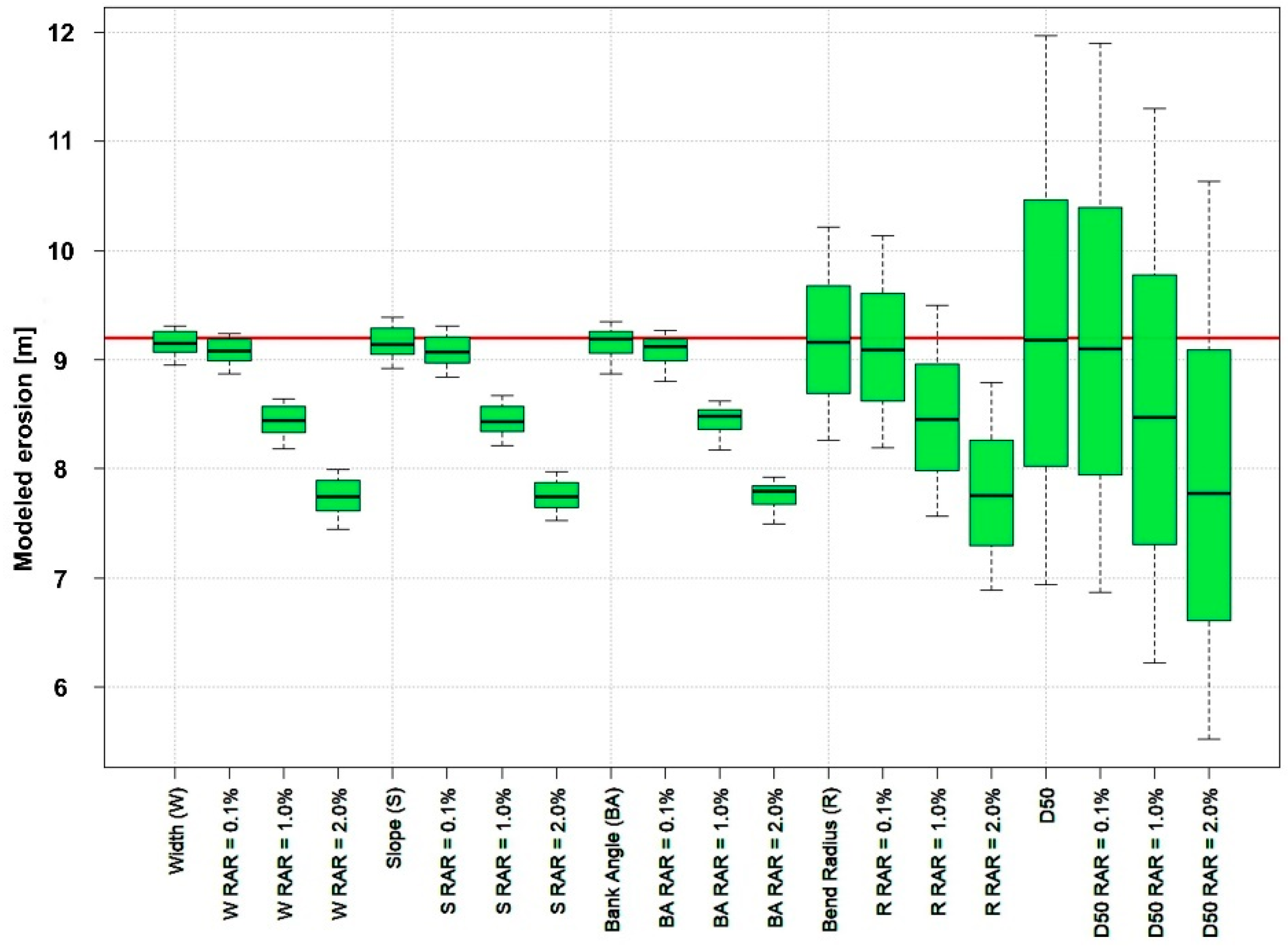
2.3. Sensitivity Analysis
3. Results
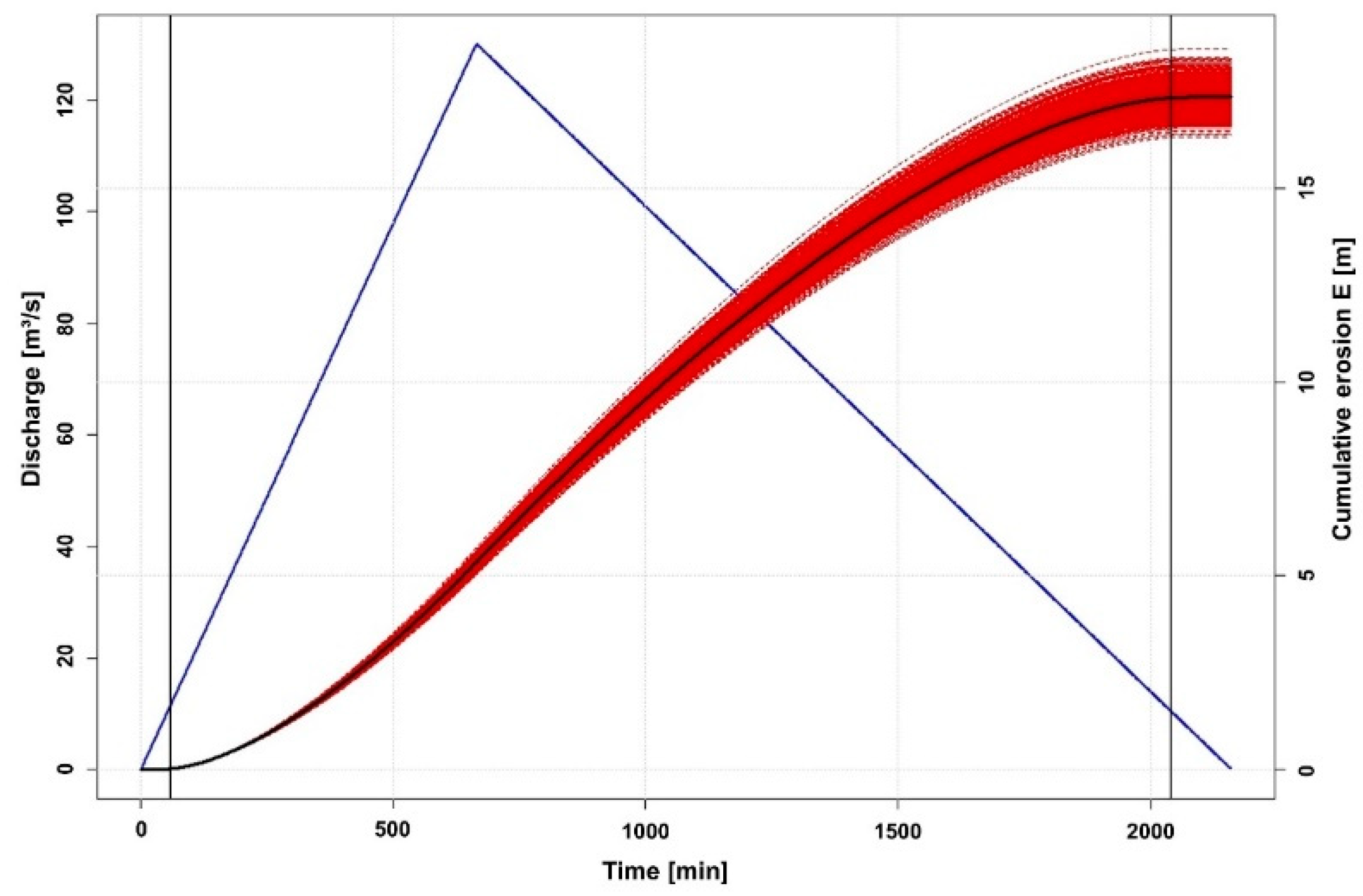
3.1. Validation
3.1.1. The Selwyn/Waikirikiri River Catchment
3.1.2. The Thur River Catchment
3.1.3. The Sulzigraben River Catchment
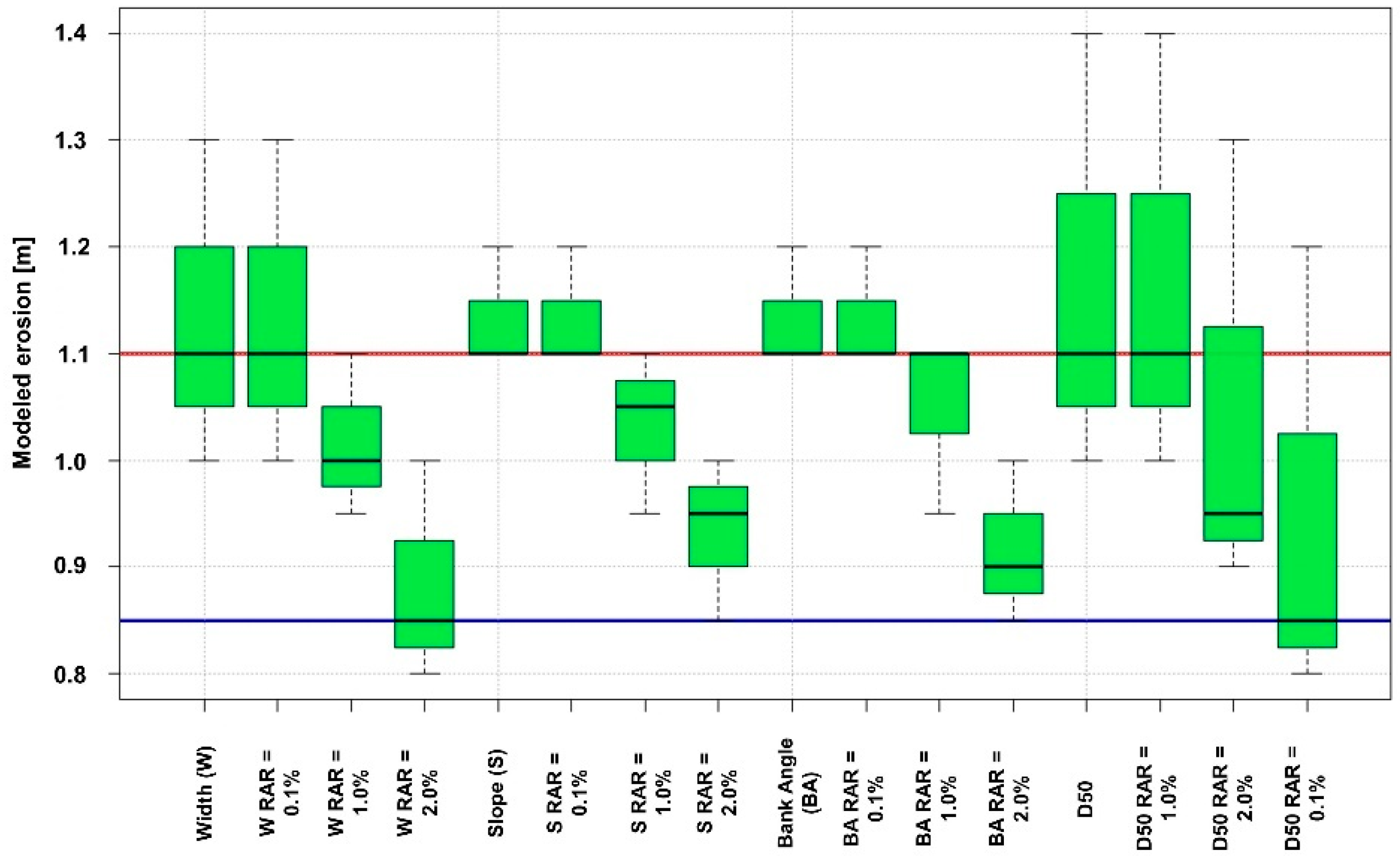
3.2. Sensitivity Analysis
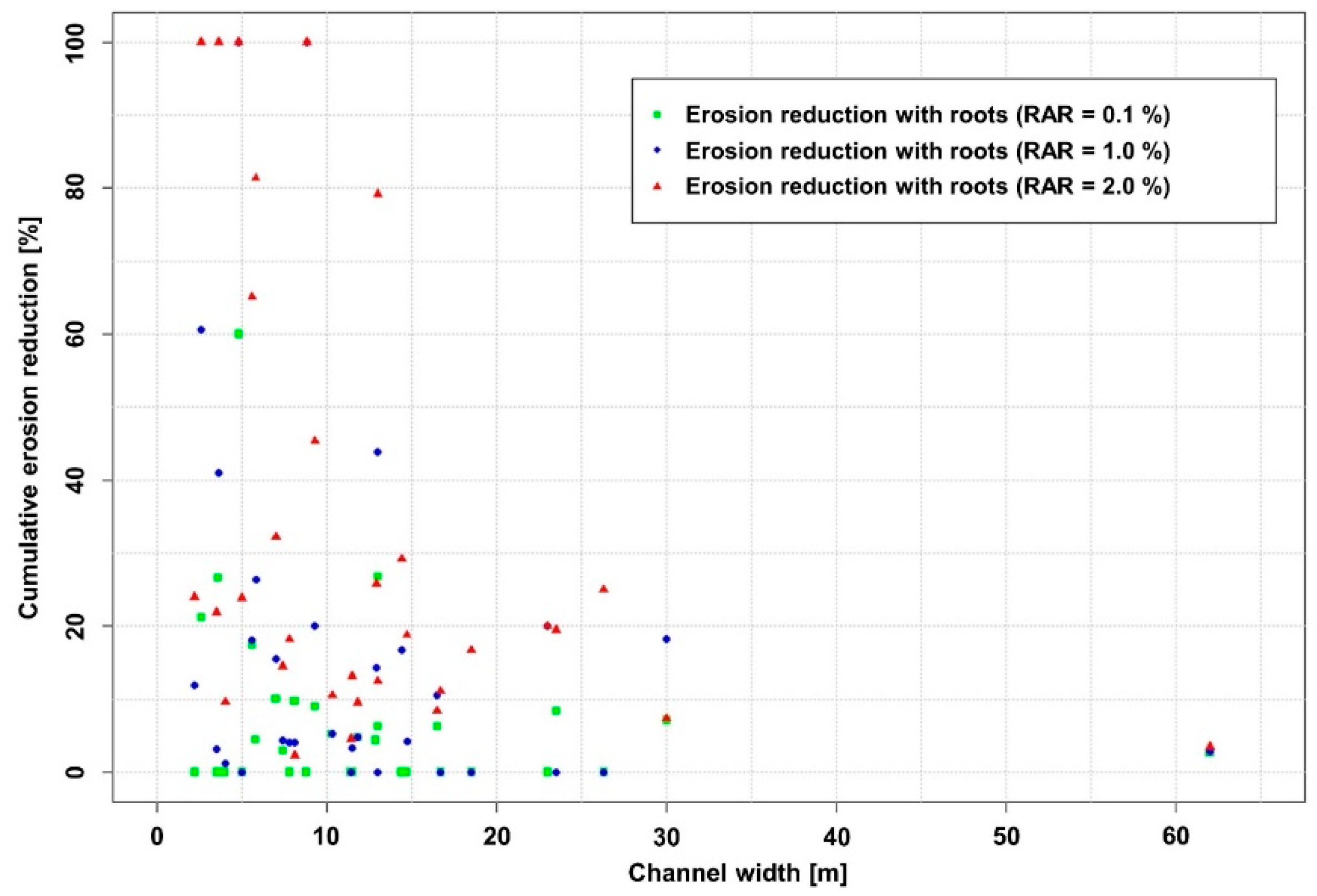
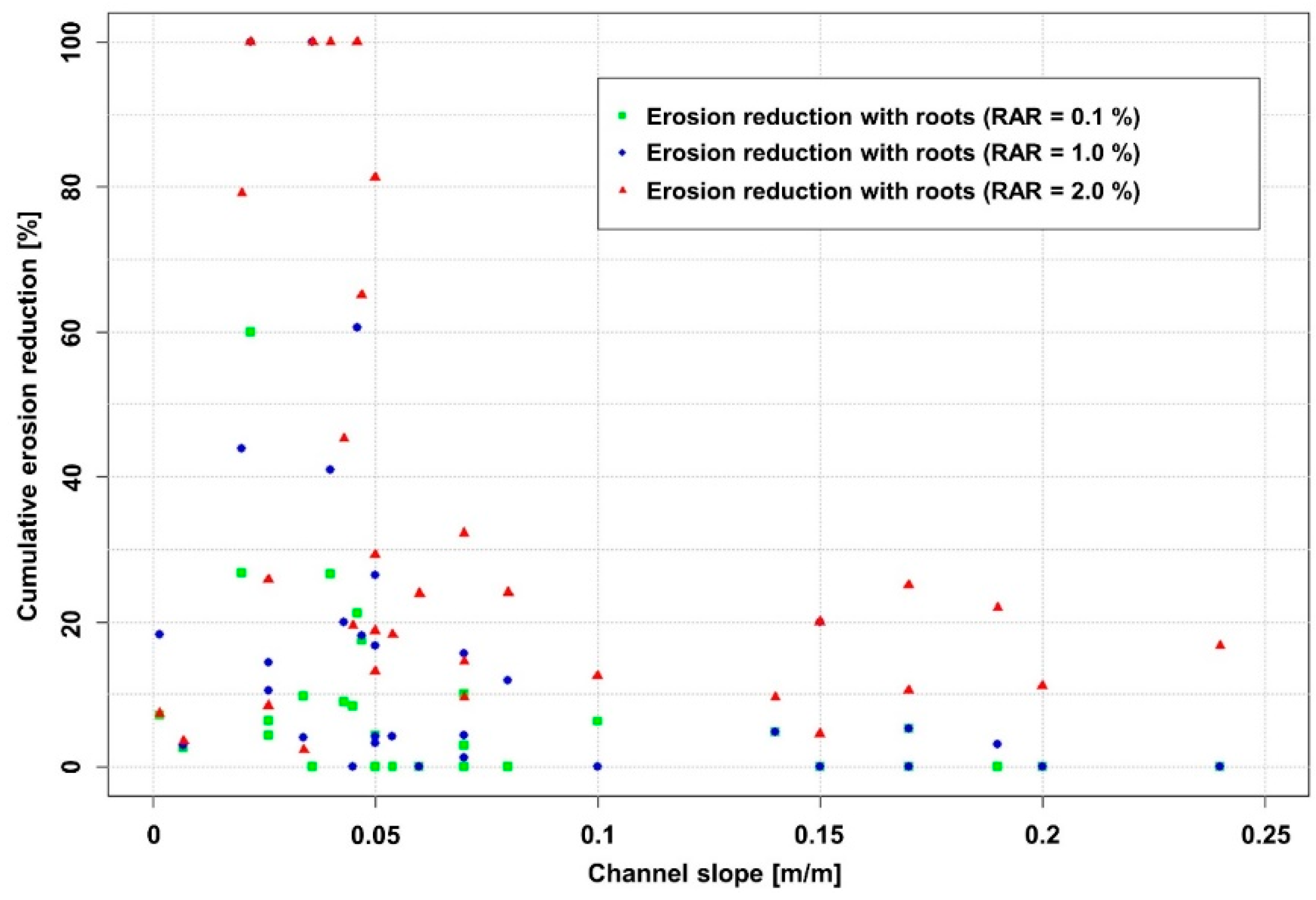
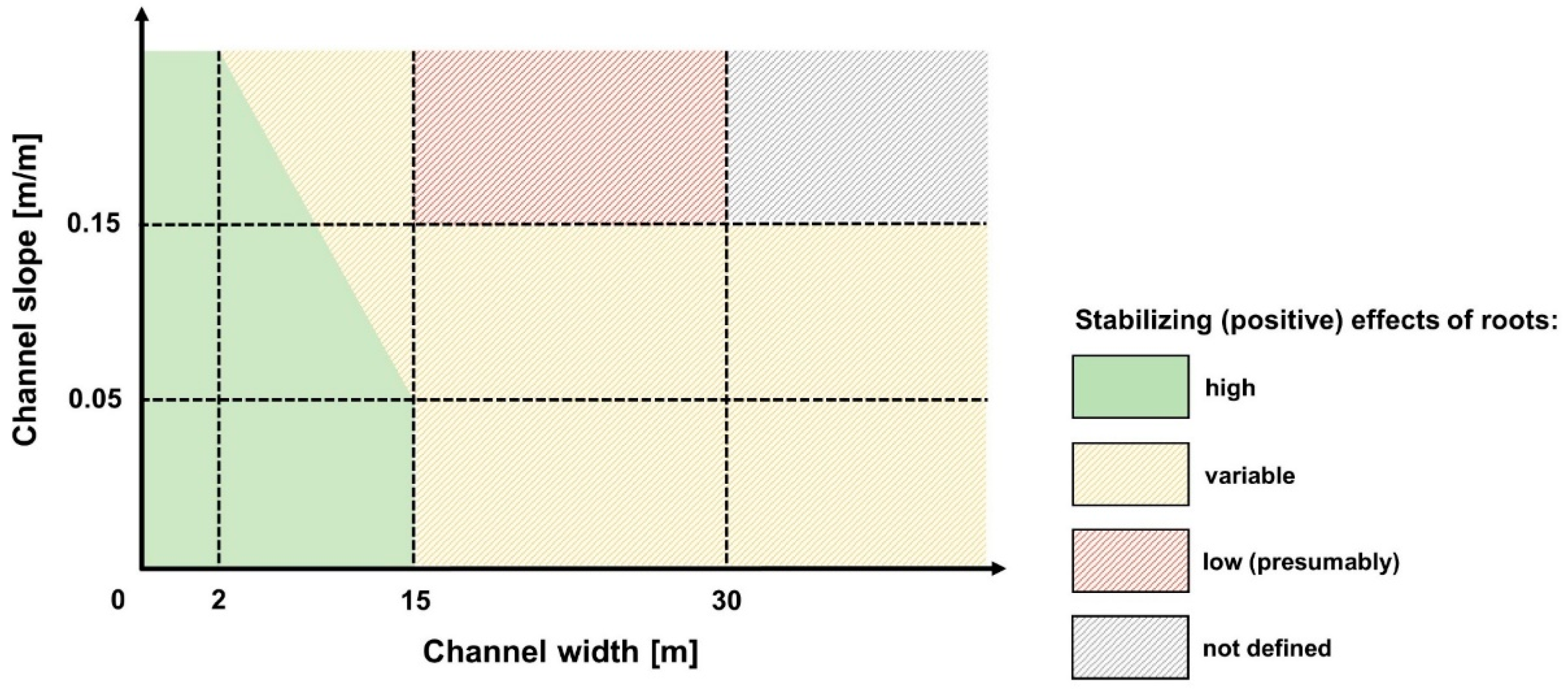
3.3. Susceptibility to Hydraulic Bank Erosion Considering the Effects of Roots
4. Discussion
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Winsemius, H.C.; Van Beek, L.P.H.; Jongman, B.; Ward, P.J.; Bouwman, A. A framework for global river flood risk assessments. Hydrol. Earth Syst. Sci. 2013, 17, 1871–1892. [Google Scholar] [CrossRef]
- Berz, G.; Kron, W.; Loster, T.; Rauch, E.; Schimetschek, J.; Schmieder, J.; Siebert, A.; Smolka, A.; Wirtz, A. World map of natural hazards—A global view of the distribution and intensity of significant exposures. Nat. Hazards 2001, 23, 443–465. [Google Scholar] [CrossRef]
- Julien, P.Y. River Mechanics; Cambridge University Press: Cambridge, UK, 2018. [Google Scholar]
- Smith, R.D.; Buffington, J.M. Effects of large woody debris on channel unit distribution in southeast Alaska. In Proceedings of the Watershed 1991, U.S. Forest Service Conference, Juneau, Alaska, 16–17 April 1991. [Google Scholar]
- Montgomery, D.R.; Buffington, J.M. Channel classification, prediction of channel response, and assessment of channel condition. In Report TFW-SI-110-93-002 prepared for the SHAMW committee of the Washington State Timber, Fish & Wildlife Agreement; University of Washington: Seattle, WA, USA, 24 June 1993; pp. 1–84. [Google Scholar]
- Cohen, A.S.; Bills, R.; Cocquyt, C.Z.; Caljon, A.G. The impact of sediment pollution on biodiversity in Lake Tanganyika. Conserv. Biol. 1993, 7, 667–677. [Google Scholar] [CrossRef]
- Piégay, H.; Darby, S.E.; Mosselman, E.; Surian, N. A review of techniques available for delimiting the erodible river corridor: A sustainable approach to managing bank erosion. River Res. Appl. 2005, 21, 773–789. [Google Scholar] [CrossRef]
- Lijklema, L.; Koelmans, A.A.; Portielje, R. Water quality impacts of sediment pollution and the role of early diagenesis. Water Sci. Technol. 1993, 28, 1–12. [Google Scholar] [CrossRef]
- Darby, S.E.; Trieu, H.Q.; Carling, P.A.; Sarkkula, J.; Koponen, J.; Kummu, M.; Conlan, I.; Leyland, J. A physically based model to predict hydraulic erosion of fine-grained riverbanks: The role of form roughness in limiting erosion. J. Geophys. Res. Earth Surf. 2010, 115. [Google Scholar] [CrossRef]
- Piégay, H.; Thevenet, A.; Citterio, A. Input, storage and distribution of large woody debris along a mountain river continuum, the Drôme River, France. Catena 1999, 35, 19–39. [Google Scholar] [CrossRef]
- Gregory, S.; Boyer, K.L.; Gurnell, A.M. Ecology and management of wood in world rivers. In Proceedings of the International Conference of Wood in World Rivers (2000: Corvallis, Or.); American Fisheries Society: Bethesda, MD, USA, 2003. [Google Scholar]
- Lassettre, N.S.; Kondolf, G.M. Large woody debris in urban stream channels: Redefining the problem. River Res. Appl. 2012, 28, 1477–1487. [Google Scholar] [CrossRef]
- Wohl, E.; Scott, D.N. Wood and sediment storage and dynamics in river corridors. Earth Surf. Process. Landf. 2017, 42, 5–23. [Google Scholar] [CrossRef]
- Janes, V.; Holman, I.; Birkinshaw, S.; O’Donnell, G.; Kilsby, C. Improving bank erosion modelling at catchment scale by incorporating temporal and spatial variability. Earth Surf. Process. Landf. 2018, 43, 124–133. [Google Scholar] [CrossRef]
- Ruiz-Villanueva, V.; Mazzorana, B.; Bladé, E.; Bürkli, L.; Iribarren-Anacona, P.; Mao, L.; Nakamura, F.; Ravazzolo, D.; Rickenmann, D.; Sanz-Ramos, M.; et al. Characterization of wood-laden flows in rivers. Earth Surf. Process. Landf. 2019, 44, 1694–1709. [Google Scholar] [CrossRef]
- Simon, A.; Collison, A.J.C. Quantifying the mechanical and hydrological effects of riparian vegetation on streambank stability. Earth Surf. Process. Landf. 2002, 27, 527–546. [Google Scholar] [CrossRef]
- Pollen, N.; Simon, A. Estimating the mechanical effects of riparian vegetation on stream bank stability using a fiber bundle model. Water Resour. Res. 2005, 41, W07025. [Google Scholar] [CrossRef]
- Docker, B.B.; Hubble, T.C.T. Quantifying root-reinforcement of river bank soils by four Australian tree species. Geomorphology 2008, 100, 401–418. [Google Scholar] [CrossRef]
- Osborne, L.L.; Kovacic, D.A. Riparian vegetated buffer strips in water-quality restoration and stream management. Freshw. Biol. 1993, 29, 243–258. [Google Scholar] [CrossRef]
- Dosskey, M.G.; Vidon, P.; Gurwick, N.P.; Allan, C.J.; Duval, T.P.; Lowrance, R. The role of riparian vegetation in protecting and improving chemical water quality in streams. JAWRA J. Am. Water Resour. Assoc. 2010, 46, 261–277. [Google Scholar] [CrossRef]
- Fetherston, K.L.; Naiman, R.J.; Bilby, R.E. Large woody debris, physical process, and riparian forest development in montane river networks of the Pacific Northwest. Geomorphology 1995, 13, 133–144. [Google Scholar] [CrossRef]
- Abbe, T.B.; Montgomery, D.R. Large woody debris jams, channel hydraulics and habitat formation in large rivers. Regul. Rivers Res. Manag. 1996, 12, 201–221. [Google Scholar] [CrossRef]
- Aarts, B.G.; Van Den Brink, F.W.; Nienhuis, P.H. Habitat loss as the main cause of the slow recovery of fish faunas of regulated large rivers in Europe: The transversal floodplain gradient. River Res. Appl. 2004, 20, 3–23. [Google Scholar] [CrossRef]
- Wohl, E. Bridging the gaps: An overview of wood across time and space in diverse rivers. Geomorphology 2016, 279, 3–26. [Google Scholar] [CrossRef]
- Wohl, E.; Angermeier, P.L.; Bledsoe, B.; Kondolf, G.M.; MacDonnell, L.; Merritt, D.M.; Palmer, M.A.; LeRoy Poff, N.; Tarboton, D. River restoration. Water Resour. Res. 2005, 41. [Google Scholar] [CrossRef]
- Partheniades, E. Erosion and deposition of cohesive soils. J. Hydraul. Div. 1965, 91, 105–139. [Google Scholar]
- Hanson, G.J.; Simon, A. Erodibility of cohesive streambeds in the loess area of the midwestern USA. Hydrol. Process. 2001, 15, 23–38. [Google Scholar] [CrossRef]
- Stecca, G.; Measures, R.; Hicks, D.M. A framework for the analysis of noncohesive bank erosion algorithms in morphodynamic modeling. Water Resour. Res. 2017, 53, 6663–6686. [Google Scholar] [CrossRef]
- Rinaldi, M.; Darby, S.E. Modelling river-bank-erosion processes and mass failure mechanisms: Progress towards fully coupled simulations. Gravel-Bed Rivers VI: Form Process Understanding to River Restoration. Dev. Earth Surf. Process. 2007, 11, 213–239. [Google Scholar]
- Lawler, D.M. Process dominance in bank erosion systems. In Lowland Floodplain Rivers; Carling, P., Petts, G.E., Eds.; Wiley: Chichester, UK, 1992; pp. 117–143. [Google Scholar]
- Couper, P.R.; Maddock, I.P. Subaerial river bank erosion processes and their interaction with other bank erosion mechanisms on the River Arrow, Warwickshire, UK. Earth Surf. Process. Landf. 2001, 26, 631–646. [Google Scholar] [CrossRef]
- Wynn, T.M.; Mostaghimi, S.; Alphin, E.F. The effects of vegetation on stream bank erosion. In Proceedings of the 2004 ASAE Annual Meeting; American Society of Agricultural and Biological Engineers: Ottawa, ON, Canada, 2004. [Google Scholar]
- Hubble, T.C.T.; Docker, B.B.; Rutherfurd, I.D. The role of riparian trees in maintaining riverbank stability: A review of Australian experience and practice. Ecol. Eng. 2010, 36, 292–304. [Google Scholar] [CrossRef]
- Pollen-Bankhead, N.; Simon, A. Hydrologic and hydraulic effects of riparian networks on streambank stability: Is mechanical root reinforcement the whole story? Geomorphology 2010, 116, 353–362. [Google Scholar] [CrossRef]
- Julian, P.J.; Torres, R. Hydraulic erosion of cohesive riverbanks. Geomorphology 2006, 76, 193–206. [Google Scholar] [CrossRef]
- Smith, H.G.; Spiekermann, R.; Dymond, J.; Basher, L. Predicting spatial patterns in riverbank erosion for catchment sediment budgets. N. Z. J. Mar. Freshwater Res. 2019, 53, 338–362. [Google Scholar] [CrossRef]
- Thorne, C.R. Processes and mechanisms of river bank erosion. In Gravel-Bed Rivers; Hey, R.D., Bathurst, J.C., Thorne, C.R., Eds.; Wiley: Chichester, UK, 1982; pp. 227–271. [Google Scholar]
- Fischenich, C. Stability Thresholds for Stream Restoration Materials; USAE Engineering Research and Development Center, Environmental Lab: Vicksburg, MS, USA, 2001. [Google Scholar]
- Liu, D.; Diplas, P.; Fairbanks, J.D.; Hodges, C.C. An experimental study of flow through rigid vegetation. J. Geophys. Res. Earth Surf. 2008, 113. [Google Scholar] [CrossRef]
- Nepf, H.; Ghisalberti, M. Flow and transport in channels with submerged vegetation. Acta Geophys. 2008, 56, 753–777. [Google Scholar] [CrossRef]
- Magilligan, F.J. Thresholds and the spatial variability of flood power during extreme floods. Geomorphology 1992, 5, 373–390. [Google Scholar] [CrossRef]
- Pasquale, N.; Perona, P. Experimental assessment of riverbed sediment reinforcement by vegetation roots. In River Flow 2014; Crc Press-Taylor & Francis Group: Leiden, The Netherlands, 2014; No. CONF; pp. 553–561. [Google Scholar]
- Bloemer, S.; Fernandes, J.P.; Florineth, F.; Geitz, P.; Gerstgraser, C.; Graf, F.; Hacker, E.; Johannsen, R.; Kovalev, N.; Markart, G.; et al. European Guidelines for Soil and Water Bioengineering. European Federation for Soil and Water Bioengineering: 2015. Available online: http://hdl.handle.net/10174/14589 (accessed on 22 March 2020).
- Van de Wiel, M.J.; Darby, S.E. A new model to analyse the impact of woody riparian vegetation on the geotechnical stability of riverbanks. Earth Surf. Process. Landf. 2007, 32, 2185–2198. [Google Scholar] [CrossRef]
- Langendoen, E.J.; Lowrance, R.R.; Simon, A. Assessing the impact of riparian processes on streambank stability. Ecohydrology 2009a, 2, 360–369. [Google Scholar] [CrossRef]
- Simon, A.; Curini, A.; Darby, S.E.; Langendoen, E.J. Bank and near-bank processes in an incised channel. Geomorphology 2000, 35, 193–217. [Google Scholar] [CrossRef]
- Pollen, N. Temporal and spatial variability in root reinforcement of streambanks: Accounting for soil shear strength and moisture. Catena 2007, 69, 197–205. [Google Scholar] [CrossRef]
- Klavon, K.; Fox, G.; Guertault, L.; Langendoen, E.; Enlow, H.; Miller, R.; Khanal, A. Evaluating a process-based model for use in streambank stabilization: Insights on the Bank Stability and Toe Erosion Model (BSTEM). Earth Surf. Process. Landf. 2017, 42, 191–213. [Google Scholar] [CrossRef]
- Lowrance, R.; Altier, L.S.; Williams, R.G.; Inamdar, S.P.; Sheridan, J.M.; Bosch, D.D.; Hubbard, R.K.; Thomas, D.L. REMM: The riparian ecosystem management model. J. Soil Water Conserv. 2000, 55, 27–34. [Google Scholar]
- Langendoen, E.J.; Alonso, C.V. Modeling the evolution of incised streams: I. Model formulation and validation of flow and streambed evolution components. J. Hydraul. Eng. 2009b, 134, 749–762. [Google Scholar] [CrossRef]
- Langendoen, E.J.; Simon, A. Modeling the evolution of incised streams. II: Streambank erosion. J. Hydraul. Eng. 2008a, 134, 905–915. [Google Scholar] [CrossRef]
- Langendoen, E.J.; Wells, R.R.; Thomas, R.E.; Simon, A.; Bingner, R.L. Modeling the evolution of incised streams. iii: Model application. J. Hydraul. Eng. 2009b, 135, 476–486. [Google Scholar] [CrossRef]
- Neitsch, S.L.; Arnold, J.G.; Kiniry, J.R.; Williams, J.R.; King, K.W. Soil and Water Assessment Tool (SWAT): Theoretical Documentation, Version 2000; Texas Water Resources Institute: College Station, TX, USA, 2002; TWRI Report TR-191. [Google Scholar]
- Gassman, P.W.; Reyes, M.R.; Green, C.H.; Arnold, J.G. The soil and water assessment tool: Historical development, applications, and future research directions. Trans. ASABE 2007, 50, 1211–1250. [Google Scholar] [CrossRef]
- Narasimhan, B.; Allen, P.M.; Coffman, S.V.; Arnold, J.G.; Srinivasan, R. Development and testing of a physically based model of streambank erosion for coupling with a basin-scale hydrologic model SWAT. JAWRA J. Am. Water Resour. Assoc. 2017, 53, 344–364. [Google Scholar] [CrossRef]
- Wilkinson, S.N.; Prosser, I.P.; Rustomji, P.; Read, A.M. Modelling and testing spatially distributed sediment budgets to relate erosion processes to sediment yields. Environ. Model. Softw. 2009, 24, 489–501. [Google Scholar] [CrossRef]
- Wilkinson, S.N.; Dougall, C.; Kinsey-Henderson, A.E.; Searle, R.D.; Ellis, R.J.; Bartley, R. Development of a time-stepping sediment budget model for assessing land use impacts in large river basins. Sci. Total Environ. 2014, 468, 1210–1224. [Google Scholar] [CrossRef]
- Hanson, G.J.; Cook, K.R. Development of excess shear stress parameters for circular jet testing. In Proceedings of the American Society of Agricultural Engineers International Meeting, Minneapolis, Minnesota, 10–14 August 1997; Paper no. 972227. pp. 1–21. [Google Scholar]
- Clark, L.A.; Wynn, T.M. Methods for determining streambank critical shear stress and soil erodibility: Implications for erosion rate predictions. Trans. ASABE 2007, 50, 95–106. [Google Scholar] [CrossRef]
- Fortier, S.; Scobey, F.C. Permissible canal velocities. Trans. Am. Soc. Civ. Eng. 1926, 89, 940–956. [Google Scholar]
- Shields, A. Anwendung der Aehnlichkeitsmechanik und der Turbulenzforschung auf die Geschiebebewegung. Ph.D. Thesis, Technical University Berlin, Berlin, Germany, 1936. [Google Scholar]
- Petit, F.; Houbrechts, G.; Peeters, A.; Hallot, E.; Van Campenhout, J.; Denis, A.C. Dimensionless critical shear stress in gravel-bed rivers. Geomorphology 2015, 250, 308–320. [Google Scholar] [CrossRef]
- Mostafa, T.S.; Imran, J.; Chaudhry, M.H.; Kahn, I.B. Erosion resistance of cohesive soils. J. Hydraul. Res. 2008, 46, 777–787. [Google Scholar] [CrossRef]
- Berenbrock, C.; Tranmer, A.W. Simulation of flow, sediment transport, and sediment mobility of the Lower Coeur d’Alene River, Idaho. In U.S. Geological Survey Scientific Investigations Report 2008-5093; US Geological Survey: Reston, VA, USA, 2008; pp. 1–164. [Google Scholar]
- Bunte, K.; Abt, S.R.; Swingle, K.W.; Cenderelli, D.A.; Schneider, J.M. Critical Shields values in coarse-bedded steep streams. Water Resour. Res. 2013, 49, 7427–7447. [Google Scholar] [CrossRef]
- Bischetti, G.B.; Chiaradia, E.A.; Simonato, T.; Spezialia, B.; Vitali, B.; Vullo, P.; Zocco, A. Root strength and root area ratio of forest species in Lombardy (Northern Italy). Plant Soil 2005, 278, 11–22. [Google Scholar] [CrossRef]
- Schwarz, M.; Cohen, D.; Or, D. Root-soil mechanical interactions during pullout and failure of root bundles. J. Geophys. Res. Earth Surf. 2010, 115. [Google Scholar] [CrossRef]
- Tron, S.; Perona, P.; Gorla, L.; Schwarz, M.; Laio, F.; Ridolfi, L. The signature of randomness in riparian plant root distributions. Geophys. Res. Lett. 2015, 42, 7098–7106. [Google Scholar] [CrossRef]
- Caflisch, F. Wurzelentwicklung und -Verstärkung von Grauerlen in Ingenieurbiologischen Massnahmen. Eine Fallstudie im Gebiet Arieschbach, Fideris (GR). Bachelor Thesis, Bern University of Applied Sciences, Zollikofen, Switzerland, 2015; pp. 1–86. [Google Scholar]
- Bischetti, G.B.; Chiaradia, E.A.; Epis, T.; Morlotti, E. Root cohesion of forest species in the Italian Alps. Plant Soil 2009, 324, 71–89. [Google Scholar] [CrossRef]
- Abdi, E.; Majnounian, B.; Rahimi, H.; Zobeiri, M.; Mashayekhi, Z.; Yosefzadeh, H. A comparison of root distribution of three hardwood species grown on a hillside in the Caspian forest, Iran. J. For. Res. 2010, 15, 99–107. [Google Scholar] [CrossRef]
- Naghdi, R.; Maleki, S.; Abdi, E.; Mousavi, R.; Nikooy, M. Assessing the effect of Alnus roots on hillslope stability in order to use in soil bioengineering. J. For. Sci. 2013, 59, 417–423. [Google Scholar] [CrossRef]
- Kölla, E. Estimating flood peaks from small rural catchments in Switzerland. J. Hydrol. 1987, 95, 203–225. [Google Scholar] [CrossRef]
- Marchi, L.; Borga, M.; Preciso, E.; Gaume, E. Characterisation of selected extreme flash floods in Europe and implications for flood risk management. J. Hydrol. 2010, 394, 118–133. [Google Scholar] [CrossRef]
- Soil Conservation Service SCS. National Engineering Handbook, Section 4; U.S. Department of Agriculture: Washington, DC, USA, 1972.
- Schirmer, M.; Luster, J.; Linde, N.; Perona, P.; Mitchell, E.A.; Barry, D.A.; Hollender, J.; Cirpka, O.A.; Schneider, P.; Vogt, T.; et al. Durisch-Kaiser, Morphological, hydrological, biogeochemical and ecological changes and challenges in river restoration—The Thur River case study. Hydrol. Earth Syst. Sci. 2014, 18, 2449–2462. [Google Scholar] [CrossRef]
- Schälchli, U.; Abbegg, J.; Hunzinger, L. Geschiebestudie Thur und Einzugsgebiet. In Ämter für Umwelt der Kantone Zürich; Thurgau: Appenzell und St. Gallen, Switzerland, 2005. [Google Scholar]
- Cattaneo, G. Hydrodynamic Simulations and Bank Stability Analysis of a Morphodynamically Active Restored River Corridor (Thur River, Switzerland). Master’ Thesis, École polytechnique fédérale de Lausanne EPFL, Lausanne, Switzerland, July 2012. [Google Scholar]
- Pasquale, N.; Perona, P.; Wombacher, A.; Burlando, P. Hydrodynamic model calibration from pattern recognition of non-orthorectified terrestrial photographs. Comput. Geosci. 2014, 62, 160–167. [Google Scholar] [CrossRef]
- Swiss Federal Office for the Environment: Discharge and water level measurements for the river Thur–Andelfingen. Available online: https://www.hydrodaten.admin.ch/en/2044.html (accessed on 2 May 2019).
- Hunziker, G. Hochwasser vom 7. Juni 2015 in der Zulg. In Ereignisanalyse; Hunziker Gefahrenmanagement: Kerzers, Switzerlands, 2015; pp. 1–36. [Google Scholar]
- Fehr, R. Einfache Bestimmung der Korngrössenverteilung von geschiebematerial mit Hilfe der Linienzahlanalyse. Schweiz. Ing. Und Archit. 1987, 38, 1104–1109. [Google Scholar]
- Wohl, E.E.; Wilcox, A. Channel geometry of mountain streams in New Zealand. J. Hydrol. 2005, 300, 252–266. [Google Scholar] [CrossRef]
- Gasser, E.; Schwarz, M.; Simon, A.; Perona, P.; Phillips, C.; Hübl, J.; Dorren, L. A review of modeling the effects of vegetation on large wood recruitment processes in mountain catchments. Earth-Sci. Rev. 2019, 194, 350–373. [Google Scholar] [CrossRef]
- ASTM. Standard Test Method for Erodibility Determination of Soil in the Field or in the Laboratory by the Jet Index Method; D 5852-00; ASTM: West Conshohocken, PA, USA, 1999; pp. 1–6. [Google Scholar]
- Wynn, T.; Mostaghimi, S. The effects of vegetation and soil type on streambank erosion, southwestern Virginia, USA. J. Am. Water Resour. Assoc. 2006, 42, 69–82. [Google Scholar] [CrossRef]
- Enlow, H.; Fox, G.; Guertault, L. Watershed variability in streambank erodibility and implications for erosion prediction. Water 2017, 9, 605. [Google Scholar] [CrossRef]
- Yuan, Y.; Khare, Y.; Wang, X.; Parajuli, P.B.; Kisekka, I.; Finsterle, S. Hydrologic and water quality models: Sensitivity. Trans. ASABE 2015, 58, 1721–1744. [Google Scholar]
- Golden, L.A.; Springer, G.S. Channel geometry, median grain size, and stream power in small mountain streams. Geomorphology 2006, 78, 64–76. [Google Scholar] [CrossRef]
- Van De Wiel, M.J. Numerical Modelling of Channel Adjustment in Alluvial Meandering Rivers with Riparian Vegetation. Ph.D. Thesis, University of Southampton, Southampton, UK, 2003. [Google Scholar]

| Model Name | Modeled Process | Effects of Vegetation | Reference |
|---|---|---|---|
| BSTEM & RipRoot | Geotechnical bank erosion, hydraulic bank erosion | Root reinforcement by adapting apparent cohesion (geotechnical bank erosion), adaption of critical shear stress (hydraulic bank erosion) based on values found in literature | [17,34,46,47,48] |
| CONCEPTS & REMM | Geotechnical bank erosion, hydraulic bank erosion | Root reinforcement by adapting apparent cohesion (geotechnical bank erosion) | [45,49,50,51,52] |
| SWAT | Hydraulic bank erosion, bed erosion | Adapting critical shear stress based on an empirical effect | [53,54,55] |
| Geotechnical bank erosion | Root reinforcement by adapting apparent cohesion | [44] | |
| SedNet | Hydraulic bank erosion | Consideration of vegetation cover (extent of vegetation cover) using a vegetation factor | [56,57] |
| Hydraulic bank erosion | Consideration of vegetation cover (extent of vegetation cover) using a vegetation factor | [36] |
| Input Parameters | Symbol | Dimension | Value |
|---|---|---|---|
| Discharge | Q | m3 s−1 | 130 |
| Duration of flood event | t | h | 38.9 |
| Mean channel width | W | m | 62 |
| Mean channel slope | S | m m−1 | 0.007 |
| Mean streambank angle | BA | ° | 85 |
| Mean bend radius | R | m | 185 |
| Median sediment diameter | D50 | mm | 27 |
| Root area ratio | RAR | % | - |
| Input Parameters | Symbol | Dimension | Value |
|---|---|---|---|
| Discharge | Q | m3 s−1 | see Table 4 |
| Duration of each flood event | t | h | 24 |
| Mean channel width | W | m | 30 |
| Mean channel slope | S | m m−1 | 0.0016 |
| Mean streambank angle | BA | ° | 45 |
| Mean bend radius | R | m | 100 |
| Median sediment diameter | D50 | mm | 10 |
| Root area ratio | RAR | % | 0.1/1/2 |
| Event | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Q | m³ s−1 | 122 | 206 | 362 | 174 | 120 | 170 | 61.9 | 340 | 501 | 390 | 492 | 628 |
| Input Parameters | Symbol | Dimension | Value |
|---|---|---|---|
| Discharge | Q | m3 s−1 | 11.4/18.9 |
| Duration of flood event | t | h | 6.5 |
| Mean channel width | W | m | 4/5 |
| Mean channel slope | S | m m−1 | 0.07 |
| Mean streambank angle | BA | ° | 29 |
| Mean bend radius | R | m | ∞ (straight reach) |
| Median sediment diameter | D50 | mm | 98 |
| Root area ratio | RARmax | % | 1 |
| Input Parameters | Symbol | Dimension | Event | Number | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | |||
| Modeled streambank erosion (no roots) | E | m | 1.37 | 3.20 | 5.90 | 2.56 | 1.32 | 2.47 | 0.10 | 5.58 | 7.75 | 6.32 | 7.64 | 9.18 |
| Standard deviation | - | m | 0.55 | 1.22 | 2.16 | 0.99 | 0.54 | 0.96 | 0.04 | 2.04 | 2.76 | 2.29 | 2.73 | 3.23 |
| Modeled streambank erosion (RAR = 0.1%) | E | m | 1.32 | 3.14 | 5.84 | 2.50 | 1.28 | 2.41 | 0.08 | 5.51 | 7.68 | 6.25 | 7.57 | 9.11 |
| Standard deviation | - | m | 0.54 | 1.20 | 2.13 | 0.97 | 0.52 | 0.94 | 0.03 | 2.02 | 2.74 | 2.27 | 2.71 | 3.21 |
| Modeled streambank erosion (RAR = 1%) | E | m | 0.93 | 2.61 | 5.20 | 2.00 | 0.89 | 1.93 | 0.01 | 4.90 | 7.05 | 5.64 | 6.95 | 8.48 |
| Standard deviation | - | m | 0.38 | 1.02 | 1.94 | 0.79 | 0.37 | 0.77 | 0.006 | 1.82 | 2.54 | 2.07 | 2.51 | 3.01 |
| Modeled streambank erosion (RAR = 2%) | E | m | 0.57 | 2.06 | 4.58 | 1.50 | 0.53 | 1.44 | 0.00 | 4.26 | 6.37 | 4.98 | 6.27 | 7.78 |
| Standard deviation | - | m | 0.25 | 0.82 | 1.72 | 0.61 | 0.23 | 0.58 | 0.00 | 1.61 | 2.33 | 1.86 | 2.29 | 2.80 |
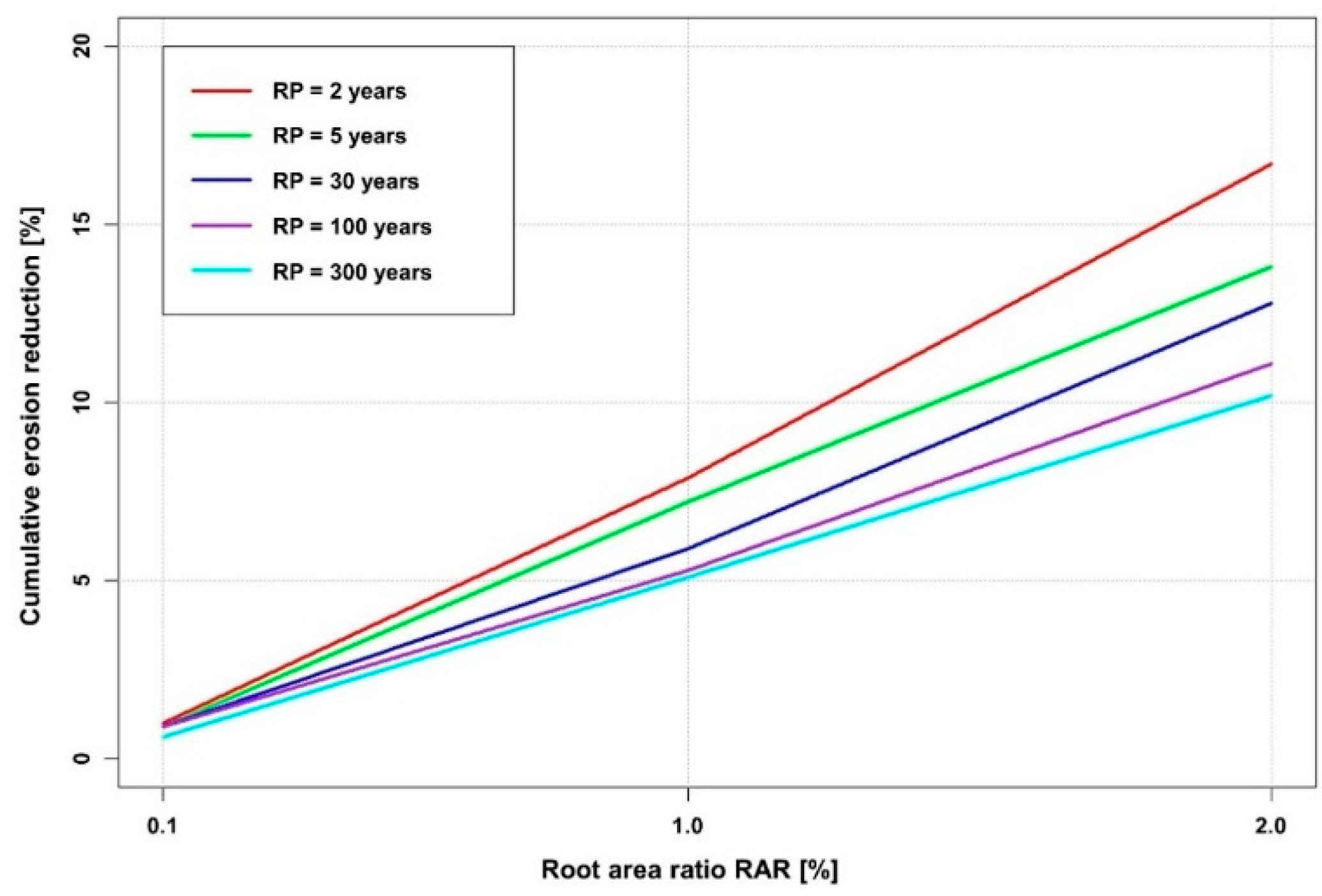
| Return Period | RAR | Cumulative Erosion Reduction |
|---|---|---|
| (Year) | (%) | (%) |
| 2 | 0.1 | 1 |
| 2 | 1 | 8 |
| 2 | 2 | 17 |
| 5 | 0.1 | 1 |
| 5 | 1 | 7 |
| 5 | 2 | 14 |
| 30 | 0 | 1 |
| 30 | 1 | 6 |
| 30 | 2 | 13 |
| 100 | 0 | 1 |
| 100 | 1 | 5 |
| 100 | 2 | 11 |
| 300 | 0.1 | 1 |
| 300 | 1 | 5 |
| 300 | 2 | 10 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Gasser, E.; Perona, P.; Dorren, L.; Phillips, C.; Hübl, J.; Schwarz, M. A New Framework to Model Hydraulic Bank Erosion Considering the Effects of Roots. Water 2020, 12, 893. https://doi.org/10.3390/w12030893
Gasser E, Perona P, Dorren L, Phillips C, Hübl J, Schwarz M. A New Framework to Model Hydraulic Bank Erosion Considering the Effects of Roots. Water. 2020; 12(3):893. https://doi.org/10.3390/w12030893
Chicago/Turabian StyleGasser, Eric, Paolo Perona, Luuk Dorren, Chris Phillips, Johannes Hübl, and Massimiliano Schwarz. 2020. "A New Framework to Model Hydraulic Bank Erosion Considering the Effects of Roots" Water 12, no. 3: 893. https://doi.org/10.3390/w12030893
APA StyleGasser, E., Perona, P., Dorren, L., Phillips, C., Hübl, J., & Schwarz, M. (2020). A New Framework to Model Hydraulic Bank Erosion Considering the Effects of Roots. Water, 12(3), 893. https://doi.org/10.3390/w12030893







