Design of PI Controllers for Irrigation Canals Based on Linear Matrix Inequalities
Abstract
1. Introduction
- -
- To provide a novel design method for PI controllers in irrigation canals.
- -
- To bring the benefits of LMI based design to irrigation canals, thus providing a design framework for linear controllers that can deal with issues as uncertainties in model parameters in a natural way.
- -
- To exploit subsystem synergies by using a centralized design to avoid undesired mutual interaction.
- -
- To make controller tuning closer to actual canal performance.
- -
- To validate and assess our results using a digital twin of ASCE Test Canal 1, which is implemented in a realistic state of the art software.
2. Materials and Methods
2.1. Problem Setting
The Linear Canal Model
2.2. Controller Design Procedure
2.2.1. Lmi Based Controller Design
- is a symmetric matrix for every and
- the dependence of the matrix function with respect to all variable decision is affine.
2.2.2. Tuning
- Penalties set by trial and error.
- Penalties proportional to the pool length of each section.
- Penalties proportional to the backwater surface area of each canal section.
2.3. Other Methods
- -
- Method 1: the resonance frequency based on the canal pool celerity.
- -
- Method 2: the resonance frequency based on the canal pool celerity and integral constants adjusted based on downstream resonance.
- -
- Method 3: the resonance frequency determined based on the maximum cross-over frequency.
- -
- Method 4: the resonance frequency determined based on the maximum cross-over frequency and integral constants adjusted based on downstream resonance.
2.4. Simulations
2.4.1. Case Study
2.4.2. Simulation Settings
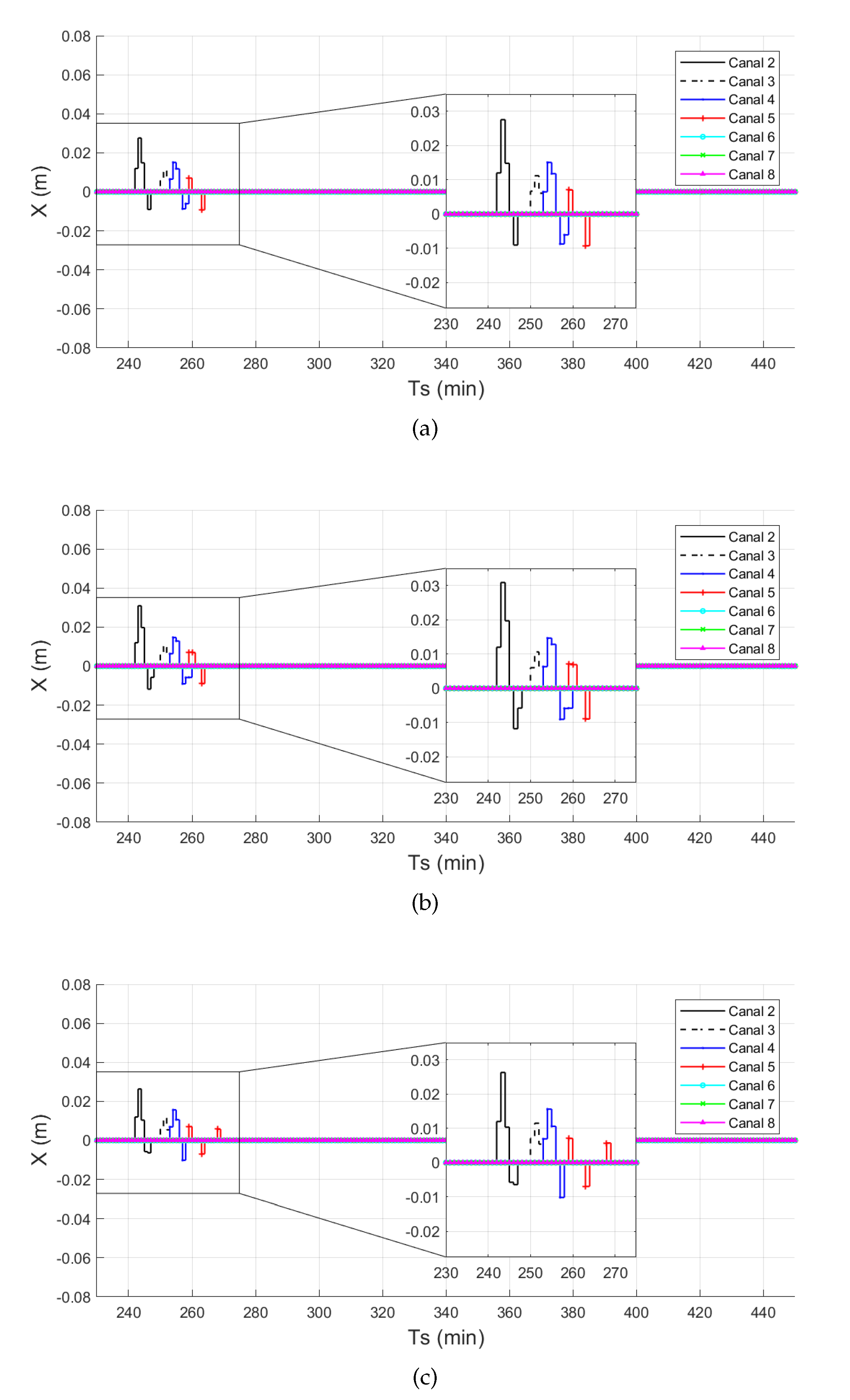
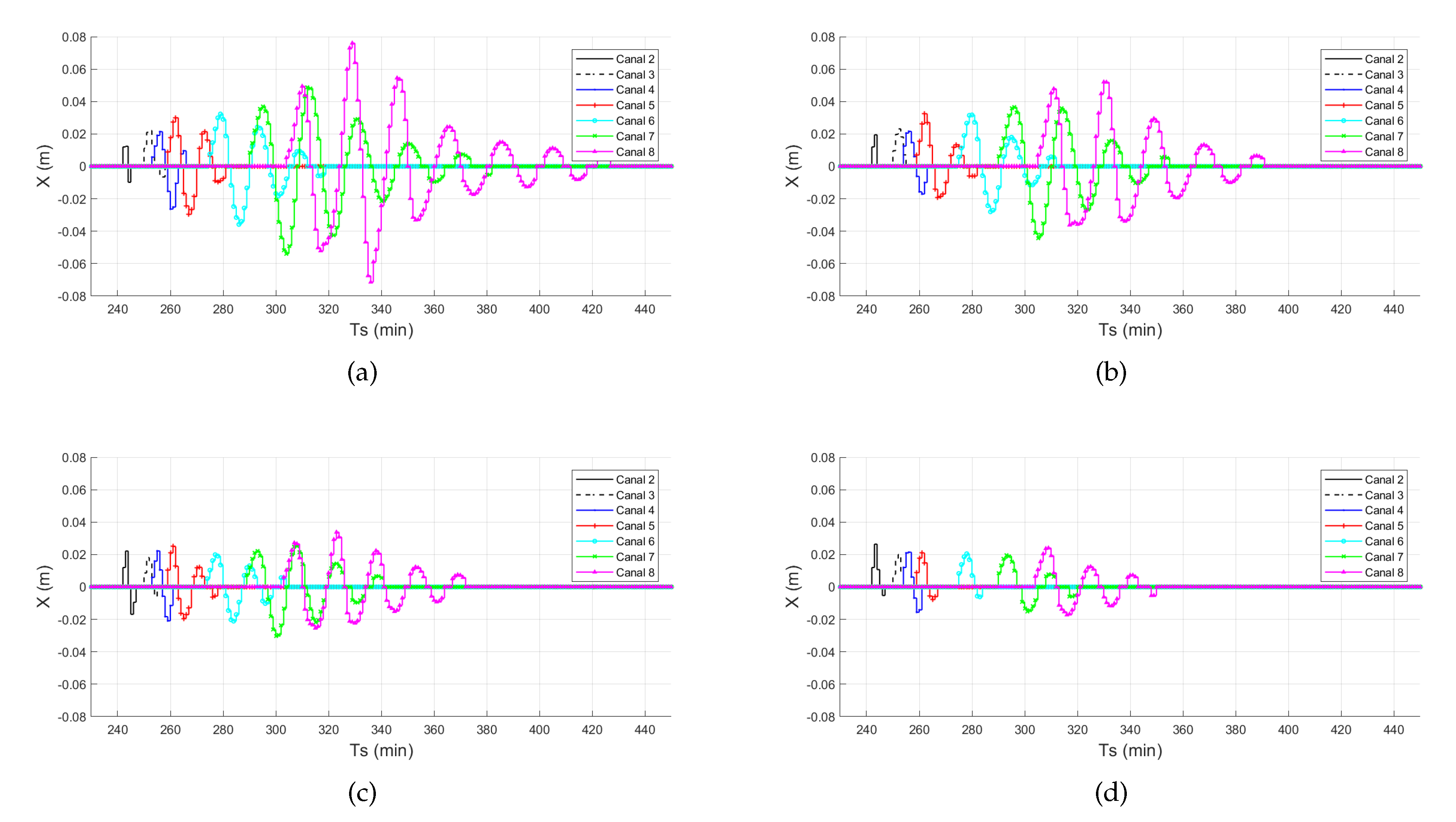
3. Results
- -
- The mean value of all the mean absolute water level error values of each pool, named as mean of mean absolute error (MMAE).
- -
- The mean value of how dispersed the absolute water level error values are with respect to its mean value, named as mean of standard deviations (MSTD).
- -
- The total sum value of how dispersed the absolute water level error values are with respect to its mean value, named as the sum of standard deviations (SSTD).
4. Discussion
4.1. Performance Indicators
4.2. Tuning and Performance
- LMI Method 3 has the best performance, presenting the best values for all but one KPI. It has the second best value for the resilience (Table 4), i.e., its great performance is achieved by slightly sacrificing the total time required to recover. Its main characteristic is the lowest maximum value as shown in Figure 2, Table 3 (MAE and IAE), and Table 5 (vulnerability).
- LMI Method 2 has the worst performance of LMI methods, however it is sufficient when all methods are jointly considered as its KPI values are above average. In particular, its response is similar to the other two LMI methods, however the performance indicators are slightly worse.
4.3. Overall Assessment
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Gleick, P.H. Water use. Annu. Rev. Environ. Resour. 2003, 28, 275–314. [Google Scholar] [CrossRef]
- Foley, J.A.; DeFries, R.; Asner, G.P.; Barford, C.; Bonan, G.; Carpenter, S.R.; Chapin, F.S.; Coe, M.T.; Daily, G.C.; Gibbs, H.K.; et al. Global consequences of land use. Science 2005, 309, 570–574. [Google Scholar] [CrossRef]
- Döll, P.; Siebert, S. Global modeling of irrigation water requirements. Water Resour. Res. 2002, 38, 8-1–8-10. [Google Scholar] [CrossRef]
- Wade, R.; Chambers, R. Managing the main system: Canal irrigation’s blind spot. Econ. Political Wkly. 1980, 15, A107–A112. [Google Scholar]
- Shahdany, S.M.H.; Firoozfar, A.; Maestre, J.; Mallakpour, I.; Taghvaeian, S.; Karimi, P. Operational performance improvements in irrigation canals to overcome groundwater overexploitation. Agric. Water Manag. 2018, 204, 234–246. [Google Scholar] [CrossRef]
- Malaterre, P.O.; Rogers, D.C.; Schuurmans, J. Classification of canal control algorithms. J. Irrig. Drain. Eng. 1998, 124, 3–10. [Google Scholar] [CrossRef]
- Burt, C.M. Regulation of Sloping Canals by Automatic Downstream Control. Ph.D. Thesis, Department of Agricultural and Irrigation Engineering, Utah State University, Logan, UT, USA, 1982; p. 172. [Google Scholar]
- Burt, C.M. Irrigation District Canal Automation-CARDD; ASAE Publication: Phoenix, AZ, USA, 1990; pp. 495–500. [Google Scholar]
- Chevereau, G.; Schwartz-Benezeth, S. BIVAL system for downstream control. In Planning, Operation, Rehabilitation and Automation of Irrigation Water Delivery Systems; ASCE: Preston, VA, USA, 1987; pp. 155–163. [Google Scholar]
- Shahverdi, K.; Monem, M.J. Construction and evaluation of the bival automatic control system for irrigation canals in a laboratory flume. Irrig. Drain. 2012, 61, 201–207. [Google Scholar] [CrossRef]
- Negenborn, R.R.; van Overloop, P.J.; Keviczky, T.; De Schutter, B. Distributed model predictive control of irrigation canals. NHM 2009, 4, 359–380. [Google Scholar] [CrossRef]
- Fele, F.; Maestre, J.M.; Hashemy, S.M.; de la Peña, D.M.; Camacho, E.F. Coalitional model predictive control of an irrigation canal. J. Process Control 2014, 24, 314–325. [Google Scholar] [CrossRef]
- Akouz, K.; Benhammou, A.; Malaterre, P.; Dahhou, B.; Roux, G. Predictive control applied to ASCE canal 2. In Proceedings of the 1998 IEEE International Conference on Systems, Man, and Cybernetics (Cat. No. 98CH36218), SMC’98, San Diego, CA, USA, 14 October 1998; Volume 4, pp. 3920–3924. [Google Scholar]
- Hashemy, S.; Monem, M.; Maestre, J.; Van Overloop, P. Application of an in-line storage strategy to improve the operational performance of main irrigation canals using model predictive control. J. Irrig. Drain. Eng. 2013, 139, 635–644. [Google Scholar] [CrossRef]
- Malaterre, P.O.; Rodellar, J. Multivariable predictive control of irrigation canals. Design and evaluation on a 2-pool model. In Proceedings of the International Workshop on Regulation of Irrigation Canals, Marrakech, Morocco, 22–24 April 1997; pp. 230–238. [Google Scholar]
- Shahdany, S.H.; Maestre, J.; Van Overloop, P. Equitable water distribution in main irrigation canals with constrained water supply. Water Resour. Manag. 2015, 29, 3315–3328. [Google Scholar] [CrossRef]
- Shahdany, S.H.; Taghvaeian, S.; Maestre, J.; Firoozfar, A. Developing a centralized automatic control system to increase flexibility of water delivery within predictable and unpredictable irrigation water demands. Comput. Electron. Agric. 2019, 163, 104862. [Google Scholar] [CrossRef]
- Tian, X.; Guo, Y.; Negenborn, R.R.; Wei, L.; Lin, N.M.; Maestre, J.M. Multi-Scenario Model Predictive Control Based on Genetic Algorithms for Level Regulation of Open Water Systems under Ensemble Forecasts. Water Resour. Manag. 2019, 33, 3025–3040. [Google Scholar] [CrossRef]
- Clemmens, A.; Replogle, J. Control of irrigation canal networks. J. Irrig. Drain. Eng. 1989, 115, 96–110. [Google Scholar] [CrossRef]
- Wahlin, B.T.; Clemmens, A.J. Performance of historic downstream canal control algorithms on ASCE test canal 1. J. Irrig. Drain. Eng. 2002, 128, 365–375. [Google Scholar] [CrossRef]
- Zamani, S.; Parvaresh Rizi, A.; Isapoor, S. The effect of design parameters of an irrigation canal on tuning of coefficients and performance of a PI controller. Irrig. Drain. 2015, 64, 519–534. [Google Scholar] [CrossRef]
- Burt, C.M.; Mills, R.; Khalsa, R.D. Improved proportional-integral (PI) logic for canal automation. J. Irrig. Drain. Eng. 1998, 124, 53–57. [Google Scholar] [CrossRef][Green Version]
- van Overloop, P.J.; Schuurmans, J.; Brouwer, R.; Burt, C.M. Multiple-model optimization of proportional integral controllers on canals. J. Irrig. Drain. Eng. 2005, 131, 190–196. [Google Scholar] [CrossRef][Green Version]
- van Overloop, P.J.; Weijs, S.; Dijkstra, S. Multiple model predictive control on a drainage canal system. Control Eng. Pract. 2008, 16, 531–540. [Google Scholar] [CrossRef]
- Karanjkar, D.; Chatterji, S.; Kumar, A. Development of linear quadratic regulator based PI controller for maximum power point tracking in solar photo-voltaic system. In Proceedings of the 2014 Recent Advances in Engineering and Computational Sciences (RAECS), Chandigarh, India, 6–8 March 2014; pp. 1–6. [Google Scholar]
- Litrico, X.; Malaterre, P.O.; Baume, J.P.; Vion, P.Y.; Ribot-Bruno, J. Automatic tuning of PI controllers for an irrigation canal pool. J. Irrig. Drain. Eng. 2007, 133, 27–37. [Google Scholar] [CrossRef]
- Lan, D.C. Research on Canal System Automation Control Based on Adaptive Parameters Fuzzy. In Applied Mechanics and Materials; Trans Tech Publications Ltd.: Stafa-Zurich, Switzerland, 2013; Volume 373, pp. 1529–1532. [Google Scholar]
- Litrico, X.; Fromion, V.; Baume, J.P.; Rijo, M. Modelling and PI control of an irrigation canal. In Proceedings of the 2003 European Control Conference (ECC), Seville, Spain, 3–5 April 2003; pp. 850–855. [Google Scholar]
- Baume, J.P.; Malaterre, P.O.; Sau, J. Tuning of PI controllers for an irrigation canal using optimization tools. In Proceedings of the USCID Workshop on Modernization of Irrigation Water Delivery Systems, Phoenix, AZ, USA, 17–21 October 1999. [Google Scholar]
- Lozano, D.; Arranja, C.; Rijo, M.; Mateos, L. Simulation of automatic control of an irrigation canal. Agric. Water Manag. 2010, 97, 91–100. [Google Scholar] [CrossRef]
- Rijo, M.; Arranja, C. Supervision and water depth automatic control of an irrigation canal. J. Irrig. Drain. Eng. 2010, 136, 3–10. [Google Scholar] [CrossRef][Green Version]
- Isapoor, S.; Montazar, A.; Van Overloop, P.; Van De Giesen, N. Designing and evaluating control systems of the Dez main canal. Irrig. Drain. 2011, 60, 70–79. [Google Scholar] [CrossRef]
- Litrico, X.; Fromion, V.; Baume, J.P. Tuning of robust distant downstream PI controllers for an irrigation canal pool. II: Implementation issues. J. Irrig. Drain. Eng. 2006, 132, 369–379. [Google Scholar] [CrossRef]
- Aguilar, J.V.; Langarita, P.; Linares, L.; Rodellar, J. Automatic control of flows and levels in an irrigation canal. IEEE Trans. Ind. Appl. 2009, 45, 2198–2208. [Google Scholar] [CrossRef]
- Alamo, T.; Normey-Rico, J.E.; Arahal, M.; Limon, D.; Camacho, E. Introducing linear matrix inequalities in a control course. IFAC Proc. Vol. 2006, 39, 205–210. [Google Scholar] [CrossRef]
- Martins, V.D.S.; Rodrigues, M. A proportional integral feedback for open channels control trough LMI design. IFAC Proc. Vol. 2011, 44, 4107–4112. [Google Scholar] [CrossRef]
- Clemmens, A.; Wahlin, B. Simple optimal downstream feedback canal controllers: ASCE test case results. J. Irrig. Drain. Eng. 2004, 130, 35–46. [Google Scholar] [CrossRef]
- Lian, F.; Chakrabortty, A.; Duel-Hallen, A. Game-Theoretic Multi-Agent Control and Network Cost Allocation under Communication Constraints. IEEE J. Sel. Areas Commun. 2017, 35, 330–340. [Google Scholar] [CrossRef]
- Lin, F.; Fardad, M.; Jovanovic, M.R. Design of Optimal Sparse Feedback Gains via the Alternating Direction Method of Multipliers. IEEE Trans. Autom. Control 2013, 58, 2426–2431. [Google Scholar] [CrossRef]
- Rotkowitz, M.; Lall, S. Decentralized Control Information Structures Preserved under Feedback. In Proceedings of the 41th IEEE Confenrence on Decision and Control, Las Vegas, NV, USA, 10–13 December 2002. [Google Scholar]
- Maestre, J. Distributed Model Predictive Control Based on Game Theory. Ph.D. Thesis, The University of Seville, Andalucia, Spain, 2010. [Google Scholar]
- Maestre, J.M.; Muñoz de la Peña, D.; Jimenez Losada, A.; Algaba, E.; Camacho, E.F. A coalitional control scheme with applications to cooperative game theory. Optim. Control Appl. Methods 2013, 35, 592–608. [Google Scholar] [CrossRef]
- Polyak, B.T.; Khlebnikov, M.V.; Shcherbakov, P. An LMI approach to structured sparse feedback design in linear control systems. In Proceedings of the 2013 European Control Conference (ECC), Zurich, Switzerland, 17–19 July 2013. [Google Scholar]
- Clemmens, A.; Kacerek, T.; Grawitz, B.; Schuurmans, W. Test cases for canal control algorithms. J. Irrig. Drain. Eng. 1998, 124, 23–30. [Google Scholar] [CrossRef]
- Wahlin, B.T. Performance of model predictive control on ASCE test canal 1. J. Irrig. Drain. Eng. 2004, 130, 227–238. [Google Scholar] [CrossRef]
- Clemmens, A.; Sloan, G.; Schuurmans, J. Canal-control needs: Example. J. Irrig. Drain. Eng. 1994, 120, 1067–1085. [Google Scholar] [CrossRef]
- Schuurmans, J.; Bosgra, O.; Brouwer, R. Open-channel flow model approximation for controller design. Appl. Math. Model. 1995, 19, 525–530. [Google Scholar] [CrossRef]
- Schuurmans, J.; Hof, A.; Dijkstra, S.; Bosgra, O.; Brouwer, R. Simple water level controller for irrigation and drainage canals. J. Irrig. Drain. Eng. 1999, 125, 189–195. [Google Scholar] [CrossRef]
- Clemmens, A.; Schuurmans, J. Simple optimal downstream feedback canal controllers: Theory. J. Irrig. Drain. Eng. 2004, 130, 26–34. [Google Scholar] [CrossRef]
- Ghainet, P.; Nemirovski, A.; Laub, A.; Chilali, M. LMI Control Toolbox-for Use with Matlab; The Math Works Inc.: Natick, MA, USA, 1995. [Google Scholar]
- Clemmens, A.; Tian, X.; van Overloop, P.J.; Litrico, X. Integrator delay zero model for design of upstream water-level controllers. J. Irrig. Drain. Eng. 2015, 143, B4015001. [Google Scholar] [CrossRef]
- Clemmens, A.; Bautista, E.; Wahlin, B.; Strand, R. Simulation of automatic canal control systems. J. Irrig. Drain. Eng. 2005, 131, 324–335. [Google Scholar] [CrossRef][Green Version]
- Liu, F.; Feyen, J.; Malaterre, P.O.; Baume, J.P.; Kosuth, P. Development and evaluation of canal automation algorithm CLIS. J. Irrig. Drain. Eng. 1998, 124, 40–46. [Google Scholar] [CrossRef]
- Hashimoto, T.; Stedinger, J.R.; Loucks, D.P. Reliability, resiliency, and vulnerability criteria for water resource system performance evaluation. Water Resour. Res. 1982, 18, 14–20. [Google Scholar] [CrossRef]
- McMahon, T.A.; Adeloye, A.J.; Zhou, S.L. Understanding performance measures of reservoirs. J. Hydrol. 2006, 324, 359–382. [Google Scholar] [CrossRef]
- Muros, F.J.; Maestre, J.M.; Algaba, E.; Alamo, T.; Camacho, E.F. Networked control design for coalitional schemes using game-theoretic methods. Automatica 2017, 78, 320–332. [Google Scholar] [CrossRef]
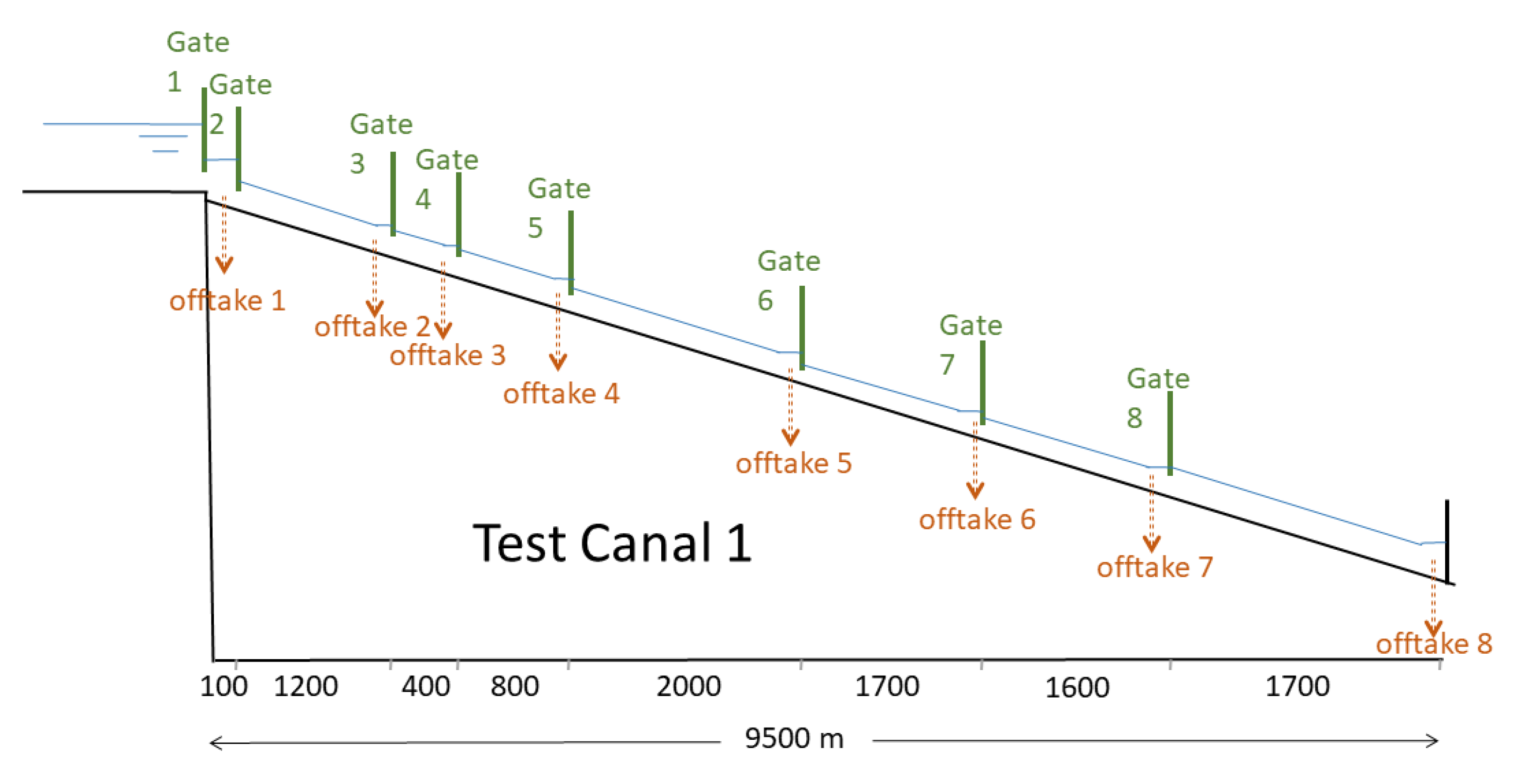
| ASCE Test Canal 1 | ||||
|---|---|---|---|---|
| Bottom Slope (m/m) | Manning’s n (-) | Side Slopes (m/m) | Drop at Each Gate (m) | /(m/m) |
| 0.002 | 0.014 | 1.5 | 1.0 | 1.45 |
| Pool Number | Pool Length (m) | Upstream Elevation (m) | Downstream Elevation (m) | Target Level (m) |
| 1 | 100 | 415.6 | 415.3 | 0.9 |
| 2 | 1200 | 408.0 | 405.6 | 0.9 |
| 3 | 400 | 403.4 | 402.6 | 0.8 |
| 4 | 800 | 399.7 | 398.1 | 0.9 |
| 5 | 2000 | 392.1 | 388.1 | 0.9 |
| 6 | 1700 | 387.4 | 384.8 | 0.8 |
| 7 | 1600 | 383.8 | 380.3 | 0.8 |
| 8 | 1700 | 379.0 | 376.1 | 0.8 |
| No. Pool | LMI Method 1 | LMI Method 2 | LMI Method 3 | |||
|---|---|---|---|---|---|---|
| 1 | 1.3079 | 0.0383 | 1.1542 | 0.0334 | 1.4104 | 0.0428 |
| 2 | 2.5170 | 0.0718 | 2.6483 | 0.0826 | 2.5172 | 0.0727 |
| 3 | 2.1069 | 0.0631 | 2.1260 | 0.0653 | 2.1411 | 0.0659 |
| 4 | 5.9515 | 0.1676 | 5.8530 | 0.1635 | 6.1181 | 0.1715 |
| 5 | 6.8866 | 0.1956 | 6.8934 | 0.1961 | 6.8971 | 0.1939 |
| 6 | 8.5417 | 0.2418 | 8.5433 | 0.2410 | 8.5357 | 0.2331 |
| 7 | 5.3328 | 0.1619 | 5.3329 | 0.1620 | 5.3329 | 0.1621 |
| Methods | MAE () | IAE () | MMAE () | MSTD () | SSTD () | ||
|---|---|---|---|---|---|---|---|
| Max | Mean | Max | Mean | ||||
| LMI Method 1 | 2.76 | 0.90 | 0.38 | 0.13 | 0.15 | 0.31 | 2.20 |
| LMI Method 2 | 3.09 | 0.93 | 0.48 | 0.16 | 0.18 | 0.35 | 2.42 |
| LMI Method 3 | 2.63 | 0.86 | 0.37 | 0.13 | 0.15 | 0.30 | 2.12 |
| PIF Method 1 | 7.60 | 3.67 | 15.04 | 4.51 | 5.21 | 3.14 | 21.96 |
| PIF Method 2 | 5.21 | 3.21 | 9.22 | 3.03 | 3.51 | 2.43 | 17.02 |
| PIF Method 3 | 3.38 | 2.47 | 5.21 | 1.85 | 2.14 | 1.69 | 11.83 |
| PIF Method 4 | 2.64 | 2.18 | 2.31 | 0.85 | 0.98 | 1.12 | 7.85 |
| RESILIENCE () | ||||||||
|---|---|---|---|---|---|---|---|---|
| Methods | Canal 1 | Canal 2 | Canal 3 | Canal 4 | Canal 5 | Canal 6 | Canal 7 | Mean |
| LMI Method 1 | 3.33 | 3.33 | 3.33 | 10.00 | 0.01 | 0.01 | 0.01 | 2.86 |
| LMI Method 2 | 3.33 | 3.33 | 3.33 | 5.00 | 0.01 | 0.01 | 0.01 | 2.15 |
| LMI Method 3 | 2.00 | 3.33 | 3.33 | 10.00 | 0.01 | 0.01 | 0.01 | 2.67 |
| PIF Method 1 | 3.33 | 2.50 | 2.00 | 2.00 | 1.43 | 1.11 | 1.11 | 1.93 |
| PIF Method 2 | 5.00 | 2.00 | 1.11 | 1.67 | 1.25 | 1.00 | 1.11 | 1.88 |
| PIF Method 3 | 5.00 | 3.33 | 1.25 | 1.11 | 1.67 | 1.43 | 1.43 | 2.17 |
| PIF Method 4 | 3.33 | 2.50 | 1.43 | 2.50 | 1.67 | 1.43 | 1.25 | 2.02 |
| VULNERABILITY () | ||||||||
|---|---|---|---|---|---|---|---|---|
| Methods | Canal 1 | Canal 2 | Canal 3 | Canal 4 | Canal 5 | Canal 6 | Canal 7 | Mean |
| LMI Method 1 | 2.76 | 1.12 | 1.51 | 0.93 | 0.00 | 0.00 | 0.00 | 0.90 |
| LMI Method 2 | 3.09 | 1.06 | 1.47 | 0.90 | 0.00 | 0.00 | 0.00 | 0.93 |
| LMI Method 3 | 2.63 | 1.15 | 1.56 | 0.71 | 0.00 | 0.00 | 0.00 | 0.86 |
| PIF Method 1 | 1.24 | 2.21 | 2.64 | 3.00 | 3.58 | 5.39 | 7.60 | 3.67 |
| PIF Method 2 | 1.95 | 2.31 | 2.16 | 3.25 | 3.17 | 4.43 | 5.21 | 3.21 |
| PIF Method 3 | 2.22 | 1.81 | 2.22 | 2.50 | 2.11 | 3.05 | 3.38 | 2.47 |
| PIF Method 4 | 2.64 | 2.00 | 2.14 | 2.10 | 2.05 | 1.96 | 2.40 | 2.18 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Arauz, T.; Maestre, J.M.; Tian, X.; Guan, G. Design of PI Controllers for Irrigation Canals Based on Linear Matrix Inequalities. Water 2020, 12, 855. https://doi.org/10.3390/w12030855
Arauz T, Maestre JM, Tian X, Guan G. Design of PI Controllers for Irrigation Canals Based on Linear Matrix Inequalities. Water. 2020; 12(3):855. https://doi.org/10.3390/w12030855
Chicago/Turabian StyleArauz, Teresa, José M. Maestre, Xin Tian, and Guanghua Guan. 2020. "Design of PI Controllers for Irrigation Canals Based on Linear Matrix Inequalities" Water 12, no. 3: 855. https://doi.org/10.3390/w12030855
APA StyleArauz, T., Maestre, J. M., Tian, X., & Guan, G. (2020). Design of PI Controllers for Irrigation Canals Based on Linear Matrix Inequalities. Water, 12(3), 855. https://doi.org/10.3390/w12030855






