Nonlinear Autoregressive Neural Networks to Predict Hydraulic Fracturing Fluid Leakage into Shallow Groundwater
Abstract
1. Introduction
2. Materials and Methods
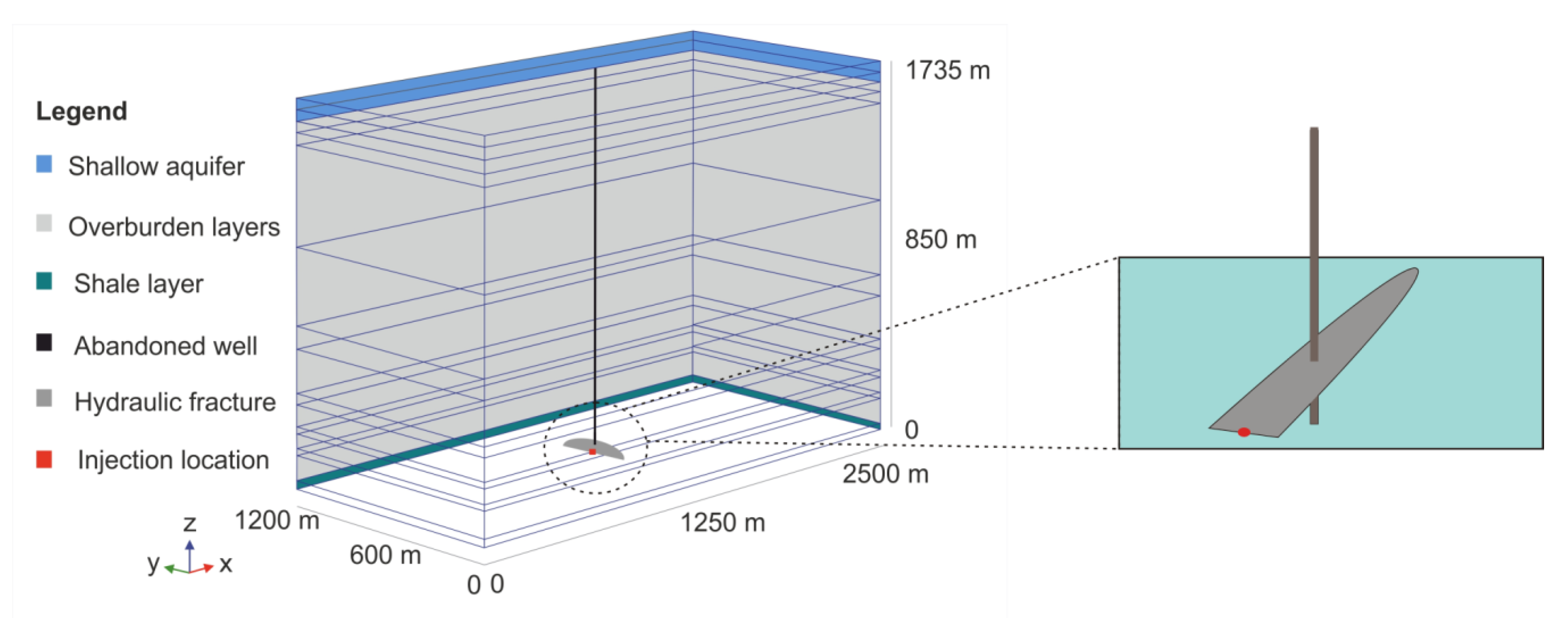
2.1. Conceptual Model for Fracturing Fluid Migration along an Abandoned Well
2.2. Data Preparation and Analysis
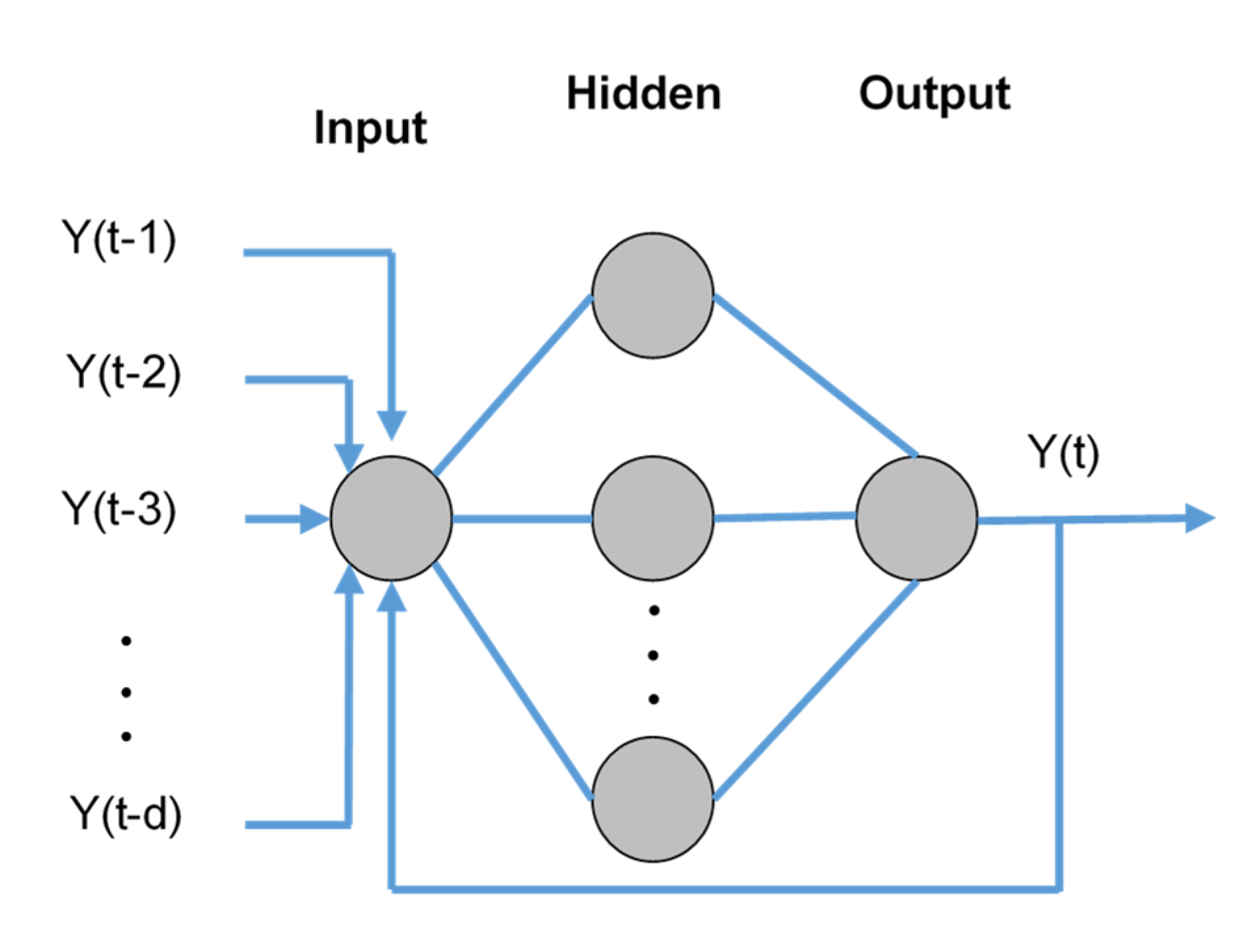
2.3. NAR Model
2.4. Training Algorithms
2.4.1. Levenberg–Marquardt
2.4.2. Bayesian Regularization
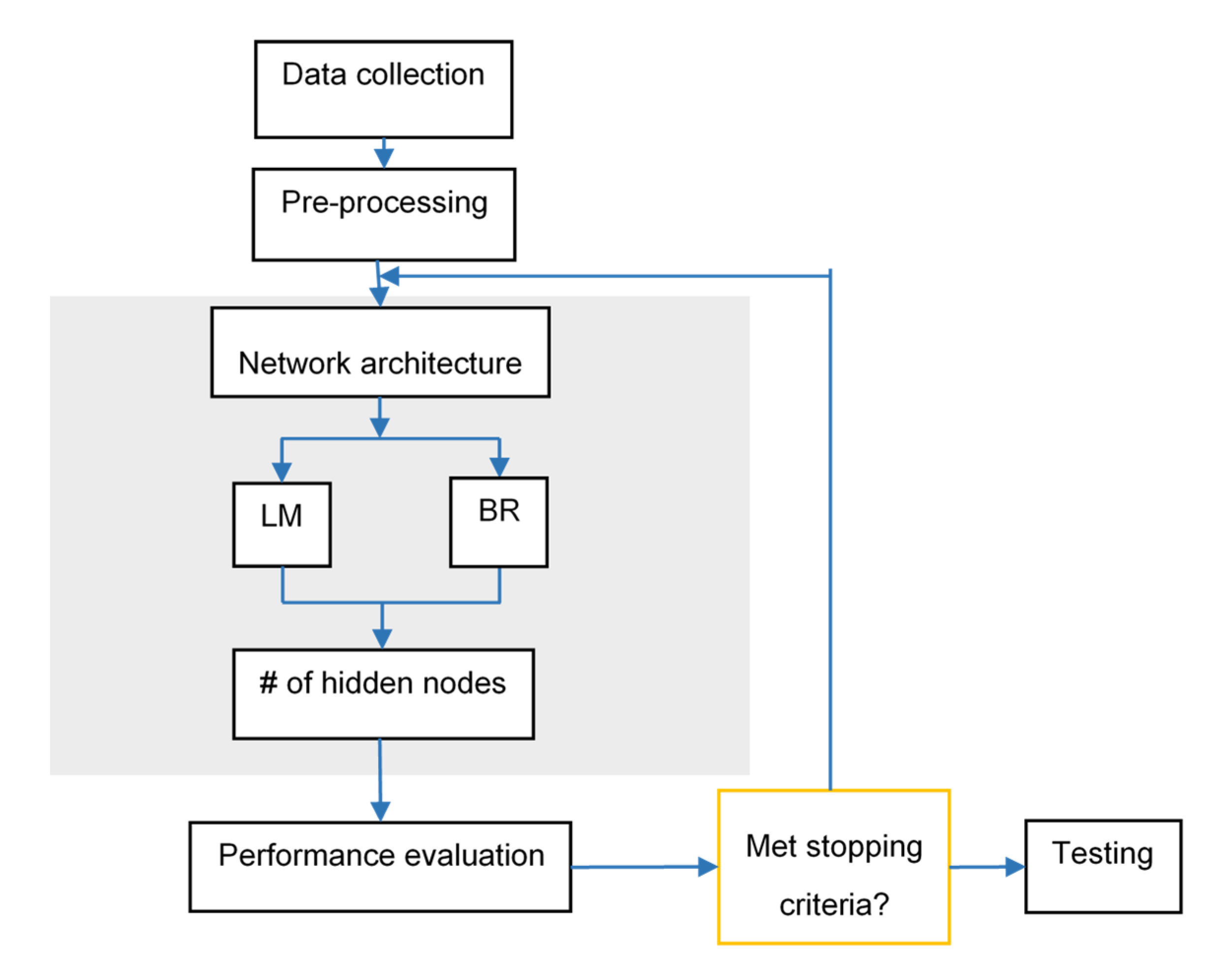
2.5. Network Architecture
2.6. Performance Evaluation
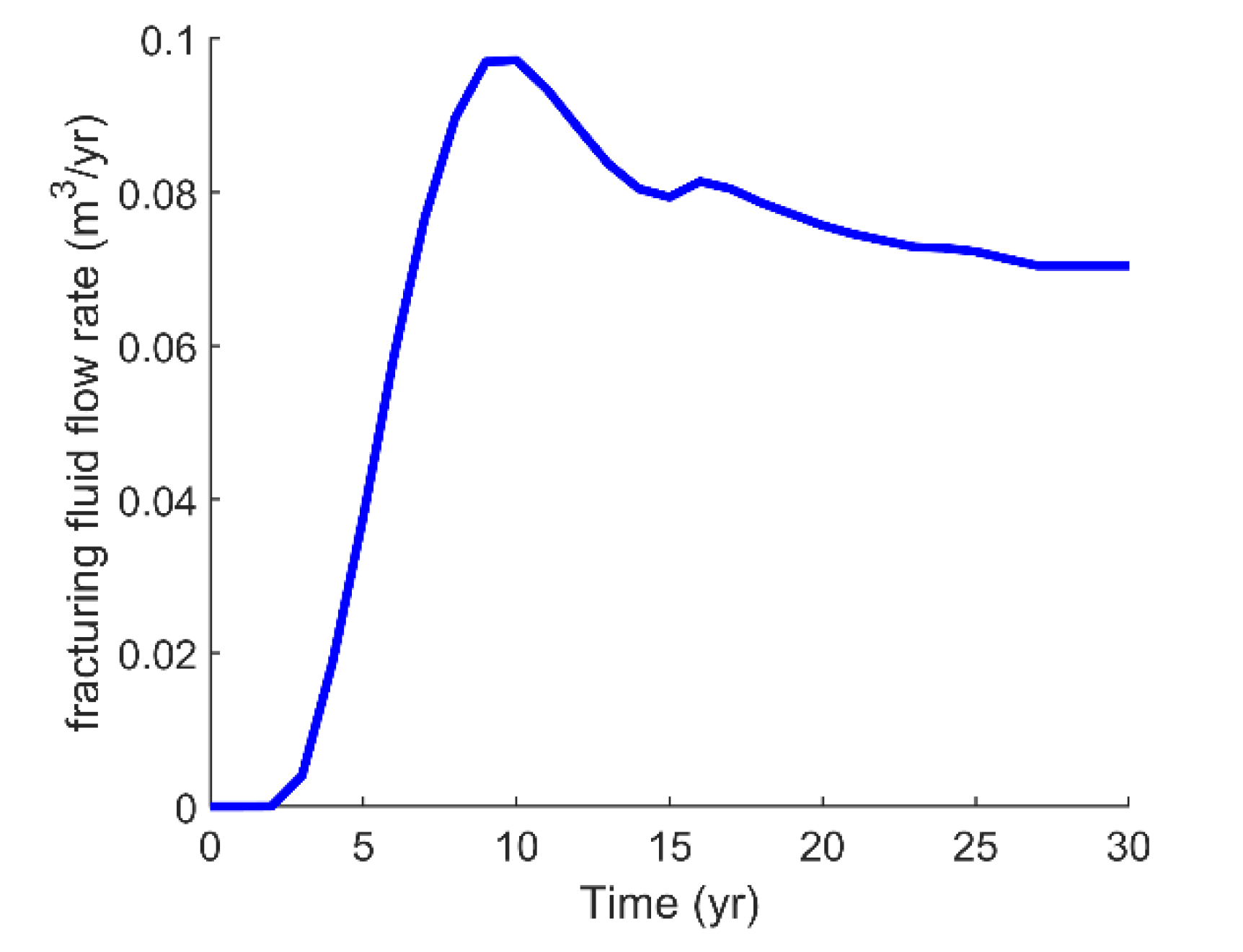
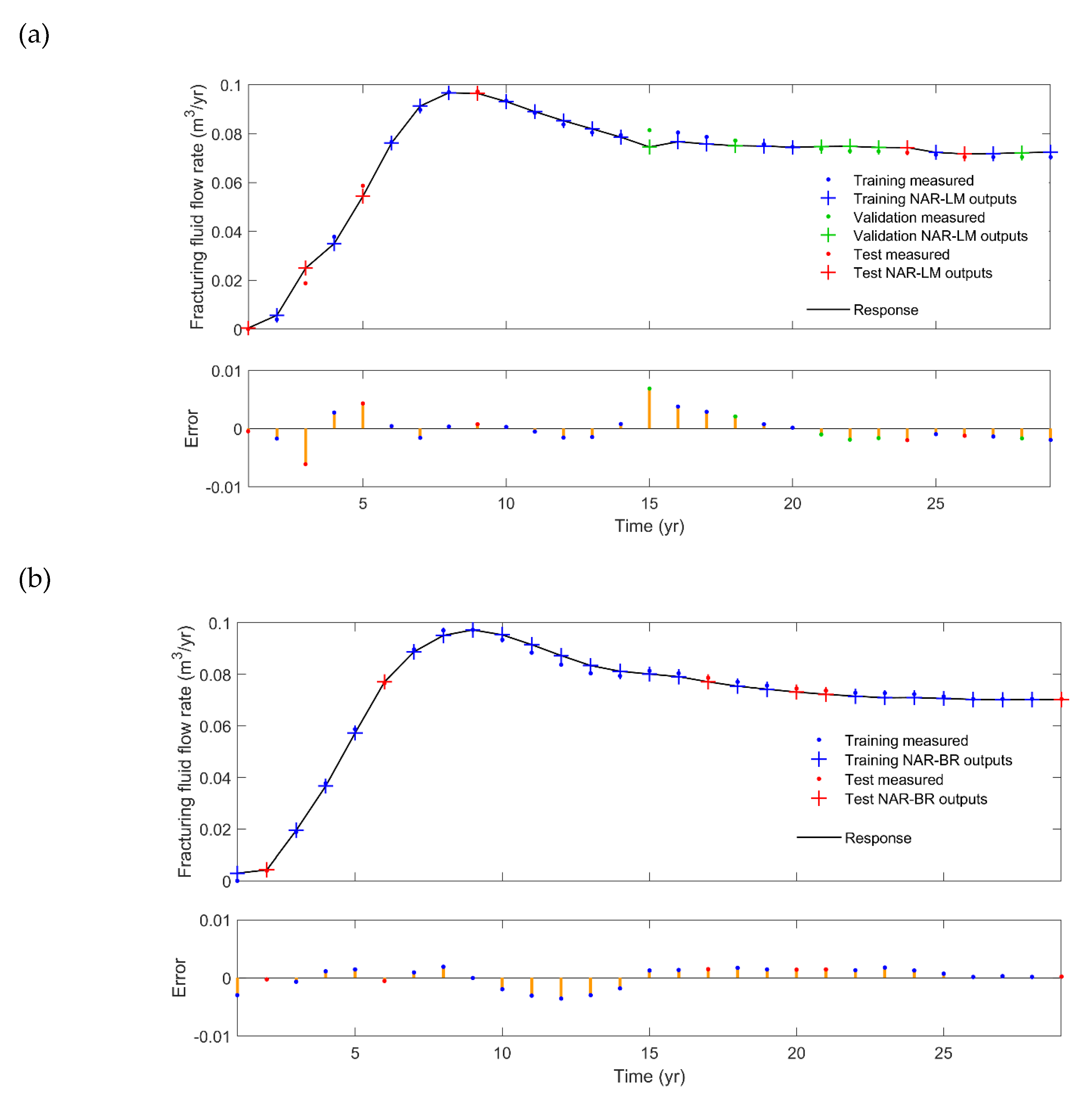
3. Results and Discussion
4. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Cook, T.; Perrin, J.; Wagener, D.V. Hydraulically Fractured Horizontal Wells Account for Most New Oil and Natural Gas Wells. Available online: https://www.eia.gov/todayinenergy/detail.php?id=34732 (accessed on 30 January 2018).
- Tatomir, A.; McDermott, C.; Bensabat, J.; Class, H.; Edlmann, K.; Taherdangkoo, R.; Sauter, M. Conceptual model development using a generic Features, Events, and Processes (FEP) database for assessing the potential impact of hydraulic fracturing on groundwater aquifers. Adv. Geosci. 2018, 45, 185–192. [Google Scholar] [CrossRef]
- Vengosh, A.; Jackson, R.; Warner, N. A critical review of the risks to water resources from unconventional shale gas development and hydraulic fracturing in the United States. Sci. Technol. 2014, 48, 8334–8348. [Google Scholar] [CrossRef] [PubMed]
- Sauter, M.; Brosig, K.; Lange, T.; Jahnke, W.; Helmig, R.; Kissinger, A.; Heitfeld, M.; Kluenker, J.; Schetelig, K. Risiken im Geologischen System bei der Fracking-Technologie Abschätzung der Auswirkungen auf Grundwasservorkommen. Wasser und Abfall 2012, 14, 16. [Google Scholar]
- Rice, A.K.; Lackey, G.; Proctor, J.; Singha, K. Groundwater-quality hazards of methane leakage from hydrocarbon wells: A review of observational and numerical studies and four testable hypotheses. Wiley Interdiscip. Rev. Water 2018, 5, e1283. [Google Scholar] [CrossRef]
- Lange, T.; Sauter, M.; Heitfeld, M.; Schetelig, K.; Brosig, K.; Jahnke, W.; Kissinger, A.; Helmig, R.; Ebigbo, A.; Class, H. Hydraulic fracturing in unconventional gas reservoirs: Risks in the geological system part 1. Environ. Earth Sci. 2013, 70, 3839–3853. [Google Scholar] [CrossRef]
- Gassiat, C.; Gleeson, T.; Lefebvre, R.; McKenzie, J. Hydraulic fracturing in faulted sedimentary basins: Numerical simulation of potential contamination of shallow aquifers over long time scales. Water Resour. Res. 2013, 49, 8310–8327. [Google Scholar] [CrossRef]
- Myers, T. Potential Contaminant Pathways from Hydraulically Fractured Shale to Aquifers. Groundwater 2012, 50, 872–882. [Google Scholar] [CrossRef] [PubMed]
- Nowamooz, A.; Lemieux, J.-M.; Molson, J.; Therrien, R. Numerical investigation of methane and formation fluid leakage along the casing of a decommissioned shale gas well. Water Resour. Res. 2015, 51, 4592–4622. [Google Scholar] [CrossRef]
- Taherdangkoo, R.; Tatomir, A.; Taylor, R.; Sauter, M. Numerical investigations of upward migration of fracking fluid along a fault zone during and after stimulation. Energy Procedia 2017, 125, 126–135. [Google Scholar] [CrossRef]
- Birdsell, D.T.; Rajaram, H.; Dempsey, D.; Viswanathan, H.S. Hydraulic fracturing fluid migration in the subsurface: A review and expanded modeling results. Water Resour. Res. 2015, 51, 7159–7188. [Google Scholar] [CrossRef]
- Reagan, M.T.; Moridis, G.J.; Keen, N.D.; Johnson, J.N. Numerical simulation of the environmental impact of hydraulic fracturing of tight/shale gas reservoirs on near-surface groundwater: Background, base cases, shallow reservoirs, short-term gas, and water transport. Water Resour. Res. 2015, 4, 2543–2573. [Google Scholar] [CrossRef] [PubMed]
- Brownlow, J.W.; James, S.C.; Yelderman, J.C. Influence of Hydraulic Fracturing on Overlying Aquifers in the Presence of Leaky Abandoned Wells. Groundwater 2016, 54, 781–792. [Google Scholar] [CrossRef] [PubMed]
- King, G.E.; Rainbolt, M.F.; Swanson, C. Frac Hit Induced Production Losses: Evaluating Root Causes, Damage Location, Possible Prevention Methods and Success of Remedial Treatments. In Proceedings of the SPE Annual Technical Conference and Exhibition, San Antonio, TX, USA, 9–11 October 2017. [Google Scholar]
- Gasda, S.E.; Bachu, S.; Celia, M.A. Spatial characterization of the location of potentially leaky wells penetrating a deep saline aquifer in a mature sedimentary basin. Environ. Geol. 2004, 46, 707–720. [Google Scholar] [CrossRef]
- Gasda, S.E.; Celia, M.A.; Wang, J.Z.; Duguid, A. Wellbore permeability estimates from vertical interference testing of existing wells. Energy Procedia 2013, 37, 5673–5680. [Google Scholar] [CrossRef]
- Taherdangkoo, R.; Tatomir, A.; Anighoro, T.; Sauter, M. Modeling fate and transport of hydraulic fracturing fluid in the presence of abandoned wells. J. Contam. Hydrol. 2019, 221, 58–68. [Google Scholar] [CrossRef] [PubMed]
- Flewelling, S.A.; Sharma, M. Constraints on upward migration of hydraulic fracturing fluid and brine. Groundwater 2014, 52, 9–19. [Google Scholar] [CrossRef]
- Birdsell, D.T.; Rajaram, H.; Lackey, G. Imbibition of hydraulic fracturing fluids into partially saturated shale. Water Resour. Res. 2015, 51, 6787–6796. [Google Scholar] [CrossRef]
- Edwards, R.W.J.; Doster, F.; Celia, M.A.; Bandilla, K.W. Numerical modeling of gas and water flow in shale gas formations with a focus on the fate of hydraulic fracturing fluid. Environ. Sci. Technol. 2017, 51, 13779–13787. [Google Scholar] [CrossRef]
- Pfunt, H.; Houben, G.; Himmelsbach, T. Numerical modeling of fracking fluid migration through fault zones and fractures in the North German Basin. Hydrogeol. J. 2016, 24, 1343–1358. [Google Scholar] [CrossRef]
- Osborn, S.G.; Vengosh, A.; Warner, N.R.; Jackson, R.B. Methane contamination of drinking water accompanying gas-well drilling and hydraulic fracturing. Proc. Natl. Acad. Sci. USA 2011, 108, 8172–8176. [Google Scholar] [CrossRef]
- Kissinger, A.; Helmig, R.; Ebigbo, A.; Class, H.; Lange, T.; Sauter, M.; Heitfeld, M.; Klünker, J.; Jahnke, W. Hydraulic fracturing in unconventional gas reservoirs: Risks in the geological system, part 2: Modelling the transport of fracturing fluids, brine and methane. Environ. Earth Sci. 2013, 70, 3855–3873. [Google Scholar] [CrossRef]
- Cao, V.; Schaffer, M.; Taherdangkoo, R.; Licha, T. Solute reactive tracers for hydrogeological applications: A short review and future prospects. Water 2020, 12, 653. [Google Scholar] [CrossRef]
- Guzman, S.M.; Paz, J.O.; Tagert, M.L.M. The use of NARX neural networks to forecast daily groundwater levels. Water Resour. Manag. 2017, 31, 1591–1603. [Google Scholar] [CrossRef]
- Loucks, D.P.; Van Beek, E. Water Resources Systems Planning and Management: An Introduction to Methods, Models and Applications. Available online: https://hydrologie.org/BIB/Publ_UNESCO/SR_999_E_2005.pdf (accessed on 15 March 2020).
- Kisi, O.; Cigizoglu, H.K. Comparison of different ANN techniques in river flow prediction. Civ. Eng. Environ. Syst. 2007, 24, 211–231. [Google Scholar] [CrossRef]
- Olyaie, E.; Banejad, H.; Chau, K.W.; Melesse, A.M. A comparison of various artificial intelligence approaches performance for estimating suspended sediment load of river systems: A case study in United States. Environ. Monit. Assess. 2015, 187, 189. [Google Scholar] [CrossRef]
- Zhang, Q.; Stanley, S.J. Forecasting raw-water quality parameters for the north Saskatchewan river by neural network modeling. Water Res. 1997, 31, 2340–2350. [Google Scholar] [CrossRef]
- Maier, H.R.; Dandy, G.C. The Use of Artificial Neural Networks for the Prediction of Water Quality Parameters. Water Resour. Res. 1996, 32, 1013–1022. [Google Scholar] [CrossRef]
- Wei, S.; Zuo, D.; Song, J. Improving prediction accuracy of river discharge time series using a Wavelet-NAR artificial neural network. J. Hydroinformatics 2012, 14, 974–991. [Google Scholar] [CrossRef]
- Ruiz, L.; Cuéllar, M.; Calvo-Flores, M.; Jiménez, M. An application of non-linear autoregressive neural networks to predict energy consumption in public buildings. Energies 2016, 9, 684. [Google Scholar] [CrossRef]
- Adamowski, J.; Fung Chan, H.; Prasher, S.O.; Ozga-Zielinski, B.; Sliusarieva, A. Comparison of multiple linear and nonlinear regression, autoregressive integrated moving average, artificial neural network, and wavelet artificial neural network methods for urban water demand forecasting in Montreal, Canada. Water Resour. Res. 2012, 48, 1–14. [Google Scholar] [CrossRef]
- Neuzil, C.E. How permeable are clays and shales? Water Resour. Res. 1994, 30, 145–150. [Google Scholar] [CrossRef]
- Edwards, R.W.; Celia, M.A. Shale gas well, hydraulic fracturing, and formation data to support modeling of gas and water flow in shale formations. Water Resour. Res. 2018, 54, 3196–3206. [Google Scholar] [CrossRef]
- Freeze, R.A.; Cherry, J.A. Groundwater prentice-hall. Eaglewood Cliffs 1979, 176, 161–177. [Google Scholar]
- Gleeson, T.; Smith, L.; Moosdorf, N.; Hartmann, J.; Dürr, H.H.; Manning, A.H.; van Beek, L.P.H.; Jellinek, A.M. Mapping permeability over the surface of the Earth. Geophys. Res. Lett. 2011, 38, L02401. [Google Scholar] [CrossRef]
- Luijendijk, E.; Gleeson, T. How well can we predict permeability in sedimentary basins? Deriving and evaluating porosity-permeability equations for noncemented sand and clay mixtures. Geofluids 2015, 15, 67–83. [Google Scholar] [CrossRef]
- EIA. World Shale Gas Resources: An Initial Assessment of 14 Regions Outside the United States; US Department of Energy: Washington, DC, USA, 2011. [Google Scholar]
- EIA. Review of Emerging Resources: US Shale Gas and Shale Oil Plays; US Department of Energy: Washington, DC, USA, 2011. [Google Scholar]
- Magri, F.; Bayer, U.; Jahnke, C.; Clausnitzer, V.; Diersch, H.J.; Fuhrman, J.; Möller, P.; Pekdeger, A.; Tesmer, M.; Voigt, H.J. Fluid-dynamics driving saline water in the North East German Basin. Int. J. Earth Sci. 2005, 94, 1056–1069. [Google Scholar] [CrossRef]
- Kissinger, A.; Noack, V.; Knopf, S.; Konrad, W.; Scheer, D.; Class, H. Regional-scale brine migration along vertical pathways due to CO2 injection--Part 2: A simulated case study in the North German Basin. Hydrol. Earth Syst. Sci. 2017, 21, 2751–2775. [Google Scholar] [CrossRef]
- Nogues, J.P.; Nordbotten, J.M.; Celia, M.A. Detecting leakage of brine or CO2 through abandoned wells in a geological sequestration operation using pressure monitoring wells. Energy Procedia 2011, 4, 3620–3627. [Google Scholar] [CrossRef][Green Version]
- Bai, M.; Reinicke, K. In Numerical Simulation of CO2 Leakage through Abandoned Wells during CO2 Underground Storage, Proceedings of the Clean Energy Systems in the Subsurface: Production, Storage and Conversion, Goslar, Germany, 21–23 May 2013; Springer: Berlin/Heidelberg, Germany, 2013; pp. 197–210. [Google Scholar]
- Pawar, R.J.; Watson, T.L.; Gable, C.W. Numerical simulation of CO2 leakage through abandoned wells: Model for an abandoned site with observed gas migration in Alberta, Canada. Energy Procedia 2009, 1, 3625–3632. [Google Scholar] [CrossRef]
- Gasda, S.E.; Nordbotten, J.M.; Celia, M.A. Determining effective wellbore permeability from a field pressure test: A numerical analysis of detection limits. Environ. Geol. 2008, 54, 1207–1215. [Google Scholar] [CrossRef]
- Nordbotten, J.M.; Celia, M.A.; Bachu, S.; Dahle, H.K. Semianalytical solution for CO2 leakage through an abandoned well. Environ. Sci. Technol. 2005, 39, 602–611. [Google Scholar] [CrossRef] [PubMed]
- Nordbotten, J.M.; Celia, M.A.; Bachu, S. Analytical solutions for leakage rates through abandoned wells. Water Resour. Res. 2004, 40, W04204. [Google Scholar] [CrossRef]
- Ebigbo, A.; Class, H.; Helmig, R. CO2 leakage through an abandoned well: Problem-oriented benchmarks. Comput. Geosci. 2007, 11, 103–115. [Google Scholar] [CrossRef]
- Celia, M.A.; Bachu, S.; Nordbotten, J.M.; Gasda, S.E.; Dahle, H.K. Quantitative estimation of CO 2 leakage from geological storage: Analytical models, numerical models, and data needs. Greenh. Gas Control Technol. 7 2005, I, 663–671. [Google Scholar]
- Da Costa Lopes, F.; Watanabe, E.H.; Rolim, L.G.B. A control-oriented model of a PEM fuel cell stack based on NARX and NOE neural networks. IEEE Trans. Ind. Electron. 2015, 62, 5155–5163. [Google Scholar] [CrossRef]
- López, M.; Valero, S.; Senabre, C.; Aparicio, J.; Gabaldon, A. Application of SOM neural networks to short-term load forecasting: The Spanish electricity market case study. Electr. Power Syst. Res. 2012, 91, 18–27. [Google Scholar] [CrossRef]
- Wang, K.W.; Deng, C.; Li, J.P.; Zhang, Y.Y.; Li, X.Y.; Wu, M.C. Hybrid methodology for tuberculosis incidence time-series forecasting based on ARIMA and a NAR neural network. Epidemiol. Infect. 2017, 145, 1118–1129. [Google Scholar] [CrossRef]
- Maier, H.R.; Dandy, G.C. Neural networks for the prediction and forecasting of water resources variables: A review of modelling issues and applications. Environ. Model. Softw. 2000, 15, 101–124. [Google Scholar] [CrossRef]
- Hagan, M.T.; Menhaj, M.B. Training Feedforward Networks with the Marquardt Algorithm. IEEE Trans. Neural Netwrok 1994, 5, 989–993. [Google Scholar] [CrossRef]
- Marquardt, D.W. An Algorithm for Least-Squares Estimation of Nonlinear Parameters. J. Soc. Ind. Appl. Math. 1963, 11, 431–441. [Google Scholar] [CrossRef]
- Sahoo, S.; Jha, M.K. Groundwater-level prediction using multiple linear regression and artificial neural network techniques: A comparative assessment. Hydrogeol. J. 2013, 21, 1865–1887. [Google Scholar] [CrossRef]
- Bishop, C. Neural Networks for Pattern Recognition; Oxford University Press: Oxford, UK, 1995. [Google Scholar]
- MacKay, D.J.C. Bayesian Interpolation. Neural Comput. 1992, 4, 415–447. [Google Scholar] [CrossRef]
- Burden, F.; Winkler, D. Bayesian regularization of neural networks. Methods Mol. Biol. 2008, 458, 25–44. [Google Scholar] [PubMed]
- Doan, C.D.; Liong, S.Y. Generalization for multilayer neural network bayesian regularization or early stopping. In Proceedings of the Asia Pacific Association of Hydrology and Water Resources 2nd Conference, Singapore, Singapore, 5–8 July 2004; pp. 5–8. [Google Scholar]
- Foresee, F.; Hagan, M.T. Gauss-Newton approximation to bayesian learning. In Proceedings of the IEEE International Conference on Neural Networks–Conference Proceedings, Houston, TX, USA, 12 June 1997; pp. 1930–1935. [Google Scholar]
- MacKay, D.J.C. A practical bayesian framework for backpropagation networks. Neural Comput. 1992, 4, 448–472. [Google Scholar] [CrossRef]
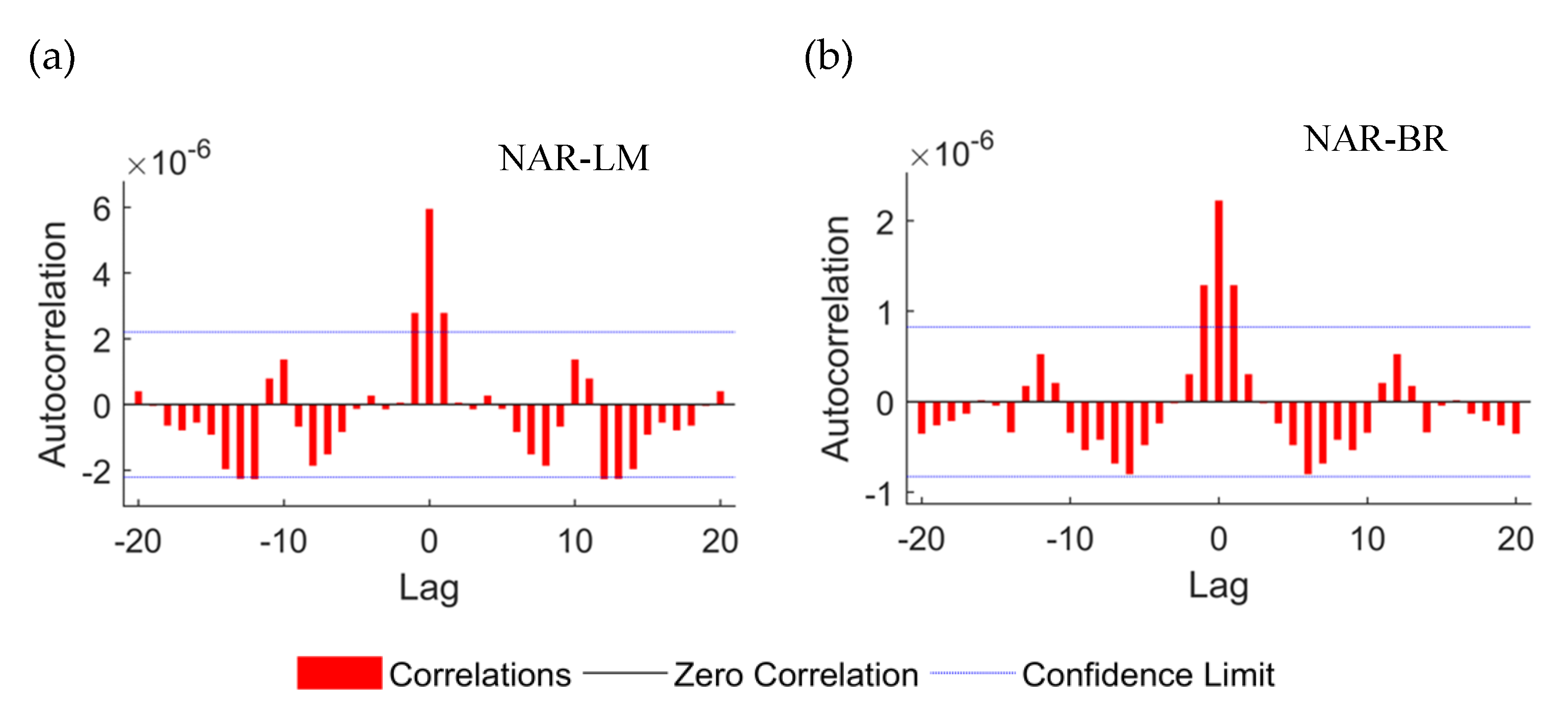
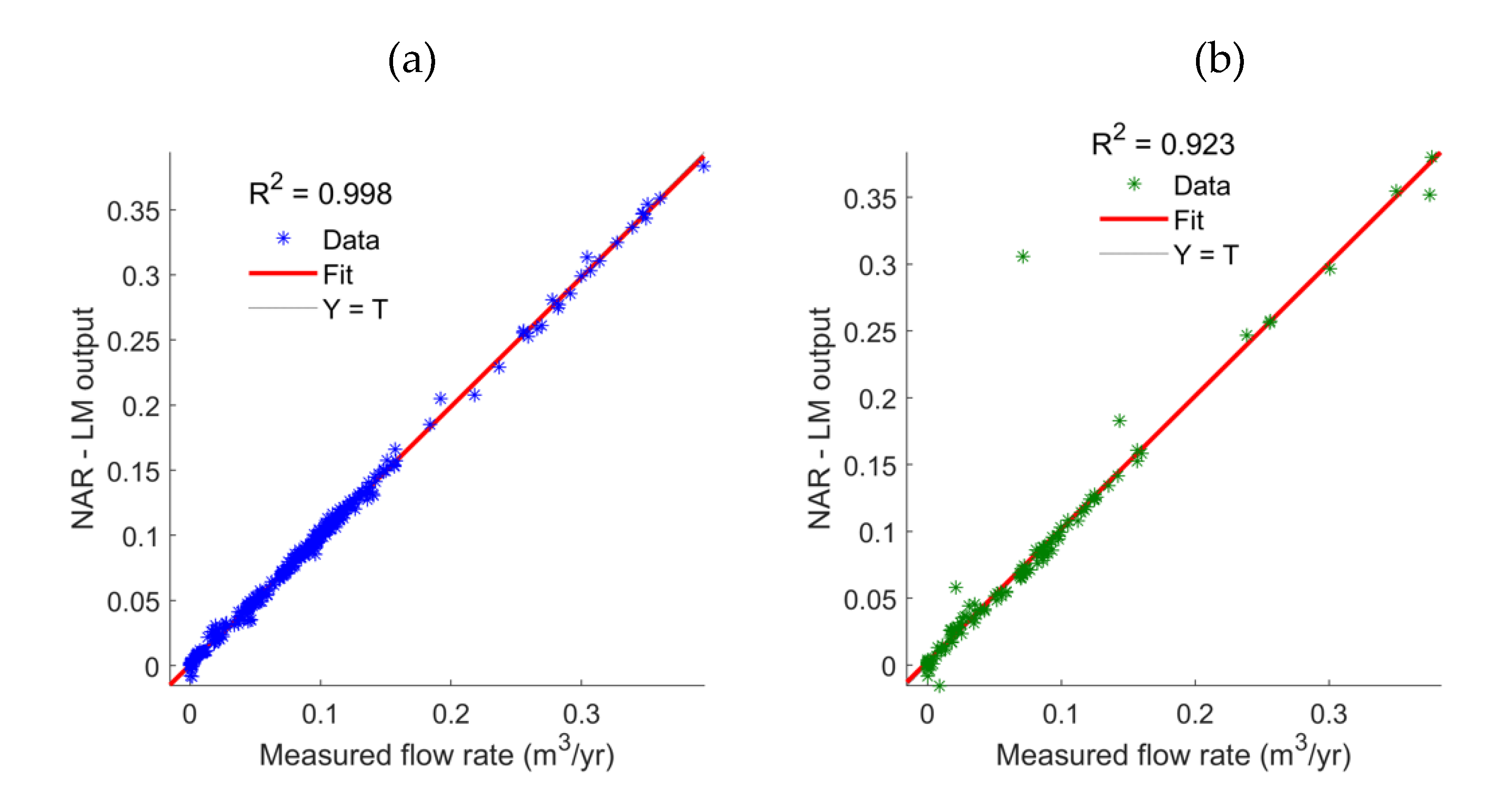
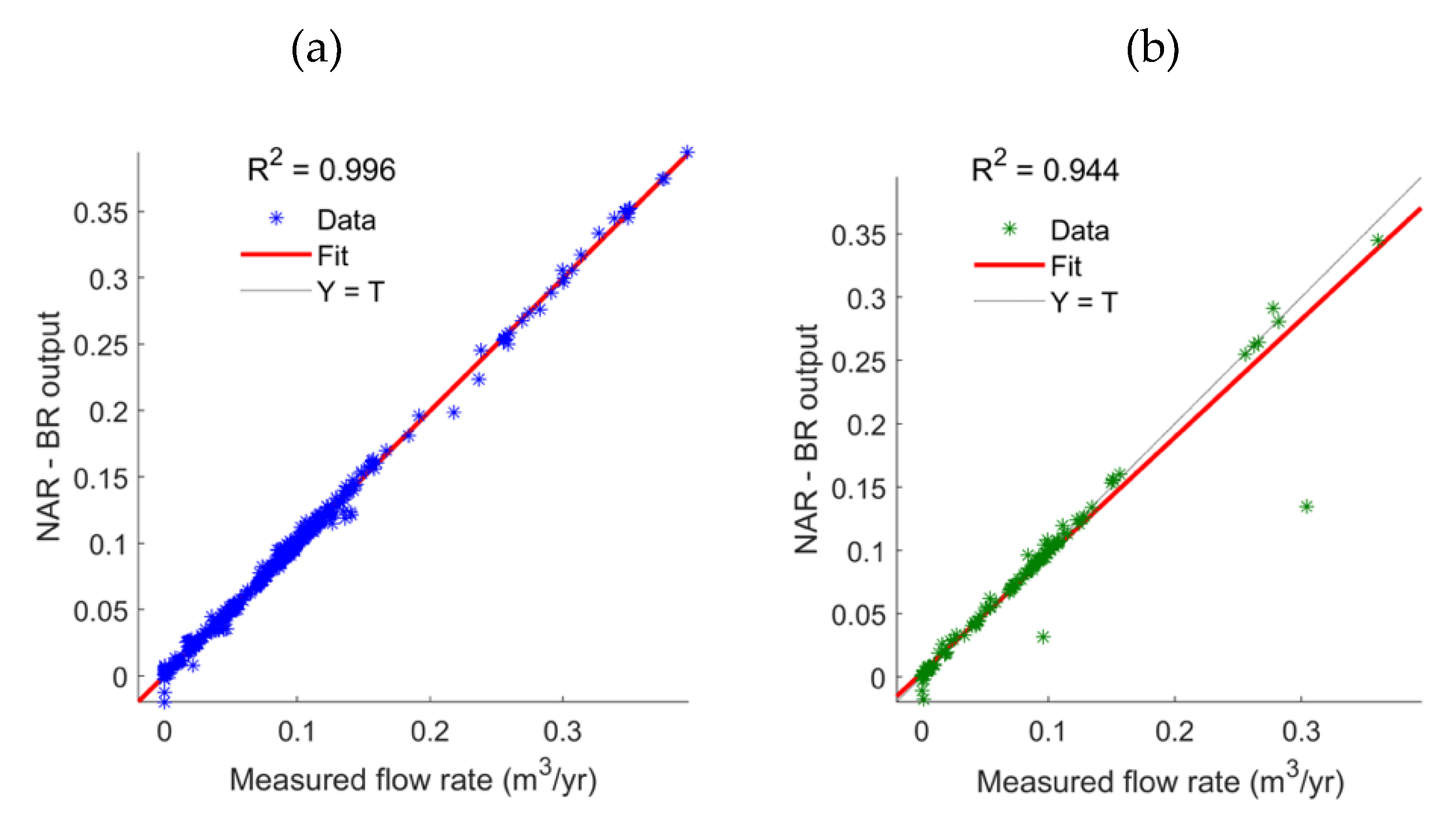
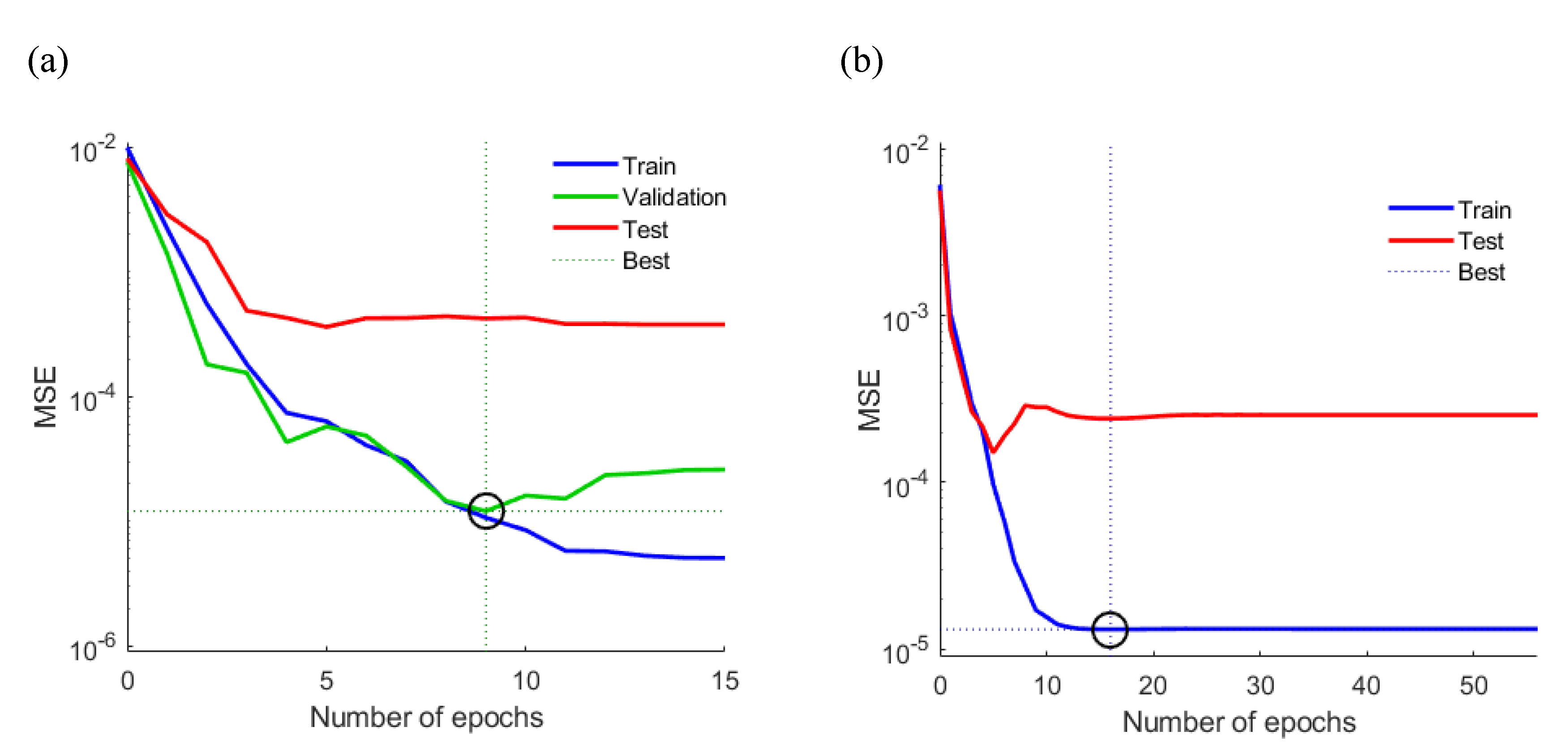
| Parameter | Unit | Base-Case Value | Min. | Max. | Source |
|---|---|---|---|---|---|
| Shale permeability | m2 | 1 × 10−19 | 1 × 10−21 | 1 × 10−18 | [12,13,34] |
| Shale porosity | 0.01 | 0.01 | 0.05 | [7,34,35,36] | |
| Overburden permeability | m2 | Depth-dependent | 1 × 10−17 | 1 × 10−15 | [7,37,38] |
| Overburden thickness | m | 1600 | 900 | 2900 | [7,39,40] |
| Salinity gradient | g/lm | 0.15 | 0.1 | 0.2 | [41,42] |
| Fracturing fluid volume | m3 | 11,365 | 11,000 | 15,000 | [8,11,13] |
| Abandoned well permeability | m2 | 1 × 10−12 | 1 × 10−17 | 1 × 10−12 | [43,44,45,46,47,48,49,50] |
| Distance of fracture plane to well | m | 0 | 0 | 15 |
| Statistical Parameter | NAR-LM | NAR-BR | |||
|---|---|---|---|---|---|
| Training | Validation | Testing | Training | Testing | |
| R2 | 0.998 | 0.996 | 0.923 | 0.996 | 0.944 |
| MSE | 1.07 × 10−5 | 1.2 × 10−5 | 4.2 × 10−4 | 1.3 × 10−5 | 2.4 × 10−4 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Taherdangkoo, R.; Tatomir, A.; Taherdangkoo, M.; Qiu, P.; Sauter, M. Nonlinear Autoregressive Neural Networks to Predict Hydraulic Fracturing Fluid Leakage into Shallow Groundwater. Water 2020, 12, 841. https://doi.org/10.3390/w12030841
Taherdangkoo R, Tatomir A, Taherdangkoo M, Qiu P, Sauter M. Nonlinear Autoregressive Neural Networks to Predict Hydraulic Fracturing Fluid Leakage into Shallow Groundwater. Water. 2020; 12(3):841. https://doi.org/10.3390/w12030841
Chicago/Turabian StyleTaherdangkoo, Reza, Alexandru Tatomir, Mohammad Taherdangkoo, Pengxiang Qiu, and Martin Sauter. 2020. "Nonlinear Autoregressive Neural Networks to Predict Hydraulic Fracturing Fluid Leakage into Shallow Groundwater" Water 12, no. 3: 841. https://doi.org/10.3390/w12030841
APA StyleTaherdangkoo, R., Tatomir, A., Taherdangkoo, M., Qiu, P., & Sauter, M. (2020). Nonlinear Autoregressive Neural Networks to Predict Hydraulic Fracturing Fluid Leakage into Shallow Groundwater. Water, 12(3), 841. https://doi.org/10.3390/w12030841






