Abstract
Effective representation of precipitation inputs is one of the essential components in hydrological model structures, especially when gauge measurements for the modelled catchment are sparse. Assessment of the impact of precipitation pre-processing is often nontrivial as precipitation data are very limited in the first place. In this paper, we demonstrate a study using a semi-distributed hydrological model, the Soil and Water Assessment Tool (SWAT) to examine the impact of different precipitation pre-processing methods on model calibration and the overall model performance with regards to the operational use. A river catchment in the UK is modelled to test against the three pre-processing methods: the Centroid Point Estimation Method (CPEM), the Grid Area Method (GAM) and the Grid Point Method (GPM). Cross-calibration and validation are then carried out by using the high-resolution Centre for Ecology & Hydrology–Gridded Estimate Areal Rainfall (CEH-GEAR) dataset. The results show that the proposed methods GAM and GPM can improve the model calibration significantly against the one calibrated with the existing CPEM method used by the model; the performance differences in the validation among the calibrated models, however, remain small and become irrelevant. The findings indicate that it is preferable to always make use of high-quality rainfall data, when available, with a better pre-processing method, even with models that are previously calibrated with low-quality rainfall inputs. It is also shown that such improvements are affected by the size of catchment and become less significant for smaller catchments.
1. Introduction
Precipitation is one of the vital forcing factors in hydrological modelling processes. The accuracy of precipitation as the input and its representation have a direct impact on the overall model performance. In the last few decades, many studies have been conducted with a focus on this, mainly due to the drive of quantifying modelling uncertainties, where inputs such as precipitation must be considered, for example [1,2].
Alongside the concerns of accuracy, the importance of spatial variability of rainfall has also been highlighted, especially over large watersheds where it is crucial to gain insight of day-to-day spatial variability of groundwater level, streamflow discharge and soil moisture content [2]. At smaller scales, rainfall variability also has a considerable impact on peak flow estimation [3]. It was reported in [4] that as the scale increases, the impact of rainfall distribution decreases and there is a shift from the spatial variability of rainfall to catchment response time distribution as the dominant factor governing runoff generation.
The effect of various spatiotemporal resolutions of precipitation on simulated runoff has also been widely investigated by, e.g., [5,6], which agreed on the necessity of adopting better rain representation input in the modelling structure. However, most of these studies are focused on specific models because precipitation pre-processing is often model dependant, although some common methods such as the Thiessen polygon method are used by many different models.
Spatial variability in precipitation influences hydrological model outputs e.g. [7], the catchment response [8] and the timing of peak runoff [9]. Schuurmans et al. [2] state that failing to consider a satisfactorily spatial distribution of precipitation will result in errors in the values of the model parameters that will be wrongly changed to compensate for errors in the rainfall input.
Hydrological model performance relative to the accuracy of spatial precipitation data has been explored by users of the Soil and Water Assessment Tool (SWAT) [10] such as [11] who studied the effect of rain gauge density on streamflow, sediment and nitrogen fluxes simulations in two small watersheds in the United States and they found that the use of higher rain gauge densities could lead to better simulations, especially for sediment fluxes. Jayakrishnan et al. [12] compared annual and monthly river flows simulated by SWAT for four catchments in the U.S. using both weather radar (Next Generation Weather Radar, NEXRAD) and rain gauges. They concluded that input of areal rainfall measured by radar gave the best estimation, despite some inherent limitations, especially the accuracy at daily time scale.
Researchers hold contrasting views on the most important inputs for model performance, with some identifying density of precipitation data, either through gages or radar [11,12]. For instance, [13] investigated the effect of the resolution of land use, soil type and rainfall data on simulating river flow in three catchments in the U.S. by constructing 18 models of each catchment and combining three land use categories, three soil types and two precipitation input scenarios. It was found that all models produced comparable values of Nash–Sutcliffe efficiency indices. The Nash–Sutcliffe efficiency index (NSE) [14] is a normalised statistic that determines the relative magnitude of the residual variance compared to the measured data variance (i.e., it indicates how well the plot of observed versus simulated data fits the 1:1 line). Their main findings were that a more refined representation of spatial data might not necessarily result in improved SWAT river flow simulations in small catchments. This may as well be attributed to other factors, such as the soil types and land use, which is possibly more dominant than the rainfall.
A more comprehensive account is given by Starks and Moriasi [15], who compared streamflow simulations from a SWAT model using four different resolutions of rainfall data in three experimental catchments of different sizes. The number of rain gauges in three scenarios varied from 1 to 7. The rainfall data obtained through weather radar, available at 4 km grids, were used in the fourth scenario. Their study produced satisfactorily calibrations for all four cases, even though the scenarios with higher rain gauge density and the radar-based rainfall showed relatively better river flow simulations.
A recent study by Masih et al. [1] used a SWAT model to compare its performance under standard precipitation input and a modified areal precipitation input obtained using the Inverse Distance and Elevation Weighting (IDEW) interpolation. This study found that the use of areal precipitation, obtained through the interpolation improved simulated streamflow.
- It is worth noting that most of those studies are based upon model simulations at large temporal scales, e.g., monthly or yearly, which has two significant implications:
- the contribution of better spatial representation from using either denser gauge networks or remote sensing data might well be smoothed away; and
- daily precipitation has a certain stochastic nature, which differs from monthly rainfall [16,17], and they may not fit the needs of day-to-day operational use.
From a modeller’s viewpoint, it would be more intriguing to explore how the way of model handling precipitation input can be improved across different scales. There is another challenging aspect of conducting such an assessment in an existing modelling system like SWAT due to parameterisation. A discussion of the benefits, as well as the drawbacks of model parameterisation, goes beyond the scope of this paper, readers can refer to [18].
An immediate impact of model parameterisation, however, is that at times models can be calibrated equally well, even though they are fed with input data (such as precipitation) that apparently are of different quality. This so-called ‘compensation of parametrisation’ makes it challenging to identify and possibly isolate the impact of various inputs by only considering model calibrations and their comparisons.
In this paper, we present a study on the impact of different precipitation pre-processing methods on the performance of a SWAT model set up for a medium-sized river catchment, the Dee catchment in the UK. We make use of a most recent, high resolution, gridded rainfall dataset—the Centre for Ecology & Hydrology (CEH) Gridded Estimates of Areal Rainfall [19] as a reference in addition to the conventional gauged rainfall data.
The objectives of this study are:
- evaluate the impact on hydrological model performance from using various methods of rainfall pre-processing above and further give recommendation where possible;
- to assess model parameterisation (via calibration) with different rainfall inputs on the overall model performance; and
- to test the utility of the new Gridded Estimate Areal Rainfall (GEAR) dataset in the context of calibrating hydrological models.
This paper is structured as follows: Section 2 introduces the study area and the datasets used in the study, followed by the description of model setup with a focus on the three pre-processing methods and the way of calibration and cross-validation. The results are discussed in detail in Section 3. Finally, several key points are concluded after the results and discussion.
2. Materials and Methods
2.1. Study Area
The Dee River originates from the mountainous area of Snowdonia National Park in North Wales in the United Kingdom. The mainstream of the river is measured 113 km long with a catchment area of 2215 km2, as shown in Figure 1. It flows eastward to the Wales–England border at the City of Chester before discharging into the Irish Sea at Liverpool Bay.
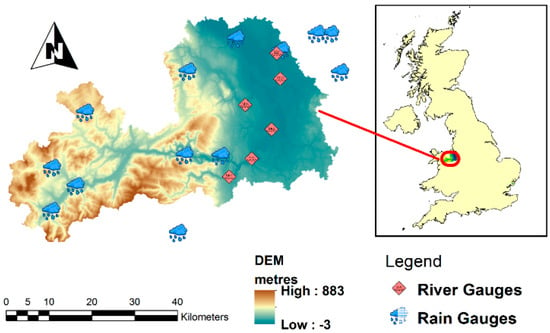
Figure 1.
The selected study catchment and locations of the rain gauges.
The annual precipitation over the basin shows a clear west-east declining trend with 1700 mm in the western part quickly reducing to 685 mm in the east where flat, lowland dominates as revealed in Figure 2. The temporal distribution of annual precipitation also demonstrates a stable seasonal pattern with wet winters (178–578) mm in December, January and February (DJF) and ordinarily dry summers (165–278 mm) in June, July and August (JJA). The Dee River originates from the mountainous area of Snowdonia with elevation reaching above 800 m, delving into a large flat area to the east barely above the sea level. For rainfall observations, there are 13 rain gauges available in the vicinity of the Dee catchment.
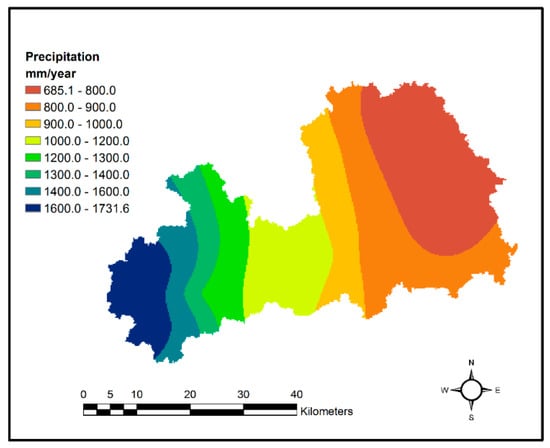
Figure 2.
The annual precipitation distribution in the Dee catchment.
2.2. Data
This study employs the SWAT model set up by [20] to assess how the difference in rainfall pre-processing technique might affect the model calibrations and its performance. The present study follows, in general, with the standard procedure of building SWAT models in terms of data preparations, namely: digital elevation model data (DEM), climatic data, soil type and vegetation data are taken from public domain sources and prepared for the two catchments over the entire study period. Table 1 summarises the use of these data and their properties.

Table 1.
Collected datasets.
For rainfall inputs, we have chosen two sources of data to help the analysis. First, the daily point rainfall measurements at the rain gauges (see Figure 1) are collected for the study period, i.e., 1992–2003. This is precisely the way that most SWAT (and many other lumped hydrological modelling processes) models follow. The second source of rainfall data are from the GEAR datasets (more details follow), which, although are still based on the underlying rain gauge measurements, are further interpolated into regular grids. In this sense, the GEAR sourced data can be seen to have already represented spatial rainfall variability using certain interpolations.
River flow data are collected at six flow gauges, again to cover the study period. Model performance is measured using the simulated river flow against the measured flow. Most data used are available in the public domain except those requested from the water management authority subject to an academic license. The summary of data are illustrated in Table 1.
The Centre for Ecology and Hydrology–Gridded Estimates of Areal Rainfall (CEH-GEAR), is a new precipitation dataset developed to provide reliable 1 km gridded estimates of daily and monthly rainfall over the UK and 3,500 km2 of the catchment area in the Republic of Ireland from 1890 to 2012 [18]. The rainfall estimates are created from the Met Office historical weather observations for the UK. The natural neighbour interpolation method [21], including a normalisation step based on average annual rainfall (AAR), was employed to create the daily and monthly rainfall over the regular 1-km grids.
A schematic representation of the interpolation procedure used to derive the CEH-GEAR daily and monthly 1 km grids is shown in Figure 3. The grids are generated using Natural Neighbour Interpolation alongside a normalisation step based on AAR, which involves two steps:
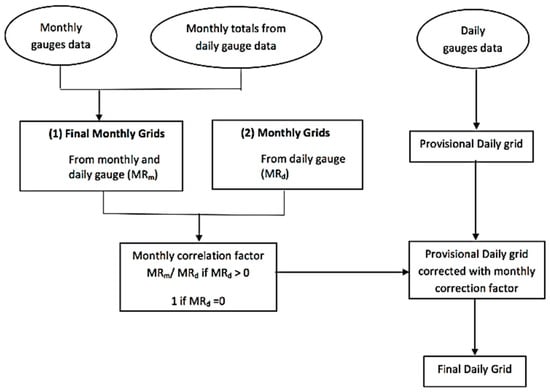
Figure 3.
Derivation of daily and monthly gridded rainfall estimates of the Centre for Ecology and Hydrology–Gridded Estimates of Areal Rainfall (CEH-GEAR) [19].
- an initial estimate from daily gauges alone;
- multiplication by a correction grid to give consistency with monthly grids that have been created from all available daily and monthly gauged data.
Readers can refer to [19] for the discussion of the derivation in details. It should be noted that weather radar data are not used in the production of the current version of CEH-GEAR although such merging would be able to improve the spatial representation of the interpolated field. This is in part due to the shorter duration of the available radar rainfall estimates (around 30 years) compared to the rain-gauge observations. Accordingly, CEH-GEAR data would have greater temporal consistency if it is solely based on rain gauge observations [19].
2.3. Modelling River Flow Using SWAT
The Soil and Water Assessment Tool, SWAT [10] is a public domain hydrological model, which has been tested in many applications worldwide. It is a physically-based continuous river basin scale model and is designed to simulate the rainfall-runoff process under various spatial and temporal scales. Moreover, this model is spatially quasi-distributed using hydrological response units (HRUs) to describe the spatial distribution of soil characteristics, land use and topography within a catchment.
The calculations in SWAT are performed for each HRU and then scaled up to the sub-basin outlet by the area of the HRU proportional to that of the sub-basin. This approach results in that the HRUs lack spatial relations typically seen in a fully distributed model, but it yields a computationally efficient calculation scheme allowing for rapid watershed simulation over long time periods [22]. The details of the model structure, applications, as well as model set-up are widely available, e.g., in [23,24].
The division of the watershed enables the model to reflect differences in evapotranspiration for different types of soil and crops. Runoff is calculated separately for each HRU and routed to obtain the total runoff for the watershed. This increases the accuracy and provides a better physical representation of the water balance [25].
When it comes to how precipitation amount is represented, the default setting of SWAT uses the values from the gauge located closest to the centroid of each sub-basin to represent the areal value for the sub-basin [1,15]. To consider the orographic effects on temperature and rainfall in mountainous areas, SWAT makes use of the elevation bands method, which allows for up to 10 elevation bands in each sub-basin that enables it to assess the differences in snow cover and snowmelt caused by orographic variation in the rainfall and temperature. This method adjusts the regional precipitation by weighing the elevation difference between the band of the rain gauge and the other bands.
Most applications of SWAT merely follow this approach as there is no explicit entry in the model user interface to conveniently alter this setting. Evidently, in some cases, such treatment does not represent well the spatial variation of the precipitation field, as it ignores the spatial heterogeneity. One can appreciate the potential impact of such treatment even without experiment because:
- the nearest gauge value may not be able to accurately represent the value at the centroid; and
- even if it can, the centroid value may not be able to represent the areal value of the sub-basin in question.
However, even using such crude estimate of sub-basin precipitation, some applications of SWAT are reported to have worked well. The reason lies in two folds: on the one hand, a denser gauge network and/or less seasonal rainfall events can mitigate the poor spatial representation of the model; on the other hand, model parameterisation can also ‘compensate’ [15]. This, in fact, inspires this study as we hope to isolate the impacts of the pre-processing techniques from the two factors mentioned, by applying cross-calibration and validation to separate model parameterisation.
2.4. Precipitation Pre-Processing Methods for the Gauge and the CEH-GEAR Data
The measured daily rainfall at 13 rain gauges in the Dee river basin have been collected from BADC and the missing data gaps in gauge observations are filled by using the Inverse Distance Weighting interpolation (IDW) method. The CEH-GEAR data (at 1 km spatial resolution) are taken without any further data screening and gap-filling operations. We applied the following three methods to pre-process the precipitation data before using them to represent (sub-) basin areal values in the SWAT model:
- the centroid point estimate method (CPEM): this is the default method used by SWAT, which estimates the areal precipitation of a sub-basin using the rainfall at the gauge closest to the centroid of the sub-basin (see Figure 4a). Apparently, only one rain gauge is used in this case for every sub-basin;
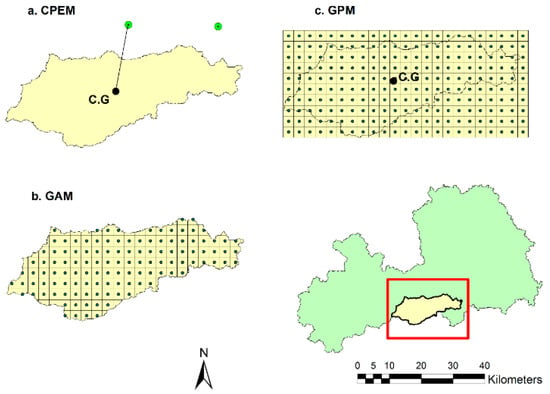 Figure 4. Methods of precipitation pre-processing for selected sub-basin in Dee River basin with (a) the centre point estimate method CPEM; (b) the grid area method GAM and (c) the grid point method GPM.
Figure 4. Methods of precipitation pre-processing for selected sub-basin in Dee River basin with (a) the centre point estimate method CPEM; (b) the grid area method GAM and (c) the grid point method GPM. - the grid-area method (GAM): this method ‘cuts out’ the target sub-basin area from the GEAR grids and takes the average of all values of the grids that either is entirely within the area or intersect with it (Figure 4b);
- the grid-point method (GPM): this method again uses the GEAR dataset except that instead of taking the average of the intersecting areas, it estimates the value at the centroid of the target sub-basin by interpolating the values of GEAR grids nearby (within a 1-km search radius) using the IDW method (see Figure 4c). The estimated centroid value is then used to represent the areal precipitation over the target sub-basin as done in CPEM.
The Inverse Distance Weighting interpolation (IDW) computes the rainfall values at un-sampled points by using the weighted average of observed data at surrounding points. Thus, this can be defined as a distance reverse function of each point from nearby points [26]. The values at un-sampled points can be determined by using a linear combination of values at a known sampled point. The IDW method depends on the theory that the unknown value of a point is more affected by closer points than by points further away. The weights are computed by:
where is the distance between the sampled and the un-sampled points. The parameter is specified as a geometric form for the weight while other specifications are possible.
The three proposed methods utilise both the gauge measurements (CPEM) and the CEH-GEAR dataset (for GAM and GPM). It should be noted that the CEH-GEAR data are also derived from gauge measurements that have been further gridded by applying the natural neighbour interpolation. To a certain degree, the GAM method effectively resembles the common Thiessen method, which obtains areal rainfall using the underlying gauge measurements averaged over the polygons. However, there are still some subtle differences, which are:
- the Thiessen polygon method is the nearest neighbour interpolation whereas the GEAR data are derived from using the natural neighbour interpolation;
- they may not use the same set of rain gauges, and more sophisticated approaches of errors corrections have been applied to produce the GEAR dataset.
Nevertheless, in terms of accounting for the spatial heterogeneity, the GAM method should be the best choice followed by GPM while the default method CPEM falls behind. Thus, we hypothesise that correspondingly, models calibrated using the methods are expected to rank in the same order regarding their performances.
2.5. Cross-Calibration and Validation of Models
We largely follow the standard approach to set up the SWAT model for the catchments. Rainfall data from the 13 gauges are used to construct the CPEM time series from 1995 to 2003. The other two-time series are produced from the CEH-GEAR dataset using the GAM and GPM methods respectively, are also generated for the same period. A daily SWAT model fed with these three rainfall time series is then calibrated over 1995–2000 and validated for the period of 2001–2003.
In all three cases, the SWAT model is calibrated and validated using the Sequential Uncertainty Fitting algorithm-SUFI2 [27]. The goodness of fit is assessed by using both the Nash–Sutcliffe Efficiency Index NSE [14] and the determination Coefficient R2 and the percent of bias (PBIAS) as defined by Equations (2)–(4):
where and are observed and the simulated river flows at time respectively. Historical flow records of the selected flow gauges (6 river gauge stations from the Dee River catchment are used to measure the performance of the model, see Table 2).

Table 2.
The river gauge stations utilised in the calibration and validation of the hydrological models (Source: National River Flow Archive, https://nrfa.ceh.ac.uk/data/).
A cross-calibration and validation approach is used to isolate the impact of model parameterisation concerning different precipitation pre-processing schema. This means that there are three (3) calibrated models for each catchment, i.e., models that are calibrated using the three pre-processed rainfall time series based on CPEM, GAM and GPM methods. These three models are then validated using three different rainfall time series as well. Therefore, in the end, there are nine (9) simulations assessed during the validation stage. Figure 5 reveals the flowchart of the modelling process of the selected study area.
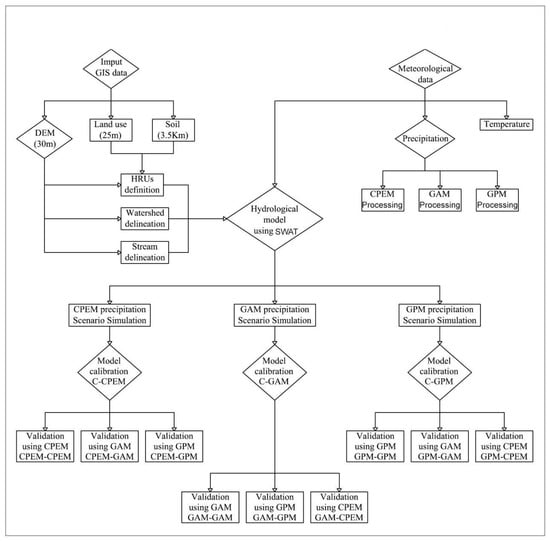
Figure 5.
Flowchart of the modelling process, input and outputs.
3. Results
As previously mentioned, the CEH-GEAR dataset is derived from rain gauge observations with an extra quality control measure before being interpolated onto the regular grids. It is therefore expected to see a good agreement between the gauge observed precipitation values and the values from the grid of the GEAR dataset that is at (nearly) the same location of the gauges.
Daily rainfall from the grids closest to the 13 gauges are extracted from the GEAR dataset and then compared with the time series of the 13 gauges. As expected, the time series are perfectly matched at the 13 locations as seen in Table 3 and Figure 6. The small deviation is likely due to the vigorous quality control measures applied to the GEAR datasets as well as the block averaging of the interpolated values.

Table 3.
Statistical comparison of precipitation of the observed and the CEH-GEAR dataset at rain gauges for a period of 1995–2003 over the Dee River basin.
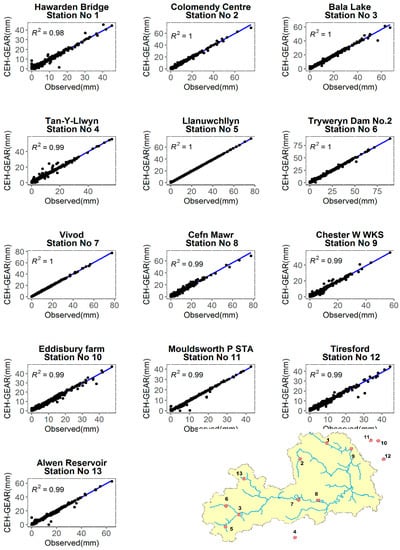
Figure 6.
Comparison of the daily precipitation observed by the gauges in the two catchments with the CEH-GEAR data at the same locations for the period of 1995–2003.
It is more useful to examine how different are the areal rainfall generated from both the gauge data and the GEAR data using the three pre-processing methods above. When it comes to the settings of SWAT, the Dee river catchments are delineated into 57 sub-basins. The six-month moving averages of the areal rainfall over the selected sub-basins in the Dee catchments are shown in Figure 7. The time series of GAM and GPM are very close (nearly identical) to each other for all the selected sub-basins.
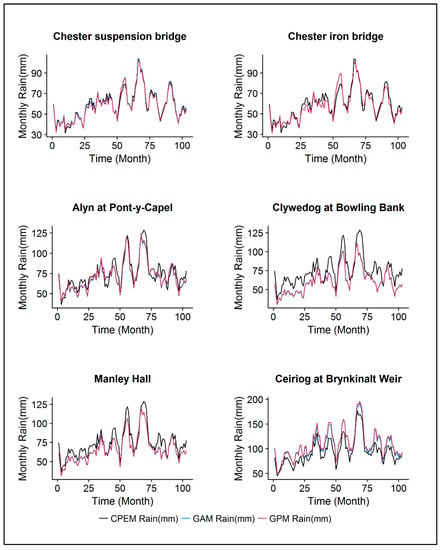
Figure 7.
Comparison of the daily precipitation observed by the gauges in the two catchments with the CEH-GEAR data at the same locations for the period of 1995–2003.
The CPEM time series, however, is remarkably different from the other two for most sub-basins. Since both the CPEM and the GPM methods use the value at the centroid of the sub-basins to represent the areal rainfall, such comparison in Figure 6 indicates that the CPEM method (which borrows the nearby gauge value) may cause a significant deviation to the representation. It also shows that the spatial variation is not as significant at smaller scales of sub-basins as both the GAM and the GPM methods produce very close results.
The cross-sub-basin distributions give contrasting pictures as seen in Figure 8. The CPEM methods produce a less varying distribution as some of the sub-basins share the same gauge. The GAM and GPM methods can reveal more details in the distribution. As to the range of the annual averages shown in Figure 8, the one from CPEM shows a range of 676–1324 mm/year and GAM 665–1749 mm/year 663–1692 mm/year for GPM respectively.
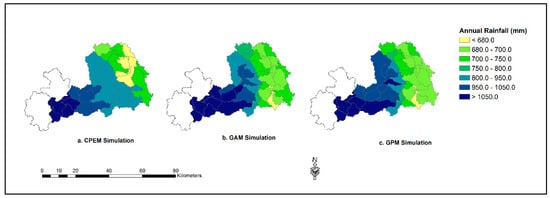
Figure 8.
Spatial distribution of annual rainfall for the three simulations at Dee river basin.
4. Discussion
To measure the impacts of precipitation pre-processing on model calibrations, we calibrated the SWAT models for the Dee catchment using the three pre-processing techniques CPEM, GAM and GPM respectively. For the Dee catchment, six river gauge stations are chosen to test the performance of the three calibrations by comparing the observed flow and the model simulated one. Further, one of the six stations, Brynkinalt Weir, is singled out to test the bias of the simulation. The performance of the three calibrated SWAT models for the Dee catchment is shown in Table 4. Clearly, both the calibrations that are driven by the GAM and GPM datasets, outperform the one using the CPEM dataset (the original setting of SWAT). The improvements are not significant in the sub-basins where the CPEM-driven model already does well, but they are more remarkable in sub-basins where it does not, e.g., the Bowling bank and the Brynkinalt Weir stations. Regarding the bias, a significant improvement can be seen for the Brynkinalt Weir sub-basins (Table 5).

Table 4.
Calibration results of three simulations of the daily Soil and Water Assessment Tool (SWAT) model for the Dee river basin for the period of 1995–2000. The numbers shown in the brackets are the sizes in Km2 of the sub-catchments represented by the station.

Table 5.
The percent of bias (PBIAS) indices of the SWAT model calibrations at the Brynkinalt Weir station.
The PBIAS index is further examined in Table 6, which includes all nine combinations of cross-validation results. Interestingly, the validations using the GPM rainfall series give better results regardless of how the models were calibrated. For the other two indices NSE and R2, out of the nine combinations of calibration-validation concerning the three different rainfall pre-processing methods (CPEM, GAM and GPM), GAM-GAM, GAM-GPM, GPM-GAM are able to achieve better results as shown in Figure 9 and Figure 10. From the perspective of practical use, it is more interesting to look at how models that are consistently calibrated and validated by the same dataset behave. In this respect, we can see that the CPEM-CPEM setting (the original SWAT settings) remains as the worst; the GPM-GPM combination is the best in the PBIAS measurements for the selected sub-basin, and overall the GAM-GAM combination does well across all sub-basins.

Table 6.
Percent of bias of three simulations of the daily SWAT model for Brynkinalt Weir station of Dee river basin for a period of 2001–2003.
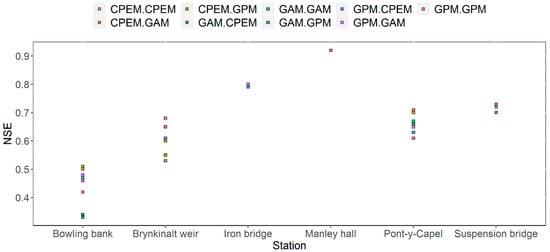
Figure 9.
Nash–Sutcliffe coefficient of cross-validated results of three simulations of the daily SWAT model of the Dee river basin for the period of 2001–2003.
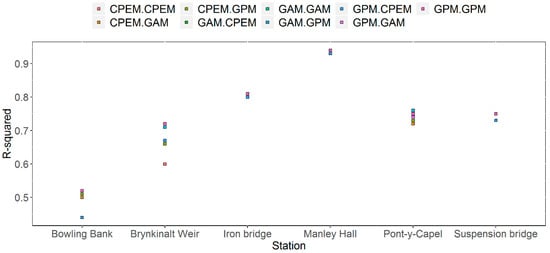
Figure 10.
Determination coefficient of cross-validated results of three simulations of the daily SWAT model of the Dee river basin for the period of 2001–2003.
The bias in model simulations can be related to the ill-parametrised model settings, but substantial bias such as the one shown in Table 6 for the sub-basin of Brynkinalt Weir is likely due to the misrepresentation of rainfall inputs. Figure 11 shows the comparison of the simulated monthly river flows from the three SWAT models against the observed one at Brynkinalt Weir station for the entire period of 1995–2003. In general, all three simulations underestimate the river flow and the most considerable bias is observed from the CPEM-driven simulation; however, both the GAM- and GPM-driven simulations can recover and get much closer after the spinning-up period of around 36 months.
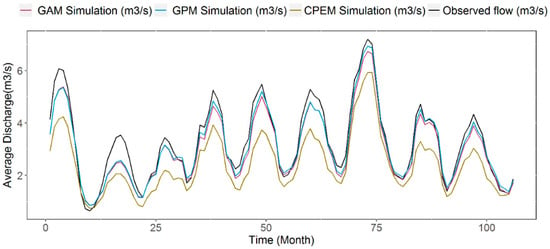
Figure 11.
The six-month moving average of monthly river flow simulations at Brynkinalt Weir for the period of 1995–2003.
A closer examination on the nine calibration-validation combinations over the validation period only (2001–2003) is revealed in Figure 12. In this case, the cumulative simulated flows are compared against the observed one. Several remarkable features are clearly present, including:
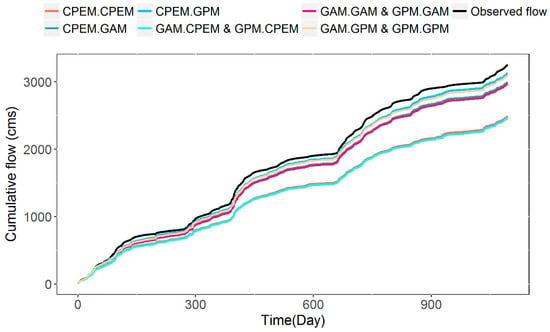
Figure 12.
Cumulative monthly flow simulations of Brynkinalt Weir station for the period of 2001–2003.
- those models calibrated using GAM and GPM data produce nearly identical results in the cross-validation when using the same precipitation data;
- those driven by the GPM data in the validation perform best, irrespective of however they are calibrated; and those driven by GAM are in the second group next to the GPM-driven one;
- the CEPM data have the worst yet very close performances regardless of how the models are calibrated;
- it is very surprising to see that the model calibrated using the CPEM time series but validated using the GPM one achieves the best result, even though the difference from the other two (GAM-GPM and GPM-GPM) is rather small.
The contents of Figure 12 effectively reconfirm what has been revealed in Figure 9 and Figure 10 by comparing the overall performance of the nine simulations. It is shown that as far as the validation is concerned, the difference caused by various choices of models is small and hence the ‘stable’ calibrations. However, the choice of feeding models with differently pre-processed rainfall inputs (datasets) does make significant improvements. In this case, the CEH-GEAR based GAM and GPM are a better choice than the rain gauge based CEPM method.
Table 7 lists the selected SWAT model parameters that are shown to be sensitive during the calibration of the selected sub-basin in Figure 4. Since the model has been subjected to three calibrations using CPEM-, GAM- and GPM-processed rainfall data, respectively, there are three sets of parameters after the calibrations. The ‘compensation’ effect can thus be indicated by the differences among the three set of parameter values, which are presented in Table 8 in terms of sensitivity values.

Table 7.
Selected SWAT parameters with its typical range for the Dee river model calibration.

Table 8.
The sensitivity of the calibrated parameters of SWAT model of the three simulations of the selected sub-basin in Figure 4.
It is worth noting, in Table 8, a clear variation of parameter sensitivity is found when switching the preprocessing methods from CPEM to GAM or GPM. In general, those parameters associated with surface runoff process, e.g., the available water capacity of the soil layer (SOL_AWC), Saturated hydraulic conductivity, mm/hr (SOL_K), the average slope of the main channel (CH_S2), become more sensitive (decreased p-values); in compassion, those related more to groundwater process are appearing less sensitive but also with less changes of p-values. This may be because the precipitation inputs become more correlated and hence leading to a better representation of the runoff process representation.
5. Conclusions
In this study, we investigated how various rainfall pre-processing methods could impact hydrological model performance. Thanks to the latest high-resolution and high-quality, gridded rainfall dataset, it was possible to measure such impact on calibration and validation of a semi-distributed model SWAT. The accompanying so-called ‘compensation’ due to model parameterisation was also studied by comparing the three distinctive models calibrated with different rainfall pre-processing methods: the centroid point estimate method (CPEM), the grid area method (GAM) and the grid point method (GPM). The models were further cross-validated over different periods to isolate the changes in performances due to model calibration (parameterisation) and the input rainfall data from different pre-processing methods. Several important points can be concluded in the following categories:
(1) The quality of the CEH-GEAR dataset and the GAM/GPM processing method. It has been shown the GEH-GEAR data are consistent with the gauge measurements with R2 greater than 0.98 for all sub-catchments; thus, can work as a reliable source for model calibration and validation. Based upon this dataset, both GAM and the GPM methods are theoretically better than the default CPEM used by SWAT, as they either take the average of the grid values or use the centroid grid value within the catchment, compared with the CPEM method using values of the gauge, which may sit outside and even farther from the catchment in question.
(2) Impact on model calibration. Both the GAM and GPM methods can improve model calibration by a considerable margin against the default setting, especially for those sub-catchments less well calibrated, e.g., with low NSE. One of such examples is the Brynkinalt Weir sub-catchment, which obtains NSE values of 0.54 from CPEM, 0.66 from GAM and 0.65 from GPM, respectively. The improvements are not as large in the smaller catchment where the rainfall distribution representativeness issue is less dominant. A remarkable finding is that the difference among the models calibrated using the three distinctive methods, in terms of parameterisation, are not as significant as we initially expected. The variation in calibrated model parameters among the models is small, although there are changes to the sensitivities of some parameters, e.g., those parameters associated with the surface runoff process become more sensitive when using GAM or GPM.
(3) Impact on cross-validation and practical implication. Six sub-catchments with nine combinations of calibration-validation using three different pre-processing methods are tested. Nash–Sutcliffe index and R2 are employed to measure the performance of the simulations at the six sub-catchments. Besides, simulated monthly flow and its cumulative at the Brynkinalt Weir station are checked against the observations. As expected, those models calibrated and validated using the same better pre-processing methods, e.g., GAM or GPM score the best. However, it is remarkable to find that a less-well-calibrated model due to the use of an inferior pre-processing method, such as CPEM, can do equally well when fed with better-pre-processed data, such as GAM or GPM during validation. In other words, it is the quality of the rainfall input data that dominates the cross-validation performance instead of how a model is calibrated. An accompanying implication is that in practice, a model previously calibrated with low-quality rainfall data can still use high-quality rainfall inputs when they become available at later times without having to be re-calibrated, which is often limited by the length of data.
(4) Impact of catchment size. The largest sub-catchment (Brynkinalt Weir, 116.0 Km2) is found to gain the most improvement compared with other sub-catchments with sizes around 10–20 Km2 (Table 4). The improvements due to the new input data/new pre-processing method become less significant when the catchment size gets smaller. Clearly, further detailed investigation with more catchments studied is needed. However, this can as well be explained by the less spatial variation of rainfall over smaller catchments than larger ones.
It should be noted that this study is based on a semi-distributed model, which still treats the rainfall inputs in a relatively lumped way, at least at the sub-basin scale. The interactions among the rainfall inputs, sub-basin parameterisation and the whole catchment response do require further studies that hopefully can identify the ‘sensitive’ areas where more sophisticated rainfall measurements and pre-processing can help significantly. Nevertheless, our study shows the value of high-quality datasets, such as the CEH-GEAR in hydrological modelling, and a practical approach to improving the SWAT simulation by adopting pre-processing methods, such as GAM and GPM, even with conventional rain gauge measurements, as they are not dependent on the CEH-GEAR data.
Author Contributions
Conceptualisation, Y.X., methodology Y.X. and S.A.A., formal analysis S.A.A. and Y.X., writing—original draft preparation S.A.A., writing—review and editing, Y.X. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Acknowledgments
The co-author Salam A. Abbas was supported by the PhD scholarship provided by the Higher Committee for Education Development in Iraq, for which we are grateful. We also thank Natural Resources Wales, the UK Centre for Ecology and Hydrology, and the British Atmospheric Data Centre for the provision of the required datasets to support this study. We would like to thank the anonymous reviewers and the editors for their valuable comments and advice, which have helped improve the quality of this paper.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Masih, I.; Maskey, S.; Uhlenbrook, S.; Smakhtin, V. Assessing the impact of areal precipitation input on streamflow simulations using the SWAT model. J. Am. Water Resour. Assoc. 2011, 47, 179–195. [Google Scholar] [CrossRef]
- Schuurmans, J.M.; Bierkens, M.F.P. Effect of spatial distribution of daily rainfall on interior catchment response of a distributed hydrological model. Hydrol. Earth Syst. Sci. 2007, 11, 677–693. [Google Scholar] [CrossRef]
- Mandapaka, P.V.; Krajewski, W.F.; Mantilla, R.; Gupta, V.K. Dissecting the effect of rainfall variability on the statistical structure of peak flows. Adv. Water Resour. 2009, 32, 1508–1525. [Google Scholar] [CrossRef]
- Segond, M.L.; Wheater, H.S.; Onof, C. The significance of spatial rainfall representation for flood runoff estimation: A numerical evaluation based on the Lee catchment, UK. J. Hydrol. 2007, 347, 116–131. [Google Scholar] [CrossRef]
- Tetzlaff, D.; Uhlenbrook, U. Effects of spatial variability of precipitation for process-orientated hydrological modelling: Results from two nested catchments. Hydrol. Earth Syst. Sci. Discuss. 2005, 2, 119–154. [Google Scholar] [CrossRef]
- Maskey, S.; Guinot, V.; Price, R. Treatment of precipitation uncertainty in rainfall-runoff modelling: A fuzzy set approach. Adv. Water Resour. 2004, 27, 889–898. [Google Scholar] [CrossRef]
- Bell, V.; Moore, R. The sensitivity of catchment runoff models to rainfall data at different spatial scales. Hydrol. Earth Syst. Sci. 2000, 4, 653–667. [Google Scholar] [CrossRef]
- Shah, S.; O’Connell, P.; Hosking, J. Modelling the effects of spatial variability in rainfall on catchment response. 2. Experiments with distributed and lumped models. J. Hydrol. 1996, 175, 89–111. [Google Scholar] [CrossRef]
- Singh, V.P. Effect of spatial and temporal variability in rainfall and watershed characteristics on stream flow hydrograph. Hydrol. Process. 1997, 11, 1649–1669. [Google Scholar] [CrossRef]
- Arnold, J.; Srinivasan, R.; Muttiah, R.; Williams, J. Large area hydrologic modelling and assessment part I: Model development. J. Am. Water Resour. Assoc. 1998, 34, 73–89. [Google Scholar] [CrossRef]
- Chaplot, V.; Saleh, A.; Jaynes, D. Effect of the accuracy of spatial rainfall information on the modeling of water, sediment, and NO3–N loads at the watershed level. J. Hydrol. 2005, 312, 223–234. [Google Scholar] [CrossRef]
- Jayakrishnan, R.; Srinivasan, R.; Santhi, C.; Arnold, J. Advances in the application of the SWAT model for water resources management. Hydrol. Process. 2005, 19, 749–762. [Google Scholar] [CrossRef]
- Cho, H.; Olivera, F. Effect of the spatial variability of land use, soil type, and precipitation on streamflows in small watersheds. J. Am. Water Resour. Assoc. 2009, 45, 673–686. [Google Scholar] [CrossRef]
- Nash, J.; Sutcliffe, J. River flow forecasting through conceptual models part I—A discussion of principles. J. Hydrol. 1970, 10, 282–290. [Google Scholar] [CrossRef]
- Starks, P.J.; Moriasi, D.N. Spatial resolution effect of precipitation data on SWAT calibration and performance: Implications for CEAP. Trans. ASABE 2009, 52, 1171–1180. [Google Scholar] [CrossRef]
- Johnson, G.L.; Hanson, C.L. Topographic and atmospheric influences on precipitation variability over a mountainous watershed. J. Appl. Meteorol. 1995, 34, 68–87. [Google Scholar] [CrossRef]
- Ly, S.; Charles, C.; Degre, A. Geostatistical interpolation of daily rainfall at catchment scale: The use of several variogram models in the Ourthe and Ambleve catchments, Belgium. Hydrol. Earth Syst. Sci. 2011, 15, 2259–2274. [Google Scholar] [CrossRef]
- Shrestha, M.K.; Recknagel, F.; Frizenschaf, J.; Meyer, W. Assessing SWAT models based on single and multi-site calibration for the simulation of flow and nutrient loads in the semi-arid Onkaparinga catchment in South Australia. Agric. Water Manag. 2016, 175, 61–71. [Google Scholar] [CrossRef]
- Keller, V.; Tanguy, M.; Prosdocimi, I.; Terry, J.; Hitt, O.; Cole, S.; Fry, M.; Morris, D.G.; Dixon, H. CEH-GEAR: 1 km resolution daily and monthly areal rainfall estimates for the UK for hydrological and other applications. Earth Syst. Sci. Data 2015, 7, 143–155. [Google Scholar] [CrossRef]
- Abbas, S.; Xuan, Y. Development of a new quantile-based method for the assessment of regional water resources in a highly-regulated river basin. Water Resour. Manag. 2019, 33, 3187–3210. [Google Scholar] [CrossRef]
- Ledoux, H.; Gold, C. An efficient natural neighbour interpolation algorithm for geoscientific modelling. In Developments in Spatial Data Handling; Springer: Berlin/Heidelberg, Germany, 2005; pp. 97–108. [Google Scholar] [CrossRef]
- Bailey, R.T.; Wible, T.C.; Arabi, M.; Records, R.M.; Ditty, J. Assessing regional-scale spatio-temporal patterns of groundwater–surface water interactions using a coupled SWAT-MODFLOW model. Hydrol. Process. 2016, 30, 4420–4433. [Google Scholar] [CrossRef]
- Abbaspour, K.; Rouholahnejad, E.; Vaghefi, S.; Srinivasan, R.; Yang, H.; Kløve, B. A continental-scale hydrology and water quality model for Europe: Calibration and uncertainty of a high-resolution large-scale SWAT model. J. Hydrol. 2015, 524, 733–752. [Google Scholar] [CrossRef]
- Gassman, P.W.; Reyes, M.R.; Green, C.H.; Arnold, J.G. The soil and water assessment tool: Historical development, applications, and future research directions. Trans. ASABE 2007, 50, 1211–1250. [Google Scholar] [CrossRef]
- Neitsch, S.L.; Arnold, J.G.; Kiniry, J.R.; Williams, J.R. Soil and Water Assessment Tool Theoretical Documentation Version; Texas Water Resources Institute: College Station, TX, USA, 2009.
- Lu, G.Y.; Wong, D.W. An adaptive inverse-distance weighting spatial interpolation technique. Comput. Geosci. 2008, 34, 1044–1055. [Google Scholar] [CrossRef]
- Abbaspour, K.; Johnson, C.; Van Genuchten, M. Estimating uncertain flow and transport parameters using a sequential uncertainty fitting procedure. Vadose Zone J. 2004, 3, 1340–1352. [Google Scholar] [CrossRef]
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).