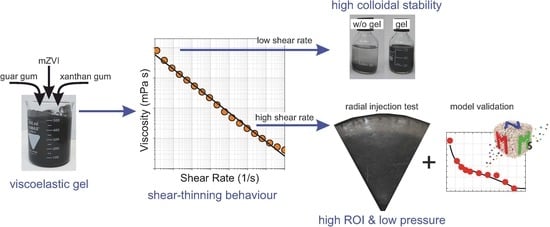
Injection of Zerovalent Iron Gels for Aquifer Nanoremediation: Lab Experiments and Modeling
Abstract
1. Introduction
2. Materials and Methods
2.1. Materials
2.2. Preparation of the mZVI Slurry
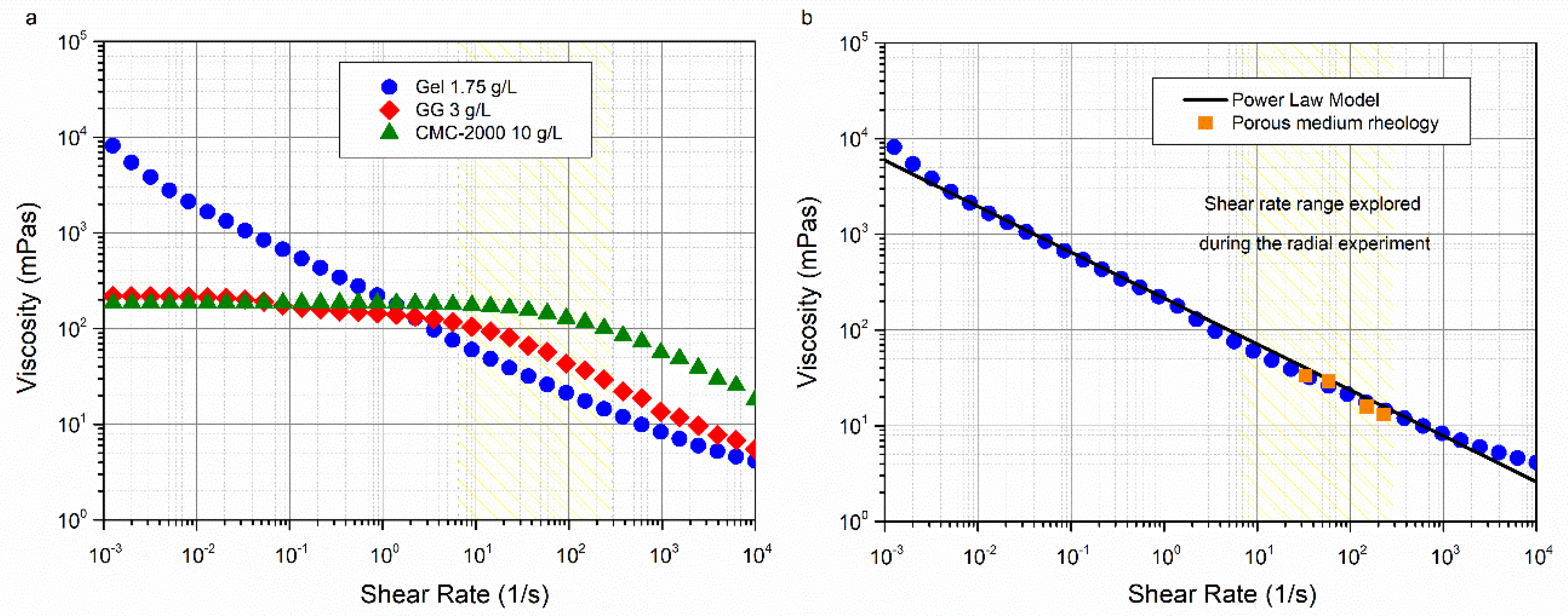
2.3. Bulk and Porous Medium Rheology
2.4. Column Transport Tests
- Pre-conditioning the porous medium with 5 pore volumes (PVs) of deionized water;
- Injecting 10 PVs of iron slurry.
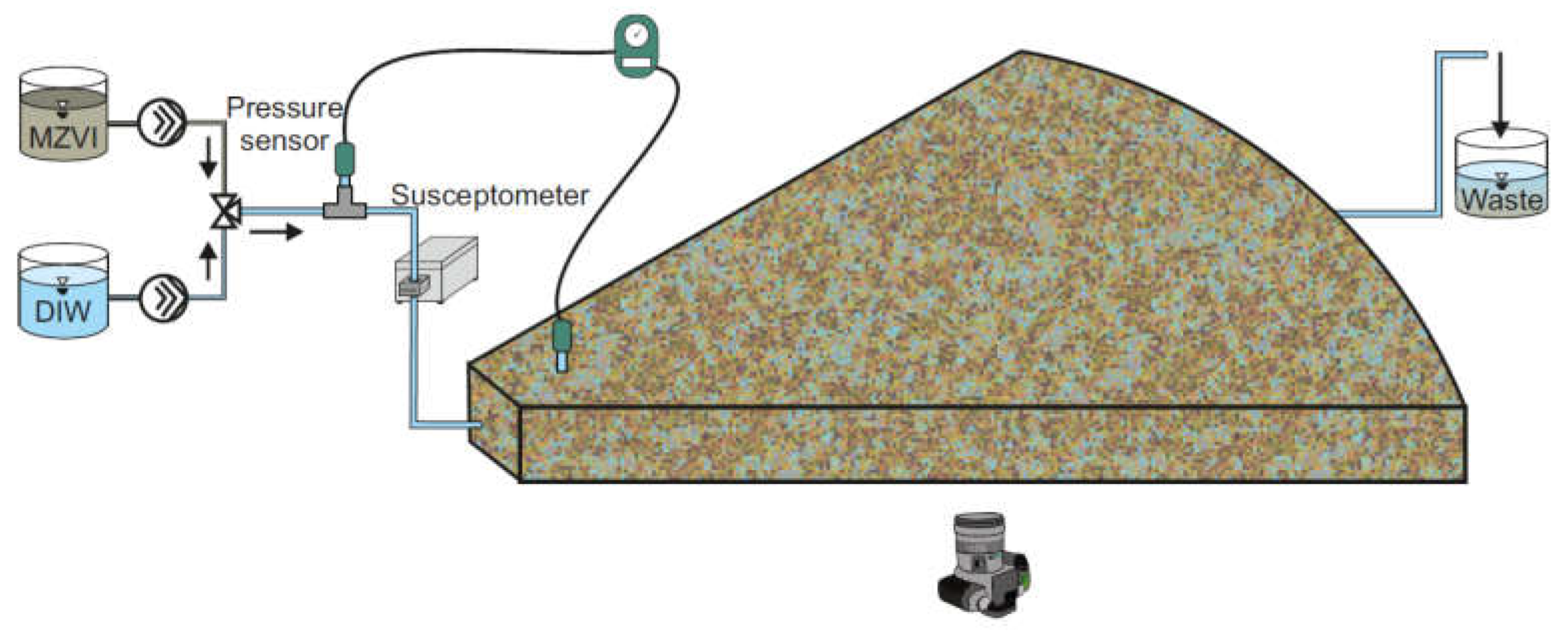
2.5. Radial Transport Test
- 2 PVs pre-conditioning with deionized water;
- 0.8 PVs of iron slurry injection.
2.6. mZVI Transport Model in Radial Geometry
- First site expressing irreversible blocking dynamics: blocking is a physicochemical deposition mechanism that typically happens when particle-particle interactions are strongly repulsive. In this case, the already deposited particles prevent suspended ones from further attachment, and a porous medium saturation can be achieved. The particle deposition rate decreases with increasing and goes to zero when the saturation concentration of deposited particles, , is reached [44,49,50].
- Second site expressing irreversible straining dynamics: straining is a physical deposition mechanism due to colloid trapping into small pore throats. Straining is likely to occur when the ratio between the size of the colloid and the sand grain is greater than, or close to, 0.5% [51,52]. In this study, a of 0.68% was found, suggesting that straining might be a relevant deposition mechanism in this system.
3. Results
3.1. Bulk and Porous Medium Rheology
3.2. Column Transport Tests and Modeling
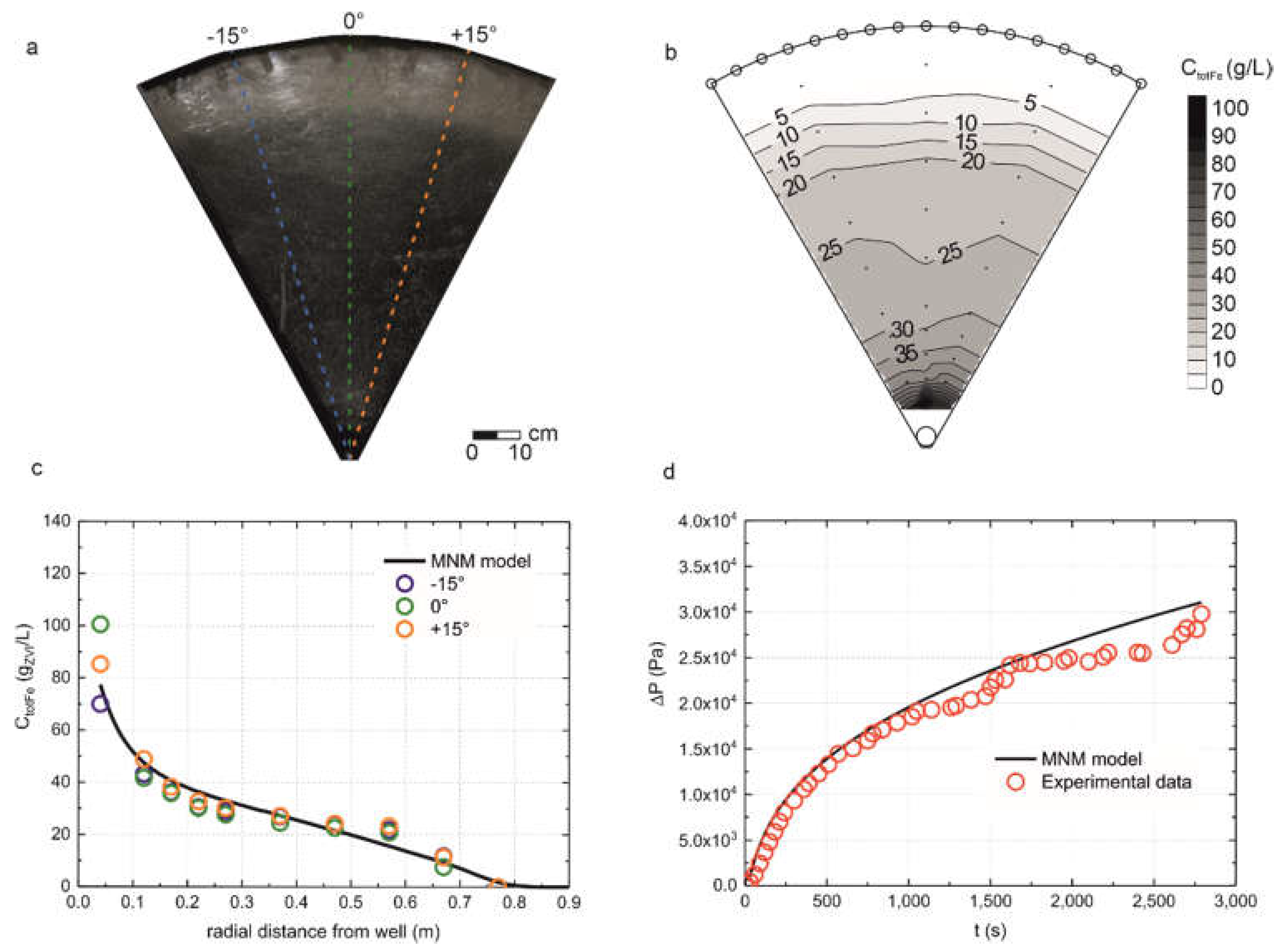
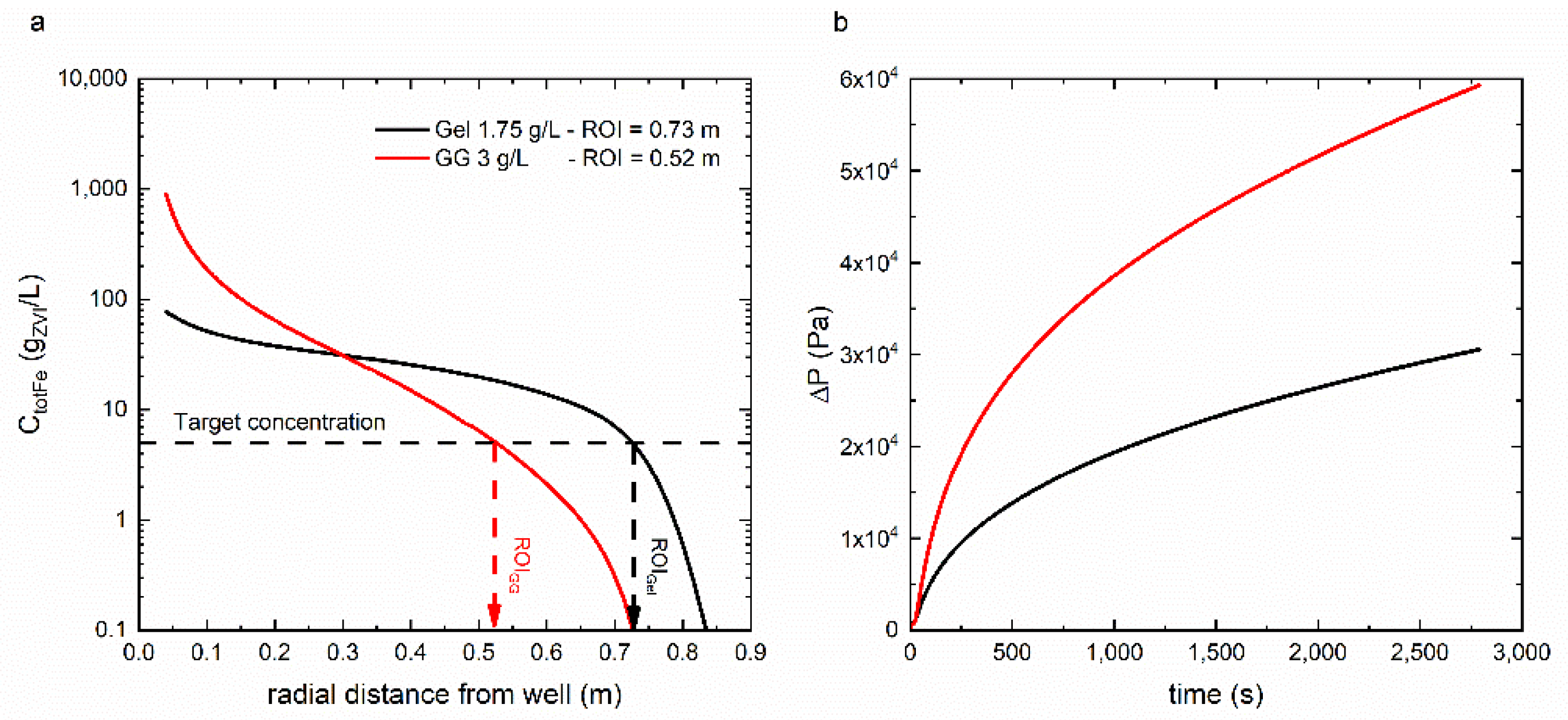
3.3. Radial Injection of mZVI Particles
4. Conclusions
Supplementary Materials
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Tosco, T.; Papini, M.; Viggi, C.; Sethi, R. Nanoscale zerovalent iron particles for groundwater remediation: A review. J. Clean. Prod. 2014, 77, 10–21. [Google Scholar] [CrossRef]
- Zhao, X.; Liu, W.; Cai, Z.; Han, B.; Qian, T.; Zhao, D. An overview of preparation and applications of stabilized zero-valent iron nanoparticles for soil and groundwater remediation. Water Res. 2016, 100, 245–266. [Google Scholar] [CrossRef] [PubMed]
- Beryani, A.; Alavi Moghaddam, M.R.; Tosco, T.; Bianco, C.; Hosseini, S.M.; Kowsari, E.; Sethi, R. Key factors affecting graphene oxide transport in saturated porous media. Sci. Total Environ. 2020, 698, 134224. [Google Scholar] [CrossRef] [PubMed]
- Gallo, A.; Bianco, C.; Tosco, T.; Sethi, R. Zerovalent iron for the remediation of contaminated aquifers. Geoing. Ambient. E Min. 2018, 155, 5–16. [Google Scholar]
- Bianco, C.; Patiño Higuita, J.E.; Tosco, T.; Tiraferri, A.; Sethi, R. Controlled Deposition of Particles in Porous Media for Effective Aquifer Nanoremediation. Sci. Rep. 2017, 7, 12992. [Google Scholar] [CrossRef] [PubMed]
- Gillies, G.; Raj, R.; Kopinke, F.D.; Georgi, A. Suspension stability and mobility of Trap-Ox Fe-zeolites for in-situ nanoremediation. J. Colloid Interface Sci. 2017, 501, 311–320. [Google Scholar] [CrossRef] [PubMed]
- Li, X.-Q.; Elliott, D.W.; Zhang, W.-X. Zero-Valent Iron Nanoparticles for Abatement of Environmental Pollutants: Materials and Engineering Aspects. Crit. Rev. Solid State Mater. Sci. 2006, 31, 111–122. [Google Scholar] [CrossRef]
- Di Molfetta, A.; Sethi, R. Clamshell excavation of a permeable reactive barrier. Environ. Geol. 2006, 50, 361–369. [Google Scholar] [CrossRef]
- Crane, R.A.; Scott, T.B. Nanoscale zero-valent iron: Future prospects for an emerging water treatment technology. J. Hazard. Mater. 2012, 211–212, 112–125. [Google Scholar] [CrossRef]
- Wang, Q.; Qian, H.; Yang, Y.; Zhang, Z.; Naman, C.; Xu, X. Reduction of hexavalent chromium by carboxymethyl cellulose-stabilized zero-valent iron nanoparticles. J. Contam. Hydrol. 2010, 114, 35–42. [Google Scholar] [CrossRef]
- Gallo, A.; Bianco, C.; Tosco, T.; Tiraferri, A.; Sethi, R. Synthesis of eco-compatible bimetallic silver/iron nanoparticles for water remediation and reactivity assessment on bromophenol blue. J. Clean. Prod. 2019, 211, 1367–1374. [Google Scholar] [CrossRef]
- Tiraferri, A.; Saldarriaga Hernandez, L.A.; Bianco, C.; Tosco, T.; Sethi, R. Colloidal behavior of goethite nanoparticles modified with humic acid and implications for aquifer reclamation. J. Nanoparticle Res. 2017, 19, 107. [Google Scholar] [CrossRef]
- Sethi, R.; Di Molfetta, A. Groundwater Engineering: A Technical Approach to Hydrogeology, Contaminant Transport and Groundwater Remediation; Springer International Publishing: Cham, Switzerland, 2019. [Google Scholar]
- Mueller, N.C.; Braun, J.; Bruns, J.; Černík, M.; Rissing, P.; Rickerby, D.; Nowack, B. Application of nanoscale zero valent iron (NZVI) for groundwater remediation in Europe. Environ. Sci. Pollut. Res. 2012, 19, 550–558. [Google Scholar] [CrossRef] [PubMed]
- Su, C.; Puls, R.W.; Krug, T.A.; Watling, M.T.; O’Hara, S.K.; Quinn, J.W.; Ruiz, N.E. A two and half-year-performance evaluation of a field test on treatment of source zone tetrachloroethene and its chlorinated daughter products using emulsified zero valent iron nanoparticles. Water Res. 2012, 46, 5071–5084. [Google Scholar] [CrossRef] [PubMed]
- Velimirovic, M.; Tosco, T.; Uyttebroek, M.; Luna, M.; Gastone, F.; De Boer, C.; Klaas, N.; Sapion, H.; Eisenmann, H.; Larsson, P.-O.; et al. Field assessment of guar gum stabilized microscale zerovalent iron particles for in-situ remediation of 1,1,1-trichloroethane. J. Contam. Hydrol. 2014, 164, 88–99. [Google Scholar] [CrossRef]
- Tosco, T.; Gastone, F.; Sethi, R. Guar gum solutions for improved delivery of iron particles in porous media (Part 2): Iron transport tests and modeling in radial geometry. J. Contam. Hydrol. 2014, 166, 34–51. [Google Scholar] [CrossRef]
- Christiansen, C.M.; Damgaard, I.; Broholm, M.; Kessler, T.; Klint, K.E.; Nilsson, B.; Bjerg, P.L. Comparison of Delivery Methods for Enhanced In Situ Remediation in Clay Till. Groundw. Monit. Remediat. 2010, 30, 107–122. [Google Scholar] [CrossRef]
- Litter, M. Iron Nanomaterials for Water and Soil Treatment; Jenny Stanford Publishing: Singapore, 2018. [Google Scholar]
- O’Carroll, D.; Sleep, B.; Krol, M.; Boparai, H.; Kocur, C. Nanoscale zero valent iron and bimetallic particles for contaminated site remediation. Adv. Water Resour. 2013, 51, 104–122. [Google Scholar] [CrossRef]
- Tiraferri, A.; Chen, K.L.; Sethi, R.; Elimelech, M. Reduced aggregation and sedimentation of zero-valent iron nanoparticles in the presence of guar gum. J. Colloid Interface Sci. 2008, 324, 71–79. [Google Scholar] [CrossRef]
- Gastone, F.; Tosco, T.; Sethi, R. Green stabilization of microscale iron particles using guar gum: Bulk rheology, sedimentation rate and enzymatic degradation. J. Colloid Interface Sci. 2014, 421, 33–43. [Google Scholar] [CrossRef]
- Dalla Vecchia, E.; Luna, M.; Sethi, R. Transport in Porous Media of Highly Concentrated Iron Micro- and Nanoparticles in the Presence of Xanthan Gum. Environ. Sci. Technol. 2009, 43, 8942–8947. [Google Scholar] [CrossRef] [PubMed]
- Cohen, M.; Yakirevich, A.; Weisbrod, N. The Role of Stabilizer Concentration in the Mobility of Carbon-Supported Nanozerovalent Iron (nZVI) in Fractured Media. Water Resour. Res. 2019, 55, 8164–8177. [Google Scholar] [CrossRef]
- Cohen, M.; Weisbrod, N. Field Scale Mobility and Transport Manipulation of Carbon-Supported Nanoscale Zerovalent Iron in Fractured Media. Environ. Sci Technol 2018, 52, 7849–7858. [Google Scholar] [CrossRef] [PubMed]
- Thombare, N.; Jha, U.; Mishra, S.; Siddiqui, M.Z. Guar gum as a promising starting material for diverse applications: A review. Int. J. Biol. Macromol. 2016, 88, 361–372. [Google Scholar] [CrossRef] [PubMed]
- Xue, W.; Huang, D.; Zeng, G.; Wan, J.; Cheng, M.; Zhang, C.; Hu, C.; Li, J. Performance and toxicity assessment of nanoscale zero valent iron particles in the remediation of contaminated soil: A review. Chemosphere 2018, 210, 1145–1156. [Google Scholar] [CrossRef] [PubMed]
- Velimirovic, M.; Simons, Q.; Bastiaens, L. Guar gum coupled microscale ZVI for in situ treatment of CAHs: Continuous-flow column study. J. Hazard. Mater. 2014, 265, 20–29. [Google Scholar] [CrossRef] [PubMed]
- Gastone, F.; Tosco, T.; Sethi, R. Guar gum solutions for improved delivery of iron particles in porous media (Part 1): Porous medium rheology and guar gum-induced clogging. J. Contam. Hydrol. 2014, 166, 23–33. [Google Scholar] [CrossRef]
- Tosco, T.; Marchisio, D.; Lince, F.; Sethi, R. Extension of the Darcy-Forchheimer Law for Shear-Thinning Fluids and Validation via Pore-Scale Flow Simulations. Transp. Porous Media 2013, 96, 1–20. [Google Scholar] [CrossRef]
- Truex, M.J.; Vermeul, V.R.; Mendoza, D.P.; Fritz, B.G.; Mackley, R.D.; Oostrom, M.; Wietsma, T.W.; Macbeth, T.W. Injection of Zero-Valent Iron into an Unconfined Aquifer Using Shear-Thinning Fluids. Groundw. Monit. Remediat. 2011, 31, 50–58. [Google Scholar] [CrossRef]
- Zhong, L.; Szecsody, J.; Oostrom, M.; Truex, M.; Shen, X.; Li, X. Enhanced remedial amendment delivery to subsurface using shear thinning fluid and aqueous foam. J. Hazard. Mater. 2011, 191, 249–257. [Google Scholar] [CrossRef]
- Luna, M.; Gastone, F.; Tosco, T.; Sethi, R.; Velimirovic, M.; Gemoets, J.; Muyshondt, R.; Sapion, H.; Klaas, N.; Bastiaens, L. Pressure-controlled injection of guar gum stabilized microscale zerovalent iron for groundwater remediation. J. Contam. Hydrol. 2015, 181, 46–58. [Google Scholar] [CrossRef] [PubMed]
- Xue, D.; Sethi, R. Viscoelastic gels of guar and xanthan gum mixtures provide long-term stabilization of iron micro- and nanoparticles. J. Nanoparticle Res. 2012, 14, 1239. [Google Scholar] [CrossRef]
- Longo, S.; Di Federico, V.; Chiapponi, L.; Archetti, R. Experimental verification of power-law non-Newtonian axisymmetric porous gravity currents. J. Fluid Mech. 2013, 731, 1–12. [Google Scholar] [CrossRef]
- Ciriello, V.; Di Federico, V. Similarity solutions for flow of non-Newtonian fluids in porous media revisited under parameter uncertainty. Adv. Water Resour. 2012, 43, 38–51. [Google Scholar] [CrossRef]
- Wexler, J.S.; Trinh, P.H.; Berthet, H.; Quennouz, N.; Du Roure, O.; Huppert, H.E.; Linder, A.; Stone, H.A. Bending of elastic fibres in viscous flows: The influence of confinement. J. Fluid Mech. 2013, 720, 517–544. [Google Scholar] [CrossRef][Green Version]
- Tatti, F.; Papini, M.P.; Sappa, G.; Raboni, M.; Arjmand, F.; Viotti, P. Contaminant back-diffusion from low-permeability layers as affected by groundwater velocity: A laboratory investigation by box model and image analysis. Sci. Total Environ. 2018, 622–623, 164–171. [Google Scholar] [CrossRef] [PubMed]
- Luciano, A.; Mancini, G.; Torretta, V.; Viotti, P. An empirical model for the evaluation of the dissolution rate from a DNAPL-contaminated area. Environ. Sci. Pollut. Res. 2018, 25, 33992–34004. [Google Scholar] [CrossRef]
- Chao, H.-C.; Rajaram, H.; Illangasekare, T. Intermediate-scale experiments and numerical simulations of transport under radial flow in a two-dimensional heterogeneous porous medium. Water Resour. Res. 2000, 36, 2869–2884. [Google Scholar] [CrossRef]
- Kobus, H.; Koschitzky, H.-P. Role of Controlled Experiments for Research on Groundwater Contamination and Remediation. In Proceedings of the Groundwater Quality: Remediation and Protection Conference, Prague, Czech Republic, 15–18 May 1995; pp. 431–438. [Google Scholar]
- Chaudemanche, C.; Budtova, T. Mixtures of pregelatinised maize starch and κ-carrageenan: Compatibility, rheology and gelation. Carbohydr. Polym. 2008, 72, 579–589. [Google Scholar] [CrossRef]
- Lindner, A.; Bonn, D.; Meunier, J. Viscous Fingering in a Shear-Thinning Fluid. Phys. Fluids 2000, 12, 256–261. [Google Scholar] [CrossRef]
- Bianco, C.; Tosco, T.; Sethi, R. A 3-dimensional micro- and nanoparticle transport and filtration model (MNM3D) applied to the migration of carbon-based nanomaterials in porous media. J. Contam. Hydrol. 2016, 193, 10–20. [Google Scholar] [CrossRef] [PubMed]
- Tosco, T.; Sethi, R. Transport of Non-Newtonian Suspensions of Highly Concentrated Micro- And Nanoscale Iron Particles in Porous Media: A Modeling Approach. Environ. Sci. Technol. 2010, 44, 9062–9068. [Google Scholar] [CrossRef] [PubMed]
- Dentz, M.; Icardi, M.; Hidalgo, J.J. Mechanisms of dispersion in a porous medium. J. Fluid Mech. 2018, 841, 851–882. [Google Scholar] [CrossRef]
- Katzourakis, V.E.; Chrysikopoulos, C.V. Modeling dense-colloid and virus cotransport in three-dimensional porous media. J. Contam. Hydrol. 2015, 181, 102–113. [Google Scholar] [CrossRef]
- Chrysikopoulos, C.V.; Syngouna, V.I.; Vasiliadou, I.A.; Katzourakis, V.E. Transport of Pseudomonas putida in a 3-D Bench Scale Experimental Aquifer. Transp. Porous Media 2012, 94, 617–642. [Google Scholar] [CrossRef]
- Kretzschmar, R.; Borkovec, M.; Grolimund, D.; Elimelech, M. Mobile subsurface colloids and their role in contaminant transport. Adv. Agron. 1999, 66, 121–193. [Google Scholar] [CrossRef]
- Katzourakis, V.E.; Chrysikopoulos, C.V. Mathematical modeling of colloid and virus cotransport in porous media: Application to experimental data. Adv. Water Resour. 2014, 68, 62–73. [Google Scholar] [CrossRef]
- Bradford, S.; Bettahar, M.; Simunek, J.; van Genuchten, M. Straining and attachment of colloids in physically heterogeneous porous media. Vadose Zone J. 2004, 3, 384–394. [Google Scholar] [CrossRef]
- Bradford, S.; Simunek, J.; Bettahar, M.; Van Genuchten, M.; Yates, S. Modeling colloid attachment, straining, and exclusion in saturated porous media. Environ. Sci. Technol. 2003, 37, 2242–2250. [Google Scholar] [CrossRef]
- Boccardo, G.; Crevacore, E.; Sethi, R.; Icardi, M. A robust upscaling of the effective particle deposition rate in porous media. J. Contam. Hydrol. 2018, 212, 3–13. [Google Scholar] [CrossRef]
- Yao, K.-M.; Habibian, M.T.; O’Melia, C.R. Water and waste water filtration. Concepts and applications. Environ. Sci. Technol. 1971, 5, 1105–1112. [Google Scholar] [CrossRef]
- Cross, M.M. Rheology of non-Newtonian fluids: A new flow equation for pseudoplastic systems. J. Colloid Sci. 1965, 20, 417–437. [Google Scholar] [CrossRef]
- Ko, C.; Elimelech, M. The “shadow effect” in colloid transport and deposition dynamics in granular porous media: Measurements and mechanisms. Environ. Sci. Technol. 2000, 34, 3681–3689. [Google Scholar] [CrossRef]
- Johnson, P.; Elimelech, M. Dynamics of colloid deposition in porous-media-blocking based on random sequential adsorption. Langmuir 1995, 11, 801–812. [Google Scholar] [CrossRef]
- Bradford, S.; Yates, S.; Bettahar, M.; Simunek, J. Physical factors affecting the transport and fate of colloids in saturated porous media. Water Resour. Res. 2002, 38, 63-1–63-12. [Google Scholar] [CrossRef]
- Homsy, G.M. Viscous Fingering in Porous Media. Annu. Rev. Fluid Mech. 1987, 19, 271–311. [Google Scholar] [CrossRef]
- Obernauer, S.; Temprano, N.; Chertcoff, R.; D’Onofrio, A.G.; Gabbanelli, S.; Rosen, M. Miscible Displacement of Polymers in Porous Medi. In Proceedings of the SPE Latin America/Caribbean Petroleum Engineering Conference, Buenos Aires, Argentina, 27–29 April 1994; p. 16. [Google Scholar]
- Bradford, S.A.; Torkzaban, S.; Walker, S.L. Coupling of physical and chemical mechanisms of colloid straining in saturated porous media. Water Res. 2007, 41, 3012–3024. [Google Scholar] [CrossRef]
| Gel Concentration (g/L) | mZVI Conc. (g/L) | Well Radius (m) | Injection Duration (min) | Simulation Radius (m) | Cell Number | Inlet Boundary Condition | |
|---|---|---|---|---|---|---|---|
| 1.75 | 20 | 0.02 | 1 | 46 | 0.9 | 300 | 3rd Type-Robin |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Mondino, F.; Piscitello, A.; Bianco, C.; Gallo, A.; de Folly D’Auris, A.; Tosco, T.; Tagliabue, M.; Sethi, R. Injection of Zerovalent Iron Gels for Aquifer Nanoremediation: Lab Experiments and Modeling. Water 2020, 12, 826. https://doi.org/10.3390/w12030826
Mondino F, Piscitello A, Bianco C, Gallo A, de Folly D’Auris A, Tosco T, Tagliabue M, Sethi R. Injection of Zerovalent Iron Gels for Aquifer Nanoremediation: Lab Experiments and Modeling. Water. 2020; 12(3):826. https://doi.org/10.3390/w12030826
Chicago/Turabian StyleMondino, Federico, Amelia Piscitello, Carlo Bianco, Andrea Gallo, Alessandra de Folly D’Auris, Tiziana Tosco, Marco Tagliabue, and Rajandrea Sethi. 2020. "Injection of Zerovalent Iron Gels for Aquifer Nanoremediation: Lab Experiments and Modeling" Water 12, no. 3: 826. https://doi.org/10.3390/w12030826
APA StyleMondino, F., Piscitello, A., Bianco, C., Gallo, A., de Folly D’Auris, A., Tosco, T., Tagliabue, M., & Sethi, R. (2020). Injection of Zerovalent Iron Gels for Aquifer Nanoremediation: Lab Experiments and Modeling. Water, 12(3), 826. https://doi.org/10.3390/w12030826